1 Introduction

Image segmentation is one of the most important steps for image analysis and image understanding. Its key goal is to divide an image into segments according to the features of the image, such as the intensity and texture, where each region has a reasonably homogeneous visual appearance or corresponds to objects or parts of objects [8].

In the field of image segmentation, the clustering method has become one of the hot topics over the last few years. The finite mixture model (FMM) [2, 16, 25], a well known clustering model, provides a flexible method to model many random phenomena. The FMM can be used for image segmentation because its k components can be used to denote k classes. In the FMM, the mixture density is used to realize the data points. The probabilistic clustering is derived according to the fitted posterior probabilities of component membership. However, it is difficult to compute the parameters of the FMM by maximum likelihood (ML) estimation. The FMM supposes the attribute of these pixels is generated by a specific finite mixture distribution. The component function of the FMM can be various statistical distributions. When the component function of the FMM is Gaussian distribution, it is called Standard Gaussian mixture model (GMM). One drawback of the FMM in image segmentation is that it supposes the pixels are independent and does not take into account the spatial relationship among the pixels.

In order to overcome the aforementioned drawback in the FMM, a spatially variant finite mixture model (SVFMM) was proposed by Sanjay et al. [20] for image segmentation where the spatial information was considered in SVFMM. The spatial information of the model was captured by MRF [9, 13]. Then the Expectation-Maximization (EM) [7] algorithm was used through ML to compute the parameters of the model. Subsequently, some models based on MRF have been proposed and applied to medical imaging segmentation [27–29]. In order to estimate the parameters of these models, EM algorithm, Markov Chain Monte Carlo (MCMC) and Variational Bayes (VB) [2, 12] approximation inference algorithm are utilized in these models, respectively.

However, the label probability proportions (the probabilities of each pixel belonging to some classes) in the SVFMM can not be obtained in closed form in the M-step of the EM algorithm. The label probability proportions are formulated as a constrained optimization problem. The results of the label probability proportions require a projection onto the unit simplex (non-negative and summing up to one components). A gradient projection algorithm is used in [20]. Convex quadratic programming is proposed for the SVFMM in [1] and it is shown to produce both better segmentations and values of the criterion function than [20]. One of the shortcomings of SVFMM in [20] and [1] is that the MRF prior lacks flexibility and it can not learn from the data. Nikou et al. [17] proposes a Gauss–Markov random field prior probability which is imposed on the label probability proportions. The parameters of the model can be estimated from the data adaptively. Concurrently, it utilizes the information in different spatial directions of the neighborhood. However, in the M-step, the label probability proportions still don’t satisfy the constraint of probability vectors.

To preserve the region boundaries in image segmentation, two synthetical models combining the class prior information with line processes [9] are proposed in [21]. In the two models, MRF smoothness priors are imposed on the label probability proportions of a spatially varying Gaussian mixture model. In the first model, the local differences between the label probability proportions are supposed to follow Gaussian distribution, at the same time the Bernoulli distribution is imposed on the binary line processes (BLP). It is a discrete line process model and the VB algorithm is used to estimate the unknown parameters of the BLP model. In the second model, the local differences between the label probability proportions are supposed to follow the continuous univariate Student’s t-distribution and the continuous line process (CLP) random variables follow a Gamma distribution. EM algorithm is used to estimate the parameters of the CLP model. But the results of the label probability proportions of the two models can not satisfy the constraint that the label probability proportions must be probability vectors. A new projection method based on a quadratic approximation is proposed to solve this problem. In order to avoid the reparatory computations in the M step of the EM, two models based on the GMM are proposed in [24] and [23], respectively. The label probability proportions in the two models are explicitly modelled as probability vectors. They both use the gradient method to estimate the models’ parameters based on minimizing the higher bound on the data negative log-likelihood. A new approach which incorporates the spatial relationships between the neighboring pixels is proposed to model the label probability proportions in [24]. We regard the model proposed in [24] as an extension of the GMM (EGMM). Considering the information that the neighboring pixels in an image are similar in some sense, the pixel value is represented by the average of its neighborhood pixels in the weight function of the label probability proportions of the model in [23]. The model in [23] is called spatial neighborhood GMM (SNGMM). A novel model for image segmentation based on the maximum likelihood estimator is proposed in [14] which is different from the pattern of SVFMM in utilizing the spatial information. The model in [14] assumes that all the pixels values are independent and identically distributed samples of generative models. The neighborhood of a pixel is regarded as its multiple observations. The likelihood of a pixel is assumed to be a weight sum of the neighborhood’s likelihood where its coefficient depends on their spatial distances to the pixel. The model in [14] based on the maximum of spatial likelihoods (MSL) is well applied to image segmentation.

The component functions of the aforementioned SVFMMs are Gaussian distribution. However, the tails of the Gaussian distribution are too short to satisfy the needs for many applications. The Student’s t-distribution has heavier tails compared with the Gaussian distribution. It is a robust alternative to the Gaussian distribution [18, 22]. The Student’s t-distribution has been successfully used in many applications, such as signal analysis [5], sequential data modelling setting [6] and speaker identification [4].

In this paper, combining the advantages of the SVFMM with robustness of the Student’s t-distribution, a spatially varying Student’s t-distribution mixture model is proposed. In the proposed model, a weight function is defined to denote the spatial relationship between the pixels, which contains the directional information of a pixel’s neighborhood. The label probability proportions of the pixels are explicitly modelled as probability vectors, they automatically satisfy the conditions of the probability vectors. Therefore the reparatory computations are not needed during the process of inference. Based on the maximum of the log-likelihood function, the gradient method is used to estimate the parameters of the proposed model. Numerical experiments have been conducted on synthetic and natural grayscale images to compare our proposed algorithm with other image segmentation algorithms. The segmentation accuracy is quantified in terms of the misclassification ratio (MCR) [29] and the probabilistic rand (PR) index [26]. The experimental results demonstrate the effectiveness and robustness of the proposed model compared with the other models.

The remainder of this paper is organized as follows. A brief review of the SVFMM and the Student’s t-distribution is given in Section 2. In Section 3, the proposed model is described in detail. Section 4 describes a number of experiments conducted to evaluate the efficiency of the proposed model. Finally, conclusions are given in Section 5.

2 Preliminary

In this section, the SVFMM is introduced firstly, then the Student’s t-distribution is reviewed briefly. In this paper x n denotes the pixel in the nth position of an image.

2.1 Spatially variant finite mixture model

The SVFMM [1, 17, 20] gives a modification of the FMM. It uses the parameter of label probability proportion π nk to denote the probability that the nth pixel belongs to the kth class. We assumes that there are K classes in the model. The nth pixel’s label probability vector is denoted by π n. The parameter vector is \(\pi^{n}=\left(\pi_{n1},\pi_{n2},..., \pi_{nK}\right)^{T}\), where T indicates the transpose of the vector. The variable π nk satisfies the constraints

$$ 0\leq \pi_{nk} \leq 1,\sum\limits_{k=1}^{K}\pi_{nk}=1; n=1,...,N, k=1,...,K. $$

Let \(\Pi=\big\{(\pi^{1})^{T},(\pi^{2})^{T},...,(\pi^{N})^{T}\big\}\) be the set of probability vectors, and Θ = {θ 1,θ 2,...,θ K } be the set of component parameters. The density function of the nth pixel is given by

$$ f\big(x_{n}|\Pi,\Theta\big)=\sum\limits_{k=1}^{K} \pi_{nk}p\big(x_{n}|\theta_{k}\big), $$

where \(p\left(x_{n}|\theta_{k}\right)\) is a Gaussian function with parameters \(\theta_{k}=\{\mu_{k},\sigma_{k}^{2}\}\), μ k and \(\sigma_{k}^{2}\) are the mean and the variance, respectively. A data set X comprises observations {x n }, where n = 1,...,N. The observations are supposed to be statistically independent. The X’s probability density function (pdf) [20] is given by

$$ f\big(X|\Pi,\Theta\big)=\prod\limits_{n=1}^{N}f\big(x_{n}|\Pi,\Theta\big). $$
(1)

A prior density based on the Gibbs distribution for the parameter set Π is introduced in [1],

$$ p(\Pi)=\frac{1}{Z}\exp(-U(\Pi)), \mbox{ with } U(\Pi)=\beta\sum \limits_{n=1}^{N}V_{N_{n}}(\Pi), $$

where Z is a normalizing constant, β is regarded as regularization parameter and the function \(V_{N_{n}}(\Pi)\) denotes the clique potential function within the neighborhood N n . The drawback of this prior probability is that the parameter β can not be estimated from the data in an easy way.

In order to overcome the aforementioned drawback, a Gauss–Markov random field prior probability for parameter Π is proposed in [17]

$$ p(\Pi)\infty \prod\limits_{k=1}^{K}\beta_{k}^{-N}\exp\left[-\frac{1}{2}\frac{\sum\limits_{n=1}^{N}\sum\limits_{m\in N_{n}}\big(\pi_{nk}-\pi_{km}\big)^{2}}{\beta_{k}^{2}}\right], $$

where the parameter β of the function is used to capture the spatial smoothness of cluster and it can be easily estimated from the data.

When the prior density is given, a posteriori pdf is given by

$$ p\big(\Pi|X;\Theta\big)\propto \prod\limits_{n=1}^{N}p(\Pi) f\big(x_{n}|\Pi,\Theta\big). $$

Then the log-density function can be obtained as follows [1]:

$$ \log \big(\Pi |X;\Theta\big)=\sum\limits_{n=1}^{N}\log\sum\limits_{k=1}^{K}\pi_{nk} p\big(x_{n}|\mu_{k},\sigma_{k}^{2}\big) +\log p(\Pi) $$
(2)

In order to estimate the parameters \(\Omega=\{\mu_{k},\sigma_{k}^{2},\pi_{nk}\}\) in (2), the EM algorithm is in general used to maximize the log of the likelihood function of the given data set. However, the result of the π nk obtained in the M-step of the EM algorithm is usually not satisfied with the constraints: 0 ≤ π nk  ≤ 1 and \(\sum \limits_{k=1}^{K}\pi_{nk} =1\). Therefore, the computation of the algorithm becomes very complex to maximize the log of the likelihood function in (2). A reparatory computation is introduced in the M-step to enforce the label probability proportion π nk to satisfy these constraints. For example, gradient projection algorithm is introduced in [20] and quadratic programming is used in [1]. After the optimization of the parameters, the label of every pixel can be obtained according to the posterior probability p(θ k |x n ) in (3)

$$ p(\theta_{k}|x_{n})=\frac{\pi_{nk}p\left(x_{n}|\theta_{k}\right)} {\sum\limits_{j=1}^{K}\pi_{nj}p\left(x_{n}|\theta_{j}\right)}. $$
(3)

2.2 The student’s t-distribution

A random variable x follows a univariate Student’s t-distribution x~St(x|μ,λ,ν), the univariate Student’s t-distribution takes the following form [2]

$$ St(x| \mu,\lambda,\nu)=\frac{\Gamma(\nu/2+1/2)}{\Gamma(\nu/2)} \left(\frac{\lambda}{\pi\nu}\right)^{1/2}\left[1+\frac{\lambda(x-\mu)^{2}} {\nu} \right]^{-\nu/2-1/2}, $$
(4)

where μ and λ are the mean and the precision of the t-distribution, respectively. The value of λ is equal to the inverse of the variance. Γ(·) is the gamma function. The parameter ν is called the t-distribution’s degrees of freedom. When ν = 1 the t-distribution becomes the Cauchy distribution. The parameter ν is used to tune the tail of t-distribution. if ν > 1, μ is the mean of x, As ν tends to infinity, the t-distribution tends to a Gaussian distribution with mean μ and precision λ [2]. Moreover, the Student’s t-distribution can be regarded as an infinite mixture of scaled Gaussian distribution, which can be rewritten in the form [2]

$$ St\big(x|\mu,\lambda,\nu\big)=\int \limits_{0}^{\infty} \mathcal{G}\big(x|\mu,(u \lambda)^{-1}\big) Gam\big(u|\nu/2,\nu/2\big)du, $$

where \(\mathcal{G}(x|\mu,(u \lambda)^{-1})\) denotes the Gaussian distribution, and Gam(u|ν/2,ν/2) is the gamma distribution. Therefore, the t-distribution provides a heavy-tailed alternative to the Gaussian distribution. The t-distribution has been successfully used as a robust alternative to the Gaussian distribution in [18, 22].

3 The proposed model

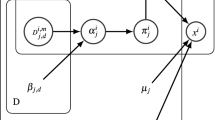
In this section, we propose a spatially varying finite mixture model whose component function is the Student’s t-distribution. A second-order neighborhood system (8 neighbors for each interior pixel) is adopted in the proposed model. There are four different adjacency types in the second-order neighborhood system. They are horizontal, vertical and two diagonal directions, as shown in Fig. 1. Let the parameter D stand for the number of adjacency types. Thus, the value of the parameter D is equal to 4.

Fig. 1
figure 1

Second-order neighborhood system. The numbers indicate the adjacency types

Full size image

Firstly, we define a function that represents the weight of the nth pixel belonging to the kth class

$$ \xi_{k}\left(x_{n}\right)=\sum\limits_{d=1}^{D}\sum\limits_{x_{i} \in N_{n}}J_{\!nd}\big(x_{n},x_{i}\big)\exp\left(-\frac{\big(x_{i}-c_{kd}\big)^{2}}{2b_{kd}^{2}}\right) $$
(5)

where N n represents the neighborhood of the nth pixel. J nd (x n ,x i ) is an identity function, its definition is given by

$$ J_{\!nd}(x_{n},x_{i}) = \left\{ \begin{array}{ll} 1, \mbox{if } x_{i}\in N_{n} \mbox{ and } x_{i} \mbox{ is $x_{n}$'s \emph{d}th adjacency type } \\ 0, \mbox{ otherwise } \end{array} \right. $$
(6)

Then the nth pixel’s label probability proportion π nk is defined as follows:

$$ \pi_{nk}=\frac{\xi_{k}\left(x_{n}\right)}{\sum\limits_{j=1}^{K}\xi_{j}\left(x_{n}\right)} =\frac{\sum\limits_{d=1}^{D}\sum\limits_{x_{i}\in N_{n}} J_{\!nd}\left(x_{n},x_{i}\right)\exp\left(-\frac{\left(x_{i}-c_{kd}\right)^{2}}{2b_{kd}^{2}}\right)} {\sum\limits_{j=1}^{K}\sum\limits_{d=1}^{D}\sum\limits_{x_{i}\in N_{n}}J_{\!nd}\left(x_{n},x_{i}\right)\exp\left(-\frac{\left(x_{i}-c_{\!jd}\right)^{2}}{2b_{\!jd}^{2}}\right)}. $$
(7)

Obviously, the label probability proportion π nk in (7) is nonnegative and subject to \(\sum\limits_{k=1}^{K}\pi_{nk}=1\). The density function of the nth pixel is given by

$$ f\left(x_{n}\right)=\sum\limits_{k=1}^{K}\pi_{nk}St\big(x_{n}|\theta_{k}\big), $$
(8)

where the pdf \(St\left(x_{n}|\theta_{k}\right)\) is the Student’s t-distribution defined in (4), whose parameters are θ k  = {μ k ,λ k }.

The log-likelihood function is given by

$$ L(\Theta)=\sum\limits_{n=1}^{N}\log f\left(x_{n}\right)=\sum\limits_{n=1}^{N} \log\left(\sum\limits_{k=1}^{K}\pi_{nk}St\big(x_{n}|\theta_{k}\big)\right). $$
(9)

There are four unknown parameters in (9). They are μ j , λ j , c jd and \(b_{\!jd}^{2}\). The derivatives of the function L with respect to μ j , λ j , c jd , \(b_{\!jd}^{2}\), respectively, can be calculated by

$$ \frac{\partial L}{\partial \mu_{j}}=\sum\limits_{n=1}^{N}\frac{\pi_{nj}}{\sum\limits_{k=1}^{K}\pi_{nk}St\left(x_{n}|\theta_{j}\right)} \cdot\frac{\lambda_{j}\left(\nu+1\right)\left(x_{n}-\mu_{j}\right)} {\nu+\lambda_{j}\big(x_{n}-\mu_{j}\big)^{2}}\cdot St\big(x_{n}|\theta_{j}\big). $$
(10)
$$ \frac{\partial L}{\partial \lambda_{j}}=\sum\limits_{n=1}^{N}\frac{\pi_{nj}}{\sum\limits_{k=1}^{K}\pi_{nk}St\left(x_{n}|\theta_{j}\right)} \cdot\frac{\nu-\nu \times\lambda_{j}(x_{n}-\mu_{j})^{2}}{2\lambda_{j}\left[\nu+\lambda_{j}(x_{n}-\mu_{j})^{2}\right]}\cdot St\big(x_{n}|\theta_{j}\big). $$
(11)
$$ \begin{array}{rll} \frac{\partial L}{\partial c_{\!jd}}&=&\sum\limits_{n=1}^{N}\frac{1}{\sum\limits_{k=1}^{K}\pi_{nj}St\big(x_{n}|\theta_{j}\big)} \cdot \frac{1 } {\left[\sum\limits_{p=1}^{K} \xi_{p}\left(x_{n}\right) \right]^{2}}\\ && .\left\{\sum \limits_{p=1, p\neq j }^{K}\xi_{p}(x_{n})\cdot St\big(x_{n}|\theta_{j}\big) -\sum \limits_{p=1, p\neq j }^{K}\xi_{p}(x_{n})\cdot St\big(x_{n}|\theta_{p}\big)\right\}\\ && \cdot \left[ \sum \limits_{x_{i} \in N_{n}} J_{id}\big(x_{n},x_{i}\big) \cdot \exp\left(-\frac{\big(x_{i}-c_{\!jd}\big)^{2}}{2b_{\!jd}^{2}}\right)\frac{x_{i}-c_{\!jd}}{b_{\!jd}^{2}} \right]. \end{array} $$
(12)
$$ \begin{array}{rll} \frac{\partial L}{\partial b_{\!jd}^{2}}&=&\sum\limits_{n=1}^{N}\frac{1}{\sum\limits_{k=1}^{K} \pi_{nj}St\big(x_{n}|\theta_{j}\big)} \cdot \frac{1 } {\left[\sum\limits_{p=1}^{K} \xi_{p}\left(x_{n}\right) \right]^{2}}\\ &&\cdot\left\{\sum \limits_{p=1, p\neq j }^{K}\xi_{p}(x_{n})\cdot St\big(x_{n}|\theta_{j}\big) -\sum \limits_{p=1, p\neq j }^{K}\xi_{p}(x_{n})\cdot St(x_{n}|\theta_{p})\right\}\\ && \cdot \left[ \sum\limits_{x_{i}\in N_{n}}J_{\!nd}(x_{n},x_{i}) \exp\left(-\frac{\big(x_{i}-c_{\!jd}\big)^{2}}{2b_{\!jd}^{2}}\right) \left(\frac{\big(x_{i}-c_{\!jd}\big)^{2}}{2b_{\!jd}^{4}}\right)\right]. \end{array} $$
(13)

After the optimization of the parameters, the posterior probability is derived as follows:

$$ St\big(\theta_{k}|x_{n}\big)= \frac{\pi_{nk}St\big(x_{n}|\theta_{k}\big)}{\sum\limits_{j=1}^{K}\pi_{nj}St\big(x_{n}|\theta_{j}\big)}. $$
(14)

Then according to a maximum a posteriori, a kth class label is assigned to the nth pixel by solution of

$$ \arg \max\limits_{k}\ \big\{St\big(\theta_{k}|x_{n}\big) \big\}. $$
(15)

We refer to the proposed model as the directional spatially varying Student’s t-distribution mixture model (DSVStMM). The gradient descend method is used to estimate the unknown parameters of the proposed model. Finally, in order to mitigate the effects of the noise, we utilize a simple competitive selection method [24] to optimize the result. The operation of the method is defined as follows: all the neighbors of one pixel belong to the same class, then set the pixel to the neighbors’ class. The method can slightly mitigate the effects of the noise.

The proposed model DSVStMM is summarized as follows.

figure b

4 Numerical experiments

We conduct some comprehensive experiments to evaluate the performance of our proposed model, compared with some state-of-the-art image segmentation models. These models are the standard GMM [2] which assumes that the relationships between the pixels are independent; the MRF-based methods which are similar to the proposed model, such as SVFMM [1], DCASV [17], CLP, BLP [21], EGMM [24] and SNGMM [23]; MSL [14] which bases on the maximum likelihood estimator and computes the likelihood of the given pixel’s neighborhood; the K-means which is used to initialize GMM, DCASV, EGMM, SNGMM and the proposed model. These models are divided into two types, one type considers that the pixels are independent of each other, the other type considers the spatial relationships of the pixels which are based on MRF and are similar to the proposed model. All of the models are implemented in MATLAB. The source code of SVFMM can be downloaded from http://www.cs.uoi.gr/kblekas/sw/MAPsegmentation.html. The source code of standard GMM, DCASV, CLP and BLP is available at http://www.cs.uoi.gr/cnikou/. We implement the algorithms for K-means, MSL, EGMM, SNGMM and the proposed model (DSVStMM) in MATLAB. For the DSVStMM model, we have selected ν = 0.001. According to (4), the value of λ must be nonnegative, so we use the absolute value of λ in (16). The loop of DSVStMM is terminated when the percentage changed of (9) between two consecutive iterations is less than 10 − 5, i.e, |ΔL/L| < 10 − 5 . These models are tested on both synthetic and natural grayscale images.

To quantify segmentation results, the misclassification ratio (MCR) [29] is adopted to evaluate the segmentation accuracy of synthetic images, the probabilistic rand (PR) index [26] is used to evaluate the image segmentation performance of the natural images. The MCR is defined as follows:

$$ \mbox{MCR}= \frac {\mbox{number of mis-classified pixels}} {\mbox{total number of pixels}}. $$

The value of MCR is bounded by the interval [0, 1], where lower values indicate better segmentation results.

The PR index measures consistency between two segmentation labels via an overlapping fraction, its definition is given by

$$ \mbox{PR}\left(S_{test}, \{S_{k} \}\right)=\frac{2}{ N \left (N-1\right)} \sum \limits_{i<j} \left[c_{ij}p_{ij}+\left(1-c_{ij}\right) \left(1-p_{ij}\right)\right]. $$

where c ij  = 1 when the pixels i and j belong to the same cluster in the test image S test , otherwise c ij  = 0. The value of the p ij can be obtained by using sample mean estimator defined as follows:

$$ p_{ij}=\frac{1}{K}\sum \limits_{k=1}^{K}\amalg\left(l_{i}^{S^{k}}=l_{j}^{S^{k}}\right). $$

where K indicates the number of the ground-truth sets, \(\amalg\big(l_{i}^{S^{k}}=l_{j}^{S^{k}}\big)\) is an identity function, whose value is equal to 1 when the pixels i and j are in the same class in the ground-truth set k, otherwise is equal to 0. The value of PR is bounded by the interval [0, 1], where the larger PR values indicate better segmentation results.

4.1 Piecewise synthetic images

To demonstrate the robustness of our model against noise, we first test the proposed model on a synthetic image (128×128 image resolution) similar to the one used in [29]. The three classes synthetic image shown in Fig. 2a is sampled from the MRF model using a Gibbs sampler. The intensities for the image with three classes are 55, 115 and 225, respectively. Figure 2b shows the original image corrupted by the mixed noise. Gaussian noise (μ = 0, σ 2 = 0.005) is added first, then the salt & pepper noise (sp = 0.08) is added to corrupt the synthetic image. The segmentation results are shown in Fig. 2c–l, respectively. As can be seen, the SVFMM can get better results than the standard GMM. However it requires K·(N + 2) parameters. That is 49158 in the first example [24]. The proposed model, DSVStMM only needs 2×K·(D + 1) parameters. In our implementation of the proposed model, D = 4, if K = 3, then the number of parameters in our model is only 30. The number of the parameters is much fewer than the SVFMM. As shown in Fig. 2k, the EGMM reduces the effect of noise significantly and can get a better image segmentation result. However, DSVStMM can reduce the effect of noise and obtain a better result than the EGMM. Its MCR is lower 5.77 % than SNGMM’s and 0.476 % than EGMM’s. We can see that the noise is reduced clearly and the edge information of the image is kept very well in Fig. 1l. In order to further test the image segmentation effectiveness of the proposed model. The experimental results obtained with various levels of mixed noise are given in Table 1. In order to reduce the randomness of the added noise and the sensitivity of the initialization, the tests are executed 10 times, then the average of the results is reported in Table 1. The results in Table 1 indicate that our proposed model has a lower MCR compared with the other models on each noise level. Its average MCR is lower 2.365 % than the EGMM’s. It shows that the proposed model is more robust against noise than EGMM. The experiments prove that the proposed model gets better segmentation results than any other model, the student’s t-distribution is more robust against noise because it owns heavy-tailed than Gaussian distribution.

Fig. 2
figure 2

First experiment (128×128 image resolution). a The original image. b Noise image with Gaussian noise (0 mean, 0.005 variance) and salt & pepper (sp = 0.08). c K-means (\(\mbox{MCR}=8.422\) %). d GMM (8.136 %). e SVFMM (\(\mbox{MCR}=6.769\) %). f DCASV (\(\mbox{MCR}=7.251\) %). g CLP (\(\mbox{MCR}=6.323\) %). h BLP (\(\mbox{MCR}=6.158\) %). i MSL (\(\mbox{MCR}=8.441\) %). j SNGMM (\(\mbox{MCR}=6.586\) %). k EGMM (\(\mbox{MCR}=1.318\) %). l DSVStMM (\(\mbox{MCR}=0.842\) %)

Full size image
Table 1 The comparison of the MCR for the first experiment
Full size table

In the second experiment, we use a synthetic four classes (K = 4) image (128×128 image resolution) as shown in Fig. 3a. The intensities of the image are 0, 85, 170 and 255, respectively. The corrupted image is shown in Fig. 3b. Mixed noise is added to corrupt the image which is Gaussian noise (μ = 0, σ 2 = 0.003) and salt & pepper (sp = 0.15). The segmentation results obtained by K-means, GMM, SVFMM, DCASV, CLP, BLP, MSL, SNGMM, EGMM and DSVStMM are shown in Fig. 3c–l, respectively. Amongst these models, the EGMM and DSVStMM get the lowest MCR, but the DSVStMM does better than the EGMM. It can be seen from the Fig. 3l that the edges and contours of the image are kept very clearer than other segmentation results. In the segmentation result of EGMM shown in Fig. 4k, the edge information is lost. The MCR of the proposed model is lower 1.190 % than EGMM. In Table 2, the results obtained (executing the test 10 times and the average of the results) for these models are presented with various mixed noise. Our proposed model gets the lowest MCR in every noise level. The MCR of the proposed model is lower 2 % or so on each noise level than EGMM. From these synthetic image tests, we can inference that the proposed model is more robust than other models against noise.

Fig. 3
figure 3

Second experiment (128×128 image resolution). a The original image. b Noise image with Gaussian noise (0 mean, 0.003 variance) and salt & pepper (\(\mbox{sp}=0.15\)). c K-means (\(\mbox{MCR}=11.029\) %). d GMM (11.664 %). e SVFMM (\(\mbox{MCR}=11.420\) %). f DCASV (\(\mbox{MCR}=11.401\) %). g CLP (\(\mbox{MCR}=11.078\) %). h BLP (\(\mbox{MCR}=11.151\) %). i MSL (\(\mbox{MCR}=11.169\)). j SNGMM (\(\mbox{MCR}=8.490\)). k EGMM (\(\mbox{MCR}=6.561\) %). l DSVStMM (\(\mbox{MCR}=5.371\) %)

Full size image
Fig. 4
figure 4

Third experiment (128×128 image resolution). a The original image. b Noise image with Gaussian noise (0 mean, 0.001 variance) and salt & pepper (\(\mbox{sp}=0.25\)). c image obtained by median filtering. d K-means (\(\mbox{MCR}=1.959\) %). e GMM (1.959 %). f SVFMM (\(\mbox{MCR}=1.959\) %). g DCASV (\(\mbox{MCR}=1.959\) %). h CLP (\(\mbox{MCR}=1.959\) %). i BLP (\(\mbox{MCR}=1.990\) %). j MSL (\(\mbox{MCR}=2.057\)). k SNGMM (\(\mbox{MCR}=1.984\)). l EGMM (\(\mbox{MCR}=1.825\) %). m DSVStMM (\(\mbox{MCR}=1.752\) %)

Full size image
Table 2 The comparison of the MCR for the second experiment
Full size table

Filtering can effectively reduce the noise. In order to test the impact of filtering before applying segmentation, a synthetic image is first corrupted by salt & pepper noise and Gaussian noise, then median filtering is used to reduce the noise, at last, all models are used to segment the image obtained by median filtering. Salt & pepper noise represents itself as randomly occurring white and black pixels. Median filtering is very effective to reduce the salt & pepper noise. Figure 4a shows the synthetic image (128×128 image resolution) which consists of four classes (K = 4) with luminance values [0, 85, 170, 255], used in the third experiment. The image shown in Fig. 4b is obtained by corrupting the original image with the salt & pepper noise (sp = 0.25) and Gaussian noise (0 mean, 0.001 variance). The image shown in Fig. 4c is obtained by median filtering acting on the image shown in Fig. 4b. It can be seen that the median filtering reduces the noise dramatically. All models are then used to segment the image obtained by median filtering. In Fig. 4d–m, we present the segmentation results of K-means, GMM, SVFMM, DCASV, CLP, BLP, MSL, SNGMM, EGMM and DSVStMM, respectively. It can be seen that the filtering affects the segmentation results obviously. The segmentation results show that most models get the same MCR. The MCR obtained by the EGMM model is lower than other models except the DSVStMM model. DSVStMM model get lower MCR than any other model. The image in Fig. 4a is corrupted by Gaussian noise (0 mean, 0.001 variance) and various levels of the salt & pepper noise, then median filtering is used to reduce the noise. The segmentation results obtained by all methods after application of the median filtering are given in Table 3. It can be seen that most models get the same MCR, while the DSVStMM gets lower MCR than any other model. It shows that the DSVStMM can effectively reduce the effects of the noise than any other model.

Table 3 The comparison of the MCR for the third experiment
Full size table

4.2 Natural images

Segmenting natural images is very difficult and challenging. It is hard to provide a good model to segment objects such as humans, animals, trees, buildings, etc. In this series of experiments, we test the proposed model on the large standard databases Amsterdam Library of Object Images(ALOI) [10] visually and the Berkeley image segmentation database [15] visually and quantitatively. In these natural images segmentation experiments, a set of natural grayscale images with and without artificial noise are used to evaluate the performance of the proposed model (DSVStMM), compared with GMM, SVFMM, DCASV, CLP, BLP, MSL, EGMM and SNGMM.

The ALOI database consists of 1000 categories, each of which contains dozens of pictures of a specific object. The ALOI database can be used to object recognition, color constancy, invariant feature extraction and image retrieval, it also offer visual evaluation of image segmentation [11]. The images shown in Fig. 5 are taken from ALOI database. In Fig. 5, the first to the third column of the first row are the original images, the forth to the seventh column of the first row are the images corrupted by mixture noise. These images are first corrupted by Gaussian noise (0 mean, 0.005 variance) and then added salt & pepper noise (sp = 0.10). The typical segmentation results are shown from the second row to the tenth row in Fig. 5 for the different models. For the segmentation results of images which are not corrupted by noise, we can see that DSVStMM yields better segmentation results than other models. The results obtained by DSVStMM own more homogeneous segmentation regions and sharper segment boundaries than other models. For the segmentation results of the corrupting images, the effect of reducing the noise by GMM model is not clear. The contours are obviously blurring of the last segmentation result of GMM. The EGMM and DSVStMM reduce the noise clearly, but EGMM is sensitive to the texture appearance. For the segmentation results of noise image, the EGMM reduce the noise effectively, but the edge and contour information of its segmentation results is blurred. However, DSVStMM yields better segmentation results than any other model. The DSVStMM not only degrades side effect of the noise for noise images but also its segmentation results keep better edge and contour information than any other model. The segmentation results obtained by DSVStMM provide the detailed information of the contours and edges. Since the component function of DSVStMM is Student’s t-distribution which has heavier tails than Gaussian distribution, the results obtained by DSVStMM show that DSVStMM can effectively process complex texture images and is more robust against noise than other models.

Fig. 5
figure 5

Segmentation examples of different methods based on the ALOI database. The first row, from the first column to the third column: the original images, from the fourth column to the seventh column, the original images corrupted by Gaussian noise (μ = 0, σ 2 = 0.005) and salt & pepper (sp = 0.10). From the second row to the tenth row, each row shows: GMM, SVMM, DCASV, CLP, BLP, MSL, EGMM, SNGMM, DSVStMM

Full size image

The Berkeley image segmentation database is considered to be used for image segmentation which consists of 300 natural color and grayscale images. Each image of the image database has 481×321 pixels. Several manual segmentation ground-truth images are provided for each image. Some natural grayscale images taken from the Berkeley image segmentation database with and without artificial noise are used to evaluate the segmentation performance visually and quantitatively. For the natural image segmentation, the proposed model is compared with the GMM, SVFMM DCASV, CLP, BLP, MSL, EGMM and SNGMM. The visual segmentation results are shown in Fig. 6. Three representative example images without noise are shown in the first column to the third column of the first row in Fig. 6; another three images are corrupted by mixture noise are shown in the forth column to the sixth column of the first row in Fig. 6. The last three images are first corrupted by Gaussian noise (0 mean, 0.003 variance) and then added salt & pepper noise (sp = 0.05). The typical segmentation results are shown from the second row to the tenth row of Fig. 6 for the different models. According to the segmentation results of these images without noise, the differences of the segmentation results of different models are not very clear. The EGMM produces very smooth segmentations, while certain texture regions may be merged into one piece. The DSVStMM favors a more contiguous segmentation for the texture region, and the information of the edges is preserved very well compared with the other models. From the segmentation results of the images with noise, we can see that the EGMM and DSVStMM both reduce the noise significantly. About the forth image, there is a plane in the sky. The segmentation results of the GMM and DCASV show that the noise is reduced poorly and the details of the plane are lost. The EGMM model can reduce noise dramatically, but the contours and edges of the segmentation results are not kept clearly. For the EGMM, much region of the sky is wrongly segmented into the plane. The segmentation result obtained by DSVStMM shows that the noise is reduced dramatically and the details of the plane are preserved very well. For the segmentation results of the fifth image, the DSVStMM not only reduces the effect of noise significantly, but also preserves the details of the balcony better than the other models. However, the information of the window and balcony is lost in the segmentation result of the EGMM for the fifth image. For the last noise image, the EGMM and DSVStMM reduce the effect of noise obviously compared with the other models, however, the tree can not be segmented correctly by the EGMM model. The tree, background and the mountain can be distinguished obviously for the segmentation results of the DSVStMM.

Fig. 6
figure 6

Segmentation examples of different methods based on the Berkeley segmentation grayscale database. The first row, from first column to the third column: the original images, from the fourth column to the sixth column, the original images corrupted by Gaussian noise (μ = 0, σ 2 = 0.003) and salt & pepper (sp = 0.05). From the second row to the tenth row, each row shows: GMM, SVMM, DCASV, CLP, BLP, MSL, EGMM, SNGMM, DSVStMM

Full size image

Next, we evaluate the performance of the DSVStMM from the objective view, as well as those of the GMM, SVFMM, DCASV, CLP, BLP, MSL, EGMM and SNGMM. In this experiment, 50 grayscale images with and without artificial noise are chosen from the Berkeley image segmentation database. The images are corrupted by mixture noise (mn) which is Gaussian noise (0 mean, 0.005 variance) and salt & pepper noise (sp = 0.10).

The PR value is used to quantify segmentation results. The PR values of image segmentation results are given in Table 4. It can be seen from the Table 4 that the differences of the segmentation results of the different models are relatively little for the images without noise. But under the noise conditions, the differences of the DSVStMM between any other model are obviously larger. At the same time the average PR of the DSVStMM is also larger than any other model. It can be seen from Table 4, the MRF-based models obtain better segmentation results than non MRF-based model under the noise conditions. The average PR of the proposed model is larger 0.04 or so than the other models. The experimental results indicate that the DSVStMM is robust against noise and produces better segmentation results. There may be two reasons for the DSVStMM producing better segmentation results. One is that the component function of DSVStMM is Student’s t-distribution which owns heavier tails than Gaussian distribution and can meet the needs of image segmentation, the other is that the models of the DSVStMM’s label probability proportions effectively represent the neighborhood relationships of the pixels.

Table 4 Comparison of image segmentation results based on berkeley grayscale images: pr index
Full size table

The execution time of the program is affected by many factors, such as the dimensions of the image and the number of segments. The dimension of the image is the most important factor. The tests given in Table 4 are performed on 481×321 images with a PC with a 2.20 GHz dual core processor and 2 GB RAM. The DSVStMM model converges after iterating averagely 84.0 times and the execution time is 4.7 s per iteration on the images in Table 4.

5 Conclusions

In this paper, we introduce an image segmentation algorithm which takes into account the spatial relationships among pixels. At the same time the directional information of the neighborhood is incorporated in the model. The number of parameters needed in the proposed model is fewer than that in other MRF-based models, so it is easier to be implemented. Furthermore, the pixels’ label probability proportions are explicitly modelled as probability vectors, thus a reparatory project step is avoided. The gradient descend method is used to estimate the parameters of the proposed model instead of the EM algorithm which is widely applied in most models. The experiments on both the synthetic and natural images show that the proposed model obtains better results than the other models. To extend the applications of the proposed model, we plan to apply the proposed model to medical imaging and bioinformatics in the future.

However, there are several improved aspects in our model. One limitation of our model is that it can be only used for grayscale images, not for color images. Another limitation is the choice of the parameter K. The number of model components K is currently set by user based on prior knowledge. This is an open question in mixture models. How to extend our model to apply in color images and adaptively choose K from the image data are our future works. In the context of image segmentation, we only use a 1-dimensional (grayscale color) feature to describe the grayscale image data. To improve the quality of image segmentation, more sophisticate features for natural images such as the Blobworld features [3] and the MRF texture features [19] will be considered to integrate into our model in the future researches.