Introduction

As compared to heat treatment, welding usually causes worsening of the initial properties of the metal, formation of an inhomogeneous structure with annealed and embrittled zones. In combination with welding stresses this worsening of the properties may give rise to various defects and even cause total fracture of welded joints in the process of welding or in service.

Under multipass welding, the metal of the weld and of the near-weld zone undergoes various and complex thermal cycles with repeated heating and cooling. This is accompanied by nonequilibrium processes of phase and structural transformations. As a rule, the metal of the deposited bead is melted one or several times when the next beads are deposited. This is followed by several more progressively damping heating cycles.

In principle, in an appropriate multipass welding process these cycles do provide a quality weld without post-welding heat treatment, because each bead of the multipass weld is first quenched and then tempered due to heating by the subsequent beads.

Development of such a process is impossible without efficient prediction of structural transformations in the weld metal.

Since the problem is complicate, the only effective way of its solution is computer simulation of the occurring processes. The statement of the problem does not allow us to avoid consideration of any of the numerous transformation processes, because each of them affects the result of the computation. Computer implementation of the method also requires steady (even if approximate) operation of all the modules without interference of the operator in any unforeseen thermal cycle, which should arise inevitably as a point of a large finite-element model of the welded structure.

The aim of the present work was to develop a set of mathematical models of decomposition of austenite under cooling of alloy steels in a welding thermal cycle and a method for determination of the parameters of these models from experimental results.

Possibilities of Simplification of the Model of Decomposition of Austenite

The factors limiting fast meeting of industrial demands are the volume and complexity of experimental determination of the parameters of transformations of specific materials rather than the intricacy of the mathematical apparatus of the models. The time and the expenses can be saved by simplifying the mathematical models of the transformations. Simplification is admissible if the aim of the simulation is estimation of the weldability and of the macroscopic properties rather than a careful study of the microstructures formed.

This dictates the choice of the model, the data for which can be obtained in an industrial laboratory from the results of tests of macroscopic specimens (with a thickness exceeding 1 mm) under the conditions imitating a welding thermal cycle with detection of such parameters as the temperature, the linear sizes, the electrical resistivity, etc. Stochastic microscopic phenomena (the number of nuclei of the new phase, the activation energy, the parameters of the microstructure, etc.) may be attracted for a quality description of the processes but not for use in the equations of the model.

An important advantage of the simulation method is the possibility of application of the published results of the studies obtained earlier for a wide circle of materials, which should be accumulated to form a data bank and to derive regression equations. This makes it possible to perform approximate computations totally without preliminary experiments. In this case test welding conducted by the method developed may be a control experiment.

The worthiness of the regression equations relating the properties of the material, the chemical composition, and the conditions of its heat treatment is preserved in the case of the use of the own experimental data. The standard for each grade of steel stipulates a considerable tolerance for the content of alloying elements. Availability of correlation relations makes it possible to allow for the effect of deviations of the chemical composition on the properties and to avoid repeated tests for each new batch of the material.

The standard approach to simulation of diffusion transformations is based on the parameters of isothermal transformation described by the Avrami equation

$$ p=1-{\left(1-{p}_s\right)}^{{\left(\frac{t}{t_s}\right)}^n}, $$
(1)

where p is the degree of the transformation (the ratio of the mass of the formed new phase to the total mass of the material participating in the transformation), t is the time from the start of the transformation, and t s and n are parameters of the process. The incubation period t s is understood as the time required for attainment of some initial degree of the transformation p s .

Unfortunately, the authors of many publications do not specify the values of p s and treat t s as the time of the start of the transformation. In fact, p s depends on the possibilities of the recording facility and commonly ranges from 1 to 5%. This complicates the use of published transformation diagrams (it has been shown experimentally in [1] that the value of t s of bainitic transformation is doubled when the sensitivity of the magnetometer increases from 0.25 to 0.004%). Formula (1) makes it possible to use parameter t s determined at any known value of p s , for example at p s = 50%.

To analyze the behavior of the parameters of Eq. (1) we should represent the diagrams of the experimental data in logarithmic coordinates. If we lay \( \overline{t} \) = ln t over one axis and \( \overline{p} \) = ln [– ln (1 – p )] over the other axis, Eq. (1) acquires a linear form

$$ \overline{p}={\overline{p}}_s+n\left(\overline{t}-{\overline{t}}_s\right). $$
(2)

Parameter n determines the slope of a part of the diagram and parameter \( {\overline{t}}_s \) = ln t s determines its shift over axis p. The experimental data of [2] show that for every kind of transformation n depends little on the temperature (the lines in the diagrams have the form of parallel rectilinear segments), whereas t s varies within the temperature range of the transformation by several orders of magnitude.

Dependence t s (T) is more complex and its full experimental plotting is quite laborious. However, in the process of arc welding the characteristic cooling rates vary from 0.1 to 500 K/sec. Therefore, the maximum time of residence of the material in the transformation interval t max does not exceed several minutes. In this connection, we are practically interested only in those parts of the transformation ranges where t s < t max.

As a rule, the main aim of the computation is determination of the final phase composition after the end of the transformations. The analysis of the dependences of the content of the products of decomposition of austenite (ferrite, pearlite, bainite) on the rates of cooling made in [3] shows that they are describable by the Avrami equation. This is explainable by the fact that at any cooling rate the initial phase (austenite) passes one and the same temperature range containing the ranges of ferritic, pearlitic and bainitic transformations. The cooling rate affects only the time of residence in each range (the time t in Eq. (1) is inversely proportional to the cooling rate w ).

The kind of dependence τ s (T) influences inconsiderably the final phase composition of the alloy. The incubation period of each transformation t s can be assumed to be constant (independent of the temperature). For the computation, we need only the mean value of t s and the boundaries of the temperature range of the transformation.

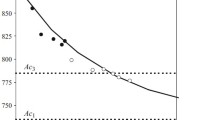
Let us consider the T s – w diagram, i.e., the dependence of the temperature of the start of ferritic transformation T s under continuous cooling on the cooling rate w (Fig. 1 a). In such system of coordinates, it has a rather simple form, which simplifies its schematic representation.

Fig. 1
figure 1

Schemes of thermokinetic (a) and isothermal (b ) diagrams of the start of transformations.

Full size image

The middle part of the diagram is almost rectilinear. The slope φ of the tangent to the curve of the start of the transformation T s (w) in every its point (Fig. 1 a ) is equal to the incubation period of the transformation at the corresponding temperature [4], i.e.,

$$ {t}_s=-\frac{dT_s}{dw}, $$
(3)

Therefore, the linearity of the part of the diagram T s implies constancy of t s in the corresponding temperature range, while the steeper regions at the ends of the diagram reflect deceleration of the transformation and growth of t s on the boundaries of the temperature range of the transformation. Formula (3) allows us to reconstruct the thermokinetic diagram of the transformation into an isothermal one.

We have mentioned already that the regions of delayed transformation present no interest under welding cooling rates; therefore, the whole of the curve describing the beginning of the transformation in Fig. 1 a may be approximated by a rectilinear segment. This is equivalent to schematic representation of the isothermal C-curve in Fig. 1 b in the form of a Π-curve.

However, we should amend the temperature ranges of the transformation interval. The equivalent temperatures of the start and finish of the transformation (T s and T f) are determined from the intersection of straight line T s with the boundaries of the range of the cooling rates at which a new phase may appear in an amount of at least p s (Fig. 1 a).

To plot the straight line T s experimentally we should test two specimens at different cooling rates matching the middle part of the rate range and detect the temperature of the start of the transformation T s (w). The tests may be conducted not only with forced cooling at the specified rates but also under natural cooling with different intensities (when the temperature decreases exponentially). In this case the cooling rate is measured in terms of the average cooling rate w = w 6/5 in the temperature range from 600 to 500°C or w = 1/t 8/5 , where t 8/5 is the time of passage through the temperature range from 850 to 500°C. Using the earlier published data (Fig. 2) we again face the problem of the level p s chosen by the authors at the start of the transformation. This level affects the obtained value of t s and the slope of the line T s (w). However, the change in p s changes only the scale of the diagram over axis w but does not influence the temperature range. For this reason, we do not need the chosen level of p s for determining the equivalent temperature of the start of the transformation T s from the diagram but should only require that it is the same for all the specimens used for plotting the diagram.

Fig. 2
figure 2

Thermokinetic diagram for steel 0.2% C – 0.3% Si – 1.75% Mn [5] with imposed cooling curves of the specimens and ranges of ferritic (F), pearlitic (P) and martensitic (M) transformations: the figures at the curves give the fractions of the formed phases in vol.%; the encircled figures give the final Vickers hardness.

Full size image

Determination of the equivalent temperature of the end of the transformation T f is somewhat more difficult. The critical cooling rate w max (Fig. 1) below which the transformation develops (i.e., the content of the given phase formed during passage of the temperature range of the transformation exceeds p s ) can be found from the results of a metallographic study of specimens after complete cooling. These results are commonly given in the published thermokinetic diagrams. Figure 2 presents an example of a diagram for a low-alloy steel with the contents of the formed phases and the final Vickers hardness deposited on the cooling curves.

Criterion for Estimation of the Phase Composition of a Steel

Analysis of published data shows that the accuracy of estimation of phase composition is commonly not high being affected by several subjective factors. The objectivity and reproducibility of the results of measurement of hardness are substantially better. At the same time, the hardness and the phase composition of a steel are correlated closely. Comprehensive data are obtained from the results of measurement of microhardness with subsequent statistical processing. Measurements of macrohardness are not comprehensive and give automatic averaging of the hardness of individual components of the structure. However, these data may be used for estimating the phase composition of the steel after cooling.

We will treat an alloy steel as a mixture of phase components having different hardness that depends only on alloying of the steel. The main phases are austenite (A), bainite (B) and martensite (M). It is expedient to combine ferrite and pearlite in a single ferrite-pearlite (FP) phase, because they have close properties and overlapping temperature ranges of the transformations. The hardness of the steel can be determined by interpolation with respect to the phase composition. Figure 3 presents the dependence of the hardness of the steel on the content of bainite phase pB in it, which has been plotted using the numerical data given in Fig. 2. It can be seen that the variation of the hardness upon transition from ferrite-pearlite structure to bainite and from bainite to martensite is linear. This means that each of the three phases of the steel has a fixed hardness value (HV FP = 170 kgf/mm2, HV B = 240 kgf/mm2, HV M = 450 kgf/mm2), which makes it possible to associate the dependence of the hardness of the steel on the cooling rate only with the changes in the phase composition, i.e.,

Fig. 3
figure 3

Proportion of the phase composition and the hardness of steel 0.2% C – 0.3% Si – 1.75% Mn [5]: 1 ) M + B; 2 ) FP + B; HV FP , HV B and HV M are the values of the hardness of the ferrite-pearlite mixture, of the bainite and of the martensite respectively; p B is the content of bainite (the scattering of the experimental points ∆p B is connected with inaccuracy of measurement of the phase composition and attains 7%).

Full size image

where the total concentration of all the phases p FP + p B + p M + p A = 1.

When the steel contains only two phases (FP + B or B + M), formula (4) permits accurate computation of the phase composition from the hardness. For this purpose, we should know the hardness of the phase components. Regression analysis of the data from atlases [3, 5,6,7] gives us the dependence of the Vickers hardness of each phase on the chemical composition, i.e.,

$$ {HV}_{\mathrm{FP}}=105+310\mathrm{C}+16\mathrm{Mn}-140\mathrm{Mo}; $$
(5)
$$ \begin{array}{l}{HV}_{\mathrm{B}}=195+136\mathrm{C}+29\mathrm{Si}+35\mathrm{Cr}+29\mathrm{Ni}+\\ {}\kern4em 132\mathrm{V}+10\mathrm{W}+173\mathrm{Al};\end{array} $$
(6)
$$ {HV}_M=289+792\mathrm{C}+37\mathrm{Si}+15\mathrm{W}. $$
(7)

Formulas (5) – (7) have been derived using the results of processing of data for 86, 45 and 100 grades of steel with R = 0.95, 0.94 and 0.97 and standard deviations of 30, 20 and 20 HV, respectively. The steels had the following alloying ranges (in wt.%): 0.01 < C < 0.5, Si < 1, Mn < 2, Cr < 2, Ni < 2, Mo < 1, V < 0.3, Nb < 0.1, Al < 0.1, Cu < 0.5, Ti < 0.05, W < 0.5 (the total content of the alloying elements did not exceed 4%). Each formula contains only those of the listed elements, the content of which affects substantially the hardness of the phase considered). The results of the computation of the hardness by formulas (5) – (7) are given as squares in Fig. 3; HV FP = 177 kgf/mm2, HV B = 230 kgf/mm2, HV M = 452 kgf/mm2.

Regression Models of Parameters of Decomposition of Austenite

In order to obtain the parameters of Avrami equation (1) we should have several pairs of values of p – t. These data can be obtained by analyzing the final phase composition of the steel after cooling at different rates. The time of residence of each specimen in the equivalent temperature range of the transformation may be determined from the difference in the abscissas of the points of intersection of the cooling curve (Fig. 2) with the boundaries of the range; the content of the formed phase can be found from the final hardness. It is desirable to use specimens in which only two phases form with different proportions of the mass fractions. The obtained pairs of values should be imposed on the diagram in logarithmic coordinates \( \overline{p}\hbox{--} \overline{t} \) . Analysis of the data of the diagram allows us to estimate the applicability of the accumulated data for determining n. If some of the points lie close to a single straight line, parameter n in this temperature range is constant and its value is equal to the slope of this line with respect to axis \( \overline{t} \).

Let us consider as an example the final phase composition of steel 09KhGSND [8] after heating to 1350°C and cooling at different rates (Fig. 4). In Fig. 5 the same data for the ferritic-pearlitic and bainitic transformations are presented in logarithmic coordinates. It can be seen from Fig. 5 that almost all the experimental points corresponding to the ferritic-pearlitic transformation are arranged near a single straight line 1. This means that the kinetics of formation of the ferrite-pearlite phase in steel 09KhGSND is describable by Eq. (1) with exponent n FP ≈ 1.

Fig. 4
figure 4

Phase composition of steel 09KhGSND as a function of cooling time τ in the temperature range of 850 – 500°C after a hold at 1350°C.

Full size image
Fig. 5
figure 5

Scheme of determination of parameters of the Avrami equation: ● (1)] concentration of the ferrite-pearlite phase p FP; ○ (2)] content of the bainite phase p B.

Full size image

In the vicinity of line 2 we observe all the light points corresponding to the concentration of bainite p B in the region of fast cooling of the steel (at t 8/5 < 5 sec). This straight line is more sloped than line 1; the exponent in Eq. (1) for bainite n B ≈ 2.4. Under slower cooling the light points lie below line 2, because bainite forms from the austenite retained after the ferritic-pearlitic transformation.

To obtain the second parameter of the Avrami equation we may use τ50, i.e., the duration of cooling in the welding thermal cycle in the temperature range 850 – 500°C, which yields 50% of the corresponding phase. The scheme of determination of this parameter from the point of intersection of the inclined line of the transformation with the line describing the level of the concentration of the phase p = 50% is presented in Fig. 5. For the ferrite-pearlite phase of steel 09KhGSND we obtain τ50FP 35 sec; for the bainite phase we obtain τ50B 6 sec.

For convenience of the computation, Eq. (1) may be transformed to

$$ p=1- \exp \left[-{\left(\frac{t}{t_{50}}\right)}^n\mathrm{In}2\right], $$
(8)

where the second parameter is the period of half-decomposition t 50 (the time of transformation of a half of the initial content of the decomposing phase). The value of t 50 can be computed if we know the boundaries T s – T f of the equivalent temperature range of the transformation, i.e.,

$$ {t}_{50}={\tau}_{50}\frac{\mathrm{In}{T}_s-\mathrm{In}{T}_{\mathrm{f}}}{\mathrm{In}\kern0.5em 850-\mathrm{In}\kern0.5em 500}. $$
(9)

The martensitic transformation may be described [9] by an equation similar to (8) but with temperature T as the argument, i.e.,

$$ p=1- \exp \left[-b\left({T}_{\mathrm{Ms}}-T\right)\right]. $$
(10)

Factor b determines the width of the temperature range of the martensitic transformation. The temperature of the lower boundary depends strongly on the content of martensite treated as the end of the transformation. To determine the parameters T Ms and b of the transformation we should cool the specimens at a high rate. In this case the other transformations will require an inconsiderable content of austenite.

The method presented makes it possible to reduce to a minimum the volume and the complexity of the tests for determining the parameters required for computer simulation of the welding process with allowance for the structural transformations. However, even a low volume of tests requires special equipment, qualified personnel and enough time for processing the data. If such resources are not available, approximate computations can be performed with the use of the results of earlier studies in the form of regression models. Though this approach has disadvantages, we should remember that its alternative is simulation of the welding process without allowance for structural transformations.

Analyzing published regression models for computing the boundaries of the temperature ranges of transformations from the chemical compositions of steels [5, 8, 10, 11] we found out that neither of the models provided enough accuracy (by the data of [5] maximum deviations from the experimental diagrams exceed 100°C).

For this reason, we processed a considerable number of diagrams from atlases [3, 5,6,7, 12] and plotted new regression models (dependences of the temperatures in °C on the contents of alloying elements in %), namely,

$$ \begin{array}{l}{T}_{\mathrm{FPs}}=895-714{\mathrm{C}+687\mathrm{C}}^2+91\mathrm{CMn}-\\ {}\kern1em 77\mathrm{Mn}+28\mathrm{Cr}-60\mathrm{Ni}-434\mathrm{Al};\end{array} $$
(11)
$$ \begin{array}{l}{T}_{\mathrm{Bs}}=700-237\mathrm{C}+20\mathrm{Si}-26\mathrm{Mn}-23\mathrm{Cr}-\\ {}\kern1em 24\mathrm{Ni}+227\mathrm{Al}-48\mathrm{Cu}-89\mathrm{V}-715\mathrm{Nb};\end{array} $$
(12)
$$ \begin{array}{l}{T}_{\mathrm{Ms}}=588-\mathrm{C}\left(597-134\mathrm{Si}-154\mathrm{Mn}\right)-\\ {}74\mathrm{Si}-92\mathrm{Mn}-12\mathrm{Cr}-20\mathrm{Ni}\hbox{-} 12\mathrm{Mo}+163\mathrm{Cu}.\end{array} $$
(13)

Formulas (11), (12) and (13) were obtained by processing 91, 96 and 160 diagrams with coefficients of multiple correlation 0.93, 0.94 and 0.92 and standard deviations 17, 15 and 10°C, respectively. They were derived with the use of only accurate enough diagrams with high enough degree of homogenization of austenite (for heating temperatures above 1000°C) and the same alloying ranges as in the hardness models [see formulas (5) – (7)]. The effect of the degree of homogenization should be studied individually (depending on the maximum heating temperature and on the time of residence in the temperature range of austenitization).

Using the same constrains for the alloying we obtained the following regression models of the parameters of the Avrami equation.

For the ferritic-pearlitic transformation

$$ \begin{array}{l}{n}_{\mathrm{FP}}=1.1-3.6\mathrm{C}+0.55\mathrm{Mn}+0.6\mathrm{C}\mathrm{r}+0.3\mathrm{Ni}-\\ {}1.95\mathrm{Cu}-0.6\mathrm{Al}+3{.6\mathrm{C}}^2-0.4{\mathrm{Mn}}^2+2.9\mathrm{MnC}\end{array} $$
(14)

(30 grades of steel, R = 0.89, standard deviation 0.08);

$$ \begin{array}{l}\kern1em \mathrm{In}\left({\tau}_{50\mathrm{FP}}\right)=0.72+1.1\mathrm{Si}+1.1\mathrm{Mn}+3.3\mathrm{Cr}+\\ {}3.5\mathrm{Ni}+3.7\mathrm{Mo}-7\mathrm{Cu}+5.3\mathrm{Al}-5.2\mathrm{Ti}+9.7\mathrm{MnC}\end{array} $$
(15)

(31 grades of steel, R = 0.94, standard deviation 0.3). For the bainitic transformation

$$ {\mathrm{n}}_{\mathrm{B}}=4-1.4\mathrm{C}+0.2\mathrm{Si}-1.2\mathrm{Mn}+1.6\mathrm{V}-2\mathrm{Cu} $$
(16)

(51 grades of steel, R = 0.87, standard deviation 0.3);

$$ \begin{array}{l}\mathrm{In}\left({\tau}_{50\mathrm{B}}\right)=-1.2+6.2\mathrm{C}+0.7\mathrm{Si}+1.25\mathrm{Mn}+\\ {}\kern3em 0.3\mathrm{Ni}+1.4\mathrm{Mo}+0.9\mathrm{V}+2\mathrm{C}\mathrm{u}\end{array} $$
(17)

(36 grades of steel, R = 0.87, standard deviation 0.4).

For factor b in the equation of the martensitic transformation (1) the analysis performed has not shown correlation with the chemical compositions of the steels. The range of scattering of the values of b varied from 0.016 to 0.032; the mean value b = 0.022 differed from the value of b = 0.011 presented in [9] for carbon steels.

We have not managed to design models for the lower boundaries of the temperature ranges of ferritic-pearlitic and bainitic transformations, because the data available were not sufficient for the purpose. These parameters influence the transformation kinetics comparatively little. In further computations the lower boundary of the ferritic-pearlitic transformation was understood as the upper boundary of the bainitic transformation, and the lower boundary of the bainitic transformation was understood as the upper boundary of the martensitic transformation.

To check the set of the regression models we used the characteristics of 140 grades of steel from atlases [3, 5,6,7, 13] for various cooling rates. The chemical compositions of the steels were used to compute the temperatures and kinetic parameters of the transformations and the hardness of the phase components. Then we computed the final phase composition for every cooling rate and used the former to compute the hardness. Comparison with the experimental data from the atlases is presented in Fig. 6. The correlation coefficient for the set of the models R = 0.9; the standard error is 37 MPa.

Fig. 6
figure 6

Comparison of computed hardness values and experimental data.

Full size image

Conclusions

  1. 1.

    The most objective and reproducible criterion of the final phase composition is the hardness of the steel, which correlates with a number of other mechanical properties.

  2. 2.

    Comparison of the results of the hardness computations with the earlier published experimental data proves worthiness of the developed models of transformations in alloy steels for various rates of cooling and of the obtained regression equations for computing the parameters of the models from the chemical compositions of the steels.