Introduction

Adhesive jointing is one of the most favorable techniques employed in composite structures, because they can reduce detrimental stress concentrations and guarantee structural integrity, contrary to the traditional ones, such as riveting and bolting [1]. However, delamination between the adherend and the finite-thickness adhesive layer due to the low bonding strength of the adhesive layer often leads to the loss of stiffness and strength of structures. A deep insight into the delamination failure mechanism requires advanced numerical methods.

Because of the very small thickness (e.g., 0.1mm) and the complicated mechanical properties of adhesive layers, modeling and simulation of the delamination failure of composites is a tough task. Currently, the cohesion theory, which was first introduced by Dugdale [2] and Barenblatt [3] to describe the discrete fracture as a separation of materials across the interface, has been demonstrated to be the most popular approach for the delamination analysis of composites, because it avoids the consideration of crack-tip singularities and can predict both the initiation and propagation of delamination cracks. The cohesive-zone model (CZM) assumes that the traction–displacement jump relationship characterizes the progressive separation of bonded interfaces.

Now, there are plenty of CZMs in terms of the shape of traction–displacement jump curves, such as bilinear [4–8], trapezoidal and polynomial [9, 10], and exponential CZMs [11–14]. These phenomenological CZMs have been successful in predicting the delamination failure of composites. However, the problems associated with ensuring the numerical convergence, which is disturbed by the “snap-back” instability as a fundamental issue in the implicit finite element analysis (FEA), poses a great challenge to a robust and accurate prediction of the delamination mechanisms of 3D composites. This problem arises essentially from the cohesive softening behavior with a nonpositive definite stiffness matrix, leading to the divergence of solutions from the equilibrium path during Newton iterations. The convergence issue is typically circumvented by introducing some advanced numerical techniques. One common numerical method is the cylindrical arc-length scheme (or the so-called Riks scheme), which attempts to trace the equilibrium path by using the arc-length search, avoiding the singular points in load responses encountered in the Newton–Raphson algorithm [4, 5, 15]. However, the Riks scheme often requires a high computational cost, because an additional constraint equation between the arc-length radius and the displacement increment have to be solved in each iteration. Another feasible scheme is to introduce an artificial viscous damping into the nonlinear stiffness equation, which regularizes the instability problem with zero or negative eigenvalues of the stiffness matrix well. Adopting this idea, Chaboche et al. [16] introduced the viscous effect into Tvergaard polynomial CZM to improve the robustness of numerical results, e.g., to eliminate “displacement jumps” in load curves, and Hamitouche et al. [17] introduced a damage rate dependence to limit the cohesive softening problem. Besides, Gao and Bower [18] introduced a fictitious small viscosity into the Xu and Needleman exponential CZM [11], and Hu et al. [19] proposed a move-limit method by building up a rigid wall to remove the instability. Although the viscous regularization scheme shows some advantages over the arc-length algorithm in improving the convergence, an unsolved issue occurs — how to select appropriate viscous parameters, which should be large enough to regularize the cohesive softening behavior, but small enough not to affect the numerical accuracy. Furthermore, it is not yet clear how some important cohesive parameters, including the cohesive strength and cohesive shape, affect the numerical convergence and computational efficiency based on the viscous regularization for simulating the delamination of composite adhesive joints.

In this research, using the mid-plane interpolation technique and ABAQUS-UEL (user element subroutine), we first develop numerical 3D finite-element codes for the bilinear CZM developed by Camanho et al.[6] and the exponential CZM proposed by Liu and Islam [14] and then introduce the artificial viscous effect into the stiffness equation in the implicit FEA to improve the numerical convergence. Then, we study the effects of different cohesive parameters, including the cohesive strength and cohesive shape, on the convergence in simulating the delamination of a composite single lap joint (SLJ) and a composite skin/stiffener panel under tension by using two mesh models. From the convergence and accuracy perspectives, this research presents some suggestions how to appropriately select the cohesive strengths and viscous parameters for a delamination analysis of composite adhesive joints by using CZMs.

1. Bilinear CZM

Camanho et al. [6] proposed a bilinear CZM. The single-mode traction- displacement jump relationships are given by

$$ \begin{array}{cc}\hfill \left\{\begin{array}{l}{T}_i=K{\Delta}_i^{\max },\kern1em {\Delta}_i^{\max}\le {\Delta}_i^c\hfill \\ {}{T}_i=\left(1-{d}_i^s\right)K{\Delta}_i^{\max },\kern1em {\Delta}_i^c\le {\Delta}_i^{\max }<{\Delta}_i^f,\hfill \\ {}{T}_i=0,\kern4em {\Delta}_i^{\max}\ge {\Delta}_i^f\hfill \end{array}\right.\hfill & \hfill \left\{\begin{array}{l}{\Delta}_i^{\max }= \max \left({\Delta}_i^{\max },\left|{\Delta}_i\right|\right),\kern0.5em i=1,2,\kern0.5em \mathrm{mode}\mathrm{s}\ \mathrm{I}\mathrm{I}\ \mathrm{and}\ \mathrm{I}\mathrm{I}\mathrm{I},\hfill \\ {}{\Delta}_3^{\max }= \max \left({\Delta}_3^{\max },{\Delta}_3\right)\mathrm{with}\ {\Delta}_3^{\max}\ge 0,\ \mathrm{mode}\ \mathrm{I}, \hfill \end{array}\right.\hfill \end{array} $$

where \( {d}_i^s=\frac{\Delta_i^f\left({\Delta}_i^{\max }-{\Delta}_i^c\right)}{\Delta_i^{\max}\left({\Delta}_i^f-{\Delta}_i^c\right)}\left(0\le {d}_i^s\le 1,\kern0.5em i=1,2,3\right) \) are damage variables,. Δ = 〚u〛 is the displacement jump vector, and u is the displacement vector, Δ f3  = 2G c1 /T c3 and Δ f1,2  = 2G c2,3 /T c1 ; T c3 and T c1  = T c2 are the maximum tractions in the normal and tangential directions, respectively; Δ c1  = Δ c2  = T c1 /K and Δ c3  = T c3 /K; G c i (i = 1, 2, 3) are mode I, II, and III delamination fracture toughnesses, respectively; Δ max i  = max(Δ max i , Δ i ) are the maximum displacement jumps in the loading history, indicating the irreversibility. In order to avoid interpenetration of the completely failed interfaces under compression, the penalty stiffness T 3 = KΔ3 (Δ3 ≤ 0) is introduced in the normal, 3-direction.

The mixed-mode traction–displacement jump relationships are written as

$$ \left\{\begin{array}{l}{T}_i=K{\Delta}_i,\kern1.5em {\Delta}_i^{\max}\le {\Delta}_i^c,\hfill \\ {}{T}_i=\left(1-{d}^s\right)K{\Delta}_i,\kern1em {\Delta}_i^c\le {\Delta}_i^{\max }<{\Delta}_i^f,\hfill \\ {}{T}_i=0,\kern4em {\Delta}_i^{\max}\ge {\Delta}_i^f,\hfill \end{array}\right. $$

where the scalar mixed-mode damage variable d s (0 ≤ d s ≤1) is written as

$$ \begin{array}{c}\hfill {d}^s=\frac{\Delta_m^f\left({\Delta}_m^{\max }-{\Delta}_m^c\right)}{\Delta_m^{\max}\left({\Delta}_m^f-{\Delta}_m^c\right)},\kern0.5em {\Delta}_m=\sqrt{\Delta_1^2+{\Delta}_2^2+{\left\langle {\Delta}_3\right\rangle}^2},\kern0.5em {\Delta}_m^{\max }= \max \left({\Delta}_m^{\max },{\Delta}_m\right),\hfill \\ {}\hfill {\Delta}_m^c=\left\{\begin{array}{l}{\Delta}_3^c{\Delta}_1^c\sqrt{\frac{1+{\beta}^2}{{\left({\Delta}_1^c\right)}^2+{\left(\beta {\Delta}_3^c\right)}^2}},\kern1em {\Delta}_3>0\hfill \\ {}\kern0.5em {\left({\Delta}_1^c\right)}^2+{\left({\Delta}_2^c\right)}^2,\kern4.5em {\Delta}_3\le 0\hfill \end{array},\kern1em {\Delta}_m^f=\left\{\begin{array}{l}\frac{2}{K{\Delta}_m^c}\left[{G}_1^c+\left({G}_2^c-{G}_1^c\right){\left(\frac{\beta^2}{1+{\beta}^2}\right)}^{\eta}\right],\kern1em {\Delta}_3>0,\hfill \\ {}\kern0.5em {\left({\Delta}_1^c\right)}^2+{\left({\Delta}_2^c\right)}^2,\kern8.5em {\Delta}_3\le 0.\hfill \end{array}\right.\right.\hfill \end{array} $$
(1)

Here, 〈 ⋅ 〉 denotes the MacAuley bracket; \( \beta =\sqrt{\left({\Delta}_1^2+{\Delta}_2^2\right)/{\Delta}_3^2}\left({\Delta}_3>0\right) \) is the mode mixity ratio, and η is the parameter defined in the B-K law [20].

2. Exponential CZM

The exponential CZM proposed by Liu et al. [14] is used. For a single-mode delamination, the damaged cohesion law T i  − Δ max i [Δ max i  = max(Δ max i , Δ i )] are written as

$$ {T}_i=e{T}_i^c/{\Delta}_i^c{\Delta}_i^{\max } \exp \left[-\frac{\Delta_i^{\max }}{\Delta_i^c}{\left(1-{d}_i^s\right)}^{-1}\right]\left(i=1,2,3\right), $$
(2)

where d s i (i = 1, 2, 3) are the damage variables in the normal and tangential directions, respectively;

$$ {d}_i^s=\frac{1- \exp \left(-\frac{\Delta_i^{\max }-{\Delta}_i^c}{\Delta_i^f-{\Delta}_i^c}\right)}{1- \exp \left(-1\right)}\left(i=1,2,3\right), $$
(3)

where Δ c i and Δ f i (i = 1, 2, 3) are the initial and critical failure displacement jumps, respectively. The critical displacement jump Δ f i (i = 1, 2, 3) in Eq.(3) can be determined by numerically solving the equation

$$ \begin{array}{c}\hfill {\displaystyle {\int}_0^{\Delta_i^f}e{T}_i^c/{\Delta}_i^c{\Delta}_i^{\max } \exp \left(-{\Delta}_i^{\max }/{\Delta}_i^c\right){\mathrm{d}\Delta}_i^{\max }}\hfill \\ {}\hfill =e{T}_i^c{\Delta}_i^c-e{T}_i^c\left({\Delta}_i^c+{\Delta}_i^f\right) \exp \left(-{\Delta}_i^f/{\Delta}_i^c\right)=\mu {G}_i^c\kern1em \left(i=1,2,3\right),\hfill \end{array} $$

where μ is a constant approximating unity, and Δ f i  = 11.76Δ c i (i = 1, 2, 3) is obtained at μ = 0.9999. The traction–displacement jump relationship T − Δmax[Δmax = max(Δmax, Δ)] for the mixed-mode delamination is assumed to be

$$ T=e{T}^c/{\Delta}^c{\Delta}^{\max } \exp \left(-\frac{\Delta^{\max }}{\Delta^c}\frac{1}{1-{d}^s}\right), $$

where d s is the scalar interfacial damage variable for the mixed-mode delamination; \( {\Delta}^c=\sqrt{{\left({\Delta}_1^c\right)}^2+{\left({\Delta}_2^c\right)}^2+{\left({\Delta}_3^c\right)}^2} \) and \( {T}^c=\sqrt{{\left({T}_1^c\right)}^2+{\left({T}_2^c\right)}^2+{\left({T}_3^c\right)}^2} \) are the equivalent critical displacement jump and the critical traction, respectively. A variable displacement jump \( \Delta =\sqrt{{\left({\Delta}_1\right)}^2+{\left({\Delta}_2\right)}^2+{\left({\Delta}_3\right)}^2} \) is assumed.

For the mixed-mode delamination, the damage variable d s is given by

$$ {d}^s=\frac{1- \exp \left(-\frac{\Delta^{\max }-{\Delta}^c}{\Delta^f-{\Delta}^c}\right)}{1- \exp \left(-1\right)}. $$
(4)

The mixed-mode critical failure displacement jump Δ f can be found numerically from the equation

$$ {\displaystyle {\int}_0^{\Delta^f}e{T}^c/{\Delta}^c{\Delta}^{\max } \exp \left(-{\Delta}^{\max }/{\Delta}^c\right){\mathrm{d}\Delta}^{\max }}=e{T}^c{\Delta}^c-e{T}^c\left({\Delta}^c+{\Delta}^f\right) \exp \left(-{\Delta}^f/{\Delta}^c\right)={G}^c, $$

where the mixed-mode fracture toughness G c is assumed to obey the B-K law [20].

The second-order tangential stiffness tensor D tan for the mixed-mode delamination is derived from Eqs.(2) and (4) by considering interpenetration of the delaminated interfaces:

$$ {D}_{ij}^{\tan }=\frac{\partial {T}_i}{\partial {\Delta}_j^{\max }}\left\{\begin{array}{l}{\delta}_{ij}\left[1-\xi {\delta}_{1j}\left\langle -{\Delta}_j^{\max}\right\rangle /{\Delta}_j^{\max}\right]\left(1-{\Delta}_j^{\max }/{\Delta}_j^c\right)e{T}_j^c{e}^{-{\Delta}_j^{\max }/{\Delta}_j^c}/{\Delta}_j^c,\kern1em 0<{\Delta}^{\max }<{\Delta}^c,\hfill \\ {}\kern1em {\delta}_{ij}\left[1-\xi {\delta}_{1j}\left\langle -{\Delta}_j^{\max}\right\rangle /{\Delta}_j^{\max}\right]\frac{T_j^c}{\Delta_j^c} \exp \left(1-\frac{\Delta_j^{\max }}{\Delta_j^c}\frac{1}{1-{d}^s}\right)\hfill \\ {}\kern1em \times \left\{1-\frac{\Delta_j^{\max }}{\Delta_j^c}\left[1-{d}^s+\frac{\partial {d}^s}{\partial {\Delta}_j^{\max }}\frac{\Delta_j^{\max }}{\Delta_j^c}\frac{1}{{\left(1-{d}^s\right)}^2}\right]\right\},\kern1em {\Delta}^c\le {\Delta}^{\max }<{\Delta}^f,\hfill \\ {}\kern8.5em 0,\kern1em {\Delta}^{\max}\le 0\kern1em \mathrm{or}\kern1em {\Delta}^{\max}\ge {\Delta}^f.\hfill \end{array}\right. $$

Here,

$$ \begin{array}{c}\hfill \frac{\partial {d}^s}{\partial {\Delta}_j^{\max }}=\frac{\partial {d}^s}{\partial {\Delta}^{\max }}\frac{\partial {\Delta}^{\max }}{\partial {\Delta}_j^{\max }},\hfill \\ {}\hfill \frac{\partial {d}^s}{\partial {\Delta}^{\max }}=\frac{1}{1- \exp \left(-1\right)}\frac{1}{\Delta^f-{\Delta}^c} \exp \left(-\frac{\Delta^{\max }-{\Delta}^c}{\Delta^f-{\Delta}^c}\right),\hfill \\ {}\hfill \frac{\partial {\Delta}^{\max }}{\partial {\Delta}_i^{\max }}=\frac{\Delta_i^{\max }}{\Delta^{\max }}\left(1+{\delta}_{1i}\frac{\left\langle -{\Delta}_i^{\max}\right\rangle }{\Delta_i^{\max }}\right),\hfill \end{array} $$

ξ is a penalty factor, and δ ij is the Kronecker delta.

3. 3D Finite-Element Formulation for Implementing CZMs

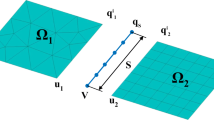
Segurado and LLorca [21] proposed a 3D finite-element formulation for implementing CZMs by adopting the midplane numerical technique. Similar to the standard isoparametric elements, a local coordinate system (ξ,η,ζ) and a global coordinate system (x, y, z) are defined. The displacement jump 〚u〛 in the local coordinate system for the cohesive element is calculated as

$$ \begin{array}{cc}\hfill \boldsymbol{\Delta} =[{\kern-2.3pt}[ \mathbf{u}]{\kern-2.3pt}] ={\boldsymbol{\upvarphi}}^T[{\kern-2.3pt}[ \mathbf{u}\left(\xi, \eta \right)]{\kern-2.3pt}], \hfill & \hfill \varphi =\varphi \left(\mathbf{n},{\tilde{\mathbf{t}}}_1,{\tilde{\mathbf{t}}}_2\right),\hfill \end{array} $$

where \( \varphi \left(\mathbf{n},{\tilde{\mathbf{t}}}_1,{\tilde{\mathbf{t}}}_2\right) \) is the 3×3 matrix transformation of the local coordinate system to the global one, and three orthogonal directions are given by

$$ \begin{array}{ccc}\hfill \mathbf{n}=\frac{\left(\frac{\partial {\mathbf{x}}^R}{\partial \xi}\times \frac{\partial {\mathbf{x}}^R}{\partial \eta}\right)}{\left\Vert \frac{\partial {\mathbf{x}}^R}{\partial \xi}\times \frac{\partial {\mathbf{x}}^R}{\partial \eta}\right\Vert },\hfill & \hfill {\tilde{\mathbf{t}}}_1=\frac{\frac{\partial {\mathbf{x}}^R}{\partial \xi }}{\left\Vert \frac{\partial {\mathbf{x}}^R}{\partial \xi}\right\Vert },\hfill & \hfill {\tilde{\mathbf{t}}}_2={\tilde{\mathbf{t}}}_1\times \mathbf{n}.\hfill \end{array} $$

The coordinate x R of a midplane point is written as

$$ {\mathbf{x}}^R=\frac{1}{2}\mathbf{H}\left(\xi, \eta \right)\left({\mathbf{I}}_{12\times 12}\kern1em \left|\kern1em {\mathbf{I}}_{12\times 12}\right.\right)\left(\mathbf{x}+\underset{\sim }{\mathbf{u}}\right) $$

where x and \( \underset{\sim }{\mathbf{u}} \) are the 24×1-node coordinate matrix and is the 24×1-node displacement matrix, respectively, for the 3D eight-node elements; H(ξ,η) is a 3×12 matrix for the 3D eight-node elements including the shape function, and I 12×12 is the identity matrix.

The relative displacement at a point (ξ,η) between element sides is interpolated as a function of the relative displacement between paired nodes

$$ [{\kern-2.3pt}[ \mathbf{u}\left(\xi, \eta \right)]{\kern-2.3pt}] =\left\{\begin{array}{c}\hfill [{\kern-2.3pt}[ {u}_1\left(\xi, \eta \right)]{\kern-2.3pt}] \hfill \\ {}\hfill [{\kern-2.3pt}[ {u}_2\left(\xi, \eta \right)]{\kern-2.3pt}] \hfill \\ {}\hfill [{\kern-2.3pt}[ {u}_3\left(\xi, \eta \right)]{\kern-2.3pt}] \hfill \end{array}\right\}=\mathbf{H}\left(\xi, \eta \right)[{\kern-2.3pt}[ {\mathbf{u}}_{\mathrm{N}}]{\kern-2.3pt}] =\mathbf{H}\left(\xi, \eta \right)\boldsymbol{\upphi} \underset{\sim }{\mathbf{u}}=\mathbf{L}\underset{\sim }{\mathbf{u}}, $$

where L is a 3×24 matrix, and −1≤ξ and η ≤1 are the local coordinates of elements; ϕ = (I 12 × 12 | I 12 × 12) is a 12×24 matrix. Finally. the nodal force vector F c (24×1 matrix) and the stiffness matrix K c (24× 24 matrix) are written as

$$ \begin{array}{c}\hfill {\mathbf{F}}_c={\displaystyle \iint {\mathbf{L}}^T{\upvarphi}^T\mathbf{T}\mathrm{d}A}={\displaystyle \iint {\mathbf{M}}^T\mathbf{T}\mathrm{d}A}={\displaystyle \sum_i{\displaystyle \sum_j{\omega}_i{\omega}_j{\mathbf{M}}^T\mathbf{T}\left|J\right|}},\hfill \\ {}\hfill {\mathbf{K}}_c=\frac{\partial {\mathbf{F}}_c}{\partial \underset{\sim }{\mathbf{u}}}={\displaystyle \iint {\mathbf{M}}^T\frac{\partial \mathbf{T}}{\partial \underset{\sim }{\mathbf{u}}}}\mathrm{d}A={\displaystyle \iint {\mathbf{M}}^T\frac{\partial \mathbf{T}}{\partial [{\kern-2.3pt}[ \mathbf{u}]{\kern-2.3pt}]}\frac{\partial [{\kern-2.3pt}[ \mathbf{u}]{\kern-2.3pt}] }{\partial \underset{\sim }{\mathbf{u}}}\mathrm{d}A}\hfill \\ {}\hfill ={\displaystyle \iint {\mathbf{M}}^T\frac{\partial \mathbf{T}}{\partial [{\kern-2.3pt}[ \mathbf{u}]{\kern-2.3pt}]}\frac{\partial [{\kern-2.3pt}[ \mathbf{u}]{\kern-2.3pt}] }{\partial \underset{\sim }{\mathbf{u}}}\mathrm{d}A}={\displaystyle \iint {\mathbf{M}}^T\frac{\partial \mathbf{T}}{\partial [{\kern-2.3pt}[ \mathbf{u}]{\kern-2.3pt}]}\mathbf{M}\mathrm{d}A}={\displaystyle \sum_i{\displaystyle \sum_j{\omega}_i{\omega}_j{\mathbf{M}}^T{\mathbf{D}}^{\tan}\mathbf{M}\left|J\right|}},\hfill \end{array} $$
(5)

where |J| is the Jacobian of the isoparametric transformation and ω is the weight; M = φL is the 3×24 shape function matrix for the 3D cohesive element.

4. Length of the Cohesive Zone

CZMs introduce a length scale, which is called the length of the cohesive zone (LCZ) due to the cohesive softening behavior. This length is defined as the distance from the crack tip to the position where the maximum cohesive traction is attained [22, 23]. If the cohesive length scale is not considered in the delamination analysis, the dissipation of delamination fracture energy cannot be accurately captured, which will lead to the mesh sensitivity problem. Therefore, the LCZ must be properly evaluated. Turon et al. [22] suggested that three elements in the cohesive zone are sufficient to predict the delamination growth, which is also adopted in this research.

5. Numerical Results and Discussion

In this research, CZMs are implemented using ABAQUS-UEL (User element subroutine), where the main task in each iteration is to update the nodal residual force F c and the element stiffness matrix K c (24× 24 matrix) in Eq. (5) for the 3D eight-node zero-thickness interface element. Due to the cohesive softening behavior, an artificial viscous force F v is introduced to improve the convergence [24]:

$$ \left\{\begin{array}{l}{\mathbf{F}}_{ext}-{\mathbf{F}}_c-{\mathbf{F}}_{\nu }=\mathbf{R},\hfill \\ {}{\mathbf{F}}_{\nu }=c{M}^{*}\boldsymbol{\upnu}, \kern1em \boldsymbol{\upnu} =\varDelta \underset{\sim }{\mathbf{u}}/\varDelta t,\hfill \end{array}\right. $$
(6)

where M * is an artificial mass matrix calculated with a unity density, v is the node velocity, \( \Delta \underset{\sim }{\mathbf{u}} \) is increment of the nodal displacement, R is the tolerance, c is a constant damping factor, and Δt is the time increment in nonlinear iterations.

In the following, two delamination cases, for a single-lap joint (SLJ) and a composite skin/stiffener panel under tension, are considered to study the numerical convergence. Because the mode II shear failure governs the delamination growth process for these two cases, the effect of the normal cohesive strength T c3 on the convergence and accuracy is very small and the value of T c3 = 40 MPa is used. The tangential cohesive strengths T c1  = T c2 are varied for comparison. In Eq. (6), it is generally assumed that c = 5 · 10–3. A very small time increment is required to guarantee the numerical precision needed (the initial, minimum, and maximum time increments were Δt = 0.0001s, 10–10, and 0.001 s, respectively).

Volokh et al. [25] showed that the convergence rates for the bilinear, parabolic, sinusoidal, and exponential CZMs were similar, but the exponential CZM with a smooth transition at the peak point turned out to be most attractive. Alfano et al. [26] found that the convergence of the trapezoidal CZM was the worst because of the severely discontinuous transitions at the peak point, leading to more iterations, although it is often superimposed to predict the ductile delamination failure of adhesive joints well [27]. By comparison, the convergence using the exponential CZM is the best, which is its great advantage over the trapezoidal CZM, especially for a coarse model. The bilinear CZM is a compromise between the numerical convergence and accuracy. In this research, the exponential and bilinear CZMs are adopted.

5.1. Delamination results for a single-lap joint (SLJ) under tension

In this section, a 3D FEA of delamination of the adhesively bonded single-lap joint (SLJ) is performed. The model geometry and material parameters taken from Panigrahi [28], as shown in Fig. 1 and are as follows: the lay-up patterns is [0]8, and the thickness of each layer was 0.125 mm. According to [14], the value of η = 2.0 is taken in Eq. (1). Campilho et al. [29], Krueger and O’Brien [30], Dattaguru et al. [31], and Pradhan and Panda [32] pointed out that a sufficiently fine mesh is strongly required to guarantee the numerical convergence and accuracy. Two mesh models were established: with 9000 solid and 300 cohesive elements for the coarse-mesh model and 13,000 solid and 600 cohesive elements for the fine-mesh model. Figure 2 shows the load–displacement curves found using the two mesh models with cohesive strengths T c1  = T c2  = 40 MPa, and Fig. 3 depicts the load–displacement curves given by the fine-mesh model and two CZMs with cohesive strengths T c1  = T c2  = 20, 40, and 60 MPa, respectively.

Fig. 1
figure 1

Schematic of an adhesively bonded single-lap joint (SLJ).

Full size image
Fig. 2
figure 2

Load–displacement curves P–Δ of SLJ obtained by models with coarse (●, ♦) and fine (×, ◄) meshes for the exponential (●, ×) and bilinear (♦, ◄) CZMs at T c1  = T c2  = 40 MPa. 1 and 2 — the initial and final delaminations, respectively.

Full size image
Fig. 3
figure 3

Load–displacement curves P–Δ of SLJ obtained by models with a fine mesh model for the exponential (*, ●, ▲) and bilinear (►, ▽, ♦) CZMs at T c1  = T c2  = 20 (*, ►), 40 (●, ▽), and 60 MPa (▼, ♦).

Full size image

For the bilinear CZM, Camanho et al. [6] suggested K = 106 N/mm3 as an accurate value for the cohesive stiffness of carbon/epoxy composites in the bilinear CZM. According to a numerical analysis, the convergence and computational efficiency were better at K = 105 N/mm3 than at K = 106 N/mm3, although they led to almost the same load responses, which were consistent with the conclusion drawn by Turon et al. [22].

It is seen from Figs. 2 and 3 that the delamination occurs suddenly and no distinct delamination evolution appears, which is in conformity with the conclusion by Campilho et al. [29] and Hu and Soutis [33]. At the same cohesive strength and delamination fracture toughness, the exponential CZM gives a higher debond load than the bilinear CZM, which is explained by a longer fracture process zone for the exponential CZM than for the bilinear CZM [29]. The convergence for the exponential CZM is better than for the bilinear CZM, because the sharp transition at the peak point in the bilinear CZM requires more iterations to reach equilibrium. In addition, Fig. 2 also shows that the effect of mesh size on the convergence is small, which implies that the coarse-mesh model is fine enough to guarantee the convergence and accuracy. From Fig. 3, it is evident the debond load increases, but the convergence is affected adversely when the cohesive strengths T c1  = T c2 increase, which was also found by Alfano and Crisfield [5], Turon et al. [22] and Liu and Islam [14]. From a numerical analysis, it follows that a delamination will not occur at T c1  = T c2 > 200 MPa for the exponential CZM and at T c1  = T c2 > 150 MPa for the bilinear CZM. Turon et al. [22] pointed out that a low cohesive strength represents the softening properties of the fracture process zone more accurately, although the stress distribution may be altered. In terms of convergence, the values of T c1  = T c2 > 80 MPa are not suggested, according to the present analysis.

From a numerical analysis,it follows that the computational time at different values of c using the exponential CZM is almost the same, but it decreases by 20% at c = 0.01 compared with that at c = 0.0001 when using the bilinear CZM. In addition, c has to increase to get convergent solutions when the cohesive strengths T c1  = T c2 are higher than 60 MPa in the bilinear CZM. Figure 4 illustrates the debond loads at the initiation of delamination for the SLJ case predicted by using two mesh models and two CZMs at T c1  = T c2 =20-80 MPa. Kim et al. [34] and Liljedahl et al. [35] studied, both experimentally and numerically, the delamination of adhesive composite joints with different adhesive materials and found that the debond loads in ductile and brittle delaminations were different. From Fig. 4, it is seen that the debond load increased greatly when the cohesive strength rose from 20 to 80 MPa, but the increase slowed down with growing cohesive strength. Thus, the values of T c1  = T c2 = 40-80 MPa turned out to be a good choice for achieving an excellent convergence and accuracy for the current adhesive material. Figure 5 shows delamination results for the SLJ at displacements of 0.584 mm (initiation of delamination) and 0.621 mm (complete delamination).

Fig. 4
figure 4

Debond loads P pred of SLJ predicted by models with coarse (1, 3) and fine (3, 4) meshes for the exponential (1, 2) and bilineat (3, 40 CZMs.

Full size image
Fig. 5
figure 5

Delaminations of SLJ at tensile displacements of 0.584mm (initial delamination) (a) and 0.621mm (complete delamination) (b).

Full size image

5.2. Delamination results for a composite skin/stiffener panel under tension

Figure 6 shows a composite skin/stiffener panel encountered in airplane structures. Material parameters and geometric sizes are taken from Krueger and O’Brien [30] and Turon et al. [7], see Table 1. The lay-up patterns of the skin and stiffener are [0/45/90/–45/+45/–45/0]s and [45/90/–45/0/90]s, respectively. The value of η =1.45 in Eq.(1) was taken from Turon et al. [7], who used the bilinear cohesive model to study the delamination of skin/stiffener panels. Orifici et al. [36] studied the delamination growth of skin/stiffener panels by using the virtual crack closure technique (VCCT) proposed by Rybicki and Kanninen [37]. Although the VCCT allows one to calculate the energy release rate and predict the crack propagation efficiently, crack initiation cannot be predicted.

Fig. 6
figure 6

Schematic of a composite skin/stiffener panel: 1 — extensometer. Dimensions in mm..

Full size image
Table 1 Material Parameters of IM6/3501-6 Composites [30, 7]
Full size table

Two mesh models were used: with 720 solid and 240 cohesive elements for the coarse model and 960 solid and 360 cohesive elements for the fine one. Figures 7 and 8 compare the effect of cohesive strengths for two CZMs. As seen, the load curves given by the two mesh models for the exponential CZM are close, but they slightly differ from those in the case of the bilinear CZM. For the exponential CZM, both mesh models show the same convergence. However, the difference between convergences becomes greater for the mesh models in the case of the bilinear CZM when the cohesive strengths T c1  = T c2 increase. For example, the difference for the computational CPU time at T c1  = T c2 < 40 MPa is 20%, but it is about 40% at T c1  = T c2 = 40-80 MPa. The effect of mesh sizes on the convergence is more distinct for the bilinear CZM than for the exponential CZM, and the computational CPU time with the fine mesh model is twice that with the coarse one.

Fig. 7
figure 7

Load–displacement curves P–Δ of the composite skin/stiffener panel obtained by models with coarse (■, □, ×) and fine (▽, ◊, ▷) meshes for the exponential (a) and bilinear (b) CZMs at T c1  = T c2  = 20 (■, ▽), 40 (□, ◊), and 60 MPa (×, ▷).

Full size image
Fig. 8
figure 8

Debond loads P pred of the composite skin/stiffener panel predicted by models with coarse (1, 3) and fine (2, 4) meshes for experimental (1, 2) and bilinear (2, 4) CZMs. 1 — the range of debond loads obtained experimentally in [7].

Full size image

From Fig. 7, it follows that high cohesive strengths T c1  = T c2 lead to a stronger interfacial bonding, and more energy is needed for propagation of the delamination crack at the same open displacement. However, convergence also becomes worse when the cohesive strengths increase. For the exponential CZM, the effect of the cohesive strengths T c1  = T c2 on the convergence is slow at T c1  = T c2 < 40 MPa, but it is improved at T c1  = T c2 > 40 MPa. For the bilinear CZM, the convergence is poor when the cohesive strengths T c1  = T c2 increase at T c1  = T c2 < 40 MPa, but gets better at T c1  = T c2 > 40 MPa. At T c1  = T c2 = 60 MPa, computational CPU time for the bilinear CZM is four times that for the exponential one. In addition, it is noted that too high or too low cohesive strengths T c1  = T c2 are not acceptable — high cohesive strengths worsen the convergence, while low ones lead to inaccurate results, see the case with T c1  = T c2 = 20 MPa in Fig. 7.

As follows from a numerical analysis, load curves are consistent at the values of c from 0.0001 to 0.01. Because the convergence in this case is poor, especially at the stage of delamination initiation, which requires many iterations and time cuts in the nonlinear FEA, the effect of viscous regularization for improving the convergence is distinct. In this case, the value of c = 0.0005 can meet the requirements of convergence and accuracy.

For this case, using the bilinear CZM, Turon et al. [7] adopted the normal strength T c3 = 61 MPa and the tangential strengths T c1  = T c2 = 68 MPa. However, they did not study the numerical convergence and computational efficiency. In this research, we compared the effect of the cohesive strengths T c1  = T c2 on the predicted debond loads, which is illustrated in Fig. 8. Figure 9 shows the process of delamination growth from its initiation at a 0.128-mm displacement to the complete delamination at a 0.184-mm displacement. The values of T c1  = T c2 = 68 MPa lead to accurate debond loads when the bilinear CZM is used. Chandra et al. [38] performed a parameter sensitivity analysis by using different CZMs for push-out tests and found the results given by the bilinear CZM were closer to experimental results than those obtained by the nonlinear CZM. However, they neglected the effect of cohesive strengths on load curves. Later, Volokh et al. [25] pointed out that the shape of different CZMs will affect the delamination fracture process at the same delamination fracture toughness and cohesive strength. Alfano [26] studied mode I and II delamination failure mechanisms by using four CZMs (bilinear, linear-parabolic, exponential, and trapezoidal), which were found to depend on the ratio between the stiffnesses of lamina and adhesive layer materials. As regards the ductile interface fracture in this case, Campilho et al. [29] showed that the length of process zone for the exponential CZM was greater than that for the bilinear CZM. Thus, the debond load predicted using the exponential CZM is larger than that given by the bilinear CZM at the same cohesive strength. In this case, the cohesive strengths T c1  = T c2 = 60-80 MPa for the bilinear CZM and T c1  = T c2 = 40-60 MPa for the exponential CZM are good choices if an excellent combination of convergence and accuracy is needed.

Fig. 9
figure 9

Delaminations in the composite skin/stiffener panel at displacements of 0.128 mm (initial delamination) (a), 0.140 mm (b), and 0.184 mm (complete delamination) (c) at T c1  = T c2 = 40 MPa. 1 — crack tip.

Full size image

6. Conclusions

CZMs have been widely used in investigating the delamination of composite structures. Unfortunately, there is still no unified CZMs able to represent the true fracture process zone under different loading conditions. Furthermore, the problem of numerical convergence emerges as a challenging issue when using CZMs in the implicit nonlinear FEA for simulating the delamination initiation and growth of composite adhesive joints.

In this paper, first 3D finite element codes are developed to implement the bilinear and exponential cohesive models for analyzing the delamination of composite adhesive joints using ABAQUS-UEL. Then, the influence of the cohesive shape and cohesive strength on the numerical convergence for a single-lap joint and a composite skin/stiffener panel under tension is studied. From a 3D FEA, four main conclusions are obtained: 1. In general, the bilinear CZM shows a worse convergence than the exponential CZM at the same cohesive strength, delamination fracture toughness, and mesh size. 2. A fine mesh size is needed to improve the convergence, especially for the bilinear CZM. 3. Relatively low cohesive strengths, e.g., T c1  = T c2 = 40-60 MPa in the exponential CZM and T c1  = T c2 = 60-80 MPa in the bilinear CZM for a SLJ and a skin/ stiffener panel, are recommended to achieve an excellent combination of convergence and accuracy. Higher cohesive strengths will worsen the numerical convergence, especially for the bilinear CZM. 4. The viscous regularization is shown to be an excellent method to improve the convergence. For a SLJ and a skin/stiffener panel, convergent solutions cannot be obtained without considering the viscous effects. From a numerical analysis, it follows that c = 0.0001-0.01 for a SLJ case and c = 0.0005-0.01 for a skin/stiffener panel are reasonable values. Finally, there should be an integrated consideration in weighting the convergence and the computational cost for selecting the cohesive shape, cohesive strength, and viscous parameters for a practical adhesive composite joint with a delamination failure.