1 Introduction

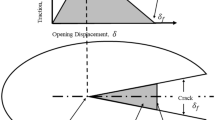
Due to the widespread use of composite laminates in various industries, it is very important to study and predict the possible failure modes in these materials [1,2,3,4]. A commonly occurring failure mode in composite laminates is delamination, which often occurs under mixed-mode I/II loading [5,6,7,8,9]. The delamination growth phenomenon is associated with the creation of a damaged zone around the crack tip called the fracture process zone (FPZ) [10,11,12,13,14]. Some toughening mechanisms in this zone, such as fiber bridging and micro-cracks formation, delay the fracture of engineering composite structures by absorbing energy, which shows the complexity of the fracture phenomenon in composite materials [15,16,17,18,19]. A simple method to quantify the effects of FPZ is the crack growth resistance curve or R-curve, which is a plot of the total dissipated energy as a function of the crack length [20,21,22,23]. Because of the presence of toughening mechanisms in the FPZ, linear elastic fracture mechanics (LEFM) is not suitable for predicting the crack growth in composite materials, and for this purpose, nonlinear fracture models are needed [24,25,26]. One of the nonlinear fracture mechanics approaches is cohesive zone model (CZM), which is based on the traction–separation laws [27,28,29]. The cohesive zone model was first proposed separately by Dugdale [30] and Barenblatt [31, 32] for studying plasticity at the crack tip. It has also been used by Hillerborg et al. [33] as a virtual crack model to analyze the crack growth in concrete. According to the efficiency of CZM, numerous attempts have been made to investigate the delamination phenomenon under different loading modes via this model and various softening shapes of CZM were developed by researchers [34,35,36,37]. In the study of mode I delamination growth in laminated composites, Sorensen et al. [38] and Tamuzs et al. [39] concluded that the bilinear CZM does not consider all FPZ toughening effects. They proposed a trilinear CZM that predicted the R-curve behavior well. Dávila et al. [40] obtained a mathematical expression for the crack growth resistance curve (R-curve) behavior of double cantilever beam (DCB) specimens using superposition of two linear softening laws. By using the same procedure, Heidari Rarani et al. [41] introduced a trilinear cohesive zone model superposed by two bilinear CZMs for simulation of mode I delamination growth in laminated composite. Shokrieh et al. [42] presented a multi-linear cohesive zone model to simulate the delamination growth under pure mode I loading. In their model, direct spring elements were used to consider the residual strength of the damaged material in the fracture process zone. In the study of delamination phenomenon in laminated composites under pure mode II loading, Ouyang [43] investigated the effect of five types of cohesive laws (equivalent linear elastic, bilinear, cubic, equivalent constant stress and exponential model) on shear fracture of an end-notched flexure (ENF) specimen using a nonlinear analytical solution. He concluded that the CZM shape has a relative influence on the critical load value in the case of short initial crack length. The trilinear cohesive zone model proposed by Heidari Rarani et al. has been extended to mode II delamination [44]. They considered four different traction–separation laws, whose shapes are bilinear, linear-exponential, trapezoidal, and trilinear, to study the delamination propagation of ENF specimens. Their results showed the superposed trilinear CZM can simulate the delamination propagation in ENF specimens more accurately than others. To model the delamination of laminated composites under mixed-mode I/II loading, De Morais et al. [45] employed finite element cohesive zone models with a bilinear softening cohesive law, which required a genetic algorithm to find optimal bilinear softening parameters. Fu and Wang [46] presented a three-linear CZM using superposition of two bilinear laws to simulate mixed-mode I/II delamination in composite laminates with large-scale fiber bridging. Their model had a good efficiency in predicting the delamination behaviors under both pure mode I and mixed-mode I/II loadings. A multi-linear CZ law was developed by Jensen et al. [47] to simulate mixed-mode delamination, but its applicability was demonstrated only by pure mode I delamination.

The studies reviewed above reveal that various shapes of softening law can have a significant influence on the analysis of crack growth problems via cohesive zone models. So that the most commonly used linear and bilinear softening laws are unable to predict the delamination behaviors of laminated composite in the presence of FPZ effects, and for this purpose, there is a need to provide multi-linear cohesive zone models. Such models remained limited in focus, dealing mostly with mode I delamination, and few studies have been conducted on mixed-mode I/II delamination. Therefore, this study aims to propose a multi-linear cohesive zone model to simulate the mixed-mode I/II delamination growth considering the effect of FPZ. To this end, the multi-linear CZM proposed for the mode I delamination growth by present authors [42] is extended to mixed-mode I/II delamination in this study and is also validated by the available experimental data in the literature. In the newly proposed model, called the extended multi-linear cohesive zone model (EML-CZ model), inclined spring elements with variable stiffness whose angle is proportional to the mixed-mode ratio are used to consider the FPZ effects. The EML-CZ model is implemented in a numerical method that works in combination with finite element results. In the following, an analytical relation is also presented to estimate the mixed-mode I/II delamination R-curve using the simulation results, and the obtained R-curves are compared with the available experimental R-curves at different mixed-mode ratios.

2 Extended multi-linear cohesive zone model

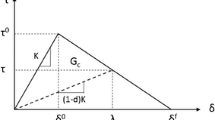
Considering the significant effects of the FPZ and related toughening mechanisms on the delamination growth in composite laminates, the extended multi-linear cohesive zone model (EML-CZ model) is proposed to simulate the initiation and propagation of mixed-mode I/II delamination. In the EML-CZ model, the residual strength of the damaged material in the FPZ considers by being placed inclined spring elements along the crack growth path and between two plies. As the crack starts to grow, the stiffness of the spring elements changes gradually according to the multi-linear traction–separation curve with an arbitrary number of line breaks in the softening zone (Fig. 1). The configuration of inclined spring elements along the crack growth path for a mixed-mode bending (MMB) specimen is shown schematically in Fig. 2.

Fig. 1
figure 1

Schematic of multi-linear traction–separation curve

Full size image
Fig. 2
figure 2

a Schematic of inclined spring elements along the crack growth path in a MMB specimen; b fiber bridging zone in a unidirectional MMB specimen

Full size image

The EML-CZ model algorithm is shown in Fig. 3. This algorithm for simulation of delamination growth in composite laminates under mixed-mode I/II loading is somewhat similar to the ML-CZ model, which is described in detail in [42]. One of the main differences is the angle of the spring elements, which is proportional to the mixed-mode ratio and is defined as

$$ \theta_{i} = Arc\cos \beta_{i} \begin{array}{*{20}c} , & {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {i = 1,2, \cdots ,t} \\ \end{array} $$
(1)

where \(\beta_{i}\) is the mixed-mode ratio, \(\theta_{i}\) is the angle of the spring elements and \(t\) is number of mixed-mode ratios.

Fig. 3
figure 3

The simulation algorithm of the EML-CZ model

Full size image

As shown in Fig. 3, another difference is that the EML-CZ model algorithm requires the material’s traction–separation curve in each desired mixed-mode ratio (\(\beta_{i}\)) as an input. For any given \(\beta_{i}\), the equivalent traction–separation law (TSL) is derived from the interpolation of pure mode I and pure mode II traction–separation laws and having the degree of mode-mixity (\(\theta_{i}\)). The interpolation formulas are based on quadratic stress interaction and are energy consistent with the modified Benzeggagh-Kenane (B-K) fracture criterion. More details about this procedure can be found in [47].

After calculating the angle of the spring elements and extracting the traction–separation curve for a given value of \(\beta_{i}\), a finite element model is prepared by ANSYS software to simulate a MMB specimen. The necessary inputs for the EML-CZ model algorithm, which are extracted from the traction–separation curve and the finite element model, are introduced in Table 1.

Table 1 The necessary inputs for the EML-CZ model algorithm
Full size table

According to Fig. 3, the algorithm is implemented in a step-by-step approach. So that in the first step, a unit load (\(P_{{{\text{unit}}}}\)) is applied to the MMB specimen, and the equations system is solved under this loading. Then, by defining a proportionality coefficient (\(\alpha_{{{11}}}\)) according to Eq. (2), the amount of load that creates a force equal to the maximum tensile strength in the first spring is calculated.

$$ \alpha_{11} = \frac{{T_{{0}} }}{{\sigma_{11} }} $$
(2)

where \(T_{0}\) is the maximum tensile strength according to the traction–separation curve and \(\sigma_{11}\) is the stress of the first spring at the first step extracted from the finite element model. Then, by applying the load resulting from multiplying this coefficient in the load of the previous step, the fracture process zone is being formed ahead of the crack tip. Therefore, the spring that had reached the maximum tensile strength can still bear the load and its stiffness should be changed according to the traction–separation curve as follows:

$$ k_{11} = \frac{{\Delta T_{1} }}{{\Delta \delta_{1} }}A_{1} $$
(3)

where \(k_{11}\) is the stiffness of the first spring (spring with the maximum tensile strength) at the first step, \(\Delta T_{1}\) is the difference between the tensile strength of break points in the first line break of the softening zone, \(\Delta \delta_{1}\) is the separation difference corresponds to \(\Delta T_{1}\), and \(A_{1}\) is the surface area on which the first spring is applied.

In the second step and onwards, two events are likely to happen: either another spring reaches the maximum tensile strength (such as the first step) or the spring involved in the FPZ reaches a break point (boundary of two line breaks with different slopes) in the softening zone of the traction–separation curve. In each step, the coefficients corresponding to both of these events should be calculated by:

$$ \begin{gathered} \alpha_{mm} = \frac{1}{{\sigma_{mm} }}\left( {T_{0} - \sum\limits_{i = 1}^{m - 1} {\alpha_{ii} \sigma_{mi} } } \right) \hfill \\ \alpha_{nm} = \frac{1}{{\sigma_{nm} }}\left( {T_{{\begin{array}{*{20}c} {{\text{last}}} & {{\text{break}}} \\ \end{array} }} - \sum\limits_{i = 1}^{m - 1} {\alpha_{ii} \sigma_{ni} } } \right)\begin{array}{*{20}c} , & {} & {n < m} \\ \end{array} \hfill \\ \end{gathered} $$
(4)

In general, the first index (\(n\)) is the spring element counter and the second one (\(m\)) is the step counter. After calculating all proportionality coefficients in each step, the one with minimum absolute value is selected and the algorithm is repeated. When the spring element reaches the maximum separation in the traction–separation curve, it is removed from the model and its stiffness value is considered zero. This process continues until the last spring element in the FPZ reaches the final break point (maximum separation point) in the softening zone of the traction–separation curve. At the end of each step, the values of load and displacement in the direction of spring elements are recorded from finite element model. Finally, all steps should be repeated for different mixed-mode ratios. The output of the EML-CZ model will be obtained as the load–displacement curves for each mixed-mode ratio.

3 Analytical assessment of R-curve behavior

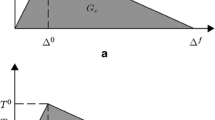
In composite laminates, the fracture process zone around the delamination crack tip involves some toughening mechanisms which cause increasing fracture resistance as the crack grows, i.e., R-curve behavior. Estimation of a mathematical equation that can express the change of the crack growth resistance (\(G_{{\text{R}}}\)) as a function of crack extension (\(\Delta a\)) is so important because using it, there is no need to do costly or time-consuming tests to calculate the fracture toughness of complex parts. In this section, an analytical relation is presented to estimate the mixed-mode I/II delamination R-curve based on potential energy stored as a result of the deformation of the inclined spring elements that simulated the FPZ in the EML-CZ model.

In general, according to the concept of the R-curve, the total strain energy release rate (\(G_{{\text{R}}}\)) for each crack extension is obtained from the sum of the strain energy release rate at delamination initiation (the fracture initiation toughness, \(G_{i}\)) and the strain energy release rate related to the FPZ or dissipated energy due to the toughening mechanisms in the FPZ (FPZ toughness, \(G_{{{\text{FPZ}}}}\)). After crack growth and reaching a certain crack extension, this energy reaches a constant value, which is called steady-state fracture toughness (\(G_{{{\text{ss}}}}\)). According to the maximum strain energy release rate criterion, the crack grows when the total strain energy release rate (\(G_{{\text{R}}}\)) reaches its critical value (\(G_{{\text{C}}}\)). The value of these three strain energy release rates should be calculated in order to extract an analytical model for the R-curve.

According to the EML-CZ model, delamination initiation occurs when the first spring element placed in the delamination crack tip reaches the final break point in the softening zone of the traction–separation curve. Therefore, the delamination initiation toughness (\(G_{i}\)) can be obtained from the summation of the elastic potential energy of the first spring element for all existing line breaks in the softening zone.

In the R-curve, the difference between the delamination initiation toughness and the steady-state fracture toughness is called the toughness caused by the fracture process zone, and the corresponding length is the FPZ length (\(L_{{{\text{FPZ}}}}\)). To calculate the energy dissipated by the toughening mechanisms in the FPZ, the following questions should be considered:

  1. 1.

    How many spring elements are involved in the FPZ for each value of the crack tip separation?

  2. 2.

    How many line breaks in the softening zone of the traction–separation curve have been crossed by each spring element?

  3. 3.

    On what slope of the softening zone of the traction–separation curve have been each spring element placed?

At any moment, the FPZ toughness (\(G_{{{\text{FPZ}}}}\)) can be obtained from the summation of the elastic potential energy of each of these spring elements at the same time.

When the FPZ is present, the R-curve starts at an initiation value and then increases to a steady-state value. This increase is the result of the development of the fracture process zone. The flat part at the end of the R-curve indicates that the effect of the existing toughness mechanisms in the FPZ is not permanent, but the fracture toughness reaches a constant value after the fully developed FPZ. According to the EML-CZ model, the stable crack growth will occur when the last spring element in the FPZ reaches the final break point (maximum separation point) in the softening zone of the traction–separation curve. Hence, the steady-state fracture toughness (\(G_{{{\text{ss}}}}\)) is obtained from the summation of the elastic potential energy of all spring elements in the FPZ when each of them passes through all the line breaks in the softening zone of the traction–separation curve.

Now, taking into account the explanations mentioned above, a mathematical relation is presented to estimate the mixed-mode I/II delamination R-curve. According to the R-curve behavior and also the investigation of various mathematical functions, the simplest function is a quadratic function in terms of crack extension when \(\Delta a < L_{{{\text{FPZ}}}}\). By applying the boundary conditions (i.e., the delamination initiation point (\(0,G_{i}\)), the delamination propagation point (\(L_{{{\text{FPZ}}}} ,G_{{{\text{ss}}}}\)), and Flattening the curve at the delamination propagation point (\(G_{{\text{R}}}^{\prime } \left( {L_{{{\text{FPZ}}}} } \right) = 0\))) in the general form of a quadratic function, we have:

$$ G_{{\text{R}}} \left( {\Delta a} \right) = \left\{ {\begin{array}{*{20}l} {Z + 2\left( {Q - 1} \right)Z\left( {\frac{{\Delta a}}{{L_{{{\text{FPZ}}}} }}} \right) + (1 - Q)Z\left( {\frac{{\Delta a}}{{L_{{{\text{FPZ}}}} }}} \right)^{2} } \hfill & {\Delta a < L_{{{\text{FPZ}}}} } \hfill \\ {QZ} \hfill & {\Delta a \ge L_{{{\text{FPZ}}}} } \hfill \\ \end{array} ,} \right.Z = \sum\limits_{{j = 1}}^{X} {\frac{1}{2}k_{j} \Delta \delta _{j}^{2} } $$
(5)

where \(Q\) is the number of spring elements in the FPZ, \(X\) is the number of line breaks in the softening zone of the traction–separation curve, \(k_{j}\) is the stiffness of spring elements (the slope of line breaks in the softening zone), \(\Delta \delta_{j}\) is the difference between the separation of break points in the traction–separation curve, \(\Delta a\) is the crack extension, and \(L_{{{\text{FPZ}}}}\) is the FPZ length.

The only required parameters of the analytical model presented in Eq. (5) to estimate the mixed-mode I/II delamination R-curve are as follows:

  • Material’s traction–separation curve in each desired mixed-mode ratio

  • Length of the fracture process zone

  • Number of spring elements in the FPZ (obtained from the EML-CZ model)

4 Results and discussion

The EML-CZ model is implemented through a user-defined material code in Matlab along with a finite element modeling in ANSYS2021-R1 to simulate a MMB specimen. SOLID185 element and COMBIN14 element have been used to model the MMB specimen and the springs, respectively. Inclined spring elements with the angle proportional to the desired mixed-mode ratio have been placed along the crack growth path and between two plies. The meshing sensitivity analysis has been performed to obtain the optimum meshing for the simulation and the hexahedral mapped mesh is selected. Also, the result of the sensitivity analysis showed that at least twenty-four spring elements should be placed in the crack growth path for convergence. The boundary and loading conditions followed the guidelines given by ASTM D6671 [48] in which the MMB specimen is constraint with a pinned support at one end and a roller support at the other end. A lever is used to load the MMB specimen in such a way that by applying an upward load at the end of the lever and a downward load at the center of the specimen, a mixed-mode loading condition is obtained. Moreover, different mixed-mode ratios can be simulated by varying the length from the point of load application to the mid-point of the specimen.

Experimental results available in [49], have been used to validate the EML-CZ model in which MMB specimens have been made of 18-ply unidirectional E-glass/Epon-826 laminate. The material properties of laminated composite are given in Table 2. The specimens have 180 × 25 × 4.1 mm dimensions and a pre-crack length of 25 mm. According to available experimental data in [49], three mixed-mode ratios (\(\beta_{i}\)) defined as the ratio of mode II strain energy release rate (SERR) over the total SERR, i.e., GII/G = 0.25, 0.5 and 0.75 have been used to implement EML-CZ model. The material’s traction–separation curves for these three mixed-mode ratios are shown in Fig. 4. These curves have been derived from the interpolation method described in detail in [47] from the traction–separation curves of pure mode I and pure mode II [50, 51].

Table 2 Material properties of unidirectional E-glass/Epon-826 laminated composite [49]
Full size table
Fig. 4
figure 4

Extracted traction–separation curve for a \(\beta = 0.25\), b \(\beta = 0.50\) and c \(\beta = 0.75\)

Full size image

In Fig. 5, the results of the EML-CZ model as the load–displacement curves under three different mixed-mode ratios are compared with the available experimental data [49] and the linear elastic fracture mechanics (LEFM) curve. The theoretical LEFM solution for the relation between the applied load and the lever displacement is described in [52].

Fig. 5
figure 5

Load–displacement curves obtained by the EML-CZ model in comparison with the experimental data [49] and the LEFM solution for three different mixed-mode ratios

Full size image

Also, a comparison between the magnitudes of the maximum load obtained by the proposed model and the experimental values in three different mixed-mode ratios is given in Table 3. As it can be seen, a good agreement between the results of the proposed EML-CZ model and the available experimental data has been generally obtained and the extracted load–displacement curves ultimately converge to the LEFM solution. The predicted maximum load is lower than the LEFM solution, which reflects the formation of FPZ before the steady-state propagation in delamination growth simulation using the proposed cohesive approach.

Table 3 A comparison between the maximum load values obtained by the EML-CZ model and the available experimental data in three different mixed-mode ratios
Full size table

To highlight the effectiveness of the EML-CZ model by applying the multi-linear traction–separation law, the algorithm has been implemented using three different softening laws including linear, bilinear, and trilinear softening laws for the MMB specimen with a mixed-mode ratio of 0.25. The obtained results in comparison with the available experimental results are shown in Fig. 6. According to Fig. 6, there is a significant difference between the load–displacement curve obtained from the linear softening law and the experimental data. This difference indicates that in this case, the all load carrying capacity of the specimen has not been used and the fracture load is predicted to be much lower than its actual value. By considering the bilinear softening law, the results were greatly improved. But in the case of the trilinear softening law, the best agreement with the experimental results has been achieved. It is concluded that by increasing the number of the line breaks in the softening zone of the traction–separation curve up to a certain number, the residual strength of the material in the FPZ can be considered and more accurate results can be predicted. This capability is so important in predicting the mixed-mode I/II delamination growth in composite laminates with R-curve effects and the EML-CZ model presented in this study provides this possibility.

Fig. 6
figure 6

A comparison between load–displacement curves obtained by the EML-CZ model with linear, bilinear, and trilinear softening laws and the available experimental data [49]

Full size image

In the following, the R-curve behavior of the MMB specimens in several mixed-mode ratios has been extracted from Eq. (5) and compared with the available experimental R-curves to evaluate the validity and the accuracy of the presented analytical model for the R-curve. The experimental results of the R-curve were obtained from [53], in which the MMB specimens were made of 12-ply unidirectional E-glass/Epon-826 composites and were tested under three mixed-mode ratios, i.e., GII/G = 0.33, 0.5 and 0.67. The analytical R-curves are plotted in Fig. 7 and compared with the available experimental data in these three mixed-mode ratios. Also, a comparison between the values of the analytical steady-state delamination toughness and the experimental values is given in Table 4. The comparison of the results clearly indicates that the results are in good agreement with the experimental data. Therefore, the new analytical model presented for the R-curve in the present study is able to accurately estimate the R-curve behavior of composite laminates in mixed-mode I/II delamination.

Fig. 7
figure 7

Analytical R-curves in comparison with the experimental data [53] for three mixed-mode ratios

Full size image
Table 4 A comparison between the analytical steady-state delamination toughness values and the experimental data for different mixed-mode ratios
Full size table

5 Conclusions

The purpose of the present study was to introduce the “extended multi-linear cohesive zone model” instead of employing the most commonly used linear and bilinear CZMs to simulate the mixed-mode I/II delamination growth in laminated composites. In the newly proposed model, called EML-CZ model, the FPZ effects were simulated by being placed inclined spring elements with an angle proportional to the mixed-mode ratio along the crack growth path. As the crack grows, the stiffness of spring elements changed gradually according to the multi-linear traction–separation curve. So, the EML-CZ model can cover all FPZ effects in the mixed-mode I/II delamination growth through applicability of implementing any arbitrary shape of softening behavior in the damaged area.

The main results obtained from this paper are as follows:

  • The load–displacement curves under different loading modes extracted from simulation were in good agreement with experimental ones.

  • Due to the existence of several types of toughening mechanisms with different strain energy release rates in the FPZ, the EML-CZ model is able to accurately predict the mixed-mode I/II delamination growth in composite laminates by increasing the number of line breaks in the softening zone. And, this is one of the main advantages of the newly presented model compared to other existing models and software capabilities.

  • The applicability of the EML-CZ model was evaluated to estimate the R-curve behavior of laminated composites in mixed-mode I/II delamination. For this purpose, an analytical relation was presented to estimate the mixed-mode I/II delamination R-curve based on potential energy of the inclined spring elements that simulated the FPZ in the EML-CZ model. This analytical model for the R-curve is a simple relationship that does not require complex parameters.

  • A good agreement was obtained between the R-curves extracted by the new model and the available experimental R-curves at different mixed-mode ratios.

The simulation algorithm of the EML-CZ model in combination with the presented analytical model for the R-curve can be used to accurately predict the mixed-mode I/II delamination growth in composite laminates.