1 Introduction

Numerical predictions of the mechanical behavior of titanium and alpha–beta titanium alloys Ti6Al4V—also known as Ti64, Ti Gr.5 or TA6V—are commonly used for the design of lightweight and high-performance components in aerospace, automotive, medical, transport industries, among others [1,2,3]. Nowadays, significant efforts have been made to accurately model part behavior until fracture, especially where structural components are concerned [4]. The mechanical behavior of the Ti6Al4V alloy shows complex plastic features, such as the tension–compression asymmetry, as known as the strength differential (SD) effect associated with twinning [5, 6], and the distortional hardening describing evolving plastic anisotropy [7, 8]. The yield strength of this alloy, as with other titanium alloys, is sensitive to both the temperature and the strain rate as its deformation mechanisms are thermally activated [9,10,11].

The most commonly used macroscopic constitutive model applied in finite element (FE) simulations of titanium alloys at room temperature is still the classical anisotropic yield criterion Hill’48 with a conventional isotropic hardening approach [12, 13]. However, more advanced models have been developed. For instance, the non-quadratic orthotropic yield functions based on multiple linear transformations Yld2011-18p and Yld2011-27p identified and validated by Aretz and Barlat [14]. Both models rely on a large number of material parameters (18 and 27, respectively) and are able to predict the earing profile in a cup-drawing test. Another model accurately representing the mechanical features of hcp materials [15] is the orthotropic yield criterion CPB06 proposed by Cazacu et al. [16], which also involves a large number of parameters. The experimental information available in the literature for the identification of the models is primarily based on uniaxial tension and/or compression tests or biaxial loading [17,18,19]. Khan et al. [20] identified and validated the orthotropic CPB06 yield criterion for the Ti6Al4V alloy and its parameters were set based on uniaxial loading conditions. Holmen et al. [21] studied several age hardened aluminum alloys showing the SD effect and calibrated a Drucker–Prager model with uniaxial tensile and compression stress–strain curves; their validation was done by comparing the load obtained from numerical simulations with experimental data of pre-notched diabolo tension and compression tests. Lee et al. [22] proposed a new model to describe the evolution of the yield surface by coupling of quadratic and non-quadratic yield functions with a non-associated flow rule. The data used for validation was the anisotropic hardening and the curvature of the yield surface of AA6181-T4. In order to choose the most suitable material model for any alloy, several scientists [23,24,25,26,27] have validated the constitutive laws with samples or parts showing different stress–strain conditions than the one used to initially characterize the models.

The current research investigates the limits of the simple Hill’48 criterion and the more advanced CPB06 model for the Ti6Al4V alloy, and is focused on associative plastic models. To quantify the prediction errors generated by these choices, different loading conditions are considered and the focused is on the full plastic strain range, from the plasticity entrance to the plastic post-necking behavior of a bulk Ti6Al4V sample (Fig. 1). Hereafter, the experimental campaign used to identify the material anisotropic behavior consists of monotonic tensile and compression tests in three orthogonal directions as well as, plane strain, and simple shear tests in one plane. The first model identification method described in Tuninetti et al. [28] was restricted to a plastic strain lower than 0.1. The present work extends the plastic strain range up to 0.2 to define a reference stress–strain curve modeled by a Voce law closer to the real behavior. The experiments used for the model evaluation (Fig. 2) cover different triaxialities; the values ranges from 0.4 to 1.2 for the tensile tests of notched samples of radii 5 mm or 1.5 mm, respectively, and higher local values for the V notch. Specimens with a through-hole for tensile loading and an elliptical cross-section for compressive loading (reaching an axial strain of 0.2 and showing barreling) complete the experimental campaign. Accurate force curves measured by load cells and displacement fields measured by digital image correlation (DIC) allow for a thorough comparison between the test campaign and the FE predictions. The Lagamine FE code developed at University of Liège since 1984 is used for the simulations [29, 30]. This nonlinear software adapted for large elastoplastic deformations uses implicit analysis to predict the mechanical behavior of materials including Cauchy stress, logarithmic strain, and displacements by several constitutive laws implemented by researchers during more than 30 years to model the behavior of metals, rocks and soils [31,32,33,34]. Each constitutive law has been implemented with an optimal integration scheme depending on the rheological model [35, 36].

Fig. 1
figure 1

a Material directions of the bulk Ti6Al4V alloy. b Experimental true stress-true strain curve for the LD direction and Voce type hardening law identified with data obtained by an extensometer (pre-necking) and DIC after the onset of necking (post-necking)

Full size image
Fig. 2
figure 2

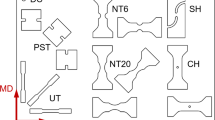
Geometries (A, B, C, D, E, F) and dimensions of the respective samples: round bars in the LD direction with a through hole, a V-notch, two notches of radii 1.5 mm and 5 mm, smooth with necking for tensile loading, and elliptical cross-section specimen in the LD direction for compressive loading with barreling

Full size image

Large strain values (higher than the one observed at the onset of necking) are obtained and sensitivity analyses are used to evaluate the influence of the reference stress–strain curve accuracy, anisotropic yield locus shape, distortional hardening, and the SD effect on the numerical prediction of the mechanical response of Ti6Al4V alloy until fracture. To this end, three material models are identified and their predictions of the load–displacement curve and the displacement field for tests involving multiaxial strain states and several values of stress triaxiality until fracture are compared with the experimental data. The first model is based on the well-known orthotropic yield criterion CPB06 with distortional hardening implemented in the Lagamine code by Gilles [35]; the second model is the anisotropic Hill’48 with distortional hardening; and the third model is the classical anisotropic Hill’48 with isotropic hardening as described by a Voce-type law. Distortional hardening for CPB06 and Hill’48 is modeled by linear interpolation of continuous yield surfaces identified at five plastic work levels. This approach allows describing different hardening rates in tension, compression, and shear. This research aims to provide a recommendation of the most suitable plasticity model for designing bulk Ti6Al4V parts that are expected to work at room temperature and low strain rates.

Section 2 of this paper presents the CPB06 and Hill’48 phenomenological yield functions and both isotropic and distortional hardening models. Section 3 identifies the properties of the Ti6Al4V alloy, provides a synthetic summary of the experimental tests, and provides material parameter set of each model. The comparison between the model yield loci and the experimental points extracted from monotonic tests is subsequently presented in Sect. 4; meanwhile, Sect. 5 focuses on analysis of the accuracy of the material model predictions for different complex loading states. Finally, Sect. 6 summarizes the main conclusions. In addition, “Appendix” provides the required equations for the mathematical transformation of the orthotropic yield criterion CPB06 into the anisotropic Hill’48.

2 Plasticity models

The three models compared are presented hereafter as, CPB06, Hill*, and Hill respectively. The CPB06 model is based on the orthotropic yield criterion developed by Cazacu et al. [16] with distortional strain hardening. The second model (Hill*) is based on the Hill’48 yield criterion with distortional strain hardening, while the third model (Hill) is the classical Hill yield locus coupled with a Voce-type isotropic strain hardening law.

2.1 CPB06 orthotropic yield criterion

The selected macroscopic orthotropic yield criterion CPB06 proposed by Cazacu et al. [16] describes both tension/compression asymmetry and anisotropic behavior. The equivalent stress is defined by:

$$\bar{\sigma } = B\left\{ {\left( {\left| {\varSigma_{1} } \right| - k\,\varSigma_{1} } \right)^{\,a} + \left( {\left| {\varSigma_{2} } \right| - k\,\varSigma_{2} } \right)^{\,a} + \left( {\left| {\varSigma_{3} } \right| - k\,\varSigma_{3} } \right)^{a} } \right\}^{{\frac{1}{a}}}$$
(1)

where k is a parameter taking into account the SD effect; a is the degree of homogeneity; and \(\varSigma_{1} ,\)\(\varSigma_{2} ,\)\(\varSigma_{3}\) are the principal values of the tensor \({\varvec{\Sigma}}\) defined by \({\varvec{\Sigma}} = {\mathbf{C}}:{\mathbf{S}}\) where C is a fourth-order orthotropic tensor that accounts for the material plastic anisotropy and S is the deviator of the Cauchy stress tensor. The tensor C represented in Voigt notations is defined as follows:

$${\mathbf{C}} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{13} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & {C_{23} } & 0 & 0 & 0 \\ {C_{13} } & {C_{23} } & {C_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right]$$
(2)

The material constant B is identified in such a way that \(\bar{\sigma }\) reduces to the yield stress in the reference direction of the material (“Appendix”), chosen as the Longitudinal Direction (LD) hereafter (Fig. 1a).

2.2 Hill’48 yield criterion

According to the Hill’48 yield criterion, the equivalent stress is defined by:

$$\bar{\sigma } = \left( {1/2\,{\varvec{\upsigma}}^{T} :{\mathbf{H}}:{\varvec{\upsigma}}} \right)^{{\frac{1}{2}}}$$
(3)

where:

$${\varvec{\upsigma}} = \left( {\begin{array}{*{20}c} {\sigma_{11} } \\ {\sigma_{22} } \\ {\sigma_{33} } \\ {\sigma_{12} } \\ {\sigma_{13} } \\ {\sigma_{23} } \\ \end{array} } \right)\;{\text{and}}\;{\mathbf{H}} = \left[ {\begin{array}{*{20}c} {G + H} & { - H} & { - G} & 0 & 0 & 0 \\ { - H} & {H + F} & { - F} & 0 & 0 & 0 \\ { - G} & { - F} & {F + G} & 0 & 0 & 0 \\ 0 & 0 & 0 & {2N} & 0 & 0 \\ 0 & 0 & 0 & 0 & {2L} & 0 \\ 0 & 0 & 0 & 0 & 0 & {2M} \\ \end{array} } \right]$$
(4)

such that F, G, H, N, L, M are material parameters that account for the plastic anisotropy.

2.3 Isotropic hardening

The hereafter called Hill model is based on the anisotropic yield criterion Hill’48 defined by Eqs. (3) and (4) combined with an isotropic hardening Voce-type law:

$$\sigma_{y} \left( {\bar{\varepsilon }_{p} } \right) = A_{0} + B_{0} \left[ {1 - \exp \left( { - C_{0} \bar{\varepsilon }_{p} } \right)} \right]$$
(5)

where \(\bar{\varepsilon }_{p}\) is the equivalent plastic strain, \(A_{0}\) is the initial yield stress, and \(B_{0}\) and \(\,C_{0}\) are the isotropic hardening saturation value and rate, respectively. The material constants \(A_{0}\), \(B_{0}\), and \(\,C_{0}\) are computed in this study from the tensile curve along the reference LD direction (Fig. 1b). Note that \(\sigma_{y}\) denotes the threshold stress whose evolution describes the size of the yield surface during plastic deformation.

2.4 Distortional hardening

Distortional hardening is applied to the CPB06 and Hill* models by determining anisotropy parameters of several yield surfaces corresponding to different levels of accumulated plastic work. By using a piece-wise linear interpolation, moreover, it is possible to obtain the yield surface corresponding to any level of accumulated work. More details can be found in [35]. The updated yield locus is described by:

$$f\left( {{\varvec{\upsigma}},\bar{\varepsilon }_{p} } \right) = \bar{\sigma }\left( {{\varvec{\upsigma}},\bar{\varepsilon }_{p} } \right) - \sigma_{y} \left( {\bar{\varepsilon }_{p} } \right)$$
(6)

For any equivalent plastic strain (\(\bar{\varepsilon }_{p}\)), the plastic work per unit volume is given by:

$$W_{p} \left( {\bar{\varepsilon }_{p} } \right) = \int_{0}^{{\bar{\varepsilon }_{p} }} {\sigma_{y} \left( {\bar{\varepsilon }_{p} } \right)\,} d\bar{\varepsilon }_{p} = \left( {A_{0} + B_{0} } \right)\bar{\varepsilon }_{p} - \frac{{B_{0} }}{{C_{0} }}\left( {1 - \exp \left( { - C_{0} \bar{\varepsilon }_{p} } \right)} \right).$$
(7)

The yield surface parameters (i.e., the anisotropy coefficients for the Hill* and CPB06 models and the SD parameter, k, for the CPB06 model) evolve as a function of the plastic work per unit volume \(W_{p}\). They are determined for several levels of \(W_{p} :\)\(W_{p}^{\left( 1 \right)} < \cdots < W_{p}^{\left( j \right)} < \cdots < W_{p}^{\left( m \right)}\), \(j = i \ldots m\), where \(W_{p}^{\left( 1 \right)}\) corresponds to the initial yielding and \(W_{p}^{\left( m \right)}\) corresponds to the highest level of plastic work reached during the experimental test before necking. For each of the individual plastic work levels, \(W_{p}^{\left( j \right)}\), \(\bar{\sigma }\) is calculated using Eq. (1) for the CPB06 model or Eq. (3) for the Hill* model. The yield surface corresponding to an intermediate level of plastic work (\(W_{p}^{\left( j \right)} \le W_{p} \le W_{p}^{{\left( {j + 1} \right)}}\)) is determined by linear interpolation.

3 Experimental procedures and materials

The forged Ti6Al4V bulk material used in this study has an α-phase volume of 94% and ellipsoidal grains with an average size of about 12 µm in the longest dimension. The bulk geometry and the reference frame are identified in Fig. 1a. The three orthogonal material directions are longitudinal (LD), transverse (TD) and short transverse (ST). A tensile test performed according to EN 10002-5:1992 at constant strain rate equal to 10−3 s−1 was used to generate the experimental stress–strain curve shown in Fig. 1b. The collection of accurate data above a strain of 0.1 requires DIC measurements as a necking zone appears at this plasticity level. These data are used for identification of the models.

Porosity measurements via optical microscopy can detect voids with dimensions larger than 0.6 μm. The initial porosity (area fraction) found from these measurements on the as-received alloy was 0.003%, and the maximum value of porosity near the crack of the fractured tensile samples was 0.8%.

The specimen geometries used for model validation are shown in Fig. 2. Tensile loading is applied on round bars (Fig. 2) with a through O-hole (geometry A), a V-notch (geometry B), and U-notches with radii R5 and R1.5 mm (geometries C and D, respectively). Furthermore, an initial elliptical cross-section specimen (geometry E), first proposed by Tuninetti et al. [37], is subjected to compressive loading. Friction between the press plates and the sample induces barreling and subsequently triaxial loading.

The tensile tests are carried out using a 100 kN electromechanical universal testing machine manufactured by Zwick. The axial displacements of the specimens are obtained by using an extensometer with 40 mm gauge length. The compression tests are performed using a servo-hydraulic testing machine. Both machines are controlled to achieve a low strain rate equal to 10−3 s−1.

Around 70% of the free surface of all the specimens are captured by three CCD cameras. The evolution of both, the major strain field and the sample geometry are computed with 3D DIC. The cross-section evolution of the samples is obtained with a procedure described by Tuninetti et al. [38]. The DIC allows measurement of the local surface strain at the necking area until fracture for the different shapes.

4 Parameter identification of the three material models

The tensile elastoplastic behavior of the Ti6Al4V alloy in the pre-necking region (with maximum strain of 0.1) has been previously characterized by Tuninetti and Habraken [7] and Tuninetti et al. [28] in the three orthogonal directions of the material (LD, TD, and ST).

In these previous studies, the orthotropic yield criterion CPB06 was identified by FE inverse modeling. The simulations covered the stress–strain data (Fig. 1c) of monotonic tensile homogeneous tests in the LD, TD and ST directions, shear and plane strain tests in the LD–ST plane; and the full-field strain measurements for compression tests in the LD, TD and ST directions. Note that these compression tests were not homogeneous due to anisotropy and the barreling effect. A sensitivity analysis for the identification method of the CPB06 yield locus based on a variable number of tests was proposed in [28] while the present article focuses on the prediction sensitivity of FE simulations describing heterogeneous tests. The research quantifies the effect of the reference stress–strain curve accuracy and of the choice between the CPB06 and Hill models as well as between distortional and isotropic hardening models.

While the set of anisotropy parameters (Cij) associated with the plastic work level of the CPB06 identification are recovered from CPB06(IJP) [28] (Table 1), the true stress-true strain curves for the full plastic strain range (even after the onset of necking) is based on [39]. LD tensile tests that are performed until fracture on smooth samples using a 3D DIC system allow the local strain and the cross-section within the localized zone of the specimens to be obtained [39]. The former and new strain hardening Voce law for the tensile reference direction LD are shown in Fig. 1b and the associated set of parameters are provided in Table 2. Finally, the FE-based inverse approach is applied to fully characterize the material model CPB06, and a new set of tension–compression asymmetry parameters k is obtained for the five levels of plastic work (Table 1). As highlighted in Sect. 1, the tensile experimental campaign used for validation, as shown in Fig. 2, is not included in the experiments used for identification. For compression, plastic strains above 0.1 are included in the experimental results for validation. It should be noted that the only difference between CPB06 (IJP) and the current CPB06 model is the distortional hardening represented by a different set of Voce (LD tensile reference curve) and SD parameters (k).

Table 1 Anisotropy coefficients [28] used in the CPB06 and CPB06(IJP) models and new SD parameters (k) for the CPB06 model at five levels of plastic work
Full size table
Table 2 Voce hardening parameters of reference LD curves identified for a strain of 0.1 or 0.2
Full size table

The Hill* material parameters presented in Table 3 are obtained by reducing the CPB06 yield criterion into the Hill’48. The methodology is presented in “Appendix”; the method is useful when data for the CPB06 model is readily available and the software selected for FE modeling does not consider the advanced constitutive law. The identification procedure is applied for the five yield surfaces defining distortional hardening in the Hill* model. Note that the new tension compression asymmetry parameter k of the CPB06 yield criterion has no effect on the material parameters of the Hill* model as the latter does not take into account the SD effect.

Table 3 Anisotropy parameters of the Hill* yield loci for five levels of plastic work obtained using the procedure explained in “Appendix”
Full size table

For the classical Hill model, an independent identification approach based on the least squares method is applied to determine the anisotropy parameters from simple shear in one plane (LD-TD) and the tensile tests in the three orthogonal material directions (Table 4).

Table 4 Anisotropy parameters of the Hill yield locus identified from simple shear and tensile tests in the three orthogonal material directions at plastic work level of 1.857 J/cm3
Full size table

Figures 3 and 4 compare cuts in the CPB06 yield surface with those from the Hill* and Hill models. The CPB06 loci are slightly larger than the Hill* ones, in turn, the Hill* loci a little larger than the Hill ones. The differences between the CPB06 and Hill* locus cuts is related to the fact that by neglecting SD effect, the Hill locus remains symmetric and cannot correctly model compression state as it is forced to pass by the LD tensile point in its identification procedure. The quadratic shape of the Hill locus limits the possible curvature in bi-axial states and shows a large difference with the CPB06 surface in these respective zones. The fact that the Hill locus is slightly smaller than Hill* one can be attributed to the least squares identification method based on tensile and shear tests. This identification approach places different emphasis on the importance of the experimental data than in the reduction of the CPB06 parameters. The close agreement of Hill and Hill* yield loci validates the developments shown in “Appendix”.

Fig. 3
figure 3

π-plane of the: a initial (Wp = 1.857 J/cm3), b final (Wp = 206.6 J/cm3) yield surfaces defined by the CPB06, Hill and Hill* models

Full size image
Fig. 4
figure 4

Comparison between the initial (left-hand side, Wp = 1.857 J/cm3) and final yield surfaces (right-hand side, Wp = 206.6 J/cm3) defined by CPB06, Hill and Hill* at three orthogonal planes: a LD-TD, b LD-ST, and c TD-ST

Full size image

5 Comparison between the model predictions and experimental results

One-eighth of the samples shown in Fig. 2 are meshed by a hexahedral BWD3D finite element based on the nonlinear three-field Hu–Washizu variational principle of stress, strain and displacement [40, 41]. A refined mesh zone was included in the notches and the through hole where the strain localization occurs (Fig. 5). The number of elements used for each modeled testing samples are 7616 for the geometries B, C and D, and 9216, 2865, 2025 for geometries A, E and F, respectively. The smooth tensile sample used for the identification of the reference tensile curve in the LD direction has also been simulated in order to compare the predictions of the cross-section of each material model with the measured values. In this case, 2025 elements are used with a refined mesh in the area where the necking appears (Fig. 5). The latter, adds interesting data of shape and load for the validation of the material models.

Fig. 5
figure 5

One-eighth of the samples meshed with eight-node hexahedral BWD3D “brick” elements

Full size image

The experimental and numerical results are compared in order to assess the ability of each implemented model to accurately predict the load and shape evolution until fracture.

Figure 6 plots the principal strain fields measured just before the crack event; the data confirm that strain values larger than 0.1 are indeed reached in tensile tests before fracture (maximum 32% for geometry D). For safety reasons, strains higher than the measured 26% local value were not targeted in the compression tests. Figure 7 shows the evolution of the axial load-axial displacement curves measured using the 40 mm initial gauge zone (placed in the middle zone) for the multiaxial tensile specimens (geometries A, B, C, D and F including necking) and with a 14 mm gauge for the compression case (geometry E). To allow objective comparisons the abscissa range is 0.8 mm for geometries A, B, and D and 1 mm for C; a range of 10 kN is covered by the load coordinate axis.

Fig. 6
figure 6

Major strain field in the final geometries measured before fracture by 3D DIC

Full size image
Fig. 7
figure 7

Axial load versus axial displacement curves for geometries A–F showing a comparison between the CPB06, Hill* and Hill model predictions and the respective experimental measurements

Full size image

As expected, given high local triaxiality and stress concentration the V-notch sample displays fracture at the earliest axial displacement. Next, for larger displacements, geometry A (i.e. the through-hole sample) with its highly concentrated and complex stress field breaks. Then, in the triaxiality level order, fractures for notched samples appear in geometry D (triaxiality evolving from 0.5 to 1.2) and later in geometry C (triaxiality from 0.4 to 0.93). The evolution of the radii in the principal directions of the material (ST, TD) and their ratio with the axial displacement are displayed in Figs. 8 and 9 using similar coordinate scales in tension and compression, respectively. The plastic anisotropy observed by the cross-section evolution is very low for tensile, showing a maximum value of axes length ratio equal to 1.04 (Fig. 9). In this material, the prediction of the axes ratios is not an accurate indicator to assess the capability of the models to predict accurate shape and load in multiaxial loading. This is confirmed by the fact that despite the CPB06 model gives less accurate predictions of axes length ratios compared to CPB06(IJP), it presents better predictions of load and geometry evolution (Figs. 7, 8).

Fig. 8
figure 8

Shape versus axial displacement curves for geometries A, C, D, E and F showing a comparison between the CPB06, Hill* and Hill model predictions and the respective DIC measurements

Full size image
Fig. 9
figure 9

Cross-section axes length ratio (ST/TD) evolution with axial displacement of the samples geometries (C, D, E, F)

Full size image

The load predictions displayed in Fig. 7 show more discrepancies between the models than the predicted geometries (Fig. 8), and is more noticeable in tension. The accuracy effect of the reference tensile curve in the LD direction is not negligible as demonstrated by comparing the CPB06 and CPB06(IJP) predicted loads; it modifies both the Voce model for CPB06 (higher hardening for CPB06(IJP) than for CPB06, Fig. 1b) and the k coefficients (affecting SD effect, but also the CPB06 shape globally).

From the results of Hill and Hill* models, the distortional hardening effect versus the isotropic hardening effect is quantified since a similar Voce model is used for the stress strain reference curve.

Comparing CPB06 and CPB06(IJP), the higher hardening curve for CPB06(IJP) explains the maximum predicted load associated with CPB06(IJP). The different predicted shape of the load curves (Fig. 7) and the geometry shape (Fig. 8), for CPB06 and CPB06(IJP) are associated with global errors quantified hereafter (Table 5). These results show the high sensitivity of the computed stress and strain fields to the Voce model identified at strain levels up to 0.1 or 0.2 and to the deduced coefficient k.

Table 5 RMSPE values (in %) of the load and the shape predictions for each geometry
Full size table

The effect of the different hardening models—i.e., isotropic or distortional hardening (Figs. 3, 4)—and the different identification method of the Hill models can be evaluated by the discrepancy between the Hill* and Hill results (Table 4 versus the first line of Table 3 or the left side drawings of Figs. 3 and 4). These differences are non-negligible. In Fig. 7, however, the load curve shapes are quite similar; only the level differs which is explained by close yield locus shapes observed in Figs. 3 and 4. The isotropic hardening model generates higher stresses compared to the distortional hardening model. The best predicted load for the Hill model relies either on Hill* for geometry C or Hill for geometry B. As depicted by the quantitative error measures presented in Table 5, the Hill and Hill* models that neglect the compression information in their identification are more accurate than the CPB06 model for the tensile tests. However, they lose their comparative advantage if compression validation is considered. To pass by the correct compression stress states, the CPB06 yield loci develop larger shapes in the different cuts presented in Figs. 3 and 4; this explains their relative high load predictions for tension cases compared to the Hill models.

Lastly, the yield locus shape and identification based on tension explain the very good agreement of the Hill load prediction in the tensile experiments versus the CPB06 model; meanwhile, the performance of the Hill models are quite poor in compression. In Fig. 8, the Hill* and CPB06 models share the same directional hardening and show agreement of the yield locus in principal tensile states, thus generating close shape prediction results. However, in a compressive state, these different yield loci generate large variations in the predicted axis lengths. In these compression cases, CPB06 predictions are closer to the experimental results.

To quantify the error of the predicted shape (S) and load (F) with the experimental data, Eq. (8) assesses the Root Mean Square Percentage Error (RMSPE) where X is either S or F and m denotes the number of experimental points considered for the computation. The RMSPE is chosen due to its sensitivity to large errors.

$${\text{RMSPE}} = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^{m} {\left( {\left| {\frac{{X_{i}^{\exp } - X_{i}^{\text{model}} }}{{X_{i}^{\exp } }}} \right| \times 100} \right)^{2} } }$$
(8)

As it can be seen, the CPB06 model, provides an excellent global load prediction with an RMSPE value equal to 2.16%, as shown in Table 5. It is worth noting that the axial direction of the validation samples under tensile loading is similar to the Voce hardening reference direction used in model identification (namely, the LD direction). This choice explains the low values of the load error for the tensile samples. However, when comparing compressive load correlation in the orthogonal direction (LT), the CPB06 model indicates greater accuracy in predicting the corresponding experimental load until fracture compared to the Hill’48 model with distortional hardening (Hill*) and the classical Hill’48 with Voce-type hardening law (Hill). The prediction capabilities of each model is summarized in Table 6 for both load and shape.

Table 6 Model features and prediction accuracy
Full size table

6 Conclusions

Three material models were identified to assess their predictions of pre- and post-necking behavior of a Ti6Al4V alloy. Experiments were performed on several sample geometries leading to different triaxial states in tension and compression. Load and displacement fields of the specimens were computed by FE Method simulations and accurately measured by load cells as well as a 3D DIC system. A quantified error between the predictions and the experimental data was provided. The three models were the following ones:

  • the orthotropic and tension–compression asymmetric yield criterion CPB06 with a distortional hardening (CPB06),

  • the anisotropic Hill’48 with distortional hardening (Hill*), and

  • the anisotropic Hill’48 with Voce isotropic hardening (Hill).

The predicted plastic behavior of the CPB06 model is satisfactory under a wide range of the loading conditions until fracture with a global error (RMSPE) equal to 2.16% for the load and 1.26% for the shape. For tensile tests, the Hill model, whose identification neglects the compression state, provides lower load errors; this advantage, however, disappears in global evaluation due to a significant error observed in the compression case. The excellent prediction capabilities of CPB06 are explained by the fact that this orthotropic advanced model describes plastic anisotropy and tension compression asymmetry of the alloy as well as the texture evolution by considering distortional hardening.

The Hill* model with distortional hardening predicts plastic behavior which is only satisfactory for positive stress triaxilities (2.4% error for the load and 1.9% for the shape); the global errors taking into account compression reach 4.5% for the load and 1.6% for the shape. Coupled with isotropic hardening, the error of the Hill model for load prediction increases to 5.4% globally and even 8.6% if only compression is considered. This poor performance is linked with the inability of the Hill’48 yield criterion to describe the SD effect of the alloy.

This study demonstrates the significant impact of distortional hardening on the quality of global model predictions. Microscopic observations, such as texture measurements and crystal plasticity research, link the evolution of the yield locus of Ti6Al4V with texture evolution. Hence, phenomenological models must take this phenomenon into account and it justifies the respective interest in distortional hardening. When large strains are present, post necking behavior has to be modeled and accurate Voce law based on true stress-true strain law identification on a large strain range should always be used; this is reflected by the lower prediction error displayed in the CPB06 model compared with the CPB06(IJP) model.

Load predictions for the specimen geometries with positive stress triaxiality are slightly overestimated by both the CPB06 and Hill* models (errors of 2.9% and 2.4%, respectively). In addition to non-perfect yield locus shapes, these errors can be explained by the fact that both models are insensitive to hydrostatic pressure and the fact that the Voce law for the reference tensile curve does not predict softening. They satisfy a condition of plastic incompressibility and neglect the initial porosity, its growth, and the nucleation of new voids in the material. The load is only slightly overestimated likely because the porosity is still relatively low even just before fracture (initial and final porosity values measured for geometry C were equal to 0.003% and 0.8%, respectively). Ongoing research targets crack prediction and the use of a Cazacu damage model sensitive to pressure [8].