1 Introduction

Die-cast aluminum alloys are increasingly used in automotive and aerospace industries to replace denser metals, thicker-walled components and higher cost materials and processes. However, there have been limited studies on predicting the ductile fracture of cast aluminum, which hinders the rational design of materials, components and processes. The objective of the current study is to characterize the plasticity and ductile fracture behavior of an AA365-T7 (trade name, Aural-2) die-cast aluminum alloy.

Metals including cast alloys oftentimes exhibit initial plastic anisotropy due to crystallographic texture created by their prior manufacturing steps. There are several possibilities to account for this anisotropy during analysis and design. The most frequently used approach employs a hardening law and the associated flow rule in conjunction with various isotropic or anisotropic yield criteria (Banabic 2010; Hershey 1954; Hill 1948; Hosford 1972; Hosford and Caddell 1993). Among these, the plastic deformation of aluminum alloys shows best agreement with non-quadratic criteria. The linear-transformation-based yield criteria proposed by Barlat et al. (2005) and Barlat et al. (2003) have been frequently used by the authors to represent the plastic deformation of a variety of aluminum alloys, e.g., Dick and Korkolis (2015), Giagmouris et al. (2010), Korkolis et al. (2010), Korkolis and Kyriakides (2008a), Korkolis and Kyriakides (2009) and Korkolis and Kyriakides (2011) and will be used in this study, as well.

Ductile fracture in metals is the result of void nucleation, growth and coalescence of microscopic voids into void sheets, which lead to material separation at the macroscale. These micromechanical fracture mechanisms have been investigated extensively both experimentally and numerically (Gurson 1977; McClintock 1968; Meyers and Chawla 1984; Rice and Tracey 1969; Thomason 1990; Tvergaard and Needleman 1984). Focusing now on cast aluminum, Mae et al. (2007) found that second-phase inclusions like silicon particles serve as void initiation sites. Similarly, due to trapped gases, changes in gas solubility between the melt and the solid, and solidification shrinkage, pores of different shapes and sizes exist in the casting and provide other possible locations for failure initiation. Recently, Toda et al. (2012) highlighted the role of solidification-induced hydrogen micropores in cast aluminum alloys on fracture, using high-resolution X-ray tomography. In their findings, these pores were more detrimental to ductility than voids initiating around second-phase particles.

It appears then that understanding void dynamics is one of the pathways to predicting ductile fracture of cast aluminum. The porous plasticity model proposed by Gurson (1977) includes void volume fraction as an internal variable related to the damage indicator. Since then, numerous phenomenological fracture criteria based on the modification of original Gurson model have been proposed in the literature Benzerga et al. (2004), Gologanu et al. (1993), Leblond et al. (1995), Nahshon and Hutchinson (2008), Pardoen and Hutchinson (2000) and Tvergaard and Needleman (1984).

Despite sound micromechanical underpinnings, such criteria can be ambiguous to calibrate and expensive to use in a simulation. Alternatively, there are several phenomenological fracture criteria based on localization analyses combined with non-porous plasticity models. These criteria (Bao and Wierzbicki 2004; Clift et al. 1990; Cockcroft and Latham 1968; McClintock 1968; Oh et al. 1979; Rice and Tracey 1969) assume that fracture occurs at a material point where a weighted measure of the accumulated plastic strain reaches a critical value.

Early studies (McClintock 1968; Oyane et al. 1980; Rice and Tracey 1969) showed that void growth is governed by the hydrostatic pressure. Therefore, classical ductile fracture criteria are formulated in terms of stress triaxiality (Benzerga and Leblond 2010; Gurson 1977; McClintock 1968). However, Coppola et al. (2009), Kim et al. (2004) and Zhang et al. (2001) have shown the dependency of ductile fracture on the deviatoric stress state represented by the Lode-angle-parameter. In that spirit, Mohr and Marcadet (2015) extended the Mohr–Coulomb to the Hosford–Coulomb criterion based on the results of a 3D localization analysis. Alternatively, Lou et al. (2012) proposed a fracture criterion based on the microscopic analysis of ductile fracture by incorporating the stress triaxiality and the maximum shear stress, and further extended it (Lou and Huh 2013) to a general expression of stress triaxiality and Lode-angle-parameter. While the above criteria assume that fracture is isotropic, Lou and Yoon (2017) proposed an anisotropic criterion by making use of a linearly transformed strain tensor.

The fracture loci predicted by these criteria have a cusp for the triaxiality of 1/3, corresponding to uniaxial tension. On the other hand, Haltom et al. (2013) and Scales et al. (2016) performed combined tension-torsion experiments on AA6061-T6 tubes and found a monotonic decrease of fracture strain with increasing triaxiality. Similar findings were reported by Ghahremaninezhad and Ravi-Chandar (2012) on AA6061-T6 sheets and Papasidero et al. (2015) on AA2024-T351 tubes. These differences could be due to specimen designs that permit localization to develop free of constraints and edge-effects, as well as the adopted measurement methods.

Besides, fracture behavior can be path-dependent (Benzerga et al. 2012). They determined difference in fracture loci for proportional and non-proportional loading, for axisymmetric stress states and stress triaxialities higher than for uniaxial loading. They also recommended to incorporate a set of internal variables to capture the essential features of path-dependent ductile fracture. Similar findings were observed in fracture experiments by Basu and Benzerga (2015). They performed experiments on round notched bars of a medium-carbon A572 Grade-50 steel with and without load path changes. Their experiments revealed a different fracture locus for each set of experiments. Occasionally, non-proportional loading arises unintentionally, e.g., in the case of notched-tension (NT) fracture specimens, as discussed by Paredes et al. (2018). In this case, the non-proportional loading path was handled by time-weighted average values of the loading parameters. However, depending on the definition of the variables, different fracture loci might be obtained.

In this study, the plasticity and ductile fracture of an Al–Si–Mg die-cast alloy (AA365-T7) are characterized using a combined experimental-numerical approach. This approach is pursued because of the inhomogeneous deformation of the fracture specimens, the development of a multi-axial stress state and the inability of experiments to capture the local fracture that usually initiates in the through-thickness mid-plane of the specimens. First, the plastic anisotropy of the alloy is probed experimentally and the Yld2004-3D yield criterion (Barlat et al. 2005) is calibrated. Then, the fracture behavior is characterized experimentally. Finite element (FE) analyses of the fracture specimens are used to determine the local stresses and strains at the onset of fracture. In that way, the fracture locus is defined. A distinction is made between fracture specimens that have proportional and non-proportional loading paths, the latter probing different fracture loci. Three fracture initiation criteria, i.e., Oyane (Oyane et al. 1980), Johnson–Cook (Johnson and Cook 1985) and Hosford–Coulomb (Mohr and Marcadet 2015) are calibrated, along with a new criterion which is a linear combination of Johnson–Cook and Oyane.

2 Plasticity modeling

The plasticity model plays an important role in the accurate prediction of the fracture strains during numerical simulations (Giagmouris et al. 2010). In this research, the anisotropic plastic behavior of the die-cast alloy is modeled using the 18-parameter non-quadratic three-dimensional anisotropic yield criterion Yld2004-3D (Barlat et al. 2005). This criterion is utilized as the plastic potential of a rate-independent, associated flow-rule, along with the isotropic hardening assumption. The Yld2004-3D criterion has been widely used in the literature to capture the anisotropic behavior of different types of aluminum alloys (Deng et al. 2015; Dick and Korkolis 2015; Korkolis and Kyriakides 2011; Tardif and Kyriakides 2012). The 3D criterion is chosen over a plane-stress, 2D one, because the stress state in the fracture specimen becomes multi-axial, including a through-thickness gradient, after the uniform deformation. This requires the use of 3D FE models, see Sect. 5.5, and hence a 3D description of plastic anisotropy.

The Yld2004-3D yield criterion is based on two linear transformations of the deviatoric stress tensor and is symmetric in tension and compression. It is expressed as:

$$\begin{aligned} \begin{aligned} \upphi&=\upphi \left( {{\varvec{\Sigma }}} \right) =\upphi \left( \tilde{\mathbf{S}} ^{{\prime }},\tilde{\mathbf{S}}^{{\prime }{\prime }} \right) \\&=\left| {\tilde{\hbox {S}} _1^{{\prime }} -\tilde{\hbox {S}} _1^{{{\prime }{\prime }}} } \right| ^{\mathrm{a}}+\left| {\tilde{\hbox {S}} _1^{{\prime }} -\tilde{\hbox {S}} _2^{\mathrm{{\prime }{\prime }}} } \right| ^{\mathrm{a}}+\left| {\tilde{\hbox {S}} _1^{{\prime }} -\tilde{\hbox {S}} _3^{\mathrm{{\prime }{\prime }}} } \right| ^{\mathrm{a}}\\&\quad +\left| {\tilde{\hbox {S}} _2^{{\prime }} -\tilde{\hbox {S}} _1^{\mathrm{{\prime }{\prime }}} } \right| ^{\mathrm{a}}+\left| {\tilde{\hbox {S}} _2^{{\prime }} -\tilde{\hbox {S}} _2^{\mathrm{{\prime }{\prime }}} } \right| ^{\mathrm{a}} \\&\quad +\left| {\tilde{\hbox {S}} _2^{{\prime }} -\tilde{\hbox {S}} _3^{{{\prime }{\prime }}} } \right| ^{\mathrm{a}}+\left| {\tilde{\hbox {S}} _3^{{\prime }} -\tilde{\hbox {S}} _1^{\mathrm{{\prime }{\prime }}} } \right| ^{\mathrm{a}}+\left| {\tilde{\hbox {S}} _3^{{\prime }} -\tilde{\hbox {S}} _2^{\mathrm{{\prime }{\prime }}} } \right| ^{\mathrm{a}}\\&\quad +\left| {\tilde{\hbox {S}} _3^{{\prime }} -\tilde{\hbox {S}} _3^{\mathrm{{\prime }{\prime }}} } \right| ^{\mathrm{a}}=4\bar{\upsigma } ^{\mathrm{a}} \\ \end{aligned} \end{aligned}$$
(1)

The exponent “a” should be 6 and 8 for body centered cubic (BCC) and face centered cubic (FCC) materials, respectively, based on crystal plasticity calculations (Hosford 1972; Logan and Hosford 1980). The quantities \(\tilde{\hbox {S}} _\mathrm{i}^{{\prime }} \) and \(\tilde{\hbox {S}} _\mathrm{j}^{{\prime }} \) are the principal stress components of the transformed deviatoric stress tensors \(\tilde{\mathbf{s}}^{{\prime }}\) and \(\tilde{\mathbf{s}}^{{\prime }{\prime }}\). These tensors are linear transformations (see Eqs. 2) of the deviatoric stress tensor \(\mathbf{s}\) through matrices \({\mathbf{C}''}\) and \({\mathbf{C}''}\) (see Eq. 3), which introduce the anisotropy. Finally, the deviatoric stress tensor \(\mathbf{s}\) is obtained from the Cauchy stress \(\varvec{\upsigma }\) tensor through the linear transformation tensor \(\mathbf{T}\) (see Eq. 4):

$$\begin{aligned} \tilde{\mathbf {s}}'= & {} {\mathbf {C^{\prime }s}} = {\mathbf {C}}^{\prime }{} \mathbf{T}{\varvec{\upsigma }} = {\mathbf {L}^{\prime }{\varvec{\upsigma }}}\nonumber \\ \tilde{\mathbf {s}}^{{''}}= & {} {\mathbf {C}^{\prime \prime }\mathbf {s}} = {\mathbf {C}^{\prime \prime }\mathbf {T}{\varvec{\upsigma }}} = {\mathbf {L}^{\prime \prime }{\varvec{\upsigma }} } \end{aligned}$$
(2)
$$\begin{aligned} \mathbf{C}= & {} \left[ \begin{array}{cccccc} {0} &{}\quad {-\hbox {c}_{12} } &{}\quad {-\hbox {c}_{13} } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {-\hbox {c}_{21} } &{}\quad {0} &{}\quad {-\hbox {c}_{23} } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {-\hbox {c}_{31} } &{}\quad {-\hbox {c}_{32} } &{}\quad {0} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {0} &{}\quad {0} &{}\quad {0} &{}\quad {\hbox {c}_{44} } &{}\quad 0 &{}\quad 0 \\ {0} &{}\quad {0} &{}\quad {0} &{}\quad 0 &{}\quad {\hbox {c}_{55} } &{}\quad 0 \\ {0} &{}\quad {0} &{}\quad {0} &{}\quad 0 &{}\quad 0 &{}\quad {\hbox {c}_{66} } \\ \end{array} \right] \end{aligned}$$
(3)
$$\begin{aligned} \mathbf{T}= & {} \frac{1}{3}\left[ \begin{array}{cccccc} {2} &{}\quad {-1} &{}\quad {-1} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {-1} &{}\quad {2} &{}\quad {-1} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {-1} &{}\quad {-1} &{}\quad {2} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {0} &{}\quad {0} &{}\quad {0} &{}\quad 3 &{}\quad 0 &{}\quad 0 \\ {0} &{}\quad {0} &{}\quad {0} &{}\quad 0 &{}\quad 3 &{}\quad 0 \\ {0} &{}\quad {0} &{}\quad {0} &{}\quad 0 &{}\quad 0 &{}\quad 3 \\ \end{array}\right] \end{aligned}$$
(4)

The 18 anisotropic coefficients are the non-zero entries of the \(\mathbf{C}^{\prime }\) and \(\mathbf{C}^{\prime }\) matrices (Barlat et al. 2005). The yield criterion reduces to the von-Mises criterion for exponent \(\hbox {a} = 2\) (or 4) and all non-zero entries in Eq. (3) equal to one.

3 Fracture modeling

3.1 Overview

Ductile fracture criteria are used to predict the onset of fracture for metals and alloys. The stress state in the fracture criteria is sometimes described by the stress triaxiality and also by the Lode-angle-parameter. The stress triaxiality is defined as the ratio of hydrostatic stress (\(\sigma _m )\) to the equivalent stress (\(\bar{\sigma } )\):

$$\begin{aligned} {\upeta }=\frac{{\upsigma }_\mathrm{m} }{\bar{\upsigma }}\quad \hbox {with}\quad {\upsigma }_\mathrm{m} =\frac{{\upsigma }_\mathrm{I} +{\upsigma }_{\mathrm{II}} +{\upsigma }_{\mathrm{III}} }{3} \end{aligned}$$
(5)

The Lode-angle-parameter is a measure of the ratio of the second and third deviatoric stress tensor invariants and is expressed as:

$$\begin{aligned} \bar{\uptheta } =1-\frac{2}{{\uppi }}\hbox {acos}\left[ {\frac{3\sqrt{3}}{2}\frac{\hbox {J}_3 }{\sqrt{\hbox {J}_2^3 }}} \right] \end{aligned}$$
(6)

In this study, the fracture locus of the die-cast alloy is probed with a combination of experiments and analysis, and three common criteria are calibrated to this locus. In addition to the existing criteria, a new criterion is proposed.

Table 1 Chemical composition of AA365-T7 die-cast alloy (wt.%)
Full size table

3.2 Selected fracture initiation criteria

The selected fracture criteria for this material are the Oyane (Oyane et al. 1980), Johnson–Cook (Johnson and Cook 1985) and Hosford–Coulomb (Mohr and Marcadet 2015) ones. The first two criteria are expressed solely in terms of stress triaxiality, while the latter is expressed in terms of stress triaxiality and Lode-angle-parameter. The Oyane criterion is micromechanically derived, using the plasticity theory of porous materials. It has two fracture parameters, “k\(_{1}\) and k\(_{2}\)” and is expressed as:

$$\begin{aligned} \bar{\upvarepsilon } _\mathrm{f} \left( {\upeta } \right) =\left( {\hbox {k}_1 {\upeta }+\hbox {k}_2 } \right) ^{-1} \end{aligned}$$
(7)

Similarly, the Johnson–Cook fracture criterion is based on the relative effects of various parameters including the stress triaxiality, strain-rate and temperature. The latter two effects are negligible for the tested material and conditions and can be ignored here. Then, the Johnson–Cook fracture criterion can be expressed in terms of three damage parameters, \(\hbox {d}_1 \), \(\hbox {d}_2 \) and \(\hbox {d}_3 \) as:

$$\begin{aligned} \bar{\upvarepsilon } _\mathrm{f} \left( {\upeta } \right) =\left[ {\hbox {d}_1 +\hbox {d}_2 \exp \left( {-\hbox {d}_3 {\upeta }} \right) } \right] \end{aligned}$$
(8)

Likewise, the Hosford–Coulomb criterion is based on the transformation from principal stress space to the space of equivalent plastic strain, stress triaxiality and Lode-angle-parameter. It consists of three parameters “m, b and c”, and the transformation constant “n”, which is typically taken as \(\mathrm{n} = 0.1\) for most metals (Roth and Mohr 2016). The criterion is expressed as:

$$\begin{aligned}&\bar{\upvarepsilon } _\mathrm{f} \left( {{\upeta },\bar{\uptheta } } \right) =\hbox {b}\left( {1+\hbox {c}} \right) ^{\frac{1}{\hbox {n}}}\left( \left\{ \frac{1}{2}\left( \left( {\hbox {f}_\mathrm{1} -\hbox {f}_\mathrm{2} } \right) ^{\mathrm{m}}+\left( {\hbox {f}_\mathrm{2} -\hbox {f}_\mathrm{3} } \right) ^{\mathrm{m}}\right. \right. \right. \nonumber \\&\qquad \left. \left. \left. +\left( {\hbox {f}_\mathrm{1} -\hbox {f}_\mathrm{3} } \right) ^{\mathrm{m}} \right) \right\} ^{\frac{1}{\mathrm{m}}}+\hbox {c}\left( {2{\upeta }+\hbox {f}_1 +\hbox {f}_3 } \right) \right) ^{-\frac{1}{\hbox {n}}} \end{aligned}$$
(9)

The functions \(\hbox {f}_\mathrm{i} \) are trigonometric functions dependent on the Lode-angle-parameter and are associated with the transformation from principal stress to Haigh-Westergaard stress space. They are defined as (Mohr and Marcadet 2015; Roth and Mohr 2016):

$$\begin{aligned} \hbox {f}_1 \left[ {\bar{\uptheta } } \right]= & {} \frac{2}{3}\hbox {cos}\left[ {\frac{{\uppi }}{6}\left( {1-\bar{\uptheta } } \right) } \right] ;\nonumber \\ \hbox {f}_2 \left[ {\bar{\uptheta } } \right]= & {} \frac{2}{3}\hbox {cos}\left[ {\frac{{\uppi }}{6}\left( {3+\bar{\uptheta } } \right) } \right] ;\nonumber \\ \hbox {f}_3 \left[ {\bar{\uptheta } } \right]= & {} -\frac{2}{3}\hbox {cos}\left[ {\frac{{\uppi }}{6}\left( {1+\bar{\uptheta } } \right) } \right] . \end{aligned}$$
(10)

3.3 Proposed new fracture criterion

A new criterion is proposed based on the linear combination of Johnson–Cook and Oyane criteria. The basic form of the fracture criterion is based on the damage accumulation concept, similar to the Johnson–Cook criterion (Johnson and Cook 1985), where it is defined as:

$$\begin{aligned} \hbox {d}=\int \frac{\hbox {d}\upvarepsilon }{{\upvarepsilon }^{\mathrm{f}}} \end{aligned}$$
(11)

In the above expression, \(\hbox {d}\upvarepsilon \) is the increment of equivalent plastic strain which occurs during an integration cycle, and \({\upvarepsilon }^{\mathrm{f}}\) is the equivalent plastic strain to fracture. Fracture occurs when d=1.0. Similarly, the Oyane criterion is based on the plasticity theory for porous materials. The volumetric strain \({\upvarepsilon }^{\mathrm{v}}\) is taken as the metric for describing ductile fracture: when it reaches a critical value \({\upvarepsilon }^{\mathrm{vf}}\), the material fractures (Oyane et al. 1980).

In proposing the new ductile fracture criterion, the concept of volumetric strain in Oyane criterion is combined into the damage definition of Johnson–Cook criterion. Assuming the normalized volumetric strain is equivalent to the damage parameter “\(\hbox {d}\)” the following fracture initiation criterion is proposed:

$$\begin{aligned} \bar{\upvarepsilon } _\mathrm{f} \left( {\upeta } \right) =\hbox {d}_0 +\hbox {d}_1 \exp \left( {\upeta } \right) +\left( {\hbox {d}_1 {\upeta }+\hbox {d}_2 } \right) ^{-1} \end{aligned}$$
(12)

The new criterion consists of three damage parameters, \(\hbox {d}_0 ,\hbox {d}_1\) and \(\hbox {d}_2 \). The first two terms in Eq. (12) are analogous to the Johnson–Cook criterion and are consistent with the finding of Hancock and Mackenzie (1976), i.e., that the strain-to-fracture decreases as the hydrostatic stress \({\upsigma }_\mathrm{m} \) increases. Similarly, the last term is equivalent to the Oyane criterion assuming damage parameter based on volumetric strain. The proposed criterion is expected to add more flexibility to the usual monotonic behavior of either the Oyane or Johnson–Cook criteria, see Fig. 18.

4 Experimental study

4.1 Overview

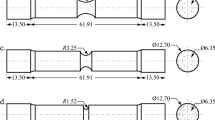
The material of this study is an Al–Si–Mg die-cast aluminum alloy (AA365-T7) in the T7 temper, received as plates of \(100\,\mathrm{mm} \times 300\,\mathrm{mm}\) in-plane dimensions and nominal thickness of 2 mm. The nominal chemical composition of this material is included in Table 1 (Hartlieb 2013). This material is also known by the trade name Aural-2. The optical images of a polished region for this material are shown in “Appendix A” (Fig. 19), showing aluminum dendrites (grey areas) with interspersed fine silicon particles (dark spots). From the die-cast plates, a total of 15 specimen geometries and orientations (with 3 repetitions for each) shown conceptually in Fig. 1 were made: 3 uniaxial tensile specimens (UT), 3 plane-strain-tension specimens (PST), 1 disk-compression specimen (DC), 3 notched-tension specimens with notch radius of 20 mm (NT20), 2 notched-tension specimens with notch radius of 6.67 mm (NT6), 2 central-hole specimens (CH) and 1 shear specimen (SH). Notice that the plate has a distinct orientation which was termed Material Direction (MD) and corresponds to the direction of molten metal flow from the gates to the risers of the die. The results from the UT, PST and DC tests are used for plasticity characterization, while those from the NT20, NT6, CH and SH tests are used for ductile fracture characterization. The engineering drawings of the plasticity and fracture specimens are shown in “Appendices B” (Fig. 20) and C (Figs. 21, 22), respectively.

4.2 Plasticity characterization

The plasticity of the material was probed using the UT, PST and DC tests. The UT and PST experiments were conducted in the material direction (MD), 45\(^{{\circ }}\) and transverse direction (TD), while the DC experiment was done in the normal direction (ND), which corresponds to the equibiaxial tension in the MD–TD plane. The UT and PST tests were performed on an MTS Landmark 370 servohydraulic testing machine of 250 kN load capacity and 176 mm stroke capacity, equipped with FlexTest software and controller and hydraulic grips. Similarly, the DC test was performed on an Instron 1350 servohydraulic testing machine with DAX software and controller, and utilizing a custom compression jig that makes use of a die-set (Baral 2015; Baral et al. 2018). All tests were performed three times; the results were reproducible in each direction.

Fig. 1
figure 1

Layout of AA365-T7 die-cast specimens on the casting plate with respect to its material direction

Full size image
Fig. 2
figure 2

True stress–strain curves from uniaxial tension experiments in MD, \(45^{{\circ }}\) and TD

Full size image

The UT experiments were performed at a cross-head displacement of 40 \(\upmu \)m/s, which induced a nominal strain-rate of \(10^{-3}\) /s in the gage-section. The full-strain-field of the test-section was acquired using the 3D Digital Image Correlation (DIC) method (Sharpe 2010; Shukla and Dally 2010). The VIC-Snap system was used to acquire the images from two 2.0 Megapixel digital cameras equipped with 35 mm Schneider lenses, and with a frame-rate of 500 ms. The images where then post-processed using the VIC-3D software. The stress–strain curves recorded are shown in Fig. 2. A mild anisotropy is observed in the flow stresses, while the uniform true strain is around 0.12 for all orientations. Though not easily distinguished in Fig. 2, the magnitude of the flow stresses is closely in this order: \({\upsigma }_{\mathrm{TD}}>{\upsigma }_{45} >{\upsigma }_{\mathrm{MD}} \). The r-values (plastic strain ratios) were calculated in all three directions from the slope of the plastic strains in the width and thickness directions. The results are shown representatively in Fig. 3. An average value out of three tests was taken for each orientation. The r-values in all orientations are less than unity and the behavior was found to be reverse of the flow stress trend, i.e., \(\hbox {r}_{\mathrm{MD}}>\hbox {r}_{45} >\hbox {r}_{\mathrm{TD}} \).

Fig. 3
figure 3

Plastic strain ratios (r-values) from uniaxial tension experiments in MD, \(45^{{\circ }}\) and TD

Full size image
Fig. 4
figure 4

a Axial (top) and transverse (bottom) strain fields in plane-strain-tension specimen in MD at the onset of fracture. b Evolution of axial and transverse strains in plane-strain–tension specimen

Full size image
Fig. 5
figure 5

Force-displacement curves from plane-strain tension experiments in MD, \(45^{{\circ }}\) and TD

Full size image
Fig. 6
figure 6

Equibiaxial plastic strain ratios \((\hbox {r}_{\mathrm{b}})\) from disk-compression experiments

Full size image

The PST experiments were performed at a cross-head displacement of 9.6 \(\upmu \)m/s, which induced a nominal strain rate close to \(10^{-3}\) /s in the gage-section. The PST geometry adopted exhibits plane-strain conditions at the center of the specimen (Tardif and Kyriakides 2012; Dick and Korkolis 2015; Tian et al. 2017). The axial and transverse strain fields obtained from the DIC at the onset of fracture are shown in Fig. 4a. As seen in that figure, the strain field is inhomogeneous and the transverse strain evolution is insignificant, especially inside the gage section. A better assessment of the plane-strain condition can be made from Fig. 4b, which shows the evolution of strains in the loading and transverse directions along the width at the horizontal centerline of the specimen. The strain in the transverse direction is close to zero in the central 40% section of the width, validating the plane-strain assumption.

Fig. 7
figure 7

Axial (left) and transverse (right) strain fields in central hole specimen at the onset of fracture

Full size image

The force-displacement (F-\(\updelta )\) curves recorded in the PST specimens are shown in Fig. 5. The displacement is extracted using a 15 mm gage-length virtual extensometer on the surface of the specimen, as shown in Fig. 4a. Like the uniaxial tension results, a mild anisotropy is observed in the PST tests, as well. The stresses in PST experiments are determined using a correction factor from FE simulation, as in our previous works (Baral et al. 2018; Dick and Korkolis 2015; Tian et al. 2017). The detailed method is described in Sect. 5.2.

Likewise, the DC experiments were performed to determine the equibiaxial plastic strain ratio \((\hbox {r}_{\mathrm{b}})\) (Barlat et al. 2003; Tian et al. 2017). The DC specimens are circular disks with 8 mm diameter. These specimens were compressed in an interrupted fashion, and the lengths along the MD and TD at subsequent deformations were measured up to 4 times per test, using a micrometer. The \(\hbox {r}_{\mathrm{b}}\) value was then determined from the slope of the plastic strains in the MD and TD as shown in Fig. 6. A total of 3 tests were done to determine an average value.

4.3 Ductile fracture characterization

The fracture locus of the die-cast alloy was probed using notched tension specimens with notch radii 20 mm and 6.67 mm (NT20 and NT6), center-hole (CH) (Dunand and Mohr 2010; Ha et al. 2018; Roth and Mohr 2014, 2016) and simple shear (SH) specimens. The S-shaped SH geometry consisting of a single ligament test-section was implemented (Water 2000; Yin et al. 2014), unlike the “butterfly” specimens (Abedini et al. 2017; Dunand and Mohr 2011; Mohr and Henn 2007) or “double shear/smiley” shear specimens (Miyauchi 1984; Till and Hackl 2013) with two gage sections, found in the literature. The notch geometry for the SH specimen was designed to avoid premature fracture initiation from the free edge boundaries using FE analysis (Ghahremaninezhad and Ravi-Chandar 2011; Mohr and Henn 2007; Roth and Mohr 2016). The selected fracture specimens cover a broad range of stress triaxialities and Lode-angle-parameters. The fracture experiments were performed using the same MTS Landmark 370 servohydraulic testing machine of 250 kN load capacity used for plasticity testing (Sect. 4.2 above). Each of these tests was performed three times; the results were generally reproducible with minor specimen-to-specimen variation between tests. In particular, the recorded force levels in the repeated tests were almost the same, while the displacements at fracture were found to have some variation, perhaps due to casting defects.

Fig. 8
figure 8

Force-displacement curves from a NT20 experiments in MD, \(45^{{\circ }}\) and TD, b NT6 experiments in MD and TD, c CH experiments in MD and TD and d SH experiments in MD. Note that the axis scales at each plot are different, depending on the specifics of each test

Full size image

The full-strain-fields of the fracture specimens were acquired using the 3D Digital Image Correlation (DIC) method. As an example, the axial and transverse logarithmic strains in the CH tests at the onset of fracture are shown in Fig. 7. As seen in the figure, the strain field is non-homogenous, with regions of higher strains found near the hole. Similar kinds of results were obtained for other types of fracture specimens. The F-\(\updelta \) curves from the NT20, NT6, CH and SH experiments are shown in Fig. 8a, b, c and d, respectively. The displacements in NT20, NT6 and CH experiments are obtained by a 30 mm virtual gage-length on the surface of the specimen, while that in the SH experiment is extracted from the center of the specimen. Also, it was observed in the experiments that the fracture in the NT tests propagated abruptly, while that in the CH and SH tests gradually.

The fracture experiments for NT20 were done in the MD, 45\(^{{\circ }}\) and TD (Fig. 8a) while those for NT6 and CH were done in MD and TD due to material availability (Fig. 8b, c). The results show some directional dependence, as the fracture resistance is found to be lower in the MD than in the TD. Also, the force level is found to be slightly lower in the MD than in the TD in these tests. Due to its lower resistance, the fracture analysis will be based on the MD results and isotropy in fracture behavior will be assumed. In addition, the SH experiments are performed in the MD only, again due to material availability (Fig. 8d).

5 Numerical study

5.1 Overview

The fracture behavior of the AA365-T7 material was examined using a combination of experiments and analysis. The strains can be probed on the surface of the specimens in a straightforward way, using the DIC method. On the other hand, the stress and strain histories at the material point of fracture initiation are impossible to obtain experimentally, as this point lies inside the specimen and the stress and strain fields are spatially non-uniform. These difficulties were overcome using the FE method. First, simulations of the fracture specimens were performed using the calibrated plasticity and hardening models. Then, the FE and material models were validated by comparing the predicted F-\(\updelta \) curve and the surface strains to the experimental ones. Finally, with the fidelity of the models thus validated, these were used to obtain the stress and strain histories at the fracture initiation point.

Fig. 9
figure 9

a Finite element model of plane-strain-tension specimen (1/8th model). b Stress correction using finite element simulation in plane-strain-tension experiment

Full size image
Table 2 Results from plasticity experiments
Full size table

5.2 Correction of plane-strain tension stress

The post-processing of the PST experiments requires more effort than the uniaxial tension tests due to the geometry of the specimen and the non-uniform fields that this induces: the edges are in a state of uniaxial tension, while the center is in a state of plane-strain tension. This leads to non-uniform stress and strain fields in the specimen, the latter shown in Fig. 4a. While the (surface) strain can be determined from the full-field strains recorded by the DIC, it is impossible to determine the actual stress in the loading direction from the force recorded during the experiment.

The stress in the PST experiment was corrected with the aid of inverse FE analysis (Baral et al. 2018; Dick and Korkolis 2015; Tian et al. 2017). A FE model identical to the PST geometry (1/8th model) was created in the non-linear implicit code Abaqus/Standard (v6.13-3), as shown in Fig. 9a. The model was meshed with quadratic, reduced-integration solid elements (C3D20R). A rate-independent, J\(_{2}\) flow theory with isotropic hardening was employed for the simulations. The actual stress in the loading direction and the apparent, average stress obtained using the total force divided by the instantaneous cross-sectional area of the specimen (i.e., F/A) are shown in Fig. 9b. Both curves were extracted from the FE model: the first one from where the plane-strain condition is valid (the lower left node at the specimen mid-plane, in Fig. 9a) and the second one using the entire mid-plane area to divide the external force. The average stress is seen to differ from the actual stress, as it neglects the non-uniform deformation in the test-section of the PST specimen. Using this stress to compute the plastic work density would lead to an error, as it is not work-conjugate to the strains measured at the center of the PST specimen (Fig. 4b). A stress correction factor was determined by dividing the actual stress by F/A (see Fig. 9b) and was then applied to the F/A measured in the actual experiment. An average correction factor of 0.946 was selected.

5.3 Calibration of yield criterion

In this study, the 18-parameter anisotropic non-quadratic 3D yield criterion Yld20004-3D (Barlat et al. 2005) was used to describe the plastic anisotropy of the die-cast AA365-T7 alloy. The results of the plasticity experiments, i.e., UT, PST and DC are summarized in Table 2. The normalized stresses in UT and PST are determined at plastic work of approx. 2 MJ/m\(^{3}\), which corresponds to a strain of \(\sim \) 1.6% in the UT-MD test. In this study, the Yld2004-3D model was calibrated using a two-step process due to the lack of sufficient experimental data points. Initially, the 10 data points from the experiments (see Table 2), together with the zero plastic strain condition for the 3 PST specimens, were used to calibrate the 8-parameter Yld2000-2D yield criterion (Banabic 2010; Barlat et al. 2003; Hosford and Caddell 1993; Korkolis and Kyriakides 2008a, b, 2009; Tian et al. 2017) using the Newton-Raphson optimization algorithm. Then, the flow stresses and r-values for UT at every 15\(^{\circ }\) angle from MD and for equibiaxial tension were predicted using the Yld2000-2D criterion. Based on this additional information, the Yld2004-3D criterion was calibrated as shown in Fig. 10, which includes the yield locus along with the contours of iso-shear lines, and stress states from experiments. The von-Mises locus is also shown for comparison. This locus is seen to miss the experimental stress points, perhaps not so much in terms of absolute value difference, but more so in terms of the resulting curvature, which controls plastic flow. The predicted stresses and r-values using Yld2004-3D are shown in Fig. 11, which shows a good agreement with experiments. The calibrated parameters for Yld2004-3D are summarized in Table 3. The yield loci from Yld2000-2D and Yld2004-3D are plotted together and shown in “Appendix D” (Fig. 23).

Fig. 10
figure 10

Yld2004-3D locus, including the contours of iso-shear lines (spaced every \(\tau /\sigma _{MD} = 0.051\)), and the von-Mises locus

Full size image
Fig. 11
figure 11

Normalized yield stress and r-value predicted by Yld2004-3D criterion along with experimentally measured values

Full size image
Table 3 Calibration parameters for Yld2004-3D
Full size table

In addition, the performance of the yield criterion can be assessed by the KBK representation (Korkolis et al. 2017). The yield condition can be written in the form \(\bar{\upsigma } ={\upsigma }_\mathrm{R} \left( {\bar{\upvarepsilon } } \right) \), where \(\bar{\upsigma } \) and \(\bar{\upvarepsilon } \) are the equivalent stress and plastic strain, respectively, and \({\upsigma }_\mathrm{R}\) is a reference stress–strain curve. The “distance” between any general stress state with deviator \(\mathbf{s}\) and the reference stress state \(\mathbf{s}_\mathrm{R} \) can be characterized by the parameter \(\hbox {cos}\uptheta =\hat{\mathbf{s}} : \hat{\mathbf{s}} _\mathrm{R} \), where the symbol ‘ : ’ denotes the double-dot product of two second-order tensors, and \(\hat{\mathbf{s}} =\mathbf{s}/\sqrt{\mathbf{s}: \mathbf{s}}\). In the same way, the experimental strain increment tensor \(\hbox {d}\hat{\varvec{\upvarepsilon }} _{\mathrm{exp}} \) can be compared with its prediction \(\hbox {d}\hat{\varvec{\upvarepsilon }} _{\mathrm{yld}} \) through the parameter \({\updelta }=\hbox {arccos}\left( {\hbox {d}\hat{\varvec{\upvarepsilon }} _{\mathrm{exp}} : \hbox {d}\hat{\varvec{\upvarepsilon }} _{\mathrm{yld}} } \right) \). Thus, any stress state \(\mathbf{s}\) can be characterized by two planar curves, namely, its distance from the yield condition, \(\bar{\upsigma } \left( \mathbf{s} \right) /{\upsigma }_\mathrm{R} =1\), and its deviation from the selected flow rule, \({\updelta }=0\), both as a function of \(\hbox {cos}\uptheta \). It is important to note that there is no 1-to-1 correspondence between \(\hbox {cos}\uptheta \) and the stress state, i.e., infinitely-many stress states can have the same \(\hbox {cos}\uptheta \). The yield condition and flow rule using the KBK representation are shown in Fig. 12a and b, respectively. As seen in the figures, the material behavior is captured much more accurately by the Yld2004-3D than by the von-Mises criterion.

5.4 Identification of post-necking hardening curve

The uniform deformation in uniaxial tension test was limited to around \(\varepsilon \approx 0.14\) at the ultimate tensile strength (UTS) in the MD. On the other hand, the predicted strains in the FE simulations of the fracture specimens are much higher (up to 0.9 equivalent plastic strain in SH specimen), which means that the post-necking hardening curve can have a significant influence on the final results. The hardening curve was represented using the combined Swift-Voce (SV) model, which gives higher flexibility in large strains than individual models, based on one of the fracture tests.

Fig. 12
figure 12

KBK representation showing the performance of von-Mises and Yld2004-3D criteria in terms of a stress and b normal to yield locus

Full size image

The Swift, Voce and combined Swift-Voce models are expressed as (Abi-Akl and Mohr 2017; Coppieters and Kuwabara 2014; Mohr and Marcadet 2015; Pack and Marcadet 2016; Sung et al. 2010; Swift 1952; Tian et al. 2017; Wang et al. 2015; Zhang and Wierzbicki 2015):

$$\begin{aligned} {\upsigma }_\mathrm{s}= & {} \hbox {k}_0 \cdot \;\left( {{\upvarepsilon }_0 +\overline{{\upvarepsilon }_\mathrm{p}} } \right) ^{\mathrm{n}} \end{aligned}$$
(13)
$$\begin{aligned} {\upsigma }_\mathrm{v}= & {} \hbox { k}_0 -\hbox {q}\cdot \hbox { exp}\left( {-{\upbeta }\cdot \overline{{\upvarepsilon }_\mathrm{p}}} \right) \end{aligned}$$
(14)
$$\begin{aligned} {\upsigma }= & {} \hbox {A}\cdot {\upsigma }_\mathrm{s} +\left( {1-\hbox {A}} \right) \;\cdot {\upsigma }_\mathrm{v} \end{aligned}$$
(15)

Initially, the Swift (1952) and Voce (Tian et al. 2017) models were fitted up to the pre-necking stress–strain curve from the uniaxial tension test in MD. Then, the post-necking hardening curve was identified by matching the F-\(\delta \) curve of the NT20-MD experiment and its FE prediction using Yld2004-3D yield criterion. This allowed identification of the post-necking hardening curve up to a true strain of 0.49. A weighting factor of 0.2 was determined between the Swift and Voce models in this way. The post-necking hardening parameters for the combined S-V model are collected in Table 4. Beyond the true strain of 0.49, the simulations use the curve extrapolated with this model. Note that while no explicit identification was performed in that latter range, a good matching of the F-\(\delta \) curve of the SH experiment by the FE model, described later, allows some confidence that the extrapolated curve is close to the actual material behavior. The entire hardening curve showing the measured, identified and extrapolated sections is shown in Fig. 13.

Table 4 Post-necking Hardening Model parameters
Full size table
Fig. 13
figure 13

Identification of post-necking hardening curve using combined Swift-Voce model

Full size image
Fig. 14
figure 14

Finite element models of the four fracture specimens, showing details of the mesh. The four central snapshots are at a scale of 1.6 times the outer two

Full size image

5.5 Finite element modeling of fracture experiments

The fracture experiments were simulated using the commercial FE package Abaqus/Standard (v6.13-13, implicit) using a user-material subroutine for the Yld2004-3D yield criterion (Giagmouris et al. 2010; Yoon et al. 2006). The 3D plasticity and FE models were required for this analysis because of the fracture initiation from the through-thickness mid-plane in most of the specimens and of the stress state being multi-axial after necking. A FE model with 1/8 size of the actual specimen was prepared for NT20, NT6 and CH specimens to take advantage of the symmetries, while a 1/2 model with symmetry in the thickness direction was created for the SH specimen. The models were meshed with quadratic, reduced-integration elements (C3D20R). A snapshot of the meshed models for all of the fracture specimens with zoomed-in regions of interest are shown in Fig. 14. The average element size in the quasi-square mesh in the gage section is approx. 0.25 mm for NT’s and CH, and 0.15 mm for SH, respectively. These sizes were determined after suitable parametric studies. In order to capture the stress gradient, a total of eight elements were arranged in the through-thickness direction. The simulations were run with two plasticity models (Yld2004-3D and von-Mises) and the combined S-V hardening model.

Fig. 15
figure 15

Equivalent plastic strain predicted by the finite element models at the onset of fracture for a NT20, b NT6, c CH and d SH specimens. Included are results of the von-Mises (left) and Yld20004-3D (right) yield criteria

Full size image
Fig. 16
figure 16

Comparison of force-displacement and strain-displacement from the experiments with predictions from finite element models for a NT20, b NT6, c CH and d SH specimens. Included are results of the von-Mises and Yld20004-3D yield criteria. The axis scales at each plot are different, depending on the specifics of each case

Full size image
Fig. 17
figure 17

Fracture locus showing the loading paths to fracture in terms of a stress triaxiality and b Lode-angle-parameter

Full size image

The plastic strain distributions from the FE models for both von-Mises and Yld2004-3D criteria are shown in Fig. 15. The strain distributions shown in FE models correspond to the onset of the fracture in the actual experiments. The plastic strains are highly localized in the through-thickness mid-plane for the NT’s and CH specimens, indicating fracture initiation from the center of these specimens and justifying the adoption of fully-3D analysis in this work. The strain in the CH specimen is concentrated near the hole, while it is distributed gradually along the transverse direction in the NT20 and NT6 specimens. The plastic strains are strongly localized within the gage section on the surface of the SH specimen.

More remarkably though, the strain gradients in NT’s are observed to be sharper in the Yld2004-3D than in the von-Mises criterion, while those in CH and SH seem comparable in both criteria. This indicates that the plasticity model plays a significant role in the prediction of fracture stresses and strains.

The fracture locus is determined by probing the fracture strains, stress triaxiality and Lode-angle-parameter from the node where fracture would initiate in the FE models, at the instant where the “global” displacement (as indicated by the virtual extensometers, see Sect. 4.3) in the FE simulations reached the experimental limit. The loading paths to fracture will be discussed more in Sect. 6.

5.6 Comparison of numerical and experimental results

The F-\(\updelta \) and strain-displacement (\(\upvarepsilon -\updelta )\) curves from the experiments and numerical simulations are shown in Fig. 16a–d for NT20, NT6, CH and SH specimens, respectively. The experimental results are compared with the FE predictions from Yld2004-3D and von-Mises criteria. The strains and displacements in both experiments and FE simulations are extracted from the surface of the specimen in the fashion described earlier (see Sect. 4.3). As seen in Fig. 16, the simulation results from the Yld2004-3D criterion generally show a better agreement than the von-Mises criterion. The von-Mises results slightly over-predict the force levels in all of the specimens and mostly miss the strain predictions as well. Although the plastic anisotropy is not severe in this material, the inability of the isotropic criterion to predict the experimental response accurately is noticeable in complex specimen geometries like the SH specimen.

6 Fracture locus and fracture initiation criteria

The ductile fracture locus of the material in the stress triaxiality (\(\upeta )\), Lode-angle-parameter (\(\bar{\uptheta } )\) and equivalent-plastic-strain-to-fracture (\(\bar{\upvarepsilon } _\mathrm{f})\) space is determined using the combined experimental-numerical approach. The loading paths to fracture are probed at the material point of the FE models with the highest equivalent plastic strain. The evolution of equivalent plastic strain of these critical points up to the fracture initiation state is shown with respect to stress triaxiality and Lode-angle-parameter in Fig. 17a, b, respectively. The stress triaxiality and Lode-angle-parameter remain more or less constant for the SH and CH specimens and are shown as solid lines, while they evolve for the NT specimens (dashed lines).

The fact that some of the specimens (i.e., SH and CH) experience proportional loading, at least at the location of fracture, while others (i.e., NT 20 and NT6) do not, casts significant doubt on whether this family of experiments is probing the same fracture locus. Clearly, plastic deformation is path-dependent; a similar path-dependence is expected for the fracture behavior. Indeed, Basu and Benzerga (2015) showed the dependence of the fracture locus on the loading paths in the triaxiality range of 0.8 and 2. It is evident that the fracture locus could be path-dependent, but the severity of this effect at triaxiality below 0.8 cannot be clearly asserted. (Note from Fig. 17a that the triaxiality range of the current study is between 0 and 0.67.)

With reference to Fig. 17, it can be seen that, except for the SH specimen, the von-Mises criterion is found to under-predict \(\bar{\upvarepsilon }_\mathrm{f} \) in comparison to Yld2004-3D. This underscores the importance of proper representation of the plastic anisotropy of the material in ductile fracture studies, as has recently begun to be appreciated (Ghahremaninezhad and Ravi-Chandar 2012; Ha et al. 2018; Haltom et al. 2013; Lou and Yoon 2017; Scales et al. 2016).

The fracture initiation criteria described in Sect. 3 are calibrated based on the Yld2004-3D results at the onset of fracture, to obtain the fracture locus for this die-cast aluminum alloy. The calibration uses a minimizing function in Matlab, based on the least-squares optimization method. Input to this procedure are the equivalent plastic strain and the stress triaxiality at the onset of fracture from all available experiments, i.e., SH, CH, NT20 and NT6. The fracture initiation loci estimated by the Oyane, Johnson–Cook, Hosford–Coulomb and the proposed criterion are shown in Fig. 18. The resulting parameters are given in Table 5. As seen in Fig. 18, the Oyane and Johnson–Cook criteria have a monotonically decreasing response, while the Hosford–Coulomb and the proposed criterion have non-monotonic responses. Given the fact that there are not enough experiments to justify the predicted loci at negative stress triaxialities, the loci are shown in dashed lines in that region. Similarly, the change of slope of the predicted locus of Hosford–Coulomb and the proposed criterion in the equibiaxial tension region (i.e., \(\eta \,=\) 0.6–0.66) cannot be fully supported by the present limited number of experiments, even more so given the non-proportional loading that the NT specimens experience. However, the proposed criterion appears to be more flexible and to provide closer approximations to the fracture strains than the other three criteria.

Fig. 18
figure 18

Fracture initiation loci estimated by the Oyane, Johnson–Cook, Hosford–Coulomb and proposed criteria

Full size image

7 Summary and conclusions

In this paper, the plasticity and ductile fracture properties of an Al–Si–Mg die-cast alloy (AA365-T7) were characterized using a combined experimental-numerical approach. A total of 15 types of experiments were performed to investigate the plasticity and fracture behavior of the material: UT, PST and DC for plasticity and NT6, NT20, CH and SH for fracture, including different orientations. In the experiments, 3D-DIC was used to capture the full-strain-fields on the specimen surface.

Finite element models of the fracture specimens were used to probe the loading paths to fracture at the critical material point. The FE results were verified by comparing their global F-\(\updelta \) and local \(\upvarepsilon -\updelta \) responses with the experiments. Since the strain predictions are more sensitive to the plasticity models adopted than the global F-\(\updelta \) response, they highlighted the differences between von-Mises and Yld2004-3D. Based on the fracture locus determined in this way, three commonly used fracture initiation criteria, i.e., the Oyane, Johnson–Cook and Hosford–Coulomb criteria and a new criterion which is a linear combination of the first two were calibrated in the triaxiality range of −1/3 and 2/3.

Table 5 Summary of fracture initiation criterion parameters
Full size table

The major conclusions from this work are:

  • The plasticity model plays an important role in the accurate prediction of the fracture strains during numerical simulations. For the particular material, and despite its limited anisotropy, the von-Mises criterion under-predicted the fracture strain, in comparison to Yld2004-3D. Similarly critical is the shape of the hardening curve at large strains.

  • A fully-3D analysis, including the description of plastic anisotropy, is required, as the stress and strain fields are spatially inhomogeneous in the fracture specimens. The 3D analysis is also required because fracture initiates in the through-thickness mid-plane of the specimens. Despite that, surface strains from DIC can be useful in establishing the fidelity of the FE and material modeling.

  • During testing, the NT6 and NT20 specimens exhibit non-proportional loading. Hence it is questionable whether they are probing the same fracture locus as the CH and SH specimens, that experience proportional loading.

  • A linear combination of two common criteria (Oyane and Johnson–Cook) is a simple way to obtain a mathematical form that is more flexible than either of the two constituents.

In closing, a natural extension of this work is to establish the path-dependence of the fracture locus, e.g., using intentionally proportional and non-proportional experiments for that purpose.