2D lattice Boltzmann investigation of saturated pool boiling using a tunable surface tension model: Prandtl number effects on film boiling

Abstract

In this paper, the saturated pool boiling is investigated using lattice Boltzmann method. The written FORTRAN code is validated in two aspects: For flow, the thermodynamic consistency test and Laplace law are applied and for heat transfer, the space- and time- averaged Nusselt number is compared with Berenson analytical solution in film boiling regime. In addition, the results of bubble generation and departure are compared with some well-known analytical solutions to show the accuracy of the code. It is confirmed that bubble departure diameter and the departure frequency are related to the gravity acceleration with powers of − 0.505 and 0.709, respectively, which is in a very good agreement with the existing analytical expressions. The present model has the ability to tune different surface tensions independent of liquid/vapor density ratio, which was unreachable using other existing numerical models of boiling. Thus, the sole effects of surface tension on boiling can also be taken into consideration using the present model. It is also shown that the departure diameter is related to the surface tension with a power of 0.485, which is in good agreement with the analytical expressions. Temperature contours are shown together with flow lines to have a better viewpoint for studying the bubble’s behavior. An intensive temperature gradient is observed in the necking area at the departure time. All the four boiling regimes in the boiling curve are simulated under constant temperature boundary condition. The Prandtl number effects on vapor bubble dynamics in the film boiling regime are investigated using the improved Shan and Chen model for the first time. Results revealed that bubbles are more resistant to depart from the vapor blanket with increasing the Prandtl number.

1 Introduction

Boiling is one of the most complicated phenomena that has many applications in different industries including aerospace industries, car factories, cooling systems and high technologic microdevices. The high non-linearity in governing equations due to mass and heat transfer, phase change and intensive density change on interface beside continuously bubble generation and departure, make the complexity of boiling. Nukiyama [1] was the first to identify different regimes in pool boiling with his well-known boiling curve. Many experimental studies were done to characterize different regimes of the boiling curve. For example, Rohsenow [2] found an expression for heat transfer in nucleation regime for different working fluids. Kutateladze [3] proposed a relation for CHF¹ point with dimensional analysis. The hysteresis phenomenon was first identified by Sakurai and Shiotsu [4]. Afterward, Ramilison and Lienhard [5] performed some experiments to study the transition regime at different contact angles. Goel et al. [6], using high-speed cameras, characterized the bubble departure in nucleate pool boiling region. To recognize the impacts of different factors on the bubble generation process, considerable researches have been done in recent years: Quan et al. [7] investigated the wetting effects of nanoparticles for a nanofluid and pointed out that nanofluids including hydrophilic nanoparticles enhance the heat flux in nucleation regime. Chen et al. [8] investigated the bubble departure diameter and its frequency in boiling nucleation regime for Methane at four different saturated pressures. They obtained a relation between bubble departure diameter and its frequency within ± 20% error. Michaie et al. [9] studied the isolated bubble dynamics for water pool boiling at pressures lower than atmospheric pressure and observed that decreasing the saturated pressure increases both the bubble departure diameter and the frequency. Abdollahi et al. [10] conducted an experiment to investigate the effects of magnetic field on boiling heat transfer. Their results revealed that applying magnetic field can considerably enhance boiling heat transfer.

Although many experiments have been performed to investigate the boiling phenomenon, still there are many unsolved questions about its complicated mechanism. In addition, recording data from inside and outside of the bubbles is a difficult work due to the small temperature and length scales. The technological improvements of computational systems have made numerical simulations an alternative to study the boiling phenomena precisely. Different numerical methods including level-set [11], Volume-of-Fluid [12], VOSET [13], Diffusive-Interface [14] and Sharp-Interface [15] methods have been used to study boiling phenomena.

All the numerical methods mentioned above are based on tracing liquid–vapor interface, which is a time-consuming process and needs solving an additional equation for each computational cell. Moreover, the computational domain must be initialized with small bubbles to start the boiling process, which makes it impossible to measure the waiting time, departure time and bubble nucleation. Identifying the liquid–vapor interface and mass transfer on the interface, the very low required computational time and easy-coding have converted the Lattice Boltzmann Method (LBM) to a powerful tool for solving engineering problems. In the following, the most recent researches on boiling using LBM are reviewed.

Ryu and Ko [16] proposed a 2D LB model for nucleation regime based on the free energy method. Sun and Li [17] studied the nucleation and bubble generation in a 3D domain using a hybrid method. Li et al. [18] investigated the boiling curve and wetting effects. Assuming constant ρc_v and using the fourth order Rung-Kutta method for discretization, they successfully modeled all the boiling regimes at low density ratio (≅ 17). A LBM study on the periodic bubble generation at high density radio was done by Begmohammadi et al. [19]. Gong and Cheng [20] modeled the periodic bubble generation, growth and departure. In their study, ρc_P and specific heat coefficients c_P = c_v were assumed to be constant in the whole domain. They successfully modeled the bubble generation process at constant temperature and constant heat flux boundary conditions. The temperature profiles inside and outside of the bubble were analyzed and the bubble waiting time was calculated under the constant heat flux condition for the first time. Later on, Zhang and Cheng [21] compared the two terms appearing in the phase change source term and confirmed that the assumptions of constant ρc_P and c_P = c_v in the whole computational domain enter no considerable error in the results. Fang et al. [22] modeled the pool boiling at high density ratio using a conjugated boundary condition. In their study, at first the bubble generation and its departure was investigated, then the heat transfer from the wall was compared with the first fluid layer heat flux near the wall and finally, the effects of reduced temperature T_r = T/T_c and cavity shape on pool boiling were studied. They concluded that the average heat flux of boiling at reduced temperature T_r = 0.68 is much higher than that at T_r = 0.86. In addition, they reported that in the boiling simulations at different cavity shapes, the circle shape has the highest heat flux, while the lowest heat flux occurs at a plane with no cavity. In their study, however, the heat transfer inside the heater was ignored. Gong and Cheng [23], in another study, analyzed the temperature distribution inside the heater and investigated the boiling curve including the effects of the heater length. In this study, it was shown that the thermal conductivity coefficient and ρc_P of the heater have no effect on nucleation and CHF, but increasing these parameters shifts the boiling curve to the left side. They noted that the conjugated boundary condition includes some errors near the wall in nucleation and transition regimes, as well as CHF point, which should be considered in calculating heat transfer from the wall.

In the present paper, we have investigated the pool boiling using an improved Shan and Chen two-phase model. A source term is added to the collision operator in order to tune different surface tensions independent of the density ratio, which was unreachable using other models of boiling. Although this source term was proposed by Li et al. [24], it has never been used for modeling the boiling process. Furthermore, the Prandtl number effects on vapor bubbles in film boiling regime are studied using the improved Shan and Chen two-phase model for the first time. Temperature contours are also shown together with flow lines to have a better viewpoint for studying the bubble’s behavior. In this paper, all physical parameters are in lattice units (mu: mass unit, ts: time step, tu: temperature unit, lu: lattice unit). The rest of the paper is organized as follows: In Sect. 2 the mathematical modeling relations are presented. In Sect. 3 the computation setup is given. In Sect. 4 the code validation is done using some well-known benchmark tests. In Sect. 5 the results are analyzed and at the end, a summary and some conclusions are provided in Sect. 6.

2 Mathematical modeling

In this section, we provide the mathematical modeling of boiling used in this paper. All the equations presented here are taken from the literature (mainly from Refs. [24,25,26]). The only minor contribution is using the previously introduced source term (C in Eq. 17) added by Li et al. [24] to the MRT lattice Boltzmann equation, which allows us to change surface tension independently from density ratio. As long as the authors know, this source term has been used for modeling droplet phenomena and it is the first time to apply it in boiling problems.

2.1 The lattice Boltzmann method

The lattice Boltzmann method is a kinematic method based on molecular collisions. The distribution function (f) plays the key role in the lattice Boltzmann model. The lattice Boltzmann equation with Bhatnagar–Gross–Krook (BGK) model in the presence of the external force (F) is expressed as [27]:

$$f_{\alpha } (x + e_{\alpha } \delta t,t + \delta t) - f_{\alpha } (x,t) = - \frac{1}{\tau }\left( {f_{\alpha } \left( {x,t} \right) - f_{\alpha }^{eq} \left( {x,t} \right)} \right) + \delta tF_{\alpha }$$

(1)

where δt = 1 is set for simplicity. Based on the BGK model, the result of the collision is a new distribution function which tends to reach its equilibrium distribution function (f^eq). τ is a time criterion that indicates whether distribution functions reach their equilibrium distribution or not. τ is called relaxation time.

The D2Q9 mesh is used here. It is a square mesh with δx = 1 that allows the particles to move only in one of the 8 defined directions. An additional direction is considered for the probability of particles that do not move. In Eq. 1, the index α denotes one of the 9 directions for spreading information and e_α is the velocity vector in α direction. x is spatial position of particles and t is time, both in lattice units.

For incompressible flows (low Mach numbers), the equilibrium distribution function is expressed as [27]:

$$f_{\alpha }^{eq} = w_{\alpha } \rho \left[ {1 + \frac{{e_{\alpha } \cdot V}}{{c_{s}^{2} }} + \frac{{\left( {e_{\alpha } \cdot V} \right)^{2} }}{{2c_{s}^{4} }} - \frac{V \cdot V}{{2c_{s}^{2} }}} \right]$$

(2)

where the ρ and V are macroscopic values of density and velocity, respectively. $c_{s} = c/\sqrt 3$ and the weighting factors, w_α, are defined as [27]:

$$w_{\alpha } = \left\{ {\begin{array}{*{20}l} {4/9} \hfill & {\alpha = 0} \hfill \\ {1/9} \hfill & {\alpha = 1 \sim 4} \hfill \\ {1/36} \hfill & {\alpha = 5 \sim 8} \hfill \\ \end{array} } \right.$$

(3)

In this paper the force scheme proposed by Li et al. [25] is adopted:

$$F_{\alpha } = w_{\alpha } \delta t\left( {1 - \frac{1}{2\tau }} \right)\left[ {\frac{{e_{\alpha } - V^{{\prime }} }}{{c_{s}^{2} }} + \frac{{\left( {e_{\alpha } \cdot V^{{\prime }} } \right)}}{{c_{s}^{4} }}e_{{_{\alpha } }} } \right] \cdot F$$

(4)

where F = F_f−f + F_f−s + F_g includes fluid–fluid force (F_f−f), fluid–solid force (F_f−s), and the gravity force (F_g). V^′ is defined as:

$$V^{\prime } = V + \varepsilon F/\left( {\left( {\tau - 0.5} \right)\psi^{2} } \right)$$

(5)

where ɛ is a parameter adjusted to reach thermodynamic consistency. ψ is interaction potential that plays an important role in calculation of intermolecular forces.

In order to achieve a more stable numerical model, collision operator with Multi Relaxation Time (MRT) is used. The MRT lattice Boltzmann equation is expressed as [27]:

$$f_{\alpha } \left( {x + e_{\alpha } \delta t,t + \delta t} \right) - f_{\alpha } \left( {x,t} \right) = - \sum\limits_{i} {\varLambda_{\alpha i} \left( {f_{i} - f_{i}^{eq} } \right)} + \delta t\left( {s_{\alpha } - \frac{1}{2}\sum\limits_{i} {\varLambda_{\alpha i} s_{i} } } \right)$$

(6)

where Λ is the relaxation time matrix and s is the force term. Comparing Eqs. 6 with 4 and 1, the force term s can be derived as:

$$s_{\alpha } = w_{\alpha } \left[ {\frac{{e_{\alpha } - V^{{\prime }} }}{{c_{s}^{2} }} + \frac{{\left( {e_{\alpha } \cdot V^{{\prime }} } \right)}}{{c_{s}^{4} }}e_{\alpha } } \right] \cdot F$$

(7)

Performing the collision step in momentum space is much convenient. This is done by multiplying the transformation matrix, M, to the right-hand side of Eq. 6:

$$M \cdot \left( {RHS{\text{ of Eq}} . ( 6 )} \right) = m = - \sum\limits_{i}^{{}} {\hat{\varLambda }_{\alpha i} \left( {\hat{f}_{i} - \hat{f}_{i}^{eq} } \right)} + \delta t\sum\limits_{i}^{{}} {\left( {I_{\alpha i} - \frac{1}{2}\hat{\varLambda }_{\alpha i} } \right)\hat{s}_{i} }$$

(8)

The matrix M in D2Q9 is expressed as [27]:

$$M = \left[ {\begin{array}{*{20}l} 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ { - 4} \hfill & { - 1} \hfill & { - 1} \hfill & { - 1} \hfill & { - 1} \hfill & 2 \hfill & 2 \hfill & 2 \hfill & 2 \hfill \\ 4 \hfill & { - 2} \hfill & { - 2} \hfill & { - 2} \hfill & { - 2} \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & { - 1} \hfill & 0 \hfill & 1 \hfill & { - 1} \hfill & { - 1} \hfill & 1 \hfill \\ 0 \hfill & { - 2} \hfill & 0 \hfill & 2 \hfill & 0 \hfill & 1 \hfill & { - 1} \hfill & { - 1} \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & { - 1} \hfill & 1 \hfill & 1 \hfill & { - 1} \hfill & { - 1} \hfill \\ 0 \hfill & 0 \hfill & { - 2} \hfill & 0 \hfill & 2 \hfill & 1 \hfill & 1 \hfill & { - 1} \hfill & { - 1} \hfill \\ 0 \hfill & 1 \hfill & { - 1} \hfill & 1 \hfill & { - 1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & { - 1} \hfill & 1 \hfill & { - 1} \hfill \\ \end{array} } \right]$$

(9)

In Eq. 8, I is the unit matrix, $\hat{f}_{i}$ and $\hat{f}_{i}^{eq}$ are distribution function and equilibrium distribution function, respectively, in momentum space and are given as:

$$\hat{f} = Mf$$

(10)

$$\hat{f}^{eq} = Mf^{eq} = \rho \left( {1, - 2 + 3\left| V \right|^{2} ,1 - 3\left| V \right|^{2} ,V_{x} , - V_{x} ,V_{y} , - V_{y} ,V_{x}^{2} - V_{y}^{2} ,V_{x} V_{y} } \right)^{T}$$

(11)

where V_x and V_y are components of macroscopic velocity (V). In Eq. 8, $\hat{\varLambda }$ is a diagonal relaxation time matrix in momentum space which is expressed as [28]:

$$\begin{aligned} \hat{\varLambda } = M\varLambda M^{ - 1} = diag\left( {s_{1} ,s_{2} ,s_{3} ,s_{4} ,s_{5} ,s_{6} ,s_{7} ,s_{8} ,s_{9} } \right) = \hfill \\ {\text{ diag}}\left( {\tau_{\rho }^{ - 1} ,\tau_{e}^{ - 1} ,\tau_{\zeta }^{ - 1} ,\tau_{j}^{ - 1} ,\tau_{q}^{ - 1} ,\tau_{j}^{ - 1} ,\tau_{q}^{ - 1} ,\tau_{{}}^{ - 1} ,\tau_{{}}^{ - 1} } \right) \hfill \\ \end{aligned}$$

(12)

where ρ, e, j and q are density quantity, energy, momentum and energy flux, respectively. ζ is related to the energy radical. τ is relaxation time which is related to the kinematic viscosity as:

$$\upsilon = \left( {\tau - 0.5} \right)c_{s}^{2}$$

(13)

From the conservation laws of mass and momentum, macroscopic density and velocity can be obtained from the distribution functions as:

$$\rho = \sum _{\alpha } f_{\alpha }$$

(14)

$$\rho V = \sum\limits_{\alpha } {f_{\alpha } } e_{\alpha } + \frac{\delta t}{2}F$$

(15)

Li et al. [29] presented the following relation for the force term $\hat{s}$ as:

$$\hat{s} = \left[ {\begin{array}{*{20}c} 0 \\ {6\left( {V_{x} F_{x} + V_{y} F_{y} } \right) + \frac{{12\varepsilon \left| F \right|^{2} }}{{\psi^{2} \left( {1/s_{2} - 0.5} \right)}}} \\ { - 6\left( {V_{x} F_{x} + V_{y} F_{y} } \right) - \frac{{12\varepsilon \left| F \right|^{2} }}{{\psi^{2} \left( {1/s_{3} - 0.5} \right)}}} \\ {F_{x} } \\ { - F_{x} } \\ {F_{y} } \\ { - F_{y} } \\ {2\left( {V_{x} F_{x} - V_{y} F_{y} } \right)} \\ {V_{x} F_{y} - V_{y} F_{x} } \\ \end{array} } \right]$$

(16)

In order to change the surface tension independently from the density ratio, Li et al. [24] added a source term to the MRT lattice Boltzmann equation that modifies the right-hand side of Eq. 8 as follows:

$$m_{new} = - \sum\limits_{i}^{{}} {\hat{\varLambda }_{\alpha i} \left( {\hat{f}_{i} - \hat{f}_{i}^{eq} } \right)} + \delta t\sum\limits_{i} {\left( {\left( {I_{\alpha i} - \frac{1}{2}\hat{\varLambda }_{\alpha i} } \right)\hat{s}_{i} + C_{i} } \right)}$$

(17)

where C_i is:

$$C = \left[ {\begin{array}{*{20}c} 0 \\ {1.5\tau_{e}^{ - 1} \left( {Q_{xx} + Q_{yy} } \right)} \\ { - 1.5\tau_{\varsigma }^{ - 1} \left( {Q_{xx} + Q_{yy} } \right)} \\ 0 \\ 0 \\ 0 \\ 0 \\ { - \tau^{ - 1} \left( {Q_{xx} - Q_{yy} } \right)} \\ { - \tau^{ - 1} Q_{xy} } \\ \end{array} } \right]$$

(18)

and Q_xx, Q_xy and Q_yy can be obtained from the following equation:

$$Q = \kappa \frac{G}{2}\psi \left( {x,t} \right)\left[ {\sum\limits_{\alpha } {w\left( {\left| {e_{\alpha } } \right|^{2} } \right)\left[ {\psi \left( {x + e_{\alpha } ,t} \right) - \psi \left( {x,t} \right)} \right]e_{\alpha } e_{\alpha } } } \right]$$

(19)

where κ is a parameter for tuning different surface tensions independently from the density ratio. In Eq. 19 w(1) = 1/3 and w(2) = 1/12 are weighting coefficients.

The streaming step can be done in velocity field as follows:

$$f_{\alpha } \left( {x + e_{\alpha } \delta t,t + \delta t} \right) = M^{ - 1} \left( {\hat{f} + m_{new} } \right)$$

(20)

2.2 Two-phase model

The Shan and Chen two-phase model is based on intermolecular forces. In this model, the intermolecular fluid–fluid force is expressed as [26]:

$$F_{f - f} \left( {x, t} \right) = - G\psi \left( {x, t} \right)\left[ \sum _{\alpha } w\left( {|e_{\alpha } |^{2} } \right)\psi \left( {x + e_{\alpha } , t} \right)e_{\alpha}\right]$$

(21)

where G is the strength of fluid–fluid interaction force. Applying the Taylor expansion of first order over Eq. 21 and using the relation between pressure and force, the pressure can be obtained as [25]:

$$P = \rho c_{s}^{2} + \frac{{Gc^{2} }}{2}\psi^{2}$$

(22)

It has been proved that using Eq. 21 for fluid–fluid interaction force leads to the following mechanical stability criterion [25]:

$$\int_{{\rho_{v} }}^{{\rho_{l} }} {\left( {P_{0} - \rho c_{s}^{2} - \frac{{Gc^{2} }}{2}\psi^{2} } \right)\frac{\psi '}{\psi }d\rho = 0}$$

(23)

where P₀ = P(ρ_v) = P(ρ_l) is the saturated pressure and ψ’ = dψ/dρ. Substituting Eq. 22 into the equation of Maxwell construction for thermodynamic consistency yields the following equation [25]:

$$\int_{{\rho_{v} }}^{{\rho_{l} }} {\left( {P_{0} - \rho c_{s}^{2} - \frac{{Gc^{2} }}{2}\psi^{2} } \right)\frac{1}{{\rho^{2} }}d\rho = 0}$$

(24)

Comparing Eqs. 23 with 24, it turns out that for preserving the thermodynamic consistency we must have:

$$\psi \propto exp \left( { - 1/\rho } \right)$$

(25)

Using Eq. 25 does not lead to an Equation of State (EOS) for a real gas [30]. In the cost of losing thermodynamic consistency, Yuan and Schaefer [31] obtained ψ from Eq. 22 so that any real EOS can be adopted in the model:

$$\psi = \sqrt {\frac{{2\left( {P_{EOS} - \rho c_{s}^{2} } \right)}}{{Gc^{2} }}}$$

(26)

It should be noted that, although G is eliminated through using Eq. 26 together with Eq. 22, it affects setting the parameter ɛ for reaching the thermodynamic consistency.

In this paper Peng-Robinson EOS is adopted, which is widely used in the literature for Water and Ammonia boiling simulations. This equation of state can be expressed as:

$$P_{EOS} = \frac{\rho RT}{1 - b\rho } - \frac{{a\left[ {(1 + 0.37464 + 1.54226\omega - 0.26992\omega^{2} )\left( {1 - \sqrt {\frac{T}{{T_{c} }}} } \right)} \right]^{2} \rho^{2} }}{{1 + 2b\rho - b^{2} \rho^{2} }}$$

(27)

with ω being the acentric factor that is dependent on the fluid structure. The parameters a = 0.45724R²T ² _c /P_c and b = 0.0778RT_c/P_c are related to critical temperature (T_c), critical pressure (P_c) and gas constant $R = \bar{R}/M$, where $\bar{R}$ is the universal gas constant and M is molecular weight. Setting smaller values of a causes thicker interface but higher density ratios are achievable [22]. In this study, the parameters in EOS are set as: a = 0.06122, b = 2/21, R = 1

In the Shan and Chen two-phase model, fluid–solid interaction force can be modeled as [26]:

$$F_{f - s} \left( {x, t} \right) = - G_{ads} \psi \left( {\rho_{w} } \right)\psi \left( {x, t} \right)\left[ { \sum _{\alpha } w\left( {|e_{\alpha } |^{2} } \right)S\left( {x + e_{\alpha } } \right)e_{\alpha } } \right]$$

(28)

where G_ads is fluid–solid interaction strength and S is a switch function that enables the fluid–solid interaction force only on a direction of fluid nodes which ends to a solid node. The virtual density ρ_v < ρ_w < ρ_l is attributed to the solid nodes in order to achieve different contact angles.

In problems such as bubble generation and detachment, the more stable way to incorporate the gravity force is [32]:

$$F_{g} = g\left( {\rho - \rho_{ave} } \right)$$

(29)

where ρ_ave is the average density of the computational domain at each time step.

2.3 Energy equation

To solve the energy equation, similar to the flow equation, a new temperature distribution function (U) is considered. The governing equation of U with SRT² operator in the presence of the source term (ϕ) is expressed as:

$$U_{\alpha } \left( {x + e_{\alpha } \delta t + \delta_{t} } \right) - U_{\alpha } \left( {x,t} \right) = - \frac{1}{{\tau_{T} }}\left( {U_{\alpha } \left( {x,t} \right) - U_{\alpha }^{eq} \left( {x,t} \right)} \right) + \delta tw_{\alpha } \phi$$

(30)

where U ^eq _α is equilibrium temperature distribution function, which is given by [27]:

$$U_{\alpha }^{eq} = w_{\alpha } T\left[ {1 + \frac{{e_{\alpha } \cdot V}}{{c_{s}^{2} }} + \frac{{\left( {e_{\alpha } \cdot V} \right)^{2} }}{{2c_{s}^{4} }} - \frac{V \cdot V}{{2c_{s}^{2} }}} \right]$$

(31)

where T is macroscopic temperature. In Eq. 30, ϕ is the source term responsible for phase change and τ_T is the thermal relaxation time that is related to thermal diffusivity by:

$$\alpha = c_{s}^{2} \left( {\tau_{T} - 0.5} \right)\delta t$$

(32)

A D2Q9 scheme is also chosen for temperature computation. The macroscopic temperature is the sum of temperature distribution functions in all directions:

$$T = \sum _{\alpha } U_{\alpha }$$

(33)

After performing some algebra, the entropy balance equation yields the following source term responsible for phase change,ϕ, as [23]:

$$\phi = \mathop {\underline{{\left\{ {T\left[ {1 - \frac{1}{{\rho c_{v} }}\left. {\frac{\partial P}{\partial T}} \right|\rho } \right]\nabla \cdot V} \right\}}} }\limits_{First Term} + \mathop {\underline{{\left\{ {\frac{1}{{\rho c_{v} }}\nabla \cdot \left( {k\nabla T} \right) - \nabla \cdot \left( {\alpha \nabla T} \right)} \right\}}} }\limits_{{\text{Sec} ond Term}}$$

(34)

where α = k/(ρc_P) is the thermal diffusivity. The derived ϕ equation consists of two terms: the first term accounts for compressibility effects and the second term considers the change in thermophysical properties in the computational domain. In most studies in the literature, the second term is neglected due to its small magnitude compared to the first term. Neglecting the second term means c_p = c_v and ρc_v = const. in the whole computational domain. In this paper, both terms of Eq. 34 are taken into consideration in order to have different special heat capacities for each phase.

Equation 34 must be discretized in the computational domain. The stable discretization method proposed by Lee and Lin [33] is used in this paper. All fluid properties (ξ) (such as thermal diffusivity and viscosity) are given by the following linear interpolation:

$$\xi = \xi_{v} + \frac{{\rho - \rho_{v} }}{{\rho_{l} - \rho_{v} }}\left( {\xi_{l} - \xi_{v} } \right)$$

(35)

3 Computation setup

The widely used characteristic length (l₀) in boiling literature represents the ratio of surface tension to buoyancy force and is given by:

$$l_{0} = \sqrt {\frac{\sigma }{g\Delta \rho }}$$

(36)

Based on the characteristic length given by Eq. 36, the characteristic velocity u₀ and the characteristic time t₀ are defined as:

$$u_{0} = \sqrt {gl_{0} }$$

(37)

$$t_{0} = \frac{{l_{0} }}{{u_{0} }}$$

(38)

Using this characteristic length, the Bond number becomes constant (Bo = gΔρ[σ/(gΔρ)]/σ = 1) and is replaced by a new non-dimensional number (L_H/l₀), where L_H is the heater length. Thus, the group of dimensionless numbers resulted from the Buckingham theorem is: (Nu, Pr, Ja, L_H/l₀)

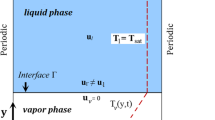
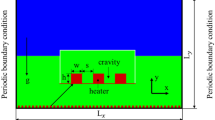
The 2D computational domain lx × ly is shown in Fig. 1 schematically. Periodic boundary conditions are imposed on the left and right sides of the computational domain and the top has the outlet boundary condition. At the bottom of the computational domain, the no-slip wall boundary condition is implemented. The length L_H with equal distance from the sides has the constant temperature T_w > T_sat and the rest of the wall is insulated.

Fig. 1

Physics, flow boundary conditions: wall boundary condition at the bottom; outflow at the top; periodic at both sides, and temperature boundary conditions: constant temperature or heat flux at the heated length (L_H) and the rest of the wall isolated; the top is at saturated temperature; both sides periodic

The initial temperature in the whole domain is the saturated temperature with the reduced temperature T_r = 0.86 and the initial density is the saturated density of liquid phase. The density ratio at the given reduced temperature is ρ_l/ρ_v = 17.1. Pr _l and Pr _v are inputs, τ_l = 0.65 and τ_v = 0.8 are set and from Eq. 13 υ_l and υ_v are obtained. Therefore, from the relation α = υ/ Pr thermal diffusivity is calculated for each of two phases and writing the Eq. 32 for τ_T, the thermal relaxation time can be obtained for each phase separately. For the calculation of specific latent heat (h_fg), the analytical expression given in Ref. [20] is used. Equalizing the dimensionless numbers to those of possible experiment setups, the gravity acceleration g = 3 × 10⁻⁵(lu ts⁻²) and specific heat c_p,l = c_v,l = 4(lu² tu ts⁻²), c_p,v = c_v,v = 2(lu² tu ts⁻²) are set. The Jacob number can be calculated as Ja = c_p,lΔT/h_fg. Contact angle (θ) and surface tension (σ) are obtained from statistic droplet test and Laplace law, respectively.

To improve the numerical stability, temperature equation is not solved during the period 0 ≤ t ≤ 2000δt. Wall temperature is also increased stepwise until the specified temperature (T_w) in the period 2000δt < t ≤ 15,000δt to smooth temperature jump. In order to enhance the bubble generation, small temperature fluctuations in the form of T(x) = T_w + 0.03T_c × sin [2π(x − lx/4)/lx] are applied in the period 15,000δt < t ≤ 25,000δt. Results are reported for times t > 30,000δt to ensure that small fluctuations are eliminated.

4 Validation

The flow validation is done for thermodynamic consistency, Laplace law, and contact angle in “Appendices 1, 2 and 3”, respectively. Here, we focus more on the heat transfer aspect of the phenomenon.

4.1 Nusselt number

In this section, the space- and time- averaged Nusselt number for film boiling is compared to the Berenson analytical expression [34], which is given as:

$$\overline{Nu} = \frac{{\bar{h}L_{H} }}{{k_{v} }} = 0.425*2\sqrt 3 \pi \left[ {\frac{{\rho_{v} \left( {\rho_{1} - \rho_{v} } \right)gh_{fg}^{{\prime }} }}{{k_{v} \mu_{v} \left( {T_{w} - T_{sat} } \right)}}} \right]^{1/4} \left[ {\frac{\sigma }{{g\left( {\rho_{1} - \rho_{v} } \right)}}} \right]^{3/8}$$

(39)

In the above equation, h ^′ _fg  = h_fg + 0.5c_p,v(T_w − T_sat) is sum of latent heat and sensible heat transfer to the vapor film. The space-averaged Nusselt number from the code is calculated using the following equation:

$$\overline{Nu}_{{_{LBM} }} \left( t \right) = \frac{{\bar{h}L_{H} }}{{k_{v} }} = - \frac{1}{{\left( {T_{w} - T_{sat} } \right)}}\frac{1}{{k_{v} }}\int\limits_{\text{Heated Area}} {k(x,2)\nabla_{y} T\left| {_{x,0} dx} \right.}$$

(40)

where local temperature gradient at the heating wall surface is evaluated using the second order central extrapolation scheme:

$$\nabla_{y} T\left| {_{x,0} } \right. = \frac{{4T\left| {_{x,1} } \right. - T\left| {_{x,2} } \right. - 3T\left| {_{x,0} } \right.}}{2\delta y}$$

(41)

In this equation, δy = 1 is lattice step in y direction. After reaching steady state condition, Eq. 40 can be integrated over a long period of time (30.76 < t ^* _a  < 60.76) to obtain the space- and time- averaged Nusselt number.

In this paper a 400 × 600lu domain is used for the simulation of film boiling and the heating length L_H = 200lu is set at constant temperature T_w. The space- and time- averaged Nusselt number from our simulation is 31.067, which has an error of 9.98% compared to the result of Berenson expression (= 34.512), that is acceptable considering the complexity of boiling phenomenon. One of the sources of this deviation is the finite length heating surface [23].

The space-averaged Nusselt number versus the dimensionless time t^* = t/t₀ is shown in the Fig. 2. The peaks and valleys in this figure are due to the continuously releasing bubbles from the vapor film.

Fig. 2

Comparison of dimensionless time evolution (t^*) of space-averaged Nusselt number ($\overline{Nu}$) predicted by the present model with the analytical expression of Berenson (Eq. 39)

4.2 Benchmark tests

Now that the code is validated for both flow and energy, the variation of bubble departure diameter and its frequency versus gravity acceleration will be compared to the well-known analytical expressions, which are used as two important benchmark problems in the literature. Furthermore, the variation of surface tension versus gravity acceleration will be compared to the analytical results, to show the ability of the written code for changing surface tension independently from the density ratio.

To generate one stable bubble, a computational domain of 200 × 600lu is considered. The heating length L_H = 10lu has constant temperature T_w with Ja = 0.2. Contact angle θ = 87.4° and surface tension σ = 0.064 are obtained numerically. The Prandtl number is set the same for both phases (Pr = 1). The process of bubble generation until its departure is shown in Fig. 3.

Fig. 3

Bubble generation, growth and departure process (L_H/l₀ = 0.54, Ja = 0.2, Pr_v = Pr_l = 1, g = 3e − 5, θ = 87.4°)

The equivalent bubble diameter is given by [35]:

$$D_{d} = \sqrt {\frac{8}{3\pi }a_{1} a_{2} }$$

(42)

where a₁ and a₂ are maximum vertical and horizontal length of the departed bubble, respectively, that can be obtained from the numerical simulation at the departure time.

The widely used analytical expression for departure diameter is obtained from equalizing the buoyancy force with surface tension at departure time and is expressed as:

$$D_{d} \propto \sqrt {\frac{\sigma }{g\Delta \rho }}$$

(43)

The constant that converts the above relation to an equality is depended on the contact angle [35]. Based on the Relation 43, the departure diameter is related to the gravity acceleration with the power of − 0.5 (D_d ∝ g^−0.5). The fitted curve for D_d versus g in the present work is of power − 0.505 (D_d ∝ g^−0.505), as shown in Fig. 4, which is in excellent agreement with the analytical expression 43.

Fig. 4

Departure diameter (left vertical axis and square marker) and departure time (right vertical axis and circle marker) versus gravity acceleration ($Ja = 0.2{ , }\theta = 87.43^\circ$). The dashed lines are fitted curves shown with their equations

The well-known equation for the departure frequency is proposed by Zuber [36]:

$$f_{d}^{ - 1} = \frac{{D_{d} }}{0.59}\left[ {\frac{\sigma g\Delta \rho }{{\rho_{l}^{2} }}} \right]^{ - 0.25}$$

(44)

From the Relation 43 we have D_d ∝ g^−0.5, thus f ⁻¹ _d  ∝ g^−0.75. Although the numerical model cannot predict the prefactor of Eq. 44 well, the power fitted curve (shown in Fig. 4) gives us f ⁻ _d  ∝ g^−0.709, which is in a very good agreement with the analytical expression 44. Maybe one of the error reasons is that the natural convection between the liquid and the heating area is not taken into consideration in the Zuber’s analytical expression [22].

In all other numerical LB models used for the simulation of boiling, the density ratio must be changed for having different surface tensions. The ability of the present model to change the surface tension independently of the density ratio makes it possible to correlate the departure diameter to the surface tension. Figure 5 shows the proportionality of surface tension to departure diameter. The predicted LB simulation gives D_d ∝ σ^0.485 that agrees well with Eq. 43.

Fig. 5

Departure diameter (square marker) versus surface tension (T_r = 0.86). The dashed line is the power fitted curve shown with its equatio

For further explanation of bubble generation process, streamlines and dimensionless temperature contour, T^* = (T − T_sat)/(T_w − T_sat), in one periodic cycle of bubble growth is depicted in Fig. 6. As shown in this figure, the bubble growth and its departure causes symmetric vortices to generate at both sides of the bubble. At the right-hand side of the growing bubble, vortices rotate clockwise and at the left-hand side, they rotate counter-clockwise, which enforce the bubble to move upward. At the necking time (t^* = 97.27), an intensive temperature gradient is appeared and temperature increases, but it disapears after bubble departure.

Fig. 6

Dimensionless temperature contour (T^*) and streamlines in a periodic cycle of bubble generation ($Ja = 0.2{ , }\theta = 87.43^\circ$): bubble nucleation (T^* = 91.27), necking (T^* = 97.27), departure (T^* = 101.08), and regeneration (T^* = 121.67). Thick solid line indicates the growing bubble interface. Units of axes and legend are shown only on the first picture to avoid repeating information

5 Results and discussion

5.1 Boiling curve

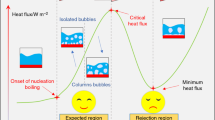
To distinguish different boiling regimes, the boiling curve is essential. The present numerical LB code can successfully simulate all the four regimes of saturated pool boiling as shown in Fig. 7. Based on this curve, heat flux from the heating surface increases linearly with Jacob number until Ja = 0.11, which is ONB³ point. The region before ONB is called free convection regime that no bubble is generated and the main reason for the fluid motion near the surface is the density difference. At the point ONB, because of bubble nucleation, the heat flux increases sharply and makes a different regime with different features called boiling nucleation regime. This regime can be divided into two different regions: (1) the region between the point ONB and the point (A), Ja = 0.13, that isolated bubbles are generated, and (2) the region between ONB and the maximum heat flux point (CHF), Ja = 0.16, that more bubble nucleation sites are active and bubbles coalesce. Boiling process at three different times is shown in Fig. 8A for point A as a sample of nucleation regime. After CHF, in the transition region, each point oscillates between nucleation and film boiling regimes. Sometimes the heating area is covered with vapor blanket and sometimes bubbles are departed from the surface separately. The process is completely unstable and each point has the potential for generating bubble. In Fig. 8B boiling process at point (B), Ja = 0.19, is shown as a sample of transition regime. With increasing the superheat, the averaged heating area places covered with vapor phase are increased and because of the vapor low thermal conductivity compared to the fluid, the heat flux decreases until the point MHF,⁴ Ja = 0.26. From this point, any further increase in superheat causes the whole heating area to be covered with vapor phase and bubbles are no longer departed from the surface but from the vapor blanket. Film boiling process at point (C), Ja = 0.3, is shown in Fig. 8C.

Fig. 7

Space and time averaged heat flux versus Jacob number known as boiling curve ($\Pr_{v} = \Pr_{l} = 1{ , }\theta = 84.6^\circ {\text{ , L}}_{H} /l_{0} = 10.7{\text{ , T}}_{r} = 0.86$). Different boiling regimes: free convection (Jacob numbers lower than that of ONB point), nucleate boiling (ONB to CHF, point A), transition region (CHF to MHF, point B), and film boiling (Jacob numbers greater than that of MHF point, point C)

Fig. 8

Boiling process in accordance with boiling curve (Fig. 7): a nucleation (point A), b transition (point B), c film boiling (point C). Units of axes and legend are shown only on the first picture to avoid repeating information

In Fig. 9 the space-averaged Nusselt number, $\overline{Nu} = \frac{{Q^{{\prime }} L_{H} }}{{k_{v} \Delta T}}$, with Q′ being the space-averaged heat flux over heating surface, versus dimensionless time t^* for points ONB, A, CHF, B, C and the point corresponded to Ja = 0.35, are compared. As can be seen from this figure, at point ONB, because of no bubble generation, the space-averaged Nusselt number is almost constant, while bubble generation causes considerable heat flux enhancement in other points. The fluctuations for points A and B are more than film boiling, clarifying that small bubbles can be departed from different parts of the heating area in nucleation and transition regimes, while in film boiling regime less number of bubbles detach from the vapor film but regularly. The CHF point has the highest space-averaged Nu number as was expected.

Fig. 9

Spaced-averaged Nu number ($\overline{Nu}$) versus dimensionless time (t^*) at points ONB, A, CHF, B, C and the point corresponded to Ja = 0.35

To analyze the film boiling, the dimensionless temperature distribution, T^*, and streamlines for boiling at point Ja = 0.35, at t^* = 49.43, are presented in Fig. 10. The thick solid line indicates the liquid–vapor interface. As shown, the vapor blanket in contact with the wall has wall temperature (T^* = 1), and far away from the wall the fluid is at saturation temperature (T^* = 0). At this time (t^* = 49.43), two symmetric bubbles are detaching from the vapor blanket, lower parts of them warmer than upper parts. Inside the bubbles, the flow lines are upward, indicating that bubbles move upward. Two vortices are generated in the space between bubbles. The vortices on the left-hand side are rotating clockwise while the vortices on the right-hand side are rotating counter-clockwise, causing the flow to move downward in the middle of the domain and then go upward from the inside of the bubbles.

Fig. 10

Dimensionless temperature contour (T^*) along with streamlines in film boiling (thick solid line indicates the liquid–vapor interface) t^* = 49.43, Ja = 0.35, Pr = 1

5.2 Effects of contact angle on pool boiling

In Fig. 11 the effect of contact angle on boiling curve is shown. As can be seen in this figure, at very low Jacob numbers (Ja < 0.06), because of no bubble generation, curves are very close to each other, meaning that boiling curve is almost independent of contact angle in this region. Increasing Jacob number in free convection region causes the hydrophobic curve (θ = 122.5°) to steepen and meet the other two curves at point Ja = 0.065. This occurs due to the fact that bubbles appear sooner at hydrophobic surfaces than hydrophilic ones, generating vortices that leads to heat transfer increase. Comparing the two curves θ = 73.2° and θ = 84.6°, it turned out that in the curve with higher wettability (θ = 73.2°) the ONB point shifted to right side and bubble generation delayed. With increasing the wettability, heat transfer generally increases and as shown in the figure, the boiling curve with θ = 73.2° is often located upper than the curve with θ = 84.6° (except for isolated bubble region). The CHF decreases and occurs at lower Jacob numbers as contact angle increases, which is also reported in Ref. [22]. This is because bubbles tend to attach to the wall with higher contact angle. The hydrophobic curve is upper than hydrophilic curves only in nucleate boiling regime since in this region the dominant factor responsible for heat transfer is the movement of nearby flow by bubble generation. This occurs more in hydrophobic surfaces because of activation of more nucleation sites. The hydrophobic surface has a high potential for film boiling, when vapor phase covers the entire heating surface. Therefore, because of low heat transfer coefficient of vapor, the hydrophobic boiling curve is lower than hydrophilic ones.

Fig. 11

Boiling curve for three different contact angles: $\theta = 73.2^\circ$ and $\theta = 84.6^\circ$ hydrophilic, and $\theta = 122.5^\circ$ hydrophobic

Contact angle effect on waiting time and departure time are given in Fig. 12. As was expected, with increasing the contact angle, both waiting time and departure time decreases, which means that hydrophobic surfaces tend to generate and depart bubbles much more than hydrophilic surfaces. More importantly, changing contact angle in hydrophobic surfaces has less effect on waiting time and departure time than in hydrophilic surfaces. Note that waiting time is measured under constant heat flux boundary condition ($Q^{{\prime \prime }} = 8.5e - 4 mu\;ts^{ - 3}$) because in this condition, when bubble appears on the surface, the temperature jump enables us to measure waiting time accurately.

Fig. 12

Contact angle effect on dimensionless waiting time (constant heat flux BC: $Q^{{\prime \prime }} = 8.5e - 4 \,mu\;ts^{ - 3}$) and departure time (constant temperature BC: Ja = 0.15)

5.3 Surface tension effects on boiling curve

In Fig. 13, the boiling curve is plotted for two different surface tensions (σ = 0.11 mu tu⁻² ts⁻², σ = 0.02 mu tu⁻² ts⁻²) at a fixed reduced temperature (T_r = 0.86). As can be seen from this figure, curves are very close to each other for Ja < 0.13, meaning that surface tension has no effects on the boiling curve in this region. As Jacob number increases, the curve with higher surface tension (σ = 0.11 mu tu⁻² ts⁻²) stands above the other one due to the fact that the liquid molecules with higher surface tension are more attracted to each other and thus, more energy is required to overcome the intermolecular forces. Comparing the two curves, it turns out that the boiling at lower surface tension (σ = 0.02 mu tu⁻² ts⁻²) has more tendency to start film boiling, while CHF occurs at the same Jacob number (Ja = 0.18) for both curves. Therefore, the transition region is shorter in the curve with lower surface tension.

Fig. 13

Surface tension effects on boiling curve ($\Pr_{v} = \Pr_{l} = 1 ,\;\theta = 84.6^\circ ,\;{\text{T}}_{r} = 0.86$)

5.4 Effects of Prandtl Number on bubbles in film boiling regime

The Prandtl number, defined as the ratio of momentum diffusivity to thermal diffusivity (Pr = υ/α), is one of the effective dimensionless numbers as mentioned in this paper. It is assumed that both the fluid and the vapor phases have the same Pr numbers for simplicity. Figure 14 gives the effects of Pr number on film boiling at Ja = 0.35. In this figure, the film boiling process is shown for four different Pr numbers (Pr = 1, Pr = 1.2, Pr = 1.4, Pr = 1.6) at three different times (t^* = 40.56, t^* = 41.83, t^* = 43.09). As shown, vapor bubbles are more resistant to depart with increasing Pr number. For example, at time t^* = 43.09, at Pr = 1 bubbles are completely departed, whereas at Pr = 1.6 they are still growing. In addition, increasing Pr number causes that bubbles get closer to each other. For instance, at Pr = 1 the two existed bubbles are growing separately, while at Pr = 1.6 they are making a unit vapor bubble. At high Pr numbers, thermal diffusivity is less than momentum diffusivity and bubble growth is less. As a result, it takes more time to depart comparing to low Pr numbers. As an example, the bubble departure at Pr = 1.2 has a delay comparing to Pr = 1.

Fig. 14

Film boiling process at Ja = 0.35 for four different Pr numbers (1, 1.2, 1.4 and 1.6) each one depicted at three times (40.56, 41.83, 43.09). Units of axes and legend are shown only on the first picture to avoid repeating information

The space-averaged Nusselt number versus dimensionless time is plotted in Fig. 15 for three different Pr numbers. As was expected, with increasing Pr number the space-averaged Nu number decreases (because the space-averaged heat flux decreases). The amplitude of the curves decreases as Pr number increases, which means that the departure has less effects on the curve of $\overline{Nu}$ with increasing Pr number.

Fig. 15

Space-averaged Nu number versus dimensionless time for three different Prandtl numbers (0.8, 1, 1.2) at Ja = 0.35

6 Concluding remarks

In this paper the saturated pool boiling is investigated using an improved pseudo-potential Lattice Boltzmann Method. The departure diameter is correlated to the surface tension numerically using the additional source term proposed by Li et al. [24], that is incorporated into the collision operator of flow equation. The boiling curve is presented and the four different boiling regimes are successfully simulated and analyzed. The contact angle and surface tension effects on boiling curve and the Pr number effects on film boiling are discussed. Based on the simulation results, the following conclusions are made:

• An intensive temperature gradient appears in the necking area at departure time, but it vanishes after bubble departure.

• Changing contact angle in hydrophilic surfaces has more effect on waiting time and departure time than in hydrophobic surfaces.

• At a fixed reduced temperature, film boiling starts sooner (at smaller Jacob numbers) as surface tension decreases.

• With increasing Pr number in film boiling regime, the effect of bubble departure on oscillations of the space-averaged Nu number curve decreases and bubbles are more resistant to depart (there is a delay).

Appendices

Appendix 1: Thermodynamic consistency

The densities of phases deviate from Maxwell construction with using Eq. 26. It is shown here that ɛ = 0.107 leads to an excellent thermodynamic consistency. To ensure the validity of the code for thermodynamic consistency, using Eq. 45, a droplet of radius R = 30lu is placed at the center of a 151 × 151lu vapor domain.

$$\rho = \frac{{\rho_{l} + \rho_{v} }}{2} - \frac{{\rho_{l} - \rho_{v} }}{2}\tanh \left[ {\frac{{2(\sqrt {(x - x_{0} )^{2} + (y - y_{0} )^{2} } - R)}}{5}} \right]$$

(45)

where (x₀, y₀) is the droplet center. Fluid–Fluid interactions are the only applied forces. In a particular reduced temperature, after 20,000 time step for reaching steady state condition, densities of phases are obtained from our numerical code. Although the interface is diffusive in this model, it is considered the point at which ρ = (ρ_l + ρ_v)/2 and is shown sharply.

A Matlab code is written to solve Eq. 24 for different saturated pressures (or reduced temperatures), which gives us the equilibrium phase densities at each reduced temperature based on Maxwell construction. In Fig. 16, densities of phases predicted by LBM at different reduced temperatures are compared with Maxwell construction. According to this figure, even at low reduced temperatures (T_r = 0.58) which leads to high density ratios (≈ 520.3), the LBM results are in a very good agreement with the analytical results of Maxwell construction.

Fig. 16

Comparison of phase densities (ρ) predicted by the present model (marked with square points) with that of Maxwell construction (Eq. 24, solid curves) for different reduced temperatures (T_r)

Appendix 2: Laplace law

In Shan and Chen two-phase model, surface tension is an output of Laplace law. The Laplace law is expressed as:

$$\Delta P = \frac{\sigma }{R}$$

(46)

where ΔP is the pressure difference between inside and outside of droplet and R is the droplet radius. According to the Laplace law, ΔP versus R is a straight line with the slope of σ. Computational domain and settings of proceeded section are used here to examine the Laplace law with our numerical code. Droplets with different radii are suspended in vapor filled domain and after reaching steady state condition, surface tension is calculated as the slope of line ΔP vs. 1/R. Different surface tensions are achievable changing the introduced variable κ. In Fig. 17, surface tension, σ, is plotted versus the variable κ. As can be seen from this figure, with increasing the variable κ, σ decays linearly which means that the variable κ is correctly applied in the code, since it has been proved that with using Eq. 19 surface tension is related to the variable κ in the form of σ ∝ (1 − κ) [24].

Fig. 17

Surface tension (slopes of lines in Fig. 5) (σ) versus the variable κ

Appendix 3: Contact angle

One of the important parameters that has considerable effects on bubble behavior is contact angle. Three kinds of forces including solid–gas (γ_sg), solid–liquid (γ_sl) and liquid–gas (γ_lg) forces, at the three-phase contact point, enforce the droplet to have a particular shape over the solid surface as shown in Fig. 18. θ is called contact angle. In the present model, different contact angles are achievable changing the parameter ρ_w. To simulate different contact angles, a droplet of radius 30 lu is placed at the point (lx/2, 3) and after reaching steady state condition (20000 δt), the contact angle is calculated using the following equation:

$$\theta = \tan^{ - 1} \left( {\frac{{b_{0} }}{{2\left( {l - a_{0} } \right)}}} \right)$$

(47)

where l = a₀/2 + b ²₀ /(8a₀). Different contact angles are simulated using the present model as illustrated in Fig. 18. Solid surfaces with θ < 90° are called hydrophilic and solid surfaces with θ > 90° are called hydrophobic.

Fig. 18

Contact angle (θ) versus the virtual density (ρ_w). The geometrical parameters (a₀ and b₀) for calculating contact angle is shown in the southwest corner. At the top, the stable shape of droplets on a wall with different contact angles is depicted (hydrophilic: θ = 48° and θ = 87.4°, hydrophobic: θ = 122.5° and θ = 150.8°)

The contact angle versus the variable ρ_w is plotted in the Fig. 18. With increasing ρ_w, ψ increases and the fluid–solid interaction force increases according to Eq. 28. Therefore, the droplet wets the solid surface more, resulting in a contact angle decrease.