1 Introduction

The rapid development of science and technology promotes the miniaturization and integration of electronic and electrical equipment, and the heat dissipation in the electronic field exceeds the threshold of 100 W/cm2 [1]. The rapid development of two-phase heat transfer technology is promoted by the urgent need for efficient cooling. During the boiling process, the vaporization latent heat transfers most of the heat, and the heat flux density during boiling is several times higher than the heat flux density of strong convection heat transfer, which provides greater heat dissipation capacity while maintaining an acceptably lower device temperature [2].

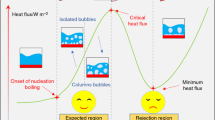
According to the different conditions under which boiling occurs, boiling heat transfer is divided into homogeneous boiling and heterogeneous boiling. Boiling with a fixed heating surface is called heterogeneous boiling. As heating progresses, the wall temperature gradually increases and exceeding the saturation temperature of the liquid. At this time, bubbles are generated at the nucleation point of the heating surface and gradually grow [3, 4]. Pool boiling is a kind of non-homogeneous boiling. Pool boiling does not necessary form a flow pipeline and only needs to provide a container to contain the working fluid [5, 6]. In recent decades, scholars have made different attempts to improve heat transfer capacity of pool boiling. Active enhancement and passive enhancement are two main ways of pool boiling enhancement [7, 8]. Active enhancement requires external power to change the dynamics of the working fluid to enhance heat transfer, but it cannot be implemented in a compact heat sink. Passive strengthening usually changes the physical structure of the heating surface without external power assistance, and the cost is low, so it is favored [9]. With the development of precision machining technology, different scholars have designed and processed microstructures of specific sizes and regularly arranged them on the heat exchange surface and explored the effect of such microstructure surfaces on heat transfer capacity of pool boiling [10]. Dong [11] et al. used thermodynamics to analyze the influence of the interaction of microstructure and wettability on heterogeneous nucleation. Their research found that under the same conditions, it is easier to form bubbles in a concave surface than in a convex or flat surface. When the bubble radius is 5–100 times larger than the curvature radius of the microstructure does bubble nucleation is enhanced by the microstructure will significantly. Deng [12] et al. prepared 12 groups of inverted Ω-shaped cavity channel structures, and the heat transfer capacity of pool boiling was studied [13]. They found that the increase of cavity leads to the increase of nucleation point density, reduces the initial superheat and improves the heat transfer coefficient. Capillary wicking ensures liquid replenishment and surface wetting under high heat flux and effectively avoids rapid heat transfer deterioration under high heat flux. Hai [14] et al. Machined micro channels on the surface of copper test rods. The effects of surface wettability, channel length and channel shape on pool boiling were studied. It is found that the micro channel provides more nucleation site, and the micro channel provides continuous liquid for bubble growth, which makes the heated surface have better gas–liquid transmission. When the heat flux is high, the bubble separation speed becomes faster, and the micro channel strengthens the liquid supplement and capillary feeding. Therefore, the wall superheat is very low. Compared with the ordinary surface, the new micro channel surface reaches 193% of the overall critical heat flow, and the HTC increase reaches 51.8 \(\mathrm{W}/{\mathrm{cm}}^{2}\cdot \mathrm{K}\). Ho [15] et al. prepared different microstructures by selective laser melting (SLM). Microstructure's effect on pool that boiled heat transfer was studied with FC-72 as medium at room temperature. On this basis, Ho [16] et al. prepared micro cavity surfaces and micro fin surfaces to compare with the Al-6061 plate. After testing, The average heat transfer coefficient (HTC) of microstructure surface increased by nearly 70%, and the CHF increased by 76%, thereby effectively improving the heat transfer characteristics of pool boiling.

Experimental methods have disadvantages of high cost, time-consuming, and difficulty in obtaining experimental details. Therefore, numerical methods have been developed. At present, Volume-of-Fluid method (VOF) is a common method to study two phase flow. However, at the study of pool boiling, there are some limitations to the VOF method. For example, it is difficult to capture all details, accurately observe the specific changes of bubble growth and separation, and reveal the physical mechanism of boiling phenomenon on the micro scale. Compared with the VOF method, the lattice Boltzmann (LBM) program for mesoscopic fluid dynamics calculations shows advantages of both the micromolecular dynamics model and macro fluid continuum model. In the lattice Boltzmann (LB) model, there is no need to track the interface, and the interface between different phases can naturally appear, deform, and migrate [17]. The LBM method can observe the behavior of bubbles from a mesoscopic perspective and directly and conveniently shows the interaction between bubbles and the liquid environment. In addition, LBM programs are easy to parallelize, which greatly improves computational efficiency.

There are many kinds of LBM multiphase flow models. Because of its simplicity and strong applicability, the pseudo potential LB model proposed by Shane and Chen [18] in 1993 has become the most popular LB multiphase model [19,20,21]. The basic idea is to use pseudo potential to represent the micro molecular interaction on the mesoscopic scale, because the phase interface is no longer a mathematical boundary, and there is no need for explicit interface tracking or interface capture technology. However, the pseudo potential model also has some problems, such as large spurious current, thermodynamic inconsistency and so on. Scholars [22, 23] use LB method to suppress these problems and increase the computational stability. Nowadays, the pseudo potential LB model has successfully simulated pool boiling on a smooth heating surface [24,25,26]. Li [27] et al. simulated gas–liquid two-phase boiling by proposing a mixed heat LB model numerically. The pool boiling curve and three boiling stages were successfully simulated, and then the pool boiling on a mixed surface that is composed of hydrophilic sidewalls and hydrophobic top micropillars was simulated. Feng [28] et al. researched the pool boiling process of the micropillar structure composed of hydrophilic sidewalls, hydrophobic tops by the multiple relaxation time (MRT) pseudo-potential model [29]. The columnar structure was found to increase the boiling heat transfer coefficient of the mixing surface. To study the influence of micropillars and holes on pool boiling nucleation, Shakeel [30] et al. used the LB method to compare the heat transfer capacity of the nucleate boiling zone of the coarse surface formed by the combination of different holes and micropillars. The saturation boiling curve is numerically simulated. The results show that the micropillar structure reduces the influence of induced flow. To analyze the pool boiling mechanism and enhance heat transfer, Zhou [31] et al. studied four different boiling bubble core cavity structures, The bubble behavior and corresponding heat transfer capacity are analyzed respectively. According to the heat flow distribution diagram, they found that the heat transfer at the bubble liquid interface and micro layer evaporation have an important influence on the growth of bubbles, which indicating that the main heat transfer mechanism of nucleate boiling is micro liquid layer evaporation.

However, previous studies using the LB method focused on the effects of different shape microstructures on bubble nucleation, bubble growth, and detachment. There are few studies on the influence of shape parameters of microstructure array by the LBM method. Consequently, a two-dimensional, solid–liquid, two-phase numerical model was established using the LB method. The effects of the structural parameters of the rectangular micro cavity array on heat transfer characteristics and bubble evolution of heating surface were studied. All cases in this paper are valuated in lattice units.

2 Method

2.1 The hybrid thermal LB model

The LB equation using MRT collision operator is as follows:

$${\text{f}}_{\alpha}\left({\mathrm{x}}+{\mathrm{e}}_{\alpha}{{\delta}}_{\mathrm{t}}\mathrm{, }{\mathrm{t}}+{\delta}_{mathrm{t}}\right) = {\mathrm{f}}_{\alpha}\left({\mathrm{x}},{\mathrm{t}}\right)-{{\mathrm{(}{\mathrm{M}}}^{-1}\Lambda \mathrm{M}\mathrm{)}}_{\alpha\beta}({\mathrm{f}}_{\beta}-{\mathrm{f}}_{\beta}^{\mathrm{ eq}})+{\delta}_{\mathrm{t}}{{\mathrm{F}}}_{\alpha}^{^{\prime}}$$
(1)
$${\text{m}}^{*}= \text{ } \text{m }\text{- }{\Lambda}\left(\text{m - }{\text{ m}}^{\text{eq}}\right)\text{+}{\delta}_{\text{t}}\left(\text{I} \, -\frac{\Lambda}{\text{2}}\right){\text{s}}$$
(2)

where \({\text{m}} \, \text{=} \, {\text{Mf}}\), \({\text{m}}^{ \, {\text{eq}}} \, \text{=} \, {\text{M}}{\text{f}}^{ \, {\text{eq}}}\), I is the unit tensor, \({\varvec{S}}\) is the force source term of the vector space \(\left(\mathrm I-0.5\mathrm\Lambda\right)\mathrm s=\mathrm{MF^\prime}\). Then the MRT LB equation can be expressed as:

$${\text{f}}_{\alpha}\left({\text{x}}\text{+}{\text{e}}_{\alpha}{{\delta}}_{\text{t}}\text{, }{\text{t}}\text{+}{\delta}_{\text{t}}\right) \, \text{=}{ \, {\text{f}}}_{\alpha}^{ \, \text{*}}\text{(x, }{\text{t}})$$
(3)

where \({\text{f}}^{*}\text{=}{\text{M}}^{-1}{\text{m}}^{*}\). In LBM, Eqs. (2) and (3) are the migration and collision processes in the lattice Boltzmann equation. The diagonal matrix \(\Lambda\) includes the relaxation time, and its expression is:

$$\Lambda=\,\text{diag}(\tau_{\rho}^{-1},\;\tau_\text{e}^{-1},\tau_{\zeta}^{-1},\;\tau_\text{j}^{-1},\;\tau_\text{q}^{-1},\;\tau_\text{j}^{-1},\;\tau_\text{q}^{-1},\tau_\text{v}^{-1},\tau_\text{v}^{-1})$$
(4)

The momentum balance matrix \({\text{m}}^{\text{eq}}\) can be obtained as follows:

$$\mathrm m^{\mathrm{eq}}=\rho(1,\,-2+3\vert\mathrm v\vert^2,1-3\vert\mathrm v\vert^2,{\mathrm v}_{\mathrm x},-{\mathrm v}_{\mathrm x},{\mathrm v}_{\mathrm y},-{\mathrm v}_{\mathrm y},\mathrm v_{\mathrm x}^2,-\mathrm v_{\mathrm y}^2,{\mathrm v}_{\mathrm x}{\mathrm v}_{\mathrm x})^{\mathrm T}$$
(5)

where \({\text{v}}\) is the macro velocity, and \(\left|{\text{v}}\right| \, =\sqrt{{\text{v}}_{\text{x}}^{2}+{\text{v}}_{\text{y}}^{2}}\). The macro density and macro velocity are calculated as:

$$\rho=\sum_\alpha f_\alpha\rho\boldsymbol v=\underset\alpha{\sum{\boldsymbol e}_{\mathbf\alpha}f_\alpha+\frac{\delta_t}2\mathbf F}$$
(6)

where \({\text{F}}=({\text{F}}_{\text{x}},{\text{F}}_{\text{y}})\) is the force acting on the system. Among them, the inter-molecular interaction force is [32]:

$${\mathbf F}_m=-G\psi\left(x\right)\underset\alpha{\mathit\sum}w_\alpha\psi\left(\mathbf x+{\mathbf e}_{\mathbf\alpha}\right){\boldsymbol e}_\alpha$$
(7)

where \(\psi\) is the pseudopotential, \({\text{G}}\) is the interaction strength, and \({\text{w}}_{\alpha }\) is the Weight coefficient. The calculation formula of pseudopotential \(\psi\) is as follows:

$$\Psi (\text{x})=\sqrt{2(\text{P}_{\text{EOS}}-\rho\text{c}^{2}_\text{s})/\text{Gc}^2}$$
(8)

where \({\text{c}} \, \text{=} \, {1}\) is the lattice unit, and \({\text{P}}_{\text{EOS}}\) is the prescribed non-ideal equation of state. The forcing term is given by:

$$\mathbf{S}=\left[\begin{array}{c}0\\ 6\mathbf{v}\cdot \mathbf{F}+\frac{\sigma {\left|{\mathbf{F}}_{m}\right|}^{2}}{{\psi }^{2}{\delta }_{t}({\tau }_{e}-0.5)}\\ -6\mathbf{v}\cdot \mathbf{F}-\frac{\sigma {\left|{\mathbf{F}}_{m}\right|}^{2}}{{\psi }^{2}{\delta }_{t}({\tau }_{\varsigma }-0.5)}\\ {F}_{x}\\ -{F}_{x}\\ {F}_{y}\\ -{F}_{y}\\ 2({v}_{x}{F}_{x}-{v}_{y}{F}_{y})\\ ({v}_{x}{F}_{y}-{v}_{y}{F}_{x})\end{array}\right]$$
(9)

where \(\sigma\) is the variation to adjust the stability. In the simulation, \(\sigma=1.2\) is for the sake of achieving thermodynamic consistency. \({\left|{\text{F}}_{\text{m}}\right|}^{2}=({\text{F}}_{\text{m}, \, {\text{x}}}^{2}+{\text{F}}_{\text{m}, \, {\text{y}}}^{2})\), F is the total force, which also contains the buoyant force given by

$${\text{F}}_{\text{b}} = ({\rho} - {\rho}_{\text{ave}}){\text{g}}$$
(10)

where \(\rho_\text{ave}\) is the the average density in the computational domain, \(g=(0,-g)\) is the gravitational acceleration.

Through the Chapman–Enskog analysis of the LB equation, the following macroscopic equations can be obtained at the Navier–Stokes level:

$${\partial }_{t}\rho +\nabla \cdot \left(\rho \mathbf{v}\right)=0$$
(11)
$${\partial }_{t}\left(\rho \mathbf{v}\right)+\nabla \cdot \left(\rho \mathbf{v}\mathbf{v}\right)=-\nabla \cdot \mathbf{P}+\nabla \cdot{\varvec{\Pi}}+{\mathbf{F}}_{b}$$
(12)

where \({\Pi}\) is the viscous stress tensor and \({\mathrm {P}}\) is the pressure tensor.

For the diffuse interface modeling of multiphase flows, Anderson et al. [33] have summarized the local balance law for entropy, which is given by (neglecting the viscous heat dissipation).

$$\rho T\frac{Ds}{Dt}=\nabla \cdot (\lambda \nabla T)$$
(13)

where \(s\) is the entropy. \({\lambda}\) is the thermal conductivity. The temperature equation can derived from Eq. (13) using the following thermodynamic relation.

$$T\mathrm{ds}={c}_{v}\mathrm{d}T+T{\left(\frac{\partial {\mathrm{p}}_{EOS}}{\partial T}\right)}_{\rho }\mathrm{d}\left(\frac{1}{\rho }\right)$$
(14)

where \({{c}_{v}}\) is the specific heat at constant volume.

The temperature equation can be written as:

$$\rho{\mathrm{c}}_{\mathrm v}\frac{\mathrm{DT}}{\mathrm{Dt}}=\nabla\cdot\left(\lambda\nabla\mathrm T\right)-\mathrm T{\left(\frac{\partial{\mathrm P}_{\mathrm{EOS}}}{\partial\mathrm T}\right)}_{\mathrm\rho}\nabla\cdot\mathrm v$$
(15)

where \({\uplambda}\) is the thermal conductivity and \({{c}_{v}}\) is the specific heat at constant volume. The finite difference method is directly used to solve Eq. (15), which can be formulated as:

$${\partial }_{t}T \text{=}-\mathbf{v}\cdot \nabla T+\frac{1}{\rho {c}_{v}}\nabla \cdot \left(\lambda \nabla T\right)-\frac{T}{\rho {c}_{v}}{(\frac{\partial {P}_{EOS}}{\partial T})}_{\rho }\nabla \cdot \mathbf{v}$$
(16)

The right-hand side of Eq. (16) is denoted by \({\text{K}}({\text{T}})\). The classical fourth-order Runge–Kutta scheme is adopted for time discretization:

$$\mathrm T^{\mathrm t+\delta\mathrm{t}}=\mathrm T^{\mathrm t}+\frac{{\delta}_{\mathrm t}}6\left({\mathrm h}_1+2{\mathrm h}_2+2{\mathrm h}_3+{\mathrm h}_4\right)$$
(17)

where \({{h}_{1}}\), \({{h}_{2}}\), \({{h}_{3}}\), and \({{h}_{4}}\) are given by:

$${\mathrm h}_1=\mathrm K\left(\mathrm T^{\mathrm t}\right),\;{\mathrm h}_2=\mathrm K\left(\mathrm T^{\mathrm t}+\frac{{\delta}_{\mathrm t}}2{\mathrm h}_2\right),\;{\mathrm h}_3=\mathrm K\left(\mathrm T^{\mathrm t}+\frac{{\delta}_{\mathrm t}}2{\mathrm h}_2\right),\;{\mathrm h}_4=\mathrm K\left(\mathrm T^{\mathrm t}+{\delta}_{\mathrm t}{\mathrm h}_3\right)$$
(18)

According to the above formula, the calculation formula of pseudopotential \({\psi}\) is as follows:

$$\psi\left(x\right)=\sqrt{2\left(P_{EOS}-\rho c_s^2\right)/GC^2}$$
(19)

In this study, the Peng-Robinson(P-R) equation of state is used:

$${\mathrm P}_{\mathrm{EOS}}=\frac{\rho\mathrm{RT}}{1-\mathrm b\rho}-\frac{\mathrm a\varphi\left(\mathrm T\right)\rho^2}{1+2\mathrm{b}\rho-\mathrm b^2\rho^{\mathit2}}$$
(20)
$$\varphi\left(\text{T}\right)=\left[{1+(0.37464+1.54226}\omega-{0.26992}\omega^2\text{)(1}-\sqrt{\text{T/}{\text{T}}_\text{C}}\text{)}\right]^2$$
(21)

where, \(a=0.45724{{R}}^{2}{T}_{C}^{2}/{P}_{C}\), \(b=0.0778{RT}_{c}/{P}_{c}\), acentric factor \({\omega} = {0.344}\). In this study we choose \({\text{a}} \, \text{=} \, \text{3/49}\), \(\text{b }\text{= 2/12}\), \({\text{R}} \, \text{=} \, {1}\) [27].

The physical meaning of Fourier number \({{F}}_{o}\) is expressed as the degree of unsteady heat and mass transfer process which can be formulated as:

$${\mathrm{F}}_{o}=\frac{\alpha t}{{L}^{2}}$$
(22)

where α is the thermal diffusivity, t is the characteristic time, and l is the characteristic length where the heat conduction occurs.

The actual physical units must be converted into dimensionless lattice units matching the lattice units. Assuming that the physical value is expressed as Q, the lattice value is expressed as Q ', and CQ is the conversion factor, the relationship between the lattice value and the physical value is expressed as follows:

$$\mathrm{Q}=\mathrm{Q{^{\prime}}}\times {\mathrm{C}}_{\mathrm{Q}}$$
(23)

The conversion between real time and lattice time is:

$$\mathrm{t}=\mathrm{t{^{\prime}}}T$$
(24)
$$T=\frac{{\nu }^{{^{\prime}}}}{\nu }{(\frac{D}{D^{\prime}})}^{2}$$
(25)

where \(D\) is the diameter and \({\nu}\) is the kinematic viscosity. And \({D}^{\prime}\) is the unit diameter of the lattice and \({\nu }^{\prime}\) is the kinematic viscosity of the lattice.

The conversion between real length and lattice length is:

$$l=l{^{\prime}}L$$
(26)
$$L=\frac{D}{D{^{\prime}}}$$
(27)

where L is the real length.

The conversion between real Velocity and lattice Velocity is:

$$\nu ={\nu }^{^{\prime}}\frac{L}{T}=\nu {^{\prime}}\frac{\upsilon }{\upsilon {^{\prime}}}\frac{D{^{\prime}}}{D}$$
(28)

The conversion between real acceleration and lattice acceleration is:

$$a={a}^{^{\prime}}\frac{L}{{T}^{2}}=a{^{\prime}}{(\frac{\upsilon }{\upsilon {^{\prime}}})}^{2}{(\frac{D{^{\prime}}}{D})}^{3}$$
(29)

The conversion between mass and lattice mass is:

$$m={m}^{^{\prime}}\mathrm{G}=m{^{\prime}}\frac{\rho }{{\rho }^{^{\prime}}}{(\frac{D}{D{^{\prime}}})}^{3}$$
(30)

The conversion between force and lattice force is:

$$F={F}^{^{\prime}}\mathrm{G}\frac{L}{{T}^{2}}=F{^{\prime}}\frac{\rho }{{\rho }^{^{\prime}}}{(\frac{\upsilon }{\upsilon {^{\prime}}})}^{2}$$
(31)

The conversion between pressure and lattice pressure is:

$$P={P}^{^{\prime}}\frac{G}{L{T}^{2}}=P{^{\prime}}\frac{\rho }{{\rho }^{^{\prime}}}{(\frac{\upsilon }{\upsilon {^{\prime}}})}^{2}{(\frac{D{^{\prime}}}{D})}^{2}$$
(32)

2.2 The simulation setup

As we all know, roughness effects play an important role in boiling heat transfer. Micro cavities on rough surfaces can promote boiling nucleation. Therefore, some scholars have prepared heating surfaces with cavities to provide artificial nucleation sites to trigger nuclear boiling in advance under small superheat [34]. On this basis, this work focuses on the influence of rectangular micro cavities structure [35,36,37] on pool boiling heat transfer performance. Deionized water was selected as the heat exchange medium in this study. Assuming that its physical property parameters are constant, the relevant physical properties are shown in Table 1. In this work, FORTRAN language was used for programming. The program is written based on the open source IDE (integrated development environment) code::block 20.03, and the compiler uses MinGW. The calculation results are analyzed and visualized by the commercial post-processing software Tecplot.

Table 1 Thermo-physical parameters of heat exchange medium
Full size table

In the LB method, in addition to discretizing the fluid into fluid particles, the physical region is also discretized into a series of lattices, and the time is discretized into a series of steps. The equation describing the motion of fluid particles is called Boltzmann equation or the corresponding discrete form. When molecules collide with each other, only two body collisions are considered, that is, it is considered that the possibility of three or more molecules colliding together at the same time is very small. The velocity distribution of each molecule is independent of other molecules, that is, the velocity of particles before collision. The external force does not affect the dynamic behavior of local collision. This work ignores the compression work of viscous heat dissipation and pressure, and is applicable to inviscid heat dissipation and compression work. All fluid properties (density, viscosity, thermal diffusivity) can be regarded as constants, except for body force term, where the fluid density is assumed to be linear with temperature.

A two dimension simulation box of \({{L}}_{{x}}\times{{L}}_{{y}}= 600 \, {l.u.} 320 \, {l.u.}\) (l.u. represents lattice units) is adopted in this study. The length of the calculation domain is 3000 μm, and the width is 1600 μm. The heat transfer medium used in this work is deionized water, and the specific parameters are shown in Table 1. In the computational domain, the bottom of the calculation domain with rectangular micro cavity is set as the heating surface. The rectangular micro cavity's depth is h, the interval is s, and the width is w. There are periodic boundaries on the left and right boundaries of the computational domain to close the system. The solid wall uses the Zou-He boundary scheme [38]. Initially, the computational domain is divided into liquid part (\({0} \le \mathrm{y} < {160}\), the green part of the calculation field) and gas part (\({160} \leqslant \, {\mathrm{y}} \, \mathrm{L}_{\mathrm{y}}\), the blue part of the calculation field), as shown in Figs. 1 and 2.

Fig. 1
figure 1

Computational domain and boundary conditions

Full size image
Fig. 2
figure 2

Comparison of temporal variations of heat flux when the wall superheat is 0.0165 with results of Q. Li et al. [27]

Full size image

At the beginning of the simulation, the two phase is in equilibrium. The initial temperature is taken as \({{T}_{s}}=0.86{{T}_{c}}\).The wall superheat is taken as \({\triangle} {T}={{T}_{b}}-{{T}_{s}}\), in which \({{T}_{b}}\) is the temperature of the heating surface and \({{T}_{s}}\) is the temperature of the top wall. The specific heat at constant volume is taken as \({{C}_{v}}={6.0}\), the gravitational constant is taken as \({g}= {3}\times{10}^{-5}\), and the thermal conductivity is taken as \({\lambda}=0.028{\rho}\).

2.3 Calculation scheme

This paper studies the influence of the depth, spacing, and width of the micro cavity. Table 2 shows examples of all cases considered in this study.

Table 2 Structural parameters of the rectangular micro cavity on the heating surface
Full size table

3 Results and discussion

3.1 Model verification

The calculation results of the heat flux change when the wall superheat is 0.0165 are compared with the previous literature [27] to verify the accuracy of the model, as shown in Fig. 2.

3.2 Pool boiling on the surface of the rectangular micro cavity structure

Figure 3 shows the heat flux curve of case 1 (h = 50 l.u. w = 50 l.u. s = 50 l.u.). At the initial stage of boiling heat transfer, the temperature difference between solid and liquid interface is large, and the heat flux increases rapidly, because the thermal conductivity of liquid is less than that of solid. When the solid wall temperature increases, the temperature difference between solid and liquid interface decreases and the heat flux decreases. At the 4000th time step, the vapor pressure in the micro cavity is greater than the surface tension and becomes the nucleation center. The evaporation of the micro liquid layer takes away most of the heat, and the downward trend of heat flow slows down. At about the 10,000 time step (\({\mathrm{F}_{o}}={5.952}\)), bubbles are generated on the wall between the micro cavities. In the initial stage of bubble formation, the number and size of bubbles are important factors affecting pool boiling heat transfer, corresponding to an rise in heat flux at the 10,000–15,000 time step (\({\mathrm{F}_{o}}=5.952-\mathrm{F}_{o}={8.928}\)) in Fig. 3. From the 4000 time step (\({\mathrm{F}_{o}}={2.3808}\)) and 10,000 time step (\({\mathrm{F}_{o}}={5.952}\)) in Fig. 4(b), it is obtainable that in heat transfer's early stages, the temperature difference of the whole surface is relatively small, which is due to the capillary action between the microstructure surfaces promoting the rapid flow of liquid in the micro cavity crevice.

Fig. 3
figure 3

Heat flux variation curve

Full size image
Fig. 4
figure 4

(a) Dynamic behavior and (b) temperature distribution of bubbles

Full size image

The bubbles grow along the side wall of the micro cavity. When the bubbles gradually grow to a sufficient size, the bubbles generated between adjacent microstructures coalesce laterally, as shown in the 20,000 time step (\({\mathrm{F}_{o}}={11.904}\)) in Fig. 4(a). The range of the three-phase contact line between bubbles and wall surface rises, and the range of the drying area of the heating wall increases, which reduces the heat transfer efficiency of the heating. This downward trend continues until around the 23,000 time step (\({\mathrm{F}_{o}}={13.6896}\)). After the 23,000 time step (\({\mathrm{F}_{o}}={13.6896}\)), the bubbles continue to grow, but under the dominant action of buoyancy, the bubbles stretch longitudinally. The tensile deformation causes the liquid block to shrink laterally, which increases the heat exchange area. Therefore, the heat flux raises. After the 35,000 time step (\({\mathrm{F}_{o}}={20.832}\)), the heat flux first decreases and then raises, as the buoyancy of the bubble raises gradually during the growth process, and the neck of bubble shrinks gradually during the upward movement of the bubble until the bubble separates from the wall. After that, the micro cavity nucleation point will continue to produce new bubbles, repeating the process of nucleation, growth, and detachment.

3.3 The influence of different micro cavity depths on boiling heat transfer

This section discusses depth's effect on pool boiling heat transfer. The micro cavity width is set to 50 l.u. the micro cavity spacing is set to 50 l.u. and the micro cavity depth is set to 30 l.u. 50 l.u. and 70 l.u. As shown in Figs. 5 and 6, the effect of micro cavity depth on heat flux is insignificant. The bubble behavior of the cavities in the three cases is similar, indicating that the micro cavity depth did not influence significantly on the boiling surface's heat transfer effect. The increase of micro cavity depth increases the heat exchange area. However, the increase of microstructure depth also increases the bubble separation resistance and liquid supplement resistance. Higher micro cavity depth is not conducive to the movement and separation of bubbles. When the increase of heat exchange area is limited, the bubble motion's effect on heat transfer is offset. Micro cavity depth's effect on heat transfer effect therefore is not obvious. As shown in Fig. 5, micro cavity depth's effect on heat flux is insignificant. The bubble behavior of the micro cavity in the three cases is similar, indicating that the micro cavity depth has little effect on the pool boiling heat transfer capacity.

Fig. 5
figure 5

Micro cavity depth's effect on bubble behavior

Full size image
Fig. 6
figure 6

Micro cavity depth's effect on heat flux

Full size image

When the time step is around 32,000 time step (\({\mathrm{F}_{o}}={11.904}\)), The bubbles are stretched and deformed under the action of the surrounding flow field to form elongated bubbles. Subsequently, the bottom of the bubble flattens during the rising process, which is similar to the simulation of Hua [39]. After the bubble is formed and separated, the upward movement of the bubbles causes the flow field to change, which has a strong shear force on the subsequently generated bubbles, making it easier for the bubbles to separate away from the wall. The subsequent formation of small bubbles further affects the area of the gas–liquid boundary and the flow field. Under the action of wake flow, bubbles will deform, break and coalesce. Then the heat flux rapidly decreases. This is because the existence of the micro cavity adds a stable vaporization core to the heating surface. The small bubbles formed by the vaporization core absorb heat, grow and polymerize in the micro cavity to form gas blocks, increase the range of three-phase contact lines, increase the thermal resistance, and hinder the backflow of surrounding liquids. With the increase in wall superheat, bubbles continue to grow and separate. The boiling heat transfer between liquid and superheated wall is strengthened again by the escape of multitudinous bubbles and the replenishment of liquid, which increases the heat flux. After 50,000 time step (\({\mathrm{F}_{o}}={23.808}\)), the boiling process is relatively stable, and the heat flux fluctuates around 0.0004.

3.4 The influence of micro cavity spacing on boiling heat transfer

In this section, in order to explore spacing's effect on pool boiling heat transfer. The micro cavity width is set to 50 l.u. the micro cavity depth is set to 50 l.u. and the micro cavity spacing is set to 30 l.u. 50 l.u. and 70 l.u. It can be seen from Fig. 7 that with the increase in micro cavity spacing, bubbles on the wall between the micro cavities are generated earlier and faster, which is also the reason why case 5 (s = 50 l.u.) has a higher heat flux before 18,000 time step (\({\mathrm{F}_{o}}={10.7136}\)), as show in Fig. 8. As the bubble grows, the gas continuously enters the bubble, which becomes larger and larger and moves upward. However, the bottom of the bubble begins to shrink, and a neck is formed between the bubble and the orifice, which becomes thinner and thinner. Eventually, the neck breaks and the air bubbles break away from the bottom. At the bubble separation point, the liquid film splits into two sub bubbles or even more bubbles, which will cause the area of phase boundary to increase. With further progression of heat transfer, the bubble diameter becomes larger, and the bubbles at the bottom of the pit merge with the bubbles at the top. Due to the uniform distribution of the micro cavity, adjacent bubbles merge with each other to form a gas film, which covers the heating surface and hinders surrounding water's reflux. Therefore, after 12,000 time step (\({\mathrm{F}_{o}}={7.1424}\)), the case 5 (s = 50 l.u.) enters the film boiling stage, and the heat transfer deteriorates rapidly. At the same wall temperature, the heat flux of case 4 (s = 30 l.u.) is lower than that of case 1 (s = 50 l.u.). The main reason is that the increase of micro cavity spacing leads to a low proportion of the wall between micro cavities on the whole heating surface. Smaller wall spacing does not easily form bubbles and is not conducive to the movement and separation of bubbles. According to Fig. 7, it can be found that case 4 (s = 30 l.u.) bubbles grow slowly and leave for a long time. With increasing time, case 5 (s = 70 l.u.) enters the film boiling stage, and the heat flux decreases significantly. For case 1 (s = 50 l.u.) and case 4 (s = 30 l.u.), due to the small micro cavity spacing, no bubbles were generated on the wall between micro cavity and did not enter the film boiling stage.

Fig. 7
figure 7

Micro cavity depth's effect on bubble behavior

Full size image
Fig. 8
figure 8

Micro cavity spacing's effect on heat flux density

Full size image

3.5 The influence of micro cavity width on boiling heat transfer

In this section, the micro cavity width is set to 50 l.u. the micro cavity depth is set to 50 l.u. and the micro cavity spacing is set to 30 l.u. 50 l.u. and 70 l.u. to explore width's effect on boiling heat transfer. According to Fig. 9, it can be found that in the early stages of boiling heat transfer, there is no significant difference in microstructure heat flux at different depths. In bubble growth's early stage, the bubble volume is small, and the micro cavity depth has no significant effect on the bubble behavior. The number and size of bubbles are important factors affecting pool boiling heat transfer. After 2000 steps, the difference in heat transfer of the three structures begins to appear. As shown in Figs. 9 and 10, the heat exchange effect is inversely proportional to the width of the micro cavity. The micro cavity's heat transfer effect surface with a width of 30 l.u. is superior than that of the other two micro cavity surfaces with wider widths. The reason is related to the capillary force decreasing with increasing micro cavity width. The capillary interaction between microstructures promotes the rapid flow of liquid in micro cavities. When the bubbles grow large enough, the bubbles generated between adjacent microstructures merge laterally, increasing the bubble volume. With the increase of bubbles, the range of three-phase contact line with the wall increases, and the range of the drying area of the heating wall increases, which reduces the heat transfer efficiency. The surrounding super cooled liquid rewetting the dry spot area becomes worse, which hinders the heat transfer. Since the size of the bubbles formed after the flow is stabilized is not much different, the effect of the number of bubbles on the boiling performance increases. Moreover, on the limited heating surface, the change of surface micro cavity width changes the number of micro cavities. The micro cavity can provide stable vaporization cores. The smaller the width, the more micro cavities on the heating surface with the same area, and the corresponding number of vaporization cores increases to strengthen the heat transfer of the heating surface.

Fig. 9
figure 9

Micro cavity width's effect on bubble behavior

Full size image
Fig. 10
figure 10

Micro cavity width's effect on heat flux

Full size image

4 Conclusions

In this paper, In this paper, the pool boiling heating model of rectangular micro cavity array is established through the mixed hot lattice Boltzmann model. To investigate surface microstructure's effect on enhanced heat transfer, this paper compares the effects of different depths (30 l.u., 50 l.u., 70 l.u.), widths (30 l.u., 50 l.u., 70 l.u.), and spacing (30 l.u., 50 l.u. 70 l.u.) of rectangular micro cavity on bubble behavior, and discusses the law and mechanism of enhanced pool boiling heat transfer. The main conclusions are as follows:

  1. (1)

    The existence of the rectangular micro cavity structure can effectively improve the pool boiling heat transfer capacity. The uniform microstructure provides a stable vaporization core, which is conducive to the early coalescence of bubbles.

  2. (2)

    Micro cavity depth has little effect on pool's heat transfer capacity boiling. Although the increased depth increases the heat exchange area, it is not conducive to the movement and separation of bubbles.

  3. (3)

    With increasing micro cavity spacing, the heat transfer performance first becomes better and then worse. The increase of micro cavity spacing not only increases the flow pores of bubbles but also increases the replenishment capacity of liquid, which is conducive to the movement and separation of bubbles. If the spacing is too large, film boiling easily occurs and the heat transfer capacity is greatly reduced.

  4. (4)

    Smaller width is beneficial to boiling heat transfer. Since capillary force decreases with increasing micro cavity width, it is conducive for supercooled liquids to enter the dry spot area for rewetting.