1 Introduction

Moving-load problems are very important in several engineering systems such as bridges traveled by vehicles or pedestrians, machine tools, pantograph collectors in railways, guideways in robotic solutions. The loads can be schematized in three different ways: moving force models if the mass involved in the motion is not relevant compared to that of the supporting systems (e.g., [1, 2]); moving mass models in cases where possible effects of load-structure interaction are negligible (i.e., the coupling between the moving subsystem and its support is assumed infinitely rigid; e.g., [3, 4]); moving oscillator models when stiffness and damping couplings between the load and the support are considered significant (e.g., [5, 6]). Recently, Cazzani et al. [7] have proposed a new approach based on mixed variables that is able to reproduce a continuous transition between a traveling mass and a traveling oscillator. Although the literature on this subject is very wide, there are still issues not fully clarified, especially among mathematical consistent formulations and technical solutions (e.g., [8]).

Concerning the simplified moving force model, it is still widely used in both scientific and technical field since it is often sufficient to answer to problems of practical interest. A typical load scheme is that of the classic Dirac delta generalized function (e.g., [9, 10]), which encompasses the jump conditions at the singular point. The usual field of application is that of mechanically-linear systems. The vibration analysis of a nonlinear beam subjected to a moving load has attracted the interest of many researchers over the last 20 years, with analytical and numerical approaches (e.g., [11, 12]). Concerning nonlinear suspended cables carrying moving loads a few studies exist (e.g., [13]), some of which turned to evaluate the effects of the traveling mass on the cable dynamic tension (e.g., [14]). To the best of the author’s knowledge, whereas the linear taut string traveled by moving loads has been extensively analyzed (e.g., [3, 15]) the situation is completely different for the nonlinear taut string.

The taut string is an idealized model of cable with evanescent sag. It is quite accurate when the natural length of the cable is smaller than the distance between the suspension points (i.e., prestressed cables). The geometric non-linearity of taut strings is rarely addressed in engineering applications, for specific objectives such as the possibility of overcoming the critical velocity (e.g., [16, 17]), whereas it is usually neglected in several problems in which it is considered of secondary importance (e.g., [18]). On the other hand, the study of the dynamics of nonlinear strings is of great interest from mathematical point of view (e.g., [19, 20]). For the description of the nonlinear dynamical response of taut strings the most used model in the literature is the Kirchhoff one, in which the longitudinal inertia is neglected and the corresponding displacement condensed (e.g. [21, 22]); with this assumption the dynamic tension component is a function of time alone. Similar problems are dealt with in the field of traveling tensioned strings, where Wickert [23] assumed the quasi-static stretch hypothesis to establish an integro-partial-differential equation for the transverse motion.

This paper is the first step towards the study of the combined effects induced by moving loads and nonlinearities on Kirchhoff taut strings, paying special attention to the dynamic change of tension, not considered in the linear model. At present a single moving force is considered supposing that its value is sufficiently small, that is the system experiences small displacements and the incremental dynamic tension is small compared to the static prestress. Therefore, the current study is limited to the weakly nonlinear dynamics of taut strings. The main purpose is to evaluate their behavior for load speeds below the string celerity through the use of semi-analytical techniques. After a summary of the equations of motion (Sect. 2), different semi-analytical solutions of the problem are obtained and critically discussed in Sect. 3. A finite-difference numerical procedure is illustrated and several numerical results are shown in Sect. 4. The final Sect. 5 highlights the strong points of the paper and its possible prospects.

2 Equations of motion

It is first presented the classic Kirchhoff model for a taut string traveled by a single force (Sect. 2.1); then the nondimensional partial differential equation is reduced to a discrete system of ordinary differential equations through the Galerkin method (Sect. 2.2).

2.1 Continuum model

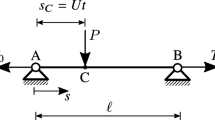
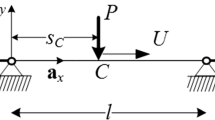
Let us consider a planar taut string of length l, mass per-unit-length m, damping coefficient \(\xi\), fixed at the two end points, (A, B), lying on the horizontal \({\mathbf {a}}_{x}\)-axis and subjected to the prestress \(T_{0}\). The curvature due to the self-weight is assumed to be negligible. The string is traveled by a vertical downward single force, \(-P{\mathbf {a}}_{y}\), which moves at a constant velocity, \(U{\mathbf {a}}_{x}\). At the initial instant \(t=0\) the force P is at the left end of the string, \(s=0\). The force occupies the instantaneous position C of abscissa \(s_{C}:=Ut\) at the generic time t (Fig. 1). Therefore, the action produced by the moving force P on the string depends on space and time, namely:

$${\mathbf {P}}=\left\{ \begin{array}{ll} -P\delta \left( s-Ut\right) {\mathbf {a}}_{y} &{} \quad \text {if}\quad 0\le t\le t_{c}\\ \mathbf {0} & \quad \text {if}\quad t>t_{c} \end{array}\right.$$
(1)

where \(\delta\) is the Dirac delta generalized function and \(t_{c}:=l/U\) is the crossing time. Accordingly, the string experiences forced vibrations in the time interval \(\left[ 0,t_{c}\right] ,\) and free damped vibrations afterwards. The attention is focused on the forced phase in the following.

Using the quasi-static stretch assumption and considering the transverse motion only, the motion equation of a taut string in the \(\left( {\mathbf {a}}_{x},{\mathbf {a}}_{y}\right)\)-plane reads (e.g., [21]):

$$\begin{aligned}&m\ddot{v}+\xi \dot{v}-\left( T_{0}+\frac{EA}{2l}\int _{0}^{l}v'^{2}\,{\mathrm {d}}s\right) v''=-P\delta \left( s-Ut\right) \\&\quad v\left( 0,t\right) =v\left( l,t\right) =0 \end{aligned}$$
(2)

v being the transverse (\({\mathbf {a}}_{y}\)-direction) displacement and EA the axial stiffness of the cable cross-section. The problem is equipped with (generally) non-homogeneous initial conditions:

$$\begin{aligned} v(s,0)=f(s),\qquad \dot{v}(s,0)=g(s) \end{aligned}$$
(3)

By defining the following nondimensional quantities:

$$\begin{aligned}\tilde{v}& =\frac{v}{l},\quad\tilde{s}=\frac{s}{l},\quad \tilde{t}=\frac{1}{l}\sqrt{\frac{T_{0}}{m}}t,\quad \tilde{P}=\frac{P}{T_{0}},\quad \tilde{U}=\frac{U}{\sqrt{T_{0}/m}},\\ \tilde{\xi }&=\xi \frac{l}{T_{0}}\sqrt{\frac{T_{0}}{m}},\quad \alpha=\frac{EA}{2T_{0}} \end{aligned}$$
(4)

where \(\alpha\) characterizes the elasticity of the cable (e.g., [24]), the dimensionless equation of motion are obtained (omitting the tilde):

$$\begin{aligned} &\ddot{v}+\xi \dot{v}-\left( 1+\alpha \int _{0}^{1}v'^{2}\,{\mathrm {d}}s\right) v''=-P\delta \left( s-Ut\right) \\&\quad v\left( 0,t\right) =v\left( 1,t\right) =0 \end{aligned}$$
(5)

It should be noted that the nondimensional transformation of the Dirac delta function reads: \(\delta \left( s-Ut\right) =\frac{1}{l}\delta \left( \tilde{s}-\tilde{U}\tilde{t}\right)\). Moreover, the term in brackets in the left member of the Eq. (5) is the dimensionless dynamic tension of the taut string: the nonlinear contribution leads to an increase of the tension from the unitary value, representative of the static prestress.

Fig. 1
figure 1

Taut string traveled by the single moving force P

Full size image

The homogeneous undamped linear problem is reduced to:

$$\begin{aligned} \begin{aligned}\ddot{v}-v''&=0\\ v\left( 0,t\right)&=v\left( 1,t\right) =0 \end{aligned} \end{aligned}$$
(6)

which admits the solution:

$$\begin{aligned} v\left( s,t\right) =\phi _{j}\left( s\right) e^{i\omega _{j}t} \end{aligned}$$
(7)

where:

$$\begin{aligned} \phi _{j}\left( s\right) =\frac{\sqrt{2}}{\omega _{j}}\sin \left( \omega _{j}s\right) ,\qquad \omega _{j}=j\pi ,\qquad j=1,2,\ldots \end{aligned}$$
(8)

are eigenfunctions which satisfy:

$$\begin{aligned} \int _{0}^{1}\phi _{i}'\phi _{j}'\,{\mathrm {d}}s=\delta _{ij} \end{aligned}$$
(9)

2.2 Discretized model

A discrete model can be derived via the classic Galerkin Method (GM). The transverse displacement v is assumed as:

$$\begin{aligned} v\left( s,t\right) =\sum _{m=1}^{N}\phi _{m}\left( s\right) q_{m}\left( t\right) \end{aligned}$$
(10)

\(\phi _{m}\) being the eigenfunctions of the linear taut string, Eq. (8), and \(q_{m}(t)\) their time-varying amplitudes. Replacing the previous expression in Eq. (5), multiplying by \(\phi _{j}\) and integrating over the string domain \(\left[ 0,1\right]\), the following equation is obtained:

$$\begin{aligned} \sum _{m=1}^{N}\int _{0}^{1}\phi _{j}\left[ \phi _{m}\ddot{q}_{j}+\xi \phi _{m}\dot{q}_{j}-\left( 1+\alpha \sum _{h=1}^{N}\sum _{k=1}^{N}\int _{0}^{1}\phi _{h}'\phi _{k}'\,{\mathrm {d}}s\,q_{h}q_{k}\right) \phi _{m}''q_{m}\right] \,{\mathrm {d}}s=-P\int _{0}^{1}\phi _{j}\delta \left( s-Ut\right) \,{\mathrm {d}}s\qquad j=1,\ldots ,N \end{aligned}$$
(11)

Using the normalized eigenfunctions, Eq. (8), and their orthogonality condition, Eq. (9), together with the property of the Dirac delta function, the generic j-th Galerkin equation becomes:

$$\begin{aligned} \ddot{q}_{j}+\xi \dot{q}_{j}+\omega _{j}^{2}q_{j}\left( 1+\alpha \sum _{h=1}^{N}q_{h}^{2}\right) =-P\omega _{j}\sqrt{2}\sin \left( \Omega _{j}t\right) \end{aligned}$$
(12)

where \(\Omega _{j}:=j\pi U=\omega _{j}U\). The forcing term in Eq. (12) shows that the traveling load induces an equivalent harmonic excitation of frequency \(\Omega _{j}\), proportional to the load speed U. The system of coupled nonlinear Galerkin equations can be summarized in matrix form as follows:

$$\begin{aligned} \begin{aligned}\left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} \ddots &{} 0\\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right] \left( \begin{array}{c} \ddot{q}_{1}\\ \ddot{q}_{2}\\ \vdots \\ \ddot{q}_{N} \end{array}\right) +\xi \left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} \ddots &{} 0\\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right] \left( \begin{array}{c} \dot{q}_{1}\\ \dot{q}_{2}\\ \vdots \\ \dot{q}_{N} \end{array}\right) +\left[ \begin{array}{cccc} \omega _{1}^{2} &{} 0 &{} 0 &{} 0\\ 0 &{} \omega _{2}^{2} &{} 0 &{} 0\\ 0 &{} 0 &{} \ddots &{} 0\\ 0 &{} 0 &{} 0 &{} \omega _{N}^{2} \end{array}\right] \left( \begin{array}{c} q_{1}\\ q_{2}\\ \vdots \\ q_{N} \end{array}\right) \\ +\alpha \left( \begin{array}{c} \omega _{1}^{2}q_{1}\left( q_{1}^{2}+q_{2}^{2}+\ldots +q_{N}^{2}\right) \\ \omega _{2}^{2}q_{2}\left( q_{1}^{2}+q_{2}^{2}+\ldots +q_{N}^{2}\right) \\ \vdots \\ \omega _{N}^{2}q_{N}\left( q_{1}^{2}+q_{2}^{2}+\ldots +q_{N}^{2}\right) \end{array}\right) =-P\sqrt{2}\left( \begin{array}{c} \omega _{1}\sin \left( \Omega _{1}t\right) \\ \omega _{2}\sin \left( \Omega _{2}t\right) \\ \vdots \\ \omega _{N}\sin \left( \Omega _{N}t\right) \end{array}\right) \end{aligned} \end{aligned}$$
(13)

Once the generic amplitude \(q_{j}(t)\) has been determined by numerical integration of Eq. (13), the solution of the problem is reconstructed by means of the Galerkin expansion (10).

3 Semi-analytical solutions

Two direct perturbation solutions on the string continuum model are described in Sects. 3.1 (Multiple Scale Method) and 3.2 (Straightforward Expansion). The solution of the linear problem is obtained as a first perturbation step.

3.1 Multiple Scale Method (MSM)

One considers a regime of small but finite displacements, for which the incremental tension is small compared with the static prestress (i.e., weakly nonlinear dynamics). Due to the absence of quadratic nonlinearities (which vanish with the initial curvature), the problem is symmetric so that a first-order analysis requires a single perturbation step.

By rescaling the variables as:

$$\begin{aligned} v\rightarrow \varepsilon ^{1/2}\,v,\quad \xi \rightarrow \varepsilon \,\xi ,\quad P\rightarrow \varepsilon ^{1/2}\,P \end{aligned}$$
(14)

the dimensionless equation of motion (divided by \(\varepsilon ^{1/2}\)) reads:

$$\begin{aligned} &\ddot{v}+\varepsilon \,\xi \dot{v}-\left( 1+\varepsilon \,\alpha \int _{0}^{1}v'^{2}\,{\mathrm {d}}s\right) v''=-P\delta \left( s-Ut\right) \\&\quad v\left( 0,t\right) =v\left( 1,t\right) =0 \end{aligned}$$
(15)

Since the excitation P is in general non-resonant, the load is ordered at the same level of the transverse displacement v; this case is also referred to as hard excitation (e.g., [21]).

Moreover, the following expansion is assumed for the unknown displacement:

$$\begin{aligned} v=v_{0}+\varepsilon \,v_{1}+\cdots \end{aligned}$$
(16)

where independent time scales are introduced, \(t_{k}=\varepsilon ^{k}t\quad (k=0,1,\ldots )\), so that the first and second time-derivatives are expressed as \(D={\mathrm {d}}_{0}+\varepsilon \,{\mathrm {d}}_{1}+\cdots\), \(D^{2}={\mathrm {d}}_{0}^{2}+2\,\varepsilon \,{\mathrm {d}}_{0}{\mathrm {d}}_{1}+\cdots\), where \({\mathrm {d}}_{k}=\frac{\partial }{\partial t_{k}}\).

The MSM perturbation equations are thus obtained:

$$\begin{aligned} \begin{aligned}\varepsilon ^{0}:&\left\{ \begin{aligned}{\mathrm {d}}_{0}^{2}v_{0}-v_{0}''&=-P\delta \left( s-Ut_{0}\right) \\ v_{0}\left( 0,t_{0},t_{1},\ldots \right)&=v_{0}\left( 1,t_{0},t_{1},\ldots \right) =0\\ v_{0}\left( s,0,0,\ldots \right)&=\breve{f}\left( s\right) ,\quad {\mathrm {d}}_{0}v_{0}\left( s,0,0,\ldots \right) =\breve{g}\left( s\right) \end{aligned} \right. \\ \varepsilon ^{1}:&\left\{ \begin{aligned}{\mathrm {d}}_{0}^{2}v_{1}-v_{1}''&=-2{\mathrm {d}}_{0}{\mathrm {d}}_{1}v_{0}-\xi {\mathrm {d}}_{0}v_{0}+\alpha v_{0}''\int _{0}^{1}v_{0}'^{2}\,{\mathrm {d}}s\\ v_{1}\left( 0,t_{0},t_{1},\ldots \right)&=v_{1}\left( 1,t_{0},t_{1},\ldots \right) =0\\ v_{1}\left( s,0,0,\ldots \right)&=0,\quad {\mathrm {d}}_{0}v_{1}\left( s,0,0,\ldots \right) =-{\mathrm {d}}_{1}v_{0}\left( s,0,0,\ldots \right) \end{aligned} \right. \end{aligned} \end{aligned}$$
(17)

For the sake of simplicity it is assumed in the following that \(\breve{f}\left( s\right) =\breve{g}\left( s\right) =0\).

From the \(\varepsilon ^{0}\)-order equation, the generating solution reads:

$$\begin{aligned} v_{0}\left( s,t_{0},t_{1},\ldots \right) =\sum _{j=1}^{N}\phi _{j}\left( s\right) x_{0j}\left( t_{0},t_{1},\ldots \right) \end{aligned}$$
(18)

The modal amplitude associated with the j-th eigenfunction, \(x_{0j}\left( t_{0},t_{1},\ldots \right)\), is the solution of the linear system:

$$\left\{ \begin{array}{ll}{\mathrm {d}}_{0}^{2}x_{0j}+\omega _{j}^{2}x_{0j}=-P\omega _{j}\sqrt{2}\sin \left( \Omega _{j}t_{0}\right) \\ x_{0j}\left( 0,0,\ldots \right)={\mathrm {d}}_{0}x_{0j}\left( 0,0,\ldots \right) =0 \end{array} \right.$$
(19)

which leads to:

$$\begin{aligned} x_{0j}=A_{j}e^{i\omega _{j}t_{0}} +\varGamma _{j}e^{i\Omega _{j}t_{0}}+\varLambda _{j}e^{i\omega _{j}t_{0}}+{\mathrm {c.c.}} \end{aligned}$$
(20)

where the term c.c. denotes the complex conjugate and:

$$\varGamma _{j}=i\frac{P\omega _{j}}{\sqrt{2}\left( \omega _{j}^{2}-\varOmega _{j}^{2}\right) },\quad \varLambda _{j}=-\frac{\Omega _{j}}{\omega _{j}}\varGamma _{j}$$
(21)

\(\varGamma _{j},\varLambda _{j}\) being purely imaginary numbers and \(A_{j}=A_{j}\left( t_{1},t_{2},\ldots \right)\) the j-th complex amplitude, which is a function of slow time scales. Note that the particular solution of Eq. (20) satisfies the initial conditions of Eq. (19) from which \(A_{j}\left( 0,\cdots \right) =0\) follows.

Replacing the generating solution (18) in the \(\varepsilon\)-order perturbation equation, observing that \(\phi _{j}''=-\omega _{j}^{2}\phi _{j}\) and accounting for the normalization condition (9), one obtains:

$$\begin{aligned} \begin{aligned} {\mathrm {d}}_{0}^{2}v_{1}-v_{1}''&=\sum _{j=1}^{N}\phi _{j}\left\{ -2i\omega _{j}{\mathrm {d}}_{1}A_{j} e^{i\omega _{j}t_{0}}-i\xi \left[ \omega _{j}A_{j}e^{i\omega _{j}t_{0}} +\varGamma _{j}\Omega _{j}e^{i\Omega _{j}t_{0}} +\omega _{j}\varLambda _{j}e^{i\omega _{j}t_{0}}\right] +\right. \\&\quad \left. -\alpha \omega _{j}^{2}x_{0j\;}\sum _{h=1}^{N}x_{0h}^{2} +{\mathrm {c.c.}}\right\} \end{aligned} \end{aligned}$$
(22)

Eq. (22) contains harmonic functions of frequency \(\omega _{j}\), generated by damping and inertia forces, and cubic combinations of the frequencies \(\omega\)’s and \(\Omega\)’s (namely, \(2\omega _{h}-\omega _{j}\), \(\omega _{h}+\Omega _{h}-\Omega _{j}\), \(\omega _{h}-\Omega _{h}+\Omega _{j}\), when \(h=j\)). To eliminate secular terms the solvability condition should be imposed requiring the vanishing of the \(\omega _{j}\)-harmonic terms (i.e., terms multiplied by \(e^{i\omega _{j}t_{0}}\)). By accounting for Eq. (20) and excluding special resonant values of \(\Omega _{j}\), the ordinary Amplitude Modulation Equations (AME) in complex form are derived:

$$\begin{aligned} \begin{aligned}&2i\omega _{j}{\mathrm {d}}_{1}A_{j}+i\xi \omega _{j}\left( A_{j} +\varLambda _{j}\right) +4\,\alpha \omega _{j}^{2}\,\varGamma _{j} \bar{\varGamma }_{j}\left( A_{j}+\Lambda _{j}\right) +\alpha \omega _{j}^{2}\,\left( A_{j}+\Lambda _{j}\right) {}^{2}\left( \bar{A}_{j}+\bar{\Lambda }_{j}\right) \\&\quad +2\alpha \omega _{j}^{2}\left[ \sum _{h=1}^{N}\varGamma _{h}\bar{\varGamma }_{h}+\left( A_{h}+\Lambda _{h}\right) \left( \bar{A}_{h}+\bar{\Lambda }_{h}\right) \right] \left( A_{j}+\Lambda _{j}\right) =0 \end{aligned} \end{aligned}$$
(23)

Setting \(A_{j}=a_{j}+ib_{j}\), with \(a_{j}:=a_{j}\left( t\right) ,\,b_{j}:=b_{j}\left( t\right)\), the AME in (real) Cartesian form are achieved:

$$\begin{aligned} \begin{aligned}&\dot{b}_{j}+\frac{1}{2}\xi \left( b_{j}-i\Lambda _{j}\right) -\frac{1}{2}\alpha \omega _{j}a_{j}\left( a_{j}^{2}+b_{j}^{2}-4\varGamma _{j}^{2}-2ib_{j}\Lambda _{j}-\Lambda _{j}^{2}\right) \\&\quad -\alpha \omega _{j}\left( \sum _{h=1}^{N}a_{h}^{2}+b_{h}^{2}-\varGamma _{h}^{2}-\Lambda _{h}^{2}-2i\Lambda _{h}b_{h}\right) a_{j}=0\\ \\&\dot{a}_{j}+\frac{1}{2}\xi a_{j}+\frac{1}{2}\alpha \omega _{j}\left( b_{j}-i\Lambda _{j}\right) \left( a_{j}^{2}+b_{j}^{2}-4\varGamma _{j}^{2}-2ib_{j}\Lambda _{j}-\Lambda _{j}^{2}\right) \\&\quad +\alpha \omega _{j}\left( \sum _{h=1}^{N}a_{h}^{2}+b_{h}^{2}-\varGamma _{h}^{2}-\Lambda _{h}^{2}-2i\Lambda _{h}b_{h}\right) \left( b_{j}-i\Lambda _{j}\right) =0 \end{aligned} \end{aligned}$$
(24)

where it has been taken into account that \({\mathrm {Re}}\left[ \varGamma _{j}\right] ={\mathrm {Re}}\left[ \varLambda _{j}\right] =0\) , \({\mathrm {Im}}\left[ \varGamma _{j}\right] =-i\varGamma _{j},\,{\mathrm {Im}}\left[ \varLambda _{j}\right] =-i\varLambda _{j}\), and that \(\varGamma _{j}^{2}\) and \(\Lambda _{j}^{2}\) are real quantities.

Equation (24) are a set of infinitely many AME’s. The infinite number is a consequence of the fact that all the modes of the string are excited by the moving force P. Since the interest is not aimed at determining fixed points of the dynamical system defined by AME’s, numerical integrations are mandatory. A finite number of involved modes must be considered with a convergence check of the solution.

Through MSM the original partial differential problem (5) has been reduced to a system of (infinite) ordinary differential equations. Differently from GM, which also supplies a set of infinite ordinary differential equations in the coupled modal coordinates, MSM filters the fast dynamics: the unknown amplitudes slowly vary in time making easier to perform numerical integrations.

Once the complex amplitude \(A_{j}\) is calculated, the j-th modal amplitude \(x_{0j}\) is rebuilt, then the first-order MSM solution \(v_{0}\) is drawn coming back to the true time t.

It is worth noting that the MSM \(\varepsilon\)-order solution, \(v_{1}\), could be obtained in a semi-analytical way through a very burdensome procedure only, once solved numerically the AME’s. In this way the advantage of using a semi-analytical method fails and the direct application of the Galerkin method, as was done in Sect. 2.2, appears much more consistent. Therefore, the MSM solution is limited to the first order although this fact may limit its accuracy, as will be shown in applications.

3.2 Straightforward Expansion (SE)

As it is well-known (e.g., [25]), SE leads to the occurrence of secular terms that can be eliminated by invoking suitable solvability conditions. This problem occurs if the interest is directed to infinite time domains (e.g., \(t\rightarrow \infty\)), in which the asymptotic series breaks down when \(t=\mathrm {O}\left( \varepsilon ^{-1}\right)\). If the interest is addressed to a finite time domain, such as \(\left[ 0,t_{c}\right]\), such drawback does not occur if \(\varepsilon t_{c}\ll 1\). Therefore, SE is expected to work properly without any correction for small displacements (e.g., of the order of \(10^{-3}\) times the span of the string) and sufficiently high load speeds (e.g., of the order of \(10^{-1}\) times the celerity of the string).

Putting Eq. (16) into Eq. (15) and separating the terms of the same order, the following perturbation equations are obtained:

$$\begin{aligned} \begin{aligned}\varepsilon ^{0}:&\left\{ \begin{aligned}\ddot{v}_{0}-v_{0}''&=-P\delta \left( s-Ut\right) \\ v_{0}\left( 0,t\right)&=v_{0}\left( 1,t\right) =0\\ v_{0}\left( s,0\right)&=\breve{f}\left( s\right) ,\quad \dot{v}_{0}\left( s,0\right) =\breve{g}\left( s\right) \end{aligned} \right. \\ \varepsilon ^{1}:&\left\{ \begin{aligned}\ddot{v}_{1}-v_{1}''&=-\xi \dot{v}_{0}+\alpha v_{0}''\int _{0}^{1}v_{0}'^{2}\,{\mathrm {d}}s\\ v_{1}\left( 0,t\right)&=v_{1}\left( 1,t\right) =0\\ v_{1}\left( s,0\right)&=0,\quad \dot{v}_{1}\left( s,0\right) =0 \end{aligned} \right. \end{aligned} \end{aligned}$$
(25)

As before, it is assumed \(\breve{f}\left( s\right) =\breve{g}\left( s\right) =0\).

The generating solution is written as:

$$\begin{aligned} v_{0}\left( s,t\right) =\sum _{j=1}^{N}\phi _{j}\left( s\right) x_{0j}\left( t\right) \end{aligned}$$
(26)

The modal amplitude \(x_{0j}\left( t\right)\), associated with the j-th eigenfunction, is the solution of the following linear system:

$$\begin{aligned} \left\{ \begin{aligned}\ddot{x}_{0j}+\omega _{j}^{2}x_{0j}&=-P\omega _{j}\sqrt{2}\sin \left( \Omega _{j}t\right) \\ x_{0j}\left( 0\right)&=\dot{x}_{0j}\left( 0\right) =0 \end{aligned} \right. \end{aligned}$$
(27)

namely:

$$\begin{aligned} x_{0j}=\varGamma _{j}e^{i\Omega _{j}t}+\varLambda _{j}e^{i\omega _{j}t}+{\mathrm {c.c.}} \end{aligned}$$
(28)

where \(\varGamma _{j}\) and \(\varLambda _{j}\) are defined in Eq. (21).

Replacing the generating solution (26) into the \(\varepsilon\)-order equation and taking into account the normalization condition (9), one obtains:

$$\begin{aligned} \begin{aligned}\varepsilon ^{1}:&\left\{ \begin{aligned}\ddot{v}_{1}-v_{1}''&=\sum _{j=1}^{N}\phi _{j}\left\{ -\xi \left( i\Omega _{j}\varGamma _{j}e^{i\Omega _{j}t}+i\omega _{j}\varLambda _{j}e^{i\omega _{j}t}\right) -\alpha \omega _{j}^{2}x_{0j}\sum _{h=1}^{N}x_{0h}^{2}+{\mathrm {c.c.}}\right\} \\ v_{1}\left( 0,t\right)&=v_{1}\left( 1,t\right) =0\\ v_{1}\left( s,0\right)&=0,\quad \dot{v}_{1}\left( s,0\right) =0 \end{aligned} \right. \end{aligned} \end{aligned}$$
(29)

The solution of the previous equation can be written as:

$$\begin{aligned} v_{1}\left( s,t\right) =\sum _{j=1}^{N}\phi _{j}\left( s\right) x_{1j}\left( t\right) \end{aligned}$$
(30)

where the \(\varepsilon\)-order modal amplitude \(x_{1j}\left( t\right)\) is the solution of:

$$\begin{aligned} \left\{ \begin{aligned}\ddot{x}_{1j}+\omega _{j}^{2}x_{1j}&=-\xi \left( i\Omega _{j}\varGamma _{j}e^{i\Omega _{j}t}+i\omega _{j}\varLambda _{j}e^{i\omega _{j}t}\right) -\alpha \omega _{j}^{2}x_{0j}\sum _{h=1}^{N}x_{0h}^{2}+{\mathrm {c.c.}}\\ x_{1j}\left( 0\right)&=\dot{x}_{1j}\left( 0\right) =0 \end{aligned} \right. \end{aligned}$$
(31)

Then, \(x_{1j}\left( t\right)\) can conveniently be expressed through the classic convolution (Duhamel) integral:

$$\begin{aligned} x_{1j}\left( t\right) =\frac{1}{\omega _{j}} \int _{0}^{t}\sin \left[ \omega _{j}\left( t-\tau \right) \right] \left[ -\xi \left( i\Omega _{j}\varGamma _{j}e^{i\Omega _{j}\tau } +i\omega _{j}\varLambda _{j}e^{i\omega _{j}\tau }\right) -\alpha \omega _{j}^{2}x_{0j}\left( \tau \right) \sum _{h=1}^{N}x_{0h}^{2} \left( \tau \right) +{\mathrm {c.c.}}\right] \,{\mathrm {d}}\tau \end{aligned}$$
(32)

Indeed, although the known terms are harmonic functions, the analytical solution is quite laborious due to the occurrence of resonances. These latter originate from the combination of the \(\omega _{j}\) frequencies (occurring for any load speed U) as well from cubic combinations of the \(\omega _{j}\) and \(\Omega _{j}\) frequencies (occurring only for special values of the load speed, even if sub-critical). For these reasons the convolution integral is more conveniently evaluated numerically. It is worth noticing that, differently from the MSM approach, the special sub-critical resonances are now accounted for.

Once \(v_{0}\left( s,t\right)\) and \(v_{1}\left( s,t\right)\) have been calculated, the response of the nonlinear taut string is determined by Eq. (16).

4 Numerical results

A fully numerical solution is introduced for validation of the semi-analytical approaches. The Finite-Difference (FD) method is applied in order to discretize the equation of motion (5) over the spatial variable s. The string is divided into \(N_{d}\) elements of equal length \(h:=1/N_{d}\) by \((N_{d}+1)\) nodes; therefore, the string transverse displacement v is evaluated in discrete form as a function of the single variable time, \(v_{j}(t):=v(s_{j},t)\), with \(s_{j}:=jh\) \((j=0,1,...,N_{d})\). The moving force P is usually assumed to move jerkily over the nodes [26]. Using the central difference technique also for the nonlinear integral term similarly to [27], the following system of coupled ordinary differential equations is obtained:

$$\begin{aligned} \ddot{v}_{j}(t)+\xi \dot{v}_{j}(t)&=\frac{v_{j+1}(t)-2v_{j}(t)+v_{j-1}(t)}{h^{2}}\cdot \nonumber \\&\quad \cdot \left\{ 1+\alpha h\left[ \frac{1}{2}\left( \frac{v_{1}(t)-v_{0}(t)}{h}\right) ^{2}+\frac{1}{2}\left( \frac{v_{N_{d}}(t)-v_{N_{d}-1}(t)}{h}\right) ^{2}+\sum _{k=1}^{N_{d}-1}\left( \frac{v_{k+1}(t)-v_{k-1}(t)}{2h}\right) ^{2}\right] \right\} +f_{j}(t) \end{aligned}$$
(33)

where the boundary conditions imply \(v_{0}(t)=v_{N_{d}}(t)=0\). The issue is the discretization of the Dirac delta function that appears in the forcing term \(f_{j}(t):=f(s_{j},t)\). It has been suggested that it can be approximated (and regularized) by a standard Gaussian function [28] or handled by combining the differential quadrature approach with the integral quadrature method (e.g., [29]). Discretizing the Dirac delta function by a standard Gaussian function, the forcing term \(f_{j}(t)\) becomes:

$$\begin{aligned} f_{j}(t)=-\frac{P}{\beta \sqrt{\pi }}\exp \left[ -\left( \frac{s_{j}-Ut}{\beta }\right) ^{2}\right] \end{aligned}$$
(34)

\(\beta\) being the regularization parameter, which has to be as small as possible to obtain an accurate representation of the Dirac delta function.

Literature values of model parameters are considered. The elasticity coefficient \(\alpha\) is assumed between 200 and 500 for metal string [21]. The moving load P is about 0.01 as for suspended cable problems interested in dynamic tension (e.g., [14]); a value of up to 0.02 is consistent with the hypothesis of weakly nonlinear dynamics. The load speed is chosen between 0.1 and 0.5 (i.e., to be neither too low nor too close to the critical value). The damping coefficient is set to the reference value of 0.01. Numerical solutions are determined through standard solvers (e.g., ode45 in \({\mathrm {MATLAB}}{}^{\circledR }\) software). As basic example, according to the aforementioned values, it is chosen \(\alpha =200\), \(P=0.01\), \(U=0.1\). The percent dynamic increase of the string tension, \(T_{d}\), is evaluated as measure of the effective nonlinearity of the problem: its value is the correction to the (unitary) static value, Eq. (5).

Figure 2 shows the convergence check on FD solutions. Differences between using 100 or 1000 elements are very limited. An improvement occurs with a smaller value of the regularization parameter \(\beta\), which is only possible for a sufficiently small step, such as \(N_{d}=1000\), to avoid numerical oscillations in the solution. In this way the discontinuity in the string deformation is described quite well (Fig. 2b). Figure 3 presents the convergence of GM varying the number of eigenfunctions considered. The solutions for \(N=20\) and \(N=30\) are almost indistinguishable; the cusp in the deformation, Fig. 3b, is obviously regularized as in the philosophy of weighted residual methods.

Fig. 2
figure 2

Convergence check of FD solution: a motion under the load, b deformed shape for force at midpoint (basic example)

Full size image
Fig. 3
figure 3

Convergence check of GM solution: a motion under the load, b deformed shape for force at midpoint (basic example)

Full size image

Using the convergence values (\(N_{d}=1000\) and \(\beta =0.001\) for FD, \(N=30\) for GM), Fig. 4 shows a comparison between the two solutions. Concerning the basic example, the agreement is very good for both the deformed shape (with the exception of the cusp, as to be expected; Fig. 4a) and for the dynamic tension (Fig. 4b). However, this example features reduced values of tension increase. In order to complete the validation between the two solutions a couple of examples in which the nonlinearity is more pronounced were considered, setting the upper extreme of the range identified for the problem parameters (i.e., \(\alpha =500\), \(P=0.02\)). Figure 5 presents the dynamic tension for two different values of U, reaching increases of up to 15% with regard to the static prestress: the agreement between the two solutions is very good. Therefore, from now on, GM will be used as reference for the semi-analytical solutions.

Fig. 4
figure 4

Comparisons between GM and FD solutions: a deformed shape for force at midpoint, b dynamic tension increment (basic example)

Full size image
Fig. 5
figure 5

Comparisons between GM and FD solutions (\(\alpha =500\), \(P=0.02\)): dynamic tension increment for a \(U=0.1\) and b \(U=0.5\)

Full size image

Concerning the basic example, Fig. 6 presents the comparison between the two perturbation solutions proposed and the Galerkin Method; moreover, the linear solution is also shown as reference. The agreement between the results is great but the effect of nonlinearity is very moderate; indeed, the linear solution is practically superimposed on the nonlinear ones and the string tension increment does not reach the one percent of the static prestress. Figure 7 is obtained by increasing the elasticity parameter \(\alpha\) from 200 to 500: the agreement among the different solutions remains good (even if MSM slightly overestimates the results) but the system behavior is still almost linear.

Fig. 6
figure 6

Comparison among semi-analytical solutions (basic example): a motion under the load, b midpoint transverse displacement, c dynamic tension increment, d deformed shape for force at midpoint

Full size image
Fig. 7
figure 7

Comparison among semi-analytical solutions (\(\alpha =500\)): a motion under the load, b dynamic tension increment

Full size image

The effect of the speed increase is analyzed in Fig. 8. When the elasticity parameter is small (\(\alpha =200\); Fig. 8a, b) the linear solution is practically exact and the dynamic increase of tension is about two percent of the static prestress. For high values of \(\alpha\) (e.g., 500; Fig. 8c, d) the nonlinearity becomes more relevant and the linear solution shows a small error. In both the situations SE solution is coincident with GM reference solution and MSM appears to be the least accurate.

Fig. 8
figure 8

Effect of speed increase (\(U=0.5\)): a, c motion under the load and b, d dynamic tension increment for \(\alpha =200,500\), respectively (\(P=0.01\))

Full size image

Finally, the effect of the load increase is taken into account in Fig. 9. Using a large value of the elasticity parameter (\(\alpha =500)\) the nonlinearity is growing in importance. When the load speed is limited (\(U=0.1\); Fig. 9a, b) both the perturbation solutions show inaccuracies compared to GM. For high load speed, \(U=0.5\) (Fig. 9c, d), SE solution leads to good results in both string motion and dynamic tension increment even if the nonlinear effect becomes relevant. Further increases in P values would result in highly nonlinear behaviors that go beyond the hypothesis of weakly nonlinear dynamics.

Fig. 9
figure 9

Effect of load increase (\(P=0.02\)): a, c motion under the load and b, d dynamic tension increment for \(U=0.1,0.5\), respectively (\(\alpha =500\))

Full size image

5 Final remarks and future developments

This paper points out the lack of literature on the problem of nonlinear taut strings traveled by moving load. Two perturbation solutions have been proposed within weakly nonlinear dynamics; a Galerkin procedure was discussed whose validity has been verified through an extensive parametric analysis; a finite-difference solution has also been identified. Three aspects can be highlighted:

  1. 1.

    the nonlinearity may have some relevance on the problem addressed; for certain combinations of the parameters involved (speed and intensity of the load, elasticity coefficient) the dynamic tension increment can achieve values close to twenty percent of the static prestress while remaining in the domain of weakly nonlinear dynamics; similar behaviors are found in the dynamics of suspended cables with moving mass ([14]), where the importance of this effect for design purposes is underlined;

  2. 2.

    between the proposed perturbation procedures, the Straightforward Expansion is pretty simple and has very good performance, paying attention to meeting its validity range; on the other hand, MSM shows larger error for low nonlinearities too, also because it has been limited to the first order expansion for consistency of analysis; on the other hand, leading MSM to second order nullifies the advantage of using a semi-analytical technique;

  3. 3.

    the Galerkin approach can be considered a good reference solution for the string nonlinear problem (as often happens in linear problems) if the aim is the analysis of global behaviors of the system; the averaging operation implicit in the use of Galerkin procedures could lead to localized problems, near the supports, as shown in [3, 4, 8, 17].

The most important prospects concern the extension of this work to (a) train of moving forces (dealt with in [26] limited to the linear range) and (b) strongly nonlinear regimes.

Improvements on Galerkin method are also possible by adding suitable quasi-static correction functions. The development of more sophisticated numerical methods can benefit from the techniques developed, e.g., in [30, 31].

The effect of damping has not been examined. It is a quantity subjected to considerable uncertainty, which can have great influence on the fatigue damage in structures under repeated loads (e.g., [32, 33]). The design of innovative damping mechanisms for controlling vibrations due to moving loads is a challenging aspect. A possible approach to smart taut string is the use of piezo-electromechanical transducers following the strategy presented, e.g., in [34,35,36,37].