Stochastic stability and dynamics of a two-dimensional structurally nonlinear airfoil in turbulent flow

Abstract

The present study considers the application of stochastic dimensional reduction (low-dimensional approximation of stochastic dynamical systems) to a 11-dimensional nonlinear aeroelastic problem exhibiting a Hopf bifurcation, with one critical mode and several stable modes. The analysis is performed close to the critical value of the bifurcation parameter (the freestream airspeed) that induces flutter in a 2-D airfoil. The system is excited by multiplicative and additive real noise processes whose power spectral densities are given by the Dryden wind turbulence model. The homogenization procedure yields a two dimensional Markov process characterized by a generator. Further simplification yields a one dimensional stochastic differential equation that characterizes the amplitude of the critical mode of the original system. This simplified low-dimensional coarse-grained model, which captures the essential stochastic dynamics close to flutter instability, is used to efficiently simulate the long-term statistics of the slow variables. The explicit forms of the homogenized drift and diffusion coefficients of the reduced stochastic differential equation are determined. The explicit formulas contain both the stochastic perturbations in the unstable and stable modes as well as the action of the nonlinear terms. The reduced order (coarse-grained) model is verified by comparison of distribution functions, obtained computationally, with the original system. Additionally, the top Lyapunov exponent found analytically compares well with the exponent obtained by numerical experiments using the original system. This analysis provides a transparent medium for applying the homogenization procedure and may be of interest to aircraft designers.

1 Introduction

In the present work, we examine the flutter characteristics of an airfoil in turbulent flow, modeled as a rigid flat plate. Turbulence is a common factor in airplane accidents, for example loss of in-flight control associated with wind gusts, which can cause substantial damage to the aircraft and injuries to crew and passengers (see Belcastro and Foster [1]). Although the effects of turbulence depend on aircraft size, we consider a nontrivial classical airfoil model as a basis for developing a unified framework for studying the effects of nonlinearity and noise in a multi-dimensional system that exhibits flutter instability (i.e. when the deterministic system undergoes a Hopf bifurcation).

The dynamics of a structurally nonlinear two dimensional airfoil has been studied numerically by Lee et al. [2] and Poirel and Price [3]. This paper provides novel, theoretically sound results for efficiently studying instabilities and associated stochastic bifurcation scenarios in the neighborhood of the flutter airspeed. Specifically, the work presented here

• revisits the stochastic multiscale problem studied in Namachchivaya and Van Roessel [4], in which the martingale problem approach is used to rigorously obtain a reduced-order representation of a dynamical system with rapidly oscillating and decaying components, driven by white noise. This paper extends the findings of Namachchivaya and Van Roessel [4] to a system driven by real noise, in this case a 2-degree-of-freedom airfoil model with wind gust/turbulence forcing. We obtain a 1-dimensional representation of the critical mode of the 11-dimensional aeroelastic system, in the vicinity of the flutter airspeed.

• validates the asymptotic results through comparison of numerical simulations of the original and reduced-order models. To the best of our knowledge, this is one of few examples in which the asymptotic solution for stability and bifurcations are compared to the numerical simulation of a 11-dimensional real application.

The main result is a 1-dimensional homogenized stochastic differential equation that captures the combined amplitude of pitch and heave oscillations when the system is close to flutter. This homogenized stochastic differential equation has the potential to serve as a computational inexpensive platform for accurately capturing the essential flutter characteristics of an airfoil undergoing instantaneous probabilistic dynamic instability. Appropriate vulnerability criterion that capture these instabilities can be formulated and incorporated in the airfoil design for improved passengers, crew, and aircraft safety. In this spirit, we derive the explicit formula for the homogenized stochastic differential equation based on model parameters. The results are hoped to be flexible enough for aircraft designers to obtain the reduced stochastic differential equations corresponding to their models. Furthermore, the homogenization procedure presented here can be adopted by other researchers who may wish to obtain accurate localized results for noisy systems in the proximity of a critical system parameter. Below, we provide an outline of the work presented here.

First, in Sect. 2, we adopt the 2-degree of freedom ordinary differential equation for a thin airfoil originally derived by Fung [5], and explain the associated aerodynamic forces. The latter entails consideration of the displaced mass and circulatory terms from aerodynamics. The circulatory terms are modified to account for the effects of horizontal and vertical components of wind gust/turbulence, as done by many authors (see, for example, [3]). The ciculatory terms are found to comprise of exponential kernels, which makes analysis mathematically intractable. Two auxiliary second order oscillators are adopted to overcome this hurdle, which increases the dimension of the system. Wind gust in the circulatory terms is modeled using two stochastic differential equations. Specifically, the time correlation of the solutions to these stochastic differential equations corresponds to the power spectral density of real turbulence determined in Yeager [6] (the Dryden model).

Second, in Sect. 3 we outline the reduction technique, which is at the crux of this work. This technique requires appropriate scalings to be introduced (for time and nonlinearities) so that the stochastic dynamics of the overall system (including noise processes) can be characterized by slow, intermediate, and fast components. Readers may be aware of asymptotic techniques that handle such multiscale problems in the deterministic context, for example the method of multiple scales (see, for example, [7]). However, in the stochastic context, the main task is to obtain a reduced-order representation using a martingale problem approach for Markov processes, which is an ideal tool for studying weak convergence of Markov processes, as explained in Ethier and Kurtz [8]. Reduced-order models were obtained with rigorous proof in Namachchivaya and Van Roessel [4] (Theorem 4.2) and are extended here without proof for the real noise case. The slow and intermediate components are associated with the “critical” and “stable” modes of the system, respectively. The fast component is the driving wind gust, enters the equations of motion as a noise process. The noise process is assumed to satisfy certain mixing conditions (Doeblin’s condition that guarantees that the fast variable rapidly attains its invariant measure) to facilitate the ensuing homogenization. The underpinning of classical homogenization is a separation of time scales, which involves the convergence of a sequence $\{x^\varepsilon (t)\}$ of processes parameterized by $\varepsilon$ to a limit process in some sense. It is important that the limit process $x^0(t)$ obtained by this procedure be much more mathematically tractable than the true physical process, and the parameter value $\varepsilon$, corresponding to the physical process, be small enough to yield a good approximation. The most widely used sense of the limit is that of weak convergence of measures as discussed in Namachchivaya and Van Roessel [4] and references therein. In essence, the problem boils down to solving a set of Poisson equations associated with the generator of the multi-scale Markov process.

Then, in Sect. 4, numerical simulations using the original and reduced-order systems are presented to validate the theoretical result obtained from solving the Poisson equations in Sect. 3. The top Lyapunov exponent (which characterizes the exponential growth rate of trajectories starting from two nearby points) for the reduced system is calculated analytically and compared with the top Lyapunov exponent obtained by numerically simulating the critical modes of the original system. Finally, in Sect. 5, we conclude with a discussion of our results.

2 The nonlinear aeroelastic dynamical system

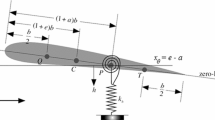
We consider a two-dimensional airfoil with two degrees of freedom (Fig. 1): a rotation around the airfoil’s elastic axis and a vertical translation (heave motion). Rotation about the elastic axis, denoted by $\alpha$, is positive when the airfoil is pitched up. Heave motion, denoted by h, is the vertical translation of the elastic axis from a mean position, and is positive downwards. The configuration $\alpha =0$ corresponds to a null angle of attack relative to the freestream. No angle of incidence is considered, so the airfoil pitch motion corresponds to the angle of attack. The pitch ($\alpha$) and heave (h) motions are governed by the following (dots represent derivative with respect to physical time t):

$$\begin{aligned} m x_\alpha b \ddot{\alpha }+m \ddot{h} + K_h h&= -L(t), \end{aligned}$$

(2.1a)

$$\begin{aligned} I_{EA}\ddot{\alpha }+m x_\alpha b \ddot{h} + K_\alpha \alpha + K_3 \alpha ^3&= M_{EA}(t). \end{aligned}$$

(2.1b)

The above equations of motion are obtained by considering the balance of aerodynamic forces and moments about the elastic axis of the airfoil. The form of (2.1) is a result of modifying the equations that govern the dynamics of a two-dimensional airfoil (see Fung [5]) to include a cubic torsional stiffness (see Poirel and Price [3]). There is no coupling between the two degrees-of-freedom when the airfoil is balanced (i.e., the center of mass coincides with the elastic axis, $x_\alpha =0$). Coupling arises from the inertia terms when $x_\alpha \ne 0$.

Fig. 1

Two-dimensional airfoil with degrees of freedom $\alpha$ and h

The terms L and $M_{EA}$ on the right hand side of (2.1a) and (2.1b) represent the aerodynamic loads: the lift force and the aerodynamic moment about the elastic axis, respectively. We now briefly review the historical development of the lift force expression. Wagner [9], developed a model for the unsteady lift acting on a two-dimensional airfoil for arbitrary pitching motion. Wagner analytically computed the effect of an idealized planar wake vorticity on the circulation around the airfoil in response to a step input for the angle of attack. Then, a model to study flutter instability was developed by Theodorsen and Mutchler [10]. Both Wagner’s and Theodorsen’s theories were derived analytically for an idealized two-dimensional flat plate airfoil moving through an inviscid, incompressible fluid. The motion of the flat plate is assumed to be infinitesimal, leaving behind an idealized planar wake. Both of these theories modified the quasi-steady thin airfoil theory (which ignores the effect of wake around the airfoil) by including the effect of the wake history on the induced circulation around the airfoil. The effect of the wake can be quite significant as it effectively reduces the magnitude of the aerodynamic forces acting on the airfoil. This reduction in turn can have a significant effect on the flutter velocity.

The quasi-steady thin airfoil theory assumes that the pitch, $\alpha$, and heave, h, motions of the airfoil are relatively small. Thus, the effects of $\dot{\alpha }$ and $\dot{h}$ appear as an effective angle of attack and an effective camber, respectively, which may be combined into a total effective angle of attack for the entire airfoil. However, thin airfoil theory breaks down for rapid maneuvers and therefore it becomes necessary to include displaced-mass and circulatory terms. Theodorsen’s model extends the quasi-steady thin airfoil theory to include displaced-mass forces and wake vorticity effects. Based on Theodorsen’s model, the lift force acting on a strip of unit span is:

$$\begin{aligned} L(t) = L^C(t) + \overbrace{\rho \pi b^2 \left\{ \ddot{h}-a_hb \ddot{\alpha } + U\dot{\alpha } \right\} }^{{=:}L^D(t)} \end{aligned}$$

(2.2)

In Eq. (2.2), $L^D (t)$ constitutes non-circulatory forces. It is associated with the fluid inertia (i.e., apparent mass forces). The circulatory forces $L^C(t)$ model the effects of boundary vorticity and shed wake convecting downstream at a constant velocity U. In the following, we describe the expression for $L^C(t)$, obtained based on the physical assumption that flow velocity at the trailing edge is finite. The equivalent of (2.2) for $M_{EA}(t)$ in (2.1b) can be obtained by similar arguments:

$$\begin{aligned} M_{EA}(t)&= \left( \frac{1}{2}+a_h\right) bL^C(t) + a_hbL^D(t) \\&\quad - \left( \frac{1}{2}-a_h\right) bL^D(t)-\frac{\rho \pi b^4}{8}\ddot{\alpha }. \end{aligned}$$

From the theory of oscillating airfoils (see Fung [5] and references therein), under bending and pitching oscillations, the circulation about the airfoil is determined by an effective downwash velocity acting at the $\frac{3}{4}$-chord point from the leading edge of the airfoil. Under constant airspeed U, circulatory lift is

$$\begin{aligned} L^C(t) = 2\pi b\rho U\hbox {w}_{\frac{3}{4}}(t)\varPhi ^W(t), \end{aligned}$$

where $\varPhi ^W(t)$ is Wagner’s indicial response function, b is half the chord length (see Fig. 1), and $\rho$ and U are the freestream density and constant airspeed, respectively. Downwash at the $\frac{3}{4}$-chord is given by

$$\begin{aligned} \hbox {w}_{\frac{3}{4}} (t) = \dot{h}(t) + U \alpha (t)+ b \dot{\alpha }(t) \left( \frac{1}{2} - a_h\right) . \end{aligned}$$

The first term $\dot{h}$ represents a uniform downwash due to vertical translation h. The second term represents uniform downwash corresponding to the pitch angle $\alpha$ (using approximation $U\sin \alpha \approx U\alpha$ for small $\alpha$). The last term represents non-uniform downwash due to $\dot{\alpha }$. Before proceeding further with the description of circulatory lift, we will recast the problem in the time-varying freestream airspeed and unsteady flow setting.

The extension of lift Eq. (2.2) to the case of time-varying airspeed was based on developments in helicopter aerodynamics theory, specifically the works of Dinyavari and Friedmann [12], Friedmann [13] and Friedmann and Robinson [14], which extended Greenberg’s theory (see Greenberg [15])to the general case of arbitrary airfoil motion and time-varying velocity. First, the airspeed U becomes a time-dependent quantity, U(t). Additionally, transient loads that occur due to external disturbances need to be modeled. Disturbance velocities that are normal to the flight path are called gusts, or turbulence, and they influence the circulatory terms. They are captured by downwash at the leading edge and at the $\frac{3}{4}$-chord-point. The circulatory terms in turn affect the airfoil motion via the aerodynamic loads. Turbulence is decomposed into longitudinal/horizontal and vertical components, $u_T$ and $\hbox {w}_T$, that are separated by $\alpha$. It is worth noting that $u_T$ and $\hbox {w}_T$ act as parametric and additive forcings to the overall system, respectively. $u_T$ enters the equations of motion as part of the freestream velocity while $\hbox {w}_T$ is equivalent to downwash at the leading edge [as can be seen in (2.9)]. This is consistent with previous work (see Poirel and Price [3] and references therein) for including gust/turbulence effects in the airfoil equations of motion.

Based on the preceding discussion, we rewrite the airspeed and circulatory lift expressions accordingly. It is assumed that non-uniformity in the flow around the airfoil is a result of small disturbances superimposed on a uniform steady flow. Hence, the airspeed term now comprises of a constant part $U_m^{\star }$ (mean airspeed) and a time varying part $u_T(t)$ (horizontal component of turbulence):

$$\begin{aligned} U(t) = U_m^{\star } + \zeta (t), \ \hbox {where} \ \ \zeta (t) = \varepsilon u_T (t), \end{aligned}$$

where $\varepsilon$ is a small scalar quantity. Equivalently, we write

$$\begin{aligned} U(t) = U_m^{\star } (1 + \epsilon ^{\star } u_T (t)), \quad \hbox {where} \quad \epsilon ^{\star } \mathop {=}\limits ^{\mathrm{def}}\frac{\varepsilon }{U_m^{\star }}. \end{aligned}$$

(2.3)

Unsteady effects due to the horizontal component of turbulence are captured using Wagner’s indicial response function $\varPhi ^W(t)$ (see Fung [5] and Wagner [9]) that has been discussed earlier. Circulatory effects due to the vertical component of turbulence are captured using Küssner’s gust penetrating function $\varPhi ^K(t)$ (see Fung [5] and Kussner [16]), and are included in the system via an additional term in $L^C(t)$. In this time-varying, unsteady flow setting, the circulatory lift term takes the following form, with time-varying airspeed and an additional component due to downwash at the leading edge (vertical component of turbulence, $\hbox {w}_T$):

$$\begin{aligned} L^C(t) = 2 \pi b \rho U(t) \hbox {w}_{\frac{3}{4}} (t) \varPhi ^W(t) + 2 \pi b \rho U(t) \hbox {w}_T (t) \varPhi ^K(t). \end{aligned}$$

(2.4)

The approximate expressions of Wagner’s and Küssner’s functions have the same form:

$$\begin{aligned} \varPhi ^I(t) \approx 1 - A_1^I e^{-b_1^I \frac{U_m^{\star } t}{b}}- A_2^I e^{-b_2^I \frac{U_m^{\star } t}{b}}, \quad t>0, \end{aligned}$$

where we use superscript $I=W,K$ to represent the expressions for Wagner’s and Küssner’s functions, respectively. The coefficients are $A_1^W = 0.165$, $A_2^W = 0.335$, $b_1^W = 0.0455$, $b_2^W = 0.3$ [17] and $A_1^K = 0.5791$, $A_2^K = 0.4208$, $b_1^K = 0.1393$, $b_2^K =1.802$ (see Leishmann [18]). Note that in the setting of (2.3), Van der Wall and Leishman [19] justified the assumption that the airspeed in $\varPhi ^W (t)$ can be set as a constant $U_m^{\star }$ when the frequency and amplitude of airspeed variations are small.

We now turn to modeling the turbulence components. The two-sided power spectral densities for the horizontal and vertical components of turbulence are given by the Dryden Model (see Yeager [6]) as

$$\begin{aligned} \mathbb {S}_{u_T}(\omega )&= \frac{\sigma _T^2 \frac{l}{U_m^{\star }}}{\pi } \frac{1}{1+\left( \frac{l}{U_m^{\star }} \omega \right) ^2}, \end{aligned}$$

(2.5a)

$$\begin{aligned} \mathbb {S}_{\mathrm{w}_T}(\omega )&= \frac{\sigma _T^2 \frac{l}{U_m^{\star }}}{2\pi } \frac{1+3\left( \frac{l}{U_m^{\star }} \omega \right) ^2}{\left( 1+\left( \frac{l}{U_m^{\star }} \omega \right) ^2\right) ^2}, \end{aligned}$$

(2.5b)

respectively. The overall characteristics are governed by the scale of turbulence l and intensity $\sigma _T^2$, which are common to both components. After transforming the above turbulence spectra into the time domain via the inverse Laplace transform (with Gaussian white noise as input and the respective turbulence velocity as the output), we arrive at the following set of stochastic differential equations for turbulence components:

$$\begin{aligned}&d u_T (t) = -\varGamma ^{\star } u_T (t) dt + \sigma _T \sqrt{\frac{2\varGamma ^{\star }}{\pi }} dW^1_t, \end{aligned}$$

(2.6a)

$$\begin{aligned}&d \hbox {w}_T (t) = \left[ -\varGamma ^{\star } \hbox {w}_T (t) + c(t) \right] dt + \sigma _T \sqrt{\frac{3\varGamma ^{\star }}{\pi }} dW^2_t, \end{aligned}$$

(2.6b)

where $c(\cdot )$ satisfies

$$\begin{aligned} d c(t) = -\varGamma ^{\star } c(t) dt + \left( 1-\sqrt{3}\right) \sigma _T\sqrt{\frac{\left( \varGamma ^{\star }\right) ^3}{\pi }} dW^2_t. \end{aligned}$$

$(W^1,W^2)$ represent two independent Wiener processes, and $\varGamma ^{\star }\mathop {=}\limits ^{\mathrm{def}}\frac{U_m^{\star }}{l}$.

We now return to the discussion of the expression for circulatory lift. Note that the expressions for circulatory lift due to downwash at the $\frac{3}{4}$-chord length (horizontal turbulence) and leading edge (vertical turbulence) are similar, differing by Wagner’s and Küssner’s functions. Therefore, we will discuss both terms simultaneously, using superscript $I=W,K$ to indicate Wagner’s and Küssner’s functions, respectively. If we consider an impulsive increment in the downwash then the circulatory lift per unit span (2.4) can be found to be

$$\begin{aligned} 2 \pi \rho b U(t) \left[ \varPhi ^I(t) \hbox {w}^I (0) + \int _{0}^{t}\hbox {w}^I(s) \frac{d \varPhi ^I(t-s)}{d s} ds \right] , \end{aligned}$$

(2.7)

where $\hbox {w}^W(\cdot )\mathop {=}\limits ^{\mathrm{def}}\hbox {w}_{3/4}(\cdot )$, $\hbox {w}^K(\cdot )\mathop {=}\limits ^{\mathrm{def}}\hbox {w}_T(\cdot )$.

Now, the memory term in (2.7) is given in terms of an exponential kernel, which constitutes to an integro-differential equation. To make analysis tractable, we would like to replace the integral portion in (2.7) with the output of a forced oscillator. Thus, let us consider an auxiliary oscillator:

$$\begin{aligned} {\ddot{\varrho }}^I + \left( b_1^I + b_2^I\right) \frac{U_m^{\star }}{b} {\dot{\varrho }}^I + b_1^I b_2^I \left( \frac{U_m^{\star }}{b}\right) ^2 \varrho ^I = \hbox {w}^I(t). \end{aligned}$$

(2.8)

A straightforward calculation (see, for example, [23]) reveals that the expression in the square brackets in (2.7) is equal to

$$\begin{aligned}&- c^I b_1^I b_2^I \left( \frac{U_m^{\star }}{b}\right) ^2 \varrho ^I - \left( A_1^I b_1^I + A_2^I b_2^I\right) \frac{U_m^{\star }}{b} {\dot{\varrho }}^I\\&\quad +\, \hbox {w}^I (0)+ \varPhi ^I(0)\hbox {w}^I(t), \end{aligned}$$

where $c^W = \frac{1}{2}$, $c^K = 1$.

All the preceeding arguments for circulatory lift force can be translated to the aerodynamic moment. In view of these arguments for aerodynamic loads, (2.1a) and (2.1b) become

$$\begin{aligned}&m x_\alpha b {\ddot{\alpha }}+m \ddot{h} + K_h h \nonumber \\&= \,-\left[ \rho \pi b^2 (\ddot{h}-a_hb \ddot{\alpha } + U (t)\dot{\alpha })\right. \nonumber \\&\quad + \,2 \pi \rho b U(t)\left[ \hbox {w}_{\frac{3}{4}}(t) \varPhi ^W (0) - {\bar{\varrho }}^W\right] \nonumber \\&\quad \left. +\, 2 \pi \rho b U_m^{\star } [\hbox {w}_T (t) \varPhi ^K (0) - {\bar{\varrho }}^K]\right] , \end{aligned}$$

(2.9a)

$$\begin{aligned}&I_{EA}\ddot{\alpha }+m x_\alpha b \ddot{h} + K_\alpha \alpha + K_3\alpha ^3 \nonumber \\&= \rho \pi b^2 \left( \ddot{h} a_hb -b\left( \frac{1}{2}-a_h\right) U(t) \dot{\alpha } - b^2 \left( a_h^2+\frac{1}{8}\right) \ddot{\alpha }\right) \nonumber \\&\quad +\, 2 \pi \rho b^2 U(t) \left( a_h + \frac{1}{2}\right) \left[ \hbox {w}_{\frac{3}{4}}(t)\varPhi ^W (0)-{\bar{\varrho }}^W\right] \nonumber \\&\quad +\, 2\pi \rho b^2 U_m^{\star } \left( a_h + \frac{1}{2}\right) [\hbox {w}_T (t) \varPhi ^K(0)- {\bar{\varrho }}^K], \end{aligned}$$

(2.9b)

with auxiliary variables

$$\begin{aligned} {\bar{\varrho }}^I&\mathop {=}\limits ^{\mathrm{def}}\varrho ^I - \hbox {w}^I(0) \\&= - \frac{b_1^I b_2^I}{2} \left( \frac{U_m^{\star }}{b}\right) ^2 \varrho ^I - \left( A_1^I b_1^I + A_2^I b_2^I\right) \frac{U_m^{\star }}{b} {\dot{\varrho }}^I, \end{aligned}$$

for $I=W,K$.

With appropriate initial conditions, (2.9) describe the system states (airfoil degrees of freedom), with appropriate forcing functions given by (2.8) (aerodynamic degrees of freedom). Equations (2.9) and (2.8), along with (2.6), represent a well-defined problem for the present study to be conducted.

The aeroelastic model (2.9) with auxiliary equations (2.8) can be combined and cast as a non-dimensionalized spring-mass-damper system with a cubic stiffness matrix:

$$\begin{aligned} {[}M][{\underline{z^{\prime \prime }}}] + {[}D(\tau )][{\underline{z^{\prime }}}] + [K(\tau )][\underline{z}] + {[}K_3][{\underline{z}}^3] = {\underline{F_{T}}} \end{aligned}$$

(2.10)

with $\begin{bmatrix} \underline{z} \end{bmatrix} \mathop {=}\limits ^{\mathrm{def}}\begin{bmatrix} \alpha&h&\varrho ^W&\varrho ^K \end{bmatrix}^{T}$, ${\underline{F_{T}}}\mathop {=}\limits ^{\mathrm{def}}\begin{bmatrix} 0&0&0&\hbox {w}_T\end{bmatrix}^T$, and $(\cdot )'$ represents derivative with respect to non-dimensional time $\tau = \frac{U_m^{\star } t}{b}$. Equation (2.10) represents a 4-degree-of-freedom nonlinear aeroelastic system excited by real noise processes, $u_T(\tau )$ and $w_T(\tau )$, modeled by (2.6). The coefficient matrices in (2.10) are shown in “Appendix 1”. We note that $\alpha$ is the only state that has not been non-dimensionalized and the others have been scaled as follows (i.e., from dimensional (t) $\rightarrow$ non-dimensional $(\tau )$):

$$\begin{aligned}&h \rightarrow b h, \quad U_m^{\star } \rightarrow b \omega _\alpha U_m, \quad u_T \rightarrow b \omega _\alpha u_T,\\&c_1 \rightarrow b \omega _\alpha c_1,\quad \hbox {w}_T \rightarrow b \omega _\alpha \hbox {w}_T,\\&\varrho ^W \rightarrow \frac{b}{\omega _\alpha U_m} \varrho ^W, \quad \varrho ^K \rightarrow \frac{b}{\omega _\alpha U_m} \varrho ^K,\\&l \rightarrow b l, \quad \sigma _T^2 \rightarrow (b \omega _\alpha )^2\sigma _T^2, \quad \epsilon ^{\star } \rightarrow \frac{1}{b \omega _\alpha }\epsilon . \end{aligned}$$

In the above, for example, $h\rightarrow bh$ is equivalent to $h=bh'$, where the prime on the non-dimensional variable on the right side of the equality is dropped for notational convenience. $\omega _\alpha$ is the natural frequency of pitch (frequency of the solution to the unforced equation). Decomposing the damping and stiffness matrices in (2.10) into their respective time invariant and time varying components:

$$\begin{aligned}{}[D(\tau )]&= [D_0] + \epsilon u_T (\tau ) [D_1], \\ [K(\tau )]&= [K_0] + \epsilon u_T (\tau ) [K_1], \end{aligned}$$

and defining $\underline{q} \mathop {=}\limits ^{\mathrm{def}}[\underline{z}, \underline{z}' ]^{T}$, (2.10) can be cast as an eight-dimensional system of differential equations in state space,

$$\begin{aligned} {{\underline{q}}_{\tau }}' = [A_0] {\underline{q}}_{\tau } + \epsilon [B_0]u_T (\tau ) {\underline{q}}_{\tau } + [C_0] {\underline{q}}_{\tau }^3 + \epsilon ^2 \wp [\hat{N}]. \end{aligned}$$

(2.11)

We shall tune the parameter $\wp$ accordingly in the ensuing analysis to see the effect of the vertical gust component (inside $[\hat{N}]$) in the framework of the original problem. For the subsequent analysis, (2.11) forms the basis of the model that will be considered and it collapses to the aeroelastic problem for the case $\wp = \frac{1}{\epsilon }$.

The system (2.11) cannot be solved explicitly. However, under some assumptions made with respect to the nonlinearities, we can obtain approximate solutions. These assumptions are based on the physics of the problem and the phenomena that one is interested in studying. To this end, we shall be more specific and study the effects of noise on systems that are close to certain bifurcation points, i.e. we analyze (2.11) in a neighborhood of a critical system parameter, $U_m=U_m^c$. We first introduce the following scalings as in Namachchivaya and Van Roessel [4]:

$$\begin{aligned} {\underline{q}}\rightarrow \epsilon \underline{q}, \quad \left( U_m-U_m^c\right) \rightarrow \epsilon ^2 \beta . \end{aligned}$$

The spatial scaling is justified from the fact that we are considering perturbations about the trivial solution in analyzing stability. Furthermore, the additive forcing is of $\mathcal O(\epsilon ^2)$ in (2.11) and so the system decays to the trivial solution at steady state.

Consider a transformation,

$$\begin{aligned} {\underline{q}}_{\tau } = [T] \left[ {v^{\epsilon }_{\tau }}\right] \end{aligned}$$

(2.12)

where [T] represents a matrix of eigenvectors of $[A_0 (U_m^c)]$ that have been arranged in accordance to the real part of the corresponding eigenvalues sorted in descending order. We remark that we also study the unfolding of the linear critical system $[A^\prime _0 (U_m^c)]$ hence giving us the flexibility to explore the bifurcation characteristics of the aeroelastic system in the vicinity of the critical airspeed. Denote by $v^{\epsilon }\mathop {=}\limits ^{\mathrm{def}}({\tilde{X}}^{\epsilon },Y^{\epsilon })\in \mathbb {R}^2\times \mathbb {R}^6$, where ${\tilde{X}}^{\epsilon }$ represents the non-dimensionalized critical modes and $Y^{\epsilon }$ represents the non-dimensionalized stable modes. Employing (2.12) and the previous arguments in (2.11), we have

$$\begin{aligned} \begin{aligned} {{v^{\epsilon }_{\tau }}}'&= {\bar{b}}^0\left( {v^{\epsilon }_{\tau }}, U_m^c\right) + \epsilon {\bar{b}}^1\left( {v^{\epsilon }_{\tau }}, u_T(\tau ), \hbox {w}_T (\tau )\right) \\&\quad + \,\epsilon ^2 {\bar{b}}^2\left( {v^{\epsilon }_{\tau }}, U_m^c\right) , \\ {v^{\epsilon }_{\tau }}&= v, \end{aligned}\end{aligned}$$

(2.13)

where the order 1 term in (2.13) is linear in $v^{\epsilon }$. The coefficient matrix is block diagonal, with the top $2\times 2$ square matrix being skew symmetric and the remaining blocks being negative definite. Details of the terms in (2.13) are given in “Appendix 1”. (2.13), (2.6a), and (2.6b) characterize the overall system.

3 Dimensional reduction

To proceed further, we define

$$\begin{aligned} {\hat{v}}_{\tau }^{\epsilon }&\mathop {=}\limits ^{\mathrm{def}}\left( {v^{\epsilon }_{\tau }}, u_T(\tau ), c(\tau ), \hbox {w}_T(\tau )\right) \\&\mathop {=}\limits ^{\mathrm{def}}\left( {\tilde{X}}_{\tau }^{\epsilon },Y_{\tau }^{\epsilon },u_T(\tau ), c(\tau ), \hbox {w}_T(\tau )\right) , \end{aligned}$$

where $({\tilde{X}}^{\epsilon },Y^{\epsilon },u_T, c, \hbox {w}_T) \in \mathbb {R}^2\times \mathbb {R}^6 \times \mathbb {R} \times \mathbb {R} \times \mathbb {R}$. $u_T$ is now the parametric noise given by the non-dimensionalized form of (2.6a) and $\hbox {w}_T$ is now the additive real noise given by the non-dimensionalized form of (2.6b), which is dependent on the now non-dimensionalized c. Let us further define

$$\begin{aligned} r= {\mathcal {R}}\left( {\hat{v}}_{\tau }^{\epsilon }\right) \overset{\text {def}}{=} \Vert {\tilde{X}}^{\epsilon }\Vert _{\mathbb {R}^2}, \quad \theta = \varTheta \left( {\hat{v}}_{\tau }^{\epsilon }\right) \overset{\text {def}}{=} \arctan \left( \frac{{\tilde{X}}^{\epsilon }_{2}}{{\tilde{X}}^{\epsilon }_{1}}\right) . \end{aligned}$$

Our goal is to study the behavior of ${\mathcal {R}}({\hat{v}}_{\tau }^{\epsilon })$ and show that the law of ${\mathcal {R}}({\hat{v}}_{\tau }^{\epsilon })$ converges to an identifiable limit as $\epsilon \rightarrow 0$. The main result is an asymptotic description of the dynamics of ${\mathcal {R}}({\hat{v}}_{\tau }^{\epsilon })$:

The law of $\{{\mathcal {R}}({\hat{v}}_{\tau }^{\epsilon });\, \tau \ge 0\}$ converges to the law of $\{{\check{r}}_{\tau };\, \tau \ge 0\}$, where ${\check{r}}$ is the solution of the stochastic differential equation:

$$\begin{aligned} { d{\check{r}}_{\tau } = b_{\mathcal {R}}({\check{r}}_{\tau })d\tau + \sigma _{\mathcal {R}}({\check{r}}_{\tau }) dW_{\tau }, \quad {\check{r}}_0 = {\mathcal {R}}(v). } \end{aligned}$$

(3.1)

$b_{\mathcal {R}}$ and $\sigma _{\mathcal {R}}$ are the homogenized drift and diffusion coefficients of ${\mathcal {R}}({\hat{v}}_{\tau }^{\epsilon })$, respectively. The homogenized drift coefficient contains two distinct components: (1) the stochastic effects from the “critical” modes comprising of the stochastic components in the stable “heavily damped” modes, and (2) the nonlinear terms.

Note that ${\mathcal {R}}({\hat{v}}_{\tau }^{\epsilon })$ is slowly varying. Therefore, we need to look on a time scale of $\mathcal O(\frac{1}{\epsilon ^2})$ to observe fluctuations. The Markov process ${\hat{v}}_{\tau }^{\epsilon }\in \mathbb {R}^{11}$ is characterized by a time-scaled generator, which will be crucial our investigation of the convergence of the laws of various processes.

3.1 Problem formulation: homogenization at a diffusive time scale

Let $(\varOmega , \mathcal {F}, \mathbb {P})$ be a probability space that characterizes the process generated from (2.13) and consider

$$\begin{aligned} ({\tilde{X}}^{\epsilon }, Y^{\epsilon }, u_T, c, \hbox {w}_T) = ({\tilde{X}}^{\epsilon } (\tilde{\omega }), Y^{\epsilon } (\tilde{\omega }) , u_T (\tilde{\omega }), c (\tilde{\omega }), \hbox {w}_T (\tilde{\omega })), \end{aligned}$$

where $\tilde{\omega } \in \varOmega$. In order to analyze the asymptotic behavior of the process generated by the time-scaled generator of (2.13) as $\epsilon \rightarrow 0$, it is necessary to remove the rapidly oscillating term $\frac{1}{\epsilon ^2} [B] {\tilde{X}}^{\epsilon }$ in ${\bar{b}}^0$ (${\bar{b}}^0$ is defined in “Appendix 1”) via a transformation

$$\begin{aligned} {\tilde{X}}_{\tau }^{\epsilon } = e^{\frac{\tau B}{\epsilon ^2}} X_{\tau }^{\epsilon }. \end{aligned}$$

(3.2)

This transformation induces an explicit $\tau$-dependence in the rate of the multi-scale process—we introduce $\theta ^{\epsilon }_{\tau } \mathop {=}\limits ^{\mathrm{def}}\frac{\omega _0 \tau }{\epsilon ^2}$ to avoid having to address time-averaging. Hence we are considering a nonlinear $\mathbb {R}^2$-valued critical process $X^{\epsilon }$, an $\mathbb {R}^6$-valued stable process $Y^{\epsilon }$, an $\mathbb {S}$-valued $\theta ^{\epsilon }$ process ($\mathbb {S}=[0,2\pi ]$), and an $\mathbb {R}^3$-valued noise process $Z^{\epsilon } \mathop {=}\limits ^{\mathrm{def}}(u_T, c, \hbox {w}_T) \in \mathbb {R}^3$. In view of the previous arguments and a time change $\tau \rightarrow \epsilon \tau$, (2.13) can be rewritten in a generic form:

$$\begin{aligned} \begin{aligned} d X^{\epsilon }_{\tau }&= \frac{1}{\epsilon }\,a^0\left( X^{\epsilon }_{\tau }, Y^{\epsilon }_{\tau }, \theta ^{\epsilon }_{\tau }, Z^{\epsilon }_{\tau }\right) d\tau + \,a^{1}\left( X^{\epsilon }_{\tau }, Y^{\epsilon }_{\tau }, \theta ^{\epsilon }_{\tau }\right) d\tau , \\ X^{\epsilon }_0&= x\in \mathbb {R}^2\,(\mathrm {critical}), \\ d Y^{\epsilon }_{\tau }&= \frac{1}{\epsilon ^2}\, b^{0}\left( Y^{\epsilon }_{\tau }\right) d\tau + \frac{1}{\epsilon }\, b^{1}\left( X^{\epsilon }_{\tau }, Y^{\epsilon }_{\tau }, \theta ^{\epsilon }_{\tau }, Z^{\epsilon }_{\tau }\right) d\tau \\&\quad +b^{2}\left( X^{\epsilon }_{\tau }, Y^{\epsilon }_{\tau }, \theta ^{\epsilon }_{\tau }\right) d\tau , \\ Y^{\epsilon }_0&=y\in \mathbb {R}^6\,(\mathrm {stable}), \\ d \theta ^{\epsilon }_{\tau }&= \frac{1}{\epsilon ^2}\,\omega _0 d\tau , \quad \theta ^{\epsilon }_0 =\theta \in \mathbb {S}, \\ d Z^{\epsilon }_{\tau }&= \frac{1}{\epsilon ^2}\, c^{0}\left( Z^{\epsilon }_{\tau }\right) d\tau + \frac{1}{\epsilon }\,g^{0}\left( Z^{\epsilon }_{\tau }\right) dW_{\tau } , \\ Z^{\epsilon }_0&=z\in \mathbb {R}^3\,(\mathrm {real \; noise}). \end{aligned} \end{aligned}$$

(3.3)

It is worth noting that augmenting the real noise processes (2.6) to Eq. (2.10) yields a 12-dimensional system (including the intrinsic $\theta$) defined by (3.3) excited by Wiener process.

Let $\mathcal {G}$ denote the generator of $Z^{\epsilon }$, which contains a diffusion term. In the limit as $\epsilon \rightarrow 0$, $\mathcal {G}$ has a unique unique invariant measure $\mu (d z)$ for each initial z, and the following limit exits for measurable f:

$$\begin{aligned} {\bar{f}}(\cdot ) = \lim _{\epsilon \rightarrow 0} \int _{\mathbb {R}^3} f(\cdot ,z,\epsilon ) \mu ^{\epsilon }(dz). \end{aligned}$$

The generator of the 12-dimensional process (3.3) is given by

$$\begin{aligned} \mathscr {L}^{\epsilon }\mathop {=}\limits ^{\mathrm{def}}\frac{1}{\epsilon ^2}\mathscr {L}_{F}^{(y,\theta ,z)} +\frac{1}{\epsilon } \mathscr {L}_{I}^{(x,y)}+\mathscr {L}_{S}^{(x,y)}, \end{aligned}$$

(3.4)

where the fast, intermediate and slow generators are defined as

$$\begin{aligned} \begin{aligned} \mathscr {L}_{F}^{(y,\theta ,z)}&\mathop {=}\limits ^{\mathrm{def}}b^{0}(y) \frac{\partial }{\partial y} +\omega _0 \frac{\partial }{\partial \theta }+\mathcal {G}, \\ \mathscr {L}_{I}^{(x,y)}&\mathop {=}\limits ^{\mathrm{def}}a^0(x,y,\theta ,z) \frac{\partial }{\partial x} + b^{1}(x,y,\theta ,z) \frac{\partial }{\partial y}, \\ \mathscr {L}_{S}^{(x,y)}&\mathop {=}\limits ^{\mathrm{def}}a^{1}(x,y,\theta ) \frac{\partial }{\partial x} + b^{2}(x,y,\theta ) \frac{\partial }{\partial y} . \end{aligned} \end{aligned}$$

For every fixed $\epsilon >0$, the processes $\left( X^{\epsilon }, Y^{\epsilon }, \theta ^{\epsilon }, Z^{\epsilon } \right)$ together form a Markov process that is characterized by the infinitesimal generator $\mathscr {L}^{\epsilon }$ acting on smooth functions. The main objective of the homogenization theory is to show that the slow process $X^{\epsilon }$ itself is a Markov process in its own right as $\epsilon \rightarrow 0$, and identify its generator $\mathscr {L}^{\dagger }$.

To sum up, our goal is to study (3.4) to (1) show that as $\epsilon \rightarrow 0$, the dynamics of the slowly varying quantity $X^{\epsilon }_{\tau }$ converges to a Markov process, and (2) identify the generator of the limiting law. Our aim is to do this via stochastic dimensional reduction, based on the results of Papanicolaou et al. [20]. The technique used here is based on that of Namachchivaya and Van Roessel [4]. To this end, we consider the Cauchy problem associated with the generator $\mathscr {L}^{\epsilon }$ in the proceeding section.

3.2 Theoretical results: stochastic dimensional reduction

Let $\mathscr {L}^{\epsilon }$ be the generator as described previously. Consider the following Cauchy problem:

$$\begin{aligned} \begin{aligned} \frac{\partial u^{\epsilon }}{\partial \tau } (x,y,\theta ,z,\tau )&= \mathscr {L}^{\epsilon } u^{\epsilon } (x,y,\theta ,z,\tau ), \\ u^{\epsilon } (x,y,\theta ,z,0)&= f(x). \end{aligned}\end{aligned}$$

(3.5)

It is well known that $u^{\epsilon } (x,y,\theta ,z,\tau )\mathop {=}\limits ^{\mathrm{def}}\mathbb {E}_{\begin{array}{c} x,y,\theta ,z \end{array}}\left[ f\left( X^{\epsilon }_{\tau }\right) \right]$ satisfies the Kolmogorov equation, with the expectation taken with respect to the probability measure of the process $X^{\epsilon }_{\tau }$. However, due to coupling between the stochastic processes, $X^{\epsilon }_{\tau }$ depends not only on the starting point x of the process $X^{\epsilon }_{\tau }$, but it also depends on the starting point $(y,\theta ,z)$ of $(Y^{\epsilon }_{\tau }, \theta ^{\epsilon }_{\tau }, Z^{\epsilon }_{\tau })$. Let us now construct an expansion:

$$\begin{aligned} \begin{aligned}&u^{\epsilon }(x,y,\theta ,z,\tau ) =u_0(x,y,\theta ,z,\tau ) + \epsilon u_1(x,y,\theta ,z,\tau ) \\&\quad +\epsilon ^2 u_2(x,y,\theta ,z,\tau ) + \ldots +\epsilon ^n u_n (x,y,\theta ,z,\tau ). \end{aligned}\end{aligned}$$

(3.6)

In this section, we describe an outline of the calculations involved in obtaining a reduced-order description of the 12-dimensional system. Details of the calculations are presented in “Appendix 2”. They are similar to the calculations of Namachchivaya and Van Roessel [4].

Substituting the expansion (3.6) into (3.5), we obtain a set of 3 Poisson equations at increasing orders of $\epsilon$. From the first of these equations, we observe that $u_0$ is only a function of x and $\tau$, i.e. $u_0(x,y,\theta ,z,\tau )=u(x,\tau )$ (see (7.1), “Appendix 2”). The remaining two non-homogeneous partial differential equations (PDEs) are forced by u. The solution of the second PDE can be obtained in terms of u by the Feynman-Kac formula. Combining results from the first two PDEs with application of the solvability condition on the third PDE gives us a PDE of the form

$$\begin{aligned} &\mathscr {L}^{\dagger \dagger } u(x,\tau ) - \frac{\partial }{\partial \tau }u(x,\tau )=0,\nonumber \\ &u(x,0)= f(x) \end{aligned}$$

(3.7)

for u, where the reduced-order generator $\mathscr {L}^{\dagger \dagger }$ is a differential operator in x only. (3.7) describes a density-valued function of a process in $\mathbb {R}^2$, the state space of $X^{\epsilon }$. By the stochastic dimensional reduction results of Papanicolaou et al. [20], we can find a stochastic process in $\mathbb {R}^2$ that is close to $X^{\epsilon }$ in distribution for small $\epsilon$ (weak limit of $X^{\epsilon }$ as $\epsilon \rightarrow 0$) based on the generator $\mathscr {L}^{\dagger \dagger }$. That $\mathbb {R}^2$ process consists of angle and amplitude coordinates, which live on $[0,2\pi ]\times \mathbb {R}\subset \mathbb {R}^2$. For studying flutter, we will be interested in the amplitude component. We obtain a stochastic differential representation of the amplitude component using $\mathscr {L}^{\dagger \dagger }$ in Sect. 3.3.

For the Feynman–Kac representation of $u_1$ and the solvability condition, the transient and invariant densities of fast processes $({\tilde{Y}}^{\epsilon },\theta ^{\epsilon },Z^{\epsilon })$ with rate $\frac{1}{\epsilon }$ in (3.3) are required (${\tilde{Y}}^{\epsilon }$ is the deterministic process equivalent to $Y^{\epsilon }$ at rate $\frac{1}{\epsilon }$; see “Appendix 2”). The coefficients of $\mathscr {L}^{\dagger \dagger }$ in (3.7) are in terms of averages with respect to the transient and invariant densities of $({\tilde{Y}}^{\epsilon },\theta ^{\epsilon },Z^{\epsilon })$. $({\tilde{Y}}^{\epsilon },\theta ^{\epsilon },Z^{\epsilon })$ are mutually independent, hence the joint density equals the product of the densities. The densities of ${\tilde{Y}}^{\epsilon }$ and $\theta ^{\epsilon }$ are known based on (3.3): ${\tilde{Y}}^{\epsilon }$ is an asymptotically stable process that decays to its initial condition and $\theta ^{\epsilon }$ varies with constant rate $\omega _0$ on a circle with radius determined by the initial conditions of x. The density of $Z^{\epsilon }$ need not be obtained explicitly. Recall that $Z^{\epsilon }$ is the stochastic process that represents the turbulence components ((2.6a), (2.6b)). Averages with respect to the density of $Z^{\epsilon }$ are obtained in terms of power spectral densities, which are determined from the Dryden model for turbulence. Hence, $\mathscr {L}^{\dagger \dagger }$ is of the form

$$\begin{aligned} \mathscr {L}^{\dagger \dagger } = \sum _{i=1}^2 {\bar{b}}_i(x) \frac{\partial }{\partial x_i} + \frac{1}{2} \sum _{i,j=1}^2 {\hat{a}}_{ij}(x) \frac{\partial ^2 }{\partial x_i \partial x_j }, \end{aligned}$$

where $\bar{b}(x)$ and ${\hat{a}}_{ij}(x)$ are in terms of power spectral densities of turbulence (see “Appendix 2” for calculations and explicit expressions).

3.3 Amplitude process

At this point we wish to determine $\mathscr {L}^{\dagger }$ that characterizes the Markov process generated by $r= {\mathcal {R}}(z) \mathop {=}\limits ^{\mathrm{def}}\Vert x\Vert _{\mathbb {R}^2}= \sqrt{x_1^2+x_2^2}$. To this end, let us apply Itô’s formula on test functions of r, $\varPhi ({\mathcal {R}}(x)) \in {\mathbf{C}}(\mathbb {R}^2)$. We have

$$\begin{aligned} \mathscr {L}^{\dagger } (\varPhi \circ {\mathcal {R}}) (x)&= \frac{d \varPhi }{d {\mathcal {R}}}({\mathcal {R}}(x)) (\mathscr {L}^{\dagger \dagger } {\mathcal {R}}) (x) \nonumber \\&\quad +\frac{1}{2} \frac{d^2 \varPhi }{d {\mathcal {R}}^2} ({\mathcal {R}}(x)) \langle d {\mathcal {R}}, d{\mathcal {R}}\rangle (x), \end{aligned}$$

(3.8)

where

$$\begin{aligned} \begin{aligned} b_{\mathcal {R}}({\check{r}}_{\tau })&=\left( \mathscr {L}^{\dagger \dagger } {\mathcal {R}}\right) (x), \quad \sigma ^2_{\mathcal {R}}({\check{r}}_{\tau }) = \langle d {\mathcal {R}}, d{\mathcal {R}}\rangle (x),\\ \langle d {\mathcal {R}}, d {\mathcal {R}}\rangle (x)&\mathop {=}\limits ^{\mathrm{def}}\sum _{i,j=1}^2{\hat{a}}_{ij}(x) \frac{\partial {\mathcal {R}}}{\partial x_i} (x)\frac{\partial {\mathcal {R}}}{\partial x_i} (x). \end{aligned} \end{aligned}$$

In view of (3.1), the homogenized coefficients are calculated to be

$$\begin{aligned} b_{\mathcal {R}}({\check{r}}_{\tau })= \delta ' \beta {\check{r}} - \bar{R} {\check{r}}^3 + \frac{{\check{r}}}{8}\left[ \kappa _1 \mathbb {S}_{u_T} (0) + \frac{3}{2} \kappa _2 \mathbb {S}_{u_T}^{\cos } (2 \omega _0) \right] + \,\frac{{\check{r}}}{8}\left[ \kappa _3 \mathbb {S}_{u_T}^{\cos ,\kappa } (\omega _0+\gamma ) + \kappa _4 \mathbb {S}_{u_T}^{\cos ,\kappa } (\omega _0-\gamma ) \right. \left. -\, \kappa _5 \mathbb {S}_{u_T}^{\sin ,\kappa } (\omega _0+\gamma ) - \kappa _6 \mathbb {S}_{u_T}^{\sin ,\kappa } (\omega _0-\gamma ) \right] + \,\frac{{\check{r}}}{4}\left[ \sum _{r=1}^4 \kappa ^{\sin , \lambda _r} \mathbb {S}_{u_T}^{\sin ,\lambda _r} (\omega _0) \right. \left. + \,\sum _{r=1}^4 \kappa ^{\cos , \lambda _r} \mathbb {S}_{u_T}^{\cos ,\lambda _r} (\omega _0)\right] + \frac{\wp }{4{\check{r}}}\kappa _{8} \mathbb {S}_{\mathrm{w}_T}^{\cos } (\omega _0), \end{aligned}$$

and

$$\begin{aligned} \sigma ^2_{\mathcal {R}}({\check{r}}_{\tau })= & {} \frac{{\check{r}}^2}{8}\left[ 2\kappa _1 \mathbb {S}_{u_T} (0) +\kappa _2 \mathbb {S}_{u_T}^{\cos } (2 \omega _0) \right] \\& + \frac{\wp }{2} \kappa _{8}\mathbb {S}_{\mathrm{w}_T}^{\cos } (\omega _0). \end{aligned}$$

We have obtained, explicitly, the homogenized results that capture the behavior of the critical modes of the 12-dimensional system (3.3). Both drift and diffusion coefficients are given in terms of parameters of the original system (2.10) (definitions of the terms involved can be found in Appendices 2 and 3). It is worth comparing the general results derived in Namachchivaya and Van Roessel [4] for the white noise case with the above drift and diffusion terms. First, the noise contributions are given interns of sine and cosine power spectral densities, as opposed to a flat power spectral density for the white noise case in Namachchivaya and Van Roessel [4]. The effects of additive noise (vertical turbulence) are given by terms with $\wp$ in the above drift and diffusion terms. Since the derivation of deterministic terms are unchanged, in the presence of cudric nonlinearities in the aeroelastic model, the modified $\mathbf{R}$ given in Namachchivaya and Van Roessel [4] can be used in the reduced model.

The reduced model (3.1) will provide a framework for computing standard statistical measures of stability, exit time laws, and stationary solutions (see Arnold et al. [21]). These results are verified in the following section.

4 Numerical results

In this section, we present various numerical results pertaining to the aeroelastic problem. The following numerical values are used (see Poirel and Price [3])

$$\begin{aligned} U_m^c=\, & {} 4.31, \quad a_h = -0.5,\quad \mu = 100,\quad r_\alpha = 0.5,\nonumber \\ x_\alpha=\, & {} 0.25,\quad k_3 = 400,\quad l=50,\quad \sigma _T=1. \end{aligned}$$

(4.1)

Note that as l goes to zero, the case of white noise results since the power spectral density becomes flat.

4.1 Results for the real noise case: parametric excitation

We present the results from using (3.8) with the numerical values sampled at different frequencies from the various power spectral densities. Figure 2 shows the cumulative distribution functions (CDFs) of the critical modes of the original system and the reduced system for the case of horizontal turbulence (i.e., $\wp = 0$). From the agreement of the plots, we can assert that the distribution of the critical modes of the original system are indeed captured by the reduced system and hence this one dimensional model can be used for investigating flutter further. The reduced system in Fig. 2 is characterized by

$$\begin{aligned}&b_{\mathcal {R}} = (0.0323 \beta +0.142336) {\check{r}} - 0.1171 {\check{r}}^3 + 3.84714 \frac{\wp }{{\check{r}}}, \\&\sigma _{\mathcal {R}}^2 =0.14725 {\check{r}}^2 + 7.69427\wp \end{aligned}$$

[based on (3.1), with $\varepsilon =0.15$, zero unfolding ($\beta = 0$), and the flow and system parameters as in (4.1))] Numerical integration for the critical and stable modes is performed using a combined predictor-corrector scheme for the deterministic drift and $\mathcal O(2)$ weak stochastic Taylor scheme, similar to that introduced in Talay [22]. A stochastic strong Taylor $\mathcal O(1.5)$ scheme is used for stochastic integration of the turbulence processes.

Fig. 2

CDF of the critical modes of the original system (dashed) and the reduced system (solid)

4.2 Stability and bifurcation analysis: parametric excitation

In investigating the stability of the critical system, the Lyapunov exponent which quantifies the degree of “sensitivity to initial conditions” (i.e., local instability in a state space) is used. For the critical system, the top Lyapunov exponent is defined as

$$\begin{aligned} \lambda \mathop {=}\limits ^{\mathrm{def}}\lim _{\tau \rightarrow \infty } \frac{1}{\tau } \ln |{\check{r}}_{\tau }| \quad \textit{almost-surely}. \end{aligned}$$

The top Lyapunov exponent gives us the rate of divergence of two trajectories that started in the vicinity of the equilibrium point after a long time. Hence, the sign and the magnitude of this value is indicative of the overall stability of the system after a long time.

It is known from Arnold et al. [21] that the top Lyapunov exponent obtained by linearizing the original system and employing Oseledec’s Multiplicative Ergodic Theorem is equivalent to the top Lyapunov exponent obtained from the homogenized system (3.1). To proceed with the analysis, let us first rewrite the homogenized drift and diffusion coefficients as

$$\begin{aligned} b_{\mathcal {R}}({\check{r}}_{\tau }) = {\mathbf{a}} {\check{r}}_{\tau } + \frac{\mathbf{c}}{2{\check{r}}_{\tau } } +{\mathbf{R }} {\check{r}}_{\tau }^3, \quad \sigma ^2_{\mathcal {R}}({\check{r}}_{\tau }) = {\mathbf{d}} {\check{r}}^2_{\tau } + {\mathbf{c}}, \end{aligned}$$

where

$$\begin{aligned} &{\mathbf{a}}= \delta ' \beta + \frac{1}{8}\left[ \kappa _1 \mathbb {S}_{u_T} (0) + \frac{3}{2} \kappa _2 \mathbb {S}_{u_T}^{\cos } (2 \omega _0) \right] + \frac{1}{8}\left[ \kappa _3 \mathbb {S}_{u_T}^{\cos ,\kappa } (\omega _0+\gamma ) + \kappa _4 \mathbb {S}_{u_T}^{\cos ,\kappa } (\omega _0-\gamma ) \right. \left. - \kappa _5 \mathbb {S}_{u_T}^{\sin ,\kappa } (\omega _0+\gamma ) - \kappa _6 \mathbb {S}_{u_T}^{\sin ,\kappa } (\omega _0-\gamma ) \right] + \frac{1}{4}\left[ \sum _{r=1}^4 \kappa ^{\sin , \lambda _r} \mathbb {S}_{u_T}^{\sin ,\lambda _r} (\omega _0) + \sum _{r=1}^4 \kappa ^{\cos , \lambda _r} \mathbb {S}_{u_T}^{\cos ,\lambda _r} (\omega _0)\right] ,\\ &{\mathbf{R}}= \frac{3}{8} \left\{ {\hat{g}}_{1:111} +{\hat{g}}_{1:122} + {\hat{g}}_{2:112} + {\hat{g}}_{2:222} \right\} , \\ &{\mathbf{d}}= \frac{1}{8}\left[ 2\kappa _1 \mathbb {S}_{u_T} (0) +\kappa _2 \mathbb {S}_{u_T}^{\cos } (2 \omega _0) \right] , \ {\mathbf{c}} = \frac{\wp }{2} \kappa _{8}\mathbb {S}_{\mathrm{w}_T}^{\cos } (\omega _0). \end{aligned}$$

We now consider the case of parametric perturbations only (i.e., ${\mathbf{c}} =0$) in analyzing the stability of the trivial solution. We note that, in the vicinity of the trivial solution, the cubic nonlinearity should have little effect on the stability of the critical system . Hence we set ${\mathbf{R}} =0$ (and valid only when ${\mathbf{R}} \le 0$ which is true for our case) for the following analysis. Application of Itô’s formula on $\ln |{\check{r}}_{\tau }|$ gives, at $\beta =0$,

$$\begin{aligned} \lambda ^R_{1} = \left( {\mathbf{a}} - \frac{\mathbf{d}}{2}\right) = 0.068711, \quad ({\check{r}}_0\,\hbox {finite}). \end{aligned}$$

It is worth noting that the drift and diffusion terms $b_{\mathcal {R}}$ and $\sigma ^2_{\mathcal {R}}$ were derived for the airfoil model in which wind gust is modeled using the Dryden model. This was accommodated by augmenting the original equations of motion (2.1) with two stochastic differential Eq. (2.6) representing colored noise that corresponds to the power spectral densities in (2.5). Hence, $\lambda _1^R$ evaluated above incorporates realistic turbulence. We have used the fact that the steady state value of the ratio of a martingale to its quadratic variation in the limit as $\tau \rightarrow \infty$ is zero. Using this result from the reduced system, the top Lyapunov exponent of the full system is estimated as $\epsilon ^2 \lambda ^R_1$. The positive top Lyapunov exponent obtained indicates that a D-bifurcation has occured, which is related to the loss of stability of the reference measure (i.e., the invariant measure associated with the trivial fixed point of the reduced random dynamical system—Dirac measure $\delta _0$ at ${\check{r}}=0$). Upon further verification of this positive sign, we can assert the almost-sure instability of the equilibrium point of the nonlinear, dissipative dynamical system when at the flutter speed (i.e., all solutions that start near the equilibrium point of the system diverge away from each other at a rate of $\epsilon ^2 \lambda ^R_1$).

Figure 3 shows the results of determining the top Lyapunov exponent of the full system by numerical integration. The same numerical scheme as in Sect. 4.1 is used for integration with $\varepsilon = 0.5$. Solid lines are the quantity $\frac{1}{\tau } \ln |r_{\tau }|$ for 10 realizations while the broken line shows the average over 2400 realizations. The linear fit of the mean solution (i.e., the slope of which is the top Lyapunov exponent of the full system, $\lambda ^F$) is shown embedded within the same plot. It is clear the actual Lyapunov exponent of the full system is $\epsilon ^2 \lambda ^F = {\mathbf{8.6497}} \times 10^{-4}$. Similarly, Fig. 4 is for the reduced system.

Fig. 3

Lyapunov exponent of the full system

Fig. 4

Lyapunov exponent of the reduced system

The Lyapunov exponent estimated by the reduced system is $\epsilon ^2 \lambda ^R_2 = {\mathbf{9.2270}} \times 10^{-4}$. We see that the analytical top Lyapunov exponent, $\lambda _1^R$, is close to its numerical counterpart, $\lambda _2^R$, and $\lambda ^R_2$ and differs from $\lambda ^F$ by $\approx$ 6 %.

Since the 2-dimensional homogenized random dynamical system (generated by (7.6) in “Appendix 2”) exhibits an $\mathbb {S}^1$-symmetry, the $({\check{r}}_{\tau },\theta )$ processes decouple and hence the ${\check{r}}_{\tau }$ process of the nonlinear system is by itself a Markov diffusion process, and its non-trivial stationary density is given by

$$\begin{aligned} p({\check{r}}) = \frac{2}{\varGamma (\nu )} \ \left( \frac{-\mathbf{R}}{\mathbf{d}}\right) ^\nu {\check{r}}^{2\nu - 1}\ \hbox {exp} \left[ \frac{\mathbf{R}}{\mathbf{d}} {\check{r}}^2\right] , \end{aligned}$$

with $\nu \mathop {=}\limits ^{\mathrm{def}}\frac{\mathbf{a}}{\mathbf{d}} - \frac{1}{2}$. In view of the definition of ${\check{r}}$, the joint stationary density is given by

$$\begin{aligned} p(x_1,x_2) = \frac{2}{\varGamma (\nu )} \ \left( \frac{-\mathbf{R }}{\mathbf{d}}\right) ^\nu \left( x_1^2 + x_2^2\right) ^{\nu - \frac{1}{2}} \ \hbox {exp} \left[ \frac{\mathbf{R }}{\mathbf{d }} \left( x_1^2 +x_2^2\right) \right] . \end{aligned}$$

We now let $\beta _{D}$ (i.e., the D-bifurcation point) be the value of $\beta$ for which $\nu = 0$ and we let $\beta _{P}$ (i.e., the Phenomenological (P)-bifurcation point) be the value of $\beta$ for which $\nu = \frac{1}{2}$. On one hand, for $\beta < \beta _{D}$, we have $\nu < 0$ and the fixed point ${\check{r}} = 0$ is asymptotically stable (i.e., the stationary probability density $p({\check{r}})$ is a delta function at ${\check{r}} = 0$). The equilibrium point of the full system looses its stability at the airspeed $U_m = U_m^c + \epsilon ^2 \beta _D$. On the other hand, for $\beta > \beta _{P}$, we have $\nu > \frac{1}{2}$ and the density is maximum at ${\check{r}} = \sqrt{\frac{\nu - \frac{1}{2}}{-{\mathbf{R}} /{\mathbf{d}} }}$. The appearance of a new peak at $\beta _{P}$ where the probability density first exhibits a crater is called a P-bifurcation point and it occurs in the full system at the airspeed $U_m = U_m^c + \epsilon ^2 \beta _P$.

Fig. 5

Bifurcation diagram for the homogenized system: Change in the distribution and density of the critical modes (x ₁, x ₂) as the bifurcation parameter β varies pass the D- and P-bifurcation points. The top figures show the cdf of the modulus $\sqrt{x_1^2+x_2^2}$, the bottom figures show the change in shape of the joint density of (x ₁, x ₂). The joint density is a δ-measure before the D-bifurcation. As the system transitions from the D- to P-bifurcation, the density stretches about the support of the δ-measure, until the P-bifurcation, where it takes a crater shape

In Fig. 5, we present the bifurcation diagram to illustrate better the D- and P-bifurcation points. Plots of the stationary densities of the reduced system are presented for an $\epsilon ^2$ neighborhood of $\beta = 0$. It is clear that at the D-bifurcation point, the top Lyapunov exponent $\lambda ^R_2$ of the reference measure is zero. For $\lambda ^R_2<0$, the trivial solution is stable and the nontrivial solution does not exist. For $\lambda ^R_2>0$, the trivial measure is unstable and hence there exists a nontrivial invariant measure. The nontrivial solution can be further examined via the two distinct growth rates of the process generated by $\mathscr {L}^{\dagger \dagger }$ given in (7.6) in “Appendix 2”. The sum of these growth rates are related through the trace formula of the Stratonovich stochastic differential equation characterized via the Hörmander equivalent of $\mathscr {L}^{\dagger \dagger }$ as done in Arnold et al. [21].

We next consider the moment stability of the response, ${\check{r}}_{\tau }$. If $\mathbb {E} [({\check{r}}_{\tau })^p ]$ tends to a finite value as $\tau \rightarrow \infty$, then the system will be stable in the p’th moment. Let us formally define the $p{\hbox {th}}$ moment Lyapunov exponent for the homogenized system with zero nonlinearity (i.e., ${\mathbf{R}} =0$) and pure horizontal turbulence

$$\begin{aligned} g(p) \mathop {=}\limits ^{\mathrm{def}}\lim _{\tau \rightarrow \infty } \frac{1}{\tau } \ln \mathbb {E} |r_{\tau }|^p \quad \hbox {for }{\check{r}}_0 \ne 0. \end{aligned}$$

Following the work of Namachchivaya and Vedula [24] and assuming that the specified conditions are satisfied, the moment Lyapunov exponent for the system can be approximated as

$$\begin{aligned} g(p) = \epsilon ^2 g_2(p) +\mathcal O(\epsilon ^2), \end{aligned}$$

where

$$\begin{aligned} g_2(p) = \frac{p}{8}\left[ 8\delta ' \beta + \kappa _2 \mathbb {S}_{u_T}^{\cos } (2 \omega _0) +\kappa _3 \mathbb {S}_{u_T}^{\cos ,\kappa } (\omega _0+\gamma ) \right. + \kappa _4 \mathbb {S}_{u_T}^{\cos ,\kappa } (\omega _0-\gamma ) - \kappa _5 \mathbb {S}_{u_T}^{\sin ,\kappa } (\omega _0+\gamma ) - \kappa _6 \mathbb {S}_{u_T}^{\sin ,\kappa } (\omega _0-\gamma ) + 2 \left( \sum _{r=1}^4 \kappa ^{\sin , \lambda _r} \mathbb {S}_{u_T}^{\sin ,\lambda _r} (\omega _0) \right. \left. \left. + \sum _{r=1}^4 \kappa ^{\cos , \lambda _r} \mathbb {S}_{u_T}^{\cos ,\lambda _r} (\omega _0) \right) \right] + \frac{p^2}{16}\left[ 2\kappa _1 \mathbb {S}_{u_T} (0)+\kappa _2 \mathbb {S}_{u_T}^{\cos } (2 \omega _0)\right] , \end{aligned}$$

and $p\in \varDelta \equiv \hbox {any compact subset in }\mathbb {R}$.

Now, the top Lyapunov exponent $\lambda _1^R$ can be found alternatively by $\lambda _1^R = g'(0)$ where the prime denotes differentiation with respect to p. Furthermore, in light of the large deviations result of Baxendale [25], the nontrivial invariant measure undergoes a P-bifurcation at $\beta _P$ corresponding to $g(-d)=0$ where $d= \hbox {dim} \ \mathbb {R}^d$. In particular, the $\beta _P$ correspoding to the homogenized equation (see Fig. 5) occurs when $d=1$.

Fig. 6

Comparison of CDFs at nonzero unfolding, at 2β _D , 10β _P and 20β _P : The top figures show the cdf of the modulus of the critical modes $\sqrt{x_1^2+x_2^2}.$ Each figure shows the comparison between the cdfs constructed using the full system (solid) and homogenized system (dashed). a–c show the joint density of the critical modes, d–f presents the joint density of pitch and pitch rate, g–i gives the joint density of heave and its rate

In Fig. 6, we present comparisons between CDFs of the reduced and full system at regions of interest, namely, $2\beta _D, 10\beta _P, 20\beta _P$ to discuss the range of validity of the homogenized stochastic differential equation for studying essential characteristics with respect to the two bifurcation points. From the relatively good agreement of the CDFs (shown at the top in Fig. 6), we can assert that the one dimensional stochastic differential equation is indeed an accurate and computationally efficient model that captures the essential flutter characteristics of the aeroelastic model. It is evident that this one-dimensional model is valid for a large region hence adding to the robustness of this model. Additionally, various joint probability densities of the aerodynamic states taken from the full system are presented in Fig. 6.

Figure 7 presents the top Lyapunov exponent obtained at various $\beta$’s from the homogenized model. These values are a good representation of the original system’s result at the prescribed $\beta$ due to the agreement of the CDFs for the range $2\beta _D$ through $20\beta _P$ shown in Fig. 6.

Fig. 7

Lyapunov exponent from the reduced model for a range of unfolding

A linear fit of the data in Fig. 7 results in $\lambda _R$ growing at a rate of ${\mathbf{0.0322}}$ with respect to $\beta$. This corresponds to a positive growth rate of ${\mathbf{4.3233}} \times 10^{-4}$ in the top Lyapunov exponent with respect to unfolding for the full aeroelastic model for the case of pure parametric excitation.

4.3 Results for the real noise case: combined excitation

The two-dimensional process $Z \mathop {=}\limits ^{\mathrm{def}}[\hbox {w}_T \ c]^T$ given by Eq. (2.6b) is linear and hence the solutions of these stochastic differential equations are gaussian. Thus, the stationary distribution of this process is distributed normally with the two statistics, $m_\infty$ and $P_\infty$:

$$\begin{aligned}&m_\infty = \begin{bmatrix} 0 \\ 0 \end{bmatrix}, \quad P_\infty = \frac{1}{\pi } \begin{bmatrix} 1&-\frac{(\varGamma ^{\star })^2}{2} \\ -\frac{(\varGamma ^{\star })^2}{2}&\,(\varGamma ^{\star })^2(1-\sqrt{3}) \end{bmatrix}, \\&\hbox {with}\, \varGamma ^{\star } = \frac{U_m^{\star }}{L}. \end{aligned}$$

The stationary joint density of $Z_t$ can be easily found via the multivarite normal distribution:

$$\begin{aligned} p_{st} (\hbox {w}_T,c)&= \frac{1}{2 \pi |P_\infty |^{1/2}} \\&\quad \times \,\exp {\left( -\frac{1}{2} (Z_t - m_\infty )^T P_\infty ^{-1}(Z_t - m_\infty ) \right) }. \end{aligned}$$

Therefore, the initial conditions for the states of the two-dimensional process $Z_t$ can now be sampled from the previous stationary probability density and hence the simulation of the full system can be facilitated. The stationary density, $p_{st} ({\check{r}})$, of the ${\check{r}}$ process in this setting is given by

$$\begin{aligned} p_{st} ({\check{r}})= \frac{2 \zeta ^{\bar{\nu }} \exp {(-\zeta )}}{\varGamma (\bar{\nu },\zeta )} \times \left( \frac{\mathbf{d }}{\mathbf{c }} \right) {\check{r}} \ \left[ \left( \frac{\mathbf{d }}{\mathbf{c }}\right) {\check{r}}^2 + 1 \right] ^{\bar{\nu } - 1} \hbox {exp} \left( \frac{\mathbf{R }}{\mathbf{d }} {\check{r}}^2\right) , \end{aligned}$$

with $\bar{\nu } \mathop {=}\limits ^{\mathrm{def}}\frac{\mathbf{a }-\frac{\mathbf{d }}{2}}{\mathbf{d }} + \zeta , \zeta \mathop {=}\limits ^{\mathrm{def}}\frac{-{\mathbf{R}}{\mathbf{c}}}{{\mathbf{d}}^2}$, $\bar{\nu }$ non-negative, and this density satisfies the stationary Fokker-Planck equation:

$$\begin{aligned} -\frac{\partial }{\partial {\check{r}}}\left( b_{\mathcal {R}}({\check{r}}) p_{st} ({\check{r}})\right) + \frac{1}{2} \frac{\partial ^2 }{\partial {\check{r}}^2}\left( \sigma _{\mathcal {R}}^2 ({\check{r}})p_{st} ({\check{r}})\right) = 0, \end{aligned}$$

with initial condition: $p_{st} ({\check{r}}_{\tau },\tau | {\check{r}}_0,\tau _0) \rightarrow \delta ({\check{r}}_{\tau } - {\check{r}}_0) \ \hbox {as} \ \tau \rightarrow \tau _0$. The homogenized coefficients $b_{\mathcal {R}} , \sigma _{\mathcal {R}}$ are given in Sect. 4.1. In view of the definition of ${\check{r}}$, the joint stationary density is given by

$$\begin{aligned} p_{st} (x_1,x_2)&=\frac{2 \zeta ^{{\bar{\nu }}} \exp {(-\zeta )}}{\varGamma (\bar{\nu },\zeta )}\\&\quad \times \,\left( \frac{\mathbf{d }}{\mathbf{c }} \right) \sqrt{x_1^2 + x_2^2} \ \left[ \left( \frac{\mathbf{d }}{\mathbf{c }}\right) \left( x_1^2 + x_2^2\right) + 1 \right] ^{{\bar{\nu }} - 1}\\&\quad \times \,\hbox {exp} \left( \frac{\mathbf{R }}{\mathbf{d }} (x_1^2 + x_2^2)\right) . \end{aligned}$$

Fig. 8

CDFs of the critical modes of the original system (dashed) and the reduced system (solid) for the case of combined excitation

In order to obtain asymptotic results, we consider the case of $\wp = 1$ and hence we are considering the vertical component of turbulence to be at $\mathcal O(\epsilon ^2)$ in the original aeroelastic model given by Eq. (2.11). Figure 8 shows the plot of the CDFs of the critical modes of the reduced and full systems at zero unfolding, $\beta =0$. Figure 8 was generated with $\varepsilon = 0.05$, using the same numerical scheme stated in Sect. 4.1. From the relatively good agreement of the CDFs in Fig. 8, we can assert the validity of this one dimensional model in capturing the essential flutter characteristics of the aeroelastic model in the vicinity of the flutter airspeed for the combined vertical and horizontal turbulence setting. Figure 9 presents the various joint probability densities taken from the full aeroelastic system whose CDF of the critical modes is given in Fig. 8. It has been verified for a range of nonzero unfolding (i.e., $\beta \ne 0$) that all normalizable joint densities (i.e., probability density) exhibit a crater shape. Thus, a D-Bifurcation does not occur in the case of combined excitation (see Fig. 5 for a lucid picture of the transition of the densities between bifurcation points). This result is commensurate with that obtained by Poirel and Price [3].

Fig. 9

Joint densities at $\beta = 0$ for combined excitation: a shows the joint density of the critical modes, b presents the joint density of heave and its rate, c gives the joint density of pitch and pitch rate

This homogenized model may further be used to study the effect of combined excitation on the full aeroelastic model for a range of nonzero unfolding. Although not considered in the present work, this homogenized model can additionally be used to accurately estimate the top Lyapunov exponent of the full aeroelastic system when excited by both multiplicative and additive noise.

5 Conclusion

We considered an 11-dimensional stochastic model that represents a 2-degree-of-freedom aeroelastic problem, with aerodynamic forcings generated by an additional 2-degree-of-freedom model and a 3-dimensional turbulence model, and extensively characterized the modeling involved. A method of stochastic dimensional reduction based on the work of Papanicolaou et al. [20], Namachchivaya and Lin [26] and Namachchivaya and Van Roessel [4] was developed, for non-white noise excitations. In developing the stochastic averaging scheme, it is assumed that the random perturbations are small, but over a long time their effects are significant. In order to understand these effects, the reduced model encoded the structure of the unperturbed dynamical system which allowed one to look at the quantities of interest on an appropriate time scale. The averaging principle permits us to obtain the equations governing the evolution of these slow variables. The method was then applied to the aeroelastic problem in the vicinity of the critical bifurcation parameter. This simplified low-dimensional coarse-grained model was used to efficiently simulate the long-term statistics of the slow variables. The goal of this technique was to obtain a one dimensional reduced model that would characterize the stochastic dynamics exhibited by the critical modes of the original system and in turn allow for aerodynamic flutter to be investigated in the presence of turbulence. This technique was facilitated by the fact that the system under consideration comprised of components that rapidly oscillate and decay, and noise processes that satisfy strong mixing conditions, so that they attain invariant measures very quickly and hence could be averaged out. Explicit formulas for the homogenized drift and diffusion coefficients were derived and these quantities were given in terms of various power spectral densities that could be readily found from the Dryden model. The formula contains terms representing contribution from the stochastic components in the stable “heavily damped” modes and the “critical” modes (this contribution was explicitly obtained for the first time in Namachchivaya and Lin [26]).

One of the key findings is that, in addition to providing a qualitative behavior of the stochastic dynamics, the results from asymptotic methods are capable of capturing the quintessence of noise-induced instability and stochastic bifurcations of the original system, as shown in Figs. 2, 3, 4, and 8. Numerical experiments were conducted for the cases of pure longitudinal and combined excitations and the CDFs of the critical modes of the original and reduced systems converged in both instances. This verifies the results obtained from the homogenization procedure. Finally, the top Lyapunov exponent was calculated analytically for the one-dimensional system and compared with the numerical value obtained from the nine-dimensional system for the case of parametric excitation. The Lyapunov exponent values were found to be relatively close to each other, allowing us to comment on the overall stability of the full system using the one-dimensional system.

Appendices

Appendix 1

The terms in (2.10) of Sect. 2 are as follows:

$$\begin{aligned} \begin{bmatrix} M \end{bmatrix}&= \begin{bmatrix} 1+\frac{a_h^2+\frac{1}{8}}{\mu r_\alpha ^2}&\frac{x_\alpha }{r_\alpha ^2}-\frac{a_h}{\mu r_\alpha ^2}&0&0\\ x_\alpha -\frac{a_h}{\mu }&1+\frac{1}{\mu }&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{bmatrix}, \\ \left[ {\begin{array}{c} {D(\tau )} \\ \end{array} } \right] &= \left[ {\begin{array}{cccc} {\frac{{u^{\epsilon } \left( {\frac{1}{2} - a_{h} } \right)^{2} }}{{\mu r_{\alpha }^{2} }}} & { - \frac{{u^{\epsilon } \left( {\frac{1}{2} + a_{h} } \right)}}{{\mu r_{\alpha }^{2} }}} & { - \frac{{2u^{\epsilon } \left( {\frac{1}{2} + a_{h} } \right)\left( {A_{1}^{W} b_{1}^{W} + A_{2}^{W} b_{2}^{W} } \right)}}{{\mu r_{\alpha }^{2} }}} & { - \frac{{2\left( {\frac{1}{2} + a_{h} } \right)\left( {A_{1}^{K} b_{1}^{K} + A_{2}^{K} b_{2}^{K} } \right)}}{{\mu r_{\alpha }^{2} }}} \\ {\frac{{u^{\epsilon } \left( {\frac{3}{2} - a_{h} } \right)}}{\mu }} & {\frac{{u^{\epsilon } }}{\mu }} & {\frac{{2u^{\epsilon } \left( {A_{1}^{W} b_{1}^{W} + A_{2}^{W} b_{2}^{W} } \right)}}{\mu }} & {\frac{{2\left( {A_{1}^{K} b_{1}^{K} + A_{2}^{K} b_{2}^{K} } \right)}}{\mu }} \\ {a_{h} - \frac{1}{2}} & { - 1} & {b_{1}^{W} + b_{2}^{W} } & 0 \\ 0 & 0 & 0 & {b_{1}^{K} + b_{2}^{K} } \\ \end{array} } \right],\\ \begin{bmatrix} K(\tau )\end{bmatrix}&= \left[ \begin{array}{ccc} \frac{1}{U_m^2} - \frac{(u^{\epsilon })^2\left( \frac{1}{2}+a_h\right) }{\mu r_\alpha ^2} &{} 0 \\ \frac{(u^{\epsilon })^2}{\mu } &{} \frac{\left( \omega _h/\omega _\alpha \right) ^2}{U_m^2} \\ -u^{\epsilon } &{} 0 \\ 0 &{} 0 \end{array}\right. \left. \begin{array}{cc} -\frac{{(u^{\epsilon })^2\left( \frac{1}{2}+a_h\right) b_1^{W} b_2^W}}{\mu r_\alpha ^2} &{} -\frac{2\left( \frac{1}{2}+a_h\right) b_1^Kb_2^K}{\mu r_\alpha ^2} \\ \frac{u^{\epsilon } b_1^Wb_2^W}{\mu } &{} \frac{2b_1^Kb_2^K}{\mu } \\ b_1^Wb_2^W &{} 0 \\ 0 &{} b_1^Kb_2^K \end{array}\right] ,\\ \begin{bmatrix} K_3 \end{bmatrix}&= \begin{bmatrix} \frac{K_3}{U_m^2}&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \end{bmatrix}, \end{aligned}$$

where $u^{\epsilon }\mathop {=}\limits ^{\mathrm{def}}1+\epsilon u_T(\tau )$, $w^{\epsilon }:=\epsilon \hbox {w}_T(\tau )$, and $\omega _h$ and $\omega _\alpha$ are the natural frequencies of heave and pitch [frequencies of the solutions to the decoupled, unforced Eq. (2.1)].

As mentioned in Sect. 2, the damping and stiffness matrices [D] and [K] can be decomposed into their respective time invariant and time varying components:

$$\begin{aligned}{}[D(\tau )]&= [D_0] + \epsilon u_T (\tau ) [D_1], \\ [K(\tau )]&= [K_0] + \epsilon u_T (\tau ) [K_1], \end{aligned}$$

where

$$\begin{aligned} \begin{bmatrix} D_0 \end{bmatrix}&= \left[\begin{array}{cccc} \frac{\left( \frac{1}{2}-a_h\right) ^2}{\mu r_\alpha ^2} &-\frac{\left( \frac{1}{2}+a_h\right) }{\mu r_\alpha ^2} & -\frac{2\left( \frac{1}{2}+a_h\right) \left( A_1^Wb_1^W+A_2^Wb_2^W\right) }{\mu r_\alpha ^2}& -\frac{2\left( \frac{1}{2}+a_h\right) \left( A_1^Kb_1^K+A_2^Kb_2^K\right) }{\mu r_\alpha ^2}\\ \frac{\left( \frac{3}{2}-a_h\right) }{\mu } & \frac{1}{\mu } & \frac{2\left( A_1^Wb_1^W+A_2^Wb_2^W\right) }{\mu } & \frac{2\left( A_1^Kb_1^K+A_2^Kb_2^K\right) }{\mu }\\ a_h-\frac{1}{2} & -1 & b_1^W+b_2^W & 0\\ 0 & 0 & 0& b_1^K+b_2^K \end{array}\right] , \\ \begin{bmatrix} D_1 \end{bmatrix}&=\left[ \begin{array}{cc} \frac{\left( \frac{1}{2}-a_h\right) ^2}{\mu r_\alpha ^2} & -\frac{\left( \frac{1}{2}-a_h\right) }{\mu r_\alpha ^2} \\ \frac{1}{\mu }\left( \frac{3}{2}-a_h\right) & \frac{1}{\mu } \\ 0 & 0 \\ 0 & 0 \end{array}\right. \left. \begin{array}{cc} -\frac{2\left( \frac{1}{2}+a_h\right) \left( A_1^Wb_1^W+A_2^Wb_2^W\right) }{\mu r_\alpha ^2} & 0\\ \frac{2\left( A_1^Wb_1^W+A_2^Wb_2^W\right) }{\mu } & 0 \\ 0 & 0 \\ 0 & 0 \end{array}\right] , \\ \begin{bmatrix} K_0 \end{bmatrix}&=\left[ \begin{array}{cc} \frac{1}{U_m^2} - \frac{\left( \frac{1}{2}+a_h\right) }{\mu r_\alpha ^2}& 0\\ \frac{1}{\mu } & \frac{\left( \omega _h/\omega _\alpha \right) ^2}{U_m^2} \\ -1 & 0 \\ 0 & 0\end{array}\right. \left. \begin{array}{cc} -\frac{\left( \frac{1}{2}+a_h\right) b_1^Wb_2^W}{\mu r_\alpha ^2} & -\frac{2\left( \frac{1}{2}+a_h\right) b_1^Kb_2^K}{\mu r_\alpha ^2}\\ \frac{u^{\epsilon } b_1^Wb_2^W}{\mu } & \frac{2b_1^Kb_2^K}{\mu } \\ b_1^Wb_2^W & 0 \\ 0 & b_1^Kb_2^K \end{array}\right] , \\ \begin{bmatrix} K_1 \end{bmatrix}&= \left[ \begin{array}{cccc} - \frac{2\left( \frac{1}{2}+a_h\right) }{\mu r_\alpha ^2} & 0 & -\frac{2\left( \frac{1}{2}+a_h\right) b_1^Wb_2^W}{\mu r_\alpha ^2} & 0 \\ \frac{2}{\mu } & 0 & \frac{b_1^Wb_2^W}{\mu } & 0 \\ -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right] . \end{aligned}$$

The coefficient matrices in (2.11) of Sect. 2 are as follows:

$$\begin{aligned} \left[ A_0\right]= & {} \left[ Z\right] ^{-1}\left[ L\right] , \quad \left[ B_0\right] = \left[ Z\right] ^{-1}\left[ Q\right] , \\ \left[ C_0\right]= & {} \left[ Z\right] ^{-1}\left[ G\right] , \quad \left[ \hat{N}\right] = \left[ Z\right] ^{-1}\left[ N\right] , \end{aligned}$$

where

$$\begin{aligned} {[}Z]= & {} \begin{bmatrix} I&0 \\ 0&[M] \end{bmatrix}, \quad [L]= \begin{bmatrix} 0&I \\ -[K_0]&-[B_0] \end{bmatrix},\\ {[}Q]= & {} \begin{bmatrix} 0&0 \\ {-[K_1]}&{-[D_1]} \end{bmatrix}\quad [G]=\begin{bmatrix} 0&0 \\ -[K_3]&0 \end{bmatrix} \\ {[}N]= & {} \begin{bmatrix} 0 \\ 0 \\ 0 \\ \hbox {w}_T\end{bmatrix}. \end{aligned}$$

The terms in (2.13) of Sect. 2 are as follows:

$$\begin{aligned}&{\bar{b}}^0\left( {v^{\epsilon }_{\tau }}, U_m^c\right) = \left[ S A_0\left( U_m^c\right) T\right] \, {v^{\epsilon }_{\tau }}= \left[ A\left( U_m^c\right) \right] {v^{\epsilon }_{\tau }},\\&{\bar{b}}^1\left( {v^{\epsilon }_{\tau }}, u_T(\tau ), \hbox {w}_T (\tau )\right) = \wp [S] [\hat{N}] + [S B_0T] u_T (\tau ) {v^{\epsilon }_{\tau }}\\&\quad = \wp [\chi ] + [\bar{B}] u_T (\tau ) {v^{\epsilon }_{\tau }}, \\&{\bar{b}}^2\left( {v^{\epsilon }_{\tau }}, U_m^c\right) = \left[ F u_{\tau }^{\epsilon }+ G \left( {v^{\epsilon }_{\tau }}\right) ^3\right] ,\\&F =\beta \left[ S A_0 '\left( U_m^c\right) T\right] = \beta \left[ A '\left( U_m^c\right) \right] ,\\&G = [S] [C_0], \\&\left( {v^{\epsilon }_{\tau }}\right) ^3 = \left[ \left( \sum _{i=1}^{8}T_{1i} v_{\tau }^{\epsilon , (i)}\right) ^3, \dots ,\left( \sum _{i=1}^{8}T_{8i} v_{\tau }^{\epsilon ,(i)}\right) ^3\right] ^T,\\&[\chi ] = \hbox {w}_T(\tau ) [S_{18}, \dots , S_{88}]^T, \hbox {where} \ [S] = [T]^{-1}. \end{aligned}$$

Due to the block diagonal form of the linear operator, $A(U_m^c)$, we can write

$$\begin{aligned} A\left( U_m^c\right)&= \left[ \begin{array}{lll}B &{} 0 &{} 0\\ 0 &{} R &{} 0\\ 0 &{} 0 &{} C\end{array}\right] , \,\hbox {where}\, B = \left[ \begin{array}{cc}0 &{} -\omega _0\\ \omega _0 &{} 0\end{array}\right] , \,\omega _0\in \mathbb {R}^{+}\\ R&= \begin{bmatrix}-\kappa&-\gamma \\ \ \gamma&-\kappa \end{bmatrix}, \,\hbox {and}\, C = \hbox {diag}(\lambda _i),\lambda _{i}<0, i=1,\dots ,4. \end{aligned}$$

The remaining terms are

$$\begin{aligned} A'\left( U_m^c\right) = \left[ \begin{array}{ll}D &{} E\\ H &{} J\end{array}\right] , [\bar{B}] = \left[ \begin{array}{ll}\bar{K} &{} \bar{M} \\ \bar{ N} &{} \bar{L}\end{array}\right] , G \left( u_{\tau }^{\epsilon }\right) ^3 = \left[ \begin{array}{l}\bar{g}_1 \left( u_{\tau }^{\epsilon }\right) \\ \vdots \\ \bar{g}_8 \left( u_{\tau }^{\epsilon }\right) \end{array}\right] , \end{aligned}$$

where D and $\bar{K}$ are $2\times 2$ matrices, E and $\bar{M}$ are $2\times 6$ matrices, H and $\bar{N}$ are $6\times 2$ matrices, and J, $\bar{L}$ are $6\times 6$ matrices, and

$$\begin{aligned} \bar{g}_m (x) \mathop {=}\limits ^{\mathrm{def}}{\hat{g}}_{m:ijk} x_i x_j x_k = {\hat{g}}_{m:111} x_1^3 + {\hat{g}}_{m:222} x_2^3+ 3{\hat{g}}_{m:122} x_1 x_2^2 + 3 {\hat{g}}_{m:112} x_1^2x_2 \end{aligned}$$

for $m = 1,\dots ,8$, and ${\hat{g}}_{m:ijk}$ are constants.

Appendix 2

Here, we describe the calculations involved in Sect. 3.2. Substituting the expansion (3.6) into (3.5), we have a set of Poisson equations at increasing orders of $\epsilon$:

$$\begin{aligned} \begin{aligned} \mathscr {L}_{F}^{(y,\theta ,z)} u_0(x,y,\theta ,z,\tau )&= b^{0}(y) \frac{\partial u_0}{\partial y}(x,y,\theta ,z,\tau ) +\omega _0 \frac{\partial u_0}{\partial \theta }(x,y,\theta ,z,\tau ) \\&\quad +\,\mathcal {G}u_0(x,y,\theta ,z,\tau ) = 0, \\ \mathscr {L}_{F}^{(y,\theta ,z)} u_1(x,y,\theta ,z,\tau )&= -a^0(x,y,\theta ,z) \frac{\partial u_0}{\partial x} (x,y,\theta ,z,\tau ) \\&\quad -\, b^{1}(x,y,\theta ,z) \frac{\partial u_0}{\partial y} (x,y,\theta ,z,\tau ), \\ \mathscr {L}_{F}^{(y,\theta ,z)} u_2(x,y,\theta ,z,\tau )&= -a^0(x,y,\theta ,z) \frac{\partial u_1}{\partial x} (x,y,\theta ,z,\tau ) \\&\quad - \,\,b^{1}(x,y,\theta ,z) \frac{\partial u_1}{\partial y} (x,y,\theta ,z,\tau ) \\&\quad - \,\left( a^{1}(x,y,\theta ) \frac{\partial u_0}{\partial x}(x,y,\theta ,z,\tau ) \right. \\&\quad \left. + \,b^{2}(x,y,\theta ) \frac{\partial u_0}{\partial y}(x,y,\theta ,z,\tau ) - \frac{\partial u_0}{\partial \tau }(x,y,\theta ,z,\tau )\right) , \\&\vdots \end{aligned} \end{aligned}$$

(7.1)

Since $\mathcal {G}$ is an operator in z alone, it is clear from the first equation of (7.1) that $u_0(x,y,\theta ,z,\tau )=u(x,\tau )$. Thus, the second and third equations of (7.1) simplifies to

$$\begin{aligned} \begin{aligned} \mathscr {L}_{F}^{(y,\theta ,z)} u_1(x,y,\theta ,z,\tau )&= -a^0(x,y,\theta ,z) \frac{\partial u}{\partial x} (x,\tau ), \\ \mathscr {L}_{F}^{(y,\theta ,z)} u_2(x,y,\theta ,z,\tau )&= -a^0(x,y,\theta ,z) \frac{\partial u_1}{\partial x} (x,y,\theta ,z,\tau ) \\&\quad - b^{1}(x,y,\theta ,z) \frac{\partial u_1}{\partial y} (x,y,\theta ,z,\tau ) \\&\quad - \left( a^{1}(x,y,\theta ) \frac{\partial u}{\partial x}(x,\tau ) - \frac{\partial u}{\partial \tau }(x,\tau )\right) . \\ \end{aligned}\end{aligned}$$

(7.2)

We first investigate the $\mathcal O(\frac{1}{\epsilon ^2})$ dynamics in (3.3) to obtain the transient and invariant measures of the fast generator $\mathscr {L}_F^{y,\theta ,z}$. Let us denote by $\psi _{\tau }$ the flow map induced by the deterministic vector field $b^{0} (y)$ of (3.3), i.e. $\psi _{\tau }(y)$ is the flow of $Y^{\epsilon }$ starting from y if it was driven only by the $\mathcal O(\frac{1}{\epsilon ^2})$ dynamics. The transient measure is a delta measure centered at $\psi _{\tau }(y)$: $\delta _{\psi _{\tau }(y)}(\eta )$. Since the vector field is asymptotically stable, we can associate a measure defined by the following limit

$$\begin{aligned} \delta _{\infty }(\eta ) = \delta _{0}(\eta ) \mathop {=}\limits ^{\mathrm{def}}\lim _{\tau \rightarrow \infty } \delta _{_{\psi _s(y)}}(\eta ). \end{aligned}$$

For the $\theta ^{\epsilon }$ process, all orbits live on a circle whose radius is dictated by the values of the initial conditions $x_1$ and $x_2$ of the process $X_{\tau }^{\epsilon }$. More precisely, contained in a closed orbit, we can associate a measure defined by the following limit

$$\begin{aligned} \delta _{\infty }(\xi )=\frac{1}{2\pi }= \lim _{\tau \rightarrow \infty } \frac{1}{\tau } \int _0^\tau \delta _{{\theta + \omega _0 s}}(\xi ) \; ds. \end{aligned}$$

For the noise process, it is natural to obtain the final results in terms of the spectral densities of the input noise $Z^{\epsilon }$ whose generator is $\mathcal {G}$. To this end, we express the solution in terms of the Green’s function $g(\zeta ,\tau ;z,0)$ for $\mathcal {G}^{*}$. The Green’s function for $\mathcal {G}^{*}$ is the solution of

$$\begin{aligned} \frac{\partial g}{\partial \tau } = \mathcal {G}^{*}g, \quad g(\zeta ,0;z,0) = \delta _0(z-\zeta ). \end{aligned}$$

Since they are independent, the transient density of the $\mathcal O(\frac{1}{\epsilon ^2})$ components is

$$\begin{aligned} p_s(y, \theta ,z, \eta ,\xi ,\zeta ) = \delta _{_{\psi _s(y)}}(\eta ) \cdot \delta _{_{\omega _0 s + \theta }}(\xi ) \cdot g(\zeta ,s;z,0). \end{aligned}$$

Now we are in a position to evaluate the PDEs (7.2). The coefficients $a^0(x,y,\theta ,z)$ and $b^{1}(x,y,\theta ,z)$ in (3.3) are both linearly dependent on the process $Z^{\epsilon }$, which invariant distribution has zero mean, so

$$\begin{aligned} \mathbb {E}\left[ a^0(x,Y^{\epsilon },\theta ^{\epsilon },Z^{\epsilon })\right] =\mathbb {E}\left[ b^{1}(x,Y^{\epsilon },\theta ^{\epsilon },Z^{\epsilon })\right] =0, \end{aligned}$$

where $\mathbb {E}[\cdot ]$ is expectation with respect to the invariant density $p_\infty$. Thus, the Fredholm alternative implies that the first equation of (7.2) has a bounded solution. Now employing the Feynman–Kac formula (see, for example, Chapter 5 of Karatzas and Shreve [27]) and defining

$$\begin{aligned} u_{x}^{\prime }(x,\tau )\mathop {=}\limits ^{\mathrm{def}}\frac{\partial u}{\partial x} (x,\tau ), \quad h(x,y,\theta ,z;\tau ) \mathop {=}\limits ^{\mathrm{def}}a^0(x,y,\theta ,z) u_{x}^{\prime }, \end{aligned}$$

the bounded solution of the first equation of (7.2) is given by

$$\begin{aligned} u_1(x,y,\theta ,z,\tau )= \mathbb{E}_{y,\theta ,z}\left[ \int _0^\infty h\left( Y_s^x,\theta ^x_s,Z_s^x; x,\tau \right) \, ds\right] = \int _0^\infty ds \; \int _{\mathbb {R}^6} \int _{\mathbb{S}} \int _{\mathbb{R}^3} a^0(x,\eta ,\xi ,\zeta ) u_{x}^{\prime } (x,\tau ) p_s(\eta ,\xi ,\zeta ; y,\theta ,z) \; d\eta d\xi d\zeta , \end{aligned} $$

(7.3)

where x and $\tau$ are parameters and the transient density does not depend on x due to the fact that the fast components of $Y^{\epsilon }, \theta ^{\epsilon }, Z^{\epsilon }$ are independent of the slow process $X^{\epsilon }$. Furthermore, we note once again that y, $\theta$ and z represent the starting points of the processes $Y^{\epsilon }_{\tau }, \theta ^x_{\tau }, Z^{\epsilon }_{\tau }$ respectively. Since $\mathbb {E}\left[ a^0(x,Y^{\epsilon },\theta ^{\epsilon },Z^{\epsilon })\right] =0$ (see above), the centering condition is automatically satisfied:

$$\begin{aligned} \int _{\mathbb {R}^6} \int _{\mathbb {S}} \int _{\mathbb {R}^3} h(\eta ,\xi ,\zeta ; x,\tau ) \ p_{\infty }(\eta ,\xi ,\zeta ) \; d\eta d\xi d\zeta = 0. \end{aligned}$$

Making use of the above expression for the transient density, (7.3) can be written as

$$\begin{aligned} u_1(x,y,\theta ,z,\tau ) = \int _0^\infty \int _{\mathbb {R}^6} \int _{\mathbb {S}} \int _{\mathbb {R}^3} a^0(x,\eta ,\xi ,\zeta ) u_{x}^{\prime } (x,\tau ) \delta _{_{\psi _s(y)}}(\eta ) \cdot \delta _{_{\omega _0 s + \theta }}(\xi ) \cdot g(\zeta ,s;z,0) \; d\eta d\xi d\zeta . \end{aligned}$$

Now, let us consider the last of the Poisson equations in (7.2) more carefully:

$$\begin{aligned} \mathscr {L}_{F}^{(y,\theta ,z)} u_2(x,y,\theta ,z,\tau )= -a^0_{j}(x,y,\theta ,z) \frac{\partial u_1}{\partial x_{j}} (x,y,\theta ,z,\tau ) - b^{1}_{j}(x,y,\theta ,z) \frac{\partial u_1}{\partial y_{j}} (x,y,\theta ,z,\tau ) - \left( a^{1}_{j}(x,y,\theta ) \frac{\partial u}{\partial x_{j}}(x,\tau ) - \frac{\partial u}{\partial \tau }(x,\tau )\right) . \end{aligned}$$

(7.4)

Note that the transient and invariant measures are not functions of the slow variable x, but only of the initial point $(y,\theta ,z)$. Keeping this in mind and integrating with respect to $\eta (=y)$ and $\xi (=\theta )$ we can rewrite (7.4) as

$$\begin{aligned} \mathscr {L}_{F}^{(y,\theta ,z)} u_2(x,y,\theta ,z,\tau ) = -a^0_{j}(x,y,\theta ,z) \int _0^\infty ds \left( \int _{\zeta \in \mathbb {R}^3} \left( \frac{\partial a^0_i}{\partial x_{j}} \left( x,{\psi _s(y)},{\omega _0 s + \theta },\zeta \right) u_{x_{i}}^{\prime } (x,\tau ) + a^0_{i} \left( x,{\psi _s(y)},{\omega _0 s + \theta },\zeta \right) u_{x_{i}x_{j}}^{\prime \prime } (x,\tau )\right) g(\zeta ,s;z,0) \; d\zeta \right) - b^{1}_{j}(x,y,\theta ,z) \int _0^\infty ds \; \frac{\partial }{\partial y_{j}} \left( \int _{\zeta \in \mathbb {R}^3} a^0_{i}(x,{\psi _s(y)},{\omega _0 s + \theta },\zeta ) u_{x_{i}}^{\prime } (x,\tau ) g(\zeta ,s;z,0) \; d\zeta \right) - \left( a^{1}_{j}(x,y,\theta ) \frac{\partial u}{\partial x_{j}}(x,\tau ) - \frac{\partial u}{\partial \tau }(x,\tau )\right) =: \varphi (x,y,\theta ,z,\tau ). \end{aligned}$$

Applying the solvability condition $\left\langle \varphi (x,y,\theta ,z,\tau ), p_{\infty }(y,\theta ,z) \right\rangle = 0$, where $p_{\infty }(y,\theta ,z)$ is in the kernel of $\mathscr {L}_{F}^{(y,\theta ,z)}$:

$$\begin{aligned} &-\int _{\mathbb {R}^6} \int _{\mathbb {S}}\int _{\mathbb {R}^3} a^0_{j}(x,y,\theta ,z) p_{\infty }(y,\theta ,z) \int _0^\infty ds \left\{ \int _{\zeta \in \mathbb {R}^3} \left( \frac{\partial a^0_{i}}{\partial x_{j}} (x,{\psi _s (y)},{\omega _0 s + \theta },\zeta ) u_{x_{i}}^{\prime } (x,\tau )\right. \right. \left. \left. + a^0_i (x,{\psi _s (y)},{\omega _0 s + \theta },\zeta ) u_{x_{i}x_{j}}^{\prime \prime } (x,\tau )\right) \right. \left. g(\zeta ,s;z,0) \; d\zeta \right) \; dy d\theta dz \\&- \int _{\mathbb {R}^6} \int _{\mathbb {S}} \int _{\mathbb {R}^3} b^{1}_{j}(x,y,\theta ,z) p_{\infty }(y,\theta ,z) \int _0^\infty ds \left( \int _{\zeta \in \mathbb {R}^3} \frac{\partial a^0_{i}}{\partial \zeta _{l}} (x,\zeta ,{\omega _0 s + \theta },\zeta )|_{\zeta ={\psi _s(y)}} \frac{\partial {\psi _s^{l}(y)}}{\partial y_j} u_{x_{i}}^{\prime } (x,\tau ) g(\zeta ,s;z,0) \; d\zeta \right) dy d\theta dz \\&- \int _{\mathbb {R}^6} \int _{\mathbb {S}}\int _{\mathbb {R}^3} p_{\infty }(y,\theta ,z) \left( a^{1}_{j}(x,y,\theta ) \frac{\partial u}{\partial x_{j}}(x,\tau ) - \frac{\partial u}{\partial \tau }(x,\tau )\right\} dy d\theta dz = 0. \end{aligned}$$

(7.5)

Equation (7.5) yields the homogenized equation for $u(x,\tau )$.

We now provide a brief overview of the computation involved at this point. The complete details can be found in Singh [11]. In order to simplify the calculations further, we look at ${\bar{b}}^1 (v^{\epsilon }, u_T,\hbox {w}_T)$, ${\bar{b}}^2 (v^{\epsilon },U_m^c)$ in (2.13) and note the change of coordinates in (3.2) that motivates an appropriate structure for the variables $a^0(x,y,\theta ,z)$, $b^{1}(x,y,\theta ,z)$, $a^{1}(x,y,\theta )$. These variables are defined in terms of the matrices $\bar{K}$, $\bar{M}$, S, $\bar{N}$, $\bar{L}$, D as given in (2.13) as well as in terms of functions of the respective noise processes: $\varphi _1 (u_T)$, $\varphi _2 (c,\hbox {w}_T)$. Furthermore, the invariant measure is given as

$$\begin{aligned} p_{\infty }(y,\theta ,z)=\frac{\delta _{0}(y) \cdot \nu _1(z_1) \cdot \nu _2(z_2,z_3)}{2 \pi }, \end{aligned}$$

where $\nu _1\cdot \nu _2$ is the invariant measure of the real noise process, which are independent. The transition density of the noise process can be decomposed as

$$\begin{aligned} g(\zeta ,s;z,0) = g_1 (\zeta _1,s;z_1,0) \cdot g_2 (\zeta _2,\zeta _3,s;z_2,z_3,0). \end{aligned}$$

We treat $\left( \zeta _2,\zeta _3\right)$ in $g_2(\zeta _2,\zeta _3,s;z,0)$ as one quantity in the analysis that follows.

We then integrate out both y and $\theta$ variables, respectively, in the solvability condition that follows from the previous remarks. We further note that the cross terms between $\varphi _1 (u_T)$, $\varphi _2 (c,\hbox {w}_T)$ have been dropped because of the independence between the horizontal and vertical noise. Additionally, we define the covariances (time correlation) in terms of functions of the respective noise processes $\varphi _1 (u_T)$, $\varphi _2 (c,\hbox {w}_T)$ as

$$\begin{aligned}\mathscr {R}_{\varphi _1}(s) \mathop {=}\limits ^{\mathrm{def}}&\mathbb {E}[\varphi _1 (u_T(\tau ))\varphi _1 (u_T({\tau +s}))] = \int _{\mathbb {R}} \varphi _1 (\zeta ) \nu _1 (\zeta ) \left( \int _{\zeta '\in \mathbb {R}} \varphi _1 (\zeta ') g_1 (\zeta ',s;z,0) \; d\zeta ' \right) d \zeta ,\\ \mathscr {R}_{\varphi _2}(s) \mathop {=}\limits ^{\mathrm{def}}&\mathbb {E}[\varphi _2 (c(\tau ),\hbox {w}_T(\tau ))\varphi _2 (c({\tau +s}),\hbox {w}_T({\tau +s}))] \int _{\mathbb {R}^2} \varphi _2 (\zeta ) \nu _2 (\zeta ) \left( \int _{\zeta '\in \mathbb {R}^2} \varphi _2 (\zeta ') g_2 (\zeta ',s;z,0) \; d\zeta ' \right) d \zeta . \end{aligned}$$

Their time integrals are the power spectral densities:

$$\begin{aligned} \begin{aligned} \mathbb {S}_{u_T} (0)&\mathop {=}\limits ^{\mathrm{def}}2 \int _0^\infty \mathscr {R}_{\varphi _1}(s) ds, \\ \mathbb {S}_{\mathrm{w}_T} (0)&\mathop {=}\limits ^{\mathrm{def}}2 \int _0^\infty \mathscr {R}_{\varphi _2}(s) ds,\\ \mathbb {S}_{u_T}^{\cos } (\omega _0)&\mathop {=}\limits ^{\mathrm{def}}2 \int _0^\infty \mathscr {R}_{\varphi _1}(s) C^0 (\omega _0 s) ds,\\ \mathbb {S}_{u_T}^{\sin } (\omega _0)&\mathop {=}\limits ^{\mathrm{def}}2 \int _0^\infty \mathscr {R}_{\varphi _1}(s) S^0 (\omega _0 s) ds,\\ \mathbb {S}_{\mathrm{w}_T}^{\cos } (\omega _0)&\mathop {=}\limits ^{\mathrm{def}}2 \int _0^\infty \mathscr {R}_{\varphi _2}(s) C^0 (\omega _0 s) ds,\\ \mathbb {S}_{\mathrm{w}_T}^{\sin } (\omega _0)&\mathop {=}\limits ^{\mathrm{def}}2 \int _0^\infty \mathscr {R}_{\varphi _2}(s) S^0 (\omega _0 s) ds, \end{aligned} \end{aligned}$$

which can be readily found from the Dryden Model. We also define the (l, j)th element:

$$\begin{aligned} {\mathcal {S}}^{\cos ,l}_{u_T,j} (\omega _0)&\mathop {=}\limits ^{\mathrm{def}}\int _0^\infty \mathscr {R}_{\varphi _1}(s) C^0 (\omega _0 s) \frac{\partial {\psi _s^{l}(y)}}{\partial y_j}|_{y=0} \ ds, \\ {\mathcal {S}}^{\sin ,l}_{u_T,j} (\omega _0)&\mathop {=}\limits ^{\mathrm{def}}\int _0^\infty \mathscr {R}_{\varphi _1}(s) S^0 (\omega _0 s) \frac{\partial {\psi _s^{l}(y)}}{\partial y_j}|_{y=0} \ ds. \end{aligned}$$

We define the various damped spectra as follows:

$$\begin{aligned} \mathbb {S}_{u_T}^{\cos , \lambda _i} (\omega _0)&\mathop {=}\limits ^{\mathrm{def}}2 \int _0^\infty e^{\lambda _i s} \mathscr {R}_{\varphi _1}(s) C^0 (\omega _0 s) ds, \\ \mathbb {S}_{u_T}^{\sin , \lambda _i} (\omega _0)&\mathop {=}\limits ^{\mathrm{def}}2 \int _0^\infty e^{\lambda _i s} \mathscr {R}_{\varphi _1}(s) S^0 (\omega _0 s) ds \end{aligned}$$

for $i= 1,\ldots ,4$, and

$$\begin{aligned} \mathbb {S}_{u_T}^{\cos , \kappa } (\omega _0)&\mathop {=}\limits ^{\mathrm{def}}2 \int _0^\infty e^{-\kappa s} \mathscr {R}_{\varphi _1}(s) C^0 (\omega _0 s) ds, \\ \mathbb {S}_{u_T}^{\sin , \kappa } (\omega _0)&\mathop {=}\limits ^{\mathrm{def}}2 \int _0^\infty e^{-\kappa s} \mathscr {R}_{\varphi _1}(s) S^0 (\omega _0 s) ds. \end{aligned}$$

Thus,

$$\begin{aligned} {\mathcal {S}}^{\cos ,l}_{u_T,j} (\omega _0)&= \begin{bmatrix} \frac{1}{8} [\mathbb {S}_{u_T}^{\cos , \kappa } (\omega _0-\gamma ) + \mathbb {S}_{u_T}^{\cos , \kappa } (\omega _0+\gamma ) ]&\frac{1}{8} [\mathbb {S}_{u_T}^{\sin , \kappa } (\omega _0-\gamma )-\mathbb {S}_{u_T}^{\sin , \kappa } (\omega _0+\gamma )]&0&0&0&0 \\ \frac{1}{8} [\mathbb {S}_{u_T}^{\sin , \kappa } (\omega _0+\gamma )-\mathbb {S}_{u_T}^{\sin , \kappa } (\omega _0-\gamma )]&\frac{1}{8} [\mathbb {S}_{u_T}^{\cos , \kappa } (\omega _0-\gamma ) + \mathbb {S}_{u_T}^{\cos , \kappa } (\omega _0+\gamma )]&0&0&0&0 \\ 0&0&\frac{1}{4}\mathbb {S}_{u_T}^{\cos , \lambda _1} (\omega _0)&0&0&0 \\ 0&0&0&\frac{1}{4}\mathbb {S}_{u_T}^{\cos , \lambda _2} (\omega _0)&0&0 \\ 0&0&0&0&\frac{1}{4}\mathbb {S}_{u_T}^{\cos , \lambda _3} (\omega _0)&0 \\ 0&0&0&0&0&\frac{1}{4}\mathbb {S}_{u_T}^{\cos , \lambda _4} (\omega _0) \end{bmatrix} , \\ {\mathcal {S}}^{\sin ,l}_{u_T,j} (\omega _0)&= \begin{bmatrix} \frac{1}{8} [\mathbb {S}_{u_T}^{\sin , \kappa } (\omega _0-\gamma ) + \mathbb {S}_{u_T}^{\sin , \kappa } (\omega _0+\gamma ) ]&\frac{1}{8} [\mathbb {S}_{u_T}^{\cos , \kappa } (\omega _0+\gamma )-\mathbb {S}_{u_T}^{\cos , \kappa } (\omega _0-\gamma )]&0&0&0&0 \\ \frac{1}{8} [\mathbb {S}_{u_T}^{\cos , \kappa } (\omega _0-\gamma )-\mathbb {S}_{u_T}^{\cos , \kappa } (\omega _0+\gamma ) ]&\frac{1}{8} [\mathbb {S}_{u_T}^{\sin , \kappa } (\omega _0-\gamma ) + \mathbb {S}_{u_T}^{\sin , \kappa } (\omega _0+\gamma )]&0&0&0&0 \\ 0&0&\frac{1}{4} \mathbb {S}_{u_T}^{\sin , \lambda _1} (\omega _0)&0&0&0 \\ 0&0&0&\frac{1}{4} \mathbb {S}_{u_T}^{\sin , \lambda _2} (\omega _0)&0&0 \\ 0&0&0&0&\frac{1}{4} \mathbb {S}_{u_T}^{\sin , \lambda _3} (\omega _0)&0 \\ 0&0&0&0&0&\frac{1}{4} \mathbb {S}_{u_T}^{\sin , \lambda _4} (\omega _0) \end{bmatrix}. \end{aligned}$$

Now, the partial differential equation (7.5) is written in terms of these power spectral densities. The homogenized generator $\mathscr {L}^{\dagger \dagger }$ will be an operator that depends only on the two dimensional slow variables $x_{\tau }$, hence the test functions associated with $\mathscr {L}^{\dagger \dagger }$ will be of the form $f(x_{\tau })$. Therefore, let f be a smooth function of x only, and the generator that produces the slow process is given by

$$\begin{aligned} \mathscr {L}^{\dagger \dagger } \mathop {=}\limits ^{\mathrm{def}}\sum _{i=1}^2 {\bar{b}}_i(x) \frac{\partial }{\partial x_i} + \frac{1}{2} \sum _{i,j=1}^2 {\hat{a}}_{ij}(x) \frac{\partial ^2 }{\partial x_i \partial x_j } \end{aligned}$$

(7.6)

with the homogenized coefficients given by

$$\begin{aligned} {\bar{b}}_i(x)= x_k\left( \beta \pi ^{\beta }_{ik} + (x_1^2 +x_2^2 ) \pi ^{\bar{g}}_{ik}\right. + \frac{1}{8}\left[ \pi ^1_{ik} \mathbb {S}_{u_T}^{\cos } (2 \omega _0) +\pi ^2_{ik} \mathbb {S}_{u_T}^{\sin } (2 \omega _0) + \pi ^3_{ik} \mathbb {S}_{u_T} (0) \right] +\frac{1}{8}\left[ \pi ^4_{ik} \mathbb {S}_{u_T}^{\cos ,\kappa } (\omega _0+\gamma ) + \pi ^5_{ik} \mathbb {S}_{u_T}^{\cos ,\kappa } (\omega _0-\gamma ) \right. \left. + \pi ^6_{ik} \mathbb {S}_{u_T}^{\sin ,\kappa } (\omega _0+\gamma ) + \pi ^7_{ik} \mathbb {S}_{u_T}^{\sin ,\kappa } (\omega _0-\gamma )\right] \left. + \frac{1}{4}\left[ \sum _{r=1}^4 \pi _{ik}^{\sin , \lambda _r} \mathbb {S}_{u_T}^{\sin ,\lambda _r} (\omega _0) + \sum _{r=1}^4 \pi _{ik}^{\cos , \lambda _r} \mathbb {S}_{u_T}^{\cos ,\lambda _r} (\omega _0)\right] \right) \end{aligned}$$

and

$$\begin{aligned} {\hat{a}}_{ij} (x)= & {} \frac{x_1^2 +x_2^2 }{8} \left[ \pi ^1_{ij} \mathbb {S}_{u_T}^{\cos } (2 \omega _0) + \pi ^2_{ij} \mathbb {S}_{u_T}^{\sin } (2 \omega _0) \right] \\&+ \frac{\wp }{2} \left[ \pi ^{8}_{ij} \mathbb {S}^{\cos }_{\mathrm{w}_T} (\omega _0) + \pi ^{9}_{ij} \mathbb {S}^{\sin }_{\mathrm{w}_T} (\omega _0) \right] \\&+ \frac{\mathbb {S}_{u_T} (0) }{4} \left( \pi ^{10}_{ij} x_1^2 + \pi ^{11}_{ij} x_2^2 + \pi ^{12}_{ij} x_1 x_2 \right) , \end{aligned}$$

where the definitions of the various $2 \times 2$ matrices $\pi ^{r}$ are given in “Appendix 3”.

Appendix 3

$$\begin{aligned} &\pi ^\beta= \begin{bmatrix} \delta '&\gamma ' \\ -\gamma '&\delta ' \end{bmatrix}, \ \pi ^{\bar{g}} = \begin{bmatrix} -\bar{R}&-\tilde{R} \\ \tilde{R}&-\bar{R} \end{bmatrix}, \\ &\pi ^1= \begin{bmatrix} \kappa _2&0 \\ 0&\kappa _2 \end{bmatrix},\ \pi ^2 = \begin{bmatrix} 0&\kappa _2 \\ -\kappa _2&0 \end{bmatrix}, \\ &\pi ^3= \begin{bmatrix} \kappa _1 - \kappa _{7}&2\sqrt{\kappa _1 \kappa _{7}} \\ -2\sqrt{\kappa _1 \kappa _{7}}&\kappa _1 - \kappa _{7} \end{bmatrix}, \ \pi ^4 = \begin{bmatrix} \kappa _3&\kappa _5 \\ -\kappa _5&\kappa _3 \end{bmatrix}, \\ &\pi ^5= \begin{bmatrix} \kappa _4&\kappa _6 \\ -\kappa _6&\kappa _4 \end{bmatrix}, \ \pi ^6 = \begin{bmatrix} -\kappa _5&\kappa _3 \\ -\kappa _3&-\kappa _5 \end{bmatrix}, \\ &\pi ^7= \begin{bmatrix} -\kappa _6&\kappa _4 \\ -\kappa _4&-\kappa _6 \end{bmatrix}, \ \pi ^{\sin , \lambda _r} = \begin{bmatrix} \kappa ^{\sin , \lambda _r}&\kappa ^{\cos , \lambda _r} \\ -\kappa ^{\cos , \lambda _r}&\kappa ^{\sin , \lambda _r} \end{bmatrix}, \\ &\pi ^{\cos , \lambda _r}= \begin{bmatrix} \kappa ^{\cos , \lambda _r}&-\kappa ^{\sin , \lambda _r} \\ \kappa ^{\sin , \lambda _r}&\kappa ^{\cos , \lambda _r} \end{bmatrix}, \ \pi ^{8} = \begin{bmatrix} \kappa _{8}&0 \\ 0&\kappa _{8} \end{bmatrix}, \\ &\pi ^{9}= \begin{bmatrix} 0&\kappa _{8} \\ -\kappa _{8}&0 \end{bmatrix}, \ \pi ^{10} = \begin{bmatrix} \kappa _1&-\sqrt{\kappa _1\kappa _{7}} \\ -\sqrt{\kappa _1\kappa _{7}}&\kappa _7 \end{bmatrix}, \\ &\pi ^{11}= \begin{bmatrix} \kappa _7&\sqrt{\kappa _1\kappa _{7}} \\ \sqrt{\kappa _1\kappa _{7}}&\kappa _1 \end{bmatrix}, \ \pi ^{12} = \begin{bmatrix} 2\sqrt{\kappa _1\kappa _{7}}&\kappa _1-\kappa _7 \\ \kappa _1-\kappa _7&- 2\sqrt{\kappa _1\kappa _{7}} \end{bmatrix},\\ &\delta' = \frac{d_{11}+d_{22}}{2},\ \gamma ' = \frac{d_{12}-d_{21}}{2},\ d_{ij} \in D,\\ &\kappa _1= ( k_{11} + k_{22})^2, \ \kappa _2 = \left\{ (k_{11} - k_{22})^2 + ( k_{12} + k_{21})^2 \right\} , \\ & \kappa _3= (m_{22}-m_{11})(n_{22}-n_{11}) + (m_{12}+m_{21})(n_{12}+n_{21}), \\ & \kappa _4= (m_{22}+m_{11})(n_{22}+n_{11}) - (m_{12}-m_{21})(n_{12}-n_{21}), \\ & \kappa _5= (m_{12}+m_{21})(n_{22}-n_{11}) - (m_{22}-m_{11})(n_{12}+n_{21}), \\ & \kappa _6= (m_{22}+m_{11})(n_{12}-n_{21}) + (m_{12}-m_{21})(n_{22}+n_{11}), \end{aligned}$$

where $m_{ij} \in \bar{M}$ and $n_{ij} \in \bar{N}$,

$$\begin{aligned} \kappa ^{\sin , \lambda _r}= & {} \left\{ -m_{1(r+2)}n_{(r+2)2} + m_{2(r+2)}n_{(r+2)1} \right\} , \\ \kappa ^{\cos , \lambda _r}= & {} \left\{ m_{1(r+2)}n_{(r+2)1} + m_{2(r+2)}n_{(r+2)2} \right\} , \end{aligned}$$

for $r = 1,\ldots ,4$,

$$\begin{aligned} \kappa _{7}= & {} (k_{12} - k_{21} )^2,\ k_{ij} \in \bar{K}, \\ \kappa _{8}= & {} \left\{ f_1^2 + f_2^2 \right\} , \end{aligned}$$

and

$$\begin{aligned} \bar{R}= & {} - \frac{3}{8} \left\{ {\hat{g}}_{1:111} +{\hat{g}}_{1:122} + {\hat{g}}_{2:112} + {\hat{g}}_{2:222} \right\} , \\ \tilde{R}= & {} - \frac{3}{8} \left\{ {\hat{g}}_{1:112} +{\hat{g}}_{1:222} - {\hat{g}}_{2:111} - {\hat{g}}_{2:122} \right\} . \end{aligned}$$