1 Introduction

As special composites whose composition changes continuously through the thickness of structure, functionally graded materials (FGMs) have received significant attention due to high performance, novel thermo-mechanical properties and resistance to ultra-high temperature. These required function enable FGMs to be widely used in various engineering fields [1, 2]. The mechanical behavior of structures made of FGMs have been of primary interest in several researches and engineering applications. Rastgo et al. [3] obtained the critical thermal buckling load using the stability equations and the Galerkin method for a curved beam made of FGM with doubly symmetric cross section. Li et al. [4] obtained the thermal buckling and postbuckling response of transversely and non-uniformly heated FGM Timoshenko beams with fixed–fixed edges through the use of the shooting method. Xiang and Yang [5] studied free and forced vibration of a laminated functionally graded beam of variable thickness subjected to initial excited thermal stresses. The effect of arbitrary boundary conditions was explored and one-dimensional steady heat conduction in the thickness direction of beam before undergoing dynamic deformation was taken into account.

With the development of material technology, the application of FGMs has been extended in devices and structures at nanoscale [6–10]. In such applications, small scale effects play an important role in mechanical characteristics, so it is necessary to consider these effects.

The nano-sized structures have a high surface-to-volume ratio and the surface stress effects play an important in their mechanical responses. Hence, the surface stress effect is one of the most important size effects to be considered in the analysis of the mechanical characteristics of nanostructures [11–13]. The reduced coordination of atoms near a free surface induces a corresponding redistribution of electronic charge that alters the binding situation [14]. As a result, excess surface energy as a superficial energy term will be attained by these atoms since a surface can be interpreted as a layer to which certain energy is attached. Moreover, the compressive and tension residual stresses may be induced in the bulk part of nanoscale structures due to the positive and negative surface stresses, respectively [15–17]. Consequently, a self-instability may accrue in the nanoscale structures because of the compressive residual stresses even in the absence of external mechanical loads [18]. Therefore, to predict the mechanical characteristics and operation of nanostructures and nanodevices accurately and subsequently to avoid the self-instability, investigation of the surface stress effects and determining the critical size of nanoscale structures are necessary.

Continuum mechanics has been proven to have the capability for solving different problems as an efficient approach corresponding to various length scales. However, at nanoscale, the length scale is much lower than usual scales considered in continuum models. Therefore, many size-dependent continuum theories have been proposed and employed to take size effects into account [19–39]. For example, Şimşek and Yurtcu [37] presented an analytical nonlocal Timoshenko beam model for bending and buckling of FG nanobeams. Recently, Barretta et al. [38] developed a variational formulation for FG nanobeams based on the nonlocal elasticity and Euler–Bernoulli beam theories. Ansari et al. [39] numerically investigated the size-dependent thermo-electro-mechanical free vibration of postbuckled piezoelectric nanobeams based on a nonlocal Timoshenko beam model. A theoretical concept based on the continuum mechanics including surface stress effects was developed by Gurtin and Murdoch [17, 40], in which the surface is simulated as a mathematical membrane of zero thickness with different material properties from the underlying bulk which is completely covered by the membrane. Gurtin–Murdoch model has the capability to incorporate the surface stress effects into the mechanical response of nanostructures as it has been applied in many studies conducted for various problems about the mechanical behaviors of structures at nanoscale.

Mogilevskaya et al. [41] considered a two-dimensional problem of multiple interacting circular nano-inhomogeneities or nano-pores based on a continuum theory of elastic material surface of Gurtin–Murdoch model. Lü et al. [42] developed a general, global theory for nano-scaled functionally graded films considering the effect of surface stress using surface elasticity theory and Kirchhoff plate theory. Intarit et al. [43] presented analytical solutions for shear and opening dislocations in an elastic half-plane with surface stresses on the basis of Gurtin–Murdoch continuum theory of elastic material surfaces. Kushch et al. [44] obtained a complete solution for the problem of multiple interacting spherical inhomogeneities with a Gurtin–Murdoch interface model including both surface tension and surface stiffness effects. Ansari et al. [45] proposed non-classical plate model to evaluate the influence of surface stress on the vibrational response of circular nanoplates using surface elasticity theory.

To mention some examples about the surface stress effect on the mechanical responses of nanobeams, Ansari and Sahmani [46] presented an exact solution for bending and buckling behaviors of nanobeams including surface stress effect. To this end, they applied Gurtin–Murdoch elasticity theory to the various types of beam theories. An attempt was made by Ansari et al. [47] to numerically investigate the postbuckling response of Euler–Bernoulli nanobeams with the consideration of the surface stress effect using Gurtin–Murdoch elasticity theory. Hashemi and Nazemnezhad [48] studied analytically nonlinear free vibration of simply-supported FG nanobeams considering surface effects. Ansari et al. [49] investigated postbuckling characteristics of Timoshenko nanobeams based on the surface elasticity theory. Sharabiani and Yazdi [50] analyzed the nonlinear free vibration of FG nanobeams based on Euler–Bernoulli beam model with surface effects by employing the direct numerical integration method. Recently, Ansari et al. [51] investigated the forced vibration response of Euler–Bernoulli FG nanobeams subjected to thermal loading by considering the local geometrical nonlinearity based on von Karman relation and surface stress effect using Gurtin–Murdoch elasticity theory. Zhang et al. [52] investigated the surface stress and piezoelectric effects on the buckling of piezoelectric nanofilms. Wang et al. [53] developed a refined Euler–Bernoulli beam model to examine the influences of chirality and surface stresses on the bending and buckling of chiral nanowires. Also, Zhang et al. [54] studied the transverse vibration of axially compressed embedded nanowires using the higher-order surface stress theory and Euler–Bernoulli beam model.

In the present investigation, by using concept of physical neutral surface and Euler–Bernoulli beam theory, a nonlinear size-dependent beam model based on Gurtin–Murdoch elasticity theory is used in order to predict the effect of surface stress on the postbuckling characteristics of FG nanobeams under different temperature changes. To this end, the surface elasticity theory is implemented into the classical Euler–Bernoulli beam theory. An analytical solution is presented to obtain postbuckling equilibrium curves of FG nanobeams with various boundary conditions in the presence of surface stress effect.

2 Mathematical formulations

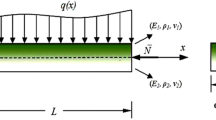
An FG nanobeam of length L and thickness h that is made from a mixture of ceramics and metals is considered as shown in Fig. 1. It is assumed that the materials at bottom surface (z = −h/2) and top surface (z = h/2) of the nanobeam are ceramics and metals, respectively. In addition to the energies associated with the bulk part, because of the considerable cohesive force between the atoms on the surface of the nanostructure, the surface energy effect should be taken into account. One way to consider such effect in a continuum manner is using the Gurtin–Murdoch surface elasticity theory [17, 32] by which the surface of the nanobeam is modeled as a two-dimensional membrane with zero thickness linking to the underlying bulk material without slipping. In the present study, a non-classical Euler–Bernoulli beam model developed within the framework of the Gurtin–Murdoch approach [51] is utilized to investigate the postbuckling of FG nanobeams subjected to external compressive axial and thermal loadings with considering the surface energy effect.

Fig. 1
figure 1

A schematic view of FG nanobeam including surface layers

Full size image

2.1 Effective material properties of FG nanobeam

The effective material properties of the FG nanobeam such as Young’s modulus (E), surface Lamé’s constants (λ s and μ s), Poisson’s ratio (v), residual surface stress (τ s), thermal coefficient (α), and thermal conductivity (K) can be determined as follows

$$E\left( z \right) = \left( {E_{m} - E_{c} } \right)V_{f} \left( z \right) + E_{c}$$
(1a)
$$\lambda^{s} \left( z \right) = \left( {\lambda_{m}^{s} - \lambda_{c}^{s} } \right)V_{f} \left( z \right) + \lambda_{c}^{s}$$
(1b)
$$\mu^{s} \left( z \right) = \left( {\mu_{m}^{s} - \mu_{c}^{s} } \right)V_{f} \left( z \right) + \mu_{c}^{s}$$
(1c)
$$\tau^{s} \left( z \right) = \left( {\tau_{m}^{s} - \tau_{c}^{s} } \right)V_{f} \left( z \right) + \tau_{c}^{s}$$
(1d)
$$\nu \left( z \right) = \left( {\nu_{m} - \nu_{c} } \right)V_{f} \left( z \right) + \nu_{c}$$
(1e)
$$\alpha \left( z \right) = \left( {\alpha_{m} - \alpha_{c} } \right)V_{f} \left( z \right) + \alpha_{c}$$
(1f)
$$K\left( z \right) = \left( {K_{m} - K_{c} } \right)V_{f} \left( z \right) + K_{c}$$
(1g)

It should be noted that the subscripts m and c stand for metal and ceramic phases, respectively. In order to describe the variation of the volume fraction of constituents, various types of functions can be utilized. In the present study, a simple power law function is employed as following to describe the volume fraction

$$V_{f} \left( z \right) = \left( {\frac{1}{2} + \frac{z}{h}} \right)^{k}$$
(2)

where k is the volume fraction exponent.

2.2 Temperature distribution

The thin FG nanobeam is considered in which the temperature values at ceramic-rich and metal-rich surfaces are equal to T c and T m , respectively. The temperature distribution can be obtained by solving the following heat conduction equation corresponding to the given boundary conditions

$$K\frac{{d^{2} T}}{{dz^{2} }} = 0 ,\quad T\left( {\frac{h}{2}} \right) = T_{m} , \quad T\left( { - \frac{h}{2}} \right) = T_{c}$$
(3)

Applying Eq. (3) along the FG nanobeam thickness results in a linear temperature distribution as follows

$$T = \left( {\frac{{T_{m} + T_{c} }}{2}} \right) + \left( {T_{m} - T_{c} } \right)\frac{z}{h}$$
(4)

2.3 Size-dependent governing equations

The developed size-dependent beam model by Ansari et al. [51] in the context of Euler–Bernoulli beam theory and Gurtin–Murdoch elasticity theory is considered. By adding the term corresponding to compressive axial load N 0 and dropping the inertia terms, the stability equations can be expressed as

$$\left( {N_{xx} + N_{xx}^{s} } \right)^{{\prime }} = 0$$
(5a)
$$\left( {M_{xx} + M_{xx}^{s} } \right)^{\prime \prime } + \left[ {\left( {N_{xx} + N_{xx}^{s} } \right)W^{\prime } } \right]^{\prime } = 0$$
(5b)

where the prime symbol denotes derivative with respect to x.

Additionally, the related boundary conditions of the nanobeam at x = 0 and x = L are expressed as [51]

$$\left( {N_{xx} + N_{xx}^{s} } \right) = 0 \quad or\quad \delta U_{0} = 0$$
(6a)
$$\left( {N_{xx} + N_{xx}^{s} } \right)W^{{\prime }} + \left( {M_{xx} + M_{xx}^{s} } \right)^{{\prime }} = 0\quad or\quad \delta W = 0$$
(6b)
$$M_{xx} + M_{xx}^{s} = 0 \quad or\quad \delta W^{{\prime }} = 0$$
(6c)

in which U 0 and W denote the displacement of neutral axis in the longitudinal and lateral directions, respectively.

The force resultants and bending moments corresponding to bulk and surface parts are defined in “Appendix”.

Integrating Eq. (6a) with respect to x, one will have

$$N_{xx} + N_{xx}^{s} = b_{1}$$
(7)

Or

$$k_{1} \left( {U_{0}^{{\prime }} + \frac{1}{2}\left( {W^{{\prime }} } \right)^{2} } \right) + k_{2} W^{{{\prime \prime }}} - N_{T} + k_{4} \left( {1 - \frac{1}{2}\left( {W^{{\prime }} } \right)^{2} } \right) = b_{1} .$$
(8)

Besides, integrating Eq. (8) once more yields

$$U_{0} = - \left\{ {\frac{1}{2}\mathop \int \limits_{ }^{ } \left( {W^{\prime } } \right)^{2} dx + \frac{{k_{2} }}{{k_{1} }}W^{\prime } - \frac{1}{{k_{1} }}\mathop \int \limits_{ }^{ } N_{T} dx + \frac{{k_{4} }}{{k_{1} }}\mathop \int \limits_{ }^{ } \left( {1 - \frac{1}{2}\left( {W^{\prime } } \right)^{2} } \right)dx} \right\} + \frac{{b_{1} }}{{k_{1} }}x + \frac{{b_{2} }}{{k_{1} }}$$
(9)

Assuming that the FG nanobeam is constrained from movement at x = 0 and that an external compressive axial load N 0 is applied at x = L, it can be expressed that \(U_{0} \left( 0 \right) = W\left( 0 \right) = W\left( L \right) = 0\), and \(U_{0} \left( L \right) = - N_{0} L/k_{1}\). By using the above boundary condition, one can obtain

$$b_{1} = - N_{0} + \left( {\frac{{\left( {k_{1} - k_{4} } \right)}}{2L}\mathop \int \limits_{ 0}^{ L} \left( {W^{{\prime }} } \right)^{2} dx + \frac{{k_{2} }}{L}\left( {W^{{\prime }} \left( L \right) - W^{{\prime }} \left( 0 \right)} \right) - N_{T} + k_{4} } \right)$$
(10a)
$$b_{2} = k_{2} W^{{\prime }} \left( 0 \right)$$
(10b)

As a result, one will have

$$\left( {M_{xx} + M_{xx}^{s} } \right)^{\prime \prime } + \left[ {\left\{ {\frac{{\left( {k_{1} - k_{4} } \right)}}{2L}\mathop \int \limits_{ 0}^{ L} \left( {W^{\prime } } \right)^{2} dx + \frac{{k_{2} }}{L}\left( {W^{\prime } \left( L \right) - W^{\prime } \left( 0 \right)} \right) - N_{T} + k_{4} } \right\} - N_{0} } \right]W^{\prime \prime } = 0$$
(11)

By inserting the bending moments defined in “Appendix” into the above equation, the governing equation can be expressed as

$$\begin{aligned} & \left( {\left( {\frac{{\left( {k_{1} - k_{3} } \right)}}{2L}\mathop \int \limits_{ 0}^{ L} \left( {W^{{\prime }} } \right)^{2} dx + \frac{{k_{2} }}{L}\left( {W^{{\prime }} \left( {L,t} \right) - W^{{\prime }} \left( {0,t} \right)} \right) - N_{T} + k_{3} } \right) - N_{0} } \right)W^{{{\prime \prime }}} \\ & \quad + k_{4} \left( { - \frac{{\left( {k_{1} - k_{3} } \right)}}{{k_{1} }}\left( {W^{{{\prime \prime 2}}} + W^{{\prime }} W^{{{\prime \prime \prime }}} } \right) - \frac{{k_{2} }}{{k_{1} }}W^{{{\prime \prime \prime \prime }}} } \right) \\ & \quad - \left( {k_{5} + k_{7} } \right)W^{{{\prime \prime \prime \prime }}} \left( {k_{4} - k_{6} } \right)\left( {W^{{{\prime \prime }2}} + W^{{\prime }} W^{{{\prime \prime \prime }}} } \right) = 0 \\ \end{aligned}$$
(12)

where

$$\begin{aligned} k_{1} & = A_{11} + 2A_{11}^{s} + b{\bar{\mathcal{A}}}^{s} , \quad k_{2} = - B_{11} - 2B_{11}^{s} - \frac{bh}{2}\Delta {\mathcal{A}}^{s} + \frac{{A_{44} }}{2}\Delta \tau^{s} + \frac{{B_{44} }}{h}\bar{\tau }^{s} , \\ k_{3} & = b\bar{\tau }^{s} + 2\theta_{11}^{s} , \quad k_{4} = B_{11} + 2B_{11}^{s} + \frac{bh}{2}\Delta {\mathcal{A}}^{s} , k_{5} = D_{11} - \frac{{B_{44} }}{2}\Delta \tau^{s} - \frac{{D_{44} }}{h}\bar{\tau }^{s} , \\ k_{6} & = \frac{bh}{2}\Delta \tau^{s} + 2\theta_{22}^{s} ,\quad k_{7} = \frac{{bh^{2} }}{4}{\bar{\mathcal{A}}}^{s} + 2D_{11}^{s} \\ \end{aligned}$$
(13)

Now, introducing the following non-dimensional parameters

$$\hat{x} = \frac{x}{L},\quad w = \frac{W}{h},\quad \beta = \frac{h}{L}$$
(14)

the non-dimensional governing equation can be obtained as

$$\left( { - \alpha_{2} \mathop \int \limits_{0}^{1} \left( {w^{{\prime }} } \right)^{2} d\hat{x} - \alpha_{3} \left[ {w^{{\prime }} \left( 1 \right) - w^{\prime}\left( 0 \right)} \right] - \bar{H} + P} \right)w^{{{\prime \prime }}} + \alpha_{1} w^{iv} =0$$
(15)

where

$$\alpha_{1} = \beta^{2} \left( {\frac{{k_{5} + k_{7} + \frac{{k_{4} k_{2} }}{{k_{1} }}}}{{A_{11m} h^{2} }}} \right),\quad \alpha_{2} = \beta^{2} \left( {\frac{{k_{1} - k_{3} }}{{2A_{11m} }}} \right),\quad \alpha_{3} = \beta^{2} \frac{{k_{2} }}{{hA_{11m} }} ,\quad \bar{H} = \frac{{k_{3} }}{{A_{11m} }}, \quad P = \frac{{N_{0} + N_{T} }}{{A_{11m} }}$$
(16)

in which A 11m is the value A 11 of a homogeneous metal nanobeam.

Moreover, the non-dimensional boundary conditions can be obtained in the following form for clamped–clamped boundary conditions

$$w\left( 0 \right) = w\left( 1 \right) = 0,w^{{\prime }} \left( 0 \right) = w^{{\prime }} \left( 1 \right) = 0$$
(17)

and it can be written for clamped-simply supported condition as

$$w\left( 0 \right) = w\left( 1 \right) = 0, \quad w^{{\prime }} \left( 0 \right) = w^{{{\prime \prime }}} \left( 1 \right) = 0$$
(18)

As well for simply supported-simply supported end condition as

$$w\left( 0 \right) = w\left( 1 \right) = 0, \quad w^{{{\prime \prime }}} \left( 0 \right) = w^{{{\prime \prime }}} \left( 1 \right) = 0$$
(19)

3 Postbuckling configuration of FG nanobeams

The non-dimensional governing Eq. (15) can be expressed as the following ordinary differential equation for the buckling problem

$$w_{s}^{iv} + \gamma^{2} w_{s}^{{{\prime \prime }}} = 0$$
(20)

where γ 2 represents the critical buckling load which can be introduced as

$$\gamma^{2} = \frac{{P - \bar{H}}}{{\alpha_{1} }} - \frac{{\alpha_{2} }}{{\alpha_{1} }}\left( {\mathop \int \limits_{0}^{1} \left( {w_{s}^{{\prime }} } \right)^{2} d\hat{x}} \right) - \frac{{\alpha_{3} }}{{\alpha_{1} }}\left( {w_{s}^{{\prime }} \left| {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right.} \right)$$
(21)

The closed-form solution for Eq. (20) gets the following form

$$w_{s} = C_{1} + C_{2} \hat{x} + C_{3} \cos \left( {\gamma \hat{x}} \right) + C_{4} \sin \left( {\gamma \hat{x}} \right)$$
(22)

in which \(C_{i} , i = 1,2, \ldots ,4\) are the unknown coefficients.

By inserting the boundary conditions in Eq. (22), an eigenvalue problem is obtained, whose characteristic equation can be derived easily by setting the coefficient matrix to zero. After that, solving the characteristic equation results in the critical buckling loads and the buckling mode shapes. Therefore, the following equations define the characteristic equation and the relevant buckling mode shapes of a clamped–clamped nanobeam as

$$2 - 2\cos \left( \gamma \right) - \gamma \sin \left( \gamma \right) = 0$$
(23a)
$$w_{s} = c\left( {1 - \frac{1 - \cos \left( \gamma \right)}{\gamma - \sin \left( \gamma \right)}\gamma \hat{x} - \cos \left( {\gamma \hat{x}} \right) + \frac{1 - \cos \left( \gamma \right)}{\gamma - \sin \left( \gamma \right)}\sin \left( {\gamma \hat{x}} \right)} \right)$$
(23b)

Accordingly, through inserting the clamped-simply supported end conditions, one will have

$$\sin \left( \gamma \right) - \gamma \cos \left( \gamma \right) = 0$$
(24a)
$$w_{s} = c\left( {1 - \frac{\gamma \cos \left( \gamma \right)}{\sin \left( \gamma \right)}\hat{x} - \cos \left( {\gamma \hat{x}} \right) + \frac{\cos \left( \gamma \right)}{\sin \left( \gamma \right)}\sin \left( {\gamma \hat{x}} \right)} \right)$$
(24b)

In addition, the characteristic equation and relevant mode shapes of a simply supported-simply supported nanobeam take the following form as

$$\sin \left( \gamma \right) = 0$$
(25a)
$$w_{s} = c\sin \left( {n\pi \hat{x}} \right)$$
(25b)

in which c is a constant.

It should be noted that by solving the linear counterpart of Eq. (15), the non-dimensional critical buckling load corresponding to the various boundary conditions can be calculated. Considering Eqs. (21), (23b), (24b) and (25b), the amplitude of the buckled FG nanobeams associated with the applied compressive axial load can be obtained.

4 Results and discussion

In this section, the postbuckling equilibrium curves of FG nanobeams subjected to thermal environment with the consideration of surface stress effect are demonstrated to indicate the influences of surface stress and thermal conditions on the nonlinear postbuckling behavior of nanobeams corresponding to different system parameters. The material properties of the FG nanobeam are tabulated in Table 1. Also, the parameter of normalized applied axial load which is used in the numerical results is defined as

$$Normalized\,applied\,axial\,load = \frac{Applied\,axial\,load\,with\,surface\,stress\,effect}{Applied\,axial\,load\,without\,surface\,stress\,effect}$$
(26)

The critical buckling loads of FG nanobeams under different types of boundary conditions corresponding to the first three buckling modes are given in Table 2. Among various boundary conditions, the nanobeams with simply supported-simply supported and clamped–clamped end supports have the minimum and maximum critical buckling loads, respectively.

Table 1 Material properties of the FG nanobeam constituents [56–58]
Full size table
Table 2 Critical buckling loads (roots of characteristic equations) for different boundary conditions
Full size table

Figure 2 contains of two parts. In the first one, the postbuckling equilibrium paths of FG nanobeams with various material property gradient indexes are plotted corresponding to the first buckling mode. It can be seen that by increasing the value of k, the equilibrium path of FG nanobeam shifts to right which means that the stiffness of nanobeam increases. In the second part of the figure, the variation of normalized applied axial load with deflection of FG nanobeam with different values of k is depicted. It can be found that the influence of material property gradient index on the normalized applied axial load is more significant for lower values of deflection. Moreover, it is observed that by increasing the deflection of FG nanobeam, the value of normalized applied axial load decreases and it tends to the value of 1. In other words, the effect of surface stress on the postbuckling behavior diminishes by increasing the deflection of nanobeam.

Fig. 2
figure 2

a Postbuckling paths of the first buckling mode for FG nanobeam with different material property gradient indexes corresponding to the classical theory, b variation of the normalized applied axial load versus maximum deflection of FG nanobeam with different material property gradient indexes \(\left( {L/h = 40,h = 1 \,{\text{nm}},\, b/h = 1,\Delta T = 300} \right)\)

Full size image

The need for considering higher buckling modes is due to the mode transitions. In the interactive buckling, a transition can happen from a stable equilibrium path to an unstable one which leads to the destruction of structure under loads lower than the critical buckling load. The interaction of different buckling modes occurs when the critical loads corresponding to the different buckling modes are close to each other [55]. This makes it necessary to determine higher buckling modes. The results shown in Figs. 3 and 4 are similar to those of Fig. 2, but they are for the second and third buckling modes, respectively. Similar anticipations observed in Fig. 2 can be seen in these figures too. Hence, it is indicated that for different buckling modes, surface stress effect on the postbuckling response of nanobeams is more prominent for lower deflections. Furthermore, this point should be said that these predictions are similar for all types of boundary conditions.

Fig. 3
figure 3

a Postbuckling paths of the second buckling mode for FG nanobeam with different material property gradient indexes corresponding to the classical theory, b variation of the normalized applied axial load versus maximum deflection of FG nanobeam with different material property gradient indexes \(\left( {L/h = 40,h = 1 \,{\text{nm}},\, b/h = 1,\Delta T = 300} \right)\)

Full size image
Fig. 4
figure 4

a Postbuckling paths of the third buckling mode for FG nanobeam with different material property gradient indexes corresponding to the classical theory, b variation of the normalized applied axial load versus maximum deflection of FG nanobeam with different material property gradient indexes \(\left( {L/h = 40,\,h = 1 \,{\text{nm}}, \,b/h = 1,\,\Delta T = 300} \right)\)

Full size image

Illustrated in Figs. 5, 6 and 7 are the postbuckling equilibrium paths of FG nanobeam with different thicknesses corresponding to the first, second and third buckling modes, respectively. In all figures, it can be observed that by increasing the thickness of nanobeam, the postbuckling equilibrium paths obtained by the classical and non-classical beam models tends to each other. In other words, surface stress effect plays more important role in the postbuckling characteristics of FG nanobeams with lower thicknesses. This pattern is the same for all types of end supports.

Fig. 5
figure 5

Postbuckling path of the first buckling mode for FG nanobeam with different thicknesses \(\left( {L/h = 40,k = 1, b/h = 1,\Delta T = 300} \right)\)

Full size image
Fig. 6
figure 6

Postbuckling path of the second buckling mode for FG nanobeam with different thicknesses \(\left( {L/h = 40,k = 1, b/h = 1,\Delta T = 300} \right)\)

Full size image
Fig. 7
figure 7

Postbuckling path of the third buckling mode for FG nanobeam with different thicknesses \(\left( {L/h = 40,k = 1, b/h = 1,\Delta T = 300} \right)\)

Full size image

Figure 8 presents the postbuckling equilibrium paths and the variation of normalized applied axial load with deflection of FG nanobeam subjected to different thermal environments. The plots are given corresponding to the first buckling mode. It is revealed that increasing the values of temperature change leads to shift the equilibrium path to right. Additionally, it causes to decrease the normalized applied axial load which means that the effect of surface stress diminishes and temperature change effect is more considerable at lower deflections. Also, similar to the observations of Figs. 2, 3 and 4, by increasing the deflection of FG nanobeams, the effect of surface stress on the postbuckling response decreases.

Fig. 8
figure 8

a Postbuckling paths of first buckling mode for FG nanobeam with different values of temperature change, b variation of normalized applied axial load versus maximum deflection of FG nanobeam with different values of temperature change \(\left( {L/h = 40,h = 1 \,{\text{nm}}, b/h = 1,k = 1} \right)\)

Full size image

5 Conclusion

The aim of present investigation was to predict the nonlinear postbuckling characteristics of FG nanobeams incorporating the effect of surface stress. A non-classical beam model on the basis of Gurtin–Murdoch elasticity theory in the framework of Euler–Bernoulli beam theory and concept of physical neutral surface was employed which has the capability to consider the effect of surface stress and von Karman-type of kinematic nonlinearity. The size-dependent nonlinear governing equations were solved analytically for different boundary conditions.

It was found that by increasing the value of material property gradient index, the equilibrium path of FG nanobeam shifts to right which means that the stiffness of nanobeam increases. In addition, it was found that the influence of material property gradient index on the normalized applied axial load is more significant for lower values of deflection. Furthermore, it was indicated that surface stress effect plays more important role in the postbuckling characteristics of FG nanobeams with lower thicknesses. Also, it was revealed that the effect of surface stress on the postbuckling behavior diminishes by increasing the deflection of nanobeam.