1 Introduction

One of the most common arterial diseases is atherosclerosis. Atherosclerosis disease is hardening of artery walls due to the growth of fatty plaques in medium and large arteries. Because fatty plaques are mainly composed of plasma lipoprotein particles such as LDL, investigation of LDL mass transfer in the artery wall is one of the important subjects in diagnosing this disease. Arterial diseases are the main cause of human deaths in most parts of the world.

In general, research activities in this field are classified into three categories: experimental, analytical and numerical methods. Wang et al. [1] studied experimentally the surface concentration of albumin in carotid artery of dog and concluded that due to Concentration Polarization (CP) phenomenon, concentration at the surface is more than its bulk value in the flow; and also as filtration velocity increases, Lumen Surface Concentration (LSC) rises. Meng et al. [2] investigated CP and showed that surface concentration strongly and inversely depends on wall shear stress (WSS), and atherosclerosis disease develops in regions with low WSS. Shukla et al. [3]; Chaturani et al. [4] and Mistra et al. [5] analytically considered blood as non-Newtonian fluid and found that the accumulation of cholesterol on artery wall increases the stenosis severity. In other studies, which are numerical studies, three different models for the artery wall are used [6]. These models include wall-free model where the artery wall is rigid and impermeable to macromolecules [7–16], fluid-wall single layer model where the artery wall is modeled as one porous domain with homogenous transfer properties [17–19] and fluid-wall multilayer model that are more complicated and divide the artery wall to more than one layer [20–27]. Each of these models is used by researchers according to whether they want to consider the effective factors on mass transfer in the lumen or wall region. Among these models, the wall-free model needs a relatively small number of parameters. This model produces good results while it is simple and there is no need to consider the flow within the artery wall. Although it cannot model the transport in the arterial wall, it would provide useful information to investigate the effective hemodynamic parameters on macromolecules surface concentration with reasonably low computational expense which make it possible to investigate the various parameters affect the LSC. By using this model, Deng et al. [14] numerically observed that under normal physiological conditions, LSC in a direct vessel is 5 to 14 %, higher than the bulk concentration and that LSC is also associated with fluid flow and changes linearly with the filtration rate and inversely with WSS. Fazli et al. [15] and Soulis and Giannoglou [16] showed that in regions with low WSS, the concentration of LDL particles is high.

On the other hand, due to stenosis in the arteries and existence of regions with low shear stress in the recirculation region, the non-Newtonian behavior of blood flow become important and it is necessary to employ the non-Newtonian models [28]. Unfortunately, macroscopic blood rheology models, such as the power law, Casson, Quemada, and Carreau-Yasuda do not provide any information on cell transport, local concentration, and wall deposition [29]. So far, the numerical results presented by researchers for mass transfer of LDL particles in blood have been based on the constant diffusion coefficient. Indeed, this coefficient cannot be constant as it is the case for viscosity when blood behaves as non-Newtonian fluid and it should be function of the shear rate, hematocrit and other factors [30].

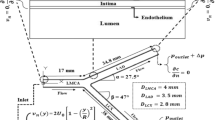
In this study, concentration of LDL near the wall of an artery with up to 60 % stenosis is obtained by means of numerical simulation. In order to get more physical and accurate results, a novel model for diffusion coefficient is introduced. The artery wall is assumed rigid and permeable to plasma. Since our goal is to investigate the parameters which affects the LSC of LDLs, the wall-free model (lumen model), where the artery wall is impermeable to macromolecules, is used for boundary condition of mass flow from the wall [6].

2 Governing equations

The blood flow is assumed laminar, steady, incompressible and fully developed and both Newtonian and non-Newtonian models are used. To simulate the flow, the non-dimensional continuity and Navier–Stokes and transfer of scalar quantity, LDL, equations are used.

$$\nabla .\varvec{u}^{\varvec{*}} = 0$$
(1)
$$\left( {\varvec{u}^{\varvec{*}} .\nabla } \right)\varvec{u}^{\varvec{*}} = - \nabla P^{*} + \nabla .\left( {\mu^{*} \nabla \varvec{u}^{\varvec{*}} } \right)$$
(2)
$$\varvec{u}^{\varvec{*}} .\nabla C^{*} = \nabla .\left( {D_{e}^{*} C^{*} } \right)$$
(3)

where \(u^{*} = \, u/U_{0}\), \( P^{*} = \, P/1/2\rho U_{0}^{2} \), \( \mu^{*} \), and \( C^{*} = \, C/C_{0} \), are non-dimensional velocity, pressure, viscosity, and LDL concentration of blood flow respectively. \( D_{e}^{*} \) is the non-dimensional effective diffusion coefficient which its value is the main concern in this paper. For the constant transport properties case, \( D_{e}^{*} \) is 2/Pe, where the Peclet number, Pe, is defined as 2U 0 R 0 /D.

In the case of Newtonian fluid, \( \mu^{*} \) is constant which equals to 2/Re, where the Reynolds number, Re, is 250 and is defined as 2ρU 0 R 0 /µ. In this equation, ρ is density of blood which equals 1,050 kg/m3, the average velocity, U 0 , is given based on the average flow rate 275 ml/min and is equal to 0.119 m/s, the radius of the artery, R 0 , is 0.35 cm, based on the diameter of the human common carotid artery, and µ is blood viscosity which equals 0.0035 kg/m.s [15]. For non-Newtonian case, non-dimensional modified Casson model is used [31, 32].

$$ \mu^{*} = \left( {\sqrt {\frac{{\frac{{\tau_{y} }}{{\rho U_{0}^{2 } }}\left( {1 - e^{{ - m\frac{{U_{0} }}{{R_{0} }}\dot{\gamma }^{*} }} } \right)}}{{\dot{\gamma }^{*} }}} + \sqrt {\frac{{\mu_{c} }}{{\rho U_{0} R_{0} }}} } \right)^{2} $$
(4)

where, µ c  = 0.0035 kg/m.s, m = 100 s and τ y  = 0.01 Pa for hematocrit of 45 % [33].

In this equation, \( \dot{\gamma }^{*} \) is non-dimensional shear strain rate and is defined as follows:

$$ \dot{\gamma }^{*} = \left[ {2\left\{ {\left( {\frac{{\partial u_{r}^{*} }}{{\partial r^{*} }}} \right)^{2} + \left( {\frac{{u_{r}^{*} }}{{r^{*} }}} \right)^{2} + \left( {\frac{{\partial u_{z}^{*} }}{{\partial z^{*} }}} \right)^{2} } \right\} + \left( {\frac{{\partial u_{r}^{*} }}{{\partial z^{*} }} + \frac{{\partial u_{z}^{*} }}{{\partial r^{*} }}} \right)^{2} } \right]^{\frac{1}{2}} $$
(5)

where z* = z/R 0 , and r* = r/R 0 are non-dimensional axial and radial directions.

The presence of red blood cells with volume fraction (hematocrit) of 40 to 50 % and their rotation affect the movement of other cells such as platelets, white blood cells, etc. Studies show that the movement of red blood cells increases the particles transfer in blood [34]. The transitive and rotational movements of cells interfere in the diffusion coefficient of particles. Diffusion coefficient of particles in blood increases due to the presence of red blood cells and by their individual rotation [35]. Cha et al. [36] determined the effective diffusion coefficient of bovine albumin in a suspension of red blood cells using TIRF method as a function of volume fraction, and showed that the diffusion coefficient of particles in the suspension of red blood cells is a function of shear rate and volume fraction (hematocrit) of the particle. So, the diffusion coefficient of platelets and other particles in blood should be modeled with an effective diffusion coefficient.

To consider the effect of shear rate on surface concentration, two cases for diffusion coefficient and viscosity are considered. In the first case, constant transport properties are assumed. In this case, viscosity coefficient is 0.0035 kg/m.s and diffusion coefficient is assumed constant. The diffusion coefficients used in this work are 2 × 10−11 m2/s, 1 × 10−11 m2/s, and 5 × 10−12 m2/s. These values are taken because the sizes of LDL particles are variable. Based on diffusion coefficient, Schmidt number, Sc, is 1.6 × 105, 3.3 × 105, and 6.6 × 105 respectively [8, 37].

In the second case, due to the non-Newtonian behavior of blood, the transport coefficients are variable and are functions of shear rate. The viscosity coefficient is expressed by the modified Casson model, Eq. (4).

The diffusivity of solute in the particle suspensions such as platelets in blood can be enhanced by increasing mixing due to the local fluid motion generated by individual red cell rotation. Based on the results obtained by Zydney and Colton [38], diffusion coefficient that is caused by the motion of RBCs is important for determining the effective diffusion coefficient for proteins and small particles. Thus, the effective diffusivity can be the sum of stationary diffusivity or Brownian molecular diffusivity (which there is no red blood cells), D s , of the solute and the shear-induced particle diffusivity or “rotation” induced diffusivity, D P . In this study, we use the following model for the diffusion coefficient of LDL particles [36].

$$ D_{e} = D_{S} + D_{P} $$
(6)

This expression is also introduced by Zydney et al. [39], but they used it for particles such as platelets, albumins, and globulins. In Eq. (6), D s is constant and it is computed from Stokes-Enistein’s equation [40, 41]. Here we modify the model and use it for LDL concentration. For LDL particles, D s is assumed to be equal to the constant diffusion coefficient and is either 5 × 10−12 m2/s, 1 × 10−11 m2/s, or 2 × 10−11 m2/s [8, 41, 42].

Keller, [43] estimated that for \( \dot{\gamma } = 500\,s^{ - 1} \), D P is about 10−9 m2/s for blood as a homogeneous fluid. This is comparable with the values of molecular diffusivity, D s , of the blood components such as O2, proteins, and platelets. The molecular diffusivity, D s , of O2, protein and platelet are about 10−9, 10−11 and 10−13 m2/s, respectively. Thus the effect of red cells is small for O2, large for proteins, and very large for platelets [29].

D P is caused by the rotational motion of RBC, similar to small-scale eddies in turbulent flow, and the random interaction of the RBCs [44]. Saadatmand et al. [41] showed that shear-induced diffusion coefficient of particles in blood is proportional to shear rate and the red blood cell radius. Their results illustrated significant enhancement of the particle diffusion due to RBC motions. The “rotation” induced diffusivity, D P , should be a function of cell radius, a, and rate of rotation, ω, i.e. [29],

$$ D_{P} = fct\left( {a,\omega } \right) $$
(7)

Now, let’s perform a dimensional analysis (or Pi-procedure). Based on the L–T system, we have:

$$ \pi_{1} = \frac{{D_{P} }}{{a^{2} \omega }} \equiv C $$
(8)

where C is a dimensionless constant. For a sphere in a 2-D channel,

$$ \omega = \frac{1}{2}\frac{du}{dy} = \frac{1}{4}\dot{\gamma } $$
(9)

Hence, from Eqs. (8) and (9),

$$ D_{P} = Ca^{2} \dot{\gamma } $$
(10)

where a is the red cell radius, and \( \dot{\gamma } \) is the shear rate.

Also, Cha et al. [35] experimentally showThe stenosis length is twice theed a linear relation between the shear-induced diffusion coefficient and the shear rate. One of the empirical relationships, which were used by Eckstein et al. [30] for \( D_{P} /a^{2} \dot{\gamma } \) is as follows [36]:

$$\frac{{D_{P} }}{{a^{2} \dot{\gamma }}} = \left\{ {\begin{array}{*{20}l} {0.025\left( {\frac{{\phi_{P} }}{0.2}} \right) \quad0 < \phi_{P} < 0.2} \\ {0.025 \quad\quad\quad\quad\!0.2 < \phi_{P} < 0.5} \\ \end{array} } \right.$$
(11)

Finally, from Eqs. (6) and (11), the following non-dimensional shear-dependent relationship is used for the effective diffusion coefficient of LDL particles in the suspension of red blood cells and hematocrit of 45 %.

$$D_{e}^{*} = \left( {\frac{{D_{s} }}{{R_{0} U_{0} }} + \frac{{0.025a^{2} }}{{R_{0}^{2} }}\dot{\gamma }^{*} } \right).$$
(12)

3 Geometry and boundary conditions

The artery is assumed axisymmetric cylinder with and without stenosis. The vessel wall is impermeable to LDL particles but plasma with constant specified filtration velocity passes through it. The filtration velocity normal to the wall is set to be constant and is 4 × 10−8 m/s [45]. As shown in Fig. 1, the upstream length proximal to the constriction, L i , is 4R 0 and the distal length downstream from the stenosis, L o , is 40R 0 . This geometry is similar to that of Ref. [8]. The geometry of the stenosis is described by the following bell-shaped Gaussian distribution profile [46].

$$R^{*} \left( {z^{*} } \right) = \left\{ {\begin{array}{*{20}l} {1.0 - \lambda e^{{ - 5(Z^{*} )^{2} }} } \hfill & {\left| {z^{*} } \right| \le 4} \hfill \\ {1.0} \hfill & {Otherwise} \hfill \\ \end{array} } \right.$$
(13)

where, 0.163 ≤ λ ≤ 0.368, the value of λ depends on the stenosis severity, and are given in Table 1. The boundary conditions for Navier–Stokes equations are as follows:

Table 1 Constant coefficient for the stenosis severities
Full size table
Fig. 1
figure 1

Geometrical description of the axisymmetric arterial stenosis and the coordinate system used in the numerical analysis

Full size image

At the inlet, z* = 0, the flow was assumed to be fully developed and unidirectional.

$$ u_{z}^{*} (0,r^{*} ) = 2\left( {1 - \left( {\frac{r}{{R_{0} }}} \right)^{2} } \right). $$
(14)
$$ u_{r}^{*} (0,r^{*} ) = 0. $$
(15)

At the outlet, the static gage pressure is set to zero. The non-slip and permeable wall boundary conditions were applied by setting the tangential and normal velocity components equal to zero and V w (constant water infiltration velocity at vessel walls), respectively [8].

$$ u_{z}^{*} \left( {z^{*} , R^{*} \left( {z^{*} } \right)} \right) = 0. $$
(16)
$$ u_{r}^{*} \left( {z^{*} , R^{*} \left( {z^{*} } \right)} \right) = \frac{{V_{w} }}{{U_{0} }}. $$
(17)

Boundary conditions for concentration of LDL at the inlet and outlet sequentially are given as follows:

$$ C^{*} \left( {0 , r^{*} } \right) = \frac{{C_{0} }}{{C_{0} }} = 1. $$
(18)
$$ \left( {\frac{{\partial c^{*} }}{{\partial z^{*} }}} \right)_{{(l^{*} ,r^{*} )}} = 0. $$
(19)
$$ \left( {\frac{{\partial c^{*} }}{{\partial r^{*} }}} \right)_{{(z^{*} ,0)}} = 0 $$
(20)

The LDL concentration was set to be uniform at the inlet [8] and zero axial concentration gradient at the outlet is used (zero flux, Newman condition) [47]. Note that C 0 is the reference concentration at the lumen inlet for LDL. Also, Eq. (20) represents symmetry across the centerline of the artery.

For the boundary condition for concentration at the wall, the lipoprotein accumulation at the luminal surface of the artery was determined by imposing a balance between convective and diffusive transports, and it states that the amount of LDL carried to the vessel wall by filtration flow is equal to the amount that diffuses back to the mainstream. This boundary condition is valid for a perfectly rejecting artery, namely, where no lipoproteins pass through the arterial wall. This equation is described as [47]:

$$ D\left(\frac{\partial C}{\partial r}\right)_{{\left( {Z, R\left( Z \right)} \right)}} = C_{w} V_{w} + P_{em} C_{w} $$
(21)

where, D is the diffusion coefficient, P em is the wall permeability, that for LDL, P em  = 0, and C w is the macromolecule concentration at the wall [47]. Finally, the following non-dimensional relationship is used at the wall [8].

$$ D_{e}^{*} \left(\frac{{\partial C^{*} }}{{\partial r^{*} }}\right)_{{(z^{*} , R^{*} \left( {z^{*} } \right))}} = C_{w}^{*} V_{w}^{*} $$
(22)

4 Numerical method

The governing equations are solved numerically by Ansys CFX software using the finite volume and algebraic multigrid methods based on the iteration [48] and coupling the pressure and velocity [49]. Convergence criterion for all equations is 10−6, and they are solved using double precision.

Structured grid is generated by Gambit software. To investigate the independency of mesh, LDL concentration profiles along the wall and in the radial direction, at a section near the end of a simple artery (without stenosis) are considered for the five different numerical grid sizes with 18,900, 24,750, 31,500, 36,900 and 43,200 cells, and it is shown that 36,900 cells are adequate. Also, LDL concentration profiles around the stenosis region for the artery with 60 % stenosis are considered with the number of meshes 52,800, 62,400, 74,880, 86,400, 96,000 and 105,600. It is found that 96,000 cells are adequate for this analysis (see Fig. 2).

Fig. 2
figure 2

Grid independent test: distributions of concentration for 60 % stenosis a along the artery wall, b along the radial direction and at the peak of the stenosis

Full size image

5 Validation of numerical results

Before presenting the main findings, we first validate our numerical results by the physical problem presented by Huang et al. [50]. The case studied was the incompressible, steady state, and Newtonian. An axisymmetric rigid tube with a smooth sinusoidal constriction that is described by the following expression:

$$ R^{*} \left( {z^{*} } \right) = 1.0 - \frac{1}{2}\sin \left( {\frac{\pi }{4}z^{*} + \frac{\pi }{2}} \right),\quad z^{*} \in [ - 2,2] $$
(23)

The stenosis length is twice the arterial diameter and has an area reduction of 75 %. The inlet, as suggested by Huang et al. [50], was placed 28 diameters before the constriction, and a uniform velocity profile was applied. The outlet was located 30 diameters downstream of the stenosis in order to reach a fully developed condition. The coordinate scales were normalized with the inlet tube radius and z* = 0 was the location of the throat. The evolution of the axial velocity profile for Reynolds number Re = 500 was compared with the experimental data presented by Huang et al. [50], as shown in Fig. 3. Results showed that the present numerical solution is in good agreement with the experimental data.

Fig. 3
figure 3

The axial velocity profiles, present results and the experimental results of Huang et al. [50] for Re = 500

Full size image

Also, in order to validate the numerical solution for concentration, LSC for Newtonian fluid with constant diffusion coefficient and simple artery for various Sc are obtained numerically and the results have been compared with the analytical solution of Johnson et al. [51] and the numerical solution of Fatouraee et al. [8] in Fig. 4. In their studies, blood was considered as a homogeneous, incompressible and Newtonian fluid, with a constant viscosity of 0.035 gr/cm.s and a mass density of 1.05 gr/cm3 for a straight segment of cylindrical artery; the vessel wall was permeable to plasma and has a filtration rate of the order of 10−8 m/s; the convective and diffusive flux of LDL into the vessel wall were so small that their effect on the LDL concentration at the luminal surface was negligible [8]. As shown in Fig. 4, our results are in a good agreement with the published analytical and numerical results and the maximum amount of deviation is less than 1 % for all cases. The results also showed that the larger the Schmidt number (i.e., the larger the lipids or the lower the diffusion coefficient), the higher the peak value of the luminal surface lipid concentration.

Fig. 4
figure 4

LSC along a simple geometry of carotid artery wall (without stenosis) for Newtonian fluid model of the present study and the analytical results from Johnson et al. [51] and Fatouraee et al. [8] for a straight segment of cylindrical artery Re = 250, V w  = 4 × 10−8 m/s, R 0  = 0.35 cm

Full size image

Moreover, in order to validate the results of the non-Newtonian model used in this study, the results of LSC for constant diffusion coefficient and simple artery for various Sc are compared with the numerical results of Fazli et al. [15] in Fig. 5. They used Carreau model as the non-Newtonian model for blood and Adina software. The results are found to be in good agreement with a maximum deviation less than 1 % for all cases.

Fig. 5
figure 5

LSC along a simple geometry of carotid artery wall (without stenosis) for non-Newtonian fluid model of the present study and the numerical results from Fazli et al. [15] for a straight segment of cylindrical artery Re = 250, V w  = 4 × 10−8 m/s, R 0  = 0.35 cm

Full size image

6 Results and discussion

Numerical simulation of LDL mass transfer in the arteries with and without stenosis, using lumen model and with filtration velocity of 10−8 m/s on the artery wall, under carotid artery steady flow has been carried out. Simulations are performed using constant transport parameters and shear-dependent parameters described for comparison. Our hypothesis is that the concentration of atherogenic lipids at the luminal surface may vary according to its location in the circulation, even if the bulk concentration remains constant.

6.1 Effect of stenosis severity on recirculation region and LSC

It is believed that hemodynamic factors, such as the wall shear stress, particle residence time, recirculation zones, arterial wall strain and wall compliance, play significant roles in the onset and localization of atherosclerosis [52, 53]. Since, recirculation region is susceptible to disease progression [54], in recent years researchers studied the transport of materials and the interaction of particles in this region [55]. In Fig. 6, recirculation regions for constant and shear-dependent transport properties cases and for 30 to 60 % stenosis are shown. As shown, there is no separation for 30 % stenosis and with increasing in stenosis severity, recirculation region is formed and it becomes larger. Recirculation zone for constant transport properties cases is longer than shear-dependent transport properties cases. It can be justified because the velocity profile is flatter for non-Newtonian flows.

Fig. 6
figure 6

Recirculation zone for Sc = 3.3 × 105, 30 % to 60 % stenosis and ϕ P  = 45 % for a constant transport properties and b shear-dependent transport properties

Full size image

In Table 2, the location of separation point, flow reattachment, the length of recirculation region, the maximum reverse velocity, and concentration in the recirculation region, for constant and shear-dependent transport properties cases and various stenosis severities are given. The results show that reverse velocity produced by shear-dependent transport properties cases is smaller than that of constant transport properties. For 30 % stenosis, where there is no separation, the maximum concentration for constant transport properties case is higher than that of shear-dependent transport properties case. It is due to the difference in velocity profiles for Newtonian and non-Newtonian fluids. But for higher stenosis severities, the maximum concentration in the recirculation region for shear-dependent transport properties cases, which has a smaller recirculation region and a lower reverse velocity, is more than that of constant transport properties cases. Moreover, for the stenosis severities of 30, 40, 50 and 60 %, the maximum of LSC has been observed for stenosis of 40 % in which the flow separation occurs for both cases. This finding is similar to the experimental and numerical results. Wang et al. [56] investigated the effect of stenosis severity of 30, 40 and 50 %, on LSC by animal experiments and found the maximum amount of LSC in stenosis of 40 %. Fazli et al. [15] considered a symmetrical 30–60 % stenosis in carotid artery with a semi-permeable wall for Newtonian and non-Newtonian fluids numerically. They showed that LSC decreased as the recirculation length is increased and reaches maximum at 40 % stenosis. On growing the severity from 40 to 50 % the length of recirculation zone increases. Consequently, due to the flow recirculation and increase in reverse velocity, LDL mixes with blood and reduces the maximum LSC from 40 to 60 %.

Table 2 Performance of constant and shear-dependent transport properties cases for different stenosis severity
Full size table

6.2 Effect of shear-dependent transport properties on LSC

Figure 7a ,b shows WSS and LSC for constant and shear-dependent transport properties cases and Sc = 6.6 × 105. A precipitous obstacle can significantly disturb the flow. From Fig. 7a, it is shown that due to the presence of the recirculation zone, the wall shear rate, and hence the wall shear stress, changes sign and becomes negative at the separation point, and then becomes positive again downstream from the reattachment point. The peak value of shear rate appears at the throat of the stenosis, where the velocity of fluid is maximum. In addition, we can see from Fig. 7a that compared to non-Newtonian case, the Newtonian fluid case has lower WSS. Since, the velocity profiles of non-Newtonian models are more uniform than the Newtonian cases, in the areas close to the wall; they have higher velocity gradient. Also, because of the shear-thinning property of the blood, the apparent viscosity of non-Newtonian fluid is larger than that of Newtonian fluids in the areas near the wall. So, the wall shear stress for non-Newtonian models is larger than the Newtonian case. This is consistent with the results of others [57–60].

Fig. 7
figure 7

a WSS and b LSC along the artery wall constant and shear-dependent transport properties for 30 to 60 % stenosis, Sc = 6.6 × 105 and ϕ P  = 45 %

Full size image

From Fig. 7b, it is apparent that the relative luminal surface concentration, C w /C 0 , in both the vortex flow region and the laminar flow region, was higher than 1.0, indicating that CP occurred in the arterial stenosis. The relative luminal surface concentration in the vortex region was significantly higher than that in the laminar flow region. Moreover, the luminal surface LDL concentration at the arterial wall was flow-dependent, varying inversely with wall shear rate [8]. Also, it can be seen from Fig. 7, for 30 % stenosis, there is no separation (WSS > 0). For shear-dependent transport properties case, LSC is lower than that of constant transport properties case, which is due to the difference in velocity profiles for Newtonian and non-Newtonian fluids. For 40 to 60 % stenosis, flow separation occurs, which is evident from WSS curves shown in Fig. 7a. Due to the existence of the recirculation region, WSS is negative and its value for constant transport properties cases is more than that of shear-dependent transport properties cases because the reverse velocity of non-Newtonian fluid is lower than that of Newtonian fluid. At the separation and reattachment points, where WSS is zero, LSC is higher for shear-dependent transport properties cases. The reason for the increase in LSC at the separation and reattachment points is that at these points, the shear rate is zero and when non-Newtonian model is used, the viscosity and consequently Sc increase strongly. It causes the concentration boundary layer thickness to reduce and LSC to increase. This finding is similar to the experimental observations of cholesterol uptake distribution along the stenosed arteries of dogs reported by Deng et al. [61] who showed that the surface concentration and, consequently, the uptake of the 3H-7-cholesterol in the arterial wall is elevated at the location of the reattachment point. Chen et al. [62] used an in vitro reverse step model and showed that the particles in blood adhered and transmigrated more in the reattachment region than in the recirculation region. They stated that the reason for this event is the higher concentration of particles in this area. Moreover, experimental studies suggest that at the separation and reattachment points, where WSS is low, LSC is high, which is an effective factor in the growth of plaques [63]. Also, angiography studies show that the atherosclerosis plaques grow downstream of stenosis, where reduction in the velocity is shown [64].

Our results suggest that changes in LSC are well correlated with changes in WSS. Also, unlike shear-dependent transport properties cases, constant transport properties cases are unable to demonstrate the increase of LSC in the reattachment point. So, it can be concluded that shear-dependent transport properties cases are more accurate than constant transport properties cases.

The diffusion coefficient variations along the longitudinal direction are also given in Fig. 8a. These variations are quite similar to wall shear rate (Fig. 8b). As it is shown, in the areas behind the stenosis, where shear rate is high, the diffusion coefficient that has a linear relationship with the shear rate, rises and after the stenosis, the shear rate decreases and the diffusion coefficient descends. In other areas, where the shear rate is almost constant, the diffusion coefficient remains almost unchanged.

Fig. 8
figure 8

a Diffusion coefficient in the longitudinal direction for 30 to 60 % stenosis, Sc = 6.6 × 105 and ϕ P  = 45 % and b shear rate in the longitudinal direction for various stenosis

Full size image

In Fig. 9, LSC for constant and shear-dependent transport properties cases in the entire length of the vessel is shown for 60 % stenosis and Sc = 6.6 × 105. At the separation and reattachment points, due to the zero WSS, we expect to have highest concentration. It is observed that for constant transport properties, LSC continues to grow after the flow reattachment point. It seems that this trend is not physical, and since the shear stress after the reattachment point does not have minimum amount, LDL concentration should not rise to this level. Shear-dependent transport properties cases give better results, because sharp increase in LSC is observed at the separation and reattachment points, and it shows less increase in LSC before the separation point and after the reattachment point. This procedure is more comparable with other results. Zhang et al. [65] studied LSC of albumin in the dog carotid artery with stenosis of 75 %, and concluded that the relative LSC in the laminar region (before the separation and after the reattachment points) is lower than relative LSC in the turbulent region (recirculation region). Thus, this result also shows the accuracy of shear-dependent transport properties cases compared to the constant transport properties cases.

Fig. 9
figure 9

LSC for constant and shear-dependent transport properties cases in the total length of the vessel for 60 % stenosis, Sc = 6.6 × 105 and ϕ P  = 45 %

Full size image

7 Conclusion

LDL particles concentration near the carotid artery walls is numerically simulated for steady flow in arteries, with symmetric 30 to 60 % stenosis and without stenosis. The lumen model, with filtration velocity of the order 10−8 m/s is used. The effects of constant and shear-dependent transport properties on the simulation result are the main concern of our study. For this purpose a new model for diffusion coefficient which consists of two parts and is based on considering the effects of rotation of red blood cells in the flow is used. The results show that the new model, the shear-dependent transport properties, unlike the constant transport properties produces physical and more accurate results. For example, the concentration of LDL in the reattachment point is increased as expected, while in case of constant transport properties, it is not shown. Also, the amount of LDL concentration in the bulk flow is predicted more accurately with our model when it is compared with the experimental results.