INTRODUCTION

Atherosclerosis is a disease of large arteries that is characterised by the accumulation of lipids in the arterial wall.10,30 The transport process of atherogenic species such as low density lipoprotein (LDL) from the bulk blood flow to and across the arterial wall contributes to lipid accumulation. This transport process is termed “arterial mass transport” and is influenced by blood flow in the lumen and transmural flow in the arterial wall.

Arterial mass transport in the fluid phase (blood lumen) has been investigated by a number of researchers using computational approaches where the arterial wall is treated as a boundary condition. This approach is generally called a “wall-free model,” and has the advantage of being computationally cheap and providing qualitative information on mass transfer in the blood lumen. It has been used to investigate oxygen12,13,18,26 – 28 and LDL transport5,6,36 – 38 in idealised as well as anatomically realistic arterial models. The common finding is that oxygen transport is limited by the fluid phase resistance, while LDL transport is limited by the resistance within the arterial wall. To provide a more detailed description of the arterial wall, a fluid-wall model which accounts for both fluid phase and tissue phase (arterial wall) transport is required. To model the multi-layered arterial wall, a fluid-wall model with a multi-layered formulation was proposed.15 This model treats the intimal and medial transport separately, but its application was limited to ideal 2D geometries due to its high computational expense.14,24 The alternative is the fluid-wall model with a single-layered formulation,21,25,32,33 which treats the intima and media of the arterial wall as one single layer of porous medium with homogeneous transport properties. It takes into account transport processes within the arterial wall without excessive computational expense.

Arterial mass transport is believed to be influenced by biomechanical forces, especially WSS.2 WSS is a tangential force that acts on the endothelium and influences the transport of macromolecules into the arterial wall from the blood lumen.22 A conventional approach to examine the influence of WSS on arterial mass transport is to assume that the transport properties of the endothelium, such as the solute permeability, are shear-dependent. An arbitrary shear-dependent permeability was assumed to investigate oxygen transport in large arteries,27,28 and zones of hypoxia were found to co-localise with regions of low WSS. Furthermore, a shear-dependent permeability based on experimental data11 was used to investigate the transport of albumin.29 However, these investigations were carried out using the wall-free model without considering transport in the arterial wall.

In the present study, a fluid-wall model, which treats the arterial wall as a single-layer of porous medium incorporating shear-dependent endothelial transport properties, was developed and used to study the effects of wall shear stress on the transport of LDL and oxygen from blood to and within the wall in an idealised model of a stenosed artery. Both flow and species transport were simulated under steady state conditions. It was assumed that LDL transport was influenced by shear-dependent hydraulic conductivity, while shear dependent permeability was assumed for oxygen transport.

METHODS

Governing Equations

Since arterial mass transport is coupled with blood flow in the fluid phase and transmural flow in the tissue phase, the model presented here includes fluid dynamics models for blood flow and transmural flow, and solute dynamics models for mass transfer.

Fluid Dynamics

Blood flow is assumed to be steady, incompressible, laminar, Newtonian and hence described by the Navier-Stokes equations

$$-\mu\nabla^2\mathbf{u}_l+\rho(\mathbf{u}_l\cdot\nabla)\mathbf{u}_l+\nabla p_l=0$$
(1)
$$\label{con}\nabla\mathbf{u}_l=0$$
(2)

in the fluid domain, where \(\mathbf{u}_l\) is blood velocity in the lumen, \(p_l\) is the pressure, μ is the dynamic viscosity of the blood, and ρ is the density of the blood.

The transmural flow in the arterial wall is modelled by Darcy’s Law

$$\mathbf{u}_w-\nabla\cdot\left(\frac{\kappa}{\mu_p}p_w\right)=0$$
(3)
$$\label{dcon}\nabla \mathbf{u}_w=0$$
(4)

in the wall domain, where \(\mathbf{u}_w\) is the velocity of the transmural flow, \(p_w\) is the pressure in the arterial wall, \(\mu_p\) is the viscosity of the blood plasma, and κ is the Darcian permeability coefficient of the arterial wall.

Solute Dynamics

Mass transfer in the blood lumen is coupled with the blood flow and modelled by the convection-diffusion equation as follows

$$\nabla\cdot(-D_l\nabla c_l+c_l\mathbf{u}_l)=0\label{cde}$$
(5)

in the fluid domain, where \(c_l\) is the solute concentration in the blood lumen, and \(D_l\) is the solute diffusivity in the lumen.

Mass transfer in the arterial wall is coupled with the transmural flow and modelled by the convection-diffusion-reaction equation as follows

$$\nabla\cdot(-D_w\nabla c_w+Kc_w\mathbf{u}_w)=r_wc_w\label{cdew}$$
(6)

in the wall domain, where \(c_w\) is the solute concentration in the arterial wall, \(D_w\) is the solute diffusivity in the arterial wall, K is the solute lag coefficient, and \(r_w\) is the consumption rate constant.

Computational Geometry and Boundary Treatments

Computational Geometry

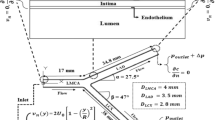
An axisymmetric stenosis with 49% area reduction was adopted. As shown in Fig. 1, the total length (z-axis) of the geometry is \(25D\), where \(D=0.004 m\) is the diameter of the non-stenosed region of the artery. The length of the stenosis is\(1D\), leaving \(4D\) upstream and \(20D\) downstream of the stenosis to minimize the effects of boundary conditions.

FIGURE 1.
figure 1

Computational geometry of a mild stenosis (49% constriction by area). Computational subdomains and dividing boundaries are denoted. The dashed line is the axis of symmetry. (a) overview of the computational geometry, the geometry was distorted for better illustration and notations; (b) details of the stenosis without distortion of the geometry.

Full size image

The axisymmetric stenosed lumen geometry was modelled by the following cosine expression:

$$\frac{r(z)}{R}=1-\frac{\delta}{D}\left(1-\cos\left(\frac{2\pi(z-z_1-z_2)}{z_2-z_1}\right)\right)$$
(7)

for \(4D<z<5D\), where r(z) is the radius of the artery at location z in the stenosis, R is the radius of the non-stenosed region of the artery, δ is the radius reduction at the throat of the stenosis (0.15D), \(z_1=4D\) is the start point of the stenosed region, and \(z_2=5D\) is the end point of the stenosed region. The wall geometry is defined as \(r=0.575D\) with a wall thickness of \(0.075D\) at the non-stenosed region and \(0.225D\) at the throat of the stenosis.

Boundary Treatments

Applying adequate boundary conditions, the system of equations can be solved in the stenosis geometry. For the Navier-stokes Equations Eq. (1) and (2), a fully developed parabolic steady velocity profile was assumed at the lumen inlet boundary \(\Gamma_{l,in}\) (see Fig. 1)

$$u(r)=2U_0\left(1-\left(\frac{2r}{D}\right)^2\right), {\rm on}\, \Gamma_{l,in}$$
(8)

where \(u(r)\) is the velocity in the axial direction at radial position r, and \(U_0\) is the mean inlet velocity. At the lumen side of the endothelial boundary \(\Gamma_{end}\), a lumen-to-wall transmural velocity in the normal direction was specified:

$$\mathbf{t}_l^T\cdot\mathbf{u}_l=0,\mathbf{u}_l\cdot\mathbf{n}_l=J_{v},{\rm on}\, \Gamma_{end}$$
(9)

where \(J_{v}\) is the transmural velocity in the normal direction, \(\mathbf{t}_l^T\) and \(\mathbf{n}_l\) are the tangent vector and normal vector of fluid subdomain \(\Omega_l\), respectively. At the lumen outlet boundary \(\Gamma_{l,out}\), a zero surface traction force condition was prescribed

$$\{-p\mathbf{I}+\mu[\nabla\mathbf{u}+(\nabla\mathbf{u})^T]\}\mathbf{n}=0$$
(10)

For Darcy’s Law Eqs. (3) and (4), an “insulation” condition was assumed for wall boundaries at the lumen inlet location \(\Gamma_{w,in}\) and at the lumen outlet location \(\Gamma_{w,out}\)

$$\mathbf{n}_w\cdot\mathbf{u}_w=0, {\rm on}\, \Gamma_{w,in}\cup\Gamma_{w,out}\label{inoutletbc}$$
(11)

where \(\mathbf{n}_w\) is the normal vector of wall subdomain \(\Omega_w\). At the wall side of the endothelial boundary \(\Gamma_{end}\), a lumen-to-wall transmural velocity in the normal direction was assumed

$$\mathbf{u}_w\cdot\mathbf{n}_w=-J_{v},{\rm on}\, \Gamma_{end}.\label{endobc2}$$
(12)

A pressure condition was prescribed at the media-adventitia interface \(\Gamma_{adv}\)

$$p_w=p_{adv}\, {\rm on}\, \Gamma_{adv}$$
(13)

As for the convection-diffusion equation (Eq. (5) in the blood lumen, a constant concentration was assumed at the lumen inlet boundary \(\Gamma_{l,in}\)

$$c_l=C_0, {\rm on}\, \Gamma_{l,in}$$
(14)

where \(C_0\) is a constant concentration. At the lumen side of the endothelial boundary \(\Gamma_{end}\), a lumen-to-wall solute flux was specified

$$-D_l\nabla c_l\mathbf{n}_l+\mathbf{u}_lc_l\mathbf{n}_l=J_{s},{\rm on}\,\Gamma_{end}$$
(15)

where \(J_{s}\) is the solute flux. At the lumen outlet boundary \(\Gamma_{l,out}\), the convective flux condition was prescribed

$$D_l\nabla c_l\mathbf{n}_l=0, {\rm on}\, \Gamma_{l,out}.\label{outletcdbc}$$
(16)

As for the convection-diffusion-reaction equation Eq. (6) in the arterial wall, an insulation condition is assumed for wall boundaries at the lumen inlet location \(\Gamma_{w,in}\) and at the lumen outlet location \(\Gamma_{w,out}\)

$$D_w\nabla c_w\mathbf{n}_w=0, {\rm on}\, \Gamma_{w,in}\cup\Gamma_{w,out}.$$
(17)

At the wall side of the endothelial boundary \(\Gamma_{end}\), a lumen-to-wall solute flux in the normal direction was assumed

$$-D_w\nabla c_w\mathbf{n}_w+\mathbf{u}_wc_w\mathbf{n}_w=J_{s},{\rm on}\, \Gamma_{end}.$$
(18)

A constant concentration was prescribed at the media-adventitia interface \(\Gamma_{adv}\)

$$c_w=c_{adv}\, {\rm on}\, \Gamma_{adv}\label{advcdbc}$$
(19)

The transmural velocity (\(J_{v}\)) in Eqs. (9) and (12) and the solute flux (\(J_{s}\)) in Eqs. (15) and (18) are given by the Kedem-Katchalsky Equations 16

$$\label{volume}J_{v}=L_{p}(\Delta p-\sigma_{d} \Delta\pi)$$
(20)
$$\label{solute}J_{s}=P\Delta c+(1-\sigma_{f})J_{v}\overline{c}$$
(21)

where \(L_{p}\) is the hydraulic conductivity of the endothelium, \(\Delta c\) is the solute concentration difference across the endothelium, \(\Delta p\) is the pressure drop across the endothelium, \(\Delta\pi\) is the oncotic pressure difference across the endothelium, \(\sigma_{d}\) is the osmotic reflection coefficient, \(\sigma_{f}\) is the solvent reflection coefficient, P is the solute endothelial permeability, and \(\overline{c}\) is the mean endothelial concentration. The first term \(P\Delta c\) of the right hand side in Eq. (21) defines the diffusive flux across the endothelium, while the second term \((1-\sigma_{f})J_{v}\overline{c}\) defines the convective flux. In the case of oxygen transport, in which the endothelial transport is dominated by diffusion,39 the convective term was not included in the simulation. Furthermore, in this preliminary study, the oncotic pressure difference \(\Delta\pi\) of Eq. (20) was neglected to de-couple the fluid dynamics from solute dynamics.

Shear-Dependent Endothelial Transport Properties

In the present study, a shear-dependent hydraulic conductivity and a shear-dependent permeability were assumed for LDL and oxygen transport, respectively.

Shear-Dependent Hydraulic Conductivity

The effect of shear stress on hydraulic conductivity (\(L_p\)) of bovine aortic endothelium was examined in vitro 3,31 under constant shear stress conditions. It was found that when exposed to higher shear stress, the endothelial monolayer presented larger hydraulic conductivity. The reported experimental data31 are summarised in Table 1. Since the experiments were conducted over a period of 240 minutes, the measured hydraulic conductivity varied with time. Here the maximal values under each shear stress condition were used to derive the relationship between shear stress and hydraulic conductivity. These experimental data were fitted with a logarithmic function to obtain a mathematical model of the shear-dependent hydraulic conductivity following the idea of a previous study,29 in which a logarithmic function was employed to fit the experimental data on albumin permeability. The resulting logarithmic function is given by

$$g(|\tau_w|)=0.4669\ln(|\tau_w|+0.015)+3.327$$
(22)

where \(|\tau_w|\) is the WSS, and g is the normalised hydraulic conductivity. This fitted curved is compared with experimental data points in Fig. 2.

FIGURE 2.
figure 2

Comparison between experimental data from 31 and fitted logarithm function. The squares are experimental data points (normalised \(L_p\)) while the line is the fitted curve.

Full size image
TABLE 1. Experimental data extracted from literature31.
Full size table

Note that Eq. (22) only accounts for the relationship between WSS and normalised hydraulic conductivity. Thus the constant coefficients in Eq. (22) need to be scaled to obtain the real value of hydraulic conductivity under varying wall shear stress in the computational geometry. Since a constant hydraulic conductivity was used for the sake of comparison, the shear-dependent hydraulic conductivity at the inlet section of the stenosis was scaled using a constant hydraulic conductivity, \(L_p=3\times 10^{-12} m s^{-1} Pa^{-1}\), which is adopted in the literature.14,15,24 Since the wall shear stress at the inlet is

$$|\tau_w|_{z=0}=\frac{8\mu U_0}{D}=1.68\, Pa,$$
(23)

the resulting shear-dependent hydraulic conductivity is given by

$$\displaylines{L_p(|\tau_w|)=0.392\times 10^{-12}\ln(|\tau_w|\cr +0.015)+2.7931\times10^{-12}.}$$
(24)

Using this relation, the value of shear-dependent hydraulic conductivity at the inlet is \(3\times 10^{-12} m s^{-1} Pa^{-1}\), which is the same as was used to define the constant \(L_p\).

Oxygen Permeability

In this study, the relationship between WSS and oxygen permeability was assumed to be linear as was assumed in previous studies.27,28

Similar to the hydraulic conductivity, a constant value of oxygen permeability \(P_{oxy}=1.96\times 10^{-4} m s^{-1}\),26 was used for comparison. Thus to ensure shear-dependent permeability at the inlet, where WSS is 1.68 Pa (see Eq. (23)), equal to the constant value above, the relationship was proposed as

$$P_{oxy}(|\tau_w|)=1.1667\times 10^{-4}|\tau_w|.$$
(25)

Numerical Details

The fluid domain was divided into 29820 quadrilateral elements for solution of the Navier-stokes equations. Quadratic formulation and linear formulation were used for velocity and pressure (\(Q_2Q_1\) element), respectively. To model the mass transfer field, the fluid domain was divided into 291213 quadrilateral elements with linear formulation yielding 293820 nodes. The wall domain was divided into 9940 quadrilateral elements with linear formulation for the simulation of transmural flow. And for the simulation of mass transport, the wall domain was divided into 77190 quadrilateral elements with linear formulation yielding 74670 nodes. A mesh sensitivity test was carried out on mass transport simulations to ensure grid independence of the obtained concentration field.

Using the computational mesh described above, the system of governing equations was solved by a commercial finite element code, Comsol Multiphysics, Version 3.2. Since the fluid dynamics computation had been decoupled from solute dynamics by neglecting the oncotic pressure difference \(\Delta\pi\) in Eq. (20), governing equations Eqs. (1)–(4) for fluid dynamics were solved first, and resulting velocity fields were then used in the solute dynamics computation. To stabilise the convection-dominated mass transfer calculation in the fluid phase, the streamline upwind Petrov-Galerkin (SUPG) method1, was used.

RESULTS

The simulation parameters for fluid dynamics were chosen to approximate physiological conditions in the human coronary artery. The diameter of the non-stenosed region of the artery was \(D=0.004\, m\), the mean velocity \(U_0=0.24\, m s^{-1}\), dynamic viscosity \(\mu=0.0035\,\,Pa\,\, s\), density \(\rho=1050\,\, kg\,\, m^{-3}\), so the resulting Reynolds number \(Re=288\). For the transmural flow, Darcian permeability \(\kappa=1\times 10^{-18}\, m^2\), pressure drop across the arterial wall \(\Delta p_w=70\, mmHg\). Under the condition of constant hydraulic conductivity \(L_p=3\times 10^{-12} m\ s^{-1} Pa^{-1}\), the resulting transmural velocity was approximately \(1.78\times 10^{-8}\, m s^{-1}\), which was similar to experimental data obtained for rabbit aortic wall.19 The constant endothelial permeability to LDL and oxygen are \(2\times10^{-10}\, m\ s^{-1}\),24 and \(1.96\times 10^{-4} m\ s^{-1},\,\) 26 respectively. The consumption rate constants in the arterial wall of LDL and oxygen were assumed to be \(1.4\times10^{-4} s^{-1},\) 14 and \(8.14\times10^{-4} s^{-1}\),39 respectively. Simulations were performed using constant transport parameters and shear-dependent parameters described earlier for comparison.

Fluid Dynamics

Variations of WSS magnitude in the axial direction of the stenosis model are shown in Fig. 3. Imposing shear-dependent hydraulic conductivity had little effect on the near-wall flow field and WSS, due to the fact that the transmural flow is several orders of magnitude smaller than the bulk flow. The two points where WSS values are zero correspond to the separation point (\(z=4.673\,D\)) and reattachment point (\(z=5.865\,D\)) respectively. The area between these two points is the flow recirculation region. The transmural velocity profiles in the immediate vicinity of the stenosis for the constant and shear-dependent hydraulic conductivity cases are compared in Fig. 4. The reduction in transmural velocity at the stenosis in both cases is caused by the higher resistance provided by the thickened wall. In the case of shear-dependent hydraulic conductivity, the transmural velocity has two minima which correspond to the separation point and the reattachment point respectively. Moreover, the transmural velocity is much lower in the post-stenotic region when the shear-dependent hydraulic conductivity is taken into account, suggesting that transmural flow is extremely sensitive to the endothelial resistance, although the endothelium represents only a thin layer of the arterial wall.

FIGURE 3.
figure 3

Wall shear stress distribution in the stenosis. The solid line is WSS calculated employing constant hydraulic conductivity. The dashed line is WSS calculated employing shear-dependent hydraulic conductivity.

Full size image
FIGURE 4.
figure 4

Comparison of transmural velocity variations in the stenosis region under constant hydraulic conductivity condition (solid line) and shear-dependent hydraulic conductivity condition (dashed line).

Full size image
FIGURE 5.
figure 5

Comparison of LDL concentration distributions in the stenosis region under constant hydraulic conductivity condition (solid line) and shear-dependent hydraulic conductivity condition (dashed line). (a) lumenal surface LDL concentration; (b) subendothelial LDL concentration.

Full size image

LDL Transport

The solute concentration profiles on both the lumen-side and wall-side of the endothelium were analysed. The lumenal surface concentration (\(c^{end}_l\)) characterises the fluid phase transport efficiency while the wall-side concentration (\(c^{end}_w\)) provides information on the degree of lipid accumulation and oxygen depletion in the subendothelial layer.

Fig. 5 shows normalised \(c^{end}_l\) and \(c^{end}_w\) of LDL in the vicinity of stenosis, where elevated concentration of LDL is observed on the lumenal surface. This is the so-called concentration polarisation phenomenon caused by high endothelial resistance to macromolecules.34 In addition, there is a large difference between \(c^{end}_l\) and \(c^{end}_w\) since most LDL particles are retained in the fluid phase at the endothelium. After the flow separation point, the concentration profiles on the lumenal surface of endothelium and the subendothelial layer exhibit dramatically different features, demonstrating that the fluid phase LDL transport is affected by transmural flow through complicated interactions between fluid phase and tissue phase transport. In Fig. 5(b), increased LDL concentration can be observed at the stenosis with both constant and shear-dependent conductivity, whereas in the post-stenotic region, elevated LDL concentration is only found when shear-dependent hydraulic conductivity is assumed, where there is a second peak of LDL accumulation at the reattachment point. This finding is similar to the experimental observations of cholesterol uptake distribution along the stenosed arteries of dogs reported by Deng et al. 7 who showed that the uptake of the 3H-7-cholesterol in the arterial wall is elevated at the location of the reattachment point. The increase of the wall-side LDL concentration is due to weaker local convective clearance effects of the transmural flow,35 which is the primary driver for mass transfer of macromolecules in the arterial wall. Specifically, in the low WSS region, where the transmural velocity is low, the LDL particles cannot be “flushed” away effectively from the subendothelial layer. This can be seen in detail in Fig. 6 where LDL concentration profiles within the wall at different axial locations are illustrated. In the case of constant hydraulic conductivity Fig. 6(a), concentration profiles at the upstream of the stenosis (\(z=3\,D\)), reattachment point (\(z=5.865\,D\)), and far downstream of the stenosis (\(z=20\,D\)) overlap with each other with a characteristic “U” shape similar to that seen in experimental observations.19 In the case of shear-dependent hydraulic conductivity Fig. 6(b), the LDL wall concentration profile at the reattachment point is different from those at the other two locations: LDL tends to accumulate in the subendothelial layer in the recirculation region because of weaker convective clearance there.

FIGURE 6.
figure 6

LDL concentration profiles in the arterial wall at different axial locations. (a) constant hydraulic conductivity condition; (b) shear-dependent hydraulic conductivity condition.

Full size image

Oxygen Transport

Fig. 7 shows the normalised \(c^{end}_l\) and \(c^{end}_w\) of oxygen for both constant permeability and shear-dependent permeability cases. It can be noted that the difference between \(c^{end}_l\) and \(c^{end}_w\) is very small due to the high oxygen permeability of the endothelium, supporting the hypothesis that \(c^{end}_l=c^{end}_w\) in the wall-free model for oxygen transport.26,35 Consequently, the oxygen concentration on the lumenal surface at the throat of the stenosis is high due to accelerated flow and consequently stronger convection present there. When employing shear-dependent permeability, higher oxygen concentrations on the lumenal surface and lower oxygen concentrations in the subendothelial layer are observed in the immediate post-stenotic region, due to reduced oxygen flux across the endothelium in the low WSS region. Figure 8 illustrates the oxygen concentration profiles in the arterial wall at different axial locations for both constant permeability and shear-dependent permeability cases. The small difference between the profiles at different locations in Fig. 8(a) are related to the oxygen concentration boundary layer development in the fluid phase, whereas in Fig. 8(b) the profile at the reattachment point, which is very low, differs considerably from that at upstream and far downstream of the stenosis.

FIGURE 7.
figure 7

Comparison of oxygen concentration distributions in the stenosis region under constant permeability condition (solid line) and shear-dependent permeability condition (dashed line). (a) lumenal surface oxygen concentration; (b) subendothelial oxygen concentration.

Full size image
FIGURE 8.
figure 8

Oxygen concentration profiles in the arterial wall at different axial locations. (a) constant permeability condition; (b) shear-dependent permeability condition.

Full size image

DISCUSSION

Effects of Shear-Dependent Endothelial Transport Properties

As pointed out previously, the endothelium, which acts as a molecular sieve, provides the predominant resistance to macromolecular (i.e. LDL) transport into the arterial wall. However, the mechanisms involved in LDL transport across the endothelium, i.e. the roles of diffusion, convection, and vesicular transport, are not fully understood. Convection, which is driven by the transmural flow, is probably the most well characterised mechanism. As for diffusion, LDL permeability calculated from the pole theory leads to much lower flux than that observed in experiments,24,25 suggesting that transport mechanisms other than physical convective diffusion play a role. Although vesicular transport is currently regarded as one of the major pathways for macromolecular transport across the endothelium,20,35 it has not been included in computational models due to its unclear mechanism. Thus, in the present study, rather than focusing on the endothelial transport itself, the influences of shear-dependent endothelial transport properties, i.e. the effects of transmural flow on LDL accumulation in the arterial wall, were examined. A scaled LDL permeability (\(P_{LDL}\)) was employed to match the experimental observation of LDL flux across the endothelium,24 and a shear-dependent hydraulic conductivity was extracted from in vitro experimental data on bovine aortic endothelium under various shear stress values.31 The transport of LDL inside the arterial wall consists of convection and diffusion. Although the magnitude of transmural velocity is only \(10^{-8} m s^{-1}\), LDL transport in the arterial wall is dominated by convection due to the extremely low diffusivity. Therefore, transmural flow, which is affected by the shear-dependent hydraulic conductivity of the endothelium, largely regulates the accumulation of LDL in the arterial wall. For example, an increase in hydraulic conductivity of the endothelium, which leads to an increase in transmural velocity with fixed endothelial permeability to LDL will reduce the accumulation of solute beyond the endothelial layer by convective clearance.35 On the other hand, by complicated interactions between lumen-side transport and wall-side transport, the accumulation of LDL on the lumenal surface is also affected by the shear-dependent hydraulic conductivity of endothelium.

The oxygen transport pathway across the endothelium is commonly considered as diffusion through the whole endothelial surface. Thus an accurate index of oxygen permeability is needed to model oxygen transport across the endothelium. A much lower oxygen permeability was used in a previous study,28 but a higher permeability of human endothelial cells suggested by Qiu and Tarbell26 was employed for our purposes. Although shear-dependent permeabilities were employed in some of the previous numerical studies on oxygen transport in the fluid phase,27,28 the question as to whether the diffusive mechanism of oxygen transport can be affected by the mechanical force remains unanswered. In the present study, an arbitrarily assumed shear-dependent permeability was employed to examine the effects of diffusive flux across the endothelium on depletion of oxygen in the arterial wall. Since oxygen transport across the endothelium is diffusion dominated and regulated by the endothelial permeability, the shear-dependent permeability to oxygen determines the oxygen flux across the endothelium. In other words, the oxygen flux across the endothelium in a region with a low local permeability is smaller,8,27,28 resulting in high oxygen concentration on the lumenal surface and hypoxia in the arterial wall.

Implication for Atherogenesis

Although the effect of WSS on mass transfer across the endothelium via shear-dependent transport properties has been a focus of much interest, our computational results suggest that WSS also has a strong influence on the concentration field of atherogenic molecules, such as LDL, within the arterial wall.

The resulting LDL concentration field obtained using shear-dependent hydraulic conductivity showed that in the region of low WSS, LDL tended to accumulate in the subendothelial layer due to weaker convective clearance effects. On the other hand, hypoxia in the arterial wall was observed in the area subject to low WSS when employing shear-dependent permeability due to smaller oxygen flux across the endothelium. Although this reduced oxygen flux was also found in earlier computational studies with a wall-free model,27,28 the concentration field indicating local hypoxia has not been found before.

Therefore, the co-localisation of low WSS, high LDL endothelial concentration on the wall-side and hypoxia in the arterial wall was found in the computational results. Since lipid accumulation and hypoxia in the arterial wall are important factors in the development of atherosclerosis,4,30 this observation of co-localisation supports the hypothesis that low WSS predisposes to atherogenesis. However, to further determine how low WSS and abnormal mass transport contribute to atherogenesis, numerical studies in anatomically realistic arterial models and more experimental data are needed.8

Limitations of Present Study

The present study has a number of limitations which are listed below.

  1. (1)

    A steady state condition was assumed although arterial flow is pulsatile, which will influence the fluid dynamics as well as the mass transfer. On one hand, under pulsatile flow conditions, the flow separation zone in the post-stenotic region will expand and contract during a cycle, resulting in oscillation of the reattachment point along the lumenal surface.17,23 This is likely to “diffuse” the focal feature of LDL concentration found near the reattachment point in the steady flow model by extending the second peak over the region encompassed by the oscillating reattachment point. On the other hand, the effect of pulsatile WSS on hydraulic conductivity was found to be strongly dependent on the degree of flow reversal.9 For pulsatile conditions with little or no reversal, there is a major increase in hydraulic conductivity over steady WSS, whilst for completely oscillatory WSS, i.e. zero mean, the effect is similar to zero shear conditions. Therefore, it could be speculated that under pulsatile flow conditions, the post-stenotic region would be subject to oscillatory WSS with low mean values; as a result, elevated LDL concentration in the subendothelial layer might be seen over a certain length along the wall before dropping to a normal level.

  2. (2)

    In the case of oxygen transport, the shear-dependent endothelial permeability to oxygen was arbitrarily assumed.

  3. (3)

    An anatomically realistic model was not examined, and consequently, the effects of complex 3D flow patterns on mass transport were not modelled.

CONCLUSION

A fluid-wall model with the single-layered arterial wall formulation was employed to study the transport of LDL and oxygen in an idealised stenosis. Shear-dependent endothelial transport properties, i.e. hydraulic conductivity and oxygen permeability, were used to investigate effects of WSS on mass transport in the arterial wall. Both LDL accumulation in the subendothelial layer and hypoxia in arterial wall were found to co-localise with low WSS. It is shown that WSS regulates the LDL accumulation in the subendothelial layer by a convective clearance mechanism, while oxygen transport would be affected by WSS if its diffusive mechanism is shear dependent. Further understanding of mechanisms involved in endothelial transport at the cellular level would enable more accurate quantitative analysis of arterial mass transport mechanisms.