1 Introduction

The aim of this paper is to study the static behavior of shell structures, which are very common structural elements. During the last sixty years, two-dimensional linear theories of thin shells and plates have been developed including important contributions by Timoshenko and Woinowsky-Krieger [1], Flügge [2], Gol’denveizer [3], Novozhilov [4], Vlasov [5], Ambartusumyan [6], Kraus [7], Leissa [8, 9], Markuš [10], Ventsel and Krauthammer [11] and Soedel [12]. All these contributions are based on the Kirchhoff-Love assumptions. This theory, named Classical Shell Theory (CST), assumes that normals to the shell middle-surface remain straight and normal to it during deformations and unstretched in length. The transverse shear deformation has been incorporated into shell theories by following the theory of Reissner-Mindlin [13], also named First-order Shear Deformation Theory (FSDT). By relaxing the assumption on the preservation of the normals to the shell middle surface after the deformation, a comprehensive analysis for elastic isotropic shells and plates was made by Kraus [7] and Gould [14, 15]. The present work is just based on the FSDT. In order to include the effect of the initial curvature a generalization of the Classical Reissner-Mindlin Theory (CRMT) has been proposed by Toorani and Lakis [16]. In this way the CRMT becomes a particular case of the Classical Toorani-Lakis Theory (CTLT). As a consequence of the use of this general theory, it is worth remarking that the stress resultants directly depend on the geometry of the structure in terms of the curvature coefficients and the hypothesis of the symmetry of the in-plane shearing force resultants and the torsional couples declines. A further improvement of the previous theories of shells has been proposed in [17]. In this last work by Toorani and Lakis, the kinematical model is generalized and the effect of the curvature is included from the beginning of the shell formulation. In this way the strain-displacement relationships and the equilibrium equations in terms of displacements and rotations have to be modified. In this paper the General Toorani-Lakis Theory (GTLT) is considered. As for the static analysis of shells, several studies have been presented earlier. In the semi-analytical methods each static and kinematic variable is transformed into a theoretical infinite Fourier series of harmonic components [18, 19]. However, the semi-analytical solutions show limitations to consider any boundary condition, stacking sequences as well as the panel geometries. It should be noticed that finite element method (FEM) does not present the above drawbacks and it represents therefore the most popular numerical tool [14, 15, 20–26]. Meshless methods are also available to solve analogous problems such as reported in literature [27–31], among others.

In the present paper, the analysis will be performed by following two different paths. In the first one, the solution is obtained by using the numerical technique termed Generalized Differential Quadrature (GDQ) method, which leads to a linear algebraic problem. The mathematical foundations and recent developments of the GDQ method as well as its major applications in engineering are discussed in detail in the book by Shu [32]. The solution is given in terms of generalized displacement components of the points lying on the middle surface of the shell. Then, numerical results will be also computed by using semi-analytical solutions and commercial programs in order to verify the accuracy of the method at issue. It appears that the interest of researches in this procedure is increasing due to its great simplicity and versatility. As shown in the literature [33], GDQ technique is a global method, which can obtain very accurate numerical results by using a considerably small number of grid points. Therefore, this simple direct procedure has been applied in a large number of cases [34–78] to circumvent the difficulties of programming complex algorithms for the computer, as well as the excessive use of storage and computer time.

After the solution of the fundamental system of five equations in terms of displacements, the generalized strains and stress resultants can be numerically evaluated by applying the Differential Quadrature rule [32] to the generalized displacements. In order to design composite structures properly, accurate stress analyses have to be performed. The determination of accurate values for interlaminar normal and shear stresses is of crucial importance. In this study, the transverse shear and normal stress profiles through the thickness are reconstructed a posteriori by simply using local three-dimensional equilibrium equations. No preliminary recovery or regularization procedure [21, 22, 25, 79, 80] on the extensional and flexural strain fields is needed when the Differential Quadrature technique is used. Based on the fact that the starting problem derives from the 3D Elasticity and that it has been simplified using the well-defined hypotheses of the FSDT, the numerical approximated solution captures well the real behavior of shells. Since the 3D Elasticity equations are always valid for the problem under consideration, it is possible to use the approximated solution to evaluate some quantities such as in-plane stresses and their derivatives and to infer others quantities of interest solving the 3D equilibrium equations such as shear and normal stresses. Thus, if the in-plane stresses and their derivatives are known, the three differential equations of the 3D elasticity can be seen as three independent differential equations of the first order that can be solved via the GDQ method along the thickness direction. The unknowns are the normal and shear stresses through the thickness. The GDQ reconstruction procedure needs only to be corrected to properly account for the boundary equilibrium conditions. GDQ results are compared with the ones obtained with semi-analytical formulations and with finite element methods. Various examples of stress profiles are presented to illustrate the validity and the accuracy of the GDQ method. Under the hypotheses of validity of the FSDT, very good agreement between the proposed procedure and the 3D FEM solution is observed without using mixed formulations and higher order kinematical models, that require an increase of the degrees of freedom [18–20, 23, 24, 26, 29, 31].

Due to the significant developments that have taken place in functionally graded materials [56–60, 73, 81], the increase in the their use in a lot of types of engineering structures in the last decades calls for improved analysis and design tools for these types of structures. Thus, in this paper, functionally graded shells are considered.

Functionally graded materials (FGMs) [81] are a class of composites that have a smooth and continuous variation of material properties from one surface to another and thus can alleviate the stress concentrations found in laminated composites. Typically, these materials consist of a mixture of ceramic and metal, or a combination of different materials, as reported in literature [81–88]. In this study, ceramic-metal graded shells of revolution with two different power-law variations of the volume fraction of the constituents in the thickness direction are considered [56, 57]. The effect of the power-law exponent and the power-law distribution choice on the mechanical behavior of functionally graded shells and panels is investigated. This paper is motivated by the lack of studies in the technical literature concerning the static analysis of doubly-curved functionally graded shells and panels and the effect of the power-law distribution choice on their mechanical behavior. The aim is to analyse the influence of constituent volume fractions and the effects of constituent material profiles on the static response of the structure. Various material profiles through the functionally graded lamina thickness are used by varying the four parameters of two power-law distributions. A parametric study is undertaken, giving insight into the effects of the material composition on the static response of doubly-curved shell structures. Static characteristics are illustrated by varying one parameter at a time, in turn. It is worth noting that a simple efficient method for accurate evaluation of the through-the-thickness distribution of shear and normal stresses in composite laminated shells under consideration can be easily applied to different generalized displacement field solutions obtained with other numerical methods and with more sophisticated kinematical models.

2 Geometry description and shell fundamental systems

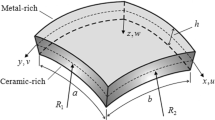
The basic configuration of the problem considered here is a laminated composite doubly-curved shell as shown in Fig. 1. The coordinates along the meridian and circumferential directions of the reference surface are φ and s, respectively. The distance of each point from the shell mid-surface along the normal is ζ. Consider a laminated composite shell made of l laminae or plies, where the total thickness of the shell h is defined as:

(1)

in which h k =ζ k+1−ζ k is the thickness of the k-th lamina or ply.

Fig. 1
figure 1

Coordinate system of a laminated composite shell

Full size image

In this study, doubly-curved shells of revolution and degenerated shells such as plates are considered. For these types of structures the expressions of the meridian curve are reported in [70, 73], so no further consideration will be introduced. The angle formed by the extended normal n to the reference surface and the axis of rotation x 3, or the geometric axis \(x'_{3}\) of the meridian curve, is defined as the meridian angle φ and the angle between the radius of the parallel circle R 0(φ) and the x 1 axis is designated as the circumferential angle ϑ as shown in [70]. For these structures the parametric coordinates (φ,s) define, respectively, the meridian curves and the parallel circles upon the middle surface of the shell. The curvilinear abscissa s(φ) of a generic parallel is related to the circumferential angle ϑ by the relation s=ϑR 0. The horizontal radius R 0(φ) of a generic parallel of the shell represents the distance of each point from the axis of revolution x 3. R b is the shift of the geometric axis of the curved meridian \(x'_{3}\) with reference to the axis of revolution x 3. The position of an arbitrary point within the shell material is defined by coordinates φ (φ 0≤φ≤φ 1), s (0≤s≤s 0) upon the middle surface, and ζ directed along the outward normal and measured from the reference surface (−h/2≤ζ≤h/2).

The present shell theory is based on the following assumptions: (1) the transverse normal is inextensible so that the normal strain is equal to zero: ε n =ε n (φ,s,ζ,t)=0; (2) the transverse shear deformation is considered to influence the governing equations so that normal lines to the reference surface of the shell before deformation remain straight, but not necessarily normal after deformation (a relaxed Kirchhoff-Love hypothesis); (3) the shell deflections are small and the strains are infinitesimal; (4) the shell is moderately thick, therefore it is possible to assume that the thickness-direction normal stress is negligible so that the plane assumption can be invoked: σ n =σ n (φ,s,ζ,t)=0; (5) the linear elastic behavior of anisotropic materials is assumed; (6) the rotary inertia and the initial curvature are also taken into account.

Consistent with the assumptions of a moderately thick shell theory reported above, the displacement field can be expressed in the following form:

(2)

where u φ , u s , w are the displacement components of points lying on the middle surface (ζ=0) of the shell, along meridian, circumferential and normal directions, respectively, while t is the time variable. β φ and β s are normal-to-mid-surface rotations. The in-plane displacements U φ and U s are assumed to vary linearly through the thickness, while W remains independent of ζ. Differently from the previous works by Tornabene [70], the displacement field has been improved taking into account the effective geometry of the shell and in particular the curvature effect has been directly introduced into the kinematical model as proposed by Toorani and Lakis [16].

Due to the changing of the kinematical model, the relationships between strains and generalized displacements along the shell reference surface (ζ=0) become the following:

(3)

In relationships (3), the first four strains \(\varepsilon_{\varphi}^{0}\), \(\varepsilon_{s}^{0}\), \(\gamma_{\varphi}^{0}\), \(\gamma_{s}^{0}\) are the in-plane meridian, circumferential and shearing components, and \(\chi_{\varphi}^{0}\), \(\chi_{s}^{0}\), \(\omega_{\varphi}^{0}\), \(\omega_{s}^{0}\) are the corresponding curvature changes. The last two components \(\gamma_{\varphi n}^{0}\), \(\gamma_{sn}^{0}\) are the transverse shearing strains. The shell is assumed to be made of a linear elastic composite laminate. Accordingly, the following constitutive equations relate internal stress resultants and internal couples with generalized strain components on the middle surface:

(4)

The elastic engineering stiffnesses depending on curvatures are defined as follows:

(5)

where the curvature radius R s for a shell of revolution is defined as:

(6)

The elastic constants \(\bar{Q}_{ij}\) can be found in Tornabene [70] and in Tornabene et al. [73], in which all the constants above introduced are explicitly defined for laminated composite and functionally graded shells and panels of revolution. κ is the shear correction factor, which is usually taken as κ=5/6, such as in the present work. In particular, the determination of shear correction factors for composite laminated structures is still an unresolved issue, because these factors depend on various parameters [23–25].

In Eqs. (4), the four components N φ , N s ,N φs , N sφ are the in-plane meridian, circumferential and shearing force resultants, and M φ , M s , M φs , M sφ are the analogous couples, while T φ , T s are the transverse shear force resultants. In the above definitions (4) the symmetry of shearing force resultants N φs , N sφ and torsional couples M φs , M sφ is not assumed as a further hypothesis, as done in Reissner-Mindlin theory. This hypothesis is satisfied only in the case of spherical shells and flat plates. The assumption under discussion is derived from the consideration that the ratios ζ/R φ , ζ/R s cannot be neglected with respect to unity.

Following the virtual work principle and the Gauss-Codazzi relations [50] for shells of revolution, five equations of equilibrium in terms of internal actions can be written for the present revolution shell element:

(7)

The first three equations in (7) represent translational equilibriums along meridian φ, circumferential s and normal ζ directions, while the last two are rotational equilibrium equations about the s and φ directions, respectively. Furthermore, the generalized external actions q φ , q s , q n , m φ , m s due to the external forces acting on the top \(q_{\varphi}^{ +} ,q_{s}^{ +} ,q_{n}^{ +}\) and bottom \(q_{\varphi}^{ -} ,q_{s}^{ -} ,q_{n}^{ -}\) surfaces of the shell can be evaluated using the static equivalence principle and can be written on the reference surface of the doubly-curved shell as:

(8)

where \(q_{\varphi}^{ +} ,q_{\varphi}^{ -} ,q_{s}^{ +} ,q_{s}^{ -} ,q_{n}^{ +} ,q_{n}^{ -}\) are the external forces in the three principal directions φ,s,ζ.

The three basic sets of equations, namely the kinematic (3), constitutive (4) and equilibrium (7) equations may be combined to give the fundamental system of equations, also known as the governing system of equations. By replacing the kinematic equations (3) into the constitutive equations (4) and the result of this substitution into the equilibrium equations (7), the complete equations of equilibrium in terms of displacement and rotational components can be written as:

(9)

where L ij , i,j=1,…,5 are the equilibrium operators. Three kinds of boundary conditions are considered, namely the fully clamped edge boundary condition (C), the soft simply supported edge boundary condition (S) and the free edge boundary condition (F). The equations describing the boundary conditions can be written as follows:

Clamped edge boundary conditions (C)

(10)
(11)

Soft simply supported edge boundary conditions (S)

(12)
(13)

Free edge boundary conditions (F)

(14)
(15)

3 Discretized equations and numerical implementation for static analysis

The Generalized Differential Quadrature method will be used to discretize the derivatives in the governing equations in terms of generalized displacements as well as the boundary conditions (see Tornabene [56] for a brief review).

Throughout the paper, the Chebyshev-Gauss-Lobatto (C-G-L) grid distribution is assumed and the coordinates of grid points (φ i ,s j ) along the reference surface are:

(16)

In Eqs. (16) N, M are the total number of sampling points used to discretize the domain in φ and s directions of the doubly-curved shell, respectively. It has been proved that, for the Lagrange interpolating polynomials, the Chebyshev-Gauss-Lobatto sampling points rule guarantees convergence and efficiency to the GDQ technique [50–52, 54].

The GDQ procedure enables one to write the equations of equilibrium in discrete form, transforming each space derivative into a weighted sum of node values of independent variables. Each approximate equation is valid in every sampling point. Thus, the whole system of differential equations can be discretized and the global assembling leads to the following set of linear algebraic equations:

(17)

In the equation’s system (17), the partitioning of matrices and vectors is set forth by subscripts b and d, which refer to the system degrees of freedom and stand for boundary and domain, respectively. In this sense, b-equations represent the discrete boundary conditions, which are valid only for the points lying on constrained edges of the shell; while d-equations are the equilibrium equations assigned on interior nodes. In particular, the explicit definition of the boundary degrees of freedom δ b and the domain degrees of freedom δ d are reported below:

(18)

For each degree of freedom, the vectors are arranged for the boundary points as follows:

(19)

and in the following way for the domain points:

(20)

The external forces f b and f d are arranged in analogous way as reported in (18)–(20). Furthermore, the external forces f b acting on the boundaries are assumed to be equal to zero (f b =0). Finally, the construction of the matrices K db ,K dd can be obtained starting from the system written in discrete form in each domain point by using the differential quadrature rule:

(21)

and following the scheme defined by the relations (18)–(20). On the contrary, the matrices K bb ,K db can be obtained starting from the definition of the boundary conditions (10)–(15) written in discrete form in each boundary point using the differential quadrature rule (21) and following the scheme defined by the relations (18)–(20). For a better comprehension of the numerical scheme illustrated above one can refer to the works [48–54, 56–59, 67], in which all the steps previously exposed are reported extensively.

In order to make the computation more efficient, static condensation of boundary degrees of freedom is performed:

(22)

The deflection of the structures considered can be determined by solving the linear algebraic problem (22). In particular, the solution procedure by means of the GDQ technique has been implemented in a MATLAB code.

With the present approach, differently from the finite element method, no integration occurs prior to the global assembly of the linear system, and this results in a further computational cost saving in favor of the Differential Quadrature technique.

4 Stress recovery from 3D elasticity equilibrium equations

The initial 2D problem (9) to be solved derives from the 3D Elasticity and it is simplified by using the well-defined hypotheses of the FSDT. Under the limit of FSDT, the numerical approximated solution captures well the real behavior of shells. Since the 3D Elasticity equations are always valid for the problem under consideration, it is possible to use the 2D approximated solution to evaluate some quantities such as in-plane stresses and their derivatives and to infer others quantities of interest (such as shear and normal stresses) by solving the 3D equilibrium equations [72, 74, 75, 77]. Thus, starting from the 3D Elasticity in orthogonal coordinates for a general doubly-curved shell [12], the 3D equilibrium equations for shells of revolution can be written as follows:

(23)

It appears that, if the stresses σ φ , σ s , τ φs and their derivatives σ φ,φ , σ s,s , τ φs,φ , τ φs,s are known in all the points of the 3D solid shell, the above three differential equations can be seen as three independent differential equations of the first order that can be solved via the GDQ method along the thickness direction ζ. It is worth noting that the third equation can be evaluated after the numerical computation of the first two unknowns τ φn , τ sn and their derivatives τ φn,φ , τ sn,s . In order to determine the unknowns at the right side of Eqs. (23), it is possible to start from the static solution in terms of the displacements obtained in the previous paragraph. Thus, after solving the static problem (22), all the displacements in the 3D solid shell can be written in discrete form using the kinematical model (2):

(24)

where T is the total number of sampling points used to discretize the domain in ζ direction. The Chebyshev-Gauss-Lobatto (C-G-L) grid distribution is assumed for the coordinate of grid points ζ m along the shell thickness direction ζ:

(25)

By using the Differential Quadrature rule [32], an approximation of the kinematic relations (3) can be obtained in discrete form:

(26)

Since the kinematic relation ε φ ,ε s ,ε φs of the 3D shell medium are the following:

(27)

by using the well-known Hooke law [18]:

(28)

and the Differential Quadrature rule [32], the derivatives of the stress components σ φ,φ , σ s,s , τ φs,φ , τ φs,s can be approximated as follows:

(29)

By considering the boundary conditions at the bottom surface of the shell, the first two 3D equilibrium equations (23) in terms of shear stresses τ φn , τ sn can be directly and independently solved at each reference surface point (φ i ,s j ). The following linear algebraic system of equations obtained via the GDQ method is used:

(30)

In order to satisfy the second boundary condition at the top surface of the shell, \(\tau_{\varphi n( ijT )} = q_{\varphi ( ij )}^{ +}\) and \(\tau_{sn( ijT )} = q_{s( ij )}^{ +}\) , respectively, the corrected profiles of the shear stresses can be defined in the following manner:

(31)

Finally, the last 3D equilibrium equation (23) can be written in discrete form and solved via the GDQ method:

(32)

where the derivatives \(\bar{\tau}_{\varphi n,\varphi} \), \(\bar{\tau}_{sn,s}\) of the shear stresses \(\bar{\tau}_{\varphi n}\), \(\bar{\tau}_{sn}\) can be approximated using the Differential Quadrature rule [32]:

(33)

In order to satisfy the second boundary condition at the top surface of the shell \(\sigma_{n( ijT )} = q_{n( ij )}^{ +}\), the correction profile of the normal stress can be defined as:

(34)

Furthermore, it is possible to use the generalized Hooke law [18] to evaluate the deformations γ φn ,γ sn ,ε n :

(35)

It is worth noting that the relations (35) do not guarantee the strain compatibility. In fact, some discontinuities can arise. However, the solution obtained in this way can be used as a good approximation of some quantities that are considered a priori fixed or negligible, when the 2D First-order Shear Deformation Theory is used. Finally, the stresses σ φ , σ s , τ φs can be corrected taking into account the contribution of the approximated deformation ε n using the following generalized Hooke expressions:

(36)

In the end, all the stress components \(\bar{\sigma}_{\varphi} \), \(\bar{\sigma}_{s}\), \(\bar{\tau}_{\varphi s}\), \(\bar{\tau}_{\varphi n}\), \(\bar{\tau}_{sn}\), \(\bar{\sigma}_{n}\) of the 3D shell medium are numerically computed using the relations (31), (34) and (36).

It should be noted that, the simple efficient method for accurate evaluation of the through-the-thickness distribution of shear and normal stresses in composite laminated shells presented above can be easily applied to different generalized displacement field solutions obtained with other numerical methods and with more sophisticated kinematical models. In fact, no restriction has been assumed about the methodology used to perform the pre-processing static analysis.

5 Numerical applications and results

In the present section, some results and considerations about the static analysis problem of laminated composite and four parameter functionally graded panels are presented. The analysis has been carried out by means of the numerical procedures discussed above. One of the aims is to compare results obtained through the GDQ method with the ones obtained with semi-analytical methods and through finite element techniques. In order to verify the accuracy of the present methodology, some comparisons have been performed. The solution procedure by means of the GDQ technique has been implemented in a MATLAB code. As illustrated below, the shear and normal stresses evaluated a posteriori by the present methodology are in good agreement with the results obtained with semi-analytical formulations and with finite element methods. The geometrical boundary conditions for a panel are identified by the same convention presented in the works [70–73].

For all the GDQ results presented below, the Chebyshev-Gauss-Lobatto grid distributions (16) with N=M=31 along the reference surface and (25) with T=101 along the shell thickness direction have been assumed.

In order to validate the GDQ numerical solution, comparisons with exact solutions of Kirchhoff-Love plates and cylindrical shell and Reissner-Mindlin cylindrical and spherical panels are shown in Table 1 and in Fig. 2. For an isotropic rectangular plate simply supported at all the edges and subjected to a sinusoidal distributed load, the well-known exact classical solution [1, 18, 74, 75] is considered:

(37)

where q nm is the maximum distributed load associated with the wave number n,m and a,b are the length of the edges of the plate, respectively. The results are obtained considering n=m=1 and q 0=q 11=−10000 Pa for a square plate (a=b=1 m) made of isotropic material with E=2.1⋅1011 Pa, ν=0.3, ρ=7800 kg/m3.

Fig. 2
figure 2

Convergence of the GDQ solution with decreasing thicknesses for a (SSSS) square plate, a (FS) annular plate, a (SSSS) cylindrical panel, a (SSSS) spherical panel, (CF) and (SF) cylindrical shells

Full size image
Table 1 Static deflection for a (SSSS) square plate at the point A=(0.5a,0.5a), for a (FS) annular plate at the point A=(R i ,0), for a (SSSS) cylindrical panel at the point A=(0.5L,0.5Δϑ)=(0.5L,0.5(ϑ 1−ϑ 0)), for a (SSSS) spherical panel at the point A=(0.5Δφ,0.5Δϑ)=(0.5(φ 1−φ 0),0.5(ϑ 1−ϑ 0)), for (CF) and (SF) cylindrical shells at the point A=(L,0) using a 31×31 Chebyshev-Gauss-Lobatto (C-G-L) grid distribution
Full size table

For an isotropic annular plate with a=R e −R i =1.5−0.5=1 m, simply supported at the outer edge (x=R e ), free at the inner edge (x=R i ) and subjected to a uniformly distributed load q 0=−10000 Pa, the well-known classical exact solution [1, 18, 74, 75] is used:

(38)

The annular plate is made of isotropic material with E=2.1⋅1011 Pa, ν=0.3, ρ=7800 kg/m3, as above.

For an isotropic cylindrical shell clamped at the top edge and free at the bottom edge and subjected to a uniformly distributed pressure load, the well-known exact classical solution [1] can be written as:

(39)

where q 0 is the internal pressure load and R,h are the radius and the thickness of the cylinder, respectively. When an isotropic cylindrical shell simply supported at the top edge and free at the bottom edge and subjected to a uniformly distributed pressure load is considered, the well-known exact classical solution [1] assumes the following form:

(40)

The results for the last two cases are obtained considering q 0=10000 Pa for cylinders (R=L=10 m, ϑ∈[0∘,360∘]) made of isotropic material with E=0.73⋅1011 Pa, ν=0.3, ρ=2700 kg/m3.

Furthermore, for isotropic cylindrical and spherical panels simply supported at all the edges and subjected to a sinusoidal distributed load the exact benchmark solutions have been obtained by Brischetto and Carrera using the Carrera’s Unified Formulation (CUF) [19–21]. The maximum distributed load q nm associated to the wave number n=m=1 is q 0=q 11=10000 Pa for a cylindrical panel (R=L=10 m, ϑ∈[−30∘,30∘]) and for a spherical panel R=10 m, φ∈[60∘,120∘], ϑ∈[−30∘,30∘]. Both of these two structures are made of isotropic material with E=0.73⋅1011 Pa, ν=0.3, ρ=2700 kg/m3.

5.1 Laminated composite shells and panels

Table 1 and Fig. 2 illustrate the convergence of the GDQ FSDT numerical solutions to the exact ones by decreasing the thickness of the structures. By plotting the ratio between the GDQ FSDT numerical solution w gdq and exact solution w exact versus the ratio h/a, well-converging results are shown and no oscillations are arisen. Thus, it is possible to conclude that the present methodology is locking-free. Finally, Table 2 shows results of the present FSDT GDQ solution compared with the higher-order solutions obtained by Shu [89] and the FSDT exact solution obtained by Carrera and Brischetto using CUF approach. The details regarding the geometry of the structures and the material mechanical properties are reported in [89]. As it appears from Table 2, GDQ results are in good agreement with the ones presented in literature for laminated shell panels.

Table 2 Dimensionless deflection for laminated spherical and cylindrical panels
Full size table

In order to assess the effectiveness of the foregoing computational procedure for the evaluation of through-the-thickness stresses, Fig. 3 presents all the stress components σ x , σ y , τ xy , τ xn , τ yn , σ n at the point C=(0.25a,0.25b) obtained using the GDQ method compared with the semi-analytical results obtained by Reddy [18] for a (90/0/90/0/90) completely simply supported square plate (a=b=1 m) with a constant thickness (h=0.1 m) and subjected to a uniformly distributed load \((q_{n}^{ +} = - 10000\mbox{ Pa})\) on the top surface of the plate. The unrecovered evaluations obtained using Eqs. (28) and the recovered evaluations derived from Eqs. (36) are reported for stresses σ x , σ y , τ xy in Fig. 3. The material properties of each lamina made of composite material are the following: E 11=137.9 GPa, E 22=E 33=8.96 GPa, G 12=G 13=7.1 GPa, G 23=6.21 GPa, ν 12=ν 13=0.3, ν 23=0.49, ρ=1450 kg/m3. As appears from Fig. 3, the discrepancy between semi-analytical and numerical results closes to zero.

Fig. 3
figure 3

Through-the-thickness variation of stress components [Pa] for a (SSSS) square plate at the point C=(0.25a,0.25a) with a (90/0/90/0/90) lamination scheme, when a uniformly distributed load \(q_{n}^{ +} = - 10000\mbox{ Pa}\) at the top surface is applied

Full size image

Figures 4, 5 and 6 show the GDQ recovered and 3D FEM displacements, strains and stresses σ x , σ y , τ xy , τ xn , τ yn , σ n for a (0/45/65) completely clamped square plate (a=b=1 m) with a constant thickness (h=0.1 m) subjected to uniformly distributed loads in the two directions x,ζ (\(q_{x}^{ +} = 10000\mbox{ Pa}\), \(q_{n}^{ +} = - 10000\mbox{ Pa}\)) on the top surface of the plate. The material properties of each lamina are the same as the previous cases of Fig. 3. The unrecovered evaluations obtained using Eqs. (28) and the recovered evaluations derived from Eqs. (36) are reported for stresses σ x , σ y , τ xy . As can be seen using the corrected stresses (36), the accuracy of the stress profiles is better than the one obtained with relations (28), even though the evaluation has been obtained using strains (35) that do not satisfy the compatibility conditions. For the three laminated plate the thickness of the middle lamina is equal to h 2=0.04 m, while the bottom and top laminae have the same thickness h 1=h 3=0.03 m. Furthermore, the 3D FEM results are obtained using 16000 brick elements with 20 nodes in Straus (or Strand) program. The FEM mesh is obtained using 10 elements through the thickness direction and 40 elements along both edges of the plate. The two solutions GDQ and 3D FEM are always in good agreement for all the examples and the quantities considered. In all the figures illustrated above, the three displacements and the six strain and stress components recovered by the GDQ method have been compared with the 3D FEM results. It appears that the GDQ results are in good agreement with those obtained with 3D FEM. Furthermore, the computational effort is remarkably small (few minutes for the GDQ results vs. some hours for the 3D FEM results) and the approximations obtained are very reliable.

Fig. 4
figure 4

Through-the-thickness variation of displacements components [m] for a (CCCC) square plate at the point C=(0.25a,0.25a) with a (0/45/65) lamination scheme, when uniformly distributed loads \(q_{x}^{ +} = 10000\mbox{ Pa}\), \(q_{n}^{ +} = - 10000\mbox{ Pa}\) at the top surface are applied

Full size image
Fig. 5
figure 5

Through-the-thickness variation of strain components for a (CCCC) square plate at the point C=(0.25a,0.25a) with a (0/45/65) lamination scheme, when uniformly distributed loads \(q_{x}^{ +} = 10000\mbox{ Pa}\), \(q_{n}^{ +} = - 10000\mbox{ Pa}\) at the top surface are applied

Full size image
Fig. 6
figure 6

Through-the-thickness variation of stress components [Pa] for a (CCCC) square plate at the point C=(0.25a,0.25a) with a (0/45/65) lamination scheme, when uniformly distributed loads \(q_{x}^{ +} = 10000\mbox{ Pa}\), \(q_{n}^{ +} = - 10000\mbox{ Pa}\) at the top surface are applied

Full size image

It is worth noting that examples illustrated above are related to moderately thick degenerate shells. The well-known FSDT validity range is:

(41)

For all the examples the ratio h/a=1/10 has been chosen. The results are good even if a limit case of the FSDT has been considered. Furthermore, it is possible to demonstrate that results improve by decreasing the plate thickness.

5.2 Functionally graded shells and panels

Typically, the functionally graded materials are made of a mixture of two constituents. In this work, it is assumed that the functionally graded material is made of a mixture of ceramic and metal constituents: Zirconia and Aluminum. Young’s modulus, Poisson’s ratio and mass density for the Zirconia are E C =168 GPa, ν C =0.3, ρ C =5700 kg/m3, and for the Aluminum are E M =70 GPa, ν M =0.3, ρ M =2707 kg/ m3, respectively. The material properties of the functionally graded shell vary continuously and smoothly in the thickness direction ζ and are functions of volume fractions of constituent materials. The Young’s modulus E(ζ), Poisson’s ratio ν(ζ) and mass density ρ(ζ) of the functionally graded shell can be expressed as a linear combination:

(42)

where ρ C ,E C ,ν C ,V C and ρ M ,E M ,ν M ,V M represent mass density, Young’s modulus, Poisson’s ratio and volume fraction of the ceramic and metal constituent materials, respectively. In this paper, the ceramic volume fraction V C follows two simple four-parameter power-law distributions [56–60, 73]:

(43)

where the volume fraction index p (0≤p≤∞) and the parameters a,b,c dictate the material variation profile through the functionally graded shell thickness. It is worth noting that the volume fractions of all the constituent materials should add up to unity:

(44)

In order to choose the three parameters a,b,c suitably, the relation (44) must be always satisfied for every volume fraction index p. By considering the relations (43), when the power-law exponent is set equal to zero (p=0) or equal to infinity (p=∞), the homogeneous isotropic material is obtained as a special case of functionally graded material. In fact, from Eqs. (44), (43) and (42) it is possible to obtain:

(45)

Some material profiles through the functionally graded shell thickness are illustrated in Fig. 7.

Fig. 7
figure 7

Variations of the ceramic volume fraction V C through the thickness for different values of the three parameters a, b, c and the power-law index p: (a) FGM 1(a=1/b=0/c/p), (b) FGM 2(a=1/b=0/c/p), (c) FGM 1(a=1/b=1/c=2/p), (d) FGM 2(a=1/b=1/c=2/p), (e) FGM 1(a=1/b=0.5/c=2/p), (f) FGM 2(a=1/b=0.5/c=2/p)

Full size image

Figures 8–13 present results for single-curved and doubly curved functionally graded panels of revolution. Figures 8 and 9 illustrate the GDQ recovered and 3D FEM stresses σ x , σ s , τ xs , τ xn , τ sn , σ n for a completely clamped cylindrical panel (L=1 m, R=2 m, ϑ∈[0∘,40∘]) with a constant thickness (h=0.06 m) subjected to a uniformly distributed load \((q_{n}^{ +} = - 10000\mbox{ Pa})\) on the top surface of the panel, while Figs. 10, 11 and 12 show the same recovered stresses σ φ , σ s , τ φs , τ φn , τ sn , σ n for a completely clamped spherical panel (R φ =R s =2.03 m, φ∈[50∘,90∘], ϑ∈[0∘,40∘]) with a constant thickness (h=0.06 m) subjected to a uniformly distributed load \((q_{n}^{ +} = - 10000\mbox{ Pa})\) on the top surface of the panel.

Fig. 8
figure 8

Through-the-thickness variation of stress components [Pa] for a functionally graded (CCCC) FGM 1(a=0/−1≤b≤0/c=2/p=10) cylindrical panel at the point C=(0.25L,10∘) when a uniformly distributed load \(q_{n}^{ +} = - 10000\mbox{ Pa}\) at the top surface is applied

Full size image
Fig. 9
figure 9

Through-the-thickness variation of stress components [Pa] for a functionally graded (CCCC) FGM 1(a=1/b=1/1≤c≤15/p=10) cylindrical panel at the point C=(0.25L,10∘) when a uniformly distributed load \(q_{n}^{ +} = - 10000\mbox{ Pa}\) at the top surface is applied

Full size image
Fig. 10
figure 10

Through-the-thickness variation of stress components [Pa] for a functionally graded (CCCC) FGM 1(a=1/b=0/c=2/0≤p≤∞) spherical panel at the point C=(60∘,10∘) when a uniformly distributed load \(q_{n}^{ +} = - 10000\mbox{ Pa}\) at the top surface is applied

Full size image
Fig. 11
figure 11

Through-the-thickness variation of stress components [Pa] for a functionally graded (CCCC) FGM 1(a=1/0≤b≤1/c=2/p=10) spherical panel at the point C=(60∘,10∘) when a uniformly distributed load \(q_{n}^{ +} = - 10000\mbox{ Pa}\) at the top surface is applied

Full size image
Fig. 12
figure 12

Through-the-thickness variation of stress components [Pa] for a functionally graded (CCCC) FGM 1(0.2≤a≤1.2/b=0.2/c=3/p=20) spherical panel at the point C=(60∘,10∘) when a uniformly distributed load \(q_{n}^{ +} = - 10000\mbox{ Pa}\) at the top surface is applied

Full size image

Figure 8 presents results for a FGM 1(a=0/−1≤b≤0/c=2/p=10) cylindrical panel, while Fig. 9 shows results for a FGM 1(a=1/b=1/1≤c≤15/p=10) cylindrical panel. Figures 8 and 9 show the recovered stresses at the point C=(0.25L,10∘). It should be noted that the corrected stresses σ x , σ s , τ xs (36), which also take into account the normal strain, are illustrated in Figs. 8 and 9 as well as in all the remaining figures. All the six stress components recovered by the GDQ method are compared with the 3D FEM results obtained using 16000 brick elements with 20 nodes in Straus (or Strand) code for the special isotropic panel made of Zirconia. The FEM mesh is obtained using 10 elements through the thickness direction and 40 elements along both edges of the cylindrical panel. As it can be seen, in Fig. 8 the variation of the stress profiles are illustrated for various values of the parameter b∈[−1,0] maintaining the same value for the other three parameters a, c, p, while Fig. 9 shows the variation of the stress profiles for different values of the parameter c∈[1,15] maintaining the same value for the other three parameters a, b, p.

In the same way, in Fig. 10 results for a FGM 1(a=1/b=0/c=2/0≤p≤∞) spherical panel are reported, while in Fig. 11 and in Fig. 12 the FGM 1(a=1/0≤b≤1/c=2/p=10) and FGM 1(0.2≤a≤1.2/b=0.2/c=3/p=20) spherical panels are considered, respectively. The corrected stresses σ φ , σ s , τ φs (36) are represented. Figures 10, 11 and 12 show the recovered stresses at the point C=(60∘,10∘). The effect of the variation of the parameter p∈[0,∞] is illustrated in Fig. 10, while in Fig. 11 and in Fig. 12 the effect of the parameters b∈[0,1] and a∈[0.2,1.2] are shown, respectively. All the six stress components recovered by the GDQ method are compared with the 3D FEM results obtained using 16000 brick elements with 20 nodes in Straus (or Strand) code for the special isotropic panel made of Zirconia. The FEM mesh is obtained using 10 elements through the thickness direction and 40 elements along both edges of the spherical panel.

As it can be seen from Figs. 8–12, when the functionally graded material degenerates into the special isotropic case of Zirconia or Aluminum, all the six stress components recovered by the GDQ method are in good agreement with those obtained with 3D FEM, as expected. It is important to note that, when the FGM 2 power-law distribution is used, the results are completely different. Thus, in order to prove this statement new results regarding the doubly-curved free-form shell panel of revolution are presented. Figure 13 illustrates the GDQ recovered stresses σ φ , σ s , τ φs , τ φn , τ sn , σ n for a FGM 2(a=1/b=0/c=2/0≤p≤∞) completely clamped free-form meridian panel. This structure has a constant thickness (h=0.06 m) and is subjected to uniformly distributed load \((q_{n}^{ +} = - 10000\mbox{ Pa})\) on the top surface. The geometrical properties , , w, R b =0 m, ϑ∈[0∘,120∘] for the free-form meridian structure involved with Fig. 12 are illustrated in Table 3 of the paper by Tornabene et al. [73]. The figure under consideration presents the stresses recovered by the GDQ method at the points C=(0.25(φ 1−φ 0)+φ 0,0.25(ϑ 1−ϑ 0)) for different values of the parameter p∈[0,∞]. Comparing the results of Fig. 13 with the ones of Fig. 10, the effect of the choice of one of the two power-law distribution FGM 1 and FGM 2 can be inferred.

Fig. 13
figure 13

Through-the-thickness variation of stress components [Pa] for a functionally graded (CCCC) FGM 2(a=1/b=0/c=2/0≤p≤∞) free-form meridian panel at the points C=(61.7004∘,30∘) when a uniformly distributed load \(q_{n}^{ +} = - 10000\mbox{ Pa}\) at the top surface is applied

Full size image

As can be seen from Figs. 4, 5 and 6 and 8–12, the GDQ numerical results show an excellent agreement with those obtained with 3D FEM without using mixed formulations and higher order kinematical models. The latter numerical procedure requires an increase of the degrees of freedom. The previous considerations are valid if all the theoretical hypotheses of moderately thick shells and plates, presented above, are satisfied. It should be noted that, increasing the thickness of the shell over the interval (41), the deformation through the thickness could be not negligible and thus the FSDT is not valid. In this case, the higher order kinematical models are needed in order to catch the real static behaviour of shells and plates, as shown in literature [18–20, 23, 24, 26, 29, 31].

6 Conclusion remarks and summary

A Generalized Differential Quadrature method application to the static analysis of functionally graded and laminated composite shells and panels of revolution has been presented to illustrate the versatility and the accuracy of this methodology. The adopted shell theory is the First-order Shear Deformation Theory. In particular, the Toorani-Lakis theory has been used as starting point to obtained the governing equations for shells. The 2D equilibrium equations have been discretized with the GDQ method producing a standard linear algebraic problem. After the solution of the fundamental system of equations, in terms of displacements of points lying on the shell middle surface, the generalized strains and stress resultants are evaluated by applying the Differential Quadrature rule to the generalized displacements. The transverse shear and normal stress profiles through the thickness are reconstructed a posteriori. The local three-dimensional equilibrium equations are used. No preliminary recovery or regularization procedure on the extensional and flexural strain fields is needed, when the Differential Quadrature technique is used. The examples presented show that the GDQ method can produce accurate results by using a small number of sampling points. Numerical solutions have been compared with those presented in literature, such as semi-analytical methods, and the 3D FEM elasticity ones obtained using commercial programs such as Straus (or Strand). The comparisons conducted with semi-analytical and FEM methods confirm that the GDQ simple numerical method provides accurate and computationally low cost results for all the structures considered. Furthermore, discretizing and programming procedures are quite easy. The GDQ results show precision and accuracy for all the cases treated, without using mixed formulations and higher order kinematical models. Two kinds of ceramic-metal graded shells of revolution, each with a four parameter power-law distribution of the volume fraction of the constituents in the thickness direction, have been considered. Various material profiles through the functionally graded shell thickness have been illustrated by varying the four parameters of the two power-law distributions. The numerical results have shown the influence of the power-law exponent, the power-law distribution choice and the choice of the four parameters on the static response of functionally graded shells considered. Within the limits of the FSDT, the proposed procedure can be applied to a huge number of engineering problems. Furthermore, it is worth noting that the simple efficient method, for accurate evaluation of the through-the-thickness distribution of shear and normal stresses in plates and shells, can be easily applied to different generalized displacement field solutions obtained with other numerical methods and with more sophisticated kinematical models.