The Brown measure of the sum of a self-adjoint element and an imaginary multiple of a semicircular element

Abstract

We compute the Brown measure of $x_{0}+i\sigma _{t}$, where $\sigma _{t}$ is a free semicircular Brownian motion and $x_{0}$ is a freely independent self-adjoint element that is not a multiple of the identity. The Brown measure is supported in the closure of a certain bounded region $\Omega _{t}$ in the plane. In $\Omega _{t},$ the Brown measure is absolutely continuous with respect to Lebesgue measure, with a density that is constant in the vertical direction. Our results refine and rigorize results of Janik, Nowak, Papp, Wambach, and Zahed and of Jarosz and Nowak in the physics literature. We also show that pushing forward the Brown measure of $x_{0}+i\sigma _{t}$ by a certain map $Q_{t}:\Omega _{t} \rightarrow {\mathbb {R}}$ gives the distribution of $x_{0}+\sigma _{t}.$ We also establish a similar result relating the Brown measure of $x_{0}+i\sigma _{t}$ to the Brown measure of $x_{0}+c_{t}$, where $c_{t}$ is the free circular Brownian motion.

1 Introduction

1.1 Sums of independent random matrices

A fundamental problem in random matrix theory is to understand the eigenvalue distribution of sums of independent random matrices. When the random matrices are Hermitian, the subordination method, introduced by Voiculescu [36] and further developed by Biane [3] and Voiculescu [37], gives a powerful method of analyzing the problem in the setting of free probability. (See Sect. 5.2 for a brief discussion of the subordination method.) For related results in the random matrix setting, see, for example, works of Pastur and Vasilchuk [30] and of Kargin [26].

A natural next step would be to consider non-normal random matrices of the form $X+iY$ where X and Y are independent Hermitian random matrices. Although a general framework has been developed for analyzing combinations of freely independent elements in free probability (see works of Belinschi, Mai, and Speicher [6] and Belinschi, Śniady, and Speicher [7]), it does not appear to be easy to apply this framework to get analytic results about the $X+iY$ case.

The $X+iY$ problem has been analyzed at a nonrigorous level in the physics literature. A highly cited paper of Stephanov [32] uses the case in which X is Bernoulli and Y is GUE to provide a model of QCD. In the case that Y is GUE, work of Janik, Nowak, Papp, Wambach, and Zahed [23] identified the domain into which the eigenvalues should cluster in the large-N limit. Then, work of Jarosz and Nowak [24, 25] analyzed the limiting eigenvalue distribution for general X and Y,  with explicit computations of examples when Y is GUE and X has various distributions [24, Sect. 6.1].

In this paper, we compute the Brown measure of $x_{0}+i\sigma _{t},$ where $\sigma _{t}$ is a semicircular Brownian motion and $x_{0}$ is an arbitrary self-adjoint element freely independent of $\sigma _{t}.$ This Brown measure is the natural candidate for the limiting eigenvalue distribution of random matrices of the form $X+iY$ where X and Y are independent and Y is GUE. We also relate the Brown measure of $x_{0}+i\sigma _{t}$ to the distribution of $x_{0}+\sigma _{t}$ (without the factor of i). Our computation of the Brown measure of $x_{0}+i\sigma _{t}$ refines and rigorizes the results of [23] and [24, 25], using a different method, while the relationship between $x_{0}+i\sigma _{t}$ and $x_{0}+\sigma _{t}$ is a new result. See Sect. 1.4 for further discussion of these works and Sects. 5.4 and 9 for a detailed comparison of results.

Our work extends that of Ho and Zhong [22], which (among other results) computes the Brown measure of $x_{0}+i\sigma _{t}$ in the case $x_{0} =y_{0}+\tilde{\sigma }_{t},$ where $\tilde{\sigma }_{t}$ is another semicircular Brownian motion, freely independent of both $y_{0}$ and $\sigma _{t}.$ In this case, $x_{0}+i\sigma _{t}$ has the form of $y_{0}+c_{2t},$ where $c_{t}$ is a free circular Brownian motion.

Our results are based on the PDE method introduced in [12]. This method has been used in subsequent works by Ho and Zhong [22], Demni and Hamdi [11], and Hall and Ho [19] and is discussed from the physics point of view by Grela, Nowak, and Tarnowski in [16]. See also the expository article [18] of the first author for an introduction to the PDE method. Similar PDEs, in which the regularization parameter in the construction of the Brown measure becomes a variable in the PDE, have appeared in the physics literature in the work of Burda, Grela, Nowak, Tarnowski, and Warchoł [9, 10].

Since this article was posted on the arXiv, three papers have appeared that extend our results have appeared. The paper [20] of Ho examines in detail the case in which $x_{0}$ is the sum of a self-adjoint element and a freely independent semicircular element, so that $x_{0}+i\sigma _{t}$ becomes the sum of a self-adjoint element and a freely independent elliptic element. The paper [21] extends the results of the present paper by allowing $x_{0}$ to be unbounded. Finally, the paper [39] of Zhong analyzes the Brown measure of $x_{0}+g,$ where g is a twisted elliptic element and $x_{0}$ is freely independent of g but otherwise arbitrary. In the case that $x_{0}$ is self-adjoint and g is an imaginary multiple of a semicircular element, Zhong’s results reduce to ours.

1.2 Statement of results

Let $\sigma _{t}$ be a semicircular Brownian motion living in a tracial von Neumann algebra $({\mathcal {A}},\tau )$ and let $x_{0}$ be a self-adjoint element of ${\mathcal {A}}$ that is freely independent of every $\sigma _{t},$ $t>0.$ (In particular, $x_{0}$ is a bounded self-adjoint operator.) Throughout the paper, we let $\mu$ be the distribution of $x_{0},$ that is, the unique compactly supported probability measure on ${\mathbb {R}}$ such that

$$\begin{aligned} \int _{{\mathbb {R}}}x^{n}~\mathrm{d}\mu (x)=\tau (x_{0}^{n}), \quad \text {for all } n\in {\mathbb {N}}. \end{aligned}$$

(1.1)

Our goal is then to compute the Brown measure of the element

$$\begin{aligned} x_{0}+i\sigma _{t} \end{aligned}$$

(1.2)

in ${\mathcal {A}}.$ (See Sect. 2 for the definition of the Brown measure.) Throughout the paper, we impose the following standing assumption about $\mu .$

Assumption 1.1

The measure $\mu$ is not a $\delta$-measure, that is, not supported at a single point.

Of course, the case in which $\mu$ is a $\delta$-measure is not hard to analyze—in that case, $x_{0}+i\sigma _{t}$ has the form $a+i\sigma _{t},$ for some constant $a\in {\mathbb {R}},$ so that the Brown measure is a semicircular distribution on a vertical segment through a. But this case is different; in all other cases, the Brown measure is absolutely continuous with respect to the Lebesgue measure on a two-dimensional region in the plane. Thus, our main results do not hold as stated in the case that $\mu$ is a $\delta$-measure.

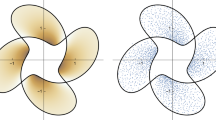
The element (1.2) is the large-N limit of the following random matrix model. Let $Y^{N}$ be an $N\times N$ random variable distributed according to the Gaussian unitary ensemble. Let $X^{N}$ be a sequence of self-adjoint random matrices that are independent of $Y^{N}$ and whose eigenvalue distributions converge almost surely to the law $\mu$ of $x_{0}.$ (The $X^{N}$’s may, for example, be chosen to be deterministic diagonal matrices, which is the case in all the simulations shown in this paper.) Then, the random matrices

$$\begin{aligned} X^{N}+i\sqrt{t}Y^{N} \end{aligned}$$

(1.3)

will converge in $*$-distribution to $x_{0}+i\sigma _{t}.$

In this paper, we compute the Brown measure of $x_{0}+i\sigma _{t}.$ This Brown measure is the natural candidate for the limiting empirical eigenvalue distribution of the random matrices in (1.3). Our main results are summarized briefly in the following theorem.

Theorem 1.2

For each $t>0,$ there exists a continuous function $b_{t}:{\mathbb {R}}\rightarrow [0,\infty )$ such that the following results hold. Let

$$\begin{aligned} \Omega _{t}=\left\{ \left. a+ib\in {\mathbb {C}}\right| ~\left| b\right| <b_{t}(a)\right\} . \end{aligned}$$

Then, the Brown measure of $x_{0}+i\sigma _{t}$ is supported on the closure of $\Omega _{t}$ and $\Omega _{t}$ itself is a set of full Brown measure. Inside $\Omega _{t}$, the Brown measure is absolutely continuous with a density that is constant in the vertical directions. Specifically, the density $w_{t}(a+ib)$ is independent of b in $\Omega _{t}$ and has the form:

$$\begin{aligned} w_{t}(a+ib)=\frac{1}{2\pi t}\left( \frac{da_{0}^{t}(a)}{da} -\frac{1}{2}\right) ,\quad a+ib\in \Omega _{t}, \end{aligned}$$

for a certain function $a_{0}^{t}.$

See Figs. 1 and 2.

Fig. 1

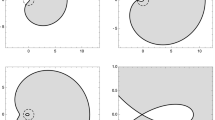
The top of the figure shows the domain $\Omega _{t}$ for the case $\mu =\frac{1}{3}\delta _{-1}+\frac{2}{3}\delta _{1}$ and $t=1.05,$ together with a simulation of the corresponding random matrix model. The bottom of the figure shows the density (in $\Omega _{t}$) of the Brown measure as a function of a

Fig. 2

The top of the figure shows the domain $\Omega _{t}$ for the case in which $\mu$ has density $3x^{2}$ on [0, 1] and $t=1/4,$ together with a simulation of the corresponding random matrix model. The bottom of the figure shows the density (in $\Omega _{t}$) of the Brown measure as a function of a

We now describe how to compute the functions $b_{t}$ and $a_{0}^{t}$ in Theorem 1.2. Recall that $\mu$ is the law of $x_{0},$ as in (1.1). We then fix $t>0$ and consider two equations:

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2}+v^{2}}~\mathrm{d}\mu (x)&=\frac{1}{t} \end{aligned}$$

(1.4)

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{x}{(a_{0}-x)^{2}+v^{2}}~\mathrm{d}\mu (x)&=\frac{a}{t}, \end{aligned}$$

(1.5)

where we look for a solution with $v>0$ and $a_{0}\in {\mathbb {R}}.$ We will show in Sect. 7.2 that there can be at most one such pair $(v,a_{0})$ for each $a\in {\mathbb {R}}.$ If, for a given $a\in {\mathbb {R}},$ we can find $v>0$ and $a_{0}\in {\mathbb {R}}$ solving these equations, we set

$$\begin{aligned} a_{0}^{t}(a)=a_{0} \end{aligned}$$

(1.6)

and

$$\begin{aligned} b_{t}(a)=2v. \end{aligned}$$

(1.7)

If, on the other hand, no solution exists, we set $b_{t}(a)=0$ and leave $a_{0}^{t}(a)$ undefined. (If $b_{t}(a)=0$, there are no points of the form $a+ib$ in $\Omega _{t}$ and so the density of the Brown measure is undefined.)

The equations (1.4) and (1.5) can be solved explicitly for some simple choices of $\mu$, as shown in Sect. 10. For any reasonable choice of $\mu ,$ the equations can be easily solved numerically.

We now explain a connection between the Brown measure of $x_{0}+i\sigma _{t}$ and two other models. In addition to the semicircular Brownian motion $\sigma _{t},$ we consider also a circular Brownian motion $c_{t}.$ This may be constructed as:

$$\begin{aligned} c_{t}=\sigma _{t/2}+i\tilde{\sigma }_{t/2}, \end{aligned}$$

where $\sigma _{\cdot }$ and $\tilde{\sigma }_{\cdot }$ are two freely independent semicircular Brownian motions. We now describe a remarkable direct connection between the Brown measure of $x_{0}+i\sigma _{t}$ and the Brown measure of $x_{0}+c_{t},$ and a similar direct connection between the Brown measure of $x_{0}+i\sigma _{t}$ and the law of $x_{0}+\sigma _{t}.$ We remark that a fascinating indication of a connection between the behavior of $x_{0} +\sigma _{t}$ and the behavior of $x_{0}+i\sigma _{t}$ were given previously in the work of Janik, Nowak, Papp, Wambach, and Zahed, discussed in Sect. 5.4. Note that since $\sigma _{t}$ has the same law as $\sigma _{t/2} +\tilde{\sigma }_{t/2},$ we can describe the three random variables in question as:

$$\begin{aligned} x_{0}+\sigma _{t}&\equiv x_{0}+\sigma _{t/2}+\tilde{\sigma }_{t/2}\\ x_{0}+c_{t}&\equiv x_{0}+\sigma _{t/2}+i\tilde{\sigma }_{t/2}\\ x_{0}+i\sigma _{t}&\equiv x_{0}+i\sigma _{t/2}+i\tilde{\sigma }_{t/2}, \end{aligned}$$

where the notation $A\equiv B$ means that A and B have the same $*$-distribution and therefore the same Brown measure.

The Brown measure of $x_{0}+c_{t}$ was computed by the second author and Zhong in [22]. They also established that the Brown measure of $x_{0}+c_{t}$ is related to the law of $x_{0}+\sigma _{t}$. We then show that the Brown measure of $x_{0}+i\sigma _{t}$ is related to the Brown measure of $x_{0}+c_{t}.$ By combining our this last result with what was shown in [22, Prop. 3.14], we obtain the following result.

Theorem 1.3

The Brown measure of $x_{0}+c_{t}$ is supported in the closure of a certain domain $\Lambda _{t}$ identified in [22]. There is a homeomorphism $U_{t}$ of $\overline{\Lambda }_{t}$ onto $\overline{\Omega }_{t}$ with the property that the push-forward of $\mathrm {Brown}(x_{0}+c_{t})$ under $U_{t}$ is equal to $\mathrm {Brown}(x_{0}+i\sigma _{t}).$ Furthermore, there is a continuous map $Q_{t}:\overline{\Omega }_{t}\rightarrow {\mathbb {R}}$ such that the push-forward of $\mathrm {Brown}(x_{0}+i\sigma _{t})$ under $Q_{t}$ is the law of $x_{0}+\sigma _{t},$ as computed by Biane.

The maps $U_{t}$ and $Q_{t}$ are described in Sects. 7.2 and 8, respectively. The map $U_{t}$ has the property that vertical line segments in $\overline{\Lambda }_{t}$ map linearly to vertical line segments in $\overline{\Omega }_{t},$ while the map $Q_{t}$ has the property that vertical line segments in $\overline{\Omega }_{t}$ map to single points in ${\mathbb {R}}.$ (See Figs. 3 and 4.) The map $Q_{t}$ is computed by first applying the inverse of the map $U_{t}$ and then applying the map denoted as $\Psi _{t}$ in Point 3 of Theorem 1.1 in [22].

Fig. 3

A visualization of the map $U_{t}:\overline{\Lambda }_{t} \rightarrow \overline{\Omega }_{t}.$ The map takes vertical segments in $\Lambda _{t}$ linearly to vertical segments in $\Omega _{t}.$ Shown for $\mu =\frac{1}{3}\delta _{-1}+\frac{2}{3}\delta _{1}$ and $t=1.05$

Fig. 4

A visualization of the map $Q_{t}:\overline{\Omega }_{t} \rightarrow {\mathbb {R}}.$ The map takes vertical segments in $\overline{\Omega }_{t}$ to single points in ${\mathbb {R}}.$ Shown for $\mu =\frac{1}{3} \delta _{-1}+\frac{2}{3}\delta _{1}$ and $t=1.05$

1.3 Method of proof

Our proofs are based on the PDE method developed in [12] and used also in [22] and [11]. (See also [18] for a gentle introduction to the method.) For any operator A in a tracial von Neumann algebra $({\mathcal {A}},\tau ),$ the Brown measure of A,  denoted $\mathrm {Brown}(A),$ may be computed as follows. (See Sect. 2 for more details.) Let

$$\begin{aligned} S(\lambda ,\varepsilon )=\tau [\log ((A-\lambda )^{*} (A-\lambda )+\varepsilon )] \end{aligned}$$

for $\varepsilon >0.$ Then, the limit

$$\begin{aligned} s(\lambda ):=\lim _{\varepsilon \rightarrow 0^{+}}S(\lambda ,\varepsilon ) \end{aligned}$$

exists as a subharmonic function. The Brown measure is then defined as:

$$\begin{aligned} \mathrm {Brown}(A)=\frac{1}{4\pi }\Delta s, \end{aligned}$$

where the Laplacian is computed in the distributional sense. The general theory then guarantees that $\mathrm {Brown}(A)$ is a probability measure supported on the spectrum of A. (The closed support of $\mathrm {Brown}(A)$ can be a proper subset of the spectrum of A.)

In our case, we take $A=x_{0}+i\sigma _{t}$, so that S also depends on t. Thus, we consider the functions:

$$\begin{aligned} S(t,\lambda ,\varepsilon )=\tau [\log ((x_{0}+i\sigma _{t}-\lambda )^{*} (x_{0}+i\sigma _{t}-\lambda )+\varepsilon )] \end{aligned}$$

(1.8)

and

$$\begin{aligned} s_{t}(\lambda )=\lim _{\varepsilon \rightarrow 0^{+}} S(t,\lambda ,\varepsilon ). \end{aligned}$$

Then,

$$\begin{aligned} \mathrm {Brown}(x_{0}+i\sigma _{t})=\frac{1}{4\pi }\Delta s_{t}(\lambda ), \end{aligned}$$

where the Laplacian is taken with respect to $\lambda$ with t fixed.

Our first main result (Theorem 3.1) is that the function S in (1.8) satisfies a first-order nonlinear PDE of Hamilton–Jacobi type, given in Theorem 3.1. Our goal is then to solve the PDE for $S(t,\lambda ,\varepsilon )$, evaluate the solution in the limit $\varepsilon \rightarrow 0,$ and then take the Laplacian with respect to $\lambda .$ We use two different approaches to this goal, one approach outside a certain domain $\Omega _{t}$ and a different approach inside $\Omega _{t},$ where the Brown measure turns out to be zero outside $\Omega _{t}$ and nonzero inside $\Omega _{t}.$ See Sects. 6 and 7.

1.4 Comparison to previous results

A different approach to the problem was previously developed in the physics literature by Jarosz and Nowak [24, 25]. Using linearization and subordination functions, they propose an algorithm for computing the Brown measure of $H_{1}+iH_{2},$ where $H_{1}$ and $H_{2}$ are arbitrary freely independent Hermitian elements. (See, specifically, Eqs. (75)–(80) in [25].) Section 6 of [24] presents examples in which one of $H_{1}$ and $H_{2}$ is semicircular and the other has various distributions.

Although the method of [24, 25] is not rigorous as written, it is possible that the strategy used there could be made rigorous using the general framework developed by Belinschi, Mai, and Speicher [6]. (See, specifically, the very general algorithm in Sect. 4 of [6]. See also [7] for further rigorous developments in this direction.) We emphasize, however, that it would require considerable effort to get analytic results for the $H_{1}+iH_{2}$ case from the general algorithm of [6]. In any case, we show in Sect. 9 that our results are compatible with those obtained by the algorithm of Jarosz and Nowak.

In addition to presenting a rigorous argument, we provide information about the Brown measure of $x_{0}+i\sigma _{t}$ that is not found in [24, 25]. First, we highlight the crucial result that the density of the Brown measure, inside its support, is always constant in the vertical direction. Although this result certainly follows from the algorithm of Jarosz and Nowak (and is reflected in the examples in [24, Sect. 6]), it is not explicitly stated in their work. Second, we give significantly more explicit formulas for the support of the Brown measure and for its density when $x_{0}$ is arbitrary. Third, we obtain (Sect. 8) a direct relationship between the Brown measure of $x_{0}+i\sigma _{t}$ and the distribution of $x_{0} +\sigma _{t}$ that is not found in [24] or [25].

Meanwhile, in Sect. 5, we also confirm a separate, nonrigorous argument of Janik, Nowak, Papp, Wambach, and Zahed predicting the domain on which the Brown measure is supported.

Finally, as mentioned previously, Sect. 3 of the paper [22] of the second author and Zhong computed the Brown measure of $y_{0}+c_{t},$ where $c_{t}$ is the free circular Brownian motion (large-N limit of the Ginibre ensemble). Now, $c_{t}$ can be constructed as $c_{t}=\tilde{\sigma } _{t/2}+i\sigma _{t/2},$ where $\sigma _{\cdot }$ and $\tilde{\sigma }_{\cdot }$ are two freely independent semicircular Brownian motions. Thus, the results of the present paper in the case where $x_{0}$ is the sum of a self-adjoint element $y_{0}$ and a freely independent semicircular element fall under the results of [22]. But actually, the connection between the present paper and [22] is deeper than that. For any choice of $x_{0},$ the region $\Lambda _{t}$ in which the Brown measure of $x_{0}+c_{t}$ is supported shows up in the computation of the Brown measure of $x_{0}+i\sigma _{t},$ as the “domain in the $\lambda _{0}$-plane” (Sect. 5.1). And then we show that the Brown measure of $x_{0}+i\sigma _{t}$ is the pushforward of the Brown measure of $x_{0} +c_{t}$ under a certain map (Sect. 8). Thus, one of the notable aspects of the results of the present paper is the way they illuminate the deep connections between $x_{0}+c_{t}$ and $x_{0}+i\sigma _{t}$.

2 The Brown measure formalism

We present here general results about the Brown measure. For more information, the reader is referred to the original paper [8] of Brown and to Chapter 11 of the monograph of Mingo and Speicher [28].

Let $({\mathcal {A}},\tau )$ be a tracial von Neumann algebra, that is, a finite von Neumann algebra ${\mathcal {A}}$ with a faithful, normal, tracial state $\tau :{\mathcal {A}} \rightarrow {\mathbb {C}}.$ Thus, $\tau$ is a norm-1 linear functional with the properties that $\tau (A^{*}A)>0$ for all nonzero elements of ${\mathcal {A}}$ and that $\tau (AB)=\tau (BA)$ for all $A,B\in {\mathcal {A}}.$ For any $A\in {\mathcal {A}},$ we define a function S by

$$\begin{aligned} S(\lambda ,\varepsilon )=\tau [\log ((A-\lambda )^{*}(A-\lambda ) +\varepsilon )],\quad \lambda \in {\mathbb {C}},~\varepsilon >0. \end{aligned}$$

It is known that

$$\begin{aligned} s(\lambda ):=\lim _{\varepsilon \rightarrow 0^{+}}S(\lambda ,\varepsilon ) \end{aligned}$$

exists as a subharmonic function on ${\mathbb {C}}.$ Then, the Brown measure of A is defined in terms of the distributional Laplacian of s:

$$\begin{aligned} \mathrm {Brown}(A)=\frac{1}{4\pi }\Delta s. \end{aligned}$$

The motivation for this definition comes from the case in which ${\mathcal {A}}$ is the algebra of all $N\times N$ matrices and $\tau$ is the normalized trace (1/N time ordinary trace). In this case, if A has eigenvalues $\lambda _{1},\ldots ,\lambda _{N}$ (counted with their algebraic multiplicities), then the function s may be computed as:

$$\begin{aligned} s(\lambda )=\frac{2}{N}\sum _{j=1}^{N}\log \left| \lambda -\lambda _{j}\right| . \end{aligned}$$

That is to say, s is 2/N time the logarithm of the absolute value of the characteristic polynomial of A. Since $\frac{1}{2\pi }\log \left| \lambda \right|$ is the Green’s function for the Laplacian on the plane, we find that

$$\begin{aligned} \mathrm {Brown}(A)=\frac{1}{N}\sum _{j=1}^{N}\delta _{\lambda _{j}}. \end{aligned}$$

Thus, the Brown measure of a matrix is just its empirical eigenvalue distribution.

If a sequence of random matrices $A^{N}$ converges in $*$-distribution to an element A in a tracial von Neumann algebra, one generally expects that the empirical eigenvalue distribution of $A^{N}$ will converge almost surely the Brown measure of A. But such a result does not always hold and it is a hard technical problem to prove that it does in specific examples. Works of Girko [14], Bai [1], and Tao and Vu [33] (among others) on the circular law provide techniques for establish such convergence results, while a somewhat different approach to such problems was developed by Guionnet, Krishnapur, and Zeitouni [17].

3 The differential equation for S

Let $\sigma _{t}$ be a free semicircular Brownian motion and let $x_{0}$ be a Hermitian element freely independent of each $\sigma _{t}$, $t>0$. The main result of this section is the following.

Theorem 3.1

Let

$$\begin{aligned} S(t,\lambda ,\varepsilon )=\tau [\log ((x_{0}+i\sigma _{t}-\lambda )^{*} (x_{0}+i\sigma _{t}-\lambda )+\varepsilon )]\quad \lambda \in {\mathbb {C}}, ~\varepsilon >0 \end{aligned}$$

and write $\lambda$ as $\lambda =a+ib$ with $a,b\in {\mathbb {R}}.$ Then, the function S satisfies the PDE

$$\begin{aligned} \frac{\partial S}{\partial t}=\frac{1}{4} \left( \left( \frac{\partial S}{\partial a}\right) ^{2} -\left( \frac{\partial S}{\partial b}\right) ^{2}\right) +\varepsilon \left( \frac{\partial S}{\partial \varepsilon }\right) ^{2} \end{aligned}$$

(3.1)

subject to the initial condition

$$\begin{aligned} S(0,\lambda ,\varepsilon )=\tau [\log ((x_{0}-\lambda )^{*}(x_{0} -\lambda )+\varepsilon )]. \end{aligned}$$

We use the notation

$$\begin{aligned} x_{t}&:=x_{0}+i\sigma _{t}\\ x_{t,\lambda }&:=x_{t}-\lambda . \end{aligned}$$

Then, the free SDEs of $x_{t,\lambda }$ and $x_{t,\lambda }^{*}$ are

$$\begin{aligned} dx_{t,\lambda }=i\,d\sigma _{t}, \qquad dx_{t,\lambda }^{*}=-i\,d\sigma _{t}. \end{aligned}$$

(3.2)

The main tool of this section is the free Itô formula. The following theorem is a simpler form of Theorem 4.1.2 of [5] which states the free Itô formula. The form of the Itô formula used here is similar to what is in Lemma 2.5 and Lemma 4.3 of [27]. For a “functional” form of these free Itô formulas, see Sect. 4.3 of [29].

Theorem 3.2

Let $({\mathcal {A}}_{t})_{t\ge 0}$ be a filtration such that $\sigma _{t}\in {\mathcal {A}}_{t}$ for all t and $\sigma _{t}-\sigma _{s}$ is free with ${\mathcal {A}}_{s}$ for all $s\le t$. Also let $f_{t}$, $g_{t}$ be two free Itô processes satisfying the free SDEs

$$\begin{aligned} df_{t}&=\sum _{k=1}^{n}a_{t}^{k}\,~d\sigma _{t}~\,b_{t}^{k}+c_{t} \,~dt \end{aligned}$$

(3.3)

$$\begin{aligned} dg_{t}&=\sum _{k=1}^{n}\tilde{a}_{t}^{k}\,~d\sigma _{t}~\,\tilde{b}_{t} ^{k}+\tilde{c}_{t}\,~dt. \end{aligned}$$

(3.4)

for some continuous adapted processes $\{a_{t}^{k},b_{t}^{k}, c_{t},\tilde{a}_{t}^{k},\tilde{b}_{t}^{k},\tilde{c}_{t}\}_{k=1}^{n}.$ Then, $f_{t}g_{t}$ satisfies the free SDE

$$\begin{aligned} d(f_{t}g_{t})=\sum _{k=1}^{n}(a_{t}^{k}\,~d\sigma _{t}~\,b_{t}^{k}g_{t} +f_{t}\tilde{a}_{t}^{k}~\,d\sigma _{t}~\,\tilde{b}_{t}^{k})+\left( c_{t} g_{t}+f_{t}\tilde{c}_{t}+\sum _{j,k=1}^{n}\tau [ b_{t}^{k} \tilde{a}_{t}^{j}]a_{t}^{k}\tilde{b}_{t}^{j}\right) \,dt. \end{aligned}$$

(3.5)

That is, $d(f_{t}g_{t})$ can be informally computed using the free Itô product rule:

$$\begin{aligned} d(f_{t}g_{t})=df_{t}\,g_{t}+f_{t}\,dg_{t}+df_{t}~dg_{t}, \end{aligned}$$

where $df_{t}~dg_{t}$ is computed using the rules

$$\begin{aligned} \,d\sigma _{t}~\,\theta _{t}~\,dt&=dt~\theta _{t} ~d\sigma _{t}=dt~d\theta _{t}~dt=0, \end{aligned}$$

(3.6)

$$\begin{aligned} d\sigma _{t}\,~\theta _{t}\,~d\sigma _{t}&=\tau [\theta _{t}]\,dt \end{aligned}$$

(3.7)

for any continuous adapted process $\theta _{t}$.

Furthermore, if a process $f_{t}$ satisfies an SDE as in (3.3), then $\tau [ f_{t}]$ satisfies

$$\begin{aligned} d\tau [ f_{t}]=\tau [ c_{t}]~dt. \end{aligned}$$

This result can be expressed informally as saying d commutes with $\tau$ and that

$$\begin{aligned} \tau [\theta _{t}~d\sigma _{t}]=0 \end{aligned}$$

(3.8)

for any continuous adapted process $\theta _{t}$.

The theorem stated above is applicable to our current situation. Let ${\mathcal {A}}_{0}$ be the von Neumann algebra generated by $x_{0}$, and ${\mathcal {B}}_{t}$ be the von Neumann algebra generated by $\{\sigma _{r}:r\le t\}$. Then, we apply Theorem 3.2 with ${\mathcal {A}}_{t}={\mathcal {A}} _{0}*{\mathcal {B}}_{t}$, the reduced free product of ${\mathcal {A}}_{0}$ and ${\mathcal {B}}_{t}$.

We shall use the free Itô formula to compute a partial differential equation that S satisfies. Our strategy is to first do a power series expansion of the logarithm and then apply the free Itô formula to compute the partial derivative of the powers of $x_{t,\lambda }^{*}x_{t,\lambda }$ with respect to t. We start by computing the time derivatives of $\tau [(x_{t,\lambda }^{*} x_{t,\lambda })^{n}].$

Lemma 3.3

We have

$$\begin{aligned} \frac{\partial }{\partial t} \tau [(x_{t,\lambda }^{*}x_{t,\lambda })]=1. \end{aligned}$$

(3.9)

When $n\ge 2$,

$$\begin{aligned} \frac{\partial }{\partial t}\tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{n}]&=-\frac{n}{2}\sum _{m=1}^{n-1}\tau [ x_{t,\lambda }^{*} (x_{t,\lambda }^{*}x_{t,\lambda })^{m-1}] \tau [x_{t,\lambda }^{*}(x_{t,\lambda }^{*} x_{t,\lambda })^{n-m-1}]\nonumber \\&\quad -\frac{n}{2}\sum _{m=1}^{n-1} \tau [ x_{t,\lambda }(x_{t,\lambda }^{*} x_{t,\lambda })^{m-1}]\tau [ x_{t,\lambda }(x_{t,\lambda }^{*} x_{t,\lambda })^{n-m-1}]\nonumber \\&\quad +n\sum _{m=1}^{n}\tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{n-m}] \tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{m-1}]. \end{aligned}$$

(3.10)

Proof

For $n=1$, we apply the free Itô formula to get

$$\begin{aligned} d(x_{t,\lambda }^{*}x_{t,\lambda })=x_{t,\lambda }^{*}(i\,d \sigma _{t})+(-i\,d\sigma _{t})x_{t,\lambda }+d\sigma _{t}\cdot d\sigma _{t} =ix_{t,\lambda }^{*}\,d\sigma _{t}-i\,d\sigma _{t}\,x_{t,\lambda }+dt \end{aligned}$$

which gives (3.9), after taking trace on both sides.

Now, we assume $n\ge 2$. We apply Theorem 3.2 repeatedly to obtain results for the product of several free Itô processes. When computing $d\tau [(x_{t,\lambda }^{*}x_{t, \lambda })^{n}],$ we obtain four types of terms, as follows:

• (1) Terms involving only one differential, either of $x_{t,\lambda }^{*}$ or of $x_{t,\lambda }$.

• (2) Terms involving two differentials of $x_{t,\lambda }$.

• (3) Terms involving two differentials of $x_{t,\lambda }^{*}$.

• (4) Terms involving a differential of $x_{t,\lambda }^{*}$ and a differential of $x_{t,\lambda }$.

We now compute $d\tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{n}]$ by moving the d inside the trace and then applying Theorem 3.2. By (3.8), the terms in Point 1 will not contribute.

We then consider the terms in Point 2. There are exactly n factors of $x_{t,\lambda }$ in $(x_{t,\lambda }^{*}x_{t,\lambda })^{n}$. Since the terms in Point 2 involve exactly two $dx_{t,\lambda }$’s, there are precisely ${\left( {\begin{array}{c}n\\ 2\end{array}}\right) }$ terms in Point 2. For the purpose of computing these terms, we label all of the $x_{t,\lambda }$’s by $x_{t,\lambda }^{(k)}$ for $k=1,\ldots ,n$. We view choosing two $x_{t,\lambda }$’s as first choosing an $x_{t,\lambda }^{(i)}$, then another $x_{t,\lambda }^{(j)}$. We then cyclically permute the factors until $dx_{t,\lambda }^{(i)}$ is at the beginning. Using the free stochastic equation (3.2) of $x_{t,\lambda }$, this term has the form:

$$\begin{aligned}&\tau [ dx_{t,\lambda }^{(i)}\,(x_{t,\lambda }^{*}x_{t,\lambda })^{m} x_{t,\lambda }^{*}\,dx_{t,\lambda }^{(j)}\,(x_{t,\lambda }^{*} x_{t,\lambda })^{n-m-2}x_{t,\lambda }^{*}]\\&\quad =-\tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{m}x_{t,\lambda }^{*}] \tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{n-m-2}x_{t,\lambda }^{*}]~dt \end{aligned}$$

where $m=j-i-1\mathrm{mod}\,n$ and we omit the labeling of all $x_{t,\lambda }$’s except $x_{t,\lambda }^{(i)}$ and $x_{t,\lambda }^{(j)}$.

If we then sum over all $j\ne i,$ we obtain

$$\begin{aligned} -\sum _{m=0}^{n-2}\tau [ x_{t,\lambda }^{*}(x_{t,\lambda }^{*} x_{t,\lambda })^{m}]\tau [ x_{t,\lambda }^{*}(x_{t,\lambda }^{*} x_{t,\lambda })^{n-m-2}]~dt. \end{aligned}$$

Since this expression is independent of i,  summing over i produces a factor of n in front. But then we have counted every term exactly twice, since we can choose the i first and then the j or vice versa. Thus, the sum of all the terms in Point 2 is

$$\begin{aligned} -\frac{n}{2}\sum _{m=0}^{n-2}\tau [(x_{t,\lambda }^{*}(x_{t,\lambda }^{*} x_{t,\lambda })^{m}]\tau [(x_{t,\lambda }^{*}(x_{t,\lambda }^{*} x_{t,\lambda })^{n-m-2}]~dt. \end{aligned}$$

(3.11)

By a similar argument, the sum of all the terms in Point 3 is

$$\begin{aligned} -\frac{n}{2}\sum _{m=0}^{n-2}\tau [ x_{t,\lambda }(x_{t,\lambda }^{*} x_{t,\lambda })^{m}]\tau [ x_{t,\lambda }(x_{t,\lambda }^{*} x_{t,\lambda })^{n-m-2}]~dt. \end{aligned}$$

(3.12)

We now compute the terms in Point 4. We can cyclically permute the factors until $dx_{t,\lambda }^{*}$ is at the beginning. Thus, each of the terms in Point 4 can be written as:

$$\begin{aligned}&\tau [ dx_{t,\lambda }^{*}(x_{t,\lambda }x_{t,\lambda }^{*})^{m} \,dx_{t,\lambda }\,(x_{t,\lambda }^{*}x_{t,\lambda })^{n-m-1}]\nonumber \\&\quad =\tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{m}] \tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{n-m-1}]~dt, \end{aligned}$$

(3.13)

where $m=0,\ldots ,n-1$. Now, there are a total of $n^{2}$ terms in Point 4, but from (3.13), we can see that there are only n distinct terms, each of which occurs n times, so that the sum of all terms from Point 4 is

$$\begin{aligned} n\sum _{m=0}^{n-1}\tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{m}] \tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{n-m-1}]~dt. \end{aligned}$$

(3.14)

We now obtain (3.10) by adding (3.11), (3.12), and (3.14) and making a change of index. $\square$

Proposition 3.4

The function S satisfies the equation:

$$\begin{aligned} \frac{\partial S}{\partial t}&=\frac{1}{2}\tau [ x_{t,\lambda } (x_{t,\lambda }^{*}x_{t,\lambda }+\varepsilon )^{-1}]^{2}\nonumber \\&\quad +\frac{1}{2}\tau [ x_{t,\lambda }^{*}(x_{t,\lambda }^{*} x_{t,\lambda }+\varepsilon )^{-1}]^{2}+\varepsilon \tau [(x_{t,\lambda }^{*} x_{t,\lambda }+\varepsilon )^{-1}]^{2}. \end{aligned}$$

(3.15)

Proof

We first show that (3.15) holds for all $\varepsilon >\Vert x_{t,\lambda }^{*}x_{t,\lambda }\Vert$. Let $\varepsilon >\Vert x_{t,\lambda }^{*}x_{t,\lambda }\Vert$. We write $\log (x+\varepsilon )$ as $\log \varepsilon +\log (1+x/\varepsilon )$ and then expand in powers of $x/\varepsilon .$ We then substitute $x=x_{t,\lambda }^{*}x_{t,\lambda },$ and then apply the trace term by term, giving

$$\begin{aligned} S(t,\lambda ,\varepsilon )=\log \varepsilon +\sum _{n=1}^{\infty } \frac{(-1)^{n-1}}{n\varepsilon ^{n}}\tau [(x_{t,\lambda }^{*} x_{t,\lambda })^{n}]. \end{aligned}$$

(3.16)

We now wish to differentiate the right-hand side of (3.16) term by term in t. We will see shortly that when we differentiate inside the sum, the resulting series still converges for $\varepsilon >\Vert x_{t,\lambda }^{*} x_{t,\lambda }\Vert$. Furthermore, since the map $t\mapsto x_{t}$ is continuous in the operator norm topology, $\Vert x_{t}\Vert$ is a locally bounded function of t. Hence, the series of derivatives converges locally uniformly in t. This, together with the pointwise convergence of the original series, will show that term-by-term differentiation is valid.

If we differentiate inside the sum in (3.16), we obtain

$$\begin{aligned} \sum _{n=1}^{\infty }\frac{(-1)^{n-1}}{n\varepsilon ^{n}} \frac{\partial }{\partial t}\tau [(x_{t,\lambda }^{*} x_{t,\lambda })^{n}]. \end{aligned}$$

(3.17)

By Lemma 3.3, the above power series becomes

$$\begin{aligned}&\frac{1}{2}\sum _{n=2}^{\infty }\sum _{m=1}^{n-1} \frac{(-1)^{n}}{\varepsilon ^{n}}\tau [ x_{t,\lambda } (x_{t,\lambda }^{*}x_{t,\lambda })^{m-1}] \tau [x_{t,\lambda }(x_{t,\lambda }^{*}x_{t,\lambda })^{n-m-1}]\nonumber \\&\quad +\frac{1}{2}\sum _{n=2}^{\infty }\sum _{m=1}^{n-1}\frac{(-1)^{n}}{\varepsilon ^{n}}\tau [ x_{t,\lambda }^{*}(x_{t,\lambda }^{*} x_{t,\lambda })^{m-1}]\tau [ x_{t,\lambda }^{*}(x_{t,\lambda }^{*} x_{t,\lambda })^{n-m-1}]\nonumber \\&\quad +\sum _{n=1}^{\infty }\sum _{m=1}^{n} \frac{(-1)^{n-1}}{\varepsilon ^{n}} \tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{n-m}] \tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{m-1}]. \end{aligned}$$

(3.18)

Note that the constant term 1 is in the last term in (3.18). The first term in (3.18) may be rewritten as:

$$\begin{aligned}&\frac{1}{2}\frac{1}{\varepsilon ^{2}}\sum _{n=0}^{\infty }\sum _{m=0}^{n} \frac{(-1)^{n}}{\varepsilon ^{n}}\tau [ x_{t,\lambda }(x_{t,\lambda }^{*} x_{t,\lambda })^{m}]\tau [ x_{t,\lambda }(x_{t,\lambda }^{*} x_{t,\lambda })^{n-m}]\\&\quad = \frac{1}{2}\left( \sum _{k=0}^{\infty } \frac{(-1)^{k}}{\varepsilon ^{k+1}}\tau [ x_{t,\lambda } (x_{t,\lambda }^{*}x_{t,\lambda })^{k}]\right) \left( \sum _{l=0}^{\infty }\frac{(-1)^{l}}{\varepsilon ^{l+1}} \tau [x_{t,\lambda }(x_{t,\lambda }^{*}x_{t,\lambda })^{l}]\right) \\&\quad = \frac{1}{2}\tau [ x_{t,\lambda }(x_{t,\lambda }^{*} x_{t,\lambda }+\varepsilon )^{-1}]^{2}. \end{aligned}$$

The second term in (3.18) differs from the first term only by replacing the $x_{t,\lambda }$ by $x_{t,\lambda }^{*}$ in the two trace terms, and is therefore computed as:

$$\begin{aligned} \frac{1}{2}\tau [ x_{t,\lambda }^{*}(x_{t,\lambda }^{*}x_{t,\lambda } +\varepsilon )^{-1}]^{2}. \end{aligned}$$

A similar computation expresses the last term in (3.18) as:

$$\begin{aligned} \sum _{n=1}^{\infty }\sum _{m=1}^{n}\frac{(-1)^{n-1}}{\varepsilon ^{n}} \tau [(x_{t,\lambda }^{*}x_{t,\lambda })^{n-m}]\tau [(x_{t,\lambda }^{*} x_{t,\lambda })^{m-1}]\ =\varepsilon \tau [(x_{t,\lambda }^{*} x_{t,\lambda }+\varepsilon )^{-1}]^{2}. \end{aligned}$$

This shows that the series in (3.17) converges to the right-hand side of (3.15). It follows that (3.15) holds for all $\varepsilon >\Vert x_{t,\lambda }^{*}x_{t,\lambda }\Vert$.

Thus, for all $\varepsilon >\max _{s\le t}\Vert x_{s,\lambda }^{*}x_{s,\lambda }\Vert$, we have

$$\begin{aligned} S(t,\lambda ,\varepsilon )&=S(0,\lambda ,\varepsilon )+\int _{0}^{t} \left\{ \frac{1}{2}\tau [ x_{s,\lambda }(x_{s,\lambda }^{*} x_{s,\lambda }+\varepsilon )^{-1}]^{2}\right. \nonumber \\&\quad \left. +\frac{1}{2}\tau [ x_{s,\lambda }^{*}(x_{s,\lambda }^{*} x_{s,\lambda }+\varepsilon )^{-1}]^{2}+\varepsilon \tau [(x_{s,\lambda }^{*} x_{s,\lambda }+\varepsilon )^{-1}]^{2}\right\} \,\mathrm{d}s. \end{aligned}$$

(3.19)

The right-hand side of (3.19) is analytic in $\varepsilon$ for all $\varepsilon >0$. We now claim that the left-hand side of (3.19) is also analytic. At each $\varepsilon >0$, we have the operator-valued power series expansion

$$\begin{aligned} \log (x_{t,\lambda }^{*}x_{t,\lambda }+\varepsilon +h) =\log (x_{t,\lambda }^{*}x_{t,\lambda }+\varepsilon ) +\sum _{n=1}^{\infty }\frac{(-1)^{n-1}h^{n}}{n} (x_{t,\lambda }^{*}x_{t,\lambda }+\varepsilon )^{-n} \end{aligned}$$

for $|h|<\Vert (x_{t,\lambda }^{*}x_{t,\lambda } +\varepsilon )^{-1}\Vert$. Taking the trace gives

$$\begin{aligned} S(t,\lambda ,\varepsilon +h)=\log (x_{t,\lambda }^{*}x_{t,\lambda } +\varepsilon )+\sum _{n=1}^{\infty }\frac{(-1)^{n-1}h^{n}}{n} \tau [(x_{t,\lambda }^{*}x_{t,\lambda }+\varepsilon )^{-n}] \end{aligned}$$

for $|h|<\Vert (x_{t,\lambda }^{*}x_{t,\lambda } +\varepsilon )^{-1}\Vert$. This shows $S(t,\lambda ,\cdot )$ is analytic on the positive real line. Since both sides of (3.19) define an analytic function for $\varepsilon >0$ and they agree for all large $\varepsilon$, they are indeed equal for all $\varepsilon >0$. Now, the conclusion of the proposition follows from differentiating both sides of (3.19) with respect to t. $\square$

Lemma 3.5

The partial derivatives of S with respect to $\varepsilon$ and $\lambda$ are given by the following formulas.

$$\begin{aligned} \frac{\partial S}{\partial \lambda }&=-\tau [ x_{t,\lambda }^{*} (x_{t,\lambda }^{*}x_{t,\lambda }+\varepsilon )^{-1}]\\ \frac{\partial S}{\partial \bar{\lambda }}&=-\tau [ x_{t,\lambda } (x_{t,\lambda }^{*}x_{t,\lambda }+\varepsilon )^{-1}]\\ \frac{\partial S}{\partial \varepsilon }&=\tau [(x_{t,\lambda }^{*}x_{t,\lambda }+\varepsilon )^{-1}]. \end{aligned}$$

Proof

By Lemma 1.1 in Brown’s paper [8], the derivative of the trace of a logarithm is given by

$$\begin{aligned} \frac{d}{du}\tau [\log (f(u))]=\tau \left[ f(u)^{-1}\frac{df}{du}\right] . \end{aligned}$$

(3.20)

The lemma follows from applying this formula. $\square$

Now we are ready to prove Theorem 3.1.

Proof of Theorem 3.1

By Lemma 3.4,

$$\begin{aligned} \frac{\partial S}{\partial t}=\frac{1}{2}\tau [ x_{t,\lambda } (x_{t,\lambda }^{*}x_{t,\lambda }+\varepsilon )^{-1}]^{2} +\frac{1}{2}\tau [ x_{t,\lambda }^{*}(x_{t,\lambda }^{*} x_{t,\lambda }+\varepsilon )^{-1}]^{2}+\varepsilon \tau [(x_{t,\lambda }^{*}x_{t,\lambda }+\varepsilon )^{-1}]^{2}. \end{aligned}$$

Using Lemma 3.5, the above displayed equation can be written as:

$$\begin{aligned} \frac{\partial S}{\partial t}=\frac{1}{2}\left( \frac{\partial S}{\partial \lambda }\right) ^{2}+\frac{1}{2}\left( \frac{\partial S}{\partial \bar{\lambda }}\right) ^{2}+\varepsilon \left( \frac{\partial S}{\partial \varepsilon }\right) ^{2}. \end{aligned}$$

Now, (3.1) follows from applying the definition of Cauchy–Riemann operators to the above equation. The initial condition holds because $x_{t}=x_{0}$ when $t=0$. $\square$

4 The Hamilton–Jacobi analysis

4.1 The Hamilton–Jacobi method

We define a “Hamiltonian” function $H:{\mathbb {R}}^{6}\rightarrow {\mathbb {R}}$ by replacing the derivatives $\partial S/\partial a,$ $\partial S/\partial b,$ and $\partial S/\partial \varepsilon$ on the right-hand side of the PDE in Theorem 3.1 by “momentum” variables $p_{a},$ $p_{b},$ and $p_{\varepsilon },$ and then reversing the overall sign. Thus, we define

$$\begin{aligned} H(a,b,\varepsilon ,p_{a},p_{b},p_{\varepsilon })=-\frac{1}{4}(p_{a}^{2} -p_{b}^{2})-\varepsilon p_{\varepsilon }^{2}, \end{aligned}$$

(4.1)

where in this case, H happens to be independent of a and b. We then introduce Hamilton’s equations for the Hamiltonian H,  namely

$$\begin{aligned} \frac{du}{dt}=\frac{\partial H}{\partial p_{u}};\quad \frac{dp_{u}}{dt} =-\frac{\partial H}{\partial u}, \end{aligned}$$

(4.2)

where u ranges over the set $\{a,b,\varepsilon \}.$ We will use the notation

$$\begin{aligned} \lambda (t)=a(t)+ib(t). \end{aligned}$$

Notation 4.1

We use the notation

$$\begin{aligned} p_{a,0},~p_{b,0},~p_{0} \end{aligned}$$

for the initial values of $p_{a},$ $p_{b},$ and $p_{\varepsilon },$ respectively.

In the Hamilton–Jacobi analysis, the initial momenta are determined by the initial positions $\lambda _{0}$ and $\varepsilon _{0}$ by means of the following formula:

$$\begin{aligned} p_{a,0}=\frac{\partial }{\partial a_{0}}S(0,\lambda _{0},\varepsilon _{0}); \quad p_{b,0}=\frac{\partial }{\partial b_{0}}S(0,\lambda _{0}, \varepsilon _{0});\quad p_{0}=\frac{\partial }{\partial \varepsilon _{0}}S(0,\lambda _{0},\varepsilon _{0}). \end{aligned}$$

(4.3)

Now, the formula for $S(0,\lambda ,\varepsilon )$ in Theorem 3.1 may be written more explicitly as:

$$\begin{aligned} S(0,\lambda ,\varepsilon )=\int _{{\mathbb {R}}} \log (\left| x-\lambda \right| ^{2}+\varepsilon )~\mathrm{d}\mu (x), \end{aligned}$$

where $\mu$ is the law of $x_{0}$, as in (1.1). We thus obtain the following formula for the initial momenta:

$$\begin{aligned} p_{a,0}&=\int _{{\mathbb {R}}}\frac{2(a_{0}-x)}{(a_{0}-x)^{2} +b_{0} ^{2}+\varepsilon _{0}}~\mathrm{d}\mu (x)\nonumber \\ p_{b,0}&=\int _{{\mathbb {R}}}\frac{2b_{0}}{(a_{0}-x)^{2} +b_{0}^{2} +\varepsilon _{0}}~\mathrm{d}\mu (x)\nonumber \\ p_{0}&=\int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2} +b_{0}^{2}+\varepsilon _{0}}~\mathrm{d}\mu (x). \end{aligned}$$

(4.4)

Provided we assume $\varepsilon _{0}>0,$ the integrals are convergent.

Proposition 4.2

Suppose we have a solution to the Hamiltonian system on a time interval [0, T] such that $\varepsilon (t)>0$ for all $t\in [0,T]$. Then, we have

$$\begin{aligned} S(t,\lambda (t),\varepsilon (t)) =S(0,\lambda _{0},\varepsilon _{0})+tH_{0}, \end{aligned}$$

(4.5)

where

$$\begin{aligned} H_{0}=H(a_{0},b_{0},\varepsilon _{0},p_{a,0},p_{b,0},p_{0}). \end{aligned}$$

We also have

$$\begin{aligned} \frac{\partial S}{\partial u}(t,\lambda (t),\varepsilon (t))=p_{u}(t) \end{aligned}$$

(4.6)

for all $u\in \{a,b,\varepsilon \}$.

We refer to (4.5) and (4.6) as the first and second Hamilton–Jacobi formulas, respectively.

Proof

The reader may consult Sect. 6.1 of [12] for a concise statement and derivation of the general Hamilton–Jacobi method. (See also the book of Evans [13].) The general form of the first Hamilton–Jacobi formula, when applied to this case, reads as:

$$\begin{aligned} S(t,\lambda (t),\varepsilon (t))=S(0,\lambda _{0},\varepsilon _{0})-tH_{0} +\int _{0}^{t}\sum _{u\in \{a,b,\varepsilon \}}p_{u} \frac{\partial H}{\partial p_{u}}~\mathrm{d}s. \end{aligned}$$

In our case, because the Hamiltonian is homogeneous of degree two in the momentum variables, $\sum _{u\in \{a,b,\varepsilon \}}p_{u} \frac{\partial H}{\partial p_{u}}$ is equal to 2H. Since H is a constant of motion, the general formula reduces to (4.5). Meanwhile, (4.6) is an immediate consequence of the general form of the second Hamilton–Jacobi formula. $\square$

4.2 Solving the ODEs

We now solve the Hamiltonian system (4.2) with Hamiltonian given by (4.1). We start by noting several helpful constants of motion.

Proposition 4.3

The quantities

$$\begin{aligned} H,~p_{a},~p_{b},~\varepsilon p_{\varepsilon }^{2} \end{aligned}$$

are constants of motion, meaning that they are constant along any solution of Hamilton’s equations (4.2).

Proof

The Hamiltonian is always a constant of motion in any Hamiltonian system. The quantities $p_{a}$ and $p_{b}$ are constants of motion because H is independent of a and b. And finally, $\varepsilon p_{\varepsilon }^{2}$ is a constant of motion because it equals $-\frac{1}{4}(p_{a}^{2}-p_{b}^{2})-H$. $\square$

We now obtain solutions to (4.2), where at the moment, we allow arbitrary initial momenta, not necessarily given by (4.3).

Proposition 4.4

Consider the Hamiltonian system (4.2) with Hamiltonian (4.1) and initial conditions

$$\begin{aligned} (a_{0},b_{0},\varepsilon _{0},p_{a,0},p_{b,0},p_{0}), \end{aligned}$$

with $p_{0}>0.$ Then, the solution to the system exists up to time

$$\begin{aligned} t_{*}=1/p_{0}. \end{aligned}$$

Up until that time, we have

$$\begin{aligned} p_{a}(t)&=p_{a,0}\\ a(t)&=a_{0}-\frac{1}{2}p_{a,0}t.\\ p_{b}(t)&=p_{b,0}\\ b(t)&=b_{0}+\frac{1}{2}p_{b,0}t\\ p_{\varepsilon }(t)&=\frac{p_{0}}{1-p_{0}t}\\ \varepsilon (t)&=\varepsilon _{0}\left( 1-p_{0}t\right) ^{2}. \end{aligned}$$

If $\varepsilon _{0}>0$, then $\varepsilon (t)$ remains positive for all $t<t_{*}$.

Proof

We begin by noting that

$$\begin{aligned} \dot{p}_{\varepsilon }=-\frac{\partial H}{\partial \varepsilon } =p_{\varepsilon }^{2}. \end{aligned}$$

We may solve this separable equation as:

$$\begin{aligned} -\left( \frac{1}{p_{\varepsilon }(t)}-\frac{1}{p_{0}}\right) =t, \end{aligned}$$

from which the claimed formula for $p_{\varepsilon }(t)$ follows. We then note that

$$\begin{aligned} \frac{d\varepsilon }{dt}&=\frac{\partial H}{\partial p_{\varepsilon }}\\&=-2\varepsilon p_{\varepsilon }\\&=-2\varepsilon \frac{p_{0}}{1-p_{0}t}. \end{aligned}$$

This equation is also separable and may easily be integrated to give the claimed formula for $\varepsilon (t).$

The formulas for $p_{a}$ and $p_{b}$ simply amount to saying that they are constants of motion, and the formulas for a and b are then easily obtained. $\square$

We now specialize the initial conditions to the form occurring in the Hamilton–Jacobi method, that is, where the initial momenta are given by (4.4). We note that the formulas in (4.4) can be written as:

$$\begin{aligned} p_{b,0}=2b_{0}p_{0} \end{aligned}$$

(4.7)

and

$$\begin{aligned} p_{a,0}=2a_{0}p_{0}-2p_{1}, \end{aligned}$$

(4.8)

where

$$\begin{aligned} p_{1}=\int _{{\mathbb {R}}}\frac{x}{(a_{0}-x)^{2} +b_{0}^{2}+\varepsilon _{0}}~\mathrm{d}\mu (x). \end{aligned}$$

(4.9)

Proposition 4.5

Suppose $a_{0},$ $b_{0},$ and $\varepsilon _{0}$ are chosen in such a way that $p_{0}=1/t,$ so that the lifetime $t_{*}$ of the system equals t. Then, we have

$$\begin{aligned} \lim _{s\rightarrow t^{-}}a(s)&=tp_{1}\\ \lim _{s\rightarrow t^{-}}b(s)&=2b_{0}\\ \lim _{s\rightarrow t^{-}}\varepsilon (s)&=0, \end{aligned}$$

where $p_{1}$ is as in (4.9).

Proof

The result follows easily from the formulas in Proposition 4.4, after using the relations (4.7) and (4.8) and setting $p_{0}=1/t$. $\square$

Definition 4.6

Let $t_{*}(\lambda _{0},\varepsilon _{0})$ denote the lifetime of the solution, namely

$$\begin{aligned} t_{*}(\lambda _{0},\varepsilon _{0})=\frac{1}{p_{0}} =\left( \int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{(a_{0}-x)^{2} +b_{0}^{2}+\varepsilon _{0}}\right) ^{-1}, \end{aligned}$$

and let

$$\begin{aligned} T(\lambda _{0}):=\lim _{\varepsilon _{0}\rightarrow 0^{+}}t_{*} (\lambda _{0},\varepsilon _{0})=\left( \int _{{\mathbb {R}}} \frac{\mathrm{d}\mu (x)}{(a_{0}-x)^{2}+b_{0}^{2}}\right) ^{-1}. \end{aligned}$$

We note that if $b_{0}=0$, then the integral in the definition of $T(a_{0}+ib_{0})$ may be infinite for certain values of $a_{0}$. Thus, it is possible for $T(a_{0}+ib_{0})$ to equal 0 when $b_{0}=0$.

Proposition 4.7

Let

$$\begin{aligned} \lambda (t;\lambda _{0},\varepsilon _{0}) \end{aligned}$$

denote the solution to the system (4.2) with $\lambda (0)=\lambda _{0}$ and $\varepsilon (0)=\varepsilon _{0}$, and with initial momenta given by (4.4). Suppose $\lambda _{0}$ satisfies $T(\lambda _{0})>t.$ Then,

$$\begin{aligned} \lim _{\varepsilon _{0}\rightarrow 0^{+}}\lambda (t;\lambda _{0}, \varepsilon _{0})=\lambda _{0}-t\int _{{\mathbb {R}}} \frac{1}{\lambda _{0}-x}~\mathrm{d}\mu (x), \end{aligned}$$

provided that $\lambda _{0}$ does not belong the closed support of $\mu$.

Proof

Using Proposition 4.4, we find that

$$\begin{aligned} \lambda (t;\lambda _{0},\varepsilon _{0})&=a(t)+ib(t)\\&=\lambda _{0}-\frac{t}{2}(p_{a,0}-ip_{b,0}). \end{aligned}$$

In the limit as $\varepsilon _{0}$ tends to zero, we have (provided $\lambda _{0}$ is not in $\mathrm {supp}(\mu )\subset {\mathbb {R}}$)

$$\begin{aligned} p_{a,0}-ip_{b,0}=\int _{{\mathbb {R}}} \frac{2(a_{0}-x)}{(a_{0}-x)^{2}+b_{0}^{2}}~\mathrm{d}\mu (x) -i\int _{{\mathbb {R}}}\frac{2b_{0}}{(a_{0}-x)^{2}+b_{0}^{2}}~\mathrm{d}\mu (x). \end{aligned}$$

It is then easy to check that

$$\begin{aligned} p_{a,0}-ip_{b,0}=2\int _{{\mathbb {R}}}\frac{1}{a_{0}+ib_{0}-x}~\mathrm{d}\mu (x), \end{aligned}$$

which gives the claimed formula. $\square$

5 The domains

5.1 The domain in the $\lambda _{0}$-plane

We now define the first of two domains we will be interested in. When we apply the Hamilton–Jacobi method in Sect. 6, we will try to find solutions with $\varepsilon (t)$ very close to zero. Based on the formula for $\varepsilon (t)$ in Proposition 4.4, it seems that we can make $\varepsilon (t)$ small by making $\varepsilon _{0}$ small. The difficulty with this approach, however, is that if we fix some $\lambda _{0}$ and let $\varepsilon _{0}$ tend to zero, the lifetime of the path may be smaller than t. Thus, if the small-$\varepsilon _{0}$ lifetime of the path—as computed by the function T in Definition 4.6—is smaller than t,  the simple approach of letting $\varepsilon _{0}$ tend to zero will not work. This observation motivates the following definition.

Definition 5.1

Let T be the function defined in Definition 4.6. We then define a domain $\Lambda _{t}\subset {\mathbb {C}}$ by

$$\begin{aligned} \Lambda _{t}=\left\{ \lambda _{0}\in {\mathbb {C}}|T(\lambda _{0})<t\right\} . \end{aligned}$$

Explicitly, a point $\lambda _{0}=a_{0}+ib_{0}$ belongs to $\Lambda _{t}$ if and only if

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{(a_{0}-x)^{2}+b_{0}^{2}}>\frac{1}{t}. \end{aligned}$$

(5.1)

This domain appeared originally in the work Biane [2], for reasons that we will explain in Sect. 5.2. The domain $\Lambda _{t}$ also plays a crucial role in work of the second author with Zhong [22]. In Sect. 5.3, we will consider another domain $\Omega _{t},$ whose closure will be the support of the Brown measure of $x_{0}+i\sigma _{t}.$ See Fig. 6 for plots of $\Lambda _{t}$ and the corresponding domain $\Omega _{t}$.

We give now a more explicit description of the domain $\Lambda _{t}$.

Proposition 5.2

For each $t>0,$ define a function $v_{t}:{\mathbb {R}} \rightarrow [0,\infty )$ as follows. For each $a_{0}\in {\mathbb {R}}$, if

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2}}~\mathrm{d}\mu (x)>\frac{1}{t}, \end{aligned}$$

(5.2)

let $v_{t}(a_{0})$ be the unique positive number such that

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2}+v_{t}(a_{0})^{2}} ~\mathrm{d}\mu (x)=\frac{1}{t}. \end{aligned}$$

(5.3)

If, on the other hand,

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2}}~\mathrm{d}\mu (x)\le \frac{1}{t}, \end{aligned}$$

(5.4)

set $v_{t}(a_{0})=0$.

Then, the function $v_{t}:{\mathbb {R}}\rightarrow [0,\infty )$ is continuous and the domain $\Lambda _{t}$ may be described as:

$$\begin{aligned} \Lambda _{t}=\left\{ \left. a_{0}+ib_{0}\in {\mathbb {C}}\right| ~\left| b_{0}\right| <v_{t}(a_{0})\right\} , \end{aligned}$$

(5.5)

so that

$$\begin{aligned} \Lambda _{t}\cap {\mathbb {R}}=\left\{ \left. a_{0} \in {\mathbb {R}}\right| v_{t}(a_{0})>0\right\} . \end{aligned}$$

(5.6)

See Fig. 5 for some plots of the function $v_{t}$. $\square$

Proof

We first note that for any fixed $a_{0},$ the integral

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2}+v^{2}}~\mathrm{d}\mu (x) \end{aligned}$$

(5.7)

is a strictly decreasing function of $v\ge 0$ and that the integral tends to zero as v tends to infinity. Thus, whenever condition (5.2) holds, it is easy to see that there is a unique positive number $v_{t}(a_{0})$ for which (5.3) holds. Continuity of $v_{t}$ is established in [2, Lemma 2].

Using the monotonicity of the integral in (5.7), it is now easy to see that the characterization of the domain $\Lambda _{t}$ in (5.5) is equivalent to the characterization in (5.1). $\square$

Fig. 5

The function $v_{t}(a)$ for the case in which $\mu =\frac{1}{3} \delta _{-1}+\frac{2}{3}\delta _{1}$

5.2 The result of Biane

We now explain how the domain $\Lambda _{t}$ arose in the work of Biane [2]. The results of Biane will be needed to formulate one of our main results (Theorem 8.2).

For any operator $A\in {\mathcal {A}},$ we let $G_{A}$ denote the Cauchy transform of A,  also known as the Stieltjes transform or holomorphic Green’s function, defined as:

$$\begin{aligned} G_{A}(z)=\tau [(z-A)^{-1}] \end{aligned}$$

(5.8)

for all $z\in {\mathbb {C}}$ outside the spectrum of A. Then, $G_{A}$ is holomorphic on its domain. If A is self-adjoint, we can recover the distribution of A from its Cauchy transform by the Stieltjes inversion formula. Even if A is not self-adjoint, $G_{A}$ determines the holomorphic moments of the Brown measure $\mathrm {Brown}(A)$ of A,  that is, the integrals of $\lambda ^{n}$ with respect to $\mathrm {Brown}(A).$ (We emphasize that these holomorphic moments do not, in general, determine the Brown measure itself.)

Let $x_{0}$ be a self-adjoint element of ${\mathcal {A}}$, and let $\sigma _{t} \in {\mathcal {A}}$ be a semicircular Brownian motion freely independent of $x_{0}.$ Define a function $H_{t}$ by

$$\begin{aligned} H_{t}(\lambda _{0})=\lambda _{0}+tG_{x_{0}}(\lambda _{0}). \end{aligned}$$

(5.9)

The significance of this function is from the following result of Biane [2], which shows that the Cauchy transform of $x_{0}+\sigma _{t}$ is related to the Cauchy transform of $x_{0}$ by the formula

$$\begin{aligned} G_{x_{0}+\sigma _{t}}(H_{t}(\lambda _{0}))=G_{x_{0}}(\lambda _{0}), \end{aligned}$$

(5.10)

for $\lambda _{0}$ in an appropriate set, which we will specify shortly. Note that this result is for the Cauchy transform of the self-adjoint operator $x_{0}+\sigma _{t}$, not for $x_{0}+i\sigma _{t}$.

We now explain the precise domain (taken to be in the upper half-plane for simplicity) on which the identity (5.10) holds. Let

$$\begin{aligned} \Delta _{t}=\left\{ \left. a_{0}+ib_{0}\right| b_{0}>v_{t}(a_{0})\right\} , \end{aligned}$$

(5.11)

which is just the set of points in the upper half-plane outside the closure of $\Lambda _{t}.$ The boundary of $\Delta _{t}$ is then the graph of $v_{t}$:

$$\begin{aligned} \partial \Delta _{t}=\left\{ a_{0}+i\left. v_{t}(a_{0}) \right| a_{0} \in {\mathbb {R}}\right\} . \end{aligned}$$

Theorem 5.3

(Biane) First, the function $H_{t}$ is an injective conformal map of $\Delta _{t}$ onto the upper half-plane. Second, $H_{t}$ maps $\partial \Delta _{t}$ homeomorphically onto the real line. Last, the identity (5.10) holds for all $\lambda _{0}$ in $\Delta _{t}$. Thus, we may write

$$\begin{aligned} G_{x_{0}+\sigma _{t}}(\lambda )=G_{x_{0}}(H_{t}^{-1}(\lambda )) \end{aligned}$$

for all $\lambda$ in the upper half-plane, where the inverse function $H_{t}^{-1}$ is chosen to map into $\Delta _{t}$.

See Lemma 4 and Proposition 2 in [2]. In the terminology of Voiculescu [34, 35], we may say that $H_{t}^{-1}$ is one of the subordination functions for the sum $x_{0}+\sigma _{t},$ meaning that one can compute $G_{x_{0}+\sigma _{t}}$ from $G_{x_{0}}$ by composing with $H_{t}^{-1}.$ Since $x_{0}+\sigma _{t}$ is self-adjoint, one can then compute the distribution of $x_{0}+\sigma _{t}$ from its Cauchy transform. We remark that Biane denotes the map $H_{t}^{-1}$ by $F_{t}$ on p. 710 of [2].

5.3 The domain in the $\lambda$-plane

Our strategy in applying the Hamilton–Jacobi method will be in two stages. In the first stage, we attempt to make $\varepsilon (t)$ close to zero by taking $\varepsilon _{0}$ close to zero. For this strategy to work, we must have $\lambda _{0}$ outside the closure of the domain $\Lambda _{t}$ introduced in Sect. 5.1. We will then solve the system of ODEs (4.2) in the limit as $\varepsilon _{0}$ approaches zero, using Proposition 4.7. Let us define a map $J_{t}$ by

$$\begin{aligned} J_{t}(\lambda _{0})=\lambda _{0}-tG_{x_{0}}(\lambda _{0}), \end{aligned}$$

(5.12)

which differs from the function $H_{t}$ in Sect. 5.2 by a change of sign. (See Sect. 5.4 for a different perspective on how this function arises.) With this notation, Proposition 4.7 says that if $\lambda (0)=\lambda _{0}$ and $\varepsilon _{0}$ approaches zero, then

$$\begin{aligned} \lambda (t)=J_{t}(\lambda _{0}), \end{aligned}$$

provided that $\lambda _{0}$ is outside the closure of $\Lambda _{t}$. Thus, the first stage of our analysis will allow us to compute the Brown measure at points of the form $J_{t}(\lambda _{0})$ with $\lambda _{0}\notin \overline{\Lambda }_{t}.$ We will find that the Brown measure is zero in a neighborhood of any such point. A second stage of the analysis will then be required to compute the Brown measure at points inside $\overline{\Lambda }_{t}$.

The discussion the previous paragraph motivates the following definition.

Definition 5.4

For each $t>0,$ define a domain $\Omega _{t}$ in ${\mathbb {C}}$ by

$$\begin{aligned} \Omega _{t}=[J_{t}(\Lambda _{t}^{c})]^{c}. \end{aligned}$$

That is to say, the complement of $\Omega _{t}$ is the image under $J_{t}$ of the complement of $\Lambda _{t}$.

See Fig. 6 for plots of the domains $\Lambda _{t}$ and $\Omega _{t}$.

Fig. 6

The regions $\Lambda _{t}$ and $\Omega _{t}$ for $\mu =\frac{1}{3} \delta _{-1}+\frac{2}{3}\delta _{1}$

We recall our standing assumption that $\mu$ is not a $\delta$-measure and we remind the reader that the set $\Delta _{t}$ in (5.11) is the region above the graph of $v_{t}$ so that $\overline{\Delta }_{t}$ is the set of points on or above the graph of $v_{t}.$

Proposition 5.5

The following results hold.

• (1) The map $J_{t}$ is well-defined, continuous, and injective on $\overline{\Delta }_{t}.$

• (2) Define a function $a_{t}:{\mathbb {R}}\rightarrow {\mathbb {R}}$ by

  $$\begin{aligned} a_{t}(a_{0})=\mathrm{Re}\,[J_{t}(a_{0}+iv_{t}(a_{0}))]. \end{aligned}$$

  (5.13)

  Then, at any point $a_{0}$ with $v_{t}(a_{0})>0,$ the function $a_{t}$ is differentiable and satisfies

  $$\begin{aligned} 0<\frac{da_{t}}{da_{0}}<2. \end{aligned}$$

• (3) The function $a_{t}$ is continuous and strictly increasing and maps ${\mathbb {R}}$ onto ${\mathbb {R}}$.

• (4) The map $J_{t}$ maps the graph of $v_{t}$ to the graph of a function, which we denote by $b_{t}.$ The function $b_{t}$ satisfies

  $$\begin{aligned} b_{t}(a_{t}(a_{0}))=2v_{t}(a_{0}) \end{aligned}$$

  (5.14)

  for all $a_{0}\in {\mathbb {R}}.$

• (5) The map $J_{t}$ takes the region above the graph of $v_{t}$ onto the region above the graph of $b_{t}$.

• (6) The set $\Omega _{t}$ defined in Definition 5.4 may be computed as:

  $$\begin{aligned} \Omega _{t}=\left\{ \left. a+ib\in {\mathbb {C}}\right| ~\left| b\right| <b_{t}(a)\right\} . \end{aligned}$$

Since $J_{t}(z)=2z-H_{t}(z)$ and $H_{t}(a_{0}+iv_{t}(a_{0}))$ is real, we see that $a_{t}(a_{0})=2a_{0}-H_{t}(a_{0}+iv_{t}(a_{0}))$. Lemma 5 of [2] and Theorem 3.14 of [22] show that $0<H_{t} ^{\prime }(a_{0}+iv_{t}(a_{0})\le 2$, which means $0\le a_{t}^{\prime } (a_{0})<2$. Thus, Point (2) improves the result to $0<a_{t}^{\prime }(a_{0})<2$.

The proof requires $\mu$ to have more than one point in its support in order to prove $a_{t}^{\prime }(a_{0}) \ne 0$. When $\mu =\delta _{0}$, it can be computed that $J_{t}(z)=z-\frac{t}{z}$ and $a_{0}+iv_{t}(a_{0})$ is the upper semicircle of radius $\sqrt{t}$. Therefore, $\mathrm{Re}\,[J_{t} (a_{0}+iv_{t}(a_{0}))]=0$ for all $a_{0}\in \Lambda _{t}\cap {\mathbb {R}}$, and its derivative is constantly 0 on $\Lambda _{t}\cap {\mathbb {R}}$.

The proof is similar to the proof in [2] of similar results about the map $H_{t}$.

Proof

Continuity of $J_{t}$ on $\overline{\Delta }_{t}$ follows from [2, Lemma 3], which shows continuity of $G_{x_{0}}$ on $\overline{\Delta }_{t}.$ To show injectivity of $J_{t}$, suppose, toward a contradiction, that $J_{t}(z_{1})=J_{t}(z_{2})$, for some $z_{1}\ne z_{2}$ in $\overline{\Delta }_{t}$. Then, using the definition (5.12) of $J_{t}$, we have

$$\begin{aligned} t(G_{\mu }(z_{2})-G_{\mu }(z_{1}))=z_{2}-z_{1}. \end{aligned}$$

This shows

$$\begin{aligned} t\int _{{\mathbb {R}}}\frac{z_{1}-z_{2}}{(z_{1}-x)(z_{2}-x)} \,\mathrm{d}\mu (x)=z_{2}-z_{1}. \end{aligned}$$

Since we are assuming that $z_{1}$ and $z_{2}$ are distinct, we can divide by $z_{1}-z_{2}$ to obtain

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{(z_{1}-x)(z_{2}-x)}=-\frac{1}{t}. \end{aligned}$$

(5.15)

Since $z_{1},z_{2}\in \overline{\Delta }_{t}$, we have $T(z_{1})\le 1/t$ and $T(z_{2})\le 1/t$. Thus, by the Cauchy–Schwarz inequality,

$$\begin{aligned} \left| \int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{(z_{1}-x) (z_{2}-x)}\right| ^{2}\le \int _{{\mathbb {R}}} \frac{\mathrm{d}\mu (x)}{|z_{1}-x|^{2}}\int _{{\mathbb {R}}} \frac{\mathrm{d}\mu (x)}{|z_{2}-x|^{2}}\le \frac{1}{t^{2}}. \end{aligned}$$

By (5.15), we have equality in the above Cauchy–Schwarz inequality. Therefore, there exists an $\alpha \in {\mathbb {C}}$ such that the relation

$$\begin{aligned} \frac{1}{\bar{z}_{2}-x}=\frac{\alpha }{z_{1}-x}, \end{aligned}$$

(5.16)

or, equivalently,

$$\begin{aligned} (\alpha -1)x=\alpha \bar{z}_{2}-z_{1} \end{aligned}$$

(5.17)

holds for $\mu$-almost every x. Since $\mu$ is assumed not to be a $\delta$-measure, we must have $\alpha =1,$ or else x would equal the constant value $(\alpha \bar{z}_{2}-z_{1})/(\alpha -1)$ for $\mu$-almost every x. With $\alpha =1,$ we find that $z_{1}=\bar{z}_{2}.$ But now if we substitute $z_{1}=\bar{z}_{2}$ into (5.15), we obtain

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{|z_{1}-x|^{2}}=-\frac{1}{t} \end{aligned}$$

which is impossible. This shows $z_{1}$ and $z_{2}$ cannot be distinct and Point (1) is established.

For Point (2), fix $a_{0}$ with $v_{t}(a_{0})>0$. We compute that

$$\begin{aligned} G_{x_{0}}^{\prime }(\lambda _{0})=-\int _{{\mathbb {R}}} \frac{\mathrm{d}\mu (x)}{(\lambda _{0}-x)^{2}} \end{aligned}$$

so that

$$\begin{aligned} \left| G_{x_{0}}^{\prime }(a_{0}+iv_{t}(a_{0}))\right| \le \int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{(a_{0}-x)^{2}+v_{t}(a_{0})^{2}} =\frac{1}{t}. \end{aligned}$$

(5.18)

We claim that this inequality must be strict. Otherwise, we would have equality in the “putting the absolute value inside the integral” inequality. This would mean, by the proof of Theorem 1.33 of [31], that

$$\begin{aligned} \frac{1}{(\lambda _{0}-x)^{2}} \end{aligned}$$

would have the same phase for $\mu$-almost every x. But since $\lambda _{0}$ is in the upper half plane, the phase of $\lambda _{0}-x$ increases from 0 to $\pi$ as x increases from $-\infty$ to $\infty$. Thus, the phase of $1/(\lambda _{0}-x)^{2}$ decreases from $2\pi$ to 0 as x increases from $-\infty$ to $\infty$. Therefore, $1/(\lambda _{0}-x)^{2}$ cannot have the same phase $\mu$-almost every x unless $\mu$ is a $\delta$-measure.

Now,

$$\begin{aligned} \frac{d}{da_{0}}G_{x_{0}}(a_{0}+iv_{t}(a_{0}))=G_{x_{0}}^{\prime }(a_{0} +iv_{t}(a_{0}))\left( 1+i\frac{dv_{t}(a_{0})}{da_{0}}\right) . \end{aligned}$$

Since (5.18) is a strict inequality,

$$\begin{aligned} \left| \frac{d}{da_{0}}G_{x_{0}}(a_{0}+iv_{t}(a_{0})) \right| ^{2}<\frac{1}{t^{2}} \left( 1+\left( \frac{dv_{t}(a_{0})}{da_{0}}\right) ^{2}\right) . \end{aligned}$$

(5.19)

Since

$$\begin{aligned} \mathrm{Im}\,[G_{x_{0}}(a_{0}+iv_{t}(a_{0}))]=-v_{t}(a_{0}) \int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{(a_{0}-x)^{2}+v_{t}(a_{0})^{2}} =-\frac{v_{t}(a_{0})}{t}, \end{aligned}$$

we have

$$\begin{aligned} \left( \frac{d}{da_{0}}\mathrm{Im}\,[G_{x_{0}}(a_{0}+iv_{t} (a_{0}))]\right) ^{2}=\frac{1}{t^{2}}\frac{dv_{t}(a_{0})}{a_{0}} \end{aligned}$$

and (5.19) becomes

$$\begin{aligned} \left( \frac{d}{da_{0}}\mathrm{Re}\,[G_{x_{0}}(a_{0}+iv_{t} (a_{0}))]\right) ^{2}<\frac{1}{t^{2}}. \end{aligned}$$

This shows, using the definition $a_{t}(a_{0})=\mathrm{Re}\,[J_{t} (a_{0}+iv_{t}(a_{0}))]$,

$$\begin{aligned} a_{t}^{\prime }(a_{0})=1-t\frac{d}{da_{0}}\mathrm{Re}\,[G_{x_{0}} (a_{0}+iv_{t}(a_{0}))]\in (0,2), \end{aligned}$$

as claimed.

We now turn to Point (3). To show that the function $a_{t}(a_{0})$ is strictly increasing with $a_{0},$ we use two observations. First, by Point (2), $a_{t}$ is increasing at any point $a_{0}$ where $v_{t}(a_{0})>0.$ Second, when $v_{t}(a_{0})=0,$ we have

$$\begin{aligned} a_{t}(a_{0})=a_{0}-t\int _{{\mathbb {R}}}\frac{1}{a_{0}-x}~\mathrm{d}\mu (x). \end{aligned}$$

(5.20)

We claim that the right-hand side of (5.20) is an increasing function of $a_{0}.$ Suppose that $a_{0}<a_{1}$ and $v_{t}(a_{0})=v_{t} (a_{1})=0$. We compute

$$\begin{aligned} a_{t}(a_{1})-a_{t}(a_{0})=(a_{1}-a_{0})\left( 1+t \int \frac{1}{(a_{1}-x)(a_{0}-x)}\,\mathrm{d}\mu (x)\right) . \end{aligned}$$

(5.21)

By Cauchy–Schwarz inequality and (5.4),

$$\begin{aligned} \left| \int \frac{1}{(a_{1}-x)(a_{0}-x)}\,\mathrm{d}\mu (x)\right| ^{2} \le \int \frac{\mathrm{d}\mu (x)}{(a_{1}-x)^{2}}\int \frac{\mathrm{d}\mu (x)}{(a_{0}-x)^{2}} \le \frac{1}{t^{2}}; \end{aligned}$$

the Cauchy–Schwarz inequality is indeed strict by the reasoning leading to (5.16) and (5.17). This proves that the right-hand side of (5.21) is positive and we have established our claim.

Consider any two points $a_{0}$ and $a_{1}$ with $a_{0}<a_{1}$; we wish to show that $a_{t}(a_{0})<a_{t}(a_{1}).$

We consider four cases, corresponding to whether $v_{t}(a_{0})$ and $v_{t}(a_{1})$ are zero or positive. If $v_{t}(a_{0})$ and $v_{t}(a_{1})$ are both zero, we use (5.20) and immediately conclude that $a_{t}(a_{0})<a_{t}(a_{1}).$ If $v_{t}(a_{0})=0$ but $v_{t}(a_{1})>0,$ then let $\alpha$ be the infimum of the interval I around $a_{1}$ on which $v_{t}$ is positive, so that $v_{t}(\alpha )=0$ and $a_{0}\le \alpha .$ Then, $a_{t}(a_{0})\le a_{t}(\alpha )$ by (5.20) and $a_{t} (\alpha )<a_{t}(a_{1})$ by the positivity of $a_{t}^{\prime }$ on I. The remaining cases are similar; the case where both $v_{t}(a_{0})$ and $v_{t}(a_{1})$ are positive can be subdivided into two cases depending on whether or not $a_{0}$ and $a_{1}$ are in the same interval of positivity of $v_{t}.$

Finally, we show that $a_{t}$ maps ${\mathbb {R}}$ onto ${\mathbb {R}}.$ Since $x_{0}$ is assumed to be bounded, the law $\mu$ of $x_{0}$ is compactly supported. It then follows easily from the condition (5.4) for $v_{t}$ to be zero that $v_{t}(a_{0})=0$ whenever $\left| a_{0}\right|$ is large enough. Thus, for $\left| a_{0}\right|$ large, the formula (5.20) applies, and we can easily see that $\lim _{a_{0} \rightarrow -\infty }a_{t}(a_{0})=-\infty$ and $\lim _{a_{0}\rightarrow +\infty }a_{t}(a_{0})=+\infty .$

For Point (4), it follows easily from Point (3) and the definition (5.13) of $a_{t}$ that $J_{t}$ maps the graph of $v_{t}$ to the graph of a function. When then note that (5.14) holds when $v_{t}(a_{0})=0$—both sides are zero. To establish (5.14) when $v_{t}(a_{0})>0$, we compute that

$$\begin{aligned} \mathrm{Im}\,[J_{t}(a_{0}+iv_{t}(a_{0}))]&=v_{t}(a_{0}) -t\mathrm{Im}\,\int _{{\mathbb {R}}}\frac{1}{a_{0}+iv_{t}(a_{0})-x}~\mathrm{d}\mu (x)\\&=v_{t}(a_{0})+tv_{t}(a_{0})\int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2} +v_{t}(a_{0})^{2}}~\mathrm{d}\mu (x)\\&=2v_{t}(a_{0}), \end{aligned}$$

by the defining property (5.3) of $v_{t}$.

For Point (5), we note that the graph of $v_{t},$ together with the point at infinity, forms a Jordan curve in the Riemann sphere, with the region above the graph as the interior of the disk—and similarly with $v_{t}$ replaced by $b_{t}.$ Since $J_{t}(\lambda _{0})$ tends to infinity as $\lambda _{0}$ tends to infinity, $J_{t}$ defines a continuous map of the closed disk bounded by $\mathrm {graph}(v_{t})\cup \{\infty \}$ to the closed disk bounded by $\mathrm {graph}(b_{t})\cup \{\infty \},$ and this map is a homeomorphism on the boundary. By an elementary topological argument, $J_{t}$ must map the closed disk onto the closed disk.

Finally, for Point (6), we use the description of $\Lambda _{t}$ in Proposition 5.2 as the region bounded by the graphs of $v_{t}$ and $-v_{t}.$ The complement of $\Lambda _{t}$ thus consists of the region on or above the graph of $v_{t}$ or on or below the graph of $-v_{t}.$ By Point (5) and the fact that $J_{t}$ commutes the complex conjugation, $J_{t}$ will map the complement of $\Lambda _{t}$ to the region on or above the graph of $b_{t}$ or on or below the graph of $-b_{t}.$ Thus, from Definition 5.4, $\Omega _{t}$ will be the region bounded by the graphs of $b_{t}$ and $-b_{t}$. $\square$

5.4 The method of Janik, Nowak, Papp, Wambach, and Zahed

We now discuss the work of Janik, Nowak, Papp, Wambach, and Zahed [23] which gives a nonrigorous but illuminating method of computing the support of the Brown measure of $x_{0}+i\sigma _{t}$. (See especially Section V of [23].) This method does not say anything about the Brown measure besides what its support should be. Furthermore, it is independent of the method used by Jarosz and Nowak in [24, 25] and discussed in Sect. 9.

Recall the definition of the Cauchy transform of an operator A in (5.8). We note that if $\lambda$ is outside the spectrum of A,  then we may safely put $\varepsilon =0$ in the function

$$\begin{aligned} S_{A}(\lambda ,\varepsilon ):=\tau [\log ((A-\lambda )^{*}(A-\lambda ) +\varepsilon )]. \end{aligned}$$

Using the formula (3.20) for the derivative of the trace of the logarithm, we can easily compute that

$$\begin{aligned} \frac{\partial }{\partial \lambda }S_{A}(\lambda ,0) =\tau [(\lambda -A)^{-1}]=G_{A}(\lambda ). \end{aligned}$$

But since $G_{A}(\lambda )$ depends holomorphically on $\lambda ,$ we find that

$$\begin{aligned} \Delta _{\lambda }S_{A}(\lambda ,0)&=4\frac{\partial }{\partial \bar{\lambda }} \frac{\partial }{\partial \lambda }S_{A}(\lambda ,0)\\&=4\frac{\partial }{\partial \bar{\lambda }}G_{A}(\lambda )\\&=0, \end{aligned}$$

so that the Brown measure is zero. This argument shows that the Brown measure is zero outside the spectrum of A.

Now, in the case $A=x_{0}+i\sigma _{t},$ the authors of [23] attempt to determine the maximum set on which the function

$$\begin{aligned} \frac{\partial }{\partial \lambda }S(t,\lambda ,0) \end{aligned}$$

remains holomorphic. We start with Biane’s subordination function identity (5.10), which we rewrite as follows. Let $\sigma$ be a fixed semicircular element, so that the law of $\sigma _{t}$ is the same as that of $\sqrt{t}\sigma .$ Then set $u=\sqrt{t},$ so that (5.10) reads as:

$$\begin{aligned} \tau [\{\lambda +u^{2}G_{x_{0}}(\lambda )-(x_{0}+u\sigma )\}^{-1}] =G_{x_{0}}(\lambda ). \end{aligned}$$

We then formally analytically continue to $u=i\sqrt{t},$ giving

$$\begin{aligned} \tau [\{\lambda -tG_{x_{0}}(\lambda )-(x_{0}+i\sqrt{t}\sigma )\}^{-1}] =G_{x_{0}}(\lambda ). \end{aligned}$$

Thus,

$$\begin{aligned} G_{x_{0}+\sigma _{t}}(\lambda +tG_{x_{0}}(\lambda ))=G_{x_{0}}(\lambda ) =G_{x_{0}+i\sigma _{t}}(\lambda -tG_{x_{0}}(\lambda )). \end{aligned}$$

In terms of the maps $H_{t}$ and $J_{t}$ defined in (5.9) and (5.12), respectively, we then have

$$\begin{aligned} G_{x_{0}+i\sigma _{t}}(J_{t}(\lambda )) =G_{x_{0}+\sigma _{t}}(H_{t}(\lambda )) \end{aligned}$$

or

$$\begin{aligned} G_{x_{0}+i\sigma _{t}}(J_{t}(H_{t}^{-1}(\lambda ))) =G_{x_{0}+\sigma _{t}} (\lambda ). \end{aligned}$$

(5.22)

We also note that from the definitions (5.9) and (5.12), we have $J_{t}(\lambda )=2\lambda -H_{t}(\lambda ),$ so that

$$\begin{aligned} J_{t}(H_{t}^{-1}(z))=2H_{t}^{-1}(z)-z. \end{aligned}$$

(5.23)

Then, since the right-hand side of (5.22) is holomorphic on the whole upper half-plane, the authors of [23] argue that the identity (5.22) actually holds on the whole upper half-plane. If that claim actually holds, we will have the identity

$$\begin{aligned} G_{x_{0}+i\sigma _{t}}(z)=G_{x_{0}+\sigma _{t}}(H_{t}(J_{t}^{-1}(z))) \end{aligned}$$

(5.24)

for all z in the range of $J_{t}\circ H_{t}^{-1},$ namely for all z (in the upper half-plane) outside the closure of $\Omega _{t}.$ An exactly parallel argument then applies in the lower half-plane. The authors thus wish to conclude that $G_{x_{0}+i\sigma _{t}}$ is defined and holomorphic on the complement of $\overline{\Omega }_{t},$ which would show that the Brown measure of $x_{0}+i\sigma _{t}$ is zero there.

We emphasize that the argument for (5.22) is rigorous for all sufficiently large $\lambda ,$ simply because the quantity $\tau [ (\lambda -A)^{-1}]$ depends holomorphically on both the complex number $\lambda$ and the operator A. But just because the right-hand side of the identity extends holomorphically to the upper half-plane does not by itself mean that the identity continues to hold on the whole upper half-plane. Thus, the argument in [23] is not entirely rigorous. Nevertheless, it certainly gives a natural explanation of how the domain $\Omega _{t}$ arises.

The identities (5.22) and (5.24) already indicate a close relationship between the operators $x_{0}+i\sigma _{t}$ and $x_{0}+\sigma _{t}.$ In Sect. 8, we will find an even closer relationship: The push-forward of the Brown measure of $x_{0}+i\sigma _{t}$ under a certain map $Q_{t}:\overline{\Omega }_{t}\rightarrow {\mathbb {R}}$ is precisely the law of $x_{0}+\sigma _{t}.$ The map $Q_{t}$ is constructed as follows: It is the unique map of $\overline{\Omega }_{t}$ to ${\mathbb {R}}$ that agrees with $H_{t}\circ J_{t}^{-1}$ on $\partial \Omega _{t}$ and maps vertical segments in $\overline{\Omega }_{t}$ to points in ${\mathbb {R}}.$

6 Outside the domain

In this section, we show that the Brown measure of $x_{0}+i\sigma _{t}$ is zero in the complement of the closure of the domain $\Omega _{t}$ in Definition 5.4. We outline our strategy in Sect. 6.1 and then give a rigorous argument in Sect. 6.2.

6.1 Outline

Our goal is to compute the Laplacian with respect to $\lambda$ of the function

$$\begin{aligned} s_{t}(\lambda )=\lim _{\varepsilon \rightarrow 0^{+}} S(t,\lambda ,\varepsilon ). \end{aligned}$$

We use the Hamilton–Jacobi method of Proposition 4.2, which gives us a formula for $S(t,\lambda (t),\varepsilon (t)).$ Since (Proposition 4.4) $\varepsilon (t) =\varepsilon _{0}(1-p_{0}t)^{2}$, we can attempt to make $\varepsilon (t)$ approach 0 by letting $\varepsilon _{0}$ approach zero. This strategy, however, can only succeed if the lifetime of the path remains at least t in the limit as $\varepsilon _{0}\rightarrow 0.$ Thus, we must take $\lambda _{0}$ for which $T(\lambda _{0})\ge t,$ where T is as in Definition 4.6. We therefore consider $\lambda _{0}$ in $\overline{\Lambda }_{t}^{c},$ where $\Lambda _{t}$ is as in Definition 5.1.

If we formally put $\varepsilon _{0}=0$, then $\varepsilon (t)=0$, and, by Proposition 4.7, we have

$$\begin{aligned} \lambda (t)=J_{t}(\lambda _{0}). \end{aligned}$$

(6.1)

Now, by Proposition 5.5, $J_{t}$ maps $\Lambda _{t}^{c}$ injectively onto $\Omega _{t}^{c}.$ Thus, for any $\lambda \in \overline{\Omega }_{t}^{c},$ we may choose $\lambda _{0}=J_{t}^{-1}(\lambda )$. Then, if we formally apply the Hamilton–Jacobi formula (4.5) with $\varepsilon _{0}=0$, we get

$$\begin{aligned} S(t,\lambda ,0)=\int _{{\mathbb {R}}}\log (|J_{t}^{-1}(\lambda )-x|^{2}) \,\mathrm{d}\mu (x)-\frac{t}{4}(p_{a,0}^{2}-p_{b,0}^{2}), \end{aligned}$$

where, with $\varepsilon _{0}=0,$ the initial momenta in (4.4) may be computed as:

$$\begin{aligned} p_{a,0}&=2\int _{{\mathbb {R}}}\frac{(a_{0}-x)}{(a_{0}-x)^{2}+b_{0}^{2}} ~\mathrm{d}\mu (x)=2\mathrm{Re}\,\int _{{\mathbb {R}}}\frac{1}{\lambda _{0}-x}~\mathrm{d}\mu (x)\\ p_{b,0}&=2\int _{{\mathbb {R}}}\frac{b_{0}}{(a_{0}-x)^{2}+b_{0}^{2}} ~\mathrm{d}\mu (x)=-2\mathrm{Im}\,\int _{{\mathbb {R}}}\frac{1}{\lambda _{0}-x}~\mathrm{d}\mu (x). \end{aligned}$$

Thus,

$$\begin{aligned} S(t,\lambda ,0)=\int _{{\mathbb {R}}}\log (|J_{t}^{-1}(\lambda )-x|^{2}) \,\mathrm{d}\mu (x)-t\mathrm{Re}\,[G_{x_{0}}(J_{t}^{-1}(\lambda _{0}))^{2}], \end{aligned}$$

(6.2)

where

$$\begin{aligned} G_{x_{0}}(\lambda )=\tau ((\lambda -x_{0})^{-1}) =\int _{{\mathbb {R}}}\frac{1}{\lambda -x}~\mathrm{d}\mu (x). \end{aligned}$$

The right-hand side of (6.2) is the composition of a harmonic function and a holomorphic function and is therefore harmonic. We thus wish to conclude that Brown measure of $x_{0}+i\sigma _{t}$ is zero outside $\overline{\Omega }_{t}$.

The difficulty with the preceding argument is that the function $S(t,\lambda , \varepsilon )$ is only known ahead of time to be defined for $\varepsilon >0.$ Thus, the PDE in Theorem 3.1 is only known to hold when $\varepsilon >0$ and the Hamilton–Jacobi formula is only valid when $\varepsilon (t)$ remains positive. We are therefore not allowed to set $\varepsilon _{0}=0$ in the Hamilton–Jacobi formula (4.5). Now, if $\lambda$ is outside the spectrum of $x_{0}+i\sigma _{t},$ then we can see that $S(t,\lambda ,\varepsilon )$ continues to make sense for $\varepsilon =0$ and even for $\varepsilon$ slightly negative, and the PDE and Hamilton–Jacobi formula presumably apply. But of course we do not know that every point in $\overline{\Omega }_{t}$ is outside the spectrum of $x_{0}+i\sigma _{t}$; if we did, an elementary property of the Brown measure would already tell us that the Brown measure is zero there.

If, instead, we let $\varepsilon _{0}$ approach zero from above, we find that

$$\begin{aligned} \lim _{\varepsilon _{0}\rightarrow 0^{+}}S(t,\lambda (t),\varepsilon (t)) =\int _{{\mathbb {R}}}\log (|J_{t}^{-1}(\lambda )-x|^{2})\,\mathrm{d}\mu (x) -t\mathrm {Re}\,[G_{x_{0}}(J_{t}^{-1}(\lambda ))^{2}]. \end{aligned}$$

(6.3)

Now, as $\varepsilon _{0}\rightarrow 0^{+},$ we can see that $\lambda (t)$ approaches $\lambda$ and $\varepsilon (t)$ approaches 0. But there is still a difficulty, because the function $s_{t}(\lambda )$ is defined as the limit of $S(t,\lambda ,\varepsilon )$ as $\varepsilon$ tends to zero with $\lambda$ fixed. But on the left-hand side of (6.3), $\lambda =\lambda (t)$ is not fixed, because it depends on $\varepsilon _{0}.$ To overcome this difficulty, we will use the inverse function theorem to show that, for each $t>0,$ the function S has an extension to a neighborhood of $(t,\lambda ,0)$ that is continuous in the $\lambda$- and $\varepsilon$-variables. Thus, the limit of S along any path approaching $(t,\lambda ,0)$ is the same as the limit with $\lambda$ fixed and $\varepsilon$ tending to zero.

6.2 Rigorous treatment

In this section, we establish the following rigorous version of (6.2), which shows that the support of the Brown measure of $x_{0}+i\sigma _{t}$ is contained in $\overline{\Omega }_{t}$. Recall that $s_{t}(\lambda )$ is the limit of $S(t,\lambda ,\varepsilon )$ as $\varepsilon$ approaches zero from above with $\lambda$ fixed.

Theorem 6.1

If $\lambda$ is not in $\overline{\Omega }_{t},$ we have

$$\begin{aligned} s_{t}(\lambda )=\int _{{\mathbb {R}}}\log (|J_{t}^{-1}(\lambda )-x|^{2}) \,\mathrm{d}\mu (x)-t\mathrm {Re}\,[G_{x_{0}}(J_{t}^{-1}(\lambda ))^{2}] \end{aligned}$$

(6.4)

and $\Delta s_{t}(\lambda )=0$.

The theorem will follow from the argument in Sect. 6.1, once the following regularity result is established.

Proposition 6.2

Fix a time $t>0$ and a point $\lambda ^{*} \in \overline{\Omega }_{t}^{c}.$ Then, the function $(\lambda ,\varepsilon )\mapsto S(t,\lambda ,\varepsilon )$ extends to a real analytic function defined in a neighborhood of $(\lambda ^{*},0)$ inside ${\mathbb {C}}\times {\mathbb {R}}$.

We will need the following preparatory result.

Lemma 6.3

If $\lambda _{0}$ is not in $\overline{\Lambda }_{t}$, there is a neighborhood of $\lambda _{0}$ in $\overline{\Lambda }_{t}^{c}$ that does not intersect $\mathrm {supp}(\mu )$.

The result of this lemma does not hold if we replace $\overline{\Lambda }_{t}^{c}$ by $\Lambda _{t}^{c}$. As a counter-example, if $\mu =3x^{2}\,dx$ on [0, 1],  then using the criterion (5.6) for $\Lambda _{t} \cap {\mathbb {R}},$ we find that $0\in \Lambda _{t}^{c}$ for small enough t,  but $0\in \mathrm {supp}(\mu )$.

Proof

It is clear that the statement of this lemma holds unless $\lambda _{0} \in {\mathbb {R}}$ since $x_{0}$ is self-adjoint.

Consider, then, a point $\lambda _{0}\in \overline{\Lambda }_{t}^{c} \cap {\mathbb {R}}.$ Choose an interval $(\alpha ,\beta )$ around $\lambda _{0}$ contained in $\overline{\Lambda }_{t}^{c} \cap {\mathbb {R}}.$ We claim that $\mu ((\alpha ,\beta ))$ must be zero. To see, note that since the points in $(\alpha ,\beta )$ are outside $\Lambda _{t},$ we have (Definition 5.1)

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2}}\,\mathrm{d}\mu (x)\le \frac{1}{t} \end{aligned}$$

for all $a_{0}\in (\alpha ,\beta )$. If we integrate the above integral with respect to the Lebesgue measure in $a_{0}$, we have

$$\begin{aligned} \int _{\alpha }^{\beta }\int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2}} \,\mathrm{d}\mu (x)\,\mathrm{d}a_{0}<\infty . \end{aligned}$$

We may then reverse the order of integration and restrict the integral with respect to $\mu$ to $(\alpha ,\beta )$ to get

$$\begin{aligned} \int _{\alpha }^{\beta }\int _{\alpha }^{\beta }\frac{1}{(a_{0}-x)^{2}} \,\mathrm{d}a_{0}\,\mathrm{d}\mu (x)<\infty . \end{aligned}$$

(6.5)

But

$$\begin{aligned} \int _{\alpha }^{\beta }\frac{1}{(a_{0}-x)^{2}}\,\mathrm{d}a_{0}=\infty \end{aligned}$$

for all $x\in (\alpha ,\beta )$. Thus, the only way (6.5) can hold is if $\mu ((\alpha ,\beta )=0$. $\square$

We now work toward the proof of Proposition 6.2. In light of the formulas for the solution path in Proposition 4.4 , we consider the map $V_{t}$ given by $V_{t}(a_{0},b_{0}, \varepsilon _{0})=(a_{t},b_{t},\varepsilon _{t}),$ where

$$\begin{aligned} a_{t}(a_{0},b_{0},\varepsilon _{0})&=a_{0}-\frac{t}{2}p_{a,0}\\ b_{t}(a_{0},b_{0},\varepsilon _{0})&=b_{0}+\frac{t}{2}p_{b,0}\\ \varepsilon _{t}(a_{0},b_{0},\varepsilon _{0})&=\varepsilon _{0} (1-p_{0}t)^{2}. \end{aligned}$$

This map is initially defined for $\varepsilon _{0}>0,$ which guarantees that the integrals (4.4) defining $p_{a,0}$ and $p_{b,0}$ are convergent, even if $b_{0}=0.$ But if $\lambda _{0}$ is in $\overline{\Lambda }_{t}^{c},$ Lemma 6.3 guarantees that $\lambda _{0}$ is outside the closed support of $\mu ,$ so that the integrals are convergent when $\varepsilon _{0}=0$ and even when $\varepsilon _{0}$ is slightly negative. Thus, for any $\lambda _{0}\in \overline{\Lambda }_{t}^{c}$, we can extend $V_{t}$ to a neighborhood of $(\lambda _{0},0)$ using the same formula. We note that when $\varepsilon _{0}=0,$ we have

$$\begin{aligned} a_{t}(a_{0},b_{0},0)+ib_{t}(a_{0},b_{0},0)=J_{t}(a_{0}+ib_{0}), \end{aligned}$$

(6.6)

as in (6.1).

Lemma 6.4

If $\lambda _{0}$ is not in $\overline{\Lambda }_{t},$ the Jacobian matrix of $V_{t}$ at $(\lambda _{0},0)$ is invertible.

Proof

If we vary $a_{0}$ or $b_{0}$ with $\varepsilon _{0}$ held equal to 0,  then $\varepsilon$ remains equal to zero, so that

$$\begin{aligned} \frac{\partial \varepsilon _{t}}{\partial a_{0}}(\lambda _{0},0) =\frac{\partial \varepsilon _{t}}{\partial b_{0}}(\lambda _{0},0)=0. \end{aligned}$$

Meanwhile, from the formula for $\varepsilon _{t},$ we obtain

$$\begin{aligned} \frac{\partial \varepsilon _{t}}{\partial \varepsilon _{0}} (\lambda _{0},0)=(1-tp_{0})^{2}. \end{aligned}$$

Thus, using (6.6), we find that the Jacobian matrix of V at $(a_{0},b_{0},0)$ has the form:

$$\begin{aligned} \left( \begin{array}{cc} K &{} *\\ 0 &{} (1-tp_{0})^{2} \end{array}\right) , \end{aligned}$$

where K is the $2\times 2$ Jacobian matrix of the map $J_{t}$.

Since $\lambda _{0}\in \overline{\Lambda }_{t}^{c},$ we have $T(\lambda _{0})=1/p_{0}>1/t,$ so that $1-tp_{0}>0.$ Furthermore, since $J_{t}$ is injective on $\overline{\Lambda }_{t}^{c},$ its complex derivative must be nonzero at $\lambda _{0},$ so that K is invertible. We can then see that the Jacobian matrix of $V_{t}$ at $(t,\lambda _{0},0)$ has nonzero determinant. $\square$

We are now ready for the proof of our regularity result.

Proof of Proposition 6.2

Define a function $\mathrm {HJ}$ by the right-hand side of the first Hamilton–Jacobi formula (4.5), namely

$$\begin{aligned} \mathrm {HJ}(a_{0},b_{0},\varepsilon _{0},t)=S(0,\lambda _{0}, \varepsilon _{0})-t\left[ \frac{1}{4}(p_{a,0}^{2}-p_{b,0}^{2}) -\varepsilon _{0}p_{0}^{2}\right] . \end{aligned}$$

(6.7)

Now take $\lambda ^{*}\in \overline{\Omega }_{t}^{c}$ and let $\lambda _{0}^{*}=J_{t}^{-1}(\lambda ^{*}),$ so that $\lambda _{0}^{*} \in \overline{\Lambda }_{t}^{c}.$ By Lemma 6.4 and the inverse function theorem, $V_{t}$ has an analytic inverse in a neighborhood U of $(\lambda ^{*},0).$ By shrinking U if necessary, we can assume that the $\lambda _{0}$-component of $V^{-1}(\lambda ,\varepsilon )$ lies in $\overline{\Lambda }_{t}^{c}$ for all $(\lambda ,\varepsilon )$ in U. We now claim that for each fixed $t>0,$ the map

$$\begin{aligned} (\lambda ,\varepsilon )\mapsto \mathrm {HJ}\circ V_{t}^{-1} (\lambda ,\varepsilon ) \end{aligned}$$

(6.8)

gives the desired analytic extension of $S(t,\cdot ,\cdot )$ to a neighborhood of $(\lambda ^{*},0).$

We first note that $\mathrm {HJ}\circ V_{t}^{-1}$ is smooth, where we use Lemma 6.3 to guarantee that the momenta in the definition of $\mathrm {HJ}$ are well defined. We then argue that for all $(\lambda ,\varepsilon )$ in U with $\varepsilon >0,$ the value of $\mathrm {HJ}\circ V_{t}^{-1}(\lambda ,\varepsilon )$ agrees with $S(t,\lambda ,\varepsilon ).$ To see this, note first that if $(\lambda ,\varepsilon )\in U$ has $\varepsilon >0,$ then the $\varepsilon _{0}$-component of $V_{t}^{-1}(\lambda ,\varepsilon )$ must be positive, as is clear from the formula for $\varepsilon _{t}(a_{0} ,b_{0},\varepsilon _{0}).$ Since, also, the $\lambda _{0}$-component of $V_{t}^{-1}(\lambda ,\varepsilon )$ is in $\overline{\Lambda }_{t}^{c},$ the small-$\varepsilon _{0}$ lifetime of the path is at least t,  so that when $\varepsilon _{0}>0,$ the lifetime is greater than t. Thus, for $(\lambda ,\varepsilon )$ in U with $\varepsilon >0,$ the first Hamilton–Jacobi formula (4.5) tells us that, indeed, $S(t,\lambda ,\varepsilon ) =\mathrm {HJ}(V_{t}^{-1}(\lambda ,\varepsilon ))$. $\square$

We now come to the proof of our main result.

Proof of Theorem 6.1

Once we know that (6.8) gives an analytic extension of $S(t,\cdot ,\cdot ),$ we conclude that the function $s_{t}$ defined as:

$$\begin{aligned} s_{t}(\lambda )=\lim _{\varepsilon \rightarrow 0}S(t,\lambda ,\varepsilon ) \end{aligned}$$

can be computed as:

$$\begin{aligned} s_{t}(\lambda )=\mathrm {HJ}\circ V_{t}^{-1}(\lambda ,0). \end{aligned}$$

(6.9)

The point of this observation is that because $\mathrm {HJ}\circ V_{t}^{-1}$ is analytic (in particular, continuous), we can compute $s_{t}(\lambda )$ by taking the limit of $\mathrm {HJ}\circ V_{t}^{-1}(\delta ,\varepsilon )$ along any path ending at $(\lambda ,0),$ rather than having to fix $\lambda$ and let $\varepsilon$ tend to zero.

Fix a point $\lambda$ in $\overline{\Omega }_{t}^{c}$ and let $\lambda _{0}=J_{t}^{-1}(\lambda )$, so that $T(\lambda _{0})\ge t$. Then, for any $\varepsilon _{0}>0,$ the lifetime of the path with initial conditions $(\lambda _{0},\varepsilon _{0})$ will be greater than t and the first Hamilton–Jacobi formula (4.5) tells us that

$$\begin{aligned} S(t,\lambda (t),\varepsilon (t))=S(0,\lambda _{0},\varepsilon _{0})-t \left[ \frac{1}{4}(p_{a,0}^{2}-p_{b,0}^{2})-\varepsilon _{0}p_{0}^{2}\right] . \end{aligned}$$

As $\varepsilon _{0}\rightarrow 0$, we find that $\lambda (t)\rightarrow J_{t}(\lambda _{0})=\lambda$ and $\varepsilon (t)\rightarrow 0.$ Thus, by (6.9) and the continuity of $\mathrm {HJ}\circ V_{t}^{-1},$ we have

$$\begin{aligned} s_{t}(\lambda )=S(0,\lambda _{0},0)-t\lim _{\varepsilon _{0}\rightarrow 0} \left[ \frac{1}{4}(p_{a,0}^{2}-p_{b,0}^{2})-\varepsilon _{0}p_{0}^{2}\right] , \end{aligned}$$

which gives the claimed expression (6.4).

Now, if $\lambda$ is outside of $\overline{\Omega }_{t},$ then $J_{t}^{-1}(\lambda )$ is outside of $\bar{\Lambda }_{t},$ which means (Lemma 6.3) that $J_{t}^{-1}(\lambda )$ is outside the support of the measure $\mu .$ It is then easy to see that $s_{t}$ is a composition of a harmonic function and a holomorphic function, which is harmonic. $\square$

7 Inside the domain

7.1 Outline

In Sect. 6, we computed the Brown measure in the complement of $\overline{\Omega }_{t}$ and found that it is zero there. Our strategy was to apply the Hamilton–Jacobi formulas with $\lambda _{0}$ in the complement of $\overline{\Lambda }_{t}$ and $\varepsilon _{0}$ chosen to be very small, so that $\lambda (t)$ is in the complement of $\overline{\Omega }_{t}$ and $\varepsilon (t)$ is also very small. If, on the other hand, we take $\lambda _{0}$ inside $\Lambda _{t}$, then (by definition) $T(\lambda _{0})<t,$ meaning that the small-$\varepsilon _{0}$ lifetime of the path is less than t. Thus, for $\lambda _{0}\in \Lambda _{t}$ and $\varepsilon _{0}$ small, the Hamilton–Jacobi formulas are not applicable at time t.

In this section, then, we will use a different strategy. We recall from Proposition 4.4 that $\varepsilon (t)=\varepsilon _{0} (1-p_{0}t)^{2}.$ Thus, an alternative way to make $\varepsilon (t)$ small is to take $\varepsilon _{0}>0$ and arrange for $p_{0}$ to be close to 1/t. Thus, for each point $\lambda$ in $\Omega _{t},$ we will try to find $\lambda _{0} \in \Lambda _{t}$ and $\varepsilon _{0}>0$ so that $p_{0}=1/t$ and $\lambda (t)=\lambda .$ (If $p_{0}=1/t$, then the solution to the system of ODEs blows up at time t,  so that technically we are not allowed to apply the Hamilton–Jacobi formulas at time t. But we will gloss over this point for now and return to it in Sect. 7.1.3.)

Once we have understood how to choose $\lambda _{0}$ and $\varepsilon _{0}$ as functions of $\lambda \in \Omega _{t},$ we will then apply the Hamilton–Jacobi method to compute the Brown measure inside $\Omega _{t}.$ Specifically, we will use the second Hamilton–Jacobi formula (4.6) to compute the first derivatives of $S(t,\lambda ,0)$ with respect to a and b. We then compute the second derivatives to get the density of the Brown measure.

7.1.1 Mapping onto $\Omega _{t}$

We first describe how to choose $\lambda _{0}$ and $\varepsilon _{0}>0$ as functions of $\lambda \in \Omega _{t}$ so that $\lambda (t)=\lambda$ and $\varepsilon (t)=0.$ If $a_{0}+ib_{0}\in \Lambda _{t},$ then $\left| b_{0}\right| <v_{t}(a_{0}).$ Then, from the defining property (5.3) of the function $v_{t},$ we see that if we take

$$\begin{aligned} \varepsilon _{0}=\varepsilon _{0}^{t}(a_{0}):=v_{t}(a_{0})^{2}-b_{0}^{2}, \end{aligned}$$

(7.1)

then $\varepsilon _{0}$ is positive and plugging this value of $\varepsilon _{0}$ into the formula (4.4) for $p_{0}$ gives

$$\begin{aligned} p_{0}=\int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2}+v_{t}(a_{0})^{2}}~\mathrm{d}\mu (x)=\frac{1}{t}, \end{aligned}$$

as desired.

It remains to see how to choose $\lambda _{0}$ so that (with $\varepsilon _{0}$ given by (7.1)) we will have $\lambda (t)=\lambda .$ Since $p_{0}=1/t,$ Proposition 4.5 applies:

$$\begin{aligned} a(t)&=t\int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2} +v_{t}(a_{0})^{2}}~\mathrm{d}\mu (x) \end{aligned}$$

(7.2)

$$\begin{aligned} b(t)&=2b_{0}. \end{aligned}$$

(7.3)

If we want $\lambda (t)$ to equal $\lambda =a+ib,$ then (7.3) immediately tells us that we should choose $b_{0}=b/2.$ We will show in Sect. 7.2 that (7.2) can be solved for $a_{0}$ as a function of a and t; we use the notation $a_{0}^{t}(a)$ for the solution.

Summary 7.1

For all $\lambda =a+ib\in \Omega _{t},$ the following procedure shows how to choose $\lambda _{0}=a_{0}+ib_{0}\in \Lambda _{t}$ and $\varepsilon _{0}>0$ so that, with these initial conditions, we will have $\lambda (t)=\lambda$ and $\varepsilon (t)=0.$ First, we use the condition

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2}+v_{t}(a_{0})^{2}}~\mathrm{d}\mu (x) =\frac{1}{t} \end{aligned}$$

to determine $v_{t}$ as a function of $a_{0}.$ Second, use the condition

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{x}{(a_{0}-x)^{2}+v_{t}(a_{0})^{2}} ~\mathrm{d}\mu (x)=\frac{a}{t} \end{aligned}$$

to determine $a_{0}$ as a function $a_{0}^{t}$ of a. Then, we take

$$\begin{aligned} b_{0}&=b/2\\ \varepsilon _{0}&=v_{t}(a_{0}^{t}(a))^{2}-b_{0}^{2}. \end{aligned}$$

7.1.2 Computing the Brown measure

Using the choices for $\lambda _{0}$ and $\varepsilon _{0}$ in Summary 7.1, we then apply the second Hamilton–Jacobi formula (4.6). Since $\lambda (t)=\lambda$ and $\varepsilon (t)=0$ and $p_{b}$ is a constant of motion,

$$\begin{aligned} \frac{\partial S}{\partial b}(t,\lambda ,0)=p_{b}(t)=p_{b,0}. \end{aligned}$$

But since, by (4.7), $p_{b,0}=2b_{0}p_{0},$ we obtain

$$\begin{aligned} \frac{\partial S}{\partial b}(t,\lambda ,0)=2b_{0}p_{0}=\frac{b}{t}, \end{aligned}$$

since we are assuming that $p_{0}=1/t.$

Similarly,

$$\begin{aligned} \frac{\partial S}{\partial a}(t,\lambda ,0)&=p_{a}(t)\\&=p_{a,0}\\&=2a_{0}p_{0}-2p_{1}.\\&=\frac{2a_{0}^{t}(a)}{t}-\frac{2a}{t}, \end{aligned}$$

where we have used (7.2) and the formula (4.8) for $p_{a,0}$.

Conclusion 7.2

The preceding argument suggests that for $\lambda =a+ib\in \Omega _{t},$ we should have

$$\begin{aligned} \frac{\partial s_{t}}{\partial a}&=\frac{2}{t}(a_{0}^{t}(a)-a)\\ \frac{\partial s_{t}}{\partial b}&=\frac{b}{t}. \end{aligned}$$

If this is correct, then the density of the Brown measure in $\Omega _{t}$ is readily computed as:

$$\begin{aligned} \frac{1}{4\pi }\left( \frac{\partial ^{2}S}{\partial a^{2}} +\frac{\partial ^{2}S}{\partial b^{2}}\right) (t,\lambda ,0) =\frac{1}{2\pi t}\left( \frac{da_{0}^{t}(a)}{da}-\frac{1}{2}\right) , \end{aligned}$$

as claimed in Theorem 1.2. In particular, the density of the Brown measure in $\Lambda _{t}$ would be independent of $b=\mathrm{Im}\,\lambda .$

7.1.3 Technical issues

The preceding argument is not rigorous, since the Hamilton–Jacobi formulas are only known to hold as long as $\varepsilon (s)$ remains positive for all $0\le s\le t.$ That is to say, if $\varepsilon (t)=0$, then we are not allowed to use the formulas at time t. We can try to work around this point by letting $\varepsilon _{0}$ approach the value $\varepsilon _{0}^{t}(\lambda _{0}):=v_{t}(a_{0})^{2}-b_{0}^{2}$ in (7.1) from above. Then, we have a situation similar to the one in (6.3), namely

$$\begin{aligned} \lim _{\varepsilon _{0}\rightarrow \varepsilon _{0}^{t}(\lambda _{0})^{+}} \frac{\partial S}{\partial a}(t,\lambda (t),\varepsilon (t))&=\frac{2}{t}(a_{0}^{t}(a)-a) \end{aligned}$$

(7.4)

$$\begin{aligned} \lim _{\varepsilon _{0}\rightarrow \varepsilon _{0}^{t}(\lambda _{0})^{+}} \frac{\partial S}{\partial b}(t,\lambda (t),\varepsilon (t))&=\frac{b}{t}, \end{aligned}$$

(7.5)

where

$$\begin{aligned} \lim _{\varepsilon _{0}\rightarrow \varepsilon _{0}^{t}(\lambda _{0})} \lambda (t)=\lambda ;\quad \lim _{\varepsilon _{0} \rightarrow \varepsilon _{0}^{t}(\lambda _{0})}\varepsilon (t)=0. \end{aligned}$$

But the Brown measure is computed by first evaluating the limit

$$\begin{aligned} s_{t}(\lambda ):=\lim _{\varepsilon \rightarrow 0^{+}} S(t,\lambda ,\varepsilon ), \end{aligned}$$

where the limit is taken as $\varepsilon \rightarrow 0$ with $\lambda$ fixed, and then taking the distributional Laplacian with respect to $\lambda .$ Since $\lambda (t)$ is not fixed in (7.4) and (7.5), it is not clear that these limits are actually computing $\partial s_{t}/\partial a$ and $\partial s_{t}/\partial b.$ The main technical challenge of this section is, therefore, to establish enough regularity of S near $(t,\lambda ,\varepsilon )$ to verify that $\partial s_{t}/\partial a$ and $\partial s_{t}/\partial b$ are actually given by the right-hand sides of (7.4) and (7.5).

7.2 Surjectivity

In this section, we show that the procedure in Summary 7.1 actually gives a continuous map of $\Lambda _{t}$ onto $\Omega _{t}.$ Given any $\lambda _{0}\in \Lambda _{t}$, choose $\varepsilon _{0} =\varepsilon _{0}^{t}(\lambda _{0})$ as in (7.1), so that

$$\begin{aligned} \lim _{s\rightarrow t}\varepsilon (s)=0. \end{aligned}$$

Then define

$$\begin{aligned} U_{t}(\lambda _{0})=\lim _{s\rightarrow t}\lambda (s). \end{aligned}$$

By Proposition 4.5, we have

$$\begin{aligned} U_{t}(a_{0}+ib_{0})=a_{t}(a_{0})+2ib_{0} \end{aligned}$$

where

$$\begin{aligned} a_{t}(a_{0})=t\int _{{\mathbb {R}}}\frac{1}{(a_{0}-x)^{2} +v_{t}(a_{0})^{2}}\,\mathrm{d}\mu (x). \end{aligned}$$

(7.6)

Since we assume $\lambda _{0}\in \Lambda _{t},$ we have $v_{t}(a_{0})>0$ and we therefore have an alternative formula:

$$\begin{aligned} a_{t}(a_{0})=\mathrm{Re}\,[J_{t}(a_{0}+iv_{t}(a_{0}))]. \end{aligned}$$

(7.7)

It is a straightforward computation to check that the right-hand sides of (7.6) and (7.7) agree, using that the identity (5.3) holds when $v_{t}(a_{0})>0.$

The main result in this section is stated in the following theorem. We remind the reader of the definition (5.12) of the map $J_{t}$.

Theorem 7.3

The following results hold.

• (1) The map $U_{t}$ extends continuously to $\overline{\Lambda }_{t}.$ This extension is the unique continuous map of $\overline{\Lambda }_{t}$ into $\overline{\Omega }_{t}$ that (a) agrees with $J_{t}$ on $\partial \Lambda _{t}$ and (b) maps each vertical segment in $\overline{\Lambda }_{t}$ linearly to a vertical segment in $\overline{\Omega }_{t}.$

• (2) The map $U_{t}$ is a homeomorphism from $\Lambda _{t}$ onto $\Omega _{t}$.

Most of what we need to prove the theorem is already in Proposition 5.5.

Proof

Proposition 5.5 showed that the right-hand side of (7.7) is continuous for all $a_{0}\in {\mathbb {R}}.$ Using this formula for $a_{t},$ we see that $U_{t}$ actually extends continuously to the whole complex plane. It is then a simple computation to check that

$$\begin{aligned} \mathrm{Im}\,J_{t}(a_{0}\pm iv_{t}(a_{0}))=\pm 2v_{t}(a_{0}). \end{aligned}$$

This formula, together with (7.7), shows that $U_{t}$ agrees with $J_{t}$ for all points in $\partial \Lambda _{t}$ having nonzero imaginary parts. Then points in $\partial \Lambda _{t}$ on the real axis are limits of points in $\partial \Lambda _{t}$ with nonzero imaginary parts. Thus, $U_{t}$ indeed agrees with $J_{t}$ on $\partial \Lambda _{t}.$ Also $U_{t}$ is linear on each vertical segment. Since $\Lambda _{t}$ is bounded by the graphs of $v_{t}$ and $-v_{t},$ it is easy to see that $U_{t}$ is the unique map with these two properties.

By Proposition 5.5, $\Omega _{t}$ is bounded by the graphs $b_{t}$ and $-b_{t},$ where the graph of $b_{t}$ is the image of the graph of $v_{t}$ under $J_{t}.$ From this result, it follows easily that $U_{t}$ is a homeomorphism. $\square$

We conclude this section by giving bounds on the real parts of points in $\Omega _{t}$, in terms of the law $\mu$ of $x_{0}.$

Proposition 7.4

Let

$$\begin{aligned} M=\sup ~\mathrm {supp}(\mu ),\quad m=\inf ~\mathrm {supp}(\mu ). \end{aligned}$$

Then

$$\begin{aligned} m<\inf (\Omega _{t}\cap {\mathbb {R}})\quad \mathrm {and} \quad \sup (\Omega _{t} \cap {\mathbb {R}})<M. \end{aligned}$$

In particular, every point $\lambda$ in $\overline{\Omega }_{t}$ has $m<\mathrm{Re}\,\lambda <M.$

Proof

Let $\tilde{a}_{0}=\sup (\Lambda _{t}\cap {\mathbb {R}})$. Then, $v_{t}(\tilde{a} _{0})=0$, which means (Proposition 5.2) that

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{(\tilde{a}_{0}-x)^{2}} \le \frac{1}{t}. \end{aligned}$$

Then

$$\begin{aligned} \sup (\Omega _{t}\cap {\mathbb {R}})=a_{t} (\tilde{a}_{0})=t\int _{{\mathbb {R}}} \frac{x\,\mathrm{d}\mu (x)}{(\tilde{a}_{0}-x)^{2}}\le M. \end{aligned}$$

Because of our standing assumption that $\mu$ is not a $\delta$-measure, this inequality is strict. The inequality for $\inf (\Omega _{t}\cap {\mathbb {R}})$ can be proved similarly. $\square$

7.3 Regularity

Define a function $\tilde{S}$ by

$$\begin{aligned} \tilde{S}(t,\lambda ,z)=S(t,\lambda ,z^{2}) \end{aligned}$$

for $z>0$.

Proposition 7.5

Fix a time $t>0$ and a point $\lambda ^{*} \in \Omega _{t}.$ Then, the function $(\lambda ,z)\mapsto \tilde{S}(t,\lambda ,z)$ extends to a real analytic function defined in a neighborhood of $(\lambda ^{*},0)$ inside ${\mathbb {C}}\times {\mathbb {R}}.$

Once the proposition is established, the function $s_{t}(\lambda ) :=\lim _{\varepsilon \rightarrow 0^{+}}S(t,\lambda ,\varepsilon )$ can be computed as $s_{t}(\lambda )=\tilde{S}(t,\lambda ,0).$ Since $\tilde{S}(t,\lambda ,z)$ is smooth in $\lambda$ and z,  we can compute $s_{t}$ (or any of its derivatives) at $\lambda ^{*}$ by evaluating $\tilde{S}(t,\lambda ,z)$ (or any of its derivatives) along any path where $\lambda \rightarrow \lambda ^{*}$ and $z\rightarrow 0.$ Thus, Proposition 7.5 will allow us to make rigorous the argument leading to 7.2. Specifically, we will be able to conclude that the left-hand sides of (7.4) and (7.5) are actually equal to $\partial s_{t}/\partial a$ and $\partial s_{t}/\partial b,$ respectively.

Remark 7.6

The function S itself does not have a smooth extension of the same sort that $\tilde{S}$ does. Indeed, since $\sqrt{\varepsilon }p_{\varepsilon }$ is a constant of motion, the second Hamilton–Jacobi formula (4.6) tells us that $\partial S/\partial \varepsilon$ must blow up like $1/\sqrt{\varepsilon }$ as we approach $(t,\lambda ^{*},0)$ along a solution of the system (4.2). The same reasoning tells us that the extended $\tilde{S}$ does not satisfy $\tilde{S}(t,\lambda ,z)=S(t,\lambda ,z^{2})$ for $z<0$. Indeed, since $\sqrt{\varepsilon }p_{\varepsilon }$ is a constant of motion, $\frac{\partial \tilde{S}}{\partial z}(t,\lambda ,z) =2\sqrt{\varepsilon }\frac{\partial S}{\partial \varepsilon } (t,\lambda , z^{2})$ has a nonzero limit as $z\rightarrow 0$. Thus, $\tilde{S}$ cannot have a smooth extension that is even in z.

To prove Proposition 7.5, we will use a strategy similar to the one in Section 6.2. For each $t>0,$ we define a map

$$\begin{aligned} W_{t}(a_{0},b_{0},\varepsilon _{0})=(a_{t},b_{t},z_{t}) \end{aligned}$$

by

$$\begin{aligned} a_{t}&=a(t,a_{0},b_{0},\varepsilon _{0})\\ b_{t}&=b(t,a_{0},b_{0},\varepsilon _{0})\\ z_{t}&=\sqrt{\varepsilon (t,a_{0},b_{0},\varepsilon _{0})} \end{aligned}$$

where a, b, $\varepsilon$ are defined as in Proposition 4.4. The last component $z_{t}$ can be expressed explicitly as:

$$\begin{aligned} z_{t}=\sqrt{\varepsilon _{0}}\left( 1-tp_{0}\right) . \end{aligned}$$

The map $W_{t}$ is initially defined only for

$$\begin{aligned} \varepsilon _{0}>\varepsilon _{0}^{t}(\lambda _{0}):=v_{t} (a_{0})^{2}-b_{0}^{2}. \end{aligned}$$

This condition guarantees that $p_{0}<1/t,$ so that the lifetime of the path is greater than t. But for each $t>0$ and $\lambda _{0}\in \Lambda _{t},$ we can extend $W_{t}$ to a neighborhood of $(a_{0},b_{0},\varepsilon _{0} ^{t}(\lambda _{0}))$, simply by using the same formulas. We note that if $\varepsilon _{0} >\varepsilon _{0}^{t}(\lambda _{0}),$ then $p_{0}<1/t$ so that $z_{t}>0$; and if $\varepsilon _{0}<\varepsilon _{0}^{t}(\lambda _{0})$ then $p_{0}>1/t$ so that $z_{t}<0.$

Lemma 7.7

For all $t>0$ and $\lambda _{0}=a_{0}+ib_{0}\in \Lambda _{t},$ the Jacobian of $W_{t}$ at $(a_{0},b_{0},\varepsilon _{0}^{t} (\lambda _{0}))$ is invertible, where $\varepsilon _{0}^{t} (\lambda _{0} )=v_{t}(a_{0})^{2}-b_{0}^{2}$.

Proof

We introduce the notations

$$\begin{aligned} q_{0}&=\int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{((a_{0}-x)^{2} +v_{t}(a_{0} )^{2})^{2}}\\ q_{1}&=\int _{{\mathbb {R}}}\frac{(a_{0}-x)\,\mathrm{d}\mu (x)}{((a_{0}-x)^{2} +v_{t}(a_{0})^{2})^{2}}\\ q_{2}&=\int _{{\mathbb {R}}}\frac{(a_{0}-x)^{2} \,\mathrm{d}\mu (x)}{((a_{0}-x)^{2}+v_{t}(a_{0})^{2})^{2}}. \end{aligned}$$

Note that $q_{0}>0$ and $q_{2}>0$. When $\varepsilon _{0}=\varepsilon _{0} ^{t}(\lambda _{0})$, we can write $p_{0}$ in terms of $q_{0}$ and $q_{2}$ as:

$$\begin{aligned} p_{0}=q_{2}+v_{t}(a_{0})^{2}q_{0}. \end{aligned}$$

(7.8)

We now compute the Jacobian matrix of $W_{t}$ at the point $(\lambda _{0},\varepsilon _{0}^{t}(\lambda _{0})),$ with $\lambda _{0}\in \Lambda _{t}.$ Using the formulas (4.4) for $p_{a,0}$ and $p_{b,0},$ we can compute that

$$\begin{aligned} \begin{array}{lll} \frac{\partial p_{a,0}}{\partial a_{0}}=2(-q_{2}+v_{t}(a_{0})^{2}q_{0}) &{} \frac{\partial p_{a,0}}{\partial b_{0}}=-4b_{0}q_{1} &{} \frac{\partial p_{a,0}}{\partial \varepsilon _{0}}=-2q_{1}\\ \frac{\partial p_{0}}{\partial a_{0}}=-2q_{1} &{} \frac{\partial p_{0}}{\partial b_{0}}=-2b_{0}q_{0} &{} \frac{\partial p_{0}}{\varepsilon _{0}}=-q_{0} \end{array}. \end{aligned}$$

The Jacobian of $W_{t}$ at $(a_{0},b_{0}, \varepsilon _{0}^{t}(\lambda _{0}))$ then has the following form:

$$\begin{aligned} DW_{t}=\begin{pmatrix} t(\frac{1}{t}+q_{2}-v_{t}(a_{0})^{2}q_{0}) &{} 2tb_{0}q_{1} &{} tq_{1}\\ -2tb_{0}q_{1} &{} t(\frac{1}{t}+p_{0}-2b_{0}^{2}q_{0}) &{} -tb_{0}q_{0}\\ 2t\sqrt{\varepsilon _{0}}q_{1} &{} 2t\sqrt{\varepsilon _{0}}b_{0}q_{0} &{} \frac{1-tp_{0}}{2\sqrt{\varepsilon _{0}}}+t\sqrt{\varepsilon _{0}}q_{0} \end{pmatrix}. \end{aligned}$$

Since $\varepsilon _{0}=\varepsilon _{0}^{t}(\lambda _{0}),$ we have $1/t=p_{0}$, and by (7.8), the (1, 1)-entry can be simplified to $2tq_{2}$. The Jacobian matrix $DW_{t}$ then simplifies to

$$\begin{aligned} DW_{t}=2t\begin{pmatrix} q_{2} &{} b_{0}q_{1} &{} \frac{1}{2}q_{1}\\ -b_{0}q_{1} &{} (q_{2}+(v_{t}(a_{0})^{2}-b_{0}^{2})q_{0}) &{} -\frac{1}{2} b_{0}q_{0}\\ \sqrt{\varepsilon _{0}}q_{1} &{} \sqrt{\varepsilon _{0}}b_{0}q_{0} &{} \frac{1}{2}\sqrt{\varepsilon _{0}}q_{0} \end{pmatrix}. \end{aligned}$$

We compute the determinant of $DW_{t}$ by first adding $-2b_{0}$ times the third column to the second column and then using a cofactor expansion along the second column. The result is

$$\begin{aligned} \det DW_{t}=4t^{3}\sqrt{\varepsilon _{0}}(q_{2}+v_{t}(a_{0})^{2}q_{0}) (q_{2}q_{0}-q_{1}^{2}) \end{aligned}$$

Now, by the Cauchy–Schwarz inequality,

$$\begin{aligned} q_{0}q_{2}-q_{1}^{2}\ge 0 \end{aligned}$$

and it cannot be an equality unless $\mu$ is a $\delta$-measure. Therefore, we conclude that $\det DW_{t}$ is positive, establishing the proposition. $\square$

Proof of Proposition 7.5

The proof is extremely similar to the proof of Proposition 6.2; the desired extension is given by the map

$$\begin{aligned} (\lambda ,z)\mapsto \mathrm {HJ}(W_{t}^{-1}(\lambda ,z)), \end{aligned}$$

where $\mathrm {HJ}$ is the Hamilton–Jacobi function in (6.7). Take $z>0$ and let $(\mu _{0},\delta _{0})=W_{t}^{-1}(\lambda ,z).$ Then, we must have $\delta _{0}>\varepsilon _{0}^{t}(\mu _{0})$ or else $z_{t}(\mu _{0},\delta _{0})=z$ would be negative. Thus, the lifetime of the path will be greater than t and the Hamilton–Jacobi formula will apply. Thus, the Hamilton–Jacobi formula (4.5) shows that $\mathrm {HJ}(W_{t} ^{-1}(\lambda ,z))$ agrees with $\tilde{S}(t,\lambda ,z)$ for $z>0$. $\square$

7.4 Computing the Brown measure

Using Proposition 7.5, we can show that the left-hand sides of (7.4) and (7.5) are actually equal to $\partial s_{t}/\partial a$ and $\partial s_{t}/\partial b$.

Corollary 7.8

For any $\lambda =a+ib$ in $\Omega _{t}$, we have

$$\begin{aligned} \frac{\partial s_{t}}{\partial a}=\frac{2}{t}(a_{0}^{t}(a)-a), \quad \frac{\partial s_{t}}{\partial b}=\frac{b}{t}, \end{aligned}$$

so that

$$\begin{aligned} \Delta s_{t}(\lambda )=\frac{2}{t} \left( \frac{da_{0}^{t}(a)}{da}-\frac{1}{2}\right) . \end{aligned}$$

Proof

Fix $t>0$ and $\lambda ^{*}\in \Omega _{t}.$ By Proposition 7.5, the function

$$\begin{aligned} s_{t}(\lambda ):=\lim _{\varepsilon \rightarrow 0^{+}} S(t,\lambda ,\varepsilon ) \end{aligned}$$

may be computed, for $\lambda$ in a neighborhood of $\lambda ^{*},$ as

$$\begin{aligned} s_{t}(\lambda )=\tilde{S}(t,\lambda ,0). \end{aligned}$$

Since $\tilde{S}$ is smooth, we can evaluate $\tilde{S}$ or any of its derivatives at $(t,\lambda ,0)$ by taking limits along any path we choose with t fixed. Thus, the left-hand sides of (7.4) and (7.5) are actually equal to $\partial s_{t}/\partial a$ and $\partial s_{t}/\partial b.$ The formula for $\Delta s_{t}$ then follows by taking second derivatives with respect to a and to b and simplifying. $\square$

We now establish our main result, a formula for the Brown measure of $x_{0}+i\sigma _{t}$.

Theorem 7.9

The open set $\Omega _{t}$ is a set of full measure for the Brown measure of $x_{0}+i\sigma _{t}.$ Inside $\Omega _{t},$ the Brown measure is absolutely continuous with a strictly positive density $w_{t}$ given by

$$\begin{aligned} w_{t}(\lambda )=\frac{1}{2\pi t}\left( \frac{da_{0}^{t}(a)}{da} -\frac{1}{2}\right) ,\quad \lambda =a+ib. \end{aligned}$$

(7.9)

Since $w_{t}(\lambda )$ is independent of b,  we see that $w_{t}$ is constant along the vertical segments inside $\Omega _{t}$.

Proof

Corollary 7.8 shows that in $\Omega _{t},$ the Brown measure of $x_{0}+i\sigma _{t}$ has a density given by (7.9). It then follows from Point (2) of Proposition 5.5 that

$$\begin{aligned} \frac{da_{0}^{t}(a)}{da}>\frac{1}{2}, \end{aligned}$$

showing that $w_{t}$ is positive in $\Omega _{t}$. It remains to show that $\Omega _{t}$ is a set of full Brown measure. Since the Brown measure is zero outside $\overline{\Omega }_{t},$ we see that $\Omega _{t}$ will have full measure provided that the boundary of $\Omega _{t}$ has measure zero. While it may be possible to prove this directly using the strategy in Sect. 7.4 of [12], we instead use the approach used in [22].

In Theorem 8.2, we will consider a probability measure $\rho _{t}$ on $\Lambda _{t}.$ We will then show that the push-forward of $\rho _{t}$ under the map $U_{t}:\Lambda _{t}\rightarrow \Omega _{t}$ agrees with $\mathrm {Brown} (x_{0}+i\sigma _{t})$ on $\Omega _{t}.$ Since the preimage of $\Omega _{t}$ under $U_{t}$ is $\Lambda _{t}$ and $\rho _{t}(\Lambda _{t})=1,$ we see that the $\mathrm {Brown}(x_{0}+i\sigma _{t})$ assigns full measure to $\Omega _{t}$. $\square$

8 Two results about push-forwards of the Brown measure

In this section, we show how $\mathrm {Brown}(x_{0}+i\sigma _{t})$ is related to two other measure by means of pushing forward under appropriate maps. To motivate one of our results, let us consider the case that $x_{0} =\tilde{\sigma }_{s}$, a semicircular element of variance s freely independent of $\sigma _{t}.$ It is known (see [4, Example 5.3] and Sect. 10.1) that in this case, the Brown measure of $\tilde{\sigma }_{s}+i\sigma _{t}$ is uniformly distributed on an ellipse. It follows that the distribution of $\mathrm{Re}\,\lambda$ with respect to $\mathrm {Brown}(\tilde{\sigma }_{s}+i\sigma _{t})$ is semicircular—which is the same (up to scaling by a constant) as the distribution of $\tilde{\sigma }_{s}+\sigma _{t}.$ (See Fig. 7.)

Point 2 of Theorem 8.2 generalizes the preceding result to the case of arbitrary $x_{0},$ in which the map $\lambda \mapsto const.\mathrm{Re}\,\lambda$ is replaced by a certain map $Q_{t}:\overline{\Omega }_{t} \rightarrow {\mathbb {R}}.$ When the distribution of $x_{0}$ is semicircular, $Q_{t}(\lambda )$ is a multiple of the real part of $\lambda ,$ as in (8.1).

Fig. 7

A random matrix approximation to the Brown measure of $x_{0} +i\sigma _{t}$ when $x_{0}$ is semicircular (left) and the distribution of the real parts of the eigenvalues (right)

Recall that $c_{t}$ denotes the circular Brownian motion. We will make use of the map $U_{t}:\overline{\Lambda }_{t}\rightarrow \overline{\Omega }_{t}$ described in Sect. 7.2, and another map $Q_{t} :\overline{\Omega }_{t}\rightarrow {\mathbb {R}}$ which we now define. Recall from Sects. 5.2 and 5.3 that the inverse of the map $J_{t}$ takes $\partial \Omega _{t}$ to $\partial \Lambda _{t}$ and that the map $H_{t}$ takes $\partial \Lambda _{t}$ to ${\mathbb {R}},$ so that $H_{t}\circ J_{t}^{-1}$ takes $\partial \Omega _{t}$ to ${\mathbb {R}}.$

Definition 8.1

Let $Q_{t}:\overline{\Omega }_{t}\rightarrow {\mathbb {R}}$ be the unique map that agrees with $H_{t}\circ J_{t}^{-1}$ on $\partial \Omega _{t}$ and maps vertical segments in $\overline{\Omega }_{t}$ to points in ${\mathbb {R}}$.

The map $Q_{t}$ is visualized in Fig. 4. In the case that $x_{0}$ is semicircular with variance s,  one can easily use the computations in Sect. 10.1 to show that

$$\begin{aligned} Q_{t}(a+ib)=\frac{s+t}{s}a. \end{aligned}$$

(8.1)

In general, we may compute $Q_{t}$ more explicitly as follows. We first map $a+ib$ to the point $a+ib_{t}(a)$ on $\partial \Omega _{t}.$ Next, we compute

$$\begin{aligned} J_{t}^{-1}(a+ib_{t}(a))=a_{0}^{t}(a)+iv_{t}(a_{0}^{t}(a)). \end{aligned}$$

Next, we use the identity $H(J_{t}^{-1}(z))=2J_{t}^{-1}(z)-z$ in (5.23). Finally, we recall that $H_{t}\circ J_{t}^{-1}$ is real-valued on $\partial \Omega _{t}.$ Thus,

$$\begin{aligned} Q_{t}(a+ib)&=\mathrm{Re}\,\{2J_{t}^{-1}[a+ib_{t}(a)]-(a+ib_{t}(a))\}\\&=2a_{0}^{t}(a)-a. \end{aligned}$$

Theorem 8.2

The following results hold.

• (1) The push-forward of the Brown measure of $x_{0}+c_{t}$ under the map $U_{t}$ in Theorem 7.3 is the Brown measure of $x_{0}+i\sigma _{t}$.

• (2) The push-forward of the Brown measure of $x_{0}+i\sigma _{t}$ under the map $Q_{t}$ is the law of $x_{0}+\sigma _{t}$.

Proof

By Theorem 3.9 in [22], the Brown measure $\rho _{t}$ of $x_{0}+c_{t}$ can be written as:

$$\begin{aligned} d\rho _{t}&=\frac{1}{\pi t}\left( 1-\frac{t}{2}\frac{d}{da_{0}} \int _{{\mathbb {R}}}\frac{x\,\mathrm{d}\mu (x)}{(a_{0}-x)^{2} +v_{t}(a_{0})^{2}}\right) ~da_{0}\,db_{0}\\&=\frac{1}{\pi t}\left( 1-\frac{1}{2} \frac{da_{t}}{da_{0}}\right) ~da_{0}\,db_{0} \end{aligned}$$

for $a_{0}+ib_{0}\in \Lambda _{t}$. Now, under the map $U_{t},$ we have $a=a_{t}(a_{0})$ and $b=2b_{0}.$ Thus,

$$\begin{aligned} d\rho _{t}&=\frac{1}{\pi t}\left( 1-\frac{1}{2} \frac{da_{t}}{da_{0}}\right) ~\frac{da_{0}^{t}}{da}da\,\frac{db}{2}\\&=\frac{1}{2\pi t}\left( \frac{da_{0}^{t}}{da} -\frac{1}{2}\right) ~da~db \end{aligned}$$

for $a+ib\in \Omega _{t}$. This last expression in the formula for the restriction of the Brown measure to $\Omega _{t}$.

Since $\rho _{t}$ is a probability measure on $\Lambda _{t},$ we find that the Brown measure of $x_{0}+i\sigma _{t}$ assigns mass 1 to $\Omega _{t}$, as noted in the proof of Theorem 7.9. Thus, there is no mass of $\mathrm {Brown}(x_{0}+i\sigma _{t})$ anywhere else and the pushforward of $\rho _{t}$ under $U_{t}$ is precisely $\mathrm {Brown}(x_{0}+i\sigma _{t})$.

To prove Point 2, we consider the unique map $\Psi _{t}:\overline{\Lambda }_{t}\rightarrow {\mathbb {R}}$ that agrees with $H_{t}$ on $\partial \Lambda _{t}$ and is constant along vertical segments in $\Lambda _{t}.$ Then, $Q_{t}=\Psi _{t}\circ U_{t}^{-1}$. (Both $Q_{t}$ and $H_{t}\circ U_{t}^{-1}$ agree with $\Psi _{t}\circ J_{t}^{-1}$ on $\partial \Omega _{t}$ and are constant along vertical segments inside $\overline{\Omega }_{t}.$) By Point 1, the push-forward of the Brown measure of $x_{0}+i\sigma _{t}$ under $U_{t}^{-1}$ is the Brown measure $\rho _{t}$ of $x_{0}+c_{t}$. By Theorem 3.13 of [22], the push-forward of the Brown measure $\rho _{t}$ by $\Psi _{t}$ of $x_{0} +c_{t}$ is the law of $x_{0}+\sigma _{t}$ and Point 2 follows. $\square$

9 The method of Jarosz and Nowak

9.1 The formula for the Brown measure

We now describe a different approach to computing the Brown measure of $x_{0}+i\sigma _{t},$ developed by Jarosz and Nowak in the physics literature [24, 25]. As discussed in the introduction, the method is not rigorous as written, but could conceivably be made rigorous using the general framework developed by Belinschi, Mai, and Speicher in [6]. (See also related results in [7].) We emphasize, however, that (so far as we know) no explicit computation of the case of $x_{0}+i\sigma _{t}$ has been made using the framework in [6].

Jarosz and Nowak work with an operator of the form $H_{1}+iH_{2},$ where $H_{1}$ and $H_{2}$ are arbitrary freely independent elements. Then on p. 10118 of [25], they present an algorithm by which the “nonholomorphic Green’s function” of $H_{1}+iH_{2}$ may be computed. In the notation of this paper, the nonholomorphic Green’s function is the function $\partial s_{t}/\partial \lambda ,$ so that the Brown measure may be computed by taking the $\bar{\lambda }$-derivative:

$$\begin{aligned} \frac{1}{\pi }\frac{\partial }{\partial \bar{\lambda }}\frac{\partial s_{t}}{\partial \lambda }=\frac{1}{4\pi }\Delta _{\lambda }s_{t}(\lambda ). \end{aligned}$$

Examples are presented in Sect. 6.1 of [24] in which $H_{2}$ is semicircular and $H_{2}$ has various different distributions. We now work out their algorithm in detail in the case that $H_{1}=x_{0}$ is an arbitrary self-adjoint element and $H_{2}=\sigma _{t}.$

We refer to [24, 25] for the framework used in the algorithm, involving “quaternionic Green’s functions.” We present only the final algorithm for computation, described in Eqs. (75)–(79) of [25], and we specialize to the case $H_{1}=x_{0}$ and $H_{2} =\sigma _{t}.$ The algorithm, adapted to our notation, is as follows. We fix a complex number $\lambda =a+ib.$ Then, we introduce three unknown quantities, complex numbers g and $g^{\prime }$ and a real number m. These are supposed to satisfy three equations:

$$\begin{aligned} B_{x_{0}}(g)&=a+\frac{m}{g} \end{aligned}$$

(9.1)

$$\begin{aligned} B_{\sigma _{t}}(g^{\prime })&=b+\frac{1-m}{g^{\prime }} \end{aligned}$$

(9.2)

$$\begin{aligned} \left| g\right|&=\left| g^{\prime }\right| , \end{aligned}$$

(9.3)

where $B_{x_{0}}$ and $B_{\sigma _{t}}$ are the “Blue’s functions,” that is, the inverse functions of the Cauchy transforms of $x_{0}$ and $\sigma _{t},$ respectively. We are supposed to solve these equations for g and $g^{\prime }$ as functions of a and b. Once this is done, we have

$$\begin{aligned} \frac{\partial s_{t}}{\partial \lambda }(a,b) =\mathrm{Re}\,g-i\mathrm{Re}\,g^{\prime }. \end{aligned}$$

(9.4)

Since $\partial /\partial \lambda =(\partial /\partial a-i~\partial /\partial b)/2,$ (9.4) may be written equivalently as:

$$\begin{aligned} \frac{\partial s_{t}}{\partial a}(a,b)&=2\mathrm{Re}\,g; \end{aligned}$$

(9.5)

$$\begin{aligned} \frac{\partial s_{t}}{\partial b}&=2\mathrm{Re}\,g^{\prime }. \end{aligned}$$

(9.6)

That is to say, the real parts of g and $g^{\prime }$ determine the derivatives of $s_{t}$ with respect to a and b,  respectively.

Proposition 9.1

The Jarosz–Nowak method when applied to $x_{0} +i\sigma _{t}$ gives the following result. We try to solve the equation

$$\begin{aligned} g=G_{x_{0}}(a+t\bar{g}) \end{aligned}$$

for g as a function of a and t,  with the solution denoted $g_{t}(a).$ Then, inside the support of the Brown measure, its density $\rho _{t}$ is a function of a and t only, namely

$$\begin{aligned} \rho _{t}(a)=\frac{1}{4\pi }\left( \frac{1}{t}+2\frac{d}{da}\mathrm{Re}\,g_{t}(a)\right) . \end{aligned}$$

(9.7)

Proof

It is known that the Blue’s function of $\sigma _{t}$ is given by $B_{\sigma _{t}}(g^{\prime })=1/g^{\prime }+tg^{\prime }.$ (This statement is equivalent to saying that the R-transform of $\sigma _{t}$ is given by $R(z)=tz,$ as in [38, Example 3.4.4].) Plugging this expression into (9.2) and simplifying, we obtain a quadratic equation:

$$\begin{aligned} t(g^{\prime })^{2}-bg^{\prime }+m=0, \end{aligned}$$

whose roots are

$$\begin{aligned} g^{\prime }=\frac{b\pm \sqrt{b^{2}-4mt}}{2t}. \end{aligned}$$

(9.8)

Assuming (as Jarosz and Nowak implicitly do) that these roots are complex, we find that

$$\begin{aligned} \mathrm{Re}\,(g^{\prime })=\frac{b}{2t}. \end{aligned}$$

(9.9)

Thus, without even using (9.1) or (9.3), we find by (9.6) that

$$\begin{aligned} \frac{\partial s_{t}}{\partial b}=\frac{b}{t}, \end{aligned}$$

which agrees with what we found in Corollary 7.8.

Meanwhile, assuming still that the roots in (9.8) are complex, we find that

$$\begin{aligned} \left| g^{\prime }\right| ^{2}&=\frac{1}{4t^{2}} (b^{2}+4mt-b^{2})\\&=\frac{m}{t}. \end{aligned}$$

Then (9.3) says that $\left| g\right| ^{2}=\left| g^{\prime }\right| ^{2}=m/t,$ so that $m=t\left| g\right| ^{2}.$ Thus, after replacing m by $t\left| g\right| ^{2},$ (9.1) becomes

$$\begin{aligned} B_{x_{0}}(g)=a+t\bar{g}. \end{aligned}$$

Since $B_{x_{0}}$ is the inverse function to $G_{x_{0}},$ this equation may be rewritten as:

$$\begin{aligned} g=G_{x_{0}}(a+t\bar{g}). \end{aligned}$$

(9.10)

We hope that this equation will implicitly determine the complex number g as a function of a (and t). We therefore write g as $g_{t}(a).$

We then substitute the expression for g in (9.5), giving

$$\begin{aligned} \frac{\partial s_{t}}{\partial a}=2\mathrm{Re}\,g_{t}(a). \end{aligned}$$

The density $\rho _{t}$ of the Brown measure is then computed as:

$$\begin{aligned} \rho _{t}(a,b)&=\frac{1}{4\pi }\left( \frac{\partial ^{2}s_{t}}{\partial b^{2}}+\frac{\partial ^{2}s_{t}}{\partial a^{2}}\right) \\&=\frac{1}{4\pi }\left( \frac{1}{t}+2\frac{d}{da}\mathrm{Re}\,g_{t}(a)\right) , \end{aligned}$$

as claimed. $\square$

Proposition 9.2

In the Jarosz–Nowak method, the quantity $\mathrm{Re}\,g_{t}(a)$ may be computed as:

$$\begin{aligned} \mathrm{Re}\,g_{t}(a)=\frac{1}{t}(a_{0}^{t}(a)-a), \end{aligned}$$

where the function $a_{0}^{t}$ is as in Summary 7.1. Thus, the formula (9.7) for the Brown measure in the Jarosz–Nowak method agrees with what we found in Theorem 7.9.

Proof

The imaginary part of the equation (9.10) for g says that

$$\begin{aligned} \mathrm{Im}\,g&=\mathrm{Im}\,\int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{a+t\bar{g}-x}\\&=t\mathrm{Im}\,g\int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{(a+t\mathrm{Re}\,g-x)^{2}+t^{2}(\mathrm{Im}\,g)^{2}}. \end{aligned}$$

Thus, at least when $\mathrm{Im}\,g\ne 0,$ we get

$$\begin{aligned} \int \frac{\mathrm{d}\mu (x)}{(a+t\mathrm{Re}\,g-x)^{2}+t^{2}(\mathrm{Im}\,g)^{2}}=\frac{1}{t}. \end{aligned}$$

(9.11)

We may now apply the equation (5.3) that defines the function $v_{t}$ with a replaced by $a+t\mathrm{Re}\,g,$ giving

$$\begin{aligned} t\mathrm{Im}\,g=\pm v_{t}(a+t\mathrm{Re}\,g). \end{aligned}$$

(9.12)

We now look at the real part of (9.10):

$$\begin{aligned} \mathrm{Re}\,g&=\mathrm{Re}\,\int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{a+t\bar{g}-x}\\&=(a+t\mathrm{Re}\,g)\int _{{\mathbb {R}}}\frac{1}{(a+t\mathrm{Re}\,g-x)^{2}+t^{2}(\mathrm{Im}\,g)^{2}}~\mathrm{d}\mu (x)\\&\quad -\int _{{\mathbb {R}}}\frac{x}{(a+t\mathrm{Re}\,g-x)^{2}+t^{2} (\mathrm{Im}\,g)^{2}}~\mathrm{d}\mu (x). \end{aligned}$$

Using (9.11) and (9.12) this equation simplifies to

$$\begin{aligned} a=t\int _{{\mathbb {R}}}\frac{x}{(a+t\mathrm{Re}\,g-x)^{2}+v_{t} (a+t\mathrm{Re}\,g)^{2}}~\mathrm{d}\mu (x). \end{aligned}$$

(9.13)

Now, if we let

$$\begin{aligned} a_{0}=a+t\mathrm{Re}\,g, \end{aligned}$$

(9.14)

then (9.13) is just the equation for a in terms of $a_{0}$ that we found in our Hamilton–Jacobi analysis (Proposition 4.5 ). Thus,

$$\begin{aligned} \mathrm{Re}\,g=\frac{1}{t}(a_{0}-a), \end{aligned}$$

as claimed. $\square$

9.2 The support of the Brown measure

We now examine the condition for the boundary of the support of the Brown measure, as given in Eq. (80) of [25]:

$$\begin{aligned} (\mathrm{Re}\,g)^{2}+(\mathrm{Re}\,g^{\prime })^{2}=\left| g\right| ^{2}. \end{aligned}$$

(9.15)

Proposition 9.3

The condition for a point $a+ib$ to be on the boundary in the Jarosz–Nowak method is that

$$\begin{aligned} b=2v_{t}(a_{0}^{t}(a)). \end{aligned}$$

Such points are precisely the boundary points of our domain $\Omega _{t}$.

Proof

We cancel $(\mathrm{Re}\,g)^{2}$ from both sides of (9.15), leaving us with

$$\begin{aligned} (\mathrm{Re}\,g^{\prime })^{2}=(\mathrm{Im}\,g)^{2}. \end{aligned}$$

Now, we have found in (9.9) that $\mathrm{Re}\,g^{\prime }=b/(2t)$ and in (9.12) that $\mathrm{Im}\,g=\pm v_{t}(a+t\mathrm{Re}\,g)/t.$ But in (9.14), we have identified $a+t\mathrm{Re}\,g$ with $a_{0}^{t}(a).$ Thus, the condition (9.15) for the boundary reads

$$\begin{aligned} \frac{b}{2t}=\pm \frac{v_{t}(a_{0}^{t}(a))}{t}, \end{aligned}$$

or $b=2v_{t}(a_{0}^{t}(a)),$ which is the condition for the boundary of $\Omega _{t}$ (Point (4) of Proposition 5.5). $\square$

10 Examples

In this section, we compute three examples, in which the law of $x_{0}$ is semicircular, Bernoulli, or uniform. Additional examples, computed by a different method, were previously worked out by Jarosz and Nowak in [24, Sect. 6.1].

We also mention that we can take $x_{0}$ to have the form $x_{0}=y_{0} +\tilde{\sigma }_{s},$ where $\tilde{\sigma }_{s}$ is another semicircular Brownian motion and $y_{0},$ $\tilde{\sigma }_{s},$ and $\sigma _{t}$ are all freely independent. Thus, our results allow one to determine the Brown measure for the sum of the elliptic element $\tilde{\sigma }_{s}+i\sigma _{t}$ and the freely independent self-adjoint element $y_{0}$. The details of this analysis will appear elsewhere.

10.1 The elliptic law

In our first example, the law $\mu$ of $x_{0}$ is a semicircular distribution with variance s. Then, $x_{0}+i\sigma _{t}$ has the form of an elliptic element $\tilde{\sigma }_{s}+i\sigma _{t}$, where $\tilde{\sigma }_{\cdot }$ and $\sigma _{\cdot }$ are two freely independent semicircular Brownian motions. The associated “elliptical law,” in various forms, has been studied extensively going back to the work of Girko [15]. The elliptical case was worked out by Jarosz and Nowak in [25, Sect. 3.6]. The Brown measure of $\tilde{\sigma }_{s}+i\sigma _{t}$ was also computed by Biane and Lehner [4, Example 5.3] by a different method. We include this example as a simple demonstration of the effectiveness of our method.

Theorem 10.1

The Brown measure of $\tilde{\sigma }_{s}+i\sigma _{t}$ is supported in the closure of the ellipse centered at the origin with semi-axes $2s/\sqrt{s+t}$ and $2t/\sqrt{s+t}$. The density of the Brown measure is constant

$$\begin{aligned} \frac{1}{4\pi }\left( \frac{1}{s}+\frac{1}{t}\right) \end{aligned}$$

in the domain.

We apply our result in this paper with $x_{0}=\tilde{\sigma }_{s}$. In the next proposition we compute $\Lambda _{t}$.

Proposition 10.2

We can parametrize the upper boundary curve of $\Lambda _{t}$ by

$$\begin{aligned} a_{0}+iv_{t}(a_{0})=\frac{(2s+t)q+it\sqrt{4(s+t)-q^{2}}}{2(s+t)}, \quad q\in [-2\sqrt{s+t},2\sqrt{s+t}]; \end{aligned}$$

(10.1)

therefore, $\Lambda _{t}$ is the ellipse centered at the origin with semi-axes $\frac{2s+t}{\sqrt{s+t}}$ and $\frac{t}{\sqrt{s+t}}$.

Proof

Recall that $\Delta _{t}$ denotes the region in the upper half plane above the graph of $v_{t}$, so that $\overline{\Delta }_{t}$ is the region on or above the graph of $v_{t}.$ Recall also that Biane [2] has shown that the function $H_{t}$ in (5.9) maps $\overline{\Delta }_{t}$ injectively onto the closed upper half plane.

In the case at hand, the Cauchy transform of $\tilde{\sigma }_{s}$ is $G_{\tilde{\sigma }_{s}}(z)=\left( z-\sqrt{z^{2}-4s}\right) /(2s)$. We can then compute the function $H_{t}$ in (5.9) as:

$$\begin{aligned} H_{t}(z)=z+tG_{\sigma _{s}}(z)=z +t\left( \frac{z-\sqrt{z^{2}-4s}}{2s}\right) , \quad z\in \overline{\Delta }_{t}. \end{aligned}$$

The inverse map $H_{t}^{-1}$ is then easily computed as:

$$\begin{aligned} H_{t}^{-1}(z)=\frac{(2s+t)z+t\sqrt{z^{2}-4(s+t)}}{2(s+t)}, \quad \mathrm{Im}\,z\ge 0. \end{aligned}$$

(10.2)

The part of the graph of $v_{t}$ where $v_{t}>0$ comes from the values of $H_{t}^{-1}$ on the real axis having nonzero imaginary part, that is, for real numbers q with $\left| q\right| <2\sqrt{s+t}.$ Plugging these numbers into (10.2) gives the claimed form (10.1). $\square$

Proposition 10.3

The boundary curve of $\Omega _{t}$ can be parametrized by

$$\begin{aligned} a+ib_{t}(a)=\frac{sq+it\sqrt{4(s+t)-q^{2}}}{s+t},\quad q \in [-2\sqrt{s+t},2\sqrt{s+t}]. \end{aligned}$$

Consequently, $\Omega _{t}$ is an ellipse centered at the origin with semi-axes $\frac{2s}{\sqrt{s+t}}$ and $\frac{2t}{\sqrt{s+t}}$.

Proof

By Proposition 10.2, the upper boundary of $\Lambda _{t}$ can be parametrized by the curve in (10.1). By Definition 5.4, we find the boundary curve of $\Omega _{t}$ by applying the map $J_{t}$ in (5.12), which satisfies $J_{t}(z)=2z-H_{t}(z)$. Thus,

$$\begin{aligned} a+ib_{t}(a)&=J_{t}(a_{0}+iv_{t}(a_{0}))\\&=\frac{sq+it\sqrt{4(s+t)-q^{2}}}{s+t}. \end{aligned}$$

which traces an ellipse centered at the origin with semi-axes $\frac{2s}{s+t}$ and $\frac{2t}{\sqrt{s+t}}$. $\square$

Proof of Theorem 10.1

The domain $\Omega _{t}$ is computed in Proposition 10.3. By Proposition 10.3 ,

$$\begin{aligned} a&=\frac{sq}{s+t}\\ a_{0}^{t}(a)&=\frac{(2s+t)q}{2(s+t)}=\frac{(2s+t)}{2s}a. \end{aligned}$$

It follows that the density of the Brown measure is

$$\begin{aligned} \frac{1}{2\pi t}\left( \frac{da_{0}^{t}(a)}{da}-\frac{1}{2}\right)&=\frac{1}{2\pi t}\left( \frac{2s+t}{2s}-\frac{1}{2}\right) \\&=\frac{1}{4\pi }\left( \frac{1}{s}+\frac{1}{t}\right) , \end{aligned}$$

as claimed. $\square$

10.2 Bernoulli case

In our second example, the law $\mu$ of $x_{0}$ is Bernoulli distributed, with mass $\alpha$ at 1 and mass $\beta =1-\alpha$ at $-1$, for $0<\alpha <1.$ The case $\alpha =1/2$ was previously analyzed in the paper of Stephanov [32] and also in Sect. V of [24] by different methods.

Denote by Q(a) the quartic polynomial

$$\begin{aligned} -4a^{4}+4t(\alpha -\beta )a^{3}-(t^{2}+4t-8)a^{2}+2t(t-2) (\alpha -\beta )a-(\alpha -\beta )^{2}t^{2}+4t-4. \end{aligned}$$

(10.3)

Then, the domain $\Omega _{t}$ and the density of the Brown measure in this example are computed in the following proposition.

Proposition 10.4

Any $\lambda \in \Omega _{t}$ satisfies $\left| \mathrm{Re}\,\lambda \right| <1$. The domain $\Omega _{t}$ is given by

$$\begin{aligned} \Omega _{t}=\left\{ a+ib\in {\mathbb {C}}\left| b^{2} <\frac{Q(a)}{(1-a^{2})^{2}}\right. \right\} \end{aligned}$$

so that

$$\begin{aligned} \Omega _{t}\cap {\mathbb {R}}=\{a\in {\mathbb {R}}|Q(a)>0\}. \end{aligned}$$

The density of the Brown measure in this Bernoulli case is given by

$$\begin{aligned} w_{t}(\lambda )=\frac{1}{4\pi }\left( -\frac{1}{t} +\frac{\beta }{(a-1)^{2}}+\frac{\alpha }{(a+1)^{2}}\right) . \end{aligned}$$

Fig. 8

The domain $\Omega _{t}$ in the Bernoulli case with a simulation of the eigenvalues (top), plotted with the density of the Brown measure (in $\Omega _{t}$) as a function of a (bottom). Shown for $\alpha =2/3$ and $t=1$

See Fig. 8.

Proof

Recall the functions $a_{0}^{t}(a)$ and $b_{t}(a)$ defined by the four equations (1.4)–(1.7). We now compute these functions for the Bernoulli case. The equations (1.4) and (1.5) take the following form in the Bernoulli case:

$$\begin{aligned} \frac{\alpha }{(a_{0}-1)^{2}+v^{2}}+\frac{\beta }{(a_{0}+1)^{2}+v^{2}}&=\frac{1}{t}\\ \frac{\alpha }{(a_{0}-1)^{2}+v^{2}}-\frac{\beta }{(a_{0}+1)^{2}+v^{2}}&=\frac{a}{t}. \end{aligned}$$

We then introduce the new variables

$$\begin{aligned} A&= (a_{0}-1)^{2}+v^{2}\\ B&= (a_{0}+1)^{2}+v^{2} \end{aligned}$$

so that

$$\begin{aligned} \frac{\alpha }{A}+\frac{\beta }{B}&=\frac{1}{t}\\ \frac{\alpha }{A}-\frac{\beta }{B}&=\frac{a}{t}. \end{aligned}$$

Then, we can solve for A and B as:

$$\begin{aligned} A=\frac{2\alpha t}{1+a},\quad B=\frac{2\beta t}{1-a}. \end{aligned}$$

We can recover $a_{0}$ and $v^{2}$ as

$$\begin{aligned} a_{0}=\frac{1}{4}(B-A)=\frac{t}{2}\frac{a+\beta -\alpha }{1-a^{2}} \end{aligned}$$

and

$$\begin{aligned} v^{2}&=\frac{A+B}{2}-a_{0}^{2}-1\\&=\frac{\alpha t(1-a)+\beta t(1+a)}{1-a^{2}} -\left( \frac{t}{2}\frac{a+\beta -\alpha }{1-a^{2}}\right) ^{2}-1\\&=\frac{Q(a)}{4(1-a^{2})^{2}} \end{aligned}$$

where Q is defined in (10.3). Recalling that $b_{t}(a)=2v$, we find that

$$\begin{aligned} a_{0}^{t}(a)=\frac{t}{2}\frac{a+\beta -\alpha }{1-a^{2}} \end{aligned}$$

(10.4)

and

$$\begin{aligned} b_{t}(a)^{2}=\frac{Q(a)}{(1-a^{2})^{2}}. \end{aligned}$$

(10.5)

Equation (10.5) gives the claimed form of the domain $\Omega _{t}.$ The density of the Brown measure is then computed from (10.4) using the formula in Theorem 7.9. $\square$

10.3 Uniform case

In our third and final example, $\mu$ is uniformly distributed on $[-1,1]$. The case in which $\mu$ is uniformly distributed on any interval can be reduced to this case as follows. First, by shifting $x_{0}$ by a constant, we can assume that the interval has the form $[-A,A].$ Once this is the case, we write

$$\begin{aligned} x_{0}+i\sigma _{t}=A\left( x_{0}/A+i\sigma _{t}/A\right) , \end{aligned}$$

where the law of $x_{0}/A$ is uniform on $[-1,1]$ and $\sigma _{t}/A$ has the same $*$-distribution as $\sigma _{t/A^{2}}.$ Thus, to compute the Brown measure in this case, we use the formulas below with t replaced by $t/A^{2}$ and then scale the entire Brown measure by a factor of A.

When $\mu$ is uniform on $[-1,1]$—in particular, symmetric about 0—the Brown measure is symmetric about the imaginary axis. The key is again solving the equations (1.4) and (1.5) that define the functions $a_{0}^{t}(a)$ and $b_{t}(a).$

Proposition 10.5

Let $v_{\max }$ be the smallest positive real number v such that

$$\begin{aligned} \frac{1}{v}=\tan \left( \frac{v}{t}\right) . \end{aligned}$$

Also let $A_{0}^{t}(v)$ be given by

$$\begin{aligned} A_{0}^{t}(v)=\sqrt{2v\cot \left( \frac{2v}{t}\right) +1-v^{2}}. \end{aligned}$$

for $\left| v\right| \le v_{\max }$. (When $v=0$, we understand the above formula as $A_{0}^{t}(0)=\sqrt{t+1}$.) Then, the following results hold.

• (1) The domain $\Omega _{t}$ has only one connected component, and is given by

  $$\begin{aligned} \Omega _{t}=\{\pm A_{t}(b/2)+iy|~\left| y\right| <b, ~\left| b\right| \le 2v_{\max }\} \end{aligned}$$

  (10.6)

  where

  $$\begin{aligned} A_{t}(v)=A_{0}^{t}(v)+\frac{t}{4}\log \left( 1-\frac{4A_{0}^{t}(v)}{(A_{0}^{t}(v)+1)^{2}+v^{2}}\right) . \end{aligned}$$

  That is, $\partial \Omega _{t}$ consists of the two curves

  $$\begin{aligned} \pm A_{t}(b/2)+ib,\quad \left| b\right| \le 2v_{\max }. \end{aligned}$$

  In particular, the function $b_{t}$ defined in (5.14) is unimodal with a peak at 0.

• (2) The domain $\Omega _{t}$ satisfies

  $$\begin{aligned} \Omega _{t}\cap {\mathbb {R}}=\left\{ a\in {\mathbb {R}}\left| \left| a\right| <\sqrt{t+1}-\frac{t}{2}\log \left( \frac{\sqrt{t+1}+1}{\sqrt{t+1}-1}\right) \right. \right\} . \end{aligned}$$

• (3) The density of the Brown measure in $\Omega _{t}$ is (as always) a function of a and t only, and the graph of this function is traced out by the curve

  $$\begin{aligned} (A_{t}(v),W_{t}(v)),\quad \left| v\right| <v_{\max }, \end{aligned}$$

  (10.7)

  where

  $$\begin{aligned} W_{t}(v)=\frac{t^{2}+4(t+2)v^{2}-t(t+4v^{2})\cos \left( 4v/t\right) -4tv\sin \left( 4v/t\right) }{4\pi t\left( -t^{2}+8v^{2}+t^{2} \cos \left( 4v/t\right) \right) }. \end{aligned}$$

  To the extent that we can compute the height $b_{t}$ of $\Omega _{t}$ as a function of a,  we can then compute the density of the Brown measure as a function of a by replacing v by $b_{t}(a)/2$ in the above expression. That is, the density $w_{t}(\lambda )$ is given by

  $$\begin{aligned} w_{t}(\lambda )=W_{t}(b_{t}(a)/2). \end{aligned}$$

  (10.8)

See Fig. 9.

Fig. 9

The domain $\Omega _{t}$ in the uniform case with a simulation of the eigenvalues (top), plotted with the density of the Brown measure (in $\Omega _{t}$) as a function of a (bottom). Shown for $t=0.1$

Before we prove Proposition 10.5, we need some computations about $v_{t}$ and $\Lambda _{t}$ from the following proposition.

Proposition 10.6

The following results about $v_{t}$ and $\Lambda _{t}$ hold.

• (1) The function $v_{t}$ is unimodal, with a peak at $a_{0}=0$. The maximum $v_{\max } = v_{t}(0)$ is the smallest positive real number v such that

  $$\begin{aligned} \frac{1}{v}=\tan \left( \frac{v}{t}\right) . \end{aligned}$$

  In particular, $v_{t}(0)< \frac{\pi t}{2}$.

• (2) The domain $\Lambda _{t}$ has only one connected component. Its boundary can be described by the two curves

  $$\begin{aligned} \pm A_{0}^{t}(v)+iv,\quad \left| v\right| \le v_{\max } \end{aligned}$$

  where

  $$\begin{aligned} A_{0}^{t}(v)=\sqrt{2v\cot \left( \frac{2v}{t}\right) +1-v^{2}}. \end{aligned}$$

  (10.9)

• (3) The domain $\Lambda _{t}$ satisfies

  $$\begin{aligned} \Lambda _{t}\cap {\mathbb {R}}= (-\sqrt{t+1}, \sqrt{t+1}). \end{aligned}$$

  (10.10)

Proof

In the uniform case, (1.4) takes the form:

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{\mathrm{d}\mu (x)}{(a_{0}-x)^{2}+v^{2}} =\frac{\arctan \left( \frac{1-a_{0}}{v}\right) +\arctan \left( \frac{1+a_{0}}{v}\right) }{2v}=\frac{1}{t}. \end{aligned}$$

(10.11)

Using the addition law of inverse tangent,

$$\begin{aligned} \arctan (A)+\arctan (B)=\arctan \left( \frac{A+B}{1-AB}\right) , \end{aligned}$$

we can easily solve for $a_{0}^{2}$ as a function of v:

$$\begin{aligned} a_{0}^{2}=2v\cot \left( \frac{2v}{t}\right) +1-v^{2}. \end{aligned}$$

(10.12)

Restricted to $a_{0}\ge 0$, (10.12) defines $a_{0}=A_{0}^{t}$ as a function of v as in (10.9).

The function $v_{t}(a_{0})$ cannot be represented as an elementary function of $a_{0}$; we, however, have proved in the preceding paragraph that $v_{t}$ restricted to $a_{0}\ge 0$ in $\Lambda _{t}$ has an inverse $A_{0}^{t}$. The function $v_{t}$ then must be strictly decreasing from 0 to $\sup (\Lambda _{t} \cap {\mathbb {R}})$; by symmetry, it is strictly increasing from $\inf (\Lambda _{t}\cap {\mathbb {R}})$ to 0. In particular, $v_{t}$ is unimodal with global maximum at $a_{0}=0$. Putting $a_{0}=0$ in (10.11), the maximum $v_{\max }=v_{t}(0)$ is the smallest positive real number v such that

$$\begin{aligned} \frac{1}{v}=\tan \left( \frac{v}{t}\right) . \end{aligned}$$

Thus, $v_{t}(0)=v_{\max }<\frac{\pi t}{2}$. This proves Point 1.

Since $v_{t}$ is unimodal, the domain $\Lambda _{t}$ has only one connected component. By Definition 5.1, $\Lambda _{t}$ is symmetric about the real axis. In our case, $\Lambda _{t}$ is also symmetric about the imaginary axis and the right-hand side of (10.9) defines an even function of v. Thus, the boundary of $\Lambda _{t}$ can be described by the curves

$$\begin{aligned} \partial \Lambda _{t}=\{(\pm A_{0}^{t}(v),v)|~\left| v\right| \le v_{\max }\}, \end{aligned}$$

which is Point 2. Since $a_{0}(v)^{2}\rightarrow t+1$ as $v\rightarrow 0$, (10.10) holds, which proves Point 3. $\square$

Proof of Proposition 10.5

In the uniform case, the equation (1.5) takes the form:

$$\begin{aligned} a&=t\int _{{\mathbb {R}}}\frac{x}{(a_{0}-x)^{2} +v_{t}(a_{0})^{2}}~\mathrm{d}\mu (x)\\&=a_{0}+\frac{t}{4}\log \left( 1-\frac{4a_{0}}{(a_{0}+1)^{2}+v_{t} (a_{0})^{2}}\right) . \end{aligned}$$

For $a\ge 0$ in $\Omega _{t}$, we can express a as a function $a=A_{t}(v)$ of $v=v_{t}(a_{0})$ using (10.9) as

$$\begin{aligned} A_{t}(v)=A_{0}^{t}(v)+\frac{t}{4}\log \left( 1-\frac{4A_{0}^{t}(v)}{(A_{0}^{t}(v)+1)^{2}+v^{2}}\right) \end{aligned}$$

(10.13)

for $0<v\le v_{\max }$.

Using the definition of $b_{t}$ in (5.14), $b_{t}(a)=2v_{t} (a_{0}^{t}(a))=2v$. Thus, $b_{t}$ is unimodal on $\Omega _{t}\cap {\mathbb {R}}$ with a peak at 0. The domain $\Omega _{t}$ has only one connected component whose boundary can be described by the two curves

$$\begin{aligned} \pm A_{t}(b/2)+ib,\quad \left| b\right| \le 2v_{\max }. \end{aligned}$$

Thus, (10.6) follows. This proves Point 1.

Using (10.10), we can compute the limit as $v\rightarrow 0$ in (10.13), from which the claimed from of $\Omega _{t} \cap {\mathbb {R}}$ follows, establishing Point 2.

Now, since both $a_{0}$ and a are functions of v when $a_{0}$ and a are nonnegative, we can compute

$$\begin{aligned} \frac{da_{0}^{t}(a)}{da}=\frac{dA_{0}^{t}(v)/dv}{dA_{t}(v)/dv}. \end{aligned}$$

(10.14)

This result also holds for negative a because $\Lambda _{t}$ and $\Omega _{t}$ are symmetric about the imaginary axis. The density of the Brown measure is then computed using Theorem 7.9. Using (10.14), the density can be expressed in terms of v as:

$$\begin{aligned} \frac{1}{2\pi t}\left( \frac{da_{0}^{t}(a)}{da}-\frac{1}{2}\right) =\frac{t^{2}+4(t+2)v^{2}-t(t+4v^{2})\cos \left( \frac{4v}{t}\right) -4tv\sin \left( \frac{4v}{t}\right) }{4\pi t\left( -t^{2}+8v^{2}+t^{2} \cos \left( \frac{4v}{t}\right) \right) }, \end{aligned}$$

establishing (10.7). Since $b_{t}(a)=2v$, we obtain (10.8), completing the proof. $\square$