Change of Support in Spatial Variance-Based Sensitivity Analysis

Abstract

Variance-based global sensitivity analysis (GSA) is used to study how the variance of the output of a model can be apportioned to different sources of uncertainty in its inputs. GSA is an essential component of model building as it helps to identify model inputs that account for most of the model output variance. However, this approach is seldom applied to spatial models because it cannot describe how uncertainty propagation interacts with another key issue in spatial modeling: the issue of model upscaling, that is, a change of spatial support of model output. In many environmental models, the end user is interested in the spatial average or the sum of the model output over a given spatial unit (for example, the average porosity of a geological block). Under a change of spatial support, the relative contribution of uncertain model inputs to the variance of aggregated model output may change. We propose a simple formalism to discuss this issue within a GSA framework by defining point and block sensitivity indices. We show that the relative contribution of an uncertain spatially distributed model input increases with its correlation length and decreases with the size of the spatial unit considered for model output aggregation. The results are briefly illustrated by a simple example.

1 Introduction

Variance-based global sensitivity analysis (GSA) is used to study how the variance of the output of a model can be apportioned to different sources of uncertainty in its inputs. Here, the term model denotes any computer code in which a response variable is calculated as a deterministic function of input variables. Originally developed in the 1990s (Sobol’ 1993), GSA is now recognized as an essential component of model building (European Commission 2009; Environmental Protection Agency 2009) and is widely used in different fields (Cariboni et al. 2007; Tarantola et al. 2002). GSA is based on the decomposition of a model output variance into conditional variances. So-called first-order sensitivity indices measure the main effect contribution of each uncertain model input to the model output variance. Based on these sensitivity indices, ranking the model inputs helps to identify inputs that should be better scrutinized first. Reducing the uncertainty on the inputs with the largest sensitivity indices (for example, by collecting additional data or changing the geographical pattern of data locations) will often result in a reduction in the variance of the model output. More generally, GSA helps to explore the response surface of a black box computer code and to prioritize the possibly numerous processes that are involved in it.

Although GSA was initially designed for models where both inputs and output can be described as real valued random variables, some recent work has extended GSA to environmental models for which both the inputs and output are spatially distributed over a two-dimensional domain and can be described as random fields (Lilburne and Tarantola 2009). In these works, the computer code under study uses maps derived from field data (for example, digital elevation models and land use maps). These maps are uncertain due to measurement errors, lack of knowledge, or aleatory variability (Brown and Heuvelink 2007; Refsgaard et al. 2007). The uncertainty of these spatial inputs is usually modeled using random fields. Model output is also spatially distributed (for example, a flood map or a pollution map). Authors use geostatistical simulation to incorporate spatially distributed model inputs into the GSA approach (Ruffo et al. 2006; Saint-Geours et al. 2010) and they display estimation procedures to compute sensitivity indices in a spatial context, either with respect to the spatial average of the model output (Lilburne and Tarantola 2009) or with respect to the values of the model output at each site of a study area (Heuvelink et al. 2010; Marrel et al. 2011; Pettit and Wilson 2010).

Nevertheless, to date, none of these studies has reported on a key issue: the link between uncertainty propagation and model upscaling/downscaling. Model upscaling is the problem of translating knowledge from smaller scales to larger (Heuvelink 1998). In many environmental models, the physical quantities considered are spatially additive (for example, porosity or evapotranspiration), that is, their large-scale properties derive from small-scale properties by simple averaging (Chilès and Delfiner 1999). In this case, the model end user is usually interested in the spatial linear average or the sum of spatial output over a given spatial unit (for example, the average porosity of a block or the total evapotranspiration over a plot of land) and model upscaling is thus reduced to a change of support problem (namely, a change of support of the end user’s output of interest). Heuvelink (1998) observed that under a change of spatial support of the model output, the relative contribution of uncertain model inputs to the variance of the aggregated model output may change. Exploring how sensitivity analysis results interact with such a change of support is thus of great importance. It would allow the modeler to check the robustness of model-based environmental impact assessment studies and better assess the confidence of their results. Knowledge of this interaction would also allow the modeler to answer the following questions: What are the model inputs that explain the largest fraction of the variance of the output over a given spatial support? For which output support size does a given spatially distributed model input contribute to the largest fraction of the variance of the model output? How does the contribution of a spatially distributed input to the variance of the model output depend on the parameters of its covariance function?

The change of support effect has been extensively discussed in geostatistics in the context of regularization theory (Journel and Huijbregts 1978). Hence, we attempt in this paper to integrate regularization theory with variance-based GSA framework. Our idea is to define site sensitivity indices and block sensitivity indices to (i) provide a simple formalism that extends variance-based GSA to spatial models when the modeler’s interest is in the spatial average or the sum of model output over a given spatial support (Sect. 2) and (ii) discuss how the relative contribution of uncertain model inputs to the variance of model output changes under model upscaling (Sect. 3). We limit our study to point-based models, that is, models for which the computation of the model output at some location uses the values of spatial inputs at that same location only (Heuvelink et al. 2010). An example is used throughout this paper to illustrate formal definitions and properties. Finally, we discuss the limits of our approach and its connections to related works in Sect. 4.

2 Variance-Based Sensitivity Indices for a Spatial Model

2.1 Description of Spatial Model $\mathcal{M}$

We want to study a computer code $\mathcal{M}$ whose output is a map and whose inputs are a map and a set of n real valued variables. Both inputs and output are uncertain and are described as random variables or random fields. More precisely, we use the following notations: let $\mathcal{D}\subset\mathbb{R}^{2}$ denote a 2D spatial domain, $\mathbf{x}\in \mathcal{D}$ a site, h the lag vector between two sites x and x′, and $v\subset\mathcal{D}$ some spatial support (block) of area |v|. We consider the model $Y= \mathcal{M}(\mathbf{U} ,Z)$ where U=(U ₁,…,U _n ) is a random vector and $\{ Z(\mathbf{x}): \mathbf{x}\in\mathcal {D} \}$ is a second-order stationary random field (SRF)—that we will often simply denote by Z(x). U and Z(x) are supposed to be independent. Covariance function C(⋅) of Z(x) is assumed to be isotropic, characterized by correlation length a∈ℝ, nugget parameter η∈[0;1[ and of the form

(1)

where ρ _a (⋅) is some valid correlogram (Cressie 1993). The model output is a two-dimensional random field $\{ Y(\mathbf{x}): \mathbf{x}\in\mathcal{D} \}$ that we will simply denote by Y(x). We assume that the first two moments of Y(x) exist. Finally, as discussed in the Introduction, we limit our study to point-based models; hence, we assume that there exists a mapping ψ:ℝⁿ×ℝ→ℝ such that

$$ \forall\mathbf{x}\in\mathcal{D} , \quad Y( \mathbf{x})= \psi \bigl[ \mathbf{U}, Z(\mathbf{x}) \bigr]. $$

(2)

A sensitivity analysis of the model $\mathcal{M}$ must be performed with respect to a scalar quantity of interest derived from spatially distributed model output Y(x). Here, we consider two different outputs of interest: the value Y(x ^∗) at some specific site $\mathbf{x}^{\ast}\in \mathcal{D}$ and the aggregated value Y _v =1/|v|∫ _v Y(x) d x over support v. Because model inputs U and Z(x) are uncertain, Y(x ^∗) and Y _v are both random variables; the sensitivity analysis will describe the relative contribution of uncertain model inputs U and Z(x) to their respective variances. (See Fig. 1.)

Fig. 1

Spatial model with uncertain inputs U and Z(x) and spatial output Y(x). The modeler is interested in the block average of Y(x) over some spatial unit v

2.2 Site Sensitivity Indices and Block Sensitivity Indices

Before defining sensitivity indices for spatial model $\mathcal{M}$, we briefly review the mathematical basis of variance-based GSA. Let us consider a model Y=G(X ₁,…,X _n ), where X _i are independent random variables and where the first two moments of Y exist. The first-order sensitivity index S _i of model input X _i is defined by

$$ S_i = \frac{\operatorname{Var} [\mathbb{E}( Y \vert X_i) ]}{\operatorname{Var} (Y )}. $$

(3)

S _i ∈[0;1] measures the main effect contribution of the uncertain model input X _i to the variance of model output Y. Sensitivity indices can be used to identify the model inputs that account for most of the variance of the model output (model inputs X _i with high first-order indices S _i ). Sum of S _i is always less than 1 and the difference 1−∑ _i S _i accounts for the contribution of the interactions between model inputs X _i to model output variance $\operatorname{Var}(Y)$. Please refer to Saltelli et al. (2008) for more details on GSA theory and on the estimation of sensitivity indices.

To extend GSA to spatial model $\mathcal{M}$, we propose to use different types of sensitivity indices to describe the relative contribution of the uncertain model inputs U and Z(x) to the variance of the model output: an index on a point support (with respect to output of interest Y(x ^∗)) and an index on a larger support (with respect to output of interest Y _v ). First-order sensitivity indices of model inputs with respect to Y(x ^∗) are called site sensitivity indices. Under the stationary hypothesis on SRF Z(x), these indices do not depend on site x ^∗, and thus will simply be denoted by S _U and S _Z

$$ S_{\mathbf{U}}= \frac{\operatorname{Var} [\mathbb{E}(Y(\mathbf {x}^\ast)\mid\mathbf{U}) ]}{\operatorname{Var} [Y(\mathbf{x}^\ast) ]} ; \qquad S_{Z}= \frac{\operatorname{Var} [ \mathbb {E}(Y(\mathbf{x}^\ast) \mid Z(\mathbf{x})) ]}{\operatorname{Var} [Y(\mathbf {x}^\ast) ]}. $$

(4)

First-order sensitivity indices of model inputs with respect to the block average Y _v are called block sensitivity indices and are denoted by S _U (v) and S _Z (v)

$$ S_{\mathbf{U}}(v)= \frac{\operatorname{Var} [\mathbb {E}(Y_v\mid\mathbf{U}) ]}{\operatorname{Var} [Y_v ]}; \qquad S_{Z}(v)= \frac {\operatorname{Var} [ \mathbb{E}(Y_v \mid Z(\mathbf{x})) ]}{\operatorname{Var} [Y_v ]}. $$

(5)

The ratio S _Z (v)/S _U (v) gives the relative contribution of model inputs Z(x) and U to the variance of the output of interest Y _v . When S _Z (v)/S _U (v) is greater than 1, the variance of Y _v is mainly explained by the variability of the 2D input field Z(x); when S _Z (v)/S _U (v) is less than 1, it is the nonspatial input U that accounts for most of $\operatorname{Var} (Y_{v} )$.

2.3 Illustrative Example

The proposed formalism for spatial GSA is illustrated by the following example. A model $Y = \mathcal{M} ( \mathbf{U}, Z )$ is used for the economic assessment of flood risk over a given floodplain $\mathcal{D}$. Z(x) is the map of maximal water levels (m) reached during a flood event. Z(x) is assumed to be a Gaussian random field with mean μ=50 and exponential covariance C(h) with C(0)=100, correlation length a=5 and nugget parameter η=0.1. U is a set of three economic parameters U ₁, U ₂, and U ₃ that determine a so-called damage function that links water levels to monetary costs. U ₁, U ₂, and U ₃ are assumed to be independent random variables following Gaussian distributions $\mathcal{N}(1.5,0.5)$, $\mathcal {N}(55,5)$, and $\mathcal{N}(10,10)$, respectively. Random field Z(x) and random vector U are supposed to be independent. Model output Y(x) is the map of expected economic damages due to the flood over the area; these damages depend on U and Z(x) through the mapping ψ

$$ \forall\mathbf{x}\in\mathcal{D}, \quad Y(\mathbf{x})= \psi \bigl[\mathbf {U}, Z( \mathbf{x}) \bigr] = U_1\cdot Z(\mathbf{x})- U_2\cdot e^{-0.036 \cdot Z(\mathbf{x})} - U_3. $$

(6)

Stakeholders are interested in two outputs: the flood damage Y(x ^∗) on a specific building $\mathbf{x}^{\ast}\in\mathcal{D}$ and the total damage |v|⋅Y _v over a district v (here, a disc of radius r=50). Here, the expression of mapping ψ and the statistical characterization of model inputs may be simple enough that exact values of sensitivity indices could be derived, but this is usually not the case in real applications in which the model is very complex. A usual alternative is to consider model $\mathcal{M}$ as a black box and estimate sensitivity indices with Monte Carlo simulation. We chose to use the estimators and the computational procedure described by Lilburne and Rarantole (2009) based on a quasirandom sampling design, using N=4096 model runs (Table 1). It appears that on a given site x ^∗, the variability of the water level map explains most of the variance of Y(x ^∗): S _Z =0.89. On a larger spatial support, the variance of the total flood damage |v|⋅Y _v is mainly due to the economic parameters U ₁, U ₂, and U ₃: S _U (v)=0.86. Thus, to improve the accuracy of damage estimation for a specific building, the uncertainty should first be reduced on the water level map Z(x); however, to improve the accuracy of total damage estimation over a large district v, the modeler should focus on reducing the uncertainty of economic parameters U ₁, U ₂, and U ₃.

Table 1 Sensitivity analysis results over N=4096 model runs with respect to the outputs of interest Y(x ^∗) and |v|⋅Y _v . Mean values with ±s.d. computed by bootstrapping (100 replicas)

3 Change of Support Effect on Block Sensitivity Indices

In this section, we assess how the ranking of uncertain model inputs based on their block sensitivity indices vary under a change of support v of model output.

3.1 Relation Between Site Sensitivity Indices and Block Sensitivity Indices

Site sensitivity indices and block sensitivity indices are related. Let $\mathbb{E}_{Z}Y(\mathbf{x})$ denote the conditional expectation of Y(x) given Z(x), that is

$$ \forall\mathbf{x}\in\mathcal{D}, \quad \mathbb{E}_{Z}Y(\mathbf {x})= \mathbb {E} \bigl[Y(\mathbf{x}) \bigm| Z( \mathbf{x}) \bigr], $$

(7)

where $\mathbb{E}_{Z}Y(\mathbf{x})$ is the transform of the input SRF Z(x) via the function $\bar {\psi}(z)= \int_{\mathbb{R}^{n}} \psi(\mathbf{u},z) f_{U}(\mathbf{u})\, d\mathbf{u}$ (Eq. (2)) where f _U (⋅) is the multivariate pdf of random vector U. Under our assumptions concerning Y(x), $\mathbb{E}_{Z}Y(\mathbf{x})$ is a second-order SRF. Let C ^∗(⋅) denote its covariance function, σ ²=C ^∗(0) its variance and $\sigma^{2}_{v}$ its block variance over support v, that is, the variance of block average $1/\vert v\vert\int_{v}\mathbb{E}_{Z}Y(\mathbf{x})\,d \mathbf {x}$. Block variance $\sigma^{2}_{v}$ is equal to the mean value of C ^∗(h) when the two extremities of lag vector h describe support v, which we denote by $\overline{C^{\ast}}(v, v)$ (Journel and Huijbregts 1978). Using these notations, it follows from Eqs. (4) and (5) that site sensitivity indices and block sensitivity indices are related by (see Appendix A for a proof)

$$ \frac{S_{Z}(v)}{S_{\mathbf{U}}(v)} = \frac{S_{Z}}{S_{\mathbf{U}}} \cdot \frac{\sigma^2_{v}}{\sigma^2} = \frac{S_{Z}}{S_{\mathbf{U}}} \cdot\frac{\overline{C^\ast}(v, v)}{C^\ast(0)}. $$

(8)

3.2 Change of Support Effect

Consider now that model $\mathcal{M}$ was initially developed to study the spatial average Y _v over the support v, and that after model upscaling the modeler is interested in the spatial average Y _V over the support V, where V≫v. We know from Krige’s relation (Journel and Huijbregts 1978) that the block variance $\sigma^{2}_{v}$ decreases with increasing size of support: $\sigma^{2}_{V}\leq\sigma^{2}_{v}$. It follows from Eq. (8) that

$$ \frac{S_{Z}(V)}{S_{\mathbf{U}}(V)} \leq \frac{S_{Z}(v)}{S_{\mathbf{U}}(v)}. $$

(9)

The fraction of the variance of the aggregated model output explained by the input random field Z(x)—compared to the fraction explained by U—is thus smaller on support V than on support v. More specifically, let us suppose that the covariance function C ^∗(⋅) of the random field $\mathbb{E}_{Z}Y(\mathbf{x})$ has a finite effective range and that the support v is large with respect to this range. To a first approximation, the block variance $\sigma^{2}_{v}$ is of the form $\sigma^{2}_{v} \simeq\sigma^{2}A/ \vert v\vert$, where A is the so-called integral range of C ^∗(⋅) and is defined by A=1/σ ²∫C ^∗(h) d h (Chilès and Delfiner 1999). It follows from Eq. (8) that

$$ \frac{S_{Z}(v)}{S_{\mathbf{U}}(v)} \simeq \frac{\vert v\vert_{\mathrm{c}}}{\vert v\vert} \quad\mbox{with} \ \vert v\vert_{\mathrm{c}}= A\cdot \frac{S_{Z}}{S_{\mathbf{U}}}. $$

(10)

Equation (10) shows that the ratio |v|_c/|v| determines the relative contribution of the model inputs Z(x) and U to the output variance $\operatorname{Var}(Y_{v})$. The larger that this ratio is, the larger the part of the output variance $\operatorname{Var}(Y_{v})$ that is explained by the input random field Z(x). For a small ratio (when the area of the support v is large compared with the critical size |v|_c), the variability of Z(x) is mainly local, and the spatial correlation of Z(x) over v is weak. This local variability averages over the support v when the aggregated model output Y _v is computed; hence, input two-dimensional random field Z(x) explains a small fraction of the output variance $\operatorname{Var}(Y_{v})$. However, for a greater ratio (that is, when the area of the support v is small compared with the critical size |v|_c), the spatial correlation of Z(x) over v is strong. The averaging-out effect is weaker; hence, model input Z(x) explains a larger fraction of the output variance $\operatorname{Var}(Y_{v})$.

3.3 Link Between Covariance Function and Lock Sensitivity Indices

Critical size $\vert v\vert_{\mathrm{c}}= A\cdot\frac {S_{Z}}{S_{\mathbf{U}}}$ depends on the covariance function C ^∗(⋅) of the random field $\mathbb {E}_{Z}Y(\mathbf {x})$, which is itself driven by the covariance function C(⋅) of the input SRF Z(x). Let us now assume that Z(x) is a Gaussian random field (GRF). $\mathbb{E}_{Z}Y(\mathbf{x})$ is then square-integrable with respect to the standard normal density. It can be decomposed into an Hermitian expansion and its covariance function C ^∗(⋅) can be written as (Chilès and Delfiner 1999; see Appendix B for a proof)

$$ C^\ast(\mathbf{h}) = \sum _{k=0}^{\infty} \lambda_k^2 \cdot \bigl[C (\mathbf{h}) \bigr]^k. $$

(11)

For most of the usual transition covariance functions (spherical, exponential, and Gaussian models), the covariance C(h) is a monotonically increasing function of correlation length a. In this case, it follows from Eq. (11) that the integral range A=1/σ ²∫C ^∗(h) d h also increases with correlation length a. An increase in correlation length a thus leads to an increase in the critical size |v|_c, and the ratio of block sensitivity indices S _Z (v) and S _U (v) satisfies (Eq. (10))

$$ \frac{\partial}{\partial a} \biggl[ \frac{S_{Z}(v)}{S_{\mathbf {U}}(v)} \biggr] \geq0. $$

(12)

The relative contribution of the uncertain model input Z(x) to the variance of the output of interest Y _v increases when the correlation length of Z(x) increases. Indeed, when correlation length a increases, the averaging-out effect that occurs when the model output is aggregated over spatial support v weakens; thus, the fraction of the output variance $\operatorname{Var}(Y_{v})$ which is explained by the input random field Z(x) increases.

Nugget parameter’s impact on the block sensitivity indices can be interpreted in the same manner. The nugget parameter η controls the relative part of pure noise in the input random field Z(x) (Eq. (1)). The smaller η is, the weaker the averaging-out effect will be when the block average Y _v is computed over the support v, and the larger the part of output variance $\operatorname{Var}(Y_{v})$ will be that is explained by Z(x). The critical size |v|_c is thus a decreasing function of nugget parameter η, and the ratio of block sensitivity indices S _Z (v) and S _U (v) satisfies (Eqs. (1), (8), (11))

$$ \frac{\partial}{\partial\eta} \biggl[ \frac{S_{Z}(v)}{S_{\mathbf {U}}(v)} \biggr] \leq0. $$

(13)

3.4 Illustrative Example

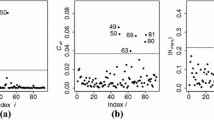
To illustrate the change of support effects on sensitivity analysis results, we performed spatial GSA on our numerical example in the following settings: varying disc-shaped support v of increasing size (Fig. 2); varying correlation length from a=1 to a=10 (Fig. 3); varying nugget parameter from η=0 to η=0.9 (Fig. 4). For each setting, we computed estimates of the output variance $\operatorname{Var}(Y_{v})$, the block sensitivity indices S _U (v), S _Z (v), and the ratio S _Z (v)/S _U (v) over N=4096 model runs. Mean values with a 95 % confidence interval were then computed for each estimate using bootstrapping (100 replicas). In accordance with Eqs. (9), (12), and (13), it appears that the block sensitivity index S _Z (v) (i) decreases when the support v increases (Fig. 2(b)), (ii) increases with the correlation length a (Fig. 3(b)), and (iii) decreases with the nugget parameter η (Fig. 4(b)). The opposite trends are observed for sensitivity index S _U (v). The change of support effect is clearly highlighted in Fig. 2(b): the contribution of the economic parameters U ₁, U ₂, and U ₃ to the variance of total flood damage |v|⋅Y _v exceeds the contribution of the water level map Z(x) when the radius r of v is greater than r _c ≃18; for radius r<r _c , the variance of total flood damage over the support v is mainly explained by the variability of the water levels Z(x). Finally, Fig. 2(c) shows that the ratio S _Z (v)/S _U (v) is proportional to 1/|v| when the support v is large enough. The theoretical curve S _Z (v)/S _U (v)=|v|_c/|v| (Eq. (10)) was fitted (least squares—R ²=0.99) on data points (for r≥20 only), yielding an estimate of the critical size |v|_c≃1,068. All calculations and figures were realized in R (Development Core Team 2009): random realizations of Z(x) were generated with the GaussRF() function from the RandomFields package (Schlather 2001), while computation of sensitivity indices was based on a modified version of the Sobol() function from the sensitivity package.

Fig. 2

GSA results depending on the size of disc-shaped support ν (with radius r and area |ν|=πr ²), for a=5, η=0.1: (a) total variance of Y _v , (b) block sensitivity indices S _U (v) (solid line) and S _Z (v) (dashed line), (c) ratio S _Z (v)/S _U (v) with fitted curve S _Z (v)/S _U (v)=|v|_c/|v| (dashed line). Error bars show 95 % confidence interval computed by bootstrapping (100 replicas)

Fig. 3

GSA results depending on correlation length a, for η=0.1 and a disc-shaped support v of radius r=50: (a) total variance of Y _v , (b) block sensitivity indices S _U (v) (solid line) and S _Z (v) (dashed line). Error bars show 95 % confidence interval computed by bootstrapping (100 replicas)

Fig. 4

GSA results depending on covariance nugget parameter η, for a=5 and a disc-shaped support v of radius r=50: (a) total variance of Y _v , (b) block sensitivity indices S _U (v) (solid line) and S _Z (v) (dashed line). Error bars show 95 % confidence interval computed by bootstrapping (100 replicas)

4 Discussion

Our first goal was to provide a formalism that extends the variance-based GSA approach to spatial models when the modeler is mainly interested in the linear average or the sum of a point-based model output Y(x) over some spatial unit v. Our approach is strongly motivated by various prior publications. Other authors had already computed site sensitivity indices (Marrel et al. 2011; Pettit and Wilson 2010) and block sensitivity indices (Lilburne and Tarantola 2009), but did so without naming them or exploring their analytical properties or their relationship. Our work is an attempt to do so. Equation (8) provides an exact relation between the site and block sensitivity indices; it may prove useful in the case of a model with a simple enough analytical expression.

Our research also sought to account for the change of support effects in the propagation of uncertainty through spatial models, within a variance-based GSA framework. We proved that the fraction of the variance of the model output that is explained by a spatially distributed model input Z(x) decreases under model upscaling; when the support v is large enough, the ratio of the block sensitivity index of spatially distributed input to the block sensitivity index of nonspatial inputs is proportional to |v|_c/|v|. The critical size |v|_c depends on the covariance function of the input SRF Z(x); it usually increases with an increase of the correlation length a or a decrease of the nugget parameter η. These findings are a translation into GSA formalism of the averaging-out effect clearly exhibited by Journel and Huijbregts (1978) in the regularization theory. Our contribution is to discuss this issue from the point of view of GSA practitioners. Formalizing the effect of a change of support on sensitivity analysis results may help modelers when they consider model upscaling; it will orientate future data gathering by identifying model inputs that will explain the largest fraction of the variance of the model output over a new spatial support. Our contribution also promotes an increased awareness of the issue of sharing out efficiently, among the various inputs used by a complex computer code, the cost of collecting field data. At some point of the model building process, the modeler will usually aim at reducing the variance of the output below a given threshold that will depend on the model use. To do so, the modeler may have to improve his knowledge on the real value of some of the model inputs, usually by collecting extra data. In this case, gathering extra field data on inputs maps that have small sensitivity indices (S _Z (v)<0.1) would be inefficient, as it would be costly but could not reduce the variance of the model output by a large fraction. Saint-Geours et al. (2011) discuss this issue on a flood risk assessment case study.

It should be noted that our approach is based on conditions that may not be met in some practical cases. First, we considered a model $\mathcal{M}$ with a single spatially distributed input Z(x). In real applications, modelers may have to deal with several spatial inputs Z ₁(x),…,Z _m (x), with different covariance functions C _i (⋅), correlation lengths a _i , and nugget parameters η _i . In this case, it can be shown that Eq. (8) still holds separately for each spatial input Z _i (x). However, no conclusion can be drawn a priori regarding how a change of support affects the relative ranking of two spatial inputs Z _i (x) and Z _j (x); the ratio of their block sensitivity indices $S_{Z_{i}}(v) /S_{Z_{j}}(v)$ will depend on the ratio of block variances $\sigma^{2}_{v, i} / \sigma^{2}_{v, j}$. Second, some environmental models are not point-based and involve spatial interactions (for example, erosion and groundwater flow models). In this case, it still may be possible to build a point-based surrogate model as a coarse approximation of the original model; if not, then the change of support properties discussed in Sect. 3 may not hold. Third, we assumed the input random field Z(x) to be stationary; if it is not, site sensitivity indices depend on site x ^∗ (Eq. (4)). It is then possible to compute maps of these indices (Marrel et al. 2011; Pettit and Wilson 2010) to discuss the spatial variability of model inputs sensitivities.

Finally, we focused on the case in which the modeler’s interest is in the spatial linear average or the sum of model output Y(x) over the support v. As discussed by Lilburne and Tarantola (2009), other outputs of interest may be considered, such as the maximum value of Y(x) over v (for example, maximal pollutant concentration over a zone), some quantile of Y(x) over v (Heuvelink et al. 2010), or the percentage of v for which Y(x) exceeds a certain threshold. To our knowledge, no study has investigated the properties of sensitivity indices computed with respect to such outputs of interest.

5 Conclusions

This paper provides a formalism to apply variance-based global sensitivity analysis to spatial models when the modeler’s interest is in the average or the sum of the model output Y(x) over a given spatial unit v. Site sensitivity indices and block sensitivity indices allow us to discuss how a change of support modifies the relative contribution of uncertain model inputs to the variance of the output of interest. We demonstrate an analytical relationship between these two types of sensitivity indices. Our results show that the block sensitivity index of an input random field Z(x) increases with the ratio |v|_c/|v|, where |v| is the area of the spatial support v and the critical size |v|_c depends on the covariance function of Z(x). Our formalization is made with a view toward promoting the use of sensitivity analysis in model-based spatial decision support systems. Nevertheless, further research is needed to explore the case of nonpoint-based models and extend our study to outputs of interest other than the average value of model output over support v.

Appendices

Appendix A: Proof of the Relation Between Site Sensitivity Indices and Block Sensitivity Indices

As mentioned in Sect. 2, we assume that the first two moments of Y(x) exist. The ratio of block sensitivity indices gives (Eq. (5))

$$ \frac{S_{Z}(v)}{S_{\mathbf{U}}(v)} = \frac{\operatorname{Var} ( \mathbb{E} [Y_v\mid Z(\mathbf{x}) ] )}{\operatorname{Var} ( \mathbb{E} [Y_v\mid \mathbf{U} ] )}. $$

(14)

The conditional expectation of block average Y _v given Z(x) gives

Thus, we have $\operatorname{Var} ( \mathbb{E} [Y_{v}\mid Z ] ) = \operatorname{Var} ( 1/\vert v\vert\int_{v}\mathbb{E}_{Z}Y(\mathbf {x})\,d\mathbf {x} ) = \sigma^{2}_{v}$ (definition of $\sigma^{2}_{v}$). Moreover, the conditional expectation of block average Y _v given input U gives

$\mathbb{E} [ Y(\mathbf{x})\mid\mathbf{U} ]$ does not depend on site x under the stationarity of SRF Z(x); thus, we have in particular $\mathbb{E} [ Y_{v}\mid\mathbf{U} ] = \mathbb {E} [ Y(\mathbf{x}^{\ast})\mid\mathbf{U} ]$, and $\operatorname{Var} ( \mathbb{E} [Y_{v}\mid\mathbf{U} ] ) = \operatorname{Var} ( \mathbb{E} [Y(\mathbf{x}^{\ast})\mid \mathbf{U} ] )$. Combining these expressions with Eq. (14) yields

$$ \frac{S_{Z}(v)}{S_{\mathbf{U}}(v)} = \frac{ \sigma^2_{v}}{\operatorname{Var}(\mathbb{E} [ Y(\mathbf {x}^\ast) \mid\mathbf{U} ])}. $$

(15)

The ratio of site sensitivity indices gives (Eq. (4))

$$ \frac{S_{Z}}{S_{\mathbf{U}}} = \frac{ \operatorname{Var}(\mathbb{E} [ Y(\mathbf{x}^\ast)\mid Z(\mathbf{x}) ])}{\operatorname{Var}(\mathbb{E} [ Y(\mathbf{x}^\ast)\bigm| \mathbf{U} ])}. $$

(16)

We notice that for point-based models $\operatorname{Var} [ \mathbb {E}(Y(\mathbf{x}^{\ast})\mid Z(\mathbf{x})) ] = \operatorname{Var} [ \mathbb{E}_{Z}Y(\mathbf{x}^{\ast}) ] = \sigma^{2}$ (definition of $\mathbb{E}_{Z}Y(\mathbf{x})$ (Eq. (7))). Finally, it follows from Eqs. (15) and (16) that

$$ \frac{S_{Z}(v)}{S_{\mathbf{U}}(v)} =\frac{S_{Z}}{S_{\mathbf{U}}} \cdot\frac{\sigma^2_{v}}{\sigma^2}. $$

Appendix B: Hermitian Expansion of Random Field $\mathbb {E}_{Z}Y(\mathbf {x})$

The random field $\mathbb{E}_{Z}Y(\mathbf{x})$ can be written (Eqs. (2), (7)) as a transformation of the Gaussian random field Z(x) through the function $\bar{\psi}: z \mapsto\int_{\mathbb{R}^{n}} \psi (\mathbf{u},z) \cdot f_{U}(\mathbf{u}) \, d\mathbf{u}$

$$\mathbb{E}_{Z}Y= \bar{\psi} ( Z ), $$

where f _U (⋅) is the multivariate pdf of random vector U. Under the hypothesis that the first two moments of Y(x) exist, random field $\mathbb{E}_{Z}Y(\mathbf{x})$ has finite expected value and finite variance. Thus, $\bar{\psi}$ belongs to the Hilbert space $L^{2}(\mathcal {G})$ of functions ϕ:ℝ→ℝ, which are square-integrable with respect to Gaussian density g(.). Hence, $\bar {\psi}$ can be expanded on the sequence of Hermite polynomials (χ _k ) _k∈ℕ, which forms an orthonormal basis of $L^{2}(\mathcal{G})$ (Chilès and Delfiner 1999)

$$\bar{\psi} = \sum _{k=0}^{\infty} \alpha_k \cdot\chi_k \quad \mbox{with~} \chi_k(z) = \frac{1}{\sqrt{k!} } \cdot\frac {1}{g(z)} \cdot \frac{\partial^k }{\partial z^k}g(z), $$

where coefficients α _k are given by: $\alpha_{k} = \int_{\mathbb{R}} \chi_{k}(z) \bar{\psi}(z) g(z) \, dz$. It follows that $\mathbb{E}_{Z}Y (\mathbf{x})$ can be written as an infinite expansion of polynomials of Z(x)

$$\forall\mathbf{x}\in\mathcal{D}, \quad\mathbb{E}_{Z}Y(\mathbf {x})= \sum _{k=0}^{\infty} \alpha_k \cdot\chi_k \bigl[Z(\mathbf{x}) \bigr]. $$

Its covariance then gives (Chilès and Delfiner 1999)

$$\operatorname{Cov} \bigl(\mathbb{E}_{Z}Y(\mathbf{x}), \mathbb {E}_{Z}Y(\mathbf{x}+ \mathbf {h}) \bigr) = \sum _{k=0}^{\infty} \alpha_k^2 \cdot \biggl[\frac{ C(\mathbf{h})}{C(0)} \biggr]^k = \sum _{k=0}^{\infty} \lambda_k^2 \cdot \bigl[ C(\mathbf{h} ) \bigr]^k, $$

where C(h) is the covariance function of GRF Z(x) and λ _k =α _k ⋅C(0)^−k/2.