Various contemporary machines and mechanisms have rotating parts in which centrifugal forces are formed in the course of rotation. This type of loading and the circular shape of rotating parts itself often play the role of causes of initiation of arc-shaped cracks, which may lead to emergency situations. This is especially important in the case of high-speed rotating loads typical, e.g., of the rotors of steam or gas turbines whose rotational speed can be as high as tens thousands revolutions per minute. This is why it is important to determine the stressed state of these parts of machines and mechanisms containing cracks, including the stress intensity factors (SIF).

The stress intensity factors determined in the process of rotation of a disk weakened by a rectilinear crack about its center are known from the literature. Thus, in [1], the values of the SIF were obtained by the method of boundary collocations for a randomly located rectilinear crack and, for a special case of eccentrically located diametric crack, the results were described by approximating relations.

However, the formation of arc-shaped cracks in a disk is possible under the action of rotating loads. For a concentric crack, the SIF were found by the boundary element method [2]. In what follows, we solve a plane problem of the theory of elasticity for a circular disk weakened by a crack randomly located along an arc of the circle rotating with a constant angular velocity. A rectilinear crack can be regarded as a special case of an arcshaped crack. We determine numerical values of the SIF and the angles of initial propagation of the crack.

Formulation of the Problem

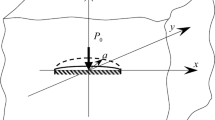
Consider an elastic isotropic circular disk of radius R bounded by a contour L 0 centered at the origin of the principal coordinate system xOy (Fig. 1). The disk is weakened by an internal arc-shaped crack randomly located along the contour L relative to a local coordinate system x 1 O 1 y 1. The O 1 x 1-axis of the local coordinate system is inclined to the Ox-axis at an angle α and the affix of its center O 1 in the principal system is given by the formula \( {z}_1^0={r}_0{e}^{i{\uptheta}_0}. \)

Fig. 1.
figure 1

General scheme of the problem.

Full size image

We assume that the edge of the disk and the crack lips are free of loads. Thus, the boundary conditions of the problem take the form

$$ N(t)+ iT(t)=0,\kern1em t\in {L}_0; $$
(1)
$$ {N}^{\pm }(t)+{iT}^{\pm }(t)=0,\kern1em t\in L, $$
(2)

where N and T are the normal and tangential components of the forces, respectively. The superscripts in formula (2) indicate the limiting values of the corresponding quantities on the crack contour L in the case where it is approached from the left (+) or from the right (–).

The disc rotates about its center with a constant angular speed ω as a result of which the stresses formed at each point of the disc for the plane stressed state take the following form in a polar coordinate system (r, θ) centered at the point O [3]:

$$ {\upsigma}_r={\upsigma}_0\left(1-\frac{r^2}{R^2}\right);\kern1em {\upsigma}_{\uptheta}={\upsigma}_0\left(1-\frac{1+3v}{3+v}\frac{r^2}{R^2}\right);\kern1em {\uptau}_{r\uptheta}=0, $$
(3)

where

$$ {\upsigma}_0=\frac{1}{8}\left(3+v\right){\uprho \upomega}^2{R}^2 $$

is the maximum level of stresses at the center of the disk, ν is Poisson’s ratio, ρ is the density of the material, and ω is the angular rotational speed of the disk. In relations (3), under the conditions of plane deformation, ν should be replaced by ν/(1− ν).

By using the well-known formulas relating the components of the stress tensor in Cartesian and polar coordinate systems [4], we find the components of stresses in the disk in Cartesian coordinates in the form

$$ \begin{array}{l}{\upsigma}_x=\frac{1}{2}\left[{\upsigma}_r+{\upsigma}_{\uptheta}-\left({\upsigma}_{\uptheta}-{\upsigma}_r\right)\operatorname{cos}2\uptheta \right];\kern1em {\upsigma}_y=\frac{1}{2}\left[{\upsigma}_r+{\upsigma}_{\uptheta}+\left({\upsigma}_{\uptheta}-{\upsigma}_r\right)\operatorname{cos}2\uptheta \right];\hfill \\ {}\kern9em {\uptau}_{xy}=\frac{1}{2}\left({\upsigma}_r-{\upsigma}_{\uptheta}\right)\operatorname{sin}2\uptheta .\hfill \end{array} $$
(4)

In the presence of a single crack, by using the boundary conditions of problem (1), (2), we obtain the following singular integral equation (SIE) of the posed problem with the help of the Kolosov–Muskhelishvili complex potentials for a disk with curvilinear cracks [5]:

$$ \frac{1}{\uppi}\underset{L}{\int}\left[K\left(t,\uptau \right){g}^{\prime }(t) dt+L\left(t,\uptau \right)\overline{g^{\prime }(t)}d\overline{t}\right]=p\left(\uptau \right),\kern1em \uptau \in L. $$
(5)

The kernels of this equation are given by the following formulas:

$$ K\left(t,\uptau \right)={f}_1\left(T,{T}^{\prime}\right)+\overline{f_2\left(T,{T}^{\prime}\right)}+{e}^{-2i\upalpha}\frac{d\overline{\uptau}}{d\uptau}\left[{T}^{\prime}\overline{g_2\left(T,{T}^{\prime}\right)}+\overline{h_2\left(T,{T}^{\prime}\right)}\right]; $$
(6)
$$ L\left(t,\uptau \right)={f}_2\left(T,{T}^{\prime}\right)+\overline{f_1\left(T,{T}^{\prime}\right)}+{e}^{-2i\upalpha}\frac{d\overline{\uptau}}{d\uptau}\left[{T}^{\prime}\overline{g_1\left(T,{T}^{\prime}\right)}+\overline{h_1\left(T,{T}^{\prime}\right)}\right], $$
(7)

where

$$ \begin{array}{l}{f}_1\left(T,{T}^{\prime}\right)=\frac{e^{i\upalpha}}{2}\left[\frac{1}{T-{T}^{\prime }}+\frac{\overline{T}}{T^{\prime}\overline{T}-{R}^2}\right];\kern1em {f}_2\left(T,{T}^{\prime}\right)=\frac{e^{-\upalpha}}{2}\frac{T^{\prime}\left(T\overline{T}-{R}^2\right)\left({T}^{\prime}\overline{T}-2{R}^2\right)}{R^2{\left({T}^{\prime}\overline{T}-{R}^2\right)}^2};\hfill \\ {}\kern6em {h}_1\left(T,{T}^{\prime}\right)=\frac{e^{i\upalpha}}{2}\left[\frac{{\overline{T}}^3}{{\left({T}^{\prime}\overline{T}-{R}^2\right)}^2}-\frac{\overline{T}}{{\left(T-{T}^{\prime}\right)}^2}\right];\hfill \end{array} $$
(8)
$$ {h}_2\left(T,{T}^{\prime}\right)=\frac{e^{-i\upalpha}}{2}\left[\frac{1}{T-{T}^{\prime }}+\frac{\overline{T}}{T^{\prime}\overline{T}-{R}^2}+\frac{\overline{T}\left({T}^{\prime}\overline{T}-3{R}^2\right)\left(T\overline{T}-{R}^2\right)}{{\left({T}^{\prime}\overline{T}-{R}^2\right)}^3}\right]; $$
(9)
$$ {g}_1\left(T,{T}^{\prime}\right)=\frac{e^{i\upalpha}}{2}\left[\frac{1}{{\left(T-{T}^{\prime}\right)}^2}-\frac{{\overline{T}}^2}{{\left({T}^{\prime}\overline{T}-{R}^2\right)}^2}\right];\kern1em {g}_2\left(T,{T}^{\prime}\right)={e}^{-i\upalpha}\frac{\left(T\overline{T}-{R}^2\right){R}^2}{{\left({T}^{\prime}\overline{T}-{R}^2\right)}^3}; $$
(10)
$$ T={te}^{i\upalpha}+{z}_1^0;\kern1em {T}^{\prime }=\uptau {e}^{i\upalpha}+{z}_1^0. $$
(11)

We determine the right-hand side of the SIE (5) by the method of superposition. To this end, we find the normal σ n and tangential τ n stresses on the crack contour in the solid disk in the form

$$ p\left(\uptau \right)=-\left({\upsigma}_n-i{\uptau}_n\right),\kern1em \uptau \in L, $$
(12)

where

$$ \begin{array}{l}{\upsigma}_n={\upsigma}_x{\mathrm{cos}}^2{\upalpha}^{\prime }+{\upsigma}_y{\mathrm{sin}}^2{\upalpha}^{\prime }-2{\uptau}_{xy}\operatorname{sin}{\upalpha}^{\prime}\operatorname{cos}{\upalpha}^{\prime };\hfill \\ {}{\uptau}_n=\left({\upsigma}_y-{\upsigma}_x\right)\operatorname{sin}{\upalpha}^{\prime}\operatorname{cos}{\upalpha}^{\prime }-{\uptau}_{xy}\left({\mathrm{cos}}^2{\upalpha}^{\prime }-{\mathrm{sin}}^2{\upalpha}^{\prime}\right),\hfill \end{array} $$
(13)

σ y , σ x , and τ xy are given by relations (3), (4), in which \( r=\sqrt{{\left(\operatorname{Re}{T}^{\prime}\right)}^2+{\left(\operatorname{Im}{T}^{\prime}\right)}^2},\uptheta =\kern0.5em \operatorname{arctan}\left(\operatorname{Im}{T}^{\prime }/\operatorname{Re}{T}^{\prime}\right), \) and the angle

$$ {\upalpha}^{\prime }=\uppi /2-\operatorname{arctan}\left(d\operatorname{Im}{T}^{\prime }/d\operatorname{Re}{T}^{\prime}\right). $$

For the single-valuedness of solution of the SIE (5), it is necessary to satisfy the auxiliary condition

$$ \underset{L}{\int }{g}^{\prime }(t) dt=0, $$
(14)

guaranteeing the single-valuedness of displacements in tracing the contour L .

The parametric equation of the crack contour L along a circular arc in the local coordinate system x 1 O 1 y 1 has the following form [4]:

$$ t=\upomega \left(\upxi \right)=1=l\frac{\left(\upxi -i\upvarepsilon \right)}{\left(-i\upxi \upvarepsilon \right)},\kern1em t\in L,\kern1em \left|\upxi \right|\le 1, $$
(15)

where ε = δ/l , l is the length of the chord connecting the crack tips, and δ is the distance from the center of the crack to this chord (Fig. 1). If ε = 0, then we get a special case of rectilinear crack. On the basis of the parametric equation of the crack contour (15), by the change of variables

$$ t=\upomega \left(\upxi \right)\le 1,\kern1em \mathrm{and}\kern1em \uptau =\upomega \left(\upeta \right),\kern1em \left|\upeta \right|\le 1, $$

in the SIE (5) and in the additional condition (14), we get a system of two integral equations in the normalized form for the derivative of the discontinuity of displacements on the crack lips g ′(ω(ξ)) ,  |ξ| ≤ 1. We numerically solve these equations by the Gauss–Chebyshev method of mechanical quadratures [4] and use their solution to find the SIF by the following formula [4]:

$$ {K}_{\mathrm{I}}^{\pm }-{iK}_{\mathrm{I}\mathrm{I}}^{\pm }=\mp \sqrt{\left|{\upomega}^{\prime}\left(\pm 1\right)\right|}\frac{u\left(\pm 1\right)}{\upomega^{\prime}\left(\pm 1\right)}, $$
(16)

where the upper signs correspond to the right tip of the crack, the lower signs correspond to its left tip, and the required function is given by the formula

$$ u\left(\upxi \right)={g}^{\prime}\left(\upomega \left(\upxi \right)\right){\upomega}^{\prime}\left(\upxi \right)\sqrt{1-{\upxi}^2}. $$

We also assume that the local fracture at both crack tips occurs by the mechanism of mode I fracture. Thus, to determine the angles of its initial propagation \( {\uptheta}_{\ast}^{\pm }, \) we use the generalized criterion of mode I fracture (σθ-criterion).

Numerical Results

The relative SIF \( {F}_{\mathrm{I},\mathrm{II}}^{\pm }={K}_{\mathrm{I},\mathrm{II}}^{\pm }/\left({\upsigma}_0\sqrt{\uppi R}\right) \) at both tips of the arc-shaped crack were found (depending on the angle of orientation of the crack α) for different values of the parameter of curvature ε = δ/l = 0, 0.1, and 0.3 and fixed relative quantities r 0 /R = 0.75, l/R = 0.24, and the angle θ0 = 0° (Fig. 2).

Fig. 2.
figure 2

Relative SIF \( {F}_{\mathrm{I}}^{\pm } \) (a) and \( {F}_{\mathrm{II}}^{\pm } \) (b) at the tips of an arc-shaped crack vs. the angle of orientation α for different values of the parameter of curvature ε = δ/l ; the solid lines correspond to the right crack tip (+) and the dashed lines correspond to the left crack tip (–).

Full size image

As follows from Fig. 2a, we get the highest values of the SIF K I for the right crack tip if the crack is maximally close to the boundary of the disk (α = 0°). As the angle α changes from 0° to 90° and the right tip moves away from the boundary, the SIF first rapidly decrease intensively and then, only for α = 90°, slightly increase. The range of the SIF K I for the right tip is much larger than for the left tip because the former is closer to the boundary of the disk.

It is worth noting that the highest values of the SIF K I are observed for the rectilinear crack (both for its right and left tips) and decrease as the curvature increases. For the right tip, the range of the SIF K II is also larger (Fig. 2b).

We considered two special cases in which an arc crack is located symmetrically about the radius of the disk. In the first case, the crack tips are directed from the boundary of the disk (concave crack; Fig. 3a), whereas in the second case, they are directed toward the boundary of the disk (convex crack; Fig. 3b). As could be expected, the SIF K I are higher for the convex crack (Table 1). For small curvatures of the convex crack, its tips approach each other. At the same time, for large curvatures, the tips move in the opposite direction. For all curvatures, the distance between the tips of the concave crack increases. However, in both cases, the crack propagates toward the boundary of the disk.

Fig. 3.
figure 3

Arc-shaped cracks whose tips are directed from the boundary of the disk for α = π/2 (a) and toward the boundary of the disk for α = 3π/2 (b).

Full size image
Table 1. Relative SIF and the Angles of Initial Propagation for Concave (α = π /2) and Convex (α = 3π /2) Cracks; r 0 / R = 0.8; l / R = 0.3
Full size table

Note that, for a concentric crack with the radius of curvature r and opening angle 2β, the obtained results agree with the available data [2] (Table 3).

We also considered the case of symmetric location of an arc-shape crack about the radius of the disk with an opening angle of 30° and a curvature angle R for different relative distances d/R from the center of the crack to the boundary of the disk for α = π/2 (Fig. 4). Note that cracks of this kind are often initiated, e.g., in the course of operation of railway wheels [6].

Fig. 4.
figure 4

Arc-shaped crack whose curvature is equal to the curvature of the disk contour for α = π/2.

Full size image

It is shown (Table 2) that the highest values of the SIF \( {K}_{\mathrm{I}}^{\pm } \) are attained for the crack located at the maximum distance from the boundary of the disk and the highest values of the SIF \( {K}_{\mathrm{II}}^{\pm }, \) on the contrary, are attained for the crack closest to the edge. For any locations of the crack, it propagates from both tips toward the boundary of the disk.

Table 2. Dependence of the Relative SIF and the Angles of Initial Propagation of an Arc-Shaped Crack on the Distance between the Crack and the Boundary of the Disk; α = π /2
Full size table
Table 3. Comparison of the Relative SIF for a Concentric Crack in a Disk (in the Numerator) with the Available Data [2] (in the Denominator)
Full size table

Conclusions

For a randomly located arc-shaped crack in a disk rotating with a constant angular speed, the maximum values of the SIF K I are attained near the tip closest to the boundary of the disk.

For an arc-shaped cracks symmetrically located about the radius of the disk, the SIF K I at both tips are always higher for the convex crack (Fig. 3b) than for the concave crack (Fig. 3a). The convex and concave cracks propagate toward the boundary of the disk.

For the symmetrically located concave crack whose radius of curvature is equal to the radius of curvature of the contour of the disk (Fig. 4), the highest values of the SIF \( {K}_{\mathrm{I}}^{\pm } \) are obtained for the crack located at the maximum distance from the boundary.