Influence of porosity on the flexural and vibration response of gradient plate using nonpolynomial higher-order shear and normal deformation theory

Abstract

The present article deals with flexural and vibration response of functionally graded plates with porosity. The basic formulation is based on the recently developed non-polynomial higher-order shear and normal deformation theory by the authors’. The present theory contains only four unknowns and also accommodate the thickness stretching effect. The effective material properties at each point are determined by two micromechanics models (Voigt and Mori–Tanaka scheme). The governing equations for FGM plates are derived using variational approach. Results have been obtained by employing a C⁰ continuous isoparametric Lagrangian finite element with eight degrees of freedom per node. Convergence and comparative study with the reported results in the literature, confirm the accuracy and efficiency of the present model and finite element formulation. The influence of the porosity, various boundary conditions, geometrical configuration and micromechanics models on the flexural and vibration behavior of FGM plates is examined.

1 Introduction

Over the last three decades, composite materials, have been the dominant emerging materials. The diversified applications of composite materials have grown steadily, penetrating and conquering new markets persistently. Further, the need of composite for the structural application has placed a high emphasis on the use of new and advanced materials which can be tailored microstructurally as per the requirement. Functionally graded materials (FGMs) are also a class of composites that have a continuous variation of material properties from one surface to another (Gupta et al. 2015). The gradation of properties in an FGM reduces the thermal stresses, residual stresses, and stress concentrations found in conventional composites.

Prediction of the realistic response of any structural component depends on its structural kinematics. In this regard, first plate theory was proposed by Kirchhoff (1850), known as Classical plate theory (CPT). This theory does not include transverse shear and normal stress hence, delivers irrational results for the thick plate. To conquer this limitation, displacement and stress based first order shear deformation theory (FSDT) was proposed by Mindlin (1951) and Reissner (1945) respectively. In FSDT, the shear correction factor is used to define the proper shear stress distribution. Its value depends on the geometric and loading conditions of the structure. To avoid restriction associated with CPT and FSDT, several higher-order shear deformation theories (HSDT) have been proposed in the last two decades. In this framework, research carried out by Basset (1890), Lo et al. (1977), Levinson (1980), Murthy (1981), Kant et al. (1982) and Reddy (1984), can be treated as a benchmark in polynomial higher-order shear deformation theory. These polynomial HSDT used Taylor series coefficients to include the shear deformation. Therefore, these are relatively complex and computationally expensive.

To circumvent the aforesaid limitations, nonpolynomial higher-order shear deformation theories have been developed in which shear strain function is used to demonstrate the shear deformation. Touratier (1991), Soldatos (1992) and Karama et al. (2009) employed sinusoidal, sinusoidal hyperbolic and exponential shear strain function respectively. Recently, Mantari (2012) investigated the flexural response of FGM plate using new sinusoidal function based HSDT with five unknowns. Thai and Choi (2013) presented cubic, sinusoidal, hyperbolic, and exponential function based HSDT to study the static and vibration response of FGM plate. Authors divided the transverse displacement in the bending and shear component to reduce the number of unknowns. Belabed et al. (2014) proposed hyperbolic function based higher-order shear deformation theory with five unknowns to investigate flexural and vibration characteristics of FGM plate. Ameur et al. (2011) showed the closed form solution to investigate the bending response of FGM plate using trigonometric shear deformation theory with four unknowns. Atmane et al. (2010) developed a new higher shear deformation theory to investigate the free vibration analysis of simply supported functionally graded plates resting on a Winkler–Pasternak elastic foundation. Nguyen (2015) presented the closed form solution of static, vibration and buckling response of FGM plate using hyperbolic higher-order shear deformation theory with four unknowns. Zenkour (2005) presented the sinusoidal shear deformation plate theory to study buckling and free vibration of simply supported FG plates. Thai and Kim (2013) presented quasi-3D sinusoidal shear deformation theory with only five unknowns for bending behavior of simply supported FGM plates. The closed form solution of free vibration response of FGM plate using four-variable refined plate theory was given by Hadji et al. (2011).

Apart from the development of such theories, several kinds of literature are available in which implementation of these theories along with 3D exact solution are given to investigate static and dynamic characteristics of the composite plate. In this framework, Reddy (2000) proposed a finite element model based on the third-order deformation theory to investigate the static and dynamic responses of FGM plate under mechanical and thermal loading. Pandya and Kant (1988) presented isoperimetric finite element formulation to investigate the static response of advanced composite plate. The flexural response of the FGM plate using collocation multiquadric radial basis functions is investigated by Ferreira et al. (2005). Wu et al. (2010) developed a modified Pagano method for three-dimensional (3-D) analysis of simply-supported, functionally graded rectangular plates under magneto-electro-mechanical loads. Jha et al. (2013) presented a free vibration response of FG elastic, rectangular, and simply supported plates based on polynomial higher order shear/shear-normal deformations theories. Alipour et al. (2010) presented a semi-analytical solution to study the vibration response of two-directional-functionally graded circular plates, resting on elastic foundations. Authors implemented Mindlin’s plate theory and the differential transformation technique to obtain the governing equations of motion. Kashtalyan (2004) presented the 3D elasticity solution for the flexural response of FGM plates, in which Young’s modulus of the plate is assumed to vary exponentially through the thickness coordinate. Lal et al. (2012) used Reddy’s third-order shear deformation theory to investigate the nonlinear bending response of FGM plate with random material properties. Prakash and Ganapathi (2006) used three-noded shear flexible plate element based on the field-consistency principle to study the free vibration and thermos-elastic buckling characteristics of circular FGM plates.

Talha and Singh (2010) investigated the static response and free vibration analysis of FGM plates using higher-order shear deformation theory with a special modification in the transverse displacement. Gupta et al. (2016a, b) used the polynomial higher order shear and normal deformation theory with 13DOF to analyze the vibration characteristics of FGM plate. Matsunaga (2009) presented Navier solution in the conjunction of two-dimensional higher-order theory to examine the flexural response of FGM plate under thermal and mechanical loads. The free vibration analysis of plates made of FGMs with an arbitrary gradient was carried out by Benachour et al. (2011) using a four-variable refined plate theory. Mantari and Soares (2013) examined the bending response of FGM plates by using a new trigonometric higher order and hybrid quasi-3D shear deformation theories.

Mojdehi et al. (2011) presented the 3D elastic solution of FGM plates based on the MLPG method and MLS approximation. Authors found that the centroidal deflection of FGM plates lies in between those of a pure ceramic and a pure metallic plate for both static and dynamic loads. Xiang and Kang (2013) used a meshless method based on thin plate spline radial basis function for the flexural response of FGM plates based on various higher-order shear deformation theories. Qian et al. (2004) studied the static and dynamic deformation of thick functionally graded elastic plates by using higher order shear and normal deformable plate theories and meshless local Petrov–Galerkin method. Zenkour (2006) presented generalized shear deformation theory for the static response of FGM plates. Effective material properties were calculated by assuming a power-law. The comparative study of the effect of various gradation laws (power-law, sigmoid or exponential function) on the mechanical behavior of FGM plates under transverse load was carried out by Chi and Chung (2006). Vaghefi et al. (2010) showed a three-dimensional solution for thick FGM plates by utilizing a meshless Petrov–Galerkin method. An exponential function was assumed for the variation of Young’s modulus through the thickness of the plate. Tamijani and Kapania (2012) used FSDT with element free Galerkin method to study the free vibration of an FG plate with curvilinear stiffeners. Zhu and Liew (2011) presented free vibration analyses of metal and ceramic FG plates with the local Kriging meshless method.

In addition, it is found from the literature (Ebrahimi and Zia 2015; Atmane et al. 2015) that during the fabrication process of FGMs, some microstructural defects i.e. micro-voids or porosities can accrue in the materials due to the large difference in solidification temperatures between the constituent materials. Wattanasakulpong and Ungbhakorn (2014), Wattanasakulpong et al. (2012) highlighted on the existence of porosities inside the FGM during multi- step sequential infiltration fabrication process. Therefore, it necessitates to include the porosity effect during computing the effective material properties of FGM plate. There are only a few reports available in the open literature dealing with the vibration and flexural analysis of FGM plate with porosity. Yahia et al. (2015) used higher-order shear deformation theories to study the wave propagation of an infinite FGM plate with porosities. The linear and nonlinear dynamic stability of a circular porous plate has been investigated to determine the critical loads in two separate studies by Magnucka-Blandzi (2010). Moreover, Mechab et al. (2016) have developed a nonlocal elasticity model for vibration of nanoplates made of porous FG material resting on elastic foundations.

Koiter (1959) and Carrrera et al. (2011) emphasized on the importance of thickness stretching effect on the structural response of the composite structure. From the aforesaid review, it is observed that most of the HSDT do not accommodate transverse normal strain which leads to the negligence of thickness stretching effect. It is also found that the available literature for the vibration and flexural response of FGM plates with porosity are relatively scarce. Therefore, the objective of the present work is set to investigate the flexural and vibration analysis of FGM plates with porosity using recently developed non-polynomial based higher-order shear and normal deformation theory by the authors’ (Gupta and Talha 2016; Gupta et al. 2017). The present theory consists of a nonlinear variation of in-plane and transverse displacement along the thickness direction and also accommodate the thickness stretching effect. The effective material properties of FGM plate with porosity are computed using newly proposed model. To implement this theory, a suitable C⁰ continuous isoparametric finite element with eight degrees of freedom (DOFs) per node is considered to minimize the computational complicacy. In order to compute the graded material properties, two micromechanics model (Voigt and Mori–Tanaka) is used with the conjunction of the power law. The influence of porosity volume fraction, volume fraction index, geometric configurations, and various boundary constraints on the flexural and vibration characteristics of FGM plates is investigated.

2 Mathematical formulation

The mathematical formulation of the actual physical problem of the FGM plates subjected to mechanical loading is presented. An FGM plate with porosity having thickness ‘h’, length ‘a’, and width ‘b’ is considered and is shown in Fig. 1.

Fig. 1

The geometric configuration of FGM Plate with porosity

2.1 Constitutive equations and material properties

The Voigt model and Mori–Tanaka are used in the present study to compute the effective material properties of FGM plate.

2.1.1 Mori–Tanaka model

According to the Mori–Tanaka scheme (Mori 1973), the effective Young’s modulus E _f and Poisson’s ratio υ _f can be calculated using effective bulk modulus (K _f ) and shear modulus (G _f ) of the FGM plate as

$$\begin{aligned} \frac{{K_{f} (z) - K_{c} }}{{K_{m} - K_{c} }} = \frac{{V_{m} }}{{1 + \left[ {1 - V_{m} } \right]\frac{{3\left[ {K_{m} + K_{c} } \right]}}{{\left[ {3K_{c} + 4G_{c} } \right]}}}} \hfill \\ \frac{{G_{f} (z) - G_{c} }}{{G_{m} - G_{c} }} = \frac{{G_{f} (z)}}{{1 + \left[ {1 - V_{m} } \right]\left( {\frac{{G_{m} + G_{c} }}{{G_{c} + f_{1} }}} \right)}}\, \hfill \\ \end{aligned}$$

(1)

where, $\,\,f_{1} = \frac{{G_{c} \left[ {9K_{c} + 8G_{c} } \right]}}{{\left[ {6K_{c} + 2G_{c} } \right]}}$ and K _c , G _c , K _m and G _m are the bulk modulus and shear modulus of ceramic and metal respectively. From Eq. (1), the effective material properties are represented as

$$E_{f} (z) = \frac{{9K_{f} (z)G_{f} (z)}}{{3K_{f} (z) + G_{f} (z)}},\,\,\,\,\upsilon_{f} (z) = \tfrac{{3K_{f} (z) - 2G_{f} (z)}}{{6K_{f} (z) + 2G_{f} (z)}}$$

(2)

2.1.2 Voigt model

The Voigt model is simple and has been adopted in most of the analyses of FGM structures (Gibson 1995). The effective material properties(p _e ) in a specific direction (along with ‘z’) is determined by

$$\begin{aligned} & V_{m} + V_{c} = 1 \\ & p_{e} = \left( {p_{c} - p_{m} } \right)V_{c} + p_{m} \\ \end{aligned}$$

(3)

where, ‘p _e ’ represents the effective material property (Young’s modulus, mass density, Poisson’s ratio), subscripts m and c represents the metallic and ceramic constituents, respectively. The volume fraction V _c is assumed to follow a simple power law in both the model as

$$V_{c} = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{n}$$

(4)

where ‘n’ is the volume fraction index. To incorporate the porosity, a new mathematical expression is modeled with the help of slight modification in the rule of mixture as given in Eq. (3). The material properties with porosity are anticipated to follow the power law in the present study and are expressed as

$$ {\rm P} = {\rm P}_{c} \left( {V_{c} - \log (1 + \lambda /2)} \right) + {\rm P}_{m} \left( {V_{m} - \log (1 + \lambda /2)} \right) $$

(5)

‘λ’ is termed as porosity volume fraction (λ < 1). λ = 0 indicates the non-porous functionally graded plate. The effective material property of porous FGM plate is given as

$$\begin{aligned} E\left( z \right) &= \left[ {E_{c} - E_{m} } \right]\left( {\frac{2z + h}{2z}} \right)^{n} - \log \left( {1 + \lambda /2} \right)\left[ {E_{c} + E_{m} } \right]\left[ {1 - \frac{2\left| z \right|}{h}} \right] + E_{m} \hfill \\ \rho \left( z \right) &= \left[ {\rho_{c} - \rho_{m} } \right]\left( {\frac{2z + h}{2z}} \right)^{n} - \log \left( {1 + \lambda /2} \right)\left[ {\rho_{c} + \rho_{m} } \right]\left[ {1 - \frac{2\left| z \right|}{h}} \right] + \rho_{m} \hfill \\ \end{aligned}$$

(6)

The linear constitutive relations of an FG plate is given by Talha and Singh (2011):

$$\left\{ \begin{aligned} \sigma_{xx} \hfill \\ \sigma_{yy} \hfill \\ \sigma_{zz} \hfill \\ \tau_{yz} \hfill \\ \tau_{zx} \hfill \\ \tau_{xy} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{12} } & 0 & 0 & 0 \\ {C_{12} } & {C_{11} } & {C_{12} } & 0 & 0 & 0 \\ {C_{12} } & {C_{12} } & {C_{11} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right]\left\{ \begin{aligned} \varepsilon_{xx} \hfill \\ \varepsilon_{yy} \hfill \\ \varepsilon_{zz} \hfill \\ \gamma_{yz} \hfill \\ \gamma_{zx} \hfill \\ \gamma_{xy} \hfill \\ \end{aligned} \right\}$$

(7)

$\begin{array}{l} C_{11} = {{E(z)(1 + \upsilon )} \mathord{\left/ {\vphantom {{E(z)(1 + \upsilon )} {(1 - 2\upsilon )(1 + \upsilon )}}} \right. \kern-0pt} {(1 - 2\upsilon )(1 + \upsilon )}} \hfill \\ C_{12} = {{\upsilon E(z)} \mathord{\left/ {\vphantom {{\upsilon E(z)} {(1 - 2\upsilon )(1 + \upsilon )}}} \right. \kern-0pt} {(1 - 2\upsilon )(1 + \upsilon )}} \hfill \\ C_{44} = C_{55} = C_{66} = {{E(z)} \mathord{\left/ {\vphantom {{E(z)} {2(1 + \upsilon )}}} \right. \kern-0pt} {2(1 + \upsilon )}} \hfill \\ \end{array}$

2.2 Displacement fields

A recently developed non-polynomial based higher-order shear and normal deformation theory by the authors’ Gupta and Talha (2016), Gupta et al. (2017) is considered to investigate the realistic flexural and vibration responses of the porous graded plates as given in Eq. (8):

$$\begin{aligned} \bar{u}(x,y,z,t) &= u_{o} (x,y,t) - z\left( {\frac{{\partial w_{b} }}{\partial x}} \right) - \psi \left[ {{ \sinh }^{ - 1} \left( {\frac{\kappa z}{h}} \right) - \left( {\frac{\kappa }{h}} \right)z} \right]\frac{{\partial w_{s} }}{\partial x} \hfill \\ \bar{v}(x,y,z,t) &= v_{o} (x,y,t) - z\left( {\frac{{\partial w_{b} }}{\partial y}} \right) - \psi \left[ {{ \sinh }^{ - 1} \left( {\frac{\kappa z}{h}} \right) - \left( {\frac{\kappa }{h}} \right)z} \right]\frac{{\partial w_{s} }}{\partial y} \hfill \\ \bar{w}(x,y,z,t) &= w_{b} (x,y,t) + \kappa { \cosh }^{2} \left( {\frac{\kappa z}{h}} \right)w_{s} (x,y,t) \hfill \\ {\text{Here,}}\,\,\psi &= - \frac{{h{ \cosh }^{2} (\kappa /2)}}{{\sqrt {\left( {1 + \kappa^{2} /4} \right)} - 1}} \hfill \\ \end{aligned}$$

(8)

where $\bar{u}$, $\bar{v}$ and $\bar{w}$ signifies the displacements of a point along the (x, y, z) coordinates. u ₀ , v ₀ , w _b and w _s are the four unknown displacement functions of mid-plane. The value of shape parameter ’κ’ is deliberated in the post-processing phase and is evaluated as 3.4.

2.3 Strain–displacement relations

The non-zero linear strains associated with the displacement field in Eq. (8) is represented as,

$$\left\{ {\varvec{\upvarepsilon}} \right\}_{6x1} = [{\mathfrak{M}}]_{6x16} \left\{ {{\bar{\mathbf{\varepsilon }}}} \right\}_{16x1}$$

(9)

where $\left\{ {\bar{\varvec{\varepsilon }}} \right\}_{16x1}$ are the components of generalized strains. The non-zero strains are given below,

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{zz} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} } \\ {\varepsilon_{yy}^{0} } \\ {\varepsilon_{zz}^{0} } \\ {\gamma_{xy}^{0} } \\ {\gamma_{xz}^{0} } \\ {\gamma_{yz}^{0} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{1} } \\ {\varepsilon_{yy}^{1} } \\ 0 \\ {\gamma_{xy}^{1} } \\ 0 \\ 0 \\ \end{array} } \right\} + f(z)\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{2} } \\ {\varepsilon_{yy}^{2} } \\ 0 \\ {\gamma_{xy}^{2} } \\ 0 \\ 0 \\ \end{array} } \right\} + \phi (z)\left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ {\gamma_{xz}^{1} } \\ {\gamma_{yz}^{1} } \\ \end{array} } \right\} + g(z)\left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ {\gamma_{xz}^{2} } \\ {\gamma_{yz}^{2} } \\ \end{array} } \right\}$$

(10)

$\begin{aligned} {\text{where,}}\,\,\,f(z) = \psi \left[ {{ \sinh }^{ - 1} \left( {\frac{\kappa z}{h}} \right) - \left( {\frac{\kappa }{h}} \right)z} \right]\,\,,\,\,g(z) = \kappa { \cosh }^{2} \left( {\frac{\kappa z}{h}} \right),\,\,\phi (z) = g^{\prime}(z),\,\,\,\,\varepsilon_{xx}^{0} = \frac{{\partial u_{0} }}{\partial x},\,\,\,\varepsilon_{yy}^{0} = \frac{{\partial v_{0} }}{\partial y},\,\,\, \hfill \\ \varepsilon_{zz}^{0} = \left( {{{2\kappa^{2} } \mathord{\left/ {\vphantom {{2\kappa^{2} } h}} \right. \kern-0pt} h}} \right)w_{s} { \cosh }\left( {\frac{\kappa z}{h}} \right)\sinh \left( {\frac{\kappa z}{h}} \right),\,\,\,\gamma_{xz}^{0} = - \left( {\frac{\kappa \psi }{h}} \right)\frac{{\partial w_{s} }}{\partial x},\,\,\,\gamma_{xz}^{1} = \kappa \psi h,\,\,\,\gamma_{xz}^{2} = \kappa \frac{{\partial w_{s} }}{\partial x}.\,\,\gamma_{yz}^{0} = - \frac{\kappa \psi }{h}\frac{{\partial w_{s} }}{\partial y},\,\,\,\gamma_{yz}^{1} = \kappa \psi h,\,\, \hfill \\ \gamma_{yz}^{2} = \kappa \frac{{\partial w_{s} }}{\partial y},\,\,\,\,\gamma_{xy}^{0} = \frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x},\,\,\gamma_{xy}^{1} = - \frac{{\partial^{2} w_{b} }}{\partial x\partial y} - \frac{\kappa \psi }{h}\frac{{\partial^{2} w_{s} }}{\partial x\partial y} - \frac{{\partial^{2} w_{b} }}{\partial x\partial y} - \frac{\kappa \psi }{h}\frac{{\partial^{2} w_{s} }}{\partial x\partial y},\,\,\,\gamma_{xy}^{2} = 2\psi \frac{{\partial^{2} w_{s} }}{\partial x\partial y} \hfill \\ \varepsilon_{xx}^{1} = - \frac{{\partial^{2} w_{b} }}{{\partial x^{2} }} - \left( {\frac{\kappa \psi }{h}} \right)\frac{{\partial^{2} w_{s} }}{{\partial x^{2} }},\,\,\,\varepsilon_{yy}^{1} = - \frac{{\partial^{2} w_{b} }}{{\partial y^{2} }} - \left( {\frac{\kappa \psi }{h}} \right)\frac{{\partial^{2} w_{b} }}{{\partial y^{2} }},\,\,\varepsilon_{xx}^{2} = \psi \frac{{\partial^{2} w_{s} }}{{\partial x^{2} }},\,\,\varepsilon_{yy}^{2} = \psi \frac{{\partial^{2} w_{s} }}{{\partial y^{2} }}\, \hfill \\ \end{aligned}$

3 Solution methodology (finite element formulation)

3.1 Element selection

In the present finite element formulation, a C⁰-continuous nine nodded isoparametric finite element with eight degrees of freedom per node (Fig. 2) is employed to discretize the plate geometry. Later, the generalized displacement vector and element geometry of the model at any point can be expressed in terms of shape functions as follows,

Fig. 2

Configuration of nine-noded finite element in natural coordinate system

$$\left\{ \Re \right\} = \sum\limits_{i = 1}^{nn} {N_{i} } \left\{ \Re \right\}_{i} ,x = \sum\limits_{i = 1}^{nn} {N_{i} } x_{i} ,y = \sum\limits_{i = 1}^{nn} {N_{i} } y_{i}$$

(11)

where {N _i }and{ℜ _i }are the shape function and displacement vector of ith node respectively. ‘nn’ is the number of nodes per element and x _i , and y _i are the Cartesian coordinate of the ith node. The shape functions at an ith node of the nine noded elements are given as:

$$N_{i} = \left\{ \begin{aligned} \frac{1}{4}\left( {\xi^{2} + \xi_{i} \xi } \right)\left( {\eta^{2} + \eta_{i} \eta } \right),\,\,\,for\,\,i = 1,2,3,4 \hfill \\ \frac{1}{2}\left( {1 - \xi^{2} } \right)\left( {\eta^{2} + \eta_{i} \eta } \right),\,\,\,for\,\,i = 5,7 \hfill \\ \frac{1}{2}\left( {\xi^{2} + \xi_{i} \xi } \right)\left( {1 - \eta^{2} } \right),\,\,\,\,for\,i = 6,8 \hfill \\ \frac{1}{2}\left( {1 - \xi^{2} } \right)\left( {1 - \eta^{2} } \right),\,\,for\,\,\,i = 9 \hfill \\ \end{aligned} \right.$$

(12)

3.2 Continuity obligation

It is obvious from Eq. (9), that the in-plane displacement (i.e. $\bar{u}$ and $\bar{v}$) encompass transverse displacement derivatives $\left( {\bar{w}} \right)$, which leads to the second order derivatives in the strain vector. Hence, it requires implementing C¹ continuity in the finite element modeling.

To eradicate the intricacy accompanying with these finite elements, the displacement field has been modified to make it appropriate for C⁰ continuous element. In this framework, the transverse displacement derivatives exist in Eq. (8) are replaced as $\frac{{\partial w_{b} }}{\partial x} = \alpha_{x} \,,\,\,\,\frac{{\partial w_{b} }}{\partial y} = \alpha_{y} \,,\frac{{\partial w_{s} }}{\partial x} = \beta_{x} \,,\,\,\frac{{\partial w_{s} }}{\partial y} = \beta_{y} \,{\text{and }}w_{s} = \beta_{z}$. After incorporating these modifications in the displacement field, four DOFs with C¹ continuity given in Eq. (8) are changed into eight DOFs with C⁰ continuity as shown in Eq. (13).

$$\begin{aligned} \bar{u}(x,y,z,t) &= u_{o} (x,y,t) - z\left[ {\alpha_{x} + \left( {\frac{\kappa \psi }{h}} \right)\beta_{x} } \right] + \psi { \sinh }^{ - 1} \left( {\frac{\kappa z}{h}} \right)\beta_{x} \hfill \\ \bar{v}(x,y,z,t) &= v_{o} (x,y,t) - z\left[ {\alpha_{y} + \left( {\frac{\kappa \psi }{h}} \right)\beta_{y} } \right] + \psi { \sinh }^{ - 1} \left( {\frac{\kappa z}{h}} \right)\beta_{y} \hfill \\ \bar{w}(x,y,z,t) &= w_{b} (x,y,t) + \kappa { \cosh }^{2} \left( {\frac{\kappa z}{h}} \right)\beta_{z} (x,y,t) \hfill \\ \end{aligned}$$

(13)

The basic field variables can be denoted mathematically as. In this procedure, the artificial constraints are introduced which are enforced variationally through a penalty approach as given in Eq. (15).

$$\frac{{\partial w_{b} }}{\partial x} - \alpha_{x} = 0\,,\,\,\,\frac{{\partial w_{b} }}{\partial y} - \alpha_{y} = 0\,,\frac{{\partial w_{s} }}{\partial x} - \beta_{x} = 0\,\,{\text{and }}\frac{{\partial w_{s} }}{\partial y} - \beta_{y} = 0$$

(14)

3.3 Energy equations

3.3.1 Strain energy of the plate

The strain energy of ith element of FGM plate is given by:

$$\begin{aligned} \varPi^{e} &= \frac{1}{2}\int_{V} {\left\{\varvec{\varepsilon}\right\}}_{i}^{T} \left\{\varvec{\sigma}\right\}_{i} dV = \,\,\frac{1}{2}\int_{v} {\left\{\varvec{\varepsilon}\right\}}_{i}^{T} \left[ {\varvec{Q}_{{\varvec{ij}}} } \right]\left\{ {{\varvec{\upvarepsilon}}_{{\mathbf{i}}} } \right\}dV \hfill \\ &= \frac{1}{2}\int_{V} {\left\{ {\bar{\varvec{\varepsilon }}} \right\}}_{i}^{T} [{\mathfrak{M}}]_{i}^{T} \left[ {\varvec{Q}_{{\varvec{ij}}} } \right][{\mathfrak{M}}]_{i} \left\{ {{\bar{\mathbf{\varepsilon }}}} \right\}_{i} dV = \frac{1}{2}\int_{A} {\left\{ {\mathbf{\Re }} \right\}}_{i}^{T} \left[ {\mathbf{B}} \right]_{i}^{T} \left[ \varvec{D} \right]\left[ {\mathbf{B}} \right]_{i} \left\{ {\mathbf{\Re }} \right\}_{i} dA \hfill \\ &= \frac{1}{2}\left\{ {\mathbf{\Re }} \right\}_{i}^{T} \left[ \varvec{K} \right]_{i} \left\{ {\mathbf{\Re }} \right\}_{i} \hfill \\ \end{aligned}$$

(15)

If ‘ne’ is the number of elements used for meshing the plate, the strain energy of the plate is given as,

$$\prod = \sum\limits_{e = 1}^{ne} {\varPi^{\left( e \right)} } ,\prod = \frac{1}{2}\sum\limits_{e = 1}^{ne} {\left\{ {\mathbf{\Re }} \right\}^{\left( e \right)T} } \left[ \varvec{K} \right]^{\left( e \right)} \left\{ {\mathbf{\Re }} \right\}^{\left( e \right)}$$

(16)

where $\left[ \varvec{K} \right]^{\left( e \right)}$ and $\left\{ {\mathbf{\Re }} \right\}^{\left( e \right)}$ are the linear stiffness matrix and displacement vector for the element, respectively.

3.3.2 Kinetic energy of the plate

The kinetic energy of FGM plate is given by:

$$\Delta = \frac{1}{2}\int_{V} {\rho \left\{ {{\dot{\mathbf{\varvec{\Lambda }}}}} \right\}}^{T} \left\{ {{\dot{\mathbf{\varvec{\Lambda }}}}} \right\}dV$$

(17)

where ‘ρ’and $\left\{ {\varvec{\Lambda}} \right\}$ are the density and global displacement vector of the plate. The global displacement field model has represented as:

$$\left\{ {\varvec{\Lambda}} \right\} = \left[ {{\bar{\mathbf{N}}}} \right]\left\{ {\mathbf{\Re }} \right\}$$

(18)

where the matrix $\left[ {{\bar{\mathbf{N}}}} \right]$ is the function of thickness coordinate which is given in “Appendix”. After substituting Eq. (18) into Eq. (17), the kinetic energy of an element is obtained as:

$$\begin{aligned} \Delta^{e} = \frac{1}{2}\int_{A} {\left( {\int_{Z} {\rho \left\{ {{\dot{\mathbf{\Re }}}} \right\}^{T} \left[ {\mathbf{N}} \right]^{T} \left[ {\mathbf{N}} \right]\left\{ {{\dot{\mathbf{\Re }}}} \right\}dz} } \right)} dA \hfill \\ = \frac{1}{2}\int_{A} {\left\{ {{\dot{\mathbf{\Re }}}} \right\}}^{T} \left[ {\mathbf{\rm M}} \right]^{(e)} \left\{ {{\dot{\mathbf{\Re }}}} \right\}dA \hfill \\ \end{aligned}$$

(19)

Kinetic energy of vibrating plate for total number of element ‘ne’ is given as

$$\Delta = \sum\limits_{e = 1}^{ne} {\Delta^{\left( e \right)} }$$

(20)

Here $\left[ {\mathbf{\rm M}} \right]^{(e)}$ is the inertia matrix of the element.

3.3.3 Work done due to transverse load

The external work done on the plate by uniformly applied load q ₀ may be written as $W_{ext}^{(e)} = \int\limits_{A} {q_{0} } (x,y)\left\{ \varvec{w} \right\}dA$

For the finite element formulation, the above equation can be written as

$$W_{ext} = \sum\limits_{e = 1}^{ne} {W_{ext}^{(e)} }$$

(21)

The total potential energy due to the applied load can be written as

$$\begin{aligned} V &= - W_{ext}^{(e)} = - \int\limits_{A} {\left\{ {\varvec{\Lambda}} \right\}}^{T} \left\{ \varvec{\mathcal{F}} \right\}dA = - \left\{ {\varvec{\Lambda}} \right\}^{(e)T} \left\{ \varvec{\mathcal{F}} \right\}^{(e)} \hfill \\ \left\{ \varvec{\mathcal{F}} \right\}^{(e)}& = \left\{ {\begin{array}{*{20}c} 0 & 0 & Q & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right\}^{T} \hfill \\ \end{aligned}$$

(22)

3.4 Governing equation

The governing equation for flexural and free vibration analysis of FG plate has been obtained using the principle of virtual work (Grover et al. 2013).

$$\int\limits_{{t_{1} }}^{{t_{2} }} {\left( {\delta L} \right)} dt = 0$$

(23)

where L is termed as Lagrangian and is demarcated as L = Π − (Δ + V). The final governing equation can be obtained by putting all the energy equations (Eqs. 16, 20 and 22) along with the energy function Π _c because of enforced artificial constraints during the conversion of C¹ continuity to C⁰ continuity. This energy function Π _c is expressed as

$$\varPi_{c} = \frac{\gamma }{2}\iint {\left[ \begin{aligned} \left( {\frac{{\partial w_{b} }}{\partial x} - \alpha_{x} } \right)^{T} \left( {\frac{{\partial w_{b} }}{\partial x} - \alpha_{x} } \right) + \left( {\frac{{\partial w_{b} }}{\partial y} - \alpha_{y} } \right)^{T} \left( {\frac{{\partial w_{b} }}{\partial y} - \alpha_{y} } \right) + \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\left( {\frac{{\partial w_{s} }}{\partial x} - \beta_{x} } \right)^{T} \left( {\frac{{\partial w_{s} }}{\partial x} - \beta_{x} } \right) + \left( {\frac{{\partial w_{s} }}{\partial y} - \beta_{y} } \right)^{T} \left( {\frac{{\partial w_{s} }}{\partial y} - \beta_{y} } \right) \hfill \\ \end{aligned} \right]}dxdy$$

(24)

Using finite element approximation Π _c is represented as:$\varPi_{c} = \frac{\gamma }{2}\left\{ {\mathbf{\Re }} \right\}^{T} \left[ {{\mathbf{K}}_{{\mathbf{c}}} } \right]\left\{ {\mathbf{\Re }} \right\}$, where $\left[ {{\mathbf{K}}_{{\mathbf{c}}} } \right]$ is the stiffness matrix due to artificial constraints. After substituting theses value in Eq. (23), the governing equation is expressed as

$$\frac{1}{2}\int\limits_{{t_{1} }}^{{t_{2} }} \delta \left[ {\left\{ {{\dot{\mathbf{\Re }}}} \right\}^{T} \left[ {\mathbf{\rm M}} \right]\left\{ {{\dot{\mathbf{\Re }}}} \right\} - \left\{ {\mathbf{\Re }} \right\}^{T} \left[ {{\mathbf{K}} + \gamma {\mathbf{K}}_{{\mathbf{c}}} } \right]\left\{ {\mathbf{\Re }} \right\}} \right]dt = 0$$

(25)

Above equations can be used to find the required governing equations for free vibration and flexural analysis by imposing the prerequisite boundary conditions as follows:

1. The generalized eigenvalue problem for free vibration of a system can be expressed as

$$\left[ {\mathbf{\rm M}} \right]\left\{ {{\ddot{\mathbf{\Re }}}} \right\} + \left[ {{\mathbf{K}} + \gamma {\mathbf{K}}_{{\mathbf{c}}} } \right]\left\{ {\mathbf{\Re }} \right\} = 0 ,$$

(26)

2. The generalized governing equation for flexural analysis may be expressed as

$$\left[ {\mathbf{K}} \right]\left\{ {\mathbf{\Re }} \right\} = \left\{ \varvec{\mathcal{F}} \right\}$$

(27)

4 Numerical results and discussion

In this section, the model validation and numerical analyses for the flexural and vibration response of the FGM plate are performed using the finite element method. A uniform 6 × 6 mesh of nine noded C^o continuous elements is employed. To prevent the shear locking phenomena, the reduced integration technique is used to integrate terms related to the transverse shear stress. The description of material properties used in the analysis is provided in Table 1.

Table 1 Properties of the FGM components

4.1 Convergence and validation of the present solution

Three test examples have been solved to show the efficacy and proficiency of the present solution along with the convergence and comparison studies. The obtained results are compared with those available in the literature. The numerical results are presented in the graphical and tabular form.

Example 1 The first example is performed for Al/Al₂O₃ square FGM plates with simply supported (SSSS) boundary condition for different values of the power law index ‘n’. The non-dimensional fundamental frequency $(\bar{\omega })$ obtained by present model are compared with those given by Belabed et al. (2014) as shown in Table 2. In Ref (Belabed et al. 2014) higher -order shear and normal deformation theory with five unknowns has been used to investigate the vibration response of FGM plate. They employed Hamilton’s principle to drive the governing equation of motion and frequency parameters have been calculated using Navier solution. The comparison study confirms that the present results are in excellent agreement with those generated by Belabed et al. (2014) even though the present model consist only four unknowns. It is also clear from the convergence study that the performance of the present formulation is good in terms of solution accuracy and the rate of convergence with mesh refinement. Based on the convergence study, in the present analysis the results are obtained at (6 × 6) mesh size, and otherwise stated.

Table 2 Comparison of linear frequency parameter $\left( {\bar{\omega } = \omega (a^{2} /h)\sqrt {\rho_{c} /E_{c} } } \right)$ for Al/Al₂O₃ (SSSS) FGM plate with different mesh size for a/h = 10

Example 2 In this example, the central deflection (w _c ) of (SSSS) Al/ZrO₂ square FGM plates with varying volume fraction indexes (n) is computed and compared with the results given by Talha and Singh (2010). The material properties of the constituent material are Em = 70 GPa N/m², $\rho_{m}$ = 2702 kg/m³ for aluminium (Al), and E _c  = 151 GPa, $\rho_{c}$ = 5700 kg/m³ for zirconia (ZrO₂). Talha and Singh (2011) used polynomial based higher-order shear deformation theory with thirteen DOF per node. It is clearly from the Fig. 3 that the solution accuracy is good for the static response for different values of volume fraction index.

Fig. 3

Comparison of central deflection of Al/ZrO₂ FGM plate

Example 3 To verify the effectiveness of the present formulation in dealing with flexural and vibration analysis of FGM plate with porosity, a convergence study is conducted in terms of different mesh size. The analysis is performed for Simply supported Ti–6Al–4V/Si₃N₄ FGM plates having a/h ratio equals to 10 with various volume fraction indices (n = 0, 1 and 10). The material properties of the constituent material are E _m  = 105.7 GPa, $\rho_{m}$ = 4429 kg/m³ for Ti–6Al–4V, and E _c  = 322.27 GPa, $\rho_{c}$ = 2370 kg/m³ for Si₃N₄. Effective material properties of FGM plate with porosity have been calculated using the mathematical expression given in Eq. (6). The non-dimensional frequency parameter is calculated using mesh sizes from (2 × 2) to (6 × 6) for different volume fraction indexes ‘n’. It is clear from the Fig. 4 that the present solution shows the excellent convergence for the frequency parameter of FGM plate with porosity.

Fig. 4

Convergence for the non-dimensional frequency of FGM plate with porosity (λ: porosity volume fraction; n: volume fraction index)

4.2 Parametric studies

In the view of the preceding discussion, it is observed that the present formulation delivers results which are in good agreement with various existing shear deformation theories of the FGM plate. In the subsequent section, the parametric studies have been carried out to explore the influence of various homogenization techniques, gradation rules, porosity volume fraction, volume fraction index, and geometric configuration on the flexural and vibration response of FGM plate.

4.2.1 Vibration analysis of FGM plate

In Table 3, the frequency parameter of fully clamped square Ti–6Al–4V/Si₃N₄ FGM plate is presented for side to thickness ratio and volume fraction indexes (n). The influence of two micromechanics model (Mori–Tanaka and Voigt model) on the frequency parameter is also discussed in the results. The non-dimensional frequency parameter is assumed as $\left( {\bar{\bar{\omega }} = \omega \left( {{{a^{2} } \mathord{\left/ {\vphantom {{a^{2} } h}} \right. \kern-0pt} h}} \right)\sqrt {{{\rho_{c} } \mathord{\left/ {\vphantom {{\rho_{c} } {E_{c} }}} \right. \kern-0pt} {E_{c} }}} } \right)$. The material properties of the constituent material are E _m  = 105.7 GPa, $\rho_{m}$ = 4429 kg/m³, υ _m  = 0.298 for Ti–6Al–4V, and E _c  = 322.27 GPa, $\rho_{c}$ = 2370 kg/m³, υ _c  = 0.25 for Si₃N₄. It is perceived from the results that by increasing side to thickness ratio, the frequency parameter increases. It is also found that the frequency parameter decreases with increase in volume fraction index ‘n’. It is evident from the results that Voigt and Mori–Tanaka models delivers same results for an isotropic plate (n = 0), whereas very small changes are seen for the rest of the values of volume fraction index ‘n’. It is observed from the results that the maximum percentage difference between the two models is 4.23%.

Table 3 Comparison of frequency parameter of (CCCC) FGM plate (Ti–6Al–4V/Si₃N₄) for various volume fraction index ‘n’ and side to thickness ratio (M–T: Mori–Tanaka)

Tables 4, 5 and 6 show the effect of various side to thickness ratios and volume fraction index on the frequency parameter of SCSC, SSSS, and CFSF FGM plate respectively. This shows the consistent behavior as discussed in the former section. Again, the maximum percentage difference in the results obtained from two different homogenization techniques (Voigt and M–T) is 4.07%. It is notable that the Mori–Tanaka model slightly overpredicts the frequency ratio as compared to Voigt model. In the succeeding sections, only Voigt model is used to compute the effective material properties of FGM plate.

Table 4 Comparison of frequency parameter of (SCSC) FGM plate (Ti–6Al–4V/Si₃N₄) for various volume fraction index ‘n’ and side to thickness ratio (M–T: Mori–Tanaka)

Table 5 Comparison of frequency parameter of (SSSS) FGM plate (Ti–6Al–4V/Si₃N₄) for various volume fraction index ‘n’ and side to thickness ratio (M–T: Mori–Tanaka)

Table 6 Comparison of frequency parameter of (CFSF) FGM plate (Ti–6Al–4V/Si₃N₄) for various volume fraction index ‘n’ and side to thickness ratio (M–T: Mori–Tanaka)

In Fig. 5a, the influence of aspect ratio (b/a) and volume fraction index ‘n’ on the frequency parameter of fully clamped FGM plate is shown. It is evident from the figure that the frequency parameter decreases with increases in aspect ratio and volume fraction index. Figure 5b–d present the variation of frequency parameter of FGM plate with aspect ratio for SCSC, SSSS, and CFSF boundary conditions respectively. It is observed form the results that for CCCC FGM plate, the frequency parameter decreases up to 33% when aspect ratio increases from 1 to 3, on the other hand, this reduction in the frequency parameter is approximately 88% for CFSF FGM. Therefore, it can be concluded that the influence of aspect ratio is more on the plate having fewer boundary constraints.

Fig. 5

Non-dimensional frequency versus aspect ratio for different volume fraction index ‘n’

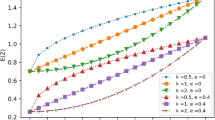
Figure 6a–d represent the effect of porosity on the non-dimensional frequency parameter of CCCC, SCSC, SSSS, and CFSF FGM plate respectively. It is observed that the frequency increases as the porosity volume fraction (λ) increase for all the boundary conditions considered herewith. It is perceived that the range of percentage increment in frequency parameter is approximately 0.5–1.5% for a/h = 5, whereas this value is increased to nearly 3.8% for a/h = 100. Hence, it is concluded that the thin plate is more sensitive to porosity as a comparison to the thick plate.

Fig. 6

Non-dimensional frequency versus side to thickness ratio for different porosity volume fraction (λ)

In Fig. 7a–d, the influence of porosity on the frequency parameter is demonstrated with the variation of volume fraction index for various boundary constraints. From the obtained results, it is noticed that the when the FGM plate is fully ceramic (n = 0), frequency parameter increases as the porosity volume fraction. But as the metal constituent increases (‘n’ increases from 1 to 10) in the FGM plate, frequency parameter decreases as the porosity volume fraction increases. It is apparent that the maximum change in the frequency is approximately 11% due to porosity when ‘n’ is 0 but this value is nearly 6% of the higher value of ‘n’.

Fig. 7

Non-dimensional frequency versus volume fraction index for different porosity volume fraction (λ)

4.2.2 Flexural response

In this section, the flexural response is performed for the FGM plate made of Ti–6Al–4V/Si₃N₄ with porosity. The transverse displacement (w), thickness coordinate (z) and the pressure (Q) applied to the top surface of the plate are presented in nondimensionalized form as

$$\bar{w} = {w \mathord{\left/ {\vphantom {w h}} \right. \kern-0pt} h},\,\,Q = {{qa^{4} } \mathord{\left/ {\vphantom {{qa^{4} } {E_{m} }}} \right. \kern-0pt} {E_{m} }}h^{4} \,\,,\bar{z} = {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0pt} h}$$

(23)

Figure 8a–b depicts the variation of non-dimensional central deflection of (Ti–6Al–4V/Si₃N₄) fully clamped FGM plate with side to thickness ratio and porosity volume fraction for n = 0 and 10. It is manifest from the results that the central deflection decreases with increase a/h ratio up to a certain limit (a/h = 50) beyond this no substantial change in the deflection occurs. It is also observed that the central deflection increases with porosity volume fraction (λ). In Fig. 8c–h, central deflection is plotted against the side to thickness ratio and porosity volume fraction with n = 0 and 10 for SCSC, SSSS, and CFSF boundary conditions respectively. In all the cases, the flexural response reflects the consistent behavior as discussed for Fig. 8a–b.

Fig. 8

Variation of central deflection with side to thickness ration and porosity volume fraction index (λ) for FGM plate (n = 1 and 10)

In Fig. 9a–d, the effect of porosity and volume fraction index on the central deflection of FGM plate is investigated for various boundary conditions. It is observed that the change in central deflection is ranged from 5 to 10% when porosity volume fraction increases from 0 to 0.4 for fully ceramic FGM plate (n = 0), whereas this percentage change is reduced to only 18–52% for the higher values of ‘n’. Therefore, it is concluded that the flexural response is significantly influenced by the porosity in the FGM plate having more volume fraction of ceramic.

Fig. 9

Variation of central deflection with volume fraction index and porosity volume fraction (λ) for FGM plate

5 Conclusions

The flexural and vibration response of functionally graded plate with porosity is analyzed using recently developed nonpolynomial higher-order shear and normal deformation theory to ensure its efficiency and applicability. This theory satisfies not only the shear stress-free boundary conditions at the top and bottom surfaces of the plate but also accommodate the thickness stretching effects. The new mathematical model is developed through the reformulation of the rule of mixture to incorporate the porosity phase in the material properties. Finite element formulation has been carried out using C⁰ isoparametric element with 72 degrees of freedom per element. Several significant effects of volume fraction of porosity, volume fraction index, geometric configuration, homogenization techniques and boundary conditions on the flexural and vibration characteristics of FGM plate are investigated. The whole analysis concludes with some significant observations that are summarized as follows:

• Porosity volume fraction is an essential parameter in structural component design. The frequency increases as the porosity volume fraction increases.

• The effect of porosity is prominent in metal whereas its effect weakens as ceramic content in the FGM plate increases.

• The effect of porosity is perceptible in thin plates.

• The presence of porosity leads to increase the deflection in all the boundary conditions considered in the present study.

• Significant changes in deflection and frequency observed for a/h < 50, but for a/h > 50 no notable changes observed in deflection and frequency.

Appendix

Notation and description of various entities associated in mathematical modelling of structural kinematics

a, b, h	Length, width and thickness of the FGM plate	E	Effective Young’s modulus
x, y, z	Cartesian coordinate	ρ	Effective mass density
u o , v o , w b	Mid-plane displacements	υ	Poisson’s ratio
w	Transverse displacement component	$\left[ {\mathbf{M}} \right]$	Mass matrix
κ	Shape parameter	$\left[ {\mathbf{K}} \right]$	Stiffness matrix
ɛ	Linear strain vector	ω	Natural frequency
V c	Volume fraction of ceramic	$\bar{w}$	Central deflection
V m	Volume fraction of metal	λ	Porosity volume fraction

$$\left[ {{\mathbf{\bar{\mathcal{N}}}}} \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {\varOmega_{1} (z)} & 0 & 0 & {\varOmega_{2} (z)} & 0 \\ 0 & 1 & 0 & 0 & {\varOmega_{1} (z)} & 0 & 0 & {\varOmega_{2} (z)} \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & {\varOmega_{3} (z)} \\ \end{array} } \right]$$

$$\varOmega_{1} (z) = - z,\,\,\,\,\,\varOmega_{2} (z) = \psi Sinh^{ - 1} \left( {\frac{\kappa z}{h}} \right) - \left( {\frac{\kappa \psi }{h}} \right),\,\,\,\,\,\,\varOmega_{3} (z) = \kappa Cosh^{2} \left( {\frac{\kappa z}{h}} \right)$$

$$\left[ {\,{\mathbf{M}}\,} \right]\,\, = \,\,\left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & z & 0 & 0 & {\varOmega_{2} (z)} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & z & 0 & 0 & {\varOmega_{2} (z)} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\varOmega_{3}^{\prime } (z)} \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\varOmega_{3} (z)} & 0 & {\varOmega_{3}^{\prime } (z)} & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\varOmega_{3} (z)} & 0 & {\varOmega_{3}^{\prime } (z)} & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & Z & 0 & 0 & {\varOmega_{2} (z)} & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]$$