1 Introduction

High-performance, microscopically inhomogeneous functionally graded materials (FGMs) have tailored composition and structural gradients with specified attributes in the chosen orientation. The FGM is created by progressively changing the composition of two materials, such as metal-ceramic. In contrast to traditional composite materials, the continuous and smooth fluctuation of the volume fractions of the two or more constituent materials in FGM eliminates the debonding between the interfaces under high loading situations. Because of these potential benefits, FGM is used for various applications such as aerospace, nuclear, civil, automotive, medical and construction [1,2,3]

Many researchers have studied the influence of various geometric parameters and boundary conditions on FGM plates for flexural and vibration responses[4, 5]. In this context, Gupta and Talha [6] examined the vibration and bending response of functionally graded plates using non-polynomial-based higher-order shear and normal deformation theory. Singh and Gupta [7] reported the influence of various cutouts and geometrical imperfections using sine and global type imperfection on the vibration response for the FGM sandwich plate using the finite element method (FEM) appoach. The authors explained the trend of frequency parameters for various parameters such as geometric imperfection, boundary condition, and volume fraction index. Zhao et al. [8] performed a study based on FEM on the porous rectangular plate using improved Fourier series using first order shear deformation theory (FSDT) for a different porosity model. According to a thorough study of the literature, a significant amount of research on strcutural response of FGM strucutres have been carried out based on approximate and closed-form solution. Most of the work reported in the literature comprises the perfect plates (without porosity and voids). However, porosities or micro voids are inevitable in FGM which comes within the structures during the manufacturing process [9, 10]. The strength of the FGM plates is reduced due to porosity and voids [11].Therefore, it is required to include porosity inclusion effect while analyzing the vibration characteristics of FGM plates. Thus, in the present work, dynamic stiffness method (DSM) is implemented to characterize the exact frequency response of porous FGM plates based on CPT in conjunction with physical neutral surface (PNS).

The dynamic stiffness method (DSM) [12] provides the exact, effective and reliable solutions to the different structural analysis. The DSM is the semi analytical method and this method has some resemblances with the finite element method (FEM) in certain aspect. The assembly procedure is the same for DSM and FEM. However, the fundamental distinction between them is the discretization approach. Different stiffness and mass matrices are created by discretizing a structural element based on its assumed shape functions in the case of FEM. In DSM, a single-element matrix comprising both stiffness and mass properties is generated by employing proper frequency-dependent form functions derived from the governing differential equation of the structural element undergoing free vibration. DSM solutions are exact since they are based on the analytical formulation of the governing differential equations. Some important literature related to DSM for plate vibration analysis is discussed in the next paragraph.

In the early 1970s, Wittrick and Williams [13] published the first study on the implementation of DSM to investigate the vibration and buckling of isotropic and anisotropic plates. Then after, many authors establishes the dynamic stiffness matrices and providing their view to researchers interested in structural analysis, But no one have discussed the general systematic approach. Thus, in the year of 1997, Boscolo and Banerjee [14] proposed a generic approach to create dynamic stiffness matrices for structural components. The authors also demonstrated that processing time might be saved using DSM analytical expressions instead of numerical approaches. Banerjee and co-authors [15,16,17] extensively employed the dynamic stiffness formulation in the vibration analysis of isotropic, orthotropic, or laminated plates using various plate theories and for varied set of boundary conditions. The authors [18, 19] developed the dynamic stiffness technique, which they applied to successfully forecast the frequency response of composite plates and plate assemblies based on several plate theories for a range of combinations of edge circumstances, in a few research publications. Recently, Kumar and Jana [20,21,22] applied the DSM technique for the vibration analysis of uniform and stepped FGM plates based on CPT theory with consideration of PNS.

The DSM is regarded as a reliable and efficient approach that may be used instead of the more popular finite element method (FEM). It is already demonstrated by various authors that processing time might be saved using DSM analytical expressions instead of numerical approaches. In their studies, many researchers have used DSM for free vibrations for isotropic and composite plates under various boundary conditions. The present work examines the influence of porosity in functionally graded materials using the DSM technique. The equilibrium equation is derived using Hamilton's principle, whereas the governing equation is developed using CPT based displacement assumptions along with the concept of physical neutral surface. The present methodology has been validated with the literature for its accuracy. The non-dimensional frequency parameter (NDFP) has been examined for the even porosity, with different volume fraction indexes and boundary conditions i.e., SSSS, SCSC, and SSSC. The effect of the porosity on the higher mode is also discussed.

2 Material and methodology

2.1 Geometrical configuration

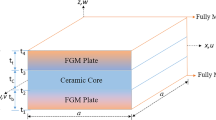
The side-to-side (a/b) and side-to-height (a/h) ratios of the plate are assumed to be 1 and 0.001, respectively. The coordinate system and plate represented in Fig. 2 are used for the mathematical formulation.

2.2 Material properties

The Al-ZrO2 metal-ceramic FGM used in this work has the parameters listed in Table 1. The variation in the material properties of the plate, particularly density (ρ) and Young's modulus (E) is given as illustrated in Eq. 1. Figure 1 depicts Young's modulus and the (z/h) ratio for various volume fraction index (k) and porosity volume fraction index (e).

Table 1 Material properties of Al and ZrO2 [23]
Full size table
Fig. 1
figure 1

Material properties variation with height for different k and e values

Full size image

2.3 Effective material property

The FGM is created by continually changing the constituents of multiphase materials according to a specified gradation law. The modified power law [24] has been employed in the current work to evaluate the effective properties (p(z)) generally young modulus and density of the FGM plate as shown in Eq. (1).

$$ p(z) = (p_{c} - p_{m} )(z/h + 1/2)^{k} + p_{m} - (e/2)(p_{c} + p_{m} ) $$
(1)

where (pc) is the ceramic properties, (pm) is the metal properties, and (e) is the volume fraction. e signifies the amount of porosity present in the material, generally, the value of e lies between 0 to 0.4, 0 depicting no porosity or perfect plate and 0.4 representing maximum porosity in the material.

2.4 Displacement field

The displacement field assumption based on classical plate theory (CPT) of porous FGM plate is as follows [25].

$$ u(x,y,z) = u_{0} (x,y) - z\frac{dw}{{dx}} $$
$$ v(x,y,z) = v_{0} (x,y) - z\frac{dw}{{dy}} $$
(2)
$$ w(x,y,z) = w_{0} (x,y) $$

FGM plates are non-homogeneous, so their physical neutral surface does not coincide with the geometrical neutral surface [20]. The coordinate system with a physical neutral surface (zns = z-z0) is introduced, where z0 is the distance between natural and geometrical neutral surfaces, as shown in Fig. 2. The reference plane is defined by (zns), which will neglect the effect of the in-plane displacement components. The modified equation of the CPT can be written as follows.

$$ u(x,y,z) = z_{ns} \frac{dw}{{dx}} = - (z - z_{0} )\frac{dw}{{dx}} $$
$$ v(x,y,z) = z_{ns} \frac{dw}{{dy}} = - (z - z_{0} )\frac{dw}{{dy}} $$
(3)
$$ w(x,y,z) = w_{0} (x,y) $$
Fig. 2
figure 2

FGM plate with the physical and geometric middle surface [20]

Full size image

The strain field can be calculated using the following equations.

$$ \varepsilon_{ii} = - z_{ns} \left( {\frac{{d^{2} w}}{{dx^{2} }}} \right),\varepsilon_{jj} = - z_{ns} \left( {\frac{{d^{2} w}}{{dy^{2} }}} \right),\gamma_{ij} = - 2z_{ns} \left( {\frac{{d^{2} w}}{dxdy}} \right) $$
(4)

In the above equation the \({\epsilon }_{ii}\),\({\epsilon }_{jj}\) Represent normal strain in x and y directions and \({\gamma }_{xy}\) Represent shear strain in the xy plane. The stress–strain relation can be developed using the generalized hooks law, as shown in Eq. 5.

$$ \left[ {\begin{array}{*{20}c} {\sigma_{ii} } \\ {\sigma_{jj} } \\ {\tau_{ij} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {q_{11} } & {q_{12} } & 0 \\ {q_{21} } & {q_{22} } & 0 \\ 0 & 0 & {q_{16} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{ii} } \\ {\varepsilon_{jj} } \\ {\gamma_{ij} } \\ \end{array} } \right] $$
(5)

where \({\sigma }_{ii}\) and \({\sigma }_{jj}\) are the normal stress and \({\tau }_{xy}\) is shear stress that is related to strain using constitutive law. The element of the material constituents is evaluated using the following equations.

$$ q_{11} = q_{22} = E(z_{n} s)/(1 - \mu^{2} )\,\,\,,q_{12} = q_{21} = \mu E(z_{n} s)/(1 - \mu^{2} ),\,\,\,q_{66} = \mu E(z_{n} s)/(1 + \mu^{{}} ) $$
(6)

As illustrated in Eq.  13, the neutral surface (z0) is obtained by equating the summation of forces at the cross section for Fx or Fy to zero.

$$ \sum\limits_{{}}^{{}} {F_{x} } = \int_{{\frac{ - h}{2} - z_{0} }}^{{\frac{h}{2} - z_{0} }} {\sigma_{xx} dA} = 0 $$
(7)
$$ z_{0} = \frac{{\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {E\left( z \right)zdz} }}{{\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {E\left( z \right)dz} }} $$
(8)
$$ = \frac{{hk(E_{c} - E_{m} )}}{2(k + 2)} = \frac{{hk(E_{rat} - 1)}}{{2(k + 2)(E_{rat} + k)}} $$
(9)

The value of the non-dimensional \(({z}_{0}/h)\) depends on both volume fraction (k) and young's modulus ratio \({E}_{rat}={E}_{c}/{E}_{m}\).

\({u}_{0}\) and \({v}_{0}\) indicate the plane's displacement, while \({w}_{0}\) represents the plate's displacement in the transverse direction as shown in Eq. 3. The plates' governing Eq. 10 are developed using Hamilton's principle, as stated in [26].

$$ D_{eq} \left( {\frac{{\partial^{4} w_{0} }}{{dx^{4} }} + 2\frac{{\partial^{4} w_{0} }}{{dx^{2} dy^{2} }} + \frac{{\partial^{4} w_{0} }}{{dx^{4} }}} \right) + I_{0} \left( {\frac{{\partial^{2} w_{0} }}{{dt^{2} }}} \right) - I_{2} \left( {\frac{{\partial^{4} w_{0} }}{{dx^{2} dt^{2} }} + \frac{{\partial^{2} w_{0} }}{{dy^{2} dt^{2} }}} \right) = 0 $$
(10)

The shear force and bending moment can be expressed in the form of a differential equation with only one variable, that is \({w}_{0}\) as given below

$$ V_{x} = - D_{eq} \left( {\frac{{\partial^{3} w_{0} }}{{dx^{3} }} + (2 - v)\left( {\frac{{\partial^{3} w_{0} }}{{dxdy^{2} }}} \right) + I_{2} \left( {\frac{{\partial^{3} w}}{{dxdt^{2} }}} \right)} \right)\delta w $$
(11)
$$ M_{xx} = - D_{eq} \left( {\frac{{\partial^{2} w_{0} }}{{dx^{2} }} + v\frac{{\partial^{2} w_{0} }}{{dy^{2} }}} \right)\varphi_{y} $$
(12)

\({w}_{0}\) is chosen in such a way that it can satisfy the Levy-type boundary condition [27]

$$ w_{0} (x,y,t) = \sum\limits_{m = 1}^{m = \infty } {w_{m} (x)e^{i\omega t} } sin(\alpha_{m} y) $$
(13)

where \(\omega \) is the angular frequency, \({w}_{m}\) maximum amplitude,\({\propto }_{m}=m\pi /L\) and m = 1,2…………\(\infty \)

The roots of the constructed differential Eq. 10 represent the natural frequency. Depending on the value of \({\propto }_{m}.\) There are two alternative solutions. [20]. The dynamic stiffness (DS) matrix formulation for case 1 is illustrated below. For case 2, the equation can be derived in the same way as it is for case 1.

Case 1 \(\left( {\alpha_{m} - \frac{{I_{2} \omega^{2} }}{{D_{eq} }}} \right) \ge \sqrt {\left( {(\frac{{I_{2} \omega^{{_{2} }} }}{{D_{eq} }})^{2} + \left( {\frac{{I_{0} \omega^{{_{2} }} }}{{D_{eq} }}} \right)} \right)}\)

$$ r_{1m} = \pm \sqrt {\left( {\alpha_{m} - \frac{{I_{2} \omega^{2} }}{{D_{eq} }}} \right) + \left( {\left( {\frac{{I_{2} \omega^{{_{2} }} }}{{D_{eq} }}} \right)^{2} + \left( {\frac{{I_{0} \omega^{{_{2} }} }}{{D_{eq} }}} \right)} \right)} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,r_{2m} = \pm \sqrt {\left( {\alpha_{m} - \frac{{I_{2} \omega^{2} }}{{D_{eq} }}} \right) - \left( {\left( {\frac{{I_{2} \omega^{{_{2} }} }}{{D_{eq} }}} \right)^{2} + \left( {\frac{{I_{0} \omega^{{_{2} }} }}{{D_{eq} }}} \right)} \right)} $$
(14)
$$ w_{m} (x) = A{}_{m}\cosh (r_{1m} x) + B_{m} \sinh (r_{1m} x) + C_{m} \cosh (r_{2m} x) + D_{m} \sinh (r_{2m} x) $$
(15)

The boundary condition for displacement and rotation is imposed on the plates. [20]

$$\begin{aligned}& x = 0,\,\,\,\,\,\,\,\,\,w_{m} = w_{a} ,\varphi_{ym} = \varphi_{ya} ,\\ & x = b,w_{m} = w_{b} ,\varphi_{ym} = \varphi_{yb}\end{aligned}$$
(16)

Similarly, force and moment at the boundaries of the plate is

$$ x = 0,\,\,\,V_{xm} = - v_{a} ,\,M_{xxm} = - m_{a} \,,\,x = b,v\,_{xm} = - v_{b} \,,\,M_{xxm} = - m_{b} $$
(17)

Appling boundary conditions for deflection and rotation at a and b (where a and b are coordinates of the boundary of the plate) are used to calculate the following matrices for deflection and rotation. [20];

$$ \left[ \begin{gathered} w_{a} \hfill \\ \varphi_{yb} \hfill \\ w_{b} \hfill \\ \varphi_{yb} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 1 & 0 \\ 0 & { - r_{1m} } & 0 & { - r_{2m} } \\ {c_{h1} } & {S_{h1} } & {C_{h2} } & {C_{h2} } \\ { - r_{1m} S_{h1} } & { - r_{1m} C_{h1} } & { - r_{2m} S_{h2} } & { - r_{2m} C_{h2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {A_{m} } \\ {B_{m} } \\ {C_{m} } \\ {D_{m} } \\ \end{array} } \right] $$
(18)

where \(C_{hi} = \cosh (r_{i} b),\,\,\,\,\,S_{hi} = \sinh (r_{i} b),\,C_{i} = \cos (r_{im} b)\,\,and\,S_{i} = \sin (r_{im} b)\,,\,i = 1,2\)

The above matrix as shown in Eq. 18 can be represented as

$$ X = AC $$
(19)

Similarly, Boscolo and Banerjee's Eq. 20 depicts the shear force and bending matrix, calculated using the boundary conditions of the shear force and the bending moment in a and b [15].

$$ \left[ \begin{gathered} v_{a} \hfill \\ m_{a} \hfill \\ v_{b} \hfill \\ m_{b} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 1 & 0 \\ {L_{1} } & 0 & {L_{1} } & 0 \\ { - R_{1} S_{h1} } & { - R_{1} C_{h1} } & { - R_{2} C_{h2} } & { - R_{2} C_{h2} } \\ { - L_{1} C_{h1} } & { - L_{1} S_{h1} } & { - L_{2} C_{h2} } & { - L_{2} S_{h2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {A_{m} } \\ {B_{m} } \\ {C_{m} } \\ {D_{m} } \\ \end{array} } \right] $$
(20)

where \( R_{i} = D_{{res}} (r^{3} - (2 - \mu )\alpha ^{2} r_{{im}} ) + r_{{im}} I_{2} \omega ^{2} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} L_{i} = D_{{res}} (r^{2} - \mu \alpha ^{2} ),{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} i = 1,2 \)

The equation can be written as

$$ F = SC $$
(21)

DSM is calculated using the analogy of F = KX and comparing the equation from X = AC and F = SC. The DSM is evaluated as shown in Eq. 22.

$$ DSM = SA^{ - 1} $$
(22)

3 Result and discussion

3.1 Validation study

To verify the present formulation, a validation study has been performed. The results obtained from the present methodology have been compared with those of Uymaz and Aydogdu [28]. The authors employed a 3D exact solution to determine the natural frequency of the Al/ZrO2 (Aluminum-Zirconia) FGM plate. The NDFP used is (\((\varpi )^{2} = \frac{{(12(1 - v^{2} )\rho_{m} \omega^{2} ab)}}{{(\pi^{4} E_{c} h^{2} )}}\)) reported in the graph. The comparative results have been shown in Fig. 3 and are found to be in good agreement with the literature.

Fig. 3
figure 3

Effect of side-to-height (a/h) and volume fraction on NDFP

Full size image

3.2 Parametric study

The NDFP of functionally graded materials is investigated using the dynamic stiffness technique. The influence of the porosity volume fraction index, volume fraction, and boundary condition on the vibration response has been investigated. This work present the first three bending modes of vibration and three boundary conditions: SSSS, SCSC, and SSSC.

Figure 4 depicts the effect of various volume fraction indexes and porosity volume fractions on the higher modes of vibration (NDFP) of FGM plates with SSSS boundary condition. The analysis is performed on a square FGM plate with a side-to-height (a/h) ratio of 0.001 whereas the material properties as given in Table 1. It is observed that the NDFP increases with the porosity volume fraction increase for the ceramic plate (k = 0). Also, the NDFP decreases with the metallic content incrases in the FGM plates (k > 0). This is expected because for ceramic, as porosity volume fraction increases, the decreament in the stiffness of the plate is less than the decreament in density. Consequently, the ratio of stiffness to mass increases. Whereas for volume fraction (k > 0) as porosity increase the stiffness decrease considerably as compared to density hence the NDFP decreases. [29]

Fig. 4
figure 4

NDFP vs. Frequency modes for SSSS boundary condition

Full size image

The variation of the the NDFP of FGM plate with the SCSC boundary condition is shown in Fig. 5a. As the clamped boundary conditions restrict rotational and displacement degrees of freedom, the frequency value is greater than the SSSS boundary conditions. The result of the SSSC boundary condition is shown in Fig. 5b. It has a greater frequency than the SSSS but a lower frequency than the SCSC. For the SSSS boundary condition, Fig. 6 shows the plot between NDPF and higher vibration modes. The impact of porosity on lower vibration modes is small, but increases for higher vibration modes. The effects of porosity on higher modes of vibration under varied boundary conditions are shown in Fig. 7a and b. Again, the results confirms that the influence of porosity in more on the higher modes of vibration for both the boundary conditions considered herewith.

Fig. 5
figure 5

NDFP vs. Frequency modes for various boundary conditions

Full size image
Fig. 6
figure 6

NDFP vs. Modes of vibration for various porosity and volume fraction indexes for SSSS boundary condition

Full size image
Fig. 7
figure 7

NDFP vs. Modes of vibration for various porosity and volume fraction indexes for SCSC and SSSC boundary condition

Full size image

4 Conclusion

The present study shows the effect of porosity on different volume fractions and boundary conditions on the NDFP of FGM plates. It has been found that the porosity in the FGM material has a prominent effect on the natural frequency. The key outcomes of the present research are stated below.

  1. 1.

    Effect of the porosity is proportional to the value of the k.

  2. 2.

    NDFP increase for pure ceramics with the inclusion of the porosity however the influence of porosity is opposite for k \(\ge\) 1.

  3. 3.

    NDPF have higher values for the SCSC and SSSC as compared to SSSS due to more restrictions at the boundaries.