Recurrent segmentation meets block models in temporal networks

Abstract

A popular approach to model interactions is to represent them as a network with nodes being the agents and the interactions being the edges. Interactions are often timestamped, which leads to having timestamped edges. Many real-world temporal networks have a recurrent or possibly cyclic behaviour. In this paper, our main interest is to model recurrent activity in such temporal networks. As a starting point we use stochastic block model, a popular choice for modelling static networks, where nodes are split into R groups. We extend the block model to temporal networks by modelling the edges with a Poisson process. We make the parameters of the process dependent on time by segmenting the time line into K segments. We require that only $H \le K$ different set of parameters can be used. If $H < K$, then several, not necessarily consecutive, segments must share their parameters, modelling repeating behaviour. We propose two variants where a group membership of a node is fixed over the course of entire time line and group memberships are allowed to vary from segment to segment. We prove that searching for optimal groups and segmentation in both variants is NP-hard. Consequently, we split the problem into 3 subproblems where we optimize groups, model parameters, and segmentation in turn while keeping the remaining structures fixed. We propose an iterative algorithm that requires $\mathcal {O} \left( KHm + Rn + R^2\,H\right)$ time per iteration, where n and m are the number of nodes and edges in the network. We demonstrate experimentally that the number of required iterations is typically low, the algorithm is able to discover the ground truth from synthetic datasets, and show that certain real-world networks exhibit recurrent behaviour as the likelihood does not deteriorate when H is lowered.

1 Introduction

A popular approach to model interactions between set of agents is to represent them as a network with nodes being the agents and the interactions being the edges. Naturally, many interactions in real-world datasets have a timestamp, in which case the edges in networks also have timestamps. Consequently, developing methodology for temporal networks has gained attention in data mining literature (Holme & Saramäki, 2012).

Many temporal phenomena have recurrent or possibly cyclic behaviour. For example, social network activity may be heightened during certain hours of day. Our main interest is to model recurrent activity in temporal networks. As a starting point we use stochastic block model, a popular choice for modelling static networks. We can immediately extend this model to temporal networks, for example, by modelling the edges with a Poisson process. Furthermore, Corneli et al. (2018) modelled the network by also segmenting the timeline and modelled each segment with a separate Poisson process.

To model the recurrent activity we can either model it explicitly, for example, by modelling explicitly cyclic activity, or we can use more flexible approach where we look for segmentation but restrict the number of distinct parameters. Such notion was proposed by Gionis and Mannila (2003) in the context of segmenting sequences of real valued vectors.

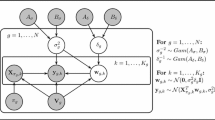
In this paper we extend the model proposed by Corneli et al. (2018) using the ideas proposed by Gionis and Mannila (2003). More formally, we consider the following problem: given a temporal graph with n nodes and m edges, we are looking to partition the nodes into R groups and segment the timeline into K segments that are grouped into H levels. Note that a single level may contain non-consecutive segments. An edge $e = (u, v)$ is then modelled with a Poisson process with a parameter $\lambda _{ijh}$, where i and j are the groups of u and v, and h is the level of the segment containing e.

This paper is an extension of a conference paper (Arachchi & Tatti, 2022). The model considered in the conference version did not allow node groups to vary over time. We extend the approach in this paper by also considering a variant where the node groups depend on the level.

To obtain good solutions for both of the variants, we rely on an iterative method by splitting the problem into three subproblems: (i) optimize groups while keeping the remaining parameters fixed, (ii) optimize model parameters $\Lambda$ while keeping the groups and the segmentation fixed, (iii) optimize the segmentation while keeping the remaining parameters fixed. We approach the first subproblem by iteratively optimizing group assignment of each node while maintaining the remaining nodes fixed. We show that such single round can be done in $\mathcal {O} \left( m + Rn + R^2H + K\right)$ time, where n is the number of nodes and m is the number of edges. Fortunately, the second subproblem is trivial since there is an analytic solution for optimal parameters, and we can obtain the solution in $\mathcal {O} \left( m + R^2H + K\right)$ time. Finally, we show that we can find the optimal segmentation with a dynamic program. Using a stock dynamic program leads to a computational complexity of $\mathcal {O} \left( m^2KH\right)$. Fortunately, we show that we can speed up the computation by using a SMAWK algorithm (Aggarwal et al., 1987), leading to a computational complexity of $\mathcal {O} \left( mKH + HR^2\right)$.

In summary, we extend a model by Corneli et al. (2018) to have recurring segments. We prove that the two variants of our main problem is NP-hard as well as several related optimization problems where we fix a subset of parameters. Navigating around these NP-hard problems we propose an iterative algorithm where a single iteration requires $\mathcal {O} \left( KHm + Rn + R^2H\right)$ time, a linear time in edges and nodes.

The rest of the paper is organized as follows. First we introduce preliminary notation, the model, and the optimization problems in Sect. 2. We then proceed to describe the iterative algorithm in Sect. 3. We present the related work in Sect. 4. Finally, we present our experiments with both fixed-membership and level-dependent membership problems in Sect. 5 and conclude the paper with discussion in Sect. 6. The computational complexity proofs are provided in Appendix.¹

2 Preliminary notation and problem definition

Assume an undirected temporal graph $G = (V, E)$, where V is a set of nodes and E is a set of edges, where each edge is tuple (u, v, t) with $u,v \in V$ and t being the timestamp. We will use $n = {\left| V\right| }$ to denote the number of nodes and $m = {\left| E\right| }$ the number of edges. For simplicity, we assume that we do not have self-loops, though the models can be adjusted for such case. We write t(e) to mean the timestamp of the edge e. We also write N(u) to denote all the edges adjacent to a node $u \in V$.

Perhaps the simplest way to model a graph (with no temporal information) is with Erdos–Renyi model, where each edge is sampled independently from a Bernoulli probability parameterized with q. Let us consider two natural extensions of this model. The first extension is a block model, where nodes are divided into k groups, and an edge (u, v) are modelled with a Bernoulli probability parameterized with $q_{ij}$, where i is the group of u and j is the group of v. Given a graph, the optimization problem is to cluster nodes into groups so that the likelihood of the model is optimized. For the sake of variability we will use the words group and cluster interchangeably.

A convenient way of modelling events in temporal data is using Poisson process: Assume that you have observed c events with timestamps $t_1, \ldots , t_c$ in a time interval T of length $\Delta$. The log-likelihood of observing these events at these exact times is equal to $c\log \lambda - \lambda \Delta$, where $\lambda$ is a model parameter. Note that the log-likelihood does not depend on the individual timestamps.

If we were to extend the block model to temporal networks, the log-likelihood of c edges occurring between the nodes u and v in a time interval is equal to $c\log \lambda _{ij} - \lambda _{ij} \Delta$, where $\lambda _{ij}$ is the Poisson process parameter and i is the group of u and j is the group of v. Note that $\lambda _{ij}$ does not depend on the time, so discovering optimal groups is very similar to discovering groups in a static model.

A natural extension of this model, proposed by Corneli et al. (2018), is to make the parameters depend on time. Here, we partition the model into k segments and assign different set of $\lambda$s to each segment.

More formally, we define a time interval T to be a continuous interval either containing the starting point $T = [t_1, t_2]$ or excluding the starting point $T = (t_1, t_2]$. In both cases, we define the duration as $\Delta \left( T\right) = t_2 - t_1$.

Given a time interval T, let us define

$$\begin{aligned} c \left( u, v, T\right) = {\left| \left\{ e = (u, v, t) \in E \mid t \in T\right\} \right| } \end{aligned}$$

to be the number of edges between u and v in T.

The log-likelihood of Poisson model for nodes u, v and a time interval T is

$$\begin{aligned} \ell \left( u, v, T, \lambda \right) = c \left( u, v, T\right) \log \lambda - \lambda \Delta \left( T\right) . \end{aligned}$$

We extend the log-likelihood between the two sets of nodes U and W, by writing

$$\begin{aligned} \ell \left( U, W, T, \lambda \right) = \sum _{u, w \in U \times W} \ell \left( u, w, T, \lambda \right) , \end{aligned}$$

where $U \times W$ is a set of all node pairs $\left\{ u, w\right\}$ with $u \in U$ and $w \in W$ and $u \ne v$. We consider $\left\{ u, w\right\}$ and $\left\{ w, u\right\}$ the same, so only one of these pairs is visited.

Given a time interval $D = [a, b]$, a K-segmentation $\mathcal {T} = T_1, \ldots , T_K$ is a sequence of K time intervals, such that $T_1 = [a, t_1], T_2 = (t_1, t_2], \ldots T_i = (t_{i - 1}, t_{i}], \ldots$, and $T_{K} = (t_{K - 1}, b]$. For notational simplicity, we require that the boundaries $t_i$ must collide with the timestamps of individual edges. We also assume that D covers the edges. If D is not specified, then it is set to be the smallest interval covering the edges.

Given a K-segmentation, a partition of nodes $\mathcal {P} = P_1, \ldots , P_R$ into R groups, and a set of $KR(R + 1)/2$ parameters $\Lambda = \left\{ \lambda _{ijk}\right\}$,² the log-likelihood is equal to

$$\begin{aligned} \ell \left( \mathcal {P}, \mathcal {T}, \Lambda \right) = \sum _{i = 1}^R \sum _{j = i}^R \sum _{k = 1}^K \ell \left( P_i, P_j, T_k, \lambda _{ijk}\right) . \end{aligned}$$

This leads immediately to the problem considered by Corneli et al. (2018).

Problem 2.1

(SFix ) Given a temporal graph G, a time interval D, integers R and K, find a node partition with R groups, a K-segmentation, and a set of parameters $\Lambda$ so that $\ell \left( \mathcal {P}, \mathcal {T}, \Lambda \right)$ is maximized.

We should point out that for fixed $\mathcal {P}$ and $\mathcal {T}$, the optimal $\Lambda$ is equal to

$$\begin{aligned} \lambda _{ijk} = \frac{ c \left( P_i, P_j, T_k\right) }{{\left| P_i \times P_j\right| } \Delta \left( T_k\right) }. \end{aligned}$$

In this paper we consider an extension of (K, R) model. Many temporal network exhibit cyclic or repeating behaviour. Here, we allow network to have K segments but we also limit the number of distinct parameters to be at most $H \le K$. If we select $H < K$, then we are forcing that certain segments share their parameters, that is, we force repeating behaviour. We do not know beforehand which segments should share the parameters.

We can express this constraint more formally by introducing a mapping ${g}:{\left[ K\right] } \rightarrow {\left[ H\right] }$ that maps a segment index to its matching parameters. We can now define the likelihood as follows: given a K-segmentation, a partition of nodes $\mathcal {P} = P_1, \ldots , P_R$ into R groups, a mapping ${g}:{\left[ K\right] } \rightarrow {\left[ H\right] }$, and a set of $HR(R + 1)/2$ parameters $\Lambda = \left\{ \lambda _{ijh}\right\}$, the log-likelihood is equal to

$$\begin{aligned} \ell \left( \mathcal {P}, \mathcal {T}, g, \Lambda \right) = \sum _{i = 1}^R \sum _{j = i}^R \sum _{k = 1}^K \ell \left( P_i, P_j, T_k, \lambda _{ijg(k)}\right) . \end{aligned}$$

We will refer to g as level mapping.

This leads to the following optimization problem.

Problem 2.2

(RSFix ) Given a temporal graph G, a time interval D, integers R, H, and K, find a node partition with R groups, a K-segmentation, a level mapping ${g}:{\left[ K\right] } \rightarrow {\left[ H\right] }$, and parameters $\Lambda$ maximizing $\ell \left( \mathcal {P}, \mathcal {T}, g, \Lambda \right)$.

We will refer to this problem as fixed membership problem.

Next we extend the previous model by allowing group memberships to vary over time. More specially, group membership of a node is attached to a level, similar to $\Lambda$. Hence, a node partition which is constrained on level is denoted as $\mathcal {P} = \left\{ P_{ih}\right\}$. The log-likelihood of this new model is given by

$$\begin{aligned} \ell \left( \mathcal {P}, \mathcal {T}, g, \Lambda \right) = \sum _{i = 1}^R \sum _{j = i}^R \sum _{k = 1}^K \ell \left( P_{ig(k)}, P_{jg(k)}, T_k, \lambda _{ijg(k)}\right) . \end{aligned}$$

Problem 2.3

(RSDep ) Given a temporal graph G, a time interval D, integers R, H, and K, find a set of H partitions of nodes $\mathcal {P}_h = P_{1h}, \ldots , P_{Rh}$, for all $h = 1,\dots , H$, into R groups, a K-segmentation, a level mapping ${g}:{\left[ K\right] } \rightarrow {\left[ H\right] }$, and parameters $\Lambda$ maximizing $\ell \left( \mathcal {P}, \mathcal {T}, g, \Lambda \right)$.

We will refer to this problem as level-dependent membership problem.

Toy examples of both models is given in Fig. 1.

Fig. 1

Toy examples of models with 4 groups, 5 segments, and 3 levels. The lightness of the color in the matrices illustrates the parameters $\Lambda$ while the color indicates which segments share the same parameters. For illustrative purposes the node groups are shown as continuous regions in matrices

3 Fast algorithm for obtaining good model

In this section we will introduce an iterative, fast approach for obtaining a good model. The computational complexity of one iteration is $\mathcal {O} \left( KHm + Rn + R^2H\right)$, which is linear in both the nodes and edges.

3.1 Iterative approach

Unfortunately, finding optimal solution for RSFix and RSDep is NP-hard.

Proposition 1

Problems 2.2–2.3 are NP-hard, even for $H = K = 1$ and $R = 2$.

Proof of Proposition 1 is in Appendix.

Consequently, we resort to a natural heuristic approach, where we optimize certain parameters while keeping the remaining parameters fixed.

Algorithm 1

Main loop of the algorithm

We split RSFix into 3 subproblems as shown in Algorithm 1. First, we find good groups, then update $\Lambda$, and then optimize segmentation, followed by yet another update of $\Lambda$.

When initializing, we select groups $\mathcal {P}$ and parameters $\Lambda$ randomly, then proceed to find optimal segmentation, followed by optimizing $\Lambda$.

The following proposition states the the complexity of Algorithm 1, and it is proven in the following subsections.

Proposition 2

The computational complexity of a single iteration of Algorithm 1 is $\mathcal {O} \left( KHm + Rn + R^2H\right)$.

Proof

The proof follows from Lemmas 3.1, 3.2, and 3.3. $\square$

Next we will explain each step in details followed by their computational complexities. Finally, we describe the difference in algorithm for RSDep .

3.2 Finding groups

Our first step is to update groups $\mathcal {P}$ while maintaining the remaining parameters fixed. Unfortunately, finding the optimal solution for this problem is NP-hard.

Proposition 3

Finding optimal partition $\mathcal {P}$ for fixed $\Lambda$, $\mathcal {T}$ and g is NP-hard, even for $H = K = 1$ and $R = 2$.

Proof of Proposition 3 is in Appendix.

Due to the previous proposition, we perform a simple greedy optimization where each node is individually reassigned to the optimal group while maintaining the remaining nodes fixed.

We should point out that there are more sophisticated approaches, for example based on SDP relaxations, see a survey by Abbe (2017). However, we resort to a simple greedy optimization due to its speed.

A naive implementation of computing the log-likelihood gain for a single node may require $\Theta (m)$ steps, which would lead in $\Theta (nm)$ time as we need to test every node. Luckily, we can speed-up the computation using the following straightforward proposition.

Proposition 4

Let $\mathcal {P}$ be the partition of nodes, $\Lambda$ set of parameters, and $\mathcal {T}$ and g the segmentation and the level mapping. Let $\mathcal {S}_h = \left\{ T_k \in \mathcal {T} \mid h = g(k)\right\}$ be the segments using the hth level.

Let u be a node, and let $P_b$ be the set such that $u \in P_b$. Select $P_a$, and let $\mathcal {P}'$ be the partition where u has been moved from $P_b$ to $P_a$. Then

$$\begin{aligned} \ell \left( \mathcal {P}^{\prime }, \mathcal {T}, g, \Lambda \right) - \ell \left( \mathcal {P}, \mathcal {T}, g, \Lambda \right) = Z + \sum _{h = 1}^H \lambda _{bah} t_h + \sum _{j = 1}^R c_{jh} \log \lambda _{ajh} - {\left| P_j\right| }\lambda _{ajh} t_h, \end{aligned}$$

where Z is a constant, not depending on a, $t_h = \Delta \left( \mathcal {S}_h\right)$ is the total duration of the segments using the hth level and $c_{jh} = c \left( u, P_j, \mathcal {S}_h\right)$, is the number of edges between u and $P_j$ in the segments using the hth level.

Proof

Let us write $\mathcal {Q}$ to be the partition obtained from $\mathcal {P}$ by deleting u, that is $Q_b = P_b \setminus \left\{ u\right\}$ and $Q_j = P_j$ for $j \ne b$. Note that

$$\begin{aligned} \ell \left( P_a^{\prime }, P_j^{\prime }, T, \lambda \right) - \ell \left( Q_a, Q_j, T, \lambda \right) = \ell \left( u, P_j^{\prime }, T, \lambda \right) \end{aligned}$$

for any T and $\lambda$. Moreover, $\ell \left( P_i^{\prime }, P_j^{\prime }, T, \lambda \right) = \ell \left( Q_i, Q_j, T, \lambda \right)$ if $i, j \ne a$. Write, for brevity, $\Delta = \ell \left( \mathcal {P}^{\prime }, \mathcal {T}, g, \Lambda \right) - \ell \left( \mathcal {Q}, \mathcal {T}, g, \Lambda \right)$. The score difference is equal to

$$\begin{aligned} \Delta&= \sum _{i \le j} \sum _{k = 1}^K \ell \left( P_i^{\prime }, P_j^{\prime }, T_k, \lambda _{ijg(k)}\right) - \ell \left( Q_i, Q_j, T_k, \lambda _{ijg(k)}\right) \\&= \sum _{j = 1}^R \sum _{k = 1}^K \ell \left( P_a^{\prime }, P_j^{\prime }, T_k, \lambda _{ajg(k)}\right) - \ell \left( Q_a, Q_j, T_k, \lambda _{ajg(k)}\right) \\&= \sum _{j = 1}^R \sum _{k = 1}^K \ell \left( u, P_j^{\prime }, T_k, \lambda _{ajg(k)}\right) \\&= \sum _{j = 1}^R \sum _{h = 1}^H \ell \left( u, P_j^{\prime }, \mathcal {S}_h, \lambda _{ajh}\right) \\&= \sum _{j = 1}^R \sum _{h = 1}^H c \left( u, P_j^{\prime }, \mathcal {S}_h\right) \log \lambda _{ajh} - t_h {\left| Q_j\right| } \lambda _{ajh} \\&= \sum _{j = 1}^R \sum _{h = 1}^H c_{jh} \log \lambda _{ajh} - t_h {\left| Q_j\right| } \lambda _{ajh} \\&= \sum _{h = 1}^H \lambda _{bah} t_h + \sum _{j = 1}^r c_{jh} \log \lambda _{ajh} - t_h {\left| P_j\right| } \lambda _{ajh}\quad . \\ \end{aligned}$$

Here we used the fact that $c \left( u, P_j, \mathcal {S}_h\right) = c \left( u, P_j^{\prime }, \mathcal {S}_h\right)$. The claim follows by setting $Z = \ell \left( \mathcal {Q}, \mathcal {T}, g, \Lambda \right) - \ell \left( \mathcal {P}, \mathcal {T}, g, \Lambda \right)$. $\square$

The proposition leads to the pseudo-code given in Algorithm 2. The algorithm computes an array c and then uses Proposition 4 to compute the gain for each swap, and consequently to find the optimal gain.

Algorithm 2

Algorithm $\textrm{F}\textsc {ind}\textrm{G}\textsc {roups}\,(\mathcal {P}, \Lambda )$ for finding groups for a fixed segmentation $\mathcal {T}$, g and parameters $\Lambda$

Lemma 3.1

FindGroups runs in $\mathcal {O} \left( m + Rn + R^2\,H + K\right)$ time.

Proof

Computing the array requires iterating over the adjacent edges, leading to $\mathcal {O} \left( {\left| N(v)\right| }\right)$ time where ${\left| N(v)\right| } = 2m$. Computing the gains requires $\mathcal {O} \left( R^2H\right)$ time.

The running time can be further optimized by modifying Line 8. There are at most 2m non-zero c[i, j] entries (across all $v \in V$), consequently we can speed up the computation of a second term by ignoring the zero entries in c[i, j]. In addition, for each a, the remaining terms

$$\begin{aligned} \sum _{h = 1}^H \lambda _{bah}d[h] - \sum _{j = 1}^R {\left| P_j\right| }\lambda _{ajh} d[h] \end{aligned}$$

can be precomputed in $\mathcal {O} \left( RH\right)$ time and maintained in $\mathcal {O} \left( 1\right)$ time. In line 9, for each node we pick the group that maximizes the gain which requires $\mathcal {O} \left( Rn\right)$ time. This leads to a running time of $\mathcal {O} \left( m + Rn + R^2H + K\right)$. $\square$

3.3 Updating Poisson process parameters

Our next step is to update $\Lambda$ while maintaining the rest of the parameters fixed. This refers to UpdateLambda in Algorithm 1. Fortunately, this step is straightforward as the optimal parameters are equal to

$$\begin{aligned} \lambda _{ijh} = \frac{ c \left( P_i, P_j, \mathcal {S}_h\right) }{{\left| P_i \times P_j\right| } \Delta \left( \mathcal {S}_h\right) }, \end{aligned}$$

where $\mathcal {S}_h = \left\{ T_k \in \mathcal {T} \mid h = g(k)\right\}$ are the segments using the hth level.

Lemma 3.2

Updating the $\Lambda$ parameters requires $\mathcal {O} \left( m + R^2H + K\right)$ time.

Proof

First we need to count the number of interactions between ith group and jth group within hth level by iterating over the edges which requires $\mathcal {O} \left( m + R^2H\right)$ time. Computing $\Delta \left( \mathcal {S}_h\right)$ requires $\mathcal {O} \left( K + H\right)$ time. Next we update parameters by executing a triple loop which runs twice over the groups and once over the levels, requiring $\mathcal {O} \left( R^2H\right)$ time. Consequently, updating the parameters requires $\mathcal {O} \left( m + R^2\,H + K\right)$ time which proves the claim. $\square$

In practice, we would like to avoid having $\lambda = 0$ as this forbids any edges occurring in the segment, and we may get stuck in a local maximum. We approach this by shifting $\lambda$ slightly by using

$$\begin{aligned} \lambda _{ijh} = \frac{ c \left( P_i, P_j, \mathcal {S}_h\right) + \theta }{{\left| P_i \times P_j\right| } \Delta \left( \mathcal {S}_h\right) + \eta }, \end{aligned}$$

where $\theta$ and $\eta$ are user parameters.

3.4 Finding segmentation

Our final step is to update the segmentation $\mathcal {T}$ and the level mapping g, while keeping $\Lambda$ and $\mathcal {P}$ fixed. Luckily, we can solve this subproblem in linear time.

Note that we need to keep $\Lambda$ fixed, as otherwise the problem is NP-hard.

Proposition 5

Finding optimal $\Lambda$, $\mathcal {T}$ and g for fixed $\mathcal {P}$ is NP-hard.

Proof of Proposition 5 is in Appendix.

On the other hand, if we fix $\Lambda$, then we can solve the optimization problem with a dynamic program. To be more specific, assume that the edges in E are ordered, and write o[e, k] to be the log-likelihood of k-segmentation covering the edges prior and including e. Given two edges $s, e \in E$, let y(s, e; h) be the log-likelihood of a segment (t(s), t(e)] using the hth level of parameters, $\lambda _{\cdot \cdot h}$. If s occurs after e we set y to be $-\infty$. Then the identity

$$\begin{aligned} o[e, k] = \max _h \max _s y(s, e; h) + o[s, k - 1] \end{aligned}$$

leads to a dynamic program.

Using an off-the-shelf approach by Bellman (1961) leads to a computational complexity of $\mathcal {O} \left( m^2 K H\right)$, assuming that we can evaluate y(s, e; h) in constant time.

However, we can speed-up the dynamic program by using the SMAWK algorithm (Aggarwal et al., 1987). Given a function x(i, j), where $i, j = 1, \ldots , m$, SMAWK computes $z(j) = \arg \max _i x(i, j)$ in $\mathcal {O} \left( m\right)$ time, under two assumptions. The first assumption is that we can evaluate x in constant time. The second assumption is that x is totally monotone. We say that x is totally monotone, if $x(i_2, j_1) > x(i_1, j_1)$, then $x(i_2, j_2) \ge x(i_1, j_2)$ for any $i_1 < i_2$ and $j_1 < j_2$.

We have the immediate proposition.

Proposition 6

Fix h. Then the function $x(s, e) = y(s, e; h) + o[s, k - 1]$ is totally monotone.

Proof

Assume four edges $s_1$, $s_2$, $e_1$ and $e_2$ with $t(s_1) \le t(s_2)$ and $t(e_1) \le t(e_2)$. We can safely assume that $t(s_2) \le t(e_1)$. We can write the difference as

$$\begin{aligned} x(s_1, e_2) - x(s_1, e_1) = y(e_1, e_2; h) = x(s_2, e_2) - x(s_2, e_1). \end{aligned}$$

Thus, if $x(s_2, e_1) > x(s_1, e_1)$, then $x(s_2, e_2) > x(s_1, e_2)$, completing the proof. $\square$

Our last step is to compute x in constant time. This can be done by first precomputing f[e, h], the log-likelihood of a segment starting from the epoch and ending at t(e) using the hth level. The log-likelihood of a segment is then $y(s, e; h) = f[e, h] - f[s, h]$, which we can compute in constant time.

Algorithm 3

Algorithm $\textrm{F}\textsc {ind}\textrm{S}\textsc {egments}\,(\mathcal {P}, \Lambda )$ for finding optimal segmentation for fixed groups $\mathcal {P}$ and parameters $\Lambda$

The pseudo-code for finding the segmentation is given in Algorithm 3. A more detailed version of the pseudo-code is given in Appendix. Here, we first precompute f[e, h]. We then solve segmentation with a dynamic program by maintaining 3 arrays: o[e, k] is the log-likelihood of k-segmentation covering the edges up to e, q[e, k] is the starting point of the last segment responsible for o[e, k], and r[e, k] is the level of the last segment responsible for o[e, k].

In the inner loop we use SMAWK to find optimal starting points. Note that we have to do this for each h, and only then select the optimal h for each segment. Note that we do define x on Line 5 but we do not compute its values. Instead this function is given to SMAWK and is evaluated in a lazy fashion.

Once we have constructed the arrays, we can recursively recover the optimal segmentation and the level mapping from q and r, respectively.

Lemma 3.3

FindSegments runs in $\mathcal {O} \left( mKH + HR^2\right)$ time.

Proof

SMAWK runs in $\mathcal {O} \left( m\right)$ time and we need to call SMAWK $\mathcal {O} \left( HK\right)$ times. Therefore it requires $\mathcal {O} \left( mKH\right)$ time to find the optimal segmentation, given precomputed f mentioned in Line 2 in Algorithm 3. To compute f, we need to compute $\alpha$ as stated in Line 5 of the detailed version of the algorithm; Algorithm 5. To compute $\alpha$, we loop over the groups twice and once over the levels which requires $\mathcal {O} \left( HR^2\right)$ time. Consequently, computational complexity of FindSegments is $\mathcal {O} \left( mKH + HR^2\right)$. $\square$

We were able to use SMAWK because the optimization criterion turned out to be totally monotone. This was possibly only because we fixed $\Lambda$. The notion of using SMAWK to speed up a dynamic program with totally monotone scores was proposed by Galil and Park (1990). Fleischer et al. (2006); Hassin and Tamir (1991) used this approach to solve dynamic program segmenting monotonic one-dimensional sequences with $L_1$ cost.

We fixed $\Lambda$ because Proposition 5 states that the optimization problem for $H < K$ cannot be solved in polynomial time if we optimize $\mathcal {T}$, g, and $\Lambda$ at the same time. Proposition 5 is the main reason why we cannot use directly the ideas proposed by Corneli et al. (2018) as the authors use the dynamic program to find $\mathcal {T}$ and $\Lambda$ at the same time.

However, if $K = H$, then the problem is solvable with a dynamic program but requires $\mathcal {O} \left( Km^2R^2\right)$ time. This may be impractical for large values of m, so using Algorithm 1 may be preferable even when $K = H$. The downside of the approach is that having more variables fixed may lead to the algorithm getting to the local optimum.

We should point out we can also approximate the aforementioned segmentation problem, if we consider it as a minimization problem and shift the cost with a constant so that it is always positive, then using algorithms by Tatti (2019); Guha et al. (2006) we can obtain $(1 + \epsilon )$-approximation with $\mathcal {O} \left( K^3 \log K \log m + K^3 \epsilon ^{-2} \log m\right)$ number of cost evaluations. Finding the optimal parameters and computing the cost of a single segment can be done in $\mathcal {O} \left( R^2\right)$ time with $\mathcal {O} \left( R^2 + m\right)$ time for precomputing. This leads to a total time of $\mathcal {O} \left( R^2(K^3 \log K \log m + K^3 \epsilon ^{-2} \log m) + m\right)$ for the special case of $K = H$.

Algorithm 4

Modified algorithm $\textrm{F}\textsc {ind}\textrm{G}\textsc {roups}\,(\mathcal {P}, \Lambda )$ for finding level-specific groups for a fixed segmentation $\mathcal {T}$, g and parameters $\Lambda$

At the end of each subproblem, the log-likelihood either improves or stays constant. Therefore our algorithm always converges and have a finite number of iterations.

3.5 Solving level-dependent membership problem

Next we present the algorithm for solving RSDep .

Finding groups We continue to use a similar greedy approach as in Algorithm 2. The only difference is that when computing gain of a node, we pick only the adjacent edges residing in a particular level and then iterate over all levels in a separate fashion. We adopt Proposition 4, except now we apply it only for one level. The modified algorithm is stated in Algorithm 4. Moreover, the running time, $\mathcal {O} \left( m + R^2Hn + K\right)$, remains the same as of Algorithm 2.

Finding Poisson parameters and segmentation These algorithms for these two subproblems remain essentially unchanged: the only difference is that we use $P_{ih}$ whenever $P_i$ is involved.

4 Related work

The closest related work is the paper by Corneli et al. (2018) which can be viewed as a special case of our approach by requiring $K = H$, in other words, while the Poisson process may depend on time they do not take into account any recurrent behaviour. Having $K = H$ simplifies the optimization problem somewhat. While the general problem still remains difficult, we can now solve the segmentation $\mathcal {T}$ and the parameters $\Lambda$ simultaneously using a dynamic program as was done by Corneli et al. (2018). In our problem we are forced to fix $\Lambda$ while solving the segmentation problem. Interestingly enough, this gives us an advantage in computational time: we only need $\mathcal {O} \left( KHm + HR^2\right)$ time to find the optimal segmentation while the optimizing $\mathcal {T}$ and $\Lambda$ simultaneously requires $\mathcal {O} \left( R^2Km^2\right)$ time. On the other hand, by fixing $\Lambda$ we may have a higher chance of getting stuck in a local maximum.

The other closely related work is by Gionis and Mannila (2003), where the authors propose a segmentation with shared centroids. Here, the input is a sequence of real valued vectors and the segmentation cost is either $L_2$ or $L_1$ distance. Note that there is no notion of groups $\mathcal {P}$, the authors are only interested in finding a segmentation with recurrent sources. The authors propose several approximation algorithms as well as an iterative method. The approximation algorithms rely specifically on the underlying cost, in this case $L_1$ or $L_2$ distance, and cannot be used in our case. Interestingly enough, the proposed iterative method did not use SMAWK optimization, so it is possible to use the optimization described in Sect. 3 to speed up the iterative method proposed by Gionis and Mannila (2003).

In this paper, we used stochastic block model (see (Holland et al., 1983; Anderson et al., 1992), for example) as a starting point and extend it to temporal networks with recurrent sources. Several past works have extended stochastic block models to temporal networks: Yang et al. (2011); Matias and Miele (2017) proposed an approach where the nodes can change group memberships over time. In a similar fashion, Xu and Hero (2014) proposed a model where the adjacency matrix snapshots are generated with a logistic function whose latent parameters evolve over time. The main difference with our approach is that in these models the group memberships of nodes are changing while in our case we keep the memberships constant and update the probabilities of the nodes. Moreover, these methods are based on graph snapshots while we work with temporal edges. In another related work, Matias et al. (2018) modelled interactions using Poisson processes conditioned by stochastic block model. Their approach was to estimate the intensities non-parametrically through histograms or kernels while we model intensities with recurring segments. For a survey on stochastic block models, including extensions to temporal settings, we refer the reader to a survey by Lee and Wilkinson (2019).

Stochastic block models group similar nodes together; here similarity means that nodes in the same group have the similar probabilities connecting to nodes from other group. A similar notion but a different optimization criterion was proposed by Arockiasamy et al. (2016). Moreover, Henderson et al. (2012) proposed a method where nodes with similar neighborhoods are discovered.

In this paper we modelled the recurrency by forcing the segments to share their parameters. An alternative approach to discover recurrency is to look explicitly for recurrent patterns (Ozden et al., 1998; Han et al., 1998, 1999; Ma & Hellerstein, 2001; Yang et al., 2003; Galbrun et al., 2019). We should point out that these works are not design to work with graphs; instead they work with event sequences. We leave adapting this methodology for temporal networks as an interesting future line of work.

Using segmentation to find evolving structures in networks have been proposed in the past: Kostakis et al. (2017) introduced a method where a temporal network is segmented into k segments with $h < k$ summaries. A summary is a graph, and the cost of an individual segment is the difference between the summary and the snapshots in the segment. Moreover, Rozenshtein et al. (2020) proposed discovering dense subgraphs in individual segments.

5 Experimental evaluation

The goal in this section is to experimentally evaluate our algorithm. Towards that end, we first test how well the algorithm discovers the ground truth using synthetic datasets. Next we study the performance of the algorithm on real-world temporal datasets in terms of running time and likelihood. We compare our results to the following baselines: the running times are compared to a naive implementation where we do not utilize SMAWK algorithm, and the likelihoods are compared to the likelihoods of the (R, K) model.

We implemented the algorithm in Python³ and performed the experiments using a 2.4 GHz Intel Core i5 processor and 16 GB RAM.

5.1 Experiments with fixed membership model

Synthetic datasets To test our algorithm, we generated 5 temporal networks with known groups and known parameters $\Lambda$ which we use as a ground truth. To generate data, we first chose a set of nodes V, number of groups R, number of segments K, and number of levels H. Next we assumed that each node has an equal probability of being chosen for any group. Based on this assumption, the group memberships were selected at random.

We then randomly generated $\Lambda$ from a uniform distribution. More specifically, we generated H distinct values for each pair of groups and map them to each segment. Note that, we need to ensure that each distinct level is assigned to at least one segment. To guarantee this, we first deterministically assigned the set of H levels to first H segments and the remaining ($K-H$) segments are mapped by randomly selecting ($K-H$) elements from H level set.

Given the group memberships and their related $\Lambda$, we then generated a sequence of timestamps with a Poisson process for each pair of nodes. The sizes of all synthetic datasets are given in Table 1.

Table 1 Experiments for the synthetic datasets

Table 2 Sizes and computational times for the real-time datasets

Fig. 2

Discovered parameters $\lambda _{\textrm{11}}(t)$, $\lambda _{\textrm{12}}(t)$ for the Synthetic-4 dataset. Parameter $\lambda _{\textrm{12}}(t)$ implies the Poisson process parameter between group 1 and group 2 as a function of time

Real-world datasets We used 7 publicly available temporal datasets. Email-Eu-1 and Email-Eu-2 are collaboration networks between researchers in a European research institution.⁴Math Overflow contains user interactions in Math Overflow web site while answering to the questions.$^{4}$ CollegeMsg is an online message network at the University of California, Irvine.$^{4}$ MOOC contains actions by users of a popular MOOC platform.$^{4}$ Bitcoin contains member rating interactions in a bitcoin trading platform.$^{4}$ Santander contains station-to-station links that occurred on Sep 9, 2015 from the Santander bikes hires in London.⁵ The sizes of these networks are given in Table 2.

Results for synthetic datasets To evaluate the accuracy of our algorithm, we compare the set of discovered groups with the ground truth groups. Here, our algorithm found the ground truth: in Table 1 we can see that Rand index (Rand, 1971) (column G) is equal to 1,

Next we compare the log-likelihood values from true models against the log-likelihoods of discovered models. To evaluate the log-likelihoods, we normalize the log-likelihood, that is we computed $\ell \left( \mathcal {P}, \mathcal {T}, g, \Lambda \right) / \ell \left( \mathcal {P}^{\prime }, \mathcal {T}^{\prime }, g^{\prime }, \Lambda ^{\prime }\right)$, where $\mathcal {P}^{\prime }, \mathcal {T}^{\prime }, g^{\prime }, \Lambda ^{\prime }$ is a model with a single group and a single segment. Since all our log-likelihood values were negative, the normalized log-likelihood values were between 0 and 1, and smaller values are better.

As demonstrated in column $LL_g$ and column $LL_f$ of Table 1, we obtained similar normalized log-likelihood values when compared to the normalized log-likelihood of the ground truth. The obtained normalized log-likelihood values were all slightly better than the log-likelihoods of the generated models, that is, our solution is as good as the ground truth.

An example of the discovered parameters, $\lambda _{11}$ and $\lambda _{12}$, for Synthetic-4 dataset are shown in Fig. 2. The discovered parameters matched closely to the generated parameters with the biggest absolute difference being 0.002 for Synthetic-4. The figures for other values and other synthetic datasets are similar.

Computational time Next we consider the computational time of our algorithm. We varied the parameters R, K, and H for each dataset. The model parameters and computational times are given in Table 2 under RSFix section. From the last column of CT in RSFix section, we see that the running times are reasonable despite using inefficient Python libraries: for example we were able to compute the model for MOOC dataset, with over 400,000 edges, under four minutes. This implies that the algorithm scales well for large networks. This is further supported by a low number of iterations, column I in RSFix section of Table 2.

Fig. 3

Computational time as a function of number of temporal edges (${\left| E\right| }$) for Synthetic-large (a, c) and Santander-large (b, d). This experiment was done with $R=3$, $K=5$, and $H=3$ using SMAWK algorithm (a–b) and naive dynamic programming (c–d). The times are in seconds in (a–c) and in hours in (d)

Next we study the computational time as a function of m, number of edges.

We first prepared 4 datasets with different number of edges from a real-world dataset; Santander-large. To vary the number of edges, we uniformly sampled edges without replacement. We sampled like a .4, .6, .8, and 1 fraction of edges.

Next we created 4 different Synthetic-large dataset with 30 nodes, 3 segments with unique $\lambda$ values but with different number of edges. To do that, we gradually increase the number of Poisson samples we generated for each segment.

From the results in Fig. 3 we see that generally computational time increases as ${\left| E\right| }$ increases. For instance, a set of 17,072 edges accounts for 18.46 s whereas a set of 34,143 edges accounts for 36.36 s w.r.t Santander-large. Thus a linear trend w.r.t ${\left| E\right| }$ is evident via this experiment.

To emphasize the importance of SMAWK, we replaced it with a stock solver of the dynamic program, and repeat the experiment. We observe in Fig. 3 that computational time has increased drastically when stock dynamic program algorithm is used. For example, a set of 34,143 edges required 3.7 h for Santander-large dataset but only 36.36 s when SMAWK is used.

Fig. 4

Normalized log-likelihood as a function of number of levels (H) for the Santander dataset (a), bitcoin dataset (b), Synthetic-5 dataset (c), and Email-Eu-1 dataset (d). This experiment is done for $R=2$, $K=20$, and $H=1, \ldots , 20$

Likelihood vs number of levels Our next experiment is to study how normalized log-likelihood behaves upon the choices of H. We conducted this experiment for $K=20$ and vary the number of levels (H) from $H=1$ to $H=20$. The results for the Santander, Bitcoin, Synthetic-5, and Email-Eu-1 dataset are shown in Fig. 4. From the results we see that generally normalized log-likelihood decreases as H increases. That is due to the fact that higher the H levels, there exists a higher degree of freedom in terms of optimizing the likelihood. Note that if $H = K$, then our model corresponds to the model studied by Corneli et al. (2018). Interestingly enough, the log-likelihood values plateau for values of $H \ll K$ suggesting that existence of recurring segments in the displayed datasets.

Effect of $\Lambda$ Next we study how does $\lambda$ parameter affect the performance of our algorithm. To conduct our study with fixed membership model, we first prepared a collection of datasets with $R=2$, $K=4$, $H=2$, and varying $\lambda$ values. Since $H=2$, we set two specific $\lambda$ values for each pair of groups. We generate $\Lambda$ as a function of $\delta$ such that $\lambda _{11\cdot } = (\delta , 0.01)$, $\lambda _{22\cdot } = (0.01, \delta )$, and $\lambda _{12\cdot } = (\delta ,\delta )$. Next, we vary $\delta$ parameter from 0.01 to 0.1. When $\delta =0.01$, each pair of $\lambda$s are set with equal values and then we gradually increase the difference between them by varying $\delta$ parameter from 0.01 to 0.1. The case $\delta =0.01$ corresponds to the event where all pairs of $\lambda$ values are equal to 0.01. $\delta = 0.1$ corresponds to the case where 2 distinct $\lambda$s are the furthest away from each other for both $\lambda _{11}$ and $\lambda _{22}$. We generated 20 number of such datasets for each $\delta$ and used the same method of generating synthetic datasets as described in Sect. 5.1.

Next we ran our algorithm across 20 different datasets for each $\delta$, and reported maximum, minimum, and average Rand indices for both group memberships and segments. To check the speed of convergence, we recorded maximum, minimum, and average number of iterations for the convergence. Interestingly, for all the datasets our algorithm always achieved Rand index of 1 for discovered groups with compared to the ground truth. Next, we will see how did the Rand index for segments vary with $\delta$.

Fig. 5

a Gives Rand index as a function of $\delta$ and b gives number of iterations as a function of $\delta$. This experiment is conducted for $R=2$, $K=4$, and $H=2$ with fixed membership model

First, let us look at Fig. 5a which shows the average, maximum, and minimum Rand index for segments as a function of $\delta$. First we observe the blue curve which corresponds to the maximum Rand index obtained. We can conclude that unless $\lambda$s are too closer to each other; i.e $\delta < 0.02$, our algorithm always produced maximum Rand index more than 0.9 which indicates the ability to produce good solutions even when the datasets get more difficult to cope up. Next let us observe the average case which reaches Rand index close to 1 after $\delta = 0.03$. Therefore we can conclude that the accuracy of discovered segments are very high as $\delta$ approaches 0.03. Similar to average case, minimum case achieves its max at 0.03 and continues the value of 0.99 afterwards. In summary, at $\delta = 0.03$, all three curves approximately coincide with each other and maintain the same streak beyond.

Second, let us observe Fig. 5b which shows the number of iterations took until the convergence. We can observe that minimum number of iterations is always 2 over all $\delta$ values that we experimented. Furthermore, average number of iterations always lies between 2 and 3.1. In the maximum case we see that the number of iterations lies between 3 and 6 which implies a fast convergence. Finally, we can conclude that the number of iterations are not directly correlated with the ground truth $\lambda$ values of the dataset.

Table 3 Experiments for the synthetic datasets

5.2 Experiments with level-dependent membership model

Synthetic datasets When generating synthetic datasets for level-dependent model, we used the same procedure as with the fixed membership model, except we assigned a group to a node depending on its specific current level. That means that a node can have several group memberships over the course of timeline depending on its timestamp instance. We prepared 5 synthetic datasets in total; characteristics and results are shown in Table 3.

First, for each dataset, we compare the normalized log-likelihood values from the ground truth model against the fixed membership and level-dependent membership models. We observe that in these datasets, discovered normalized log-likelihood value obtained using level-dependent membership model (column $LL_d$) is always approximately equal and even slightly better than the ground truth (column $LL_g$). As shown in $LL_f$ column, even though fixed membership model produces a competitive score, the values are always worse than the ground truth. Next, we compare the group sets discovered using level-dependent model, with the ground truth groups. Here, we can see that Rand index (column G) is equal to 1 except for Synthetic-d-4. Finally, we see the running times which are shown in last column of Table 3. For over 100,000 edges, our algorithm converges in less than a minute.

Real-world datasets For each dataset, we conducted the experiments based on two group membership models. The statistics of discovered log-likelihood values for real-world datasets are shown in Table 2 under RSDep section. First, let us look at column $LL_d$ and $LL_f$ in RSDep section. For all datasets, normalized log-likelihood values obtained for level-dependent membership model are better than fixed membership model. This phenomenon illustrates that level-dependent membership model utilizes its higher degree of freedom while optimizing group memberships with compared to the case where memberships remain constant. The datasets Email-Eu-2, CollegeMsg, and MOOC have a significant gap between the likelihood values of two models indicating that the level-dependent model fit these datasets better. Nevertheless, MathOverflow dataset creates nearly equal likelihood results with both models that group membership of a node stays almost constant over all the segments is evident.

Likelihood vs number of levels Next we study the effect of H towards obtained normalized log-likelihood. We conducted this experiment for $K=20$ and $R = 2$, then vary the number of levels (H) from $H=1$ to $H=20$. For each level, we repeated the experiment 20 times and took the minimum of normalized log likelihood values over all such repetitions. The results for the Synthetic-2, Santander, Bitcoin, and Email-Eu-2 dataset are shown in Fig. 6. From the results we see that generally normalized log-likelihood decreases as H increases. That is due to the fact that higher the H levels, there exists more flexibility in terms of optimizing the group memberships. For Synthetic-2 the log-likelihood values generally are plateauing indicating no significant variation in model parameters from $H=2$ which is the ground truth number of H levels. Same plateauing behaviour is evident in Email-Eu-2 dataset after $H=15$ suggesting recurrent segments even if group memberships are allowed to vary from segment to segment.

Fig. 6

Normalized log-likelihood as a function of number of levels (H) for the Synthetic-2 dataset (a), Santander dataset (b), Bitcoin dataset (c), and Email-Eu-2 dataset (d). This experiment is done for $R=2$, $K=20$, and $H=1, \ldots , 20$. The reported scores are minimum of 20 restarts

Fig. 7

a Gives Rand index as a function of $\delta$ and b gives number of iterations as a function of $\delta$. This experiment is conducted for $R=2$, $K=4$, and $H=2$ with level-dependent model

Effect of $\Lambda$ Next, we study the affect of $\lambda$s towards the performance of our algorithm using level-dependent membership model. As described at the end of Sect. 5.1, we adhered to the same process of generating $\lambda$ varying datasets. Only difference here is that group memberships are also allowed to vary based on the level. Over all the datasets, our algorithm achieved Rand index of 1 for discovered group memberships. Next, we will observe the Rand index for discovered segments.

First, let us look at Fig. 7a which shows the average, maximum, and minimum Rand index for segments as a function of $\delta$. For the max case, we can observe that unless $\delta < 0.02$ our algorithm could discover segments with a Rand index value more than 0.99. For the average case, we can initially observe an increasing trend between $\delta = 0.01$ and $\delta = 0.08$. Afterwards, the curve tends to fluctuate from $\delta = 0.08$ to $\delta = 0.2$ and becomes constant at Rand index of 0.99 after $\delta = 0.4$. For the minimum case, we can see that Rand index tends to fluctuate until $\delta < 0.2$ and then reaches its maximum at $\delta = 0.4$ and continues to be approximately constant at its max afterwards. In summary, at $\delta = 0.04$, all three curves coincide with each other at a value close to 1.

Second, let us observe Fig. 7b which shows the number of iterations took until the convergence. We can observe that minimum number of iterations is always either 2 or 3. For the average case, average number of iterations always lies between 3 and 5 which shows a sufficiently fast convergence on average. Among all cases we experimented, except 2 outlier cases, in all other cases maximum number of iterations lies below 10. Similar to fixed membership model, we can not observe any trend that varies with $\delta$.

5.3 Case study

Finally we present a case study based on London cycling hire usage dataset$^{4}$ in which the interactions were occurred on 9th of September, 2015. The size of this network is given in Table 2. Our goal is to discover how the clusters are partitioned, that is, can we find some hidden pattern behind their locations and how did the $\lambda$ parameters behave during the course of the day, that is, whether our model can discover peak and non-peak recurrent patterns accurately. We conducted the experiment for $R = 5$, $K = 5$, and $H = 2$. That is, we are interested in segmenting the day into 5 segments with only 2 levels with the intention of finding peak and non-peak hours using Algorithm 1.

First, let us look at the clusters obtained from London cycling dataset which are shown in Fig. 8. In general, we can observe that the stations which are geographically close to each other are most likely to be partitioned together into the same cluster. This is due to the fact that the stations which are grouped together are most likely to interact with the stations from other clusters and the stations within the same cluster in similar fashion.

Fig. 8

Clusters found by our algorithm using London cycling hire usage dataset. Cluster 1, 2, 3, 4, and 5 are denoted by blue, yellow, green, pink, and red markings respectively (Color figure online)

Fig. 9

Discovered parameters $\Lambda$ and the segmentation for London cycling data ($R=5$, $K=5$, and $H=2$). The $\Lambda$ values are scaled by $10^6$ for the sake of presentation

Figure 9 shows how did the $\lambda$ parameters vary during the day. Interestingly we can clearly observe 2 peak segments during the day; approximately, one peak segment lies in the morning from 7.15 AM to 9.30 AM and the other peak segment lies in the evening from 4 PM to 7.45 PM. We can observe in Fig. 9 that the highest interaction levels of $10^{-5}$ were attained for both $\lambda _{\textrm{14}}(t)$ and $\lambda _{\textrm{44}}(t)$ which means that cluster 4 which has shown in Fig. 8 in blue color interacts with its geographically overlapping cluster 1 which is shown in pink color more frequently while keeping its intra-cluster interactions more busier with compared to other clusters.

On the other hand, we can observe in Fig. 9 that $\lambda _{\textrm{12}}(t)$, $\lambda _{\textrm{23}}(t)$, and $\lambda _{\textrm{35}}(t)$ record the least levels of interactions ticking. To justify our observed result, we see the geographic closeness between cluster 1 and 2, cluster 2 and 3, and cluster 3 and 5. It is evident in Fig. 8 that above cluster pairs are not clustered together as its neighbouring counterparts thus the interaction levels have become too low when compared to other inter-cluster interactions.

6 Concluding remarks

In this paper we introduced a problem of finding recurrent sources in temporal network: we introduced a stochastic block model with recurrent segments. We proposed two variants of this problem where group membership of a node was fixed over the course of timeline and group memberships were varying from segment to segment.

We showed that finding optimal groups and recurrent segmentation in both variants was NP-hard. Therefore, to find good solutions we introduced an iterative algorithm by considering 3 subproblems, where we optimize groups, model parameters, and segmentation in turn while keeping the remaining structures fixed. We demonstrate how each subproblem can be optimized in $\mathcal {O} \left( m\right)$ time. Here, the key step is to use SMAWK algorithm for solving the segmentation. This leads to a computational complexity of $\mathcal {O} \left( KHm + Rn + R^2H\right)$ for a single iteration. We show experimentally that the number of iterations is low, and that the algorithm can find the ground truth using synthetic datasets.

The paper introduces several interesting directions: Gionis and Mannila (2003) considered several approximation algorithms but they cannot be applied directly for our problem because our optimization function is different. Adopting these algorithms in order to obtain an approximation guarantee is an interesting challenge. We used a simple heuristic to optimize the groups. We chose this approach due to its computational complexity. Experimenting with more sophisticated but slower methods for discovering block models, such as methods discussed in Abbe (2017), provides a fruitful line of future work.

Appendices

Appendix A: Proofs

Proof of Proposition 1

Assume that we are given an instance of MaxCut, that is, a static graph H with n nodes and $m \ge n$ edges. Define

$$\begin{aligned} r = 2^6(n + 1)^2\quad \text {and}\quad \alpha = \max (2^{20} m^2, r^2)\quad . \end{aligned}$$

The temporal graph G consists of two copies of H: we will denote the nodes of the copies with $U = u_1, \ldots , u_n$ and $V = v_1, \ldots , v_n$. We connect the nodes in U (and V) to match the edges in H at timestamp 1. We connect the corresponding nodes $u_i$ and $v_i$ with $n\alpha$ cross edges at timestamp 0. We also add two sets of r nodes, which we will denote by X and Y, and connect each node pair (x, y), where $x \in X$ and $y \in Y$, with $\alpha$ edges at timestamp 0.

We set $H = K = 1$, which forces the segmentation to be a single segment [0, 1].

Set $R = 2$. Let $\mathcal {P} = \left\{ P_1, P_2\right\}$ be the optimal solution, and let $\Lambda$ be its parameters.

We will prove in Lemma A.1 that $X \subseteq P_1$ and $Y \subseteq P_2$ or $X \subseteq P_2$ and $Y \subseteq P_1$. Moreover, $u_i \in P_1$ implies that $v_i \in P_2$ and $v_i \in P_1$ implies $u_i \in P_2$.

This immediately implies that $\lambda _{11} = \lambda _{22}$. Moreover, since $r > n$, we have $\lambda _{12}> \alpha /4 > 1 \ge \lambda _{11}$.

Let us define $C_i = U \cap P_i$ and $D_i = V \cap P_i$. Write x to be the number of cross edges between $C_1$ and $C_2$.

Let $C_1' \cup C_2' = U$ be the maximum cut, and let $D_1' \cup D_2' = V$ be the corresponding cut in V. Define $\mathcal{P}' = \left\{ X \cup C'_1 \cup D'_2, Y \cup C'_2 \cup D'_1\right\}$. Write $x'$ to be the number of cross edges between $C_1'$ and $C_2'$. By optimality $x' \ge x$.

The log-likelihood of $\mathcal {P}'$ is

$$\begin{aligned} \ell \left( \mathcal {P}^{\prime }\right)&\ge \ell \left( \mathcal {P}^{\prime }, \Lambda \right) \\&= (2m - 2x^{\prime }) \log \lambda _{11} + 2x^{\prime } \log \lambda _{12} + Z \\&\ge (2m - 2x) \log \lambda _{11} + 2x \log \lambda _{12} + Z \\&= \ell \left( \mathcal {P}\right) \ge \ell \left( \mathcal {P}^{\prime }\right) , \end{aligned}$$

where

$$\begin{aligned} Z = \alpha (n^2 + r^2)\log \lambda _{12} - 2m - \alpha (n^2 + r^2). \end{aligned}$$

We have shown that $x' = x$, proving the NP-hardness of finding $\mathcal {P}$ with the optimal likelihood. $\square$

Lemma A.1

Let $\mathcal {P}$ be the partition as defined in the proof of Proposition 1. Then $X \subseteq P_1$ and $Y \subseteq P_2$ or $X \subseteq P_2$ and $Y \subseteq P_1$. Moreover, $u_i \in P_1$ implies that $v_i \in P_2$ and $v_i \in P_1$ implies $u_i \in P_2$.

Proof

To prove the lemma we will need several counters: let us define $a_i = {\left| P_i \cap X\right| }$, $b_i = {\left| P_i \cap Y\right| }$, $c_i = {\left| P_i \cap U\right| }$, and $d_i = {\left| P_i \cap V\right| }$. We also write $x_i = a_i + b_i$, $y_i = c_i + d_i$ and $z_i = x_i + y_i$.

Define $k_{ij}$ to be the number of cross edges between U and V in (i, j)th group of $\mathcal {P}$. Similarly, let $m_{ij}$ to be the number of edges in U and V (that is, the cross edges are excluded) in (i, j)th group of $\mathcal {P}$. Note that $k_{12} + k_{11} + k_{22} = n$ and $m_{12} + m_{11} + m_{22} = 2\,m$.

The parameters for $\mathcal {P}$ are

$$\begin{aligned} \lambda _{12}&= \frac{\alpha a_1 b_2 + \alpha a_2 b_1 + \alpha n k_{12} + m_{12}}{z_1z_2}, \\ \lambda _{11}&= \frac{\alpha a_1 b_1 + \alpha n k_{11} + m_{11}}{{z_1 \atopwithdelims ()2}}, \end{aligned}$$

and

$$\begin{aligned} \lambda _{22} = \frac{\alpha a_2 b_2 + \alpha n k_{22} + m_{22}}{{z_2 \atopwithdelims ()2}}. \end{aligned}$$

Let us define $\mathcal {P}^{\prime } = \left\{ X \cup U, Y \cup V\right\}$. Note that the parameters for $\mathcal {P}^{\prime }$ are equal to

$$\begin{aligned} \lambda _{12}' = \frac{\alpha n^2 + \alpha r^2}{(r + n)^2} \quad \text {and}\quad \lambda _{11}^{\prime } = \lambda _{22}^{\prime } = \frac{m}{{n + r \atopwithdelims ()2}}. \end{aligned}$$

To prove the claim we will assume that $a_1 b_1 + a_2 b_2 > 0$ or $k_{12} < n$, and show that $\ell \left( \mathcal {P}'\right) > \ell \left( \mathcal {P}\right)$ which is a contradiction.

First, note that we can write the score difference as

$$\begin{aligned} \ell \left( \mathcal {P}'\right) - \ell \left( \mathcal {P}\right) = A + B + C, \end{aligned}$$

where

$$\begin{aligned} A&= \alpha (a_1 b_2 + a_2 b_1 + n k_{12}) \log \frac{\lambda _{12}^{\prime }}{\lambda _{12}},\\ B&= \alpha (a_1b_1 + n k_{11}) \log \frac{\lambda _{12}^{\prime }}{\lambda _{11}} + \alpha (a_2b_2 + n k_{22}) \log \frac{\lambda _{12}^{\prime }}{\lambda _{22}}, \end{aligned}$$

and

$$\begin{aligned} C = m_{11} \log \frac{\lambda _{11}^{\prime }}{\lambda _{11}} + m_{22} \log \frac{\lambda _{11}^{\prime }}{\lambda _{22}} + m_{12} \log \frac{\lambda _{11}^{\prime }}{\lambda _{12}}. \end{aligned}$$

(1)

We claim that

$$\begin{aligned} A \ge 0,\quad B > \alpha 2^{-7}, \quad \text {and}\quad C \ge 2m \log \frac{1}{4\alpha n r^2}. \end{aligned}$$

This proves the lemma since

$$\begin{aligned} B + C&> \alpha 2^{-7} - 2m \log 4 \alpha n r^2 \\&\ge \alpha 2^{-7} - 8m \log \alpha \\&\ge \alpha 2^{-7} - 8m \sqrt{\alpha } \\&= \sqrt{\alpha } \left( \sqrt{\alpha }2^{-7} - 8m \right) \ge 0. \end{aligned}$$

We will first bound C. Since we may have at most $\alpha n$ edges per node pair, we have $\lambda _{11}, \lambda _{12}, \lambda _{22} \le \alpha n$. Moreover, since $r > n$, we have $\lambda _{11}^{\prime } \ge (r + n)^{-2} \ge r^{-2}/4$. The bound follows from Eq. (1).

Next we will bound B. Assume that $x_1, x_2 \ge 2n$. Our next step is to upper bound $\lambda _{11}$ and $\lambda _{22}$. In order to do this, first note that since $m_{11} \le \alpha / 2$ and $k_{11} \le y_1$, we have

$$\begin{aligned} \frac{m_{11} + \alpha n k_{11}}{{y_1 \atopwithdelims ()2} + y_1 x_1} \le \alpha \frac{1/2 + n y_1 }{{y_1 \atopwithdelims ()2} + 2n y_1 } \le \alpha \frac{1/2 + n y_1 }{1 + 2n y_1 } = \alpha / 2. \end{aligned}$$

In addition, since $x_1 \ge 3$, we have

$$\begin{aligned} \alpha \frac{a_1b_1}{{x_1 \atopwithdelims ()2}} \le 2\alpha / 3\quad . \end{aligned}$$

We can combine the two bounds, leading to

$$\begin{aligned} \lambda _{11} = \frac{\alpha a_1b_1 + m_{11} + \alpha n k_{11}}{{z_1 \atopwithdelims ()2}} = \frac{a_1b_1 + m_{11} + \alpha n k_{11}}{{x_1 \atopwithdelims ()2} + {y_1 \atopwithdelims ()2} + y_1 x_1} \le 2\alpha /3. \end{aligned}$$

The same bound holds for $\lambda _{22}$.

Since $r \ge 4n$, we have $\lambda _{12}^{\prime } \ge 17\alpha /25$. Thus,

$$\begin{aligned} B \ge \alpha (a_1b_1 + a_2b_2 + nk_{11} + nk_{22}) \log \frac{17 \times 3}{25 \times 2} > \alpha 2^{-7}. \end{aligned}$$

Assume now that $x_1 < 2n$. Then $a_2 + b_2 = x_2> 2r - 2n > 1.5 r$. Since $a_2, b_2 \le r$, we must have $a_2, b_2 \ge r/2$. Moreover, using the previous arguments, we have

$$\begin{aligned} \log \frac{\lambda _{12}'}{\lambda _{22}} \ge 2^{-7} \quad \text {and}\quad \log \frac{\lambda _{12}'}{\lambda _{11}} \ge \log \frac{17}{25n} . \end{aligned}$$

Consequently,

$$\begin{aligned} B&= \alpha (a_2b_2 + nk_{22}) \log \frac{\lambda _{12}^{\prime }}{\lambda _{22}} + \alpha (a_1b_1 + nk_{11}) \log \frac{\lambda _{12}^{\prime }}{\lambda _{11}} \\&\ge \alpha \left( \frac{r^2}{2^9} - 4 n^2 \log \frac{25 n}{17}\right) \\&\ge \alpha (8(n + 1)^4 - 4 n^2 \log 2 n) \\&\ge \alpha (8(n + 1)^4 - 8 n^{4}) \ge \alpha > \alpha 2^{-7}. \end{aligned}$$

Finally we will bound A by showing that $\lambda _{12} \le \lambda ^{\prime }_{12}$. Assume for simplicity that $x_1 \le x_2$. Let us define

$$\begin{aligned} N = a_1 b_2 + a_2 b_1 + 1 + nk_{12}\quad . \end{aligned}$$

Assume that $z_1, z_2 \ge r$. We claim that $N \le r^2 + (z_1 - r)(z_2 - r)$, which leads to

$$\begin{aligned} \lambda _{12} \le \alpha \frac{N}{z_1z_2} \le \alpha \frac{r^2 + (z_1 - r)(z_2 - r)}{z_1z_2} = \alpha - \alpha \frac{2nr}{z_1z_2}. \end{aligned}$$

Here the first inequality holds since $m_{12} \le 2m \le \alpha$. The right hand side achieves its maximum when $z_1z_2$ is maximized, that is, $z_1 = z_2 = n + r$. In such case, the upper bound is equal to $\lambda _{12}^{\prime }$.

To prove the claim, first note that

$$\begin{aligned} nk_{12} \le \max (y_1, y_2) \min (y_1, y_2) = y_1y_2 \end{aligned}$$

(2)

with the equality holding if and only if $k_{12} = y_1 = y_2 = n$.

Assume that $x_1 = x_2 = r$. If $a_1b_1 + a_2b_2 > 0$, then

$$\begin{aligned} N = r^2 - a_1b_1 + a_2b_2 + 1 + nk_{12} \le r^2 + y_1y_2 = r^2 + (z_2 - r)(z_1 - r). \end{aligned}$$

Assume $a_1b_1 + a_2b_2 = 0$. Then $k_{12} < n$, and the inequality is strict in Eq. (2). Consequently,

$$\begin{aligned} N = r^2 + n k_{12} + 1 \le r^2 + y_1y_2 = r^2 + (z_2 - r)(z_1 - r) \end{aligned}$$

Assume now that $x_1 \le x_2 - 1$. Since a node in $(X \cup Y) \cap P_1$ is connected to r nodes, we must have $a_1 b_2 + a_2 b_1 \le x_1r$. Due to the assumption, $x_1 \le r - 1$ and $x_2 \ge r + 1$, which leads to

$$\begin{aligned} k_{12}&\le \min (y_1, y_2) \\&= \min (z_1 - x_1, z_2 - x_2) \\&\le \min (z_1 - x_1, z_2 - r) \end{aligned}$$

and

$$\begin{aligned} N&\le x_1 r + 1 + n \min (z_1 - x_1, z_2 - r) \\&\le (r - 1)r + 1 + n \min (z_1 - r + 1, z_2 - r) \\&\le r^2 + (1 + n - r) + n \min (z_1 - r, z_2 - r) \\&\le r^2 + \max (z_1 - r, z_2 - r)\min (z_1 - r, z_2 - r) \\&= r^2 + (z_2 - r)(z_1 - r). \end{aligned}$$

As a final case assume that $z_1 < r$. If $x_1 = z_1$, then

$$\begin{aligned} \lambda _{12} \le \alpha \frac{rz_1}{z_1 z_2} \le \alpha \frac{r}{r + 2n} = \alpha \frac{r^2}{r^2 + 2nr} \le \alpha \frac{r^2 + n^2}{r^2 + 2nr + n^2} = \lambda _{12}^{\prime }. \end{aligned}$$

If $x_1 < z_1$, then

$$\begin{aligned} N \le x_1r + 1 + n (z_1 - x_1) \le z_1r \end{aligned}$$

and again

$$\begin{aligned} \lambda _{12} \le \alpha \frac{N}{z_1z_2} \le \frac{zr_1}{z_1z_2} \le \lambda _{12}^{\prime }. \end{aligned}$$

The case for $z_2 < r$ is symmetrical.

We have now proven our claim, and thus proved that $\lambda _{12} \le \lambda _{12}'$. Consequently, $A \ge 0$. $\square$

Proof of Proposition 3

To prove NP-hardness we will reduce the MaxCut problem, where we are asked to partition graph into 2 subgraphs and maximize cross-edges.

Assume that we given a static graph H. We will use H as our temporal graph G by setting the edges to the same timestamp, say t. We also set $H = K = 1$, and use $R = 2$ groups. We also set the segmentation $\mathcal {T} = {[t, t]}$.

Select two values $\alpha < \beta$ and set the parameters $\lambda _{11} = \lambda _{22} = \alpha$ and $\lambda _{12} = \beta$.

Let $P_1, P_2$ be a partition of the nodes and let x be the number of the inner edges, that is, edges (u, v, t) with $u, v \in P_1$ or $u, v \in P_2$. Note that $m - x$ is the number of cross edges.

The log-likelihood is then equal to

$$\begin{aligned} \ell \left( \mathcal {P}, \mathcal {T}, g, \Lambda \right) = x \log \alpha + (m - x) \log \beta , \end{aligned}$$

which is maximized when $m - x$ is maximized since $\beta > \alpha$. Since $m - x$ is the number of cross-edges, this completes the proof. $\square$

Proof of Proposition 5

Assume that we given an instance of 3-Matching, that is, a domain X of size n, where n is divisible by 3, and a collection $\mathcal {S}$ of m sets such that $S \subseteq X$ and ${\left| S\right| } = 3$ for each $S \in \mathcal {S}$. The problem whether there is a disjoint subcollection in $\mathcal {S}$ covering X is known to be NP-complete.

Let $\mathcal {T} = \left\{ S \subseteq X \mid {\left| S\right| } = 3, S \notin \mathcal {S}\right\}$ be the complement collection of $\mathcal {S}$. For each $i \le j \le n$, define $c_{ij}$ to be the number of sets in S containing i and j,

$$\begin{aligned} c_{ij} = {\left| \left\{ S \in \mathcal {S} \mid \left\{ i, j\right\} \subset S\right\} \right| }. \end{aligned}$$

To construct the dynamic graph G we will use 5 sets of nodes, namely $\left\{ u\right\}$, A, B, C, D. The first set consists only of one node u. Every edge will be adjacent to u. The second set A contains as many nodes as there are sets in $\mathcal {T}$. For each $i \in T_j \in \mathcal {T}$, we add an edge $(u, a_j)$ at timestamp i. The third set B contains $\sum _{i < j} c_{ij}$ nodes which we divide further into $n(n - 1)/2$ sets $B_{ij}$ with ${\left| B_{ij}\right| } = c_{ij}$. For each $i < j$ we connect nodes in $B_{ij}$ with u at timestamp i and at timestamp j. The fourth set C contains $n(m - c_{ii})$ nodes which we divide further into n sets $C_{i}$ with ${\left| C_{i}\right| } = m - c_{ii}$. For each $i \le n$ we connect nodes in $C_i$ with u at timestamp i. The fifth set D contains nw nodes, where $w = 24n^6$, which we divide further into n sets $D_{i}$ with ${\left| D_{i}\right| } = w$. For each $i \le n$ we connect w nodes with u at timestamp i.

We will set $K = n$ and $H = n / 3$. We set R to be the number of nodes and set the partition $\mathcal {P}$ to be the partition where each node is contained in its own group. We require for a segmentation to start from 0. Since there are only n timestamps, the segmentation consists of n segments of form $(i - 1, i]$ or [0, 1].

Let g be the optimal grouping of segments and let $\Lambda$ be its parameters. We first claim that g groups timestamps into groups of 3. To prove this assume that there is a group of size $y = 1,2$. Then there is another group with a size of $x \ge 6 - y$. Let $g^{\prime }$ be a mapping where we move $3 - y$ timestamps from the larger group to the smaller group and let $\Lambda ^{\prime }$ be the new optimal parameters.

The number of edges adjacent to A, B, and C can be bound by $3n^3 +2n^2m + nm \le 6n^5$. Moreover, the non-zero parameters can be bound by $\lambda ^{\prime } \ge 1/n$ and $\lambda \le 1$. Consequently, the score difference can be bound by

$$\begin{aligned} \ell \left( g^{\prime }\right) - \ell \left( g\right) \ge 6n^5(\log 1/n - \log 1) + Z(x) \ge 6n^6 + Z(x), \end{aligned}$$

where Z(x) is equal to

$$\begin{aligned} w \left( (x - 3 + y)\log \frac{1}{x - 3 + y} + 3 \log \frac{1}{3} - x\log \frac{1}{x} - y \log \frac{1}{y}\right) . \end{aligned}$$

The derivative of Z(x) with respect to x is equal to $\log (x / (x - 3 + y)) > 0$, that is, Z(x) is at smallest when $x = 6 - y$. A direct calculation shows that Z(x) is the smallest when $y = 2$, leading to

$$\begin{aligned} \ell \left( g^{\prime }\right) - \ell \left( g\right)&\ge -6n^6 + w \left( 6 \log \frac{1}{3} - 4\log \frac{1}{4} - 2 \log \frac{1}{2}\right) \\&> -6n^6 + w/4 = 0. \end{aligned}$$

In summary, $\ell \left( g^{\prime }\right) > \ell \left( g\right)$ which is a contradiction. Thus, g groups of segments to size of at least 3. Since $K = 3H$, the groups are exactly of size 3.

Our next step is to calculate the impact of a single group to the score. In order to do that first note that for any $i < j$ there are

$$\begin{aligned} {n \atopwithdelims ()3} - c_{ij} + c_{ij} = {n \atopwithdelims ()3} \end{aligned}$$

edges joining the same nodes at timestamp i and timestamp j. Similarly, there are

$$\begin{aligned} {n \atopwithdelims ()3} - c_{ii} + \left( \sum _{i < j} c_{ij}\right) + m - c_{ii} + w = {n \atopwithdelims ()3} + m + w \end{aligned}$$

edges adjacent to node i.

Consider a set S of size 3 induced by g. Assume that $S \notin \mathcal {T}$. Then there are $3{n \atopwithdelims ()3}$ parameters in $\Lambda$ associated with the group with value 2/3, and $3(m + w)$ parameters with value 1/3. The remaining parameters are 0. Consequently, the impact to the score is equivalent to

$$\begin{aligned} \alpha = 6 {n \atopwithdelims ()3} \log 2/3 + 3(m + w) \log 1/3. \end{aligned}$$

Assume that $S \in \mathcal {T}$. Then using exclusion-inclusion principle, there are $3{n \atopwithdelims ()3} - 3$ parameters with value 2/3, $3(m + w) + 3$ parameters with value 1/3, one parameter with value 3/3 and the remaining parameters are 0. Consequently, the impact to the score is equivalent to

$$\begin{aligned} \beta = 6{n \atopwithdelims ()3} \log 2/3 - 6\log 2/3 + 3(1 + m + w) \log 1/3\quad . \end{aligned}$$

We immediately see that

$$\begin{aligned} \alpha - \beta = 6 \log 2/3 - 3 \log 1/3 = 3 \log 4/3 > 0\quad . \end{aligned}$$

Let k be the number of groups induced by g that are in $\mathcal {S}$. Then the score is equal to

$$\begin{aligned} \ell \left( g\right) = k \alpha + (H - k) \beta - {\left| E(G)\right| }. \end{aligned}$$

Since $\alpha > \beta$, there is a disjoint subcollection in $\mathcal {S}$ covering X if and only if $\ell \left( g\right) = H \alpha - {\left| E(G)\right| }$. $\square$

Appendix B: Detailed pseudo-code for FindSegments 

Algorithm 5

Algorithm $\textrm{F}\textsc {ind}\textrm{S}\textsc {egments}\,(\mathcal {P}, \Lambda )$ for finding optimal segmentation for fixed groups $\mathcal {P}$ and parameters $\Lambda$