A new approach to estimation of the proportional hazards model based on interval-censored data with missing covariates

Abstract

This paper discusses the fitting of the proportional hazards model to interval-censored failure time data with missing covariates. Many authors have discussed the problem when complete covariate information is available or the missing is completely at random. In contrast to this, we will focus on the situation where the missing is at random. For the problem, a sieve maximum likelihood estimation approach is proposed with the use of I-spline functions to approximate the unknown cumulative baseline hazard function in the model. For the implementation of the proposed method, we develop an EM algorithm based on a two-stage data augmentation. Furthermore, we show that the proposed estimators of regression parameters are consistent and asymptotically normal. The proposed approach is then applied to a set of the data concerning Alzheimer Disease that motivated this study.

1 Introduction

It is well-known that the proportional hazards model is one of the most commonly used models for regression analysis of failure time data, and a great deal of literature has been established for fitting it to right-censored or interval-censored data. By interval-censored data, we mean that the failure time of interest is observed only to belong to an interval instead of being known exactly, and it is apparent that they include right-censored data as a special case (Sun 2006). Among others, the fields that often generate interval-censored data include demographical, epidemiological, financial, medical and sociological studies. In the following, we will discuss the fitting of the proportional hazards model to interval-censored failure time data when some covariates may have missing observations.

As discussed by many authors, missing data can arise due to many circumstances and in general, their analysis highly depends on the censoring mechanism (Little and Rubin 2002). For the situation, a naive approach is the so-called complete-case (CC) method, which bases the analysis only on the complete part of the data or throw away the subjects with missing information. It is apparent that the CC method not only may be inefficient but also could yield biased estimation when the missing data mechanism depends on the observed data (Lipsitz et al. 1994; Little and Rubin 2002; Qi et al. 2005). Instead of the CC method, some alternatives could be the multiple imputation procedure and the estimating equation approach. As pointed out by many authors, when the missing is missing at random (MAR), the focus of this paper, the maximum likelihood approach may be preferred or should be used.

Several maximum likelihood methods have been proposed for regression analysis of right-censored failure time data with missing covariates under the proportional hazards model when the missing is MAR (Chen et al. 2002; Chen and Little 1999; Zhou and Pepe 1995). However, it does not seem to exist an established approach for interval-censored data when some covariates may be missing at random except Wen and Lin (2011), who proposed a semiparametric maximum likelihood estimation procedure under the proportional hazards model. However, they only considered current status data or case I interval-censored data, a special case of the general interval-censored data discussed here. In the following, we will consider the estimation of the proportional hazards model when one faces case II interval-censored data with missing covariates and propose a sieve maximum likelihood estimation approach. The method can be easily implemented and makes use of I-spline functions to approximate the underlying cumulative hazard function in the model.

The remainder of this paper is organized as follows. We will begin in Sect. 2 with introducing the model and assumptions that will be used throughout the paper and then present the resulting likelihood function. The proposed sieve maximum likelihood estimation approach will be derived in Sect. 3, and in particular, for the determination of the proposed estimators, an EM algorithm is developed. Section 4 establishes the asymptotic properties of the proposed estimators of regression parameters. Some results obtained from a simulation study are presented in Sect. 5 and suggest that the proposed approach works well in practical situations. Section 6 provides an application and some discussion and concluding remarks are given in Sect. 7.

2 Models, assumptions and likelihood functions

Consider a failure time study that involves n independent subjects and let $T_i$ and $\mathbf{X_i}$ denote the failure time of interest and a p-dimensional vector of covariates associated with subject i. In the following, suppose that for each subject, there exist two monitoring variables or observation times $U_i$ and $V_i$ with $U_i < V_i$, and instead of observing $T_i$, one observes only $U_i$ and $V_i$ and the indicator variables $\delta _{1i} = I (T_i<U_i)$, $\delta _{2i} = I (U_i\leqslant T_i<V_i)$ and $\delta _{3i} = 1 - \delta _{1i}-\delta _{2i}$. That is, we only know if the failure for subject i has occurred before $U_i$, during the examination interval $[U_i, V_i)$ or after V and observe case II interval-censored data (Sun 2006).

To describe the covariate effect on $T_i$, we will assume that given the covariates $\mathbf{X_i}$, the cumulative hazard function of $T_i$ has the form

$$\begin{aligned} \Lambda _i (t|{\mathbf{X_i}}) = \Lambda _0 (t) \, \text{ exp }\{{{\beta '}} \mathbf{X_i}\} , \end{aligned}$$

(1)

where $\Lambda _0 (t)$ denotes an unspecified baseline cumulative hazard function and ${\varvec{\beta }}$ a p-dimensional vector of regression parameters. That is, $T_i$ follows the proportional hazards model. In the following, we will assume that given the covariate $\mathbf{X_i}$, the failure time $T_i$ is independent of the observation times $U_i$ and $V_i$ or we have the independent interval censoring.

Under the assumptions above, if there was no missing covariate, the likelihood function would have the form

$$\begin{aligned} L_c ( \beta , \gamma , \Lambda _0 ) = \prod _{i=1}^{n} \, f(U_i, V_i, \delta _{1i}, \delta _{2i}, \delta _{3i}|{\mathbf{X_i}}; \beta , \Lambda (t)) \, f({\mathbf{X_i}}; \gamma ) . \end{aligned}$$

In the above, $f({\mathbf{X_i}}; \gamma )$ denotes the density function of the covariate with the unknown parameter $\gamma$ and

$$\begin{aligned}&f(U_i, V_i, \delta _{1i}, \delta _{2i}, \delta _{3i}|{\mathbf{X_i}}) \propto [1 - \text{ exp }\{-\Lambda _0 (V_i)\text{ exp }(\beta '{\mathbf{X_i}})\}]^{\delta _{1i}}\nonumber \\&\quad \times \,[\text{ exp }\{ -\Lambda _0 (U_i)\text{ exp }(\beta '{\mathbf{X_i}})\}-\text{ exp }\{-\Lambda _0(V_i)\text{ exp }(\beta '{\mathbf{X_i}})\}]^{\delta _{2i}}\nonumber \\&\quad \times \, [\text{ exp }\{-\Lambda _0 (U_i)\text{ exp }(\beta '{\mathbf{X_i}})\}]^{\delta _{3i}} , \, \, \, i=1, \ldots , n. \end{aligned}$$

(2)

It follows that we would have the log likelihood function

$$\begin{aligned} l_n (\beta , \gamma , \Lambda _0 )= & {} \text{ log }[L_c({\theta },\beta , \gamma , \Lambda (t))]\nonumber \\= & {} \sum _{i=1}^n\text{ log }[f(U_i, V_i, \delta _{1i}, \delta _{2i}, \delta _{3i}|{\mathbf{X_i}}; \beta , \Lambda (t))] +\sum _{i=1}^n \text{ log }[f({\mathbf{X_i}}; \gamma )]\nonumber \\= & {} l_{1} (\beta , \Lambda _0 ) \, + \, l_{2} (\gamma ) . \end{aligned}$$

(3)

It is easy to see that one can maximize $l_{1} ( \beta , \Lambda _0 )$ and $l_{2} (\gamma )$ separately if the goal is to estimate $\beta$, $\gamma$ and $\Lambda _0$, or can ignore $l_{2} (\gamma )$ since $\gamma$ is usually not of interest. As will be seen below, we have to estimate $\beta$, $\gamma$ and $\Lambda _0$ together when there are missing covariates. Now suppose that some covariates may be missing and the covariate can be written as ${\mathbf{X_i}} ' = ({\mathbf{X_i^{obs}}}' , {\mathbf{X_i^{mis}}} ' )$, where $\mathbf{X_i^{obs}}$ denotes the components of the covariates that are known or can be observed and $\mathbf{X_i^{mis}}$ the components of the covariates that are missing. Also suppose that we can write the density function of the covariates as

$$\begin{aligned} f(\mathbf{X_i^{obs}}, \mathbf{X_i^{mis}}; \gamma )\propto f(\mathbf{X_i}^{obs})f(\mathbf{X_i^{mis}}|\mathbf{X_i^{obs}}; \gamma ) . \end{aligned}$$

Let $R_{i} = ( R_{i 1}, ... , R_{i p} )'$ denote the missing indicator with $R_{i j} = 1$ if the jth component of the covariate associated with subject i is observed and 0 otherwise. In the following, we will assume that the covariate is missing at random, meaning that

$$\begin{aligned} f(R_i|U_i, V_i, \delta _{1i}, \delta _{2i}, \delta _{3i}, {\mathbf{X_i^{mis}}}, {\mathbf{X_i^{obs}}} ) = f(R_i|U_i, V_i, \delta _{1i}, \delta _{2i}, \delta _{3i}, {\mathbf{X_i^{obs}}} ) \end{aligned}$$

for the conditional density function of $R_i$. Then the observed likelihood function has the form

$$\begin{aligned} L_o( {{\theta }} ) = \prod _{i=1}^{n} \, \int f(U_i, V_i, \delta _{1i}, \delta _{2i}, \delta _{3i}|{\mathbf{X_i^{mis}}}, {\mathbf{X_i^{obs}}}; \beta , \Lambda (t))f(\mathbf{X_i^{obs}}, \mathbf{X_i^{mis}}; \gamma )\mathbf{d}{\mathbf{X_i^{mis}}} , \end{aligned}$$

where ${{\theta }} = ( \beta , \gamma , \Lambda _0 )$. In the next section, we will discuss estimation of ${{\theta }}$ by maximizing $L_o ( {{\theta }} )$.

3 Sieve maximum likelihood estimation

In this section, we will discuss estimation of ${{\theta }}$ by maximizing $L_o ( {{\theta }} )$ with the focus on making inference about $\beta$. For this, it is apparent that it would be difficult directly to maximize it and thus we will develop an EM algorithm. Before presenting the algorithm, we will first discuss the use of the sieve approach and then the data augmentation.

It is well-known that the sieve approach can be used to approximate an unknown function in order to reduce the number of unknown parameters and the computational burden (Ma et al. 2015; Zhao et al. 2015; Li et al. 2017). More specifically, for the estimation here, we suggest to approximate the baseline cumulative hazard function $\Lambda _0 (t)$ by monotone spline functions such as

$$\begin{aligned} \Lambda _{n}(t)=\sum \limits _{l=1}^{s+k_n}\alpha _lI_l(t) \end{aligned}$$

(Ramsay 1988). In the above, $\{I_l(t), l=1, \ldots , s+k_n\}$ are integrated spline basis functions with the order s and the number of knots $k_n$, and the $\alpha _l'$s are nonnegative coefficients that ensure monotonicity of $\Lambda _{n} (t)$. The degree s determines the smoothness of the true baseline cumulative hazard function and is often taken to be 1, 2, or 3, which corresponds to linear, quadratic, or cubic basis functions, respectively. In practice, for the choice of s and $k_n$, one commonly used method is to try different values of them and compare the obtained results. As an alternative, one could also use the AIC to choose the values of s and $k_n$ that give the smallest AIC, and more discussion on this is given below.

Now we discuss the data augmentation and for this, we will first assume that all covariates have been observed. Then the log likelihood function $l_{1}(\beta , \Lambda (t))$ would have the form

$$\begin{aligned} l_1(\beta , \Lambda _0 )= & {} \sum \limits _{i=1}^n\text{ log } \left\{ \left[ 1-\text{ exp }\{-\Lambda _0 (V_i)\text{ exp }(\beta '{\mathbf{X_i}})\} \right] ^{\delta _{1i}}\right. \nonumber \\&\times \left[ \text{ exp }\{-\Lambda _0 (U_i)\text{ exp }(\beta '{\mathbf{X_i}})\}-\text{ exp }\{-\Lambda _0 (V_i)\text{ exp }(\beta '{\mathbf{X_i}})\} \right] ^{\delta _{2i}}\nonumber \\&\left. \quad \left[ \text{ exp }\{-\Lambda _0 (U_i)\text{ exp }(\beta '{\mathbf{X_i}})\} \right] ^{\delta _{3i}} \right\} . \end{aligned}$$

(4)

By replacing $\Lambda _0$ with $\Lambda _n$, we have that

$$\begin{aligned} l_{1}^{*}(\beta , \alpha _l)= & {} \sum \limits _{i=1}^n \text{ log }\left\{ [1-\text{ exp }\left\{ -\left( \sum \limits _{l=1}^{s+k_n}\alpha _l I_l(V_i)\right) \text{ exp }(\beta '{\mathbf{X_i}})\right\} ]^{\delta _{1i}}\nonumber \right. \\&\times \,\left[ \text{ exp }\left\{ -\left( \sum \limits _{l=1}^{s+k_n}\alpha _lI_l(U_i)\right) \text{ exp }(\beta '{\mathbf{X_i}})\right\} \nonumber \right. \\&\left. -\,\text{ exp }\left\{ -\left( \sum \limits _{l=1}^{s+k_n} \alpha _l I_l(V_i)\right) \text{ exp }(\beta '{\mathbf{X_i}})\right\} \right] ^{\delta _{2i}}\nonumber \\&\left. \times \,\left[ \text{ exp }\left\{ -\left( \sum \limits _{l=1}^{s+k_n}\alpha _l I_l(U_i)\right) \text{ exp }(\beta '{\mathbf{X_i}})\right\} \right] ^{\delta _{3i}}\right\} . \end{aligned}$$

(5)

Note that as pointed out by McMahan et al. (2013), the direct maximization of the function above with the traditional algorithm would suffer numerical instability. Also one may often get local maximizers and have other issues like convergence. In the following, we will augment the observed data.

Let $N_i(t)$ denote the latent Poisson process with the mean function $\Lambda _n (t) \text{ exp }\{\beta '{} \mathbf{X_i}\}$, $i=1, \ldots , n$, and define $Z_i = N_i(t_{1i})$ and $W_i=N_i(t_{2i})-N_i(t_{1i})$ for $\delta _{1i}=0$, where $t_{1i}=V_i I(\delta _{1i}=1)+U_i I(\delta _{1i}=0)$, and $t_{2i}=V_i I(\delta _{2i}=1)+U_i I(\delta _{3i}=1)$. Then $Z_i$ and $W_i$ are Poisson random variables with means $\Lambda _{n}(t_{1i})\text{ exp }\{\beta '{} \mathbf{X_i}\}$ and $\{\Lambda _{n}(t_{2i})-\Lambda _{n}(t_{1i})\}\text{ exp }\{\beta '\mathbf{X_i}\}$, respectively, and they are independent given $\delta _{1i}=0$. Furthermore, note that if $T_i$ is left-censored or interval-censored, we have that

$$\begin{aligned} P(T_i\leqslant t_{1i})=P(N_i(t_{1i})>0) =P(Z_i>0)=1-\text{ exp }\{-\Lambda _{n}(V_i)\text{ exp }(\beta '{\mathbf{X_i}})\} , \end{aligned}$$

or

$$\begin{aligned} P(t_{1i}<T_i\leqslant t_{2i})= & {} P\{N_i(t_{1i})=0, N_i(t_{2i})>0\} =P(Z_i=0, W_i>0)\\= & {} \text{ exp }\{-\Lambda _{n}(U_i)\text{ exp }(\beta '{\mathbf{X_i}})\}-\text{ exp }\{-\Lambda _{n}(V_i)\text{ exp }(\beta '{\mathbf{X_i}})\} , \end{aligned}$$

and for right-censored $T_i$, we have that

$$\begin{aligned} P(T_i\geqslant t_{2i})=P\{N_i(t_{2i})=0\} =P(Z_i=0, W_i=0) =\text{ exp }\{-\Lambda _{n}(U_i)\text{ exp }(\beta '{\mathbf{X_i}})\} . \end{aligned}$$

Thus if the $Z_i$’s and $W_i$’s were observed, the log likelihood function corresponding to $l_{1}^{*}(\beta , \alpha _l)$ would have the form

$$\begin{aligned} l_{1}^{**}(\beta , \alpha _l)= & {} \sum \limits _{i=1}^n \, \text{ log }\{ P_{Z_i}(Z_i)P_{W_i}(W_i)^{\delta _{2i} +\delta _{3i}}\{\delta _{1i}I(Z_i>0)\\&+\,\delta _{2i}I(Z_i=0, W_i>0)+\delta _{3i}I(Z_i=0, W_i=0)\}\} . \end{aligned}$$

In the above, $P_A(.)$ denotes the probability function associated with the random variable A.

In addition, note that one can decompose or write $Z_i$ and $W_i$ as

$$\begin{aligned} Z_i = \sum \limits _{l=1}^k \, Z_{il}, \, W_i=\sum \limits _{l=1}^k \, W_{il} , \end{aligned}$$

the summation of k independent Poisson random variables $Z_{il}$’s and $W_{il}$’s with means $\alpha _l I_l(t_{1i})$ $\text{ exp }(\beta '{\mathbf{X_i}})$ and $\alpha _l\{I_l(t_{2i})-I_l(t_{1i})\}\text{ exp }(\beta '{\mathbf{X_i}})$, respectively. Then by treating $\{ \, (Z_i, W_i, Z_{il}, W_{il},\mathbf{X_{i}^{mis}}) \, \}$ to be known, we would have the complete log likelihood function

$$\begin{aligned} l_{1}^{***}(\beta , \alpha _l)= & {} \sum \limits _{i=1}^n\sum \limits _{l=1}^k \text{ log }\left\{ P_{Z_{il}}(Z_{il})P_{W_{il}}(W_{il})^{\delta _{2i}+\delta _{3i}} \right. \\&\left. \times \, \{\delta _{1i}I(Z_i>0)+\delta _{2i}I(Z_i=0, W_i>0)+\delta _{3i}I(Z_i=0, W_i=0)\}\right\} \end{aligned}$$

corresponding to $l_{1}^{*}(\beta , \alpha _l)$.

Now we are ready to discuss the two steps of the proposed EM algorithm. Let ${\mathbf{O_i}}=(U_i, V_i, \delta _{1i}, \delta _{2i}, \delta _{3i}, \mathbf{X_i^{obs}}, \mathbf{R_i})$ denote the observed data on subject i and $\theta ^\mathbf{(d)}=(\beta ^{(d)'}, \alpha _l^{(d)'}, \gamma ^{(d)'})^{'}$ the estimator of the parameters given after the d iterations. In the E-step of the $(d + 1)$th iteration, we need to determine the expectation $Q ( {\theta }|{\theta }^\mathbf{(d)}) = E [ l_{1}^{***}(\beta , \alpha _l) + l_2 ( \gamma ) | \mathbf{O_i} , \theta ^\mathbf{(d)}]$ or

$$\begin{aligned} Q(\theta |\theta ^\mathbf{(d)})= & {} \sum \limits _\mathbf{i=1}^\mathbf{n}\sum \limits _\mathbf{l=1}^\mathbf{k}[\{\mathbf{E}(\mathbf{Z_{il}}|\mathbf{O_i},{\theta }^\mathbf{(d)} )+(\delta _{\mathbf{2i}} +\delta _{\mathbf{3i}})\mathbf{E}(\mathbf{W_{il}}|\mathbf{O_i},{\theta }^\mathbf{(d)})\}\times \{\mathbf{log}(\alpha _l)+\beta _1'{\mathbf{X_i^{obs}}}\}\\&+\,\{\beta _2'E(Z_{il}{\mathbf{X_i^{mis}}}|\mathbf{O_i},{\theta }^\mathbf{(d)})+\beta _2'(\delta _{i2}+\delta _{i3})E(W_{il}{\mathbf{X_i^{mis}}}|\mathbf{O_i},{\theta }^\mathbf{(d)})\}\\&- \,\alpha _l\text{ exp }(\beta _1'{\mathbf{X_i^{obs}}})E(\text{ exp }(\beta _2'{\mathbf{X_i}^{mis}}|\mathbf{O_i},{\theta }^\mathbf{(d)}))\{(\delta _{1i}+\delta _{2i})I_l(V_i)+\delta _{3i}I_l(U_i)\}]\\&+\,\sum \limits _{i=1}^n \int \text{ log }\{f(\mathbf{X_i^{obs}}, \mathbf{X_i^{mis}}; \gamma )\}{} \mathbf{f}(\mathbf{X_i^{mis}}|\mathbf{O_i},\theta ^\mathbf{(d)})\mathbf{d}{\mathbf{X_i^{mis}}} + \mathbf{l} (\theta ^\mathbf{(d)}) . \end{aligned}$$

In the above, $\beta _1$ and $\beta _2$ denote the components of $\beta$ corresponding to the observed and missing covariates, respectively, and $l (\theta ^\mathbf{(d)})$ is a function of $\theta ^\mathbf{(d)}$ free of $\theta$.

For the determination of the expectations above, we need to calculate

$$\begin{aligned} E(Z_{il}|\mathbf{O_i},{\theta }^\mathbf{(d)} )=\frac{\alpha _l^{(d)}I_l(V_i)E(Z_i|\mathbf{O_i},\theta ^\mathbf{(d)})}{\Lambda ^{(d)}(V_i)}, \end{aligned}$$

and

$$\begin{aligned} E(W_{il}|\mathbf{O_i},{\theta }^\mathbf{(d)} )=\frac{\alpha _l^{(d)}\{I_l(V_i)-I_l(U_i)\}\times E(W_i|\mathbf{O_i},\theta ^\mathbf{(d)} )}{\Lambda ^{(d)}(V_i)-\Lambda ^{(d)}(U_i)}, \end{aligned}$$

where $\Lambda ^{(d)}(\cdot )=\sum \nolimits _{l=1}^k\alpha _l^{(d)}I_l(\cdot )$. Note that if there are no missing covariates, by following Wang et al. (2016), we have that

$$\begin{aligned} E(Z_i|\mathbf{O_i},{\theta ^\mathbf{(d)}} )=\frac{\Lambda ^{(d)}(V_i)\text{ exp }(\beta _1^{(d)'}{\mathbf{X_i}^\mathbf{obs}} +\beta _2^{(d)'}{\mathbf{X_i}^\mathbf{mis}})\delta _{1i}}{1-\text{ exp }\{-\Lambda ^{(d)}(V_i)\text{ exp }(\beta _1^{(d)'}{\mathbf{X_i}^\mathbf{obs}} +\beta _2^{(d)'}{} \mathbf{X_i}^\mathbf{mis})\}} , \end{aligned}$$

and

$$\begin{aligned} E(W_i|\mathbf{O_i},{\theta ^\mathbf{(d)}} )=\frac{\{\Lambda ^{(d)}(U_i)-\Lambda ^{(d)}(V_i)\}\text{ exp }(\beta _1^{(d)'}{\mathbf{X_i}^\mathbf{obs}} +\beta _2^{(d)'}{\mathbf{X_i}^\mathbf{mis}})\delta _{2i}}{1-\text{ exp }[-\{\Lambda ^{(d)}(U_i) -\Lambda ^{(d)}(V_i)\}\text{ exp }(\beta _1^{(d)'}{\mathbf{X_i}^\mathbf{obs}}+\beta _2^{(d)'}{\mathbf{X_i}^\mathbf{mis}})]} . \end{aligned}$$

When there exist missing categorical covariates, by following Herring and Ibrahim (2001), we have that

$$\begin{aligned} E(Z_i|\mathbf{O_i},{\theta ^\mathbf{(d)}} )=\sum \limits _{x_{i}^\mathbf{mis}(j)}\frac{\Lambda ^{(d)}(V_i)\text{ exp }(\beta _1^{(d)'}{\mathbf{X_i}^\mathbf{obs}} +\beta _2^{(d)'}{x_{i}^\mathbf{mis}(j)})\delta _{1i}p_{ij}}{1-\text{ exp }\{-\Lambda ^{(d)}(V_i)\text{ exp }(\beta _1^{(d)'}{\mathbf{X_i}^\mathbf{obs}}+\beta _2^{(d)'}x_{i}^\mathbf{mis}(j))\}} , \end{aligned}$$

and

$$\begin{aligned} E(W_i|\mathbf{O_i},{\theta ^\mathbf{(d)}} )=\sum \limits _{x_{i}^\mathbf{mis}(j)}\frac{\{\Lambda ^{(d)}(U_i) -\Lambda ^{(d)}(V_i)\}\text{ exp }(\beta _1^{(d)'}{\mathbf{X_i}^\mathbf{obs}}+\beta _2^{(d)'}{x_{i}^\mathbf{mis}(j)})\delta _{2i}p_{ij}}{1 -\text{ exp }[-\{\Lambda ^{(d)}(U_i)-\Lambda ^{(d)}(V_i)\}\text{ exp }(\beta _1^{(d)'}{\mathbf{X_i}^\mathbf{obs}}+\beta _2^{(d)'}{x_{i}^\mathbf{mis}(j)})]} . \end{aligned}$$

Here $\mathbf{X_{i}^\mathbf{mis}(j)}$ denotes the jth possible missing data pattern for subject i and $p_{ij}$ the conditional probability of a given missing data pattern, which can be estimated in the dth iteration of the EM algorithm by

$$\begin{aligned} p_{ij}= & {} P({\mathbf{X_i}^\mathbf{mis}} = x_{i}^\mathbf{mis}(j)|\mathbf{O_i,\theta ^\mathbf{(d)}} )\\= & {} \frac{f(U_i, V_i, \delta _{1i}, \delta _{2i}, \delta _{3i}|{{\mathbf{X_i}^\mathbf{obs}}, x_i^\mathbf{mis}(j)})f({\mathbf{X_i}^\mathbf{obs}}, x_i^\mathbf{mis}(j); \gamma ^{(d)})}{\sum \limits _{x_{i}^\mathbf{mis}(j)} f(U_i, V_i, \delta _{1i}, \delta _{2i}, \delta _{3i}|{{\mathbf{X_i}^\mathbf{obs}}, x_i^\mathbf{mis}(j)})f({\mathbf{X_i}^\mathbf{obs}}, x_i^\mathbf{mis}(j); \gamma ^{(d)})} . \end{aligned}$$

For the situation where missing covariates are continuous, the calculation, which will be described at “Appendix I”, will involve integrations and do not have the closed forms.

In the M-step of the $(d + 1)$th iteration, we need to maximize $Q ({{\theta }}, {{\theta }}^{(d)})$. For this, one can solve the following score equations

$$\begin{aligned} \frac{\partial Q}{\partial \beta _1}= & {} \sum \limits _{i=1}^n[\{E(Z_{i}|\mathbf{O_i},{\theta ^\mathbf{(d)}} )+\delta _{2i}E(W_{i}|\mathbf{O_i},{\theta ^\mathbf{(d)}})\}-\{(\delta _{2i}+\delta _{1i})\Lambda (V_i)+\delta _{3i}\Lambda (U_i)\} \nonumber \\&\text{ exp }(\beta _1'{\mathbf{X_i}^\mathbf{obs}})E(\text{ exp }(\beta _2'{\mathbf{X_i}^\mathbf{mis}}))|\mathbf{O_i},{\theta ^\mathbf{(d)}})]{\mathbf{X_i}^\mathbf{obs}}=0, \end{aligned}$$

(6)

$$\begin{aligned} \frac{\partial Q}{\partial \beta _2}= & {} \sum \limits _{i=1}^n\left[ \{E(Z_i{\mathbf{X_i}^\mathbf{mis}}|\mathbf{O_i},{\theta ^\mathbf{(d)}} )+\delta _{2i}E(W_i{\mathbf{X_i}^\mathbf{mis}}|\mathbf{O_i},{\theta ^\mathbf{(d)}})\}\nonumber \right. \\&-\,\{(\delta _{2i}+\delta _{1i})\Lambda (V_i)+\delta _{3i}\Lambda (U_i)\}\nonumber \\&\left. \times \,\text{ exp }(\beta _1'{\mathbf{X_i}^\mathbf{obs}})\frac{\partial E(\text{ exp }(\beta _2'{\mathbf{X_i}^\mathbf{mis}}|\mathbf{O_i},{\theta ^\mathbf{(d)}}))}{\partial \beta _2}\right] =0,\end{aligned}$$

(7)

$$\begin{aligned} \frac{\partial Q}{\partial \alpha _l}= & {} \sum \limits _{i=1}^n[\alpha _l^{-1}\{E(Z_{il}|\mathbf{O_i},{\theta ^\mathbf{(d)}} )+\delta _{2i}E(W_{il}|\mathbf{O_i},{\theta ^\mathbf{(d)}})\}\nonumber \\&-\,\{(\delta _{2i}+\delta _{1i})I_l(V_i)+\delta _{3i}I_l(U_i)\} \nonumber \\&\times \,\text{ exp }(\beta _1'{\mathbf{X_i}^\mathbf{obs}})E(\text{ exp }(\beta _2'{\mathbf{X_i}^\mathbf{mis}}|\mathbf{O_i},{\theta ^\mathbf{(d)}}))]=0, \end{aligned}$$

(8)

$$\begin{aligned} \frac{\partial Q}{\partial \gamma }= & {} \sum \limits _{i=1}^n\frac{\partial [\int \text{ log }\{f(\mathbf{X_i}^\mathbf{obs}, \mathbf{X_i}^\mathbf{mis}; \gamma )\}f(\mathbf{X_i}^\mathbf{mis}|\mathbf{O_i},\theta ^\mathbf{(d)})d{\mathbf{X_i}^\mathbf{mis}}]}{\partial \gamma ^{(d)}}=0 . \end{aligned}$$

(9)

In the above,

$$\begin{aligned}&\frac{\partial E(\text{ exp }(\beta _2'{\mathbf{X_i}^\mathbf{mis}}|\mathbf{O_i},{\theta ^\mathbf{(d)}}))}{\partial \beta _2}=\sum \limits _{x_{i}^\mathbf{mis}(j)}\text{ exp }\left( \beta _2'{ x_i^\mathbf{mis}(j)}\right) x_i^\mathbf{mis}(j)p_{ij},\\&E({\mathbf{X_i}^\mathbf{mis}}|\mathbf{O_i},{\theta ^\mathbf{(d)}})=\sum \limits _{x_{i}^\mathbf{mis}(j)}x_{i}^\mathbf{mis}(j)p_{ij},\\&E(Z_i{\mathbf{X_i}^\mathbf{mis}}|\mathbf{O_i},{\theta ^\mathbf{(d)}} )=\sum \limits _{x_{i}^\mathbf{mis}(j)}\frac{\Lambda ^{(d)}(V_i)\text{ exp }(\beta _1^{(d)'}{\mathbf{X_i}^\mathbf{obs}}+\beta _2^{(d)'}{x_{i}^\mathbf{mis}(j)})x_{i}^\mathbf{mis}(j)\delta _{1i}p_{ij}}{1-\text{ exp }\{-\Lambda ^{(d)}(V_i)\text{ exp }(\beta _1^{(d)'}{\mathbf{X_i}^\mathbf{obs}}+\beta _2^{(d)'}x_{i}^\mathbf{mis}(j))\}}, \end{aligned}$$

and

$$\begin{aligned}&E(W_i{\mathbf{X_i}^\mathbf{mis}}|\mathbf{O_i},{\theta ^\mathbf{(d)}} )\\&\quad =\sum \limits _{x_{i}^\mathbf{mis}(j)}\frac{\{\Lambda ^{(d)}(U_i)-\Lambda ^{(d)}(V_i)\}\text{ exp }(\beta _1^{(d)'}{\mathbf{X_i}^\mathbf{obs}}+\beta _2^{(d)'}{x_{i}^\mathbf{mis}(j)})x_{i}^\mathbf{mis}(j)\delta _{2i}p_{ij}}{1-\text{ exp }[-\{\Lambda ^{(d)}(U_i)-\Lambda ^{(d)}(V_i)\}\text{ exp }(\beta _1^{(d)'}{\mathbf{X_i}^\mathbf{obs}}+\beta _2^{(d)'}{x_{i}^\mathbf{mis}(j)})]}. \end{aligned}$$

The proposed EM algorithm can be summarized as follows.

Step 1. Select the initial estimates $\beta _1^{(0)}, \beta _2^{(0)}, \alpha _l^{(0)}$ and $\gamma ^{(0)}$.

Step 2. At the $(d+1)$th iteration, compute the conditional expectations $E({Z_{i}{} \mathbf{X_i}^\mathbf{mis}}|{} \mathbf{O_i},{\theta ^\mathbf{(d)}})$, $E({W_{i}{} \mathbf{X_i}^\mathbf{mis}}|\mathbf{O_i},{\theta ^\mathbf{(d)}})$, $E(Z_{il}|\mathbf{O_i},{\theta ^\mathbf{(d)}})$, $E(W_{il}|\mathbf{O_i},{\theta ^\mathbf{(d)}})$, $E( Z_{i}|\mathbf{O_i},{\theta ^\mathbf{(d)}})$, and $E(W_i|\mathbf{O_i},{\theta ^\mathbf{(d)}})$.

Step 3. Obtain $\hat{\beta }_\mathbf{1}^{(d+1)}$ and $\hat{\beta }_\mathbf{2}^{(d+1)}$ by solving the Eqs. (6) and (7) with

$$\begin{aligned} \alpha _l^{*(d)}({\beta })=\frac{\sum \nolimits _{i=1}^n\{E(Z_{il}|\mathbf{O_i},{\theta ^\mathbf{(d)}} )+\delta _{2i}E(W_{il}|\mathbf{O_i},{\theta ^\mathbf{(d)}})\}}{\sum \nolimits _{i=1}^n[\{(\delta _{2i}+\delta _{1i})I_l(V_i)+\delta _{3i}I_l(U_i)\}\text{ exp }(\beta _1'{\mathbf{X_i}^\mathbf{obs}})E(\text{ exp }(\beta _2'{\mathbf{X_i}^\mathbf{mis}}|\mathbf{O_i},{\theta ^\mathbf{(d)}}))]}\nonumber \\ \end{aligned}$$

(10)

Step 4. Obtain ${\hat{\alpha }}_l^{(d+1)}({\beta })$ by solving the Eq. (8) and applying the Quasi-Newton method or the Eq. (10) given $\hat{\beta }_\mathbf{1}^{(d+1)}$, $\hat{\beta }_\mathbf{2}^{(d+1)}$.

Step 5. Obtain $\hat{\gamma }^{(d+1)}$ by solving the Eq. (9).

Step 6. Repeat Steps 2–5 until a pre-specified converge criterion is satisfied.

Note that for the application of the method proposed above, one needs to specify $f(\mathbf{X}; \gamma )$, the density function of the covariates. For this, based on Herring and Ibrahim (2001), the standard option is joint normal distribution, Bernoulli distribution or the logistic regression model if missing covariates are continuous, binary, or categorical, respectively. More discussion on this is given below.

4 Asymptotic properties

Let ${{\hat{\theta }}}_n = ( {{\hat{\beta }}}_n , {{\hat{\gamma }}}_n , {{\hat{\Lambda }}}_n )$ denote the sieve maximum likelihood estimator of $\theta$ defined in the previous section and ${{\hat{\theta }}}_n^* = ( {{\hat{\beta }}}_n , {{\hat{\Lambda }}}_n )$. Now we will establish the asymptotic properties of ${{\hat{\theta }}}_n^*$. For this, let $\theta _0^* = ( \beta _{0}, \Lambda _0 )$ denote the true value of $\theta ^*$ and define the distance between $\theta ^{1} = ( {\beta _1}^{1}, {\beta _2}^{1}, \Lambda ^{1} )$ and $\theta ^{2} = ({\beta _1}^{2}, {\beta _2}^{2} , \Lambda ^{2})$ as

$$\begin{aligned} d ( \theta ^{1} , \theta ^{2} ) = \{ \, || {\beta _1}^{1} - {\beta _1}^{2} ||^{2} +|| {\beta _2}^{1} - {\beta _2}^{2} ||^{2}+ || \Lambda ^{1} - \Lambda ^{2} ||_2^{2} \, \}^{1/2} . \end{aligned}$$

In the above, ||v|| denotes the Euclidean norm of a vector v and $||\Lambda ^{1} - \Lambda ^{2}||_2^{2} = \int [ \{\Lambda ^{1}(u) - \Lambda ^{2}(u) \}^{2} + \{ \Lambda ^{1}(v) - \Lambda ^{2}(v)\}^2 ] d f ( u , v )$, where f(u, v) represents the joint density function of U and V. Then we have the following consistency and asymptotic normality results.

Theorem 1

Assume that the regularity conditions given in “Appendix A.2” hold. Then as $n\rightarrow \infty$, we have that $d ( {{\hat{\theta }}}_n , \theta _0 ) \rightarrow 0$ almost surely and

$$\begin{aligned} \sqrt{n} ( {{\hat{\beta }}}_n - \beta _0 ) \rightarrow N(0, \Sigma ) \end{aligned}$$

in distribution with $\Sigma$ given in “Appendix A.2”.

The proof of the results above is sketched in “Appendix A.2”. For inference about $\beta$, it is apparent that one needs to estimate $\Sigma$ and one common approach would be to employ the Louis’s Formula. However, it can be seen below that this would be computationally intensive for the situation considered here and thus by following Wen and Lin (2011) and others, we propose to employ the nonparametric bootstrap method (Efron 1981; Su and Wang 2016). Specifically, let Q be an integer and for each $1\le q \le Q$, draw a new data set, denoted by $O^{(q)}$, of the sample size n with replacement from the original observed data $\{ \, O_i ; \,i = 1,\ldots , n \, \}$. Let ${{\hat{\beta }}}^{(q)}_n$ denote the estimator of $\beta$ defined above based on the bootstrap samples $O^{(q)}$, $q = 1, ... , Q$. respectively. Then one can estimate the covariance matrix of ${{\hat{\beta }}}_n$ by using the sample covariance matrix of the ${{\hat{\beta }}}_n^{(q)}$’s and the numerical results below suggest that this approach seems to work well.

5 A simulation study

In this section, we present some results obtained from a simulation study to evaluate the finite sample performance of the sieve maximum likelihood estimation procedure proposed in the previous sections. In the study, it was assumed that there exist two covariates $\mathbf{X_{i}^{obs}}$ and $\mathbf{X_{i}^{miss}}$. Note that as discussed above, we can write $f(\mathbf{X^{obs}}, \mathbf{X^{miss}};\gamma )$ as

$$\begin{aligned} f(\mathbf{X_{i}^{obs}}, \mathbf{X_{i}^{mis}}; \gamma )=f(\mathbf{X_{i}^{obs}})f(\mathbf{X_{i}^{mis}}|\mathbf{X_{i}^{obs}}; \gamma ) . \end{aligned}$$

For the generation of the covariates, we assumed that $f(\mathbf{X_{i}^{obs}})$ is Bernoulli(0.6) or normal(1, 0.25), and set $f(\mathbf{X_{i}^{miss}}\mid \mathbf{X_{i}^{obs}})$ to be

$$\begin{aligned} Bernoulli\left( 0.5\mathbf{X_{i}^{obs}}+0.73(1-\mathbf{X_{i}^{obs}})\right) \, \text {or} \,normal(1.5+\mathbf{X_{i}^{obs}},0.25) . \end{aligned}$$

Given the covariates, the failure times of interest $T_i$’s were generated based on model (1) with $\Lambda _0 (t) = t^3$, t or $\Lambda _{0}(t)=log(1+t)$. For the missing mechanism, we considered the following two situations

$$\begin{aligned} P(R_{i}=1|O_{i})=\frac{\text{ exp }\{U+V+\mathbf{X^{obs}_{i}}\}}{{1+\text{ exp }\{U+V+\mathbf{X^{obs}_{i}}\}}} , \end{aligned}$$

and

$$\begin{aligned} P(R_{i}=1|O_{i})=\frac{\text{ exp }\{0.22U+0.22V+0.22{ \mathbf{X}^{obs}_{i}}\}}{{1+\text{ exp }\{0.22U+0.22V+0.22\mathbf{X^{obs}_{i}}\}}}, \end{aligned}$$

which will be referred to as set-ups I and II and correspond to the missing rates of $30\%$ and $40\%$, respectively. For the generation of the observation times or censoring intervals, it was assumed that the $U_i$’s and $V_i$’s follow the uniform distribution over the region $\{(u,v): 0\le u\le 0.28, u+0.8\le v \le 1.2\}$. The results given below are based on the sample size $n = 200$ with 1000 replications.

Table 1 Estimation of regression parameters $\beta _{1}$ and $\beta _{2}$ with $\Lambda _{0}(t) = t^{3}$, $30\%$ missing and censoring rates

Table 1 gives the obtained results on estimation of the regression parameters $\beta _1$ and $\beta _2$ with their true values being $\{0.2, 0.5\}$ and $\{0.5, 1\}$, respectively, and under the set up I for the missing mechanism. Here for the I-spline approximation to the cumulative baseline hazards function, we took $s = 3$, the degree or order of the spline basis functions, and $k_n = 5$, the number of knots, and chose the knots equally spaced between the smallest and largest observation times by following Wang et al. (2016). In the table, we calculated the estimated bias given by the average of the estimates minus the true value (Bias), the sample standard error (SE), the average of the estimated standard error (ESE), and the $95\%$ empirical coverage probability (CP). For comparison, we also applied the naive or complete data approach, which deletes the subjects with missing covariates, and the full data approach, assuming no missing covariates, which are denoted by CC and Full in the table, respectively. In addition, we also considered the most commonly used multiple imputation method (Horton and Kleinman 2007; Schomaker and Heumann 2018), denoted by MI in the table.

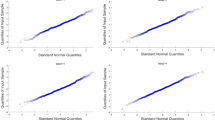
One can see from Table 1 that the proposed method seems to give good performance, which is similar to that of the Full approach. Both are better than the CC method and in particular, the CC methods gave larger biases. The results also suggest that the proposed method gave much better performance than the multiple imputation method, which clearly should not be used for estimation of $\beta _2$. In addition, the results on the coverage probabilities indicate that the normal approximation to the distribution of the proposed estimator appears to be reasonable. To further see this, we investigated the quantile plots of the standardized estimator against the standard normal distribution and present them in Fig. 1, which again suggest the normal approximation is appropriate.

Fig. 1

Quantile plots of the standardized estimates of a $\beta _1$ with $\beta _{1} = \beta _2 =0.5$, (b) $\beta _{2}$ with $\beta _{1} = \beta _2 =0.5$, c $\beta _1$ with $\beta _{1} = 0.5$ and $\beta _2 = 1$, and d $\beta _2$ with $\beta _{1} = 0.5$ and $\beta _2 = 1$

Table 2 Estimation of regression parameters $\beta _{1}$ and $\beta _{2}$ with $\Lambda _{0}(t) = t^{3}$ and $40\%$ missing rate and $30\%$ censoring rate

Table 3 Estimation of regression parameters $\beta _{1}$ and $\beta _{2}$ with $\Lambda _{0}(t) = t$ and $30\%$ missing rate and $30\%$ censoring rate

Table 4 Estimation of regression parameters $\beta _{1}$ and $\beta _{2}$ with continuous covariates, $\Lambda _{0}(t)=t^{3}$, and $30\%$ missing and censoring rates

Table 5 Estimation of regression parameters $\beta _{1}$ and $\beta _{2}$ with $\Lambda _{0}(t)=log(1+t)$ and $30\%$ missing and censoring rates

Table 6 Estimation of regression parameters $\beta _{1}$ and $\beta _{2}$ with $\Lambda _{0}(t) = t^{3}$ and $30\%$ missing rate and $50\%$ censoring rate

Tables 2, 3, 4, 5 and 6 present the estimation results obtained similarly as Table 1. Specifically, in Tables 2 and 3, the same set-up as Table 1 was used except that Table 2 considered the set up II for the missing mechanism and Table 3 used $\Lambda _0 (t) = t$. In Table 4, instead of discrete covariates, both covariates were generated from the normal distribution mentioned above and Table 5 investigated the situation where $\Lambda _{0}(t)=log(1+t)$ with all other set-ups being the same as in Table 1. Instead of 30% censoring rate, we considered 50% censoring rate in Table 6 also with the other set-ups being the same as in Table 1. One can see that in all situations, the proposed method and the Full approach gave similar performance and both seem to do well. In contrast, both the CC method and the multiple imputation method may yield biased estimates and low coverage probabilities.

As pointed out above, the focus here has been on the situation with missing at random and a natural question is how the proposed method would perform if one faces non-ignorable missing. To see this, we repeated the study giving Table 1 except that instead of set up I for the missing mechanism, we considered the following mechanism

$$\begin{aligned} P(R_{i}=1|O_{i})=\frac{\text{ exp }\{0.5U+0.22V+0.22{ \mathbf{X}^{obs}_{i}}+0.22{ \mathbf{X}^{miss}_{i}}\}}{{1+\text{ exp }\{0.5U+0.22V+0.22{ \mathbf{X}^{obs}_{i}}+0.22\mathbf{X^{miss}_{i}}\}}} . \end{aligned}$$

Table 7 gives the results on estimation of the regression parameters $\beta _1$ and $\beta _2$ given by the four methods discussed above and they suggest that again both the proposed method and the Full method gave good performance. However, the CC and multiple imputation methods did not seem to provide reasonable results. Of course, one may be careful about the proposed method since no theoretical justification can be provided yet.

Table 7 Estimation of regression parameters $\beta _{1}$ and $\beta _{2}$ with $\Lambda _{0}(t) = t^{3}$ and $30\%$ missing and censoring rates under the non-ignorable missing mechanism

6 An application

Now we apply the sieve maximum likelihood estimation procedure proposed in the previous sections to the set of data arising from Alzhehelmer’s Disease Neuroimaging Initiative, discussed by Li et al. (2020) among others. It is a longitudinal study and among others, one variable of interest is the Alzheimers disease (AD) conversion. Due to the nature of the study, only interval-censored data are available on the occurrence time of the AD conversion, and the participants in the study are classified into three groups based on their cognitive conditions, cognitively normal, mild cognitive impairment and Alzheimer’s disease. By following Li et al. (2020) and others, we will focus on the patients in the mild cognitive impairment group to determine significant baseline prognostic factors or covariates for the AD conversion.

The data consist of five baseline covariates. They are the Rey Auditory Verbal Learning Test (RAVLT), the Middle temporal gyrus (MidTemp) from Neuroimaging, the participants’s Alzheimer’s Disease Assessment Scale 13 items (ADAS13), the functional assessment questionnaire score (FAQ), and the participant’s baseline age (Age). Among the 396 participants in the mild cognitive impairment group, around $20\%$ of them have missing information on the MidTemp. Also there are 3 subjects with missing ADAS13 and 3 subjects with missing FAQ, and in the analysis below, we will exclude these six subjects for simplicity. As mentioned above, Li et al. (2020) discussed the same problem but they only considered the situation where there do not exist missing covariates.

Table 8 Analysis results of Alzhehelmer’s Disease data

Table 8 presents the analysis results given by the proposed sieve maximum likelihood estimation procedure, including the estimated covariate effect (Estimate), the estimated standard error (SE) and the p-value for testing the covariate effect being zero. For comparison, we also include in the table the results given by Li et al. (2020) based on the 316 subjects with complete information on the MidTemp. One can see that the proposed method suggests that except Age, all other four covariates, RAVLT, MidTemp, ADAS13 and FAQ, had significant effects on the AD conversion. In contrast, the approach that ignored the missing information indicates that MidTemp may only have some mild effect and ADAS13 had no effect on predicting the AD conversion. In addition, as expected, the proposed method gave more efficient estimates than Li et al. (2020) for all covariates.

7 Discussion and concluding remarks

In this paper, we discussed the inference about the proportional hazards model when one faces interval-censored failure time data with missing covariates, and for the problem, a sieve maximum likelihood estimation procedure was proposed. In the method, I-spline functions were employed to approximate the unknown baseline cumulative hazard function and a Poisson-based EM algorithm was developed. The proposed estimator of regression parameters were shown to be consistent and asymptotically normal, and the numerical studies indicated that the proposed method seems to work well for practical situations and should be used when covariates are missing at random.

As pointed out above, the focus here has been on the situation where covariates may be missing at random, meaning that the missingness depends only on the observed values. It is worth to note that sometimes one may face more complicated situations where the missingness could depend on both observed and missing values, which is often referred to as nonignorable missing (Du et al. 2021). For the latter case, a valid inference procedure usually requires one to make some assumptions on or model the missingness, and it is easy to see that for the situation, one could often have to deal with the model misspecification issue.

There exist several directions for future research. One is that the focus here has been on the proportional hazards model (1) and it is apparent that the same type of missing data could happen to other commonly used regression models such as the additive hazards model or the linear transformation model. It would be useful to develop some estimation procedures similar to that proposed above for these latter models. In the preceding sections, we have assumed that covariates are time-independent and it is clear that sometimes there may exist time-dependent covariates. Thus it would be helpful to generalize the proposed approach to allow for time-dependent covariates. Also in the above, it has been assumed that we observe case II interval-censored data and as pointed out by some authors, in practice, one may face a more general type of interval-censored data, case K interval-censored data (Sun 2006; Wang et al. 2016). It is apparent that the method given above cannot be directly applied to this latter situation and in other words, some generalizations of it are needed.

Appendix

1.1 A.1.E-step of the EM algorithm for continuous covariates

In the E-step of the EM algorithm developed in Sect. 3, we need to calculate the expectations $E(Z_i|\mathbf{O_i},\theta ^\mathbf{(d)} )$ and $E(W_i|\mathbf{O_i},\theta ^\mathbf{(d)} )$. As described there, when missing covariates are categorical, they are some summations and can be expressed in the closed form. However, for continuous covariates, this will not be the case and instead we have to deal with the integrals that do not have a closed form. More specifically, we have that

$$\begin{aligned} E(Z_i|\mathbf{O_i},\theta ^\mathbf{(d)} )= & {} \int _{\mathbf{X_{miss}}}\frac{\varvec{\Lambda }^{(\mathbf{d})}(\mathbf{V_i})\mathbf{exp}(\beta _\mathbf{1}^{(\mathbf{d})'}{\mathbf{X_i}^\mathbf{obs}}+\beta _\mathbf{2}^{(\mathbf{d})'}{} \mathbf{X_{i}^{miss}})\delta _\mathbf{1i}}{1-\mathbf{exp}\{-\varvec{\Lambda }^{(\mathbf{d})}(\mathbf{V_i})\mathbf{exp}(\beta _\mathbf{1}^{(\mathbf{d})'}{\mathbf{X_i}^\mathbf{obs}}+\beta _\mathbf{2}^{(\mathbf{d})'}{} \mathbf{X_{i}^{miss}})\}}\\&\times p(\mathbf{X_{i}^{miss}}|{\mathbf{O_i}},{\theta ^{(\mathbf{d})}} )\mathbf{dX_{i}^{miss} }, \end{aligned}$$

and

$$\begin{aligned} E(W_i|\mathbf{O_i},\theta ^\mathbf{(d)} )= & {} \int _\mathbf{{{X_{i}^{miss}}}}\frac{\{{\varvec{\Lambda }}^{\mathbf{(d)}}(\mathbf{U_i}) -{\varvec{\Lambda }}^{\mathbf{(d)}}(\mathbf{V_i})\}{\mathbf{exp}}(\beta _\mathbf{1}^{(\mathbf{d})'}{\mathbf{X_i}^{\mathbf{obs}}} +\beta _\mathbf{2}^{(\mathbf{d})'}{} \mathbf{X_{i}^{miss}})\delta _{\mathbf{2i}}}{1-{\mathbf{exp}}[-\{{\varvec{{\Lambda }}}^{(\mathbf{d})}(\mathbf{U_i})- {\varvec{\Lambda }}^{(\mathbf{d})}(\mathbf{V_i})\}\text{ exp }(\beta _\mathbf{1}^{(\mathbf{d})'}{\mathbf{X_i}^{\mathbf{obs}}}+\beta _\mathbf{2}^{(\mathbf{d})'}{} \mathbf{X_{i}^{miss}})]}\\&\times p(\mathbf{X_{i}^{miss}}|{\mathbf{O_i}},{\theta ^{(\mathbf{d})})}{} \mathbf{dX_{i}^{miss}} \end{aligned}$$

by using the notation defined before.

To calculate the integrals above, by following Herring and Ibrahim (2001), one can employ the Monte-Carlo estimation approach, which draws the sample from

$$\begin{aligned} p_{ij}= & {} P(\mathbf{X_i^{mis}}|{\mathbf{O_i},\theta ^\mathbf{(d)}} )=\frac{\mathbf{f}(\mathbf{U_i}, \mathbf{V_i}, \delta _{\mathbf{1i}}, \delta _{\mathbf{2i}}, \delta _{\mathbf{3i}}|{{\mathbf{X_i}^{\mathbf{obs}}},\mathbf{X_i}^{\mathbf{mis}}})\mathbf{f}({\mathbf{X_i}^{\mathbf{obs}}}, \mathbf{X_i}^{\mathbf{mis}}; \gamma ^{(\mathbf{d})})}{\int _{\mathbf{X_{i}^{mis}}} \mathbf{f}(\mathbf{U_i}, \mathbf{V_i}, \delta _{\mathbf{1i}}, \delta _{\mathbf{2i}}, \delta _{\mathbf{3i}}|{{\mathbf{X_i}^{\mathbf{obs}}}, \mathbf{X_i}^{\mathbf{mis}}})\mathbf{f}({\mathbf{X_i}^{\mathbf{obs}}}, \mathbf{X_i}^{\mathbf{mis}}; \gamma ^{(\mathbf{d})})}\\\propto & {} \mathbf{f}(\mathbf{U_i}, \mathbf{V_i}, \delta _{1i}, \delta _{2i}, \delta _{3i}|{{\mathbf{X_i}^{\mathbf{obs}}}, \mathbf{X_i}^{\mathbf{mis}}})\mathbf{f}({\mathbf{X_i}^{{\mathbf{obs}}}}, \mathbf{X_i}^{\mathbf{mis}}; \gamma ^{(\mathbf{d})}) . \end{aligned}$$

Note that $f(U_i, V_i, \delta _{1i}, \delta _{2i}, \delta _{3i}|{{\mathbf{X_i}^{\mathbf{obs}}}, \mathbf{X_i}^{\mathbf{mis}}})$ is log-concave (Ibrahim et al. 1999) and if $f({\mathbf{X_i}^{\mathbf{obs}}},\mathbf{X_i}^{\mathbf{mis}};\gamma ^{(\mathbf{d})})$ belongs to the exponential family, the logrithm of $P(\mathbf{{ X_i^{mis}}}|{\mathbf{O_i},\theta ^\mathbf{(d)}} )$ is concave. It follows that one can use the Gibbs sampler (Gilks and Wild 1992) and adaptive rejection algorithm (Gilks and Wild 1992) to sample from $P({ \mathbf{X_i^{mis}}}|{\mathbf{O_i},\theta ^\mathbf{(d)}} )$.

More specifically for the determination of $E(Z_i|\mathbf{O_i},\theta ^\mathbf{(d)} )$, for each subject with missing covariate $\mathbf{X_{i}^{miss}}$, we first apply the Gibbs sampler and adaptive reject algorithm to draw the sample $s_{i,1},...,s_{i,n_{i}}$ of size $n_i$ from $p(\mathbf{X_{i}^{miss}|O_{i}},\theta ^{\mathbf{(d)}})$. Then the conditional expectation can be approximated by

$$\begin{aligned} E(Z_i|\mathbf{O_i},\theta ^\mathbf{(d)} )=\frac{1}{\mathbf{n_{i}}}\sum _{\mathbf{k=1}}^{\mathbf{n_{i}}}\frac{{\varvec{\Lambda }}^{(\mathbf{d})}(\mathbf{V_i}){\mathbf{exp}}(\beta _\mathbf{1}^{(\mathbf{d})'}{\mathbf{X_i^{obs}}}+\beta _\mathbf{2}^{(\mathbf{d})'}{\mathbf{s_{i,k}}})\delta _{\mathbf{1i}}}{1-{\mathbf{exp}}\{-{{\varvec{\Lambda }}}^{(\mathbf{d})}(\mathbf{V_i}){\mathbf{exp}}(\beta _\mathbf{1}^{(\mathbf{d})'}{\mathbf{X_i^{obs}}}+\beta _\mathbf{2}^{(\mathbf{d})'}{} \mathbf{s}_{\mathbf{i,k}})\}} . \end{aligned}$$

In comparison to the categorical covariate situation, the above operation can be regarded as replacing each $x_{i}^{miss}$ by $n_{i}$ sampled values with equal weight. It is apparent that $E(W_i|\mathbf{O_i},\theta ^\mathbf{(d)} )$ can be calculated similarly.

1.2 A.2.Proofs of the asymptotic properties

In this Appendix, we will sketch the proof for the consistency and asymptotic normality of the proposed estimators given in Theorem 1 by employing the empirical process theory and nonparametric techniques. Define ${P}f=\int f(x)dP(x)$ and ${P}_n f = n^{-1} \sum \limits _{i=1}^{n} f(X_i)$ for a function f, a probability function P and a sample $X_1, \ldots , X_n$. For the proof, we need the following regularity conditions.

• (A1) Assume that $\Lambda (\tau _1)<\infty$, $\Lambda (\tau _2)<\infty$, and there exists a positive constant a such that $P ( V - U> a ) > 0$. Also the union of the supports of U and V is contained in the interval $[r_1, r_2]$ with $0<r_1<r_2< +\infty$.

• (A2) The function $\Lambda _0$ is continuously differentiable on $[r_1, r_2]$, and satisfies $M^{-1}<\Lambda _0(r_1)<\Lambda _0(r_2)< M$ for some positive constant M.

• (A3) The set of covariates (X, Z) has bounded support.

• (A4) The conditional distribution $f(\mathbf{X_i^{mis}}|\mathbf{X_i^{obs}}; \gamma )$ is identifiable and has continuous second-order derivatives with respect to $\gamma$, and $-E_0[\partial ^2/\partial \gamma ^2)\text{ log }f(\mathbf{X_i^{mis}}|\mathbf{X_i^{obs}}; \gamma _0)]$ is positive definite.

• (A5) For any $({\theta }, \varvec{\Lambda })$ near $({ \theta _\mathbf{0}}, {\varvec{\Lambda }_\mathbf{0}})$, ${P}_0(\text{ log }L({\theta , \varvec{\Lambda }})-\text{ log }L({\theta _\mathbf{0}, \varvec{\Lambda }_\mathbf{0}})\leqslant -K(||\theta -\theta _\mathbf{0}||^2+||\varvec{\Lambda }-\varvec{\Lambda }_\mathbf{0}||^2)$ for a fixed constant $K>0$.

First we will prove the consistency and for this, we will verify the conditions of Theorem 5.7 of Van der Vaart (1998). Let $BV_\omega [r_1, r_2]$ denote the functions whose total variation in $[r_1, r_2]$ are bounded by a given constant. Then the class of functions

$$\begin{aligned} F_\omega =\left\{ \int \limits _{0}^{U_k}\text{ exp }\{\beta ^{T}X_i\}d\Lambda (s): \Lambda \in BV_\omega [r_1, r_2]\right\} \end{aligned}$$

is a convex hull of functions $\{I(U_k\geqslant s)\text{ exp }\{\beta ^{T}X_i\}$ and thus it is a Donsker class. Furthermore,

$$\begin{aligned} \text{ exp }\left( -\int \limits _{0}^{U_k}\text{ exp }\{\beta ^{T}X_i\}d\Lambda (s)\right) -\text{ exp }\left( -\int \limits _{0}^{U_{k+1}}\text{ exp }\{\beta ^{T}X_i\}d\Lambda (s)\right) \end{aligned}$$

is bounded away from zero. Therefore, $l(\theta , {\hat{\alpha }}|\mathbf{O})=\text{ log }L(\theta , {\hat{\alpha }}|\mathbf{O})$ belongs to some Donsker class due to the preservation property of the Donsker class under Lipschitz-continuous transformations. Then we can conclude that $\sup _{\theta \in \Theta _n}|{P}_nl(\theta , {\hat{\alpha }}|\mathbf{O})-{P}_nl(\theta _0, {\hat{\alpha }}|\mathbf{O})|$ converges in probability to 0 as $n\rightarrow 0$.

Now we verify that another condition of Theorem 5.7 of Van der Vaart (1998) also holds. That is, for any $\varepsilon >0$, we have

$$\begin{aligned} \sup _{d(\theta , \theta _0)>\varepsilon }Pl(\theta ,{\hat{\alpha }}|\mathbf{O}) <Pl(\theta _0, {\hat{\alpha }}|\mathbf{O}) . \end{aligned}$$

Note that this condition is satisfied if we can prove the model is identifiable. According to condition (A4) and similar arguments to the proof of Theorem 2.1 of Chang et al. (2007), we can show the identifiability of the model parameters. Now, by Theorem 5.7 of Van der Vaart (1998), we have $d({\hat{\theta }}_n, \theta _0)= o_p(1)$, which completes the proof of consistency.

Before proving the asymptotic normality, we will need to establish the convergence rate. For this, we will first define the covering number of the class ${{\mathcal {L}}}=\{l(\theta ,{\hat{\alpha }}|\mathbf{O}):\theta \in \Theta \}$ and establish a needed lemma.

Lemma 1

Assume that Conditions (A1), (A3)–(A4) hold. Then the covering number of the class ${{\mathcal {L}}} = \{l(\theta ,{\hat{\alpha }}|\mathbf{O}): \theta \in \Theta \}$ satisfies

$$\begin{aligned} N(\epsilon , {{\mathcal {L}}}, L_2(P))=O(\epsilon ^{-1}). \end{aligned}$$

Proof of Lemma 1

The proof is similar to that of Zeng et al. (2016) and Hu et al. (2017) and thus omitted.

To establish the convergence rate, for any $\eta >0$, define the class ${{\mathcal {F}}}_\eta =\{l(\theta _{n0}, {\hat{\alpha }}|\mathbf{O})-l(\theta , {\hat{\alpha }}|\mathbf{O}): \theta \in \Theta , d(\theta , \theta _{n0})\leqslant \eta \}$ with $\theta _{n0}=(\beta _0,\Lambda _{n0})$. Following the calculation of (Shen and Wong 1994, p. 597), we can establish that $\text{ log }N_{[]}(\epsilon , {{\mathcal {F}}}_{\eta }, \parallel .\parallel _{2})\leqslant CN \text{ log }(\eta /\epsilon )$ with $N=m+1$, where $N_{[]}(\epsilon , {{\mathcal {F}}}_{\eta }, d)$ denotes the bracketing number (see the Definition 2.1.6 in Van Der Vaart and Wellner 1996) with respect to the metric or semi-metric d of a function class ${{\mathcal {F}}}$. Moreover, some algebraic calculations lead to $\parallel l(\theta _{n0},{\hat{\alpha }}|\mathbf{O})-l(\theta , {\hat{\alpha }}|\mathbf{O})\parallel _{2}^2\leqslant C\eta ^2$ for any $l(\theta _{n0}, {\hat{\alpha }}|\mathbf{O})-l(\theta , {\hat{\alpha }}|\mathbf{O})\in {{\mathcal {F}}}_\eta$. Therefore, by Lemma 3.4.2 of Van Der Vaart and Wellner (1996), we obtain

$$\begin{aligned} E_p\parallel n^{1/2}(P_n-P)\parallel _{{\mathcal {F}}_{\eta }}\leqslant CJ_\eta (\epsilon , {{\mathcal {F}}}_\eta , \parallel .\parallel _{2})\left\{ 1+\frac{J_\eta (\epsilon ,{{\mathcal {F}}}_\eta , \parallel .\parallel _{2})}{\eta ^2n^{1/2}}\right\} , ~~~~~~~~(S) \end{aligned}$$

where $J_{[ ]}(\eta , {{\mathcal {F}}}_\eta , \parallel .\parallel _{2})=\int _{0}^\eta \{logN_{[]}(\epsilon , {{\mathcal {F}}}_{\eta }, \parallel .\parallel _{2})\}^{1/2}d\epsilon$. The right-hand side of (S) yields $\phi _n(\eta )=C\eta ^{1/2}(1+\frac{\eta ^{1/2}}{\eta ^{2} n^{1/2}}M_1),$ where $M_1$ is a positive constant. Then $\phi _n(\eta )/\eta$ is a decreasing function, and $n^{2/3}\phi _n(-1/3)=O(n^{1/2})$. According the theorem 3.4.1 of Van Der Vaart and Wellner (1996), we can conclude that $d({\hat{\theta }}, \theta _0)=O_p(n^{-1/3})$.

Now we prove the asymptotic normality of ${\hat{\beta }}_n$. Following the proof of Theorem 2 in Zeng et al. (2016), one can obtain that

$$\begin{aligned} \sqrt{n} ( {{\hat{\beta }}}_n - \beta _0 )=(E[\{l_\beta -l_\Lambda (s^*)\}\{l_\beta -l_\Lambda (s^*)\}^{T})^{-1}G_n\{l_\beta -l_\Lambda (s^*)\}+o_p(1), \end{aligned}$$

where $l_\beta$ is the score function for $\beta$, $l_\Lambda (s^*)$ is the score function along this submodel $d\Lambda _{\epsilon , s^*}=(1+\epsilon s^*)d\Lambda$. This implies that the influence function for ${\hat{\beta }}_n$ is exactly the efficient influence function, so that $\sqrt{n} ( {{\hat{\beta }}}_n - \beta _0 )$ converges to a zero-mean normal random vector whose covariance matrix attains the semiparametric efficiency bound. $\square$