Introduction

Researchers are working on nanomaterials for various technological usages. Battery cells, solar energy, renewable energy resources, cancer therapy, and biological importance are examples of nanomaterials. The synthesis of nanomaterials and the stable dispersion of the nanocomposites in the common working liquid are recently used in heat transfer analysis and medication. Choi [1] explained in his paper that the accumulation of nanoparticles considerably improved the thermo-physical properties of base liquids. Choi is mainly attributed with the invention of the term “nanofluid.” The most exciting aspect of these nanomaterials is their ultra-fine size, which ranges from 1 to 100 nm. While just examining a 5% volume concentration of nanoparticles, Eastman et al. [2] estimated a rise of 60% in the thermal enhancement using the CuO, Al2O3, and Cu nanoparticles. Because of nanofluids’ unique properties, a number of scientists and academics have indicated an interest in researching different elements of nanofluid flow along with heat exchange phenomena. To address the enhanced heat transmission capacities of nanofluids, Yusuf [3] investigated the dynamics of nanofluid flows with irreversibility analysis. Abdelsalam and Bhatti [4] conducted a numerical investigation into the characteristics of a hybrid nanofluid model containing nano-diamonds and silica. The study focused on a catheterized tapered artery, exploring three distinct configurations under the influence of both a magnetic field and heat transfer. A mathematical model for convective energy transmission of a nanocomposite in conjunction with a flat plate in a two-slip process combination is also put out by Kuznetsov and Nield [5]. Numerous researchers have conducted in-depth studies on the movement of nanofluids and the transfer of energy, such as those by [6,7,8,9,10].

The combination of two chemically distinct nanoparticles in the same base liquid performs hybrid nanofluid. Micromachining, medicinal lubricating, mobility, acoustical, maritime constructions, and solar heating are only a few of the business, intellectual, and technological implications of hybrid nanofluid. Hybrid nanofluid is receiving a lot of interest from designers, researchers, and engineers. To comprehend the rheological characteristics of flow using hybrid nanofluids, numerous scientists and researchers have recently carried out theoretical and numerical studies. The first investigation into the thermophysical transmission capabilities of hybrid nanofluids was published by Jana et al. [11]. The uses, synthesis, and thermos-physical characteristics of hybrid composites were looked into by Sarkar et al. [12] and Nasir et al. [13], respectively. Based on Tiwari and Das’ nanofluid simulation theory, Devi and Devi [14] improved the thermal properties for nanocomposites and used them on an expanding stream model. The same kind of approach for the improvement of energy transmission can be seen in [15,16,17,18,19,20]. These ideas were used to enhance thermal efficiency in a more reliable way.

The effect of buoyancy and stability phenomena over the rotating sphere is examined by Rajasekaran et al. [21]. The movement normally starts inside the viscous layer and then, becomes completely established and steady after a while. The flow is often independent of circumstances at the stagnation point, the upper end, or far above since the accelerating instability and friction force are handled over a short period. Mahdy [22], in contrast, investigated the Casson fluid flow in terms of the stagnation point considering the sphere surface. Mahdy and Hossam [23] presented the time-dependent flow of the nanofluid over the surface of a gyrating sphere for the applications of heat transfer. The flow phenomena in a rotating system using the same idea were done by Chamkha et al. [24]. The same kind of approach can also be seen in [25,26,27,28]. In the case where shear strain is trifling, the Casson fluid exhibits elastic behavior, and in the case when the shear strain is considerable, the Casson fluid exhibits Newtonian behavior. Recently, the numerical investigation and various features of nanofluid are studied by Nasir et al. [29]. Boyd et al. [30] scrutinized the Casson fluid, in terms of varying blood flow. In the spinning sphere’s forward stagnation zone, under various wall circumstances, Chamkha et al. [31] looked into the unstable heat and mass transport flow.

Substantial practical implementations of the computation of nonlinear convectional flow over a rotational sphere include spin-stabilized rockets, textile painting, simulation of several geoscience vortices, conditioning of rotational parts of machines and spinning equipment layout. Therefore, for the past few decades, it has been essential to analyze boundary layer flow caused by sphere rotations in stationary fluid or a uniform streaming. Sir George Stokes [32] was the first to investigate the flow carried on a sphere’s spinning in 1845. Howarth [33] examined the stream across a spinning sphere after a period had passed and determined an approximation to the solutions for the flow away from the equator. In their later publications, Raza et al. [34], Acharya et al. [35] and Dawar and Acharya [36] proposed theoretical solutions to the issue under the presumption of boundary layer approach. Recently, Patil et al. [37] examined the mix convectional nanofluid stream with triple diffusive effect over a rotating sphere for cooling purposes in various industrial disciplines.

Following a comprehensive review of the available literature, we have chosen to offer an analytical approach focused on the fundamental themes related to the Casson flow of hybrid nanofluids. In the current research, unsteady motion, heat and mass transport for hybrid nanofluids including CuO and Cu nanoparticles that are flowing through a sphere are examined. To study the flow phenomena, a variety of mathematical and physical performances are used, including chemical reaction, MHD, and second-order convection. Finally, the physical depiction of the collected analytical results for various essential aspects is visualized graphically as well as in tabular form. The results of current model have potential advantages in the biomedical applications, transport mechanism in capillaries, design and production of spherical designed components, spacecraft, manufacturing of ship, temperature control of twisting parts of machines, configuration of spinning industrial equipment, etc., in which nonlinear convectional stream can help by supplying various control parameters to improve thermal and mass transport in the production of spherical bodies. Additionally, in the industrial sectors, the construction and assembling of spherical shapes utilize diffusive liquids such as hydrogen and ammonia and nanoparticles to control heat and mass transport.

Flow configuration and mathematical formulation

Description of physical problem

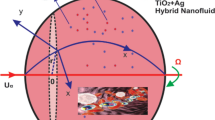
Let us investigate the unsteady mixed convection flow of Casson hybrid nanofluid across a gyrating sphere’s stagnation area. Blood is the basic fluid, and it includes two types of nanomaterials: copper oxide and copper. As indicated in Fig. 1a, W denotes the sphere’s angular velocity. The x-axis and y-axis are perpendicular to each other which is defined on the surface of sphere. Transverse perception is used to describe the flow field and magnetic field \(B(t) = B_{0} t^{{\frac{ - 1}{2}}}\). The sphere’s surface temperature and concentration are assumed as \(T_{{\text{w}}}\) and \(C_{{\text{w}}}\), whereas the surrounding temperature and concentration are \(T_{\infty }\) and \(C_{\infty }\), respectively, unknown. Moreover, the following is the rheological formulation for a Casson fluid [37]:

$$ \tau_{{{\text{mn}}}} = \left\{ {2\left( {\frac{{P_{{\text{y}}} }}{{\sqrt {2\pi } }} + \mu_{{\text{c}}} } \right),e_{{{\text{mn}}}} ,\;\;\pi > \pi_{{\text{c}}} ,\;\;\;\;2\left( {\frac{{P_{{\text{y}}} }}{{\sqrt {2\pi_{{\text{c}}} } }} + \mu_{{\text{c}}} } \right),e_{{{\text{mn}}}} ,\;\;\pi < \pi_{{\text{c}}} } \right.. $$
(1)

Here, the alteration rate mechanisms are \(e_{{{\text{mn}}}} \cdot e_{{{\text{mn}}}} = \pi\) and \(e_{{{\text{mn}}}} = (m,n)\), \(\mu_{{\text{c}}}\) dynamic viscosity, \(\pi_{{\text{c}}}\) critical value of non-Newtonian model and \(P_{{\text{y}}}\) represents a fluid of yield stress.

Fig. 1
figure 1

A two-dimensional configuration of physical problem

Full size image

Governing flow equations

The effects of Ohmic heating and viscosity dissipations are not considered in these ideas. The governing equations can be expressed as follows, as shown in [26,27,28, 32, 38]:

$$ \frac{{\partial \left( {ru} \right)}}{\partial x} + \frac{{\partial \left( {rv} \right)}}{\partial y} = 0 $$
(2)
$$ \begin{aligned} \frac{\partial u}{{\partial t}} + & u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} - \left( {\frac{{w^{2} }}{r}} \right)\frac{\partial r}{{\partial x}} = \frac{\partial U}{{\partial t}} + U\left( {\frac{\partial U}{{\partial x}}} \right) - \frac{{\sigma_{{{\text{hnf}}}} B_{0}^{2} }}{{\rho_{{{\text{hnf}}}} }}\left( {u - U} \right) + \upsilon_{{{\text{hnf}}}} \left( {1 + \frac{1}{\beta }} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\eta_{0} }}{{\rho_{{{\text{hnf}}}} }}.\frac{{\partial^{4} u}}{{\partial y^{4} }} \\ & \; + \frac{gx}{L}\left[ {\left( {T - T_{\infty } } \right)\left( {\beta^{*}_{\text T} } \right)_{{{\text{hnf}}}} + \left( {T - T_{\infty } } \right)^{2} \left( {\beta^{*}_{\text T} } \right)_{{{\text{hnf}}}}^{2} + \left( {T - T_{\infty } } \right)\beta^{*}_{{\text{C}}} + \left( {C - C_{\infty } } \right)^{2} \beta_{{\text{C}}}^{2*} } \right], \\ \end{aligned} $$
(3)
$$ \frac{\partial w}{{\partial t}} + u\frac{\partial w}{{\partial x}} + v\frac{\partial w}{{\partial y}} + \left( \frac{wu}{r} \right)\frac{\partial r}{{\partial x}} = \upsilon_{{{\text{hnf}}}} \left( {1 + \frac{1}{\beta }} \right)\frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{{\eta_{0} }}{{\rho_{{{\text{hnf}}}} }}\frac{{\partial^{4} w}}{{\partial y^{4} }} - \frac{{\sigma_{{{\text{hnf}}}} B_{0}^{2} w}}{{\rho_{{{\text{hnf}}}} }}, $$
(4)
$$ \frac{\partial T}{{\partial t}} + u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \alpha_{{{\text{hnf}}}} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{16}{{3\left( {\rho Cp} \right)_{{{\text{hnf}}}} }}\left( {\frac{{\sigma^{*} T_{\infty }^{*} }}{{k^{*} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \tau \left( {D_{{\text{B}}} \frac{\partial T}{{\partial y}}\frac{\partial C}{{\partial y}} + \frac{{D_{{\text{m}}} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial y}}} \right)^{2} } \right), $$
(5)
$$ \frac{\partial C}{{\partial t}} + u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} = D_{{\text{m}}} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{T} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - k_{{\text{r}}} \left( {C - C_{\infty } } \right). $$
(6)

The physical conditions are [35, 36]:

$$ \left. \begin{gathered} {\text{For}}\;\;t < 0:\;\;\;\;T \to T_{\infty } ,\;\;C \to C_{\infty } \;{\text{and}}\;u = v = w = 0, \hfill \\ \;\;\;\;\;\;\;y = 0:\;\;\;u = v = 0\;{\text{and}}\;w = \Omega \left( t \right)r. \hfill \\ {\text{for}}\;\;t \ge 0:\;\;\;\; - \frac{k}{h}\left( {\frac{\partial T}{{\partial y}}} \right) = \left( {T_{{\text{f}}} - T} \right),D\left( {\frac{\partial C}{{\partial y}}} \right) + \frac{D}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial y}}} \right) = 0, \hfill \\ \;\;\;\;\;\;C \to C_{\infty } ,T \to T_{\infty } \;{\text{and}}\;u \to U,w \to 0. \hfill \\ \end{gathered} \right\} $$
(7)

In \(x,y\) and \(z\) directions, the expressions \(u,\,v\) and \(w\) are explained. \(g\) represent acceleration due to gravity, \(\beta\) is the Casson parameter, \(\eta_{0}\) denotes couple stress parameter, \(\tau = \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{hnf}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}\) is the ratio of heat capacity with base fluid \(\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}}\) and heat capacity of hybrid nanofluid \(\left( {\rho c_{{\text{p}}} } \right)_{{{\text{hnf}}}}\), \(\left( {D_{B} ,D_{T} } \right)\) represent the Brownian and thermophoresis terms, respectively, \(B_{0}\) is the magnitude of the magnetic field, \(k_{r}\) chemical reaction rate, \(hnf\) state hybrid nanofluid fluids such as \(\mu_{{{\text{hnf}}}}\) define viscosity, \(\rho_{{{\text{hnf}}}}\) represent density, \(\sigma_{{{\text{hnf}}}}\) denotes electrical conductivity, \(k_{{{\text{hnf}}}}\) signify thermal conductivity a of hybrid nanofluid. The thermal properties of the base fluid and solid materials are calculated utilizing the correlations provided in Tables 1 and 2.

Table 1 Thermal properties of \({\text{CuO}}\)/blood [3]
Full size table
Table 2 Thermal properties of \({\text{CuO}} + {\text{Cu}}/{\text{blood}}\) [3]
Full size table

In this work, copper and copper oxide, two different types of nanomaterials, are examined. Tables 2 and 3 provide a description of these materials’ thermophysical properties, including base fluid. Table 3 summarizes the thermos-physical features of fundamental liquids, nanofluids, and hybrid nanofluids. In Tables 1 and 2, \(\phi_{1} = \phi_{2} = 0\) denotes base liquid, whereas \(\phi_{1}\) and \(\phi_{2}\) stand for \({\text{CuO}}\) and \({\text{CuO}}\), respectively. Initially, \({\text{CuO}}\) transmitted into the base liquid to make nanofluid, and after that, \({\text{Cu}}\) distributed to create the hybrid nanofluid. Table 3 displays the numerical information for the base liquid and nanomaterials employed in this experiment.

Table 3 Experimental results of the materials [3]
Full size table

The similarity variables are used as.

$$ \left. \begin{gathered} u = f^{\prime } \left( \eta \right)\left( \frac{Ax}{t} \right),w = G\left( \eta \right)\left( \frac{Bx}{t} \right),U\left( {t,x} \right) = \frac{Ax}{t},\Omega \left( t \right) = \frac{B}{t},\eta = y\left( {\frac{2}{{v_{{\text{f}}} t}}} \right), \hfill \\ v = - Af\left( \eta \right)\left( {\frac{{2v_{{\text{f}}} }}{t}} \right),\theta \left( \eta \right)\left( {T_{{\text{w}}} - T_{\infty } } \right) = T - T_{\infty } ,\phi \left( \eta \right)\left( {C_{{\text{w}}} - C_{\infty } } \right) = C - C_{\infty } , \hfill \\ \end{gathered} \right\} $$
(8)

The aforementioned similarity variables in Eq. (2)–(6) are used to get the following form:

$$ \begin{gathered} \left( {1 + \frac{1}{\beta }} \right)f^{\prime \prime \prime } + \frac{{\mu_{{\text{f}}} }}{{\mu_{{{\text{hnf}}}} }}\frac{{\rho_{{{\text{hnf}}}} }}{{\rho_{{\text{f}}} }}A\left[ {ff^{\prime \prime } - \frac{1}{2}\left( {1 - f - \frac{1}{2}\eta f^{\prime \prime } } \right) + \frac{A}{2}\left( {1 - (f^{\prime})^{2} + \lambda G^{2} } \right)} \right] + \hfill \\ \frac{{\mu_{{\text{f}}} }}{{\mu_{{{\text{hnf}}}} }}\left[ {\frac{A}{2}\left( {{\text{Gr}}\theta + {\text{Gr}}_{1} \theta^{2} - {\text{Gc}}\Phi - {\text{Gc}}_{1} \Phi^{2} } \right) - \frac{1}{2}M\left( {f^{\prime } - 1} \right) - k^{*} f^{(v)} } \right] = 0, \hfill \\ \end{gathered} $$
(9)
$$ \left( {1 + \frac{1}{\beta }} \right)G^{\prime \prime } + \frac{{\mu_{{\text{f}}} }}{{\mu_{{{\text{hnf}}}} }}\frac{{\rho_{{{\text{hnf}}}} }}{{\rho_{{\text{f}}} }}\left[ {A\left( {fG^{\prime } - f^{\prime } G} \right) + \frac{1}{2}\left( {G + \frac{1}{2}\eta G^{\prime } } \right)} \right] - \frac{{\mu_{{\text{f}}} }}{{2\mu_{{{\text{hnf}}}} }}M\,G - k^{*} G^{\rm{iv}} = 0, $$
(10)
$$ \left( {\frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }} + \frac{3}{4}{\text{Rd}}} \right)\theta^{\prime \prime } + \frac{{\left( {\rho cp} \right)_{{{\text{hnf}}}} }}{{\left( {\rho cp} \right)_{f} }}\Pr \left( {{\text{Af}}\theta^{\prime } + {\text{Nt}}(\theta^{\prime } )^{2} + {\text{Nb}}\theta^{\prime } \Phi^{\prime } + \frac{1}{4}\eta \theta^{\prime } } \right) = 0, $$
(11)
$$ \left( {1 - \phi_{1} } \right)\left( {1 - \phi_{2} } \right)\Phi^{\prime\prime} + AScf\Phi^{\prime} - \frac{1}{4}ErSc\Phi + \frac{Nt}{{Nb}}\theta^{\prime\prime} = 0. $$
(12)

The physical conditions after transformation become.

$$ \left. \begin{gathered} f^{\prime } \left( 0 \right) = 0 = f\left( 0 \right),G\left( 0 \right) = 1,\theta^{\prime } \left( 0 \right) = Bi\left( {\theta \left( 0 \right) - 1} \right),{\text{Nt}}\theta^{\prime } \left( 0 \right) + {\text{Nb}}\Phi^{\prime } \left( 0 \right) = 0, \hfill \\ f^{\prime } \left( \infty \right) \to 1,G\left( \infty \right) = \theta \left( \infty \right) = \Phi \left( \infty \right) \to 0 \hfill \\ \end{gathered} \right\} $$
(13)

The model parameters that control movement, energy transmission and concentration phenomena are as follows:

Schmidt, Prandtl, Reynolds numbers, linear and nonlinear Grashof numbers are \({\text{Sc}} = \frac{{v_{{\text{f}}} }}{{D_{{\text{B}}} }},{\text{Pr}} = \frac{{\mu_{{\text{f}}} c_{{\text{p}}} }}{{k_{{\text{f}}} }},{\text{Re}} = \frac{Ux}{{v_{{\text{f}}} }},{\text{Gr}} = \frac{{g\beta^{ * } \left( {T_{{\text{w}}} - T_{\infty } } \right)\rho_{{\text{f}}} x^{4} }}{{\upsilon_{{\text{f}}}^{2} L}},{\text{Gr}}^{*} = \frac{{g\left( {\beta^{ * } } \right)^{2} \left( {T_{{\text{w}}} - T_{\infty } } \right)^{2} x^{4} }}{{\upsilon_{{\text{f}}}^{2} L}},\lambda^{*} = {\text{Gr}} + {\text{Gr}}^{*} ,\) Couple stress parameter, Biot number, linear and nonlinear Buoyancy ratio are \(k^{*} = \frac{{2A\eta_{0} }}{{\rho_{{\text{f}}} \upsilon_{{\text{f}}}^{2} }},B_{{\text{i}}} = \frac{h}{{k_{{\text{f}}} }}\sqrt {\frac{{\upsilon_{{\text{f}}} }}{2}} ,{\text{Nr}} = \frac{{g\beta_{{\text{C}}} \left( {C_{{\text{w}}} - C_{\infty } } \right)x^{4} }}{{\upsilon_{{\text{f}}}^{2} L}},N_{1} = \frac{{g\left[ {\beta_{{\text{C}}} \left( {C_{{\text{w}}} - C_{\infty } } \right)} \right]^{2} x^{4} }}{{\upsilon_{{\text{f}}}^{2} L}},\) the Brownian motion factor, thermophoresis factor, the rotation factor, mixed convection factor and magnetic field factor are defined as \({\text{Nb}} = \tau \frac{{D_{B} C_{\infty } }}{{v_{{\text{f}}} }},Nt = \tau \frac{{D_{{\text{T}}} \left( {T_{{\text{w}}} - T_{\infty } } \right)}}{{v_{{\text{f}}} T_{\infty } }},\lambda = \left( \frac{B}{A} \right)^{2} ,\lambda^{ * } = \frac{{{\text{Gr}}}}{{{\text{Re}}^{2} }},M = \frac{{\sigma B_{0}^{2} }}{{\rho_{{\text{f}}} }}.\)

Drag force and heat transfer rate

The engineering-relevant thermofluidic quantities in this study are \(C_{{{\text{fx}}}} ,C_{{{\text{fz}}}}\) and \({\text{Nu}}\) whose dimensionless form is:

$$ \left. \begin{gathered} \left( {{\text{Re}}^{\frac{1}{2}} A^{\frac{1}{2}} } \right)C_{{{\text{fx}}}} = 2\mu_{{{\text{hnf}}}} \left( {\rho_{f} U^{2} } \right)^{ - 1} \left( {\frac{\partial u}{{\partial y}}} \right)_{y = 0} = 2\sqrt 2 \left( {1 - \phi_{1} } \right)^{ - 2.5} \left( {1 - \phi_{2} } \right)^{ - 2.5} f^{\prime \prime } (0), \hfill \\ \left( {{\text{Re}}^{\frac{1}{2}} A^{\frac{1}{2}} } \right)C_{{{\text{fz}}}} = 2\mu_{{{\text{hnf}}}} \left( {\rho_{f} U^{2} } \right)^{ - 1} \left( {\frac{\partial w}{{\partial y}}} \right)_{y = 0} = - 2\sqrt 2 \lambda \left( {1 - \phi_{1} } \right)^{ - 2.5} \left( {1 - \phi_{2} } \right)^{ - 2.5} G^{\prime } (0), \hfill \\ \left( {{\text{Re}}^{{\frac{ - 1}{2}}} A^{\frac{1}{2}} } \right)Nu = \frac{{ - k_{{{\text{hnf}}}} }}{{(T_{{\text{w}}} - T_{\infty } )k_{{\text{f}}} }}\left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0} = - 2\left( {\frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }} + \frac{3}{4}Rd} \right)\theta^{\prime } (0). \hfill \\ \end{gathered} \right\} $$
(14)

Analytical (OHAM) and numerical procedures

The solution of the proposed model is obtained by the well-known optimal homotopy analysis method (OHAM). The trial solutions \(f_{0} = \eta \left( {1 - e^{ - \eta } } \right),\) \(G_{0} = e^{ - \eta } ,\)\(\Theta_{0} = \frac{{B_{{\text{i}}} }}{{1 + B_{{\text{i}}} }}e^{ - \eta } ,\)\(\Phi_{0} = - \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\frac{{B_{{\text{i}}} }}{{1 + B_{{\text{i}}} }}e^{ - \eta }\) for the velocity, temperature, and concentration profiles are deliberated as above. [39] briefly described OHAM ability to manage a set of differential equations. Therefore, OHAM has been used in this situation to resolve the governing Eqs. (9)–(12) associated with the model problem under investigation. The computation is performed using the Mathematica program for both numerical and OHAM tasks. The Nusselt number values are provided in Table 4 by comparing the results with [28], and the skin friction values are displayed in Fig. 8 and Table 3 by comparison with the published results of [28] and [34] to validate the correctness of this approach. This investigation makes it obvious that the current solutions and the preceding results are in excellent agreement.

Table 4 Impact of \(M,A\) and \({\text{Rd}},{\text{Nb}}\) on Nusselt number
Full size table

Result and discussion

The influence of the various embedded parameters considering hybrid nanofluids has been examined numerically and graphically in this work. The proposed model is authenticated through comparison with the published work [28]. The validation of the obtained results is further used for the impact of various embedded parameters. The nanomaterials volume fraction is limited up to 5% means \(0.01 \le \,\phi = \phi_{1} + \,\phi_{2} \,\, \le 0.05\) for both the nanofluids (\({\text{CuO}}\)) and Hybrid nanofluid (\({\text{CuO}} + {\text{Cu}}\)). The parameters influence is shown in Figs. 3–8 for the velocity, temperature and concentration distributions. Figure 1a depicts the physical aspects of the suggested mathematical model. The solid nanomaterials \({\text{Cu}}\) and \({\text{CuO}}\) are employed in the blood to accomplish hybrid nanofluids. This geometry is utilized in the laboratory for blood testing purposes as apparatus. In reality, blood is tested for several drugs in a laboratory that includes diverse instruments such as sphere. The magnetic field is applied vertically as illustrated in the geometry, with the remainder of the discussion taking place in mathematical modeling. Figure 2a, b, c and d shows the OHAM and numerical method comparison for velocities, heat and concentration profile, respectively.

Fig. 2
figure 2

a–d Comparison of OHAM technique and numerical scheme (shooting method) for a \(f^{\prime } \left( \eta \right)\), b \(G\left( \eta \right)\), c \(\theta \left( \eta \right)\) and d \(\Phi \left( \eta \right)\)

Full size image

Velocity field \(f^{\prime } \left( \eta \right)\)

Figure 3a, b, c and d shows how the velocity distribution of the nanofluid is affected by different magnitudes of the important factors in this section. The impact of the \(\beta\) (Casson variable) on the profile of velocity components is shown schematically in Fig. 3a. As shown in the figure, increasing the \(\beta\) variable ranges reduce the \(f^{\prime } \left( \eta \right)\) inside the vicinity of boundary layer. When the Casson parameter approaches \(\infty\), the substance turns into a Newtonian fluid. The elastic kinematic viscosity tends to raise as the magnitude increases, but the effective stress decreases. The fluid motion is slowed as a result of the impact. The fact that hybrid nanofluid has a greater resistance than nanofluid should also be addressed. Figure 3b illustrates the impact of various \(\lambda\) rotation factor values on nanofluid and hybrid nanofluid velocity profiles. Raising the rotation parameter values enhances the speed of nanofluid. The figure shows that increasing the range of \(\lambda\) allows the gyration to become considerably more dynamic, which aids lot further in the spinning effects, which decelerates the hybrid nanofluid progress. Figure 3c displays the velocity curve for distinct \(k^{*}\) values. The hybrid nanofluid and nanofluid velocity distributions decrease as \(k^{*}\) increases, as illustrated in the graph. It is a straightforward explanation. As the size of \(k^{*}\) rises, both the flow of nanofluid and hybrid nanofluid slow, deteriorating the opposing resistance, which is analogous to a noticeable fall in apparent viscosity. Figure 3d shows how the \(\phi_{1} ,\,\phi_{2}\) affects the \(f^{\prime } \left( \eta \right)\) profile. The velocity slows down as the nanoparticle volume fraction increases. Larger values of the \(\phi_{1} ,\,\phi_{2}\) lead the momentum boundary layer to have a declining characteristic. The huge decline in nanofluid velocity is also less than that found in hybrid nanofluids, according to the researchers. Variations in nanofluid and hybrid nanofluid velocity for \(\lambda^{*}\)(mixed convection parameters) are shown in Fig. 6. As \(\lambda^{*}\) range widens, the velocity profile improves. As the magnitude of \(\lambda^{*}\) increases, a general rise in nanofluid movement is seen, which might be connected to the high buoyancy force. In this study, hybrid nanofluid was found to outperform nanofluid in terms of performance.

Fig. 3
figure 3

a–d Performance of a \(\beta\), b \(\lambda\), c \(k^{*}\) and d \(\phi_{1} ,\phi_{2}\) vs. \(f^{\prime } \left( \eta \right)\)

Full size image

Velocity field \(G\left( \eta \right)\)

The influence of the mixed convection, magnetic parameters and nanoparticles volume fraction is displayed in Fig. 4a, b and c. Variations in nanofluid and hybrid nanofluid velocity for \(\lambda^{*}\)(mixed convection parameters) are shown in Fig. 4a. As \(\lambda^{*}\) range widens, the velocity profile improves. As the magnitude of \(\lambda^{*}\) increases, a general rise in nanofluid movement is seen, which might be connected to the high buoyancy force. In this study, hybrid nanofluid was found to outperform nanofluid in terms of performance. Nanocomposites, which are trailed by hybrid nanomaterials, have a suitable trend. The effect of \(M\) is shown in Fig. 4b. In this case, opposing friction known as “Lorentz force” boosts with enhancing magnitude of the magnetic parameters and consequently the fluid motion reduced. The magnetic field represents the ratio of hydro-magnetic body force to viscous force, so an increase in \(M\) parameter results in a significant hydro-magnetic body force, which reduces the velocity of fluid. In this case, controlling nanoparticle fluid flow with an induced magnetic field is a viable option. Figure 4c depicts the influence of \(\phi = \phi_{1} + \phi_{2}\). It is worth noting that as the \(\phi_{1} ,\,\phi_{2}\) parameter is enhanced, the flow of both nanofluids drops sharply. The momentum boundary layer shrinks as the value of both (nano and hybrid) nanofluid increases, which is the fundamental cause of this scenario. The velocity of the hybrid nanocomposite declines significantly in contrast to the nanofluid, as seen by such a curved graphic.

Fig. 4
figure 4

a–d Performance of a \(\lambda^{*}\), b \(M\), c \(\phi_{1} ,\phi_{2}\) vs. \(G\left( \eta \right)\)

Full size image

Variation in hybrid nanofluid thermal profile

The impact of the parameters like \(\,M,\,A,\,\left( {\phi_{1} ,\,\phi_{2} } \right),\,Rd\) and \({\text{Nt}}\), versus thermal profiles is displayed in Fig. 5a, b, c, d and e. Figure 5a portrays the effect of M on the thermal distribution. It is assumed that when \(M\) rises, the temperature of both liquids climbs with it. According to science, when the Ohmic heating influence happens, a significant quantity of heat is produced because of the induced magnetic field that is being used, which raises the thermal behavior of the both (nano and hybrid) nanofluids. In this situation, hybrid nanofluid performs better than regular nanofluid. Figure 5b exhibits the variation of \(A\) on \(\theta \left( \eta \right)\) for both (nano and hybrid) nanofluids. This figure demonstrates that \(\theta \left( \eta \right)\) profile in this plot is performing as \(A\) appears to be dropping. The \(\theta \left( \eta \right)\) profile decreases as \(A\) increases, implying that the thermal contact medium decrease as \(A\) increases.

Fig. 5
figure 5

a–d Performance of a \(M\), b \(A\), c \(\phi_{1} ,\phi_{2}\), d \(N_{{\text{t}}}\) and e \({\text{Rd}}\) vs. \(\theta \left( \eta \right)\)

Full size image

Figure 5c describes the effect of \(\phi_{1} ,\,\phi_{2}\) on \(\theta \left( \eta \right)\). Rising \(\phi_{1} ,\,\phi_{2}\) values cause the temperature of \({\text{CuO}}\;{\text{and}}\;{\text{Cu}} + {\text{CuO}}\) nanofluids to rise. Convective movement from a heated surface to a cooler side is stronger with greater the range of \(\phi_{1} ,\,\phi_{2}\). In reaction, the thermal behavior of both (nano and hybrid) nanofluid increases. In addition, hybrid nanocomposites behaves more effectively than nanofluid. Figure 5d shows the \(\theta \left( \eta \right)\) of both \({\text{CuO}}\;{\text{and}}\;{\text{Cu}} + {\text{CuO}}\) nanofluids as a function of the \({\text{Nt}}\). The temperature field becomes stronger and the thermal boundary layer thicker as the range of \({\text{Nt}}\) rises. By ensuring that nanomaterials on the sphere heated boundary flows rapidly toward the surrounding static liquid, the thermophoretic power increases heat energy. It is significant to remember that when the \(N_{t}\) increases, the temperature and thickness of the thermal boundary layer expand. As a result, one may expect the thermal boundary layer to expand in the presence of the \(N_{{\text{t}}}\). The variation of \(\theta \left( \eta \right)\) for \({\text{Rd}}\) is shown in Fig. 5e. The temperature filed of both (nano and hybrid) nanofluid lowers as the \({\text{Rd}}\) increases. Since increasing the radiation parameter lowers the average absorption coefficient, initiating in poor energy absorption by both types of fluid.

Concentration field

The effect of various model factors on concentration fields \(\Phi \left( \eta \right)\) is highlighted in Fig. 6a, b, c and d. In Fig. 6a, the divergence of \(\Phi \left( \eta \right)\) with Schmidt number \({\text{Sc}}\) is seen. For nanofluids and hybrid nanofluids, increasing the Schmidt number has a lessening influence on the \(\Phi \left( \eta \right)\) profile. The greater the Schmidt number, the less efficient species diffusion is, leading particles to scatter and, as a result, a drop in the \(\Phi \left( \eta \right)\) profile. Figure 6b depicts the impact of \(\phi_{1} ,\,\phi_{2}\) (volumetric fractions of nanomaterials) on \(\Phi \left( \eta \right)\) fields. As may be observed in the graph, \(\Phi \left( \eta \right)\) is showing a downward trend in \(\phi_{1} ,\,\phi_{2}\). The increase in \(\phi_{1} ,\,\phi_{2}\) was found to compensate for the reduction in solute concentration. Figure 6c displays the impact of \({\text{Nb}}\) on \(\Phi \left( \eta \right)\). As the \({\text{Nb}}\) grows, the concentration field declines. Micro-mixing, which improve thermophysical characteristics, is frequently achieved via Brownian motion. When a result, as the amount of \({\text{Nb}}\) increases, so does the amount of nanoparticles concentration. Figure 6d depicts a chemical reaction \({\text{Er}}\) vs concentration profile. The concentration profile is decayed by the chemical reaction parameter, and this impact is considerably stronger when utilizing \({\text{Cu}}\) and \({\text{CuO}}\) hybrid nanofluids. The heat transfer rate has been displayed for the increasing values of the thermophoretic parameter and volume fraction in Fig. 7a and b. Also, Fig. 7c and d illustrates the variations of average Nusselt number with remarkable factors of the present work, e.g., \(M,A,{\text{Rd}}\) and \({\text{Nb}}\). We have computed the skin friction coefficient profile for fluid flow in order to validate our findings in Fig. 8. We determined that the outcomes produced by using \(M = 0,A = 0,\phi = 0\) are in very good accord with [34]. The hybrid nanofluid is comparatively more effective to enhance the heat transfer as compared to the traditional fluids. In the case of \(f^{\prime \prime } (0)\) and \(G^{\prime } \left( 0 \right)\), Table 4 shows a comparison of predicted results with Rana et al. [28] previously published study. The current findings show a strong connection with existing studies, supporting the quality of our numerical data. The numerical findings for \(f^{\prime\prime}(0)\) and \(G^{\prime } \left( 0 \right)\) for nanofluid and hybrid nanofluid are presented against \(k^{*} ,\,M,\,\,(\,\phi_{1} ,\,\,\phi_{2} )\) in Table 5 to show how different factors impact these physical characteristics in engineering fields. \(f^{\prime } (0)\) and \(G^{\prime}\left( 0 \right)\) are inextricably linked to \(k^{*} ,\phi_{1} ,\,\,\phi_{2} ,M\). As a result, the fascinating phenomena of nanofluids and hybrid nanofluids are being investigated. Table 5 also showed that when nanofluid was compared to hybrid nanofluid, hybrid nanofluid was found to be superior than nanofluid. On the other hand, Table 6 shows how the \(\phi_{1} ,\,\,\phi_{2}\), \({\text{Rd}},{\text{Nt}},(\phi_{1} ,\phi_{2} )\) parameters affect the Nusselt number \({\text{Nu}}\). It is essential to keep in mind that \({\text{Nu}}\) and \(Rd,{\text{Nt}},(\phi_{1} ,\phi_{2} )\) are directly related. \({\text{Nu}}\) for nanofluids and hybrid nanofluids is improved as a result of \(Rd,{\text{Nt}},(\phi_{1} ,\phi_{2} )\) being strengthened. A percent rise in \({\text{Nu}}\) has been linked to an increase in nanofluid. In the case of a hybrid nano-liquid, an increase in nanofluid between 0.01 and 0.02 will increase the thermal conductivity by 5.8% and 11.947%, respectively. Additionally, as shown in Table 6, the same value of \(\phi_{1} ,\,\,\phi_{2}\) was discovered when nanofluid increased thermal efficiency by 2.576% and 5.197%. Table 7 shows convergence of the OHAM-BVPh 2.0 package up to 15 orders of accuracy for nanofluid and hybrid nanofluid, respectively.

Fig. 6
figure 6

a–d Performance of a \({\text{Sc}}\), b \(\phi_{1} ,\phi_{2}\), c \(N_{{\text{b}}}\) and d \({\text{Er}}\) vs. \(\Phi \left( \eta \right)\)

Full size image
Fig. 7
figure 7

a–d Impact of a \({\text{Nt}}\), b \(\phi_{1} ,\phi_{2}\), c \({\text{M, A}}\) and d \({\text{Rd}},{\text{Nb}}\) on Nusselt number

Full size image
Fig. 8
figure 8

Compression of present outcomes with [34] for various values of \(\lambda\)

Full size image
Table 5 Skin friction valuation when \(A = 1.6,\phi_{1} = 0.04\)
Full size table
Table 6 Heat transfer rate when \(A = 1.6,Nb = 0.4\)
Full size table
Table 7 The OHAM convergence
Full size table

Concluding remarks

This research work aims investigating the behavior of a nonlinear convective CuO-Cu hybrid nanofluid flow, considering the impact of temperature-responsive characteristics of water (physical properties). The flow is investigated over a complex revolving sphere geometry, which bears important practical applications in fields of medication and manufacturing. The current analysis also considers aspects like radiation, nonlinear convection, couple stress, and magnetic effects in the nanofluid flow. The governing system of PDEs are solved using advanced analytical methods known as OHAM. The following concise conclusions are drawn from the extensive analysis presented above:

  • As the quantity of nanoparticles \((\phi_{1} ,\,\phi_{2} )\) and the strength of the magnetic field \(M\) intensified, there was a drop in the \(f\left( \eta \right)\), \(G\left( \eta \right)\) velocity dispersion values along the \(x\) and \(y\)-axes. Nonetheless, an upward trend was observed as the \(\lambda^{*}\) value increased.

  • The hybrid CuO–Cu nanoparticles have a greater rate of heat transmission than CuO (mono-particles).

  • By enhancing the magnitude of \(k^{*} ,\,M,\,\,(\,\phi_{1} ,\,\,\phi_{2} )\) parameters, it is anticipated that the values of \(f^{\prime } (0)\) and \(G^{\prime } \left( 0 \right)\) in the x- and y-direction for nanofluid and hybrid nanofluid would be improved.

  • As \((\phi_{1} ,\,\phi_{2} ),\,\,N_{t}\) and \(M\) parameter is improved, temperature distribution grows. Additionally, CuO–Cu nanofluid leads CuO in terms of thermal performance.

  • A growth in the range of \(\Phi \left( \eta \right)\) was discovered when the values of \((\phi_{1} ,\,\phi_{2} )\,\) and \({\text{Sc}}\) are elevated.

  • The most recent research used to be quite useful in practice, particularly for industrial and medicinal applications.

  • The results portray that increasing values of \(\phi_{1} ,\,\,\phi_{2}\) from 0.01 to 0.02 improves the heat penetration by 5.8% and 11.947%, respectively, while enhancing conductivity by 2.576% and 5.197% for roughly the same level of \(\phi_{1} ,\,\,\phi_{2}\).

  • During the quantitative examination, hybrid nanomaterials were discovered to have the most effective behavior as compare to nanofluid inside base fluid.

  • The findings demonstrate that nanofluid and hybrid nanofluid effectively correlate with existing work [27] and [34].

  • The future work should explore the features of ternary nanofluid flow to systematically inspect transportation phenomena and concentration profiles. Therefore, imminent research endeavors might focus on the entropy generation, some other factors such as EMHD, porosity, nonlinear energy source and thermal radiation, and the rheological behaviors of both Newtonian and non-Newtonian nanofluids. Furthermore, the explanation of a useful ternary nanofluid flow model, involving various aspects, is warranted, as is the employment of a pursued machine learning approach and numerical simulations.