Numerical approach of Fe₃O₄-ethylene glycol heat and mass transfer magneto nanofluid flow past a porous shrinking sheet with chemical reaction and thermal radiation

Abstract

The primary goal of this work is to study the effect of nonlinear chemical reaction and heat source or sink on the entropy generation analysis of a nanofluid composed of Fe₃O₄ and ethylene glycol flowing through a shrinking surface in the incidence of partial slip, and thermal radiations have been explored. As a result, we provide a unique investigation into the development and comprehension of a mathematical model for a non-Newtonian nanoliquid flow in a magnetic and porous media circumstance. Fe₃O₄ nanoparticles are dispersed in ethylene glycol to create the nanofluid. The basic governing constitutive PDEs are rehabilitated into nonlinear ODE’s by suitable resemblance transformations. Employing the Keller–Box procedure, the numerical outcome of the resulting collection of governing equations is found. Using various figures, the effects of essential factors on the nanofluid flow, mass and heat transportation, friction factor, Nusselt number, and entropy generation are determined and explored. High values of suction and velocity slip factor are observed to increase the velocity, while a porosity factor and nanoparticle volume fraction decrease the velocity. Heat conduction in the system is enhanced by the heat source and viscous dissipation. A chemical reaction decreased the solutal concentration to lower amounts. The model is applicable to energy systems and thermally enhanced industrial flow operations. The research is applicable to enrobing procedures for electric-conductive nanomaterials, which have potential applications in aircraft, smart coating transport phenomena, and other sectors. The findings of the present study are also juxtaposed with those seen in prior research endeavours.

Introduction

Due to their inadequate thermal conductivity, regular fluids have traditionally been reserved out of widespread usage in a variety of manufacturing and technology disciplines. As a consequence, conventional fluids should not be used for thermal transmission. In contrast, metals that are elements are more thermally conductive. As a consequence, spreading such extraordinarily conductive particles into our typical liquids would serve as a gold standard approach. Following that, the resulting fluids may have improved heat conductivity. Conventional cooling fluids, such as ethylene glycol and viscous water, consume lower thermal conductivities, which limits the effectiveness of heat transfer. Choi and Eastman [1] were the first to use the term nanofluid. In general, nanofluids often contain a volume proportion of nano-particles of up to 5%, which increases heat transfer efficiency. Nanofluids are created by combining nanoparticles with commonly used fluids such as polymer solutions, oil, water, and biofluids. Nanofluid flow research has advanced significant relevance in the fluid dynamics community due to its multiple remarkable applications in several commercial and technical sectors, including geothermal power extraction, fibre glass, the fabrication of plastic panes, hot rolling, and so on. The rate of thermal transmission is determined by the thermophysical properties of the refrigeration system. The addition of nanoparticles to refrigerants can assist with this. Consequently, thermal transport becomes more efficient. Consequently, the exploration of nanoparticles or nanofluids is one of the most prevalent fields of study. Nanofluids have piqued the interest of several authors in recent years owing to their extensive range of applicability’s in science and industry. In view of this, nanofluids are extremely important in contemporary technologies and fields of engineering [2,3,4,5,6,7]. Sheikholeslami et al. [8] investigated the implication of magneto nanofluid heat flow across an extending flat plate. In their study, Khan and Hafeez [9] examined the combined effects of slip-flow and heat transmission on the performance of nanofluids flowing over a porous radiative diminishing sheet. Azmi et al. [10] conducted a comprehensive examination and analysis of the literature on the heat transfer enhancement properties and applications of ethylene glycol nanofluids. Mebarek-Oudina and Chabani [11] conducted research on applications of nanofluid and thermal transfer improvement strategies in various enclosures. The inspiration of the Lorentz force on a Casson fluid flow caused by dusty elements with hybrid nanofluid across a stretched sheet was studied by Khan et al. [12].

Magnetohydrodynamics (MHD) is the study of the magnetic characteristics of electrically conducting materials. MHD boundary layer with thermal and solutal transport across surfaces is used in a wide range of technical and geo-physical uses, including packed-bed catalytic reactors, nuclear reactor cooling, and oil recovery. The exploration of magnetohydrodynamic fluid flow has important applications in a diversity of industrial industries, including the creation of heat exchangers, MHD acceleration devices, pumps, bearings, and flow metres. Many chemical engineering procedures such as metallurgy and extrusion of polymers, entail chilling a molten liquid as it is extended into a cooling system. Several new studies have been attentive to the influence of magnetic fields on nanofluid flow concerns. Bahiraei and Hangi [13] reviewed the thermal transmission properties of magnetic nanofluids. Gholinia et al. [14] explored the effect of MHD on ethylene glycol nanoliquid flow across a vertical porous rotating cylinder. The transport features of MHD nanofluid flow in a porous media were explored by Sheikholeslami et al. [15]. The natural convection of a nanofluid consisting of Fe₃O₄ particles dispersed in water was explored by Sheikholeslami and Ganji [16], with a specific focus on the influence of an external magnetic field. In their study, Muhaimin et al. [17] conducted an analysis to investigate the impact of suction on the magnetohydrodynamic (MHD) heat transfer flow along a declining sheet. The study conducted by Hayat et al. [18] examines the impact of magnetohydrodynamics (MHD) on the rotating flow of a second-grade fluid as it passes over a declining surface. In their study, Hafidzuddin et al. [19] examined the effects of transpiration on the flow of a magnetohydrodynamic (MHD) heat transfer fluid across a nonlinear surface that undergoes elongation or shrinkage. Mishra et al. [20] scrutinized the impact of heat source/sink on MHD Ag–${\mathrm{H}}_{2}\mathrm{O}$ nanofluid flow along an extending/diminishing porous channel. Krishna and Chamkha [21] conducted a study on the impact of ion slip on the magnetohydrodynamic (MHD) boundary layer flow of nanoliquid over an infinite vertical surface surrounded by a porous medium. Veera Krishna et al. [22] examined the implications of Hall on magneto rotating mixed convective fluid flow across an infinite porous vertical sheet. There are a few intriguing publications [23,24,25,26,27,28] that explore the influence of MHD with porous media conditions.

It is crucial to comprehend the features of flow over porous materials for various applications in science and engineering. Knowledge of transport procedures in porous media is crucial for numerous fields of science, chemical, aerospace, including powder metallurgy, geohydrology, mechanical, and petroleum engineering, to mention a few. As a result, application processing, and also scientific studies and periodicals, have provided porous material with a lot of attention. Ahmad and Pop [29] studied the mixed convection flow over a vertical flat surface comprising nanoliquids from a porous medium. The effectiveness of thermal transmission for a nanofluid submerged in a porous medium while moving with Brownian motion is deliberate by Dogonchi et al. [30]. Following that, Haq et al. [31] considered nanofluids in porous material under the influence of heat radiation and successfully generated a dual outcome that originated on the results. However, Hayat et al. [32] sought to investigate nanofluid for unsteady fluid flow in porous media with varied flow factor influences. Following that, various investigations were conducted to better understand the heat transmission characteristics of nanofluids in porous media. The study conducted by Soid et al. [33] investigated the phenomenon of magnetohydrodynamic (MHD) radiative heat transfer in the context of flow through an elongating or decreasing sheet. The study of fluid flow phenomena on a stretched sheet has emerged as a popular research area in recent years due to its wide range of applications in several scientific and commercial disciplines. This sort of study has potential benefits for several applications, such as the production of rubber sheets, preparation of glass fibres, spinning of melt, cooling of metallic plates, and others. The fluid flow of a nanofluid over an extended surface in a boundary layer was discussed by Khan and Pop [34]. A Numerical analysis of the heat transmission nanofluid flow past a nonlinear increasing sheet was done by Rana and Bhargava [35]. Turkyilmazoglu [36] spoke about the inspiration of heat transmission on micropolar fluid via a dwindling porous sheet.

Thermal radiation has a significant impact on manufacturing and engineering procedures. These procedures require operation at a high temperature under a variety of non-isothermal circumstances and in situations where convective thermal transmission factors are reduced. Radiative thermal transmission is incorporated into the models of relevant apparatus, hyper-sonic flights, space vehicles, and turbines with gas, among others. Hayat et al. [37] observed a wider range of nonlinear heat radiation values, which expanded the temperature field. Ghadikolaei et al. [38] examined the influence of MHD micropolar dusty fluid along with graphene oxide engine oil nanoparticles in a porous media past a stretched surface with radiation. Nayak [39] conducted a study on the influence of radiation on the flow of 3D magneto nanofluid flow through a dwindling surface with viscous dissipation. Mahanthesh et al. [40] examined the influence of radiation on mixed convection nanofluid flows on a vertical sheet. The impact of heat radiation on the natural convection of Fe₃O₄–H₂O nanofluid was explored by Sheikholeslami and Shamlooei [41]. Ramesh et al. [42] investigated the radiative Carreau nanofluid flow in a micro-channel with magnetic characteristics.

In contrast to earlier studies' focus on the first order of chemical reactions $(m=1)$, more recent studies have attempted to examine the higher order of chemical reactions. Chemical reactions have a diversity of particle uses in engineering and research, including the chemical sector, evaporation at the surface of a water body, deposition of chemical vapour, chemical engineering, and several others. According to a research by Rajani et al. [43], they studied the flow of the nanofluid with Brownian motion while taking higher-order chemical interactions into consideration. They found that the augmentation rate in species solutal curves is less important for advanced-order chemical processes compared to lower-order reactions. Sajid et al. [44] inspected the effect of the heat source on micropolar fluid along a heated wall incorporated with an nth-order chemical reaction. The impact of a chemical reaction on the Walters-B nanofluid's MHD stagnation point fluid flow under Newtonian thermal and solutal situations was addressed by Qayyum et al. [45] in their study. Venkateswarlu et al. [46] conducted a computational examination of the MHD flow of chemical reaction and heat production over a varying vertical plate. Under slip conditions, Rahman et al. [47] have determined the impact of nanofluid flow past a diminishing wall. References [48,49,50,51,52,53] have accounts of successful research into the nth order of the chemical process.

The process of transferring thermal energy from one area to another is accompanied by a phenomenon known as energy deterioration. In several thermal industrial processes, the phenomenon of energy degradation poses a significant risk as it diminishes the efficiency of heat structures. Minimization entropy generation is used as a metric to quantify the increase in thermal efficiency. Entropy is generated by several phenomena such as friction, heat radiation, chemical reactions, and electrical resistance. The regulation of temperature via cooling and heating processes has significant importance across several industries and construction sectors, particularly in relation to energy consumption and the operation of electrical equipment. Therefore, it is essential to optimize the formation of entropy in order to prevent any compromise of immutability, which may adversely impact the efficiency of a given system. The quantification of energy dissipation resulting from heat transfer and friction is assessed by the observation of entropy generation. In 1982, Bejan [54] made the discovery that the calculation of irreversibility could be derived from the rate of entropy generation. The present discourse aims to elucidate the concept of irreversibility and its inherent relationship with the generation of entropy across several scientific and thermal engineering disciplines, Bejan conducted in-depth study and analysis. Qing et al. [55] explored the entropy production on the MHD flow of nanofluids through a permeable linearly expanding or declining porous surface. Bhatti et al. [56] conducted a numerical analysis to examine the entropy generation in the context of radiative magnetohydrodynamic (MHD) nanofluid flow through a porous diminishing sheet. Hayat et al. [57] investigated the irreversibility associated with energy minimization in the context of nanofluid flow over a curved surface with partial slip effect, taking into account the presence of a Darcy Forchheimer medium. The study conducted by Rashid et al. [58] explored the flow of magnetohydrodynamic (MHD) nanofluid across a diminishing wall while considering the generation of entropy. Entropy formation in MHD nanoliquid flow across a nonlinear stretched surface with Navier's velocity slip and convective thermal transmission was examined by Seth et al. [59]. Additional pertinent studies in this field might be seen in the cited sources [60, 61].

This research aims to establish a mathematical model for Fe₃O₄-ethylene glycol magneto nanofluid flow along a dwindling porous surface subject to radiation and chemical reaction. Viscous dissipation and a porous media have been considered while doing the study. The internal friction that determines the temperature gradient is controlled by viscous dissipation. This important trait provides the foundation for several industrial uses, including the cooling of nuclear reactors, chemical and food processing, oil drilling, and biotechnology. Viscous dissipation alters the distribution of temperature by acting as a primary energy source. Moreover, there is a lack of study conducted by other scholars about the potential consequences associated with governing variables, namely the velocity slip factor and the nanoparticles volume fraction parameter. In order to establish the impacts of the aforementioned regulating parameters, the first objective of this investigation is to advance the work of Humphries et al. [63]. According to the authors, these contributions distinguish the current analysis from that of Humphries et al. [63], primarily because the numerical findings achieved in this work are novel and original. This study briefly examines the impact of the frictional factor, rate of heat and mass transfer on selected control variables, including suction, velocity slip, heat generation/sink, chemical reaction, viscous dissipation, and nanoparticles volume fraction factors. The utility of the proposed method is demonstrated through simulation results, which are compared to previously published results in order to show the efficacy of the proposed results. The current work is of critical importance for geothermal energy storage systems employing spherical underground tanks, heat exchanger technology, and next-generation solar film gleaners.

Formulation of the problem

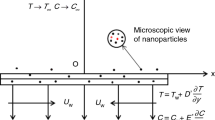
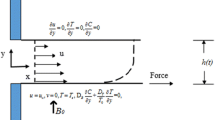
Consider the 2-D incompressible flow of a nanofluid composed of Fe₃O₄ and ethylene glycol in the direction of a diminishing sheet with a permeable medium. In the context of fluid dynamics, when fluid flow occurs along the horizontal axis x and the vertical axis y, it may be seen that y > 0 indicates the presence of the fluid's actively involved volume. Let us consider the scenario where B(x) represents an applied magnetic field that is perpendicular to the fluid flow, characterized by a velocity u = ax (as seen in Fig. 1). The species concentration and heat at the surface of the plates are specified by ${C}_{\mathrm{w}}={C}_{\infty }+{C}_{0}{x}^{\text{n}}$ and ${T}_{\mathrm{w}}={T}_{\infty }+{T}_{0}{x}^{\text{n}}$ correspondingly, here ${C}_{\infty }$ and ${T}_{\infty }$ are the concentration and temperature, far away from the plate, with repute to the ambient fluid. ${C}_{0}>0$ denotes the concentration representative and ${T}_{0}$ resembles the nanofluid temperature characteristic. The leading equations for the continuity, thermal, momentum, and nanofluid species concentration for nanofluids may be given as (Humphries et al. [63]; Zainodin et al. [64])

Fig. 1

Graphical depiction and flow diagram

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{{\mu }_{\mathrm{nf}}}{{\rho }_{\mathrm{nf}}}\frac{{\partial }^{2}u}{{\partial y}^{2}}-\frac{{\nu }_{\mathrm{nf}}}{{K}_{\mathrm{p}}}u-\frac{{\sigma }_{\mathrm{nf}}{B}^{2}\left(x\right)}{{\rho }_{\mathrm{nf}}}u$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\,{\alpha }_{\mathrm{nf}}\frac{{\partial }^{2}T}{\partial {y}^{2}}-\frac{1}{{\left(\rho {C}_{\mathrm{p}}\right)}_{\mathrm{nf}}}\frac{\partial {q}_{\mathrm{r}} }{\partial y}+\frac{Q\left(T-{T}_{\infty }\right)}{{\left(\rho {C}_{\mathrm{p}}\right)}_{\mathrm{nf}}}+\frac{{\mu }_{\mathrm{nf}}}{{\left(\rho {C}_{\mathrm{p}}\right)}_{\mathrm{nf}}}{\left(\frac{\partial u}{\partial y}\right)}^{2}$$

(3)

$$u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D\frac{{\partial }^{2}C}{\partial {y}^{2}}-{K}^{*}{\left(C-{C}_{\infty }\right)}^{\text{m}}$$

(4)

The problems with physical boundary constraints are.

$$u=-Ux+l\frac{\partial u}{\partial y},v=-{v}_{\rm x},T={T}_{\mathrm{w}}\left(x\right)={T}_{\infty }+{T}_{0}{x}^{n},C={C}_{\mathrm{w}}\left(x\right)={C}_{\infty }+{C}_{0}{x}^{n} \;\mathrm{at }\;y=0$$

$$u\to u=0,T\to {T}_{\infty }, C\to {C}_{\infty } \;\mathrm{as} \;y\to \infty$$

(5)

In this context, $u$ and $v$ represent the velocity components in the $x$ and $y$ axes, respectively. $B(x)$ denotes the magnetic field factor, while ${v}_{\rm x}$ represents the velocity of mass transmission through the wall. It is important to note that ${v}_{\rm x}>0$ corresponds to suction, whilst ${v}_{\rm x}<0$ corresponds to injection.

The heat flux ${q}_{\mathrm{r}}$ via the Rosseland estimation is

$${q}_{\mathrm{r}}=-\frac{{\sigma }^{*}}{3{k}^{*}}\frac{\partial {T}^{4}}{\partial y}$$

(6)

Here ${k}^{*}$ designates the factor of mean absorption. Now substitute Eq. (5) in Eq. (3), we have

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\,{\alpha }_{\mathrm{nf}}\frac{{\partial }^{2}T}{\partial {y}^{2}}-\frac{16{\sigma }^{*}{T}_{\infty }^{3}}{{3{k}^{*}\left(\rho {C}_{\mathrm{p}}\right)}_{\mathrm{nf}}}\frac{{\partial }^{2}T }{\partial {y}^{2}}+\frac{Q\left(T-{T}_{\infty }\right)}{{\left(\rho {C}_{\mathrm{p}}\right)}_{\mathrm{nf}}}+\frac{{\mu }_{\mathrm{nf}}}{{\left(\rho {C}_{\mathrm{p}}\right)}_{\mathrm{nf}}}{\left(\frac{\partial u}{\partial y}\right)}^{2}$$

(7)

The thermal conductivity can be expressed as:

where ${\mu }_{\mathrm{nf}}=\frac{{\mu }_{\mathrm{f}}}{{\left(1-\varphi \right)}^{2.5}},{\rho }_{\mathrm{nf}}=\left(1-\varphi \right){\rho }_{\mathrm{f}}+\varphi {\rho }_{\mathrm{s}}, {\left(\rho {C}_{\mathrm{p}}\right)}_{\mathrm{nf}}=\left(1-\varphi \right){\left(\rho {C}_{\mathrm{p}}\right)}_{\mathrm{f}}+\varphi {\left(\rho {C}_{\mathrm{p}}\right)}_{\mathrm{s}}$

$${k}_{\mathrm{nf}}=\left[\frac{{k}_{\mathrm{s}}+2{k}_{\mathrm{f}}-2\varphi \left({f}_{\mathrm{f}}-{k}_{\mathrm{s}}\right)}{{k}_{\mathrm{s}}+2{k}_{\mathrm{f}}+\varphi \left({f}_{\mathrm{f}}-{k}_{\mathrm{s}}\right)}\right],{\alpha }_{\mathrm{nf}}=\frac{{k}_{\mathrm{nf}}}{{\left(\rho {C}_{\mathrm{p}}\right)}_{\mathrm{nf}}},\frac{{\sigma }_{\mathrm{nf}}}{{\sigma }_{\mathrm{f}}}=1+\left[\frac{3\left(\frac{{\sigma }_{\mathrm{s}}}{{\sigma }_{\mathrm{f}}}-1\right)\varphi }{\left(\frac{{\sigma }_{\mathrm{s}}}{{\sigma }_{\mathrm{f}}}+2\right)-\left(\frac{{\sigma }_{\mathrm{s}}}{{\sigma }_{\mathrm{f}}}-1\right)\varphi }\right]$$

(8)

The non-dimensional and similarity variables are

$$u = axf^{\prime } \left( \eta \right),v = - \left( {\nu {\text{a}}} \right)^{{\frac{1}{2}}} f\left( \eta \right),\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{{\text{w}}} - T_{\infty } }},\phi \left( \eta \right) = \frac{{\left( {C - C_{\infty } } \right)}}{{\left( {C_{{\text{w}}} - C_{\infty } } \right)}} \;\& \;\eta = y\left( {\frac{a}{\nu }} \right)^{{\frac{1}{2}}}$$

(9)

Equations (2) and (6) are of the form after performing the similarity conversions.

$$f^{{\prime \prime \prime }} + B_{1} B_{2} ff^{{\prime \prime }} - B_{1} B_{2} f^{{\prime 2}} - B_{2} Mf\prime - B_{1} B_{2} Kf^{\prime } = 0$$

(10)

$$B_{2} \left( {B_{3} + \frac{4}{{3R}}} \right)\theta ^{{\prime \prime }} + {\text{Pr}}.B_{2} B_{4} \left( {f\theta ^{\prime } - nf^{\prime } \theta + \beta \theta } \right) + {\text{Ec}}.{\text{Pr}}.f^{{\prime \prime 2}} = 0$$

(11)

$$\phi ^{{\prime \prime }} + {\text{Sc}}.\left[ {f\phi ^{\prime } - n.f^{\prime } \phi - Kr.\phi ^{m} } \right] = 0$$

(12)

And transformed boundary constraints are

$$\left. {\begin{array}{*{20}c} {f\left( \eta \right) = S,f^{\prime } \left( \eta \right) = - 1 + \lambda f^{{\prime \prime }} \left( \eta \right),\;\theta \left( \eta \right) = 1,\;\phi \left( 0 \right) = 1\;{\text{at}}\;\eta = 0} \\ {f^{\prime } (\eta ) \to 0,\;\theta (\eta ) \to 0,\phi \left( \eta \right) \to 0\;{\text{as}}\;\eta \to \infty } \\ \end{array} } \right\}$$

(13)

where $\mathrm{Pr}=\frac{{\nu }_{\mathrm{f}}}{{\alpha }_{\mathrm{f}}}, K=\frac{{\nu }_{\mathrm{f}}}{a{K}_{\mathrm{p}}},\beta =\frac{Q}{a{\left(\rho {C}_{\mathrm{p}}\right)}_{\mathrm{f}}}, M=\frac{2L\sigma {B}_{0}^{2}}{\rho }, \lambda =l{\left(\frac{a}{\nu }\right)}^\frac{1}{2},R=\frac{{k}^{*}{k}_{\mathrm{f}}}{4{\sigma }^{*}{T}_{\infty }^{3}}$ and $\mathrm{Ec}=\frac{{u}_{\mathrm{w}}^{2}}{{C}_{\text{p}}({T}_{\mathrm{w}}-{T}_{\infty })},$

$${\text{Sc}} = \frac{{\nu _{{\text{f}}} }}{D},\;{\text{Kr}} = \frac{{K^{*} \Delta C^{{\text{m} - 1}} }}{a}$$

And also $B_{1} = \left[ {1 - \phi \left( {1 - \frac{{\rho _{{\text{s}}} }}{{\rho _{{\text{f}}} }}} \right)} \right],\;B_{2} = \left( {1 - \phi } \right)^{{2.5}} ,\;B_{3} = \frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }},\;B_{4} = 1 - \phi + \frac{{\phi \left( {\rho C_{{\text{p}}} } \right)_{{\text{s}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}$.

In this context, the drag force, Nusselt number, and Sherwood numbers must be denoted as (Thermo-physical characteristics of nanoparticles are mentioned in Table 1)

Table 1 Thermo-physical attributes of ethylene glycol and ${\mathrm{Fe}}_{3}{\mathrm{O}}_{4}$ nanoparticle

$${C}_{\mathrm{f}}=\frac{{\tau }_{\mathrm{w}}}{\rho {u}_{\mathrm{w}}^{2}}=\frac{{\mathrm{Re}}_{\rm x}^{-\frac{1}{2}}}{{B}_{1}}{f}^{{\prime}^{\prime}}\left(0\right)\Rightarrow {B}_{1}{C}_{\mathrm{f}}{\mathrm{Re}}_{\rm x}^\frac{1}{2}={f}^{{\prime}^{\prime}}\left(0\right)$$

(14)

$${\mathrm{Nu}}_{\rm x}=-\frac{{k}_{\mathrm{nf}}x}{{k}_{\mathrm{f}}\left({T}_{\mathrm{w}}-{T}_{\infty }\right)}{\left(\frac{\partial T}{\partial y}\right)}_{y=0}=-\frac{{k}_{\mathrm{nf}}}{{k}_{\mathrm{f}}}{\mathrm{Re}}_{\rm x}^{-\frac{1}{2}}{\theta }^{\mathrm{^{\prime}}}\left(0\right), \mathrm{then}\quad \frac{{k}_{\mathrm{f}}}{{k}_{\mathrm{nf}}}{\mathrm{Nu}}_{\rm x}{\mathrm{Re}}_{\rm x}^{1/2}=-{\theta }^{\mathrm{^{\prime}}}\left(0\right).$$

(15)

$${\mathrm{Sh}}_{\rm x}=-\frac{x}{D\left({C}_{\mathrm{w}}-{C}_{\infty }\right)}{\left(D\frac{\partial C}{\partial y}\right)}_{y=0}\;\mathrm{then}\; {\mathrm{Re}}_{\rm x}^{-\frac{1}{2}}{\mathrm{Sh}}_{\rm x}=-{\phi }^{\mathrm{^{\prime}}}\left(0\right)$$

(16)

Analysis of entropy generation

A comprehensive comprehension of the mechanisms behind entropy generation is crucial for gaining insight into the irreversibility of thermal energy inside a certain system. The depletion of available energy in industrial and technological processes is mostly attributed to the creation of entropy. The entropy generation significantly influences the presentation of heat equipment such as energy engines, thermal pumps, freezers, and power plants. Given the considerable importance of the matter, it is essential to ascertain the rate at which entropy is generated inside a system in order to optimize the system's energy for optimal operational performance. The equation governing the generation of entropy in the context of non-steady magnetohydrodynamic (MHD) nanofluid flow under the influence of radiation and viscosity is derived from the second law of thermodynamics, as stated in Reference [65].

$${S}_{\mathrm{G}}=\frac{{k}_{\mathrm{nf}}}{{T}_{\infty }^{2}}\left[{\left(\frac{\partial T}{\partial x}\right)}^{2}+\left(1+\frac{16{\sigma }^{*}{T}_{\infty }^{3}}{3{k}^{*}{k}_{\mathrm{f}}}\right){\left(\frac{\partial T}{\partial y}\right)}^{2}\right]+\frac{{D}_{\mathrm{B}}}{{T}_{\infty }}\left(\frac{\partial T}{\partial y}\right)\left(\frac{\partial \phi }{\partial y}\right)+\frac{{D}_{\mathrm{B}}}{{T}_{\infty }}{\left(\frac{\partial \phi }{\partial y}\right)}^{2}+\frac{{\mu }_{\mathrm{nf}}}{{T}_{\infty }}{\left(\frac{\partial u}{\partial y}\right)}^{2}+\frac{\sigma {B}_{0}^{2}}{{T}_{\infty }}{u}^{2}+\frac{{\nu }_{\mathrm{nf}}}{{k}_{\mathrm{nf}}}{u}^{2}$$

(17)

The entropy production rate distinctive is specified by

$${\left({S}_{\mathrm{G}}\right)}_{0}=\frac{{k}_{\mathrm{nf}}\left(\Delta T\right)}{{x}^{2}{T}_{\infty }^{2}}$$

(18)

Using Eqs. (17) and (18), we obtain the entropy generation number

$${N}_{\mathrm{s}}=\frac{{S}_{\mathrm{G}}}{{\left({S}_{\mathrm{G}}\right)}_{0}}$$

(19)

From Eqs. (17), (18) and (19), the entropy production number may be specified as:

$$N_{{\text{s}}} = \left( {1 + \frac{{4R}}{3}} \right)\theta ^{{\prime 2}} \left( \eta \right){\text{Re}}_{{\text{x}}} + \frac{{{\text{Br}}}}{\Omega }f^{{\prime \prime 2}} \left( \eta \right){\text{Re}}_{{\text{x}}} + \frac{{{\text{Br}}}}{\Omega }\left( {M + k} \right)f^{{\prime 2}} \left( \eta \right) + \gamma \left[ {\Omega ^{\prime } .\frac{1}{{\Omega ^{2} }}\phi ^{{\prime 2}} + \frac{1}{\Omega }\theta ^{\prime } \phi ^{\prime } } \right]$$

(20)

where $\mathrm{Br}=\frac{{\mu }_{\mathrm{nf}}}{{k}_{\mathrm{nf}}}\frac{{u}_{\mathrm{w}}^{2}}{\Delta T}$ is the Brinkman number, $\Omega = \frac{{\Delta T}}{{T_{\infty } }},\Omega ^{\prime } = \frac{{\Delta \phi }}{{\phi _{\infty } }}$ is the difference in dimensionless temperature and concentration, $\gamma =\frac{D\left({\phi }_{\mathrm{w}}-{\phi }_{\infty }\right)}{{k}_{\mathrm{nf}}}$ refers to the nanoparticle mass transfer factor and ${\mathrm{Re}}_{\rm x}=\frac{{u}_{\rm x}l}{\nu }$ is the Reynolds number.

Method of solution

A variety of numerical approaches may be used to solve the altered, nonlinear, boundary value problems described by Eqs. (10)–(12). In this section, we implement Keller's widespread, second-order precise implicit finite difference approach. Recent research has used this approach in the context of MHD and rheological flows. The Keller box technique begins by reducing the multi-degree and order connected ODEs specified in (10)–(12) to a set of linear-order equations. These equations are then discretized using finite difference approximations in each coordinate direction with suitable step lengths. The Keller Box Scheme consists of four fundamental phases.

• Convert the higher-order set of ordinary differential equations to 1st order.

• Implement discretization by using finite difference.

• Quasi-linearization of nonlinear algebraic equations.

• Tridiagonal Block elimination of linear algebraic equations.

Equations (10)–(12) along with boundary circumstances (13) are firstly represented as a set of 1st-order equations. For this, we use new dependent variables $f^{\prime } = p,p^{\prime } = q,\theta = v,\theta ^{\prime } = g,\phi = s,\phi ^{\prime } = t$

As a result, we get the following seven first-order equations:

• 1. ${f}^{\prime}=p \quad (21)$

• 2. ${p}^{\prime}=q \quad (22)$

• 3. ${\theta }^{\prime}=g \quad (23)$

• 4. ${\phi }^{\prime}=t \quad (24)$

• 5. ${q}^{\prime}+{B}_{1}{B}_{2}fq-{B}_{1}{B}_{2}{p}^{2}-{B}_{2}Mp-{B}_{1}{B}_{2}Kp=0 \quad (25)$

• 6. $B_{2} \left( {B_{3} + \frac{4}{{3R}}} \right)g^{\prime} + {\text{Pr}}.B_{2} B_{4} \left( {fg - npv + \beta v} \right) + {\text{Ec}}.{\text{Pr}}.q^{2} = 0\quad (26)$

• 7. $t^{\prime}+\mathrm{Sc}.\left[ft-n.ps-Kc.{s}^{m}\right]=0 \quad (27)$

the boundary circumstances in terms of new variables are:

$$\left.\begin{array}{c}f\left(\eta \right)=S,p\left(\eta \right)=-1+\lambda q\left(\eta \right),v\left(\eta \right)=1,s\left(0\right)=1 \;at\; \eta =0\\ p(\eta )\to 0,v(\eta )\to 0,s\left(\eta \right)\to 0 \;as\; \eta \to \infty \end{array}\right\}$$

(28)

Expand the first-order derivatives using the finite difference approach in Eqs. (21–27). The equations are nonlinear; thus, we linearize them using Newton's method. Then we get.

$$\begin{aligned} {\text{i}}{\text{.}}\;\frac{{f_{\rm j} - f_{{\rm j - 1}} }}{{h_{\rm j} }} & = \frac{{p_{\rm j} + p_{{\rm j - 1}} }}{2} = p_{{\rm j - \frac{1}{2}}} \\ & \Rightarrow f_{\rm j} - f_{{\rm j - 1}} - \frac{{h_{\rm j} }}{2}\left( {p_{\rm j} + p_{{\rm j - 1}} } \right) = 0 \\ & \Rightarrow (f_{\rm j} + \delta f_{\rm j} ) - (f_{{\rm j - 1}} + \delta f_{{\rm j - 1}} ) - \frac{{h_{\rm j} }}{2}\left( {\left( {p_{\rm j} + p\zeta _{\rm j} } \right) + \left( {p_{{\rm j - 1}} + p_{{\rm j - 1}} } \right)} \right) = 0 \\ & \Rightarrow \delta f_{\rm j} - \delta f_{{\rm j - 1}} - \frac{{h_{\rm j} }}{2}\left( {\delta p_{\rm j} + \delta p_{{\rm j - 1}} } \right) = (f_{{\rm j - 1}} - f_{\rm j} ) + h_{\rm j} p_{{\rm j - \frac{1}{2}}} = \left( {r_{1} } \right)_{{\rm j - \frac{1}{2}}} \\ \end{aligned}$$

$$\begin{aligned} {\text{ii}}{\text{.}}\;\frac{{p_{\rm j} - p_{{\rm j - 1}} }}{{h_{\rm j} }} & = \frac{{q_{\rm j} + q_{{\rm j - 1}} }}{2} = q_{{\rm j - \frac{1}{2}}} \\ & \Rightarrow p_{\rm j} - p_{{\rm j - 1}} - \frac{{h_{\rm j} }}{2}\left( {q_{\rm j} + q_{{\rm j - 1}} } \right) = 0 \\ & \Rightarrow (p_{\rm j} + \delta p_{\rm j} ) - (p_{{\rm j - 1}} + \delta p_{{\rm j - 1}} ) - \frac{{h_{\rm j} }}{2}\left( {\left( {q_{\rm j} + \delta q_{\rm j} } \right) + \left( {q_{{\rm j - 1}} + \delta q_{{\rm j - 1}} } \right)} \right) = 0 \\ & \Rightarrow \delta p_{\rm j} - \delta p_{{\rm j - 1}} - \frac{{h_{\rm j} }}{2}\left( {\delta q_{\rm j} + \delta q_{{\rm j - 1}} } \right) = (p_{{\rm j - 1}} - p_{\rm j} ) + h_{\rm j} q_{{\rm j - \frac{1}{2}}} = \left( {r_{2} } \right)_{{\rm j - \frac{1}{2}}} \\ \end{aligned}$$

$$\begin{aligned} {\text{iii}}.\;\frac{{v_{\rm j} - v_{{\rm j - 1}} }}{{h_{\rm j} }} & = \frac{{g_{\rm j} + g_{{\rm j - 1}} }}{2} = g_{{\rm j - \frac{1}{2}}} \\ & \Rightarrow v_{\rm j} - v_{{\rm j - 1}} - \frac{{h_{\rm j} }}{2}\left( {g_{\rm j} + g_{{\rm j - 1}} } \right) = 0 \\ & \Rightarrow (v_{\rm j} + \delta v_{\rm j} ) - (v_{{\rm j - 1}} + \delta v_{{\rm j - 1}} ) - \frac{{h_{\rm j} }}{2}\left( {\left( {g + \delta g_{\rm j} } \right) + \left( {g_{{\rm j - 1}} + \delta g_{{\rm j - 1}} } \right)} \right) = 0 \\ & \Rightarrow \delta v_{\rm j} - \delta v_{{\rm j - 1}} - \frac{{h_{\rm j} }}{2}\left( {\delta g_{\rm j} + \delta g_{{\rm j - 1}} } \right) = (v_{{\rm j - 1}} - v_{\rm j} ) + h_{\rm j} g_{{\rm j - \frac{1}{2}}} = \left( {r_{3} } \right)_{{\rm j - \frac{1}{2}}} \\ \end{aligned}$$

$$\begin{aligned} {\text{iv}}.\;\frac{{s_{\rm j} - s_{{\rm j - 1}} }}{{h_{\rm j} }} & = \frac{{t_{\rm j} + t_{{\rm j - 1}} }}{2} = t_{{\rm j - \frac{1}{2}}} \\ & \Rightarrow s_{\rm j} - s_{{\rm j - 1}} - \frac{{h_{\rm j} }}{2}\left( {t_{\rm j} + t_{{\rm j - 1}} } \right) = 0 \\ & \Rightarrow (s_{\rm j} + \delta s_{\rm j} ) - (s_{{\rm j - 1}} + \delta s_{{\rm j - 1}} ) - \frac{{h_{\rm j} }}{2}\left( {\left( {t_{\rm j} + \delta t} \right) + \left( {t_{{\rm j - 1}} + \delta t_{{\rm j - 1}} } \right)} \right) = 0 \\ & \Rightarrow \delta s_{\rm j} - \delta s_{{\rm j - 1}} - \frac{{h_{\rm j} }}{2}\left( {\delta t_{\rm j} + \delta t_{{\rm j - 1}} } \right) = (s_{{\rm j - 1}} - s_{\rm j} ) + h_{\rm j} t_{{\rm j - \frac{1}{2}}} = \left( {r_{4} } \right)_{{\rm j - \frac{1}{2}}} \\ \end{aligned}$$

$$\begin{aligned} & {\text{v}}{\text{.}}\;\left( {\frac{{q_{{\text{j}}} - q_{{{{\mathrm{j} - 1}}}} }}{{h_{{\text{j}}} }}} \right) - B_{1} B_{2} \left( {p^{2} } \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} + B_{1} B_{2} \left( {fq} \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} - B_{2} \left( {M + B_{1} K} \right)\left( {\frac{{p_{{\text{j}}} + p_{{{{\mathrm{j} - 1}}}} }}{2}} \right) = 0 \\ & \quad \Rightarrow \left( {q_{{\text{j}}} - q_{{{{\mathrm{j} - 1}}}} } \right) - h_{{\text{j}}} \left[ {B_{1} B_{2} \left( {p^{2} } \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} - B_{1} B_{2} \left( {\frac{{f_{{\text{j}}} + f_{{{{\mathrm{j} - 1}}}} }}{2}} \right)\left( {\frac{{q_{{\text{j}}} + q_{{{{\mathrm{j} - 1}}}} }}{2}} \right) + B_{2} \left( {M + B_{1} K} \right)\left( {\frac{{p_{{\text{j}}} + p_{{{{\mathrm{j} - 1}}}} }}{2}} \right)} \right] = 0 \\ & \quad \Rightarrow \left( {q_{{\text{j}}} + \delta q_{{\text{j}}} - q_{{{{\mathrm{j} - 1}}}} - \delta q_{{{{\mathrm{j} - 1}}}} } \right) - h_{{\text{j}}} B_{1} B_{2} \left( {p_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}}^{2} + p_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} \left( {\delta p_{{\text{j}}} + \delta p_{{{{\mathrm{j} - 1}}}} } \right)} \right) \\ & \quad \quad + B_{1} B_{2} h_{{\text{j}}} \left[ {\left( {fq} \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} + \frac{1}{2}f_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} \left( {\delta q_{{\text{j}}} + \delta q_{{{{\mathrm{j} - 1}}}} } \right) + \frac{1}{2}q_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} \left( {\delta f_{{\text{j}}} + \delta f_{{{{\mathrm{j} - 1}}}} } \right)} \right. \\ & \quad \quad \left. { - B_{2} \left( {M + KB_{1} } \right)\left( {\frac{{p_{{\text{j}}} + \delta p_{{\text{j}}} + p_{{{{\mathrm{j} - 1}}}} + \delta p_{{{{\mathrm{j} - 1}}}} }}{2}} \right)} \right] = 0 \\ & \quad \Rightarrow \left( {\delta q_{{\text{j}}} - \delta q_{{{{\mathrm{j} - 1}}}} } \right) - h_{{\text{j}}} B_{1} B_{2} \left( {p_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} \left( {\delta p_{{\text{j}}} + \delta p_{{{{\mathrm{j} - 1}}}} } \right)} \right) \\ & \quad \quad + B_{1} B_{2} h_{{\text{j}}} \left[ {\frac{1}{2}f_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} \left( {\delta q_{{\text{j}}} + \delta q_{{{{\mathrm{j} - 1}}}} } \right) + \frac{1}{2}q_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} \left( {\delta f_{{\text{j}}} + \delta f_{{{{\mathrm{j} - 1}}}} } \right)} \right. \\ & \quad \quad \left. { - B_{2} \left( {M + B_{1} K} \right)\left( {\frac{{\delta p_{{\text{j}}} + \delta p_{{{{\mathrm{j} - 1}}}} }}{2}} \right)} \right] \\ & \quad \quad = \left( {q_{{{{\mathrm{j} - 1}}}} - q_{{\text{j}}} } \right) + h_{{\text{j}}} B_{1} B_{2} p_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}}^{2} - B_{1} B_{2} h_{{\text{j}}} \left( {fq} \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} + B_{2} h_{{\text{j}}} \left( {M + B_{1} K} \right)p_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} \\ & \quad \quad = \left( {r_{5} } \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} \\ & \quad \Rightarrow \delta q_{{\text{j}}} \left( {m_{1} } \right)_{{\text{j}}} + \left( {m_{2} } \right)_{{\text{j}}} \delta q_{{{{\mathrm{j} - 1}}}} + \left( {m_{3} } \right)_{{\text{j}}} \delta p_{{\text{j}}} + \left( {m_{4} } \right)_{{\text{j}}} p_{{{{\mathrm{j} - 1}}}} + \left( {m_{5} } \right)_{{\text{j}}} \delta f_{{\text{j}}} + \left( {m_{6} } \right)_{{\text{j}}} \delta f_{{{{\mathrm{j} - 1}}}} = \left( {r_{5} } \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} \\ {\text{where}}\;\left( {m_{1} } \right)_{{\text{j}}} & = 1 + B_{1} B_{2} \frac{{h_{{\text{j}}} }}{2}f_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} ,\;\left( {m_{2} } \right)_{{\text{j}}} = - 1 + B_{1} B_{2} \frac{{h_{{\text{j}}} }}{2}f_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} = \left( {m_{1} } \right)_{{\text{j}}} - 2.0 \\ \left( {m_{3} } \right)_{{\text{j}}} & = h_{{\text{j}}} B_{1} B_{2} p_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} - \frac{{h_{{\text{j}}} }}{2}B_{2} \left( {M + B_{1} K} \right) = \left( {m_{4} } \right)_{{\text{j}}} ,\left( {m_{5} } \right)_{{\text{j}}} = B_{1} B_{2} \frac{{h_{{\text{j}}} }}{2}q_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} = \left( {m_{6} } \right)_{{\text{j}}} \;{\text{and}}\; \\ \left( {r_{5} } \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} & = \left( {q_{{{{\mathrm{j} - 1}}}} - q_{{\text{j}}} } \right) + h_{{\text{j}}} B_{1} B_{2} p_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}}^{2} - B_{1} B_{2} h_{{\text{j}}} \left( {fq} \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} + B_{2} h_{{\text{j}}} \left( {M + B_{1} K} \right)p_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} \\ \end{aligned}$$

$$\begin{aligned} & {\text{vi}}.\;B_{2} \left( {B_{3} + \frac{4}{{3R}}} \right)\left( {\frac{{g_{{\text{j}}} - g_{{{\text{j}} - 1}} }}{{h_{{\text{j}}} }}} \right) + {\text{Pr}}B_{2} B_{4} \left[ {\left( {fg} \right)_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} - n\left( {pv} \right)_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} + \beta \left( {\frac{{v_{{\text{j}}} + v_{{{\text{j}} - 1}} }}{2}} \right)} \right] + {\text{Pr}}{\text{.Ec}}{\text{.}}\left( {q^{2} } \right)_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} = 0 \\ & \Rightarrow B_{2} \left( {B_{3} + \frac{4}{{3R}}} \right)\left( {g_{{\text{j}}} + \delta g_{{\text{j}}} - g_{{{\text{j}} - 1}} - \delta g_{{{\text{j}} - 1}} } \right) + h_{{\text{j}}} {\text{Pr}}B_{2} B_{4} \beta \left( {\frac{{v_{{\text{j}}} + \delta v_{{\text{j}}} + v_{{{\text{j}} - 1}} + \delta v_{{{\text{j}} - 1}} }}{2}} \right) \\ & \quad \quad + h_{{\text{j}}} {\text{Pr}}B_{2} B_{4} \left[ {\left( {fg} \right)_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} + \frac{1}{2}f_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} \left( {\delta g_{{\text{j}}} + \delta g_{{{\text{j}} - 1}} } \right) + \frac{1}{2}g_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} \left( {\delta f_{{\text{j}}} + \delta f_{{{\text{j}} - 1}} } \right)} \right. \\ & \quad \quad \left. { - n\left\{ {\left( {pv} \right)_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} + \frac{1}{2}p_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} \left( {\delta v_{{\text{j}}} + \delta v_{{{\text{j}} - 1}} } \right) + \frac{1}{2}v_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} \left( {\delta p_{{\text{j}}} + \delta p_{{{\text{j}} - 1}} } \right)} \right\}} \right] \\ & \quad \quad + {\text{Ec}}{\text{.Pr}}.h_{{\text{j}}} \left\{ {q_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}}^{2} + q_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} \left( {\delta q_{{\text{j}}} + \delta q_{{{\text{j}} - 1}} } \right)} \right\} = 0 \\ & \Rightarrow B_{2} \left( {B_{3} + \frac{4}{{3R}}} \right)\left( {\delta g_{{\text{j}}} - \delta g_{{{\text{j}} - 1}} } \right) \\ & \quad \quad + \frac{{h_{{\text{j}}} }}{2}{\text{Pr}}B_{2} B_{4} \left[ {f_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} \left( {\delta g_{{\text{j}}} + \delta g_{{{\text{j}} - 1}} } \right) + g_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} \left( {\delta f_{{\text{j}}} + \delta f_{{{\text{j}} - 1}} } \right)} \right. \\ & \quad \quad \left. { - n\left\{ {p_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} \left( {\delta v_{{\text{j}}} + \delta v_{{{\text{j}} - 1}} } \right) + v_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} \left( {\delta p_{{\text{j}}} + \delta p_{{{\text{j}} - 1}} } \right)} \right\}} \right] \\ & \quad \quad + {\text{Ec}}{\text{.Pr}}{\text{.}}h_{{\text{j}}} \left\{ {q_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} \left( {\delta q_{{\text{j}}} + \delta q_{{{\text{j}} - 1}} } \right)} \right\} + h_{{\text{j}}} {\text{Pr}}B_{2} B_{4} \beta \left( {\frac{{\delta v_{{\text{j}}} + \delta v_{{{\text{j}} - 1}} }}{2}} \right) \\ & = B_{2} \left( {B_{3} + \frac{4}{{3R}}} \right)\left( {g_{{{\text{j}} - 1}} - g_{{\text{j}}} } \right) - h_{{\text{j}}} {\text{Pr}}B_{2} B_{4} \beta v_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} - h_{{\text{j}}} {\text{Pr}}B_{2} B_{4} \left[ {\left( {fg} \right)_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} - n\left( {pv} \right)_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} } \right] \\ & \quad \quad + {\text{Ec}}{\text{.Pr}}.h_{{\text{j}}} q_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}}^{2} = \left( {r_{6} } \right)_{{{\text{j}} - \frac{{\text{1}}}{{\text{2}}}}} \\ \end{aligned}$$

$$\begin{aligned} & \Rightarrow \left( {n_{1} } \right)_{{\text{j}}} \delta g_{{\text{j}}} + \left( {n_{2} } \right)_{{\text{j}}} \delta g_{{{{\mathrm{j} - 1}}}} + \left( {n_{3} } \right)_{{\text{j}}} \delta f_{{\text{j}}} + \left( {n_{4} } \right)_{{\text{j}}} \delta f_{{{{\mathrm{j} - 1}}}} + \left( {n_{5} } \right)_{{\text{j}}} \delta v_{{\text{j}}} + \left( {n_{6} } \right)_{{\text{j}}} \delta v_{{{{\mathrm{j} - 1}}}} + \left( {n_{7} } \right)_{{\text{j}}} \delta p_{{\text{j}}} + \left( {n_{8} } \right)_{{\text{j}}} \delta n_{{{{\mathrm{j} - 1}}}} + \left( {n_{9} } \right)_{{\text{j}}} \delta q_{{{{\mathrm{j} - 1}}}} + \left( {n_{{10}} } \right)_{{\text{j}}} \delta q_{{{{\mathrm{j} - 1}}}} = \left( {r_{6} } \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} \\ & {\text{where}}\;\left( {n_{1} } \right)_{{\text{j}}} = B_{2} \left( {B_{3} + \frac{4}{{3R}}} \right) + \frac{{h_{{\text{j}}} }}{2}{\text{Pr}}B_{2} B_{4} \left[ {f_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} } \right],\;\left( {n_{2} } \right)_{{\text{j}}} = \left( {n_{1} } \right)_{{\text{j}}} - 2*B_{2} \left( {B_{3} + \frac{4}{{3R}}} \right) \\ \left( {n_{3} } \right)_{{\text{j}}} & = \frac{{h_{{\text{j}}} }}{2}{\text{Pr}}B_{2} B_{4} \left[ {g_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} } \right] = \left( {n_{4} } \right)_{{\text{j}}} ,\left( {n_{5} } \right)_{{\text{j}}} = \frac{{h_{{\text{j}}} }}{2}{\text{Pr}}B_{2} B_{4} \left[ { - n..p_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} + \beta } \right] = \left( {n_{6} } \right)_{{\text{j}}} ,\;\left( {n_{7} } \right)_{{\text{j}}} \\ & = \frac{{h_{{\text{j}}} }}{2}{\text{Pr}}B_{2} B_{4} \left[ { - n..v_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} } \right] = \left( {n_{8} } \right)_{{\text{j}}} ,\left( {n_{9} } \right)_{{\text{j}}} = h_{{\text{j}}} {\text{EcPr}}q_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} = \left( {n_{{10}} } \right)_{{\text{j}}} \;{\text{and}}\;\left( {r_{6} } \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} = B_{2} \left( {B_{3} + \frac{4}{{3R}}} \right)\left( {g_{{{{\mathrm{j} - 1}}}} - g_{{\text{j}}} } \right) \\ & \quad - h_{{\text{j}}} {\text{Pr}}B_{2} B_{4} \beta v_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} - h_{{\text{j}}} {\text{Pr}}B_{2} B_{4} \left[ {\left( {fg} \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} - n\left( {pv} \right)_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}} } \right] + {\text{Ec.Pr}}.h_{{\text{j}}} q_{{{{\mathrm{j} - }}\frac{{\text{1}}}{{\text{2}}}}}^{2} \\ \end{aligned}$$

$$\begin{aligned} & {\text{vii}}.\;\left( {\frac{{t_{\text{j}} - t_{{\text{j} - 1}} }}{{h_{\text{j}} }}} \right) + {\text{Sc}}\left[ {\left( {ft} \right)_{{\text{j} - \frac{1}{2}}} - n.\left( {{{ps}}} \right)_{{\text{j} - \frac{1}{2}}} - {{Kc}}.\left( {s^{\text{m}} } \right)_{{ \text{j} - \frac{1}{2}}} } \right] = 0~\;{\text{then}} \\ & \Rightarrow \left( {t_{\text{j}} + \delta t_{\text{j}} - t_{{\text{j} - 1}} - \delta t_{{\text{j} - 1}} } \right) \\ & \quad + {\text{Sc}}h_{\text{j}} \left[ {\left\{ {\left( {ft} \right)_{{ \text{j} - \frac{1}{2}}} + \frac{1}{2}f_{{\text{j} - \frac{1}{2}}} \left( {\delta t_{\text{j}} + \delta t_{{\text{j} - 1}} } \right) + \frac{1}{2}t_{{\text{j} - \frac{1}{2}}} \left( {\delta f_{\text{j}} + \delta f_{{\text{j} - 1}} } \right)} \right\}} \right. \\ & \quad - n\left\{ {\left( {ps} \right)_{{ \text{j} - \frac{1}{2}}} + \frac{1}{2}p_{{\text{j} - \frac{1}{2}}} \left( {\delta s_{\text{j}} + \delta s_{{\text{j} - 1}} } \right) + \frac{1}{2}s_{{\text{j} - \frac{1}{2}}} \left( {\delta p_{\text{j}} + \delta p_{{\text{j} - 1}} } \right)} \right\} \\ & \quad \left. { - {{Kc}}.\left\{ {\left( {s^{\text{m}} } \right)_{{ \text{j} - \frac{1}{2}}} + ms_{{\text{j} - \frac{1}{2}}} \left( {\delta s_{\text{j}} + \delta s_{{\text{j} - 1}} } \right)} \right\}} \right] = 0 \\ & \Rightarrow \left( {\delta t_{\text{j}} - \delta t_{{\text{j} - 1}} } \right) \\ & \quad + \frac{1}{2}{\text{Sc}}h_{\text{j}} \left[ {\left\{ {f_{{\text{j} - \frac{1}{2}}} \left( {\delta t_{\text{j}} + \delta t_{{\text{j} - 1}} } \right) + t_{{\text{j} - \frac{1}{2}}} \left( {\delta f_{\text{j}} + \delta f_{{\text{j} - 1}} } \right)} \right\}} \right. \\ & \quad \left. { - n\left\{ {p_{{\text{j} - \frac{1}{2}}} \left( {\delta s_{\text{j}} + \delta s_{{\text{j} - 1}} } \right) + s_{{\text{j} - \frac{1}{2}}} \left( {\delta p_{\text{j}} + \delta p_{{\text{j} - 1}} } \right)} \right\} - Kc.\left\{ {2ms_{{\text{j} - \frac{1}{2}}} \left( {\delta s_{\text{j}} + \delta s_{{\text{j} - 1}} } \right)} \right\}} \right] \\ & = \left( {t_{{\text{j} - 1}} - t_{\text{j}} } \right) - {\text{Sc}}h_{\text{j}} \left[ {\left( {ft} \right)_{{ \text{j} - \frac{1}{2}}} - n\left( {ps} \right)_{{ \text{j} - \frac{1}{2}}} - Kc.\left( {s^{\text{m}} } \right)_{{ \text{j} - \frac{1}{2}}} } \right] = \left( {r_{7} } \right)_{{ \text{j} - \frac{1}{2}}} \\ & \left( {p_{1} } \right)_{ \text{j}} \delta t_{\text{j}} + \left( {p_{2} } \right)_{ \text{j}} \delta t_{{\text{j} - 1}} + \left( {p_{3} } \right)_{ \text{j}} \delta f_{\text{j}} + \left( {p_{4} } \right)_{ \text{j}} \delta f_{{\text{j} - 1}} + \left( {p_{5} } \right)_{ \text{j}} \delta s_{\text{j}} + \left( {p_{6} } \right)_{ \text{j}} \delta s_{{\text{j} - 1}} + \left( {p_{7} } \right)_{ \text{j}} \delta p_{\text{j}} + \left( {p_{8} } \right)_{ \text{j}} \delta p_{{\text{j} - 1}} \\ & = \left( {r_{7} } \right)_{{ \text{j} - \frac{1}{2}}} \\ & \left( {p_{1} } \right)_{ \text{j}} = 1 + \frac{{h_{\text{j}} {\text{Sc}}}}{2}f_{{\text{j} - \frac{1}{2}}} ,\quad \left( {p_{2} } \right)_{ \text{j}} = \left( {p_{1} } \right)_{ \text{j}} - 2.0,\left( {p_{3} } \right)_{ \text{j}} = \frac{{h_{\text{j}} {\text{Sc}}}}{2}t_{{\text{j} - \frac{1}{2}}} = \left( {p_{4} } \right)_{ \text{j}} ,\left( {p_{5} } \right)_{ \text{j}} = \frac{1}{2}{\text{Sc}}.h_{\text{j}} \left( { - n*p_{{\text{j} - \frac{1}{2}}} - Kc*2*m*s_{{\text{j} - \frac{1}{2}}} } \right) \\ & \left( {p_{6} } \right)_{ \text{j}} ,\;~\left( {p_{7} } \right)_{ \text{j}} = \frac{1}{2}{\text{Sc}}.h_{\text{j}} s_{{\text{j} - \frac{1}{2}}} = \left( {p_{8} } \right)_{ \text{j}} \;{\text{and}} \\ & \left( {r_{7} } \right)_{{ \text{j} - \frac{1}{2}}} = \left( {t_{{\text{j} - 1}} - t_{\text{j}} } \right) - {\text{Sc}}h_{\text{j}} \left[ {\left( {ft} \right)_{{ \text{j} - \frac{1}{2}}} - n\left( {ps} \right)_{{ \text{j} - \frac{1}{2}}} - Kc.\left( {s^{\text{m}} } \right)_{{ \text{j} - \frac{1}{2}}} } \right] \\ \end{aligned}$$

the boundary constraints are:

$$\eta =0: {f}_{0}=S,{p}_{0}=-1+\lambda {q}_{0},{v}_{0}=1,{s}_{0}=1$$

$$p_{\rm j} \to 0,v_{\rm j} \to 0,s_{\rm j} \to 0{ }\;{\text{as}}\;\eta \to \infty$$

The whole linearized system is actually written as a block matrix, where each member of the coefficient matrix is a separate matrix. A linear tridiagonal system of equations is obtained. It may be expressed as $A\delta =r$ in a vector–matrix form. The block elimination approach may be utilized to solve this tridiagonal matrix. This process is repetitive until the convergence criterion is met.

Appropriate initial guesses have been selected in order to improve the accuracy of this method. The following first predictions are determined using boundary criteria.

$$f\left( \eta \right) = S + \frac{1}{{\left( {1 + \lambda } \right)}}\left( {e^{ - \eta } - 1} \right),\theta \left( \eta \right) = e^{ - \eta } ,\phi \left( \eta \right) = e^{ - \eta }$$

The technique presented demonstrates a high level of reliability, exhibiting second-order consistency and ease of implementation, hence yielding a very desirable result. The coherence of the design is influenced by the modification of the accompanying initial estimations. The Thomas approach is used for the resolution of the previously specified difference equations in a block-matrix representation. The existing study used a fixed grid size of $\Delta \eta =0.006$, which offers six decimal places of precision as ${\eta }_{\infty }\to 3$ for the majority of the values shown in the table, with a tolerance for error of ${10}^{-6}$ in all circumstances.

Results and discussion

It is not possible to find an analytical solution to the ordinary differential equation (ODE) that was constructed using Eqs. (10) through (12), coupled with the boundary condition Eq. (13). Due to the nonlinear nature of the ODE, it is also hard to derive accurate solutions to the problems. This study focuses on the development of numerical calculations for the Fe₃O₄-ethylene glycol nanofluid as it flows over a contracting sheet with porous media. Additionally, the analysis includes an examination of the entropy generation calculation. Figures 2–35 illustrate the effects of various important physical factors, including velocity slip, viscous dissipation, radiation parameter, chemical reaction, Schmidt number, nanoparticle volume fraction, and porosity factor, on entropy generation, fluid velocity, heat profile, Sherwood number, Nusselt number, and friction factor. Table 2 presents a comparative analysis between the current research results and the solutions proposed by Bhattacharyya [62] and Humphries [63]. The provided results were in strong agreement with the data obtained from existing study.

Fig. 2

Variation of $K$ on $f^{\prime}(\eta )$

Fig. 3

Variation of $K$ on $\theta (\eta )$

Fig. 4

Variation of $S$ on velocity curve

Fig. 5

Variations of $S$ on $\theta (\eta )$

Fig. 6

Variations of $S$ on $\phi (\eta )$

Fig. 7

Variations of $\phi$ on velocity curve

Fig. 8

Variation of $\phi$ on $\theta (\eta )$

Fig. 9

Variation of M on velocity gradient

Fig. 10

Variation of R on $\theta (\eta )$

Fig. 11

Effect of $\beta$ on $\theta (\eta )$

Fig. 12

Effect of $\mathrm{Ec}$ on $\theta (\eta )$

Fig. 13

Effect of $\mathrm{Pr}$ on $\theta (\eta )$

Fig. 14

Effect of $\phi$ on friction factor

Fig. 15

Variation of $K$ on entropy generation number $\mathrm{Ns}$

Fig. 16

Impact of $\beta$ on $\mathrm{Ns}$

Fig. 17

Variation of $\phi$ on $\mathrm{Ns}$

Fig. 18

Variation of $S$ on $\mathrm{Ns}$

Fig. 19

Variation of $\lambda$ on Ns

Fig. 20

Variation of $\mathrm{Ec}$ on $\mathrm{Ns}$

Fig. 21

Variation of $\lambda$ on velocity curve

Fig. 22

Variation of $\lambda$ on $\theta (\eta )$

Fig. 23

Variation of $\lambda$ on $\upphi \left(\eta \right).$

Fig. 24

Effect of $n$ on $\theta (\eta )$

Fig. 25

Effect of $n$ on $\phi \left(\eta \right).$

Fig. 26

Variation of $\phi \;{\text{versus}}\;S\;{\text{versus}}\;R$ on Nusselt number

Fig. 27

Variation of $\phi \;{\text{versus}}\;{\text{Ec}}\;{\text{versus}}\;R$ on Nusselt number

Fig. 28

Effect of $Kr$ on concentration gradient

Fig. 29

Effect of ${\varvec{m}}$ on concentration gradient

Fig. 30

Effect of ${\varvec{S}}{\varvec{c}}$ on concentration gradient

Fig. 31

Effect of ${\varvec{K}}{\varvec{r}}$ on Ns

Fig. 32

Effect of ${\varvec{S}}{\varvec{c}}$ on Ns

Fig. 33

${\text{Sc}}\;{\text{versus}}\;n$ on Sherwood number

Fig. 34

$Kr\,\mathrm{ versus }m$ on Sherwood number

Fig. 35

${\text{Sc}}\;{\text{versus}}\;Kr$ on Sherwood number

Table 2 Comparison quantities of skin friction for various values of $S$ with $M = 2, R=0.5, Pr=6.2$, $\beta =0.2, n=0.1$ fixed, when $Kr = {\text{Sc}} = \phi = K = {\text{Ec}} = \lambda = 0$ $.$

Figure 2 depicts the effects of the porosity factor K on the velocity field. Higher porosity factor K values have the capacity to diminution velocity profiles. As shown in Fig. 3, the thermal gradient increases as the porosity factor K increases. Figures 4 and 3 depict the velocity and temperature curves for numerous suction factor quantities, respectively. According to Fig. 4, velocity increases slightly as S increases. As shown in Fig. 5, as S increases, the thermal field of fluids decreases monotonically. Figure 6 reveals the influence of suction factor on species concentration. From the figure, it is observed that concentration gradient increased when enhancing the suction parameter.

Figures 7 and 8 depict the activation of the heat and flow fields in response to the nanoparticle volume fraction ϕ. Figure 7 demonstrates a noticeable deceleration in fluid velocity as the values of ϕ grow. As seen in Fig. 8, the augmentation of ϕ leads to a simultaneous rise in both the thermal layer width and fluid temperature.

Figure 9 illustrates the nondimensional velocity $f^{\prime}$ at different levels of the magnetic field factor M. It is apparent that the velocity derivative $(f^{\prime})$ of the Fe₃O₄-ethylene glycol nanofluid increases as the magnetic field (M) increases in the scenario of a decreasing sheet. Figure 11 serves as an illustrative example of the impact of the non-uniform heat generation/sink component on the temperature curve. The figure demonstrates a positive correlation between the increase in β and the enhancement of thermal boundary layer performance. In the presence of a heat source parameter, the energy has the potential to be discharged into the stream. This energy has a role in enhancing the thermal boundary layer.

In Figs. 10 and 12, the variation in the dimensionless temperature field $(\theta (\eta ))$ related to different values of the thermal radiation parameter $\mathrm{Rd}$ and Eckert number $\mathrm{Ec}$ is examined. Developed temperature and a denser thermal boundary layer are connected with a bigger thermal radiation parameter, as seen in Fig. 10. Due to the enhancement of the temperature field, the larger radiation imparts a considerable quantity of heat to the fluid. Figure 12 illustrates the effect of the Eckert number. Owing to frictional heating, the consequence of the Eckert number is an upsurge in temperature and boundary layer thickness. For low-velocity fluids, viscous dissipation can be neglected. Figure 13 portrays the effects of the Prandtl Number $\mathrm{Pr}$ on temperature gradient. Growing the Prandtl number declines the temperature outline. The thermal diffusivity is inverse to the Prandtl parameter. Greater estimates of the Prandtl parameter indicate less thermal diffusivity, resulting in a reduction in temperature distribution. An increase in the Prandtl number tends to reduce thermal diffusivity, which delays the diffusion of temperature and consequently reduces the thermal sketch. Figure 14 provides a visual representation of the influence of variables M and ϕ on the surface drag force, often referred to as the skin factor. The presented figures illustrate a consistent rise in the drag force at the surface as the quantities of M and ϕ grow. This observation may be inferred from the correlation between these two variables.

Figures 15 and 16 provide an explanation about the impact of the heat source component β and the porosity factor K on the profiles of entropy generation (Ns). There is a clear correlation between the increase in values of K and β, and the corresponding rise in the variable Ns. As the volume proportion of nanoparticles increases, the Ns demonstrates a decreasing trend, as seen in Fig. 17. Figure 18 illustrates the impact of the suction factor (S) on the Ns. The phenomenon of fluid friction and heat transfer leads to an observable increase in the profile of entropy production rates up to a certain point, beyond which it is lowered by increasing the value of S.

Figures 19 and 20 exemplify the effects of the velocity slip factor and viscous dissipation on the entropy production factor Ns. When the velocity slip factor λ is increased, the width of the entropy optimization is reduced. According to Fig. 20, it can be seen that an increase in the values of Ec corresponds to a concurrent increase in the level of entropy optimization.

Figures 21–23 depict the impact of velocity slip on solutal, heat, and velocity gradients. The presented data illustrate that in the presence of slippage, the velocity of the Fe₃O₄-ethylene glycol nanofluid near the surface does not align with the decreasing velocity caused by the slip boundary circumstance. Furthermore, the transmission of the pulling force from the shrinking surface to the nanofluid is only partial. Consequently, increasing the magnitude of partial slip leads to an amplification of the momentum boundary layer, while concomitantly diminishing the curves representing temperature and species concentrations. Figure 24 illustrates the correlation between the variable n and the temperature curve. The thermal curve shows an increasing trend as the amounts of n increase. The impact of stretching sheet factor $n$ on concentration curves is implicated in Fig. 25. It reveals that the Solutal curves enhance when the values of $n$ rise.

Figure 26 illustrates the correlation between the variables R, S, and ϕ with respect to the Nusselt number. The visual representation indicates that an increase in all these parameters leads to a corresponding increase in the heat transfer rate. Figure 27 illustrates the impact of radiation, nanoparticle volume fraction ϕ, and viscous dissipation factors on the Nusselt number. It is evident that a rise in the quantities of R leads to a corresponding increase in the Nusselt number. However, a contrary tendency is found when the amounts of Ec are increased. Figure 28 displays the impacts of chemical reaction parameter (Kr) on the concentration field. It is clear that stronger $(Kr)$ decreases the concentration of nanoparticles, and that a thicker solute border layer destructive chemical rate (Kr > 0) increases the mass transfer rate, decreasing the concentration of nanoparticles.

Figure 29 depicts the $m$ influence on the concentration curve. This means that the effect of $m$ increased mass transport, which increased the concentration field and lowered the concentration boundary layer thickness. Sc is a significant quantity in mass transport phenomena. Schmidt number Sc is linked to nanoparticle concentration diffusion. Figure 30 shows how adding Sc improves the concentration profile. The Schmidt number (Sc) is the kinematic viscosity to molecular diffusion coefficient ratio. Higher Sc promotes more molecular diffusivity, resulting in a decrease in the concentration gradient of nanoparticles. Figure 31 depicts the effect of Schmidt number on entropy production in a Fe₃O₄-ethylene glycol nanofluid. The entropy production for different values of chemical reaction parameter impact is shown in Fig. 32. Both the Schmidt number and the chemical reaction parameters increase entropy generation, whereas the opposite effect is seen further from the wall. Because the emission rate of heat energy near the sheet is lowered in this location, the entropy generation is maximized.

Figure 33 depicts the influence of Schmidt number (Sc) and n on the mass transmission rate. The graph demonstrates that an increase in both factors decreases the Sherwood number profile. The relationship between Kr and m in relation to the Sherwood number is depicted in Fig. 34. The graphs revealed a decline in value alongside an increase in the values of both chemical reaction and $m$. Here, it can be observed that particle collisions during a chemical reaction reduce the mass transfer rate. Figure 35 explains how the Schmidt number Sc and chemical reaction factor Kr affect the rate of mass transmission. The quantities of the Sherwood number behave as a decreasing function of Kr & Sc, as seen in Fig. 35.

Tables 3 and 4 provide an overview of the effects of various non-dimensional regulating parameters on the friction factor and Nusselt number, resulting in variances. The data shown in the table demonstrates a clear relationship between the variables Kr, Ec, n, K, and β, and their impact on the Nusselt number. Enhancing the values of Kr, Ec, n, K, and β sequentially leads to a decrease in the Nusselt number. Conversely, when the quantities of R, S, λ, M, and Pr are increased, a reversal pattern is seen, resulting in an enhancement of the Nusselt number. Furthermore, it has been shown that an increase in the amounts of S and M is associated with an elevation in the friction factor. Conversely, a contrasting outcome may be noticed when Kr, K, and λ experience an increase. The impacts of different flow parameters on local Sherwood number have been calculated and are shown in Table 5 in order to analyze the behavior of certain quantities of engineering importance. From Table 5, it can be observed that the Sherwood number tends to increase with the Schmidt number, velocity slip factor, suction parameter, and magnetic field parameter; however, the value of this physical quantity decreases with an increase in the chemical reaction parameter, $m$, and porosity factor.

Table 3 Computation of numerical values for skin friction coefficient for various values of $M, K, \lambda , Kr, S$ when $\mathrm{Sc} = R = {\mathrm{Ec}} = 0.1, n = 0.2, \beta = 0.5, \mathrm{Pr} = 6.2.$

Table 4 Computation of numerical values for Nusselt number for various values of $M, Kr, {\text{Sc}}, S, \lambda , Kr, n,\beta , \mathrm{Ec} , \mathrm{Pr}$ when $Sc = 0.1.$

Table 5 Computation of numerical values for Sherwood number for various values of $M, Kr, \mathrm{Sc}, S, \lambda , Kr, n$ when $R = {\mathrm{Ec}} = 0.1, \beta = 0.5, Pr = 6.2.$

Conclusions

The present study is to demonstrate the two-dimensional radiative MHD heat and mass transfer flow of a Fe₃O₄-ethylene glycol nanofluid over a permeable shrinking sheet. The study also considers the combined impacts of velocity slip, chemical reaction, and viscous dissipation. The complicated nature of the PDE's for thermal, fluid flow, and mass transfer is reduced by transforming it into a system of ordinary differential equations, which is then numerically solved by using the Keller–Box procedure for different amounts of the governing factors. The numerical results are represented by graphs and tables. The primary findings of this investigation are as follows:

• A rise in the thermal radiation and an increase in the Eckert number both have a significant impact on the temperature field.

• The concentration of nanoparticles decreases as the value of the chemical reaction rises.

• Eckert number, porosity factor, and the existence of a heat source all contribute to increased entropy, although nanoparticle volume fraction, suction, and velocity slip factors reduce entropy creation.

• As Sc increases, the intensity of the concentration gradient decreases and speeds up the mass transfer rate.

• The flow is slowed down by increasing the Prandtl number, which also lowers temperatures values

• The temperature profiles of the nanoparticles slow down when suction parameters are increased, but they speed up as heat generation/absorption and viscous dissipation parameters are amplified.

• The enhancement in heat transmission was seen with an increase in the porosity (K) of the medium, whereas the velocity field on the surface exhibited a contrasting trend.

• The velocity curves exhibited an increase in response to an increase in the velocity slip factor, whereas the temperature and concentration curves showed a drop.