Introduction

Over the past several years, researchers have paid close attention to the development of enhanced heat transfer fluids. To fulfill the industrial and technical demands, a smart liquid with improved heat capability is desirable. Nanotechnology is a rapidly expanding field in this modern age of advancement, where things are becoming smaller in size and getting better in the terminology of appropriate features. An area of particular importance is the preparation of products at the atomic and molecular levels for specific industrial purposes. One of the main ingredients of nanotechnology is nanofluid, which is primarily utilized to handle heat transfer challenges effectively. To fulfill the industrial and technical demands, a smart fluid with outstanding thermal capability is desirable. Choi [1] in 1955 published an innovative heat transfer fluid that is based on nanotechnology called as nanofluid. A nanofluid is a suspension created in a base fluid by the uniform dispersion of very tiny dimension particles. The use of nanoparticles significantly enhances the thermophysical characteristics of conventional heat transfer fluid, hence increasing its heat transfer coefficient. Due to the widespread recognition, nanofluids are now extensively employed in a variety of industries, including automotive, electronics, solar energy, biomedical, oil recovery, food stuff, aerodynamics, geothermal systems, crude oil extractions, groundwater pollution, thermal insulation, heat exchanger, storage of nuclear waste, bulging construction, agriculture, thermal power plants, nuclear reactions, technologically advanced procedures, cost-effective and efficient cooling system refrigerators (see Das et al. [2], Nield and Bejan [3], Shenoy et al. [4] and Merkin et al. [5]). A nanofluid is a suspension that includes a host fluid and the uniform dispersion of very tiny particles. These particles have sizes ranging between 1 and 100 nm, and the material of these particles may be polymers, metals, metal oxides or other materials. An application of nanoadditives essentially augments the thermal parameters of conventional energy transport media, hence increasing its heat transfer coefficient. Convective flows in nanofluids have extensive engineering applications in aerodynamics, geothermal systems, building thermal insulation, heat exchanger, microelectronics, cancer therapy and others. In all of these applications, the heat conductivity of nanosuspension has a strong impact on the efficiency of the energy transport phenomenon. For such reason, scientists have continuously scrutinized the advantages and disadvantages of the nanosuspensions application (see Shenoy et al. [4] and Merkin et al. [5]).

Numerical simulation is an accessible and effective method for studying the problems of convective energy and mass transport. Interest in such studies is caused by a wide range of applications of the results obtained, including the rocket science, instrumentation, micro- and radio electronics, heating of buildings, etc. One of the striking examples of the application of the results is the development of cooling systems for heat-generated sources of various types. In such systems, good results are shown by the use of nanofluids as working fluids due to the possibility of varying their thermophysical properties by nanoparticles. Thus, Miroshnichenko et al. [6] have analyzed free convective energy and mass transport of Al2O3/H2O nanosuspension in a tilted open chamber having local hot element. It has been assumed that the top boundary of the cavity is open, and the nanoliquid penetrates into the chamber through it. The analysis has been carried out employing the Oberbeck–Boussinesq equations written using dimensionless stream function, vorticity and temperature. The influence of the cavity inclination angle, the heater position and the nanoparticles concentration has been demonstrated. It has been revealed that the optimal selection of the considered parameters makes it possible to minimize the average temperature of the heater. The most efficient cooling of the thermally producing blocks is observed when it is placed in the center of the cavity at an angle of inclination of the chamber equaled to π/3. A computational analysis of thermal convection of Al2O3/H2O nanoliquid inside a closed chamber with a thick bottom wall heated unevenly (according to the sinusoidal law) has been carried out by Bouchoucha et al. [7]. The finite volume technique has been employed to work out the control equations. The outcomes have been shown as streamlines, isotherms, local and average Nu profiles for different values of the Rayleigh number, nanoadditives concentration and the thickness of the bottom wall. The outcomes obtained have shown a decrease in the mean Nu with an increase in the thickness of the bottom wall. Bondarenko et al. [8] have visualized the natural convective flow of Al2O3/H2O nanosuspension in a closed square chamber with a thermally producing block. Cooling of the cavity occurs from the vertical walls. The impact of the nanoadditives concentration and the location of the heater on transport phenomena in the cavity and heat removal from the heated element has been shown. The authors have revealed that an inclusion of nanoadditives can improve the cooling phenomenon when the energy source is close to the vertical cold surface. Mahmoodi [9] has presented results of mathematical modeling of natural convection of nanofluids (Ag/H2O, Cu/H2O, Ti2O/H2O) inside closed 2D chamber with a flat horizontal/vertical heater in the center of the cavity and cold vertical walls. The results have shown that Ag/H2O nanofluid has more effective properties for heat removing from the heater for high Ra. Low Rayleigh numbers have reflected low sensitivity to the type of nanofluids.

Keramat et al. [10] have numerically examined the free convection of alumina–water nanosuspension within closed H-shaped cavity with baffle at 104 < Ra < 106. It has been demonstrated that a raise of Ra and nanoadditives volume fraction enhances the energy transport inside the cavity. Islam et al. [11] have conducted the computational analysis of CNT-water nanosuspension thermal convection within a triangular chamber under the sinusoidal heating influence from the bottom wall by employing the finite difference technique. The outcomes have shown that an increment in Ra results to a raise of the fluctuations amplitude in the average Nusselt number. Nabwey et al. [12] have presented results of numerical calculation of Cu/H2O nanofluid heat transfer within an inclined U-chamber in the presence of local energy element and magnetic field. The obtained data have illustrated that the location of the heating section and the value of the Hartmann number have the most essential impact on the energy transport strength in the chamber. Alsabery et al. [13] have scrutinized the mixed convection of Al2O3/H2O nanosuspension inside 2D chamber with wavy vertical walls and isothermal heating from the bottom boundary or solid inner block. The obtained outcomes reflect significant changes in the flow structure with a raise of the nanoadditives concentration and the introduction of a solid element on the bottom wall compared to a flat isothermal boundary. Reviews on the researches of energy transport in various regions filled with nanofluids under different boundary conditions have been presented by Narankhishig et al. [14] and Sheikholeslami and Rokni [15]. The problems of convective heat transfer under the magnetic impact have been shown by Narankhishig et al. [14], while Sheikholeslami and Rokni [15] have presented the results of numerical simulation of nanosuspension heat and mass transport under the magnetic impact inside different cavities. Two models have been shown, namely MHD and FHD.

It should be noted that copper nanoparticles are among the most effective carriers among different nanoadditives owing to high heat conductivity of the copper. Selimefendigil et al. [16] have simulated the mixed convection in a square porous chamber filled with a CuO/H2O nanosuspension. The cavity contains a porous insert in the lower part and a rotating adiabatic cylinder in the central part of the body. The chamber is warmed from the lower border and cooled from the upper boundary. The impact of Ra, the angular velocity of rotation, the nanoadditives volume fraction, the Darcy number, and the position of the cylinder in the cavity on the performance of the thermal system has been shown. The authors have shown that energy transport strength increases with a growth of Ra, angular velocity of rotation of the cylinder and nanoadditives volume fraction, and Da. Vijaybabu [17] has demonstrated simulation data of the convective motion of CuO/H2O nanosuspension in a closed square chamber having isothermally heated round porous body. It has been found that the flow rate of a liquid increases with an increment in Da and nanoadditives volume fraction in the working liquid. Mathematical modeling of heat transfer of CuO/H2O nanosuspension in a porous chamber with open areas has been performed by Biswas et al. [18]. The porous medium has been modeled taking into account the Darcy–Brinkman–Forchheimer approach. The results have shown that the heat transfer rate of the host liquid is highly dependent on the governing parameters (Reynolds number, Darcy number, Richardson number, porosity, nanoparticles volume fraction and cavity geometry parameter). An assessment of the efficiency of heat removal by adding nanoparticles to the working medium has been performed. Sivasankaran et al. [19] have analyzed the thermal convection of CuO/H2O nanosuspension in a tilted chamber having thermally producing porous medium. In the simulation, a local heat non-equilibrium model has been employed. The chamber is warmed from the horizontal bottom border and cooled from the vertical boundaries. The results obtained have shown that the energy transport strength decreases with a raise of the nanoadditives volume fraction for the case of high Rayleigh numbers. The intensification of energy transfer is achieved by increasing the values of the modified conductivity coefficient and the porosity of the material. A numerical study of the thermal convection of water-based nanoliquids with the addition of Cu, Al2O3, TiO2 nanoadditives in regions of various geometries with warmed and cooled cylinders has been carried out by Garoosi et al. [20]. The simulation results have shown that at low Ra, the energy transport strength decreases with a change in the shape of the body from square to triangular. It has been also found that for each Rayleigh number, an optimal nanoadditives concentration with high energy transport strength inside the chamber can be defined. Emami et al. [21] have examined the thermal convection of a water-based nanofluid with the addition of copper particles in a tilted porous chamber. The influence of chamber tilted angle, heater shape, properties of nanosuspension and porous medium on the energy transport characteristics has been examined. The results have shown that the choice of heater shape (side or corner heating) and angle of inclination at different nanofluid concentrations and different properties of the porous medium can greatly affect the heat transfer characteristics. Bouzerzour et al. [22] have demonstrated the results of free convection simulation within annulus filled with CuO/H2O nanofluids in the presence of local heaters. The results have shown the best heat removal at high Ra and the nanoadditives concentration.

In some cases, alumina particles are added to the base fluid along with copper oxide particles. Such combination can intensify the heat transport within the chamber. Thus, the thermogravitational energy transport of Cu/Al2O3/H2O hybrid nanosuspension in a partially open square chamber with a fixed isothermally heated vertical partition under the magnetic impact has been scrutinized by Du et al. [23]. The finite difference procedure has been used to work out the Navier–Stokes equations. The results have shown that an increment in the nanoadditives concentration in the liquid enhances the rate of heat transfer inside the cavity. Mixed convection within horizontal channel under the magnetic impact has been examined computationally by Nath and Murugesan [24]. The impact of the magnetic field tilted angle and the characteristics of the nanofluid on the hydrodynamics of the flow in the channel has been shown. Rana et al. [25] have demonstrated the outcomes of computational analysis of hybrid nanoliquid in closed cavity with inner bodies of different types by employing the Galerkin finite element algorithm. The authors have shown a strong dependence of the mean Nu on the volume concentration of nanoparticles. Valuable published papers on classical viscous fluids and nanofluids are also those by Roy [26–29], Roy et al. [30], Parvin et al. [31], Saha et al. [32], Sajid and Ali [33], Sajid and Bicer [34, 35], Sajid et al. [36 ,37], and Hawaz et al. [38].

It can be seen from the presented brief review that studies on heat transfer in areas filled with two-phase liquids have been started recently and require additional analysis. Motivated by the preceding work, the primary goal of this present research is to present a mathematical modeling of the thermogravitational energy transport of CuO/H2O nanosuspension in a closed square chamber with an energy source of periodic heat generation and cooling vertical walls. The thermophysical properties of the working liquid considered are dependent on temperature and the nanoadditives volume fraction. The obtained results are related to the modeling of passive cooling systems for heating elements and various thermal systems. CuO/H2O is chosen as the nanoparticle since it has been widely used in numerous studies. The initial nanoparticles concentration (C0) have been considered in the range between 0.0 and 0.04. It should be noted that the use of CuO as nanoparticles is an effective way to intensify heat transfer due to the high thermal conductivity properties of copper oxide. Moreover, the considered temperature- and concentration-dependent relations for the thermal conductivity and dynamic viscosity have been verified my many authors for the considered nanoparticles material.

Mathematical model and basic assumptions

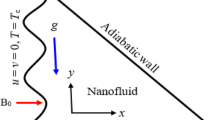
The schematic model of considered natural convection problem is shown in Fig. 1. The thermogravitational energy transport of a viscous nanofluid (a mixture of water and copper oxide nanoparticles) in a closed chamber having thermally producing solid block placed on the lower border is considered. The volumetric heat generation of the source is described by the following relation \(Q\left( t \right) = 0.5Q_{0} \left\{ {1 - \cos \left( {ft} \right)} \right\}\). The vertical borders of the chamber are assumed to be isothermally cooling, while the horizontal surfaces are considered to be adiabatic. The force of gravity is directed vertically downward. The chamber is saturated with a Newtonian heat-conducting water-based nanosuspension. It is supposed that water and nanoadditives are in heat equilibrium, and only Brownian diffusion and thermal diffusion are considered as the main mechanisms of the relative motion of nanoparticles inside the carrier medium. The thermal properties of the nanoparticle material and water are given in Table 1. It is also assumed that the properties of a nanoliquid depend on temperature and the nanoadditives volume fraction.

Fig. 1
figure 1

Physical model

Full size image
Table 1 Thermal properties of the working fluid and nanoadditives material
Full size table

The transport of mass, momentum and energy within the chamber is assumed to be 2D, laminar, with a negligible effect of viscous dissipation and the work of pressure forces. The Boussinesq approximation is used to describe the influence of the buoyancy force. Considering these conditions, the governing equations can be formulated as follows (see Astanina et al. [39, 40]):

$$\frac{{\partial \overline{u}}}{{\partial \overline{x}}} + \frac{{\partial \overline{v}}}{{\partial \overline{y}}} = 0$$
(1)
$$\rho_{{{\text{nf}}}} \left( {\frac{{\partial \overline{u}}}{\partial t} + \overline{u}\frac{{\partial \overline{u}}}{{\partial \overline{x}}} + \overline{v}\frac{{\partial \overline{u}}}{{\partial \overline{y}}}} \right) = - \frac{\partial p}{{\partial \overline{x}}} + 2\frac{\partial }{{\partial \overline{x}}}\left( {\overline{\mu }_{{{\text{nf}}}} \left( {T,C} \right)\frac{{\partial \overline{u}}}{{\partial \overline{x}}}} \right) + \frac{\partial }{{\partial \overline{y}}}\left[ {\overline{\mu }_{{{\text{nf}}}} \left( {T,C} \right)\left( {\frac{{\partial \overline{u}}}{{\partial \overline{y}}} + \frac{{\partial \overline{v}}}{{\partial \overline{x}}}} \right)} \right]$$
(2)
$$\begin{aligned} \rho_{{{\text{nf}}}} \left( {\frac{{\partial \overline{v}}}{\partial t} + \overline{u}\frac{{\partial \overline{v}}}{{\partial \overline{x}}} + \overline{v}\frac{{\partial \overline{v}}}{{\partial \overline{y}}}} \right) & = - \frac{\partial p}{{\partial \overline{y}}} + 2\frac{\partial }{{\partial \overline{y}}}\left( {\overline{\mu }_{{{\text{nf}}}} \left( {T,C} \right)\frac{{\partial \overline{v}}}{{\partial \overline{y}}}} \right) \\ & \quad + \frac{\partial }{{\partial \overline{x}}}\left[ {\overline{\mu }_{{{\text{nf}}}} \left( {T,C} \right)\left( {\frac{{\partial \overline{u}}}{{\partial \overline{y}}} + \frac{{\partial \overline{v}}}{{\partial \overline{x}}}} \right)} \right] + \left( {\rho \beta } \right)_{{{\text{nf}}}} g\left( {T - T_{c} } \right) \\ \end{aligned}$$
(3)
$$\begin{aligned} \left( {\rho c} \right)_{{{\text{nf}}}} \left( {\frac{\partial T}{{\partial t}} + \overline{u}\frac{\partial T}{{\partial \overline{x}}} + \overline{v}\frac{\partial T}{{\partial \overline{y}}}} \right) & = \frac{\partial }{{\partial \overline{x}}}\left( {k_{{{\text{nf}}}} \frac{\partial T}{{\partial \overline{x}}}} \right) + \frac{\partial }{{\partial \overline{y}}}\left( {k_{{{\text{nf}}}} \frac{\partial T}{{\partial \overline{y}}}} \right) \\ & \quad + \left( {\rho c} \right)_{{\text{p}}} \left\{ {\overline{D}_{{\text{B}}} \left( {\frac{\partial C}{{\partial \overline{x}}}\frac{\partial T}{{\partial \overline{x}}} + \frac{\partial C}{{\partial \overline{y}}}\frac{\partial T}{{\partial \overline{y}}}} \right) + \frac{{\overline{D}_{{\text{T}}} }}{{T_{{\text{c}}} }}\left[ {\left( {\frac{\partial T}{{\partial \overline{x}}}} \right)^{2} + \left( {\frac{\partial T}{{\partial \overline{y}}}} \right)^{2} } \right]} \right\} \\ \end{aligned}$$
(4)
$$\frac{\partial C}{{\partial t}} + \overline{u}\frac{\partial C}{{\partial \overline{x}}} + \overline{v}\frac{\partial C}{{\partial \overline{y}}} = \frac{\partial }{{\partial \overline{x}}}\left( {\overline{D}_{{\text{B}}} \frac{\partial C}{{\partial \overline{x}}} + \frac{{\overline{D}_{{\text{T}}} }}{{T_{{\text{c}}} }}\frac{\partial T}{{\partial \overline{x}}}} \right) + \frac{\partial }{{\partial \overline{y}}}\left( {\overline{D}_{{\text{B}}} \frac{\partial C}{{\partial \overline{y}}} + \frac{{\overline{D}_{{\text{T}}} }}{{T_{{\text{c}}} }}\frac{\partial T}{{\partial \overline{y}}}} \right)$$
(5)
$$\left( {\rho c} \right)_{{{\text{hs}}}} \frac{\partial T}{{\partial t}} = k_{{{\text{hs}}}} \left( {\frac{{\partial^{2} T}}{{\partial \overline{x}^{2} }} + \frac{{\partial^{2} T}}{{\partial \overline{y}^{2} }}} \right) + Q\left( t \right)$$
(6)

The nanosuspension density, thermal capacity and heat parameter of volumetric expansion of a nanofluid are determined as follows:

$$\rho_{{{\text{nf}}}} = \left( {1 - C} \right)\rho_{{\text{f}}} + C\rho_{{\text{p}}}$$
(7)
$$\left( {\rho c} \right)_{{{\text{nf}}}} = \left( {1 - C} \right)\left( {\rho c} \right)_{{\text{f}}} + C\left( {\rho c} \right)_{{\text{p}}}$$
(8)
$$\left( {\rho \beta } \right)_{{{\text{nf}}}} = \left( {1 - C} \right)\left( {\rho \beta } \right)_{{\text{f}}} + C\left( {\rho \beta } \right)_{{\text{p}}}$$
(9)

The Brownian diffusion parameter \(\overline{D}_{{\text{B}}}\) can be determined on the basis of the Einstein–Stokes relation in the form \(\overline{D}_{{\text{B}}} = \frac{{k_{{\text{B}}} }}{{3\pi \mu_{{\text{f}}} \left( T \right)d_{{\text{p}}} }}T\); to determine the thermal diffusion parameter \(\overline{D}_{{\text{T}}}\), we can use the relation of the form \(\overline{D}_{{\text{T}}} = C\left[ {\frac{{\mu_{{\text{f}}} \left( T \right)}}{{\rho_{{\text{f}}} }}} \right]\left( {\frac{{0.26 \cdot k_{{\text{f}}} }}{{2k_{{\text{f}}} + k_{{\text{p}}} }}} \right)\). Here, \(k_{{\text{B}}} = 1.3807 \times 10^{ - 23} \;{\text{J}}\;{\text{K}}^{ - 1}\) is the Boltzmann parameter, dp is the nanoadditives size.

The nanosuspension heat conductivity is determined based on the Chon model [41] in the form:

$$\frac{{k_{{{\text{nf}}}} }}{{k_{f} }} = 1 + 64.7 \cdot C^{0.764} \left( {\frac{{d_{{\text{f}}} }}{{d_{{\text{p}}} }}} \right)^{0.369} \left( {\frac{{k_{{\text{f}}} }}{{k_{{\text{p}}} }}} \right)^{0.7476} {\text{Pr}}_{{\text{T}}}^{0.9955} \;{\text{Re}}^{1.2321}$$
(10)

Here, \({\text{Pr}}_{{\text{T}}} = \frac{{\mu_{{\text{f}}} \left( T \right)}}{{\rho_{{\text{f}}} \alpha_{{\text{f}}} }}\) is the Prandtl number, \({\text{Re}} = \frac{{\rho_{{\text{f}}} k_{{\text{B}}} }}{{3\pi \left[ {\mu_{{\text{f}}} \left( T \right)} \right]^{2} l_{{\text{f}}} }}T\) is the Reynolds number, \(l_{{\text{f}}} = 0.17\;{\text{nm}}\) is the mean free path of the host liquid molecule (see Chon et al. [41]). The presented relation (10) makes it possible to analyze the influence of the size of nanoparticles and temperature on the heat conductivity of a nanofluid in a wide range of temperatures at \(1\% \le C \le 9\%\) (see Chon et al. [41] and Abu-Nada et al. [42]).

The nanosuspension viscosity is determined as follows (see Chon et al. [41], Abu-Nada et al. [42], Haddad et al. [43] and Nguyen et al. [44]):

$$\begin{aligned} \mu_{{{\text{nf}}}} \left( {T,C} \right) & = - 0.6967 \times 10^{ - 3} + \frac{{1.5937 \times 10^{ - 2} }}{T - 273.15} + 1.238 \times 10^{ - 3} C + \frac{1.35614}{{\left( {T - 273.15} \right)^{2} }} \\ & \quad - 0.259 \times 10^{ - 3} C^{2} - 3.088 \times 10^{ - 2} \left( {\frac{C}{T - 273.15}} \right) - \frac{19.65274}{{\left( {T - 273.15} \right)^{3} }} + 0.01593 \times 10^{ - 3} C^{3} \\ & \quad + 4.38206 \times 10^{ - 3} \left( {\frac{{C^{2} }}{T - 273.15}} \right) + 0.147573\frac{C}{{\left( {T - 273.15} \right)^{2} }} \\ \end{aligned}$$
(11)

The dynamic viscosity of water is (see Chon et al. [41] and Nguyen et al. [44]):

$$\mu_{{\text{f}}} \left( T \right) = 2.414 \times 10^{ - 5} \times 10^{{247.8/\left( {T - 140} \right)}}$$
(12)

The formulated dimensional partial differential Eqs. (1) to (6) can be dimensionalized using the following relations:

$$\begin{aligned} x & = {{\overline{x}} \mathord{\left/ {\vphantom {{\overline{x}} L}} \right. \kern-\nulldelimiterspace} L},\quad y = {{\overline{y}} \mathord{\left/ {\vphantom {{\overline{y}} L}} \right. \kern-\nulldelimiterspace} L},\quad \tau = t\sqrt {{{g\beta_{{\text{f}}} \Delta T} \mathord{\left/ {\vphantom {{g\beta_{{\text{f}}} \Delta T} L}} \right. \kern-\nulldelimiterspace} L}} ,\quad u = {{\overline{u}} \mathord{\left/ {\vphantom {{\overline{u}} {\sqrt {g\beta_{{\text{f}}} \Delta TL} }}} \right. \kern-\nulldelimiterspace} {\sqrt {g\beta_{{\text{f}}} \Delta TL} }}, \\ v & = {{\overline{v}} \mathord{\left/ {\vphantom {{\overline{v}} {\sqrt {g\beta_{{\text{f}}} \Delta TL} }}} \right. \kern-\nulldelimiterspace} {\sqrt {g\beta_{{\text{f}}} \Delta TL} }},\quad \theta = {{\left( {T - T_{{\text{c}}} } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{{\text{c}}} } \right)} {\Delta T}}} \right. \kern-\nulldelimiterspace} {\Delta T}},\quad \phi = {C \mathord{\left/ {\vphantom {C {C_{0} }}} \right. \kern-\nulldelimiterspace} {C_{0} }},\quad M = {{\mu_{{{\text{nf}}}} \left( {T,C} \right)} \mathord{\left/ {\vphantom {{\mu_{{{\text{nf}}}} \left( {T,C} \right)} {\mu_{{\text{f}}} \left( {T_{{\text{c}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\mu_{{\text{f}}} \left( {T_{{\text{c}}} } \right)}}, \\ K & = {{k_{{{\text{nf}}}} \left( {T,C} \right)} \mathord{\left/ {\vphantom {{k_{{{\text{nf}}}} \left( {T,C} \right)} {k_{{\text{f}}} }}} \right. \kern-\nulldelimiterspace} {k_{{\text{f}}} }},\quad D_{{\text{B}}} = {{\overline{D}_{{\text{B}}} \left( T \right)} \mathord{\left/ {\vphantom {{\overline{D}_{{\text{B}}} \left( T \right)} {\overline{D}_{{\text{B}}} \left( {T_{{\text{c}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\overline{D}_{{\text{B}}} \left( {T_{{\text{c}}} } \right)}},\quad D_{{\text{T}}} = {{\overline{D}_{{\text{T}}} \left( {T,C} \right)} \mathord{\left/ {\vphantom {{\overline{D}_{{\text{T}}} \left( {T,C} \right)} {\overline{D}_{{\text{T}}} \left( {T_{{\text{c}}} ,C_{0} } \right)}}} \right. \kern-\nulldelimiterspace} {\overline{D}_{{\text{T}}} \left( {T_{{\text{c}}} ,C_{0} } \right)}} \\ \end{aligned}$$
(13)

Also with the use of new dimensionless stream function ψ \(\left( {u = \frac{\partial \psi }{{\partial y}}, \, v = - \frac{\partial \psi }{{\partial x}}} \right)\) and vorticity \(\omega = \frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}\), therefore, the non-dimensional control equations are

$$\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial y^{2} }} = - \omega$$
(14)
$$\begin{aligned} \frac{\partial \omega }{{\partial \tau }} + u\frac{\partial \omega }{{\partial x}} + v\frac{\partial \omega }{{\partial y}} & = \frac{1}{{1 - \phi C_{0} + \phi C_{0} \cdot {{\rho_{{\text{p}}} } \mathord{\left/ {\vphantom {{\rho_{{\text{p}}} } {\rho_{{\text{f}}} }}} \right. \kern-\nulldelimiterspace} {\rho_{{\text{f}}} }}}}\sqrt {\frac{{{\text{Pr}}}}{{{\text{Ra}}}}} \left[ {\frac{{\partial^{2} \left( {M\omega } \right)}}{{\partial x^{2} }} + \frac{{\partial^{2} \left( {M\omega } \right)}}{{\partial y^{2} }}} \right] \\ & \quad + \frac{{1 - \phi C_{0} + \phi C_{0} \cdot {{\left( {\rho \beta } \right)_{{\text{p}}} } \mathord{\left/ {\vphantom {{\left( {\rho \beta } \right)_{{\text{p}}} } {\left( {\rho \beta } \right)_{{\text{f}}} }}} \right. \kern-\nulldelimiterspace} {\left( {\rho \beta } \right)_{{\text{f}}} }}}}{{1 - \phi C_{0} + \phi C_{0} \cdot {{\rho_{{\text{p}}} } \mathord{\left/ {\vphantom {{\rho_{{\text{p}}} } {\rho_{{\text{f}}} }}} \right. \kern-\nulldelimiterspace} {\rho_{{\text{f}}} }}}}\frac{\partial \theta }{{\partial x}} + \frac{2}{{1 - \phi C_{0} + \phi C_{0} \cdot {{\rho_{{\text{p}}} } \mathord{\left/ {\vphantom {{\rho_{{\text{p}}} } {\rho_{{\text{f}}} }}} \right. \kern-\nulldelimiterspace} {\rho_{{\text{f}}} }}}}\sqrt {\frac{{{\text{Pr}}}}{{{\text{Ra}}}}} \\ & \quad \times \left[ {\frac{{\partial^{2} M}}{{\partial x^{2} }}\frac{\partial u}{{\partial y}} - \frac{{\partial^{2} M}}{{\partial y^{2} }}\frac{\partial v}{{\partial x}} + \frac{{\partial^{2} M}}{\partial x\partial y}\left( {\frac{\partial v}{{\partial y}} - \frac{\partial u}{{\partial x}}} \right)} \right] \\ \end{aligned}$$
(15)
$$\begin{aligned} \frac{\partial \theta }{{\partial \tau }} + u\frac{\partial \theta }{{\partial x}} + v\frac{\partial \theta }{{\partial y}} & = \frac{1}{{\left[ {1 - \phi C_{0} + \phi C_{0} \cdot {{\left( {\rho c_{{\text{p}}} } \right)_{{\text{p}}} } \mathord{\left/ {\vphantom {{\left( {\rho c_{{\text{p}}} } \right)_{{\text{p}}} } {\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}} \right. \kern-\nulldelimiterspace} {\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}} \right]\sqrt {{\text{Ra}} \cdot {\text{Pr}}} }}\left[ {\frac{\partial }{\partial x}\left( {K\frac{\partial \theta }{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {K\frac{\partial \theta }{{\partial y}}} \right)} \right] \\ & \quad + \frac{{D_{{\text{B}}} \cdot C_{0} }}{{\left[ {\phi C_{0} + \left( {1 - \phi C_{0} } \right) \cdot {{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} } \mathord{\left/ {\vphantom {{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} } {\left( {\rho c_{{\text{p}}} } \right)_{{\text{p}}} }}} \right. \kern-\nulldelimiterspace} {\left( {\rho c_{{\text{p}}} } \right)_{{\text{p}}} }}} \right]{\text{Le}}\sqrt {{\text{Ra}} \cdot {\text{Pr}}} }}\left( {\frac{\partial \phi }{{\partial x}}\frac{\partial \theta }{{\partial x}} + \frac{\partial \phi }{{\partial y}}\frac{\partial \theta }{{\partial y}}} \right) \\ & \quad + \frac{{D_{{\text{T}}} \cdot {\text{Nt}}}}{{\left[ {\phi C_{0} + \left( {1 - \phi C_{0} } \right) \cdot {{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} } \mathord{\left/ {\vphantom {{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} } {\left( {\rho c_{{\text{p}}} } \right)_{{\text{p}}} }}} \right. \kern-\nulldelimiterspace} {\left( {\rho c_{{\text{p}}} } \right)_{{\text{p}}} }}} \right]\sqrt {{\text{Ra}} \cdot {\text{Pr}}} }}\left[ {\left( {\frac{\partial \theta }{{\partial x}}} \right)^{2} + \left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} } \right] \\ \end{aligned}$$
(16)
$$\begin{aligned} \frac{\partial \phi }{{\partial \tau }} + u\frac{\partial \phi }{{\partial x}} + v\frac{\partial \phi }{{\partial y}} & = \frac{1}{{{\text{Le}}\sqrt {{\text{Ra}} \cdot {\text{Pr}}} }}\left[ {\frac{\partial }{\partial x}\left( {D_{{\text{B}}} \frac{\partial \phi }{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {D_{{\text{B}}} \frac{\partial \phi }{{\partial y}}} \right)} \right] \\ & \quad + \frac{{{\text{Nt}}}}{{C_{0} \sqrt {{\text{Ra}} \cdot {\text{Pr}}} }}\left[ {\frac{\partial }{\partial x}\left( {D_{{\text{T}}} \frac{\partial \theta }{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {D_{{\text{T}}} \frac{\partial \theta }{{\partial y}}} \right)} \right] \\ \end{aligned}$$
(17)
$$\frac{\partial \theta }{{\partial \tau }} = \frac{{{{\alpha_{{{\text{hs}}}} } \mathord{\left/ {\vphantom {{\alpha_{{{\text{hs}}}} } {\alpha_{{\text{f}}} }}} \right. \kern-\nulldelimiterspace} {\alpha_{{\text{f}}} }}}}{{\sqrt {{\text{Pr}} \cdot {\text{Ra}}} }}\left( {\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }} + \frac{{k_{{\text{f}}} }}{{2k_{{{\text{hs}}}} }}\left\{ {1 - \cos \left( {\gamma \tau } \right)} \right\}} \right)$$
(18)

The formulated equations are affected with conditions:

$$\begin{aligned} \tau = 0{:} & \quad \psi = \omega = \theta = 0,\quad \phi = 1; \\ \tau > 0{:} & \quad \psi = 0,\quad \omega = - \frac{{\partial^{2} \psi }}{{\partial x^{2} }},\quad \theta = 0,\quad \frac{\partial \phi }{{\partial x}} = - \frac{{{\text{Le}} \cdot {\text{Nt}}}}{{C_{0} }}\frac{{D_{{\text{T}}} }}{{D_{{\text{B}}} }}\frac{\partial \theta }{{\partial x}}\quad {\text{at}}\quad x = 0\quad {\text{and}}\quad x = 1; \\ & \quad \psi = 0,\quad \omega = - \frac{{\partial^{2} \psi }}{{\partial y^{2} }},\quad \frac{\partial \theta }{{\partial y}} = 0,\quad \frac{\partial \phi }{{\partial y}} = 0\quad {\text{at}}\quad y = 0\quad {\text{and}}\quad y = 1; \\ & \quad \psi = 0,\quad \omega = - \frac{{\partial^{2} \psi }}{{\partial \overline{n}^{2} }},\quad \left\{ {\begin{array}{*{20}l} {\theta_{{\text{f}}} = \theta_{{{\text{hs}}}} ,} \hfill \\ {\frac{{k_{{\text{f}}} }}{{k_{{{\text{hs}}}} }}\frac{{\partial \theta_{{\text{f}}} }}{{\partial \overline{n}}} = \frac{{\partial \theta_{{{\text{hs}}}} }}{{\partial \overline{n}}},} \hfill \\ \end{array} } \right.\quad \frac{\partial \phi }{{\partial \overline{n}}} = - \frac{{{\text{Le}} \cdot {\text{Nt}}}}{{C_{0} }}\frac{{D_{{\text{T}}} }}{{D_{{\text{B}}} }}\frac{{\partial \theta_{{\text{f}}} }}{{\partial \overline{n}}}\quad \left| {{\text{at}}\;{\text{the}}\;{\text{surface}}\;{\text{heater}}} \right. \\ \end{aligned}$$
(19)

Here, \({\text{Ra}} = {{g \cdot \left( {\rho \beta } \right)_{{\text{f}}} \cdot \Delta T \cdot L^{3} } \mathord{\left/ {\vphantom {{g \cdot \left( {\rho \beta } \right)_{{\text{f}}} \cdot \Delta T \cdot L^{3} } {\left[ {\mu_{{\text{f}}} \left( {T_{{\text{c}}} } \right) \cdot \alpha_{{\text{f}}} } \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\mu_{{\text{f}}} \left( {T_{{\text{c}}} } \right) \cdot \alpha_{{\text{f}}} } \right]}}\) is the Rayleigh number, \({\text{Le}} = {{\alpha_{{\text{f}}} } \mathord{\left/ {\vphantom {{\alpha_{{\text{f}}} } {\overline{D}_{{\text{B}}} \left( {T_{{\text{c}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\overline{D}_{{\text{B}}} \left( {T_{{\text{c}}} } \right)}}\) is the Lewis number, \({\text{Nt}} = {{\overline{D}_{{\text{T}}} \left( {T_{{\text{c}}} {,}C_{0} } \right) \cdot \Delta T} \mathord{\left/ {\vphantom {{\overline{D}_{{\text{T}}} \left( {T_{{\text{c}}} {,}C_{0} } \right) \cdot \Delta T} {\left( {\alpha_{{\text{f}}} \cdot T_{{\text{c}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\alpha_{{\text{f}}} \cdot T_{{\text{c}}} } \right)}}\) is the thermal diffusion coefficient, and auxiliary functions M, K, DB and DT have the following form:

$$\begin{aligned} M & = \left\{ { - 69.67 + \frac{1593.7}{{\theta \Delta T + T_{{\text{c}}} - 273.15}} + 123.8 \cdot \phi C_{0} + \frac{135614.0}{{\left[ {\theta \Delta T + T_{c} - 273.15} \right]^{2} }} - 25.9 \cdot \left( {\phi C_{0} } \right)^{2} } \right. \\ & \quad - \frac{{3088.0 \cdot \phi C_{0} }}{{\theta \Delta T + T_{{\text{c}}} - 273.15}} - \frac{1965274.0}{{\left[ {\theta \Delta T + T_{{\text{c}}} - 273.15} \right]^{3} }} + 1.593 \cdot \left( {\phi C_{0} } \right)^{3} + \frac{{438.206 \cdot \left( {\phi C_{0} } \right)^{2} }}{{\theta \Delta T + T_{{\text{c}}} - 273.15}} \\ & \quad {{\left. { + \frac{{14757.3 \cdot \phi C_{0} }}{{\left[ {\theta \Delta T + T_{{\text{c}}} - 273.15} \right]^{2} }}} \right\}} \mathord{\left/ {\vphantom {{\left. { + \frac{{14757.3 \cdot \phi C_{0} }}{{\left[ {\theta \Delta T + T_{{\text{c}}} - 273.15} \right]^{2} }}} \right\}} {\left( {2.414 \cdot 10^{{\frac{247.8}{{T_{{\text{c}}} - 140}}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2.414 \cdot 10^{{\frac{247.8}{{T_{{\text{c}}} - 140}}}} } \right)}} \\ \end{aligned}$$
$$\begin{aligned} K & = 1 + 64.7\left( {\phi C_{0} } \right)^{0.764} \left( {\frac{{d_{{\text{f}}} }}{{d_{{\text{p}}} }}} \right)^{0.369} \left( {\frac{{k_{{\text{f}}} }}{{k_{{\text{p}}} }}} \right)^{0.7476} \left( {\frac{{2.414 \times 10^{ - 5} \times 10^{{\frac{247.8}{{\theta \Delta T + T_{{\text{c}}} - 140}}}} }}{{\rho_{{\text{f}}} \alpha_{{\text{f}}} }}} \right)^{0.9955} \\ & \quad \times \left\{ {\frac{{\rho_{{\text{f}}} k_{{\text{B}}} }}{{3\pi l_{{\text{f}}} }}\frac{{\theta \Delta T + T_{{\text{c}}} }}{{5.8274 \times 10^{ - 10} \cdot 10^{{\frac{495.6}{{\theta \Delta T + T_{{\text{c}}} - 140}}}} }}} \right\}^{1.2321} \\ \end{aligned}$$
$$D_{{\text{B}}} = \frac{{T \cdot \mu_{{\text{f}}} \left( {T_{{\text{c}}} } \right)}}{{T_{c} \cdot \mu_{{\text{f}}} \left( T \right)}} = 10^{{\frac{247.8 \cdot \theta \Delta T}{{\left( {T_{{\text{c}}} - 140} \right) \cdot \left( {\theta \Delta T + T_{{\text{c}}} - 140} \right)}}}} \left[ {\theta \frac{\Delta T}{{T_{{\text{c}}} }} + 1} \right]$$
$$D_{{\text{T}}} = \frac{{C \cdot \mu_{{\text{f}}} \left( T \right)}}{{C_{0} \cdot \mu_{{\text{f}}} \left( {T_{{\text{c}}} } \right)}} = \phi \cdot 10^{{\frac{247.8 \cdot \theta \Delta T}{{\left( {\theta \Delta T + T_{{\text{c}}} - 140} \right) \cdot \left( {140 - T_{{\text{c}}} } \right)}}}}$$

The formulated governing equations of nanofluid thermal convection within a closed chamber with a hot element of periodic heat generation with additional restrictions (19) have been worked out using the finite difference methodology on a uniform calculation mesh. The developed mathematical model has been tested using the natural convection problems inside isothermally heated cavities (see Ho et al. [45] and Saghir et al. [46]). Table 2 demonstrates a comparison of the obtained results with the data of other researchers. It can be found that the received data have a good agreement with experimental and numerical outcomes.

Table 2 Comparison of mean Nu with results of Ho et al. [45] and Saghir et al. [46]
Full size table

The developed solution method has been tested for sensitivity to grid parameters for Ra = 106, Pr = 6.52, Le = 9415.6, C0 = 0.04, γ = 0.01, Nt = 2.56–7, δ = 0.4 (see Fig. 2). The results obtained show a periodic change in the average temperature due to periodic heat generation from the local source. Time moments around τ = 150 and τ = 314 characterize the peaks of heat generation oscillations from the heater according to the selected ratio. The use of different grid dimensions for the maximum heat flux leads to small differences between the values of the average heater temperature due to the uniform grid type. It should be noted that these differences decrease when the grid is crunched. Taking into account this grid convergence and computational time, the uniform mesh of 100 × 100 elements has been employed for further calculations.

Fig. 2
figure 2

Influence of grid parameters on average heater temperature at Ra = 106, Pr = 6.52, Le = 9415.6, Nt = 2.56–7, C0 = 0.04, γ = 0.01, δ = 0.4

Full size image

Results and discussions

Computational studies of the problem have been solved for Ra = 106, Pr = 6.52, Le = 9415.6, Nt = 2.56–7, C0 = 0.00 − 0.04, γ = 0.01 − 0.1, δ = 0.1–0.7, τ = 0 − 500. The major attention was employed to the influence of these dimensionless parameters on thermogravitational energy transport within a closed area saturated with nanosuspension in the presence of a heating element with periodic generation.

Figure 3 reflects the influence of the volumetric thermal production oscillation frequency γ on the distribution of the streamlines and isothermal for other fixed parameters: C0 = 0.04 and τ = 500. Uniform heating of the cavity is observed for any value of γ. The isolines are distributed symmetrically about the average section along the x-coordinate through the heater. Two convective symmetrical cells are formed with cores in the region above the source, which reflects an appearance of ascending and descending convective flows in the chamber due to the cooling effect from the vertical walls.

Fig. 3
figure 3

Isotherms Θ and streamlines Ψ for C0 = 0.04: a − γ = 0.01, b − γ = 0.05, c − γ = 0.1

Full size image

An increase in the volumetric thermal production oscillation frequency γ enhances the energy transport in the chamber. The convective cores will mix closer to the upper boundary of the cavity. In addition, a decrease in the values of isotherms is observed. The convective plume above the heater narrows at the base and expands near the upper adiabatic wall, reflecting an increase in heat removal from the source. Thus, increasing the intensity of heat generation from the heater leads to increased movement of the suspension in the cavity and mixing of nanoparticles with the base liquid, which leads to improved heat removal.

In more detail, the influence of γ on heat and mass transfer can be estimated from the change in the average temperature of the heater, which is shown in Fig. 4. As noted above, the distribution of Θavg has a periodic nature of change. An increase in γ results to a reduction in the period and amplitude of oscillations. It should be noted that the maximum temperature is observed at the minimum value of the considered parameter, while the minimum value is reached at the maximum γ. The transition from a heat dissipation parameter value of 0.01 to 0.1 reduces the average temperature by 20%.

Fig. 4
figure 4

Time variations of the mean heater temperature at C0 = 0.04 and different values of γ

Full size image

Figure 5 presents the influence of the initial fraction of nanoadditives (C0) on the convective energy transport in the considered chamber for fixed dimensionless parameters: γ = 0.05 and τ = 500. The change in C0 has insignificant effect on the streamlines and isotherms. When passing from C0 = 0.00 to C0 = 0.04, there is a slight shift of the streamlines Ψ and isotherms Θ to the heater. It can be explained by the steady state of the process for the considered time point, at which the fluid flow calms down, and the displacement of the base fluid with nanoparticles is established. It the same time, the dependences of the average source temperature did not change (see Fig. 6).

Fig. 5
figure 5

Isotherms Θ and streamlines Ψ at γ = 0.05, δ = 0.04: a − C0 = 0.00, b − C0 = 0.02, c − C0 = 0.04

Full size image
Fig. 6
figure 6

Change in the average temperature of the heater at γ = 0.05 and different C0

Full size image

Figure 7 shows the influence of C0 on the mean Nu along the energy source at γ = 0.05. The results show a strong change in the values of the Nusselt number when going from C0 = 0.0 to C0 = 0.02. Further increase in C0 has no noticeable effect on Nuavg. Thus, the addition of nanoparticles CuO into the base liquid leads to an increase in the intensification of heat transfer at the source surface by 25%, which indicates the intensification of heat exchange.

Fig. 7
figure 7

Time variations of the mean Nu at γ = 0.05 and different C0

Full size image

Numerical calculations of thermogravitational convection in a chamber has been performed for various positions of the heat-producing solid block (δ = l/L). The obtained distributions of isotherms and streamlines for various δ and for C0 = 0.04, γ = 0.05 are shown in Fig. 8. The distribution of streamlines demonstrates a symmetrical flow structure respect to the hot element location. It should be noted that for δ = 0.1, 0.7, one huge convective cell appears with a core in the central part of the cavity. When the source is displaced to the right isothermal boundary, the convective cells are aligned, and at δ = 0.4 (see Fig. 8d), a completely symmetrical flow with respect to the central section is observed. A further raise of δ results to a repetition of the initial flow pattern in the reflected form. Moving the source to different parts of the cavity away from the center enhances the cooling effect of the vertical walls with increasing boundary layers between the source and the boundaries.

Fig. 8
figure 8

Effect of the position of the hot element on isotherms Θ and isolines of Ψ at C0 = 0.04, γ = 0.05 for different hot element location δ: a − δ = 0.1, b − δ = 0.2, c − δ = 0.3, d − δ = 0.4, e − δ = 0.5, f − δ = 0.6, g − δ = 0.7

Full size image

The distributions of the integral characteristics of energy transport at different locations of the heater (average temperature source is in Fig. 9 and the mean Nu at the source is in Fig. 10) reflect a weak influence of δ. In any case, results illustrate a periodic change in the considered parameters due to the oscillation of the volumetric heat generation of the heater. For clarity, the time moment up to τ = 200 has been considered and the central position of the source relative to the middle section (δ = 0.4) as well as the symmetrical locations of the relative central section (δ = 0.1 and δ = 0.7, δ = 0.3 and δ = 0.5) have been considered. The minimum temperature in this case is observed at the central location of the heater (δ = 0.4), while the displacement of the source increases the temperature, and the temperature values for symmetrical locations coincide: δ = 0.1 and δ = 0.7, δ = 0.3 and δ = 0.5.

Fig. 9
figure 9

Time variations of the mean heater temperature at γ = 0.05, C0 = 0.04 and different δ

Full size image
Fig. 10
figure 10

Time variations of the mean Nu at γ = 0.05, C0 = 0.04 and different δ

Full size image

In addition, the time dependences of the mean Nusselt number (Fig. 10) reflects nonsignificant differences for various values of δ due to the conservation of the heat flux and by compensating for the effect of cooling walls with a symmetric arrangement.

Figure 11 shows the dynamics of flow development in the cavity using the example of isotherms Θ and isolines of the stream function Ψ during one oscillation period. For this, the case of C0 = 0.02, γ = 0.05 and the last considered oscillation period for τ = 445–485 have been considered. The following time points have been used: τ = 445 (Fig. 11a), τ = 455 (Fig. 11b), τ = 465 (Fig. 11c), τ = 475 (Fig. 11d), and τ = 485 (Fig. 11e). The resulting distributions clearly reflect the evolution of convective flows in the cavity during the oscillation period. It should be noted that the intensification of heat and mass transfer is achieved at τ = \(T_{\uptau }\)/2 (Fig. 11c), where \(T_{\uptau }\) is the oscillation period. The presence of CuO solid particles in the base fluid improves the thermal conductivity properties of the suspension and improves the properties of the passive cooling system.

Fig. 11
figure 11

Isotherms Θ and isolines of Ψ at C0 = 0.02, γ = 0.05 for different moments of one period of oscillation: a − τ = 445, b − τ = 455, c − τ = 465, d − τ = 475, e − τ = 485

Full size image

Conclusions

A numerical investigation of the phenomenon of convective energy and mass transport in a closed square chamber saturated with H2O/CuO nanosuspension under the impact of an energy source of periodic heat generation has been carried out. The cavity has been cooled from the vertical walls of a constant low temperature. The control equations have been written using the dimensionless stream function, vorticity, temperature and solved by the finite difference method using a developed C++ programming code. As a result of the present research the following conclusions have been obtained:

  • The introduction of copper nanoparticles results to an increase in energy transport rate in the cavity compared to a pure working liquid.

  • The periodic law of source heating leads to a periodic change in the integral characteristics of heat transfer such as Θavg and Nuavg. In this case, the intensity of heat generation is reflected in the change in the periods and amplitudes of the distributions.

  • Changing the location of the heater does not lead to qualitative changes in the characteristics of heat transfer.

  • An addition of nanoparticles into the water-based fluid and varying the properties of the working fluid and heat transport can improve the heat transfer by 20–25%.

The analyzed problem and obtained results can be considered as the further development of one of the main directions of hydrodynamics and thermophysics, namely the optimization of thermal systems with heating elements of complex types (for the present research using the periodic inner heating). Therefore, the novelty of the present research is related to analysis of cooling schemes for solid element of periodic volumetric heat generation using nanofluids of variable physical properties. Such analysis is performed for the first time taking into account the published papers. In addition, the conclusions about the influence of the heater position on the heat transfer rate and nanofluid convective flows strength within the cavity are new.