Introduction

Investigation of natural convection flows due to the interior heat generation within a confined reactor having wavy wall and filled with porous media has been attracted researcher’s contemplation from many years owing to the vast applications in many engineering fields. Some enchanting engineering applications of such flows are the cooling processes for microelectronic devices, heat exchangers, solar collectors, underground cable systems, roughened surface in cooling devices [1, 2] and so forth. To enhance the convection procedures and thereby system performances, interior heat generation and heat losses through the confined surfaces could take a momentous role from the technological aspects. Applications noted above could be classified into two categories by considering nature of heating. When heat is produced from different thermal conditions employed in the boundary of confined reactor, it is called external heating. On the other hand, when heat is produced due to the presence of interior heat sources, it is called interior heating. Vast works have been done considering external heating, but very few works have been done for the case of interior heating. In the present study, chemically reacting fluid which actually produces heat within the confined reactor is considered.

The impacts of amplitude wavelength ratio on natural convective flow inside a two wall wavy enclosure were numerically investigated by Das and Mahmud [3]. They showed that the periodic nature in Nusselt number graphs is removed by raising the amplitude wavelength ratio under large values of Grashof number. Shu and Zhu [4] numerically investigated natural convection flow in an annulus bounded by a cool exterior square and hot interior circular cylinders. They used a super elliptic function to approximate the exterior square cylinder so that a coordinate transformation could easily transform the annulus into rectangular region. Findings obtained from their study established a critical value of aspect ratio for which different flow patterns and temperature characteristics were found at high Rayleigh numbers. Yang [5,6,7,8] introduced a new integral transform and used this to analyze the differential equation of heat transfer problem. Wang and Chen [9] numerically investigated forced convection in a channel having wavy lower wall. They used a simple coordinate transformation that converted the wavy channel into parallel wall channel. Waviness in local Nusselt number graphs was shown due to the presence of wavy lower wall, and the amplitude of these waves increased significantly with the increase in amplitude wavelength ratio of wavy wall at high Reynolds number. Dormohammadi et al. [10] conducted a numerical investigation to optimize the heat transfer and entropy generation of nanofluid flow in a channel containing two sinusoidal wavy walls. They found optimal heat transfer and entropy generation for a particular values of wavelength ratio (λ = 1) and wave amplitude ratio (α = 0.2) and suggested those values to design an optimal wavy wall heat exchanger. Effects of different wave shapes on corrugated channel performance were numerically investigated by Salami et al. [11]. They examined for three different waves namely triangular, trapezoidal and sinusoidal and then concluded that trapezoidal waves produce the maximum Nusselt number and friction factor for any set of values of flow parameters. Oztop et al. [12] numerically conducted an investigation on natural convective flow inside an enclosure comprising two wavy horizontal walls. Their interest was on the wave amplitude and two types Rayleigh numbers. They expressed the heat transfer as a decreasing function of the waviness of both wavy walls by portioning the ratio of internal and external Rayleigh number greater than unity and less than unity. The impacts of ambient oscillating temperature on natural convective flow inside a closed vessel containing chemically reacting fluid were numerically studied by Roy [13]. He showed that the flow patterns and temperature characteristics are periodic in time and thermal explosion occurs for higher values of Frank-Kamenetskii number under the large values of Rayleigh number. Varol and Oztop [14] performed an investigation on natural convective flow inside a shallow enclosure containing a wavy hot lower wall. The wavy wall was expressed by a sinusoidal function, and numerical simulation was conducted by the computational software CFDRC. Findings revealed that heat transfer could be ameliorated by diminishing the wave length and diminished by raising Rayleigh number and aspect ratio.

Cheong et al. [15] ran an investigation on natural convection inside a porous cavity having wavy vertical wall to examine the impacts of aspect ratio on flow patterns and heat transfer. Convection ensued owing to temperature variety between two vertical walls of cavity. The results revealed that waviness in right wall improves heat transfer that gains its supreme state when the aspect ratio is equal to unity. Chen et al. [16] numerically simulated natural convection inside a fluid-saturated non-Darcy porous cavity containing bent vertical walls to examine the impacts of dimensionless parameters on streamlines and heat transfer. Two straight walls were retained at adiabatic thermal condition, and the bent walls were considered to be isothermal where right wall was highly heated than left wall. Finite volume-based SIMPLEC scheme was ascribed to solve the model equations. Their one enchanting result was that three vortices (top, bottom and middle of cavity) are produced at low Darcy–Rayleigh number and among two of that vortices (top and bottom) vanishes and the middle one is wrenched into two at high Darcy–Rayleigh number. Akbarzadeh et al. [17] conducted a numerical investigation to examine the combined effects of nanofluid, wavy walls and porous medium inside a heat exchanger duct. The second-order upwind method was implemented to discretize all the governing equations, and then, SIMPLE algorithm was applied to solve the equations. The results obtained in their study revealed that heat transfer of the system can be importantly enhanced by a combination of wavy walls, nanofluid and porous medium.

Allali et al. [18] conducted an investigation to show the interaction between natural convection and thermal explosion in an enclosed porous cavity where the flow governing equations were formed by using Darcy law and heat was generated from an exothermic reaction. Horizontal and vertical walls were maintained at surrounding temperature and adiabatic thermal condition, respectively. They found some critical values of Frank-Kamenetskii and Rayleigh number and predicted that thermal explosion and solution characteristics depend upon convection and nature of boundary conditions, respectively. Natural convection flow inside a porous concentric annulus containing chemically reacting fluid was examined by Roy and Gorla [19]. They varied the values of physical parameters and radius of annulus to observe their impacts on streamlines and isotherms. The results revealed that flow strength and maximum temperature within the annulus could be improved by increasing the values of radius of annulus and physical parameters excluding Forchheimer drag parameter.

In the present study, our aim is to simulate natural convective flow inside a confined 2D porous reactor bounded by a complex wavy lower wall. Non-Darcian model is imposed to govern the model equations. Heat is presumed to be generated by an exothermic chemical reaction. A coordinate transformation is applied to convert the physical domain into rectangular domain, and then, FDS is employed to solve the transformed equations. The results in terms of streamlines, isotherms and local Nusselt number at the lower and upper walls are displayed varying all the introduced physical parameters.

Formulation of the model

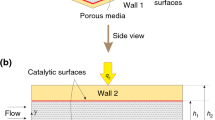
Natural convection flow within a 2D confined reactor bounded by the plane surfaces except the lower wall is considered. A complex wavy wall is placed as the lower wall of the reactor. The reactor is fulfilled with an isotropic, homogeneous, fluid-saturated porous medium having fluid that can generate heat. The walls of the reactor are maintained at an ambient temperature Ta. The physical domain and the computational domain of the model are pictured in Fig. 1a, b, respectively. U and V are, respectively, the components of the velocity along the X- and Y-axes for physical domain and along the ξ- and η-axes for computational domain. The variable T stands for the temperature. It is assumed that heat is generated within the reactor by a single-step exothermic reaction when a reactant A produces product B [20,21,22].

$$A \to B + {\text{heat}},\quad {\text{rate}} = k_{0} a {\text{e}}^{- {\text{E}}/ {\text{RT}}}$$
(1)

where k0 and a are the pre-exponential factor and species concentration, respectively. E and R are known as the activation energy and universal gas constant. respectively. The concentration of the reactant is supposed to be constant by supplying sufficient reactant in the reactor.

Fig. 1
figure 1

Transformation of a the physical domain \((X,Y)\) to b the computational domain \((\xi ,\eta )\)

Full size image

With a view to formulating the model, the confined reactor containing fluid-saturated porous medium and heat producing fluid is taken into consideration as a continuum and a thermal equilibrium exists between the fluid phases and solid. The constant behavior of the thermophysical properties is also considered. Boussinesq approximation is taken into consideration so that the change in density with temperature can be neglected from all terms except the buoyancy term. The governing equations which describe this type of porous medium can be formulated using Forchheimer and Brinkman modifications known as non-Darcian model [23, 24]. Considering the above assumptions, the governing equations in terms of dimensionless variables can be expressed as

$$\frac{\partial u}{\partial x} + \frac{\partial u}{\partial y} = 0$$
(2)
$$\frac{\partial u}{\partial \tau } + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = - \frac{\partial p}{\partial x} + { \Pr }\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - \frac{ \Pr }{\text{Da}}u - \frac{F}{{\sqrt {\text{Da}} }}u\left| {\varvec{v}} \right|$$
(3)
$$\frac{\partial v}{\partial \tau } + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = - \frac{\partial p}{\partial y} + { \Pr }\left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - \frac{ \Pr }{\text{Da}}v - \frac{F}{{\sqrt {\text{Da}} }}v\left| {\varvec{v}} \right| + {\text{PrRa}}\theta$$
(4)
$$\frac{\partial \theta }{\partial \tau } + u\frac{\partial \theta }{\partial x} + v\frac{\partial \theta }{\partial y} = \frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }} + K_{\text{f}} e^{\theta }$$
(5)

where \(\left| {\varvec{v}} \right| = \sqrt {u^{2} + v^{2} }\) and the dimensionless variables are defined by

$$\begin{aligned} x & = \frac{X}{{L_{\text{Y}} }},\quad y = \frac{Y}{{L_{\text{Y}} }},\quad \tau = \frac{t\alpha }{{L_{\text{Y}}^{2} }},\quad u = \frac{{UL_{\text{Y}} }}{\alpha },\quad \\ v & = \frac{{VL_{\text{Y}} }}{\alpha } ,\quad \theta = \frac{E}{{RT_{\text{a}}^{2} }}\left( {T - T_{\text{a}} } \right),\quad p = \frac{{PL_{\text{Y}}^{2} }}{{\rho \alpha^{2} }},\quad s_{\text{w}} (x) = \frac{{S_{\text{w}} (X)}}{{L_{\text{Y}} }} .\\ \end{aligned}$$
(6)

Note that length of the reactor along the X-axis and Y-axis are, respectively, LX and LY. P, t, α, F and ρ are, respectively, the pressure, time, thermal diffusivity, Forchheimer drag parameter and the density of the fluid. The function sw(x) introduced in Eq. (6) represents the lower wavy wall of the reactor. In our study, it is defined by

$$s_{\text{w}} (x) = - \sum\limits_{i = 1}^{n} {A_{\text{i}} \text{sec}\,h [e_{\text{i}} (x - x_{\text{i}} )]}$$
(7)

where Ai, ei and n are the constants that determine the amplitude of a wave, the enlargement of a wave along the x-axis and the number of waves in the lower wavy wall, respectively. Also, the constant xi represents the critical point at which the function sw(x) gains its highest value.

The dimensionless parameters introduced in Eqs. (2)–(5), Pr, Da, Ra and Kf are the Prandtl number, Darcy number, Rayleigh number and Frank-Kamenetskii number, respectively. These parameters are defined as:

$${ \Pr } = \frac{\nu }{\alpha },\quad {\text{Da}} = \frac{K}{{L_{\text{Y}}^{2} }},\quad {\text{Ra}} = \frac{{g\beta RT_{\text{a}}^{2} L_{\text{Y}}^{3} }}{E\alpha \nu }\quad {\text{and}}\quad K_{\text{f}} = \frac{{EQk_{0} ae^{{ - E/RT_{\text{a}} }} L_{\text{Y}}^{2} }}{{RT_{\text{a}}^{2} \rho C_{\text{P}} \alpha }}$$
(8)

where υ, K, g, β and CP are, respectively, kinematic viscosity, permeability of the porous medium, acceleration due to gravity, coefficient of thermal expansion and specific heat at constant pressure. The Frank-Kamenetskii number is used to explain the explosion in the reactor. This number is obtained by performing the Frank-Kamenetskii approximation under the assumption \(\frac{{RT_{\text{a}} }}{E} \ll 1\) in the last term of Eq. (5) [25].

It is assumed that at the beginning of time, the fluid is at rest and the temperature of the fluid is uniformly distributed throughout the reactor. Also, no-slip velocity boundary conditions are considered at the reactor walls for any time. Thus the boundary conditions considered in this study are in the form of dimensionless variables:

$$\begin{aligned} & u = v = 0\,{\text{ and }}\,\theta = 0\quad \forall \, x,y\,{\text{ when}}\,\tau = 0 \\ & \left. {\begin{array}{*{20}l} {u = v = 0\,{\text{ and }}\,\theta = 0\quad {\text{for}}\,0 \le x \le L,\,y = s_{\text{w}} (x), \, 1} \hfill \\ {u = v = 0\,{\text{ and }}\,\theta = 0\quad {\text{for}}\,0 < y < 1,\,x = 0, \, L} \hfill \\ \end{array} } \right\}\quad \tau > 0 \\ \end{aligned}$$
(9)

where \(L = L_{\text{X}} /L_{\text{Y}}\). With a view to eliminating the pressure gradient term and then forming the vorticity-stream function formulation, we now define the stream function, ψ, and vorticity, Ω, by

$$u = \frac{\partial \psi }{\partial y},\,v = - \frac{\partial \psi }{\partial x}\,{\text{and}}\,\varOmega = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}.$$
(10)

Thus, the vorticity-stream function formulation is of the form

$$\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial y^{2} }} = - \varOmega$$
(11)
$$\begin{aligned} \frac{\partial \varOmega }{\partial \tau } + u\frac{\partial \varOmega }{\partial x} + v\frac{\partial \varOmega }{\partial y} & = { \Pr }\left( {\frac{{\partial^{2} \varOmega }}{{\partial x^{2} }} + \frac{{\partial^{2} \varOmega }}{{\partial y^{2} }}} \right) - \left( {\frac{ \Pr }{\text{Da}} + \frac{F}{{\sqrt {\text{Da}} }}\left| {\varvec{v}} \right|} \right)\varOmega \\ & \quad - \frac{F}{{\sqrt {\text{Da}} }}\left( {u\frac{{\partial \left( {\left| {\varvec{v}} \right|} \right)}}{\partial y} - v\frac{{\partial \left( {\left| {\varvec{v}} \right|} \right)}}{\partial x}} \right) + {\text{PrRa}}\frac{\partial \theta }{\partial x} \\ \end{aligned}$$
(12)

subject to the boundary conditions

$$\begin{aligned} & \psi = 0,\quad \frac{\partial \psi }{\partial y} = 0\,{\text{and}}\,\theta = 0\quad \forall \, x,y\,{\text{ when}}\,\tau = 0 \\ & \left. {\begin{array}{*{20}l} {\psi = 0,\quad \frac{\partial \psi }{\partial y} = 0\,{\text{and}}\,\theta = 0\quad {\text{for}}\,0 \le x \le L,\,y = s_{\text{w}} (x), \, 1} \hfill \\ {\psi = 0,\quad \frac{\partial \psi }{\partial y} = 0\,{\text{and}}\,\theta = 0\quad {\text{for}}\,0 < y < 1,\,x = 0, \, L} \hfill \\ \end{array} } \right\}\quad \tau > 0. \\ \end{aligned}$$
(13)

To make the numerical calculation easy, a coordinates transformation is required so that the irregular boundary of the physical domain is transformed into a regular shape in the computational domain. Using an algebraic transformation by introducing a new set of independent variables \((\xi ,\eta )\), the physical domain enclosed by \(0 \le x \le L\) in the x-direction and enclosed by the curve \(y = s_{\text{w}} (x)\) at the lower wall and the line \(y = 1\) at the upper wall can be transformed into the rectangular computational domain enclosed by \(0 \le \xi \le L\) and \(0 \le \eta \le 1\). The transformation used in this study is:

$$\left. {\begin{array}{*{20}l} {x = x(\xi ,\eta ) = \xi } \hfill \\ {y = y(\xi ,\eta ) = s_{\text{w}} (\xi ) + \eta (1 - s_{\text{w}} (\xi ))} \hfill \\ \end{array} } \right\}.$$
(14)

Now, by substituting Eq. (14) into Eqs. (11), (12) and (5), the governing equations are transformed a wavy wall reactor into a rectangular reactor. The transformed equations are:

$$\nabla^{2} \psi = - \varOmega$$
(15)
$$\begin{aligned} & \frac{\partial \varOmega }{\partial \tau } + \frac{1}{J}uy_{\eta } \frac{\partial \varOmega }{\partial \xi } + \frac{1}{J}\left( {v - uy_{\xi } } \right)\frac{\partial \varOmega }{\partial \eta } = { \Pr }\nabla^{2} \varOmega - \left( {\frac{ \Pr }{\text{Da}} + \frac{F}{{\sqrt {\text{Da}} }}\left| {\varvec{v}} \right|} \right)\varOmega \\ & \quad - \frac{F}{{\sqrt {\text{Da}} }}\frac{1}{J}\left( { - vy_{\eta } \frac{{\partial \left( {\left| {\varvec{v}} \right|} \right)}}{\partial \xi } + (u + vy_{\xi } )\frac{{\partial \left( {\left| {\varvec{v}} \right|} \right)}}{\partial \eta }} \right) + {\text{PrRa}}\frac{1}{J}\left( {y_{\eta } \frac{\partial \theta }{\partial \xi } - y_{\xi } \frac{\partial \theta }{\partial \eta }} \right) \\ \end{aligned}$$
(16)
$$\frac{\partial \theta }{\partial \tau } + \frac{1}{J}uy_{\eta } \frac{\partial \theta }{\partial \xi } + \frac{1}{J}\left( {v - uy_{\xi } } \right)\frac{\partial \theta }{\partial \eta } = \nabla^{2} \theta + K_{\text{f}} e^{\theta }$$
(17)

where

$$\begin{aligned} u & = \frac{1}{J}\frac{\partial \psi }{\partial \eta },\,v = - \frac{1}{J}\left( {y_{\eta } \frac{\partial \psi }{\partial \xi } - y_{\xi } \frac{\partial \psi }{\partial \eta }} \right),\,\varOmega = \frac{1}{J}\left( {y_{\eta } \frac{\partial v}{\partial \xi } - y_{\xi } \frac{\partial v}{\partial \eta } - \frac{\partial u}{\partial \eta }} \right),\,J = y_{\eta } \\ \nabla^{2} & = \frac{1}{{J^{2} }}\left( {y_{\eta }^{2} \frac{{\partial^{2} }}{{\partial \xi^{2} }} + \left( {1 + y_{\xi }^{2} } \right)\frac{{\partial^{2} }}{{\partial \eta^{2} }} - 2y_{\xi } y_{\eta } \frac{{\partial^{2} }}{\partial \xi \partial \eta } + (2y_{\xi } y_{\xi \eta } - y_{\eta } y_{\xi \xi } )\frac{\partial }{\partial \eta }} \right) \\ y_{\xi } & = (1 - \eta )s_{\text{w}}^{\prime } (\xi ),\,y_{\eta } = 1 - s_{\text{w}} (\xi ),\,y_{\xi \xi } = (1 - \eta )s_{\text{w}}^{\prime \prime } (\xi ),\,y_{\xi \eta } = - s_{w}^{\prime } (\xi ). \\ \end{aligned}$$

Equations (15)–(17) are solved subject to the following boundary conditions

$$\begin{aligned} & \psi = 0, \, \frac{\partial \psi }{\partial \eta } = 0\,{\text{ and }}\,\theta = 0\,\forall \, \xi ,\eta \,{\text{when }}\tau = 0 \\ & \left. {\begin{array}{*{20}l} {\psi = 0, \, \frac{\partial \psi }{\partial \eta } = 0\,{\text{ and }}\,\theta = 0\,{\text{for}}\,0 \le \xi \le L,\,\eta = 0, \, 1} \hfill \\ {\psi = 0, \, \frac{\partial \psi }{\partial \eta } = 0\,{\text{ and }}\,\theta = 0\,{\text{for}}\,0 < \eta < 1,\,\xi = 0, \, L} \hfill \\ \end{array} } \right\}\quad \tau > 0 .\\ \end{aligned}$$
(18)

To besiege the thermal explosion in the reactor, it is important to know how the heat is released from the reactor to the surroundings by the reactor side walls as the heat is generated within the reactor by the exothermic reaction. A fantastic quantity that describes the heat transfer characteristics is the local Nusselt number, Nu, which is calculated at the side walls of the reactor. Now, we define the local Nusselt number, Nu, by

$${\text{Nu}} = \frac{{L_{\text{Y}} h}}{\lambda }$$
(19)

where λ is the thermal conductivity of the fluid and h is the heat transfer coefficient which is defined by

$$h = \frac{\lambda }{{T_{\text{r}} - T_{\text{a}} }}\left( {\frac{\partial T}{\partial n}} \right)$$
(20)

where \({\partial \mathord{\left/ {\vphantom {\partial {\partial n}}} \right. \kern-0pt} {\partial n}}\) refers the differentiation with respect to the coordinate normal to the wall of the reactor, Tr represents the reference temperature and

$$\frac{\partial T}{\partial n} = \sqrt {\left( {\frac{\partial T}{\partial X}} \right)^{2} + \left( {\frac{\partial T}{\partial Y}} \right)^{2} } .$$
(21)

The expression for Nusselt number in the coordinates \((\xi ,\eta )\) is given by

$${\text{Nu}}_{\xi } = \frac{1}{{y_{\eta } }}\sqrt {1 + y_{\xi }^{2} } \frac{\partial \theta }{\partial \eta }$$
(22)

where \({\text{Nu}}_{\xi } = \frac{{E(T_{\text{r}} - T_{\text{a}} ){\text{Nu}}}}{{RT_{\text{a}}^{2} }}\).

Numerical method

The flow governing Eqs. (15) and (16) in transformed coordinates (ξ, η) subject to the boundary condition (18) are solved by applying FDS to produce numerical solutions. The diffusion terms are split by central difference scheme, whereas the convective terms are split by an upwind difference scheme. Uniform step sizes, \(\Delta \xi = {{12} \mathord{\left/ {\vphantom {{12} {(m_{\xi } - 1)\,{\text{and}}\,}}} \right. \kern-0pt} {(m_{\xi } - 1)\,{\text{and}}\,}}\Delta \eta = {1 \mathord{\left/ {\vphantom {1 {(m_{\eta } - 1)}}} \right. \kern-0pt} {(m_{\eta } - 1)}}\), where mξ and mη are the number of grid points along the ξ and η directions, respectively, are used to discretize the flow domain. The stream function, ψ, is evaluated from Eq. (15) by utilizing the finite difference method together with successive over relaxation (SOR) technique. After getting the stream function, the velocity components u and v are obtained from the expression for u and v given in Eq. (17). After that, the vorticity Ω and the temperature θ are obtained from Eq. (16) and (17), respectively. Similar technique may be followed to calculate all the quantities in every time steps.

In any study, it is important to show whether the results figured in the study are grid independent or not. Because of this, to show the grid independency four different sizes of grid are considered. The results in terms of absolute percentage error for maximum stream function and maximum temperature in the reactor are presented in Table 1. Here, absolute percentage errors are calculated by using the following relation.

$${\text{Absolute}}\,{\text{percentage}}\,{\text{error}}\, (\% )= \left| {q(m_{{{\text{j}} + 1}} \times n_{{{\text{j}} + 1}} ) - q(m_{\text{j}} \times n_{\text{j}} )} \right| \times 100$$
(23)

where the quantity q stands for maximum stream function or maximum temperature and \(m_{\text{j}} = L \times 2^{\text{j}} + 1\) and \(n_{\text{j}} = 2^{\text{j}} + 1\) are the number of grid points along the ξ and η directions, respectively. From Table 1, it is seen that the absolute percentage error for any two consecutive grids is less than 1% and this error decreases as the grid size increases. Also, the maximum stream function and maximum temperature with time for different grid sizes are plotted in Fig. 2 which showed that the difference between any two consecutive curves is very small and the curves for grids 193 × 17 and 385 × 33 are almost overlapping. This indicates that grids larger than 193 × 17 will produce the grid independence solution. As a result, we have taken the grid 193 × 17 throughout our all calculations to minimize the simulation time and cost.

Table 1 Grid independence study (τ = 2.0, Ra = 104, Pr = 1.0, Kf = 2.0, Da = 10−3, F = 0.5, Ai = 0.3, ei = 4.0 and n = 4)
Full size table
Fig. 2
figure 2

Comparison of a maximum stream function and b maximum temperature with time for different grid sizes (τ = 2.0, Ra = 104, Pr = 1.0, Kf = 2.0, Da = 10−3, F = 0.5, Ai = 0.3, ei = 4.0 and n = 4)

Full size image

To ensure the validity of our numerical code, a comparison has been made of our result with the numerical results of Khanafer et al. [26] and Oztop et al. [12] and the experimental results of Krane and Jesse [27]. It is worth mentioning that our considered physical model reduces to the model of Khanafer et al. [26] and Oztop et al. [12] if we set Ai = 0.0 and L = 1.0. Also, the flow governing Eqs. (11), (12) and (5) reduce to the flow governing equations of Khanafer et al. [26] for pure fluid and Oztop et al. [12] if we set F = 0.0, 1/Da = 0.0 and Kf = 0.0. Temperature at the vertically middle point along the length of the enclosure is shown in Fig. 3 when the values of the dimensionless parameters Ra = 105 and Pr = 0.7. It is seen that our result makes a good harmony with the results obtained from [26] to [27].

Fig. 3
figure 3

Comparison of the present study with studies of Khanafer et al. [26], Oztop et al. [12] and Krane and Jesse [27] for temperature at the vertical midpoint along the width of the enclosure

Full size image

Results and discussion

Numerical simulations are conducted for 2D natural convective flow inside a fluid-saturated non-Darcy porous reactor having a complex wavy bottom wall. The dimensionless parameters that generate the flow are Pr, Da, Ra and Kf. The results that are presented here are chosen to elucidate the flow patterns and temperature distribution along with heat transfer characteristics at the lower and top wall of the reactor. The following results are figured for steady case of exothermic reaction at dimensionless time variable τ = 2.0, while the values of other parameters are Ra = 104, Pr = 1.0, Kf = 2.0, Da = 10−3, F = 0.5, Ai = 0.3, ei = 4.0 and n = 4 when values are not noted in the respective figure.

Improvement of streamlines and isotherms with time, τ

The improvement of streamlines and isotherms in the reactor with increasing time is displayed in Figs. 4 and 5, respectively. It is observed from these figures that both the temperature and the strength of flow speedily increase and reach to a steady state (Figs. 4d–f, 5e, f). Two vortices are formed between every two consecutive peaks of wave where they have the equal but opposite directed strength. This opposite characteristics happen as the relatively cooler particles go upward because of the buoyancy force and spin in clockwise and anticlockwise directions. Totally, eight vortices are produced in the reactor where each vortex is separated by the stream function having zero magnitude which occurs at the peak and trough of the every waves. It is also observed from Fig. 5 that four high-temperature regions are formed along the vertically midsection of the reactor and at the peak of every waves. This region is symmetrical about y-axis if the produced vortices are symmetrical (the isotherms and streamlines allocated at the second and third peak). On the other hand, asymmetrical characteristics are observed in the high-temperature region and produced vortices if both are asymmetrical (the isotherms and streamlines allocated at the second and third peak).

Fig. 4
figure 4

Improvement of streamlines with time, τ

Full size image
Fig. 5
figure 5

Improvement of isotherms with time, τ

Full size image

Changes in streamlines and isotherms with increasing Darcy number, Da

Changes in flow patterns and isotherms with increasing Darcy number, Da, are displayed in Figs. 6 and 7, respectively. The results reveal that the strength of vortices increases for increasing the Darcy number while the maximum temperature in the reactor decreases. It is also observed that for low values of Da (Fig. 6a, b), center of all the vortices excluding adjacent to vertical walls is under the horizontal line passes through the vertically middle point of the reactor. And the center moves upward and reaches to this horizontal line when Da is equal to 10−2 (Fig. 6d). In other words, it can be told that center of all the vortices moves upward as the Darcy number increases. This happens because higher values of Darcy number indicate the porous medium with more permeability which creates low resistance when fluid flows through the reactor. Therefore, fluid can spontaneously transfer from one place to another through the porous medium and the strength of vortices is heightened. Also, the increasing strength of vortices assists to distribute heat uniformly near the center of the vortices. Consequently, the maximum temperature decreases with increasing Darcy number.

Fig. 6
figure 6

Changes in streamlines with increasing Darcy number, Da

Full size image
Fig. 7
figure 7

Changes in isotherms with increasing Darcy number, Da

Full size image

Changes in streamlines and isotherms with increasing Frank-Kamenetskii number, K f

The impacts of Frank-Kamenetskii number, Kf, on fluid flow and temperature distribution are described by Figs. 8 and 9, respectively. Figures evidently show that a momentous increase in the strength of the vortices and the highest temperature is occurred due to the increase in the values of Kf. Heat is generated within the reactor by the exothermic chemical reaction, and this can be described by only the Frank-Kamenetskii number, Kf. Higher values of Kf generate more heat in the reactor and increase the temperature of the reactor as the heat loss by the side walls remains constant. As a consequence, the strength of vortices increases and the center of vortices moves upward. Also, the highest temperature increases and is inspissated above the peak of each waves where two opposite directed vortices are separated.

Fig. 8
figure 8

Changes in streamlines with increasing Frank-Kamenetskii number, Kf

Full size image
Fig. 9
figure 9

Changes in isotherms with increasing Frank-Kamenetskii number, Kf

Full size image

Changes in streamlines and isotherms with increasing Rayleigh number, Ra

Impacts of Rayleigh number, Ra, on fluid flows and temperature distributions are described by Figs. 10 and 11, respectively. The results reveal that the strength of vortices abruptly increases due to increase the values of Rayleigh number while the maximum temperature slightly decreases. It is important to mention that the Rayleigh number imparts the strength of convection. AS a result, the strength of vortices is higher for higher values of the Rayleigh number. Besides, more convection of heat occurred near the boundary walls cause more heat loss through the boundary walls to the neighboring environments. Consequently, the maximum temperature in the reactor is markedly decreased due to increase in the Rayleigh number.

Fig. 10
figure 10

Changes in streamlines for different values of the Rayleigh number, Ra

Full size image
Fig. 11
figure 11

Changes in isotherms with increasing the Rayleigh number, Ra

Full size image

Changes in streamlines and isotherms for different values of Forchheimer drag parameter, F

The impact of Forchheimer drag parameter, F, on the streamlines and temperature distribution is described by Figs. 12 and 13, respectively. The results elicit that the strength of vortices decreases with increasing values of the Forchheimer drag parameter while the maximum temperature increases. The Forchheimer drag parameter, F, represents a clogging force of order two in simulating the fluid flow in a porous medium. Increase of values F from 0.0 through 0.5 and 1.0 yields a potential improvement in Forchheimer drag which is the cause of deceleration of flow, that is, reduces the strength of vortices. It is anticipated that more chaotic effects are generated for larger values of F for the case of fluid flow in porous medium. Maximum temperature, however, is slightly increased with a increase in F.

Fig. 12
figure 12

Changes in streamlines with increasing the Forchheimer drag parameter, F

Full size image
Fig. 13
figure 13

Changes in isotherms with increasing the Forchheimer drag parameter, F

Full size image

Changes in streamlines and isotherms for variable heights of amplitude, A i

Impacts of variable heights of amplitude on streamlines and temperature distributions are illustrated by Figs. 14 and 15, respectively. Two layouts A1 = 0.1, A2 = 0.2, A3 = 0.3, A4 = 0.4 (Figs. 14a, 15a) and A1 = 0.1, A2 = 0.3, A3 = 0.2, A4 = 0.4 (Figs. 14b, 15b) and their opposite layouts (Figs. 14c, 15c); Figs. 14d and 15d, respectively, are considered. The results elicit that the strength of vortices depends upon the height of wave amplitude for the both layouts. The vortex of highest strength is produced right to the wave of the highest amplitude where it is contiguous to the right wall. On the other hand, the vortex of highest strength is produced left to the wave of highest amplitude where it is contiguous to the left wall. However, the maximum temperature occurs above the wave of the highest amplitude and stays nearly unchanged for any layouts of the height of amplitude. The thinnest vortex is produced right to the wave with the smallest amplitude when this wave is adjacent to the left wall of the reactor and left to the same wave when this wave is adjacent to the right wall of the reactor. On the other hand, the thickest vortex is produced to the opposite side of the same wave where the thinnest vortex is produced. Variable shapes in the vortex are happened due the variable heights of amplitude of the waves. The temperature above every wave is relatively higher with relatively higher amplitude of wave.

Fig. 14
figure 14

Changes in streamlines for variable heights of the amplitude, Ai

Full size image
Fig. 15
figure 15

Changes in isotherms for variable heights of the amplitude, Ai

Full size image

Improvement of Nusselt number with time, τ

Improvements of heat transfer are illustrated by the Nusselt number, Nuξ, and graphs at the lower and upper walls which are shown in Fig. 16. The results reveal that heat transfer gradually raises at the both walls as time flows and it reaches to a steady state when the least value of non-dimensional time is 2.0. No heat transfers are noticed at junctions of every two walls of reactor. Oscillating behaviors are shown in heat transfer characteristics at the both walls because of waviness in lower wall. And the amplitude of oscillation in Nusselt number graphs increases as time flows. At the upper wall, the highest heat transfer occurs at the point which is exactly above the every peaks of the lower wall and the lowest at the point which is exactly above the every trough of the lower wall. At the lower wall, the highest heat transfer occurs at the points which are neither the peak nor the trough of a wave, and they are the points lie between the peak and trough of the wave. And the lowest temperature occurs at the each peaks of the wave. However, the heat transfer rate at the wavy wall is relatively weaker than the plane wall. This happens because the highest temperature regions are created more close the upper wall than the lower wall.

Fig. 16
figure 16

Changes in the Nusselt number, Nuξ, at the a lower and b upper walls with time, τ

Full size image

Nusselt number variations with the change of Darcy number, Da

Impacts of Darcy number on Nusselt number graphs at lower and upper walls are shown in Fig. 17a, b, respectively. The results reveal that for a particular value of Darcy number, heat transfer is higher in upper wall than in lower wall. Also, at the upper wall the highest rate of heat transfer increases and the lowest decreases as the Darcy number increases. In other words, higher permeability of porous medium indicates higher the highest rate of heat transfer at the upper wall. The opposite characteristics in the highest heat transfer and the similar characteristics in the lowest heat transfer at the lower wall are noticed when the values of the Darcy number increases. There are three optimum values of the Nusselt number occur between every two peaks of the wavy lower wall where only optimum value of Nusselt number occurs between the portion of the upper wall above the same two peaks of the lower wall. The difference between these optimum values occurred in the lower wall decreases as the Darcy number increases. This happens because the temperature gradient near the lower wall decreases with increasing Darcy number.

Fig. 17
figure 17

Nusselt number, Nuξ, variations at the a lower and b upper walls with the change of Darcy number, Da

Full size image

Nusselt number variations with the change of Rayleigh number, Ra

Impacts of Rayleigh number on the Nusselt number at the lower and upper walls are shown in Fig. 18a, b, respectively. The results reveal that at the upper wall, the highest rate of heat transfer increases and the lowest decreases as the Rayleigh number increases. At the lower wall the highest rate of heat transfer decreases and also the lowest decreases as the Rayleigh number increases. Nusselt number curves are concave up at the portions of lower wall which are concave down (between x = 2 and x = 4; x = 5 and x = 7; x = 8 and x = 10). The concavity of these curves decreases with the increasing values of the Rayleigh number.

Fig. 18
figure 18

Changes in the Nusselt number, Nuξ, at the a lower and b upper walls for different values of Rayleigh number, Ra

Full size image

Nusselt number variations with the change of Frank-Kamenetskii number, K f

Impacts of Frank-Kamenetskii number on Nusselt number at lower and upper walls are displayed in Fig. 19a, b, respectively. The results reveal that Nusselt number graphs are oscillating at the both wavy and plane walls for every value of Frank-Kamenetskii number and these oscillations increase with increasing Kf. Also, heat transfer is greater in upper wall than in lower wall for any values of Kf. However, heat transfer at both walls raises with increasing Frank-Kamenetskii number. Also the difference between the highest and lowest heat transfer raises with increasing Kf, that is, the amplitude of the curves of Nusselt number increases as the values of Kf increase. This happens due to the more heat generation from the exothermic reaction when the value of Kf is higher. Fluid particles with high temperature flow very close to the reactor walls that causes high-temperature gradient at the reactor walls.

Fig. 19
figure 19

Changes in the Nusselt number, Nuξ, at the a lower and b upper walls for different values of Frank-Kamenetskii number, Kf

Full size image

Nusselt number variations with the change of Forchheimer drag parameter, F

Impacts of Forchheimer drag parameter on Nusselt number at lower and upper walls are shown in Fig. 20a, b, respectively. The results reveal that at upper wall, the highest heat transfer is noticed at the points that are exactly above the every peaks of lower wall and this rate slightly decreases with the increase of F. Besides, at lower wall the highest heat transfer is noticed at the points that are neither the peaks nor the trough of the wavy wall and this rate slightly increases with the increase of F.

Fig. 20
figure 20

Changes in the Nusselt number, Nuξ, at the a lower and b upper walls for different values of Forchheimer drag parameter, F

Full size image

Conclusions

Numerical simulation of 2D natural convection flow in a closed reactor containing complex wavy lower wall and filled with non-Darcy porous medium containing a heat generating fluid was carried out in this study. The dimensionless vorticity and energy equations which govern the fluid flow were solved in transformed coordinates by using the finite difference method. Employing dimensionless numbers and wave amplitude, the following conclusions were noticed.

  • Higher values of Frank-Kamenetskii number significantly improve the strength of vorticity and the highest temperature. Heat transfer rate can be significantly enhanced at the both walls by increasing the Frank-Kamenetskii number in the range 0.5 ≤ Kf ≤ 3.0.

  • Though the strength of vorticity considerably increases due to the increase in the Darcy number, the highest temperature slightly decreases. Similar behaviors in flow patterns and temperature distributions are observed due to changing the Rayleigh number like Darcy number.

  • Strength of vorticity can only be decelerated by increasing the Forchheimer drag parameter. Inconsiderable changes in maximum temperature and heat transfer at both walls are observed due to changing the Forchheimer drag parameter.

  • Strength of vorticity is higher within the vortex produced contiguous to the wave with highest amplitude. And the highest temperature always occurs at the above of this wave.

  • At the upper wall, the highest heat transfer rate is observed at the points that are exactly above the each peaks of wavy lower wall and this rate increases with the increase in every physical parameters introduced in our study except Forchheimer drag parameter.

  • At the lower wall, the highest heat transfer is observed at the points that are neither the peaks nor troughs of wavy lower wall and this rate increases due to increasing the Frank-Kamenetskii number and Forchheimer drag parameter and decreases due to increasing the Darcy and Rayleigh number.