Introduction

The study of buoyancy driven flow which formally known as natural convection within enclosures considering different geometrical shapes had been studied a lot due to their outstanding applications related to energy consumption and conversion such as food processing [1] sustainable building [2], solar air heaters [3], different shapes of solar collectors [4,5,6,7], materials processing [8], chemical reactions [9], cooling systems of nuclear chemical reactor [10,11,12], heat exchangers [13, 14], etc. Many of previous works were presented to study the phenomenon of natural convection within different shape of enclosures such as square [15,16,17], rectangular [18,19,20], triangular [21], trapezoidal [22,23,24], rhombus [25], circular [26], parallelogrammic [27], elliptical [28, 29], wavy [30] utilizing different numerical method such as finite difference, finite element and finite volume formulation. Based upon the previous publications, there is abundant in the studies regarding the simple shapes while there is gap regarding the more complex shapes such as wavy-shaped enclosure.

Some of the studies of natural convection within simple shapes of enclosures had been presented by numerous researchers. The convection within square enclosure had been investigated by Goodarzi et al. [31, 32]. Also, MHD effect on natural convection within square enclosure had been studied by Pordanjani et al. [33] using FORTRAN code based upon finite volume method. Goodarzi et al. [34] used finite volume formulation to study the influence of Rayleigh number along with the geometric aspect ratio on natural convection heat transfer as well as the entropy generation within nanofluid filled rectangular enclosure.

The multi-layers systems had been taken a lot of attention and studied recently by various researchers. Mehryan et al. [35] used finite element method to study the natural convection within a square enclosure filled by solid layer, porous medium layer in addition to the third nanofluid layer considering thermal non-equilibrium model. Hussain and Rahomey [36] studied the natural convection within square enclosure considering different inner bodies (circle, elliptical, triangular, rhombus and rectangular). The space between them and been filled by nanofluid in the right layer with porous medium saturated with the same nanofluid in the left layer.

The wavy enclosure had been studied by many researchers that used finite volume formulation considering the existence of internal heat generation [37]. The influence of wavy patterns on heat transfer in addition to the entropy generation of Cu-water nanofluid enclosure had been investigated via finite volume formulation by [38, 39]. The results showed that entropy generation and Nusselt number reduces with increasing of nanofluid loading. Also, the influence of different types of nanofluid such as TiO2-water, Cu-water and Al2O3-water on heat transfer thermal rate and the generation of entropy within complex wavy enclosure that had been simulated numerically using formulation based upon finite volume scheme [40]. The finite difference scheme used to study the natural convection as well as entropy generation in triangular-wavy porous enclosure under wide range of Darcy number in addition to Rayleigh number along with number of undulations [41]. The undulation increases the entropy generation in a comparison with that of without undulations. The influence of inclined magnetic field on inclined square-wavy enclosure filled by nanofluid considering heater in the corner had been investigated by Sheremet et al. [42] utilizing finite difference methodology. The CVFEM used to study the influence of magnetic field on complex wavy enclosure filled by Fe3O4-water nanofluid under wide range of dimensionless numbers such as Hartmann and Rayleigh numbers, nanofluid loading in addition to the amplitude of sinusoidal wall [43]. Finite difference method had been used by Reference [44] to examine the natural convection within wavy enclosure heated partially from its left sidewall and filled by nanofluid and porous medium. Alrowaili et al. [45] studied the natural convection in MHD wavy enclosure considering three different wavy walls (Out-Out, In-In, In-Out) surfaces using finite element method. The results showed that In-In wavy pattern reveals the lowest convection transport.

The existence of inner body within wavy enclosure had been received attention by Nemours researchers considering the influence of the shape of inner bodies, their size and position. Many researchers used finite element method in this specific subject to examine the influence of inner cylindrical body size on natural convection within wavy enclosure [46]. The results indicate that there is a critical value of inner cylinder diameter which if it increases beyond this value, a reduction in heat transfer will be noted. Also, a comparison between the wavy and circular enclosure had been done which leads to prove that the wavy shape reveals better heat transfer rate more than the circular shape. The influence of inner rotating solid cylinder immersed in a porous wavy enclosure heated partially studied from its bottom wall had been studied by Alsabery et al. [47]. The magnetic field on natural convection between circular cylinder in a wavy enclosure had been demonstrated by [48, 49]. The inner wavy body had been studied within wavy enclosure had been studied by [50, 51]. For example, Abdulkadhim et al. [51] studied the inner wavy body on natural convection within a nanofluid-porous wavy enclosure using local thermal equilibrium model. In another study where local thermal non-equilibrium model had been utilized to study the natural convection between inner cylindrical body immersed in a nanofluid-porous wavy enclosure [52]. Also, Dogonchi and Hashim [53] studied the natural convection within wavy enclosure filled by nanofluid considering the existence of inner rhombus body using CVFEM to examine the impact of inner body. It was obtained that for better heat transfer, the decreasing of the size of inner body is recommended. The inner square enclosure within wavy enclosure had been reported by [54]. The elliptical inner body within wavy enclosure under the influence of magnetic field had been examined by [55] by finite element method. The space had been filled by nanofluid and porous medium. Darcy–Forchheimer model had been used for treating the porous medium. Ganesh et al. [56] studied the fluid flow considering fins and inner circular body in a wavy enclosure filled by MWCNT and proposed new correlations of Nusselt number. Mourad et al. [57] studied the MHD free convection as well as entropy generation between Koch Snowflake located inside wavy enclosure filled by nanofluid and porous medium.

Recently, more attention had been given to the complex shapes of enclosure like U-shape [58], I-shaped [59], F-shape [60], E-shape [61]. For example, [62] used lattice Boltzmann scheme to study the magnetic field on natural convection within incinerator enclosure considering the inner hot block body.

As indicated above, these results had the application within the study of heat transfer in a shell and tube heat exchanger in industrial systems. Also, the Darcy–Brinkman model had been used for the modeling of fluid flow saturated with porous medium started by Darcy model. After that, two extensions of Darcy model had been proposed. The first model was due to Forchheimer that used for moderate and high Reynolds number by addition of nonlinear term to Darcy model. Unfortunately, this model still not able to predict the flow through high porosity and confined media. The second extension was introduced to Darcy model by Brinkman, which included a second-order viscous term with an equivalent viscosity for the porous medium. This modification allows the use of no-slip conditions on confining walls and gives accurate results at higher porosity values.

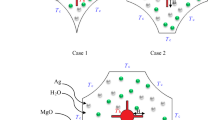
It can be seen that there are serious limitations on the combined enclosures which they are a combination of more than single enclosure. This case is the most case that closes to the real industrial applications. Besides, there are limitations in the I-shape enclosure studies in spite its applications in shell and tube heat exchangers thermal systems in the industrial applications [59, 63,64,65,66,67,68]. So, it can be seen that there is no published study focuses on studying of the natural convection within I-shaped along with wavy-walled enclosure with the existence of inner elliptical body considering the influence of four cases of different wavy patterns under inclined magnetic field when the enclosure filled by nanofluid and porous medium. In this way, the objective of the present work is to illustrate the influence of the wavy patterns under four different cases (In-In, In-Out, Out-In, Out-Out), magnetic field, distance between the wavy walls, number of undulations and position of the inner body on the fluid flow intensity along with the heat transfer.

Mathematical model

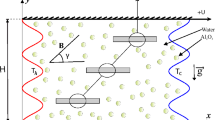
The natural convection in an I-shaped wavy enclosure filled by nanofluid in the right layer along with porous medium saturated with the same nanofluid in the left layer considering the existence of inner elliptical body had been solved via finite element method. Darcy–Brinkman model had been used to modeless the porous media considering the local thermal equilibrium approach between nanofluid and porous medium. The inclined magnetic field had been applied to show its impact on fluid flow and heat transfer. Four different cases of wavy patterns which they are (Case 1: In-In, Case 2: In–Out, Case 3: Out-In, Case 4: Out-Out) to show their impact on fluid flow and heat transfer will studied had been discussed in Fig. 1. The assumptions had been listed below:

  • The fluid flow is laminar along with incompressible under steady and two-dimensional

  • No slip conditions had been applied to all of the elliptical as well as the walls of the enclosure while the interface wall which separates the left and right layer had been considered to be permeable.

  • Local thermal equilibrium model had been applied between the porous medium and nanofluid

  • Darcy-Brinkman had been used to predict the fluid flow within the porous medium

  • Constant nanofluid thermophysical properties while Boussinesq approximation had been considered to treat the density in the body force of momentum equation

Fig. 1
figure 1

The physical model and the selected CFD cases of the present problem

Full size image

The governing equations for the present multi-layers systems had been written below in the dimensionless form for each layer:

  • For right region (nanofluid layer):

$${\text{Continuity}}$$
$$\frac{{\partial U}}{{\partial X}} + \frac{{\partial V}}{{\partial Y}} = 0$$
(1)
$${\text{X}} - {\text{momentum}}$$
$$\begin{aligned} U\frac{{\partial U}}{{\partial X}} + {\text{V}}\frac{{\partial V}}{{\partial Y}} = & - \frac{{\partial P}}{{\partial X}} + \frac{{\mu _{{{\text{nf}}}} }}{{\rho _{{{\text{nf}}}} \alpha _{{\text{f}}} }}\left( {\frac{{\partial ^{2} U}}{{\partial X^{2} }} + \frac{{\partial ^{2} U}}{{\partial Y^{2} }}} \right) \\ & + PrHa^{2} \left( {Vsin\left( \gamma \right)cos\left( \gamma \right) - Usin^{2} \left( \gamma \right)} \right) \\ \end{aligned}$$
(2)
$$Y - {\text{momentum }}$$
$$\begin{gathered} U\frac{\partial V}{{\partial X}} + {\text{V}}\frac{\partial V}{{\partial Y}} = - \frac{\partial P}{{\partial Y}} + \frac{{\mu_{{{\text{nf}}}} }}{{\rho_{{{\text{nf}}}} \alpha_{{\text{f}}} }}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{\left( {\rho \beta } \right)_{{{\text{nf}}}} }}{{\rho_{{\text{f}}} \beta_{{{\text{nf}}}} }}Ra\theta + Ha^{2} PrV\left( {Usin\left( \gamma \right)cos\left( \gamma \right) - Vcos^{2} \left( \gamma \right)} \right). \hfill \\ \end{gathered}$$
(3)
$${\text{Energy }}$$
$$U\frac{\partial \theta }{{\partial X}} + {\text{V}}\frac{\partial \theta }{{\partial Y}} = \frac{{\alpha_{{{\text{nf}}}} }}{{\alpha_{{\text{f}}} }}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right).$$
(4)

  • For left layer (Nanofluid-Porous medium layer):

$${\text{Continuity}}$$
$$\frac{\partial U}{{\partial X}} + \frac{\partial V}{{\partial Y}} = 0.$$
(5)
$$X - {\text{momentum }}$$
$$\begin{gathered} U\frac{\partial U}{{\partial X}} + {\text{V}}\frac{\partial V}{{\partial Y}} = - \varepsilon^{2} \frac{\partial P}{{\partial X}} + \varepsilon \frac{{\mu_{{{\text{nf}}}} }}{{\rho_{{{\text{nf}}}} \alpha_{{\text{f}}} }}\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \varepsilon^{2} \frac{{\mu_{{{\text{nf}}}} }}{{\rho_{{{\text{nf}}}} \alpha_{{\text{f}}} }}\frac{U}{Da} + PrHa^{2} \left( {Vsin\left( \gamma \right)cos\left( \gamma \right) - Usin^{2} \left( \gamma \right)} \right){ } \hfill \\ \end{gathered}$$
(6)
$$Y - {\text{momentum }}$$
$$\begin{gathered} U\frac{\partial V}{{\partial X}} + {\text{V}}\frac{\partial V}{{\partial Y}} = - \varepsilon^{2} \frac{\partial P}{{\partial Y}} + \varepsilon \frac{{\mu_{{{\text{nf}}}} }}{{\rho_{{{\text{nf}}}} \alpha_{{\text{f}}} }}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) - \varepsilon^{2} \frac{{\mu_{{{\text{nf}}}} }}{{\rho_{{{\text{nf}}}} \alpha_{{\text{f}}} }}\frac{V}{Da} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \varepsilon^{2} \frac{{\left( {\rho \beta } \right)_{{{\text{nf}}}} }}{{\rho_{{\text{f}}} \beta_{{{\text{nf}}}} }}Ra\theta + \varepsilon^{2} Ha^{2} PrV\left( {Usin\left( \gamma \right)cos\left( \gamma \right) - Vcos^{2} \left( \gamma \right)} \right). \hfill \\ \end{gathered}$$
(7)
$${\text{Energy}}$$
$$U\frac{\partial \theta }{{\partial X}} + {\text{V}}\frac{\partial \theta }{{\partial Y}} = \frac{{\alpha_{{{\text{eff}}}} }}{{\alpha_{{\text{f}}} }}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right)$$
(8)

The thermo-physical properties of the nanoparticle and water had been inserted in Table 1. Additionally, the following formula for determination the properties of nanofluid [69]:

$$\alpha_{{{\text{na}}}} = \frac{{k_{{{\text{na}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{nf}}}} }}$$
(9)
$$\rho_{{{\text{na}}}} = \left( {1 - \phi } \right)\rho_{{{\text{bf}}}} + \phi \rho_{{{\text{sp}}}}$$
(10)
$$\rho c_{{\text{p}}} = \left( {1 - \phi } \right)\left( {\rho c_{{\text{p}}} } \right)_{{{\text{bf}}}} + \phi \left( {\rho c_{{\text{p}}} } \right)_{{{\text{sp}}}}$$
(11)
$$\left( {\rho \beta } \right)_{{{\text{na}}}} = \left( {1 - \phi } \right)\left( {\rho \beta } \right)_{{{\text{bf}}}} + \phi \left( {\rho \beta } \right)_{{{\text{sp}}}}$$
(12)
Table 1 Thermophysical properties of nanofluid [75]
Full size table

The correlations for determination of dynamics viscosity and thermal conductivity are based upon [70,71,72,73]:

$$\mu_{{{\text{na}}}} = \frac{{\mu_{{{\text{bf}}}} }}{{\left( {1 - \phi } \right)^{2.5} }}$$
(13)
$$\frac{{k_{{{\text{na}}}} }}{{k_{{{\text{bf}}}} }} = \frac{{k_{{{\text{sp}}}} + 2k_{{{\text{bf}}}} - 2\phi \left( {k_{{{\text{bf}}}} - k_{{{\text{sp}}}} } \right)}}{{k_{{{\text{sp}}}} + 2k_{{{\text{bf}}}} + 2\phi \left( {k_{{{\text{bf}}}} - k_{{{\text{sp}}}} } \right)}}$$
(14)

The effective thermal conductivity as well as the coefficient of thermal diffusion can be obtained as indicated below:

$$k_{{{\text{eff}}}} = \left( {1 - \varepsilon } \right)k_{{{\text{sp}}}} + \varepsilon k_{{{\text{na}}}}$$
(15)
$$\alpha_{{{\text{eff}}}} = \frac{{k_{{{\text{eff}}}} }}{{\left( {\rho c_{p} } \right)_{{{\text{na}}}} }}$$
(16)

Additionally, electrical nanofluid conductivity can be obtained from the equation inserted below [74]:

$$\frac{{\sigma_{{{\text{na}}}} }}{{\sigma_{{{\text{bf}}}} }} = 1 + \frac{{3\left( {\frac{{\sigma_{{{\text{sp}}}} }}{{\sigma_{{{\text{bf}}}} }} - 1} \right)\phi }}{{\left( {\frac{{\sigma_{{{\text{sp}}}} }}{{\sigma_{{{\text{bf}}}} }} + 2} \right) - \left( {\frac{{\sigma_{{{\text{sp}}}} }}{{\sigma_{{{\text{bf}}}} }} - 1} \right)\phi }}$$
(17)

The thermal boundary conditions that had been applied into the permeable surfaces between the right layer (nanofluid) and the left layer (nanofluid and porous medium) may be defined as inserted below:

$$\theta_{{{\text{po}}}} = \theta_{{{\text{na}}}} , \frac{{\partial \theta_{{{\text{na}}}} }}{\partial X} = \frac{{K_{{{\text{eff}}}} }}{{K_{{{\text{na}}}} }}\frac{{\partial \theta_{{{\text{po}}}} }}{\partial X}, \Psi_{{{\text{po}}}} = \Psi_{{{\text{na}}}} , \frac{{\partial \Psi_{{{\text{na}}}} }}{\partial X} = \frac{{\partial \Psi_{{{\text{po}}}} }}{\partial X}, \Omega_{{{\text{po}}}} = \Omega_{{{\text{na}}}} ,$$
$$\frac{{\partial \Omega_{\text{na}} }}{\partial X} = \frac{{\partial \Omega_{\text{po}} }}{\partial X}, \mu_{\text{po}} \left( {\frac{{\partial U_{\text{po}} }}{\partial Y} + \frac{{\partial V_{\text{po}} }}{\partial X}} \right) = \mu_{\text{na}} \left( {\frac{{\partial U_{\text{na}} }}{\partial Y} + \frac{{\partial V_{\text{na}} }}{\partial X}} \right), P_{\text{po}} = P_{\text{na}} , \frac{{\partial P_{\text{po}} }}{\partial X} = \frac{{\partial P_{\text{na}} }}{\partial Y}$$

  • Boundary conditions

The boundary conditions had been as indicated below:

  • The left wall in addition to the inner elliptical body had been kept at isotherm hot temperature

  • The right wall had been kept at isotherm cold temperature

  • The top and bottom walls are adiabatic

  • Nusselt number

Nusselt number can be obtained as indicated below along the hot left side wall:

$$Nu_{{\text{L}}} = \frac{{k_{{{\text{eff}}}} }}{{k_{{\text{f}}} }}\frac{\partial \theta }{{\partial n}} , \overline{Nu} = \frac{1}{l}\mathop \int \limits_{0}^{l} Nu_{\text{L}} \left( \varphi \right)d\varphi$$
(18)

Mesh and Validation

The Galerkin finite element formulation used in the present work to solve the dimensionless partial differential equations. Besides, Newton–Raphson method had been utilized to treat the discretized the equations in each layer. The errors of the convergence criteria had been set to be equal to 10–7 for each variable.

$${\raise0.7ex\hbox{${\sum \left| {\xi_{{{\text{i}},{\text{j}}}}^{n + 1} - \xi_{{{\text{i}},{\text{j}}}}^{n} } \right|}$} \!\mathord{\left/ {\vphantom {{\sum \left| {\xi_{{{\text{i}},{\text{j}}}}^{n + 1} - \xi_{{{\text{i}},{\text{j}}}}^{n} } \right|} {\left| {\xi_{{{\text{i}},{\text{j}}}}^{n + 1} } \right|}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left| {\xi_{{{\text{i}},{\text{j}}}}^{n + 1} } \right|}$}} \le 10^{ - 7}$$
(19)

Numerical grid generation had been presented in Fig. 2a for different four wavy patterns. Also, mesh independent test had been presented in Fig. 2b. The flowchart of the numerical solution is presented in Fig. 2c. The present results based upon CFD code had been validated with significant researchers. Firstly, a validation with the case of inner circular cylinder located within square enclosure in terms of contours (Fig. 3) and Nusselt number (Fig. 4) of the previous results presented by Kim et al. [76]. Secondly, a validation in terms of streamlines of the present CFD code with Nikfar and Mahmoodi [77] had been presented in Fig. 5. Finally, another four validations had been presented in Table 2 in terms of Nusselt number. All of these comparisons reveal that the present CFD code is in a good agreement with the previous published works.

Fig. 2
figure 2figure 2

a Numerical grid generation for four cases of wavy patterns b Mesh independent test for Case 1 c Flowchart of the solution procedure

Full size image
Fig. 3
figure 3

A comparison between the present results and Kim et al. [76] in terms of streamlines and isotherms

Full size image
Fig. 4
figure 4

A comparison between the present results and Kim et al. [76] in terms of Nusselt number

Full size image
Fig. 5
figure 5

Validation of the present results with Nikfar and Mahmoodi [77]

Full size image
Table 2 Average absolute deviation of the present work with the previous published works
Full size table

The average absolute deviation (A.A.D) is an important indicator that reflects the accuracy of the numerical results and it is given by the formula inserted below:

Relative Deviation

$${\text{RD}}_{{\text{i}}} = \frac{{Nu_{{\text{present study}}} - Nu_{{\text{previous study}}} }}{{Nu_{{\text{present study}}} }}$$
(20)
$${\text{Average Absolute Deviation}}\,\,A.A.D. = \frac{{\mathop \sum \nolimits_{i = 1}^{i = n} \left| {RD_{{\text{i}}} } \right|}}{n}$$
(21)

The maximum absolute deviation (A.A.D.) of this study is 0.007 as indicated in Table 2.

Results and discussion

In this section, the influence of various physical in addition to the geometrical dimensionless parameters on fluid flow strength and heat transfer will be discussed in full-details.

The influence of number of undulations

In this section, the influence of number of undulations \((1\le N\le 4)\) considering four different cases of wavy patterns on streamlines and isotherms with and without magnetic field had been presented in Figs. 6–9.

Fig. 6
figure 6

Streamlines contours in the absence of magnetic field considering different cases of wavy patterns and different number of undulations at \(Ra={10}^{6}, Ha=0, Da=0.001, \phi =0.02,\gamma =45^\circ\)

Full size image
Fig. 7
figure 7

Isotherms contours in the absence of magnetic field considering different cases of wavy patterns and different number of undulations at \(Ra={10}^{6}, Ha=0, Da=0.001,\gamma =45^\circ , \phi =0.02\)

Full size image
Fig. 8
figure 8

Streamlines contours in the existence of the magnetic field considering different cases of wavy patterns and different number of undulations at \(Ra={10}^{6}, Ha=60, Da=0.001,\gamma =45^\circ , \phi =0.02\)

Full size image
Fig. 9
figure 9

Isotherm lines contours in the existence of the magnetic field considering different cases of wavy patterns and different number of undulations at \(Ra={10}^{6}, Ha=60, Da=0.001,\gamma =45^\circ , \phi =0.02\)

Full size image

Firstly, considering the absence of magnetic field to examine the influence of number of undulations along with the impact of wavy shape patterns on fluid flow strength and isotherms is presented via Figs. 6 and 7. So regarding the streamlines as shown in Fig. 6, it, may be noted that when the number of undulations is \((N=1)\), Case 3 reveals the highest strength in fluid flow as its maximum stream function \(\left|{\Psi }_{\mathrm{max}}\right|=34.229\) while Case 2 reveals the lowest fluid flow strength as its maximum stream function \(\left|{\Psi }_{\mathrm{max}}\right|=30.1766\) which make Case 3 (Out-In) better than Case 2 (In–Out) by 13.42%. The physical reason behind this is due to stenosis between the inner hot elliptical body and the right cold walls which increases the impact between the fluid molecules. It can be seen that increasing the number of undulations beyond (\(N=1)\) leads reduce the strength of the fluid flow because increases the wavy surfaces resist the free movement of the nanofluid. Additionally, the influence of wavy patterns is negligible. However, increasing the number of undulations leads to decreasing the fluid flow strength for most of the cases as the area of the wall increases which makes the resistance of internal wavy surfaces increases and resist the movement of nanofluid as its kinetic energy decreases. On the other side, the influences of number of undulations and wavy patterns on isotherms are demonstrated via Fig. 7. It can be seen that the hottest region is on the top area of the enclosure as it denser while the cold isotherms lines are on the lower side of the enclosure. Besides, it can be seen that the wavy patterns completely changes the distribution of isotherms lines in a comparison with the number of undulations.

Secondly, considering the existence of magnetic field to examine the influence of number of undulations along with the impact of wavy shape patterns on fluid flow strength and isotherms is presented via Figs. 8 and 9. It can be seen that the magnetic field at \((Ha=60)\), an obvious reduction for all of the cases of wavy patterns and number of undulations. For example, if a comparison had been made between the stream function with and without magnetic field i.e., at \(Ha=0\) and \(Ha=60\), respectively considering Case 1. It is an obvious the magnetic field reduces the stream function by 48.95%. So, it can be seen that the impact of magnetic field on the fluid flow strength is higher than the impact of wavy patterns and the number of undulations. It can be seen as illustrated in Fig. 9 that the magnetic field changes the distribution of isotherms obviously in a comparison in the case of absence of the magnetic field.

The influence of distance between wavy walls

In this section, the influence of distance between the wavy walls considering four different cases of wavy patterns with and without magnetic field had been presented via Figs. 10, 11, 12 and 13. The number of undulations is fixed to\((N=1)\). The selected distance between wavy walls had been taken as\(\left(B=0.8-1.4\right)\). Considering the absence of magnetic field and regarding Fig. 10, which show the strong relation between the distance between wavy walls and the wavy patterns on the stream function which reveals the strength of the fluid flow. It can be seen that at\(B=0.8\), the stream function values would be for Case 2 > Case 3 > Case 4 > Case 1. Also, regardless the wavy shape patterns, the fluid flow would be at its minimum values when the distance parameter between two wavy walls is at\(B=0.8\). In this way i.e., at \(B=0.8\), Case 1 reveals the lowest fluid flow strength with maximum stream function\(\left|{\Psi }_{\mathrm{max}}\right|=23.270\). This is noted by two inner cells that formed above and below the inner elliptical body because the distance between the elliptical body and wavy walls too small which break down the natural convection currents into two inner cells. Considering Case 1, it can be seen that increasing the distance parameter between two wavy walls into\(B=1.0\), leads to improve the fluid flow strength by 41.17%. However, further increasing of the wavy walls distance had negligible impact on the fluid flow strength for all cases of wavy patterns. The impact of the distance between the wavy walls on isotherms had been presented in Fig. 11 which clearly influences on their distribution.

Fig. 10
figure 10

Streamlines contours in the absence of the magnetic field considering different cases of wavy patterns and different distance between wavy patterns at \(Ra={10}^{6}, Ha=0, Da=0.001,\gamma =45^\circ , \phi =0.02\)

Full size image
Fig. 11
figure 11

Isotherm lines contours in the absence of the magnetic field considering different cases of wavy patterns and different distance between wavy patterns at \(Ra={10}^{6}, Ha=0, Da=0.001,\gamma =45^\circ , \phi =0.02\)

Full size image
Fig. 12
figure 12

Streamlines contours in the existence of the magnetic field considering different cases of wavy patterns and different distance between wavy patterns at \(Ra={10}^{6}, Ha=60, Da=0.001,\gamma =45^\circ , \phi =0.02\)

Full size image
Fig. 13
figure 13

Isotherm lines contours in the existence of the magnetic field considering different cases of wavy patterns and different distance between wavy patterns at \(Ra={10}^{6}, Ha=60, Da=0.001,\gamma =45^\circ , \phi =0.02\)

Full size image

The magnetic field taken into account to examine its effect on streamlines and isotherms had been shown via Figs. 12 and 13, respectively. The results when the magnetic field and the distance parameter between the wavy walls are crucial. W.r.t. Figure 12 there are many important point. Firstly, for all four cases of wavy walls, it can be seen that there is increasing in the fluid flow strength with increasing of the distance parameter between wavy walls but in a lower rate in a comparison with the case of the absence of magnetic field that had been illustrated in Fig. 10. For example, taking Case 1 it can be seen that increasing the distance between wavy walls from \((B=0.8)\) into \((B=1.4)\) leads to improve the fluid flow strength by 16.07%. The impact of magnetic field and the distance between wavy walls are presented in Fig. 13 which clearly change the distribution of isotherms in a comparison with the absence of magnetic field.

The influence of inner elliptical body position

The influence of inner elliptical body position on fluid flow and heat transfer had been presented in terms of streamlines and isotherms in Figs. 14 and 15, respectively, for four different cases of wavy walls patterns.

Fig. 14
figure 14

Streamlines contours considering different cases of wavy patterns under different position of inner elliptical body at \(Ra={10}^{6}, Ha=0, Da=0.001,\gamma =45^\circ , \phi =0.02\)

Full size image
Fig. 15
figure 15

Isotherm lines contours considering different cases of wavy patterns under different position of inner elliptical body at \(Ra={10}^{6}, Ha=0, Da=0.001,\gamma =45^\circ , \phi =0.02\)

Full size image

Firstly, w.r.t. Figure 14, it can be seen that for all wavy patterns that moving of the inner elliptical body from the center of the enclosure into the top region leads to an obvious reduction in the fluid flow strength while its movement into the lower region reveals better fluid flow strength. For example, considering Case 1 when the inner body located at the center \((\delta =0.8)\), the absolute maximum stream function \(\left|{\Psi }_{\mathrm{max}}\right|=32.852\) while when it moves into the top at \(\left(\delta =1.3\right)\), the absolute maximum stream function \(\left|{\Psi }_{\mathrm{max}}\right|=19.304\) while when it moves to the lower region at \(\left(\delta =0.3\right),\) the absolute maximum stream function \(\left|{\Psi }_{\mathrm{max}}\right|=34.019\). The same behavior is noted for other wavy patterns. However, the magnitude of fluid flow strength is different from wavy patterns to another patterns along with the position of inner elliptical body. For example, at \((\delta =0.8)\), the fluid flow strength of Case 3 > Case 1 > Case 4 > Case 2 while at \((\delta =0.3)\), Case 4 > Case 2 > Case 3 > Case 1. On the other hand at \((\delta =1.3)\), Case 4 > Case 2 > Case 1 > Case 3. It is also noted that two inner cells had been created above and below the inner elliptical body when it positioned at the center while these inner cells had been broken into on one inner cell located above the inner body when it moved toward the lower region while the inner cell formed below the inner body when the latter moved toward the top region.

Secondly, w.r.t. isotherms that had been presented in Fig. 15, it can be seen that when the inner body located in the bottom region more hot isotherms lines distributed among the area of the enclosure while location of the inner body in the top region leads to a lot of cold isotherms lines fills the enclosure area.

The influence of selected parameters on Nusselt number

The most important dimensionless parameter in heat transfer analysis which in the indicator of heat transfer bettering is Nusselt number. So, this section will explain this idea in-full details.

The influence of different wavy patterns along with the number of undulations in the absence of magnetic field i.e., at \(\left(Ha=0\right)\) had been shown in Fig. 16. It can be seen that increasing the number of undulations reduces the Nusselt number which turn in reduction of heat transfer. It can be seen that when the number of undulations is \((N=1)\), the Nusselt number of Case 3 > Case 1 > Case 4 > Case 2. This behavior of Nusselt number remains the same when the number of undulations increases into \((N=2)\). However, increasing the number of undulations into \((N=3)\), make Nusselt number of wavy shape of Case 1 had the highest value in a comparison with that of Case 2 which had the lowest Nusselt number. While increasing the number of undulations into \((N=4)\) leads to make Nusselt number of Case 3 had the highest value along with keeping Case 2 had the lowest Nusselt number. It can see that based upon the numerical observations that in the absence of magnetic field that the influence of number of undulations and the wavy patterns are high as illustrated in Fig. 16. While considering the influence of magnetic field at Fig. 17 which reveals that the impact of magnetic field is higher than the influence of wavy walls patterns. For example, when the number of undulations are \((N=3, 4)\), there are similar contribution on Nusselt number for Case 1 and Case 2. As well as approximately similar value of Nusselt number for Case 3 and Case 4. Additionally, Nusselt number of Case 3 and Case 4 are higher than that of Case 1 and Case 2.

Fig. 16
figure 16

Nusselt number variation w.r.t. number of undulations considering different cases of wavy patterns in the absence of magnetic field at \(Ra={10}^{6}, Da=0.001, Ha = 0, \gamma =45^\circ\)

Full size image
Fig. 17
figure 17

Nusselt number variation w.r.t. number of undulations considering different cases of wavy patterns in the existence of magnetic field at \(Ra={10}^{6}, Da=0.001, Ha = 60, \gamma =45^\circ\)

Full size image

The influence of the distance between the wavy walls had been shown via Figs. 18 and 19 without and with magnetic field, respectively. Considering Fig. 18, it can be seen that increasing the distance between wavy walls for all four cases of the wavy patterns leads to enhance the heat transfer by increasing the dimensionless value of Nusselt number. For example, for Case 1 increasing the distance from \(B=0.8\) into \(B=1.4\) leads to increase Nusselt number by 31.67%. On the other hands when the magnetic field effect taken into account as shown in Fig. 19, it can be seen that still increasing the distance between the wavy patterns enhance Nusselt number but lower than that in the absence of magnetic field. It is worthy to mention that in the existence of the magnetic field, Case 4 had the lowest Nusselt number in a comparison with the other cases of wavy patterns.

Fig. 18
figure 18

Nusselt number variation w.r.t. distance between wavy walls considering different cases of wavy patterns in the absence of magnetic field at \(Ra={10}^{6}, Da=0.001, Ha = 0\)

Full size image
Fig. 19
figure 19

Nusselt number variation w.r.t. distance between wavy walls considering different cases of wavy patterns in the existence of magnetic field at \(Ra={10}^{6}, Da=0.001, Ha = 60, \gamma =45^\circ\)

Full size image

The impact of the position of inner body is illustrated via Figs. 20 and 21 without and with the magnetic field, respectively. Three different positions of inner elliptical body had been selected which they are at the center \((\delta =0.8)\), at the top region \((\delta =1.3)\), at the bottom region \((\delta =0.3)\). It can be seen for Case 1 as shown in Fig. 20 that when the inner elliptical body moves from the center into the top, Nusselt number decreases from \(Nu=14.8685\) into \(Nu=7.5926\) while movement the inner elliptical body from the center top into the bottom leads to enhance the heat transfer rate by increasing of Nusselt number about 67.70%. In this way, it can be seen that the similar trends is observed for all wavy patterns. Also, in Fig. 21 which show the behavior of Nusselt number with the position of inner elliptical body inner the influence of magnetic field. It may be noted that the magnetic field make a notice difference and the influence of wavy shape patterns more strong in a comparison of that in the absence of magnetic field.

Fig. 20
figure 20

Nusselt number variation w.r.t. vertical position of the elliptical inner body considering different cases of wavy patterns in the absence of magnetic field at \(Ra={10}^{6}, Da=0.001, Ha = 0\)

Full size image
Fig. 21
figure 21

Nusselt number variation w.r.t. vertical position of the elliptical inner body considering different cases of wavy patterns in the existence of magnetic field at \(Ra={10}^{6}, Da=0.001, Ha = 60, \gamma =45^\circ\)

Full size image

Conclusions

The present work examines numerically the influence of wavy patterns on fluid flows and heat transfer considering the existence of inner elliptical body under the impact of magnetic field. The major results can be summarized as indicated below:

  • The influence of wavy shape patterns is higher when the number of undulations \((N=1)\).

  • Case 3 is highest than Case 2 by 13.42% in terms of fluid flow strength.

  • Increasing Hartmann number from \(Ha=0\) into \(Ha=60\) leads to an obvious reduction in the fluid flow by 48.95%.

  • Case 4 along with locating the inner elliptical body in the bottom of the enclosure reveals the best strength in the fluid flow.

  • For bettering the thermal rate of heat transfer, it is recommended to move the inner elliptical body downwards for all cases of wavy patterns.

  • Increasing the number of undulations along with Hartmann number reduces the heat transfer rate.

  • Nusselt number improved with increasing the parameter of the distance between the wavy walls