Introduction

The natural convection within confined enclosures of different shapes filled partly by fluid and partly with porous medium saturated by the same fluids had been take a lot of numerical and experimental investigation for its importance applications such as heat exchangers, fuel cell, solar collectors, cooling of electronic equipment in addition to the nuclear thermal systems, drying processes, fluid flow of geophysics, pollution of ground water, etc. There are serious problem in augmentation of the heat transfer using of the traditional fluids which is due to low thermal conductivities so the researchers introduced the concepts of nanofluid which is a promoting techniques in the augmentation of heat transfer. Besides, corrugating the wall of the enclosure is recommending technique in improving the thermal performance of the system. So, here a full—description to the most important studies that covers these techniques will be reviewed comprehensively.

The nanofluid filled regular and simple shapes of enclosure had been studied abundantly. For example, Ghasemi et al. (2011) studied the influence of magneto-hydrodynamics applied uniformly in a horizontal direction on natural convection in a square enclosure. They examined the influence of Hartmann number, Rayleigh number in addition to the nanofluid loading on heat transfer rate and behavior of fluid flows. The results indicate that there would be an improving in the rate of heat transfer as the Hartmann number decreases along with increasing of Rayleigh number. While the heat transfer may be increases or decreases when the nanofluid is adding will be highly influenced by Rayleigh and Hartmann number. Izadi et al. (2014) utilized finite volume method to examine the influence of different heat source and sink position on the mixed convection within a square enclosure considering Al2O3-water nanofluid filled the space. Control volume finite element formulation had been utilized by Bouhalleb and Abbassi (2015) to analyze the transient thermogravitional flow in an inclined rectangular enclosure. It heated sinusoidally from its left sidewall while the right sidewall kept at cold temperature. The influence of aspect ratio, angle of enclosure inclination in addition to the nanofluid loading had been discussed in full-details. They found that increasing or decreasing the aspect ratio leads to different behaviors on Nusselt number which the latter increases as nanofluid loading increases. Izadi (2020) and Izadi et al. (2020) studied the natural convection within isosceles triangular enclosure filled by Al2O3–Cu/water hybrid nanofluid with porous medium. The two-phase mixture approach and Darcy–Brinkman model had been used to simulate the nanofluid and porous medium, respectively. The natural convection within triangular enclosure considering the Brownian motion along with magnetic field had been studied by Ghasemi and Aminossadati (2010), Mahmoudi et al. (2012), Ghasemi and Aminossadati (2010) and Mahmoudi et al. (2012). Also, Saleh et al. (2011) examined the problem of natural convection within trapezoidal enclosure filled by Al2O3–water and Cu–water nanofluids using finite difference method. They developed new correlations of Nusselt number. The results showed that Cu–water nanofluid is recommended in heat transfer more than Al2O3. Mehryan et al. (2020a, b) studied the natural convection within a trapezoidal enclosure with flexible partition using finite element formulation. It had been indicated that the best heat transfer rate was at zero inclination angle and reduces with increasing the inclination angle of the trapezoidal enclosure. Hussein & Mustafa (2017) studied the thermally driven flow in a parallelogrammic enclosure open from its top wall and filled with Cu–water nanofluid using finite volume method. The enclosure is heated partially from its bottom wall while the tilted wall is maintained at cold temperature. The selected dimensionless parameters of this study are Rayleigh number, position of the heat source, inclination angle of the two cold walls of the enclosure in addition to the nanofluid concentration. The results show that increasing nanofluid loading along with the dimensionless value of Rayleigh number improves noticeably the Nusselt number. Also, for better heat transfer it is better to locate the heat source closed to the left sidewall with tilting angle of \(60^\circ\).

The nanofluid filled complex shapes of enclosure investigated by many researchers. For example, Cho et al. (2013) utilized finite volume formulation to examine the influence of different types of nanofluids particles such as Cu, Al2O3 and TiO2 filled complex wavy enclosure on natural convection as well as entropy generation. Additionally, the authors investigated the influence of wavy surface amplitude and length in addition to Rayleigh number on fluid flow and heat transfer. The results indicate that Cu nanoparticle reveals the best performance in terms of heat transfer and lowest generation of entropy. Sadeghi et al. (2020) studied the natural convection in a novel-complex enclosure shape filled with Al2O3 nanofluid with internal heat generation along with inclined magnetic field using finite element scheme. The enclosure includes trapezoidal heater and wavy cold wall. The influence of Hartmann and Rayleigh numbers, concentration of nanoparticle and its shapes, trapezoidal heater location and parameter of internal heat generation on fluid flow and heat transfer were examined. The results show that the impact of heat generation at low value of Rayleigh number was so significant. Also, applying of horizontal magnetic field can suppress the natural convection heat transfer.

The nanofluid saturated with porous medium studied a lot using various models like LTE, LTNE, Darcy model, Darcy–Brinkmann model etc. For example, Ahmed and Rashed (2019) illustrated the MHD buoyancy driven flow in a wavy enclosure filled by nanofluid and porous medium along with internal heat generation using finite difference approach. Izadi et al. (2019) used finite element method to study the non-uniform magnetic field applied from two semi-circular hot cylinders. The gap filled by hybrid nanofluid and porous medium considering the local thermal non-equilibrium model under various selected parameters like the magnetic source power ratio, coefficient of porosity, Hartmann and Rayleigh number. Kadhim et al. (2020) studied the natural convection in a wavy enclosure using finite element method. The enclosure was filled by two different layers, the right layer filled by Cu–Al2O3 hybrid nanofluid while the left layer filled by porous medium saturated by the same hybrid nanofluid. Darcy–Brinkmann model had been used to model the porous layer. The researchers examined the influence of Rayleigh number, porous layer width, Darcy number, number of undulations, inclination angle and the nanofluid loading. The results showed that using of hubrid nanofluid reveals better augmentation in Nusselt number in a comparison with Al2O3–water nanofluid. Besides, Rayleigh and Darcy number were strongly influenced on the Nusselt number. Mehryan et al. (2020a, b) used LTNE to simulate the natural convection within Ag–MgO/water nanofluid in porous square enclosure. The porous medium had been treated via Darcy model.

The existence of inner body considering various shapes within different shapes of enclosure had been studied considering the influence of inner body size, position, number and shapes etc. For example, the influence of inner body locations that moved in vertical, horizontal and diagonal direction had been studied by Abdulkadhim (2019), Hussain and Hussein (2010), Kim et al. (2008), Lee et al. (2010) and Majdi et al. (2019). Also, Yoon et al. (2012) studied utilizing immersed boundary scheme which is based upon formulation of finite volume approach the natural convection between two inner circular cylinder immersed in a square enclosure considering the influence of various size and Rayleigh number. The results showed that reduction of the size of the inner circular cylinders leads to increasing of the dependency on Rayleigh number. Kefayati and Tang (2018) used lattice Boltzmann scheme to study the influence of one cylinder of circular and elliptical shape on natural convection within square enclosure under various inclination angle. They examined the influence of various inner body position and size under diverse Rayleigh number values. Roy (2018) studied using finite difference method the natural convection between three different shapes of inner shapes (circular, elliptical and rectangular) immersed in a nanofluid square enclosure. The results indicate that using of inner circular cylinder reveals better rate in thermal heat transfer more than rectangular and elliptical shapes. Wang et al. (2021) studied the transient convection considering various inner circular body positions moved in the vertical direction immersed in square enclosure. The results indicate that the inner body position is highly affects on the fluid flow behavior and heat transfer field. Bhowmick et al. (2020) studied the influence of magnetic field on entropy generation and natural convection of square enclosure with pair of circular cylinders located immersed in a porous medium. They illustrate the impact of distance between the inner cylinders along with Darcy, Hartmann and Rayleigh number. The results displayed that the thermal rate of heat transfer augmented as there was an increasing in the dimensionless distance between the inner circular cylinders. Yan et al. (2020) used finite element method to study the natural convection within square enclosure filled by nanofluid and porous medium considering inner hot elliptical body under inclined magnetic field. Alsabery et al. (2020) studied the location and the size of inner solid body of squared shape on the rate of heat transfer utilizing two-phase nanofluid model. Shehzad et al. (2021) studied the influence of different inner hot and cold pipes with a fin attached to them on the natural convection within square heat exchangers.

The natural convection within more complex shapes like C-shape, H-shape, U-shape and especially I-shaped had been received little attention despite their importance in engineering applications (Armaghani et al. 2020; Keramat et al. 2020; Ma et al. 2019a, b, 2020; Malekpour et al. 2018; Mohebbi et al. 2017). For example, Armaghani et al. (2020) studied the influence of inclined magnetic field along with heat generation in I-shaped enclosure filled by nanofluid and porous medium. Also, Ma et al. (2020) studied the inclined magnetic field within I-shaped enclosure with multi-square inner bodies considering nanofluid filled the gap.

Thus, it can be seen and according to the best authors’ knowledge that there are serious limitations in the complex shapes of enclosures especially the I-shapes enclosure despite its applications in the shell and tube heat exchangers industry. The I-shaped enclosure is a combination of more than one enclosure which is the real case in the industrial engineering projects. Besides, there is no study up to date that discuss the inclined magnetic field in I-shaped enclosure with wavy walls filled by multi-layers of nanofluid and porous medium considering four different cases of inner bodies (circular, square, rhombus and triangular) using finite element method. In this way, this paper will be the first attempt to solve this problem under wide range of Rayleigh number, Darcy number, Hartmann number in addition to the influence of different thermal management of the inner bodies.

Mathematical model

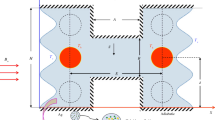
The computational CFD model used in the present study will be presented here considering many assumptions. Firstly, the physical model is presented in Fig. 1 which consists of a three-dimensional view for the enclosure with the internal circular bodies along with the two-dimensional view of the enclosure that contain the two layers. The right layer consists of nanofluid while the left layer consists of porous medium saturated with the same nanofluid. Four different cases of inner body shapes had been included in the present work. Case 1, 2, 3 and 4 represent circular, square, rhombus and triangular shapes, respectively. With respect to the thermal boundary conditions, the top and bottom wall of the enclosure are fully insulated. The right and left wall included the wavy, horizontal and the vertical parts which form the I-shape are kept at isotherm hot and cold temperature, respectively. Also, different boundary conditions of the inner body had been selected in order to examine the influence of the inner body conditions and its position on the heat transfer and fluid flows.

Fig. 1
figure 1

The influence of thermophysical properties

Full size image

Governing equations

The governing equations of the nanofluid and porous medium under the assumptions inserted below;

  • The fluid flow of the two layers within the enclosure are considered to be laminar,

  • The left layer which consists of the porous medium had been modeled via Darcy–Brinkman model.

  • Local thermal equilibrium between the each layer had been considered

  • The influence of thermal radiation and the internal heat generation, Soret and Dufour are ignoring.

  • Only the density is considered to be changed in the momentum equations and treated via Boussinesq approximation while the thermophysical nanofluid properties are assumed to be constant.

In this way and based upon the above mentioned conditions, the final form of the governing equations may be written as indicated below (Al-Zamily 2014; Hussain and Rahomey 2019; Sheikholeslami et al. 2013);

$$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0$$
(1)
$$X-momentum$$
$$U\frac{\partial U}{\partial X}+\mathrm{V}\frac{\partial V}{\partial Y}=-{C}_{1}\frac{\partial P}{\partial X}+{C}_{2}\frac{{\mu }_{na}}{{\rho }_{na}{\alpha }_{bf}}\left(\frac{{\partial }^{2}U}{\partial {X}^{2}}+\frac{{\partial }^{2}U}{\partial {Y}^{2}}\right)-{C}_{3}\frac{{\mu }_{na}}{{\rho }_{na}{\alpha }_{bf}}\frac{U}{Da}+{C}_{1}Pr{Ha}^{2}\left(Vsin\left(\gamma \right)cos\left(\gamma \right)-U{sin}^{2}\left(\gamma \right)\right)$$
(2)
$$Y-momentum$$
$$U\frac{\partial V}{\partial X}+\mathrm{V}\frac{\partial V}{\partial Y}=-{C}_{1}\frac{\partial P}{\partial Y}+{C}_{2}\frac{{\mu }_{na}}{{\rho }_{na}{\alpha }_{bf}}\left(\frac{{\partial }^{2}V}{\partial {X}^{2}}+\frac{{\partial }^{2}V}{\partial {Y}^{2}}\right)-{C}_{3}\frac{{\mu }_{nf}}{{\rho }_{nf}{\alpha }_{f}}\frac{V}{Da}+{C}_{1}\frac{{\left(\rho \beta \right)}_{na}}{{\rho }_{bf}{\beta }_{na}}Ra\theta +{C}_{1}{Ha}^{2}Pr\left(Usin\left(\gamma \right)cos\left(\gamma \right)-V{cos}^{2}\left(\gamma \right)\right)$$
(3)
$$Energy$$
$$U\frac{\partial \theta }{\partial X}+\mathrm{V}\frac{\partial \theta }{\partial Y}={C}_{4}\left(\frac{{\partial }^{2}\theta }{\partial {X}^{2}}+\frac{{\partial }^{2}\theta }{\partial {Y}^{2}}\right)$$
(4)

Considering the following dimensionless parameter

$$\mathrm{X}=\frac{\mathrm{x}}{\mathrm{L}}, \mathrm{Y}=\frac{\mathrm{y}}{\mathrm{L}},\mathrm{ U}=\frac{\mathrm{uL}}{{\mathrm{\alpha }}_{\mathrm{f}}},\mathrm{ V}=\frac{\mathrm{vL}}{{\mathrm{\alpha }}_{\mathrm{f}}},\mathrm{ P}=\frac{{\mathrm{pL}}^{2}}{{\uprho }_{\mathrm{nf}}{\mathrm{\alpha }}_{\mathrm{f}}^{2}},\uptheta =\frac{\mathrm{T}-{\mathrm{T}}_{\mathrm{c}}}{{\mathrm{T}}_{\mathrm{h}}-{\mathrm{T}}_{\mathrm{c}}},\mathrm{ Ra}=\frac{\mathrm{g}{{\upbeta }_{\mathrm{f}}\mathrm{L}}^{3}\Delta \mathrm{T}}{{\upnu }_{\mathrm{f}}{\mathrm{\alpha }}_{\mathrm{f}}},\mathrm{ Da}=\frac{{k}_{p}}{{L}^{2}},\mathrm{ Pr}=\frac{{\upnu }_{\mathrm{f}}}{{\mathrm{\alpha }}_{\mathrm{f}}}$$
(5)

The coefficients in the Eqs. 2–4 are as indicated below;

Right Layer (Nanofluid Layer): \({C}_{1}=1, {C}_{2}=1,{C}_{3}=0 \, and \, {C}_{4}={\alpha }_{nf}/{\alpha }_{f}\)

Left Layer (Nano-Porous Layer): \({C}_{1}={\varepsilon }^{2}, {C}_{2}=\varepsilon ,{C}_{3}={\varepsilon }^{2} \, and \, {C}_{4}={\alpha }_{eff}/{\alpha }_{f}\)

The fluid flow distributions within the wavy enclosure are represented in term of stream function as indicated below;

$$U=\frac{\partial\Psi }{\partial Y} , V=-\frac{\partial\Psi }{\partial X}$$
(6)
$${U}_{na}=\frac{\partial {\Psi }_{na}}{\partial Y} , {V}_{na}=\frac{\partial {\Psi }_{na}}{\partial X}$$
(7)

Which leads to the dimensionless equation;

$$\frac{{\partial }^{2}\Psi }{\partial {X}^{2}}+\frac{{\partial }^{2}\Psi }{\partial {Y}^{2}}=\frac{\partial \mathrm{U}}{\partial Y}-\frac{\partial \mathrm{V}}{\partial X}$$
(8)
$$\frac{{\partial }^{2}{\Psi }_{na}}{\partial {X}^{2}}+\frac{{\partial }^{2}{\Psi }_{na}}{\partial {Y}^{2}}=\frac{\partial {\mathrm{U}}_{na}}{\partial Y}-\frac{\partial {\mathrm{V}}_{na}}{\partial X}$$
(9)

The thermophysical nanofluid properties are inserted below (Table 1);

Table 1 Thermo-physical properties of water and nanoparticles (Al2O3) at T = 25 °C (Motlagh and Soltanipour 2017)
Full size table
$${\alpha }_{na}=\frac{{k}_{na}}{{\left(\rho {C}_{p}\right)}_{na}}$$
(10)
$${\rho }_{na}=\left(1-\phi \right){\rho }_{bf}+\phi {\rho }_{sp}$$
(11)
$${\left(\rho {c}_{p}\right)}_{na}=\left(1-\phi \right){\left(\rho {c}_{p}\right)}_{bf}+\phi {\left(\rho {c}_{p}\right)}_{sp}$$
(12)
$${\left(\rho \beta \right)}_{na}=\left(1-\phi \right){\left(\rho \beta \right)}_{bf}+\phi {\left(\rho \beta \right)}_{sp}$$
(13)

As regards the dynamic viscosity, Brinkman correlations have been taken into account in the numerical simulation (Chamkha and Ismael 2013; Garoosi et al. 2015; Oztop and Abu-Nada 2008)

$${\mu }_{na}=\frac{{\mu }_{bf}}{{\left(1-\phi \right)}^{2.5}}$$
(14)

Maxwell approach considered for thermal conductivity (Abdelmalek et al. 2020; Bessaïh et al. 2017; Sheremet et al. 2016)

$$\frac{{k}_{nf}}{{k}_{bf}}=\frac{{k}_{sp}+2{k}_{bf}-2\phi \left({k}_{bf}-{k}_{sp}\right)}{\left({k}_{sp}+2{k}_{bf}\right)+\phi \left({k}_{bf}-{k}_{sp}\right)}$$
(15)

The electrical conductivity of the mixture of nanofluid are expressed as indicated below;

$$\frac{{\sigma }_{na}}{{\sigma }_{bf}}=1+\frac{3\left(\frac{{\sigma }_{sp}}{{\sigma }_{bf}}-1\right)\phi }{\left(\frac{{\sigma }_{sp}}{{\sigma }_{bf}}+2\right)-\left(\frac{{\sigma }_{sp}}{{\sigma }_{bf}}-1\right)\phi }$$
(16)

The thermal diffusivity \({\alpha }_{eff}\) in addition to the thermal conductivity effectiveness \({k}_{eff}\) are given by:

$${\alpha }_{eff}=\frac{{k}_{eff}}{{\left(\rho {c}_{p}\right)}_{na}}$$
(17)
$${k}_{eff}=\left(1-\varepsilon \right){k}_{sp}+\varepsilon {k}_{na}$$
(18)

Boundary conditions

The boundary conditions in this study are presented in shown in Fig. 1 and indicated below;

The left walls including the horizontal, vertical and wavy parts are kept at hot temperature:

$${T}_{h}=1, U=V=0$$

The right wall including the horizontal, vertical and wavy parts are kept at cold temperature:

$${T}_{c}=0, U=V=0$$

The top and bottom walls are insulated \(\frac{\partial T}{\partial Y}=0, U=V=0\)

The inner bodies are located at hot and cold temperature as indicated in the results.

Also, with respect to the permeable surface’s boundary conditions that separate the nanofluid and porous medium may be defined as indicated below;

$${\theta }_{po}={\theta }_{na}, \frac{\partial {\theta }_{na}}{\partial X}=\frac{{K}_{eff}}{{K}_{na}}\frac{\partial {\theta }_{po}}{\partial X}, {\Psi }_{po}={\Psi }_{na},\frac{\partial {\Psi }_{po}}{\partial X}=\frac{\partial {\Psi }_{na}}{\partial X}, {\Omega }_{po}={\Omega }_{na}, \frac{\partial {\Omega }_{na}}{\partial X}=\frac{\partial {\Omega }_{po}}{\partial X}, {\mu }_{po}\left(\frac{\partial {\mathrm{U}}_{po}}{\partial Y}+\frac{\partial {\mathrm{V}}_{po}}{\partial X}\right)={\mu }_{na}\left(\frac{\partial {\mathrm{U}}_{na}}{\partial Y}+\frac{\partial {\mathrm{V}}_{na}}{\partial X}\right), {\mathrm{P}}_{po}={\mathrm{P}}_{na}, \frac{\partial {\mathrm{P}}_{na}}{\partial X}=\frac{\partial {\mathrm{P}}_{po}}{\partial Y}$$

Nusset number

Nusselt number had been determined on the inner hot body from the equation inserted below;

$${Nu}_{L}=\frac{{k}_{nf}}{{k}_{f}}\frac{\partial \theta }{\partial n}, \overline{Nu }=\frac{1}{l}{\int }_{0}^{l}{Nu}_{L}\left(\varphi \right)d\varphi$$
(19)

With respect to the determination of total Nusselt number for the case of multi-inner hot bodies, it had been predicted by summing all of the Nusselt number at each hot inner body.

Validation and mesh independent study

In order to check the accuracy of the present numerical CFD results, validations with significant researchers are presented. First validation is with Malekpour et al. (2018) results in terms of Nusselt number for I-shaped enclosure filled with nanofluid along with applied magnetic field uniformly in the horizontal direction. The results are presented in Table 2 and graphed in Fig. 2 under wide range of Rayleigh and Hartmann numbers.

Table 2 Validation of the present work with Malekpour et al. (2018)
Full size table
Fig. 2
figure 2

Validation of the present work with Malekpour and Karimi Malekpour et al. (2018) in terms of Nusselt number at \(\varphi =0.04, Ha=0\)

Full size image

It can be seen that the present good agreement with their results. Besides that two different cases of validation in terms of streamlines and isotherms had been presented in Figs. 3 and 4. The first validation presented, in Fig. 3, with Ma et al. (2020) for I-shaped nanofluid enclosure with multi-inner body of square shape considering applied magnetic field under \(\phi =0, Ha=0, Ra={10}^{6}\). Also, in Fig. 4, A validation with results found by Hussain and Rahomey (2019) for inner circular body embedded in a square enclosure filled partially by nanofluid and partially by porous medium with the same nanofluid at \(Ra={10}^{6}, Da={10}^{-3},\phi =0\) was presented. Again it can be seen that there is excellence agreement with each study.

Fig. 3
figure 3

Validation in terms of streamlines and isotherms with Ma et al. Ma et al. (2020)

Full size image
Fig. 4
figure 4

Validation in terms of streamlines and isotherms with Hussain and Rahomey Hussain & Rahomey (2019)

Full size image

With respect to the numerical grid generation and independent study that presented in Fig. 5. Due to the CPU memory, various number of numerical element generation had been test for high Rayleigh number to check the error that may occur at \(Ra={10}^{6},Da={10}^{-3},\phi =0.02, Ha=20\). It can be seen that when the number of element are 28,146 leads to the same Nusselt number at number of element are 32,234 so there is no necessity in increasing the number of elements and the time of numerical solution. That’s why we use, in our all calculations, 28,146 elements.

Fig. 5
figure 5

Mesh generation for the enclosure (top image) and mesh independent study in terms of Nusselt number (bottom image)

Full size image

Results and discussion

The present section discuss the numerical results of natural convection heat transfer within I-shaped wavy-walled enclosure filled by nanofluid saturated with porous medium (left layer) and the same nanofluid (right layer) under wide range of Rayleigh number \(({10}^{4}\le Ra\le {10}^{6})\), Darcy number \(({10}^{-5}\le Da\le {10}^{-1})\), Hartmann number \((0\le Ha\le 60)\) considering three different positions of the hot inner body along with four different cases of the shapes of inner body (circle, square, rhombus and triangle) for three different number of the hot source inner body \(\left(1\le No\le 3\right)\) and three different positions \(\left(0.3\le Y\le 1.3\right)\). The influence of these mentioned dimensionless parameters on heat transfer and fluid flow are presented in terms of streamlines, isotherms in addition to Nusselt number.

The influence of dimensionless numbers on fluid flow and heat transfer

Since many dimensionless parameters under investigated, we start by illustrating the influence of Rayleigh, Darcy and Hartmann numbers along with four different shapes of inner body on fluid flow and heat transfer. First of all, the influence of Rayleigh number and the inner body shape is presented in terms of streamlines and isotherms in Figs. 6a, b, respectively.

Fig. 6
figure 6

a Streamlines contours considering different inner hot shapes under various Rayleigh number at \(Da=0.001, \varphi =0.02, Ha=0\). b Isotherms contours considering different inner hot shapes under various Rayleigh number at \(Da=0.001, \varphi =0.02, Ha=0\)

Full size image

With respect to Fig. 6a, at low Rayleigh number \((Ra={10}^{4})\), where the power intensity of natural convection is low and the conductive mode of heat transfer is the dominant mode, it can be seen that there are just two inner vortices formed closed to each shape of the inner body on the nanofluid region (right layer) while the streamlines on the nano-porous region (left layer) does not contain any circulation which reflect the lower strength of the fluid flow. This is due to the porous medium which plays as additional resistance to the fluid flow in addition to the low Rayleigh number. This can be observed from the low stream function value which is influenced by the inner body shape. For example, the strength of fluid flow for \(\mathrm{Case }4>Case 3>\mathrm{Case }2>Case 1\) which makes the triangular shape (Case 4) recorded the better case in terms of the best fluid flow strength while the inner circular body gives the lowest strength of the fluid flow.

With increasing the Rayleigh number into \(\left(Ra={10}^{6}\right),\) which reflect the changing of the heat transfer mode from the conduction mode into the thermogravitational (natural convection) mode leading to increasing the fluid flow strength for each case of the inner body shape. For example, the strength for \(\mathrm{Case }3>Case 1>\mathrm{Case }2>Case 4\) which makes the triangular shape reveals the lowest case in terms of fluid flow strength while the rhombus shape give the best fluid flow strength. It is worthy to mention that increasing the Rayleigh number helps more nanofluid to penetrate from the right layer into the left layer due to increasing the permeability of the porous medium which leads to the formation of the inner vortices in many regions within the enclosure at high Rayleigh number.

With respect to Fig. 6b, which reveals the isotherms under various dimensionless values of Rayleigh number considering four different cases of inner body, it can be seen that the isotherms lines at low Rayleigh number \(\left(Ra={10}^{4}\right)\) are vertical which reflect the conduction heat transfer mode is dominant while at high Rayleigh number \((Ra={10}^{6})\), the shapes of isotherms lines obviously changed into the non-uniform curved lines which is an indication of the thermogravitional mode is dominated. It can be seen that the behavior of isotherms are similar regardless the inner body shape.

The influence of Darcy number and the inner body shape is presented in terms of streamlines and isotherms in Fig. 6b and 7a, respectively. Firstly, with respect to the Fig. 7a which illustrates the influence of various Darcy number and different four cases of inner body shape on the fluid flow strength. By constriction our analysis on the left layer of the enclosure which contains (porous medium saturated with nanofluid) and following the influence of Darcy number along with the inner body shape, it can be noted that at low Darcy number \(\left(Da={10}^{-5}\right),\) there is no inner vortices formed while as the Darcy number increases into \(Da={10}^{-1}\), more inner vortices formed which means that the fluid flow strength is increasing as Darcy number increases. The physical reason behind this, is that increasing the dimensionless value of Darcy number leads to an obvious increment in the permeability of the porous medium which helps nanofluid to penetrate into the left layer leading to increases the convection heat transfer mode because the conductive mode is dominant at low Darcy number and this is obvious also from the shape of the streamlines in the left layer as there is no inner cells which reflect low fluid flow strength. Also, the shape of inner body had great impact on the fluid flow strength. For example, at low Darcy number \(\left(Da={10}^{-5}\right)\), the maximum stream function of the left layer for \(\mathrm{Case }1>Case 2>\mathrm{Case }3>Case 4\), while at high Darcy number \(\left(Da={10}^{-5}\right)\), the maximum stream function of the left layer for \(\mathrm{Case }2>Case 4>\mathrm{Case }3>Case 1\). Thus, at low Darcy number Case 1 which represents the inner circular shape had the highest fluid flow strength while the lowest fluid flow strength was when the inner shape is triangular. Actually, at low Darcy number the influence of inner body shape had great influence on the fluid flow characteristics. On the other hand, at high Darcy number Case 1 which is the inner circular shapes recorded the lowest case in the fluid flow strength while the square shape is better in the enhancing the fluid flow strength.

Fig. 7
figure 7

a Streamlines contours considering different inner hot shapes under various Darcy number at \(Ra={10}^{6}, \varphi =0.02, Ha=0\). b Isotherms contours considering different inner hot shapes under various Darcy number at \(Ra={10}^{6}, \varphi =0.02, Ha=0\)

Full size image

With respect to the Fig. 7b, which examines the isotherms under various Darcy number and different cases of inner body shape, it can be seen obviously that increasing Darcy number leads to change the isotherm lines from the vertical lines as the conduction heat transfer is dominant at low Darcy number into curved-horizontal lines at high Darcy number.

With respect to the magnetic field influence on fluid flow and heat transfer which is presented in Fig. 8a, b. Firstly, the influence of Hartmann number considering different shapes of inner body had been presented in Fig. 8a. It can be seen that the Hartmann number influence strongly on the fluid flow contours because increasing Hartmann number leads to reduce the fluid flow strength. For example, for case 1, it can be seen that maximum stream function reduces from \({\Psi }_{max}=29.6179\) at \(Ha=0\), into \({\Psi }_{max}=13.2388\) at \(Ha=60\) which makes this behavior is quite reverse to the influence of Rayleigh number on the strength of the fluid flow. This behavior is similar for all of the other cases of inner body shapes but at different rate. For example, in the absence of magnetic field \(\left(Ha=0\right),\) it can be seen that the maximum stream function for different cases of inner body shape is \(\mathrm{Case }3>Case 1>\mathrm{Case }2>Case 4\) while increasing the Hartmann number into \(\left(Ha=60\right)\), leads for further decrement in the maximum stream function which makes it for \(\mathrm{Case }2>Case 4>\mathrm{Case }1>Case 3\). The physical reason behind this is that increasing the Hartmann number is an indication of increasing the electromagnetic force which its role is to reduce the natural convection buoyancy force and reduces the fluid flow strength. With respect to Fig. 8b which shows that increasing Hartmann number slightly reduces on the isotherms.

Fig. 8
figure 8

a Streamlines contours considering different inner hot shapes under various Hartman number at \(\mathrm{Ra}={10}^{6},\mathrm{ \varphi }=0.02,\mathrm{ Da}=0.001\). b Isotherms contours considering different inner hot shapes under various Hartman number at \(\mathrm{Ra}={10}^{6},\mathrm{ \varphi }=0.02,\mathrm{ Da}=0.001\)

Full size image

The influence of inner hot body number

The influence of number of inner hot pipe for each of the four selected cases of the inner body shape (circle, square, rhombus and triangular) on streamlines and isotherm are presented in Fig. 9a, b, respectively.

Fig. 9
figure 9

a Streamlines contours considering different number of inner hot shapes at \(Ra={10}^{6}, \varphi =0.02, Da=0.001, Ha=20\). b Isotherms contours considering different number of inner hot shapes at \(Ra={10}^{6}, \varphi =0.02, Da=0.001, Ha=20\)

Full size image

With respect to Fig. 9a, it may be noted that regardless the inner body shape, increasing the number of inner hot body from \(N=1\) into \(N=2\), leads to increasing the fluid flow strength by increasing the maximum stream function. Also, further increasing the number of hot body for \(No=3\), leads to slight reduction the fluid flow strength. For example, regarding Case 1 the maximum stream function increases from \({\Psi }_{max}=18.3070\) into \({\Psi }_{max}=27.9309\) and then reduces into \({\Psi }_{max}=25.0989\) when the number of inner hot body increases from \(No=1, 2\), and 3, respectively. It is worthy to mention, that the inner body shape along with the number of inner hot body had great impact of the strength of fluid flow. For example, when the number of inner hot body is \(No=1\), the maximum stream function for \(Case 4>Case 2>Case 1>Case 3\) which make the fluid flow strength of Case 4 which represents the triangular shape had the highest fluid flow strength. The influence of inner body shape for further increasing of inner hot body number is approximately negligible with slight better augmentation in fluid flow strength for Case 1 at \(No=1\).

With respect to the isotherms as shown in Fig. 9-b it can be seen that increasing the number of hot inner body leads to increase the hot temperature lines in the left layer (nanofluid saturated with the porous medium) as the hot lines resulted from the inner hot bodies will combine with the hot line resulted from the left wall of the enclosure.

The influence of position of the inner hot body

The influence of three different inner body position which they are based on the position of the inner hot body are bottom when the distance between the position of the inner hot body and the base of the insulated enclosure wall is \(Y=0.3\), in the same manner, center \(Y=0.8\) and top \(Y=1.3\) on streamlines and isotherms are presented in Fig. 10a, b, respectively. Firstly, with respect to the streamlines which is presented in Fig. 10a, so for Case 1 which indicate the circular shape of inner body by following its position when moved the inner hot body up and down, that the fluid flow strength because the maximum stream function increases from \({\Psi }_{max}=17.0935\) when it located at \(Y=0.3\) into \({\Psi }_{max}=24.1271\) when it located at \(Y=0.8\). However, more upward movement leads to a reduction in the fluid flow strength into \({\Psi }_{max}=16.1245\) at \(Y=1.3\). This behavior is repeated to Case 2 and Case 3 except Case 4 because the fluid flow strength decreases as the inner hot triangular body moved upward. It worthy to mention that the influence of inner hot body shape is negligible on fluid flow strength when it is located at the center and top of the enclosure while the influence of inner body location when it located at the bottom of the enclosure is strong especially for the Case 4 which is the triangular shape.

Fig. 10
figure 10

a Streamlines contours considering different position of inner hot shapes at \(Ra={10}^{6}, \varphi =0.02, Da=0.001, Ha=20\). b Isotherms contours considering different position of inner hot shapes at \(Ra={10}^{6}, \varphi =0.02, Da=0.001, Ha=20\)

Full size image

With respect to Fig. 10b which shows the isotherms clearly influenced by the position of the inner body shape.

Nusselt number

The Nusselt number is the most important parameters in the augmentation of heat transfer rate. So the influence of the mentioned parameters on Nusselt number will be discussed in full details to draw the major conclusions.

The influence of Rayleigh number considering different inner body shape on average Nusselt number along the inner hot body had been displayed in Fig. 11. It can be seen that increasing Rayleigh number leads to an increasing in the Nusselt number because of increasing the fluid flow strength and natural convection rate which increasing the rate impact between the fluid molecules which increasing the thermal energy transferred from the hot inner body into the enclosure area. This increasing of Rayleigh number changed the mode of heat transfer into the thermogravitional (natural convection) mode. It is also noted that the inner body shape plays an important role in the augmentation of Nusselt number which leads to improving the thermal rate of heat transfer. For example, Nusselt number for \(Case 1>Case 3>Case 2>Case 4\).

Fig. 11
figure 11

Nu with respect to Ra for different shapes of inner body at \(\varphi =0.02, Da=0.001, Ha=0\)

Full size image

With respect to the influence of Darcy number as illustrated in Fig. 12 which shows obviously that increasing Darcy number improves Nusselt number because increasing Darcy number leads to augmentation of natural convection and buoyancy force which changed the mode of heat transfer from the conductive mode into the convection. Again, Nusselt number for \(Case 1>Case 3>Case 2>Case 4\).

Fig. 12
figure 12

Nu with respect to Da for different shapes of inner body at \(\varphi =0.02, Ra={10}^{5}, Ha=0\)

Full size image

Besides, increasing Hartmann number leads to express more resistance of the MHD force to the movement of the fluid flow which leads to a reduction of Nusselt number as shown in Fig. 13 which makes its influence is quite reversible to the influence of Rayleigh and Darcy number. It may be noted that influence of Hartmann number on Nusselt number is highly affected by the inner body shape of each case. For example, the reduction in Nusselt number for \(Case 1>Case 3>Case 2>Case 4\) which makes Case 4 is the best solution to reduce the heat transfer reduction in a comparison with the other cases.

Fig. 13
figure 13

Nu with respect to Ha for different shapes of inner body at \(\varphi =0.02, Ra={10}^{5}, Da=0.001\)

Full size image

Also, the influence of MHD angle on the Nusselt number is presented in Fig. 14. Different behaviors of Nusselt number is obtained based upon the angle of magnetic field inclination angle. When \(0^\circ \le \gamma \le 30^\circ\), it is observed that increasing the inclination angle of magnetic field leads to decreasing in the Nusselt number for all of the inner body shapes. When \(\gamma \ge 30^\circ\), it can be seen that the influence of angle of MHD is positive on the Nusselt number as the latter increases as the magnetic field angle increases for all of the inner body shape. It can be seen that Nusselt number for \(Case 1>Case 3>Case 2>Case 4\) for the entire magnetic field angle of inclination.

Fig. 14
figure 14

Nu with respect to MHD Angle for different shapes of inner body at \(\varphi =0.02, Ra={10}^{5}, Da=0.001, Ha=60\)

Full size image

The influence of nanofluid loading is showed in Fig. 15 for various inner body shapes. It can be seen that Nusselt number increases as the nanofluid loading increases. It can be seen again that the inner body shape plays an important role in the enhancement of Nusselt number which Case 1 indicate the best case in the augmentation of heat transfer while the Case 4 record the lowest improving in Nusselt number.

Fig. 15
figure 15

Nu with respect to nanofluid loading for different shapes of inner body at \(\varphi =0.02, Ra={10}^{5}, Da=0.001\)

Full size image

The impact of number of inner hot bodies on the Nusselt number is presented in Fig. 16. It can be seen that for all numbers of inner bodies and various shapes, there would be an increasing of Nusselt number with increasing of Rayleigh number. However, it can be seen that Nusselt number is in its highest value when the number of inner heater bodies is \(No=1\) for all shapes (circle, square, rhombus and triangle). It is observed that when the number of inner bodies are \(No=3\), leads to reduce Nusselt number for all of the four cases of inner body shapes. It is noted that at low Rayleigh there is no change on Nusselt when the number of inner hot bodies for all cases are \(No=1, 2\). While the deviation (difference) in Nusselt number for \(No=1, 2\) increases as Rayleigh number increases.it is obtained that Case 1 reveals better augmentation of Nusselt number for all cases.

Fig. 16
figure 16

Nu with respect to Rayleigh number for various number of inner hot pipes considering different shapes at \(\varphi =0.02, Ra={10}^{6}, Da=0.001, Ha=20\)

Full size image

Finally, with respect to the influence of the inner hot body location on Nusselt number is discussed in Figs. 17 and 18. It can be seen that when the inner hot body start moving upwards, there would be a reduction in Nusselt number for all of the shapes of inner bodies. Besides that, the Nusselt number for \(Case 1>Case 3>Case 2>Case 4\) in any position of inner bodies.

Fig. 17
figure 17

Nu with respect to Rayleigh number under various location of inner hot body considering different shapes at \(\varphi =0.02, Ra={10}^{6}, Da=0.001, Ha=20\)

Full size image
Fig. 18
figure 18

Nu with respect to various position of inner hot body considering different shapes at \(\varphi =0.02, Ra={10}^{6},\) \(Da=0.001, Ha=20\)

Full size image

Conclusion

  1. 1.

    Increasing Ra, Da, nanofluid loading and reducing the Ha leads to augmentation of heat transfer

  2. 2.

    Best location in terms of best strength of fluid flow was for triangular shapes when its located at the bottom of the enclosure

  3. 3.

    Increasing the number of inner heated body into \(N=2\), leads to highest fluid flow strength. However, further increasing of number of the heated body leads to reduce the fluid flow strength

  4. 4.

    For various values of Ra, Da, Ha, \({\gamma }_{MHD}\), \(\phi\), Case 1 which represent the circular shapes reveals the highest augmentation in Nusselt number followed by Case 3 (rhombus), Case 2 (square) and Case 4 (triangular) reveals the lowest improving in heat transfer rate.

  5. 5.

    The magnetic field inclination angle reveals different behavior on heat transfer rate where it was concluded that increasing its value from \(0^\circ\) into \(30^\circ\) leads to reduces the Nusselt number. further increasing of magnetic field angle more than \(30^\circ\) leads to increasing of Nusselt number