Significance of nonlinear thermal radiation in 3D Eyring–Powell nanofluid flow with Arrhenius activation energy

Abstract

In this paper, a mathematical analysis for three-dimensional Eyring–Powell nanofluid nonlinear thermal radiation with modified heat plus mass fluxes is investigated. To enhance the dynamical and physical study of structure, the slip condition is introduced. A Riga plate is employed for avoiding boundary-layer separation to diminish the friction and pressure drag of submarines. To evaluate the heat transfer, the Cattaneo–Christov heat flux model is implemented via appropriate transformation. A comparison between bvp4c results and shooting technique is made. Graphical and numerical illustrations are presented for prominent parameters.

Introduction

In recent years, non-Newtonian fluids due to their extensive role in engineering and industrial applications have attracted the attention of a large number of researchers. These include Reiner–Philippoff fluid, Casson fluid, Carreau fluid, micropolar fluid, Prandtl fluid, power law fluid, Eyring–Powell fluid and Prandtl–Eyring fluid. Such fluids can be used in the processing of chemical; that is why, a number of researchers are investigating non-Newtonian fluids in the process of polymers and in chemical engineering. Besides, nanofluids containing small nanomaterial particles like molecules or atoms are ejected in a base fluid [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Nanofluid is a fluid typical of nanomaterials coined by Choi and Eastman [21]. The modern convection agents have a point of view that a broad range of production and industrial characteristic plays an important role in the heat transfer in such liquids. Due to this fact, nanoparticles have been used in the past decades as attractive agents in the formation of fluids to maximize heat transfer in industrial automation. By controlling the nanoscale stage in the development of practical tools, materials and systems, they make a significant contribution to nanotechnology. These include inertia, Magnus brown absorption, thermophoresis, liquid precipitation and gravity. Boungiorno et al. [22] examined the vital role in the growth of the non-homogenous scientific equilibrium for the convective transportation of nanoparticles with convectional boundaries. He also developed possible slipping tools for Brownian motion and thermophoresis in nanofluids. Powell and Eyring [23] have introduced fluid model called Eyring–Powell fluid. Patel and Timol [24] developed the Eyring–Powell models more efficient and significant as compared to the power law model, but it was rather complex in nature. Simultaneously, concern was to argue that this fluid’s dynamic existence is believed to be resulted from the fluids kinetic theory more than its matter-of-fact expression. The fluid model of Eyring-Powell is used to design the manufacturing in material flows. This model also reduces the viscous fluid flow of the Eyring–Powell fluid to a moveable surface at low and high shear concentrations, as investigated by Hayat et al. [25]. Akbar et al. [26] discussed Eyring–Powell magneto-fluid flow numerically past the stretching sheet by employing the finite difference method. As various non-Newtonian fluid system equations are complex as compared to Navier–Stokes equations, obtaining the solutions of these equations is much difficult but more significant due to the simplicity and ease of Eyring–Powell model and vital in chemical engineering processes. Hayat et al. [27] illustrated Eyring–Powell fluid for Newtonian heat and magnetohydrodynamics, and even today, it is of great significance to improve the mathematical modeling of non-Newtonian fluids [28,29,30,31,32,33,34,35]. Eldabe et al. [36] explored Eyring–Powell fluid for MHD within the variable viscosity effects which has been examined in [37]. Islam et al. [38] reported the disturbance of the Eyring–Powell fluid. Akbar and Nadeem [39] argued an endoscope transfer and heating structure of Eyring–Powell fluid. Sirohi et al. [40] examined the fluid flow of Eyring–Powell near a dynamic plate utilizing various techniques. Nadeem et al. [41] discussed the peristaltic flux of Eyring–Powell fluid. The effect of dual stratification by Eyring–Powell has been inspected by Jayachandra et al. [42]. Yoon and Ghajar [43] offered a brief description of the effect of varying large and small viscosities of shear rate by using Powell–Eyring fluid to understand the nature of fluid time range. Agbaje et al. [44] investigated the incompressible nanoflow limits stage of Eyring–Powell. Gailitis and Lielausis [45] invented the Riga electromagnetic actuator surface, which consists of definitely arranged magnets and electrode sets. Ahmad et al. [46] examined the impact of zero normal mass and heat flux on the motion of nanofluid flowing across a Riga layer. The flow problem was determined by two techniques: (1) the shooting method and (2) bvp4c. Iqbal et al. [47] performed the analysis of nanofluid flow to a variable-thick Riga plate with bioconvection, heat convection and mass flow elements within the flow region. Khan et al. [48] investigated Powell–Eyring MHD fluid by considering the elements of thermophysics. The stretching surface with boundary conditions flow of nanofluid is available in [49]. Goodarzi et al. [50] used two types of mixture model and narrow cavity channel to describe the laminar and turbulent nanofluid case flow. Riaz et al. [51] studied the Eyring–Powell fluid for heat and mass transfer. Three-dimensional Eyring–Powell nanofluids through the stretch sheet were proposed by Gireesha et al. [52]. Hayat et al. [53] determined their three-dimensional previous-degree nanofluid flow instead of utilizing the stretching layer to evaluate the thermal influence flow. Hayat et al. [54] reported Maxwell nanofluid with heat transfer source/sink effects for a three-dimensional boundary-layer flow. Hedayati et al. [55] highlighted the nanofluid flow in a channel. Most of these slip systems are similar to the Fukui–Kaneko (FK) slip demarcation flow model [56], the Maxwell first-order boundary slip flow model [57], the nominal injunction slip surface flow model [58] and the second command slip boundary flow method [59]. Kinetic theory for gases is the origin of these models. These models are used in engineering and science problems. In addition, for chemical reaction, the least required energy to reactants is the activation energy. In chemical industry, oil emulsions, water mechanics and food processing play important roles, and due to concentration, a variance in mixture-type mass transfer process happens. Geothermal reservoirs have been studied for exothermic or endothermic reactions with the aid of activation energy, where activation energy plays an important role in alternate convective flows [60]. Techniques of numerical methods of fractional control problem were reported using the Chebyshev polynomial technique by Zhang et al. [61]. Shafique et al. [62] provided the concept of rotating viscoelastic flow by numerical approaches for chemical reactions and activation energy species for convoluted and nonlinear Fokker–Planck formula. Hemeda and Eladdad [63], along with an integrated scheme, provided the concept of an iterative technique. Asadollahi and Esmaeeli [64] studied two-dimensional simulation of condensation liquid behavior on micro-object with moving walls. They found that an increase in Weber number leads to liquid breakup and consequently this mechanism provides an effective way for removing the condensed liquid from micro-devices surfaces. Their presented results reveal the liquid evolutionary performance and breaking up over time which is ultimately a controllable situation for manipulating the walls velocity. Few useful numerical techniques can be seen in [65,66,67]. Furthermore, Khan et al. [68] inspected non-Fourier heat flux model on viscoelastic fluid. Nadeem and Muhammad [69] studied the flow of heat from Cattaneo–Christov model and its influence on stratification saturated with porous medium. Hayat et al. [70] discussed chemically reactive double stratified stream via Fourier theory of heat change. Salahuddin et al. [71] applied the variable thicknesses of the Cattaneo–Christov experiment on Williamson fluid via stretched sheet. Recently, Cattaneo–Christov model on Powell–Eyring fluid has been discussed by Hayat et al. [72] with variable thermal conductivity. Powell–Eyring fluid study has not been given a wide coverage. There is little literature available to support over the extended surface flow of non-Newtonian fluid from the Eyring–Powell. However, using the concept of non-Fick’s theory of mass flux and non-Fourier’s theory of thermal flux, Eyring–Powell fluid over a Riga plate with nonlinear thermal energy and activation energy has not been discussed yet.

Model

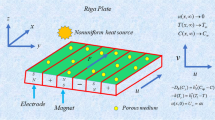
Let us consider a three-dimensional Eyring–Powell nanofluid with nonlinear thermal radiation, activation energy and the non-Fourier heat transfer and non-Fick’s mass flux passing over bidirectional stretching sheet as shown in Fig. 1. Let the stretching velocity about x-direction and y-direction be $\tilde{u} = ax,\,\tilde{v} = by$, respectively. The region $z \ge 0$ is occupied by the fluid. Let us consider the temperature and the nanoparticle’s concentration $\tilde{T}_{\text{f}} ,\,\tilde{C}_{\text{f}}$ are constant and assume that they are better than the ambient high temperature and the concentration $\tilde{T}_{\infty } ,\,\tilde{C}_{\infty }$ (Fig. 1).

Fig. 1

Flow geometry

A three-dimensional Eyring–Powell model of energy and nanoparticle’s concentration with activation energy and nonlinear thermal radiation [73, 74] can be expressed by

$$\left( {\frac{{\partial \tilde{u}}}{\partial x} + \frac{{\partial \tilde{v}}}{\partial y} + \frac{{\partial \tilde{w}}}{\partial z}} \right) = 0,$$

(1)

$$\begin{aligned} \left( {\tilde{u}\frac{{\partial \tilde{u}}}{\partial x} + \tilde{v}\frac{{\partial \tilde{u}}}{\partial y} + \tilde{w}\frac{{\partial \tilde{u}}}{\partial z}} \right) & = \left( {\nu + \frac{1}{\rho \varGamma a}} \right)\frac{{\partial^{2} \tilde{u}}}{{\partial z^{2} }} - \frac{1}{{2\rho \varGamma a^{3} }}\left( {\frac{{\partial \tilde{u}}}{\partial z}} \right)^{2} \frac{{\partial^{2} \tilde{u}}}{{\partial z^{2} }} \\ & \quad - \frac{{\sigma^{*} B_{0}^{2} }}{\rho }\tilde{u} - \frac{\nu \varphi }{{K^{*} }}\tilde{u} + \frac{{\pi j_{0} M_{0} }}{8\rho }\exp \left( {\frac{ - \pi }{{\alpha_{1} }}z} \right), \\ \end{aligned}$$

(2)

$$\begin{aligned} \left( \tilde{u}\frac{{\partial \tilde{v}}}{\partial x} + \tilde{v}\frac{{\partial \tilde{v}}}{\partial y} + \tilde{w}\frac{{\partial \tilde{v}}}{\partial z} \right) = \left( {\nu + \frac{1}{\rho \varGamma a}} \right)\frac{{\partial^{2} \tilde{v}}}{{\partial z^{2} }} \\ \quad - \frac{1}{{2\rho \varGamma a^{3} }}\left( {\frac{{\partial \tilde{v}}}{\partial z}} \right)^{2} \frac{{\partial^{2} \tilde{v}}}{{\partial z^{2} }} - \frac{{\sigma B_{0}^{2} }}{\rho }\tilde{v} - \frac{\nu \varphi }{{K^{*} }}\tilde{v}, \end{aligned}$$

(3)

The Fourier and the Fick laws can be expressed as follows:

$$\vec{q} + \varOmega_{\text{E}} \left( {\frac{{\partial \vec{q}}}{\partial t} + \tilde{V} \cdot \nabla \vec{q} - \vec{q} \cdot \nabla \tilde{V} + \left( {\nabla \cdot \tilde{V}} \right)\vec{q}} \right) = - k\nabla \tilde{t},$$

(4)

$$\vec{j} + \varOmega_{\text{C}} \left( {\frac{{\partial \tilde{j}}}{\partial t} + \tilde{V} \cdot \nabla \vec{j} - \vec{j} \cdot \nabla \tilde{V} + \left( {\nabla \cdot \tilde{V}} \right)\vec{j}} \right) = - D_{\text{B}} \nabla \tilde{C},$$

(5)

$$\begin{aligned}\left( \tilde{u}\frac{{\partial \tilde{T}}}{\partial x} + \tilde{v}\frac{{\partial \tilde{T}}}{\partial y} + \tilde{w}\frac{{\partial \tilde{T}}}{\partial z} + \varOmega_{\text{E}} \phi_{\text{E}} \right) = \alpha \frac{{\partial^{2} \tilde{T}}}{{\partial z^{2} }}\\ \quad + \tau \left\{ {D_{\text{B}} \frac{{\partial \tilde{C}}}{\partial z}\frac{{\partial \tilde{T}}}{\partial z} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{{\partial \tilde{T}}}{\partial z}} \right)^{2} } \right\} - \frac{1}{{\left( {\rho c} \right)_{\text{p}} }}\frac{{\partial \tilde{q}_{\text{r}} }}{\partial z}, \end{aligned}$$

(6)

$$\left( \tilde{u}\frac{\partial C}{\partial x} + \tilde{v}\frac{{\partial \tilde{C}}}{\partial y} + \tilde{w}\frac{{\partial \tilde{C}}}{\partial z} + \varOmega_{\text{C}} \phi_{\text{C}} \right) = D_{\text{B}} \left( {\frac{{\partial^{2} \tilde{C}}}{{\partial z^{2} }}} \right) + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{{\partial^{2} \tilde{T}}}{{\partial z^{2} }}} \right) - Kr^{2} \left( {\tilde{C} - \tilde{C}_{\infty } } \right)\left( {\frac{{\tilde{T}}}{{\tilde{T}_{\infty } }}} \right)^{n} \exp \left( {\frac{{ - E_{\text{a}} }}{{K_{1} \tilde{T}}}} \right),$$

(7)

The associated boundary conditions can be given as follows:

$$\tilde{u} = \tilde{u}_{\text{w}} \left( x \right) + \alpha_{0} \frac{{\partial \tilde{u}}}{\partial z},w = 0, - k\frac{{\partial \tilde{T}}}{\partial z} = h_{\text{f}} \left[ {\tilde{T}_{\text{f}} - \tilde{T}} \right],\;{\text{at}}\;z = 0,\tilde{v} = \tilde{v}_{\text{w}} \left( y \right) + \alpha_{0} \frac{{\partial \tilde{v}}}{\partial z},$$

(8)

$$\tilde{u} \to 0,\tilde{v} \to 0,\tilde{T} \to \tilde{T}_{\infty } ,\tilde{C} \to \tilde{C}_{\infty } ,z \to \infty .$$

(9)

Radiative heat flux can be addressed by

$$\tilde{q}_{\text{r}} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial \tilde{T}^{4} }}{\partial z} = - \frac{{16\sigma^{*} \tilde{T}^{3} }}{{3k^{*} }}\frac{{\partial \tilde{T}}}{\partial z}.$$

(10)

Substituting expression (10) in Eq. (6), we get,

$$\begin{aligned} \left( {\tilde{u}\frac{{\partial \tilde{T}}}{\partial x} + \tilde{v}\frac{{\partial \tilde{T}}}{\partial y} + \tilde{w}\frac{{\partial \tilde{T}}}{\partial z} + \varOmega_{\text{E}} \phi_{\text{E}} } \right) & = \alpha \frac{{\partial^{2} \tilde{T}}}{{\partial z^{2} }} + \tau \left\{ {D_{\text{B}} \frac{{\partial \tilde{C}}}{\partial z}\frac{{\partial \tilde{T}}}{\partial z} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{{\partial \tilde{T}}}{\partial z}} \right)^{2} } \right\} \\ & \quad + \frac{{16\sigma^{*} }}{{3k^{*} \left( {\rho c} \right)_{\text{p}} }}\frac{\partial }{\partial z}\left( {\tilde{T}^{3} \frac{{\partial \tilde{T}}}{\partial z}} \right), \\ \end{aligned}$$

(11)

where

$$\begin{aligned} \phi_{\text{E}} & = \tilde{u}^{2} \frac{{\partial^{2} \tilde{T}}}{{\partial x^{2} }} + \tilde{v}^{2} \frac{{\partial^{2} \tilde{T}}}{{\partial y^{2} }} + \tilde{w}^{2} \frac{{\partial^{2} \tilde{T}}}{{\partial z^{2} }} + 2\tilde{u}\tilde{v}\frac{{\partial^{2} \tilde{T}}}{\partial x\partial y} + 2\tilde{v}\tilde{w}\frac{{\partial^{2} \tilde{T}}}{\partial y\partial z} + 2\tilde{u}\tilde{w}\frac{{\partial^{2} \tilde{T}}}{\partial x\partial z} + \left( \begin{aligned} \tilde{u}\frac{{\partial \tilde{u}}}{\partial x} + \tilde{v}\frac{{\partial \tilde{u}}}{\partial y} \hfill \\ + \tilde{w}\frac{{\partial \tilde{u}}}{\partial z} \hfill \\ \end{aligned} \right)\frac{{\partial \tilde{T}}}{\partial x} \\ & \quad + \left( {\tilde{u}\frac{{\partial \tilde{v}}}{\partial x} + \tilde{v}\frac{{\partial \tilde{v}}}{\partial y} + \tilde{w}\frac{{\partial \tilde{v}}}{\partial z}} \right)\frac{{\partial \tilde{T}}}{\partial y} + \left( {\tilde{u}\frac{{\partial \tilde{w}}}{\partial x} + \tilde{v}\frac{{\partial \tilde{w}}}{\partial y} + \tilde{w}\frac{{\partial \tilde{w}}}{\partial z}} \right)\frac{{\partial \tilde{T}}}{\partial z}, \\ \end{aligned}$$

(12)

$$\begin{aligned} \phi_{\text{C}} & = \tilde{u}^{2} \frac{{\partial^{2} \tilde{C}}}{{\partial x^{2} }} + \tilde{v}^{2} \frac{{\partial^{2} \tilde{C}}}{{\partial y^{2} }} + \tilde{w}^{2} \frac{{\partial^{2} \tilde{C}}}{{\partial z^{2} }} + 2\tilde{u}\tilde{v}\frac{{\partial^{2} \tilde{C}}}{\partial x\partial y} + 2\tilde{v}\tilde{w}\frac{{\partial^{2} \tilde{C}}}{\partial y\partial z} + 2\tilde{u}\tilde{w}\frac{{\partial^{2} \tilde{C}}}{\partial x\partial z} + \left( \begin{aligned} \tilde{u}\frac{{\partial \tilde{u}}}{\partial x} + \tilde{v}\frac{{\partial \tilde{u}}}{\partial y} \hfill \\ + \tilde{w}\frac{{\partial \tilde{u}}}{\partial z} \hfill \\ \end{aligned} \right)\frac{{\partial \tilde{C}}}{\partial x} \\ & \quad + \left( {\tilde{u}\frac{{\partial \tilde{v}}}{\partial x} + \tilde{v}\frac{{\partial \tilde{v}}}{\partial y} + \tilde{w}\frac{{\partial \tilde{v}}}{\partial z}} \right)\frac{{\partial \tilde{C}}}{\partial y} + \left( {\tilde{u}\frac{{\partial \tilde{w}}}{\partial x} + \tilde{v}\frac{{\partial \tilde{w}}}{\partial y} + \tilde{w}\frac{{\partial \tilde{w}}}{\partial z}} \right)\frac{{\partial \tilde{C}}}{\partial z}. \\ \end{aligned}$$

(13)

Let us introduce the following transformation:

$$\begin{aligned} \eta & = \sqrt {\frac{a}{v}z^{2} } ,\tilde{u} = axf^{\prime } \left( \eta \right),\tilde{v} = ayg^{\prime } \left( \eta \right),\tilde{w} = - \sqrt {av} \left( {f\left( \eta \right) + g\left( \eta \right)} \right), \\ \theta (\eta ) & = \frac{{\tilde{T} - \tilde{T}_{\infty } }}{{\tilde{T}_{\text f} - \tilde{T}_{\infty } }},\phi \left( \eta \right) = \frac{{\tilde{C} - \tilde{C}_{\infty } }}{{\tilde{C}_{\text w} - \tilde{C}_{\infty } }}. \\ \end{aligned}$$

(14)

Applying similarity transformation to the governing equation, the nonlinear dimensional expressions are reduced to the following expressions:

$$\left( {1 + \omega - \omega f^{\prime \prime } \left( \eta \right)} \right)f^{\prime \prime \prime } \left( \eta \right) + \left( {f\left( \eta \right) + g\left( \eta \right)} \right)f^{\prime \prime } \left( \eta \right) - K_{1} f^{\prime } \left( \eta \right) - \left( {f^{\prime } \left( \eta \right)} \right)^{2} + Qe^{ - B\eta } = 0,$$

(15)

$$\left( {1 + \omega - \omega g^{\prime \prime } \left( \eta \right)} \right)g^{\prime \prime \prime } \left( \eta \right) + (f\left( \eta \right) + g\left( \eta \right))g^{\prime \prime } \left( \eta \right) - K_{1} g^{\prime } \left( \eta \right) - \left( {g^{\prime } \left( \eta \right)} \right)^{2} = 0,$$

(16)

$$\begin{aligned} & \left( {1 + \varepsilon_{1} \theta } \right)\theta '' + \left[ {\frac{4}{3}N_{\text{r}} \left( {1 + \left( {\theta_{\text{w}} - 1} \right)\theta } \right)^{3} } \right]\theta '' + \left[ {\varepsilon_{1} + \left( {1 + \left( {\theta_{\text{w}} - 1} \right)\theta } \right)^{2} \left( {4N_{\text{r}} \left( {\theta_{\text{w}} - 1} \right)} \right)\theta '^{2} } \right] \\ & \quad + \Pr \left( {f\left( \eta \right) + g\left( \eta \right)} \right)\theta '\left( \eta \right) + N_{\text{B}} \theta '\left( \eta \right)\phi '\left( \eta \right) + N_{\text{T}} \left( {\theta '\left( \eta \right)} \right)^{2} - \delta_{\text{t}} \left( {f + g} \right)\left( {f' + g'} \right)\theta ' \\ & \quad + \left( {f + g} \right)^{2} \theta '' = 0, \\ \end{aligned}$$

(17)

$$\begin{aligned} & \phi ''\left( \eta \right) + S_{\text{c}} \left( {f\left( \eta \right) + g\left( \eta \right)} \right)\phi '\left( \eta \right) + \frac{{N_{\text{T}} }}{{N_{\text{B}} }}\theta ''\left( \eta \right) - S_{\text{c}} \sigma (1 + \delta \theta )^{n} \exp \left( {\frac{{ - E_{1} }}{1 + \delta \theta }} \right)\phi \left( \eta \right) \\ & \quad - \delta_{\text{c}} \left( {f + g} \right)\left( {f' + g'} \right)\phi (\eta ) + \left( {f + g} \right)^{2} \phi ''(\eta ) = 0, \\ \end{aligned}$$

(18)

$$f\left( 0 \right) = g\left( 0 \right) = 0,f\left( 0 \right) = 1 + \alpha f''\left( 0 \right),g'\left( 0 \right) = \lambda + \alpha g''\left( 0 \right),$$

(19)

$$f'\left( \eta \right) = 0,g'\left( \eta \right) = 0,\theta \left( \eta \right) = 0,\phi \left( \eta \right) = 0\;{\text{as}}\;\eta \to 0,$$

(20)

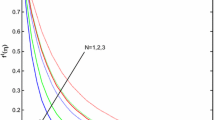
where the porosity parameter is $K_{1}$, dimensionless constant $B$, customized Hartmann number $Q$, radiation parameter $N_{\text{r}}$, non-dimensional fluid parameter $\omega$, Prandtl number $\Pr$, velocity slip parameter $\alpha$, Schmidt number Sc, thermophoresis number $N_{\text{T}}$, Brownian motion $N_{\text{B}}$, activation energy $E_{1}$, chemical reaction parameter $\sigma$, heat parameter $\delta$, Biot number $\gamma$, recreation for temperature diffusion $\delta_{\text{t}}$ and time relaxation for mass diffusion $\delta_{\text{c}}$, which are expressed as follows:

$$\begin{aligned} E_{1} & = \frac{{E_{\text{a}} }}{{k_{1} T_{\infty } }},\quad K_{1} = \frac{{\sigma^{ * } B_{0}^{2} }}{{a\rho_{\text{f}} }} + \frac{{v_{f} \varphi }}{{aK^{ * } }},\quad \Pr = \frac{v}{a},\quad {\rm N}_{\text{B}} = \frac{{\tau D_{\text{B}} }}{v}\left( {\tilde{C}_{\text{w}} - \tilde{C}_{\infty } } \right),\quad \alpha = \alpha_{0} \left( {\frac{\nu }{a}} \right)^{{ - \frac{1}{2}}} ,\quad \gamma = \frac{h}{k}\sqrt {\frac{v}{a}} ,\quad \lambda = \frac{b}{a}, \\ \quad \sigma & = \frac{{k_{\text{r}}^{2} }}{a},\quad \delta = \frac{{b^{3} x^{2} }}{{2\nu c^{2} }},\quad \mu = \nu \rho ,\quad N_{\text{T}} = \frac{{\tau D_{\text{T}} }}{{vT_{\infty } }}\left( {\tilde{T}_{\text{f}} - \tilde{T}_{\infty } } \right),\quad \omega = \frac{1}{\mu \varGamma a},\quad N_{\text{r}} = \frac{{4\sigma T_{\infty }^{3} }}{{k^{*} k}}, \\ \quad S_{\text{c}} & = \frac{\alpha }{{D_{\text{B}} }},\quad \delta_{\text{t}} = b\lambda_{\text{E}} ,\quad \,\delta_{\text{c}} = b\lambda_{\text{C}} ,\quad Q = \frac{{\pi M_{0} J_{0} }}{{8\rho a^{2} x}},\quad B = \frac{\pi }{{\alpha_{1} }}\left( {\sqrt {\frac{\nu }{a}} } \right). \\ \end{aligned}$$

(21)

To drive the skin friction coactive $\tilde{C}_{\text{f}}$, the Newton method is used. The Fourier law is implemented to find the value of the Nusselt number ${\text{Nu}}_{\text{x}}$. Also to find the value of local Sherwood number ${\text{Sh}}_{\text{x}}$, the Fick’s laws have been utilized. Finally, the quantities of interest can be written as:

$$C_{\text{fx}} = \frac{{\tau_{\text{wx}} }}{{\rho U_{\text{u}}^{2} }},\quad C_{\text{fy}} = \frac{{\tau_{\text{wy}} }}{{\rho U_{\text{w}}^{2} }},\quad {\text{Nu}}_{\text{x}} = \frac{{xq_{\text{w}} }}{{k_{1} \left( {\tilde{T}_{\text{w}} - \tilde{T}_{\infty } } \right)}},\quad {\text{Sh}}_{\text{x}} = \frac{{xq_{\text{m}} }}{{k_{1} \left( {\tilde{C}_{\text{w}} - \tilde{C}_{\infty } } \right)}}.$$

(22)

$\tau_{\text{wx}} ,\,\tau_{\text{wy}}$ are the barrage shear stress next to x-axis and y-axis, respectively, which are defined as:

$$\tau_{\text{wx}} = \mu \left( {\frac{{\delta \tilde{u}}}{\delta z} + \frac{{\delta \tilde{w}}}{\delta x}} \right)_{z = 0} ,\,\,\tau_{\text{wy}} = \mu \left( {\frac{{\delta \tilde{v}}}{\delta z} + \frac{{\delta \tilde{w}}}{\delta y}} \right)_{z = 0},$$

(23)

where

$$h_{\text{m}} = - D_{\text{B}} \left( {\frac{{\delta \tilde{C}}}{\delta z}} \right)_{{{\text{z}} = 0}} ,\quad h_{\text{m}} = - k\left( {\frac{{\delta \tilde{T}}}{\delta z}} \right)_{{{\text{z}} = 0}} .$$

(24)

Substituting (22) to (24), we get

$$C_{\text{fx}} \text{Re}_{\text{x}}^{0.5} = - f''\left( 0 \right),\quad C_{\text{fy}} \text{Re}_{\text{y}}^{0.5} = - g''\left( 0 \right),\quad \frac{{{\text{Nu}}_{\text{x}} }}{{\text{Re}_{\text{x}}^{0.5} }} = - \theta '\left( 0 \right),\quad \frac{{{\text{Sh}}_{\text{x}} }}{{\text{Re}_{\text{x}}^{0.5} }} = - \phi '\left( 0 \right).$$

(25)

Here, the local Reynolds number on relied stretching velocity, local Sherwood number and local Nusselt number are denoted, respectively, as $\text{Re}_{\text{x}} ,\,\text{Re}_{\text{y}} ,\,{\text{Sh}}_{\text{x}} ,\,{\text{Nu}}_{\text{x}}$.

Numerical procedure

The set of nonlinear coupled differential equations with dimensionless boundaries as described in (14)–(19) have been solved to find numerical results for velocity, high temperature and concentration by utilizing Lobatto IIIa finite difference shooting method bvp4c via computational software MATLAB.

Let us consider

$$\begin{aligned} & f = l_{1} ,\frac{{{\text{d}}f}}{{{\text{d}}\eta }} = l_{2} ,\frac{{{\text{d}}^{2} f}}{{{\text{d}}\eta ^{2} }} = l_{3} ,\frac{{{\text{d}}^{3} f}}{{{\text{d}}\eta ^{3} }} = l_{3}^{'} ,g = l_{4} ,\frac{{{\text{d}}g}}{{{\text{d}}\eta }} = l_{5} ,\frac{{{\text{d}}^{2} g}}{{{\text{d}}\eta ^{2} }} = l_{6} ,\frac{{{\text{d}}^{3} g}}{{{\text{d}}\eta ^{3} }} = l_{6}^{'} ,\theta = l_{7} ,\frac{{{\text{d}}\theta }}{{{\text{d}}\eta }} = l_{8} , \\ & \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta ^{2} }} = l_{8}^{'} ,\phi = l_{9} ,\phi ^{'} = l_{{10}} ,\phi ^{{''}} = l_{{10}}^{'} , \\ & \left. {\begin{array}{*{20}l} {l_{3}^{'} = \frac{1}{{(1 + \omega - \omega l_{3} )}} - \left( {\left( {l_{1} + l_{4} } \right)l_{3} + K_{1} l_{2} + l_{2}^{2} + Qe^{{ - B\eta }} } \right),} \hfill \\ {l_{6}^{'} = \frac{1}{{(1 + \omega - \omega l_{6} )}}\left( {(l_{1} + l_{4} )l_{6} + k_{1} l_{5} + l_{5}^{2} } \right),} \hfill \\ {l_{8}^{'} = \frac{1}{{\left( {1 + \varepsilon _{1} l_{7} + \left( {l_{1} + l_{4} } \right)^{2} } \right)\left( {\frac{4}{3}\left( {N_{{\text{r}}} \left( {1 + \left( {\theta _{{\text{w}}} - 1} \right) + l_{7} } \right)^{3} } \right)} \right)}}\left[ \begin{gathered} - \varepsilon _{1} - \left( {1 + \left( {\theta _{{\text{w}}} - 1} \right)l_{7} } \right)^{2} \left( {4N_{{\text{r}}} \left( {\theta _{{\text{w}}} - 1} \right)} \right)l_{8}^{2} \hfill \\ - P_{{\text{r}}} \left[ {\left( {l_{1} + l_{4} } \right)l_{8} } \right] - N_{{\text{B}}} l_{8} l_{{10}} - N_{{\text{T}}} l_{8}^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\, + \delta _{t} \left( {l_{1} + l_{4} } \right)\left( {l_{2} + l_{5} } \right)l_{8} \hfill \\ \end{gathered} \right],} \hfill \\ {l_{{10}}^{'} = \frac{1}{{\left( {1 + \left( {l_{1} + l_{4} } \right)^{2} } \right)}}\left( { - S_{{\text{c}}} \left( {l_{1} + l_{4} } \right)l_{{10}} - \frac{{N_{{\text{T}}} }}{{N_{{\text{B}}} }}l_{8}^{'} + S_{{\text{c}}} \sigma \left( {1 + \delta l_{7} } \right)^{n} \exp \left( {\frac{{ - E_{1} }}{{1 + \delta l_{7} }}} \right)l_{9} + \delta _{{\text{c}}} \left( {l_{1} + l_{4} } \right)\left( {l_{2} + l_{5} } \right)l_{9} } \right),} \hfill \\ {l_{1} \left( 0 \right) = l_{4} \left( 0 \right) = 0,l\left( 0 \right) = 1 + \alpha l_{3} \left( 0 \right),l_{5} \left( 0 \right) = \lambda + \alpha l_{6} \left( 0 \right),} \hfill \\ {l_{8} \left( 0 \right) = - \gamma \left( {1 - l_{7} \left( 0 \right)} \right),\,l_{9} \left( 0 \right) = 1,\,{\text{at}}\,z = 0} \hfill \\ {l_{2} \left( \eta \right) = 0,\,l_{5} \left( \eta \right) = 0,l_{7} \left( \eta \right) = 0,l_{9} \left( \eta \right) = 0\,{\text{as}}\,\eta \to 0} \hfill \\ \end{array} } \right\} \\ \end{aligned}$$

(26)

Discussion

The 3D Eyring–Powell fluid through a stretching slip with activation energy and velocity slip for different parameters is sketched in Figs. 2–32. Figure 2 demonstrates the combined effects of porosity and magnetic parameter $K_{1}$ on $f^{\prime}$. It is seen that velocity decreases with higher $K_{1}$. Actually, by enhancing the magnetic parameter, the Lorentz forces or struggle forces increase, and due to this reason, the flow of fluid slows down or components of velocity profile decline in fluid. Figure 3 illustrates the effects of $K_{1}$ on $g^{\prime}$. It is experiential that with the higher values of $K_{1}$, velocity component $g^{\prime}$ reduces. In Fig. 4, the effect of $K_{1}$ on temperature distribution $\theta^{\prime}$ is shown. It is noted that temperature distribution $\theta^{\prime}$ boosts up when $K_{1}$ is increased. In Fig. 5, the exploration impacts of $K_{1}$ on volumetric concentration $\phi^{\prime}$ are depicted. The volumetric concentration $\phi^{\prime}$ increases with higher $K_{1}$. Figure 6 shows the impacts of velocity profile $f^{\prime}$ on modified Hartmann number $Q$. It is seen that the velocity is enhanced by higher values of $Q$. Physically, increasing modified Hartmann number $Q$ leads to the conflicting behavior with the magnetic parameter as observed previously. Higher modified Hartmann number $Q$ values raise the magnetization flanked by the plates, which ultimately assist in accelerating the flow, i.e., the reverse influence to Lorentz magnetic pull force connected with the magnetic field. This characteristic is exclusively linked with Riga plates. Therefore, velocities are decreased for the situation where the modified Hartmann number $Q$ disappears, and the Riga plate becomes a straight plate in this situation. Figure 7 illustrates the velocity profile for slip parameter $\alpha$. The velocity profile $f^{\prime}$ decreases for higher value of $\alpha$. In Fig. 8, the consequence of $\alpha$ on velocity component $g^{\prime}$ is depicted. It is noticed that the velocity component $g^{\prime}$ decreases when $\alpha$ is increased. In Fig. 9, the effects of $\alpha$ on temperature $\theta$ are shown in which an increase in $\alpha$ causes a rise in $\theta$. Figure 10 illustrates the effects of $\alpha$ on volumetric concentration $\phi$. It is clearly seen that an increase in $\alpha$ causes a reduction in $\phi$. Figure 11 shows the stretching parameter $\beta$ on velocity report $f^{\prime}$ where reduction in velocity $f^{\prime}$ is observed with increasing $\beta$. Figure 12 reveals the variations of $g^{\prime}$ for altering principles of $\beta$. Augmentation in stretching parameter $\beta$ leads to a faster pressure group which causes an increase in velocity. Figure 13 represents the graph of stretching parameter $\beta$ against heat distribution $\theta$. It is exposed that $\theta$ decreases with higher $\beta$. Figure 14 represents the volume friction $\phi^{\prime}$ via stretching parameter $\beta$ in which volume friction $\phi^{\prime}$ reduces by increasing $\beta$. Figures 15 and 16 illustrate the effect of Biot number $\left( \gamma \right)$ on the temperature distribution $\theta$ and volumetric concentration profile $\varphi$, respectively. It is seen that Biot number $\gamma$ is directly proportional to the temperature and volumetric concentration profile. Figure 17 shows the witness that thermal distribution increases when one increased the radiation parameter. Physically, one can say that the radiation parameter increases the heat energy between the particles of fluid. It charges them up. Thus, the heat boosts up with the addition of radiation. In Fig. 18, we see that the radiation parameter $N_{\text{r}}$ has direct influence on concentration $\phi$. It clearly reveals that the enhancement in radiation parameter $N_{\text{r}}$ enhances its volume friction $\phi$. Obviously, the phenomenon in which fluid particles get thermal heat energy has a prominent impact on temperature and volume friction. Figure 19 demonstrates Prandtl $\Pr$ for temperature coefficient. It is perceived that temperature behavior has an opposite trend with increasing $\Pr$. Physically, a rise in Prandtl $\Pr$ causes low heat penetration, which causes a decrease in the thickness of thermal boundary layer. Figure 20 displays the part of $\Pr$ on concentration; here, $\Pr$ is inversely proportional to the concentration trend , which suggests that concentration decreases with increasing $\Pr$. Figures 21 and 22 reveal the consequence of thermophoresis number $N_{\text{t}}$ for temperature distribution $\theta$ as well as volume friction of nanoparticles $\phi$, respectively. It is detected that a rise in the aspect of thermophoresis number $N_{\text{t}}$ results in the rise in temperature and volume friction. Figure 23 visualizes the effect of temperature ratio parameter $\theta_{\text{n}}$ on temperature sharing $\theta$ in which temperature distribution is boosted up with an increment in temperature relative amount of parameter $\theta_{\text{n}}$. Figure 24 shows the blow of Schmidt number $S_{\text{c}}$ over $\phi$ in which a rise in $S_{\text{c}}$ yields a drop in concentration. Figure 25 exhibits the effect of relaxation for heat diffusion $\delta_{\text{t}}$ on temperature distribution. In Fig. 25, a decrease in temperature against relaxation for heat diffusion $\delta_{\text{t}}$ is viewed. The sway of time is for collection diffusion $\delta_{\text{c}}$ versus attentiveness profile, which is shown in Fig. 26. The volumetric concentration of nanomaterials is clearly decomposed with an increment in the values of point relaxation for mass diffusion $\delta_{\text{c}}$. The conductivity of Brownian motion parameter on volume friction is plotted in Fig. 27. Escalating $N_{\text{b}}$ results in a decrease in volume friction. Physically, $N_{\text{b}}$ creates a continuous motion between the particles of fluids. This motion enhances chaotic movements, which uplifts the kinetic energy and thus causes the devaluation in the nanoparticle’s concentration profiles. Figure 28 elucidates the effect of the Arrhenius activation energy on volumetric concentration profile $\phi$. Intensifying the value of parameter $E_{1}$, the nanoparticle concentration profiles rise. From Figs. 29–32, it is perceived that on top of the dimensionless rapidity components, heat distribution and the volumetric application profile give a good agreement of shooting technique and the bvp4c technique. A dual comparison is also presented in Tables 1–4 in which firstly the values of different parameters against existing reported results are taken into account and secondly it has been prepared in between two different techniques. It can easily be seen that our applied numerical scheme has produced exactly the same results with the existing shooting technique. An excellent agreement is established when a comparison has been made between current analysis and available results [47,48,49, 72, 75]. In Tables 1 and 3, the values of $- f^{\prime\prime}\left( 0 \right)$ are provided against parameters $M$ and $\lambda$, while Tables 2 and 4 give the insight into values of same parameters when produced against $- g^{\prime\prime}\left( 0 \right)$. Additionally, some new results of local Nusselt number and Sherwood number for different physical parameters are also reported in Tables 5 and 6, respectively. It is analyzed that local Nusselt number $- \theta^{\prime}\left( 0 \right)$ rises with $\Pr ,\gamma ,N_{\text{b}} ,Q$, but it diminishes with $\delta_{\text{T}} ,\delta_{\text{E}} ,N_{\text{T}}$. The basic purpose of Table 6 is to represent the various impacts of the key parameters $\Pr ,\delta_{\text{T}} ,\delta_{\text{E}} ,\gamma ,N_{\text{T}} ,N_{\text{b}}$ on Sherwood number $\phi^{\prime}\left( 0 \right)$. As for increasing values of $N_{\text{T}} ,E,\gamma$ getting the higher variation in $\phi^{\prime}\left( 0 \right)$, the negative behavior is observed for the cases of $N_{\text{r}} ,N_{\text{b}}$

Fig. 2

Profile of $f'\left( \eta \right)$ against $K_{1}$

Fig. 3

Profile of $g'\left( \eta \right)$ against $K_{1}$

Fig. 4

Profile of $\theta \left( \eta \right)$ against $K_{1}$

Fig. 5

Profile of $\phi \left( \eta \right)$ against $K_{1}$

Fig. 6

Profile of $f'\left( \eta \right)$ against $Q$

Fig. 7

Profile of $f'\left( \eta \right)$ against $\alpha$

Fig. 8

Profile of $g'\left( \eta \right)$ against $\alpha$

Fig. 9

Profile of $\theta \left( \eta \right)$ against $\alpha$

Fig. 10

Profile of $\phi \left( \eta \right)$ against $\alpha$

Fig. 11

Profile of $f'\left( \eta \right)$ against $\beta$

Fig. 12

Profile of $g'\left( \eta \right)$ against $\beta$

Fig. 13

Profile of $\theta \left( \eta \right)$ against $\beta$

Fig. 14

Profile of $\phi \left( \eta \right)$ against $\beta$

Fig. 15

Profile of $\theta \left( \eta \right)$ against $\gamma$

Fig. 16

Profile of $\phi \left( \eta \right)$ against $\gamma$

Fig. 17

Profile of θ(η) against $N_{\text{r}}$

Fig. 18

Profile of ϕ(η) against $N_{\text{r}}$

Fig. 19

Profile of θ(η) against $\Pr$

Fig. 20

Profile of ϕ(η) against $\Pr$

Fig. 21

Profile of θ(η) against $N_{\text{T}}$

Fig. 22

Profile of ϕ(η) against $N_{\text{T}}$

Fig. 23

Profile of θ(η) against $\theta_{\text{n}}$

Fig. 24

Profile of ϕ(η) against $S_{\text{c}}$

Fig. 25

Profile of θ(η) against $\delta_{\text{t}}$

Fig. 26

Profile of ϕ(η) against $\delta_{\text{c}}$

Fig. 27

Profile of ϕ(η) against $N_{\text{B}}$

Fig. 28

Profile of ϕ(η) against E₁

Fig. 29

Comparison of $\Pr$ by shooting method

Fig. 30

Comparison of $N_{\text{T}}$ by shooting method

Fig. 31

Comparison of $N_{\text{B}}$ by shooting method

Fig. 32

Comparison of $N_{\text{r}}$ by shooting method

Table 1 Statistical shooting assessment and outcomes from bvp4c with Hayat et al. [72] and Freidoonimehr and Rahimi [75] for $f^{\prime\prime}\left( 0 \right)$ when $\gamma = M = 0,\delta_{\text{t}} = 0,\delta_{\text{c}} = 0,Q = 0$ also all extended parameters are zero

Table 2 Statistical shooting assessment and outcomes from bvp4c with Hayat et al. [72] and Freidoonimehr and Rahimi [75] for $- g^{\prime\prime}\left( 0 \right)$ when $\gamma = M = 0,\delta_{\text{t}} = 0,\delta_{\text{c}} = 0,Q = 0$ also all extended parameters are zero

Table 3 Statistical shooting assessment and outcomes from bvp4c with Freidoonimehr and Rahimi [75] and Wang [76] for $f^{\prime\prime}\left( 0 \right),$ when $\gamma = M = 0,\delta_{\text{t}} = 0,\delta_{\text{c}} = 0,Q = 0$ also all extended parameters are zero

Table 4 Statistical shooting assessment and outcomes from bvp4c with Freidoonimehr and Rahimi [75] and Wang [76] for $- g^{\prime\prime}\left( 0 \right)$ when $\gamma = M = 0,\delta_{\text{t}} = 0,\delta_{\text{c}} = 0,Q = 0$ also all extended parameters are zero

Table 5 Local Nusselt number $- \theta \left( 0 \right)$ versus $\Pr ,\delta_{\text{T}} ,\delta_{\text{E}} ,\theta_{\text{w}} ,N_{\text{r}} ,\gamma ,N_{\text{t}} ,N_{\text{b}} ,Q$

Table 6 Local Sherwood number $- \phi^{\prime}\left( 0 \right)$ versus $\Pr ,\delta_{\text{T}} ,\delta_{\text{E}} ,E,N_{\text{r}} ,\gamma ,N_{\text{t}} ,N_{\text{b}}$

Conclusions

The quantitative findings of this study are as follows:

• Velocity decreases with higher values of magnetic parameter because of Lorentz forces, whereas temperature boosts up.

• Velocity and concentration decrease with higher values of slip parameter; however, the reverse conductivity is noted for temperature distribution.

• Velocity, temperature and concentration decline with rising values of stretching parameter.

• Enhancement of radiation parameter leads to enhancement of volume friction.

• The temperature distribution decreases with relaxation heat diffusion.