Introduction

Rayleigh–Bénard convection (RBC) is a well-known convective phenomenon that occurs in nature and it has applications in many fields including the heat exchangers. In RBC, the following external mechanisms are considered as regulating mechanisms of heat transport:

  1. 1.

    Gravity modulation.

  2. 2.

    Boundary temperature modulation.

  3. 3.

    Rotational modulation.

Gravity modulation is essentially g-jitter or time-periodic body force, i.e., gravity-aligned oscillation of the Rayleigh–Bénard system. Modulated gravitational field effect on RBC has been of interest since long. Low-amplitude perturbation caused by crew motions, solar drag and other sources are experienced in a space-based experiment. The study on effect of gravitation modulation is of primary importance in such an experiment. It was Gershuni and Zhukhovitskii [1] who first reported the influence of g-jitter in an infinite extent horizontal plane confined with a Newtonian liquid. Gresho and Sani [2] investigated the effect of gravity modulation on a simple pendulum and reported a useful mechanical analogy. The effect of modulations of vertical temperature gradient and gravitational field on onset of convection using both physically realistic boundaries and free boundaries was studied by Greshuni et al. [3]. An excellent review on gravity modulation was reported by Davis [4]. Biringen and Peltier [5] studied numerically the effect of sinusoidal and random modulations in different liquids by varying Prandtl number, and they concluded that compared to random modulation, sinusoidal modulation has effective stabilizing property in the three-dimensional RBC. Using high-frequency gravity modulation, Wheeler et al. [6] performed a linear stability analysis of RBC and reported the primary importance of frequency of modulation. Recently, Siddheshwar and Kanchana [7] and Siddheshwar and Meenakshi [8] studied the influence of three different wave-types of gravity-aligned oscillations (triangle, square and trigonometric sine) and showed that the influence of all the three types of wave-forms is to stabilize the Rayleigh–Bénard system in the presence/absence of nanoparticles and compared to the triangle wave-form, trigonometric sine wave-form transports maximum heat.

Venezian [9] made a linear stability analysis of the temperature-modulated RBC. Venezian [9] considered small amplitudes of modulation and obtained the shift in the critical Rayleigh number as a function of the driving frequency. Modulation of thermal instability at low frequency was investigated by Rosenblat and Herbert [10]. A classical Bénard problem with both steady and time-periodic components of modulation was considered by Rosenblat and Tanaka [11] in order to study the linear stability of the problem. Experimental and theoretical works on RBC under periodic external modulation was done by Ahlers et al. [12]. Schmitt and Lucke [13] derived an amplitude equation for convective rolls when the temperatures of the horizontal boundaries are modulated sinusoidally in time. Siddheshwar et al. [14] showed that the effect of temperature modulation on heat transfer depends not only on the frequency of temperature modulation but also on the phase difference. The combined effect of temperature modulation and rotation on RBC was investigated by Singh and Singh [15] using the classical Floquet theory. They studied harmonic and subharmonic natures of instability depending upon the Coriolis force, frequency and amplitude.

The effect of rotation on onset of RBC was initiated by Chandrasekhar [16]. He showed that the disturbances in the liquid layer due to rotation results in a delay of the onset of convection. Bhattacharjee [17] showed that the threshold of convection can be raised or lowered depending on the Prandtl number and rotation speed. Küppers and Lortz [18] considered high rotation rates because of which the stable steady-state convective flow makes a direct transition to a weakly turbulent state. A number of laboratory studies confirmed that the onset of convection is indeed time-dependent [19, 20] although the mechanism for time dependence is different. Recently, Geurts and Kunnen [21] and Kooij et al. [22] studied heat transfer in a Rayleigh–Bénard configuration consisting of a vertical cylinder which is rotating about one of its axis and the rotation rate is modulated harmonically in time. For particular rotation rate, they observed an enhancement in heat transport.

Another innovative way of enhancing the heat transfer in RBC is using nanoliquid (Newtonian liquid suspended with dilute concentration of 10–100 nm sized metal/nonmetal particles or carbon nanotubes) as a working medium. The keyword, nanoliquid, is introduced by Choi [23] who showed that there is a tremendous enhancement in thermal conductivity of baseliquid due to nanoparticles suspension. Thereafter, so many nanoliquid-related investigations were appeared in the literature using different nanomaterials and base liquids. A review on this aspect is provided by Azmi et al. [24] and Pinto and Firrelli [25]. Quite recently, Esfahani and Feshalami [26] made an interesting study on onset and heat transport in RBC in different nanoliquids using new empirical models. After peer review of the literature, it becomes apparent that compared to the study on modulation-imposed RBC in Newtonian liquids the study on modulation-imposed RBC in Newtonian nanoliquids is sparse. Yadav et al. [27] studied thermal instability of rotating nanofluids using the Galerkin method. The analytical expression of the critical Rayleigh number for both non-oscillatory and oscillatory cases was discussed. Bhadauria and Agarwal [28] studied the effect of rotation in a linear stability analysis of convection involving a Newtonian nanoliquid and explained the effect of various parameters on the critical Rayleigh number. Even though Yadav et al. [27] and Bhadauria and Agarwal [28] studied RBC in a Newtonian nanoliquid, they used base liquid properties in their study. The present study deviates from the study on RBC in nanoliquids reported by these investigators in the sense that the thermophysical properties of nanoliquids are included in the two-phase model. The two-phase model used in the present paper is proposed by Siddheshwar et al. [29] for the case of non-modulated system and used by many investigators [30,31,32,33,34,35]. Siddheshwar et al. [29] in their paper called this model as the generalized Buongiorno two-phase model. We retain this name for the model in the current study also.

In some applications, for instance in the thermoacoustic engine [36] there is a need to regulate convection and have either a standing wave or traveling wave. Suppression of convection may be achieved by imposing suitable acoustics (modulation of acceleration or by vibration). Similarly in pulse tube cryocoolers, the convection is suppressed by acoustic. Thus, gravity modulation or vibration plays an important role in such devices to stabilize thermal convection. Rotational modulated RBC is an non-isothermal system that can throw light on a mixing process. An additional advantage in such mixing processes can be had by usage of nanoparticles/nanotubes of high thermal conductivity that might help in adding more vigor to a mixing process and might also help in the visualization of such a process. These above applications motivate the present study. The present study includes three different ways of modulating Rayleigh–Bénard convective system externally with same amplitude and frequency. The three different modulations considered in the paper are: gravity, boundary temperature and rotational modulations. Though the amplitude and the frequency of all the three modulations are assumed to be same, the outcome of these modulations is not similar, and this is because the gravity modulation and rotational modulation affect the momentum equation whereas the boundary temperature modulations affect the heat equation and the former modulations retain symmetry of the conduction state but the latter one induces a nonlinear conduction profile [37]. Due to these variations in modulations, there will be shift in the threshold of onset of convection and change in the Nusselt number value. An added advantage in heat transfer or in flow visualization can be had by the addition of nanoparticles/nanotubes in the base liquid. Thus, the present study throws light on many application situations. Five nanoparticles, two nanotubes and four base liquids are considered in the paper to obtain a combination of twenty-eight nanoliquids. The feasibility of using these nanoparticles/nanotubes are also discussed in the paper. The generalized Buongiorno two-phase model is used for the description of the nanoliquids. Using a truncated Fourier series representation, the generalized Lorenz model is obtained for each modulation problem. The Lorenz model is then transformed to the respective Ginzburg–Landau model using the method of multiscales [38]. The solution of the Ginzburg–Landau model is used in quantifying the heat transport in terms of the Nusselt number. With this background of the literature and mention on importance of the problem, we now move on to the formulation of the RBC problem in the presence of different types of modulations and in the presence/absence of nanoparticles.

Mathematical formulation

Description of the Rayleigh–Bénard convection setup

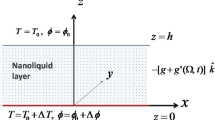
Let us consider an infinite extent horizontal nanoliquid layer between two thin parallel plates, \(z=0\) and \(z=h\). The upper and lower plates are maintained at constant temperatures \(T_0\) and \(T_0+\Delta T (\Delta T>0)\). Further, since the working medium is considered to be a nanoliquid and two-phase model is adopted in the study we assume the upper and lower plates are maintained at constant nanoparticle concentrations \(\phi _0\) and \(\phi _0+\Delta \phi (\Delta \phi >0),\) respectively. The system is subject to stress-free, isothermal and isonanoparticle concentration boundary conditions. The schematic of the setup is provided in Fig. 1.

Fig. 1
figure 1

Schematic of Rayleigh–Bénard convection problem

Full size image

Governing equations for nanoliquids

The governing system of equations in dimensional form for studying two-dimensional Rayleigh–Bénard convection (independent of the horizontal co-ordinate, y) in nanoliquids using the generalized Buongiorno two-phase model with the assumption of the Oberbeck–Boussinesq approximation and the small-scale convective motion are:

$$\begin{aligned}&\nabla \cdot \mathbf {q}=0, \end{aligned}$$
(1)
$$\begin{aligned}&\rho _\mathrm{nl}\dfrac{\partial \mathbf {q}}{\partial t} =- \nabla p +\mu _\mathrm{nl}\nabla ^2 \mathbf {q} \nonumber \\&\quad +\left[ \rho _\mathrm{nl}-(\rho \beta _1)_\mathrm{nl}(T-T_0) + (\rho \beta _2)_\mathrm{nl} (\phi -\phi _0)\right] \mathbf {g}, \end{aligned}$$
(2)
$$\begin{aligned}&(\rho \texttt {C}_\mathrm{p})_\mathrm{nl}\left[ \dfrac{\partial T}{\partial t}+ (\mathbf {q}\cdot \nabla ) T\right] = k_\mathrm{nl}\nabla ^2 T,\end{aligned}$$
(3)
$$\begin{aligned}&\dfrac{\partial \phi }{\partial t}+ (\mathbf {q}\cdot \nabla )\phi = D_\mathrm{B} \nabla ^2 \phi + \dfrac{D_\mathrm{Th}}{T_0}\nabla ^2 T, \end{aligned}$$
(4)

where \(\mathbf {q}=(u,w)\) is the velocity vector in m, t is time in s, p is the pressure in Pa, \(\mathbf {g}=(0,0, -g)\), acceleration due to gravity in \(\text {m}\,\text {s}^{-2}\), T is the temperature in K, \(\phi\) is the normalized nanoparticles/nanotube volume fraction, \(\mu _\mathrm{nl}\), \(\rho _\mathrm{nl}\), \(\beta _{1_\mathrm{nl}}\), \(\beta _{2_\mathrm{nl}}\), \(\texttt {C}_{p_\mathrm{nl}}\) and \(k_\mathrm{nl},\) respectively represent dynamic viscosity (in \(\text {kg}\,\text {ms}^{-1}\)), density (in \(\text {kg}\,\text {m}^{-2}\)), thermal expansion coefficient (in \(\text {K}^{-1}\)), nanoparticles/nanotube expansion coefficient (in \(\text {kg}^{-1}\)), specific heat (in \(\text {J}\,\text {kg}^{-1}\,\text {K}^{-1}\)) and thermal conductivity (in \(\text {W}\,\text {m}^{-1}\,\text {K}^{-1})\) of nanoliquid and are calculated using either phenomenological laws or mixture theory (see Table 1).

The term, \(n\), in Hamilton-Crosser model represents the shape factor for spherical shaped nanoparticles, \(n=3\) for nanotubes \(n=3.75\).

The term, \(D_\mathrm{B}\) and \(D_\mathrm{Th}\) represent the diffusion coefficients and are defined as:

$$\begin{aligned} D_\mathrm{B}=\dfrac{K_\mathrm{B} T}{3\pi \mu _\mathrm{nl}d_\mathrm{h}} \text { and } D_\mathrm{Th}=0.26\dfrac{k_\mathrm{nl}}{2k_\mathrm{nl}+k_\mathrm{np}}\dfrac{\mu _\mathrm{nl}}{\rho _\mathrm{nl}}\chi \end{aligned}$$
(5)

where \(d_\mathrm{h}\) denotes hydrodynamic diameter. In the paper, we considered both spherical-shaped nanoparticles and nanotubes. For nanoparticles \(d_\mathrm{h}=d_\mathrm{np}\), average diameter of nanoparticles and in the case of nanotubes,

$$\begin{aligned} d_\mathrm{h}=\dfrac{l}{\log \left( \dfrac{l}{d_\mathrm{nt}}\right) +0.32}, \end{aligned}$$
(6)

where \(d_\mathrm{nt}\) denotes the nanotube diameter and l is the length of nanotubes.

Table 1 Thermophysical properties of nanoliquids using phenomenological laws and mixture theory
Full size table

The governing system of Eqs. (1)–(4) is subject to stress-free, isothermal and iso-nanoparticles’ concentration boundary condition:

$$\begin{aligned} \left. \begin{aligned} u=0,w=0,\;S_{xz} =0, T=T_0+\Delta T,\phi =\phi _0+\Delta \phi \text { at } z=0 \\ u=0,w=0,\;S_{xz} =0,T=T_0,\phi =\phi _0 \text { at } z=h \end{aligned} \right\} , \end{aligned}$$
(7)

where u and w are the ith and kth-components of velocity vector, \(\mathbf {q}\) and \(S_{xz}=\mu_\mathrm{nl}\left(\dfrac{\partial u}{\partial z}+\dfrac{\partial w}{\partial x}\right)\).

We now impose time-periodic external driving forces to the aforementioned hydrodynamical system to study the influence of various parameters on heat transport. We first study the effect of time-periodic gravity-aligned oscillations on Rayleigh–Bénard convection in Newtonian liquids as well as Newtonian nanoliquids.

Gravity modulation

Modulation of gravitational force is achieved by periodically oscillating the nanoliquid layer vertically with time, t (see Fig. 2). Thus, the gravitational acceleration in the equation of linear momentum (2) now takes the form:

$$\begin{aligned} \mathbf {g}=(0,0, -[g+g'(\omega ,t)]), \end{aligned}$$
(8)

where \(\omega\) is frequency of modulation.

Fig. 2
figure 2

Schematic of the gravity-modulated Rayleigh–Bénard convection problem

Full size image

In the quiescent basic state, we have

$$\begin{aligned} \mathbf {q}=0, \;p=p_\mathrm{b}(z), \;T=T_\mathrm{b}(z),\; \phi =\phi _\mathrm{b}(z), \end{aligned}$$
(9)

Using Eq. (9) in the governing Eqs. (1)–(4) and substituting boundary condition (7), we get the temperature and the nanoparticles’ distribution determined by conduction and are given below:

$$\begin{aligned} \left. \begin{aligned} T_\mathrm{b}(z)= & {} \left( 1-\dfrac{z}{h}\right) \Delta T+T_0,\\ \phi _\mathrm{b}(z)= & {} \left( 1-\dfrac{z}{h}\right) \Delta \phi +\phi _0 \end{aligned} \right\} . \end{aligned}$$
(10)

We apply the following perturbations (due to an external heating and the vertical vibration) on the basic state solution:

$$\begin{aligned} \left. \begin{aligned} \mathbf {q}=\mathbf {q}'(x,z,t), \, p=p_\mathrm{b}(z)+p'(x,z,t),\\ T=T_\mathrm{b}(z)+T'(x,z,t), \,\phi =\phi _\mathrm{b}(z)+\phi '(x,z,t) \end{aligned}\right\} , \end{aligned}$$
(11)

where \(T_\mathrm{b}\) and \(\phi _\mathrm{b}\) are obtained from Eq. (10).

Using the perturbations (11) in Eqs. (2)–(4), we get the governing equation in perturbed form. We eliminate the pressure term in the resulting equations and we introduce the following stream function, \(\psi\):

$$\begin{aligned} u=-\dfrac{\partial \psi }{\partial z}, \quad w=\dfrac{\partial \psi }{\partial x}, \end{aligned}$$
(12)

that yields the following system of partial differential equations:

$$\begin{aligned}&\rho _\mathrm{nl} \dfrac{\partial }{\partial t}(\nabla ^2 \psi ) = \mu _\mathrm{nl}\nabla ^2 \psi + \left[ g+g'(\omega ,t)\right] \nonumber \\&\qquad \left( (\rho \beta _1)_\mathrm{nl}\dfrac{\partial T'}{\partial x} -(\rho \beta _2)_\mathrm{nl}\dfrac{\partial \phi '}{\partial x}\right) , \end{aligned}$$
(13)
$$\begin{aligned}&(\rho \texttt {C}_\mathrm{p})_\mathrm{nl}\left[ \dfrac{\partial T'}{\partial t}+ \dfrac{\partial \psi }{\partial x}\dfrac{\partial T'}{\partial z}-\dfrac{\partial \psi }{\partial z}\dfrac{\partial T'}{\partial x}+\dfrac{\partial \psi }{\partial x}\dfrac{\hbox {d}T_\mathrm{b}}{\hbox {d}z}\right] \nonumber \\&\quad =k_\mathrm{nl}\nabla ^2 T', \end{aligned}$$
(14)
$$\begin{aligned}&\dfrac{\partial \phi '}{\partial t}+\dfrac{\partial \psi }{\partial x}\dfrac{\partial \phi '}{\partial z}-\dfrac{\partial \psi }{\partial z}\dfrac{\partial \phi '}{\partial x}-\dfrac{\partial \psi }{\partial x}\dfrac{\hbox {d} \phi _\mathrm{b}}{\hbox {d}z} \nonumber \\&\quad = D_\mathrm{B} \nabla ^2 \phi '+\dfrac{D_\mathrm{Th}}{T_0}\nabla ^2 T'. \end{aligned}$$
(15)

Introducing the following nondimensional variables

$$\begin{aligned} \begin{aligned}&(X,Z)=\left( \dfrac{x}{h},\dfrac{z}{h}\right) , \, \tau =\dfrac{\alpha _\mathrm{bl}t}{h^2}, \, {\varPsi }=\dfrac{\psi }{\alpha _\mathrm{bl}},\\&{\varTheta }= \dfrac{T'}{\Delta T}, \, {\varPhi }= \dfrac{\phi '}{\Delta \phi }, \end{aligned} \end{aligned}$$
(16)

into Eqs. (13)–(15), we get the governing equations in nondimensional form as:

$$\begin{aligned} \dfrac{1}{\hbox {Pr}_\mathrm{nl}}\dfrac{\partial }{\partial \tau } ( \nabla ^2 {\varPsi })= & {} a_1 \nabla ^4 {\varPsi }+ \left[ 1+g_\mathrm{m}(\omega ,\tau )\right] \hbox {Ra}_\mathrm{nl}a_{1}^2 \dfrac{\partial {\varTheta }}{\partial X} \nonumber \\&-\left[ 1+g_\mathrm{m}(\omega ,\tau )\right] \hbox {Ra}_{\phi _\mathrm{nl}}a_{1}^2 \dfrac{\partial {\varPhi }}{\partial X} \end{aligned}$$
(17)
$$\begin{aligned} \dfrac{\partial {\varTheta }}{\partial \tau }= & {} a_1 \nabla ^2 {\varTheta }+\dfrac{\partial {\varPsi }}{\partial X}-J({\varPsi },{\varTheta }), \end{aligned}$$
(18)
$$\begin{aligned} \dfrac{\partial {\varPhi }}{\partial \tau }= & {} \dfrac{a_1}{\hbox {Le}_\mathrm{nl}} \nabla ^2 {\varPhi }+\dfrac{a_1N_{\mathrm{A}_\mathrm{nl}}}{\hbox {Le}_\mathrm{nl}} \nabla ^2 {\varTheta }\nonumber + \dfrac{\partial {\varPsi }}{\partial X}- J({\varPsi }, {\varPhi }), \end{aligned}$$
(19)

where \(\hbox {Pr}_\mathrm{nl} = \dfrac{\mu _\mathrm{nl}}{\rho _\mathrm{nl}\alpha _\mathrm{nl}}\) is the nanoliquid Prandtl number, \(a_1 =\dfrac{\alpha _\mathrm{nl}}{\alpha _\mathrm{bl}}\) is the diffusivity ratio, \(\hbox {Ra}_\mathrm{nl} = \dfrac{(\rho \beta _1)_\mathrm{nl} \Delta T h^3 g}{ \mu _\mathrm{nl} \alpha _\mathrm{nl}}\) is the thermal Rayleigh number, \(\hbox {Ra}_{\phi _\mathrm{nl}} = \dfrac{(\rho _\mathrm{np}-\rho _\mathrm{nl}) \Delta {\varPhi }h^3 g }{ \mu _\mathrm{nl} \alpha _\mathrm{nl}}\) is the concentration Rayleigh number, \(\hbox {Le}_\mathrm{nl} = \dfrac{\alpha _\mathrm{nl}}{D_\mathrm{B} \Delta {\varPhi }}\) is the Lewis number, \(N_{\mathrm{A}_\mathrm{nl}} = \dfrac{D_\mathrm{Th} \Delta T}{D_\mathrm{B} T_0 \Delta {\varPhi }}\) is the modified diffusivity ratio. In Eqs. (18) and (19), \(J({\varPsi },{\varTheta })\) and \(J({\varPsi }, {\varPhi })\) are Jacobians defined as \(J({\varPsi },{\varTheta })=\dfrac{\partial {\varPsi }}{\partial X}\dfrac{\partial {\varTheta }}{\partial Z}-\dfrac{\partial {\varPsi }}{\partial Z}\dfrac{\partial {\varTheta }}{\partial X}\) and \(J({\varPsi },{\varPhi })=\dfrac{\partial {\varPsi }}{\partial X}\dfrac{\partial {\varPhi }}{\partial Z}-\dfrac{\partial {\varPsi }}{\partial Z}\dfrac{\partial {\varPhi }}{\partial X}\) and in Eq. (17), \(g_\mathrm{m}(\omega , \tau ) = \dfrac{g'(\omega , \tau )}{g}\) arises due to gravity modulation.

It is clear from the definition of nondimensional parameter that the governing Eqs. (17)–(19) involve the thermophysical properties of nanoliquids which deviates the present study with the classical Buongiorno model [41].

The boundary condition (7) in nondimensional form written as:

$$\begin{aligned} \left. \begin{aligned} {\varPsi }= \dfrac{\partial ^2}{\partial Z^2}\left( \dfrac{\partial {\varPsi }}{\partial X}\right) ={\varTheta }={\varPhi }=0 \text { at } Z=0,1. \end{aligned}\right. \end{aligned}$$
(20)

By previous instigation [32], it is now well-known that the minimal mode truncated Fourier series representation is good enough to approximate solution. Hence using a minimal truncated representation we perform a weakly nonlinear stability analysis in the next subsection.

Weakly nonlinear stability analysis

We assume the solution to the stream function, temperature and nanoparticles’ concentration as the following minimal mode truncation form:

$$\begin{aligned} {\varPsi }= & {} \dfrac{\sqrt{2}a_1 \delta ^2}{\pi ^2 \kappa _\mathrm{c}} {\mathcal {A}}(\tau )\sin (\pi \kappa _\mathrm{c} X)\sin (\pi Z), \end{aligned}$$
(21)
$$\begin{aligned} {\varTheta }= & {} \dfrac{\sqrt{2}}{\pi r_\mathrm{nl}} {\mathcal {B}}(\tau )\cos (\pi \kappa _\mathrm{c} X)\sin (\pi Z) \nonumber \\&-\dfrac{1}{\pi r_\mathrm{nl}} {\mathcal {C}}(\tau )\sin (2\pi Z), \end{aligned}$$
(22)
$$\begin{aligned} {\varPhi }= & {} \dfrac{\sqrt{2}}{\pi } {\mathcal {L}}(\tau )\cos (\pi \kappa _\mathrm{c} X)\sin (\pi Z) \nonumber \\&+\dfrac{1}{\pi } {\mathcal {M}}(\tau )\sin (2\pi Z), \end{aligned}$$
(23)

where \(r_\mathrm{nl}= \dfrac{\hbox {Ra}_\mathrm{nl}\pi ^2 \kappa _\mathrm{c}^2}{\delta ^6}\), \(\kappa _\mathrm{c}\) is the critical wave number and \(\delta ^2=\pi ^2 (1+\kappa _\mathrm{c}^2)\). The coefficient of amplitudes, \({\mathcal {A}},{\mathcal {B}},{\mathcal {C}},{\mathcal {L}}\) and \({\mathcal {M}}\) represent the scaling. With these scalings, we get the generalized Lorenz model which resembles the classical Lorenz model in the limiting case (in the absence of modulation and nanoparticles).

Substituting the solution (21)–(23) into the governing Eqs. (17)–(19) and using orthogonality condition with the corresponding eigenfunctions \(\sin (\pi \kappa _\mathrm{c} X)\sin (\pi Z)\), \(\cos (\pi \kappa _\mathrm{c} X)\sin (\pi Z)\) and \(\sin (2\pi Z)\), we get the following generalized Lorenz system which involves the properties of nanoparticles and base liquid and the influence of the gravity-aligned oscillation:

$$\begin{aligned} \dfrac{1}{ \hbox {Pr}_\mathrm{nl}}\dfrac{\hbox {d}{\mathcal {A}}}{\hbox {d}\tau _1}= & {} a_1 \left( -{\mathcal {A}}+\left[ 1+g_\mathrm{m}(\omega ,\tau _1)\right] {\mathcal {B}} \right. \nonumber \\&\quad \left. -\left[ 1+g_\mathrm{m}(\omega ,\tau _1)\right] r_{\phi _\mathrm{nl}}{\mathcal {L}}\right) , \end{aligned}$$
(24)
$$\begin{aligned} \dfrac{\hbox {d}{\mathcal {B}}}{\hbox {d}\tau _1}= & {} a_1 (r_\mathrm{nl} {\mathcal {A}}-{\mathcal {B}}-{{\mathcal {A}}}{{\mathcal {C}}}), \end{aligned}$$
(25)
$$\begin{aligned} \dfrac{\hbox {d}{\mathcal {C}}}{\hbox {d}\tau _1}= & {} a_1 ({{\mathcal {A}}}{{\mathcal {B}}}-b_1{\mathcal {C}}),\end{aligned}$$
(26)
$$\begin{aligned} r_\mathrm{nl}\dfrac{\hbox {d}{\mathcal {L}}}{\hbox {d}\tau _1}= & {} a_1\left( r_\mathrm{nl} {\mathcal {A}}-\dfrac{N_{\mathrm{A}_\mathrm{nl}}}{\hbox {Le}_\mathrm{nl}} {\mathcal {B}}- \dfrac{r_\mathrm{nl}}{\hbox {Le}_\mathrm{nl}}{\mathcal {L}}+r_\mathrm{nl}{{\mathcal {A}}}{{\mathcal {M}}}\right) ,\end{aligned}$$
(27)
$$\begin{aligned} r_\mathrm{nl}\dfrac{\hbox {d}{\mathcal {M}}}{\hbox {d}\tau _1}= & {} a_1\left( \dfrac{ b_1N_{\mathrm{A}_\mathrm{nl}}}{\hbox {Le}_\mathrm{nl}}{\mathcal {C}}-\dfrac{b_1r_\mathrm{nl}}{\hbox {Le}_\mathrm{nl}} {\mathcal {M}}-r_\mathrm{nl}{{\mathcal {A}}}{{\mathcal {L}}}\right) , \end{aligned}$$
(28)

where \(\tau _1=\delta ^2 \tau\), \(r_{\phi _\mathrm{nl}}= \dfrac{\hbox {Ra}_{\phi _\mathrm{nl}}\pi ^2 \kappa _\mathrm{c}^2}{\delta ^6}\) and \(b_1=\dfrac{4\pi ^2}{\delta ^2}\).

In the paper, the gravity modulation is taken to be a trigonometric sine function, viz., \(g_\mathrm{m}(\omega , \tau _1) = \epsilon ^2\delta _2 \sin (\omega \tau _1)\). The factor \(\epsilon ^2\) is included with the amplitude, \(\delta _2\), to emphasize that the modulation considered in the paper to be of small amplitude that facilitates the use of a regular perturbation expansion in Eqs. (24)–(28) in terms of \(\epsilon\):

$$\begin{aligned} \left[ \begin{matrix} {\mathcal {A}} \\ {\mathcal {B}} \\ {\mathcal {C}}\\ {\mathcal {L}}\\ {\mathcal {M}}\\ r_\mathrm{nl} \end{matrix} \right]= & {} \left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{matrix} \right] +\epsilon \left[ \begin{matrix} A_1 \\ B_1\\ C_1 \\ L_1 \\ M_1 \\ 0 \end{matrix} \right] \nonumber \\&+\epsilon ^2 \left[ \begin{matrix} A_2 \\ B_2 \\ C_2 \\ L_2 \\ M_2 \\ r_2 \end{matrix} \right] + \epsilon ^3 \left[ \begin{matrix} A_3 \\ B_3\\ C_3 \\ L_3 \\ M_3 \\ 0 \end{matrix} \right] + \cdots \end{aligned}$$
(29)

We assume the time variations only at the small scale \(\tau _1^* = \epsilon ^2 \tau _1\) and hence \(g_\mathrm{m}(\omega ^*, \tau _1^*)= \epsilon ^2 \delta _2 \sin (\omega ^* \tau _1^*)\) where \(\omega ^*=\dfrac{\omega }{\epsilon ^2}\). The nondimensional parameter, \(N_{\mathrm{A}_\mathrm{nl}}\), describes the thermophoretic effect and is assumed to be weak and arises in the order of \(\epsilon ^2\). For the sake of mathematical convenience, we define the operators

$$\begin{aligned}&\texttt {L} = \left[ \begin{matrix} -a_1 &{} \quad a_1 &{} \quad 0 &{} \quad -a_1 r_{\phi _\mathrm{nl}} &{} \quad 0 \\ a_1 &{} \quad a_1 &{} \quad 0 &{} \quad 0 &{} \quad 0\\ 0 &{} \quad 0 &{} \quad -b_1a_1 &{} \quad 0 &{} \quad 0\\ a_1 &{} \quad 0 &{} \quad 0&{} \quad -\dfrac{a_1}{\hbox {Le}_\mathrm{nl}} &{} \quad 0\\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad -\dfrac{a_1 b_1}{\hbox {Le}_\mathrm{nl}} \end{matrix} \right] \text { and } \nonumber \\&U_\mathrm{i} = \left[ \begin{matrix} A_\mathrm{i} \\ B_\mathrm{i} \\ C_\mathrm{i} \\ L_\mathrm{i} \\ M_\mathrm{i} \end{matrix} \right] , \quad i = 1(1)3. \end{aligned}$$
(30)

On applying regular perturbation Eq. (29) into the governing system of Eqs. (24)–(28) and extracting \(o(\epsilon )\), \(o(\epsilon ^2)\) and \(o(\epsilon ^3)\) on either side of the resulting equations, we get system of homogeneous/nonhomogeneous equations.

At \(o(\epsilon )\), we get a homogeneous system:

$$\begin{aligned} \texttt {L}U_1 = 0, \end{aligned}$$
(31)

Solving the above system, we get the following solution

$$\begin{aligned}&[A_1, \, B_1, \, C_1, \, L_1, \, M_1]^{\mathrm{Tr}} \nonumber \\&\quad = [{\mathcal {A}}_{1_0}, \, {\mathcal {A}}_{1_0}, \, 0, \, \hbox {Le}_{\mathrm{nl}}{\mathcal {A}}_{1_0}, \, 0]^{\text{Tr}}, \end{aligned}$$
(32)

where \({\mathcal {A}}_{1_0}\) is an arbitrary function of \(\tau _1^*\).

At \(o(\epsilon ^2)\), we get a nonhomogeneous system:

$$\begin{aligned} \texttt {L}U_2 = [R_{21},R_{22},R_{23},R_{24},R_{25}]^\mathrm{Tr}, \end{aligned}$$
(33)

where

$$\begin{aligned}&R_{21} = 0, R_{22} = a_1 A_1 C_1, R_{23} = -a_1 A_1 B_1, \nonumber \\&R_{24} = - A_1 M_1, R_{25} = - A_1 L_1. \end{aligned}$$
(34)

Substituting the solution of first-order system, i.e., Eq. (32), in the (33) and solving the resultant equations, we get solution of second-order system:

$$\begin{aligned}&[A_2, \, B_2, \, C_2, \, L_2, \, M_2]^\mathrm{Tr} \nonumber \\&\quad = \left[ 0, \, 0, \, \dfrac{1}{b_1}{\mathcal {A}}_{1_0}^2, \, 0, \, \dfrac{-\hbox {Le}_\mathrm{nl}^2}{b_1}{\mathcal {A}}_{1_0}^2\right] ^\mathrm{Tr}, \end{aligned}$$
(35)

At \(o(\epsilon ^3)\), we get a nonhomogeneous system:

$$\begin{aligned} \texttt {L}U_3 = [R_{31},R_{32},R_{33},R_{34},R_{35}]^\mathrm{Tr}, \end{aligned}$$
(36)

where

$$\begin{aligned} \left. \begin{aligned} R_{31} =\dfrac{1}{\hbox {Pr}_\mathrm{nl}}\dfrac{\hbox {d}A_1}{\hbox {d}\tau _1^*}-a_1 \hbox {Pr}_\mathrm{nl} \delta _2 \sin (\omega ^* \tau _1^*)B_1 + a_1 \hbox {Pr}_\mathrm{nl} r_{\phi _\mathrm{nl}} \delta _2 \sin (\omega ^* \tau _1^*)L_1,\\ R_{32} = \dfrac{\hbox {d}B_1}{\hbox {d} \tau _1^*}-a_1 r_2 A_1 +a_1 A_1 C_2, \\ R_{33} = -a_{1}(A_1 B_2 +A_2 B_1)+\dfrac{\hbox {d}C_1}{\hbox {d}\tau _1^*},\\ R_{34} = - a_1(A_1M_2+A_2M_1)+\dfrac{\hbox {d}L_1}{\hbox {d}\tau _1^*}-a_1r_2 A_1 +a_1 \dfrac{N_{\mathrm{A}_\mathrm{nl}}}{\hbox {Le}_\mathrm{nl}}B_1+\dfrac{1}{\hbox {Le}_\mathrm{nl}}L_1,\\ R_{35} = a_1(A_1L_2+A_2L_1)+\dfrac{\hbox {d}M_1}{\hbox {d}\tau _1^*}+\dfrac{a_1b_1r_2}{\hbox {Lev}}M_1. \end{aligned} \right\} . \end{aligned}$$
(37)

At the third-order system, we determine the amplitude, \({\mathcal {A}}_{1_0}\), using the Fredholm solvability condition which states that ‘the inhomogeneous terms must be orthogonal to the solution of the homogenous system’, i.e.,

$$\begin{aligned} R_{31}\hat{A_1}+R_{32}\hat{B_1}+R_{33}\hat{C_1}+R_{34}\hat{L_1}+R_{35}\hat{M_1}=0, \end{aligned}$$
(38)

where \((\hat{A_1},\hat{B_1},\hat{C_1},\hat{L_1}, \hat{M_1})\) denote the solution of adjoint system (31).

Equation (38) yields to the Ginzburg–Landau equation:

$$\begin{aligned} \dfrac{\hbox {d}{\mathcal {A}}_{1_0}(\tau _1^*)}{\hbox {d}\tau _1^*} = Q_1 {\mathcal {A}}_{1_0}(\tau _1^*)-Q_2 {\mathcal {A}}_{1_0}^3(\tau _1^*). \end{aligned}$$
(39)

The expressions for the coefficients \(Q_1\) and \(Q_2\) are, respectively, given by:

$$\begin{aligned} \left. \begin{aligned} Q_1 = \dfrac{a_1 \hbox {Pr}_\mathrm{nl}\left[ r_{2}+N_{\mathrm{A}_\mathrm{nl}}r_{\phi _\mathrm{nl}}+ \delta _2 \sin (\omega ^* \tau _1^*)(r_0-r_{\phi _\mathrm{nl}}\hbox {Le}_\mathrm{nl})\right] }{1+\hbox {Pr}_\mathrm{nl}(r_0-\hbox {Le}_\mathrm{nl}^2r_{\phi _\mathrm{nl}})},\\ Q_2 = \dfrac{ \hbox {Pr}_\mathrm{nl}(r_0-\hbox {Le}_\mathrm{nl}^3r_{\phi _\mathrm{nl}})}{b_1 \left[ 1+\hbox {Pr}_\mathrm{nl}(r_0-\hbox {Le}_\mathrm{nl}^2r_{\phi _\mathrm{nl}})\right] }, \end{aligned} \right\} . \end{aligned}$$
(40)

On taking \(r_{\phi _\mathrm{nl}}=0\) in Eq. (39), we arrive at the Ginzburg–Landau equation for Newtonian liquids reported by Siddheshwar [42].

We next study the influence of boundary temperature modulation on Rayleigh–Bénard convection in Newtonian liquids and Newtonian nanoliquids.

Boundary temperature modulation

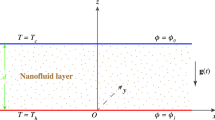
The boundary temperature modulation in Rayleigh–Bénard convection is achieved by imposing externally a time-periodic boundary temperature with small amplitude, \(\epsilon ^2 \delta _2\), phase difference, \(\varphi\), and frequency, \(\omega\). In the problem of the generalized Buongiorno two-phase model, it is necessary to consider the wall introduction of nanoparticles’ concentration in addition to wall temperature. The schematic of the problem is shown in Fig. 3. The governing system of equations in dimensional form for studying Rayleigh–Bénard convection in nanoliquids using a two-phase model are Eqs. (1)–(4).

Fig. 3
figure 3

Schematic of Rayleigh–Bénard convection with boundary temperature modulation

Full size image

The external imposed wall temperatures (Venezian [9]) are

$$\begin{aligned} \left. \begin{aligned} T=T_0+\dfrac{\Delta T}{2}\left[ 1+\epsilon ^2\delta _2\cos (\omega t)\right] \quad \text {at} \quad z=0,\\ T=T_0-\dfrac{\Delta T}{2}\left[ 1-\epsilon ^2\delta _2\cos (\omega t+\varphi )\right] \quad \text {at} \quad z=h, \end{aligned} \right\} . \end{aligned}$$
(41)

Similarly, for wall introduction of concentration we need to take:

$$\begin{aligned} \left. \begin{aligned} \phi =\phi _0+\dfrac{\Delta \phi }{2}\left[ 1+\epsilon ^2\delta _2\cos (\omega t)\right] \quad \text {at} \quad z=0,\\ \phi =\phi _0-\dfrac{\Delta \phi }{2}\left[ 1-\epsilon ^2\delta _2\cos (\omega t+\varphi )\right] \quad \text {at} \quad z=h, \end{aligned} \right\} . \end{aligned}$$
(42)

The velocity, pressure, temperature and nanoparticles’ concentration fields in the quiescent basic state are given by

$$\begin{aligned}&q_\mathrm{b} (z)=(0,0), \;\; p=p_\mathrm{b}(z,t), \;\; T_\mathrm{b}=T_\mathrm{b} (z,t), \\&\phi _\mathrm{b}=\phi _\mathrm{b}(z,t), \end{aligned}$$

which satisfy the following equations:

$$\begin{aligned} -\dfrac{\hbox {d} p_\mathrm{b}}{\hbox {d} z}= & {} [\rho _\mathrm{nl}-(\rho \beta )_\mathrm{nl}(T_\mathrm{b}-T_0)]g, \end{aligned}$$
(43)
$$\begin{aligned} \dfrac{\partial T_\mathrm{b}}{\partial t}= & {} \alpha _\mathrm{nl}\dfrac{\partial ^2T_\mathrm{b}}{\partial z^2}, \end{aligned}$$
(44)
$$\begin{aligned} \dfrac{\partial \phi _\mathrm{b}}{\partial t}= & {} D_\mathrm{B}\dfrac{\partial ^2\phi _\mathrm{b}}{\partial z^2}+\dfrac{D_\mathrm{T}}{T_0}\dfrac{\partial ^2T_\mathrm{b}}{\partial z^2}. \end{aligned}$$
(45)

Equations (44) and (45) consist of the sum of a steady part and an oscillating part:

$$\begin{aligned} T_\mathrm{b}=T_\mathrm{s}(z)+\epsilon ^2T_1(z,t), \end{aligned}$$
(46)
$$\begin{aligned} {\phi _{\mathrm{b}}}={\phi _{\text{s}}}(z)+\epsilon ^2 \phi _1(z,t). \end{aligned}$$
(47)

Solving Eqs. (43)–(45) with the help of Eqs. (46) and (47) and using the boundary conditions (41) and (42), we get

$$\begin{aligned} T_\mathrm{b}(z,t)= & {} T_0+\Delta T\left( \frac{1}{2}-\frac{z}{h}\right) \nonumber \\&+ \epsilon ^2\delta _2\text {Re}\{[a(\lambda _1) \text {e}^{\uplambda {\text{z}}}+a(-\lambda ) \text {e}^{-\uplambda {\text{z}}}]\text {e}^{\text {-i}\upomega {\text{t}}}\}, \end{aligned}$$
(48)
$$\begin{aligned} \phi _\mathrm{b}(z,t)= & {} \phi _0+\Delta \phi \left( \frac{1}{2}-\frac{z}{h}\right) \nonumber \\&+\epsilon ^2\delta _2\text {Re}\{[a(\lambda _1) \text {e}^{\uplambda _1 {\text{z}}}+a(-\lambda _1)\text {e}^{-\uplambda _1 {\text{z}}}] \text {e}^{\text {-i}\upomega {\text{t}}}\} \nonumber \\&+ N_{\mathrm{A}_\mathrm{nl}} \left[ \dfrac{\lambda ^2}{\lambda ^2-\lambda _1^2} \left[ \left( \dfrac{\text {e}^{\uplambda _1 {\text{z}}}-\text {e}^{-\uplambda _1 {\text{z}}}}{\text {e}^{\uplambda _1 {\text{h}}}-\text {e}^{-\uplambda _1 {\text{h}}}}\right) \right. \right. \nonumber \\& \qquad \left. \left( a'(\lambda ,\lambda _1)+a'(-\lambda ,-\lambda _1) \right) +a'(-\lambda ,-\lambda _1)\right) \nonumber \\& \qquad +a(\lambda )(\text {e}^{-\uplambda _1 {\text{z}}}-\text {e}^{\uplambda {\text{z}}}) \nonumber \\& \qquad \left. \left. +a(-\lambda )(\text {e}^{-\uplambda _1 {\text{z}}}-\text {e}^{\uplambda {\text{z}}})\right] \right] , \end{aligned}$$
(49)

where

$$\begin{aligned}&a'(\lambda ,\lambda _1) = \dfrac{\Delta T}{2}\left[ \dfrac{\text {e}^{\text {-i} \varphi }-\text {e}^{-\uplambda {\text{h}}}}{\text {e}^{\uplambda {\text{h}}}-\text {e}^{-\uplambda {\text{h}}}}\right] \left( \text {e}^{\uplambda {\text{h}}}-\text {e}^{\uplambda _1 {\text{h}}}\right) ,\end{aligned}$$
(50)
$$\begin{aligned}&a(\lambda _1)=\dfrac{\Delta T}{2}\left[ \dfrac{\text {e}^{\text {-i}\varphi }- \text {e}^{-\uplambda {\text{h}}}}{\text {e}^{\uplambda {\text{h}}}-\text {e}^{-\uplambda {\text{h}}}}\right] , \nonumber \\&\quad \lambda =(1-\text {i})\sqrt{\frac{\omega h^2}{2\alpha _\mathrm{nl}}}, \end{aligned}$$
(51)
$$\begin{aligned}&a(\lambda _1) = \dfrac{\Delta \phi }{2}\left[ \dfrac{\text {e}^{\text {-i}\varphi } -\text {e}^{-\uplambda _1 {\text{h}}}}{\text {e}^{\uplambda _1 {\text{h}}}-\text {e}^{-\uplambda _1 {\text{h}}}}\right] , \nonumber \\&\quad \lambda _1=(1-\text {i})\sqrt{\frac{\omega h^2}{2D_\mathrm{B}}}. \end{aligned}$$
(52)

Applying perturbations (11) on the basic state solution (48) and (49) and introducing the stream function (12) and the scaling (16), the governing equations take the form:

$$\begin{aligned} \dfrac{1}{\hbox {Pr}_\mathrm{nl}}\dfrac{\partial }{\partial \tau } ( \nabla ^2 {\varPsi })= & {} a_1 \nabla ^4 {\varPsi }+ \hbox {Ra}_\mathrm{nl}a_{1}^2 \dfrac{\partial {\varTheta }}{\partial X} - \hbox {Ra}_{\phi _\mathrm{nl}}a_{1}^2 \dfrac{\partial {\varPhi }}{\partial X} \end{aligned}$$
(53)
$$\begin{aligned} \dfrac{\partial {\varTheta }}{\partial \tau }= & {} a_1 \nabla ^2 {\varTheta }-J({\varPsi },{\varTheta }) \nonumber \\&-\left[ \epsilon ^2 \delta _2 f(Z,\tau )-1\right] \dfrac{\partial {\varPsi }}{\partial X}, \end{aligned}$$
(54)
$$\begin{aligned} \dfrac{\partial {\varPhi }}{\partial \tau }= & {} \dfrac{a_1}{\hbox {Le}_\mathrm{nl}} \nabla ^2 {\varPhi }+\dfrac{a_1N_{\mathrm{A}_\mathrm{nl}}}{\hbox {Le}_\mathrm{nl}} \nabla ^2 {\varTheta }- J({\varPsi }, {\varPhi }) \nonumber \\&-\left[ \epsilon ^2 \delta _2 [g(Z,\tau )+N_{\mathrm{A}_\mathrm{nl}} g_1(Z,\tau )]-1\right] \nonumber \\&\dfrac{\partial {\varPsi }}{\partial X} , \end{aligned}$$
(55)

where

$$\begin{aligned} f(Z,\tau )= & {} \hbox {Re}\lbrace A(\lambda ) \text {e}^{\uplambda {\text{Z}}}+A(\lambda )\text {e}^{-\uplambda {\text{Z}}} \rbrace \text {e}^{-{\text{i}}\upomega ^* \uptau }, \end{aligned}$$
(56)
$$\begin{aligned} A(\lambda )= & {} \dfrac{\lambda }{2}\left( \dfrac{\text {e}^{{\text{i}}\varphi }-\text {e}^{-\uplambda }}{\text {e}^{\uplambda }-\text {e}^{-\uplambda }}\right) , \;\; \lambda = (1-i) \sqrt{\dfrac{\omega ^*}{2 a_1}}, \end{aligned}$$
(57)
$$\begin{aligned} g(Z,\tau )= & {} \hbox {Re}\lbrace A_1(\lambda _1) \text {e}^{\uplambda _1 {\text{Z}}}+A_1(-\lambda _1)\text {e}^{-\uplambda _1 {\text{Z}}} \rbrace \text {e}^{-{\text{i}}\upomega ^* \uptau }, \end{aligned}$$
(58)
$$\begin{aligned} A_1(\lambda _1)= & {} \dfrac{\lambda _1}{2}\left( \dfrac{\text {e}^{{\text{i}}\varphi }-\text {e}^{-\uplambda _1}}{\text {e}^{\uplambda _1}-\text {e}^{-\uplambda _1}}\right) ,\;\; \lambda _1 = (1-i) \sqrt{\dfrac{\omega ^*\hbox {Le}_\mathrm{nl}}{2 a_1}},\end{aligned}$$
(59)
$$g_{1} (Z,\tau )\lambda _{1} \left[ {M(\lambda _{1} ,\lambda ) + M(\lambda _{1} , - \lambda )} \right]({\text{e}}^{{\uplambda _{1} Z}} + {\text{e}}^{{ - \uplambda _{1} Z}} ) - N(\lambda _{1} ,\lambda )(\lambda _{1} {\text{e}}^{{ - \uplambda _{1} Z}} + \lambda {\text{e}}^{{\uplambda {\text{Z}}}} ) + N(\lambda _{1} , - \lambda )(\lambda {\text{e}}^{{\uplambda {\text{Z}}}} - \lambda _{1} {\text{e}}^{{ - \uplambda _{1} {\text{Z}}}} ),$$
(60)
$$M(\lambda _{1} ,\lambda ) = \frac{{\lambda _{1} }}{2}\frac{1}{{1 - \left( {\frac{{\lambda _{1} }}{\lambda }} \right)^{2} }}\left( {\frac{{{\text{e}}^{{ - {\text{i}}\varphi }} - {\text{e}}^{{ - \uplambda _{1} }} }}{{{\text{e}}^{{\uplambda _{1} }} - {\text{e}}^{{ - \uplambda _{1} }} }}} \right)\left( {\frac{{{\text{e}}^{\uplambda } - {\text{e}}^{{ - \uplambda _{1} }} }}{{{\text{e}}^{{\uplambda _{1} }} - {\text{e}}^{{ - \uplambda _{1} }} }}} \right),$$
(61)
$$N(\lambda _{1} ,\lambda ) = \frac{1}{{2\left( {1 - \left( {\frac{{\lambda _{1} }}{\lambda }} \right)^{2} } \right)}}\left( {\frac{{{\text{e}}^{{ - {\text{i}}\varphi }} - {\text{e}}^{{ - \uplambda _{1} }} }}{{{\text{e}}^{{\uplambda _{1} }} - {\text{e}}^{{ - \uplambda _{1} }} }}} \right).$$
(62)

Weakly nonlinear stability analysis

Following the procedure of Sec. (2.3), we get the fifth-order Lorenz model for the boundary temperature-modulated convection problem in the form:

$$\begin{aligned} \dfrac{1}{ \hbox {Pr}_\mathrm{nl}}\dfrac{\hbox {d}{\mathcal {A}}}{\hbox {d}\tau _1}= & {} a_1 \left( {\mathcal {B}}-{\mathcal {A}}-r_{\phi _\mathrm{nl}}{\mathcal {C}}\right) , \end{aligned}$$
(63)
$$\begin{aligned} \dfrac{\hbox {d}{\mathcal {B}}}{\hbox {d}\tau _1}= & {} a_1 ( r_\mathrm{nl} {\mathcal {A}}-{\mathcal {B}}- {\mathcal {A}}{\mathcal {C}}-2\epsilon ^2r_\mathrm{nl} \delta _2 F(\tau ) {\mathcal {A}}),\end{aligned}$$
(64)
$$\begin{aligned} \dfrac{\hbox {d}{\mathcal {C}}}{\hbox {d}\tau _1}= & {} a_1 ( {\mathcal {A}}{\mathcal {B}}-b{\mathcal {C}}),\end{aligned}$$
(65)
$$\begin{aligned} r_\mathrm{nl}\dfrac{\hbox {d}{\mathcal {L}}}{\hbox {d}\tau _1}= & {} a_1\left( r_\mathrm{nl} {\mathcal {A}}-\dfrac{ N_{\mathrm{A}_\mathrm{nl}}}{\hbox {Le}_\mathrm{nl}}{\mathcal {B}}-\dfrac{r_\mathrm{nl}}{\hbox {Le}_\mathrm{nl}}{\mathcal {L}}+ r_\mathrm{nl} {\mathcal {A}}{\mathcal {M}}\right. \nonumber \\&\left. +2\epsilon ^2 \delta ^2 r_\mathrm{nl} \left[ G(\tau )+\epsilon ^2 N_{\mathrm{A}_\mathrm{nl}} G_1(\tau )\right] {\mathcal {A}} \right) ,\end{aligned}$$
(66)
$$\begin{aligned} r_\mathrm{nl}\dfrac{\hbox {d}{\mathcal {M}}}{\hbox {d}\tau _1}= & {} a_1\left( \dfrac{ b_1 N_{\mathrm{A}_\mathrm{nl}}}{\hbox {Le}_\mathrm{nl}}{\mathcal {C}}-\dfrac{b_1 r_\mathrm{nl}}{\hbox {Le}_\mathrm{nl}}{\mathcal {M}}- r_\mathrm{nl} {\mathcal {A}}{\mathcal {L}}\right) , \end{aligned}$$
(67)

where

$$\begin{aligned} F(\tau )= & {} \int _{X=0}^{\frac{2\pi }{\pi \kappa _\mathrm{c}}} \int _{Z=0}^1 f(Z,\tau ) \cos ^2(\pi \kappa X)\sin ^2(\pi Z)\hbox {d}X \hbox {d}Z,\end{aligned}$$
(68)
$$\begin{aligned} G(\tau )= & {} \int _{X=0}^{\frac{2\pi }{\pi \kappa _\mathrm{c}}} \int _{Z=0}^1 g(Z,\tau ) \cos ^2(\pi \kappa X)\sin ^2(\pi Z)\hbox {d}X \hbox {d}Z,\end{aligned}$$
(69)
$$\begin{aligned} G_1(\tau )= & {} \int _{X=0}^{\frac{2\pi }{\pi \kappa _\mathrm{c}}} \int _{Z=0}^1 g_1(Z,\tau ) \cos ^2(\pi \kappa X)\sin ^2(\pi Z)\hbox {d}X \hbox {d}Z. \end{aligned}$$
(70)

Using an identical procedure to that in subsection (2.3), the Ginzburg–Landau equation for the boundary temperature modulation problem may be obtained in the form:

$$\begin{aligned} \dfrac{\hbox {d}{\mathcal {A}}_{1_0}(\tau _1^*)}{\hbox {d}\tau _1^*} = Q_3 {\mathcal {A}}_{1_0}(\tau _1^*)-Q_4 {\mathcal {A}}_{1_0}^3(\tau _1^*), \end{aligned}$$
(71)

where

$$\begin{aligned} \left. \begin{aligned} Q_3 = \dfrac{a_1 \hbox {Pr}_\mathrm{nl}(r_{2}+N_{\mathrm{A}_\mathrm{nl}}r_{\phi _\mathrm{nl}}-2\delta _2 [r_0F(\tau )+r_{\phi _\mathrm{nl}}\hbox {Le}_\mathrm{nl}G(\tau )])}{1+\hbox {Pr}_\mathrm{nl}(r_0-\hbox {Le}_\mathrm{nl}^2r_{\phi _\mathrm{nl}})},\\ Q_4 = \dfrac{a_1 \hbox {Pr}_\mathrm{nl}(r_0-\hbox {Le}_\mathrm{nl}^3r_{\phi _\mathrm{nl}})}{b_1 \left[ 1+\hbox {Pr}_\mathrm{nl}(r_0-\hbox {Le}_\mathrm{nl}^2r_{\phi _\mathrm{nl}})\right] }. \end{aligned} \right\} . \end{aligned}$$
(72)

Having obtained the Ginzburg–Landau equation of the gravity-modulated and boundary temperature-modulated convection problems, we next derive the time-dependent Ginzburg–Landau equation for Rayleigh–Bénard convection in Newtonian liquids and Newtonian nanoliquids in the presence of rotational modulation.

Rotational modulation

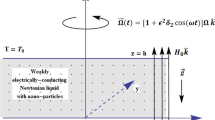
In the case of rotational modulation, the nanoliquid layer is assumed to be in rotation about the axis of z, with a constant angular velocity, \(\mathbf {\Omega }\). The motion described here occurs as it in a way as it appears to an observer at rest in a frame rotating about the same axis and with the same angular velocity. The governing system of equations in dimensional form for studying two-dimensional Rayleigh–Bénard convection in nanoliquids are given in Eq. (1)–(4) with an additional term \(2\rho _{\mathrm{nl}_0}(\mathbf {q}\times \mathbf {\Omega })\) in the linear momentum Eq. (2). The term \((\mathbf {q}\times \mathbf {\Omega })\) represents the Coriolis acceleration (see Chandrasekhar [16]) with the time-periodic angular acceleration, \(\mathbf {\Omega }(t) ={\varOmega }[1+\epsilon ^2\delta _2\cos (\omega t)]\) and \(\epsilon ^2\delta _2\) is its amplitude and \(\omega\) is frequency. Schematic of the same is shown in Fig. 4.

Fig. 4
figure 4

Schematic of rotationally modulated Rayleigh–Bénard convection problem

Full size image

The basic state solution of the rotational modulation problem is given by Eq. (10). Superimposing the perturbation, (11), on the basic state solution and using the resultant equations in Eqs. (1)–(4), eliminating the pressure and introducing the stream function, we get the nondimensional form of the governing equations to study rotating Rayleigh–Bénard convection in nanoliquids in the following form:

$$\begin{aligned}&\rho _\mathrm{nl}\dfrac{\partial }{\partial t}(\nabla ^2 \psi ) = \mu _\mathrm{nl}\nabla ^2 \psi +2\rho _{\mathrm{nl}_0} {\varOmega }[1+\epsilon ^2\delta _2\cos (\omega t)] \dfrac{\partial v}{\partial z} \nonumber \\&\qquad +(\rho \beta )_\mathrm{nl}\dfrac{\partial T'}{\partial x}g -(\rho \beta )_{\phi } \dfrac{\partial \phi '}{\partial x}g, \end{aligned}$$
(73)
$$\begin{aligned}&\rho _\mathrm{nl}\left[ \dfrac{\partial v}{\partial t}+J(\psi , v)\right] \nonumber \\&\quad = \mu _\mathrm{nl} \nabla ^2 v + 2\rho _{\mathrm{nl}_0} {\varOmega }[1+\epsilon ^2\delta _2\cos (\omega t)] \dfrac{\partial \psi }{\partial z}, \end{aligned}$$
(74)
$$\begin{aligned}&(\rho \texttt {C}_\mathrm{p})_\mathrm{nl}\left[ \dfrac{\partial T'}{\partial t}+ \dfrac{\partial \psi }{\partial x}\dfrac{\partial T'}{\partial z}-\dfrac{\partial \psi }{\partial z}\dfrac{\partial T'}{\partial x}+\dfrac{\partial \psi }{\partial x}\dfrac{\hbox {d}T_\mathrm{b}}{\hbox {d}z}\right] \nonumber \\&\quad =k_\mathrm{nl}\nabla ^2 T', \end{aligned}$$
(75)
$$\begin{aligned}&\dfrac{\partial \phi '}{\partial t}+\dfrac{\partial \psi }{\partial x}\dfrac{\partial \phi '}{\partial z}-\dfrac{\partial \psi }{\partial z}\dfrac{\partial \phi '}{\partial x}-\dfrac{\partial \psi }{\partial x}\dfrac{\hbox {d} \phi _\mathrm{b}}{\hbox {d}z}\nonumber \\&\quad = D_\mathrm{B} \nabla ^2 \phi '+\dfrac{D_\mathrm{Th}}{T_0}\nabla ^2 T', \end{aligned}$$
(76)

where v describes the local spinning motion of a continuum point observed in rotating frame of reference.

Introducing the nondimensional variables as in Eq. (16) and with \(V = \dfrac{h}{\alpha _\mathrm{bl}}v\) into the governing Eqs. (73)–(76), we get

$$\begin{aligned} \dfrac{1}{\hbox {Pr}_\mathrm{nl}}\dfrac{\partial ( \nabla ^2 {\varPsi })}{\partial \tau }= & {} a_1 \nabla ^4 {\varPsi }- a_1 \sqrt{Ta_\mathrm{nl}}[1+\epsilon ^2\delta _2\cos (\omega \tau )]\dfrac{\partial V}{\partial Z} \nonumber \\&+\hbox {Ra}_\mathrm{nl}a_{1}^2 \dfrac{\partial {\varTheta }}{\partial X} -\hbox {Ra}_{\phi _\mathrm{nl}}a_{1}^2 \dfrac{\partial {\varPhi }}{\partial X}, \end{aligned}$$
(77)
$$\begin{aligned} \dfrac{\partial V}{\partial \tau }= & {} a_1\hbox {Pr}_\mathrm{nl} \nonumber \\&\left( \nabla ^2 V +\sqrt{Ta_\mathrm{nl}}[1+\epsilon ^2\delta _2\cos (\omega \tau )] \dfrac{\partial {\varPsi }}{\partial Z}\right) \nonumber \\&-J({\varPsi },V), \end{aligned}$$
(78)
$$\begin{aligned} \dfrac{\partial {\varTheta }}{\partial \tau }= & {} a_1 \nabla ^2 {\varTheta }+ \dfrac{\partial {\varPsi }}{\partial X}- J({\varPsi },{\varTheta }), \end{aligned}$$
(79)
$$\begin{aligned} \dfrac{\partial {\varPhi }}{\partial \tau }= & {} \dfrac{a_1}{\hbox {Le}_\mathrm{nl}} \nabla ^2 {\varPhi }+\dfrac{a_1N_{\mathrm{A}_\mathrm{nl}}}{\hbox {Le}_\mathrm{nl}} \nabla ^2 {\varTheta }\nonumber \\&+ \dfrac{\partial {\varPsi }}{\partial X}- J({\varPsi }, {\varPhi }), \end{aligned}$$
(80)

where \(\hbox {Ta}_\mathrm{nl}=\left( \dfrac{2h^2\rho _0 {\varOmega }}{\mu _\mathrm{nl}}\right) ^2\) is the Taylor number which characterizes the rotation rate. Equations (77)–(80) are solved subject to stress-free, isothermal and iso-nanoparticles’ concentration boundary conditions defined in Eq. (20).

Weakly nonlinear stability analysis

We make a weakly nonlinear stability analysis of the system by assuming the stream function, temperature and nanoparticles’ concentration as in Eqs. (21)–(23) and for V, we assume:

$$\begin{aligned} V= & {} \dfrac{\sqrt{2}a_1 \delta ^2}{\pi ^2} {\mathcal {D}}(\tau )\sin (\pi \kappa X)\cos (\pi Z)\nonumber \\&+\dfrac{\delta ^3}{\pi ^2}{\mathcal {E}} \sin (2\pi \kappa _\mathrm{c} X). \end{aligned}$$
(81)

Substituting Eqs. (21)–(23) and (79) in Eqs. (77)–(80) and taking the orthogonality condition with the eigenfunctions associated with the considered minimal modes, we get

$$\begin{aligned} \dfrac{\hbox {d}{\mathcal {A}}}{\hbox {d}\tau _1}= & {} a_1\hbox {Pr}_\mathrm{nl}\nonumber \\&\left( {\mathcal {B}}-{\mathcal {A}}- \hbox {ta}_\mathrm{nl}[1+\epsilon ^2\delta _2\cos (\omega ^* \tau _1)]{\mathcal {D}}- r_{\phi _\mathrm{nl}}{\mathcal {L}}\right) , \end{aligned}$$
(82)
$$\begin{aligned} \dfrac{\hbox {d}{\mathcal {B}}}{\hbox {d}\tau _1}= & {} a_1 ( r_\mathrm{nl} {\mathcal {A}}-{\mathcal {B}}- {\mathcal {A}}{\mathcal {C}}),\end{aligned}$$
(83)
$$\begin{aligned} \dfrac{\hbox {d}{\mathcal {C}}}{\hbox {d}\tau _1}= & {} a_1 ( {{\mathcal {A}}}{{\mathcal {B}}}-b_1{\mathcal {C}}),\end{aligned}$$
(84)
$$\begin{aligned} r_\mathrm{nl}\dfrac{\hbox {d}{\mathcal {L}}}{\hbox {d}\tau _1}= & {} a_1\left( r_\mathrm{nl} {\mathcal {A}}-\dfrac{ N_{\mathrm{A}_\mathrm{nl}}}{\hbox {Le}_\mathrm{nl}}{\mathcal {B}}-\dfrac{r_\mathrm{nl}}{\hbox {Le}_\mathrm{nl}}{\mathcal {L}}+r_\mathrm{nl} {{\mathcal {A}}}{{\mathcal {M}}}\right) ,\end{aligned}$$
(85)
$$\begin{aligned} r_\mathrm{nl}\dfrac{\hbox {d}{\mathcal {M}}}{\hbox {d}\tau _1}= & {} a_1\left( \dfrac{ b_1N_{\mathrm{A}_\mathrm{nl}}}{\hbox {Le}_\mathrm{nl}}{\mathcal {C}}-\dfrac{b_1 r_\mathrm{nl}}{\hbox {Le}_\mathrm{nl}} {\mathcal {M}}- r_\mathrm{nl} {{\mathcal {A}}}{{\mathcal {L}}}\right) , \end{aligned}$$
(86)
$$\begin{aligned} \dfrac{\hbox {d}{\mathcal {D}}}{\hbox {d}\tau _1}= & {} a_1 (\hbox {Pr}_\mathrm{nl} ta_\mathrm{nl}[1+\epsilon ^2\delta _2\cos (\omega ^* \tau _1)] {\mathcal {A}}- \hbox {Pr}_\mathrm{nl}{\mathcal {D}})\nonumber \\&-{{\mathcal {A}}}{{\mathcal {E}}}, \end{aligned}$$
(87)
$$\begin{aligned} \dfrac{\hbox {d}{\mathcal {E}}}{\hbox {d}\tau _1}= & {} -\hbox {da}_1 \hbox {Pr}_\mathrm{nl}{\mathcal {E}}+a_1^2{\mathcal {A}}{\mathcal {D}}, \end{aligned}$$
(88)

where \(d=\kappa ^2 b_1\) and \(\hbox {ta}_\mathrm{nl}=\sqrt{\dfrac{\hbox {Ta}_\mathrm{nl}\pi ^2}{\delta ^6}}\).

We now use the following regular perturbation expansion in Eqs. (82)–(88) in addition to small time scale and a weak thermophoretic effect:

$$\begin{aligned} \left[ \begin{matrix} {\mathcal {A}} \\ {\mathcal {B}} \\ {\mathcal {C}}\\ {\mathcal {L}}\\ {\mathcal {M}}\\ {\mathcal {D}}\\ {\mathcal {E}}\\ r_\mathrm{nl} \end{matrix} \right]= & {} \left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ r_0 \end{matrix} \right] +\epsilon \left[ \begin{matrix} A_1 \\ B_1\\ C_1 \\ L_1 \\ M_1 \\ D_1 \\ E_1 \\ 0 \end{matrix} \right] +\epsilon ^2 \left[ \begin{matrix} A_2 \\ B_2 \\ C_2 \\ L_2 \\ M_2 \\ D_2 \\ E_2 \\ r_2 \end{matrix} \right] \nonumber + \epsilon ^3 \left[ \begin{matrix} A_3 \\ B_3\\ C_3 \\ L_3 \\ M_3 \\ D_3 \\ E_3 \\ 0 \end{matrix} \right] + \cdots \end{aligned}$$
(89)

Following the procedure of Sec. (2.3), we can get the Ginzburg–Landau equation in the form:

$$\begin{aligned} \dfrac{\hbox {d}{\mathcal {A}}_{1_0}(\tau _1^*)}{\hbox {d}\tau _1^*} = Q_5 {\mathcal {A}}_{1_0}(\tau _1^*)-Q_6 {\mathcal {A}}_{1_0}^3(\tau _1^*), \end{aligned}$$
(90)

where

$$\begin{aligned} \left. \begin{aligned} Q_5 = \dfrac{a_1 \hbox {Pr}_\mathrm{nl}\left[ r_{2}+N_{\mathrm{A}_\mathrm{nl}}r_{\phi _\mathrm{nl}}-2\delta _2 \cos (\omega ^*\tau _1^*)\hbox {ta}_\mathrm{nl}^2\right] }{1+\hbox {Pr}_\mathrm{nl} (r_0-\hbox {Le}_\mathrm{nl}^2r_{\phi _\mathrm{nl}})-\hbox {ta}_\mathrm{nl}^2},\\ Q_6 = \dfrac{\left[ a_1 \hbox {Pr}_\mathrm{nl}(r_0-\hbox {Le}_\mathrm{nl}^3 r_{\phi _\mathrm{nl}})-\dfrac{a_1b_1\;ta_\mathrm{nl}^2}{\hbox {d}\;\hbox {Pr}_\mathrm{nl}}\right] }{b_1\left[ 1+ \hbox {Pr}_\mathrm{nl}(r_0-\hbox {Le}_\mathrm{nl}^2r_{\phi _\mathrm{nl}})-\hbox {ta}_\mathrm{nl}^2\right] } \end{aligned} \right\} . \end{aligned}$$
(91)

The Ginzburg–Landau equations (39), (71) and (90) obtained from gravity, boundary temperature and rotation modulations, respectively, are analytically intractable due to their non-autonomous nature. The coefficient of the linear term of the Ginzburg–Landau equations depends on amplitude and frequency of modulation. \(r_0\) and \(r_2\) in the Ginzburg–Landau equations (39), (71) and (88) are scaled Rayleigh number and scaled correction Rayleigh number. Without loss of generality, we assume \(r_0=r_\mathrm{c}\), critical Rayleigh number for unmodulated system, and from previous investigation [7] we found that \(r_2\simeq 1\). We use Mathematica 8.0 to numerically solve the Ginzburg–Landau equations by using the initial condition \(A_{1_0}(0)=1\). Using this solution, we next quantify the heat transport in terms of the Nusselt number.

Estimation of heat transport at lower plate

The thermal Nusselt number, \(\hbox {Nu}_\mathrm{nl}(\tau _1^*)\), is defined as:

$$\begin{aligned} \hbox {Nu}_\mathrm{nl}(\tau _1^*)= & {} 1+\dfrac{k_\mathrm{nl}}{k_\mathrm{bl}}\left[ \dfrac{\int _0^{\frac{2\pi }{\pi \kappa _\mathrm{c}}}\left( \dfrac{\partial {\varTheta }}{\partial Z}\right) \hbox {d}X}{\int _0^{\frac{2\pi }{\pi \kappa _\mathrm{c}}}\left( \dfrac{\hbox {d}{\varTheta }_\mathrm{b}}{\hbox {d}Z}\right) \hbox {d}X}\right] _{Z=0}, \end{aligned}$$
(92)

where \({\varTheta }_\mathrm{b} =\dfrac{T_\mathrm{b}-T_0}{\Delta T}\). Substituting Eqs. (10) and (22) in Eq. (92) and completing the integration, we get

$$\begin{aligned} \hbox {Nu}_\mathrm{nl}(\tau _1^*)=1+\left( \dfrac{k_\mathrm{nl}}{k_\mathrm{bl}}\right) \dfrac{2}{r_\mathrm{nl}}C(\tau _1^*). \end{aligned}$$
(93)

Using first- and second-order solutions of \(C(\tau _1^*)\), we get

$$\begin{aligned} \hbox {Nu}_\mathrm{nl}(\tau _1^*)=1+\dfrac{2}{b_1} \left( \dfrac{k_\mathrm{nl}}{k_\mathrm{bl}}\right) \left( 1-\dfrac{1}{r_\mathrm{nl}}\right) {\mathcal {A}}_{1_0}(\tau _1^*)^2. \end{aligned}$$
(94)

The time-averaged Nusselt number (mean Nusselt number), \(\overline{\hbox {Nu}_\mathrm{nl}(\tau _1^*)}\), for Eq. (94) is given by:

$$\begin{aligned} \overline{\hbox {Nu}_\mathrm{nl}(\tau _1^*)}= \dfrac{1}{\left( \dfrac{2\pi }{\omega ^*}\right) } \displaystyle {\int _{0}^{\dfrac{2\pi }{\omega ^*}}\hbox {Nu}_\mathrm{nl}(\tau _1^*)\hbox {d}\tau _1^*}. \end{aligned}$$
(95)

From Eq. (95), it is clear that the mean Nusselt number is calculated in the interval \(\left[ 0, \dfrac{2\pi }{\omega ^*}\right]\). The amplitude, \({\mathcal {A}}_{1_0}(\tau _1^*)\), in Eq. (94) is the solution of the Ginzburg–Landau equations (39), (71) and (90) of gravity, boundary temperature and rotation modulations, respectively. Using this solution, we calculate the mean Nusselt number for different values of amplitude and frequency of modulation.

Results and discussion

The individual effect of time-periodic modulations of the gravity field, boundary temperature and the rotation of the channel on Rayleigh–Bénard convection in nanoliquids is studied in the paper using the generalized Buongorno two-phase model. Using a truncated Fourier series representation, the generalized Lorenz model is derived for all the three modulated problems. Method of multiscales is then employed to reduce the Lorenz model into a Ginzburg–Landau model. Using the Ginzburg–Landau equation, the amplitude is obtained numerically and the Nusselt number is evaluated as a quadratic function of the amplitude. The results and their discussion is focused mainly on the following aspects:

  1. 1.

    Studying the influence of nanoparticles (nanotubes) on heat transport in the presence/absence of modulation.

  2. 2.

    Discussing the effect of gravity, boundary temperature and rotational modulations on heat transport in Newtonian liquids and Newtonian nanoliquids.

  3. 3.

    Explaining the individual effects of three types of modulation and comparing them.

  4. 4.

    Recovering results of single-phase model from those of two-phase.

  5. 5.

    Qualitative comparison of the present results with those of previous experimental and numerical works.

Influence of nanoparticles (nanotubes) on heat transport in the presence/absence of modulation

The Nusselt number for four Newtonian liquids (\(\chi =0\)) and for twenty-eight Newtonian nanoliquids (\(\chi =0.05\)) are presented. Twenty-eight Newtonian nanoliquids are studied by making a combination of four Newtonian liquids with five nanoparticles and two nanotubes. The transmission electron microscope (TEM) pictures of these nanoparticles (nanotubes) of size >100 nm are shown in Fig. 5. The actual physical values of Newtonian liquids, nanoparticles and nanotubes are used in the study. Their thermophysical properties are tabulated in Tables 2–4. Tables 2–4 clearly show that the thermal conductivity of all Newtonian liquids is less than 1 whereas the nanoparticles made from metals and metal oxides and carbon nanotubes have their thermal conductivity in the range 8 to 6600. The feasibility study on these eleven nanoparticles and two carbon nanotubes is explained well by Kanchana and Zhao [43]. They argued that enhanced heat transport in Newtonian liquids due to nanoparticles (nanotubes) not only depends on thermal conductivity of nanoparticles (nanotubes) but also the contribution of other thermophysical properties of nanoparticles (nanotubes) also counts.

Table 2 Thermophysical properties of four base liquids at \(300^{\circ }\,\hbox {K}\) [43]
Full size table
Table 3 Thermophysical properties of five nanoparticles at \(300^{\circ }\,\hbox {K}\) [43]
Full size table
Table 4 Thermophysical properties of carbon nanotubes at \(300^{\circ }\,\hbox {K}\) [43]
Full size table
Fig. 5
figure 5

The transmission electron microscope (TEM) pictures of nanoparticles and nanotubes in >100 nm size [44]

Full size image

It is pretty clear from Table 5 that smaller the particle size, greater the surface area and hence better the particle activity. Thus, in this sense the nanoparticles are very sensitive than the microparticles. In fact, the thermal instability is lower for the nanoliquid compared to the base liquid [45]. Therefore, nanoparticles (nanotubes) have to be dispersed in the base liquid very gently, there should be no violent vibration and friction. They should also be protected from moisture, heat and sunlight. Nanoparticles possess an attractive force and such a force becomes stronger as size decreases and hence there will be a maximum possibility of agglomeration. To avoid agglomeration, varieties of surfactants are being used [46]. The stability of nanoparticles in base liquid depends heavily on the surfactants, the base liquid, size of particles and molecular weight. For example, the stability of colloidal copper in Ethylene glycol and Engine oil is retained for a longer time when compared to that in water [47, 48]. With this brief information on nanoparticles, we now see the influence of nanoparticles on heat transport using the nondimensional parameters which characterize the nanoliquid properties.

Table 5 Details of material in nano size as per US Research Nanomaterials, Inc [44]
Full size table

The values of nondimensional parameters, Prandtl number (Pr), modified diffusivity ratio (\(N_{\mathrm{A}_\mathrm{nl}}\)), Lewis number (\(\hbox {Le}_\mathrm{nl}\)) and nanoparticle concentration Rayleigh number (\(\hbox {Ra}_{\phi _\mathrm{nl}}\)) for different nanoliquids are documented in Table 6 for \(\chi =0.05\). It is apparent from this table that the effect of nanoparticles (nanotubes) is to reduce the Prandtl number and enhance the nanoparticle concentration Rayleigh number, Lewis number and thermal diffusivity ratio. All these nondimensional parameters characterize the nanoliquid properties. We now try to understand the influence of these parameters on heat transport.

Prandtl number correlates the momentum transport and the thermal transport. Decrease in Prandtl number essentially means that the thermal transport dominates over the momentum transport and hence facilitates the heat transfer. Lewis number correlates the mass transport and the thermal transport. Increase in Lewis number due to nanoparticles (nanotubes) in base liquid means that the thermal transport dominates over the mass transport which improves the heat transfer much better. The modified diffusivity ratio signifies the relative importance of thermophoresis (Soret-type cross-diffusion) and molecular diffusion. Increase in the value of the modified thermal diffusivity ratio means thermophoresis has increasing influence on heat transport with an improvement in it. The nanoparticle concentration Rayleigh number is the analog of the thermal Rayleigh number, and this correlates the buoyancy force due to concentration difference and viscous force. Increase in the value of the concentration Rayleigh number means that the buoyancy force due to concentration becomes more important than the viscous force and this also favors enhanced heat transfer. Thus the perception from the above results is that the influence of nanoparticles (nanotubes) in base liquid is to enhance heat transport. The percentage of enhancement of heat transport due to nanoparticles (nanotubes) in base liquid is presented in Table 7.

The values of mean Nusselt number for twenty-eight nanoliquids at different volume fractions of nanoparticles (nanotubes) in the absence of modulation are documented in Table 7. From Table 7, it is clear that dilute concentrations of nanoparticles (nanotubes) in base liquids lead to a significant increase in heat transfer. Maximum heat transfer enhancement is noticed in glycerin-based SWCNTs while the minimum one is in water-based titania nanoparticles.

Tables 8–10 present values of the mean Nusselt number for gravity, boundary temperature and rotational modulations for Newtonian liquids and Newtonian nanoliquids. These tables reiterate the results of the no-modulation problem, viz., nanoparticles (nanotubes) in base liquid enhance the heat transport irrespective of the values of amplitude and frequency of modulation. There is quite a change in the value of the mean Nusselt number due to modulations and this is discussed in the succeeding subsection.

Table 6 Values of various parameters concerning twenty-eight nanoliquids for volume fraction, \(\chi =0.05\), at \(300^{\circ }\,\hbox {K}\)
Full size table
Table 7 Nusselt number of twenty-eight nanoliquids for different values of volume fraction, \(\chi\), calculated using the Nusselt number for water \(=\) 2.00332, ethylene-glycole \(=\) 2.05386, engine oil \(=\) 2.05615 and glycerin \(=\) 2.05615
Full size table

Results from modulation

When a time-periodic modulation is imposed on a Rayleigh–Bénard convection system involving Newtonian liquids or Newtonian nanoliquid layers, then the flow in the system gets disturbed. The rate of heat transport in such a system thereby alters. In the past few decades, different types of modulation in hydrodynamics have been studied with great interest. The interest lies not only in the mechanics of this new class of problems but also with the immense possibilities for applications, e.g., using modulation, enhancement of heat transport or higher efficiency can be attained in various processing techniques. The present paper is an attempt to study the individual effect of three types of modulations on heat transport and seek the merits and demerits of such modulations. The three types of modulations considered in the paper are:

  1. 1.

    Gravity modulation,

  2. 2.

    Boundary temperature modulation and

  3. 3.

    Rotational modulation.

We now discuss the effect of gravity modulation on heat transport in the Rayleigh–Bénard convection problem involving Newtonian liquids or Newtonian nanoliquids. When such liquid layer vibrates vertically with small amplitude, \(\epsilon ^2 \delta _2\) and low frequency, \(\omega ^*\), their momentum and heat transports modifies. The values of the average Nusselt number for four Newtonian liquids and twenty-eight Newtonian nanoliquids for different values of \(\delta _2\) and \(\omega ^*\) are documented in Table 8. From Table 8, it is clear that the effect of increase in the amplitude of modulation is to increase the mean Nusselt number whereas the effect of increase in frequency of modulation is to decrease the same. Comparing Table 8 with Table 7, it is apparent that at \(\omega ^*=5\) the effect of gravity modulation is to enhance heat transport of the system. However, when \(\omega ^*\) increases in value slightly beyond 5 it has an opposing influence. Thus, if we choose gravity modulation as a regulating mechanism of heat transfer in any application frequency of modulation is a dominant factor than the amplitude.

Let us now move on to the discussion of the effect of boundary temperature modulation. The present work focuses on two types of boundary temperature modulations:

  1. 1.

    In-phase modulation (synchronous) and

  2. 2.

    Out-of-phase modulation (asynchronous).

\(\varphi =0^{\circ }\) represents in-phase modulation and \(\varphi \ne 0^{\circ }\) represents the out-of-phase modulation. The schematic of in-phase and out-of-phase modulations for cosine function is shown in Fig. 6. The values of mean Nusselt number for Newtonian liquids and Newtonian nanoliquids for in-phase and out-of-phase temperature modulations are documented in Table 9. From the table, it is clear that there is no influence of modulation in the case of in-phase modulation. Further, modulation has less influence in the case when the phase difference is \(\varphi =\pi\). The effect of the amplitude on mean Nusselt number as a function of the phase difference for four different frequencies (\(\omega ^*=0.6,1,3\) and 5) is shown in Fig. 7. It can be easily seen that the mean Nusselt number decreases with increase in frequency. The effect of increase in phase difference is to decrease \({\overline{\hbox {Nu}}}_\mathrm{nl}\) in \(\left[ 0,\pi \right]\) while it increases with \(\varphi\) in \(\left[ \pi ,2\pi \right]\). When the phase difference takes the values \(\varphi =\dfrac{\pi }{2}\) and \(\varphi =\dfrac{3\pi }{2}\) the effect of boundary temperature modulation is most significant. When the results documented in Table 9 are seen in conjunction with the schematic in Fig. 6, we may conclude that:

  1. 1.

    Odd multiples of \(\dfrac{\pi }{2}\) have significant effect and even multiples of \(\dfrac{\pi }{2}\) do not have or have less influence on the heat transport and

  2. 2.

    the modulation is significant when there is a phase-lag of the sinusoidal temperature at the lower plate compared to that at the upper plate.

This suggests that in-phase modulation cannot be used to regulate heat transport and this result is true for all Newtonian liquids and Newtonian nanoliquids (see Table 9). Thus, the choice of phase difference and frequency of modulations are very important factors in the case of boundary temperature modulation.

Rotational modulation is achieved by rotating the liquid layer uniformly about the fixed axis of Z. Taylor number characterizes the rotation rate. Table 10 shows the values of the mean Nusselt number in the presence/absence of rotational modulation for Newtonian liquids and Newtonian nanoliquids for a value of \(\hbox {Ta}_\mathrm{nl}=100\) and for different values of \(\omega ^*\) and \(\delta _2\). From the tables, it is apparent that the effect of small values of \(\delta _2\) is to enhance the heat transport whereas the effect of increasing \(\omega ^*\) is to diminish the same. The rate of enhancement due to amplitude is less than the rate of diminishment due to frequency of rotational modulation. Figure 8 is the plot of \(\overline{ \hbox {Nu}_\mathrm{nl}}\) versus scaled Rayleigh number, \(r_\mathrm{nl}\), for different values of \(\hbox {Ta}_\mathrm{nl}\) for a representative nanoliquid, viz., water–copper nanoliquid. Figure 8 reveals that as we increase \(\hbox {Ta}_\mathrm{nl}\), \(\overline{ \hbox {Nu}_\mathrm{nl}}\) decreases which implies that the effect of rotation is to diminish heat transport. Overall, we conclude that the frequency of modulation and the Taylor number are dominant parameters that influence heat transport the most in the case of rotational modulation.

Fig. 6
figure 6

Schematic of in-phase and out-of-phase temperature modulations for a cosine function of time and for four different values of phase difference, \(\varphi\)

Full size image
Fig. 7
figure 7

Variation of \(\overline{\hbox {Nu}_\mathrm{nl}}\) with phase difference \(\varphi\) for water–copper nanoliquid and for different values of \(\delta _2\) and for \(\omega ^*\)

Full size image
Fig. 8
figure 8

Plots of \(\overline{\hbox {Nu}_\mathrm{nl}}\) versus \(r_\mathrm{nl}\) for water–copper nanoliquid and different values of \(\hbox {Ta}_\mathrm{nl}\) and for \(r_\mathrm{nl}=5\), \(\delta _2=0.1\) and \(\omega ^*=5\)

Full size image
Table 8 Values of \(\overline{\hbox {Nu}_\mathrm{nl}}\) for twenty-eight Newtonian nanoliquids for different values of \(\delta _2\), \(\omega ^*\) and for \(\chi =0.05\) in the case of gravity modulation
Full size table
Table 9 Variation of \(\overline{\hbox {Nu}_\mathrm{nl}}\) in the case of in-phase and out-of-phase temperature modulations for \(r_\mathrm{nl}=5\), \(\delta _2=0.1\), \(\omega ^*=5\)
Full size table
Table 10 Values of \(\overline{\hbox {Nu}_\mathrm{nl}}\) for twenty-eight Newtonian nanoliquids for different values of \(\delta _2\), \(\omega ^*\) and for \(\chi =0.05\) in the presence rotation modulation
Full size table

Explanation for the observed individual effects of three types of modulations

On observing the coefficient of the linear term in the algebraic part of the Ginzburg–Landau equations (39), (69) and (88) of gravity, temperature and rotation modulations, respectively, one can easily see that the modulation-related quantities appear only in this term. The quantities \(Q_1\), \(Q_3\) and \(Q_5\) are growth-related terms while \(Q_2, Q_4\) and \(Q_6\) play their designated role of keeping the solution bounded. It is thus fairly clear that a closer inspection of \(Q_1\), \(Q_3\) and \(Q_5\) would throw more light on the effect of modulation on the amplitude and thereby the Nusselt number. Figure 9 is a plot of \(Q_1\), \(Q_3\) and \(Q_5\) versus \(\tau _1^*\) for a fixed value of the parameters appearing in them. The figure clearly reveals that

$$\begin{aligned} \overline{Q_1}>\overline{Q_3}>\overline{Q_5}. \end{aligned}$$
(94)

On seeing this result in conjunction with those of the average Nusselt number, we may conclude that the Nusselt number is highest for gravity modulation for which the mean, \(\overline{Q_1}\) is highest. It is obvious that the one with the maximum area under the curve has maximum heat transfer. We made similar computation with \(Q_2\), \(Q_4\) and \(Q_6\) and these reiterate what is said above.

Fig. 9
figure 9

Variation of \(Q_1, Q_3\) and \(Q_5\) with time for \(\delta _2=0.1\), \(\omega ^*=5\), \(\chi =0.05\) and \(r_\mathrm{nl}=5\)

Full size image

Recovering results of single-phase model from those of two-phase

As mentioned in the introduction to the paper, the generalized Buongiorno two-phase model allows one to deduce the results of the single-phase model from that of the two-phase. Siddheshwar and Kanchana [31, 32] showed that the results pertaining to single-phase model [49,50,51,52,53] and references therein) can be recovered as a limiting case of the generalized Buongiorno two-phase model by taking nanoparticles concentration Rayleigh number, \(\hbox {Ra}_{\phi _\mathrm{nl}}=0\). In the present paper, we found that the results of Siddheshwar and Kanchana [31, 32] are true in the presence of modulation also (see Fig. 10).

Fig. 10
figure 10

Variation of \(\overline{\hbox {Nu}_\mathrm{nl}}\) with \(r_\mathrm{nl}\) for water–copper nanoliquid and for \(\delta _2=0.1\) and for \(\omega ^*=5\) for gravity, temperature and rotational modulations

Full size image

Qualitative comparison of the present results with those of previous experimental and numerical works

The experimental findings of Swaminathan et al. [54], Niemela Donnelly [55] and Niemela et al. [56] and the numerical findings of Gresho and Sani [2] and Elhajjar et al. [57] on Rayleigh–Bénard convection in the presence/absence of different types of modulations for rigid boundaries are summarized in Table 11. From previous investigations [31, 32, 58, 59], we know that in the presence/absence of nanoparticles:

$$\begin{aligned} \hbox {Nu}^{[ {\rm FF}]}>\hbox {Nu}^{[{\rm RR}]}, \end{aligned}$$
(97)

and

$$\begin{aligned} \hbox {Nu}_\mathrm{nl}^{[\text { Rectangular enclosure }]}<\hbox {Nu}_\mathrm{nl}^{[\text { Classical RBC }]}, \end{aligned}$$
(98)

where FF and RR, respectively, represent the free boundaries and the rigid boundaries.

In the present investigation, we obtained \(Nu_\mathrm{nl}=2.8507 (>1.586)\) for water–alumina nanoliquids in the absence of modulations at volume fraction, \(\chi =0.08\). These satisfies the relation (98) implying the present investigation is in reasonably good agreement with previous investigation.

Though we have made a qualitative comparison of results obtained in the present study with previous investigations, some of these remains to be experimentally proven, more so because all the experimental works mentioned in Table 11 were done by using low Prandtl number liquids [54,55,56]. The reason for such a choice of Prandtl number is to retain the liquid layer as thin as possible so that it is easy to do experiment in the presence of modulation. Experimenting in the presence of modulation for a nanoliquid layer is quite a challenging task and is still unattempted one.

Having discussed the results of the paper in the next section, we draw a general conclusion.

Table 11 Results from previous works and qualitative comparison with those of present work
Full size table

Conclusion

Based on the results and their discussion, we now come to the following conclusion:

  1. 1.

    Effect of dilute concentration of nanoparticles (nanotubes) in base liquid leads to enhancement in heat transport in both no-modulation and also in the case of the three types of modulation problems.

  2. 2.

    In the case of gravity-modulated Rayleigh–Bénard convection in Newtonian liquids and Newtonian nanoliquids, the following results are true:

    1. (1)

      \({\overline{\hbox {Nu}}}_\mathrm{nl}^{\delta _2 =0} > {\overline{\hbox {Nu}}}_\mathrm{nl}^{\delta _2 \ne 0}\).

    2. (2)

      The effect of increasing \(\omega ^*\) is to diminish the heat transport and effect of increasing \(\delta _2\) is to enhance the heat transport.

    3. (3)

      \(\omega ^*\) effect on \(\overline{\hbox {Nu}_\mathrm{nl}}\) is more significant than that of \(\delta _2\).

  3. 3.

    In the case of boundary temperature-modulated Rayleigh–Bénard convection in Newtonian liquids and Newtonian nanoliquids, we observe the following:

    1. (1)

      \([\overline{\hbox {Nu}_\mathrm{nl}}]_{\delta _2=0}\approx [\overline{\hbox {Nu}_\mathrm{nl}}]_{\delta _2\ne 0}\) for \(\varphi =0\).

    2. (2)

      \([\overline{\hbox {Nu}_\mathrm{nl}}]_{\delta _2=0}<[\overline{\hbox {Nu}_\mathrm{nl}}]_{\delta _2\ne 0}\) or \([\overline{\hbox {Nu}_\mathrm{nl}}]_{\delta _2=0}>[\overline{\hbox {Nu}_\mathrm{nl}}]_{\delta _2\ne 0}\) for all values of \(\varphi\) and depending on the value of \(\omega ^*\).

    3. (3)

      \([{\overline{\hbox {Nu}}}_\mathrm{nl}]_{\varphi =0}<[{\overline{\hbox {Nu}}}_\mathrm{nl}]_{\varphi \ne 0}\) or \([{\overline{\hbox {Nu}}}_\mathrm{nl}]_{\varphi =0}>[{\overline{\hbox {Nu}}}_\mathrm{nl}]_{\varphi \ne 0}\) depending on the choice of \(\omega ^*\) and \(\varphi\).

  4. 4.

    In the case of rotationally modulated Rayleigh–Bénard convection in Newtonian liquids and Newtonian nanoliquids, we observe the following:

    1. (1)

      \(\overline{\hbox {Nu}_\mathrm{nl}}^{\delta _2 =0} > \overline{\hbox {Nu}_\mathrm{nl}}^{\delta _2 \ne 0}\).

    2. (2)

      The effect of increasing \(\omega ^*\) and \(\hbox {Ta}_\mathrm{nl}\) is to diminish the heat transport and effect of increasing \(\delta _2\) is to enhance the heat transport.

    3. (3)

      The influence of \(\omega ^*\) and \(\hbox {Ta}_\mathrm{nl}\) on \(\overline{\hbox {Nu}_\mathrm{nl}}\) is more significantly than that of \(\delta _2\).

  5. 5.

    Comparing the three types of modulation considered in the paper, it must be observed that both gravity and rotational modulation problems involve non-static configurations. In the case of temperature modulation, however, the system is static. It appears from the results and the above observations that temperature modulation is best suited to regulate convection and heat transport.