1 Introduction

There has been surging interest in heat transfer applications due primarily to implications in refrigeration and automotive industries where the enhanced surfaces are widely used on their heat exchangers. As a result of this there is an aggressive competition in the process industry to incorporate this technology in heat exchangers. A major limitation against enhancing the heat transfer in such engineering systems is the inherently poor thermal conductivity of conventional liquids, including water. Therefore, for more than a century since Maxwell’s theory in 1873, scientists and engineers have made a great effort to break this fundamental limit by dispersing millimeter or micrometer sized particles in liquids. However, the major problem with the use of such large sized particles is the agglomeration of these particles in liquids. The agglomeration of microparticles results in not only the rapid sedimentation and clogging of microchannels but also in the decreasing of thermal conductivity of liquids. An innovative modern way of heat transfer enhancement in liquids to overcome problems faced in microparticles is to include nano-sized particles (1–100 nm), in short called nanoparticles, in base liquids. Contribution of nanoparticles in engineering applications is well explained by Colangelo et al. [14].

The usage of carbon nanotubes in base liquids is trending now. This is because carbon nanotubes offer higher thermal conductivity enhancement and a larger surface area than the spherical shaped nanoparticles. Carbon nanotubes are made by a number of layers of carbon sheets. Carbon nanotubes with a layer of carbon sheet is called single-walled carbon nanotubes (SWCNTs) and carbon nanotubes with multiple layers of carbon sheet is called multi-walled carbon nanotubes (MWCNTs). Base liquids with nanoparticles are called nanoliquids, the word coined by Choi [13]. We extend this definition to include nanotubes in place of nanoparticles.

There are two models available for studying Rayleigh–Bénard convection in nanoliquids :

  1. (a)

    Khanafer–Vafai–Lightstone (KVL) single-phase model (see [24]) and

  2. (b)

    Buongiorno two-phase model (see [11]).

Although nanoliquids are solid–liquid mixtures, the single-phase model conventionally used in most studies of Rayleigh–Bénard convection assumes the nanoliquid as a single phase (homogeneous) liquid. In fact, due to the extremely small size and low concentration of the suspended nanoparticles, the particles are assumed to move with same velocity as the liquid. A good number of papers have appeared on convection in nanoliquids using the single-phase model (Ghasemi and Aminossadati [18], Jou and Tzeng [21], Abu-Nada et al. [1], Tiwari and Das [49], Sheremet et al. [35], Siddheshwar and Meenakshi [42], Meenakshi and Siddheshwar [29], Siddheshwar and Veena [44] and Kanchana et al. [23]). Buongiorno [11] showed that there are several factors such as gravity, friction between the liquid and solid particles, Brownian forces, sedimentation and dispersion that may affect a nanoliquid flow. Consequently, the slip velocity between the liquid and solid particles cannot be neglected while simulating nanoliquid flows. Buongiorno [11] developed a transport equation to study the movement between the solid and liquid particles. Using the Buongiorno transport equation, Tzou [50, 51] studied the onset of convection in a horizontal layer of a nanoliquid heated uniformly from below and found that as a result of Brownian motion and thermophoresis of nanoparticles, the critical Rayleigh number is much lower, by one to two orders of magnitude, than that of a base liquid. Kim et al. [25, 26] investigated the onset of convection in a horizontal nanoliquid layer using a two-phase model and modified the three quantities, namely, the thermal expansion coefficient, the thermal diffusivity, and the kinematic diffusivity that appear in the definition of the Rayleigh number. Many authors (Nield and Kuznetsov [31], Roberts and Walker [34], Agarwal et al. [3], Yadav et al. [57], Noghrehabadi and Samimi [32], Agarwal and Bhadauria [2], Umavathi [52] and references therein) have investigated various influences on Rayleigh Bénard convection in nanoliquids using the Buongiorno two-phase model. Recently Maheshwary et al. [27] made a comprehensive report on effect of concentration, particle size and particle shape on thermal conductivity of titania/water based nanofluid. They showed that concentration has a more significant effect than shape and size of the particles on the thermal conductivity of the nanofluid. In literature there are many review articles connecting enhancement in thermal conductivity due to nanoparticles/nanotubes and thereby heat transfer enhancement (see Wang and Mujumdar [55], Murshed et al. [30], Shima and Philip [36], Usri et al. [53], Angayarkanni and Philip [4], Pinto and Fiorelli [33], Azmi et al. [5] and references therein).

The single-phase model used by many investigators incorporates information on thermophysical properties of nanoliquids whereas the two-phase model does not get explicitly into the modeling of nanoliquid properties like density, heat capacity, volumetric expansion coefficient, dynamic viscosity, thermal conductivity, Brownian and thermophoretic coefficients in terms of the volume fraction of the nanoparticles and the corresponding properties of nanoparticles and base liquid. Siddheshwar et al. [47, 48] were the first to give details of such an exercise for Rayleigh–Bénard convection in nanoliquids by incorporating thermophysical properties into the classical Buongiorno model. Siddheshwar and Kanchana [40, 41] extended this idea to Rayleigh–Bénard convection in nanoliquids occupying different types of enclosures. Recently Kanchana and Zhao [22] studied the effect of internal heat generation/absorption on Rayleigh–Bénard convection in nanoliquids. They made a feasibility study among different types of nanoparticles and provided a vital information for choosing an appropriate nanoparticle in the liquid for a desired thermal engineering problem addressing heat removal.

Modulated gravitational fields on Rayleigh–Bénard convection have been of classical interest because of the induced change in the stability bounds. The problem involving the effect of time-periodic gravity modulation in a liquid layer was first studied by Gershuni and Zhukhovitskii [16]. Gresho and Sani [19] developed a useful mechanical analogy by considering the effect of gravity modulation on a simple pendulum. The effect of gravity and temperature modulations on the stability of equilibrium in a plane horizontal layer with free and rigid boundaries was presented by Gershuni et al. [17]. Biringen and Peltier [7] studied the effect of sinusoidal and random modulations on three-dimensional Rayleigh–Bénard convection at 1g and \(\mu g\) and they confirmed the result of Gresho and Sani [19]. Wheeler et al. [56] used the averaging method and the Floquet theory to analyze the stability of directional solidification problem under high-frequency gravity modulation. There are many other works that deal with gravity modulation effect on convection in different liquids (see Malashetty and Padmavathi [28], Bhadauria [6], Boulal et al. [9], Shu et al. [37], Siddheshwar [38], Siddheshwar et al. [45], Siddheshwar and Abraham [39], Siddheshwar et al. [46] and Siddheshwar and Revathi [43]).

From the review of literature it is observed that all the works mentioned above deal with trigonometric sine type of gravity oscillation. In the paper we focus attention on studying the influence of three different types of time-periodic gravity-aligned oscillation on onset and heat transport in nanoliquids. Three types of gravity modulation considered in the paper are trigonometric sine, triangular and square wave forms. Further, we also note that all the reported works on nonlinear stability of Rayleigh–Bénard convection in the presence of sinusoidal gravity modulation have made use of the Lorenz model for investigation. In view of the above observation it is clear that the following five important aspects concerning the nonlinear stability of nanoliquids warrant consideration:

  1. a.

    Treating convection in nanoliquids in a way that is different from the classical binary liquid convection (Buongiorno approach),

  2. b.

    Connecting the results of Khanafer–Vafai–Lightstone model (see Khanafer et al. [24]) and the generalized Buongiorno two-phase model (see Siddheshwar et al. [47]),

  3. c.

    Deriving the Ginzburg–Landau equation from the Lorenz model (see Siddheshwar and Kanchana [40]),

  4. d.

    Studying the influence of three different types of time-periodic gravity-aligned oscillations on onset and the heat transport and

  5. e.

    Comparing results on onset and heat transport in Newtonian liquids with/without nanoparticles and carbon nanotubes.

After peer review of literature we noticed that the modulated Rayleigh–Bénard convection problem as handled in this paper is new in its limiting case as well, i.e., Newtonian liquid without nanoparticles/nanotubes.

2 Mathematical formulation for Rayleigh–Bénard convection

2.1 Problem description

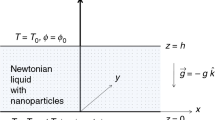
Consider an infinite extent horizontal nanoliquid layer. \(z=0\) and \(z=h\) represent the lower and upper boundaries of the layer and are held at temperatures \(T_0+\varDelta T (\varDelta T>0)\) and \(T_0\) and at nanoparticle concentration \(\phi _0+\varDelta \phi (\varDelta \phi >0)\) and \(\phi _0\) respectively. Here \(T_0\) and \(\phi _0\) are temperature and nanoparticle/nanotube volume fraction at upper plate, \(\varDelta T\) and \(\varDelta \phi\) are temperature and nanoparticles/nanotube volume fraction differences between two plates respectively. The horizontal layer is subject to time-periodic gravity-aligned oscillations and thus the gravity term is having an additional time-dependent component \(g'(\varOmega ,t)\) with frequency \(\varOmega\). Further, the horizontal boundaries are assumed to be stress-free, isothermal and isonanoparticle concentration. The vertical boundaries are assumed to be far away and hence there is no effect of the vertical boundaries on the dynamics in the bulk of the nanoliquid. The schematic of the Rayleigh–Bénard convection configuration is shown in Fig. 1.

Fig. 1
figure 1

Schematic of the Rayleigh–Bénard convection problem with time-periodic vertical oscillations

Full size image

2.2 Mathematical formulation

The governing system of equations in dimensional form for studying the Rayleigh–Bénard convection problem with time-periodic vertical oscillations using the two-phase model of Siddheshwar et al. [47] are: Conservation of mass

$$\begin{aligned} \nabla \cdot \mathbf {q}=0, \end{aligned}$$
(1)

Conservation of linear momentum

$$\begin{aligned} &\rho _{nl} \dfrac{\partial \mathbf {q}}{\partial t} = - \nabla p +\mu _{nl}\nabla ^2 \mathbf {q}\\ &\quad +\left[ \rho _{nl}-(\rho \beta _1)_{nl}(T-T_0) + (\rho \beta _2)_{nl} (\phi -\phi _0)\right] \mathbf {g}, \end{aligned}$$
(2)

Conservation of energy

$$\begin{aligned} (\rho \texttt {C}_p)_{nl}\left[ \dfrac{\partial T}{\partial t}+ (\mathbf {q}\cdot \nabla ) T\right] = k_{nl}\nabla ^2 T, \end{aligned}$$
(3)

Conservation of nanoparticle volume fraction

$$\begin{aligned} \dfrac{\partial \phi }{\partial t}+ (\mathbf {q}\cdot \nabla )\phi = D_B \nabla ^2 \phi + \dfrac{D_{Th}}{T_0}\nabla ^2 T. \end{aligned}$$
(4)

In writing Eq. (3) we have neglected the Brownian motion effects being aware that previous studies (Tzou [51], Tzou [50], Nield and Kuznetsov [31], Yadav et al. [57]) clearly point to the validity of this assumption. For mathematical tractability we consider two-dimensional rolls in the (x, z)-plane. Hence all the physical quantities defined in the governing Eqs. (1)–(4) are independent of y. Thermally induced instabilities dominate hydrodynamic instabilities. Thus, the acceleration term \((\mathbf {q} \cdot \nabla )\mathbf {q}\) has been neglected in the equation of linear momentum. This also means that we are considering only small scale convective motion (see Siddheshwar et al. [45]). The physical quantities involved in the governing Eqs. (1)–(4) are \(\mathbf {q}\), velocity vector with horizontal and vertical velocity component u and w respectively, \(\rho _{nl}\), density in \(kg/m^2\), t, time in s, p, pressure in Pa, \(\mu _{nl}\), dynamic coefficient of viscosity in kg/ms, \((\beta _1)_{nl}\), thermal expansion coefficient in 1/K, \((\beta _2)_{nl}\), concentration analog of thermal expansion coefficient in 1/kg, T, temperature in K, \(T_0\), temperature of upper boundary in K, \(\phi\), normalized nanoparticle/nanotube volume fraction, \(\mathbf {g} = (0,0,-[g+g'(\varOmega ,t)]\), where g is acceleration due to gravity in \(m/s^2\), \(g'(\varOmega ,t)\) is time-dependent modulated gravity, \((\texttt {C}_p)_{nl}\), heat capacity in \(J/[kg-K]\), \(k_{nl}\), thermal conductivity in \(W/[m-K]\), \(D_B =\dfrac{(k_{B0} T)}{3\pi \mu _{bl}d_{np}}\), Brownian diffusion coefficient and \(D_{Th} = 0.26 \dfrac{k_{bl}}{2k_{bl}+k_{np}}\dfrac{\mu _{bl}}{\rho _{bl}}\chi\), thermophoretic diffusion coefficient, where \(\chi\) is the volume fraction of nanoparticles/nanotube and is defined as

$$\begin{aligned} \chi = \dfrac{\text { Volume fraction of nanoparticles \,/\, nanotubes}}{\text { Volume fraction of (nanoparticles \,/ \,nanotubes \,+\, baseliquid)}}. \end{aligned}$$
Table 1 Thermophysical properties of four base liquids at \(300^{\circ }\hbox {K}\) (Siddheshwar et al. [47])
Full size table
Table 2 Thermophysical properties of five nanoparticles at \(300^{\circ }\hbox {K}\) (Siddheshwar et al. [47])
Full size table
Table 3 Thermophysical properties of carbon nanotubes at \(300^{\circ }\hbox {K}\) (Siddheshwar et al. [41])
Full size table

The subscript bl and np refer to baseliquid and nanoparticle/nanotube thermophysical properties and are documented in Tables 1, 2 and 3. The subscript nl refers to nanoliquid properties and these properties are calculated using either the phenomenological laws or mixture theory:

Phenomenological laws :

$$\begin{aligned} \dfrac{\mu _{nl}}{\mu _{bl}}& {}= \dfrac{1}{(1-\chi )^{2.5}}, (\text{Brinkman model }[10])\\ \dfrac{k_{nl}}{k_{bl}}& {}= \frac{\left( \dfrac{k_{np}}{k_{bl}} +(n-1)\right) -(n-1)\chi \left( 1-\dfrac{k_{np}}{k_{bl}}\right) }{\left( \dfrac{k_{np}}{k_{bl}}+(n-1)\right) +\chi \left( 1-\dfrac{k_{np}}{k_{bl}}\right) },(\text{Hamilton-Crosser model } [20]) \end{aligned}$$

Mixture theory [24]:

$$\begin{aligned} \left. \begin{aligned} \dfrac{(\rho \texttt {C}_p)_{nl}}{(\rho \texttt {C}_p)_{bl}}=(1-\chi )+\chi \dfrac{(\rho \texttt {C}_p)_{np}}{(\rho \texttt {C}_p)_{bl}}, \\ \dfrac{(\rho \beta )_{nl}}{(\rho \beta )_{bl}}=(1-\chi )+\chi \dfrac{(\rho \beta )_{np}}{(\rho \beta )_{bl}}, \\ \alpha _{nl}=\dfrac{k_{nl}}{(\rho \texttt {C}_p)_{nl}}, \; \dfrac{\rho _{nl}}{\rho _{bl}}=(1-\chi )+\chi \dfrac{\rho _{np}}{\rho _{bl}}, \end{aligned} \right\}. \end{aligned}$$

In the Hamilton Crosser model, n is the shape factor with \(n=3\) for spherical shaped nanoparticles and \(n=3.75\) for nanotubes. The specific heat and thermal expansion coefficient of nanoliquids are calculated using the following expressions :

$$\begin{aligned} (\texttt {C}_p)_{nl} = \dfrac{(\rho \texttt {C}_p)_{nl} }{\rho _{nl}}, \beta _{nl} = \dfrac{(\rho \beta )_{nl}}{\rho _{nl}}. \end{aligned}$$

At the basic state the nanoliquid is assumed to be at rest and hence the pressure, temperature and the nanoparticle concentration vary in the \(z-\)direction only and are given by

$$\begin{aligned} \mathbf {q_b}=(0,0),\; p=p_b(x,z),\; T=T_b(z),\; \phi =\phi _b(z). \end{aligned}$$
(5)

Using Eq. (5) in the governing Eqs. (1)–(4), we get the solution of the basic temperature and nanoparticle concentration as follows :

$$\begin{aligned} \left. \begin{aligned} T_b(z)& {}= \left( 1-\dfrac{z}{h}\right) \bigtriangleup T+T_0,\\ \phi _b(z)& {}= \left( 1-\dfrac{z}{h}\right) \bigtriangleup \phi +\phi _0 \end{aligned} \right\} . \end{aligned}$$
(6)

We superimpose perturbations on the basic state solution as given below:

$$\begin{aligned} \mathbf {q}=\mathbf {q}',\; p=p_b+p',\; T=T_b+T',\; \phi =\phi _b+\phi ', \end{aligned}$$
(7)

where the prime denotes the perturbation. An external heating and a time-periodic oscillation perturb the system. Substituting the expression (7) in Eqs. (2)–(4), using the basic state solution (6), eliminating the pressure and introducing the stream function, \(\psi\), in the form:

$$\begin{aligned} u=-\dfrac{\partial \psi }{\partial z},\quad w=\dfrac{\partial \psi }{\partial x}, \end{aligned}$$
(8)

we get the governing equation as given below:

$$\begin{aligned}&\rho _{nl}\left( \dfrac{\partial }{\partial t}(\nabla ^2 \psi )\right) = \mu _{nl}\nabla ^2 \psi +(\rho \beta _1)_{nl} \left[ g+g'(\varOmega ,t)\right] \dfrac{\partial T'}{\partial x} \nonumber \\&\quad -(\rho \beta _2)_{nl}\left[ g+g'(\varOmega ,t)\right] \dfrac{\partial \phi '}{\partial x},\end{aligned}$$
(9)
$$\begin{aligned}&(\rho \texttt {C}_p)_{nl}\left[ \dfrac{\partial T'}{\partial t}+ \dfrac{\partial \psi }{\partial x}\dfrac{\partial T'}{\partial z}-\dfrac{\partial \psi }{\partial z}\dfrac{\partial T'}{\partial x}+\dfrac{\partial \psi }{\partial x}\dfrac{dT_b}{dz}\right] =k_{nl}\nabla ^2 T', \end{aligned}$$
(10)
$$\begin{aligned}&\dfrac{\partial \phi '}{\partial t}+\dfrac{\partial \psi }{\partial x}\dfrac{\partial \phi '}{\partial z}-\dfrac{\partial \psi }{\partial z}\dfrac{\partial \phi '}{\partial x}-\dfrac{\partial \psi }{\partial x}\dfrac{d \phi _b}{dz}\\ &\quad = D_B \nabla ^2 \phi '+\dfrac{D_{Th}}{T_0}\nabla ^2 T'. \end{aligned}$$
(11)

Using the following non-dimensional variables

$$\begin{aligned} &\begin{aligned} (X,Z)=\left(\dfrac{x}{h},\dfrac{z}{h}\right) ,\quad \tau =\dfrac{\alpha _{bl}t}{h^2},\quad \varPsi =\dfrac{\psi }{\alpha _{bl}}, \varTheta = \dfrac{T'}{\bigtriangleup T},\\ &\quad \varPhi = \dfrac{\phi '}{\bigtriangleup \phi }, \end{aligned} \end{aligned}$$
(12)

Equations (9)–(11) can be written in the non-dimensional form as:

$$\begin{aligned} \dfrac{1}{Pr_{nl}}\dfrac{\partial }{\partial \tau } (\nabla ^2 \varPsi )& {} = a_1 \nabla ^4 \varPsi + \left[ 1+g_m(\varOmega , \tau )\right] Ra_{nl}a_{1}^2 \dfrac{\partial \varTheta }{\partial X} \nonumber \\&-\left[ 1+g_m(\varOmega , \tau )\right] Ra_{\phi _{nl}}a_{1}^2 \dfrac{\partial \varPhi }{\partial X}, \end{aligned}$$
(13)
$$\begin{aligned} \dfrac{\partial \varTheta }{\partial \tau }& {}= a_1 \nabla ^2 \varTheta +\dfrac{\partial \varPsi }{\partial X}-J(\varPsi ,\varTheta ), \end{aligned}$$
(14)
$$\begin{aligned} \dfrac{\partial \varPhi }{\partial \tau }& {}= \dfrac{a_1}{Le_{nl}} \nabla ^2 \varPhi +\dfrac{a_1N_{A_{nl}}}{Le_{nl}} \nabla ^2 \varTheta + \dfrac{\partial \varPsi }{\partial X}- J(\varPsi , \varPhi ), \end{aligned}$$
(15)

where \(Pr_{nl} = \dfrac{\mu _{nl}}{\rho _{nl}\alpha _{nl}}\) is the nanoliquid Prandtl number which characterizes the speed of propagation of momentum and energy in the nanoliquid flow, \(a_1 =\dfrac{\alpha _{nl}}{\alpha _{bl}}\) is the diffusivity ratio, \(Ra_{nl} = \dfrac{(\rho \beta )_{nl} \varDelta T h^3 g}{ \mu _{nl} \alpha _{nl}}\) is the thermal Rayleigh number which represents the balance of energy released by the buoyancy force and the energy dissipation by viscous and thermal effects, \(Ra_{\phi _{nl}} = \dfrac{(\rho _{np}-\rho _{nl}) \varDelta \varPhi h^3 g }{ \mu _{nl} \alpha _{nl}}\) is the concentration Rayleigh number which is analog of thermal Rayleigh number, \(Le_{nl} = \dfrac{\alpha _{nl}}{D_B \varDelta \varPhi }\) is the Lewis number which is the ratio of thermal and mass diffusivities, \(N_{A_{nl}} = \dfrac{D_{Th} \varDelta T}{D_B T_0 \varDelta \varPhi }\) is the modified diffusivity ratio which signifies the relative importance of thermophoresis (Soret-type cross-diffusion) and molecular diffusion. The dimensionless parameters as defined earlier are based on nanoliquid properties and not on just base liquid ones. This is very much unlike the case of the classical Buongiorno model [11]. In Eqs. (14) and (15), \(J(\varPsi ,\varTheta )\) and \(J(\varPsi , \varPhi )\) are Jacobian defined as \(J(\varPsi ,\varTheta )=\dfrac{\partial \varPsi }{\partial X}\dfrac{\partial \varTheta }{\partial Z}-\dfrac{\partial \varPsi }{\partial Z}\dfrac{\partial \varTheta }{\partial X}\) and \(J(\varPsi ,\varPhi )=\dfrac{\partial \varPsi }{\partial X}\dfrac{\partial \varPhi }{\partial Z}-\dfrac{\partial \varPsi }{\partial Z}\dfrac{\partial \varPhi }{\partial X}\) and in Eq. (13), \(g_m(\varOmega , \tau ) = \dfrac{g'(\varOmega , \tau )}{g}\) is arise due to gravity modulation. There are three different types of time-periodic oscillations (also called g-gitter or gravity modulation) are considered in the paper (see Fig. 2), viz.,

Case (i): Gravity modulation by trigonometric sine wave-form

$$\begin{aligned} g_m(\varOmega , \tau ) =\delta f_1(\varOmega , \tau ) =\delta \sin (\varOmega \tau ), \end{aligned}$$
(16)

Case (ii) : Gravity modulation by triangular wave-form

$$\begin{aligned} g_m(\varOmega , \tau )=8\delta f_2(\varOmega , \tau ) = \dfrac{8\delta }{\pi ^2} \sum _{n=1,3,5,\cdots }^{\infty } \dfrac{(-1)^{\frac{(n-1)}{2}}}{n^2} \sin (n\varOmega \tau ), \end{aligned}$$
(17)

Case (iii) : Gravity modulation by square wave-form

$$\begin{aligned} g_m(\varOmega , \tau ) = \delta f_3(\varOmega , \tau )& {}= \delta \left[ H\left( \dfrac{\varOmega \tau }{\pi } \right) -H\left( \dfrac{\varOmega \tau }{\pi } -1\right) \right] -1 \nonumber \\ & {}= \dfrac{4\delta }{\pi }\sum _{n=1,3,5,\cdots }^\infty \dfrac{1}{n}\sin (n\varOmega \tau ), \end{aligned}$$
(18)

where \(H\left( \dfrac{\varOmega \tau }{\pi }\right)\) is the Heaviside step function, \(\delta\) is the amplitude of modulation and \(\varOmega\) is the frequency. In cases (ii) and (iii), the Fourier series of \(f_2\) and \(f_3\) in \(\left[ 0 ,\dfrac{2\pi }{\varOmega }\right]\) are used.

Equations (13)–(15) are solved subject to stress-free, isothermal, iso-nanoparticle concentration boundary conditions on the horizontal boundaries:

$$\begin{aligned} \varPsi = \dfrac{\partial ^2}{\partial Z^2}\left( \dfrac{\partial \varPsi }{\partial X}\right) =\varTheta =\varPhi =0\; \text { at } \;Z=0,1, \end{aligned}$$
(19)

and the periodicity conditions in the \(X-\) direction:

$$\begin{aligned} \left. \begin{aligned} \varPsi \left( X \pm \dfrac{2\pi }{\pi \kappa _c},Z\right) =\varPsi (X,Z),\\ \varTheta \left( X\pm \dfrac{2\pi }{\pi \kappa _c}, Z\right) =\varTheta (X,Z), \\ \varPhi \left( X\pm \dfrac{2\pi }{\pi \kappa _c}, Z\right) =\varPhi (X,Z), \end{aligned}\right\} , \end{aligned}$$
(20)

where \(\kappa _c\) is the critical wave number of the convecting cell. Using a minimal mode truncated Fourier series representation we make a weakly nonlinear stability analysis of the system (13)–(20) and derive a generalized Lorenz model in the next section.

Fig. 2
figure 2

Schematic of wave forms for \(\varOmega ^*=4\pi\)

Full size image
Fig. 3
figure 3

Plot of the critical stationary Rayleigh number, \(Ra_{nl_c}\), versus the concentration Rayleigh number, \(Ra_{\phi _{nl}}\), diffusivity ratio, \(N_{A_{nl}}\) and the Lewis number, \(Le_{nl}\), for trigonometric sign modulation and for water-copper nanoliquid

Full size image

3 Weakly nonlinear stability analysis

Minimal modes to describe the nonlinear interaction for the present problem is five-mode with the stream function, temperature and the nanoparticle concentration taken as follows:

$$\begin{aligned} \varPsi& {}= \dfrac{\sqrt{2}a_1 \eta ^2}{\pi ^2 \kappa } A(\tau )\sin (\pi \kappa X)\sin (\pi Z), \end{aligned}$$
(21)
$$\begin{aligned} \varTheta& {}= \dfrac{\sqrt{2}}{\pi r_{nl}} B(\tau )\cos (\pi \kappa X)\sin (\pi Z)-\dfrac{1}{\pi r_{nl}} C(\tau )\sin (2\pi Z), \end{aligned}$$
(22)
$$\begin{aligned} \varPhi& {}= \dfrac{\sqrt{2}}{\pi } L(\tau )\cos (\pi \kappa X)\sin (\pi Z)+\dfrac{1}{\pi } M(\tau )\sin (2\pi Z), \end{aligned}$$
(23)

where \(r_{nl}= \dfrac{Ra_{nl}\pi ^2 \kappa ^2}{\eta ^6}\) and \(\eta =\pi \sqrt{1+\kappa _c^2}\).

Substituting Eqs. (21)–(23) into Eqs. (13)–(15) and multiplying the resultant equations by eigenfunctions \(\sin (\pi \kappa X)\sin (\pi Z)\), \(\cos (\pi \kappa X)\sin (\pi Z)\) and \(\sin (2\pi Z)\) and integrating with respect to X and Z over one wave length, viz., \(\int _{Z=0}^1 \int _{X=0}^{\frac{2\pi }{\kappa _c \pi }} dX dZ\), which involve both rotating and counter-rotating Rayleigh–Bénard cells, we get the generalized Lorenz model in the form

$$\begin{aligned} \dfrac{1}{ Pr_{nl}}\dfrac{dA}{d\tau _1}& {}= a_1 \left( \left[ 1+g_m(\varOmega ,\tau _1)\right] B-A-\left[ 1+g_m(\varOmega ,\tau _1)\right] r_{\phi _{nl}}L\right) , \end{aligned}$$
(24)
$$\begin{aligned} \dfrac{dB}{d\tau _1}& {}= a_1 (r_{nl} A-B-AC), \end{aligned}$$
(25)
$$\begin{aligned} \dfrac{dC}{d\tau _1}& {}= a_1 (AB-bC), \end{aligned}$$
(26)
$$\begin{aligned} r_{nl}\dfrac{dL}{d\tau _1}& {}= a_1\left( r_{nl} A-\dfrac{ N_{A_{nl}}}{Le_{nl}}B-\dfrac{r_{nl}}{Le_{nl}}L+r_{nl}AM\right) , \end{aligned}$$
(27)
$$\begin{aligned} r_{nl}\dfrac{dM}{d\tau _1}& {}= a_1\left( \dfrac{ bN_{A_{nl}}}{Le_{nl}}C-\dfrac{br_{nl}}{Le_{nl}}M-r_{nl}AL\right) , \end{aligned}$$
(28)

where \(\tau _1=\eta ^2 \tau\), \(r_{\phi {nl}}= \dfrac{Ra_{\phi _{nl}}\pi ^2 \kappa ^2}{\eta ^6}\) and \(b=\dfrac{4\pi ^2}{\eta ^2}\).

Using the linearized version of the Lorenz model (24)–(28) we first make a linear stability analysis under the following subsections:

  1. 1.

    Validity of the principle of exchange of stabilities in the case of the no-modulation problem and justification for using it in the modulation problem and

  2. 2.

    Obtain the expression for the critical Rayleigh number and the correction Rayleigh number using Venezian [54] approach in the case of the modulation problem.

Fig. 4
figure 4

Plot of the critical Rayleigh number versus frequency of modulation, \(\varOmega ^*\), for different waveforms and for water-copper nanoliquid(left) and for water (right)

Full size image

3.1 Linear stability analysis

Linear stability analysis involves infinitesimal amplitudes and hence we neglect the nonlinear terms in the Lorenz model (24)–(28). That gives us the following system of ordinary differential equations:

$$\begin{aligned} \dfrac{1}{ Pr_{nl}}\dfrac{dA}{d\tau _1}& {}= a_1 \left( \left[ 1+g_m(\varOmega ,\tau _1)\right] B-A-\left[ 1+g_m(\varOmega ,\tau _1)\right] r_{\phi _{nl}}L\right) , \end{aligned}$$
(29)
$$\begin{aligned} \dfrac{dB}{d\tau _1}& {}= a_1 (r_{nl} A-B), \end{aligned}$$
(30)
$$\begin{aligned} r_{nl}\dfrac{dL}{d\tau _1}& {}= a_1\left( r_{nl} A-\dfrac{ N_{A_{nl}}}{Le_{nl}}B-\dfrac{r_{nl}}{Le_{nl}}L\right) . \end{aligned}$$
(31)

3.1.1 Validity of the principle of exchange of stabilities (PES) in the case of the no-modulation problem and justification for using it in the modulation problem

With the intention of showing the PES is valid for the unmodulated convection we assume the amplitudes A, B and L of Eqs. (29)–(31) to vary as \(e^{i\omega \tau _1}\) which leads to:

$$\left[ {\begin{array}{*{20}c} { - \left( {\frac{1}{{Pr_{{nl}} }}i\omega + a_{1} } \right)} & {a_{1} } & { - a_{1} r_{{\phi _{{nl}} }} } \\ {a_{1} r_{{nl}} } & { - (i\omega + a_{1} )} & 0 \\ {a_{1} r_{{nl}} } & {\frac{{ - a_{1} N_{{A_{{nl}} }} }}{{Le_{{nl}} }}} & { - \left( {i\omega + \frac{{a_{1} }}{{Le_{{nl}} }}} \right)r_{{nl}} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} A \\ B \\ L \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right],$$
(32)

where \(\omega\) is the natural frequency. The condition for a non-trivial solution of the above system is given by:

$$\left| {\begin{array}{*{20}c} { - \left( {\frac{1}{{Pr_{{nl}} }}i\omega + a_{1} } \right)} & {a_{1} } & { - a_{1} r_{{\phi _{{nl}} }} } \\ {a_{1} r_{{nl}} } & { - (i\omega + a_{1} )} & 0 \\ {a_{1} r_{{nl}} } & {\frac{{ - a_{1} N_{{A_{{nl}} }} }}{{Le_{{nl}} }}} & { - \left( {i\omega + \frac{{a_{1} }}{{Le_{{nl}} }}} \right)r_{{nl}} } \\ \end{array} } \right| = 0.$$
(33)

Solving the determinant (33) for \(r_{nl}\) we get the expression of the critical scaled Rayleigh number for oscillatory mode of convection as follows :

$$\begin{aligned} (r_{nl})^{osc}= P(\omega ^2)+i\omega \; N(\omega ^2), \end{aligned}$$
(34)

where \(P(\omega ^2)\) and \(N(\omega ^2)\) given by

$$\begin{aligned} P(\omega ^2)& {}= 1 +\dfrac{a_1^2r_{\phi _{nl}}( Le_{nl}-N_{A_{nl}})}{a_1^2+Le_{nl}^2\omega ^2}-\omega ^2 \left( \dfrac{1}{a_1^2Pr_{nl}}-\dfrac{Le_{nl}^2r_{\phi _{nl}}}{a_1^2 +Le_{nl}^2\omega ^2}\right) ,\end{aligned}$$
(35)
$$\begin{aligned} N(\omega ^2)& {}= \dfrac{\left( 1+Pr_{nl}\right) }{a_1 Pr_{nl} }+\dfrac{a_1 r_{\phi _{nl}} Le_{nl} (1+ N_{A_{nl}}- Le_{nl})}{(a_1^2+Le_{nl}^2 \omega ^2)}. \end{aligned}$$
(36)

Solving the equation \(N(\omega ^2)=0\) we get the expression for the frequency of oscillations in unmodulated convection as:

$$\begin{aligned} \omega ^2 = -\left( \dfrac{a_1^2\left[ 1+Pr_{nl}+Pr_{nl} Le_{nl} r_{\phi _{nl}}(1+N_{A_{nl}}-Le_{nl})\right] }{ Le_{nl}^2(1+Pr_{nl})}\right) . \end{aligned}$$
(37)

It is quite obvious from the expression (37) that the oscillatory unmodulated convection is possible only when

$$\begin{aligned} Le_{nl}>1+N_{A_{nl}}. \end{aligned}$$
(38)

Computation (see Table 4) reveals that this inequality cannot be realised for all nanoliquids considered and hence we may discount the oscillatory motion in our problem and thereby implying the validity of ‘the principle of exchange of stabilities’ for unmodulated convection. The nanoparticle/nanotube effect is weak due to dilute concentration, the modulation considered is of small amplitude and not-so-large frequency and hence this is assumed not to dramatically change the underlying nature of stationary mode of unmodulated convection at onset.

Table 4 Thermophysical properties of twenty eight nanoliquids for volume fraction, \(\chi =0.05\), at \(300^{\circ }\hbox {K}\)
Full size table

3.1.2 Expression for the critical stationary Rayleigh number and the correction Rayleigh number for the modulation problem

To find the expression of critical stationary Rayleigh number and its correction we follow the Venezian [54] approach. We take the gravity modulation to be of first-order in \(\epsilon _1\), a very small amplitude, and assuming that the thermophoretic effect is weak and to be first-order in \(\epsilon _1\) and hence we expand amplitudes, A, B, L and scaled Rayleigh number, \(r_{nl}\), in the form:

$$\begin{aligned} \left. \begin{aligned} A=A_0+\epsilon _1 A_1+{\epsilon _1}^2 A_2 +\cdots \\ B=B_0+\epsilon _1 B_1+{\epsilon _1}^2 B_2 +\cdots \\ L=L_0+\epsilon _1 L_1+{\epsilon _1}^2 L_2 +\cdots \\ r_{nl}=r_{0}^L+\epsilon _1 r_1^L+{\epsilon _1}^2 r_2^L+\cdots \end{aligned} \right\} . \end{aligned}$$
(39)

Using Eq. (39) in the Eqs. (29)–(31) and equating terms of the same order in \(\epsilon _1\) on either side of the resulting equation, we get

$$\begin{aligned}&O({\epsilon _1}^0): {\mathcal {L}}_1 W_0=0, \end{aligned}$$
(40)
$$\begin{aligned}&O({\epsilon _1}^1): {\mathcal {L}}_1 W_1=[R^L_{21} \; R^L_{22} \; R^L_{23}]^{Tr}, \end{aligned}$$
(41)
$$\begin{aligned}&O({\epsilon _1}^2): {\mathcal {L}}_1 W_2=[R^L_{31} \; R^L_{32} \; R^L_{33}]^{Tr}, \end{aligned}$$
(42)

where Tr represents the transpose, \({\mathcal {L}}_1\) and \(W_i\), \(i=0,1,2\) are operators defined as:

$${\mathcal {L}}_1 = \left[\begin{matrix} -\left(\frac{1}{Pr_{nl}}\frac{d}{d\tau _1}+a_1\right) & a_1 & -a_{1} r_{\phi _{nl}} \\ r_{0}^{L} a_{1} & -\left(\frac{d}{d\tau_{1}}+a_{1}\right) & 0 \\ r_{0}^{L} a_{1} & 0 & -r_{0}^{L}\left(\frac{d} {d\tau_{1}}+\frac{a_{1}}{Le_{nl}}\right) \end{matrix} \right],$$
(43)

\(W_i=[A_i, \;\;B_i,\;\; L_i]^{Tr}\) and \(R^L_{21}\), \(R^L_{22}\), \(R^L_{23}\), \(R^L_{31}\), \(R^L_{32}\) and \(R^L_{33}\) are given by

$$\begin{aligned} \left. \begin{aligned} R^L_{21}&=a_1\overline{g_m(\varOmega ^*, \tau _1)}B_0-a_1\overline{g_m(\varOmega ^*, \tau _1)}r_{\phi _{nl}}L_0 \\ R^L_{22}&=r_1^La_1 A_0,\;\; R^L_{23}=r_1^La_1 A_0-\dfrac{a_1r_1^L L_0}{Le_{nl}}\\ \end{aligned}\right\} , \end{aligned}$$
(44)
$$\begin{aligned} \left. \begin{aligned} R^L_{31}&=a_1\overline{g_m(\varOmega ^*, \tau _1)}B_1-a_1\overline{g_m(\varOmega ^*, \tau _1)}r_{\phi _{nl}}L_1 \\ R^L_{32}&=r_2^La_1 A_0,\;\; R^L_{33}=r_2^La_1 A_0\dfrac{a_1 N_{A_{nl}}B_0}{Le_{nl}}-\dfrac{a_1r_2^L L_0}{Le_{nl}}\\ \end{aligned}\right\} , \end{aligned}$$
(45)

where \(\varOmega ^*=\dfrac{\varOmega }{\epsilon _1}\) and the over bar on \(g_m(\varOmega ^*, \tau _1)\) denotes the time-average in \(\left[ 0,\frac{2\pi }{\varOmega ^*}\right]\).

The solution of the homogeneous system of equations, (40), yields:

$$\begin{aligned} W_0=[A_0,\;r_0^L A_0,\;Le_{nl} A_0]^{Tr}. \end{aligned}$$
(46)

with the critical Rayleigh number :

$$\begin{aligned} (r_{0}^{L})^{s}=1+r_{\phi _{nl}} Le_{nl}. \end{aligned}$$
(47)

We now use on Eqs. (41) and (42) the solvability condition which states that ‘the inhomogeneous terms must be orthogonal to the solution of the homogenous equation’. This yields

$$\begin{aligned} r_1^{L}=0 \end{aligned}$$
(48)

and

$$\begin{aligned} r_2^{L}& {}= Re\left[ \dfrac{a_1(r_0^{L}-r_{\phi _{nl}}Le_{nl}) \left[ r_0^{L}(i\varOmega ^* Le_{nl}-a_1)-r_{\phi _{nl}}Le_{nl}(i\varOmega ^*-a_1)\right] }{(i\varOmega ^*-a_1)(i\varOmega ^* Le_{nl}- a_1) \left( \frac{i\varOmega ^*}{a_1 Pr_{nl}}-1+\frac{a_1 r_0}{a_1-i\varOmega ^*}+\frac{a_1 r_{\phi _{nl}}Le_{nl}}{a_1-i\varOmega ^* Le_{nl}}\right) }\right] \nonumber \\&-N_{A_{nl}}r_{\phi _{nl}}, \end{aligned}$$
(49)

where Re denotes the real part. In the next subsection we derive the first-order Ginzburg–Landau model from the fifth-order Lorenz model using the method of multiscales.

Table 5 Values of \(\overline{Nu_{nl}}\) for four Newtonian liquids and twenty eight Newtonian nanoliquids (\(\chi =0.05\)), \(r_{nl}=5\), \(\varOmega ^*=5\) and for different values of \(\delta\) and for different types of gravity-aligned oscillation
Full size table
Table 6 Values of \(\overline{Nu_{nl}}\) for twenty eight Newtonian nanoliquids (\(\chi =0.05\)), \(r_{nl}=5\), \(\delta =0.1\), for different values of \(\varOmega ^*\) and for different types of gravity- aligned oscillation
Full size table

3.2 Derivation of the Ginzburg–Landau model from the Lorenz model

Consider the following regular perturbation expansion for the amplitudes and the scaled Rayleigh number:

$$\begin{aligned} \left[ \begin{matrix} A \\ B \\ C\\ L\\ M\\ r_{nl_c} \end{matrix} \right] = \left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ r_0^L \end{matrix} \right] +\epsilon _2 \left[ \begin{matrix} A_1 \\ B_1\\ C_1 \\ L_1 \\ M_1 \\ 0 \end{matrix} \right] +\epsilon _2^2 \left[ \begin{matrix} A_2 \\ B_2 \\ C_2 \\ L_2 \\ M_2 \\ r_2^N \end{matrix} \right] + \epsilon _2^3 \left[ \begin{matrix} A_3 \\ B_3\\ C_3 \\ L_3 \\ M_3 \\ 0 \end{matrix} \right] + \cdots , \end{aligned}$$
(50)

where \(\epsilon _2\) is a small amplitude which is different from \(\epsilon _1\) and \(\epsilon _1\) = O(\(\epsilon _2^2\)). The essential difference between \(\epsilon _1\) and \(\epsilon _2\) is that the former was chosen from the modulation term with small amplitude and latter concerns finite amplitude convection. We assume the small time-scale, \(\tau _1^* = \epsilon _2^2 \tau _1\) and a weak thermophoretic effect, \(\epsilon _2^2 N_{A_{nl}}\) and that the gravity modulation is of second-order correction in \(\epsilon _2\). For the sake of convenience let us define the operators \({\mathcal {L}}_2\) and V as follows:

$${\mathcal {L}}_2 = \left[ \begin{array}{ccccc} -a_1 &{} a_1 &{} 0 &{} -a_1 r_{\phi _{nl}} &{} 0 \\ r_0^L a_1 &{} a_1 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} -ba_1 &{} 0 &{} 0\\ r_0^L a_1 &{} 0 &{} 0&{} -r_0^L\dfrac{a_1}{Le_{nl}} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{r_0^L a_1 b}{Le_{nl}} \end{array} \right] \text { and } \quad V_i = \left[ \begin{array}{c} A_i \\ B_i \\ C_i \\ L_i \\ M_i \end{array} \right] , i = 1(1)3.$$
(51)

Substituting Eq. (50) in Eqs. (24)–(28) and on comparing the like powers of \(\epsilon _2\) on either side of the resulting equations, we get the following equations at various orders:

First-order system:

$$\begin{aligned} {\mathcal {L}}_2 V_1 = 0, \end{aligned}$$
(52)

Second-order system:

$$\begin{aligned} {\mathcal {L}}_2 V_2 = [R_{21},R_{22},R_{23},R_{24},R_{25}]^{Tr}, \end{aligned}$$
(53)

Third-order system:

$$\begin{aligned} {\mathcal {L}}_2V_3 = [R_{31},R_{32},R_{33},R_{34},R_{35}]^{Tr}, \end{aligned}$$
(54)

where

$$\begin{aligned} \begin{aligned} R_{21}&= 0, R_{22} = a_1 A_1 C_1, R_{23} = -a_1 A_1 B_1, R_{24} = - A_1 M_1, R_{25} = - A_1 L_1, \end{aligned} \end{aligned}$$
(55)
$$\begin{aligned} \left. \begin{aligned} R_{31}&=\dfrac{1}{Pr_{nl}}\dfrac{dA_1}{d\tau _1^*}-a_1 Pr_{nl} g_m(\varOmega ^*, \tau _1^*)B_1 + a_1 Pr_{nl} r_{\phi _{nl}} g_m(\varOmega ^*, \tau _1^*) L_1,\\ R_{32}&= \dfrac{dB_1}{d \tau _1^*}-a_1 r_2^N A_1 +a_1 A_1 C_2, \\ R_{33}&= -a_{1}(A_1 B_2 +A_2 B_1)+\dfrac{dC_1}{d\tau _1^*},\\ R_{34}&= - a_1(A_1M_2+A_2M_1)+\dfrac{dL_1}{d\tau _1^*}-a_1r_2^N A_1 +a_1 \dfrac{N_{A_{nl}}}{Le_{nl}}B_1+\dfrac{1}{Le_{nl}}L_1,\\ R_{35}&= a_1(A_1L_2+A_2L_1)+\dfrac{dM_1}{d\tau _1^*}+\dfrac{a_1br_2^N}{Le_{nl}}M_1, \end{aligned} \right\} , \end{aligned}$$
(56)

where \(\varOmega ^*=\dfrac{\varOmega }{\epsilon _2^2}\).

The solution of the first- and second-order systems is given by

$$\begin{aligned}{}[A_1,\;B_1,\; C_1,\; L_1,\; M_1] & {}= [A_{1},\; A_{1},\; 0,\; Le_{nl}A_{1},\; 0]^{Tr}, \end{aligned}$$
(57)
$$\begin{aligned}{}[A_2,\;B_2,\;C_2,\;L_2,\;M_2]& {}= [0, \; 0,\; \dfrac{1}{b}A_{1}^2, \;0,\; \dfrac{-Le_{nl}^2}{b}A_{1}^2]^{Tr}. \end{aligned}$$
(58)

For the purpose of determining the amplitude, \(A_{1}\), we consider the Fredholm solvability condition as :

$$\begin{aligned} \sum _{j=1}^5 R_{ij} \hat{V_1} = 0, \end{aligned}$$
(59)

where \(\hat{V_1}\) represents the solution of the adjoint system of Eq. (52).

The expression for correction Rayleigh number, \(r_2^N\), is obtained by considering the solubility condition for steady part of third-order system which is given by

$$\begin{aligned} r_2^N=-(\overline{g_m(\varOmega ^*, \tau _1^*)}+r_{\phi _{nl}} N_{A_{nl}}). \end{aligned}$$
(60)

Substituting \(i=3\) in Eq. (59) and on using Eqs. (52) and (56) in the resulting equation, we get the Ginzburg–Landau equation in the form:

$$\begin{aligned} \dfrac{dA_{1}(\tau _1^*)}{d\tau _1^*} = \left[ Q_1+ g_m(\varOmega ^*, \tau _1^*) Q_2\right] A_{1}(\tau _1^*)-Q_3 A_{1}^3(\tau _1^*), \end{aligned}$$
(61)

where

$$\begin{aligned} \left. \begin{aligned} Q_1&= \dfrac{a_1 Pr_{nl}(r_{2}^N+N_{A_{nl}}r_{\phi _{nl}})}{1+Pr_{nl}(r_0^L-Le_{nl}^2r_{\phi _{nl}})}, Q_2 = \dfrac{a_1 Pr_{nl}(r_{0}^L- r_{\phi _{nl}}Le_{nl})}{1+Pr_{nl}(r_0^L-Le_{nl}^2r_{\phi _{nl}})},\\ Q_3&= \dfrac{\eta ^2 Pr_{nl}(r_0^L-Le_{nl}^3r_{\phi _{nl}})}{4\pi ^2 \left[ 1+Pr_{nl}(r_0^L-Le_{nl}^2r_{\phi _{nl}})\right] } \end{aligned} \right\} . \end{aligned}$$
(62)

The Ginzburg–Landau equation (61) with its non-autonomous nature is analytically intractable. Hence we use Mathematica 8.0 to solve the equation numerically with the initial condition \(A_1(0)=1\).

In the next section we quantify the heat transport in terms of the Nusselt number at the lower boundary within a wave-length distance in the horizontal direction.

Table 7 Values of \(\overline{Nu_{nl}}\) for twenty eight Newtonian nanoliquids for \(r_{nl}=5\), \(\delta =0.1\), \(\varOmega ^*=5\) for different values of \(\chi\) and for different types of gravity-aligned oscillation
Full size table

4 Estimation of heat transport in nanoliquids at the lower plate in the presence/absence of gravity modulation

The thermal Nusselt number, \(Nu_{nl}(\tau _1^*)\), is defined as:

$$\begin{aligned} Nu_{nl}(\tau _1^*) & {}= \dfrac{\text { Heat\; transport \;by\; (conduction \,+\,convection)} }{\text { Heat \;transport \;by \;conduction }} \end{aligned}$$
$$\begin{aligned} & {}= 1+\dfrac{k_{nl}}{k_{bl}}\left[ \dfrac{\int _0^{\frac{2\pi }{\pi \kappa _c}}\left( \dfrac{\partial \varTheta }{\partial Z}\right) dX}{\int _0^{\frac{2\pi }{\pi \kappa _c}}\left( \dfrac{d\varTheta _b}{dZ}\right) dX}\right] _{Z=0}, \end{aligned}$$
(63)

where \(\varTheta _b(Z) =\dfrac{T_b(Z)-T_0}{\varDelta T}\).

Substituting Eqs. (6) and (22) in Eq. (63), we get

$$\begin{aligned} Nu_{nl}(\tau _1^*)=1+\left( \dfrac{k_{nl}}{k_{bl}}\right) \dfrac{2}{r_{nl}}C(\tau _1^*). \end{aligned}$$
(64)

Using Eqs. (50), (57) and (58) in (64), we get

$$\begin{aligned} Nu_{nl}(\tau _1^*)=1+\dfrac{2}{b} \left( \dfrac{k_{nl}}{k_{bl}}\right) \left( 1-\dfrac{1}{r_{nl}}\right) {\mathcal {A}}_{1}(\tau _1^*)^2. \end{aligned}$$
(65)

To have a detailed discussion on the heat transfer we define the time-averaged Nusselt number (mean Nusselt number), \(\overline{Nu_{nl}(\tau _1^*)}\), as follows :

$$\begin{aligned} \overline{Nu_{nl}(\tau _1^*)}= \dfrac{1}{\left( \dfrac{2\pi }{\varOmega ^*}\right) } \displaystyle {\int _{0}^{\dfrac{2\pi }{\varOmega ^*}}Nu_{nl}(\tau _1^*)d\tau _1^*}, \end{aligned}$$

where \(\left[ 0, \dfrac{2\pi }{\varOmega ^*}\right]\) is the interval chosen to calculate the mean Nusselt number. With the necessary background for analysing the results prepared in the previous sections, in what follows we discuss the results obtained and draw a few conclusions.

Table 8 Values of \(\overline{Nu_{nl}}\) for twenty eight Newtonian nanoliquids (\(\chi =0.05\)) for \(r_{nl}=5\), \(\delta = 0.1\), \(\varOmega ^*=5\) and for different types of gravity- aligned oscillation using the single-phase model (\(Ra_{\phi _{nl}}=0\))
Full size table

5 Results and discussion

The effect of gravity modulation on Rayleigh–Bénard convection in nanoliquids is studied in the paper using the generalized Buongiorno two-phase model with thermophysical properties determined from the phenomenological laws or the mixture theory. Three different types of gravity modulation effects on onset of convection and the heat transport are investigated in the paper. Before we move on to the discussion on the results of the paper we need to mention that the results, their discussion and thereby the conclusion drawn lean heavily on the actual values of thermophysical properties of nanoliquids (see Table 4) determined by using thermophysical properties of the base liquids and the nanoparticles/nanotubes (see Tables 1, 2, 3). This shift from the classical approach to convection makes the outcome of the paper more valuable in the context of Rayleigh–Bénard convection of real Newtonian nanoliquids or real Newtonian liquid.

Table 9 Results from previous works and qualitative comparison with those of present work
Full size table

In the present problem the principle of exchange of stabilities is valid and hence the stationary mode of convection is the preferred one at onset. The following general results can be qualitatively obtained from Fig. 3:

$$\begin{aligned} \dfrac{dRa_{nl_c}}{dN_{A_{nl}}}<0,\;\; \quad \dfrac{dRa_{nl_c}}{dRa_{\phi _{nl}}} <0,\;\; \quad \dfrac{dRa_{nl_c}}{dLe_{nl}} >0, \end{aligned}$$
(66)

where \(Ra_{nl_c}=Ra_{nl_0}+\epsilon _1^2 Ra_{nl_2}\). The above general results especially that for the Lewis number in Eq. (66), have been arrived at by considering the fact that \(Le_{nl}<N_{A_{nl}}\) which in turn means that \(Ra_{{nl}_c}<Ra_{{bl}_c}\). The data documented in Table 4 and Fig. 3 point to this fact. Thus the linear stability analysis clearly shows that the onset of convection is advanced in the base liquid when a dilute concentration of nanoparticles/nanotubes is introduced.

Figure 4 reveals that for the modulated system the following are true :

  1. (a)

    For \(\varOmega ^*<2.3\)

    1. (i)

      \(Ra_{nl_c}^{T}<Ra_{nl_c}^{TS}<Ra_{nl_c}^S\) and \(Ra_{bl_c}^{T}<Ra_{bl_c}^{TS}<Ra_{bl_c}^S\)

    2. (ii)

      \(Ra_{nl_c}^{\delta =0}<Ra_{nl_c}^{\delta \ne 0}\) and \(Ra_{bl_c}^{\delta =0}<Ra_{bl_c}^{\delta \ne 0}\)

    3. (b)

      For \(\varOmega ^*>2.3\)

    4. (i)

      \(Ra_{nl_c}^{T}>Ra_{nl_c}^{TS}>Ra_{nl_c}^S\) and \(Ra_{bl_c}^{T}>Ra_{bl_c}^{TS}>Ra_{bl_c}^S\)

    5. (ii)

      \(Ra_{nl_c}^{\delta =0}>Ra_{nl_c}^{\delta \ne 0}\) and \(Ra_{bl_c}^{\delta =0}>Ra_{bl_c}^{\delta \ne 0}\)

Further, \(Ra_{nl_c}<Ra_{bl_c}\) is true for all three types of modulation and also for the no modulation case.

With a clear knowledge as to what the observed effect of nanoparticles/nanotubes and the gravity modulation on onset of convection is, we now move on to discuss the results on nonlinear stability analysis and what it has to say in the post-onset regime of Rayleigh–Bénard convection.

The non-autonomous fifth-order Lorenz model is reduced to the non-autonomous first-order Ginzburg–Landau equation using the method of multiscales. Using the Ginzburg–Landau equation, one of the amplitudes is obtained numerically and the Nusselt number is evaluated as a quadratic function of the amplitude. The mean Nusselt number for four Newtonian liquids (\(\chi =0\)) and for twenty-eight Newtonian nanoliquids (for \(\chi =0.05\)) are presented for different modulations.

From Table 5 it is apparent that amongst the three modulations, triangular wave facilitates least heat transport and square wave facilitates maximum heat transport. Having a look at Fig. 2 it can be inferred that the wave form that has the maximum area under its curve facilitates maximum heat transport. Further, the Table 5 clearly shows that the following results are true:

  1. (i)

    \(\overline{Nu}_{nl}^{\delta =0} > \overline{Nu}_{nl}^{\delta \ne 0}\) for all three modulations and is true for both Newtonian liquids (NL) and Newtonian nanoliquids (NNL),

  2. (ii)

    \(\overline{Nu}_{nl}<\overline{Nu}_{bl}\) for all three modulations and also for the no modulation case.

Table 6 documents the effect of frequency \((\varOmega ^*)\) of modulation on the mean Nusselt number. The effect of increasing \(\varOmega ^*\) is to decrease the heat transport in the case of all three types of modulation and the result is true for Newtonian liquid as well as Newtonian nanoliquids.

Table 7 reiterates the fact that dilute concentrations of nanoparticle/nanotube when dispersed uniformly in Newtonian liquid facilitates enhanced heat transfer.

The generalised fifth-order Lorenz model in Eqs. (24)–(28) reduces to the third-order Lorenz model associated with the single-phase model of Khanafer et al. [24]. This can be seen on taking \(r_{\phi _{nl}}=0\) in the fifth-order Lorenz model. With \(r_{\phi _{nl}}=0\), Eqs. (24)–(28) get uncoupled from L and M resulting in the third-order Lorenz model (see Siddheshwar and Meenakshi [42] for no modulation):

$$\begin{aligned} \dfrac{1}{ Pr_{nl}}\dfrac{dA}{d\tau _1} & {}= a_1 \left( \left[ 1+g_m(\varOmega ,\tau _1)\right] B-A\right) , \end{aligned}$$
(67)
$$\begin{aligned} \dfrac{dB}{d\tau _1} & {}= a_1 (r_{nl} A-B-AC), \end{aligned}$$
(68)
$$\begin{aligned} \dfrac{dC}{d\tau _1} & {}= a_1 (AB-bC), \end{aligned}$$
(69)

which is the Lorenz model obtained for single-phase. Table 8 clearly points to the fact that the single-phase model under predicts the mean Nusselt number in comparison with that by the generalized two-phase model of the current paper. This result can be comprehended by seeing the results documented in Table 8 in conjunction with Table 5.

The experimental and numerical results on Rayleigh–Bénard convection in Newtonian nanoliquids in the presence/absence of gravity modulation for rigid boundaries are summarized in Table 9. The findings of the present study for free boundaries are compared with these results by recollecting the results of classical Rayleigh–Bénard convection on different boundaries (see Chandrasekhar [12]) we may write that :

$$\begin{aligned} Ra^{[FF]}<Ra^{[RF]}<Ra^{[RR]}\quad \text { and }\quad Nu^{[FF]}>Nu^{[RF]}>Nu^{[RR]}, \end{aligned}$$
(70)

where FF, RF and RR represents the free-free, rigid-free and rigid-rigid boundaries. We note here that the classical results on boundary effect on onset of convection holds good in the presence of nanoparticles/nanotubes also. Thus the relation (70) is true in the case of nanoliquid also, i.e.,

$$\begin{aligned} Ra_{nl}^{[FF]}<Ra_{nl}^{[RF]}<Ra_{nl}^{[RR]} \quad \text { and } \quad Nu_{nl}^{[FF]}>Nu_{nl}^{[RF]}>Nu_{nl}^{[RR]}. \end{aligned}$$
(71)

The results reported from Fig. 4 and Table 5 for water are in line with the experimental and numerical findings of Gresho and Sani [19], Biringen and Peltier [8] and Yu et al. [58] mentioned in Table 9.

Comparing the results of present problem with the enclosure problem of Siddheshwar and Kanchana [40, 41] we may conclude :

$$\begin{aligned} Nu_{nl}^{[\text { Rectangular\; enclosure }]}<Nu_{nl}^{[\text { Classical \;RBC }]},\;\; \forall \text { nanoliquids}. \end{aligned}$$
(72)

The Nusselt number for water-alumina nanoliquids without gravity modulation at volume fraction, \(\chi =0.08\) is 2.8507 which is greater than the value obtained by Elhajjar et al. [15] for rectangular enclosure (see Table 9). Hence the relation (72) is satisfied in the present study. Thus the present study reiterates the numerical and experimental results obtained by earlier investigators. In fact, the results of the weakly nonlinear stability analysis of the present study can serve as an initial value for numerical studies of the full equations and this will form the topic for a separate major study. With this remark we now draw some general conclusions in the next section.

6 Conclusion

The effect of three different wave-types of time-periodic gravity-aligned oscillations on Rayleigh–Bénard convection in Newtonian liquids and in Newtonian nanoliquids is studied in the paper using the generalized Buongiorno two-phase model. The principle of exchange of stabilities is shown to be valid in the case of no modulation problem and justification is provided for using it in the modulation problem and hence the stationary mode of convection considered to be a preferred one at onset. It is shown that the addition of dilute concentration of nanoparticles/nanotubes to Newtonian liquids leads to advancement of convection. The result may because the effect of increasing \(Ra_{\phi _{nl}}\) and \(N_{A_{nl}}\) is to advance the onset of convection. The Nusselt number is obtained using the solution of Ginzburg–Landau equation which is in turn derived from Lorenz model using the method of multiscales. It is shown that effect of increasing amplitude of gravity modulation is to increase the heat transport whereas the effect of increasing frequency of gravity modulation is to decrease the heat transport. This is true for all three types of modulation. Further, the Nusselt number in the presence of modulation is less than that in its absence. When we see the following results on the onset of convection and heat transport:

  1. (i)

    \(Ra_{nl_c}^{T}<Ra_{nl_c}^{TS}<Ra_{nl_c}^{S}\), for \(\varOmega ^*<2.3\),

  2. (ii)

    \(Ra_{nl_c}^{T}>Ra_{nl_c}^{TS}>Ra_{nl_c}^{S}\), for \(\varOmega ^*>2.3\),

  3. (iii)

    \(\overline{Nu_{nl}}^{T}<\overline{Nu_{nl}}^{TS}<\overline{Nu_{nl}}^{S}\)    \(\forall \varOmega ^*.\)

Seeing this in conjunction with Fig. 2 we may conclude that the wave-form that has the maximum area under its curve helps transport maximum heat. Results on convection using the Khanafer–Vafai–Lightstone single-phase model (Ref. [24]) can be obtained as a limiting case of those obtained by the generalized Buongiorno two-phase model of Siddheshwar et al. [47]. In the presence/absence of gravity modulation we may conclude that the single-phase model under predicts heat transport compared to that by two-phase model. The generalized Buongiorno two-phase model uses actual thermophysical values for nanoliquids and thus dealing with Rayleigh–Bénard convection in nanoliquids is different from that of binary liquid convection. The two-phase model gives useful information for experimentalists who may seek information on the suitability of a particular nanoliquid and for a given application situation. The results of the present study makes a qualitative confirmation of the numerical and experimental studies of Gresho and Sani [19], Biringen and Peltier [8], Yu et al. [58] and Elhajjar et al. [15].