Introduction

Nanofluid is defined as a fluid, which uses metal or nonmetallic particles in nano sizes as nanoparticles in the base fluid. Previously, more research was done to measure and model the thermal conductivity, but in recent years, there has been much research on nanofluid heat transfer. Nanofluid is a fluid with nanoparticles in sizes from 1 to 100 nm, which has a high thermal conductivity and heat transfer coefficient relative to the base fluid.

The idea of adding solid particle in ordinary fluids to increase heat transfer was first proposed by Maxwell [1] about a century ago, but due to the large size of the solid metal particles (in millimeter and microsize), problems such as instability and sedimentation of these particles arose. Choi [2] was the first to use the term nanofluid for a fluid having nanoparticles. He showed that the addition of a small amount of nanoparticles (for example, 1% volume fraction) to the base fluid nearly doubles the thermal conductivity coefficient. Other researchers, including Xuan and Li [3], showed that increasing volume fraction about 1–5% could increase the ratio of effective thermal conductivity to the thermal conductivity of the base fluid by 20%. Wang et al. [4] proposed a model to predict the thermal conductivity of the nanofluid. The model was suitable for low volume fractions of nanofluid with metallic. The comparison of the above model with experimental results in a nanoparticle diameter of 50 nm and a volume fraction of less than 0.05 has an acceptable agreement. Hwang et al. [5] measured the thermal conductivity coefficient of four nanofluid types and showed that the thermal conductivity is linear with the volume fraction of nanoparticles. They also stated that the thermal conductivity measured in the experiments was larger than that obtained from theoretical models, and the thermal conductivity of the nanofluid in comparison with the base fluid in the volume fraction of 1% was 11.3%. Nie et al. [6] examined various mechanisms to increase the thermal conductivity and showed that in a given size of nanoparticles, the thermal conductivity is proportional to temperature and inversely proportional to viscosity. Sankar et al. [7] used a theory based on the molecular dynamics model to estimate the thermal conductivity of the nanofluid. They showed that by increasing the volume fraction from 1 to 7%, the thermal conductivity coefficient increases and the temperature increase also increases the thermal conductivity coefficient. Two approaches based on conservation equations have been adopted in the literature to investigate the numerical heat transfer of nanofluids: single-phase model and two-phase model (see Wang and Mujumdar [8]). In Ghaffari et al. [9], a two-phase numerical study of the thermal and hydrodynamic effects of the turbulent flow of the nanofluid in the curved horizontal tube was performed using a mixture model. They measured numerically the mixed convection of the turbulent flow of nanofluid containing water and aluminum oxide in the inlet region of a curved tube. They also considered the governing equations in the form of three-dimensional cylindrical coordinates. To analyze the thermal and hydrodynamic parameters, they used a mixed multiphase model and also studied the effects of buoyancy force, centrifugal force and the volume fraction of nanoparticles. Their results show that the volume fraction of nanoparticles has no significant effect on the skin friction coefficient, but its effect on the thermal parameters and the turbulence intensity of the flow is high and the results are close to the experimental and numerical work carried out by others. Rostamani et al. [10] investigated numerically the forced convection of the nanofluid through the channel. The studied flow regime was a turbulent and two-dimensional channel, and the assumption of constant thermal heat flux was used on the channel wall. The nanoparticles used were a mixture of copper oxide, titanium oxide and aluminum oxide and water base fluid. The boundary condition of the constant heat flux along the wall was applied, and the thermophysical properties of the temperature-dependent nanofluid were considered. Their results showed that with the increasing of the volume fraction, the shear stress at the wall and the heat transfer rate increased. Also, for a given Reynolds number and volume fraction, the copper oxide nanoparticles improved the heat transfer rate rather than the nanoparticles of aluminum and titanium oxide. Mirmasoumi et al. [11] studied the effect of the average diameter of nanoparticles on the mixed convection heat transfer in a nanomaterial. The geometry studied in this work, the horizontal tube and the nanofluid, was water with aluminum oxide nanoparticles. Flow is a fully developed, laminar method of solving this problem, and the numerical model used is two-phase mixture model. In this case, it is assumed that constant heat flux is applied along the wall; all the physical properties of the fluid are assumed to be constant, except for the density that changes linearly with temperature. The boundary conditions at the inlet part of the pipe are such that the specified inlet temperature and the input velocity are fixed in the axial direction, and in other directions, zero is considered. Laminar and turbulent mixed convection heat transfer of nanofluids in a rectangular shallow cavity using a two-phase mixture model is studied by Goodarzi et al. [12]. Garoosi et al. [13] studied mixed convection heat transfer of nanofluid in a two-sided lid-driven cavity with several pairs of heaters and coolers inside using two-phase mixture model. Armaghani et al. [14,15,16,17,18,19] used the Buongiorno two-phase model for modeling the forced convection heat transfer of nanofluid in LNTE and LTE porous channel. Rashidi et al. [20, 21] studied steady two-dimensional, viscous incompressible MHD nanofluid flow. They concluded that the presence of magnetic field leads to decrease the nanofluid velocity and increase the nanofluid temperature. Effects of the external magnetic field on flow and heat transfer are investigated by Sheikholeslami et al. [22, 23]. Their results show that the Nusselt number is an increasing function of the Reynolds number, the nanoparticle volume fraction and the magnetic number. The Euler and mixture two-phase models for turbulent flow of alumina nanofluid inside a horizontal tube are compared by Hejazian et al. [24]. They showed the mixture model was in a better agreement with experimental results for the estimation of average Nusselt number. It is worth mentioning that many references on nanofluids can be found in the books by Das et al. [25], Nield and Bejan [26], and Shenoy et al. [27], and in the review papers by Buongiorno et al. [28], Kakaç and Pramuanjaroenkij [29], Wong and Leon [30], Manca et al. [31], Mahian et al. [32], Sheikholeslami and. Ganji [33], Meyes et al. [34], etc.

The purpose of this study is to investigate the heat transfer and pressure drop of nanofluid in a three-dimensional rectangular channel using two-phase approach. The fluid flow was considered to be turbulent and the effect of parameters such as volume fraction, aspect ratio and diameter of nanoparticles on thermal and hydrodynamic parameters was investigated.

Problem definition and mathematical formulation

Geometry

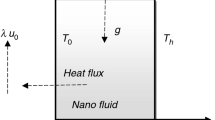
The geometry studied in this work is a 3D channel with length L, width 2a and height 2b as shown in Fig. 1. The fluid used is the water, and aluminum oxide particles were used as nanoparticles in the base fluid.

Fig. 1
figure 1

Geometry of the problem

Full size image

Governing equations

Continuity equation

The general form of the continuity equation is as follows:

$$\nabla \cdot \left( {\rho_{\text{m}} V_{\text{m}} } \right) = 0.$$
(1)

In the above equation, Vm is the mean mass velocity of the mixture and ρm is the density of the mixture as defined below,

$$V_{\text{m}} = \frac{{\sum\nolimits_{k = 1}^{n} {\phi_{\text{k}} \rho_{\text{k}} V_{\text{k}} } }}{{\rho_{\text{m}} }}\;\& \;\rho_{\text{m}} = \sum\limits_{k = 1}^{n} {\phi_{\text{k}} \rho_{\text{k}} } .$$
(2)

In the above equation, ϕk is the volume fraction of the k-phase.

Momentum equation

$$\nabla \cdot (\rho_{\text{m}} V_{\text{m}} V_{\text{m}} ) = - \nabla P + \nabla \cdot (\tau - \tau_{t} ) + \nabla \cdot \left( {\phi_{\text{k}} \rho_{\text{k}} V_{\text{dr,k}} V_{\text{dr,k}} } \right) - \rho_{\text{m}} \beta_{\text{eff}} g(T - T_{i} )$$
(3)
$$\tau = \mu_{\text{eff}} \nabla V_{\text{m}} ,\;\tau_{t} = - \sum\limits_{k = 1}^{n} {\phi_{\text{k}} \rho_{\text{k}} } \overline{{V_{\text{k}}^{\prime } V_{\text{k}}^{\prime } }} .$$
(4)

n is the number of secondary phases and \(V^{\prime }\) is the fluctuating velocity. \(V_{{{\text{dr}},k}}\) is equal to the spin velocity defined for the kth secondary phase as follows:

$$V_{\text{dr,k}} = V_{\text{k}} - V_{\text{m}} .$$
(5)

The relative velocity (slip) is defined as the speed of the second phase (particles, p) relative to the velocity of the first phase (base fluid, f), as follows:

$$V_{\text{pf}} = V_{\text{p}} - V_{\text{f}} .$$
(6)

Also, the relationship between the spin velocity and slip velocity is as follows:

$$V_{{{\text{dr}},{\text{p}}}} = V_{\text{pf}} - \sum\limits_{k = 1}^{n} {\frac{{\phi_{\text{k}} \rho_{\text{k}} }}{{\rho_{\text{m}} }}} V_{\text{fk}} .$$
(7)

Finally, the slip or relative velocity between the two phases, which is considered to be the interaction between the two phases, is calculated from the following relation known as Manning’s relation (see Nie et al. [6]).

$$V_{\text{pf}} = \frac{{\rho_{\text{p}} d_{\text{p}}^{2} }}{{18\mu_{\text{f}} f_{\text{drag}} }}\frac{{\left( {\rho_{\text{p}} - \rho_{\text{m}} } \right)}}{{\rho_{\text{p}} }}a.$$
(8)

In the above relation, f is the drag function, which is derived from the relation of Schiller and Neumann [31]:

$$f_{\text{drag}} = \left\{ {\begin{array}{*{20}l} {1 + 0.15Re_{\text{p}}^{0.687} ,} \hfill & {Re_{\text{p}} \le 1000} \hfill \\ {0.0183Re_{\text{p}} ,} \hfill & {Re_{\text{p}} \ge 1000} \hfill \\ \end{array} } \right\}.$$
(9)

In this case, Rep and acceleration a are defined as follows:

$$a = g - (V_{\text{m}} \cdot \nabla )V_{\text{m}}$$
(10)
$$Re_{\text{P}} = \frac{{V_{\text{m}} d_{\text{p}} }}{{\nu_{\text{eff}} }}.$$
(11)

Second-phase volume fractional equation

The second-phase fractional equation for the two-phase flow is as follows:

$$\nabla \cdot (\phi_{\text{p}} \rho_{\text{p}} V_{\text{m}} ) = - \nabla \cdot (\phi_{\text{p}} \rho_{\text{p}} V_{\text{dr,p}} ).$$
(12)

Energy equation

$$\nabla \cdot \sum\limits_{k = 1}^{n} {\left( {\phi_{\text{k}} V_{\text{k}} (\rho_{\text{k}} E_{\text{k}} + P)} \right)} = \nabla \cdot \left( {k_{\text{eff}} \nabla T - C_{\text{p}} \rho_{\text{m}} \overline{{V^{\prime } T^{\prime } }} } \right),$$
(13)

where keff is the effective thermal conductivity of the nanofluid and \(T^{\prime }\) is the fluctuating temperature. Ek in the above relationship is defined as follows:

$$E_{\text{k}} = h_{\text{k}} - \frac{P}{{\rho_{\text{k}} }} + \frac{{V_{\text{k}}^{2} }}{2},$$
(14)

where hk in the above equation is the sensible enthalpy of the k-phase.

Turbulence model

The simplest “complete models” of turbulence are two-equation models in which the solution of two separate transport equations allows the turbulent velocity and length scales to be independently determined. The standard k − ε model falls within this class of turbulence model and has become the workhorse of practical engineering flow calculations. In this work, the turbulent flow is modeled by the of the two-equation k − ε model of Shah and London [35]. In this model, the turbulent kinetic energy equation is as follows:

$$\nabla \cdot (\rho_{\text{m}} V_{\text{m}} k) = \nabla \cdot \left( {\frac{{\mu_{\text{t,m}} }}{{\sigma_{k} }}\nabla k} \right) + G_{\text{k,m}} - \rho_{\text{m}} \varepsilon + G_{\text{b}} .$$
(15)

Also, the energy dissipation rate of the turbulent kinetic energy is as follows:

$$\nabla \cdot (\rho_{\text{m}} V_{\text{m}} \varepsilon ) = \nabla \cdot \left( {\frac{{\mu_{\text{t,m}} }}{{\sigma_{\varepsilon } }}\nabla \varepsilon } \right) + \frac{\varepsilon }{K}(c_{1} G_{\text{k,m}} - c_{2} \rho_{\text{m}} \varepsilon ).$$
(16)

In the above relationships, the terms and constants are defined as follows:

$$\mu_{\text{t,m}} = \rho_{\text{m}} c_{\mu } \frac{{k^{2} }}{\varepsilon },\quad G_{\text{k,m}} = \mu_{\text{t,m}} \left( {\nabla V_{\text{m}} + (\nabla V_{\text{m}} )^{T} } \right),\quad G_{\text{b}} = \beta g_{\text{i}} \alpha_{\text{T}} \mu_{\text{t}} \frac{\partial T}{{\partial x_{\text{i}} }}$$
(17)
$$c_{1} = 1.44,\quad c_{2} = 1.92,\quad c_{\upmu} = 0.09,\quad \sigma_{\text{k}} = 1,\quad \sigma_{\upvarepsilon} = 1.3.$$
(18)

Physical properties

Effective nanofluid density (see Baqaie et al. [16]):

$$\rho_{\text{eff}} = (1 - \phi )\rho_{\text{f}} + \phi \rho_{\text{p}} .$$
(19)

Nanofluid thermal capacity (see Baqaie et al. [16]):

$$(C_{\text{p}} )_{\text{eff}} = \left[ {\frac{{(1 - \phi )(\rho C_{\text{p}} )_{\text{f}} + \phi (\rho C_{\text{p}} )_{\text{p}} }}{{\rho_{\text{eff}} }}} \right].$$
(20)

Thermal conductivity coefficient:

Kahn et al. [2], who considered the Brownian motion and the mean diameter of the nanoparticles, obtained the thermal conductivity of the nanofluid as follows:

$$\frac{{k_{\text{eff}} }}{{k_{\text{f}} }} = 1 + 64.7 \times \phi^{0.746} \left( {\frac{{d_{\text{f}} }}{{d_{\text{p}} }}} \right)^{0.369} \left( {\frac{{k_{\text{p}} }}{{k_{\text{f}} }}} \right)^{0.746} \times Pr^{0.9955} \times Re^{1.2321} .$$
(21)

In the above relationships, the terms and constants are as follows:

$$Pr = \frac{{\mu_{\text{f}} }}{{\rho_{\text{f}} \alpha_{\text{f}} }}$$
(22)
$$Re = \frac{{\rho_{\text{f}} B_{\text{c}} T}}{{3\pi \mu^{2} l_{\text{bf}} }}$$
(23)
$$\mu = A \times 10^{{\frac{B}{T - C}}} ,\quad C = 140\;{\text{K}},\quad B = 247\;{\text{K}},\quad A = 2.414 \times 10^{ - 5} ({\text{Pa}}\;{\text{s}}),\quad B_{\text{c}} = 1.3807 \times 10^{ - 23} \left( {\frac{J}{K}} \right).$$
(24)

Viscosity:

The effective viscosity of the nanofluid from Mirmasoumi et al.’s relationship (see Mirmasoumi and Behzadmehr [11]), which is a function of temperature, mean diameter of nanoparticles, the volume fraction of nanoparticles, nanoparticle density and physical properties of the base fluid, is obtained as follows:

$$\mu_{\text{nf}} = \mu_{\text{f}} + \frac{{\rho_{\text{p}} V_{\text{B}} d_{\text{f}}^{2} }}{72C\delta },$$
(25)

where the VB of the Brownian Speed and δ is obtained from the following equation:

$$V_{\text{B}} = \frac{1}{{d_{\text{p}} }}\sqrt {\frac{{18k_{\text{b}} T}}{{\pi \rho_{\text{p}} d_{\text{p}} }}}$$
(26)
$$\delta = \sqrt[3]{{\frac{\pi }{6\phi }}}d_{\text{p}}$$
(27)

and C in Eq. (25) is obtained from the following equation:

$$C = \mu_{\text{f}}^{ - 1} \left[ {(c_{1} d_{\text{p}} + c_{2} )\phi + (c_{3} d_{\text{p}} + c_{4} )} \right].$$
(28)

It should be noted that in the equation above the constants are considered as follows:

$$C_{1} = - \;0.113 \times 10^{ - 5} ,\quad C_{2} = - \;0.277 \times 10^{ - 5} ,\quad C_{3} = - \;0.09 \times 10^{ - 5} ,\quad C_{4} = - \;0.039 \times 10^{ - 5} .$$
(29)

Volumetric expansion coefficient:

The thermal expansion coefficient of the nanofluid is obtained from the following equation (see Schiller and Neumann [36]):

$$\beta_{\text{nf}} = \left[ {\frac{1}{{1 + \frac{{(1 - \phi )\rho_{\text{f}} }}{{\phi \rho_{\text{s}} }}}}\frac{{\beta_{\text{s}} }}{{\beta_{\text{f}} }} + \frac{1}{{1 + \frac{\phi }{1 - \phi }\frac{{\rho_{\text{s}} }}{{\rho_{\text{f}} }}}}} \right]\beta_{\text{f}} .$$
(30)

Boundary conditions

Inlet BCs:

$$V_{x} = V_{y} = 0,\quad V_{z} = V_{0} \;\& \;T = T_{0} .$$

For turbulent the below condition is used:

$$k = \frac{3}{2}(IV_{0} )^{2} ,\quad \varepsilon = C_{\upmu}^{0.75} \frac{{K^{1.5} }}{{0.1D_{\text{h}} }},\quad C_{\upmu} = 0.09,$$
(31)

where \(I = 0.16Re^{{ - \frac{1}{8}}} .\)

Wall BCs:

$$\begin{aligned} - k_{\text{eff}} \frac{\partial T}{\partial n} = q_{\text{w}} \hfill \\ V_{\text{x}} = V_{\text{y}} = V_{\text{z}} = 0 \hfill \\ \end{aligned}$$
(32)

and below for turbulent:

$$k = 0,\varepsilon = 0.$$

Outlet BCs:

In the channel outlet (z = 100), the static pressure is assumed to be p0, and also the mass balance is used.

Numerical method and validation

Figure 2 shows the grid of the channel, which is denser in the boundary of the entrance and near the walls due to the high gradient of the speed and the network temperature. The finite volume method was used to discretize the governing equations, and SIMPLEC algorithm was used for velocity and pressure coupling. Also, the second-order upwind scheme has been used for modeling convection terms. The simulation of the nanofluid is carried out using finite volume method. Two-equation \(K - \varepsilon\) model is used for modeling turbulence. In this work, the grid sensitivity study of the results was investigated by applying different mesh. The results of this study were in the aspect ratio of 1 and volume fraction of 3% and other fixed parameters appeared in Table 1:

Table 1 Fixed parameters for grid study
Full size table
Fig. 2
figure 2

Channel variable grid

Full size image

The grid study is appeared in Table 2.

Table 2 Grid sensitivity study
Full size table

Therefore, the number of nodes in different directions is 30 × 60 × 30.

Table 3 shows time of running for the different above-mentioned fixed parameters coding in computer with RAM 4.00 GB and CPU core i3 2.73 GH characteristics (Fig. 2).

Table 3 CPU time for different Ri
Full size table

Results and discussion

In this work, the modeling of the turbulent flow of aluminum oxide nanofluid was done in a rectangular channel in the three-dimensional model. In this study, the effect of different parameters such as volume fraction, aspect ratio and diameter of nanoparticles on thermal and hydrodynamic parameters such as Nusselt number and friction coefficient was investigated. The results of this research are shown in Figs. 3 and 4. In order to study and validate the solving method, the Nusselt number obtained from this work was compared with the Ditos–Bolter [37] relationship as well as the Darcy friction coefficient with a maximum error value of almost 9% (see Cebeci and Cousteix [38], for example). It should be noted that this comparison is carried out for pure water flow for forced convection.

Fig. 3
figure 3

Comparison of Nusselt number obtained from modeling with Ditos–Bolter model in different Reynolds number

Full size image
Fig. 4
figure 4

Comparison of friction coefficient with methods of Belazius and Putukhov for different Reynolds number

Full size image

Volume fraction effect on heat transfer

In this section, the effect of a change in the nanoparticle volume fraction on the forced convection heat transfer of the turbulent flow of nanofluid of aluminum oxide water into a rectangular channel and in the conditions of Re = 50,000, Ri = 0.01, AR = 0.75, Dh = 0.01 m, L/Dh = 100 was investigated. For this purpose, the volume fraction of nanoparticles containing 0, 1, 3 and 5% of aluminum oxide nanoparticles in water was used. The diameter of the aluminum oxide nanoparticles used in this study is 28 nm. The physical properties of the aluminum oxide nanoparticles and of the water base fluid are considered for the inlet temperature (Ti = 20 °C). Given that the physical properties of the nanofluid are a function of the volume fraction of nanoparticles, for each volume fraction, the physical properties of the fluid change. Figure 5 shows the profile of non-dimensional temperature variation. It should be noted that the dimensionless temperature is defined as follows:

$$T^{ * } = \frac{{T - T_{i} }}{{\left( {\frac{{q_{\text{w}} d_{\text{h}} }}{{k_{\text{eff}} }}} \right)}}.$$
(33)
Fig. 5
figure 5

Dimensionless temperature on a line perpendicular to the channel axis for L/Dh = 100

Full size image

By increasing the volume fraction of nanoparticles in a given Reynolds and Richardson numbers, the constant thermal fluxes on the walls and the conduction heat transfer coefficient increase, and the effect of these results will lead to a decrease in the non-dimensional temperature, with the minimum amount of non-dimensional temperature at the channel center and its maximum value occurred near the walls.

The following non-dimensional axial velocity changes in different volume fraction of nanoparticles on an imaginary line perpendicular to the axis of the channel at the point z = 80 are shown in Fig. 6. In this figure, it can be seen that due to the increase in the volume fraction, the dimensionless axial velocity changes are not significant; this is due to the fact that the hydrodynamic development depends on Reynolds number, and in all the fractional volumes used in this section, the Reynolds number is constant, so the axial speed profiles will coincide. That is, in fact, with the increase in the volume fraction of nanoparticles, the flow regime will not change. The maximum velocity is at the center of the channel, and its lowest value is near the walls; also, due to forced convection of the flow and the absence of secondary flows, the dimensionless axial velocity is symmetrical to the horizontal and vertical center lines. By increasing the volume fraction of nanoparticles from 0 to 5%, the value of this number increases.

Fig. 6
figure 6

Dimensionless axial velocity on a line perpendicular to the channel axis for L/Dh = 100

Full size image

As seen in Fig. 7, at the beginning of the channel, due to the low difference in the temperature of the nanofluid and the wall temperature, the Nusselt number is high, but gradually and over the channel, the temperature difference increases, and as a result, the Nusselt number decreases to reach a constant value in the developed region. The Nusselt number is the ratio of the convection to the conduction heat transfer, by increasing the volume fraction of nanoparticles, the transfer of heat convection and conduction of nanofluid increases, but the amount of increase in convection is higher than conduction.

Fig. 7
figure 7

Nusselt number along the channel in L/Dh = 100

Full size image

With increasing volume fraction of nanoparticles in constant Reynolds number, the values of the physical properties of nanofluids and therefore the inlet velocity change.

Figure 8 shows variations in the mean skin friction coefficient along the channel. At the beginning of the channel, due to the high gradient velocity and therefore high shear stress, this coefficient is high but gradually decreases along the channel due to the reduction in the velocity gradient, which amounts to a constant amount during developed region. As shown in Fig. 7, with increasing volume fraction of nanoparticles, the skin friction coefficient is constant and does not change. The flow regime depends on the Reynolds number. Therefore, in the fixed Reynolds number with the change in the nanoparticle volume fraction, the mean frictional coefficient of the channel wall is constant. The coefficient of skin friction of the channel is defined as:

Fig. 8
figure 8

Skin friction coefficient along the channel in L/Dh = 100

Full size image

Aspect ratio effect on the thermal and hydrodynamic parameters

In this section, the effect of changing the aspect ratio of the channel on the thermal and hydrodynamic parameters of the nanofluid in the turbulent forced convection heat transfer is considered. In all this section, Reynolds number is 30,000 and Richardson number is 0.01. The channel is considered to have a hydraulic diameter of 0.01 m and a channel length of 100. The aspect ratio (height-to-width) of the channel has been considered in four aspect ratios of 0.25, 0.5, 0.75 and 1. Considering that in each aspect ratio the hydraulic diameter of the channel is constant, and given that the geometric characteristics of the cross section of the channels are different, the total amount of heat input is different to the channel.

In Fig. 9, the amount of dimensionless temperature increases with increasing aspect ratio. By increasing the aspect ratio for constant Reynolds and Richardson numbers, the dimesnionless temperature profiles decrease. Interaction of nanofluids dimensionless temperature and reduction in heat loss against the walls of the channel lead to an increase in the dimensionless temperature of nanofluids, by increasing the aspect ratio (Fig. 10).

Fig. 9
figure 9

Dimensionless temperature on the perpendicular line for L/Dh = 100

Full size image
Fig. 10
figure 10

Dimensionless transversal velocity for L/Dh = 100

Full size image

In Fig. 11, due to the decrease in temperature difference with increasing aspect ratio, the amount of forced convection coefficient increases with increasing aspect ratio. In all aspect ratios, the amount of heat transfer coefficient at the beginning of the channel is high due to the low variation in wall temperature and the nanofluid temperature, but gradually decreases the value of this coefficient by moving the length of the channel due to the increase in the temperature difference until to having a constant value in the developed region. In Fig. 12, the coefficient of skin friction at the beginning of the channel is due to the high gradient velocity, which is large and reduces in the direction of the channel’s axis to a constant value in the developed hydrodynamic region. As can be seen in the figure, with increasing aspect ratio, the skin friction coefficient of the channel increases. The effects of the geometry of the cross section of flow can increase the coefficient of skin friction of the channel by increasing the aspect ratio.

Fig. 11
figure 11

Heat transfer coefficient in L/Dh = 100

Full size image
Fig. 12
figure 12

Friction coefficient along the channel for L/Dh = 100

Full size image

Effect of the nanoparticles diameter on thermal and hydrodynamic parameters

In this section, the effect of changing the diameter of the nanoparticles on thermal and hydrodynamic parameters in mixed and forced convection is investigated. This study has been done in a 3% volume fraction and a diameter of nanoparticles of 20, 30 and 90 nm. The inlet temperature is assumed to be 20 °C, and the input properties are considered in this temperature. To investigate the effect of nanoparticle diameter on forced convection transfer heat, the Reynolds number is 30,000 and the Richardson number is 0.01. The channel has a hydraulic diameter of 0.01 m, a 0.75 aspect ratio and a channel length of 100.

In Fig. 13, it can be seen that increasing the average diameter of nanoparticles in a constant Reynolds number, the dimensionless axial velocity does not change significantly. According to Fig. 14, with the increasing mean diameter of the nanoparticles, the thermal conductivity coefficient, the thermal constant heat flux on the walls and the nanofluid temperature are reduced, which results in an increase in the nanofluid dimensionless temperature. With the increase in the average diameter of the nanoparticles for the constant Reynolds and Richardson numbers, the Prandtl number decreases, and this leads to the thermal development that occured earlier.

Fig. 13
figure 13

Axial velocity perpendicular to axis for L/Dh = 100

Full size image
Fig. 14
figure 14

Dimensional temperature variations on the perpendicular line for L/Dh = 100

Full size image

It is seen in Fig. 15 that the heat convection coefficient at the beginning of the channel is high due to the gradient of its extreme temperature, and when moving in the direction of flow, the amount of heat convection coefficient decreases to reach a constant value in the developed region. It is also seen in this figure that the increase in the diameter of the nanoparticles decreases the heat convection coefficient, because with the increase in the diameter of the nanoparticles, the thermal heat flux changes on the channel walls and, consequently, the nanofluid temperature, which due to the relationship of the forced heat convection coefficient, reduces the heat convection coefficient by increasing the diameter of the nanoparticles.

Fig. 15
figure 15

Heat convection coefficient over channel length for L/Dh = 100

Full size image

In Fig. 16, variation in the coefficient of skin friction along the channel for the forced turbulent flow of nanofluid in the constant Reynolds and Richardson is shown by increasing the diameter of the nanoparticles. As shown in this figure, the skin friction coefficient in the aspect ratio of 0.75 with increasing diameter of the nanoparticles has no significant changes.

Fig. 16
figure 16

Skin friction coefficient along the channel for L/Dh = 100

Full size image

Conclusions

In this study, nanofluid turbulent mixed convection of water and aluminum oxide in a three-dimensional channel with a rectangular cross section by using a two-phase mixture was analyzed. The effect of nanoparticle volume fraction on thermal and hydrodynamic parameters was studied. The results show that with increasing volume fraction of nanoparticles in constant Reynolds and Richardson number, dimensionless temperature reduces and Nusselt number increases, but dimensionless axial velocity and skin friction coefficient changes are not significant. It should be noted that in mixed convection heat transfer, the velocity and temperature profiles are not symmetrical due to the presence of secondary flow due to buoyancy force, and the minimum temperature and maximum velocity toward the wall of the bottom of the channel tend to be. About the aspect ratio, the results of this survey show that increasing the aspect ratio, the dimensionless temperature, the heat convection coefficient, Nusselt number and the skin friction coefficient of the channel increase. Also, by increasing the aspect ratio, the maximum axial velocity was not changed. In the nanoparticle diameter section, the results of this study show that in the constant volume fraction, Reynolds and Richardson number, with an increase in the mean diameter of the nanoparticles, dimensionless temperature increases and forced heat convection coefficient and the Nusselt number decrease. Also, the increase in mean diameter of nanoparticles has no significant effect on the dimensionless axial velocity and the mean skin friction coefficient of the channel.