Introduction

In engineering, cooling and heating are two processes that are important for increasing the efficiency of a thermodynamic system. Thus, a continuous demand for efficient heat exchangers is present. However, a limit for existing heat exchangers has already been reached. Hence, new fluids for efficient heat transfer are developed. One of these fluids is nanofluids. A nanofluid is a mixture of a base fluid and nanometre-sized (1–100 nm) particles. The base fluid is usually water. The development in technology enabled the use of nanofluids in: heat transfer devices [34, 36], domestic refrigeration [1], solar energy panels [20, 23], for heat transfer in porous media [15], etc.

Experiments giving a detailed view of nanofluid flow and heat transfer are difficult to perform. Indirect measurements, such as measuring the temperature in a setup including nanofluids are much easier and more often done. A test case, where nanofluid flows through a heated section of a straight pipe, is popular among experimentalists. One of the first authors who measured the heat transfer of a water–\(\hbox {Al}_2\) \(\hbox {O}_3\) nanofluid in a heated pipe was Wen and Ding in [42]. Colla et al. [9] performed experimental measurements of a similar test case for the water–\(\hbox {TiO}_2\) nanofluid. Ghodsinezhad et al. [13] experimentally investigated the water–\(\hbox {Al}_2\) \(\hbox {O}_3\) nanofluid cavity flow. The measurements revealed that the nanoparticles enhance the heat transfer. Arani and Amani [5] observed the pressure loss of a water–\(\hbox {TiO}_2\) nanofluid. The experimental investigation showed that at high Reynolds numbers, the pressure loses increase. Thus, the viscosity of a nanofluid has to be assigned in the pipe flow. Kumar et al. [19] presented a theoretical approach to determine the dynamic viscosity of a nanofluid, while Mishra et al. [26] presented a brief review on the viscosity of nanofluids. Recently, Ambreen and Kim [4] reviewed the heat transfer and pressure drop correlations. In the experimental measurements, the mixture of nanoparticles and water must be homogeneous and isotropic. Wen et al. [43] demonstrated an experiment where they have shown that the nanoparticles do not stay afloat in the nanofluid at normal conditions, but slowly settle down to the bottom. Saidur et al. [35] presented a similar experiment, they included a stabilizing agent that enabled the nanoparticles to stay afloat in a nanofluid. However, the agent can change the physical properties of the nanofluid. Paltra et al. [28] presented an experimental study of forced convection flow boiling for two nanofluids. They investigated the thermal-hydraulic phenomena of water and nanoparticles through high-speed visualization. Kouloulias et al. [18] visualized the subcooled pool boiling in nanofluids. The outcome of his work presented a step forward to evaluate the applicability of nanofluids in cooling applications via heat transfer.

Another challenge is the measuring of thermal conductivity. To simulate the nanofluid flow in heating and cooling application the thermal conductivity must be accurately determined. Moldoveanu et al. [27] measured the thermal conductivity of a hybrid nanofluid with a comprehensive regression analysis. To measure the thermal conductivity, Ebrahimi et al. [10] modified the transient hot-wire to accurately measure the thermal conductivity of a low viscosity nanofluid. The measured thermal conductivity of the nanofluid was found to be in a good agreement with the Maxwell model [22]. Xu et al. [44] presented a novel method that they defined as the steady flow method to measure the thermal conductivity of nanofluids under flow conditions. Yildiz et al. [45] compared the theoretical and experimental thermal conductivity model to examine the thermal performance of a hybrid nanofluid. They showed that a hybrid nanofluid has the same heat transfer properties at a lower nanoparticle volume fraction compared to a mono-nanofluid. Tong at el. [41] examined the exergy efficiency of a flat-plate solar panel. They observed that the efficiency of the solar panel with nanofluid improved for over 50% compared with a regular fluid.

For the simulation of a multiphase fluid flow, two approaches can be employed: the Euler–Euler method and the Euler–Lagrange method. The Euler–Euler method, which was used in this study, considers the nanoparticles and water as two continuous phases. On the other hand, the Euler–Lagrange method considers the nanoparticles as a dispersed phase. Simulating the nanofluid flow is difficult because there are no numerical models known that cloud properly predicts the mechanisms that are present in the nanofluid flow. Cardellini et al. [8] performed a direct numerical simulation of nanofluid flow. Fasano et al. [12] also performed a direct numerical simulation of nanofluids to determine their physical properties. However, direct numerical investigations of a nanofluid flows are very costly. Hence, different models were tested to simulate the flow. Akbari et al. [2] compared the VOF (volume of fluid) model and the single-phase model. They concluded that the VOF model is better for the simulation of the nanofluid flow. Sekrani and Poncet [37] simulated the nanofluid flow in a pipe. They presented that the heat transfer coefficient was smaller when calculated with the single-phase model then of the VOF model. On the other hand, Fard et al. [11] compared the heat transfer coefficient of a nanofluid and water in a heated pipe. Shahmohammadi and Jafari [38] simulated the laminar and turbulent flow of a nanofluid in a pipe with barriers. They used different multiphase models to investigate fluid flow characteristics. Khalili et al. [16] employed the mixture model to simulate the flow of a nanofluid in a circular enclosure. Goutam and Manosh [33] numerically observed the entropy generation of a turbulent flow, for water–\(\hbox {Al}_2\) \(\hbox {O}_3\) and water–\(\hbox {TiO}_2\) nanofluids. They employed the mixture model to simulate the turbulent flow of a nanofluid in a heated pipe. Their observations have shown that the water–\(\hbox {TiO}_2\) nanofluid is thermodynamically more efficient. Ravnik et al. [30] presented a Euler–Lagrange method to simulate the natural convection of a nanofluid in an enclosed cavity. Sharaf et al. [39] numerical investigated the migration and convective heat transfer of nanoparticles in a nanofluid with the Euler–Lagrange method.

To determine the variable that has the most impact on the heat transfer performance of the nanofluid, Ravnik et al. [31] presented stochastic modelling using the boundary–domain integral method. The results have shown that the volume fraction of nanoparticles has an impact on the heat transfer performance of the nanofluid. On the other hand, Alsabery et al. [3] employed the inhomogeneous Bungiorno’s two-phase model to present the effects of an inhomogeneous nanofluid on the convective heat transfer. Sheikholeslami et al. [40] employed the neural network for the prediction of the nanofluid heat transfer performance. The results revealed that the heat transfer intensified by the rise of nanoparticles volume fraction. Mikhailenko et al. [24] investigated the convective heat transfer of a nanofluid in a rotating nanofluid cavity with sinusoidal temperature boundary condition. They analysed the effect of Rayleigh number, Taylor number and nanoparticles volume fraction of the fluid flow and heat transfer.

In this study, the Bungiorno’s single-phase mixture model [7] was employed to observe the flow of a water–\(\hbox {TiO}_2\) nanofluid in a heated pipe. The physical properties of the nanofluid are obtained from empirical correlations taking into account to varying temperature and concentration fields. An additional conservation equation is employed to estimate the volume fraction of nanoparticles in the fluid. An extended version of this model was presented by Malvandi et al. [21]. Minea et al. [25] tested the single-phase and the Bungiorno’s mixture model. The results have shown that there is no agreement between the experimental results and the numerical results if a homogeneous and isotropic nanofluid model is used. Ravnik et al. [32] reviewed different Euler–Euler models for the simulation of nanofluid flow. An investigation using the single-phase model was presented by Ravnik and Škerget [29]. They simulated the fluid motion with the boundary-domain integral numerical method. The results have shown an enhancement of the heat transfer.

The main focus in this paper is to simulate the mixed flow of a nanofluid with inhomogeneous distribution of nanoparticles. The Bungiorno’s mixture model includes an additional equation to solve the volume fraction of nanoparticles. However, the numerical implementations of this model have shown [24] that the model does not agree well with experimental data in the case when homogenous nanofluid is considered. Furthermore, there is a possibility of nanoparticles settling to the bottom of the circular pipe and thus decreasing the heat transfer coefficient. Because of that, the numerical investigation in this paper was focused on the mass fraction nanoparticle distribution in the pipe. Additionally, we focused on the inlet of the pipe.

The article is split into three sections. In the first section, we show the governing equations and present the two employed models. Secondly, we describe the numerical example. Thirdly, we show the results, and in the last section, we present our conclusions.

Governing equations and models

In the present work, we consider an incompressible, Newtonian, steady and laminar fluid flow in a copper pipe. The system is split into a solid and fluid part. The solid part is heated with a heat flux. The temperature filed in the solid part is determined with this equation:

$$\begin{aligned} k_{\mathrm{cu}}\varDelta {T}=0, \end{aligned}$$
(1)

where \(k_{\mathrm{cu}}\) is the thermal conductivity of copper. We employed the Euler–Euler approach and modelled the fluid flow using the following system of equations:

$$\begin{aligned}&\mathbf {\nabla }\cdot \mathbf {v}=0, \end{aligned}$$
(2)
$$\begin{aligned}&(\mathbf {v}\cdot \mathbf {\nabla })\mathbf {v}=-\frac{{1}}{\rho _{\mathrm{nf}}}\mathbf {\nabla }p+\nu _{\mathrm{nf}} \varDelta {\mathbf {v}}-\beta _{\mathrm{nf}} \mathbf {g}\varDelta \rho _{\mathrm{nf}}, \end{aligned}$$
(3)
$$\begin{aligned}&\mathbf {\nabla }\cdot (\rho _{\mathrm{nf}}\mathbf {v}h)=\mathbf {\nabla }\cdot (k_{\mathrm{nf}}\mathbf {\nabla }T), \end{aligned}$$
(4)

where \(\mathbf {v}\) is the velocity vector field, T is the temperature field, p is the pressure field, h is the specific enthalpy and \(\rho _{\mathrm{nf}}\) (density of nanofluid), \(\varDelta \rho _{\mathrm{nf}}\) (density difference), \(\nu _{\mathrm{nf}}\) (kinematic viscosity of nanofluid), \(\beta _{\mathrm{nf}}\) (thermal expansion of nanofluid), \(k_{\mathrm{nf}}\) (thermal conductivity of nanofluid) are the thermodynamic properties of the nanofluid. In the system of equations that we wrote above: Eq. (2) is the mass conservation equation, Eq. (3) is the momentum transport equation and (4) is the energy conservation equation. Steady state was considered in order to facilitate comparison with the experiment. Additionally, from an engineering point of view, state operation of heat exchangers and other thermal devices is of primary importance.

The thermodynamic properties of a nanofluid depend on the thermodynamic properties of water and the volume fraction \(\psi\) of nanoparticles. The natural convection was simulated with the Boussinesq approximation of Buoyancy in Eq. (3): \(\beta _{\mathrm{nf}} \mathbf {g}\varDelta \rho _{\mathrm{nf}}\). Thermodynamic properties of water depend on temperature. The properties of water were presented in [14]. The density of pure water \(\rho _\mathrm{f(T)}\):

$$\begin{aligned} \rho _\mathrm{f(T)}&=1.31839028583\cdot 10^{-9}\cdot T^5-4.1415691320879\cdot 10^{-7}\cdot T^4\nonumber \\&+0.0000627465524729587\cdot T^{3}-0.00812457260548172 \cdot T^2\nonumber \\&+0.0554068116720146 \cdot T+999.90837195736\; \left[ \frac{{\rm kg}}{{\rm m^3}}\right] , \end{aligned}$$
(5)

the thermal conductivity of pure water \(k_\mathrm{f(T)}\):

$$\begin{aligned} k_\mathrm{f(T)}&= 0.0000000000074354379\cdot T^{5}+ 2.43717635743 \cdot 10^{-9}\cdot T^{4}\nonumber \\&-0.0000002889967610567 \cdot T^{3}+5,15309471096903\cdot 10^{-6}\cdot T^2\nonumber \\&+0.00185267131276284 \cdot T+0.561293060017584\; \left[ \frac{{\rm W}}{{\rm mK}}\right] , \end{aligned}$$
(6)

the specific heat capacity of pure water \(c_{\mathrm{pf}}(T)\):

$$\begin{aligned} c_{\mathrm{p,f}}(T)&=4.088550653591\cdot 10^{-8}\cdot T^{5}+ 0.0000117146192195605 \cdot T^4\nonumber \\&-0.00137712095636289 \cdot T^3+ 0.0902711920148249\cdot T^2\nonumber \\&-2.99500832260219 \cdot T+4217.11488982432\; \left[ \frac{{\rm J}}{{\rm kgK}}\right] , \end{aligned}$$
(7)

and the kinematic viscosity of pure water \(\vartheta _\mathrm{f(T)}\):

$$\nu _{{{\text{f(T)}}}} = \frac{{2.414 \cdot 10^{{ - 5}} \cdot 10^{{\frac{{247.8}}{{(T + 133.15)}}}} }}{{\rho _{{{\text{f(T)}}}} }}\;\left[ {\frac{{{\text{m}}^{2} }}{{\text{s}}}} \right].$$
(8)

The single-phase model assumes the nanofluid to be a new continuous fluid with changed properties, which depend on temperature and on the volume fraction of particles \(\psi\). The density of the nanofluid is determined with the mass conservation law for mixtures [17]: \(\rho _{{{\text{nf}}}} c_{{{\text{p}},{\text{nf}}}} = \rho _{{\text{f}}} c_{{{\text{p,f}}}} (1 - \psi ) + \rho _{{\text{p}}} c_{{{\text{p,p}}}} \psi ,\) where \(c_{{\rm p,p}}\) is the specific heat capacity of nanoparticles. The nanofluid thermal expansion coefficient \(\beta _{{\rm nf}}\) is defined by this equation: \(\beta _{{\rm nf}}=\rho _{\rm f} \beta _{\rm f}(1-\psi )+\rho _{{\rm p}}\beta _{{\rm p}}\psi\). The kinematic viscosity \(\vartheta _{{\rm nf}}\) of a nanofluid is defined with the fluid kinematic viscosity that contains particles of a spherical shape. This equation was presented by Brinkman [6]:

$$\begin{aligned} \vartheta _{\mathrm{nf}}=\frac{{\rho _\mathrm{f}}}{\rho _{\mathrm{nf}}}\frac{{\vartheta _\mathrm{f}}}{(1-\psi )^{2.5}}. \end{aligned}$$
(9)

Thermal conductivity of a nanofluid is determined with the Maxwell–Garnett equation [22]:

$$\begin{aligned} k_{\mathrm{nf}}=k_\mathrm{f}\frac{{k_{\rm p}}+2k_{\rm f}-2\psi (k_{\rm f}-k_{\rm p})}{k_{\rm p}+2k_{\rm f}+\psi (k_{\rm f}-k_{\rm p})}. \end{aligned}$$
(10)

where \(k_\mathrm{p}\) is the thermal conductivity of nanoparticles. The single-phase model solves Eqs. (2), (3) and (4) using appropriate pressure, velocity and temperature boundary conditions.

In this work, we foresee that the volume fraction of nanoparticles in the pipe volume changes due to the nanofluid motion. Thus, the nanofluid properties not only depend on the temperature but also on the spatially varying nanoparticle concentration. Convection and two diffusive processes are accounted for: Brownian diffusion (\(\mathbf {j_\mathrm{B}}\)) and thermophoresis (\(\mathbf {j_\mathrm{T}}\)). Hence, an additional conservation equation is set up to model the volume fraction \(\psi\) of nanoparticles in the pipe [7]:

$$\begin{aligned} (\mathbf {v}\cdot \mathbf {\nabla })\psi =-\mathbf {\nabla }\cdot (\mathbf {j_{\rm B}}+\mathbf {j_{\rm T}}). \end{aligned}$$
(11)

where \(\mathbf {j_{\rm B}}\) is determined with the Fick’s constitution model and \(\mathbf {j_{\rm T}}\) is defined with the Fourier’s constitution model. With this, we can rewrite the Eq. (11) into:

$$\begin{aligned} (\mathbf {v}\cdot \mathbf {\nabla })\psi =-\mathbf {\nabla }\cdot (\rho _{\rm p}D_{{\rm B}}\mathbf {\nabla }\psi +\rho _{\rm p}D_{\rm T}\mathbf {\nabla }T), \end{aligned}$$
(12)

where \(D_\mathrm{B}\) stands for the Brownian diffusion coefficient and \(D_\mathrm{T}\) is the diffusion coefficient of the thermophoresis. The \(D_\mathrm{B}\) coefficient is modelled with the Stokes–Einstein equation:

$$\begin{aligned} D_{\mathrm{B}}=\frac{{k_\mathrm{BT}}}{3\pi \vartheta _{\rm f}\rho _{\rm f}d_{\rm p}}, \end{aligned}$$
(13)

where \(k_\mathrm{B}\) is the Boltzmann constant and \(d_{\rm p}\) is the particle diameter. The thermophoresis diffusion coefficient is modelled by [7]:

$$\begin{aligned} D_{\mathrm{T}}=0.26\frac{{k_{\rm f}}}{2k_{\rm f}+k_{\rm p}}\frac{{\rho _{\rm f}}\vartheta _{\rm f}}{\rho _{\rm p}}\frac{{\psi }}{T}. \end{aligned}$$
(14)

The energy conservation equation (4) needs to be adapted, to include the added heat flux due to the changing nanoparticle volume fraction. Thus, we reformulate Eq. (4) in the way that we write an additional source (\(\rho _{\rm p}c_{{\rm p,p}}(\mathbf {j_{\rm B}}+\mathbf {j_\mathrm{T}})\mathbf {\nabla }T\)) that adds the heat flux of the changing volume fraction of nanoparticles to the energy equation:

$$\begin{aligned} \rho _{\mathrm{nf}}c_{{\rm p,nf}}(\mathbf {v}\cdot \mathbf {\nabla }) T=\mathbf {\nabla }\cdot (k_{\mathrm{nf}}\mathbf {\nabla }T)+\rho _{\rm p}c_{{\rm p,p}}(\mathbf {j_{\rm B}}+\mathbf {j_\mathrm{T}}) \cdot \mathbf {\nabla }T. \end{aligned}$$
(15)

We replace \(j_{\rm B}\) and \(j_\mathrm{T}\) in Eq. (15) with Fick’s constitution model and Fourier’s constitution model. Thus, we can write this form of the energy conservation equation for the mixture model:

$$\begin{aligned} \rho _{\mathrm{nf}}c_{{\rm p,nf}}(\mathbf {v}\cdot \mathbf {\nabla }) T=\mathbf {\nabla }\cdot (k_{\mathrm{nf}}\mathbf {\nabla }T)+\rho _{\rm p}c_{{\rm p,p}}(D_{\mathrm{B}}\mathbf {\nabla }\psi +D_{\mathrm{T}}\mathbf {\nabla }T)\cdot \mathbf {\nabla }T \end{aligned}$$
(16)

The Bungiorno’s mixture model solves the nanofluid flow with the mass conservation law equation (2), the momentum transport equation (3), energy conservation equation (16) and volume fraction conservation equation for nanoparticles in Eq. (13).

Mass fraction

In the Bungiorno’s mixture model, described above, we solve for the volume fraction of nanoparticles. However, in this study, we used the commercial CFD package Ansys CFX. In this program, only the conservation equation for the mass fraction can be used. Thus, we have to replace the volume fraction \(\psi\) in Eq. (12) and in Eq. (15) with the mass fraction \(\xi\). The mass and volume fractions are related by: \(\psi =\frac{{\rho _{\mathrm{nf}}}}{\rho _{\rm p}}\xi .\) We rewrite Eq. (12) into the mass fraction conservation equation:

$$\begin{aligned} (\mathbf {v}\cdot \mathbf {\nabla })\xi =-\mathbf {\nabla }\cdot (\rho _{\mathrm{nf}}D_{\mathrm{B}}\mathbf {\nabla }\xi + D_{\mathrm{B}}\xi \mathbf {\nabla }\rho _{\mathrm{nf}}+\rho _{\mathrm{nf}}D_\mathrm{T}\mathbf {\nabla }T). \end{aligned}$$
(17)

Furthermore, we also must replace the volume fraction in the energy Eq. (16):

$$\begin{aligned}&\rho _{\mathrm{nf}}c_{{\rm p,nf}}(\mathbf {v}\cdot \mathbf {\nabla }) T=\mathbf {\nabla }\cdot (k_{\mathrm{nf}}\mathbf {\nabla }T)\nonumber \\&\quad +c_{{\rm p,p}}(\rho _{\mathrm{nf}}D_{\mathrm{B}}\mathbf {\nabla }\xi +D_{\mathrm{B}}\xi \mathbf {\nabla }\rho _{\mathrm{nf}} +\rho _{\mathrm{nf}}D_{\mathrm{T}}\mathbf {\nabla }T)\cdot \mathbf {\nabla }T. \end{aligned}$$
(18)

Finally, in order to determine the diffusion coefficient \(D_\mathrm{T}\) Eq. (14), we calculate the volume fraction by using the mass fraction field obtained from (17).

Numerical example

We simulated the nanofluid flow in a heated copper pipe. The numerical model was prepared based on the experimental investigation that was presented by Colla et al. [9]. Four different cases were simulated. In each case, we changed the heating power and the mass flow rate. For the first case, the heating power was \(P=100W\), inlet temperature of the nanofluid was \(T_{{\rm in}}=20.66\) °C and \({\dot{m}}=0.0063\frac{{\rm kg}}{{\rm s}}\), second case \(P=100\) W, inlet temperature \(T_{{\rm in}}=21.05\) °C and \({\dot{m}}=0.0083\frac{{\rm kg}}{{\rm s}}\), third case \(P=200W\), \(T_{{\rm in}}=20.72\) °C and \({\dot{m}}=0.00506\frac{{\rm kg}}{{\rm s}}\), last case \(P=200\) W, \(T_{{\rm in}}=20.83^oC\) and \({\dot{m}}=0.0063\frac{{\rm kg}}{{\rm s}}\). The average nanoparticle mass fraction at inlet was \(\xi _0=0.0106\) and \(\xi _0=0.0254\).

Fig. 1
figure 1

Illustration of the computational domain on a cross-plane (z–y). Two domains are modelled. The copper pipe domain and the nanofluid domain

Full size image

We modelled a solid and fluid domain. The two domains were meshed with structured and hexahedral elements. In Fig. 1, we present the cross section of the pipe and the two domains. On the right of the figure, we illustrate the meshed pipe cross section. The number of mesh elements was 1,375,000. Minea et al. [25] tested three mesh densities and validated that this was the optimal density. The diameter of the pipe was 12 mm, wall thickens was 2mm and the pipe length was 2 m. We simulated the flow with the water–\(\hbox {TiO}_2\) nanofluid. In the experimental investigation, the pipe was not heated nonuniformly. Thus, we split the pipe into nine sections over the x-axis. The copper pipe was included into our model (see Fig. 1), and heat transfer through the pipe material was simulated. The boundary conditions were prescribed at the outer rim of the copper material. The outer rim of the copper pipe was split into nine section. For each section, a different heat flux was measured in the experimental investigation presented by Colla et al. [9]. The heat flux for each section of the outer rim is presented in Table 1.

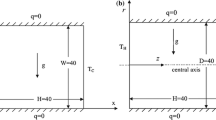
Table 1 The heat flux \(\left[ \frac{{\rm W}}{{\rm m^2}}\right]\) on the outer rim for nine sections of the pipe for the 100W and 200W cases. The heat flux values correspond to experimentally determined ones [9]
Full size table

In the fluid, we simulated the nanofluid flow and forced and natural convection of heat, in copper, we considered diffusion of heat. The nanoparticles were considered in thermal equilibrium with the fluid. In Fig. 2, we present the numerical model of a heated pipe.

Fig. 2
figure 2

An illustration of the modelled domain. The pipe was split into nine section. Each section was heated with a different heat flux. Thus, the temperature of the nanofluid increased over the length of the pipe

Full size image

At the inlet, we assumed that the nanofluid mixture was inhomogeneous. Thus, we choose a mathematical function of \(\xi (y)\) to describe the inhomogeneous distribution of nanoparticles in the nanofluid in the vertical (y) direction. Two distributions were considered: a linear type and a sigmoid type. The linear function that was defined as follows:

$$\begin{aligned} \xi (y)=\xi _0\left( 1-\frac{{ky}}{R}\right) , \end{aligned}$$
(19)

where \(\xi _0\) is the mass fraction, \(R=0.004\) is the pipe radius and \(k=0.35\) is a constant. The second mathematical function is a sigmoid that was defined like this:

$$\begin{aligned} \xi (y)=\left\{ \begin{array}{cc} \xi _0+\alpha (-1+A(1+Be^{\rm{C\frac{{y}}{R}})^{-1}}) &{} \qquad y<0 \\ \xi _0+\alpha (1-A(1+Be^{\rm{-C\frac{{y}}{R}})^{-1}}) &{} \qquad y\ge 0 \end{array}\right. \end{aligned}$$
(20)

where \(\xi _0\) is the mass fraction, \(R=0.004\) is the pipe radius, \(A=1+e^{\gamma \beta }\), \(B=e^{\gamma \beta }\) and \(C=\gamma\). The function is an approximation of the mass fraction of nanoparticles in the nanofluid. The sigmoid function approximates the mass fraction of nanoparticles in the nanofluid at the pipe inlet, which makes the distribution of nanoparticles at the inlet inhomogeneous. The nanoparticles are more likely to be found at the lower end of the pipe and less likely at the upper end. We have used this function to emulate the possible sedimentation of nanoparticles.

The values of the coefficients are \(\alpha =0.01(1+e^{\gamma \beta })^{-1}\), \(\beta =0.8\) and \(\gamma =10\). To determine the values of k, \(\alpha\), \(\beta\) and \(\gamma\), we performed a number of simulations and chose the values which fitted the experimental results best. In Fig. 3, we present shapes of the mathematical functions \(\xi (y)\) that were used to model nanoparticle distribution.

Fig. 3
figure 3

The mass fraction \(\xi\)(y) on the inlet boundary condition (Inlet in Fig. 2), for different mass fraction of nanoparticles, \(\xi _0=0.0106\) (left) and \(\xi _0=0.0254\) (right)

Full size image

At the inlet, a parabolic profile was prescribed, which was calculated based on the inlet nanofluid temperature and mass rate \({\dot{m}}\). The following expression was used \(\mathbf {v}=\left[ v_{\rm x},0,0\right]\):

$$\begin{aligned} v_{\rm x}=2\frac{{\dot{m}}}{\rho _{\mathrm{nf}}A}\left( 1-\frac{{y^2+z^2}}{R^2}\right) , \end{aligned}$$
(21)

A is the pipe cross section. The velocity profile is illustrated in Fig. 4. At the outlet the static pressure was set to 0Pa.

Fig. 4
figure 4

The velocity profile that was set for the boundary condition on the inlet of the pipe, where \(\xi _0\) of nanoparticles was 0.0106 (left) and 0.0254 (right)

Full size image

At the walls of the pipe, mass flux of nanofluid vanishes. In order to implement this boundary condition, we set no slip velocity at the wall and \(\mathbf {j_{\rm B}}\)+\(\mathbf {j_\mathrm{T}}=0\). This enables

$$\begin{aligned} 0=\rho _{\mathrm{nf}}D_{\mathrm{B}}\mathbf {\nabla }\xi + D_{\mathrm{B}}\xi \mathbf {\nabla }\rho _{\mathrm{nf}}+\rho _{\mathrm{nf}}D_\mathrm{T}\mathbf {\nabla }T. \end{aligned}$$
(22)

an estimate for \(\mathbf {\nabla }\xi\)

$$\begin{aligned} \mathbf {\nabla }\xi =-\frac{{\rho _{\mathrm{nf}}}D_{\mathrm{B}}\mathbf {\nabla }\xi + D_{\mathrm{B}}\xi \mathbf {\nabla }\rho _{\mathrm{nf}}+\rho _{\mathrm{nf}}D_\mathrm{T}\mathbf {\nabla }T}{\rho _{\mathrm{nf}}D_{\rm B}}, \end{aligned}$$
(23)

that ensures zero mass flux at the wall section of the pipe.

The density of nanoparticles \(\hbox {TiO}_2\) is \(\rho _{\rm p}=3972{\rm kg}{\rm m^{-3}}\), nanoparticle diameter is \(d_{\rm p}=70\) nm, heat capacity is \(c_{{\rm p,p}}=711{\rm J}{\rm kg}^{-1}{\rm K}^{-1}\), thermal conductivity \(k_{\rm p}=8.6{\rm W}{\rm m}^{-1}{\rm K}^{-1}\) and thermal expansive coefficient is \(\beta _{\rm p}=0.000254{1}{\rm K}^{-1}\). Numerical simulations were performed accounting for variable nanofluid properties, which were estimated based on the temperature and nanoparticle concentration fields. The nanofluid flow was solved by employing the mass conservation law equation (2), the momentum transport equation (3), energy conservation equation (18) and mass fraction conservation equation for nanoparticles in Eq. (17).

Pressure scheme

In order to perform the surface integration of the pressure gradient in the momentum equation, pressure values are required at the control volume faces, where the integration takes place. In this paper, we used the CFX standard pressure discretization, which interpolates the pressure on the faces using the cell centre values. Since in our case we are dealing with buoyancy, we use trilinear interpolation to improve the accuracy. To handle the pressure–velocity coupling, ANSYS CFX uses a co-located (non-staggered) grid layout, so that the control volumes are identical for all transport equations. By applying a momentum-like equation to each integration point, an expression for the advection velocity at each integration point is obtained. This expression includes the pressure redistribution term, which is spatially accurate to the third order and is usually much smaller than the average of the vertex velocities, especially if the grid is fine enough.

Results and discussion

In this section, we present the results of the tested numerical models. We compared the results with the results that were presented in [25]. In Fig. 5, we present the measured and simulated temperature of the wall to observe the impact of the nanofluid on the heat transfer.

Fig. 5
figure 5

Temperature of the pipe wall. The wall was heated with a 100W heater and the nanoparticles mass fraction was \(\xi _0=0.0106\). Mass flow rate was \({\dot{m}}=0.0063{\rm kg}{\rm s}^{-1}\) (left) and \({\dot{m}}=0.0083{\rm kg}{\rm s}^{-1}\) (right)

Full size image

As the pipe length is relatively short, the main reason for the inhomogeneous distribution of nanoparticles is their distribution at the inlet. By inhomogeneous distribution of nanoparticles at the inlet, we model a possible gravitational effect, which could occur in the piping before the test section. As the particles travel through the pipe, they redistribute further according to the forces acting on them. This is modelled by the nanoparticle volume fraction transport equation (12), which takes into account Brownian diffusion and thermophoresis. In the first part of the numerical testing Fig. 5, the nanoparticle mass fraction in the fluid was 1.06%. The agreement between the experiment and the numerical testing was the best with the sigmoid distribution of nanoparticle concentration at the inlet Fig. 5 (left). On the other hand, increasing the mass flow rate, the linear function gave a better agreement between the numerical and experimental results Fig. 5 (right). The velocity of the fluid is higher, thus the particles have a greater momentum. The mass fraction of nanoparticles on the pipe inlet is approximately linear.

Fig. 6
figure 6

Temperature of the pipe wall. The wall was heated with a 200W heater and the nanoparticles mass fraction was \(\xi _0=0.0106\) (top) and \(\xi _0=0.0254\) (bottom). Mass flow rate was \({\dot{m}}=0.00506{\rm kg}{\rm s}^{-1}\) (left) and \({\dot{m}}=0.0063{\rm kg}{\rm s}^{-1}\) (right)

Full size image

In Fig. 6, we present the results of four test cases where the heating power was 200 W. The chosen heating power and mass flow rate do not influence the numerical results. Also for these four cases, the sigmoid inlet nanoparticle concentration distribution has the best agreement with the experimental results.

Fig. 7
figure 7

Vertical mass fraction profiles \(\xi (y)\) through the centre of the pipe at different locations x and different inlet mass fraction boundary conditions: linear mass fraction distribution (left) and sigmoid mass fraction distribution (right). The wall was heated with a 200W heater. Mass fraction \(\xi _0=0.0106\) (top) and \(\xi _0=0.0254\) (bottom)

Full size image

The mass flow rate does indeed have an effect on the accuracy of the model prediction (Figs. 5 and 6). It seems that the model describes cases where advection dominates over diffusion better and where natural convection is less important better. However, the effect of mass flow on the result accuracy is small compared to the effect of inhomogeneous nanoparticle distribution. Numerical results that were presented by Minea et al. [25] show simulations with homogenous particle distribution can not yield good agreement, regardless of the mass flow rate considered. Thus, the need to consider inhomogeneous nanoparticle distribution is essential.

In Fig. 7, we present the vertical mass fraction profiles \(\xi (y)\) at several locations along the pipe. The shape of the mass fraction profile differs at different locations in the pipe. The three-dimensional flow field, which forms in the pipe mixes the nanofluid and contributes to the diminishing nanoparticle mass fraction in the centre. We observe a similar profile characteristics for \(\xi _0=0.0106\) (top) and \(\xi _0=0.0254\) (bottom). The mass fraction profile changes with the length of the pipe.

Fig. 8
figure 8

Temperature of the pipe wall. The wall was heated with a 100 W heater (left) and 200 W heater (right). The nanoparticles mass fraction was \(\xi _0=0.0106\) (top) and \(\xi _0=0.0254\) (bottom). Mass flow rate was \({\dot{m}}=0.0063{\rm kg}{\rm s}^{-1}\)

Full size image

Lastly, we present the temperature distribution on the pipe inner wall Fig. 8. We increased the wall heating power from 100W to 200W. The mass flow rate was constant \({\dot{m}}=0.0063{\rm kg}{\rm s}^{-1}\). We observed that both inhomogeneous cases agree with some experimental measurements. The worst agreement was for the case \(\xi _0=0.0254\) and 100W heating power Fig. 8 (bottom–left).

Numerical tests have shown that simulation results depend strongly on the mass fraction profile that was defined as the boundary condition at the inlet of the pipe. The mass fraction profile \(\xi (y)\) changed over the length of the pipe. Hence, the nanofluid properties changed over the length of the pipe. Comparing the results of the wall temperature that were presented in this study with the results of the study that were presented by Minea et al. [25], we observed that the impact of the mass fraction equation (17) in the Bungiorno mixture model on the nanofluid flow is negligible. The pipe is too short for the nanoparticle concentration changes along the pipe to have a non-negligible effect. In Figs. 5, 6 and 8, we observed that the wall temperature that was presented by Minea et al. [25] is always below the wall temperature that was measured in the experimental measurements. However, changing the inlet nanoparticle distribution from a homogeneous to inhomogeneous, the results are in a better agreement with the experimental measurements.

Conclusions

We performed numerical simulations of a laminar nanofluid flow and heat transfer at different flow conditions. This study aimed to show the influence of the inhomogeneous nanoparticle distribution in the nanofluid on the heat transfer. We observed a big impact of the inlet nanoparticle distribution on the results. A good agreement with an experiment was reached with different mathematical functions that described the nanoparticle distribution at the inlet of the pipe. Since the simulated pipe was short, the inlet distribution had a much larger impact on the results that the redistribution of nanoparticles in the pipe due to convention, Brownian diffusion and thermophoresis.