Toward a modeling study of thermal conductivity of nanofluids using LSSVM strategy

Abstract

In the present study, a comprehensive model based on least square support vector machine algorithm (LSSVM) was developed to estimate thermal conductivity of nanofluids. The model assessed the thermal conductivity of 29 different nanofluids. The representative nanofluids were composed of nine base fluids, including water, ethylene glycol, transformer oil, engine oil, R113, DI Water, monoethylene glycol, paraffin, and oil. Al₂O₃, TiO₂, CuO, ZnO, Al, and Cu nanoparticles were employed in the corresponding nanofluids. A collection of 1109 experimental samples from reliable sources was used. In addition, the present model can estimate the thermal conductivity of nanofluids as a function of temperature, diameter, nanoparticle volume fraction as well as the thermal conductivity of the nanoparticles and the base fluid. The proposed LSSVM structure was optimized by particle swarm optimization technique where the outcomes proved great accuracy of the model for estimating the thermal conductivity of nanofluids. Moreover, statistical observations showed superior predictive ability of LSSVM model than other previous available correlations. Namely, the average relative deviation percent of 2.46 and 3.10%, and R-squared values of 0.9954 and 0.9914 were resulted for training and testing stages of LSSVM model, respectively.

Introduction

Extensive utilizations of heat transfer phenomena in industrial instruments underlie their great significance in the corresponding efficiency. Further, economic heat transfer processes are characterized by the required volume of such instruments, which is, in turn, related to their efficiency [1, 2]. Therefore, the required power consumption and thus processing cost decrease with an increase in the heat transfer efficiency of the working fluid passing through the heat transfer devices. Numerous investigations have been carried out in order to enhance the efficiency of heat transfer [3,4,5]. Increasing the effective surface area, utilization of vibration technique and application of microscale channels are such investigations that can improve the efficiency of heat transfer. As demonstrated in Fig. 1, one can observe remarkable attentions on nanofluid systems based on annually published articles. This figure was prepared based on publications recorded in Google Scholar, which are searched in January 2018 by three relevant topics such as “nanofluids”, “nanofluids thermal conductivity”, and “nanofluids viscosity” during various years. As can be seen, the main investigated subject regarding the nanofluid systems refers to the thermal conductivity (42%), followed by viscosity (58%). On the other hand, the thermal conductivity of the working fluid in the heat transfer systems is identified as an important factor as to improve the heat transfer efficiency. Owning to low thermal conductivity of traditional working heat transfer fluids, for example, water (H₂O), ethylene glycol (EG), and different oils, their thermal conductivity can be increased through the addition of a few solid nanoparticles to such aforementioned fluids [6, 7]. These nanoparticles help to have a simple fluidized process, avoiding critical issues, such as the blockage of channels, precipitation of particles, and erosion due to their nano-sized structures. A new aspect of nanofluids was familiarized by Chol [8] considering the suspension of nanoparticles in a base fluid. In addition, a practical application of nanofluids in microchannels was also introduced [9]. Recently, numerous studies have been carried out in order to predict the nanofluids thermal conductivity using simple empirical correlations and some analytical solutions. A simple correlation was proposed by Maxwell [10] in 1904 for determining the nanofluid’s effective thermal conductivity. This correlation can be employed in order to estimate the thermal conductivity in dilute suspensions containing microparticles; however, this correlation could not show an accurate estimation of the thermal conductivity of nanofluids high deviations between correlation and experimental results [11,12,13,14].

Fig. 1

Year-wise published research records on different areas of nanofluids from Google scholar (2003–2017)

Several studies have reported the measured thermal conductivity of nanofluids together with the effective parameters. Such parameters found to be the volume fraction of nanoparticles and their size, the aggregation, morphology and the physicochemical properties of the solid particles, as well as temperature, and the nature of the base fluid. In addition, many efforts have been made to proposing theoretically a new mechanism for thermal conductivity enhancement. An investigation was carried out by Vatani et al. [15] to estimate effective thermal conductivity of nanofluids based on broad data gathering from recent articles. They compared the outcomes of their model with seven previous other correlations and concluded that all the models cannot be accurately applied for different nanofluids; nonetheless, these available correlations are quite popular in the estimation of nanofluid’s thermal conductivity. As a result, highly accurate estimation of thermal conductivity of nanofluids is a stimulating subject which must be addressed. Moreover, measuring the thermal conductivity of nanofluids seems to be time-consuming and costly while limited effective parameters can be investigated during the experiments [16]. On the other hand, the proposed available models can also cover inadequate ranges of working conditions. Accordingly, developing an accurate model to indicate the relationships between relevant parameters determining the thermal conductivity of nanofluids was found to be a serious issue. An investigation was carried out by Baghban et al. to estimate heat transfer coefficient of the nanofluids containing the silica nanoparticles as a function of Reynolds number, Prandtl number, and mass fraction nanofluid by the adaptive neuro-fuzzy inference system (ANFIS), artificial neural network (ANN), support vector machine (SVM), least square support vector machine (LSSVM), genetic programming (GP), principal component analysis (PCA), and committee machine intelligent system (CMIS) [17].

To address such issue employing artificial intelligence, such as the artificial neural networks (ANNs), fuzzy inference systems, and support vector machines, which typically result in precise outcomes, has been recommended by numerous studies in several fields [18,19,20,21,22,23]. ANN is known as a promising technique to find optimal solutions for complicated problems leading to a considerably time- and/or cost-saving procedure. Thanks to the rapid process of the ANN, it  has broadly applications in numerous studies in order to estimate the thermophysical properties of nanofluids, i.e., thermal conductivity, density, and viscosity [24,25,26,27]. An artificial neural network model has been proposed by Hojjat et al. [28] to estimate the thermal conductivity of non-Newtonian nanofluids. The inputs of their model were based on the operating temperature, the concentration and thermal conductivity of nanoparticles. In addition, another model developed by Papari et al. [29] was based on a diffusion neural network approach. Such model was employed to predict the thermal conductivity of certain nanofluids containing multi-walled carbon nanotubes. The nanofluids were synthesized in four base fluid including oil, decene, distilled water, and ethylene glycol. A couple of structures of ANN model were also applied by Longo et al. [30] in order to predict the thermal conductivity of Al₂O₃ and TiO₂ nanopowders in water as the base fluid. The model was developed as a function of temperature, volume fraction, thermal conductivity, and the average size of nanoparticle. Hemmati Esfe et al. [31] modeled the thermal conductivity of Al₂O₃–Water nanofluid at different temperatures and solid volume fractions using ANN method. Recently, another embranchment of artificial intelligence called least square support vector machine has been employed by numerous scholars in such fields [19,20,21]. However, this technique has been rarely utilized in order to estimate the physical properties of nanofluids [32]. It would be worth mentioning that all previously proposed models can only be applied for limited nanofluids with poor accuracy to estimate thermal conductivity. Hence, the present work aims to present a more wide-ranging model for estimating the thermal conductivity of nanofluids.

Available correlations

Several operative medium models have been employed to predict the effective thermal conductivity of nanofluids. The correlation-based models, such as Maxwell correlation [33], Hamilton and Crosser correlation [34], and Bruggeman correlation [35] could predict the effective thermal conductivity of nanofluid as a function of volume fraction, the thermal conductivity of particle, and thermal conductivity of base fluid. Apart from these conventional correlation-based approaches, newly proposed strategies are also explained here. The effect of a nanolayer around a particle was considered by new approaches, such as Yu–Choi’s [36], Leong’s et al. [37], Xie et al.’s [38], and Sohrabi’s models [39]. It is worth to mention that Sohrabi’s [39], Koo and Kleinstreuer’s [40], and Xu et al.’s models [41] considered the effect of convective heat transfer caused by Brownian motion in their models. Moreover, an investigation was carried out by Evans et al. [42] in order to show the dependence of thermal conductivity of nanofluids on clustering and interfacial thermal resistance. The following literature surveys encompass extensive conducted studies by researchers to predict thermal conductivity of nanofluids.

Maxwell correlation

This correlation (Eq. 1) is considered as the preliminary developed correlation which can predict the effective thermal conductivity of nanofluids [33]. Accurate outcomes of this model are resulted for low volume fractions of spherical particles.

$$K_{\text{eff}} = \frac{{K_{\text{p}} + 2K_{\text{f}} + 2\phi \left( {K_{\text{p}} - K_{\text{f}} } \right)}}{{K_{\text{p}} + 2K_{\text{f}} - \phi \left( {K_{\text{p}} - K_{\text{f}} } \right)}}K_{\text{f}}$$

(1)

Here k_eff, k_f, and k_p refer to the effective thermal conductivity of nanofluid, the thermal conductivity of the base fluid, and thermal conductivity of particle, respectively. $\phi$ stands for the volume fraction of the particle.

Hamilton and Crosser correlation (H–C model)

The main advantage of H–C model compared with Maxwell model is that the H–C model considered the effect of the particle shapes in their formulation. This model is formulated as below [34]:

$$K_{\text{eff}} = \frac{{K_{\text{p}} + \left( {n - 1} \right)K_{\text{f}} - \left( {n - 1} \right)\phi \left( {K_{\text{p}} - K_{\text{f}} } \right)}}{{K_{\text{p}} + \left( {n - 1} \right)K_{\text{f}} - \phi \left( {K_{\text{p}} - K_{\text{f}} } \right)}}K_{\text{f}} ,\quad n = \frac{3}{\psi }$$

(2)

In the above correlation, the term n refers to the empirical shape factor and ψ stands for the sphericity, which is the ratio of the surface area of a sphere with unit volume to the surface area of the particle. In the case of n = 3, both H–C and Maxwell correlations are identical.

Bruggeman correlation

For spherical particles, the Bruggeman model [35] has more satisfactory prediction compared to the Maxwell model. This model uses another averaging technique with no restrictions on the concentration of inclusions. This model is formulated as follows:

$$K_{\text{eff}} = \left\{ {\frac{1}{4}\left[ {\left( {3\phi - 1} \right)\frac{{K_{\text{p}} }}{{K_{\text{f}} }} + \left( {2 - 3\phi } \right)} \right] + \frac{1}{4}\sqrt {\left[ {\left( {3\phi - 1} \right)^{2} \left( {\frac{{K_{\text{p}} }}{{K_{\text{f}} }}} \right)^{2} + \left( {2 - 3\phi } \right)^{2} + 2\left( {2 + 9\phi - 9\phi^{2} } \right)\left( {\frac{{K_{\text{p}} }}{{K_{\text{f}} }}} \right)} \right]} } \right\}K_{\text{f}}$$

(3)

All above available correlations had satisfactory accuracy for the large size of particles (micro- and millimeter), but their approximation for nano-size particles shows significant deviations.

The Yu and Choi model

A proper investigation was carried out by Yu and Choi [36] to show the effect of a nanolayer around a particle in nanofluids for calculating the corresponding thermal conductivity. Moreover, they assumed a quite low particle volume concentration in the base fluid. Accordingly, the equivalent thermal conductivity of the equivalent particles k_pe can be expressed as [43]:

$$K_{\text{pe}} = \frac{{\left[ {2\left( {1 - \sigma } \right) + \left( {1 + \beta } \right)^{3} \left( {1 + 2\sigma } \right)} \right]\sigma }}{{ - \left( {1 - \sigma } \right) + \left( {1 + \beta } \right)^{3} \left( {1 + 2\sigma } \right)}}K_{\text{p}}$$

(4)

where $\beta = \frac{h}{a}$ in which h refers to the thickness of the nanolayer and a stands for the radius of particle. In addition, the definition of σ is $\sigma = \frac{{k_{\text{lr}} }}{{K_{\text{p}} }}$ in which k_lr denotes the nanolayer thermal conductivity and k_p is the thermal conductivity of particle. Yu and Choi modified the above correlation with the following formula by combining with the Maxwell model, which is shown as follows:

$$K_{\text{pe}} = \frac{{K_{\text{pe}} + 2K_{\text{f}} + 2\left( {K_{\text{e}} - K_{\text{f}} } \right)\left( {1 + \beta } \right)^{3} \phi }}{{K_{\text{pe}} + 2K_{\text{f}} - \left( {K_{\text{e}} - K_{\text{f}} } \right)\left( {1 + \beta } \right)^{3} \phi }}K_{\text{f}}$$

(5)

It should be mentioned that there is a limiting case as σ = 1 in the Yu–Choi model. Accordingly, this model can help us to have forward computations for thermal conductivity of nanofluids in the presence of a nanolayer.

Leong et al.’s correlation

The proposed formula by Leong et al. [37] to determine the effective thermal conductivity of nanofluids was developed via solving the energy equation in spherical coordinates at steady-state condition which is presented as below:

$$k_{\text{eff}} = \frac{{\left( {k_{\text{p}} - k_{\text{lr}} } \right)\phi k_{\text{lr}} \left[ {2\gamma_{1}^{3} - \gamma_{2}^{3} + 1} \right] + \left( {k_{\text{p}} - 2k_{\text{lr}} } \right)\gamma_{1}^{3} \left[ {\phi \gamma_{2}^{3} \left( {k_{\text{lr}} - k_{\text{f}} } \right) + k_{\text{f}} } \right]}}{{\gamma_{1}^{3} \left( {k_{\text{p}} + 2k_{\text{lr}} } \right) - \left( {k_{\text{p}} - k_{\text{lr}} } \right)\phi \left[ {\gamma_{1}^{3} + \gamma_{2}^{3} - 1} \right]}}$$

(6)

In above expression, $\gamma_{1} = 1 + \frac{h}{2a}$ and $\gamma_{2} = 1 + \frac{h}{a}$ and also k_lr refers to the thermal conductivity of the interfacial nanolayer. As can be concluded from the Leong et al. model, the effective thermal conductivity is related to the particle’ radius (a), interfacial nanolayer thickness (h), volume fraction ($\phi$), and the thermal conductivity of the particle (k_p) and the base fluid (k_f). The Maxwell model can be obtained from this formula when k_lr = k_f and h = 0. Leong et al.’s model used the general solution for the base liquid temperature field (T_f). By this modification, the model can be reduced to the Maxwell model by either setting h = 0 or k_lr = k_f.

Xie et al.’s model

Another investigation was carried out by Xie et al. [38] to propose a model for thermal conductivity of nanofluids in the presence of a nanolayer with spherical shell and thickness (h) around the particle. The following formula indicates their model as:

$$k_{\text{eff}} = k_{\text{f}} + 3\theta \phi_{\text{T}} k_{\text{f}} + \frac{{3\theta^{2} \phi_{\text{T}}^{2} }}{{1 - \theta \phi_{\text{T}} }}k_{\text{f}}$$

(7)

Here, term θ can be obtained by:

$$\theta = \frac{{\left( {\frac{{k_{\text{lr}} - k_{\text{f}} }}{{k_{\text{lr}} + 2k_{\text{f}} }}} \right)\left[ {\left( {1 + \frac{h}{a}} \right)^{3} - \frac{{\left( {\frac{{k_{\text{p}} - k_{\text{f}} }}{{k_{\text{p}} + 2k_{\text{f}} }}} \right)}}{{\left( {\frac{{k_{\text{f}} - k_{\text{lr}} }}{{k_{\text{f}} + 2k_{\text{lr}} }}} \right)}}} \right]}}{{\left( {1 + \frac{h}{a}} \right)^{3} + 2\left( {\frac{{k_{\text{lr}} - k_{\text{f}} }}{{k_{\text{lr}} + 2k_{\text{f}} }}} \right)\left( {\frac{{k_{\text{p}} - k_{\text{lr}} }}{{k_{\text{p}} + 2k_{\text{lr}} }}} \right)}}$$

(8)

$\phi_{\text{T}}$ which refers to the total volume fraction of nanoparticles and nanolayers are defined as follows:

$$\phi_{\text{T}} = \phi \left( {1 + \frac{h}{a}} \right)^{3}$$

(9)

The thermal conductivity of the nanolayer (k_lr) can be introduced as:

$$k_{\text{lr}} = \frac{{k_{\text{f}} \left[ {\frac{{k_{\text{p}} }}{{k_{\text{f}} }}\left( {1 + \frac{h}{a}} \right) - 1} \right]^{2} }}{{\left\{ {\left[ {\frac{{k_{\text{p}} }}{{k_{\text{f}} }}\left( {1 + \frac{h}{a}} \right) - 1} \right] - \frac{h}{a}} \right\}{ \ln }\left\{ {1 + \left[ {\frac{{k_{\text{p}} }}{{k_{\text{f}} }}\left( {1 + \frac{h}{a}} \right) - 1} \right]} \right\} + \frac{h}{a}\left[ {\frac{{k_{\text{p}} }}{{k_{\text{f}} }}\left( {1 + \frac{h}{a}} \right) - 1} \right]}}$$

(10)

A similar model developed by Sohrabi et al. [39] showed the effect of the convective heat transfer caused by the Brownian motion. They considered linear and nonlinear profiles for the thermal conductivity of the nanolayer. As Xie et al., they did not directly use such profiles in their main equations and an average value of the nanolayer thermal conductivity was employed to determine the effective thermal conductivity of nanofluids.

Koo and Kleinstreuer’s model

The model developed by Koo and Kleinstreuer [13] predicts the thermal conductivity of nanofluids as a function of k_static and k_Brownian. The former term (k_static) in the thermal conductivity is owing to the higher thermal conductivity of the nanoparticles, while the latter (k_Brownian) implies the effect of Brownian motion. The above-mentioned conventional Maxwell model is employed for determining static term, and Brownian motion effects are defined as expressed by the following formula.

$$k_{\text{Brownian}} = 5 \times 10^{4} \beta \phi \rho_{\text{f}} C_{{{\text{p}},{\text{f}}}} \sqrt {\frac{{k_{\text{B}} Tf}}{{\rho_{\text{p}} d_{\text{p}} }}}$$

(11)

The density of particles and base fluid is shown by ρ_p and ρ_f, respectively; also T and c_p,f refer to the operating temperature and specific heat capacity of the base fluid, respectively. k_B is the Boltzmann’s constant, and d_p stands for the particle diameter. The empirical terms in formulation 11 (β and f) are obtained by accurate experimental measurements. In addition, Koo and Kleinstreuer [40] suggested a method for determining β, while f can be obtained based on the following expression.

$$f = \left( { - 134.63 + 1722.3\phi } \right) + \left( {0.4705 - 6.04\phi } \right)T$$

(12)

Indeed, developing expressions for f and β are a problematic issue because of their complications. Hence, Xu et al. [41] suggested another model to address this problem.

Xu et al.’s model

Another strategy similar to Koo and Kleinstreuer model was proposed by Xu et al. [41]. The thermal conductivity of nanofluids is composed of two terms of static and dynamic conductivity. The dynamic term in this model differs from the one in Koo and Kleinstreuer model [13]. They assumed that the distribution of the nanoparticle sizes is fractal, resulting in the following expression for the dynamic part of the thermal conductivity of nanofluids.

$$k_{\text{Dynamic}} = k_{\text{f}} C\frac{{Nu \times d_{\text{f}} \left( {2 - D_{\text{f}} } \right)D_{\text{f}} \left[ {\left( {\frac{{d_{\text{p, max}} }}{{d_{\text{p, min}} }}} \right)^{{1 - D_{\text{f}} }} - 1} \right]^{2} }}{{Pr\left( {1 - D_{\text{f}} } \right)^{2} \left( {\frac{{d_{\text{p, max}} }}{{d_{\text{p, min}} }}} \right)^{{2 - D_{\text{f}} }} - 1}} \times \frac{1}{{\bar{d}_{\text{p}} }}$$

(13)

Here D_f is defined as:

$$D_{\text{f}} = 2 - \frac{\ln \phi }{{\ln \left( {\frac{{d_{{{\text{p}},{\text{mx}}}} }}{{d_{\text{p,min}} }}} \right)}}$$

(14)

C, $\bar{d}_{\text{p}}$, d_f, d_p,min, and d_p,max refer to empirical coefficient, average diameter, diameter of the liquid molecule, minimum and maximum particle diameters, respectively. In addition, Xu et al. employed Tomotika et al. [44] approach presented in the following equation to determine Nusselt number while assuming $\frac{{d_{\text{p, max}} }}{{d_{\text{p, min}} }}$ = 0.001 is:

$$Nu = 2 + 0.5RePr + O\left( {Re^{2} Pr^{2} } \right)$$

(15)

The formulations of Reynolds and Prandtl number are expressed as:

$$Re = \frac{{d_{\text{p}} u_{\text{p}} }}{{\vartheta_{\text{f}} }}$$

(16)

$$Pr = \frac{{\mu_{\text{f}} C_{{{\text{p}},{\text{f}}}} }}{{k_{\text{f}} }}$$

(17)

In above formulations, the velocity of particles is represented by u_p. μ_f and υ_f refer to the dynamic and kinematic viscosity of the base fluid, respectively. Moreover, the values of c for deionized water and ethylene glycerol (EG) were assumed by 85.0 and 280.0, respectively.

Evans et al.’ model

Since clusters can be simply created by nanoparticles [45, 46], the fractal theory is typically applied to investigate such effect [47]. Evans et al. [42] believed that clustering can be as a consequence of rapid heat transfer along long distances. This is because of the conduction heat transfer rate through the solid particles is greater than that of liquid media. Hence, they studied the effect of clusters on thermal properties of nanofluids including the thermal conductivity and interfacial thermal resistance. Three models were utilized regularly to evaluate the effect of clusters including Bruggeman model, Nan et al. model [48], and Maxwell model. Accordingly, the following formula was obtained for the effective thermal conductivity of nanofluids.

$$k_{\text{eff}} = \frac{{\left( {k_{\text{cl}} + 2k_{\text{f}} } \right) + 2\phi_{\text{cl}} \left( {k_{\text{cl}} - k_{\text{f}} } \right)}}{{\left( {k_{\text{cl}} + 2k_{\text{f}} } \right) - \phi_{\text{cl}} \left( {k_{\text{cl}} - k_{\text{f}} } \right)}}k_{\text{f}}$$

(18)

The volume fraction and thermal conductivity of the clusters are represented by $\phi_{\text{cl}}$ and k_cl, respectively. They proved that size of a cluster increases with a rise of the effective thermal conductivity.

It should be noted that in all above-mentioned existing models, various physical mechanisms were used to determine the thermal conductivity enhancement of the nanofluids.

Theory of least square support vector machine (LSSVM)

Although ANN-based models result in promising outcomes, they are not reproducible. This is because of changing the optimization bases and unsystematic initialization of this type of models. The support vector machine (SVM) supersedes ANN-based models by applying a range of inputs from nonlinear functions to multi-dimensional mappings. Input and output spaces are connected by linear decision surface. The SVM-based models need fewer adjustable parameters compared to ANN-based models. In addition, SV-based models must not set the number of hidden layers and corresponding neurons for these models, leading to more accurate generalization [49, 50].

Least square support vector machine (LSSVM), developed by Suykens and Vandewalle [49] in 1999, showed to be simpler than SVM. Some linear equations with support vectors were used to eliminate the quadratic programming problems, to reduce sophistications of optimization. In LSSVM models, the regression error is estimated by the difference between calculated values by LSSVM and the experimental values, whereas in SVM method, regression error is computationally optimized. In LSSVM, the optimization process is done as [51, 52]:

$$L_{\text{LSSVM}} = \frac{1}{2}w^{\text{T}} w + \mu \mathop \sum \limits_{i = 1}^{n} e_{\text{i}}^{2}$$

(19)

It is used in the equation below:

$$y_{\text{i}} = w^{\text{T}} g\left( {x_{\text{i}} } \right) + b + e_{\text{i}} ,\quad i = 1, 2, 3, \ldots , n$$

(20)

where w is the weight vector, T is transposed matrix, µ shows a relation of single and total regression weight errors, e_i is the regression error dependent on entire data, g(x) is a function of the mapping, and b is the bias term. W (regression weight coefficient) will be defined by applying Lagrangian multiplier (α_i) and an input vector (x_i) as:

$$w = \mathop \sum \limits_{i = 1}^{n} \alpha_{\text{i}} x_{\text{i}} \;{\text{in which}}\;\alpha_{\text{i}} = \, 2\mu e_{\text{i}}$$

(21)

The equation above will be modified by considering a linear relationship between dependent and independent parameters as:

$$y = \mathop \sum \limits_{i = 1}^{n} \alpha_{\text{i}} x_{\text{i}}^{\text{T}} x + b$$

(22)

Then, Lagrange multiplier (α_i) will be obtained as:

$$\alpha_{\text{i}} = \frac{{y_{\text{i}} - b}}{{x_{\text{i}}^{\text{T}} x + \left( {2\mu } \right)^{ - 1} }}$$

(23)

The kernel function is combined with Eq. (23) as to modify it and make it usable for nonlinear constraints, so we would have:

$$y = \mathop \sum \limits_{i = 1}^{n} \alpha_{\text{i}} k\left( {x_{\text{i}} ,x} \right) + b$$

(24)

where Kernel function [k(x_i, x)] is defined as:

$$k\left( {x_{\text{i}} ,x} \right) = g\left( {x_{\text{i}} } \right) \cdot g\left( x \right)^{\text{T}}$$

(25)

The most common type of Kernels used in performing the LSSVM method is Gaussian radial basis function. Kernels (RBF kernels) and their samples are as follows:

$$k\left( {x_{\text{i}} ,x} \right) = \exp \left( {\frac{{x_{\text{i}} - x^{2} }}{{\sigma^{2} }}} \right)$$

(26)

In which σ² is squared bandwidth and needs to be optimized by an optimization algorithm during the training process.

Results and discussion

Data preparation

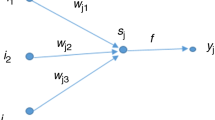
Consistency and accuracy of the proposed models above highly depend on applied experimental data, which should be accessible and precise in order to implement the model [19, 21]. A comprehensive model was developed in the current study through using 1109 experimental data points for estimating dimensionless thermal conductivity of 29 different nanofluids at different particle diameter size, temperature, and volume fraction [11, 53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78]. It is worth mentioning that this model is applied for spherical nanoparticles. The name of studied nanofluids, ranges of temperature, particle diameters, and volume fractions together with their references are presented in Table 1. Moreover, the thermal conductivity of particles and base fluids is also summarized in Table 2. The next stage after data preparation and recognition is to select the input and output variables of the LSSVM model. The input variables of suggested LSSVM model were the temperature (K), particle diameter (nm), volume fraction (v), the thermal conductivity of nanoparticle (W m⁻¹ K⁻¹), and thermal conductivity of the base fluid (W m⁻¹ K⁻¹). On the other hand, the thermal conductivity of nanofluid was considered as the outcome of the model. Scheme of input and output variables of the proposed model is represented in Fig. 2. In order to train and evaluate the model, all gathered data points were divided into two subcategories, namely the test and train group. A quarter of data points was chosen as testing data, and the remained 75% was employed to train the LSSVM approach.

Table 1 Diameter, temperature, and volume fraction ranges of experimental data points

Table 2 Thermal conductivity of nanoparticle and base fluid

Fig. 2

Parameters used for implementation of the model

Model development and evaluation

Radial basis function (RBF) kernel renders high-speed computations owing to the fewer tuning terms as compared to others; such function was chosen as an operative and applicable kernel function in line with other studies. As already discussed, employing the proposed model which uses LSSVM approach with RBF kernel function deals with a significant problem, i.e., finding model tuning parameters of $\gamma$ and σ² (where $\gamma$ refers to the regularization term and σ² identifies the kernel sample variance). Such parameters play a remarkable role in order to achieve a satisfactory LSSVM model with high capability of approximations and globalizations.

The present research uses the particle swarm optimization (PSO) technique for determining optimal values of aforementioned tuning parameters. The objective of this optimization algorithm is to reach a less value of mean absolute relative error (MARE) of testing samples as a cost function. The optimization process was continued several epochs as efforts to obtain a possible global optimum based on the defined fitness function. Figure 3 illustrates a diagram of PSO–LSSVM model applied in the present work. Moreover, specifications of the proposed model are presented in Table 3.

Fig. 3

Schematic diagram of proposed PSO–LSSVM model

Table 3 Details of trained LSSVM model

A comparison between estimated and experimental thermal conductivity of nanofluid at three stages of training, testing, and total dataset for the LSSVM model is illustrated in Fig. 4. As is clearly seen in this figure, the estimated and actual thermal conductivities of nanofluid cover each other properly. Furthermore, the approximations by the proposed LSSVM model were assessed by applying various approaches such as the statistical and graphical confirmations. The cross-scheme of the suggested model which is created through scheming estimated against experimental data points of nanofluid’ thermal conductivity is illustrated in Fig. 5. An excellent agreement between estimated and experimental nanofluid thermal conductivity values at different stages (i.e., train, test, and total’s) is observed in this figure.

Fig. 4

Experimental versus estimated thermal conductivities for: a training data, b testing data, c total data

Fig. 5

Regression plots between experimental and estimated thermal conductivities for: a training data, b testing data, c total data

Figure 6 represents the percentage of absolute errors between the estimated thermal conductivity of nanofluid and experimental values. As can be seen, the vertical axis refers to the absolute error percent and the horizontal axes are assigned to the experimental thermal conductivity of nanofluid. Results from this figure indicate that the resulting errors by the LSSVM model range mostly between 5 and – 5%, confirming the promising performance ability of the proposed model. Apart from these graphical evaluations, a few popular statistical techniques which are expressed base on the following equations were applied. This can help to validate the superior application of our proposed model.

Fig. 6

Absolute deviation of the proposed LSSVM model

$$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {y_{\text{Pred}} \left( i \right) - y_{\text{Exp}} \left( i \right)} \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {y_{\text{Pred}} \left( i \right) - \bar{y}_{\text{Exp}} } \right)^{2} }}$$

(27)

$$\% {\text{AARD}} = \frac{100}{N}\mathop \sum \limits_{i = 1}^{N} \frac{{\left( {y_{\text{Pred}} \left( i \right) - y_{\text{Exp}} \left( i \right)} \right)}}{{y_{\text{Exp}} \left( i \right)}}$$

(28)

$${\text{RMSE}} = \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {y_{\text{Pred}} \left( i \right) - y_{\text{Exp}} \left( i \right)} \right)^{2} }}{N}} \right)^{0.5}$$

(29)

$${\text{STD}} = \mathop \sum \limits_{i = 1}^{N} \left( {\frac{{\left( {y_{\text{Pred}} \left( i \right) - \bar{y}_{\text{Exp}} \left( i \right)} \right)^{2} }}{N}} \right)^{0.5}$$

(30)

The corresponding statistical analyses of the LSSVM model at three stages of train, test and total data points are summarized in Table 4. It is found that the LSSVM model results in high values of R-squared and low values of AARD, RMSE, and STD. These analyses strongly justify the applicability and consistency of the proposed model in order to estimate the thermal conductivity of nanofluids.

Table 4 Statistical analyses obtained from the LSSVM model

Several comparisons were carried out between the outcomes of the proposed LSSVM model and other previous correlations. Figure 7 shows the predicted dimensionless thermal conductivities of Al₂O₃–water nanofluid with particle diameter and temperature of 38.4 nm and 324 K, respectively, resulted from the models by Chon et al. [11], Murshed et al. [36], Nan et al. [38], Yu and Choi [48], Xie et al. [59], and Mintsa et al. [60] together with the ones from the proposed LSSVM model. The dimensionless thermal conductivity increases with an increase in the nanoparticle volume fraction. As can be seen, there is a great agreement between the LSSVM outcomes compared with other correlations. These correlations are simple and cannot be applied in different range of conditions. In addition, the dimensionless thermal conductivity of Ag–water nanofluid with a particle diameter of 63 nm at 343 K is obtained from the proposed model in this work, and correlations such as the Hamilton and Crosser [34], Timofeeva et al. [61], Wasp et al. [79], and Godson et al. [80] are compared in Fig. 8. Among these four correlations, after our LSSVM model, Godson et al. have satisfactory performance in order to apply in Ag–water system. This comparison clearly indicates an accurate prediction of the results from the present model proposed in this study with the corresponding experimental dimensionless thermal conductivities. Figure 9 shows the dimensionless thermal conductivity of carbon nanotube–water nanofluid predicted by Thang et al.’s correlation [62] as well as our proposed model at three different temperatures for d_p = 9 nm. In addition, another comparison of this correlation with LSSVM model for carbon nanotube–water nanofluid for different particle sizes at 296.15 K is indicated in Fig. 10. As can be seen for carbon nanotube–water nanofluid system, Thang et al.’s correlation cannot predict accurately the dimensionless thermal conductivity. Moreover, Fig. 11 shows the outcomes of the proposed LSSVM model and four other correlations developed by Patel et al. [81], Azmi et al. [82], and Vajjha and Das [83] for predicting the dimensionless thermal conductivity of CuO–water nanofluid with d_p = 24 nm and T = 298.15 K. Patel et al. have better accuracy than other two correlations for estimating dimensionless thermal conductivity in CuO–water system. In addition, the dimensionless thermal conductivity of TiO₂–EG nanofluid at 298.15 K resulted from Jang et al. correlation [84] and the proposed LSSVM model at different nanoparticle sizes and volume fractions is illustrated in Fig. 12. As can be found by all above comparisons, the LSSVM model proposed in this work shows an invaluable predictive ability to determine the dimensionless thermal conductivity of nanofluids.

Fig. 7

Comparison of LSSVM model with different models to estimate dimensionless thermal conductivity of Al₂O₃–water nanofluid

Fig. 8

Comparison of LSSVM model with different models to estimate dimensionless thermal conductivity of Ag–water nanofluid

Fig. 9

Comparison of LSSVM model with Thang et al. model to estimate dimensionless thermal conductivity of CNT–water nanofluid at different temperatures

Fig. 10

Comparison of LSSVM model with Thang et al. model to estimate dimensionless thermal conductivity of CNT–water nanofluid for different particle sizes

Fig. 11

Comparison of LSSVM model with different models to estimate dimensionless thermal conductivity of CuO–water nanofluid

Fig. 12

Comparison of LSSVM model with Jang et al. models to estimate dimensionless thermal conductivity of TiO₂–EG nanofluid for different volume fractions and size particles

Outlier detection and sensitivity analysis

It has been found that the data points used in the modeling study can highly influence the predictive performance of the resultant model [85]. Owning to different measurement errors of experimental databases in the literature, analysis of outlier for applied data points can lead to erroneous measured data points. In order to carry out the outlier analysis, the leverage mathematical approach is usually used to calculate the residual values and Hat matrix of input data points as expressed below [86].

$$H = X\left( {X^{\text{T}} X} \right)^{ - 1} X^{\text{T}}$$

(31)

In the above equation, X stands for $m \times n$ matrix in which the terms m and n refer to the number of experimental measurements and parameters of our model, respectively. The main diagonal of Hat matrix can provide the Hat values. Consequently, a graphical illustration by William’s plot indicates the valid and suspected data points. These results are shown in Fig. 13 to detect outliers. A warning leverage value ($H^{*}$) in this figure was calculated by:

Fig. 13

Outlier analysis of the proposed LSSVM model

$$H^{*} = 3\left( {n + 1} \right)/m$$

(32)

Furthermore, the leverage boundary has been indicated by the green line and those data points which have higher Hat values (H) than this warning value H^* are introduced as outliers. Two other red lines presented in this figure are also referred to the standardized residuals boundaries with the values ranging + 3 and − 3. Accordingly, the valid data points are also situated within these boundaries.

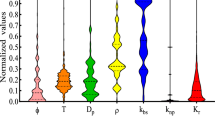
Sensitivity analysis is a popular statistical technique to show the relationship between inputs and output. The effect of inputs on output term is determined by the relevancy factor (r). We can find the most effective variables on thermal conductivity of nanofluids for the present case. The relevancy factor is varied between − 1 and + 1. The higher value of this term is assigned to a specific input variable, indicating the more influence of this input variable on the corresponding output. The positive value is due to an increasing effect, and its negative value shows a decreasing effect. A mathematical formulation of relevancy factor is defined as follows [87]:

$$r = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {X_{{{\text{k}},{\text{i}}}} - \bar{X}_{\text{k}} } \right)\left( {Y_{\text{i}} - \bar{Y}} \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {X_{{{\text{k}},{\text{i}}}} - \bar{X}_{\text{k}} } \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} \left( {Y_{\text{i}} - \bar{Y}} \right)^{2} } }}$$

(33)

where $X_{{{\text{k}},{\text{i}}}}$, $\bar{X}_{\text{k}}$, $Y_{\text{i}}$, and $\bar{Y}$ refer to the “i”th input value, the average value of the kth input, the “i”th output value, and the average value of output, respectively. Hence, as demonstrated in Fig. 14, the values of nanofluid dimensionless thermal conductivity show a direct relationship between temperature, the thermal conductivity of base fluid, and volume fraction. Thermal conductivity of base fluid is the most effective parameter, and the particle diameter has the lowest effect on thermal conductivity of nanofluid. As can be seen, a number of sixty data points were detected as outliers.

Fig. 14

Sensitivity analysis of parameters used for the developed model

Conclusions

According to the results from statistical analyses and graphical illustrations, we can find significant conclusions as follows:

• A comprehensive databank adopted from previously published articles was used in the present study, and the successful performance of our LSSVM model was shown in order to estimate thermal conductivity of nanofluids.

• Optimizing tuning parameters of LSSVM strategy by PSO algorithm led to encouraging results for predicting thermal conductivity of nanofluids. In addition, a satisfactory agreement was observed between the outcomes of the proposed LSSVM model and experimental values with obtained R² and AARD % of 0.9913 and 3.10%, respectively.

• A comparison of the LSSVM results with 15 different correlations indicates great accuracy. Further, the corresponding predictive capability of our model was greatly accepted. Moreover, we can see a great generalization ability of the LSSVM model to estimate thermal conductivity of different nanofluids.

• The present model is highly nonlinear and complicated. As a result, through using the LSSVM approach, which is a connectionist technique with low tuning parameters, can help to overcome any drawbacks and issues that one might face.

Appendix: Program

I have developed a graphical user interface (GUI) version of the model as illustrated in Fig. 15. This program is an exe file presented in supplementary content, and it needs Matlab software version 2012 (64bit) before running. As indicated, three input parameters (temperature, diameter, and volume fraction) should be given and by choosing one of nanofluid in the panel and then clicking on calculate button, the thermal conductivity of nanofluid is obtained.

Fig. 15

GUI version of developed model for estimation of thermal conductivity of nanofluid