Q ₀’s and resonance energies used in k ₀-NAA compared with estimations based on ENDF/B-VII.1 cross section data

Abstract

In k ₀-NAA the modified Høgdahl convention is used for the description of the activation by neutrons. In this convention Q ₀, the ratio between the resonance integral and thermal cross section, is modified to account for non-ideal behavior of the neutron epithermal flux. For this correction an effective resonance energy, E _res, is needed. In this work Q ₀ and E _res are calculated using neutron capture cross section data from the nuclear database ENDF/B-VII.1. The results are compared with k ₀-nuclear data. Special attention was given to new Q ₀’s and $E_{\text{res}}$’s for non-1/v nuclides to be used in the extended Høgdahl convention.

Introduction

In the k ₀-method for neutron activation analysis [1–4] the nuclear parameters for activation using epithermal neutrons are Q ₀ (resonance integral divided by cross section at v = 2200 m/s) and effective resonance energy, E _res. These parameters take into account the resonances in the capture cross section distribution and were mostly calculated using nuclear cross-section data. Most of them were calculated 30 years ago [5]. Often it was mentioned “re-determination desired” [1] or for E _res “should be adequately refined and updated” [5]. In this work the latest nuclear datafile ENDF/B-VII.1 [6] was used for the calculations. Besides recalculating the existing Q ₀ values, also new Q ₀ values were calculated for non-1/v nuclides for which the resonances extend to the thermal energy region and thus also affect the resonance integral in due to epithermal neutrons below the Cd cut-off energy. The latter data is of importance for use in the extended Høgdahl convention [7].

Theory

Neutrons used for activation analysis are typically produced in a nuclear reactor; they can be divided into three groups based on their energy, see Fig. 1. The fission process in the reactor produces fast neutrons. The typical energy is 0.7 MeV with an energy distribution that can be described by a Watt distribution. These neutrons are slowed down by moderation resulting in an epithermal spectrum with a 1/E flux distribution. When completely slowed down the neutrons are called thermal neutrons and the energy spectrum follows a Maxwell–Boltzmann distribution centered at the local neutron temperature. A more accurate description is given by Trkov [8]. The present paper is based on the principles and assumptions made in the currently used k ₀-literature.

Fig. 1

Typical schematic neutron spectrum of a nuclear reactor

Fig. 2

Division in thermal and epithermal flux in the Høgdahl convention by irradiating under a 1 mm Cd-cover

The k ₀-formula for the calculation of element concentrations is based on the Høgdahl convention that divides the neutron flux into two regimes, the thermal region and the epithermal region. For practical experimental reasons the division is made by covering the samples using 1 mm of cadmium and filtering the thermal neutrons, see Fig. 2. Cadmium absorbs or reflects essentially all neutrons that have an energy lower than the Cd “cut-off” energy, E _Cd that is taken to be 0.55 eV. The fast or fission neutrons are not taken into account separately from the epithermal neutrons. The neutron spectrum is characterized by the ratio of thermal (sub Cd) to epithermal flux, f.

The epithermal flux is ideally following a 1/E distribution but in practical situations it follows a 1/E ^1+α distribution. The flux distribution characteristic parameters f and α (describing the non-ideal epithermal flux) are reactor and channel specific. In Fig. 3 an overview is given of all reactors and channels used in the early years of the k ₀ research [1]. It is clear that there is a correlation between f and α. Closer to the core, there are more epithermal neutrons compared to thermal (lower f) and the spectrum is closer to 1/E (α near zero); farther away, or more moderated, the epithermal flux deviates more from 1/E.

Fig. 3

Flux parameters for reactors and channels used in the early years of k ₀ [1], the trend line equals α = 0.135 log(f)−0.175

The activation by (n,γ) reactions depends on the probability of capturing a neutron and is described by the energy dependent cross section of a target nuclide. A typical cross section distribution is given in Fig. 4.

Fig. 4

Typical cross section distribution for (n,γ) activation and neutron energy distribution

For most of the nuclides used for neutron activation the cross section follows a 1/v distribution in the thermal energy region and shows resonances in the epithermal energy flux region. The 1/v behavior in the thermal region makes the activation, relative to a 1/v monitor, independent of the neutron density energy distribution or neutron temperature. Typically the 1/v-cross section is described as σ(v) = σ(v ₀)·v ₀ /v or σ(E) = σ(E ₀).√E ₀ /√E, where v ₀ is 2200 m/s which corresponds to a temperature of 293.59 K or an energy of 0.0253 eV. Non 1/v nuclides show resonances in the thermal energy region as well as in the epithermal region.

Q ₀(α)

The activation by epithermal neutrons is described by a resonance integral, I ₀. In the k ₀-method, the activation term for 1/E epithermal neutrons is described using Q ₀, which is the ratio between the resonance integral I ₀ and σ ₀. For an ideal 1/E epithermal spectrum and for a non-ideal epithermal flux distribution, 1/E ^1+α, the integral is given as:

$$I_{0} = \int\limits_{{E_{\text{Cd}} }}^{\infty } {\sigma (E)\frac{1}{E}{\text{d}}E}\quad {\text{or}}\quad I_{0} (\alpha ) = \int\limits_{{E_{\text{Cd}} }}^{\infty } {\sigma (E)\frac{{E_{a}^{\alpha } }}{{E^{1 + \alpha } }}{\text{d}}E} ,$$

(1)

where E _a is an arbitrary energy which can be omitted if the energies are taken in eV. Since the epithermal flux distribution is channel dependent it is necessary to have an analytical expression for I ₀(α) related to I ₀. To achieve this, the concept of effective resonance energy, Ē _res, was developed. Ē _res represents “the energy of a single virtual resonance which gives the same resonance activation rate as all the resonances for the isotope” [5]. The resonance cross section integral is separated into a fraction that is determined by the cross sections for the resonances only $I^{\prime}_{0} (\alpha )$, and a fraction that is determined by the 1/v cross section:

$$I^{\prime}_{0} (\alpha ) = I_{0} (\alpha ) - \int\limits_{{E_{\text{Cd}} }}^{\infty } {\sigma_{0} \sqrt {E_{0} /E} \frac{{E_{a}^{\alpha } }}{{E^{1 + \alpha } }}{\text{d}}E} = I_{0} (\alpha ) - \frac{{2\sqrt {E_{0} /E_{\text{Cd}} } \sigma_{0} }}{{(1 + 2\alpha )E_{\text{Cd}}^{\alpha } }} = I_{0} (\alpha ) - \frac{{0.429\sigma_{0} }}{{(1 + 2\alpha )0.55^{\alpha } }}.$$

(2)

If we define that the resonances are comprised in one peak at effective resonance energy, Ē _res, it simply follows from Eq. 1 that:

$$\bar{E}_{\text{res}} (\alpha ) = E_{a} \left( {\frac{{I^{\prime}_{0} (\alpha )}}{{I^{\prime}_{0} }}} \right)^{ - 1/\alpha } .$$

(3)

$I^{\prime}_{0} (\alpha )$ can be numerically evaluated from evaluated neutron cross-section data files like ENDF/B- VII.1. It must be emphasized that the resulting resonance energy depends on α. This dependence can be approximated by [5]:

$$E_{\text{res}} (\alpha ) = \bar{E}_{\text{res}} e^{ - p\alpha } .$$

(4)

The effect of this α dependence as well as the effect of uncertainty in Ē _res on the final results was found to be small and only one effective resonance energy is used [11].

In the “modified” Høgdahl convention, the expression for Q ₀(α) can now be written for a 1/E ^1+α flux distribution by combining Eqs. (2) and (3) and dividing by σ ₀, resulting is:

$$Q_{0} (\alpha ) = \left( {\frac{{Q_{0} - 0.429}}{{\bar{E}_{\text{res}}^{\alpha } }} + \frac{0.429}{{(1 + 2\alpha )0.55^{\alpha } }}} \right)E_{a}^{\alpha } .$$

(5)

The complete k ₀-formula [1–4] using a modified Høgdahl convention is written as:

$$\rho_{a} (\mu g/g) = \frac{{\left( {\frac{{N_{\text{p}} /t_{\text{c}} }}{\text{SDCW}}} \right)_{a} }}{{\left( {\frac{{N_{\text{p}} /t_{\text{c}} }}{\text{SDCw}}} \right)_{m} }} \cdot \frac{1}{{k_{0,m} (a)}} \cdot \frac{{G_{{{\text{th}},m}} f + G_{e,m} Q_{0,m} (\alpha )}}{{G_{{{\text{th}},a}} f + G_{e,a} Q_{0,a} (\alpha )}} \cdot \frac{{\varepsilon_{p,m} }}{{\varepsilon_{p,a} }} \cdot 10^{6} ,$$

(6)

with ρ is the mass fraction of analyte, a, m the analyte and co-irradiated monitor, f the thermal to epithermal flux ratio, G _th , G _e the thermal and epithermal self-shielding factors.

The effect of differences in nuclear data on the concentration can, if self-shielding is not relevant, be calculated using:

$$\frac{{\rho_{2} }}{{\rho_{1} }} = \frac{{f + Q_{0,1} (\alpha )}}{{f + Q_{0,2} (\alpha )}}$$

(7)

Q ₀’s for non-1/v nuclides

Non-1/v nuclides are called this way because their cross section for (n,γ)-reactions is not following a 1/v distribution in the thermal energy region as most nuclides do.

These nuclides are originally not analyzed in the k ₀-method using the Høgdahl activation convention but through the Westcott convention [9]. The main difference between the two methods is that the split up in epithermal and thermal flux is different. For non-1/v behavior in the thermal energy region Westcott introduced a nuclide specific g(T _n)-factor. This factor is an integral similar to the resonance integral, based on the assumption that the neutron distribution follows Maxwell’s law for one neutron temperature.

Recently the “Extended” Høgdahl convention was introduced that allows analyzing non-1/v nuclides as well [7]. It was argued and proven that only at the expense of a small loss of accuracy this rather simple extension will work very well:

$$\rho_{a} (\mu g/g) = \frac{{\left( {\frac{{N_{\text{p}} /t_{\text{c}} }}{\text{SDCW}}} \right)_{a} }}{{\left( {\frac{{N_{\text{p}} /t_{\text{c}} }}{\text{SDCw}}} \right)_{m} }} \cdot \frac{1}{{k_{0,m} (a)}} \cdot \frac{{G_{{{\text{th}},m}} f + G_{e,m} Q_{0,m} (\alpha )}}{{G_{th,a} fg_{a} (T_{N} ) + G_{e,a} Q_{0,a} (\alpha )}} \cdot \frac{{\varepsilon_{p,m} }}{{\varepsilon_{p,a} }} \cdot 10^{6} .$$

(8)

The virtue of this method is that all the old reactor parameters can be used and no recalibration is needed. The neutron temperature can be measured using a Lu-monitor but as well by using the reading of the moderator temperature. g(T _n) factors for all k ₀-nuclides were recently reviewed and calculated using the ENDF/B VII.1 data file [10]. A difficulty in implementing the “Extended” Høgdahl convention was caused by the fact that no Q ₀’s were available.

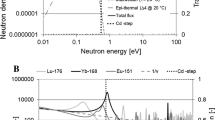
In the Westcott convention the epithermal nuclear activation parameter called s ₀ is also based on the resonance integral. The integration starts at a much lower energy in order to take into account all epithermal neutrons that extend to well below 0.55 eV, see Fig. 5. This is different from the Høgdahl convention for which the integration starts at the Cd cut-off or 0.55 eV. Another major difference is the fact that in the Westcott convention the 1/v component is omitted from the resonance integral.

Fig. 5

Epithermal flux lower energy spectrum and non-1/v cross section data

For a 1/v nuclide the relation between Q ₀ and s ₀ is given as [9]:

$$s_{0} = \sqrt {\frac{4T}{{\pi T_{0} }}} (Q_{0} - 0.429)$$

(9)

In the case of non-1/v nuclides the transformation is somewhat more difficult since the cross section distribution in this region is dominated by resonances [9]:

$$s_{0} = \sqrt {\frac{4T}{{\pi T_{0} }}} (Q_{{0,{\text{total}}}} - gb),$$

(10)

where Q _0,total is based on the integral over the total epithermal energy region, g is Westcott’s “g-factor” and b (~1.17) is the 1/v total resonance integral.

Westcott did a thorough investigation on the epithermal neutron energy distribution at low energies. He found a few different options to describe the measured epithermal flux distributions. He finally opted for a simplified distribution similar to the monotonic cut-off function as used for the Cd-transmission. He found based on the Δ₄(E) function an effective cut-off energy, μkT _n, with μ = 3.7 as a good approximation for a heavy water or a graphite moderator and μ = 2.1 for a water moderated reactor. Taking this into account, Q _0,total refers to the resonance integral over the whole epithermal energy region, starting at μkT _n.

Since the integration of Q ₀ normally starts at 0.55 eV the major resonance peak of for instance Lu-176 is left out of the integral, see Fig. 5. For the extended Høgdahl convention, in order to account for the activity produced by neutrons in this energy region, this extra integral area has to be taken into account and added to the normal Q ₀. For 1/v nuclides the cross section in the low energy region of the epithermal spectrum still follows the 1/v cross section distribution. In order to be equivalent with the Høgdahl convention for 1/v nuclides it is proposed in this work to add for non-1/v nuclides only the non-1/v area in the region between μkT _n and 0.55 eV. This extra part of Q ₀, which now depends on μ and T _n or on reactor type and neutron temperature, is called in this work $Q_{{\mu ,T_{\text{n}} }} \left( \alpha \right)$. For 1/v nuclides $Q_{{\mu ,T_{\text{n}} }} \left( \alpha \right)$ = 0. These Extended Q ₀′s, including $Q_{{\mu ,T_{\text{n}} }} \left( \alpha \right)$ for non-1/v nuclides, can be treated in the same way as normal Q ₀’s for the Høgdahl convention, including the adjustment for α with resonance energies using Eq. 5.

For 1/v nuclides this small part of the resonance integral, between μkT _n and 0.55 eV, $Q_{{1/\nu ,\mu ,T_{\text{n}} }} \left( \alpha \right)$ (Eq. 11), is included in the thermal activation when using the Høgdahl convention. $Q_{{1/\nu ,\mu ,T_{\text{n}} }} \left( \alpha \right)$ causes the differences in results between Høgdahl and the Westcott convention as found in Ref [7].

$$Q_{{1/v,T_{\text{n}} }} (\alpha ) = \frac{1}{{\sigma_{0} }}\int\limits_{{\mu kT_{n} }}^{{E_{\text{Cd}} }} {\sigma_{0} } \sqrt {\frac{{E_{0} }}{E}} \frac{1}{{E^{1 + \alpha } }}dE = \frac{{2\sqrt {E_{0} /\mu kT_{n} } }}{{(1 + 2\alpha )(\mu kT_{n} )^{\alpha } }} - \frac{{2\sqrt {E_{0} /E_{\text{Cd}} } }}{{(1 + 2\alpha )E_{\text{Cd}}^{\alpha } }}$$

(11)

which makes Q _{1/v,2.1,20 °C}(0) = 0.952, Q _{1/v,3.7,20 °C}(0) = 0.611, Q _{1/v,2.1,100 °C}(0) = 1.345, Q _{1/v,3.7,100 °C}(0) = 0.493.

The extended Q ₀’s are temperature dependent like $s_{0}$’s and make the extended Høgdahl convention nearly as accurate as the Westcott convention.

Results

The trapezoidal numerical integration method was used to calculate $Q_{0} (\alpha)$’s using Eq. 12 for all nuclides in the k ₀-database [11] based on the lin–lin cross-section data for (n,γ)-capture as found in ENDF/B-VII.1. From these results Q ₀’s and resonance energies were derived. The upper level, E1, of the integral 2 MeV was used.

$$Q_{0} = \frac{1}{{\sigma_{0} }}\int\limits_{{E_{\text{Cd}} }}^{E1} {\sigma (E)\frac{1}{E}{\text{d}}E}\quad {\text{and}}\quad Q_{0} (\alpha ) = \frac{1}{{\sigma_{0} }}\int\limits_{{E_{\text{Cd}} }}^{E1} {\sigma (E)\frac{1}{{E^{1 + \alpha } }}{\text{d}}E}$$

(12)

The effect of the differences in E _res and Q ₀ on the concentration (Eq. 5) is used to check the relevance of the differences. For this f and α parameters of a relevant irradiation channel were chosen since they affect the concentration results. This was done based on an empirical relation between f and α. This relation was established using the parameters of the three reactors used by De Corte and Simonits in the early years of the k ₀-method and is given in Fig. 3. The chosen parameters are α = 0.03 and f = 32.3. Based on the data in Fig. 3 the range of $\alpha$’s was chosen to be −0.03 to 0.37.

Effective resonance energies

The most appropriate method for determination of effective resonance energies was found to be to fit Eq. 5 directly by optimizing E _res to the integrated Q ₀(α) based on the ENDF/B VII.1 data file. An example is given in Fig. 6. A least squares fit for the $\alpha$’s between −0.03 and 0.2 was used.

Fig. 6

Q ₀(α) from ENDF/B VII.1 fitted using Eq. 5 for the determination of E _res and compared to data from the k ₀-database [11]

The determined resonance energies are compared to the data in the k ₀-database, see Fig. 7. The results from these calculations are comprised in Table 1 and compared to the k ₀-data file. The effect of the differences on the concentration determination is also given in Fig. 7.

Fig. 7

The ratio between the resonance energies from this work and the k ₀-database is shown in the left graph (Ce-140 is outside graph range) and the right hand graph shows the effect on the concentration for an irradiation in a channel with f = 32.3 and α = 0.03

Table 1 Effective resonance energies (in eV) based on ENDF/B-VII.1 data compared with k ₀-database [11]

A comparison between Q ₀’s from ENDF/B-VII.1 and the k ₀-database is made in Table 2 and in Fig. 8. In Fig. 8 also the effect on concentration is given.

Table 2 Q ₀’s based on integrated ENDF/B-VII.1 data compared with k ₀-database [11]

Fig. 8

The ratio between Q ₀ from this work and the k ₀-database is shown in the left graph and the right hand graph shows the effect on the concentration for an irradiation in a channel with f = 32.3 and α = 0.03

Q₀ for non 1/v nuclides

The epithermal neutrons with energies below the Cd cut-off energy contribute to the resonance integral significantly in case of resonances in this region. To evaluate to which extent resonances affect the integral in this region sub-Cd Q ₀’s are calculated. The integral limits chosen are 3.7kT _n with T _n = 20 °C and as upper limit the Cd cut-off energy 0.55 eV.

To visualize the results, this partial integral is plotted versus the regular Q ₀ in Fig. 9. The 1/v integral for this region is equal to 0.611, Eq. 11. The figure shows that only non-1/v nuclides, as expected, deviate from the 1/v integral. A thorough investigation of these sub Cd-Q ₀’s showed that only for Eu-151, Yb-168 and Lu-176 a significant effect can be expected.

In Table 3, the “extended” Q ₀’s [sub Cd-Q ₀ corrected for the 1/v contribution, Q _1/v,μ,Tn(α)] for these nuclides are tabulated. It must be noted that these extended Q ₀’s cannot be used for epithermal (Cd-covered) activation. For irradiation under Cd cover the tabulated “normal” Q ₀’s in Table 3 should be used.

Table 3 Extended Q ₀’s and effective resonance energies for Eu-151, Yb-168 and Lu-176

The effective resonance energies in Table 3 were determined using the fit procedure described above for each temperature. It was found that Eq. 5 fits the data very well (average deviation less than 1 %). From Fig. 10 one can conclude that only one resonance energy for all temperatures is needed per nuclide except for Eu-151 (μ = 2.1) and one extended Q ₀ is needed except for Lu-176 (μ = 3.7) because these show strong temperature dependence.

Fig. 9

Q ₀ (μ = 3.7, T _n = 20 °C) below the cut-off energy of Cd for all nuclides in the k ₀-database

Fig. 10

Q ₀’s for Eu-151, Yb-168 and Lu-176 and effective resonance energies for μ = 2.1 (light water) and 3.7 (heavy water and graphite) and different temperatures are given

Discussion

Effective resonance energy

The effective resonance energies ultimately used in the present k ₀-database [11] are weighted averages of all resonances in the cross section distribution as tabulated by Mughabghab [12, 13] and were determined by Jovanovic in the early eighties [5]. The approach of measuring effective resonance energies was developed in the same period [14] as well but only one measured Ē _res is used (Ru-96) in the present k ₀-nuclear database.

Recently new measurements were reported. Budak et al. [15] measured the resonance energies of the Gd-159 and Hf-179 target nuclides, showing good agreement with the adopted values. Arbocco et al. [16] measured “k ₀, Q ₀ and effective resonance energies for 37 isotopes” and determined 28 effective resonance energies using a new “α-vector” method. The results for Ē _res show reasonably to good comparison to the present adopted values except for the low Q ₀ (≤5) and good agreement for Q ₀’s of these nuclides.

Trkov compared the k ₀-database with an averaged E _res(α) determined using Eq. 2 with integration limits 0.55 eV to 2 MeV and Eq. 3 for $\alpha$’s between −0.1 and 0.1 based on recent cross section data [8]. Trkov reported differences of up 110 % (for Zr-94), the calculations from this work give similar results. In the present work the effective resonance energy were determined based on fitting Eq. (5) to numerically integrated $Q_{0} (\alpha )$’s for $\alpha$’s between −0.03 and 0.25. Methods based on the calculated E _res(α) fail if Q ₀ is very low and thus close to the 1/v cross section which is the case for 12 of the 101 nuclides investigated.

All effective resonance energies in the latest 2012 k ₀ data table [11] were already published in 1987 [1], except for some of the “non-1/v” nuclides (Lu-176, Eu-151 and Yb-168). At that time no data was given for S-36, Ca-46, Os-184 and Hg-204 because the necessary cross section data was available but not trustworthy. Even in the latest nuclear data table ENDF/B-VII.1 the data for these nuclides are still not useful. These data seem to be only relevant to neutron activation analysts and therefor there is a lack of funding and/or interest of nuclear scientists. The Q ₀’s for these nuclides were never measured because their values are too low for an accurate assessment. The adopted values of Q ₀ are all less than 2. This also indicates that the relevance of the resonance energy of these nuclides is not high, as illustrated in Fig. 7. Because Q ₀’s are given for these nuclides one can raise the question which Ē _res to use. In literature some state a value of 1 eV and others propose 1000 eV. Verheijcke [17] used an empirical equation based on a general trend that between Ē _res and I₀. However since there are no data we propose in this work a correction for Q ₀(α) for these four nuclides using Ē _res is 1 eV.

Q ₀’s

Most of the Q ₀’s in the k₀-library were measured (55 %). The rest were only calculated from nuclear data or literature present at that time. These nuclides often got a remark “redetermination desirable”, no uncertainty is given and this is still the case in the present k ₀-data library. The aim now was to see whether there is any change or improvement in the nuclear data.

From Fig. 7 one has to conclude that the differences in Ē _res are not giving a significant effect on the concentration between old and new data. The significant differences in Q ₀ (effect >5 % in concentration for a channel with f = 32 and α = 0.03) are seen for 19 nuclides of which 10 are from measured Q ₀’s, see Fig. 8. The most significant effects of differences in Q ₀’s are seen for four of the Sn-isotopes and for Zr-96 which is a monitor for α determination.

Q ₀’s and effective resonance energies for non-1/v nuclides

s ₀ data for Lu-176 were calculated by Westcott at the end of the fifties and although the cross section data used by him was based on only two resonances, those data were very similar to the data in ENDF/B-VII.1. The comparison of his s ₀ data with those obtained by converting the Q ₀’s of this work to $s_{0}$’s using Eq. 10 is good (Table 4). The s ₀ of Yb-168 was measured by De Corte in the beginning of the eighties and it is significantly different from that calculated from the present nuclear data [2]. The s ₀ calculated from the Q ₀ of Eu-151 seems to be much lower than that of Kim and Gryntakis in 1975 [18].

Table 4 Comparison between $s_{0}$’s from literature and $s_{0}$’s calculated from Q ₀’s from this work for Lu-176, Eu-151, Yb-168

The effect on the concentration of the temperature dependence of the resonance energy of Eu-151 is small, see Table 3; however the effect of the temperature for the extended Q ₀ of Lu is significant. The effect of reactor type or μ is significant for both mentioned parameters.

The new extended Q ₀’s for Lu-176, Eu-151 and Yb-168, are now for the first time calculated for use in the Extended Høgdahl convention and can now be used for gaining experience about the quality of these values.

Conclusion

Adopting the effective resonance energies calculated in this work using ENDF/B-VII.1 data will have only a very small effect on the analysis results. On the other hand, the newly calculated Q ₀’s show some large differences relative to those currently in use and one can conclude that there might be some significant effects on the concentrations measured by the k ₀ method if the irradiation conditions are significantly different from the irradiation conditions used for the determination of the $k_{0}$’s. The difference can be larger than a few % for some 20 nuclides.

“Extended” Q ₀’s were calculated for the first time for use in the new Extended Høgdahl convention. With these new Q ₀’s it should be possible to perform k ₀-NAA for Eu, Yb and Lu with no extra effort and with accuracy comparable to that achievable when using 1/v nuclides.