Properties of Solution Set of Tensor Complementarity Problem

Abstract

In this paper, a new subclass of tensors is introduced and it is proved that this class of new tensors can be defined by the feasible region of the corresponding tensor complementarity problem. Furthermore, the boundedness of solution set of the tensor complementarity problem is equivalent to the uniqueness of solution for such a problem with zero vector. For the tensor complementarity problem with a strictly semi-positive tensor, we proved the global upper bounds of its solution set. In particular, such upper bounds are closely associated with the smallest Pareto eigenvalue of such a tensor.

1 Introduction

The nonlinear complementarity problem was introduced by Cottle in his Ph.D. thesis in 1964. In the last decades, many mathematical workers have concentrated a lot of their energy and attention on this classical problem because of a multitude of interesting connections to numerous disciplines and a wide range of important applications in operational research, applied science and technology such as optimization, economic equilibrium problems, contact mechanics problems, structural mechanics problem, nonlinear obstacle problems, traffic equilibrium problems, and discrete-time optimal control. For more details, see [1–4] and references therein. Well over a thousand articles and several books have been published on this classical subject, which has developed into a well-established and fruitful discipline in the field of mathematical programming.

The linear complementarity problem is a special case of nonlinear complementarity problem. It is well known that the linear complementarity problem has wide and important applications in engineering and economics (Cottle et al. [5]; Han et al. [3]). Cottle and Dantzig [6] studied the existence of solution of the linear complementarity problem with the help of the structure of the matrix. Some relationships between the uniqueness and existence of solution of the linear complementarity problem and semi-monotonicity of the matrices were showed by Eaves [7], Karamardian [8], Pang [9, 10] and Gowda [11], respectively. Cottle [12] studied some classes of the complete matrix (a matrix is called complete iff the matrix and all its principal submatrices are the same class of matrix) and obtained that each complete matrix that the linear complementarity problem has a solution is a strictly semi-monotone matrix.

The tensor complementarity problem, as a special type of nonlinear complementarity problems, is a new topic emerged from the tensor community, inspired by the growing research on structured tensors. At the same time, the tensor complementarity problem as a natural extension of the linear complementarity problem seems to have similar properties to the problem and to have its particular and nice properties other than ones of the classical linear complementarity problem. So how to obtain the nice properties and their applications of the tensor complementarity problem will be very interesting by means of the special structure of higher-order tensor (hypermatrix).

The notion of the tensor complementarity problem is used firstly by Song and Qi [13], and they showed the existence of solution for such a problem with some classes of structured tensors. In particular, they showed that the nonnegative tensor complementarity problem has a solution if and only if all principal diagonal entries of such a tensor are positive. Che et al. [14] showed the existence of solution for the symmetric positive definite tensor complementarity problem and copositive tensors. Luo et al. [15] studied the sparsest solutions to tensor complementarity problems. Song and Qi [16] studied the solution of the semi-positive tensor complementarity problem and obtained that a symmetric tensor is (strictly) semi-positive if and only if it is (strictly) copositive.

In this paper, we study the properties of solution set of the tensor complementarity problem by means of the special structure of tensors. We first introduce a new subclass of tensors and give its two equivalent definitions by means of the tensor complementarity problem. Subsequently, it is proved that each tensor that the tensor complementarity problem has a solution is a subclass of such tensors. Furthermore, it be proved that the solution set of the tensor complementarity problem is bounded if and only if such a problem with zero vector has unique solution. We finally present the global upper bounds for solution of the tensor complementarity problem with a strictly semi-positive tensor with the help of the smallest Pareto eigenvalue of such a tensor.

2 Preliminaries

Throughout this paper, we use small letters $x, y, v, \alpha , \ldots$ for scalars, small bold letters $\mathbf{x}, \mathbf{y}, \ldots$ for vectors, capital letters $A, B, \ldots$ for matrices, bold capital letters $\mathbf{A}, \mathbf{B}, \ldots$ for tensors. All the tensors discussed in this paper are real. Let $I_n := \{ 1,2, \ldots , n \}$, and ${\mathbb {R}}^n:=\{\mathbf{x}=(x_1, x_2,\ldots , x_n)^\top : x_i\in {\mathbb {R}}, i\in I_n\}$, ${\mathbb {R}}^n_{+}:=\{\mathbf{x}\in {\mathbb {R}}^n:\mathbf{x}\ge \mathbf{0}\}$, ${ {\mathbb {R}}}^n_{-}:=\{\mathbf{x}\in {\mathbb {R}}^n: \mathbf{x}\le \mathbf{0}\}$, ${\mathbb {R}}^n_{++}:=\{\mathbf{x}\in {\mathbb {R}}^n:\mathbf{x}>\mathbf{0}\}$, where ${\mathbb {R}}$ is the set of real numbers, $\mathbf{x}^\top$ is the transpose of a vector $\mathbf{x}$, and $\mathbf{x}\ge \mathbf{0}$ ($\mathbf{x}>\mathbf{0}$, $\mathbf{x}\le \mathbf{0}$) means $x_i\ge 0$ ($x_i>0$, $x_i\le 0$) for all $i\in I_n$.

Let F be a nonlinear function from ${ {\mathbb {R}}}^n$ into itself. The nonlinear complementarity problem is to find a vector $\mathbf{x} \in { {\mathbb {R}}}^n$ such that

$$\begin{aligned} \mathbf{x} \ge \mathbf{0}, F(\mathbf{x}) \ge \mathbf{0}, \text{ and } \mathbf{x}^\top F(\mathbf{x}) = 0, \end{aligned}$$

or to show that no such vector exists. Let $A = (a_{ij})$ be an $n \times n$ real matrix and $F(\mathbf{x})=\mathbf{q} + A\mathbf{x}$. Then such a nonlinear complementarity problem is called the linear complementarity problem, denoted by LCP$(A, \mathbf{q})$, i.e., to find $\mathbf{x} \in {\mathbb {R}}^n$ such that

$$\begin{aligned} \mathbf{x} \ge \mathbf{0}, \mathbf{q} + A\mathbf{x} \ge \mathbf{0}, \text{ and } {} \mathbf{x}^\top (\mathbf{q} + A\mathbf{x}) = 0, \end{aligned}$$

or to show that no such vector exists.

In 2005, Qi [17] introduced the concept of positive (semi-)definite symmetric tensors. A real mth-order n-dimensional tensor (hypermatrix) $\mathbf{A} = (a_{i_1\cdots i_m})$ is a multi-array of real entries $a_{i_1\cdots i_m}$, where $i_j \in I_n$ for $j \in I_m$. If the entries $a_{i_1\cdots i_m}$ of a tensor $\mathbf{A}$ are invariant under any permutation of their indices, then $\mathbf{A}$ is called a symmetric tensor. We denote the zero tensor by $\mathbf{O}$. Let $\mathbf{x} \in {\mathbb {R}}^n$. Then $\mathbf{A} \mathbf{x}^{m-1}$ is a vector in ${\mathbb {R}}^n$ with its ith component as

$$\begin{aligned} \left( \mathbf{A} \mathbf{x}^{m-1}\right) _i: = \sum _{i_2, \ldots , i_m=1}^n a_{ii_2\cdots i_m}x_{i_2}\cdots x_{i_m} \end{aligned}$$

for $i \in I_n$. Then $\mathbf{A} \mathbf{x}^m$ is a homogeneous polynomial of degree m, defined by

$$\begin{aligned} \mathbf{A} \mathbf{x}^m:= \mathbf{x}^\top (\mathbf{A} \mathbf{x}^{m-1})= \sum _{i_1,\ldots , i_m=1}^n a_{i_1\cdots i_m}x_{i_1}\cdots x_{i_m}. \end{aligned}$$

A tensor $\mathbf{A}$ is called positive semi-definite if for any vector $\mathbf{x} \in {\mathbb {R}}^n$ and an even number m, $\mathbf{A} \mathbf{x}^m \ge 0$, and is called positive definite if for any nonzero vector $\mathbf{x} \in {\mathbb {R}}^n$ and an even number m, $\mathbf{A} \mathbf{x}^m > 0$. Recently, miscellaneous structured tensors are widely studied, for example Zhang et al. [18] and Ding et al. [19] for M-tensors, Song and Qi [20] for P–($P_0$)tensors and B–($B_0$)tensors, Qi and Song [21] for B–($B_0$)tensors, Song and Qi [22] for infinite and finite dimensional Hilbert tensors, Song and Qi [23] for E-eigenvalues of weakly symmetric nonnegative tensors and references therein.

Definition 2.1

Let $\mathbf{A} = (a_{i_1\cdots i_m})$ be a real mth-order n-dimensional tensor.

• (i) The tensor complementarity problem, denoted by TCP$(\mathbf{A},\mathbf{q})$, is to find $\mathbf{x} \in {\mathbb {R}}^n$ such that

  $$\begin{aligned}&\mathbf{x} \ge \mathbf{0} \end{aligned}$$

  (1)
  $$\begin{aligned}&\mathbf{q} + \mathbf{A}{} \mathbf{x}^{m-1} \ge \mathbf{0} \end{aligned}$$

  (2)
  $$\begin{aligned}&\mathbf{x}^\top (\mathbf{q} + \mathbf{A}{} \mathbf{x}^{m-1}) = 0 \end{aligned}$$

  (3)

  or to show that no such vector exists.

• (ii) A vector $\mathbf{x}$ is said to be (strictly) feasible iff $\mathbf{x}$ satisfies the inequality (1) and (strict) inequality (2).

• (iii) The TCP$(\mathbf{A}, \mathbf{q})$ is said to be (strictly) feasible iff a (strictly) feasible vector exists.

• (iv) The set of all feasible vector of the TCP$(\mathbf{A}, \mathbf{q})$ is said to be its feasible region.

• (v) The TCP$(\mathbf{A}, \mathbf{q})$ is said to be solvable iff there is a feasible vector satisfying the Eq. (3).

• (vi) $\mathbf{A}$ is called a Q -tensor [13] iff the TCP$(\mathbf{A}, \mathbf{q})$ is solvable for all $\mathbf{q}\in {\mathbb {R}}^n$.

• (vii) $\mathbf{A}$ is called a R $_0$-tensor [13] iff the TCP$(\mathbf{A}, \mathbf{0})$ has unique solution.

• (viii) $\mathbf{A}$ is called a R -tensor [13] iff it is a $R_0$-tensor and the TCP$(\mathbf{A}, \mathbf{q})$ has unique solution for $\mathbf{q}=(1,1,\ldots ,1)^\top$.

Let $\mathbf{w}=\mathbf{q} + \mathbf{A}{} \mathbf{x}^{m-1}$. Then a feasible vector $\mathbf{x}$ of the TCP$(\mathbf{A}, \mathbf{q})$ is its solution if and only if

$$\begin{aligned} x_iw_i=x_iq_i+x_i\left( \mathbf{A}{} \mathbf{x}^{m-1}\right) _i=0 \text{ for } \text{ all } i\in I_n. \end{aligned}$$

(4)

Recently, Song and Qi [13] extended the concepts of (strictly) semi-monotone matrices to (strictly) semi-positive tensors.

Definition 2.2

Let $\mathbf{A} = (a_{i_1\cdots i_m})$ be a real mth-order n-dimensional symmetric tensor. $\mathbf{A}$ is said to be

• (i) semi-positive iff for each $\mathbf{x}\ge 0$ and $\mathbf{x}\ne \mathbf{0}$, there exists an index $k\in I_n$ such that

  $$\begin{aligned} x_k>0 \text{ and } \left( \mathbf{A} \mathbf{x}^{m-1}\right) _k\ge 0; \end{aligned}$$

• (ii) strictly semi-positive iff for each $\mathbf{x}\ge \mathbf{0}$ and $\mathbf{x}\ne \mathbf{0}$, there exists an index $k\in I_n$ such that

  $$\begin{aligned}x_k>0 \text{ and } \left( \mathbf{A} \mathbf{x}^{m-1}\right) _k>0;\end{aligned}$$

• (iii) a P -tensor (Song and Qi [20]) iff for each $\mathbf{x}$ in ${\mathbb {R}}^n$ and $\mathbf{x}\ne \mathbf{0}$, there exists $i \in I_n$ such that

  $$\begin{aligned} x_i \left( \mathbf{A} \mathbf{x}^{m-1}\right) _i > 0; \end{aligned}$$

• (iv) a P $_0$-tensor (Song and Qi [20]) iff for every $\mathbf{x}$ in ${\mathbb {R}}^n$ and $\mathbf{x}\ne \mathbf{0}$,, there exists $i \in I_n$ such that $x_i \not = 0$ and

  $$\begin{aligned} x_i \left( \mathbf{A} \mathbf{x}^{m-1}\right) _i \ge 0; \end{aligned}$$

• (v) copositive (Qi [24]) if $\mathbf{A}\mathbf{x}^m\ge 0$ for all $\mathbf{x}\in {\mathbb {R}}^n_+$;

• (vi) strictly copositive (Qi [24]) if $\mathbf{A}{} \mathbf{x}^m>0$ for all $\mathbf{x}\in {\mathbb {R}}^n_+\setminus \{\mathbf{0}\}$.

Lemma 2.1

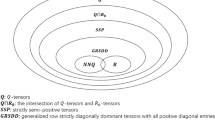
(Song and Qi [13, Corollary 3.3,Theorem 3.4]) Each strictly semi-positive tensor must be a R-tensor, and each R-tensor must be a Q-tensor. A semi-positive $R_0$-tensor is a Q-tensor.

Song and Qi [25] introduced the concept of Pareto H-(Z-)eigenvalue and used it to portray the (strictly) copositive tensor. For the number and computation of Pareto H-(Z-)eigenvalue see Ling et al. [26] and Chen et al. [27].

Definition 2.3

Let $\mathbf{A} = (a_{i_1\cdots i_m})$ be a real mth-order n-dimensional tensor. A real number $\mu$ is said to be

• (i) Pareto H-eigenvalue of $\mathbf{A}$ iff there is a nonzero vector $\mathbf{x}\in {\mathbb {R}}^n$ satisfying

  $$\begin{aligned} \mathbf{A}{} \mathbf{x}^m=\mu \mathbf{x}^\top \mathbf{x}^{[m-1]}, \ \mathbf{A}{} \mathbf{x}^{m-1}-\mu \mathbf{x}^{[m-1]} \ge \mathbf{0},\ \mathbf{x}\ge \mathbf{0}, \end{aligned}$$

  (5)

  where $\mathbf{x}^{[m-1]}=(x_1^{m-1},x_2^{m-1},\ldots ,x_n^{m-1})^\top$.

• (ii) Pareto Z-eigenvalue of $\mathbf{A}$ iff there is a nonzero vector $\mathbf{x}\in {\mathbb {R}}^n$ satisfying

  $$\begin{aligned} \mathbf{A}{} \mathbf{x}^m=\mu (\mathbf{x}^\top \mathbf{x})^{\frac{m}{2}}, \ \mathbf{A}{} \mathbf{x}^{m-1}-\mu (\mathbf{x}^\top \mathbf{x})^{\frac{m}{2}-1}{} \mathbf{x} \ge \mathbf{0},\ \mathbf{x}\ge \mathbf{0}. \end{aligned}$$

  (6)

Lemma 2.2

(Song and Qi [25, Theorem3.1,3.3,Corollary3.5]) Let a symmetric tensor $\mathbf{A}$ be strictly copositive. Then

• (i) $\mathbf{A}$ has at least one Pareto H-eigenvalue $\lambda (\mathbf{A}):=\mathop {\mathop {\min }\nolimits _{\mathbf{x}\ge 0}}\nolimits _{\Vert \mathbf{x}\Vert _{m=1}} \mathbf{A}{} \mathbf{x}^m$ and

  $$\begin{aligned} \lambda (\mathbf{A})=\min \{\lambda : \lambda \text{ is } \text{ Pareto } \text{ H-eigenvalue } \text{ of } {} \mathbf{A}\}>0, \end{aligned}$$

  (7)

  where $\Vert \mathbf{x}\Vert _m=\left( \sum \nolimits _{i=1}^{n}|x_i|^m\right) ^{\frac{1}{m}}$;

• (ii) $\mathbf{A}$ has at least one Pareto Z-eigenvalue $\mu (\mathbf{A}):=\mathop {\mathop {\min }\limits _{\mathbf{x}\ge 0}}\limits _{\Vert \mathbf{x}\Vert _2=1 }\mathbf{A}{} \mathbf{x}^m$ and

  $$\begin{aligned} \mu (\mathbf{A})=\min \{\mu : \mu \text{ is } \text{ Pareto } \text{ Z-eigenvalue } \text{ of } \mathbf{A}\}>0. \end{aligned}$$

  (8)

3 Solution of the TCP$(\mathbf{A}, \mathbf{q})$

3.1 S-tensor and Feasible Solution of the TCP$(\mathbf{A}, \mathbf{q})$

We first introduce the concept of the S-tensor, which is a natural extension of S-matrix [5].

Definition 3.1

Let $\mathbf{A} = (a_{i_1\cdots i_m})$ be a real mth-order n-dimensional tensor. $\mathbf{A}$ is said to be a

• (i) S -tensor iff the system

  $$\begin{aligned} \mathbf{A}{} \mathbf{x}^{m-1}>\mathbf{0}, \ \mathbf{x}>\mathbf{0} \end{aligned}$$

  has a solution;

• (ii) S $_0$-tensor iff the system

  $$\begin{aligned} \mathbf{A}{} \mathbf{x}^{m-1}\ge \mathbf{0}, \ \mathbf{x}\ge \mathbf{0},\ \mathbf{x}\ne \mathbf{0} \end{aligned}$$

  has a solution.

Proposition 3.1

Let $\mathbf{A}$ be a real mth-order n-dimensional tensor. Then $\mathbf{A}$ is a S-tensor if and only if the system

$$\begin{aligned} \mathbf{A}{} \mathbf{x}^{m-1}>\mathbf{0}, \ \mathbf{x}\ge \mathbf{0} \end{aligned}$$

(9)

has a solution.

Proof

It follows from Definition 3.1 that the necessity is obvious. Now we show the sufficiency. In fact, if there exists $\mathbf{y}$ such that

$$\begin{aligned} \mathbf{A}{} \mathbf{y}^{m-1}>\mathbf{0}, \ \mathbf{y}\ge \mathbf{0}. \end{aligned}$$

Clearly, $\mathbf{y}\ne \mathbf{0}$. Since $\mathbf{A}{} \mathbf{y}^{m-1}$ is continuous on $\mathbf{y}$, it follows that

$$\begin{aligned} \mathbf{A}(\mathbf{y}+t\mathbf{e})^{m-1}>\mathbf{0} \end{aligned}$$

for some small enough $t>0$, where $\mathbf{e}=(1,1,\ldots ,1)^\top$. It is obvious that $\mathbf{y}+t\mathbf{e}>0$. So $\mathbf{A}$ is an S-tensor. $\square$

Now, by means of the solution of the TCP$(\mathbf{A},\mathbf{q})$, we may give the following equivalent definition of S-tensor.

Theorem 3.1

Let $\mathbf{A}$ be a real mth-order n-dimensional tensor. Then $\mathbf{A}$ is a S-tensor if and only if the TCP $(\mathbf{A}, \mathbf{q})$ is feasible for all $\mathbf{q}\in {\mathbb {R}}^n$. Meanwhile, each Q-tensor must be an S-tensor.

Proof

Let $\mathbf{A}$ is a S-tensor. Then it follows from Definition 3.1 of S-tensor that there exists $\mathbf{y}$ such that

$$\begin{aligned} \mathbf{A}{} \mathbf{y}^{m-1}>\mathbf{0}, \ \mathbf{y}>\mathbf{0}. \end{aligned}$$

So for each $\mathbf{q}\in {\mathbb {R}}^n$, there exists some scalar $t>0$ such that

$$\begin{aligned} \mathbf{A}(\root m-1 \of {t}{} \mathbf{y})^{m-1}=t\mathbf{A}{} \mathbf{y}^{m-1}\ge -\mathbf{q}. \end{aligned}$$

Clearly, $\root m-1 \of {t}{} \mathbf{y}> \mathbf{0}$, and so $\root m-1 \of {t}\mathbf{y}$ is a feasible vector of the TCP$(\mathbf{A},\mathbf{q})$.

On the other hand, if the TCP$(\mathbf{A}, \mathbf{q})$ is feasible for all $\mathbf{q}\in {\mathbb {R}}^n$, we take $\mathbf{q}<\mathbf{0}$. Let $\mathbf{z}$ is a feasible solution of the TCP$(\mathbf{A},\mathbf{q})$. Then

$$\begin{aligned} \mathbf{z}\ge \mathbf{0} \text{ and } {} \mathbf{q} + \mathbf{A}{} \mathbf{z}^{m-1} \ge \mathbf{0}, \end{aligned}$$

and hence

$$\begin{aligned} \mathbf{A}{} \mathbf{z}^{m-1} \ge -\mathbf{q} > \mathbf{0}. \end{aligned}$$

So $\mathbf{z}$ is a solution of the system (9). It follows from Proposition 3.1 that $\mathbf{A}$ is an S-tensor. $\square$

3.2 $R_0$-Tensor and Boundedness of Solution Set of the TCP$(\mathbf{A},\mathbf{q})$

Theorem 3.2

Let $\mathbf{A}$ be a real mth-order n-dimensional tensor. Then the following three conclusions are equivalent:

• (i) $\mathbf{A}$ is $R_0$-tensor;

• (ii) For each $\mathbf{q}\in { {\mathbb {R}}}^n$ and each $t, s\in { {\mathbb {R}}}$ with $t>0$, the set

  $$\begin{aligned} \varGamma (\mathbf{q},s,t)=\{\mathbf{x}\ge \mathbf{0}: \mathbf{q}+\mathbf{A}{} \mathbf{x}^{m-1}\ge \mathbf{0} \text{ and } {} \mathbf{x}^\top \mathbf{q}+t\mathbf{A}{} \mathbf{x}^m\le s\} \end{aligned}$$

  is bounded;

• (iii) For each $\mathbf{q}\in {\mathbb {R}}^n$, the solution set of the TCP $(\mathbf{A},\mathbf{q})$ is bounded.

Proof

(i) $\Rightarrow$ (ii). Suppose that there exist $\mathbf{q}'\in {\mathbb {R}}^n$, $s'\in {\mathbb {R}}$ and $t'>0$ such that the set $\varGamma (\mathbf{q}',s',t')$ is not bounded. Let a sequence $\{\mathbf{x}^k\}\subset \varGamma (\mathbf{q}',s',t')$ be an unbounded sequence. Then the sequence $\{\frac{\mathbf{x}^k}{\Vert \mathbf{x}^k\Vert }\}$ is bounded, and so there exists $\mathbf{x}'\in { {\mathbb {R}}}^n$ and a subsequence $\{\frac{\mathbf{x}^{k_j}}{\Vert \mathbf{x}^{k_j}\Vert }\}$ such that

$$\begin{aligned} \lim _{j\rightarrow \infty }\frac{\mathbf{x}^{k_j}}{\Vert \mathbf{x}^{k_j}\Vert }=\mathbf{x}'\ne \mathbf{0} \text{ and } \lim _{j\rightarrow \infty }\Vert \mathbf{x}^{k_j}\Vert =\infty . \end{aligned}$$

From the definition of $\varGamma (\mathbf{q}',s',t')$, it follows that

$$\begin{aligned} \frac{\mathbf{q}'}{\Vert \mathbf{x}^{k_j}\Vert ^{m-1}}+\mathbf{A}(\frac{\mathbf{x}^{k_j}}{\Vert \mathbf{x}^{k_j}\Vert })^{m-1}\ge \mathbf{0} \text{ and } \frac{\mathbf{x}^\top \mathbf{q}'}{\Vert \mathbf{x}^{k_j}\Vert ^m}+t'{} \mathbf{A}(\frac{\mathbf{x}^{k_j}}{\Vert \mathbf{x}^{k_j}\Vert })^m\le \frac{s'}{\Vert \mathbf{x}^{k_j}\Vert ^m}, \end{aligned}$$

(10)

and hence, by the continuity of $\mathbf{A}{} \mathbf{x}^m$ and $\mathbf{A}\mathbf{x}^{m-1}$, let $j\rightarrow \infty$,

$$\begin{aligned} \mathbf{A}(\mathbf{x}')^{m-1}\ge \mathbf{0} \text{ and } {} \mathbf{A}(\mathbf{x}')^m\le 0. \end{aligned}$$

Since $\mathbf{x}'\ge \mathbf{0}$, we have

$$\begin{aligned} \mathbf{A}(\mathbf{x}')^m=(\mathbf{x}')^\top \mathbf{A}(\mathbf{x}')^{m-1}\ge 0. \end{aligned}$$

Thus, $\mathbf{A}(\mathbf{x}')^m=0$, and hence, $\mathbf{x}'$ is a nonzero solution of the TCP$(\mathbf{A},\mathbf{0})$. This contradicts the assumption that $\mathbf{A}$ is $R_0$-tensor.

(ii) $\Rightarrow$ (iii). It follows from the definition of $\varGamma (\mathbf{q},s,t)$ that

$$\begin{aligned} \varGamma (\mathbf{q},0,1)=\{\mathbf{x}\ge \mathbf{0}: \mathbf{q}+\mathbf{A}\mathbf{x}^{m-1}\ge \mathbf{0} \text{ and } {} \mathbf{x}^\top (\mathbf{q}+\mathbf{A}\mathbf{x}^{m-1})= 0\}. \end{aligned}$$

That is, $\varGamma (\mathbf{q},0,1)$ is the solution set of the TCP$(\mathbf{A},\mathbf{q})$. So the conclusion follows.

(iii) $\Rightarrow$ (i). Suppose $\mathbf{A}$ is not $R_0$-tensor. Then the TCP$(\mathbf{A},\mathbf{0})$ has a nonzero solution $\mathbf{x}^*$, and so $\mathbf{x}^*\in \varGamma (\mathbf{0},0,1)$. Since $\mathbf{x}^*\ne \mathbf{0}$, $\tau \mathbf{x}^*\in \varGamma (\mathbf{0},0,1)$ for all $\tau >0$. Therefore, the set $\varGamma (\mathbf{0},0,1)$ is not bounded. This contradicts the assumption (iii). So $\mathbf{A}$ is $R_0$-tensor. $\square$

It is known that each semi-positive tensor is an $R_0$-tensor and each $P_0$-tensor is a semi-positive tensor (Song and Qi [13]). The following conclusions are obvious.

Corollary 3.1

Let $\mathbf{A}$ be a semi-positive tensor. Then for each $\mathbf{q}\in {\mathbb {R}}^n$, the solution set of the TCP $(\mathbf{A},\mathbf{q})$ is bounded.

Corollary 3.2

Let $\mathbf{A}$ be a $P_0$-tensor. Then for each $\mathbf{q}\in {\mathbb {R}}^n$, the solution set of the TCP $(\mathbf{A},\mathbf{q})$ is bounded.

3.3 Solution of TCP$(\mathbf{A},\mathbf{q})$ with Strictly Semi-positive Tensors

In this section, we discuss the global upper bound for solution of TCP$(\mathbf{A},\mathbf{q})$ with strictly semi-positive and symmetric tensor $\mathbf{A}$. Song and Qi [16] showed the following conclusion about a symmetric tensor.

Lemma 3.1

(Song and Qi [16, Theorem 3.2,3.4]) Let $\mathbf{A} = (a_{i_1\cdots i_m})$ be a real mth-order n-dimensional tensor. Then a symmetric tensor $\mathbf{A}$ is strictly semi-positive if and only if it is strictly copositive. Moreover, the TCP $(\mathbf{A}, \mathbf{q})$ has a unique solution $\mathbf{0}$ for $\mathbf{q} \ge \mathbf{0}$ when $\mathbf{A}$ is strictly semi-positive.

Theorem 3.3

Let a symmetric tensor $\mathbf{A} = (a_{i_1\cdots i_m})$ be strictly semi-positive. If $\mathbf{x}$ is a solution of the TCP $(\mathbf{A}, \mathbf{q})$, then

$$\begin{aligned} \Vert \mathbf{x}\Vert _m^{m-1}\le \frac{\Vert (-\mathbf{q})_+\Vert _m}{\lambda (\mathbf{A})}, \end{aligned}$$

(11)

where $\lambda (\mathbf{A})$ is defined in Lemma 2.2 (i), $\Vert \mathbf{x}\Vert _m:=\left( \sum \limits _{i=1}^n|x_i|^m\right) ^{\frac{1}{m}}$ and $\mathbf{x}_+:=\left( \max \{x_1,0\},\max \{x_2,0\},\ldots ,\max \{x_n,0\}\right) ^\top$.

Proof

It follows from Lemmas 2.2 and 3.1 that

$$\begin{aligned} \lambda (\mathbf{A})=\min \{\lambda ; \lambda \text{ is } \text{ Pareto } \text{ H-eigenvalue } \text{ of } {} \mathbf{A}\}=\mathop {\mathop {\min }\limits _{\mathbf{y}\ge 0}}\limits _{\Vert \mathbf{y}\Vert _m=1}{} \mathbf{A}{} \mathbf{y}^m>0. \end{aligned}$$

(12)

Since $\mathbf{x}$ is a solution of the TCP$(\mathbf{A}, \mathbf{q})$, we have

$$\begin{aligned} \mathbf{A}{} \mathbf{x}^{m}-\mathbf{x}^\top (-\mathbf{q})=\mathbf{x}^\top (\mathbf{A}\mathbf{x}^{m-1}+\mathbf{q})=0,\ \mathbf{A}{} \mathbf{x}^{m-1}+\mathbf{q}\ge \mathbf{0} \text{ and } {} \mathbf{x}\ge \mathbf{0}. \end{aligned}$$

Suppose that $\mathbf{q}\ge \mathbf{0}.$ Then $\mathbf{x}=\mathbf{0}$ by Lemma 3.1, and the conclusion is obvious. So we may assume that $\mathbf{q}$ is not nonnegative; then, $\mathbf{x}\ne \mathbf{0}$ (suppose not, $\mathbf{x}=\mathbf{0}$, $\mathbf{A}{} \mathbf{x}^{m-1}+\mathbf{q}=\mathbf{q}$, which contradict to the fact that $\mathbf{A}{} \mathbf{x}^{m-1}+\mathbf{q}\ge \mathbf{0}$). Therefore, we have

$$\begin{aligned} \frac{\mathbf{A}{} \mathbf{x}^m}{\Vert \mathbf{x}\Vert ^m_m}=\mathbf{A}\left( \frac{\mathbf{x}}{\Vert \mathbf{x}\Vert _m}\right) ^m\ge \lambda (\mathbf{A})>0. \end{aligned}$$

Thus, we have

$$\begin{aligned} 0<\Vert \mathbf{x}\Vert ^m_m\lambda (\mathbf{A})\le \mathbf{A}{} \mathbf{x}^{m}=\mathbf{x}^\top (-\mathbf{q})\le \mathbf{x}^\top (-\mathbf{q})_+\le \Vert \mathbf{x}\Vert _m\Vert (-\mathbf{q})_+\Vert _m. \end{aligned}$$

The desired conclusion follows. $\square$

Theorem 3.4

Let a symmetric tensor $\mathbf{A} = (a_{i_1\cdots i_m})$ be strictly semi-positive. If $\mathbf{x}$ is a solution of the TCP $(\mathbf{A}, \mathbf{q})$, then

$$\begin{aligned} \Vert \mathbf{x}\Vert _2^{m-1}\le \frac{\Vert (-\mathbf{q})_+\Vert _2}{\mu (\mathbf{A})}, \end{aligned}$$

(13)

where $\mu (\mathbf{A})$ is defined in (8) in Lemma 2.2.

Proof

It follows from Lemma 2.2 and 3.1 that

$$\begin{aligned} \mu (\mathbf{A})=\min \{\mu : \mu \text{ is } \text{ Pareto } \text{ Z-eigenvalue } \text{ of } {} \mathbf{A}\}=\mathop {\mathop {\min }\limits _{\mathbf{y}\ge 0}}\limits _{\Vert \mathbf{y}\Vert _2=1}\mathbf{A}{} \mathbf{y}^m>0. \end{aligned}$$

(14)

Similarly, we also may assume that $\mathbf{q}$ is not nonnegative; then, $\mathbf{x}\ne \mathbf{0}$, and so

$$\begin{aligned} \frac{\mathbf{A}{} \mathbf{x}^m}{\Vert \mathbf{x}\Vert ^m_2}=\mathbf{A}\left( \frac{\mathbf{x}}{\Vert \mathbf{x}\Vert _2}\right) ^m\ge \mu (\mathbf{A})>0. \end{aligned}$$

Thus, we have

$$\begin{aligned} 0<\Vert \mathbf{x}\Vert ^m_2\mu (\mathbf{A})\le \mathbf{A}{} \mathbf{x}^{m}=\mathbf{x}^\top (-\mathbf{q})\le \mathbf{x}^\top (-\mathbf{q})_+\le \Vert \mathbf{x}\Vert _2\Vert (-\mathbf{q})_+\Vert _2. \end{aligned}$$

The desired conclusion follows. $\square$

We now introduce a quantity for a strictly semi-positive tensor $\mathbf{A}$.

$$\begin{aligned} \beta (\mathbf{A}):=\mathop {\mathop {\min }_{\mathbf{x}\ge 0}}\limits _{\Vert \mathbf{x} \Vert _\infty =1}\max _{i \in I_n}x_i(\mathbf{A}{} \mathbf{x}^{m-1})_i, \end{aligned}$$

(15)

where $\Vert \mathbf{x}\Vert _\infty :=\max \{|x_i|;i\in I_n\}$. It follows from the definition of strictly semi-positive tensor that $\beta (\mathbf{A})>0$. Then the following equation is well defined in Theorem 3.5.

Theorem 3.5

Let a real mth-order n-dimensional tensor $\mathbf{A} = (a_{i_1\cdots i_m})$ be strictly semi-positive. If $\mathbf{x}$ is a solution of the TCP $(\mathbf{A}, \mathbf{q})$, then

$$\begin{aligned} \Vert \mathbf{x}\Vert _\infty ^{m-1}\le \frac{\Vert (-\mathbf{q})_+\Vert _\infty }{\beta (\mathbf{A})}. \end{aligned}$$

(16)

Proof

Suppose that $\mathbf{q}\ge \mathbf{0}.$ Then $\mathbf{x}=\mathbf{0}$ by Lemma 3.1, and the conclusion is obvious. So we may assume that $\mathbf{q}$ is not nonnegative, and similarly to the proof technique of Theorem 3.3, we have $\mathbf{0}\le \mathbf{x}\ne \mathbf{0}$. It follows from the definition of $\beta (\mathbf{A})$ and (4) that

$$\begin{aligned} 0<\Vert \mathbf{x}\Vert ^m_\infty \beta (\mathbf{A})\le & {} \max \limits _{i \in I_n}x_i(\mathbf{A}{} \mathbf{x}^{m-1})_i = \max \limits _{i \in I_n}x_i(-\mathbf {q})_i\\= & {} \max \limits _{i \in I_n}x_i((-\mathbf {q})_+)_i\le \Vert x\Vert _\infty \Vert (-\mathbf {q})_+\Vert _\infty . \end{aligned}$$

The desired conclusion follows. $\square$

It is well known that the nonlinear complementarity problem with pseudo-monotone and continuous function F has a solution if it has a strictly feasible point $x^*$ (i.e., $\mathbf{x}^*\ge 0,\ F(\mathbf{x}^*)>0$) ([3, Theorem 2.3.11]). A function F from ${\mathbb {R}}^n_+$ into itself is called pseudo-monotone iff for all vectors $\mathbf{x},\mathbf{y} \in {\mathbb {R}}^n_+$,

$$\begin{aligned} (\mathbf{x} -\mathbf{y} )^\top F(\mathbf{y}) \ge 0\ \Rightarrow \ ( \mathbf{x} -\mathbf{y} )^\top F(\mathbf{x})\ge 0. \end{aligned}$$

Now we give an example to certify the function F deduced by a strictly semi-positive tensor is not pseudo-monotone. However, the corresponding nonlinear complementarity problem has a solution by Lemma 2.1.

Example 3.1

Let $\mathbf{A} = (a_{i_1i_2i_3}) \in T_{3, 2}$ and $a_{111}=1$, $a_{122}=1$, $a_{211}=1$, $a_{221}=-2$, $a_{222}=1$ and all other $a_{i_1i_2i_3}=0$. Then

$$\begin{aligned} \mathbf{A} \mathbf{x}^2=\left( \begin{array}{ll}x_1^2&{}+x_2^2\\ x_1^2&{}-2x_1x_2+x_2^2\end{array}\right) . \end{aligned}$$

Clearly, $\mathbf{A}$ is strictly semi-positive, and so it is a Q-tensor.

Let $F(\mathbf{x})=\mathbf{A}{} \mathbf{x}^{2}+\mathbf{q}$ for $\mathbf{q}=(-\frac{3}{2},-\frac{1}{2})^\top$. Then F is not pseudo-monotone. In fact,

$$\begin{aligned} F(\mathbf{x})=\mathbf{A} \mathbf{x}^2+\mathbf{q}=\left( \begin{array}{ll}x_1^2&{}+x_2^2-\frac{3}{2}\\ (x_1^2&{}-x_2)^2-\frac{1}{2}\end{array}\right) . \end{aligned}$$

Take $\mathbf{x}=(1,0)^\top$ and $\mathbf{y}=(1,1)^\top$. Then

$$\begin{aligned} \mathbf{x}-\mathbf{y}=\left( \begin{array}{ll}0\\ -1\end{array}\right) ,\ F(\mathbf{x})=\left( \begin{array}{ll}-\frac{1}{2}\\ \frac{1}{2}\end{array}\right) \text{ and } F(\mathbf{y})=\left( \begin{array}{ll}\frac{1}{2}\\ -\frac{1}{2}\end{array}\right) . \end{aligned}$$

Clearly, we have

$$\begin{aligned} (\mathbf{x}-\mathbf{y})^\top F(\mathbf{y})=0\times \frac{1}{2}-1 \times (- \frac{1}{2})>0. \end{aligned}$$

However,

$$\begin{aligned} (\mathbf{x}-\mathbf{y})^\top F(\mathbf{x})=0\times (-\frac{1}{2})-1\times \frac{1}{2}<0, \end{aligned}$$

and hence F is not pseudo-monotone. $\square$

4 Conclusions

In this paper, we discussed the equivalent relationships between the feasible solution of the tensor complementarity problem and a class of tensors. It is showed that the solution set of the tensor complementarity problem is bounded if and only if such a complementarity problem with zero vector has unique solution. By means of two constants with respect to the smallest Pareto eigenvalue of tensor, we proved the global upper bounds for solution of the tensor complementarity problem with a strictly semi-positive and symmetric tensor. A new quantity is introduced for a strictly semi-positive tensor. For a strictly semi-positive tensor (not symmetric), the global upper bounds for such a tensor complementarity problem are proved by means of such a new quantity.