Predictability and Scaling in a BTW Sandpile on a Self-similar Lattice

Abstract

This paper explores the predictability of a Bak–Tang–Wiesenfeld isotropic sandpile on a self-similar lattice, introducing an algorithm which predicts the occurrence of target events when the stress in the system crosses a critical level. The model exhibits the self-organized critical dynamics characterized by the power-law segment of the size-frequency event distribution extended up to the sizes $\sim L^{\beta }$, $\beta = \log _3 5$, where L is the lattice length. We establish numerically that there are large events which are observed only in a super-critical state and, therefore, predicted efficiently. Their sizes fill in the interval with the left endpoint scaled as $L^{\alpha }$ and located to the right from the power-law segment: $\alpha \approx 2.24 > \beta$. The right endpoint scaled as $L^3$ represents the largest event in the model. The mechanism of predictability observed with isotropic sandpiles is shown here for the first time.

1 Introduction

Self-organized criticality (SOC) is prescribed to various observed systems and processes [21, 37]. A system is said to be self-organized and critical if its stationary state is attained without parameter tuning and is characterized by power-laws. The first model with SOC was defined by Bak, Tang, and Wiesenfeld [3]. They introduced a mechanism (the BTW mechanism) which balances two multi-scale processes: a constant slow loading and a quick stress-release. This mechanism was constructed on a square lattice, each cell of which contains grains of sand. A constant slow loading of sand into randomly chosen cells makes them unstable when a threshold is passed. As soon as a cell becomes unstable it topples, transmitting grains to neighboring cells. The transmission continues while the unstable cells exist. The whole, and sometimes long, process of the transmissions, which continues between two successive additions of grains, is called an event or an avalanche. The stress-release is defined by dissipation at the boundary of the lattice: unstable boundary cells transmit some of their grains out of the lattice. An analogue of the construction with the sandpile gave birth to the title of the model.

The BTW mechanism can be implemented in various ways. The choice of the transmission rules and the definition of neighbors determine the model specification. The above definition of SOC, obviously, is not rigorous and, as far as we know, has not yet been fully formalized mathematically (but fully accepted by the researchers). The BTW model and its generalization to any Abelian sandpiles (where the order the unstable cells topple in does not affect the system dynamics) have been proved to possess a stationary state [7]. However, the stationary state belongs to an abstract space (of measures defined on operators which transform the configurations of the stable cells from one to another) which is not linked to the grains explicitly. In spite of the existence of a fixed point (in an appropriate abstract space) the total amount of sand in the lattice fluctuates with time. The corresponding fluctuations are of interest in various applications.

The distribution of model avalanches with respect to their size has a power-law segment that turns to a more rapid decay in the domain of extreme events [4]. The value of the power-law exponent determines the universality class of the model. It has been shown that there are only two universality classes among a broad set of the isotropic specifications of the BTW mechanism [4]. The class depends on whether the transmission of the grains from the unstable cells is deterministic or random [19, 22].

Scale invariance, seen through the (truncated) power-law distributions, characterizes many real-life systems and processes. Examples include the distribution of earthquakes [12], forest fires [18], financial crashes [20], solar flares [1], sunspot groups [32], natural language [11], armed conflicts [28], and other quantities [36]. SOC is associated with at least some of these examples [37]. In contrast to the discussed BTW-like models, the observed power-law exponents vary from sample to sample. The BTW mechanism together with other artificial systems generating SOC are applied to model the above real-life processes. Evidently, the transmission of the grains does not replicate these processes. When sandpiles, or other simulation models, are used in applications, the design of the specification has to follow the observable system in a plausible way. Then the adequacy of the model is estimated through the reproduction of the regularities established by real systems. Thus, the existence of only a few universality classes limits the area of the applicability of the BTW mechanism defined on the square lattice. When the adjustment of the exponent is desired, one constructs the BTW mechanism on graphs or self-similar structures [5, 6, 8, 16, 31]. The topology of these structures affects the relevance of the model. For instance, the usage of self-similar objects without “holes” is more natural when seismic processes are investigated.

As the sequence of events in sandpile models exhibits properties found in earthquakes and solar flares, scholars have attempted to apply synthetic regularities to forecast the corresponding extremes [13, 35]. The comparative analysis of the specific prediction algorithms in various models of earthquakes gives evidence that the BTW model, in contrast to other models, fails the forecasting tests [26]. Other authors, see e.g. [2], agree with the general unpredictability of the BTW model, arguing that the size of the forthcoming large avalanche is impossible to forecast. Based on this, Geller et al. [10] declared the unpredictability of large earthquakes. The unpredictability of the BTW model is unexpected, as the sequence of the events ruled by the BTW mechanism is characterized by the correlation of numerous quantities [17, 27]. Shapoval and Shnirman [29, 30] established that large events are predictable in the BTW model. They introduced precursors of large events: a general increase in sand grains in the lattice and a high concentration of active areas in the lattice, i.e., where the number of grains is large. Garber et al. [9] also predicted large events in the BTW model but used only information regarding the size of consecutive events without any internal characteristics of the system. The both groups of authors deal with relatively small lattices. Efficiently predicted avalanches are located to the right of the scale-invariant part of the size-frequency event distribution. This property corresponds to a more general conclusion regarding the growth in the prediction efficiency with the size of the forecasting events, which holds for synthetic and real processes [14, 25].

The number of the cells along the lattice side represent the characteristic size L of the system. The right boundary of the power-law segment of the size-frequency event follows a power-law function of L. Other scaling laws are also observed; e.g., the size of the largest avalanche is scaled as $L^3$. The scaling of predictable events in the BTW model has not yet been revealed. We note that one should design the models with finite and, likely, moderate L for astrophysical and seismic applications.

This paper proposes a theory which explains somewhat controversial claims regarding the predictability of BTW-like models and agrees with the general results on the predictability of extremes in complex systems. In our framework, the prediction is explored with several lattices in order to relate the prediction to the lattice length. This idea is natural in statistical physics when one studies regularities which are universal with respect to system size. We choose the model introduced by Shapoval and Shnirman [31] who constructed the BTW mechanism on a self-similar lattice by defining the load of each cell proportionally to its area. Such loading corresponds to the multi-scale heterogeneity of a seismic region [33], in contrast to that in the original BTW model. Motivated by the analysis of predictability as a property of models, rather than by the search for the best forecasting algorithm, we introduce the total stress in the system as a precursor of large events. This is a well-known precursor used in real-life processes when extremes are characterized by an activation scenario and a growth in activity precedes large stress releases. The efficiency of prediction algorithms is estimated with the Molchan diagram which incorporates statistical type I and II errors [23, 24].

The rest of the paper is organized in the following way. The model is defined in Sect. 2. Section 3 introduces a general approach to the evaluation of the prediction efficiency. Section 4 contains the main results of the paper, specifying and evaluating our prediction algorithm. Section 5 concludes.

2 Model

The description of the model follows paper Shapoval and Shnirman [31]. It is repeated here for the sake of completeness.

2.1 Self-similar Lattice

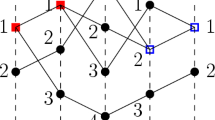
We define a self-similar lattice that consists of cells of different sizes. The smallest cells determine the unit of measurements. The (linear) length of the lattice is $L=3^{n}$, where n is the depth of self-similarity realized in the computations. At the thermodynamic limit, n tends to $+\infty$. The self-similar lattice is defined with a recursive algorithm. At the beginning, a large single square with length L is divided into 9 identical squares. The four corner cells (shown in grey in Fig. 1) are indivisible during the further construction of the lattice. The other five cells are divisible. All the divisible cells of the length L/3 are split into 9 identical squares. At the kth step of the recursion, all divisible cells of the size $L/3^{k-1}$ are split into 9 identical squares. The corner cells are called indivisible whereas the other cells are divisible. When the recursion is applied $n-1$ times, the smallest squares are $L/3^n \times L/3^n = 1 \times 1$. They are indivisible too. The constructed self-similar lattice is denoted by ${\hat{C}}_{n,L}$. The indivisible squares are the cells of the lattice. Let $C_{k,L}$ be the indivisible cells constructed at the step $k-1$. Then ${\hat{C}}_{n,L} = \cup _{k=1}^{n-1} C_{k,L}$.

Fig. 1

Divisible (in white) and indivisible (in grey) cells that appear when an $L/3^{k-1} \times L/3^{k-1}$-square is split into 9 smaller squares of size $L/3^k \times L/3^k$

2.2 Configurations

We assume that the cells $c \in {\hat{C}}_{n,L}$ are numbered in an arbitrary way; I is the number of the cells. Two cells are called neighbours if they share an edge, or part of an edge. The threshold $H_i$ of the cell $c_i$ is defined as the number of the neighbours of the cell $c_i$ in our lattice which is folded into a torus by gluing the opposite edges. The folding into a torus is used only for the definition of the thresholds. Let ${\mathcal {N}}(c_i)$ be the set that consists of the neighbours of the cell $c_i$; $|{\mathcal {N}}(c_i)|$ denotes the number of these neighbours. Then $H_i = |{\mathcal {N}}(c_i)|$ if $c_i$ is an inner cell of the lattice. The inequality $H_i > |{\mathcal {N}}(c_i)|$ holds for the boundary cells, Fig. 2.

Fig. 2

Self-similar lattice ${\hat{C}}_{3,L}$. The thresholds are written inside the cells

For any $i=1\ldots , I$ the cell $c_i$ contains $h_i \in {\mathbb {Z}}$ grains. The cell $c_i$ is stable if $h_i < H_i$. The numbers $h_i$, $i=1\ldots , I$, constitute a configuration. A configuration is called stable if $h_i < H_i$ for all $i=1,\ldots , I$.

2.3 Dynamics

The dynamics of the configurations caused by falling of the grains and their redistribution over the lattice is defined as in the original paper by Bak et al. [3] (the difference is in the geometry of the lattice, not in the mechanism generating the dynamics). The initial configuration corresponds to the empty lattice: $h_i = 0$ for all $i=1,\ldots , I$. Clearly, it is stable.

At each time moment a current stable configuration is transformed into another one in the following way. Initially, a cell $c_i$ is chosen at random. The probability ${\mathsf {P}}$ of choosing the cell $c_i$ is proportional to the area of the cell. Formally, if $c_i \in C_{r,L}$ then ${\mathsf {P}}\sim 3^{-2r}$. A grain falls on the chosen cell:

$$\begin{aligned} h_i \longrightarrow h_i+1. \end{aligned}$$

If $h_i$ is still less than $H_i$ then a stable configuration is obtained and a new time moment starts.

If $h_i = H_i$, then the stability of the configuration is violated. Then the sandpile in the cell $c_i$ topples and the grains are transferred to the neighbouring cells equally:

$$\begin{aligned}&h_{i}\rightarrow h_{i}-H_{i} \end{aligned}$$

(1)

$$\begin{aligned}&h_{j}\rightarrow h_{j}+1,\quad \forall j: c_j\in {\mathcal {N}}(c_i) \end{aligned}$$

(2)

The transfer defined by (1) and (2) conserves the total number of grains in the lattice when an inner cell topples. If at least one neighbour of the toppled cell becomes unstable, the transfers continue. In other words, the rules (1) and (2) are applied while there are unstable cells $c_i$ in the lattice. The subsequent transfers occurred during a single time moment are called an avalanche. The size of the avalanche is the number of the cells that become unstable during the avalanche. Each cell is counted as many times as it becomes unstable. Each avalanche is finite because the transfers at the boundary are dissipative. We note that the stable configuration occurred after the avalanche does not depend on the order of toppling (because the order in which any two unstable cells topple does not affect the configuration). This property is called Abelian.

2.4 Power-Law Distribution of Avalanches

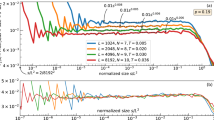
The size-frequency probability distribution of avalanches is known to follow a truncated power-law $1/s^{\gamma }$ with the exponent $\gamma = 2-2/\beta$, where $\beta =\log _3 5$ is the similarity exponent of the lattice [31]. We denote $f_L(s)$ as the fraction of the avalanches with the size s, $s=1,2,\ldots$, and display the dependence $f_L(s)$ on s for several values of the lattice length L in Fig. 3a. The right end of the power-law segment and the tail located to the right are badly observed with the chosen axes. Therefore, we turn from $f_L(s)$ to the function $F_L(s)$ which gathers the avalanches into bins whose length is constant in a logarithmic scale:

$$\begin{aligned} F_L(s)=\sum \limits _{\sigma \in {[}s/\varDelta s, s\varDelta s{)}} f_L(\sigma ), \end{aligned}$$

(3)

where 1.495 is assigned to $\varDelta s$. The choice of bin length is performed in order to improve the visibility of the graphs and is never used for any estimates. Note that the focus on $F_L(s)$ instead on $f_L(s)$ increases the exponent of the power-law from $-\gamma$ to $-\gamma +1$, as it follows from the integration:

$$\begin{aligned} \int _{s/\varDelta s}^{s\varDelta s} \pmb {\sigma ^{-\gamma }}\,d\sigma = {\left\{ \begin{array}{ll} \frac{1}{1-\gamma } \big ( (\varDelta s)^{1-\gamma } - (\varDelta s)^{\gamma -1} \big ) \cdot \pmb {s^{1-\gamma }}, &{} \text {if } \gamma \ne 1, \\ 2\ln \varDelta s \cdot \pmb {s^0}, &{} \text {if } \gamma = 1. \end{array}\right. } \end{aligned}$$

The scaling $s \rightarrow s/L^{\beta }$ combines the upper boundary of the power-law segment, Fig. 3b.

Fig. 3

The size-frequency distribution of avalanches shown with (a) the empirical density $f_L(s)$ (following the power-law $L^{-\gamma }$) and (b) zoomed “integrated” density $F_L(s)$ obtained through $f_L(s)$-binning over the intervals $[s/\varDelta s, s\varDelta s)$ of constant logarithmic bins (which increases the power-law exponent by 1); $\beta =\log _3 5 \approx 1.465$, $\gamma = 2-2/\beta$, $\varDelta s=1.495$

3 The Evaluation of the Prediction Algorithms

The efficiency of the prediction algorithms based on different mechanisms is comparable when they output the same quantities. Following Molchan [24], we consider the fail-to-predict rate $\nu$ and the alarm rate $\tau$ as such quantities. Namely, let E be the sequence of events that occur within the time interval $[t_0, t_1]$. A part $E^*$ of them is the subject of the prediction. The selection into $E^*$ is based on the physical properties of interest, such as energy released during large earthquakes. For example, one can be interested in the prediction of extreme events or specific events that follow the extremes.¹ The events from $E^*$ are called target events. The prediction algorithms are designed to predict the time of their occurrence. We require the output of any prediction algorithm to be the set of the time intervals, in which the target events are expected. One can say that an alarm is switched on for the time intervals selected by the prediction algorithm. Avoiding a new term, each interval itself can also be referred to as an alarm. Each alarm $[t_b, t_e] \subset [t_0, t_1]$ is switched on in advance. Let ${\mathcal {T}}$ be the set of all alarms. Then an event from $E^*$ is called predicted if it occurs at a time moment that belongs to ${\mathcal {T}}$. Otherwise, the event is unpredicted. The fail-to-predict rate $\nu$ is defined as the number of unpredicted events in $E^*$ divided by the number of all events in $E^*$. Further, $\tau$ is the fraction of the alarms in the whole considered time interval: $\tau = \sum _{[t_b,t_e]\in {\mathcal {T}}} (t_b-t_e) / (t_1 - t_0)$. The fail-to-predict and alarm rates correspond to the statistical errors of types I and II respectively.

By this moment, the pair $(\nu , \tau )$ characterises any prediction algorithm A which is designed to predict the target events from $E^*\subset E$ occurred within the considered time interval $[t_0, t_1]$. Now we are going to evaluate the efficiency of the algorithms, following algorithms, following [23, 24]. Consider two elementary algorithms. The first algorithm always switches the alarm on. Then ${\mathcal {T}}= [t_0, t_1]$, $\nu = 0$, $\tau = 1$. The second algorithm always switches the alarm off. Then ${\mathcal {T}}= \emptyset$, $\nu = 1$, $\tau = 0$. A random switching of the alarms on and off leads to the pairs $(\nu , \tau )$ such that $\nu + \tau \approx 1$. The equality is exact if the quantities $\nu$ and $\tau$ are rigorously defined in probabilistic terms (see, Molchan [24]). We note that if an algorithm A with the alarms ${\mathcal {T}}$ results in some $(\nu , \tau )$ then the algorithm ${\bar{A}}$ setting the alarms $[t_0,t_1] \setminus {\mathcal {T}}$ produces the outcome $(1-\nu , 1-\tau )$. Therefore, we reduce the consideration of all possible prediction outcomes from $[0,1]\times [0,1]$ to the triangle that is located below the diagonal $\nu + \tau = 1$ in the $(\nu , \tau )$-space. Then an algorithm $A = A(\nu , \tau )$ is clearly more efficient than another algorithm $A'(\nu ',\tau ')$ if $\nu < \nu '$ and $\tau < \tau '$. However, the case of the algorithms differently ordered with respect to the two rates requires the definition of the efficiency comparison. There are numerous ways to define a goal function $g(\nu ,\tau )$ which is monotone increasing with respect to their variables. As in [24], we pick $g(\nu , \tau ) = \nu + \tau$ and say that the algorithm $A(\nu ,\tau )$ is more efficient than $A'(\nu ', \tau ')$ if $\nu + \tau < \nu ' + \tau '$. The values $\varepsilon = \nu + \tau$ and $1 - \varepsilon$ are respectively called the loss and the efficiency of the algorithm $A(\nu ,\tau )$. Then $1 - \varepsilon = (1 - \nu ) - \tau$ is interpreted as the proportion of the target events characterized by non-random prediction.

We insist that the evaluation of the prediction algorithms in terms of the rates $\nu$ and $\tau$ is performed with just the outcome but not the mechanism of the algorithms. Therefore, arbitrary algorithms are comparable. We only add that the adjustment of any algorithm and the computation of the rates must be performed with different samples.

4 Prediction Efficiency in the Model

4.1 Adjustment of the Algorithm

In this section we construct an algorithm that predicts when large events occur in our model. This algorithm switches alarms on when the total number of grains on the lattice exceeds a critical value. Each alarm is set for a fixed-length time interval. However the alarm can be prolonged if the surplus of grains can be detected when the alarm is on. Alarm is switched off early if the target event occurs. As a result, the number of subsequent time moments when the alarm is on, in general, differs.

Here are the details of the algorithm. By definition, the target events $E^*$ in our model are the avalanches whose size s is greater than some level ${\mathcal {S}}_*$ (whereas the set E consists of all observed avalanches). In other words, the avalanches with the sizes from the half-bounded interval $({\mathcal {S}}_*, +\infty )$ form the set of the target events. The left endpoint ${\mathcal {S}}_*$ of the interval is a parameter of the prediction problem that has to affect the efficiency of the algorithm. Let $Q(t) = \sum _{i \in I} h_{i}(t)$ be the number of grains on the whole lattice when a grain has been added and there has been a possible sand redistribution at time t.

Then we introduce two parameters of the algorithm: the threshold $Q^*$ of the sand on the lattice and the duration $T^*$ of the alarms. The algorithm switches an alarm on for the interval $[t+1, t+T^*]$ at the time moment t if $Q(t) > Q^*$. In other words, $t' \in {\mathcal {T}}$ if and only if there is the time moment $t \in [t'-T^*, t'-1]$ such that $Q(t) > Q^*$. From this definition it follows that the alarm can continue when the functional Q(t) leaves the critical zone $Q > Q^*$. The alarm $[t+1, t+T^*]$ can be prolonged at some $t'' \in [t+1, t+T^*]$ for the interval $(t+T^*, t''+T^*]$ if $Q(t'') > Q^*$. The prolongation occurs as many times as the inequality $Q(t) > Q^*$ holds and the alarm is on. The alarm $[t+1, t+T^*]$ is terminated at some $t''' \in [t+1, t+T^*]$ if the target event occurs at $t'''$.

Our algorithm is fully defined by the parameters $Q^*$ and $T^*$. Therefore, the output of the algorithm, which is the pair $(\nu , \tau ) = (\nu (Q^*, T^*), \tau (Q^*, T^*))$ of the rates, is also fully defined by these parameters when the catalogue is fixed. Initially, the algorithm is applied to a training set of model events. Scanning a (broad part of the) two-dimensional space of the parameters, we select and fix such values $T^*$ and $Q^*$ that minimize $\nu (Q^*, T^*) + \tau (Q^*, T^*)$ in the training set. Then the algorithm with these parameters $T^*$ and $Q^*$ is applied to another time series to find the prediction efficiency.

4.2 Prediction Efficiency

The adjustment of the parameter $Q^*$ is illustrated for the largest avalanches (their number is 93) occurred on the $3^5 \times 3^5$ lattice in Fig. 4. This is so called Molchan diagram² that exhibits the two errors of the prediction algorithm as a function of the parameters. The adjustment leads us to $Q^* = 15260$, which corresponds to the prediction loss in $\nu + \tau \approx 0.35$ obtained with the training set. We admit that a better efficiency can be achieved with another choice of the parameters. However, it is likely that our result is close to the optimal one. When the parameter $Q^*$, the number of the grains on the lattice, decreases, the prediction loss $\nu +\tau$ drops, then attains its minimum (which is close to 0.35), and, later on, increases. Typically, the minimum of $\nu + \tau$ is attained when $\nu$ and $\tau$ take close values. Therefore, $\min \{\nu , \tau \}$ can be considered as another measure of the prediction loss. Furthermore, we will focus on $\nu + \tau$ as the quality of the prediction outcome.

Fig. 4

The Molchan diagram: the implicit dependence of the error rate on the alarm rate, given the alarm length $T^* = 3$ and variable total number $Q^*$ of the grains on the lattice (written next to the points). The blue dot is obtained with the parameters adjusted with the training sample

In Fig. 5, we illustrate the efficiency of the prediction algorithm applied to $L \times L$ lattices and various left endpoints ${\mathcal {S}}_*$ of the target event sizes. This figure starts at the left at sizes that correspond to the existence of the prediction, i. e., the loss function $\varepsilon = \nu + \tau$ significantly deviates from 1. These sizes are located to the right of the power-law segment of the size-frequency avalanche distribution displayed in Fig. 3a. Associating extremes with the fast decay of the size-frequency relationship at the right, one can claim that our algorithm is efficient only for extremes.

Fig. 5

The loss $\varepsilon$ of the prediction algorithm as a function of the left endpoint ${\mathcal {S}}_*$ of the target event sizes for the train (yellow) and test (red) catalogues and four lattices, which differ in the length L. The number of target events observed with several computations is written next to the corresponding point. The 0.95 error bars are shown by black vertical segments for selected outputs; the dashed lines are defined by (7)

According to the definition of the loss function $\varepsilon$, it exhibits the inefficiency of the prediction. The better the prediction is, the smaller the values of $\varepsilon$ is observed. Red curves of Fig. 5 imply that for any given L, the efficiency of the prediction increases with growth in the size of target events. A linear function rather accurately follows the increment in efficiency with the growth of ${\mathcal {S}}_*$ observed for $L = 3^4$ and $L = 3^5$. On one hand, a turn to a faster drop at the right observed with $L = 3^5$ may be an artifact caused by relatively small number of the target events (50 and 39 for the last two points at the left in Fig. 5b). On the other hand, this number is not too small. Anyway, we argue that the improvement of the efficiency observed through drop in $\varepsilon$ is not worse than linear.

The most efficient prediction in $\nu \approx 0.09$ and $\tau \approx 0.09$ is attained with $L = 3^4$. The simulation of the $3^5 \times 3^5$ lattice results in the loss of 0.29 and 0.35 recorded for the first two points at the right in Fig. 5b. The efficiency in $\varepsilon = 0.3$ requires much longer catalogues for $L \ge 3^6$ than we are able to generate in a reasonable time. The sum of the errors crosses 0.6 if $L = 3^6$ and just shows up the efficiency ($\varepsilon \in [0.75, 0.8]$) if $L = 3^7$.

We also display the loss function obtained with the training time series (yellow curves in Fig. 5). While the number of target events is large, the loss functions computed with the training and testing time series almost coincide. The two curves expectedly start deviating when the time series contain hundreds of target events. Nevertheless, their patterns follow each other in the domain where the values of the functions are clearly different. Such an agreement evidences in favour of the reliability of the estimated prediction efficiency.

The difference between the loss obtained with the training and the testing catalogues gives an estimate of the level of uncertainty in the prediction results. Other estimates are obtained with the error bars constructed as if the prediction loss $\varepsilon$ were the probability of success in the Bernulli trials (0.95-quantile is chosen in the illustration in Fig. 5d). The error bars agree with the distance between the yellow and red curves in Fig. 5.

Fig. 6

The critical threshold $Q^* = Q^*(\mathcal {S_*})$ adjusted for the predictions of the events with the size $s > \mathcal {S_*}$ and $L = 3^5$; the efficiency of these predictions are in Fig. 5b

We recall that the threshold $Q^*$, the upward cross of which launches the alarms, is adjusted with the training set to minimize the loss function. These optimized values of the threshold $Q^*$ slowly rise with the growth in the left endpoint of the target events, Fig. 6. The approximation of this steady growth by a linear function may worth further analysis. As a function of L, the threshold follows a general scaling $Q^* \sim L^{\beta }$ observed for the number of grains (this statement is not supported by a figure). The adjusted duration of the alarm is 1 for a majority of the values of ${\mathcal {S}}_*$, but it starts slowly rising for the extremes.

4.3 The Relationship Between the Left Endpoint of the Target-Event Size and the Lattice Length

We solve the equation $\varepsilon ({\mathcal {S}}_{*},L) = \mathrm {const}$ for several values of the constant and represent the solutions denoted as ${\mathcal {S}}_{*,\varepsilon }(L)$ and shown in Fig. 5. A power function

$$\begin{aligned} {\mathcal {S}}_{*,\varepsilon }(L) \approx C_{\varepsilon } L^{\alpha }, \end{aligned}$$

(4)

with the same exponent $\alpha$ is used to fit all points we obtained with different $\varepsilon$. A general relationship between L and ${\mathcal {S}}_{*,\varepsilon }(L))$ remains open since small values of $\varepsilon$ are not attained with our computer experiments.

Fig. 7

The left endpoint ${\mathcal {S}}_{*,\varepsilon }(L)$ of the sizes of the target events as a function of the lattice length L, given several values of the loss $\varepsilon$

The size of avalanches scaled as $L^{\alpha }$, $\alpha \approx 2.24$, is larger than the right endpoint of the power-law segment scaled as $L^{\beta }$, $\beta = \log _3 5$. Therefore, the left endpoint ${\mathcal {S}}_{*,\varepsilon }$ of the size of the target events, predictable with a positive efficiency $1-\varepsilon$, is located on the tail of the size-frequency probability distribution, Fig. 8.

Fig. 8

The full size-frequency distribution of avalanches shown with the “integrated” density $F_L(s)$ including the part marked by the rectangles of the corresponding color that highlights the target events predicted with $\varepsilon \in [0.1, 0.8]$ (and shown in Fig. 5) in order to show their location. (The left upper and right lower corners of each rectangle $({\mathcal {S}}_{*,0.8}(L), F_L({\mathcal {S}}_{*,0.8}(L)))$ and $({\mathcal {S}}_{*,0.1}(L), F_L({\mathcal {S}}_{*,0.1}(L)))$ respectively, indicate the left endpoints of the size of the target events which are predicted with the loss 0.8 and 0.1 respectively. The rectangle itself is for illustrative purpose only.)

Now we return to Figs. 5 and combine the prediction efficiencies found for different lattice lengths (and the testing time series) into a single graph by using the normalization (4). The normalized endpoint $s_{*,\varepsilon }(L)$ of the target events is

$$\begin{aligned} s_{*,\varepsilon }(L) = {\mathcal {S}}_{*,\varepsilon }(L) / L^{\alpha }. \end{aligned}$$

(5)

According to Fig. 9, the normalization collapses the efficiency curves in the intersection of their domains. The curves are likely to attain a universal pattern with respect to the lattice length. This is expressed by a function which relates the normalized left endpoint of the target event sizes to the prediction efficiency.

We conjecture that the collapsed part of the graph in Fig. 5 is linear (as in Fig. 9):

$$\begin{aligned} s_{*,\varepsilon }(L) \approx -K_1\varepsilon + K_2 \end{aligned}$$

(6)

with the following estimates of the constants: $K_1 \approx 0.42$, $K_2 \approx 0.37$. The fit (6) is constructed with all points of Fig. 9 except the points characterized by the largest ${\mathcal {S}}_{*,\varepsilon }(L)$ for each L.

Fig. 9

The normalized left endpoint $s_{*,\varepsilon }(L) = {\mathcal {S}}_{*,\varepsilon }(L) / L^{\alpha }$ of the target event sizes as a function of the prediction loss $\varepsilon$ for given values of L. The linear approximation (shifted to make it visible) is dashed

Equations (5) and (6) lead to the following conjecture regarding the universal dependence of the prediction efficiency on the lattice length and the left endpoint of the target events:

$$\begin{aligned} \varepsilon ({\mathcal {S}}_*, L) = \frac{K_2}{K_1} - \frac{{\mathcal {S}}_*}{K_1L^{\alpha }}. \end{aligned}$$

(7)

The graph constructed with Eq. (7) is shown in Fig. 5 with dashed lines.

The substitution of 0 for $\varepsilon$ into (7) gives an estimate of the left endpoint of the target events which are predicted with the absolute efficiency ($\varepsilon = 0$):

$$\begin{aligned} {\mathcal {S}}_{*,0} = K_2L^{\alpha } \approx 0.37 L^{\alpha }. \end{aligned}$$

The extrapolation of the pattern (6) towards $\varepsilon = 0$ gives only an estimate regarding the most efficient prediction, which requires additional numerical or theoretical justifications.

The scaling exponent $\alpha \approx 2.24$ is located between the exponents $\beta =\log _3 5 \approx 1.465$ and 3 representing the scaling of the upper bound of the power-law segment in the size-frequency distribution and the size of the largest avalanche respectively. The scaling $L^3$ for the largest avalanche in the model ($h_i = H_i-1$ for all i, and a new grain falls into the center of the lattice) is obtained numerically and not discussed here.

5 Conclusion

This paper examines the predictability of extreme events in a BTW sandpile on a self-similar lattice. We design and evaluate an algorithm which predicts the occurrence of extreme events in advance by switching alarms on when the total number of grains on the lattice exceeds a threshold, Sect. 4.1. This condition indicates that the system has become overloaded and, as a result, super-critical. Overloading as the precursor of stress-release is frequently used when predicting the occurrence of extreme events [15].

Following Molchan [23], the efficiency of a prediction algorithm is defined with the fail-to-predict and alarm rates $\nu$ and $\tau$, which are inferred from type I and II statistical errors, Sect. 3. The most efficient prediction obtained numerically in the model is characterized by $\nu \approx \tau \approx 0.09$: $91\%$ of the target events are predicted whereas the alarm continues $9\%$ of the time. As far as we know, such an effective prediction algorithm has never been designed for BTW-like sandpiles.

The efficiency of the prediction depends on the system length and the size of the target events. For any given lattice, larger events are better predicted, Fig. 5. The target events which admit efficient prediction are larger than the upper bound of scale-free avalanches, Fig. 8. This statement reconciles the general conclusions regarding the unpredictability of sandpiles [2, 10, 26] with specific examples of predictability in related systems [14, 34]. Unpredictability is related to scale-free avalanches, whereas efficient predictions are constructed for extreme events. We note that the predictability frontier found by our specific algorithm may generally be shifted to the domain of smaller avalanches, if another algorithm is designed (as in Garber et al. [9] for a BTW sandpile).

The quantitative analysis of the prediction is performed with the sum of the rates $\varepsilon = \nu + \tau$ called the prediction loss. Smaller values of $\varepsilon$ indicate more effective predictions. The conjecture (7), confirmed by Fig. 9, relates the loss $\varepsilon$ to the system length L and the left endpoint ${\mathcal {S}}_*$ of the size of the target events: $\varepsilon \approx 0.88 - {\mathcal {S}}_* / (0.42L^{\alpha })$.

We argue that the avalanches of size $C L^{\alpha }$ with $\alpha = 2.24$ are marginal: smaller avalanches are unpredictable with our algorithm, whereas larger avalanches are fully predictable. The quality of the prediction algorithm changes from absolute inefficiency to full efficiency at the avalanches of size $C L^{\alpha }$, Fig. 7. The level of efficiency depends on the constant C.

On the first sight, the prediction of extreme avalanches seems to be doable if one knows everything about the system. In particular, large events are very unlikely to occur when the number of grains in the lattice is small. Furthermore, the largest avalanches (with the size of $\sim L^3$) are expected only when the lattice is filled with the grains almost fully. Our results go far beyond these naive statements (which have never been quantified for sandpiles). We build the prediction algorithm on the level of stress accumulated by the system, which is the main quantity regulating the criticality. This algorithm predicts large avalanches with the absolute efficiency. Their size is located between $\sim L^{\alpha }$ and $\sim L^3$, thus, filling the interval of the sizes. In other words, extreme events that admit an efficient prediction by our algorithm are rare, as they do not belong to the scale-free segment of the size-frequency relationship. However, the set of these extremes is not too thick, as their lower bound is located quite far from the size of the largest avalanche on the lattice.

To conclude, we exploit the level of criticality, represented by the total number of grains in the lattice, to predict the occurrence of large avalanches. When the system becomes super-critical a large avalanche is expected, but its exact size may be impossible to estimate. Earlier, researchers were tempted to interpret such uncertainty as unpredictability. However, we draw the opposite conclusion when establishing that the extremes, the size of which are scaled as $L^{\alpha }$, occur only in a super-critical state. This property opens the door for the construction of efficient prediction algorithms and, in particular, allows us to forecast the occurrence of large avalanches based on the level of stress in the system. The detailed links between the geometry of the system, the self-similarity of oscillations around the critical point, and the prediction efficiency are worth further study. The predictability of real systems may depend on system geometry represented by the self-similarity exponent as well as the total stress accumulated by the system. If geometry does affect predictability, then the prediction of strong earthquakes should vary from region to region, as (geological) faults are characterized by different fractal geometry.