1 Introduction

In recent years, there has been a growing interest [1,2,3,4,5,6,7,8,9] in characterizing trajectories conditioned on rare events. Such questions appear in a wide range of topics, including protein folding [10], chemical reactions [11, 12], stochastic models of gene expression [13], atmospheric activities [14], glassy systems [15, 16], disordered media [17]. One motivation is to find efficient algorithms where the rare events become typical such that they are computationally easy to generate [2, 11, 18,19,20,21]. To calculate the probability of rare events one needs to understand how these rare events are created and how they relax. In these activities, a major interest concerns conditioning on an atypical value of an empirical observable, such as the integrated current, the empirical density, the entropy production, or the activity [22,23,24,25,26,27,28]. How do the fluctuations get affected by such conditioning, and what is the effective dynamics in this conditioned ensemble? These are questions we address in this present work.

For Markov processes, in particular, for systems with few degrees of freedom and evolving according to a Langevin equation, it is known [1, 8, 15, 16, 23, 29,30,31,32,33] how to describe the conditioned dynamics when the time window for the empirical observable is large. In this paper, we see how the same ideas [29] can be extended to systems with many degrees of freedom.

We work here in the steady state of a one-dimensional diffusive system of length L coupled with reservoirs at the boundary, as shown in Fig. 1. Under a diffusive re-scaling of space i and time \(\tau \), defining \(\left( \frac{i}{L},\frac{\tau }{L^2}\right) \equiv (x,t)\) for large L, these systems are described [34,35,36,37,38,39] by a hydrodynamic density \(\rho (x,t)\) and current j(x, t) whose time evolution is governed by a fluctuating hydrodynamics equation

$$\begin{aligned} \partial _t\rho (x,t)=-\partial _x j(x,t)\qquad \text {with}\qquad j(x,t)=-D(\rho (x,t))\; \partial _x\rho (x,t)+\eta (x,t) \end{aligned}$$
(1a)

where \(D(\rho )\) is the diffusivity and \(\eta (x,t)\) is a Gaussian white noise with zero mean and covariance

$$\begin{aligned} \left\langle \eta (x,t)\eta (x',t')\right\rangle =\frac{1}{L}\sigma (\rho (x,t))\; \delta (x-x')\;\delta (t-t') \end{aligned}$$
(1b)

where \(\sigma (\rho )\) is the mobility. The density \(\rho (x,t)\) could be the density of particles or of energy depending on the system. The microscopic details of the system are embedded in the functions \(D(\rho )\) and \(\sigma (\rho )\). The pre-factor \(\frac{1}{L}\) in the covariance of \(\eta (x,t)\) is due to coarsegraining, which makes the noise strength weak for large L [34, 36, 39, 40].

Fig. 1
figure 1

A diffusive system of length L coupled with two reservoirs at different densities \(\rho _a\) and \(\rho _b\) at the boundary

Full size image

Our interest is in the statistics of the steady state density \(\rho (x)\) when conditioned on the integrated current \(Q_T\) over a time interval [0, T], for large T. Individual statistics of \(\rho (x)\) and \(Q_T\) have already been studied [36, 40,41,42,43,44,45,46,47,48,49]. For the conserved dynamics (1), when the density is bounded inside the bulk, the probability \(P(Q_T)\) of \(Q_T\) for large T has a large deviation description and the large deviation function is independent of where the current is measured [42, 43, 49]. On the other hand, in the steady state, the probability of \(\rho (x)\) has also a large deviation form when the system size L is large [36, 40, 41, 44]. These two probabilities are given by

$$\begin{aligned} P(Q_T=q\, T)\sim e^{-T\,L\, {\varPhi }(q)}\qquad \text {and} \qquad P[\rho (x)]\sim e^{-L\, {\mathcal {F}}[\rho (x)]} \end{aligned}$$
(2)

for T and L both being large, where \({\varPhi }(q)\) and \({\mathcal {F}}[\rho (x)]\) are the corresponding large deviation functions. Here, the precise meaning of the symbol \(\sim \) is that \(\lim _{L\rightarrow \infty }\lim _{T\rightarrow \infty }\frac{\log P(Q_T=qT)}{L\; T}=-{\varPhi }(q)\) and \(\lim _{L\rightarrow \infty }\frac{\log P[\rho (x)]}{L}=-{\mathcal {F}}[\rho (x)]\).

In contrast to (2), the conditioned probability of \(\rho (x,t)\) depends (as we will see in regions I, II, III, IV, and V of Fig. 2) on where \(Q_T\) is measured. Therefore, we define an empirical observable

$$\begin{aligned} Q_T^{(\alpha )}=\int _0^1 dx\,\alpha (x) \int _0^T dt\, j(x,t)\qquad \text {with}\qquad \int _0^1 dx\, \alpha (x)=1. \end{aligned}$$
(3)

Here, \(\alpha (x)\) is arbitrary except for the normalizationFootnote 1 in (3). A choice of \(\alpha (x)=\delta (x-x_0)\) corresponds to the current being measured at \(x_0\).

We denote by \({\mathcal {P}}_t^{(\alpha )}[\rho (x)\vert Q]\) the conditioned probability of a density profile \(\rho (x)\) at time t given that \(Q_T^{(\alpha )}\) takes value Q while the system is in its steady state. For large T and L, it has the large deviation form

$$\begin{aligned}&{\mathcal {P}}_t^{(\alpha )}[\rho (x)\vert Q=qT]\sim e^{-L \, \psi _t^{(\alpha )}[\rho (x), q]} \end{aligned}$$
(4)

where \(\psi _t^{(\alpha )}[\rho (x), q]\) is the conditioned large deviation function.

Fig. 2
figure 2

A schematic time evolution of the density profile \(\rho (x,t)\) when conditioned on \(Q_T^{(\alpha )}\) in (3) measured over a large time interval [0, T]. The system starts in its steady state far in the past, then reaches a quasi-stationary state for \(1\ll t\) and \(1\ll T-t\), and finally for \(t\gg T\) it relaxes to its steady state. Different shaded regions denote different parts of the evolution: (I) \(t<0\), (II) \(t\ge 0\) but small, (III) \(1\ll t\) and \(1\ll T-t\), (IV) \(T-t> 0\) but small, and (V) \(t\ge T\)

Full size image

Our goal is to determine this conditioned large deviation function \(\psi _t^{(\alpha )}[\rho (x), q]\). For the diffusive systems studied in this paper, cross-correlations of the density and the current can be derived from \(\psi _t^{(\alpha )}[\rho (x), q]\). This way, the function plays the role of free energy [36] in an ensemble where q is fixed. Large deviation functions are also important in understanding non-equilibrium phase transitions in theoretical models [27, 43, 47, 49,50,51] and in experiments [52].

In this paper, we will give \(\psi _t^{(\alpha )}[\rho (x), q]\) at \(t=0\), in the intermediate quasi-stationary state (\(t\gg 1\) and \(T-t\gg 1\)), and at \(t=T\) (indicated in Fig. 2) for diffusing independent particles and for the symmetric simple exclusion process [36]. Our results for the latter are in a perturbation expansion in small density. A hydrodynamic description of these two examples is given by (1) with \(D(\rho )=1\) and \(\sigma (\rho )=2\rho \) for the diffusing independent particles, and \(D(\rho )=1\) and \(\sigma (\rho )=2\rho (1-\rho )\) for the symmetric simple exclusion process.

We shall start by a microscopic calculation on these models where we determine the conditioned probability in terms of the left and right eigenvectors associated to the largest eigenvalue of a tilted matrix [29]. Then, taking a hydrodynamic limit of the conditioned probability we derive \(\psi _t^{(\alpha )}[\rho (x), q]\). For example, in the quasi-stationary state (regime III in Fig. 2), we will see that

$$\begin{aligned} \psi _t^{(\alpha )}[\rho (x), q]\equiv \psi _\text {qs}[\rho (x), q]=\psi _\text {left}^{(\alpha )}[\rho (x), q]+\psi _\text {right}^{(\alpha )}[\rho (x), q] \end{aligned}$$
(5)

up to an additive constant (subscript “qs” denotes “quasi-stationary”), where \(\psi _\text {left}^{(\alpha )}\) and \(\psi _\text {right}^{(\alpha )}\) are related [29] to the left and right eigenvectors of a tilted matrix (see Sect. 2.5 for a precise definition). We will see later that these two functions \(\psi _\text {left}^{(\alpha )}[\rho (x), q]\) and \(\psi _\text {right}^{(\alpha )}[\rho (x), q]\) have in fact the following physical interpretation in terms of the large deviation function defined in (4).

$$\begin{aligned} \psi _\text {left}^{(\alpha )}[\rho (x), q]&=\psi _0^{(\alpha )}[\rho (x), q]-{\mathcal {F}}[\rho (x)] \end{aligned}$$
(6a)
$$\begin{aligned} \psi _\text {right}^{(\alpha )}[\rho (x), q]&=\psi _T^{(\alpha )}[\rho (x), q] \end{aligned}$$
(6b)

up to an additive constant, where \({\mathcal {F}}[\rho (x)]\) is the unconditioned large deviation function of the density, as defined in (2).

We shall show (see (28)) that \(\psi _\text {left}^{(\alpha )}\) and \(\psi _\text {right}^{(\alpha )}\) have a simple dependence on \(\alpha (x)\), which cancels in the expression (5) for \(\psi _\text {qs}[\rho (x), q]\). In other regions of Fig. 2, e.g. at \(t=0\) and \(t=T\), \(\psi _t^{(\alpha )}[\rho (x), q]\) does depend on \(\alpha (x)\).

In addition, we shall see that the conditioned dynamics for large T, can be effectively described by a fluctuating hydrodynamics equation with an additional driving field, which can be expressed in terms of \(\psi _\text {left}^{(\alpha )}\) and \(\psi _\text {right}^{(\alpha )}\). For example, in the quasi-stationary regime, the path \(\rho (x,t)\) leading to a fluctuation at \(t_0\) with \(1\ll t_0\) and \(1\ll T-t_0\) (illustrated in Fig. 3), follows, for \(t< t_0\),

$$\begin{aligned} \partial _t\rho (x,t)=\partial _x \left\{ D(\rho )\partial _x\rho -\sigma (\rho )\left( {\varPhi }'(q)\, \alpha (x)+\partial _x \frac{\delta \psi ^{(\alpha )}_\text {right}}{\delta \rho (x,t)}\right) +\eta (x,t)\right\} \end{aligned}$$
(7a)

with \(\eta (x,t)\) being a Gaussian white noise of zero mean and covariance (1b). Similarly, the path \(\rho (x,t)\) for subsequent relaxation (\(t\ge t_0\)) follows

$$\begin{aligned} \partial _t\rho (x,t)=\partial _x \left\{ D(\rho )\partial _x\rho -\sigma (\rho )\left( {\varPhi }'(q)\, \alpha (x)-\partial _x \frac{\delta \psi ^{(\alpha )}_\text {left}}{\delta \rho (x,t)} \right) +\eta (x,t)\right\} \end{aligned}$$
(7b)

Comparing (7b) with (1a) one can see that, in the quasi-stationary regime, the effect of conditioning on (3) is a driving field \(E={\varPhi }'(q)\, \alpha (x)-\partial _x \frac{\delta \psi ^{(\alpha )}_\text {left}}{\delta \rho (x,t)}\). Similarly, for (7a) the driving field is \(E+\partial _x \frac{\delta \psi _{\text{ q }s}}{\delta \rho (x,t)}\), as seen from (5). In absence of conditioning, (7a) reduces to the effective dynamics found in [53].

These equations (7), including the noise, are expected to hold in the whole quasi-stationary regime. That in this regime the noise part is of the form given in (7) is not surprising. Afterall, the microscopic dynamics is a Markov process and it is known that the dynamics in the conditioned ensemble is also a Markov process [1, 8, 23, 29].

Fig. 3
figure 3

A schematic path \(\rho (x,t)\) leading to a fluctuation in density at \(t=t_0\) in the quasi-stationary regime, and its subsequent relaxation to the quasi-stationary density \({\bar{\rho }}_\text {qs}(x)\)

Full size image

In the later part of this paper, we shall show that these results are consistent with a macroscopic approach starting from (1) for a rather general \(D(\rho )\) and \(\sigma (\rho )\). In this approach, \(\psi _\text {left}^{(\alpha )}\) and \(\psi _\text {right}^{(\alpha )}\) are solution of the Hamilton–Jacobi equations

$$\begin{aligned}&\int _0^1 dx\, \bigg \{ \frac{\sigma (\rho )}{2} \left( \partial _x \frac{\delta \psi ^{(\alpha )}_\text {left}}{\delta \rho (x,t)}-{\varPhi }'(q)\alpha (x)+ \frac{D(\rho )\partial _x\rho }{\sigma (\rho )}\right) ^2 -\frac{(D(\rho )\partial _x\rho )^2}{2\sigma (\rho )}\bigg \} \nonumber \\&\quad =\,{\varPhi }'(q)\,q -{\varPhi }(q) \end{aligned}$$
(8a)
$$\begin{aligned}&\int _0^1 dx\, \bigg \{ \frac{\sigma (\rho )}{2} \left( \partial _x \frac{\delta \psi ^{(\alpha )}_\text {right}}{\delta \rho (x,t)}+{\varPhi }'(q)\alpha (x)- \frac{D(\rho )\partial _x\rho }{\sigma (\rho )}\right) ^2 -\frac{(D(\rho )\partial _x\rho )^2}{2\sigma (\rho )}\bigg \}\nonumber \\&\quad ={\varPhi }'(q)\,q-{\varPhi }(q) \end{aligned}$$
(8b)

One should note that all our results for the conditioned process are in the large T limit.

We present this paper in the following order. In Sect. 2, we discuss the microscopic framework for analyzing the conditioned probability in a general lattice gas model and introduce conditioned large deviation function in the hydrodynamic limit. Our calculation is in a weighted ensemble, which is known [1, 8, 23, 29,30,31] to be equivalent to the conditioned process in the large T limit (through an equivalence of ensembles). We use this procedure to derive \(\psi _t^{(\alpha )}[\rho (x), q]\) for the diffusing independent particles in Sect. 3, and for the symmetric simple exclusion process in Sect. 4. Using this microscopic approach we describe the conditioned dynamics in Sect. 5. In Sects. 6 and 7, we show how our expressions of the large deviation function \(\psi _t^{(\alpha )}[\rho (x), q]\) fit with the Hamilton–Jacobi equations derived from a macroscopic approach starting from the fluctuating hydrodynamics description (1).

2 Microscopic Analysis Using the Tilted Matrix

Let us first recall a few earlier results [1, 8, 16, 23, 29,30,31,32, 54] for a Markov process conditioned on an empirical measure by writing them for the two examples: (a) diffusing independent particles and (b) the symmetric simple exclusion process. These are defined on a finite one-dimensional lattice of L sites where particles jump between neighboring sites following a continuous time \(\tau \) update rule (see Figs. 4 and 5). The jump rates at the boundary correspond to coupling to reservoirs of density \(\rho _a\) and \(\rho _b\) [36]. In both examples, a configuration is specified by the set of occupation variables \({\mathbf {n}}\equiv \{n_1,\ldots ,n_L\}\).

The microscopic analogue of the empirical observable (3) is

(9)

where \(\varvec{\lambda }\equiv \{\lambda _0,\ldots ,\lambda _L\}\) with \(\lambda _i\) being real valued parameters. A jump from site \(i+1\) to i is counted as a jump from site i to \(i+1\) with a negative sign. (Here, \(i=0\) denotes the left reservoir and \(i=L+1\) denotes the right reservoir.) Similar to the condition in (3) we consider

$$\begin{aligned} \sum _{i=0}^{L}\lambda _i=1. \end{aligned}$$
(10)
Fig. 4
figure 4

Transition rates for independent particles on a one-dimensional chain coupled with reservoirs of density \(\rho _a\) and \(\rho _b\). The number of particles \(n_i\ge 0\) at a site i is arbitrary

Full size image
Fig. 5
figure 5

Transition rates of particles in the symmetric simple exclusion process on a one-dimensional chain coupled with reservoirs of density \(\rho _a\) and \(\rho _b\). A site is occupied at most by one particle at a time

Full size image

2.1 Tilted Matrix

Instead of conditioning on the value of \({\mathcal {Q}}_N^{(\varvec{\lambda })}\), it is more convenient [1, 8, 29,30,31, 54] to work in the ensemble where events are weighted by a factor \(e^{\kappa {{\mathcal {Q}}_N^{(\varvec{\lambda })}}}\). By analogy [1, 8, 23, 29, 31, 33, 55] with equilibrium thermodynamics, we shall refer to this ensemble as the canonical ensemble and the ensemble where \({\mathcal {Q}}_N^{(\varvec{\lambda })}\) is fixed as the micro-canonical ensemble. For large N, these two ensembles are equivalent (see Sect. 2.3).

In the canonical ensemble, we need to introduce the following tilted matrix [29]

$$\begin{aligned} {\mathcal {M}}_\kappa ^{(\varvec{\lambda })}({\mathbf {n}}',{\mathbf {n}})= {\left\{ \begin{array}{ll}e^{\kappa \sum _{i=0}^{L}\lambda _i \, {\mathcal {J}}_{i}\left( {\mathbf {n}}',{\mathbf {n}}\right) }{\mathcal {M}}_0({\mathbf {n}}',{\mathbf {n}}) \qquad &{} \text {for }{\mathbf {n}}'\ne {\mathbf {n}},\\ -{\sum }_{{\mathbf {n}}''\ne {\mathbf {n}}}{\mathcal {M}}_0({\mathbf {n}}'',{\mathbf {n}}) \qquad &{}\text {for }{\mathbf {n}}'= {\mathbf {n}} \end{array}\right. } \end{aligned}$$
(11)

where \({\mathcal {M}}_0({\mathbf {n}}',{\mathbf {n}})\) is the transition rate from configuration \({\mathbf {n}}\) to \({\mathbf {n}}'\) in the original (without condition) dynamics and for this transition,

$$\begin{aligned} {\mathcal {J}}_{i}({\mathbf {n}}',{\mathbf {n}})= {\left\{ \begin{array}{ll} 1, &{} \text {if a particle jumps from } i \text { to } i+1,\\ -1, &{} \text {if a particle jumps from } i+1 \text { to } i,\\ 0, &{} \text {if no particle jumps between } i \text { and } i+1. \end{array}\right. } \end{aligned}$$

The scaled cumulant generating function of \({\mathcal {Q}}_N^{(\varvec{\lambda })}\), defined by

$$\begin{aligned} \mu (\kappa )=\lim _{N\rightarrow \infty }\frac{\log \left\langle e^{\kappa {{\mathcal {Q}}_N^{(\varvec{\lambda })}}}\right\rangle }{N}, \end{aligned}$$
(12)

is the largest eigenvalue of \({\mathcal {M}}_\kappa ^{(\varvec{\lambda })}\) [29] such that

$$\begin{aligned} \sum _{{\mathbf {n}}}{\mathcal {M}}_\kappa ^{(\varvec{\lambda })}({\mathbf {n}}',{\mathbf {n}})\,{\mathcal {R}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})&=\mu (\kappa )\,{\mathcal {R}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}}') \end{aligned}$$
(13a)
$$\begin{aligned} \sum _{{\mathbf {n}}'}{\mathcal {L}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}}')\,{\mathcal {M}}_\kappa ^{(\varvec{\lambda })}({\mathbf {n}}',{\mathbf {n}})&= \mu (\kappa )\,{\mathcal {L}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}}) \end{aligned}$$
(13b)

where \({\mathcal {R}}^{(\kappa ,\varvec{\lambda })}\) and \({\mathcal {L}}^{(\kappa ,\varvec{\lambda })}\) are the associated right and left eigenvectors, respectively.

At times of our interest, namely \(\tau =0\), \(\tau =N\), and in the quasi-stationary regime, the probability \(P_\tau ^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})\) of a configuration \({\mathbf {n}}\) in the canonical ensemble can be expressed (see [8, 29, 56]) in terms of these eigenvectors up to normalization constants.

  • At time \(\tau =0\),

    $$\begin{aligned} P_0^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})={\mathcal {L}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})\;{\mathcal {R}}^{(0,\varvec{\lambda })}({\mathbf {n}}) \end{aligned}$$
    (14a)

  • at time \(\tau =N\),

    $$\begin{aligned} P_N^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})={\mathcal {R}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}}) \end{aligned}$$
    (14b)

  • and in the quasi-stationary regime, i.e.\(1\ll \tau \) with \(1\ll N-\tau \),

    $$\begin{aligned} P_\text {qs}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})={\mathcal {L}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})\,{\mathcal {R}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}}). \end{aligned}$$
    (14c)

2.2 Dependence on \(\lambda \)

In our examples, the number of particles is conserved inside the bulk of the system, which means

$$\begin{aligned} {\mathcal {J}}_{i-1}({\mathbf {n}}',{\mathbf {n}})-{\mathcal {J}}_{i}({\mathbf {n}}',{\mathbf {n}})=n_i'-n_i \end{aligned}$$

for all \(1\le i\le L\) and equivalently

$$\begin{aligned} {\mathcal {J}}_{i}({\mathbf {n}}',{\mathbf {n}})={\mathcal {J}}_{0}({\mathbf {n}}',{\mathbf {n}})-\sum _{j=1}^{i}(n_j'-n_j). \end{aligned}$$

This conservation of particles leads to a symmetry of the tilted matrix and its eigenvectors. To see this, we use the above relation in (11). Here, using \(\sum _{i=1}^{L}\lambda _i\sum _{j=1}^{i} n_j=\sum _{i=1}^{L} n_i\sum _{j\ge i}^{L}\lambda _j\) and the normalization (10) we get

$$\begin{aligned} \left[ e^{\kappa \sum _{i=1}^{L}n_i' \sum _{j\ge i}^{L}\lambda _j }\right] {\mathcal {M}}_\kappa ^{(\varvec{\lambda })}({\mathbf {n}}',{\mathbf {n}})\left[ e^{-\kappa \sum _{i=1}^{L}n_i \sum _{j\ge i}^{L}\lambda _j }\right]&= {\mathcal {M}}_{\kappa }({\mathbf {n}}',{\mathbf {n}}) \end{aligned}$$

where \({\mathcal {M}}_{\kappa }\) is the tilted matrix for the case where \(\lambda _0=1\) and \(\lambda _i=0\) for rest of the sites. Denoting the eigenvectors of \({\mathcal {M}}_{\kappa }\) as \(({\mathcal {R}}^{(\kappa )},\,{\mathcal {L}}^{(\kappa )})\), we get

$$\begin{aligned} {\mathcal {R}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})\left[ e^{\kappa \sum _{i=1}^{L}n_i\sum _{j\ge i}^{L}\lambda _j}\right]&= {\mathcal {R}}^{(\kappa )}({\mathbf {n}}) \end{aligned}$$
(15a)
$$\begin{aligned} {\mathcal {L}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})\left[ e^{-\kappa \sum _{i=1}^{L}n_i\sum _{j\ge i}^{L}\lambda _j}\right]&= {\mathcal {L}}^{(\kappa )}({\mathbf {n}}). \end{aligned}$$
(15b)

Moreover, the eigenvalue \(\mu (\kappa )\) is same in the two cases, which shows that it is independent of \(\lambda \).

This gives the \({{\varvec{\lambda }}}\)-dependence of the probabilities (14). For example, using (15) in (14c) we see that in the quasi-stationary regime, the probability \(P_\text {qs}^{(\kappa ,\varvec{\lambda })}\) is independent \(\varvec{\lambda }\) (given the normalization in (10)),

$$\begin{aligned} P_\text {qs}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})\equiv P_\text {qs}^{(\kappa )}({\mathbf {n}}). \end{aligned}$$
(16)

2.3 An Equivalence of Ensembles: Canonical Versus Micro-canonical

For large time N, there is [1, 8, 23, 29,30,31] an equivalence between the canonical ensemble and the micro-canonical ensemble, where \({\mathcal {Q}}_N^{(\varvec{\lambda })}\) is fixed. In this equivalence, the conditioned probability \({\mathcal {P}}_\tau ^{(\varvec{\lambda })}({\mathbf {n}}\vert {\mathcal {Q}})\) of a configuration \({\mathbf {n}}\) at time \(\tau \) given \({\mathcal {Q}}_N^{(\varvec{\lambda })}={\mathcal {Q}}\) is related to the probability \(P_\tau ^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})\) in the canonical ensemble by

$$\begin{aligned} {\mathcal {P}}_\tau ^{(\varvec{\lambda })}({\mathbf {n}}\vert {\mathcal {Q}}=vN)\simeq P_\tau ^{(\phi '(v),\varvec{\lambda })}({\mathbf {n}}) \qquad \text {for large time }N, \end{aligned}$$
(17)

where \(\phi (v)\) is the Legendre transform of the eigenvalue \(\mu (\kappa )\), defined by

$$\begin{aligned} \phi (v)=v\, \kappa -\mu (\kappa )\qquad \text {with } \mu '(\kappa )=v. \end{aligned}$$
(18)

This also means [36, 42, 43, 49] that the probability of \({\mathcal {Q}}_N^{(\varvec{\lambda })}\) has a large deviation form given by

$$\begin{aligned} P({\mathcal {Q}}_N^{(\varvec{\lambda })}=vN)\sim e^{-N\phi (v)} \qquad \text { for large time } N. \end{aligned}$$
(19)

In this work, our results for the micro-canonical ensemble are obtained from the canonical ensemble using the equivalence (17).

2.4 Hydrodynamic Limit

Our main interest is the probability in the hydrodynamic limit, which is defined in the scaled coordinates \((x,t)\equiv (\tfrac{i}{L},\tfrac{\tau }{L^2})\) for large L, with \(N=L^2T\) and \(\lambda _i=\frac{1}{L}\alpha (x)\) such that

$$\begin{aligned} {\mathcal {Q}}_N^{(\varvec{\lambda })}\simeq L\,Q_T^{(\alpha )}\qquad \text {for large }L, \end{aligned}$$

with \(Q_T^{(\alpha )}\) given in (3). In this hydrodynamic limit,

$$\begin{aligned} \phi \left( v=\frac{q}{L}\right) \simeq \frac{1}{L}{\varPhi }(q),\qquad \qquad \mu (\kappa )\simeq \frac{1}{L}\chi (\kappa ) \end{aligned}$$
(20)

and they are related (due to (18)) by

$$\begin{aligned} {\varPhi }(q)=q\, \kappa -\chi (\kappa )\qquad \text {for } \chi '(\kappa )=q. \end{aligned}$$
(21)

This scaling (20) is well known [42, 43, 48, 49] and this will be confirmed in our examples.

For the probability of occupation variables \({\mathbf {n}}\), taking a hydrodynamic limit means [36, 38, 57] coarse-graining the system over boxes of width w with \(1\ll w\ll L\), such that each box has a total density \(\rho (x)\) which varies smoothly on the hydrodynamic scale x. If \(P({\mathbf {n}})\) is the probability of a microscopic configuration \({\mathbf {n}}\), then the probability \(P[\rho (x)]\) of a hydrodynamic density profile \(\rho (x)\) is

$$\begin{aligned} \sum _{{\mathbf {n}}\in \rho (x)}P({\mathbf {n}}) \simeq P[\rho (x)] \end{aligned}$$
(22)

where the summation is over all \({\mathbf {n}}\) that correspond to the profile \(\rho (x)\) (see for example Sect. 3).

The right eigenvector \({\mathcal {R}}^{(\kappa ,\varvec{\lambda })}\) has an interpretation of a probability (see (14b)) and therefore, its hydrodynamic limit is similarly defined by

$$\begin{aligned} \sum _{{\mathbf {n}}\in \rho (x)}{\mathcal {R}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})\simeq r^{(\kappa ,\alpha )}[\rho (x)] \end{aligned}$$
(23a)

In comparison, \({\mathcal {L}}^{(\kappa ,\varvec{\lambda })}\) by itself does not have an interpretation of a probability. Considering (14a, 14c), we define the hydrodynamic limit for the left eigenvector as

$$\begin{aligned} {\mathcal {L}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})\simeq \ell ^{(\kappa ,\alpha )}[\rho (x)] \end{aligned}$$
(23b)

for each configuration \({\mathbf {n}}\) that corresponds to the profile \(\rho (x)\). (Note that in contrast to (23a) there is no summation over \({\mathbf {n}}\) in (23b).)

Using this construction of the hydrodynamic limit in (23), we see that the probability in (14) leads to the probability of density \(\rho (x)\), which

  • at \(t=0\) is given by

    $$\begin{aligned} P_{t=0}^{(\kappa ,\alpha )}[\rho (x)]\simeq \, \ell ^{(\kappa ,\alpha )}[\rho (x)]\;r^{(0,\alpha )}[\rho (x)], \end{aligned}$$
    (24a)

  • at \(t=T\) is given by

    $$\begin{aligned} P_{t=T}^{(\kappa ,\alpha )}[\rho (x)]\simeq \, r^{(\kappa ,\alpha )}[\rho (x)], \end{aligned}$$
    (24b)

  • and in the quasi-stationary regime (\(1\ll t\) and \(1\ll T-t\)) is given by

    $$\begin{aligned} P_\text {qs}^{(\kappa ,\alpha )}[\rho (x)]\equiv P_\text {qs}^{(\kappa )}[\rho (x)]\simeq \, \ell ^{(\kappa ,\alpha )}[\rho (x)]\; r^{(\kappa ,\alpha )}[\rho (x)], \end{aligned}$$
    (24c)

    up to normalization constants.

Remark

Note that to obtain both (24a) and (24c) we have replaced the sum \(\sum _{{\mathbf {n}}\in \rho (x)}{\mathcal {L}}({\mathbf {n}}){\mathcal {R}}({\mathbf {n}})\) by \(\ell [\rho (x)]\sum _{{\mathbf {n}}\in \rho (x)}{\mathcal {R}}({\mathbf {n}})\) for large L. We will see that this relation is satisfied for the two models that we consider in this paper. It is expected to remain valid for more general diffusive systems [58].

2.5 Large Deviation Function

In our examples we shall see that the hydrodynamic limit of the eigenvectors have a large deviation form given by

$$\begin{aligned}&\displaystyle r^{(\kappa ,\alpha )}[\rho (x)]\sim e^{-L\,\psi _\text {right}^{(\kappa ,\alpha )}[\rho (x)]} \end{aligned}$$
(25a)
$$\begin{aligned}&\displaystyle \ell ^{(\kappa ,\alpha )}[\rho (x)]\sim e^{-L\,\psi _\text {left}^{(\kappa ,\alpha )}[\rho (x)]} \end{aligned}$$
(25b)

Using them in (24) gives

$$\begin{aligned} {\mathcal {P}}_t^{(\kappa ,\alpha )}[\rho (x)]\sim e^{-L\,\psi _t^{(\kappa ,\alpha )}[\rho (x)]} \end{aligned}$$
(26)

with the large deviation function

  • at \(t=0\),

    $$\begin{aligned} \psi _0^{(\kappa ,\alpha )}[\rho (x)]=\psi _\text {left}^{(\kappa ,\alpha )}[\rho (x)]+\psi _\text {right}^{(0,\alpha )}[\rho (x)] \end{aligned}$$
    (27a)

  • at \(t=T\),

    $$\begin{aligned} \psi _T^{(\kappa ,\alpha )}[\rho (x)]=\psi _\text {right}^{(\kappa ,\alpha )}[\rho (x)] \end{aligned}$$
    (27b)

  • and in the quasi-stationary regime, i.e.\(t\gg 1\) and \(T-t\gg 1\),

    $$\begin{aligned} \psi _t^{(\kappa ,\alpha )}[\rho (x)]\equiv \psi _{\text {qs}}^{(\kappa )}[\rho (x)]= \psi _\text {left}^{(\kappa ,\alpha )}[\rho (x)]+\psi _\text {right}^{(\kappa ,\alpha )}[\rho (x)] \end{aligned}$$
    (27c)

where all these equalities are up to an additive constant (independent of \(\rho (x)\)).

Remark

From (15) we see that the large deviation functions in (25) have a simple dependence on \(\alpha (x)\), given by

$$\begin{aligned} \psi ^{(\kappa , \alpha )}_\text {right}[\rho (x)]&=V^{(\kappa )}_\text {right}[\rho (x)]+\kappa \int _0^1dx\, \rho (x)\int _x^1dy\,\alpha (y) \end{aligned}$$
(28a)
$$\begin{aligned} \psi ^{(\kappa , \alpha )}_\text {left}[\rho (x)]&=V^{(\kappa )}_\text {left}[\rho (x)]-\kappa \int _0^1dx\, \rho (x)\int _x^1dy\,\alpha (y) \end{aligned}$$
(28b)

where \(V^{(\kappa )}_\text {right}[\rho (x)]\) and \(V^{(\kappa )}_\text {left}[\rho (x)]\) are the large deviation functions associated to \({\mathcal {R}}^{(\kappa )}\) and \({\mathcal {L}}^{(\kappa )}\) in (15) (following a definition similar to (23) and (25)).

3 Independent Particles

In this section, we analyze the simple case of a system of independent particles with transition rates defined in Fig. 4. Considering the symmetry (15) it is sufficient to analyze the case \(\lambda _0=1\), and \(\lambda _i=0\) for \(i\ge 1\). In the rest of our analysis, we shall consider this case, unless explicitly stated otherwise.

In this case the tilted matrix (11) is

$$\begin{aligned} \left[ {\mathcal {M}}_\kappa \cdot {\varOmega }\right] ({\mathbf {n}})&=e^{\kappa }\rho _a {\varOmega }(n_1-1,\ldots )+e^{-\kappa }(n_1+1){\varOmega }(n_1+1,\ldots )\\&\quad +(n_L+1){\varOmega }(\ldots ,n_L+1)+\rho _b {\varOmega }(\ldots ,n_L-1) \\&\quad +\sum _{i=1}^{L-1}\bigg [(n_i+1){\varOmega }(\ldots ,n_i+1,n_{i+1}-1,\ldots )\\&\quad +(n_{i+1}+1){\varOmega }(\ldots ,n_i-1,n_{i+1}+1,\ldots )\bigg ]\\&\quad -(\rho _a+2n_1+\ldots +2n_L+\rho _b){\varOmega }({\mathbf {n}}) \end{aligned}$$

where \({\varOmega }({\mathbf {n}})\) is the component of an arbitrary state vector \(\varvec{{\varOmega }}\) in the configuration space.

The eigenvalue equations (13) become

$$\begin{aligned} \left[ {\mathcal {M}}_\kappa \cdot {\mathcal {R}}^{(\kappa )}\right] ({\mathbf {n}})&=\mu (\kappa )\;{\mathcal {R}}^{(\kappa )}({\mathbf {n}}) \end{aligned}$$
(29a)
$$\begin{aligned} \left[ {\mathcal {L}}^{(\kappa )} \cdot {\mathcal {M}}_\kappa \right] ({\mathbf {n}})&=\mu (\kappa )\;{\mathcal {L}}^{(\kappa )}({\mathbf {n}}) \end{aligned}$$
(29b)

One can check that the right and left eigenvectors are of the form

$$\begin{aligned} {\mathcal {R}}^{(\kappa )}({\mathbf {n}})&=\prod _{i=1}^{L}\frac{a_i^{n_i}}{n_i!}e^{-a_i} \end{aligned}$$
(30a)
$$\begin{aligned} {\mathcal {L}}^{(\kappa )}({\mathbf {n}})&=\prod _{i=1}^{L}b_i^{n_i} \end{aligned}$$
(30b)

where \((a_i, b_i)\) are positive numbers to be determined. With this ansatz the eigenvalue equations (29) lead to

$$\begin{aligned} e^{-\kappa }a_1+ a_L-\rho _a-\rho _b-\mu (\kappa ) +\sum _{i=1}^{L}\left[ e^{\kappa \delta _{i,1} }\frac{a_{i-1}}{a_{i}}+\frac{a_{i+1}}{a_i}-2\right] n_i=0\\ e^{\kappa }\rho _a b_1+ \rho _b b_L-\rho _a-\rho _b-\mu (\kappa ) +\sum _{i=1}^{L}\left[ e^{-\kappa \delta _{i,1} }\frac{b_{i-1}}{b_i}+\frac{b_{i+1}}{b_i}-2\right] n_i=0 \end{aligned}$$

with \(a_0=\rho _a\), \(a_{L+1}=\rho _b\), and \(b_0=1=b_{L+1}\). As the occupation variables \(n_i\) are arbitrary, for the equations to be satisfied, their coefficients must vanish. This leads to a set of coupled linear equations for \(a_i\) and \(b_i\), which can be easily solved, and we get, for \(1\le i\le L\),

$$\begin{aligned} a_i&= \rho _a\left( 1-\frac{i}{L+1}\right) e^{\kappa }+\rho _b\frac{i}{L+1} \end{aligned}$$
(31a)
$$\begin{aligned} b_i&=\left( 1-\frac{i}{L+1}\right) e^{-\kappa }+\frac{i}{L+1} \end{aligned}$$
(31b)

with the largest eigenvalue

$$\begin{aligned} \mu (\kappa )=\mu _\text {ni}(\kappa )=\frac{\rho _a}{L+1}\left( e^{\kappa }-1 \right) +\frac{\rho _b}{L+1}\left( e^{-\kappa }-1 \right) \end{aligned}$$
(32)

3.1 Hydrodynamic Limit

In the hydrodynamic limit, from (32) it is easy to confirm (20), which gives

$$\begin{aligned} \chi (\kappa )\equiv \chi _{\text {ni}}(\kappa )=\rho _a\left( e^{\kappa }-1 \right) +\rho _b\left( e^{-\kappa }-1 \right) \end{aligned}$$
(33)

For the hydrodynamic limit of the right eigenvector, defined in (23a), we decompose the system into \(M=L/w\) boxes each containing w sites and define

$$\begin{aligned} r^{(\kappa )}(\rho _1,\ldots ,\rho _{M})=\sum _{{\mathbf {n}}}{\mathcal {R}}^{(\kappa )}({\mathbf {n}}) \end{aligned}$$

where the sum is over all configurations with \(\rho _m w\) particles in the m-th box. Then, using (30a) we get

$$\begin{aligned} r^{(\kappa )}(\rho _1,\ldots ,\rho _{M})=\prod _{m=1}^{M}\left\{ \sum _{n_{m_1}}\cdots \sum _{n_{m_w}}\left[ \frac{a_{m_1}^{n_{m_1}}}{n_{m_1}!}\cdots \frac{a_{m_w}^{n_{m_w}}}{n_{m_w}!}e^{-a_{m_1}\cdots -a_{m_w}}\right] \,\delta _{\rho _m w ,\sum _i n_{m_i}}\right\} \end{aligned}$$

where \(m_i\) denotes the site index of the i-th site of the mth box, and \(\delta _{i,j}\) is the Kronecker delta. Using an identity

$$\begin{aligned} \sum _{n_1=0}^{\infty }\sum _{n_2=0}^{\infty }\frac{a_{1}^{n_{1}}}{n_{1}!}\frac{a_{2}^{n_{2}}}{n_{2}!}\,\delta _{n,n_1+n_2}=\frac{(a_{1}+a_2)^{n}}{n!} \end{aligned}$$

and that \(a_{i}\) is slowly varying such that \(a_{i}\simeq a(\frac{m w}{L})\) when the site i is in the m-th box, and defining \(\rho _{m}= \rho (\frac{m w}{L})\) we get

$$\begin{aligned} r^{(\kappa )}(\rho _1,\ldots ,\rho _{M})\simeq \prod _{m=1}^{M} \frac{\left[ w\,a(\frac{m w}{L})\right] ^{w\, \rho (\frac{m w}{L})}}{[w\, \rho (\frac{m w}{L})]!}\; e^{-w\,a(\frac{m w}{L})} \end{aligned}$$

Then, for \(1\ll w\ll L\), using the Stirling’s formula we get (following the definition (23a, 25a, 28a))

$$\begin{aligned} r^{(\kappa )}(\rho _1,\ldots ,\rho _{M})\simeq r^{(\kappa )}[\rho (x)]\sim e^{-L\,V_\text {right}^{(\kappa )}[\rho (x)]} \end{aligned}$$

with

$$\begin{aligned} V^{(\kappa )}_\text {right}[\rho (x)]= H_\text {ni}[\rho (x),a(x)] \end{aligned}$$
(34a)

where we defined

$$\begin{aligned} H_\text {ni}[\rho (x),a(x)]= \int _0^1 dx \left[ \rho (x)\log \frac{\rho (x)}{a(x)} -\rho (x)+a(x)\right] \end{aligned}$$
(34b)

and

$$\begin{aligned} a(x)= \rho _a\left( 1-x\right) e^{\kappa }+\rho _b x \end{aligned}$$
(34c)

For the left eigenvector, the hydrodynamic limit (23b) is simple to construct from (30b), which (following the definition (23b, 25b, 28b)) leads to \(\ell ^{(\kappa )}[\rho (x)]\sim e^{-L\,V_\text {left}^{(\kappa )}[\rho (x)]}\) with

$$\begin{aligned} V^{(\kappa )}_\text {left}[\rho (x)]=\int _0^1 dx&\,\rho (x)\log \frac{1}{b(x)} \end{aligned}$$
(35a)

and

$$\begin{aligned} b(x)= e^{-\kappa }(1-x)+ x \end{aligned}$$
(35b)

Remark

The \(\kappa =0\) corresponds to the case without a condition on the empirical observable. So, the steady state large deviation function of density \({\mathcal {F}}_\text {ni}[\rho (x)]=V_\text {right}^{(0)}[\rho (x)]\) is

$$\begin{aligned} {\mathcal {F}}_\text {ni}[\rho (x)]=H_\text {ni}[\rho (x),{\bar{\rho }}_\text {free}(x)]\qquad \text {with }\quad {\bar{\rho }}_\text {free}(x)=\rho _a(1-x)+\rho _b x \end{aligned}$$
(36)

3.2 Large Deviation Function

Expressions for \(\psi ^{(\kappa ,\alpha )}_\text {left}\) and \(\psi ^{(\kappa ,\alpha )}_\text {right}\) for an arbitrary \(\alpha (x)\) follow from (28). Using this result in (27) we get the large deviation function at three different times, all of which are of the form

$$\begin{aligned} \psi _t^{(\kappa ,\alpha )}[\rho (x)]=H_\text {ni}[\rho (x),{{\bar{\rho }}}_{t}^{(\kappa ,\alpha )}(x)] \end{aligned}$$
(37)

with the average density profile

  • at \(t=0\),

    $$\begin{aligned} {{\bar{\rho }}}_{0}^{(\kappa ,\alpha )}(x)={\bar{\rho }}_\text {free}(x)\left[ (1-x)e^{-\kappa \int _0^{x}dy\alpha (y)}+\, x\,e^{\kappa \int _x^{1}dy \alpha (y)}\right] \end{aligned}$$
    (38a)

  • at \(t=T\),

    $$\begin{aligned} {{\bar{\rho }}}_{T}^{(\kappa ,\alpha )}(x)=\rho _a(1-x)e^{\kappa \int _0^{x}dy\alpha (y)}+\rho _b\, x\,e^{-\kappa \int _x^{1}dy \alpha (y)} \end{aligned}$$
    (38b)

  • and in the quasi-stationary regime,

    $$\begin{aligned} {{\bar{\rho }}}_\text {qs}(x)={\bar{\rho }}_\text {free}(x)+x(1-x)\left[ \rho _a\left( e^{\kappa }-1 \right) +\rho _b\left( e^{-\kappa }-1 \right) \right] \end{aligned}$$
    (38c)

4 Symmetric Simple Exclusion Process

In this section, we analyze the one-dimensional symmetric simple exclusion process with the transition rates defined in Fig. 5. We indicate how to perform a low-density expansion. Our results will be limited to the first two terms in this expansion, although it is straightforward to extend our approach to higher orders. Considering the symmetry (15) we will analyze only the case \(\lambda _0=1\), and \(\lambda _i=0\) for \(i\ge 1\).

4.1 A Representation of the Eigenvectors

A configuration can be specified by the position of the particles. In a configuration with m occupied sites \(\{i_1,\ldots ,i_m\}\) we denote the component of the eigenvectors as

$$\begin{aligned} {\mathcal {R}}^{(\kappa )}({\mathbf {n}})\equiv {\mathcal {R}}^{(\kappa )}(i_1,\ldots ,i_m)\qquad \text {and}\qquad {\mathcal {L}}^{(\kappa )}({\mathbf {n}})\equiv {\mathcal {L}}^{(\kappa )}(i_1,\ldots ,i_m) \end{aligned}$$
(39)

We normalize such that the component of both eigenvectors in the empty configuration is 1.

4.2 A perturbation Solution for Small Density

For finite L, the Perron-Frobenius theorem [59] assures that the largest eigenvalue of the tilted matrix is non-degenerate. Expressions of the eigenvalue and eigenvectors exist [60, 61], but it is hard to extract from them the large scale behaviors. Here, we use a perturbation expansion in small \(\rho _a\) and \(\rho _b\), where it is possible to systematically solve the eigenvalue equation order by order. We write

$$\begin{aligned} \mu (\kappa )&=\mu _0(\kappa )+\mu _1(\kappa )+\mu _2(\kappa )+\cdots \end{aligned}$$
(40a)
$$\begin{aligned} {\mathcal {R}}^{(\kappa )}&= {\mathcal {R}}_0^{(\kappa )}+{\mathcal {R}}_1^{(\kappa )}+{\mathcal {R}}_2^{(\kappa )}+\cdots \end{aligned}$$
(40b)
$$\begin{aligned} {\mathcal {L}}^{(\kappa )}&= {\mathcal {L}}_0^{(\kappa )}+{\mathcal {L}}_1^{(\kappa )}+{\mathcal {L}}_2^{(\kappa )}+\cdots \end{aligned}$$
(40c)

with increasing orders in \(\rho _a\) and \(\rho _b\).

For \(\rho _a=\rho _b=0\), all \({\mathcal {R}}_n^{(\kappa )}=0\) except for the empty configuration and one has \(\mu _0(\kappa )=0\). Considering that the injection rates of particles into the system are of order one in density whereas the extraction rates are of order zero, it is also clear that at order n in \(\rho _a\) and \(\rho _b\), the \({\mathcal {R}}_n^{(\kappa )}\) of configurations with more than n occupied sites vanish. (This is evident in the block-diagonal structure of the tilted matrix given in Appendix A.) Therefore,

$$\begin{aligned}&{\mathcal {R}}_0^{(\kappa )}(i)=0,\\&{\mathcal {R}}_0^{(\kappa )}(i,j)={\mathcal {R}}_1^{(\kappa )}(i,j)=0,\\&{\mathcal {R}}_0^{(\kappa )}(i,j,k)={\mathcal {R}}_1^{(\kappa )}(i,j,k)={\mathcal {R}}_2^{(\kappa )}(i,j,k)=0, \end{aligned}$$

and so on. Here we present the solution up to only the second order.

The equations one needs to solve up to the second order in \(\rho _a\) and \(\rho _b\) are given in the Appendix A. Since at this order \({\mathcal {R}}_2^{(\kappa )}\) of configurations with 3 or more occupied sites vanish, the hierarchy closes. For arbitrary L, we get the solution

$$\begin{aligned} \mu _1(\kappa )&=\frac{\rho _a}{L+1}\left( e^{\kappa }-1 \right) +\frac{\rho _b}{L+1}\left( e^{-\kappa }-1 \right) \end{aligned}$$
(41a)
$$\begin{aligned} \mu _2(\kappa )&=- \frac{\left( e^\kappa -1\right) ^2}{6(L+1)^2}\left[ 2L\left( \rho _a^2+\rho _a\rho _be^{-\kappa }+\rho _b^2e^{-2\kappa }\right) + \rho _a^2+4\rho _a\rho _be^{-\kappa }+\rho _b^2e^{-2\kappa }\right] \end{aligned}$$
(41b)

in agreement with an earlier result [56]. The right eigenvector, up to the second order, is given by

$$\begin{aligned}&{\mathcal {R}}_1^{(\kappa )}(i)= \,e^{\kappa }\rho _a\left( 1-\frac{i}{L+1}\right) +\rho _b\frac{i}{L+1} \end{aligned}$$
(42a)
$$\begin{aligned}&{\mathcal {R}}_2^{(\kappa )}(i)= \,e^{\kappa }\rho _a^2\left( 1-\frac{i}{L+1}\right) +\rho _b^2\frac{i}{L+1} \nonumber \\&\quad -\left( e^\kappa \rho _a-\rho _b\right) ^2\frac{i}{6L}\left( 1-\frac{i}{L+1}\right) \left[ e^{-\kappa }\left( 2-\frac{i}{L+1}\right) +1+\frac{i}{L+1}\right] \end{aligned}$$
(42b)
$$\begin{aligned}&{\mathcal {R}}_2^{(\kappa )}(i,j) - {\mathcal {R}}_1^{(\kappa )}(i){\mathcal {R}}_1^{(\kappa )}(j) = -\frac{\left( \rho _a e^\kappa -\rho _b\right) ^2}{(L+1)}\frac{i}{L}\left( 1-\frac{j}{L+1}\right) \qquad \text {for }j\ge i \end{aligned}$$
(42c)

As the probabilities (14) are always a product of a left and a right eigenvector, we will only need the following orders for the left eigenvector.

$$\begin{aligned}&{\mathcal {L}}_0^{(\kappa )}(i)= e^{-\kappa }\left( 1-\frac{i}{L+1}\right) +\frac{i}{L+1} \end{aligned}$$
(43a)
$$\begin{aligned}&{\mathcal {L}}_1^{(\kappa )}(i)= \left( e^{-\kappa }-1\right) ^2\frac{i}{6L}\left( \frac{i}{L+1}-1\right) \left[ e^{\kappa }\rho _a\left( 2-\frac{i}{L+1}\right) +\rho _b\left( 1+\frac{i}{L+1}\right) \right] \end{aligned}$$
(43b)
$$\begin{aligned}&{\mathcal {L}}_0^{(\kappa )}(i,j)- {\mathcal {L}}_0^{(\kappa )}(i)\; {\mathcal {L}}_0^{(\kappa )}(j)= -\frac{\left( e^{-\kappa }-1\right) ^2}{(L+1)}\frac{i}{L}\left( 1-\frac{j}{L+1}\right) \qquad \text {for }j\ge i \end{aligned}$$
(43c)

Remarks

  • For the symmetric simple exclusion process, the eigenvalue equation can be systematically solved to arbitrary order. The “miracle” which makes an explicit solution possible in practice is that at every order, the eigenvectors are low degree polynomials of the site indices i. This is special to the exclusion process, and may not apply to other diffusive systems.

  • At the first order in \(\rho _a\) and \(\rho _b\), the expressions of eigenvalue and eigenvectors coincide with that of the independent particles case in Sect. 3.

4.3 Cumulants of the Occupation Variable

One can then derive the cumulants of the occupation variables from the probability (14). For example, at time \(\tau =N\), using (14b) and the representation (39) we get

$$\begin{aligned} \left\langle n_i \right\rangle&=\frac{1}{{\mathcal {N}}}\bigg ({\mathcal {R}}^{(\kappa )}(i)+\sum _{j\ne i}{\mathcal {R}}^{(\kappa )}(i,j)+\cdots \bigg )\\ \left\langle n_i n_j \right\rangle&=\frac{1}{{\mathcal {N}}}\bigg ({\mathcal {R}}^{(\kappa )}(i,j)+\sum _{k\ne i,j}{\mathcal {R}}^{(\kappa )}(i,j,k)+\cdots \bigg ) \end{aligned}$$

where the normalization \({\mathcal {N}}=1+\sum _i{\mathcal {R}}^{(\kappa )}(i)+\sum _i\sum _{j\ne i}{\mathcal {R}}^{(\kappa )}(i,j)+\cdots \).

Using this with the perturbation solution of the eigenvectors we can construct a perturbation expansion of the cumulants for the low density limit. For example, at the second order in \(\rho _a\) and \(\rho _b\), the average occupation of a site i at time \(\tau =N\) is

$$\begin{aligned} \left\langle n_i \right\rangle ={\mathcal {R}}_1^{(\kappa )}(i)+{\mathcal {R}}_2^{(\kappa )}(i)-\left( {\mathcal {R}}_1^{(\kappa )}(i)\right) ^2+\sum _{j\ne i}\left( {\mathcal {R}}_2^{(\kappa )}(i,j)- {\mathcal {R}}_1^{(\kappa )}(i){\mathcal {R}}_1^{(\kappa )}(j)\right) +\cdots \end{aligned}$$
(44a)

and the connected correlation

$$\begin{aligned} \left\langle n_i n_j\right\rangle _c={\mathcal {R}}_2^{(\kappa )}(i,j)- {\mathcal {R}}_1^{(\kappa )}(i){\mathcal {R}}_1^{(\kappa )}(j)+\cdots \end{aligned}$$
(44b)

For time \(\tau =0\) and for the quasi-stationary state (see (14)) we can similarly write the average occupations and their correlations by replacing \({\mathcal {R}}^{(\kappa )}\) by \({\mathcal {R}}^{(0)}{\mathcal {L}}^{(\kappa )}\) or \({\mathcal {R}}^{(\kappa )}{\mathcal {L}}^{(\kappa )}\) in (44).

4.4 Hydrodynamic Limit

It is straightforward to take the hydrodynamic limit of the expressions (42) and (43), which can be used to derive the hydrodynamic limit of the cumulants of the occupation variables. For large L, we define

$$\begin{aligned} \ell ^{(\kappa )}(x)&\simeq {\mathcal {L}}_0^{(\kappa )}(x\,L)+{\mathcal {L}}_1^{(\kappa )}(x\,L) \nonumber \\&=e^{-\kappa }(1-x)+ x-\frac{1}{6}(e^{-\kappa }-1)^2x(1-x)\left[ e^{\kappa }\rho _a(2-x)+\rho _b(1+x)\right] \end{aligned}$$
(45)

and

$$\begin{aligned} g_\text {left}^{(\kappa )}(x,y)&\simeq L\;\left[ {\mathcal {L}}_0^{(\kappa )}(xL,yL)- {\mathcal {L}}_0^{(\kappa )}(xL)\; {\mathcal {L}}_0^{(\kappa )}(yL)\right] \nonumber \\&=-(e^{-\kappa }-1)^2 x(1-y)\qquad \text {for }y\ge x. \end{aligned}$$
(46)

Similarly, from (42) we define

$$\begin{aligned} r^{(\kappa )}(x)&\simeq {\mathcal {R}}_1^{(\kappa )}(x\,L)+{\mathcal {R}}_2^{(\kappa )}(x\,L) \nonumber \\&=e^{\kappa }\left( \rho _a+\rho _a^2\right) (1-x)+\left( \rho _b+\rho _b^2 \right) x \nonumber \\&\quad -\frac{1}{6}(e^{\kappa }\rho _a-\rho _b )^2 x (1-x)\left[ 1+x+\left( 2-x\right) e^{-\kappa } \right] \end{aligned}$$
(47)

and

$$\begin{aligned} g_\text {right}^{(\kappa )}(x,y)&\simeq L\;\left[ {\mathcal {R}}_2^{(\kappa )}(xL,yL)- {\mathcal {R}}_1^{(\kappa )}(xL)\; {\mathcal {R}}_1^{(\kappa )}(yL)\right] \nonumber \\&=-(e^{\kappa }\rho _a-\rho _b )^2 x(1-y)\qquad \text {for }y\ge x. \end{aligned}$$
(48)

Remark

In taking the hydrodynamic limit of the perturbation expansion we have assumed that the limits of large L and small density can be exchanged. We will see that the resulting large deviation functions are consistent with the macroscopic analysis in Sect. 7.2.

4.4.1 Cumulants of Density

At time \(\tau =0\), in the quasi-stationary regime, and at \(\tau =L^2 T\) (the hydrodynamic time \(t=T\)) the cumulants of the occupation variables are of the form (see (44))

$$\begin{aligned} \langle n_{xL}\rangle&\simeq {{\bar{\rho }}}(x)=u(x)\left[ 1-u(x)\right] +\int _0^1dy\;c(x,y) \end{aligned}$$
(49a)
$$\begin{aligned} \langle n_{xL} \; n_{yL}\rangle _c&\simeq \frac{1}{L}c(x,y) \end{aligned}$$
(49b)

for large L, up to the second order in \(\rho _a\) and \(\rho _b\), where

  • at \(t=0\),

    $$\begin{aligned} u(x)&=\ell ^{(\kappa )}(x)r^{(0)}(x) \end{aligned}$$
    (50a)
    $$\begin{aligned} c(x,y)&= \ell ^{(\kappa )}(x)\ell ^{(\kappa )}(y)g_\text {right}^{(0)}(x,y)+r^{(0)}(x)r^{(0)}(y)g_\text {left}^{(\kappa )}(x,y) \end{aligned}$$
    (50b)

  • in the quasi-stationary state,

    $$\begin{aligned} u(x)&=\ell ^{(\kappa )}(x)r^{(\kappa )}(x) \end{aligned}$$
    (51a)
    $$\begin{aligned} c(x,y)&= \ell ^{(\kappa )}(x)\ell ^{(\kappa )}(y)g_\text {right}^{(\kappa )}(x,y)+r^{(\kappa )}(x)r^{(\kappa )}(y)g_\text {left}^{(\kappa )}(x,y) \end{aligned}$$
    (51b)

  • at \(t=T\),

    $$\begin{aligned} u(x)=r^{(\kappa )}(x)\qquad \text {and}\qquad c(x,y)= g_\text {right}^{(\kappa )}(x,y) \end{aligned}$$
    (52)

Explicit expressions of the cumulants are given in Appendix B.

4.4.2 Large Deviation Function

Here, we show how to derive a small density expansion of the large deviation function in (26) from the above expansion of the cumulants of the density.

Take an arbitrary probability distribution \(P({\mathbf {n}})\) where the occupation variables are either 0 or 1. Then, one can write

$$\begin{aligned} \prod _{i=1}^{L} e^{h_i n_i}= \ \prod _{i=1}^{L} \left[ 1 + n_i \left( e^{h_i}-1\right) \right] \end{aligned}$$

where \(h_i\) are real valued parameters. If one expands this product, averages over \(P({\mathbf {n}})\), and uses the fact that cumulants of order k scale like \(\rho _a\) and \(\rho _b\) to the power k, then one gets, for finite L,

$$\begin{aligned} \log \left\langle \prod _{i=1}^{L} e^{h_i n_i}\right\rangle&= \sum _{i=1}^{L}\langle n_i \rangle \left( e^{h_i} -1 \right) - {1 \over 2} \sum _{i=1}^{L}\langle n_i \rangle ^2 \left( e^{h_i} -1 \right) ^2 \\&\quad + \sum _{i=1}^{L}\sum _{j>i}^{L} \left\langle n_i n_j \right\rangle _c \left( e^{h_i} -1 \right) \left( e^{h_j} -1 \right) + \cdots \end{aligned}$$

In the hydrodynamic limit, when \(h_{i} \simeq h(\frac{i}{L})\), \(\left\langle n_{i} \right\rangle \simeq {\bar{\rho }}(\frac{i}{L})\), and \(\left\langle n_{i} n_{j} \right\rangle _c \simeq {1 \over L} c(\frac{i}{L},\frac{j}{L})\), we get for the generating functional

$$\begin{aligned} \log \left\langle \prod _{i=1}^{L} e^{h_i n_i}\right\rangle \simeq L \, {\mathcal {G}}[h(x)] \end{aligned}$$

with

$$\begin{aligned} {\mathcal {G}}[h(x)]&= \int _0^1 dx \, \left( e^{h(x)} -1\right) {\bar{\rho }}(x)- {1 \over 2} \int _0^1 dx \, \left( e^{h(x)} -1\right) ^2 {\bar{\rho }}(x)^2 \nonumber \\&\quad + \int _0^1 dx \int _x^1 dy \left( e^{h(x)} -1\right) \left( e^{h(y)} -1\right) c(x,y)+ \cdots \end{aligned}$$
(53)

Then, \(P[\rho (x)]\) has [7, 36] the large deviation form (26) with the large deviation function \(\psi [\rho (x)]\) given by the Legendre transformation

$$\begin{aligned} \psi [\rho (x)] = \int _0^1 dx \, h(x) \, \rho (x) \, - \, {\mathcal {G}}[h(x)] \end{aligned}$$
(54)

where h(x) is the solution of \(\frac{\delta {\mathcal {G}}[h]}{\delta h(x)}=\rho (x)\).

The small density expansion of (53, 54) is then straightforward to get from the perturbation expansion of the cumulants. It gives

$$\begin{aligned} \psi [\rho (x)]\simeq H_\text {sep}[\rho (x),{{\bar{\rho }}}(x), c(x,y) ] \end{aligned}$$
(55a)

where up to the second order in \(\rho _a\) and \(\rho _b\),

$$\begin{aligned} H_\text {sep}[\rho (x),{{\bar{\rho }}}(x), c(x,y) ]&=\int _0^1 dx \left[ \rho (x)\log \frac{\rho (x)}{{\bar{\rho }}(x)}+(1-\rho (x))\log \frac{1-\rho (x)}{1-{\bar{\rho }}(x)}\right] \nonumber \\&\quad -\frac{1}{2}\int _0^1dx \int _0^1dy \left( \frac{\rho (x)}{{\bar{\rho }}(x)}-1\right) \left( \frac{\rho (y)}{{\bar{\rho }}(y)}-1\right) c(x,y) \end{aligned}$$
(55b)

The expression (55) remains valid at all times with \({\bar{\rho }}(x)\) and c(x, y) being replaced by their expressions in Sect. 4.4.1. For the unconditioned case, where \({\bar{\rho }}(x)\) and c(x, y) are given by (49) for \(\kappa =0\), one can verify that this perturbation expansion result is consistent with previously known expressions [36, 40, 44].

4.4.3 Small Density Expansion of \(\chi (\kappa )\), \(V_\text {left}^{(\kappa )}\) and \(V_\text {right}^{(\kappa )}\)

It is straightforward to take the hydrodynamic limit of (41), which confirms (20) at the level of a small density expansion with

$$\begin{aligned} \chi (\kappa )=\rho _a\left( e^{\kappa }-1 \right) +\rho _b\left( e^{-\kappa }-1 \right) -\frac{1}{3}\left( 1-e^{-\kappa } \right) ^2\left( e^{2\kappa }\rho _a^2+e^\kappa \rho _a\rho _b+\rho _b^2 \right) +\cdots \end{aligned}$$
(56)

This is in agreement with earlier findings in [42, 56].

For \(\lambda _0=1\) and \(\lambda _i=0\) for \(i\ge 1\), the large deviation functions \(\psi _\text {left}^{(\kappa ,\alpha )}\equiv V_\text {left}^{(\kappa )}\) and \(\psi _\text {right}^{(\kappa ,\alpha )}\equiv V_\text {right}^{(\kappa )}\) (see (28)). An expression for \(V_\text {left}^{(\kappa )}\) can be derived by taking the hydrodynamic limit (23b, 25b) of \({\mathcal {L}}^{(\kappa )}\). For a configuration \({\mathbf {n}}\), where the occupation variables are either 0 or 1, we write

$$\begin{aligned} \log {\mathcal {L}}^{(\kappa )}=\sum _i n_i\; \log {\mathcal {L}}^{(\kappa )}(i)+\sum _{i<j}n_in_j \;\log \left[ 1+\frac{{\mathcal {L}}^{(\kappa )}(i,j)-{\mathcal {L}}^{(\kappa )}(i){\mathcal {L}}^{(\kappa )}(j)}{{\mathcal {L}}^{(\kappa )}(i) {\mathcal {L}}^{(\kappa )}(j)}\right] +\cdots \end{aligned}$$

using the representation in (39). Then, from the perturbation expansion (40c, 43) and taking the hydrodynamic limit (23b, 25b) we get

$$\begin{aligned} V_\text {left}^{(\kappa )}[\rho ]=\int _0^1 dx \; \rho (x)\log \frac{1}{\ell ^{(\kappa )}(x)}-\frac{1}{2}\int _0^1dx \int _0^1dy \, \frac{\rho (x)\; \rho (y)}{\ell ^{(\kappa )}(x)\;\ell ^{(\kappa )}(y)}\;g^{(\kappa )}_{\text {left}}(x,y)+\cdots \end{aligned}$$
(57)

where \(\ell ^{(\kappa )}(x)\) and \(g_\text {left}^{(\kappa )}(x,y)\) are defined in (45) and (46).

In comparison, it is harder to derive an expression for \(V_\text {right}^{(\kappa )}\) by taking the hydrodynamic limit of the expression (42) for \({\mathcal {R}}^{(\kappa )}\). It is much easier to derive using the relation (27b) and the result (49, 55) at time T. This gives

$$\begin{aligned} V_\text {right}^{(\kappa )}[\rho (x)]&=H_\text {sep}\left[ \rho (x),{\bar{\rho }}_T(x), g_\text {right}^{(\kappa )}(x,y) \right] \end{aligned}$$
(58a)
$$\begin{aligned} \text {with}\quad {\bar{\rho }}_T(x)&=r^{(\kappa )}(x)\left( 1-r^{(\kappa )}(x)\right) + \int _0^1dy\,g_\text {right}^{(\kappa )}(x,y) \end{aligned}$$
(58b)

up to the second order in \(\rho _a\) and \(\rho _b\), and an additive constant.

Remark

We have checked (details in Appendix C) that the result (57), and the expression of \(\psi _\text {qs}^{(\kappa )}\) and \(\psi _T^{(\kappa )}\) obtained from (55) satisfy the relation (27c).

5 Effective Dynamics

In the canonical ensemble, the biased dynamics is Markovian and one can write [1, 5, 6, 8, 23, 29, 62] the transition rates in terms of the tilted Matrix. For example, in the quasi-stationary regime, the transition rate \(W_{\text {qs}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}}',{\mathbf {n}})\) from a microscopic configuration \({\mathbf {n}}\) to another configuration \({\mathbf {n}}'\) is given by [29]

$$\begin{aligned} W_{\text {qs}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}}',{\mathbf {n}})= \frac{{\mathcal {L}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}}')}{{\mathcal {L}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})}\,{\mathcal {M}}_\kappa ^{(\varvec{\lambda })}({\mathbf {n}}',{\mathbf {n}}) \qquad \text {for }{\mathbf {n}}'\ne {\mathbf {n}}. \end{aligned}$$
(59a)

This means, a spontaneous fluctuation at time \(\tau _0\) in the quasi-stationary regime (\(1\ll \tau _0\) and \(1 \ll N-\tau _0\)), relaxes following this dynamics (59a).

Similarly, the path leading to a spontaneous fluctuation can be described by a time reversal of (59a). The transition rate of this time-reversed process can be constructed [63] using the quasi-stationary distribution (14c), which gives

(59b)

For the two examples considered in this paper (the independent particles and the symmetric simple exclusion process), it is straightforward to see that the effective dynamics (59a) with (11) correspond to re-weighting the jump rates of particles (see Figs. 4 and 5): the jump rate for a particle from site i to \(i+1\) is weighted by a factor \(e^{E_i}\), whereas the jump rate from \(i+1\) to i is weighted by \(e^{-E_i}\), where

$$\begin{aligned} E_i({\mathbf {n}})=\kappa \, \lambda _i+\log \frac{{\mathcal {L}}^{(\kappa ,\varvec{\lambda })}(\widehat{{\mathbf {n}}})}{{\mathcal {L}}^{(\kappa ,\varvec{\lambda })}({\mathbf {n}})}\qquad \qquad \text {for all }0\le i\le L, \end{aligned}$$
(60a)

with

$$\begin{aligned} {\widehat{n}}_j=n_j-\delta _{j,i}+\delta _{j,i+1} \qquad \qquad \text {for all } 1\le j\le L. \end{aligned}$$
(60b)

Similar re-weighting of jump rates can be seen for the time reversed dynamics (59b). We note that, in general, the jump rates for the dynamics are non-local functions of the occupation variables \({\mathbf {n}}\).

5.1 Hydrodynamic Limit

In the large L limit, when \(x=\frac{i}{L}\) and \(\lambda _i=\frac{1}{L}\alpha (x)\), (60) becomes

$$\begin{aligned} E_i({\mathbf {n}})\simeq \frac{1}{L}e(x)\qquad&\text {with}\qquad e(x)=\kappa \,\alpha (x)-\partial _x\frac{\delta \psi _\text {left}^{(\kappa ,\alpha )}}{\delta \rho (x)}. \end{aligned}$$
(61)

In a hydrodynamic description (1), the effect of such a weak bias can be incorporated (see [64] for another example) within the linear response theory, where e(x) acts as an external driving field. This leads to the following dynamics.

Relaxation

A spontaneous fluctuation of hydrodynamic density in the quasi-stationary state relaxes following \(\partial _t\rho (x,t)=-\partial _x j(x,t)\) with

$$\begin{aligned} j(x,t)=-D(\rho (x,t))\partial _x\rho (x,t)+\sigma (\rho (x,t))\left\{ \kappa \,\alpha (x)-\partial _x\frac{\delta \psi _\text {left}^{(\kappa ,\alpha )}}{\delta \rho (x,t)} \right\} +\eta (x,t) \nonumber \\ \end{aligned}$$
(62a)

where \(\eta (x,t)\) is a Gaussian white noise of zero mean and covariance (1b).

A somewhat similar analysis based on (59b) leads to the following dynamics:

Fluctuation

The path leading to a fluctuation in the quasi-stationary state is described by \(\partial _t \rho (x,t)=-\partial _x j(x,t)\) with

$$\begin{aligned} j(x,t)=-D(\rho (x,t))\partial _x\rho (x,t)+\sigma (\rho (x,t))\left\{ \kappa \,\alpha (x)+\partial _x\frac{\delta \psi _\text {right}^{(\kappa ,\alpha )}}{\delta \rho (x,t)} \right\} +\eta (x,t) \nonumber \\ \end{aligned}$$
(62b)

Remarks

  • The time evolution of the most probable density profile leading to a fluctuation and its subsequent relaxation are the zero noise case of (62b) and (62a). We have verified this explicitly for the independent particles starting from their microscopic dynamics. For the symmetric simple exclusion process, we checked this up to the second order in a low density expansion.

  • The effective dynamics (7) in the micro-canonical ensemble are readily obtained from (62) using the ensemble equivalence (21).

6 Macroscopic Analysis

The two examples discussed in Sects. 3 to 5 are governed [36, 39, 42, 53], for large L, by the fluctuating hydrodynamics equation (1). Our goal here is to show that the large deviation functions (34, 35) and (57, 58) are consistent with a macroscopic approach. Besides this, the macroscopic analysis applies for a general class of models where the microscopic details enter in the terms \(D(\rho )\) and \(\sigma (\rho )\).

Much of the results can be inferred by drawing an analogy of (1) to a Langevin equation in the weak noise limit, as in [29]. In this analogy, a simple quantity is the generating function, which for (1) is defined by

$$\begin{aligned} G_T^{(\kappa ,\alpha )}[r(x), s(x)]=\int dQ\, e^{L\kappa \, Q}P^{(\alpha )}_T[r(x),Q\vert s(x)] \end{aligned}$$
(63)

where \(P^{(\alpha )}_T[r(x),Q\vert s(x)]\) is the joint probability of a density profile \(\rho (x,T)=r(x)\) at the hydrodynamic time \(t=T\), and \(Q_T^{(\alpha )}=Q\) in (3), given the density \(\rho (x,0)=s(x)\) at \(t=0\). Similarly to the Langevin equation [29], one expects, for large L and T, the generating function to have the form

$$\begin{aligned} G_T^{(\kappa ,\alpha )}[r(x), s(x)]\sim e^{T\, L\, \chi (\kappa )-L\, \psi ^{(\kappa , \alpha )}_\text {right}[r(x)]-L\, \psi ^{(\kappa , \alpha )}_\text {left}[s(x)]} \end{aligned}$$
(64)

where \(\chi (\kappa )\), \(\psi ^{(\kappa , \alpha )}_\text {right}\), and \(\psi ^{(\kappa , \alpha )}_\text {left}\) are the same quantities as in (20) and (25). Starting from (64) we now obtain a variational formulation as in [34,35,36, 40].

6.1 A Variational Formulation

For large L, the probability of a certain time evolution of \(\rho (x,t)\) and j(x, t) inside the time window [0, T], which follows (1) is given by [34, 36]

$$\begin{aligned} P[\rho (x,t),j(x,t)]\sim \exp \left[ -L\int _0^1 dx \int _0^T dt \frac{(j(x,t)+D(\rho )\partial _x\rho (x,t))^2}{2\sigma (\rho )} \right] \end{aligned}$$
(65)

where \(\sim \) means that sub-leading terms in large L are neglected. Using this, the generating function (63) can be written as a path-integral

$$\begin{aligned} G_T^{(\kappa ,\alpha )}[r(x), s(x)]\sim \int {\mathcal {D}}[\rho ,j]e^{L S_T^{(\kappa ,\alpha )}[\rho ,j]} \end{aligned}$$
(66a)

with

$$\begin{aligned} S_{t_f-t_i}^{(\kappa ,\alpha )}[\rho ,j]=\int _{t_i}^{t_f}dt\int _0^1dx\left\{ \kappa \,\alpha (x) j(x,t)- \frac{(j(x,t)+D(\rho )\partial _x\rho (x,t))^2}{2\sigma (\rho )}\right\} \end{aligned}$$
(66b)

with \(t_i=0\) and \(t_f=T\). The path integral in (66a) is over all paths \(\{\rho (x,t),j(x,t)\}\) satisfying \(\partial _t\rho =-\partial _x j\) with the initial density profile \(\rho (x,0)=s(x)\) and the final density profile \(\rho (x,T)=r(x)\).

For large L and T, assuming a single optimal path, we get the large deviation form (64) with

$$\begin{aligned} T\, \, \chi (\kappa )-\, \psi ^{(\kappa , \alpha )}_\text {right}[r(x)]-\, \psi ^{(\kappa , \alpha )}_\text {left}[s(x)]=\max _{\rho ,j} S_T^{(\kappa ,\alpha )}[\rho ,j] \end{aligned}$$
(67)

where the optimization is over all paths \((\rho (x,t),j(x,t))\) satisfying the conditions mentioned earlier.

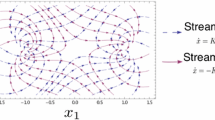
In a rather general class of systems [49], the optimal path for (67) starts at the given density profile \(\rho (x,0)=s(x)\) but soon becomes time independent \(\rho (x,t)={\bar{\rho }}_\text {qs}(x)\) and remains at this density until only close to the final time T where it changes to \(\rho (x,T)=r(x)\). (This assumption for the time independence of the optimal profile for \(t\gg 1\) and \(T-t\gg 1\) is equivalent to assuming the additivity principle [42].) This is illustrated in the schematic in Fig. 6. In this paper, we shall only consider situations where this scenario holds. For examples where this breaksdown see [48, 65].

Remarks

  1. 1.

    The probability (65) does not include the contribution of reservoirs. This applies to density profiles \(\rho (x)\) which are fixed at the boundary, i.e.\(\rho (0,t)=\rho _a\) and \(\rho (1,t)=\rho _b\). This is justified when the coupling with the reservoirs is strong, so that fluctuations of density at the boundary relax to the reservoir density in a time scale much faster than the hydrodynamic time scale.

  2. 2.

    The formula (67) means

    $$\begin{aligned} \chi (\kappa )=\lim _{T\rightarrow \infty }\frac{1}{T}\max _{\rho ,j} S_T^{(\kappa ,\alpha )}[\rho ,j] \end{aligned}$$
    (68)

    which leads to the well-known result [36, 42]

    $$\begin{aligned} \chi (\kappa )=\max _{q}\left\{ \kappa \; q- {\varPhi }(q)\right\} ;\quad {\varPhi }(q)=\min _{{\bar{\rho }}_\text {qs}}\int _0^1dx\frac{\left( q+D({\bar{\rho }}_\text {qs})\partial _x{\bar{\rho }}_\text {qs}(x)\right) ^2}{2\sigma ({\bar{\rho }}_\text {qs})} \end{aligned}$$
    (69)

    which agrees [36, 42] with (33) and (56) for the independent particles and for the symmetric simple exclusion process.

Fig. 6
figure 6

A schematic of the optimal evolution of density for the variational problem (67), where at the intermediate time the density is time independent \({\bar{\rho }}_\text {qs}(x)\)

Full size image

6.2 Hamilton–Jacobi Equation

In (67), the deviation of the optimal path from \({\bar{\rho }}_\text {qs}(x)\) near \(t=0\) and \(t=T\) (see Fig. 6) are important and they contribute to \(\psi ^{(\kappa , \alpha )}_\text {right}\) and \(\psi ^{(\kappa , \alpha )}_\text {left}\). Here, we show how this variational formula (67) leads to a pair of Hamilton–Jacobi equations for \(\psi ^{(\kappa , \alpha )}_\text {right}\) and \(\psi ^{(\kappa , \alpha )}_\text {left}\).

We start by deriving the equation for \(\psi ^{(\kappa , \alpha )}_\text {left}\). For this, we use (see remark after Eq. (24))

$$\begin{aligned} G_T^{(\kappa ,\alpha )}[r(x), s(x)]\simeq \int {\mathcal {D}}[\rho ]\; G_{T-t}^{(\kappa ,\alpha )}[r(x), \rho (x)]\; G_t^{(\kappa ,\alpha )}[\rho (x), s(x)] \end{aligned}$$
(70)

for \(0< t< T\), which can be seen from the definition (63). We consider infinitesimal \(t>0\) but large T, such that \(T-t\) is large. This means, we can use (64) for \(G_{T-t}^{(\kappa ,\alpha )}[r(x), \rho (x)]\). On the other hand, using the Action formulation (66) we write, for an infinitesimal t,

$$\begin{aligned} G_t^{(\kappa ,\alpha )}[\rho (x), s(x)]\sim \exp \left[ t\,L\int _0^1dx\left\{ \kappa \,\alpha (x) j(x)- \frac{(j(x)+D(s)\partial _x s(x))^2}{2\sigma (s)}\right\} \right] \end{aligned}$$

where \(\rho (x)\simeq s(x)-t\, \partial _x j(x)\). Using this in (70) and a saddle point analysis for large L we get

$$\begin{aligned}&\psi ^{(\kappa , \alpha )}_\text {left}[s(x)]\simeq t\chi (\kappa )-\max _{j(x)}\left\{ -\psi ^{(\kappa , \alpha )}_\text {left}[s(x)-t\, \partial _x j(x)]\right. \\&\quad \left. +\,t\int _0^1dx\left( \kappa \,\alpha (x) j(x)- \frac{(j(x)+D(s)\partial _x s(x))^2}{2\sigma (s)}\right) \right\} \end{aligned}$$

Expanding \(\psi ^{(\kappa , \alpha )}_\text {left}[s(x)-t\, \partial _x j(x)]\) in a Taylor series up to linear order in t, and then using an integration by parts, we get

$$\begin{aligned} \chi (\kappa )&\simeq \max _{j(x)}\left\{ \frac{\delta \psi ^{(\kappa , \alpha )}_\text {left}}{\delta s(1)} j(1)-\frac{\delta \psi ^{(\kappa , \alpha )}_\text {left}}{\delta s(0)} j(0)\right. \nonumber \\&\quad \left. +\int _0^1dx\left[ \left( \kappa \,\alpha (x)-\partial _x \frac{\delta \psi ^{(\kappa , \alpha )}_\text {left}}{\delta s(x)}\right) j(x)- \frac{(j(x)+D(s)\partial _x s(x))^2}{2\sigma (s)}\right] \right\} \end{aligned}$$
(71)

For density profiles which are fixed at the boundary (see the remark 1 in Sect. 6.1), one can see from (28, 35, 57) that

$$\begin{aligned} \frac{\delta \psi ^{(\kappa , \alpha )}_\text {left}}{\delta s(x)}=0\qquad \text {at } x=0 \text { and at } x=1, \end{aligned}$$
(72)

for the two systems we study in this paper. Similar conditions occurred already in earlier works [34, 53]. Using this in (71) and optimizing over j(x) leads to

$$\begin{aligned} \int _0^1dx\left[ \frac{\sigma (s)}{2}\left( \partial _x \frac{\delta \psi ^{(\kappa , \alpha )}_\text {left}}{\delta s(x)}-\kappa \,\alpha (x)+\frac{D(s)s'(x)}{\sigma (s)}\right) ^2 - \frac{(D(s) s'(x))^2}{2\sigma (s)}\right] =\chi (\kappa ) \end{aligned}$$
(73a)

where we denote \(s'(x)\equiv \partial _xs(x)\).

A similar analysis (by considering small decrement around the time T) leads to an analogous equation for \(\psi ^{(\kappa , \alpha )}_\text {right}\) .

$$\begin{aligned} \int _0^1dx\left[ \frac{\sigma (r)}{2}\left( \partial _x \frac{\delta \psi ^{(\kappa , \alpha )}_\text {right}}{\delta r(x)}+\kappa \,\alpha (x)-\frac{D(r)r'(x)}{\sigma (r)}\right) ^2 - \frac{(D(r) r'(x))^2}{2\sigma (r)}\right] =\chi (\kappa ) \nonumber \\ \end{aligned}$$
(73b)

These two are the Hamilton–Jacobi equations associated to the variational problem (67). Their micro-canonical analogue (8) can be obtained by the ensemble equivalence (21).

6.3 Optimal Path

In (71) the optimal current

$$\begin{aligned} j_\text {opt}(x)=-D(s)\partial _x s(x)+\sigma (s)\left( \kappa \,\alpha (x)-\partial _x \frac{\delta \psi ^{(\kappa , \alpha )}_\text {left}}{\delta s(x)}\right) \end{aligned}$$
(74)

This means that the optimal path \(\rho _\text {opt}(x,t)\) near \(t=0\) follows

$$\begin{aligned} \partial _t \rho _\text {opt}=\partial _x \left\{ D(\rho _\text {opt})\partial _x \rho _\text {opt}-\sigma (\rho _\text {opt})\left( \kappa \,\alpha (x)-\partial _x \frac{\delta \psi ^{(\kappa , \alpha )}_\text {left}}{\delta \rho _\text {opt}}\right) \right\} \end{aligned}$$
(75)

It is straightforward to extend the argument for \(t\ge 0\) but \(T-t\gg 1\) (region II of Fig. 2) and show that the dynamics is the same.

A similar analysis in the derivation of (73b) shows that the optimal path \(\rho _\text {opt}(x,t)\) in region IV of Fig. 2 is described by

$$\begin{aligned} \partial _t \rho _\text {opt}=\partial _x\left\{ D(\rho _\text {opt})\partial _x \rho _\text {opt}-\sigma (\rho _\text {opt})\left( \kappa \,\alpha (x)+\partial _x \frac{\delta \psi ^{(\kappa , \alpha )}_\text {right}}{\delta \rho _\text {opt}}\right) \right\} \end{aligned}$$
(76)

In the quasi-stationary state (76) also describes the optimal path leading to a fluctuation and (75) describes the optimal path of relaxation (see illustration in Fig. 3).

6.4 Fixed point of the dynamics

Using (73) we show in Appendix D that along the optimal path (75),

$$\begin{aligned} \frac{d}{dt}\psi _\text {qs}^{(\kappa )}[\rho _\text {opt}(x,t)]=-\int _0^1dx\,\frac{\sigma (\rho _\text {opt}(x,t))}{2}\left( \partial _x \frac{\delta \psi _\text {qs}^{(\kappa )}[\rho _\text {opt}(x,t)]}{\delta \rho _\text {opt}(x,t)}\right) ^2 \end{aligned}$$
(77)

with \(\psi _\text {qs}^{(\kappa )}\) given in (27c). Since \(\sigma (\rho )\) is positive, this means \(\frac{d}{dt}\psi _\text {qs}^{(\kappa )}[\rho _\text {opt}(x,t)]=0\) if and only if \(\partial _x\frac{\delta \psi _\text {qs}^{(\kappa )}[\rho _\text {opt}(x,t)]}{\delta \rho _\text {opt}(x,t)}=0\). (The case \(\kappa =0\) has been discussed earlier in [53].)

The examples we consider here have a unique quasi-stationary density \({\bar{\rho }}_\text {qs}\), where \(\frac{\delta \psi _\text {qs}^{(\kappa )}}{\delta {{\bar{\rho }}}_\text {qs}(x)}=0\). Then (77) implies that \({\bar{\rho }}_\text {qs}\) is an attractive fixed point of (75) (see Fig. 3).

For \({\bar{\rho }}_\text {qs}\) the optimal current (74) is \(j_\text {opt}=\chi '(\kappa )\), which can be seen from (69). Then, we get

$$\begin{aligned} -D({\bar{\rho }}_\text {qs})\partial _x {\bar{\rho }}_\text {qs}+\sigma ({\bar{\rho }}_\text {qs})\left( \kappa \,\alpha (x)-\partial _x \frac{\delta \psi ^{(\kappa , \alpha )}_\text {left}}{\delta {\bar{\rho }}_\text {qs}(x)}\right)&=\chi '(\kappa ) \end{aligned}$$

which leads to

$$\begin{aligned} \partial _x \frac{\delta \psi ^{(\kappa , \alpha )}_\text {left}}{\delta {\bar{\rho }}_\text {qs}(x)}=\kappa \,\alpha (x)-\frac{\chi '(\kappa )+D({\bar{\rho }}_\text {qs})\partial _x {\bar{\rho }}_\text {qs}(x)}{\sigma ({\bar{\rho }}_\text {qs})} \end{aligned}$$
(78a)

A similar calculation for (76) lead to

$$\begin{aligned} \partial _x \frac{\delta \psi ^{(\kappa , \alpha )}_\text {right}}{\delta {\bar{\rho }}_\text {qs}(x)} =-\kappa \,\alpha (x)+\frac{\chi '(\kappa )+D({\bar{\rho }}_\text {qs})\partial _x {\bar{\rho }}_\text {qs}(x)}{\sigma ({\bar{\rho }}_\text {qs})} \end{aligned}$$
(78b)

These give conditions for the solution of (73). It is well-known [53, 66] that, there are multiple solutions of a Hamilton–Jacobi equation. For the two examples studied in this work, the relevant solution of (73) follows the boundary condition (78) and (see (72))

$$\begin{aligned}&\frac{\delta \psi ^{(\kappa , \alpha )}_\text {left}}{\delta \rho (x)}=0\quad \text {and} \quad \frac{\delta \psi ^{(\kappa , \alpha )}_\text {right}}{\delta \rho (x)}=0 \qquad \text {at } x=0\text { and } x=1,\nonumber \\&\quad \hbox { for density profiles}~\rho (x)\nonumber \\&\quad \hbox { with } \rho (0)=\rho _a \hbox { and } \rho (1)=\rho _b. \end{aligned}$$
(79)

6.5 Conditioned Stochastic Dynamics

In Sect. 5 we have shown using a microscopic analysis that, in the quasi-stationary state, conditioned dynamics is given by a fluctuating hydrodynamics equation (62). Here, we give a derivation using the macroscopic approach.

In the quasi-stationary state, if \({\mathcal {P}}[\rho ,j\vert \rho _i]\) is the probability of a path \(\left\{ \rho (x,t),j(x,t)\right\} \) in a time window \([t_i,t_f]\) (for \(1\ll t_i<t_f\) and \(1\ll T-t_f\)) given an initial density \(\rho (x,t_i)=\rho _i(x)\), then using (63) and (66b) one can write

$$\begin{aligned} {\mathcal {P}}[\rho ,j\vert \rho _i]=\frac{G_{T-t_f}^{(\kappa ,\alpha )}[\rho _T,\rho _f]\; e^{L S_{t_f-t_i}^{(\kappa ,\alpha )}}}{G_{T-t_i}^{(\kappa ,\alpha )}[\rho _T,\rho _i]} \end{aligned}$$

where we denote \(\rho (x,t_f)=\rho _f(x)\) and \(\rho (x,T)=\rho _T(x)\). Then, for large L, using (26) and (64) we get

$$\begin{aligned} {\mathcal {P}}[\rho ,j\vert \rho _i]\sim e^{-L (t_f-t_i)\chi (\kappa )+L \psi _\text {left}^{(\kappa ,\alpha )}[\rho _i]-L \psi _\text {left}^{(\kappa ,\alpha )}[\rho _f]+ L S_{t_f-t_i}^{(\kappa ,\alpha )}[\rho ,j]} \end{aligned}$$
(80)

This expression can be simplified by using

$$\begin{aligned} \psi _\text {left}^{(\kappa ,\alpha )}[\rho _f]-\psi _\text {left}^{(\kappa ,\alpha )}[\rho _i]&=\int _0^1 dx \int _{t_i}^{t_f}dt\, \partial _t\rho \,\frac{\delta \psi _\text {left}^{(\kappa ,\alpha )}[\rho ]}{\delta \rho (x,t)}\\&= \int _0^1 dx \int _{t_i}^{t_f}dt\, j(x,t)\,\partial _x\left( \frac{\delta \psi _\text {left}^{(\kappa ,\alpha )}[\rho ]}{\delta \rho (x,t)}\right) \end{aligned}$$

where the last equality is obtained by using \(\partial _t\rho =-\partial _x j\), integration by parts, and the boundary condition (79). In addition, we use (73a) to write

$$\begin{aligned}&(t_f-t_i)\chi (\kappa )\\&\quad =\int _0^1dx\int _{t_i}^{t_f}dt\left[ \frac{\sigma (\rho )}{2}\left( \partial _x \frac{\delta \psi ^{(\kappa , \alpha )}_\text {left}}{\delta \rho (x,t)}-\kappa \,\alpha (x)+\frac{D(\rho )\partial _x\rho (x,t)}{\sigma (\rho )}\right) ^2 - \frac{(D(\rho )\partial _x \rho (x))^2}{2\sigma (\rho )}\right] \end{aligned}$$

Using the above two results in (80) and following a simple algebra we get

$$\begin{aligned} {\mathcal {P}}[\rho ,j\vert \rho _i]\sim e^{L \,{\widehat{S}}[\rho ,j]} \end{aligned}$$
(81a)

with the Action

$$\begin{aligned} {\widehat{S}}[\rho ,j]=-\int _{t_i}^{t_f}dt\int _0^1dx\frac{\left\{ j(x,t)+D(\rho )\partial _x\rho (x,t)+\sigma (\rho )\left( \partial _x \frac{\delta \psi ^{(\kappa , \alpha )}_\text {left}}{\delta \rho (x,t)}-\kappa \,\alpha (x) \right) \right\} ^2}{2\sigma (\rho )} \nonumber \\ \end{aligned}$$
(81b)

Comparing with (65) one can clearly see that the conditioned dynamics in the quasi-stationary state is given by a fluctuating hydrodynamics equation \(\partial _t\rho (x,t)=-\partial _x j(x,t)\) with j(x, t) in (62a). This describes, how a spontaneous fluctuation relaxes in the quasi-stationary state.

On the other hand, (62b) shows the path leading to a fluctuation. This is given by a time reversal of (62a), which can be constructed (for example see eq. 2.15 of [53]) by using that \(P_\text {qs}^{(\kappa ,\alpha )}[\rho ]\) is the steady state of (62a). This gives a fluctuating hydrodynamics equation \(\partial _t\rho (x,t)=-\partial _x \left\{ j(x,t)+\sigma (\rho )\partial _x\frac{\delta \psi _\text {qs}^{(\kappa )}}{\delta \rho (x,t)}\right\} \) with the j(x, t) in (62a). Then, using (27c) one gets (62b).

7 Solution in Specific Examples

Here, we show how to check that the results for \(\psi _\text {left}^{(\kappa ,\alpha )}\) and \(\psi _\text {right}^{(\kappa ,\alpha )}\) derived in Sects. 3 and 4 using a microscopic analysis, are indeed solution of the Hamilton–Jacobi equations (73).

7.1 Independent Particles

In this case, using (28b) and (33) in (73a) we get

$$\begin{aligned} \int _0^1dx\left[ \rho (x)\left( \partial _x \frac{\delta V^{(\kappa )}_\text {left}}{\delta \rho (x)}\right) ^2+\rho '(x)\left( \partial _x \frac{\delta V^{(\kappa )}_\text {left}}{\delta \rho (x)}\right) \right] =\rho _a\left( e^{\kappa }-1 \right) +\rho _b\left( e^{-\kappa }-1 \right) \end{aligned}$$
(82)

Expression (35a) for \(V^{(\kappa )}_\text {left}\) gives

$$\begin{aligned} \partial _x \frac{\delta V^{(\kappa )}_\text {left}}{\delta \rho (x)}= \frac{(e^{-\kappa }-1)}{b(x)}\qquad \text {and}\qquad \left( \partial _x \frac{\delta V^{(\kappa )}_\text {left}}{\delta \rho (x)}\right) ^2=(e^{-\kappa }-1)\left( \frac{1}{b(x)}\right) ' \end{aligned}$$

With this, the left hand side of (82) becomes

$$\begin{aligned} (e^{-\kappa }-1)\int _0^1dx\left[ \rho (x)\left( \frac{1}{b(x)}\right) '+\frac{\rho '(x)}{b(x)}\right]&=(e^{-\kappa }-1)\int _0^1dx\left( \frac{\rho (x)}{b(x)}\right) '\\&=(e^{-\kappa }-1)\left( \frac{\rho (1)}{b(1)}-\frac{\rho (0)}{b(0)}\right) \end{aligned}$$

From the boundary condition \(\rho (0)=\rho _a\), \(\rho (1)=\rho _b\), and using (35b) we see that the above expression agrees with the right hand side of (82).

Moreover, one can check that the solution (28b, 35a) is consistent with the boundary condition (78, 79).

A similar calculation shows that \(\psi _\text {right}^{(\kappa )}\) in (28a, 34a) is a solution of (73b) with the boundary condition (78, 79).

7.2 Symmetric Simple Exclusion Process

In this case, our solution for \(\psi _\text {left}^{(\kappa ,\alpha )}\) and \(\psi _\text {right}^{(\kappa ,\alpha )}\) in (28, 57, 58) are for small density. We have explicitly verified, up to the second order in density, that these are solutions of the Hamilton–Jacobi equations (73) and they satisfy the boundary condition (78, 79). The analysis is similar to that of the independent particles in Sect. 7.1. In fact, at the leading order in density, they are identical.

8 Summary

In the present work we have tried to determine the probability of the density (4) in a diffusive many-particle system conditioned on the time-integrated current (3) for large T. This is a generalization to extended systems of earlier works on conditioned stochastic processes [8, 16, 23, 29,30,31,32]. We mostly worked with the canonical ensemble where dynamics is weighted by the current (3). However, the equivalence of ensembles allows to make predictions for the conditioned process (see Sect. 2). We give explicit expressions for a system of independent particles (Sect. 3) and the symmetric simple exclusion process (Sect. 4).

In the hydrodynamic limit, the conditioned probability of the density \(\rho (x)\) is characterized by the large deviation function \(\psi _t^{(\kappa ,\alpha )}[\rho ]\) in (26). For the two systems considered in this paper, we have calculated \(\psi _t^{(\kappa ,\alpha )}[\rho ]\) at three different times of the evolution, namely, at \(t=0\), at \(t=T\), and in the quasi-stationary regime. These are, in general, related by (see (27))

$$\begin{aligned} \psi _0^{(\kappa ,\alpha )}[\rho ]+\psi _T^{(\kappa ,\alpha )}[\rho ]=\psi _\text {qs}^{(\kappa ,\alpha )}[\rho ]+{\mathcal {F}}[\rho ] \end{aligned}$$
(83)

with \({\mathcal {F}}\) defined in (2).

In the second half of the paper, we used a macroscopic approach, where \(\psi _t^{(\kappa ,\alpha )}\) is expressed (see (27)) in terms of \(\psi _\text {left}^{(\kappa ,\alpha )}\) and \(\psi _\text {right}^{(\kappa ,\alpha )}\), which are solutions of a pair of Hamilton–Jacobi equations (73). These solutions also act as the potential for an additional field that drives the conditioned process (see (62) and Sect. 6.5). Using this macroscopic approach we verified the microscopic results for the two specific examples (see Sect. 7).

The macroscopic formulation is expected to work for a wide class of diffusive systems where the microscopic details enter in the two functions \(D(\rho )\) and \(\sigma (\rho )\) in (1). This is in the spirit of the macroscopic fluctuation theory [34]. It would be interesting to find more examples for explicit solutions of \(\psi _\text {left}^{(\kappa ,\alpha )}\) and \(\psi _\text {right}^{(\kappa ,\alpha )}\) using both the microscopic and the macroscopic approach. Because the SSEP conditioned on the current is known to be described by an XXX spin chain with additional boundary terms, one could try to relate our results to other choices of boundary densities and \(\kappa \) by a rotational symmetry [67, 68]. For systems on a ring, where the unconditioned state is in equilibrium, the calculation may be simpler. However, due to the periodic boundary condition, the optimal profile in the quasi-stationary state could become time dependent (see [48, 65, 69]), in contrast with the two examples studied in the present work.

In the unconditioned case (\(\kappa =0\)), the spatial correlations of density follow simple differential equations [39, 70], whose solutions can be formally expressed in terms of a Green’s function. It would be interesting to see if there are similar equations for the conditioned case, especially in the quasi-stationary state.