From Ecology to Finance (and Back?): A Review on Entropy-Based Null Models for the Analysis of Bipartite Networks

Abstract

Bipartite networks provide an insightful representation of many systems, ranging from mutualistic networks of species interactions to investment networks in finance. The analyses of their topological structures have revealed the ubiquitous presence of properties which seem to characterize many—apparently different—systems. Nestedness, for example, has been observed in biological plant-pollinator as well as in country-product exportation networks. Due to the interdisciplinary character of complex networks, tools developed in one field, for example ecology, can greatly enrich other areas of research, such as economy and finance, and vice versa. With this in mind, we briefly review several entropy-based bipartite null models that have been recently proposed and discuss their application to real-world systems. The focus on these models is motivated by the fact that they show three very desirable features: analytical character, general applicability, and versatility. In this respect, entropy-based methods have been proven to perform satisfactorily both in providing benchmarks for testing evidence-based null hypotheses and in reconstructing unknown network configurations from partial information. Furthermore, entropy-based models have been successfully employed to analyze ecological as well as economic systems. As an example, the application of entropy-based null models has detected early-warning signals, both in economic and financial systems, of the 2007–2008 world crisis. Moreover, they have revealed a statistically-significant export specialization phenomenon of country export baskets in international trade, a result that seems to reconcile Ricardo’s hypothesis in classical economics with recent findings on the (empirical) diversification industrial production at the national level. Finally, these null models have shown that the information contained in the nestedness is already accounted for by the degree sequence of the corresponding graphs.

1 Introduction

“Data is the New Oil” has become the unofficial slogan for the enthusiasts of technological progress in the recent decade [95]. New data sources have created new economic and political possibilities. Catalyzed by the need for new analytical and numerical tools, the theory of complex networks has gained much attention, since the interplay between different data agents can often be expressed in the shape of a network, and new methods for the analyses of such structures have been designed.

A prominent network type found in many real-world systems is the so-called bipartite network, which is characterized by the presence of two distinct types of nodes. Examples are user-movie databases, plant-pollinator ecosystems, author-article collaborations, or financial bank-asset networks. Although purely data-based analyses provide valuable insights into interaction mechanisms, recent results have shown that such network structures contain more information than is apparent at first sight. In particular, several techniques have been designed based on statistical physics and information theory, which provide the possibility to filter statistically relevant signals from the network that otherwise remain hidden when the data is taken at face value [50, 81, 82, 87, 90].

Network theory is by nature interdisciplinary and has thus created a vast vocabulary and a plethora of tools. Due to the interaction patterns of many biological systems, the analysis of bipartite networks has been very popular in ecology and its methodologies have spread to other ares of research. Here, we present a brief review of insights that have been gained in the areas of ecological, economic, and financial networks. Our focus, however, lies on bipartite network modeling, with a particular attention to entropy-based null models and their applications. We shall show that seemingly genuine network characteristics, such as nestedness, can be traced back to basic properties like the degree sequence of the nodes. For this purpose, appropriately defined benchmarks models are used that are as unbiased and general as possible. Furthermore, we review how such null models can be used to reconstruct networks when only partial or noisy data is available, and how this method can be applied to asses systemic risk in financial networks [31, 50, 87]. In addition, we illustrate how Ricardo’s specialization hypothesis in international trade [77] can be reconciled with the apparently contradicting export diversification signal that has been observed [21], and how early warning signs are revealed preceding the financial crisis of 2008 [81].

Network theory has found wide-spread applications in different fields of scientific research. In this article, we focus on bipartite undirected networks, in which we can distinguish between two distinct types of nodes. They are ordered in two separate layers such that links only exists between, but not within, layers. The structure of the network can be expressed in a biadjacency matrix, with nodes of one type along the rows and nodes of the other type along the columns. Due to the ubiquity of network structures in science, different fields have created different vocabularies. For instance, in ecology the biadjacency matrix is commonly known as the interaction matrix when the interaction between species is studied. Analogously, research on the occurrence of organisms in different environments uses the presence-absence matrix. Furthermore, in economic and financial networks one may use the expression ownership matrix. We will use the general term biadjacency matrix in the following. Regarding the number of connections attached to each node, we refer to them as degrees, which is more common than marginal totals in ecology.

In the following sections, we review major insights that have emerged from the study of bipartite networks. We shall focus initially on several open problems in ecological, economic, and financial networks. Subsequently, we present entropy-based null models for bipartite structures that have appeared in recent literature. Finally, we shall discuss how their application has helped in finding solutions for the aforementioned issues.

2 Open Problems in Ecological Networks

The analysis of networks has a long tradition in the field of biology and ecology. Research on food webs, for instance, can be dated back to the pioneering works of Elton in 1927 [38]. Food webs capture the predator-prey relationships between different species: squirrels eat plants but are hunted by snakes, which fall prey to foxes. Directed links in these networks express the flow of biomass, and species can be order in hierarchical layers (known as trophic levels) according to their position in the food chain.

Ecology studies the interactions among species, or between species and their natural environments. Some typical examples are plants and pollinators, or organisms and their habitats. In these cases, one can distinguish between two different types of nodes that populate two distinct layer of a bipartite network. If the interactions between the species or environments are mutually beneficial and cooperative, for example in the case of pollinators and plants, such bipartite networks are often referred to as mutualistic networks.

2.1 Bipartite Motifs

Motifs are defined as n-node subgraphs that are overrepresented in empirical networks and have been labeled as “the building blocks of complex networks” [64]. In directed networks, such as food webs, the smallest nontrivial motifs can be built out of three nodes, leading to 13 distinct patterns [64]. Different motifs are assumed to serve different functions in the network. In genetic transcription networks, for example, is has been observed that certain motifs regulate the expression of genes [4] (for an overview of the motifs and their function, see, e.g.,  [85]).

Analyzing networks from ecology, engineering, biochemistry and neurobiology, in [64] it has been observed that different network types show distinct motif abundances. Hence, the question arises whether one can predict global network characteristics from the presence and temporal changes of such structures. Finding motifs in monopartite networks can generally be computationally intensive and different algorithms have been proposed (see [98] for a survey).

Here, we will concentrate on bi-cliques, i.e. motifs in undirected bipartite networks. We shall use the vocabulary presented in [80], since, in our opinion, this nomenclature makes it easier to grasp the shape of the motifs. As an example, the M-, W-, X-, as well as the V-, $\varLambda$-, and the V$_n$-motifs, are shown in Fig. 1.

Fig. 1

Illustration of several undirected bipartite motifs. The nomenclature is based on the visual shape of the structures. Top: closed motif in which all nodes of one layer are connected to those of the other. Bottom: open motif that capture node similarities in terms of common nearest neighbors in the opposite bipartite layer

The simplest motifs are the bi-cliques $K_{1,2}$ and $K_{2,1}$, also known as $\varLambda$- and V-motifs, that are composed of two nodes in the same and one node in the opposite layer. They draw exactly a “$\varLambda$” and a “V” between the layers, as illustrated in Fig. 1.

Let us call the two layers L and $\varGamma$ and indicate the respective nodes with $i\in L$ and $\alpha \in \varGamma$. A binary bipartite network can be represented by a biadjacency matrix, i.e. a rectangular matrix $\mathbf{M}$ of dimension $N_L \times N_{\varGamma }$, whose elements $m_{i\alpha }$ are 1 if nodes i and $\alpha$ are connected, 0 otherwise. We can easily express the number of V-motifs between the nodes i and j of the upper layer L as

$$\begin{aligned} V^{ij}=\sum _{\alpha \in \varGamma } m_{i\alpha }m_{j\alpha },\quad i,j\in L. \end{aligned}$$

(1)

The $\varLambda _{\alpha \beta }$-motifs are defined analogously for the nodes of the lower layer, $\alpha , \beta \in \varGamma$. $\hbox {V}^{ij}$ captures the number of neighbors that the node couple (i, j) has in common. The motifs can be easily generalized to more than two nodes by including n legs that are all attached to the same node in the opposite layer, as shown in Fig. 1. We will call them $V_n$ and $\varLambda _n$ (with $\text {V}=\text {V}_2$ and $\varLambda =\varLambda _2$), or in standard graph theory $K_{2,n}$ and $K_{n, 2}$. V- and $\varLambda$-motifs thus represent the number of connections shared between 2 or more nodes belonging to the same layer.

A more complex class of motifs is represented by the so called closed motifs. The M-, W- and X-motifs are illustrated on the top in Fig. 1 and are referred to as $K_{2,2}$, $K_{3,2}$ and $K_{2,3}$ in graph theory. We can express them in terms of the biadjacency matrix and write, for instance, for the total number of X-motifs

$$\begin{aligned} X=\sum _{i<j}\sum _{\alpha <\beta }m_{i\alpha }m_{j\alpha }m_{i\beta } m_{j\beta }. \end{aligned}$$

(2)

The other mentioned closed motifs can be described similarly.

Bipartite motifs can even account for non-existing links, which is the case, for example, of the popular checkerboards, introduced by Diamond [32] for the study of the avifauna of Vanuatu’s islands. A checkerboard considers the case of mutual exclusions of two species. The total number of checkerboards is in the biadjacency matrix is thus

$$\begin{aligned} C=\sum _{i<j}\sum _{\alpha <\beta }m_{i\alpha }(1-m_{j\alpha })(1-m_{i\beta }) m_{j\beta }. \end{aligned}$$

(3)

Togetherness, T, is defined in a similar way and counts how many times two species interact together with the same species, avoiding, at the same time, the interaction with other ones. In formulas,

$$\begin{aligned} T=\sum _{i<j}\sum _{\alpha <\beta }m_{i\alpha }m_{j\alpha }(1-m_{i\beta }) (1-m_{j\beta }). \end{aligned}$$

(4)

In [89], the authors show that C and T differ by a constant term.

As a final comment to the present section, note that although all the motifs so far involve several links, they are all multi-linear in the corresponding biadjacency matrix. This fact is particular convenient for analytical calculations, as we will see in the following.

2.1.1 Motifs Analysis in Mutualistic Networks

In ecology, finding patterns that explain the distribution of species in different habitats, e.g. islands, forest, or even parasitic hosts, or why certain organisms interact with others, is a major concern. In this context, the frequency of motifs permits to highlight hidden structures in the architecture of the biological system. A clear example is the case of the study of the avifauna of Vanuatu’s islands, [32]. Considering birds and their island habitats as the two layers of a bipartite network, the abundance of checkerboards is analyzed in order to understand co-existing behaviors. This question triggered a long debate about the correct null model to test statistically significance of the measurements [27, 33, 48, 78]. An agreement was achieved with the work of [78], who proposed a rewiring randomization in which the degree sequence is fixed for both layers, as well as the average bird population of the islands bird species occupy. The authors observe a statistically significant abundance of checkerboards, suggesting a peculiar colonization pattern that increases the mutual exclusions of some species.

Checkerboards and togetherness in a bipartite network can be measured using, for example, the package released by Dormann et al. [35].

2.2 Nestedness

From the study of ecological systems, the insight has emerged that species in sites of lower biodiversity also populate environments with larger biodiversity. This concept is called nestedness and in mutualistic networks translates into the fact that specialists’ interactions, i.e. organisms that interact only with a small number of other species, are a subset of those of generalist organisms. This phenomenon is also present in other biological bipartite systems [8]: for example, it has been observed that species occupying different island of an archipelago describe a nested structure. Larger islands are those able to sustain a greater number of species and smaller islands host just a subset of them. It has been hypothesized that this observation is due to an original ecosystem comprising all islands, which has subsequently been divided into an archipelago by disruptive geological events. From a general heterogeneity of species in the original environment, the limited resources of the new ecosystems force some species to (local) extinction, if their population exceed the sustainable limit on the respective island. Thus, smaller islands host a subset of the species hosted by bigger islands, depending on the sustainable population of different species. Studying the effect of a fragmented habitat on the population of animals permits to design the best strategies for the conservation of rare species [23, 34, 41, 63].

The concept of nestedness is reflected in the structure of the biadjacency matrix: rows and columns can be sorted in such a way that the matrix is approximately triangular, as shown in Fig. 2. The role of such a structure is debated, as we will see in the following, but nevertheless it is constantly present in different mutualistic or antagonistic system.

Fig. 2

Illustration of three different matrices of the same dimensions and number of links (filled squares). The left-most matrix can be packed more densely into a triangular shape than the other two and has the highest nestedness. Notice how “shorter” rows (columns) are completely contained in “longer” rows (columns). The nestedness clearly decreases to the right. Figure courtesy of [67] published under CC license

In the last decades, several metrics to capture the nestedness phenomenon have been proposed in literature, with the first attempt dating back to the nestedness temperature [8]. After ordering rows and columns in the biadjacency matrix into a state of “maximum packing”, a line is drawn on the matrix representing the boundary of the expected fully nested matrix. Then, a quantity called “temperature” is defined by considering the absence in the packed part and the presence in the empty side of interactions, weighted by their distance from the boundary. In [3], the authors show that the nestedness temperature is not maximal for disordered system, since random matrices have a intermediate value of nestedness, and proposed the NODF (“Nestedness metric based on Overlap and Decreasing Fill”) to solve the problem. Using the definition Eq. (1), let us define the number of V-motifs for two nodes (i, j) with different degrees as $\tilde{V}_{ij}=(1-\delta _{k_i, k_j})V_{ij}$, where $\delta$ is the Kroenecker delta and $k_i$ the degree of node i. The NODF can be written as

$$\begin{aligned} \text {NODF}=2\dfrac{\sum _{i<j}\frac{\tilde{V}_{ij}}{\text {min}\{k_i, k_j\}}+\sum _{\alpha <\beta }\frac{\tilde{\varLambda }_{\alpha \beta }}{\text {min}\{k_\alpha , k_\beta \}}}{N_\varGamma (N_\varGamma -1)+N_L(N_L-1)}, \end{aligned}$$

(5)

where $\tilde{\varLambda }_{\alpha \beta }$ is analogous to $\tilde{V}_{ij}$ and defined on the layer $\varGamma$. Although Eq. (5) may seem slightly mysterious at first sight, we can observe some interesting properties. First, it is independent of the order of elements in the matrix and receives a contribution from each node couple of the same layer, if the respective nodes have different degrees. Second, normalizing each contribution by the minimum degree restricts it value to the range 0 (no overlap between neighbors) to 1 (if all the neighbors of the node with the smaller degree are also shared by the higher degree node). Finally, the overall denominator normalizes the NODF by accounting for the number of couples considered in the calculation. It can be shown that such a normalization induces a bias in the NODF towards the longer layer [80]: if, without loss of generality, $N_L\gg N_\varGamma$, then the main contribution to the NODF will come from the layer L. Because of this peculiarity, sometimes the nestedness is captured by considering separately the contribution from each of the two layers. Nevertheless, some scholars argued about the possibility of disregarding the contribution of couple of nodes with the same degree and, for instance, Bastolla et al. [13] provided a different measure considering such terms.

For nested species abundances in different habitats, a certain agreement about the role of nestedness has been reached: the geological division of a rich original ecosystem in an archipelago forces species to survive with the limited resources of smaller islands. Thus, species on smaller islands are more exposed to the risk of extinction, and the surviving species are a subset of those hosted on bigger islands [8]. Instead, the role of nestedness for the properties of ecological mutualistic networks underwent a deeper debate. On the one hand, it has been argued that nestedness generally increases biodiversity by reducing competition [13] and favors the stability of the network [94]. On the other hand, the authors of  [88] claim that nested interactions are inherently less stable compared to random interactions. Although predator-prey interactions seem to stabilize the networks, mutualistic and competitive interactions do not [2].

An important contribution to the discussion was put forward in [91]: the authors show that the attempts of a species to increase its abundance in a mutualistic network drives the system to a more nested configuration. In this scenario, species abundances start from general initial conditions and growth is shown to be higher if the number of mutualistic interactions is lower. Moreover, the abundance of the rarest species is connected to the resilience of the network, i.e. the speed at which the system, after small perturbations, returns to an equilibrium.

Despite these efforts, no consensus about the importance of nestedness has yet been reached. Moreover, also the origin of nestedness is highly debated: James et al. [57] show that the correlation between persistence and nestedness is present when nestedness correlates even with the connectance of the network. Hence, it is not clear which variable , i.e. whether connectance or nestedness, captures at best the properties of the system.

2.3 Monopartite Projections and Communities

When studying mutualistic networks, the question naturally arises whether one can find groups of highly cooperative species, or groups of organisms that compete for the same resources. In plant-pollinator networks, an example for the former would be a community of plants and pollinators that live in symbiosis and benefit from cooperation. Contrary to that, an example for the latter would be a collection of insects that compete for the same pollen. In ecology, these substructures are referred to as compartments [93]. In the following, we shall adopt the network vocabulary and call them modules or communities. They describe collections of nodes that are more closely related to each other than to individuals in other communities.

The problem of finding communities between nodes of the same layer can be found throughout different fields of complex networks analysis, from ecological, to financial, to economic networks. For this problem, several tools have been presented in the literature (for an overview, see, e.g. [42]). A popular approach is to perform a monopartite projection, i.e. to project the bipartite network on one of its layers. In the resulting graph, nodes are connected if they share at least one neighbor in the original bipartite network. Note that the procedure discards parts of the original information—in general, it is not possible to reconstruct the original bipartite network from the projection. Moreover, there is no clear guideline on how to set the link weights in the projection. It has been shown that the communities found in binary projections can be incorrect and misleading and that weighted projections should generally be preferred [51]. Nonetheless, simply setting the weights equal to the number of neighbors in the original network is quantitatively biased [102]. Inspired by the importance of collaborations in the author-article network of scientific coauthors, Newman proposed that links in the author projection should be corrected by a factor $1 / (d - 1)$, where d is the degree of the collaboration paper [68, 69]. Despite these efforts, a systematic exploration of how weight should be set remains open. At the same time, the question of which links carry statistically relevant information is neglected.

3 Open Problems in Economic Networks

Seminal works in classical economics date back to Adam Smith’s fundamental “The Wealth of Nations” in 1776 [86]. In the wake of Smith’s publication, David Ricardo devoted parts of his intellectual endeavors to economics, which culminated in his famous “Principles of Political Economy and Taxation” [77]. His most important legacy is probably the concept of comparative advantage, which expresses the fact that some nations can produce certain products more efficiently than others. As a result, Ricardo advocated the idea that nations should concentrate their resources only on their most advantageous industries. According to him, combining industrial specialization with free trade would be favorable for all countries and foster national economic growth.

Nowadays, international exportations and importations are recorded on a yearly basis and made available by the UN Comtrade Database.¹ This allows us to scrutinize trade relations and test hypotheses of classical economics with the help of state-of-the-art tools in data analysis and network theory. In fact, the global structure of trade interactions can be expressed as the so-called International Trade Network (ITN), also known as World Trade Web, in which nodes correspond to countries and link weights to trade volumes in US$. Countries can share directed links with different weights, corresponding to products of different categories.

International trade is one of the main global stages on which countries interact, and the ITN has been extensively studied due to its importance for economic growth and to address questions like globalization and the spreading of economic shocks [36]. For example, regarding the number of trade partners, it has been shown that the network is generally disassortative, i.e. that countries with few trade partners tend to interact with nations with many partners [46, 83]. When trade volumes are taken into account, however, it has been observed that high-degree countries trade most intensively with other high-degree countries [40]. Although product-specific trade volumes are very heterogeneous [12], the aggregate link weights distribution is almost log-normal [6, 12]. Country-specific trade volumes depend strongly on national GDP and their distributions reach from truncated log-normality to Pareto-log-normality [6].

Trade can also be studied at an even finer level, when links are drawn among regional industries instead of countries. Using the World Input-Output Database, it has been shown that global production systems are still regionally organized and industries are asymmetrically connected, leading to possible shock amplification from regional fluctuations to the global scale [24].

3.1 Diversification in Trade

Recent developments on the ITN have been triggered by the suggestion that trade networks should be considered as bipartite with countries in one layer and products in the other layer [45]. The setup is illustrated in Fig. 3. The proposal is motivated by the observation that importers and exporters have intrinsically different motivations for connecting to trade partners [45]. In particular, the rationale is that a strong exporter should also be a good producer, such that the productive capabilities of a country can be inferred from its exported products. This statement, however, has its caveats: for instance, a strong exporter may indeed be good producer, but the inverse may not necessarily be true. In fact, isolated nations have more problems in exporting wares to other countries, even if the internal production prospers. Despite these particular cases, in general studying the exports of different countries can give us information about their industrial production.

For their analyses, the authors of [45] have made use of methodologies developed for mutualistic networks and analyzed the properties of the country-product network using the revealed comparative advantage (RCA), also knows as Balassa index [11]. The RCA compares the relative monetary importance of a particular product among all exports of a country (its export basket) to the global average and assigns a value to each link accordingly, as explained in detail in Appendix A. By pruning links sequentially for different RCA threshold values, in [45] the authors separate the core and periphery of the network and showed that degree distributions are truncated power laws. The networks emerging from the pruning procedure are considered as binary, since each existing link expresses the fact that a certain country is a relevant exporter of a particular product at some threshold value.

Fig. 3

Illustration of a part of the country-product exportation network. Both Italy and Germany are strong exporters of cars and pharmaceutical products, whereas only Italy has a comparative advantage in wine production (“Wine” by Thengakola, “Car” and “pills” by alrigel from the Noun Project. All icons are under the CC license)

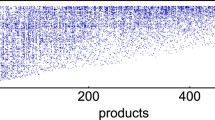
A fundamental observation that emerges from the binarized ITN, when only relevant exportations with RCA $\ge 1$² are kept, is the approximately triangular structure of its biadjacency matrix, as illustrated in Fig. 4: some countries have large export basket and others have small ones, just like some product have only few exporters and others many. The crucial fact is that the smaller export baskets are contained in the bigger ones. The ITN therefore exhibits the nestedness property [22, 29, 53,54,55, 92, 101], which we have already observed for mutualistic networks in the previous section. In the context of the bipartite trade network, this observation is striking, since it contradicts theories of classical economics. As mentioned above, according to Ricardo one would expect a specialization of exportation, which should be observable through a block-diagonal structure of the biadjacency matrix. Instead, the matrix is approximately triangular, as shown in Fig. 4, which corresponds to an increasing diversification of exportations, as has also been mentioned in [21]. The most developed countries export all products, from the most sophisticated to the most basic ones, whereas less developed countries are able to export just few low technology items.

3.2 Product and Country Space

A considerable amount of work on the bipartite trade network has been devoted to the analyses of relations among products and among countries. An intuitive approach would be to project the bipartite network on its two layers, respectively. However, this approach is generally problematic—in fact, in the case of the ITN the projected networks are almost completely connected with link densities of over 93% [82], leading to trivial properties.

To address this question, in [22] the authors apply Minimal Spanning Forests to the country and the product projections. Unexpectedly, they find that neighboring countries compete over the same market rather than diversifying their export baskets [22].

A different approach has been chosen by Hidalgo et al. [55], who construct the “product space” by connecting products that are similar according to a specific metric. The distance between two products is essentially measured as the conditional probability that a country exports both of them as measured on the data [55]. They observe that more sophisticated goods, such as vehicles and machinery, occupy the core of the network, whereas less sophisticated ones, e.g. vegetables or crude oil, populate the periphery. Given the topology of the product space, they argue that less developed countries get trapped in the periphery because of a lack of connections to the more valuable products in the core [55].

Another proposal for inferring the possible evolution of the industrialization of countries is proposed in [101]: from the binary bipartite network of trade, the authors are able to obtain a forest of products, discounting the degree sequence of both layers.

All methods revised here do not rely on the application of unbiased null model, but use different ingredients in order to highlight possible dynamics that may describe the industrialization of countries. None of them discusses the statistical significance of their findings, but rather use some of the features of the bipartite network to propose an explanation for their observations. In order to correctly project the information contained in the bipartite network, more involved methodologies are needed.

Fig. 4

Biadjacency matrix of the International Trade Network for the year 2000 with countries sorted from top to bottom and products from left to right in increasing fitness and complexity, respectively. Links in the network are shown as black dots. The overall triangularity of the matrix is correlated with the nestedness of the system

3.3 Economic Complexity

The bipartite structure of the ITN encodes information on non-tradable capabilities of countries [5], such as their infrastructure, education system, patent rights, and industry-specific knowledge. As mentioned above, the fact that a country is capable of exporting a certain product signals that its industry is advanced enough to compete in global markets [5]. Consequently, the country has the necessary latent capabilities to manufacture the product, which should be reflected in the composition of its export basket.

In order to capture how the industrial capabilities shape national economies, Hidalgo and Hausmann proposed the so-called method of reflections [53, 54]. This method is linear in the biadjacency matrix and consists of iteratively assigning a quantity to each node that depends on those of its neighbors and their degrees. As the authors point out, the resulting “complexities” of countries correlate with their GDPs. Unfortunately, the convergence of the algorithm is not guaranteed [76].

This problem was remediated in [22, 29, 92] and a non-linear recursive algorithm was proposed, which gave rise to the so-called economic complexity framework. The capabilities of countries were labeled as their fitness and the level of sophistication of the products as their complexity. Although some convergence issues are still present, it has been shown that fitness and complexity rankings of countries and products are stable even in absence of convergence [76].

In [30] the authors study the evolution of countries in terms of their fitness (intangible assets assessing competitiveness) and GDP per capita (GDPpc, a monetary measure). They observe a strong heterogeneity in the country dynamics and identify several regimes, such as a “poverty trap” in the low fitness regime, and a laminar region for high fitness countries. In conclusion, they argue that the overall heterogeneous evolution dynamics cannot be assessed with classical regression tools and that methods from dynamical systems theory would be more appropriate [30].

In a recent study, the evolution of products has been analyzed in an analogous way [5]. Similar to countries, the dynamic of products is observed in the complexity-logPRODY space, with logPRODY being a monetary measure defined as the average weight of a product exporter’s GDPpc [5]. As the authors observe, products tend to move towards an asymptotic zone with product-specific asymptotic markets. Interestingly, the asymptotic markets seem to be determined by the product complexities and are characterized by high competition [5].

Even though the study of the International Trade Network has enjoyed much attention in the last decade, it is striking that the topic of early warning signals detection in economic networks has received relatively little attention. This comes as a surprise, since financial and trade relation are strongly connected: in the aftermath of the crisis, world merchandise exports fell by 22% [100]. As we shall see in the next section, the problem of detecting early structural changes in economic systems can be tackled by adopting the same methodology employed for financial systems, i.e. by comparing the observed networks with properly-defined benchmarks.

4 Open Problems in Financial Networks

Financial institutions form a global system of investments and money lending. In the aftermath of the 2008 financial crisis, correctly assessing systemic risk and shock propagation has become a top priority for policy makers and regulators. Contrary to previous beliefs, the financial network has revealed itself to be more unstable than expected due to the complex structure of its connections [7, 14, 19, 25, 59].

Financial stress can be transmitted through two main channels: direct exposure due to bilateral agreements, such as credit swap contracts [49], and indirect exposure due to portfolio overlaps [1, 37, 44]. Whereas the first gives rise to a monopartite inter-bank network, the second presents itself naturally as a bipartite financial institutions-assets network.

Interest in the inter-bank network has surged in the fields of public administration and academic research ever since the bankruptcy of Lehman Brothers and the subsequent turmoil. An important contribution of network theory has been to shift the paradigm from the dogma “too big to fail” to “too central to fail” [15]. To quantify the financial risk associated to different institutions including network effects, the so-called “DebtRank” was introduced in [15].

Indirect exposures, on the other hand, can be created through bank portfolio overlaps. In a bank-asset network, financial institutions are ordered along one layer and assets (or asset classes) along the other. Financial contagion can be created through the effects of fire sales spillovers: a sudden drop in the value of an asset can trigger a cascade of sell-orders, which leads to asset illiquidity [20, 28, 49, 50, 84, 87]. This phenomenon can put banks in distress, who may react by selling other assets, thereby causing further devaluation dynamics.

In an recent article, a dynamical model for the analysis of shocks in the bank-asset network has been presented and applied to the Venezuelan banking system [60]. The authors show that their model is able to capture temporal changes in the structure of the network and that some assets with small capitalization can cause significant global shocks [60]. Fire sale spillovers have also been analyzed by [49], who have introduced a metric to asses the systemic risk of the bank-asset network.

Despite these significant advancements, the analysis of financial network is often hindered by a lack of detailed data. The model in [60], for instance, uses balance sheets for the model construction – but often, such information is available only in aggregate and detailed asset holdings are undisclosed. Many tools of financial analysis therefore rely on aggregate data, resulting in unrealistically dense networks and a biased underestimation of systemic risk [87]. As a consequence, improved methods are necessary that reconstructed the network in a more realistic way while avoiding systematic bias [87].

4.1 Systemic Risk

Be $\mathbf{W}$ the weighted biadjacency matrix of a bipartite network in which connections carry weights. We can obtain the node strengths by summing over the rows and columns, respectively. Let us index the banks with $i\in L$ and the assets with $\alpha \in \varGamma$. In the financial context, the vertex strengths are often described as the total asset size of a bank (or market value of their portfolio), $V_i = \sum _{\alpha } w_{i\alpha }$, and the market capitalization of an asset, $C_\alpha = \sum _{i} w_{i\alpha }$ [31, 87]. It is possible to remap the matrix entries in such a way that banks choose their portfolio weights proportional to their market value and the asset’s capitalization:

$$\begin{aligned} w^{CAPM}_{i\alpha } = \frac{V_i C_\alpha }{w}, \end{aligned}$$

(6)

where we have used $w = \sum _{i', \alpha '} w_{i'\alpha '}$ This model is called capital asset pricing model (CAPM, [61, 66]). As has been shown in [31] and is illustrated in Fig. 5, these matrix weights give a good approximation of the systemic risk of the system measured in terms of the metric introduced by [49], despite the fact that networks of return price correlations show little agreement with real cases [16, 17]. However, without the use of a null model, little can be said about the precision of the risk predictions [31].

Fig. 5

Aggregate vulnerability of the bank-asset network calculated with the metric calculated by Greenwood et al. [49] using the whole data (solid black line) and the CAPM matrix weights, which require only the node strengths (dotted red line). Figure courtesy of [31] (Color figure online)

5 Bipartite Exponential Random Graph

Statistical null models can be used as comparison benchmarks in order to verify whether real systems show unusual properties. For this purpose, they should be unbiased and formulated as general as possible. This notwithstanding, null models may maintain certain characteristics of the empirical network that should be discounted. Let us define the set of all possible networks, called ensemble, with the same node composition as the empirical network, but different number of links. To each member of the ensemble we will assign a probability that depends on some property of the original network that should be maintained. By comparing the ensemble characteristics with the actual network, we can observe how constraining certain information on the ensemble captures some features of the real system. If the quantities measured on the real network are correctly reproduced, then the constraints are enough to explain such a behavior. If, however, the real network shows a statistically significant deviation, this information cannot be explained by the constraints and represent a non-trivial information about the structure of the empirical network. In these sections, we review the extension of the exponential random graph model (ERGM) to bipartite networks, motivated by the fact that its monopartite version has enjoyed considerable success in the past [47, 58, 71]. More detailed derivations of the null models can be found in the Appendix B and in [80, 82, 90].

5.1 Bipartite Erdős-Rényi Random Graph

Let us consider an empirical binary bipartite network, expressed by its biadjacency matrix $\mathbf{M}^*$ with layer dimensions $N_L$ and $N_\varGamma$. Quantities measured on the real system will be marked with an asterisk. We start by constructing the set of all possible networks with the same layer dimensions: this set, the ensemble $\mathcal {G}_B$, runs from the empty network (without any links) to the fully connected network (in which all possible $N_{L} \times N_\varGamma$ links are realized).

Be $G_B \in \mathcal {G}_\text {B}$ an element of the ensemble $\mathcal {G}_\text {B}$ of bipartite networks with fixed layer dimensions. The most general and unbiased probability distribution over the ensemble can be obtained by maximizing the Shannon entropy [71], defined as

$$\begin{aligned} S=-\sum _{G_\text {B}\in \mathcal {G}_\text {B}} P(G_\text {B}) \ln \big (P(G_\text {B})\big ). \end{aligned}$$

(7)

Assume now that we have measured some quantities $\mathbf {C}$ of the real network, for example the number of edges. We want the corresponding ensemble expectation value $\langle \mathbf {C}\rangle$ to reflect the same value, i.e. we constrain the expectation value of the observable in such a way that $\langle \mathbf {C}\rangle \equiv \mathbf {C}^*$. It can be shown that the probability of observing the generic graph $G_\text {B}\in \mathcal {G}_\text {B}$ is, as in [58],

$$\begin{aligned} P(G_\text {B}|{\varvec{\theta }})=\dfrac{e^{-{\varvec{\theta }} \cdot \mathbf {C}(G_\text {B})}}{\mathcal {Z}({\varvec{\theta }})}, \end{aligned}$$

(8)

where ${\varvec{\theta }}$ is the vector of Lagrange multipliers associated to the constraints $\mathbf {C}$, and $\mathbf {C}(G_\text {B})$ is the value of the constraints on the graph $G_\text {B}$. $\mathcal {Z}({\varvec{\theta }})$ is the partition function known from statistical physics,

$$\begin{aligned} \mathcal {Z}({\varvec{\theta }}) =\sum _{G'_\text {B}\in \mathcal {G}_\text {B}} e^{-{\varvec{\theta }}\cdot \mathbf {C}(G'_\text {B})}, \end{aligned}$$

(9)

and its exponent the graph Hamiltonian, $\mathcal {H} ={\varvec{\theta }}\cdot \mathbf {C}$ [71]. Assuming that the network quantities $\mathbf {C}$ can be expressed analytically in terms of the biadjacency matrix, $\mathbf {C}\equiv \mathbf {C}(\mathbf{M})$, we can see that the probability $P(G_B|{\varvec{\theta }})$ for a given graph only depends on the Lagrange multipliers. The trick is to derive their values by maximizing the likelihood of observing the real network in the ensemble, $\mathcal {L}\equiv \ln P(G^*_B)$ [47]. This is equivalent to explicitly imposing $\langle \mathbf {C} \rangle =\mathbf {C}^*$ on the ensemble. Summarizing, the ERGM formulation essentially relies on two steps: first, the maximization of the entropy under some constraints, and second the likelihood maximization. The result of the former is a functional relation that describes how the probabilities per link depend on the Lagrangian multipliers. In the latter, on the other hand, the Lagrangian multipliers are explicitly calculated, essentially deriving them from the real network. In principle, different approaches can be used in order to obtain the values of the Lagrange multipliers ${\varvec{\theta }}$; the likelihood maximization permits to find the most similar configuration to the actual network.

The formalism above extends the exponential random graph [71] to networks with bipartite structure. It is well known that constraining the number of links $E^*$ in the ERGM framework returns the Erdős-Rényi random graph [39]. In analogy, imposing the same constraints on the ensemble $\mathcal {G}_B$ gives us the bipartite random graph (BiRG, as it is called in  [82]), in which all links have the same probability $p = E / N_L N_\varGamma$. The derivation of the BiRG is shown in the Appendix B.

5.2 Bipartite Configuration Model

In the previous paragraphs, we have derived the bipartite exponential random graph by focusing on the simplest constraint possible, the total number of edges E. In this section, we shall proceed by considering the degree sequence as a local, node specific property.

In the realm of monopartite networks, the configuration model (CM,  [26, 65, 68, 71]) has enjoyed a variety of application. It is constructed using the degree sequence of the real network and can be extended to the bipartite case, giving rise to the bipartite configuration model (BiCM, [80]). Constraining the degree sequence of both layers, L and $\varGamma$, corresponds to imposing two series of Lagrange multipliers, ${\varvec{\theta }}$ and ${\varvec{\rho }}$, respectively. With some algebra, it can be shown that the probability distribution becomes [80]

$$\begin{aligned} P(G_B|{\varvec{\theta }}, {\varvec{\rho }}) = \prod _{i, \alpha }(p_\text {BiCM})_{i\alpha }^{m_{i\alpha }} \big (1-(p_\text {BiCM})_{i\alpha }\big )^{1-m_{i\alpha }}, \end{aligned}$$

(10)

where the probability per link reads

$$\begin{aligned} (p_\text {BiCM})_{i\alpha }=\frac{e^{-(\theta _i + \rho _\alpha )}}{1+e^{-(\theta _i+\rho _\alpha )}}, \quad i\in L, \alpha \in \varGamma \end{aligned}$$

(11)

The Lagrange multiplicators can be recovered through the maximization of the likelihood $\mathcal {L}$ of observing the empirical network, as shown in Appendix B.

Note that Eq. (10) factorizes into the single link probabilities. This is very convenient for analytical calculations, for example for the multi-linear bipartite motifs, such as the V-motif in Eq. (1) and the X-motif in Eq. (2).

Other less strict null models can be defined through the relaxation of the constraints. For instance, imposing only the degree sequence of one layer leads to the bipartite partial configuration model (BiPCM, [82]). The choice of the null model generally depends on the information that one wishes to discount.

5.2.1 Validated Projections

The BiCM can be used to safely project the information contained in the bipartite network on one network layer, discounting the information from the degree sequence [50, 82, 90]. The idea is to compare the observed co-occurrence of links between nodes on the same layer (or, otherwise stated, the number of V-motifs between nodes on the same layer) with the expectations from the null model. In the BiCM, given a node couple, the probabilities for the V-motifs insisting on them are independent and, in general, different [82]. Thus, the distribution of such V-motifs is Poisson-Binomial, the generalization of a binomial distribution to independent events with different success probability [56]. The comparison between the observations with the expectation of the null model can be captured by a p-value, such that we obtain one p-value for every node couple: p-values are analyzed through a multiple hypothesis test and only statistically significant V-motif abundances are validated, leading to a monopartite network with only statistically relevant links. This methods is known in literature as the grand canonical projection algorithm and is described in detail in [50, 82, 90].

5.3 Bipartite Configuration Models for Weighted Networks

The ERGM bipartite framework can be easily extended from binary to weighted networks. In weighted bipartite networks, nodes are characterized by their degrees and strengths, i.e. the sum over the weight of their edges. One may intuitively be inclined to extend the BiCM to its weighted counterpart, the bipartite weighted configuration model (BiWCM [31], see Appendix B), by simply exchanging the degree with strength constraints. However, it has been shown for monopartite networks that such a null model performs very badly in capturing the essential features of the actual network [62]. This is due to the fact that it ignores the information on the network topology that is contained in the binary degree sequence. As the authors of [62] point out, non-trivial degree and strength sequences complement each other in the network reconstruction. The constraints should thus be modified accordingly: in Sect. 8 we shall see how a bipartite system guides us to the definition of a proper null model in the financial context.

6 Results in Ecological Networks

6.1 Degree Sequence in Biological Bipartite Networks

Entropy-based approaches for the analysis of biological systems are well present in literature [9, 52], but they have rarely been employed for the analysis of bipartite networks. Contrary to this general tendency, Williams [97] has used the aforementioned BiRG to assess the significance of the degree distribution in mutualistic networks. The author has sampled the ensemble of the BiRG and compared the observed degree distribution with the frequencies expected from the null model by implementing the likelihood ratio statistics. The calculation is repeated for every element of a sample of the BiRG ensemble and the values are compared. The comparison shows that the degree distribution of mutualistic networks, besides being strongly skewed, can be usually explained just by the total number of links. The result is even more striking, considering that its monopartite analogous has not such a good performance [96].

6.2 Nestedness (Reprise)

The study of nestedness has enjoyed considerable attention in ecology. Yet despite those efforts, doubts about its origin and significance persist, as we have seen in Sect. 2. To address this matter, Johnson et al. [67] highlight that a null model should be implemented in order to state if the nestedness of a particular system is a genuine quantity, or whether it is already captured by the degree sequence. By applying an approximation of the configuration model presented in [26, 65, 68, 71], which is valid for sparse networks, they argue that nestedness naturally derives from degree heterogeneities and disassortative degree-degree correlation, i.e. the tendency of low degree nodes to connect to high degree nodes. As they point out, finite null models, such as the approximated configuration model [26, 65, 68, 71], tend to be dissassortative and nested. Studying 60 empirical networks, they conclude that in almost 90% of them the observed nestedness can be described by a degree-conserving null model.

The results of Johnson et al. [67] have been refined and re-interpreted in a recent work by Payrató Borrás et al. [72], which has been published during the writing of the present review. Based on a comparison between the NODF values and the BiCM expectations of 167 different biological systems, they conclude that the observed nestedness can indeed be explained by the null model and are thus accounted for by the degree sequence.

7 Results in Economic Networks

7.1 Network Validation in Trade

In the following paragraphs, we review some recent results that have been obtained through the application of the binary BiCM in the area of international trade.

To compare the empirical network with the null model, we shall make us of z-scores. Be $Q(G_B)$ a quantities that we can measure on the network $G_B$. Eq. (11) gives us the tools to calculate its expectation value $\langle Q \rangle$ and the standard deviation $\sigma _Q$ on the BiCM ensemble. The z-score is defined as

$$\begin{aligned} z(Q) = \frac{Q^* - \langle Q \rangle }{\sigma _Q} \end{aligned}$$

(12)

and expresses the discrepancy between the observed and the expectation value in terms of standard deviations.

7.1.1 Nestedness and Specialization

The bipartite export network of countries and products is nested, meaning that smaller export baskets are contained in larger ones [22, 29, 53,54,55, 92, 101]. As we have seen in the previous paragraph, by using the BiCM it is possible to show that the nestedness of mutualistic networks is explained by their degree sequence [67, 72]. The same idea has been tested for the trade network [80]: the authors show that the nestedness of the International Trade Network (ITN) could be reproduced by the BiCM, thereby highlighting that the observed connection between degree sequence and nestedness also holds in non-ecological systems. However, the authors also argue that the BiCM cannot fully reproduce the disassortativity of the ITN, leading to the conclusion that the degree sequence alone is not enough to explain why strong exporters preferably connect to weak exporters.

In the nested representation of the bipartite trade matrix (as shown in Fig. 4), countries and products are typically ordered in increasing fitness and complexity along the rows and columns, respectively. Although the algorithm for calculating their values may not converge, it has been shown that the rankings are stable nonetheless [75]. Since the degree-constrained BiCM recovers the nestedness of the network, one may thus question its ability to reproduce the fitness and complexity rankings. This matter was addressed in [80], in which the authors show that the degree distributions for countries and products can be accurately reproduced when they are ranked by fitness and complexity, respectively. However, the model does not reproduce the exact fitness and complexity rankings: even when the observed values are close to the null model expectations, the distributions over the BiCM ensemble are broad, as shown in Fig. 6. Despite the fact that fitness is positively correlated with the degree sequence, highlighted by the tendency of the expectations to follow the real ranks in Fig. 6, it contains information that is not accounted for by the latter.³ A similar behavior is observed for the product complexity rankings.

Fig. 6

Boxplots for the expected fitness rankings against the actual values for the year 2000. The country with the highest rank 1 (Germany) has the highest fitness, the one with lowest rank 146 (Iraq) has the lowest fitness. Red dots represent the averages on the ensemble. While the expected ranks are close to the observed ones, the vertical distribution intervals are quite large. We annotate those countries whose ranks diverge the most from the expectations of the null model: the countries whose real fitness values are much higher than expected are above the identity line. Ireland, Norway, Singapore and Israel have thus much higher empirical ranks, whereas Morocco’s, Kenya’s and Gambia’s are much lower (Color figure online)

Fig. 7

The images shows the biadjacency matrix in Fig. 4 with links as white dots. The z-scores of the connectivity with respect to the BiCM are shown as a superimposed color map (gray shading). Higher link abundances than expected are shown as lighter colors, and lower abundances as dark colors. The smaller exporters on the top focus on the most basic products, as shown in the upper-left corner by the z-scores $(z\sim 30)$. The most developed countries on the bottom, on the other hand, specialize on the most sophisticated products, as measured by the scores in the lower-right $(z\sim 25)$. Moreover, they export basic products much less than expected, as can be seen in the the lower-left corner $(z\sim -20)$. This suggests that countries diversify their export baskets as much as possible while specializing on the most sophisticated products they are able to export. Figure modified from [90] (Color figure online)

Fig. 8

Illustration of the product network with colors according to the occupation density of country communities, i.e. the density of links existing between the corresponding product and country communities [90]. Left: Advanced economies occupy the core of the network, which contains high technology items. Right: Developing economies occupy much more the periphery with less sophisticated product rather than the center. Figure courtesy of [90] (Color figure online)

The analysis of the triangular structure of the country-product matrix has been extended in [90]. Discounting the degree sequence and comparing empirical with expected link abundances, the authors observed a specialization signal within the overall export diversification tendency. Figure 7 shows the phenomenon quantitatively using the empirical biadjacency matrix and the z-scores of the expected number of links as a heat map. “Hotter” (whitish) colors represent higher z-score values, “colder” (dark) colors lower values. The high z-scores stretch from the upper-left to the lower-right and illustrate that countries concentrate their exports on more complex products more than expected, while still exporting basic goods as well. As a consequence, stating that exports baskets are nested is only partially true, since the density in the baskets of more developed countries remains biased towards more exclusive products.

These conclusions can also be drawn from validated monopartite projection of the bipartite trade network (see Sect. 5.2.1). Figure 8 shows the link density between different areas of the product network and advanced economies (left) and developing economies (right): in both cases, the network is not populated uniformly, since the former tend to occupy preferentially the highly technological items in the core of the network, whereas the latter focus their export on lower complexity products that belongs to the periphery of the validated product network. In this sense, developed countries, given the size of their export basket, tend to specialize their exports towards the most exclusive products.

The previous result on the biadjacency matrix and the product network therefore reconcile the apparent conflict between Ricardo’s argument of export specification and the overall diversification reported in literature [21]. Nevertheless, let us stress that the specialization phenomenon is a higher-order feature of the bipartite network of trade: in fact, it can be uncovered only by discounting the degree sequence information.

7.1.2 Motif Validation in Trade

Evolution of Bipartite Motifs of Countries

In the economic literature, acronyms are often used to refer to countries that supposedly share similar features in their economic development and institutional frameworks. Famous examples are the G7 (Canada, the USA, Italy, France, Germany, the UK, Japan), which share a large part of the global GDP, and the five rising BRICS economies (Brazil, Russia, India, China, South Africa). Further groups are, e.g., the MINT countries (Mexico, Indonesia, Nigeria, Turkey) that show interesting economic developments [70] and the south European “PIGS” (Portugal, Italy Greece, Spain) that were struggling during the 2008 financial crisis [43].

Using the bipartite International Trade Network, it is possible to quantify the similarities within these country groups in terms of their $\text {V}_n$-motifs, n being the number of members. In [81], the authors compare the real trade network with the randomized BiCM ensemble to observe if such similarities are genuine or can just be attributed to the dimension of the export baskets, i.e. the country node degrees. They applied the BiCM to the product-country trade network and calculated the number of $\text {V}_n$-motifs for each country group, where n is the number of members.

Fig. 9

Comparison of the observed numbers of V$_n$-motifs (see Sect. 2.1). The green dots represent the empirical quantity measured on the real network, the box plot the expectation value distribution according to the BiCM. The whiskers capture the 0.15th and the 99.85th percentile. Whereas the BRICS and G7 are compatible with the null model predictions, PIGS, Tiger Cubs and the ex-Warsaw Pact countries show abundances that are not explainable in terms of the degree sequences alone. Figure courtesy of [81] (Color figure online)

Figure 9 compares the number of $\text {V}_n$-motifs for different country groups [81]: green dots represent the values observed in the data, whereas the box-plots capture the probability distribution of the ensemble. In panel (c) we can see that the observations for the “PIGS” lie clearly above the box-plot whiskers, which indicates that the similarities are not merely due to their export baskets sizes. This is true even before the 2008 crisis, although the discrepancy gradually increases over time. The BRICS in panel (a), on the contrary, show export basket overlaps that are compatible with the null model. The MINT countries in panel (f) do not have a single export item in common. As a consequence, both MINT and BRICS groupings cannot be justified from the observation of similar industrial capabilities alone (see also [29, 92]).

Contrary to that, strong similarities can be observed in the Tiger Cubs (Thailand, Indonesia, Malaysia, Philippines, Vietnam), which have experienced a recent industrialization process similar to the original Four Asian Tigers (Hong Kong, Singapore, South Korea, Taiwan). Panel (d) in Fig. 9 shows a statistically significant signal of V$_n$-motifs, which gradually diminishes in intensity. This indicates that their recent industrial developments have begun to diverge, progressively turning into a differentiation in their exports. Similarly, the impact of a common communist industrialization program can be observed in the exports of ex-Warsaw Pact countries that are now part of the European Union (such as Poland, Romania, and Hungary) well into the years 2000, see panel (e) in Fig. 9. After joining the EU, the signal has progressively declined. The composition of the G7 group, on the other hand, can be simply attributed to their degrees, i.e. to the dimensions of their export baskets: panel (b) shows that no statistically significant signal can be detected.

Closed Motifs evolution Closed motifs are more complex combinations of links and capture mesoscopic structural properties of the network. For instance, a X-motif measures how many times two countries compete on the world market by sharing more than two products in their export basket. A high number of X-motifs indicates that their export baskets are very similar on a global level. Several scholars [99] suggest that an excessive degree of similarity in industrialization and exportation weakens the International Trade Network and makes is more prone to stress. A diversification of industrial capabilities, on the other hand, would make the system more resilient.

Fig. 10

a–c show the abundance of closed motifs (see Sect. 2.1) in the ITN network from 1995 until 2010. It is apparent that they increased until the financial crisis struck and dropped after 2007. The values are compared with the BiCM expectations in (d) using z-scores. Before the crisis, abundances were strongly underrepresented and increasing significantly already from 2003 onwards, indicating a global change of the network. Figure courtesy of [81] (Color figure online)

Following the trends in Fig. 10a–c, we can observe an increase in the number of closed motifs, i.e. of the similarity of export baskets, before the financial crisis [81]. This development comes to an abrupt halt in 2008 and abundances drop from that point on. Notice that this evolution only illustrates what happened in the wake of the crisis and does not provide any early-warning signal. However, comparing the observations with the null model, a very different picture arises, as illustrated in panel (d): all three motifs occur less in the network than would be expected from the BiCM. Z-scores are predominantly negative, with values as small as -3 to -4 for the X- and M-motifs. They are relatively stable until 2003, from which point on we observe a clear trend towards greater z-scores, i.e. towards a better agreement with the null model. Thus when the crisis struck in 2008, the ITN had already undergone significant structural changes in the preceding five years, which eventually fade out around 2010.

Note that the latter results do not imply any causal relation, as discussed in [81]. However, the dramatic evolution of the closed motifs anticipated the crisis. In that sense it can be regarded as an early-warning signal, since it informs us that the network is changing globally such that the resilience of the whole system is modified, making it more vulnerable to external shocks.

Moreover, it is worth underlining that these observations cannot be made without the benchmark of the null model. Considering only the data limits us to the simple observation of abrupt trend changes in motif abundances. Only the comparison with the BiCM reveals a clear signal of anticipating structural change. Analyses as the one presented here provide effective tools to monitor systems such as the ITN, and offer deep insights to policy makers.

In summary, recent results on the International Trade Network obtained through the comparison with the BiCM have shown that many apparently genuine properties can be traced back to the degree sequence, i.e. the number of exporters of a product and the size of the export basket of a country.

8 Results in Financial Networks

8.1 Systemic Risk (Reprise)

Financial stress can propagate among banks through asset portfolio overlaps. As indicated in Sect. 4.1, the capital asset pricing model (CAPM) performs well at assessing the systemic risk due to fire sales spillover effects in the bipartite bank-asset network of financial US institutions [31]. Their data is derived from quarterly reports which disclose the single positions in the bank portfolios. Hence, the authors could compare the risk estimations due to aggregate exposures, considering only the node strengths, with measures that take also the degrees into account. Risk is measured using the metric defined by Greenwood et al. [49].

Although the CAPM framework replicates the systemic risk well (see Fig. 5), without a proper model little can be said about the precision of the risk prediction. Hence, the maximum entropy capital asset pricing model has been proposed (MECAPM, [31], see Appendix B), for which the portfolio weights are constrained as $\langle w_{i\alpha }\rangle = w^{CAPM}_{i\alpha }$. With $N_L$ and $N_\varGamma$ being the numbers of banks and portfolios, the MECAPM thus uses $N_L \times N_\varGamma$ conditions. As shown in Appendix B, the single link probabilities read [31, 87]

$$\begin{aligned} \left( p_{CAPM}\right) _{i\alpha } = \frac{w^{CAPM}_{i\alpha }}{1 + w^{CAPM}_{i\alpha }} \end{aligned}$$

(13)

and the probability for a particular graph, $P(G_B)$, is geometrically distributed [31].

Fig. 11

Quartile of banks with the highest indirect risk as measured by [31] during the interval 2001–2014. Top: MECAPM (dashed line, grey shading); Middle: BiECM (blue squares, blue shading); Bottom: BiWCM (red crosses, red shading). The shaded areas and their partial overlaps illustrate the corresponding distributions. Although all three models systematically underestimate the systemic risk, MECAPM outperforms the best. Figure courtesy of [31] (Color figure online)

Since strength and degree information can complement each other, in analogy to the monopartite case in [62] the authors of [31] have also included the so-called bipartite enhanced configuration m odel (BiECM, [31]), on which degrees and strength constraints are imposed.

The results of the analysis are summarized in Fig. 11 for the banks with the highest systemic exposures in the data. The BiWCM refers to the weighted counterpart of the BiCM, in which node strengths instead of node degrees are constrained (see Appendix B and [31]). Although all three models systematically underestimate risk, the MECAPM clearly outperforms the other two models [31]. Notice that the BiWCM performs very badly, underestimating the risk as much as $-80\%$. Errors are relatively large, as we can see from the shaded areas.

A possible reason for the large error intervals in Fig. 11 has been suggested in [87], pointing to the fact that the MECAPM predicts very dense network configurations. In fact, from  Eq. (13) we can see that the link probabilities quickly approach 1 for $w_{i\alpha }^{CAPM} \gg 1$. This issue has been taken up in [87], which proposes the so-called enhanced capital asset pricing model (ECAPM, [87]). Using only the strength sequences $C_i$ and $V_\alpha$ of the asset capitalization and portfolio market value, respectively, this approach aims at reconstructing the network topology while imposing the CAPM link weights.

Firstly, the topology of the network is established by using the BiCM under the assumption that the Lagrange multipliers are proportional to node-specific fitness values, represented by their strengths [87]. In analogy to the BiCM (see Appendix B), this yields

$$\begin{aligned} (p_{ECAPM})_{i\alpha } = \frac{z V_i C_\alpha }{1 + z V_i C_\alpha },\quad \forall i \in L, \alpha \in \varGamma , \end{aligned}$$

(14)

where z absorbs the proportionality constants.

Secondly, the link weights are reconstructed using the CAPM model while taking the network topology into consideration. Instead of setting $w_{i\alpha } = V_i C_\alpha / w$, a correction factor is applied [87]

$$\begin{aligned} w_{i\alpha }= & {} m_{i\alpha } \frac{V_i C_\alpha }{w\ (p_{ECAPM})_{i\alpha }} \nonumber \\= & {} (V_i C_\alpha + z^{-1}) \frac{m_{i\alpha }}{w}, \end{aligned}$$

(15)

where $m_{i\alpha }$ is 0 or 1 depending on the link presence. As pointed out in [87], the weight expectations of the ECAPM correspond with those of the MECAPM and thus the CAPM [87]. However, the former reconstructs the network topology separately, which compensates the high network densities for the latter.

The difference between the ECAPM and the MECAPM has been tested in [87] on a data set of security holdings of European institutions (Security Holding Statistics, SHS) collected by the European Central Bank from 2009 to 2015. The empirical difference is visible in Fig. 12, which compares the node degrees with node strengths. The MECAPM shows continuously high degrees and does not capture the real distribution, which illustrates the observation made for Eq. (13). Even though the ECAPM underestimates degrees for small strength values, it better reproduces the data.

Fig. 12

Relation between the strengths and degrees of the nodes in [87]. The security holder portfolios have certain market values $V_i$ (the “banks”) and issued security assets have a market capitalization $C_\alpha$ (the “assets”). The ECAPM follows the real empirical data much closer than the MECAPM, which systematically overestimates the degrees. Figure courtesy of [87] (Color figure online)

Since both MECAPM and ECAPM reproduce the same weights, they estimate the same systemic risks as measured with the metric introduced in [49]. However, reconstructing the topology as in [87] significantly decreases the uncertainty of the risk metric. In particular, comparing the errors of the MECAPM and ECAPM yields

$$\begin{aligned} \sigma _{S_i}^{MECAPM} \propto V_i^{1/2}\sigma _{S_i}^{ECAPM}, \end{aligned}$$

(16)

where $V_i$ is the value of institution i and $S_i$ its systematicness [87]. The fluctuations in the ECAPM framework are thus systematically smaller than in MECAPM and motivate the application of a degree as well as strength reconstruction.

Fig. 13

Left: Fraction of financial institutions in the validated monopartite projection. The values decrease only slightly, with temporary reduction around 2009. Right: Average degree in the monopartite projection of financial institutions. Notice the salient dip in 2009 after the beginning of the crisis. Figure courtesy of [50] (Color figure online)

8.2 Portfolio Overlap Projection

The risk of fire sales has also been treated in [50] using a different methodology. Contrary to [31] and [87], they do not consider weighted networks but instead the binary bipartite network between financial institutions and their assets holding in the years 1991–2013. Instead of calculating the systemic risk measure on the null model, they focus on the overlap matrix of portfolios, which expresses the number of assets that financial institutions share, i.e. the number of their V-motifs (see Eq. (1)). By applying the grand canonical projection algorithm [82] with a Bonferroni correction for the p-value testing, and thus comparing the observed values $\hbox {V}^*$ with their BiCM expectations and validating only statistically significant links, they obtain a network of financial institutions containing only relevant links that are not accounted for by the degree sequences.

As Fig. 13 shows, the fraction of institutions that have at least one significant edge in the validated network remains relatively constant. In spite of this seemingly innocuous development, the similarity of these nodes increase very quickly, as illustrated in Fig. 13. In particular, notice how the similarity increases before the 2007–2008 financial crisis. After a drop in 2009, it took up pace and has reached levels even higher than before the crisis [50].

In conclusion, the authors point out that the validated projection method can recover those financial institutions that would be at risk of suffering the greatest losses in cases of financial distress [50].

9 Conclusions and Outlook

In this review, we have presented several recent methods designed for the statistical analysis of bipartite network. Interestingly, despite the fact that bipartite networks have been considered deeply in ecology, and many analytical quantities of interest originate from the study of, e.g., species interaction networks, recent techniques for statistical significance testing have been formulated in a -seemingly- completely different context, namely economic and financial systems. However, while the latter has benefited greatly from the progress made in ecology, many of the analytical tools commonly employed in socio-economic networks seem not to have been recognized yet as potentially useful for ecological systems, apart from few exceptions [67, 72, 97]. However, the recent application of the bipartite configuration model, originally formulated for the study of international trade, has already shed some light on a better understanding of the origin of nestedness. In a similar way, validating similarities among insect species could provide insights on their competition in isolated environments. Furthermore, the resilience studies of economic and financial bipartite networks can catalyze the study of extinction spillovers in the standard ecological framework. This work aims at bridging the gap between these two—apparently—distant areas which can benefit greatly from sharing advancements across scientific fields.

A straightforward example is provided by the detection of mesoscale structures in bipartite networks, such as communities and motifs. Although motifs have been popularized in biological science, recently proposed techniques to overcome the limitations of modularity maximization have not yet crossed the borders of graph theory, and their application in ecological networks is still in an embryonic stage [10]. The same holds true for the multiplex formalism [73]. The cross-disciplinary importance of these topics is clearly shown by the idea of considering social networks as “mutualistic” information ecosystems. In this context, has been found that mesoscale structures may be correlated to the emergence of collective attention [18], in particular when a transition from a modular to a nested structure is observed. These results also underline the general need to develop dynamical models to study the evolution of bipartite networks.

An application that has benefited from both, the concepts developed in ecology and the methods designed for social networks, are so-called recommender systems [102]. Briefly speaking, these algorithms suggest “users” their next “choices”, be they movies to watch or items to buy, among others. Although many recommendation algorithms exist, an interesting example is provided by those which are built upon the idea of a resource-allocation dynamic taking place on the network. Other concepts such as specialization and interaction have inspired models able to reproduce observed patterns in both ecological and social systems [79].

Some of the statistical methods presented in this review have been recently employed and extended for the study of tripartite structures to asses the relationship between technology and economic development [74]. In this network, the three layers consist of technologies, countries, and products, and the analysis aims at quantifying the probability of jumping from a given technology in one layer to a given product in another one, while accounting for all possible paths through the intermediate countries layer. Although the null model employed in this approach is, in fact, a combination of two distinct bipartite configuration models, the paper certainly represents an interesting direction for future research.

Appendices

Appendix: Revealed Comparative Advantage

The revealed comparative advantage (RCA, also knows as Balassa index [11]), rescales the product export volumes in order to determine whether countries are relevant exporters of products. Be e(c, p) the export value of product p in country c’s export basket. The RCA is calculated by comparing the monetary importance of p in c’s export basket to the global average,

$$\begin{aligned} \text {RCA}_{c, p} = \frac{e(c, p)}{\sum _{p'} e(c, p')} \big / \frac{\sum _{c'}e(c', p)}{\sum _{c', p'} e(c', p')} . \end{aligned}$$

(17)

A country is a relevant exporter if RCA $\ge 1$. Using the RCA, the weighted country-product biadjacency matrix can be binarized by keeping only those matrix entries that identify relevant exports and setting them to 1.

Appendix: Bipartite Exponential Random Graph Model

We report some of the null models that have been obtained through entropy maximization and which have been applied to binary and weighted bipartite networks. In the following, all quantities marked with an asterisk refer to the real networks, expressed by their binary ($\mathbf{M}^*$) or weighted ($\mathbf{W}^*$) biadjacency matrix. The layer dimensions are $N_L$ and $N_\varGamma$.

1.1 Bipartite Random Graph

Constraining the expected number of links in the graph ensemble yields an extension of the Erdős-Rényi random graph to bipartite networks, the bipartite random graph (BiRG). The constraint $C \equiv E = \sum _{i,\alpha }m_{i\alpha }$, and thus the Lagrange multiplier $\theta$ as well, is scalar. The partition function can be calculated easily:

$$\begin{aligned} \mathcal {Z}_\text {BiRG}(\theta )= & {} \sum _{G_\text {B} \in \mathcal {G}_\text {B}}e^{-\theta E(G_\text {B})}\nonumber \\= & {} (1+e^{-\theta })^{N_L N_\varGamma }. \end{aligned}$$

(18)

The probability per graph reads

$$\begin{aligned} P(G_G|\theta )= & {} \dfrac{e^{-\theta E}}{(1+e^{-\theta })^{N_L N_\varGamma }}\nonumber \\= & {} \left( p_\text {BiRG}\right) ^E(1-p_\text {BiRG})^{N_L N_\varGamma -E}, \end{aligned}$$

(19)

where $p_\text {BiRG} \equiv \dfrac{e^{-\theta }}{1+e^{-\theta }}$ is the probability of observing a bipartite link between any node couple $i\in L$, $\alpha \in \varGamma$. Notice that $p_\text {BiRG}$ is uniform and independent of the links. Since Eq. (19) is a Binomial distribution, we see that the probability of observing a generic graph $G_\text {B}$ in the ensemble reduces to the problem of observing $E(G_\text {B})$ successful trials with the same probability $p_\text {BiRG}$. We can obtain an analytical expression for the Lagrange multiplier $\theta$ and thus for the link probability by maximizing the likelihood, which reads

$$\begin{aligned} \mathcal {L}=\ln P(G^*|\theta )=-\theta \, E^*- N_LN_\varGamma \ln (1+e^{-\theta }), \end{aligned}$$

(20)

and returns

$$\begin{aligned} p_\text {BiRG}=\frac{E^*}{N_L\,N_\varGamma }. \end{aligned}$$

(21)

1.2 Bipartite Partial Configuration Model

Without loss of generality, we constrain the degree sequence on the layer L such that $\langle k_i\rangle =k_i^*,\,\forall i \in L$. For each node degree $k_i$, we introduce one associated Lagrange multiplier, $\theta _i$. This gives us the bipartite partial configuration model (BiPCM, [82]). Following the same procedure as in Eq. (18), we can obtain

$$\begin{aligned} \mathcal {Z}_\text {BiPCM}({\varvec{\theta }}) =\prod _{i,\alpha }1+e^{-\theta _i}. \end{aligned}$$

(22)

The probability per graph reads

$$\begin{aligned} P(G_B|{\varvec{\theta }})= & {} \prod _{i,\alpha } (p_\text {BiPCM})_i^{m_{i\alpha }} \big (1-(p_\text {BiPCM})_i\big )^{1-m_{i\alpha }}\nonumber \\= & {} \prod _{i}(p_\text {BiPCM})_i^{k_i} \big (1-(p_\text {BiPCM})_i\big )^{N_\varGamma - k_i}, \end{aligned}$$

(23)

where $(p_\text {BiPCM})_i=\frac{e^{-\theta _i}}{1+e^{-\theta _i}}$ is the probability of connecting the node i with any of the node of the opposite layer $\varGamma$. The link probabilities are not uniform, but depend on the Lagrange multipliers of the nodes $i\in L$. The factors in the product in Eq. (23) express the probabilities of observing exactly the constrained node degrees: the probability of the degree $k_i$ of the node $i \in L$ is given by the probability of observing $k_i$ successes trials of a binomial distribution with probability $(p_\text {BiPCM})_i$. Maximizing the likelihood $\mathcal {L}$ returns the explicit expressions for the link probabilities:

$$\begin{aligned} (p_\text {BiPCM})_i=\dfrac{k_i^*}{N_\varGamma }. \end{aligned}$$

(24)

1.3 Bipartite Configuration Model

In the monopartite configuration model, the degrees of all the nodes are constrained. Analogously, in the bipartite configuration model (BiCM, [80]) the degrees of the two layer degree sequences are constrained, such that $\langle k_i\rangle = k_i^*,\,\forall i\in L$, and $\langle k_\alpha \rangle =k_\alpha ^*,\,\forall \alpha \in \varGamma$. If ${\varvec{\theta }}$ and ${\varvec{\rho }}$ are the corresponding Lagrange multipliers, the partition function reads [80]

$$\begin{aligned} \mathcal {Z}_\text {BiCM}({\varvec{\theta }}, {\varvec{\rho }})=\prod _{i,\alpha }1+e^{-(\theta _i + \rho _\alpha )}, \end{aligned}$$

(25)

following essentially the same strategy used in Eq. (18). Again, the probability per graph factorizes in a product of probabilities per link:

$$\begin{aligned} P(G_B|{\varvec{\theta }}, {\varvec{\rho }})= & {} \prod _{i, \alpha } \dfrac{e^{-(\theta _i + \rho _\alpha ) m_{i\alpha }}}{1+e^{-(\theta _i+\rho _\alpha )}}\nonumber \\= & {} \prod _{i, \alpha } (p_\text {BiCM})_{i\alpha }^{m_{i\alpha }} \big (1-(p_\text {BiCM})_{i\alpha }\big )^{1-m_{i\alpha }}, \end{aligned}$$

(26)

where the probability per link reads

$$\begin{aligned} (p_\text {BiCM})_{i\alpha }=\frac{e^{-(\theta _i + \rho _\alpha )}}{1+e^{-(\theta _i+\rho _\alpha )}}, \quad i\in L, \alpha \in \varGamma \end{aligned}$$

(27)

Compared to the probability distributions of the BiRG and BiPCM, we can see that the BiCM distribution is more general and corresponds to the product of different Bernoulli events with link-specific success probabilities. Note that the distribution factorizes and link probabilities are independent. Maximizing the likelihood returns the equation system [80]

$$\begin{aligned} \left\{ \begin{array}{c} \sum _\alpha \dfrac{e^{-(\theta _i+\rho _\alpha )}}{1+e^{-(\theta _i + \rho _\alpha )}}=k_i^*,\quad \forall i\in L,\\ \\ \sum _i\dfrac{e^{-(\theta _i+\rho _\alpha )}}{1+e^{-(\theta _i+\rho _\alpha )}}=k_\alpha ^*,\quad \forall \alpha \in \varGamma . \end{array}\right. \end{aligned}$$

(28)

Solving this system allows us to evaluate the Lagrange multipliers and ultimately obtain the graph probabilities.

1.4 Bipartite Weighted Configuration Model

Constraining the node strengths as $\langle s_i \rangle = s^*_i, \forall i\in L$, and $\langle s_\alpha \rangle = s^*_\alpha , \forall \alpha \in \varGamma$, yields the bipartite weighted configuration model (BiWCM, [31]). Be ${\varvec{\theta }}$ and ${\varvec{\rho }}$ the corresponding Lagrange multipliers. As shown in [31], the partition function is

$$\begin{aligned} \mathcal {Z}_\text {BiCM}({\varvec{\theta }}, {\varvec{\rho }}) = \prod _{i,\alpha } \frac{1}{ 1 - e^{-(\theta _i +\rho _\alpha )}}. \end{aligned}$$

(29)

The graph probability yields

$$\begin{aligned} P(G_B|{\varvec{\theta }}, {\varvec{\rho }}) = \prod _{i, \alpha } \left( e^{-(\theta _i +\rho _\alpha )}\right) ^{w_{i\alpha }} (1 - e^{-(\theta _i +\rho _\alpha )}). \end{aligned}$$

(30)

Similar to the BiCM, the Lagrange multipliers can be obtained by solving an equation system, which reads [31]

$$\begin{aligned} \left\{ \begin{array}{c} \sum _\alpha \dfrac{e^{-(\theta _i + \rho _\alpha )}}{1 - e^{-(\theta _i +\rho _\alpha )}} = s_i^*,\quad \forall i\in L,\\ \\ \sum _i\dfrac{e^{-(\theta _i +\rho _\alpha )}}{1 - e^{-(\theta _i + \rho _\alpha )}} = s_\alpha ^*,\quad \forall \alpha \in \varGamma .\\ \end{array}\right. \end{aligned}$$

(31)

1.5 Bipartite Enhanced Configuration Model

The bipartite enhanced configuration model (BiECM, [31]) is a bipartite extension of the monopartite enhanced configuration model introduced in [62]. Both, degrees as well as strengths, are constrained.

Be $\theta _i$ and $\theta _\alpha$ the constraints associated to the degrees, and $\rho _i$ and $\rho _\alpha$ those associated to the strengths for the nodes $i\in \text {L}$ and $\alpha \in \varGamma$, respectively. Using the short-hand notation $\phi _i = e^{-\rho _i}, \xi _\alpha = e^{-\rho _\alpha }, \psi _i = e^{-\theta _i}$ and $\gamma _\alpha = e^{-\theta _\alpha }$, the partition function reads [31]

$$\begin{aligned} \mathcal {Z}_{BiECM}({\varvec{\theta }}, {\varvec{\rho }}) = \prod _{i, \alpha } \frac{1 - \phi _i \xi _\alpha ( 1 - \psi _i \gamma _\alpha )}{1 - \phi _i \xi _\alpha }. \end{aligned}$$

(32)

Consequently, the network probability is given by

$$\begin{aligned} P(G_B) = \prod _{i, \alpha } \frac{(1 - \phi _i \xi _\alpha ) (\phi _i\xi _\alpha )^{w_{i\alpha }} (\psi _i\gamma _\alpha )^{\varTheta (w_{i\alpha })}}{1- \phi _i \xi _\alpha (1 - \psi _i\gamma _\alpha )} \end{aligned}$$

(33)

and factorizes in single link probabilities. The values of the Lagrange multipliers can be obtained through a nonlinear system of equations, as shown in the Appendix of [31].

1.6 Maximum Entropy Capital Asset Pricing Model

The elements of the weighted biadjacency matrix can be rescaled to yield the quantities of the capital asset pricing model (CAPM, [61, 66]). In the financial context, the vertex strengths are often described as the total asset size of a bank (or market value of their portfolio), $V_i = \sum _{\alpha } w_{i\alpha }$, and the market capitalization of an asset, $C_\alpha = \sum _{i} w_{i\alpha }$ [31, 87]. In the CAPM, banks choose their portfolio weights proportional to their market value and the asset’s capitalization:

$$\begin{aligned} w^{CAPM}_{i\alpha } = \frac{V_i C_\alpha }{w}, \end{aligned}$$

(34)

where we have used $w = \sum _{i', \alpha '} w_{i'\alpha '}$ The probability distribution for the MECAPM yields [31]

$$\begin{aligned} P(G_B) = \prod _{i, \alpha } \left[ 1 - \left( p_{CAPM}\right) _{i\alpha }\right] ^{w_{i\alpha }} \left( p_{CAPM}\right) _{i\alpha }, \end{aligned}$$

(35)

where the probability per link reads

$$\begin{aligned} \left( p_{CAPM}\right) _{i\alpha } = \frac{w^{CAPM}_{i\alpha }}{1 + w^{CAPM}_{i\alpha }}. \end{aligned}$$

(36)

Note that $P(G_B)$ is geometrically distributed for $w_{i\alpha } \in \mathbb {N}$ [31]. The link probabilities can be easily calculated using the identity in Eq. (34).

1.7 Enhanced Capital Asset Pricing Model

The so-called enhanced capital asset pricing model (ECAPM, [87]) reconstructs the link topology and subsequently the link weights. Their method makes only use of the strength sequence and is composed of two steps.

Firstly, the topology of the network is reconstructed by using the BiCM under the assumption that the exponential Lagrange multipliers $x_i \equiv \text {e}^{-\theta _i}$ and $y_\alpha \equiv \text {e}^{-\theta _\alpha }$ are proportional to node-specific fitness values, represented by their strengths:

$$\begin{aligned} x_i\equiv & {} \sqrt{z_\varGamma } s_i,\quad \forall i \in L\nonumber \\ y_\alpha\equiv & {} \sqrt{z_L} s_\alpha ,\quad \forall \alpha \in \varGamma . \end{aligned}$$

(37)

Constraining the network density with the total number of links $\langle E\rangle \equiv E^*$, the parameter $z = \sqrt{z_\varGamma z_L}$ can be estimated using [87]

$$\begin{aligned} \langle E \rangle = \sum _{i, \alpha } \frac{z V_i C_\alpha }{1 + z V_i C_\alpha },\quad \forall i \in L, \alpha \in \varGamma , \end{aligned}$$

(38)

Subsequently, the single link probabilities are simply given by the BiCM expression in Eq. (11), substituting the Lagrange multipliers with the expressions (37):

$$\begin{aligned} (p_{ECAPM})_{i\alpha } = \frac{z V_i C_\alpha }{1 + z V_i C_\alpha },\quad \forall i \in L, \alpha \in \varGamma , \end{aligned}$$

(39)

where z absorbs the proportionality constants.

Secondly, the link weights are reconstructed using the CAPM model while taking the network topology into consideration. Instead of setting $w_{i\alpha } = V_i C_\alpha / w$, a correction factor is applied [87]

$$\begin{aligned} w_{i\alpha }= & {} m_{i\alpha } \frac{V_i C_\alpha }{w\ (p_{ECAPM})_{i\alpha }} \nonumber \\= & {} (V_i C_\alpha + z^{-1}) \frac{m_{i\alpha }}{w}, \end{aligned}$$

(40)

where $m_{i\alpha }$ is 0 or 1,depending the link is present in the graph or not.