1 Introduction

The combinatorial problem of enumeration of dimer covers of graphs (aka domino tilings) has attracted interest from a diverse range of perspectives. These include statistical mechanics, combinatorics, and algorithm complexity studies. In their groundbreaking papers, P. W. Kasteleyn, M. E. Fisher and H. V. N. Temperley [9, 19, 20, 26], showed that for planar graphs the pure dimer problem admits a simple solution in terms of a Pfaffian of what is now known as the Kasteleyn matrix. The pure dimer partition functions is different in this sense from its monomer-dimer extension, for which its evaluation is computationally hard and thus not of simple Pfaffian form [17].

Extensive research has been devoted to various facets of dimer coverings, specially in the case of planar and bipartite graphs. Examples include the close relation between the partition functions of the dimer cover and of the Ising model [10, 20, 24], non-existence of phase transitions [16], structure of the model’s correlation functions, the arctic circle phenomenon [7], continuum limits and their description in terms of (conformal) field theory. More on this may be found in the overviews [4, 8, 21] and references therein.

Our focus here is on the Pfaffian structure seen in some of the model’s correlation functions. For operators to which this applies the 2n correlation functions can be determined from just the corresponding two point function. The proofs bear close similarity to the methods which have recently been developed for planar Ising spin models [2]. In analogy to the latter, the method relies on a combinatorial relation, which is valid for general graphs, combined with topological implications of planarity.

It was already noted that for planar graphs the boundary monomer correlation functions, whose explicit definition is restated below, are given by Pfaffians of the corresponding 2-point functions [12, 25]. The relation is less simple for the bulk monomer correlation functions, but it was pointed out that these can be written as products of two Pfaffians [3].

We start by giving an elementary geometric proof of the Pfaffian structure of the boundary monomer functions. The derivation also explains why these functions do not have the Pfaffian structure in the bulk. Furthermore, we formulate more explicitly than was done in the literature the model’s disorder operators, and show that the expectation values of products of order–disorder operators yield correlation functions which are simultaneously Pfaffian throughout the bulk and reduce to the simpler monomer correlation functions for sites along a boundary line.

The disorder operators can be viewed as incomplete implementations of the dimer model’s \(Z_2\) gauge symmetry. From this perspective, their construction and basic properties are similar to those of the corresponding concept for the Ising model, as discussed by L. P. Kadanoff and H. Ceva [18].

The combinatorial and topological arguments presented here parallel the analogous discussion of planar Ising model in the introductory sections of [2]. An essential tool is a path integral representation of a duplicated system, which is referred to as the double dimer model. The latter has been studied by R. Kenyon and D. Wilson (cf. [22, 23] and references therein) and is related to the monopole-dimer model recently studied in [5].

2 Dimer Covers and Monomer Correlations

Given a finite graph \(\mathcal {G}= ( \mathcal {V} , \mathcal {E}) \) of vertex set \( \mathcal {V} \), a perfect matching or dimer cover is a subset of the edge set, \(\omega \subset \mathcal E\), such that every vertex is covered by exactly one edge. The set of perfect matchings is denoted \(\Omega _ \mathcal {G}\). The dimer-cover partition function counts the number of the graph’s perfect matchings.

Perfect matchings can also be weighted through a complex-valued edge function \(K \,: \mathcal E \mapsto \mathbb {C}\). Given such an edge weight, the weighted dimer-cover partition function is

$$\begin{aligned} Z_{ \mathcal {G}, K} \ := \ \sum _{\omega \in \Omega _\mathcal {G}} \chi _K(\omega ) \end{aligned}$$
(2.1)

with

$$\begin{aligned} \chi _K(\omega ) := \prod _{b\in \omega } K_b \, . \end{aligned}$$

Of particular interest is the effect on the dimer-cover partition function of the removal of a collection of sites, \( M \subset \mathcal {V}\), which are regarded as covered by separate monomers. The collection of perfect matchings of the remaining vertices is denoted by \(\Omega _\mathcal {G}(M) \) and

$$\begin{aligned} Z_{\mathcal {G},K}(M) \ := \ \sum _{\omega \in \Omega _\mathcal {G}(M)} \chi (\omega ) \end{aligned}$$
(2.2)

stands for the weighted partition function of the monomer-depleted graph. It should be noted that not all graphs admit a perfect matching. In particular if M is of odd cardinality, then at least one of the factors in \( Z_{\mathcal {G},K}\times Z_{\mathcal {G},K}(M) \) vanishes. For simplicity, we shall concentrate in this paper on the case \( Z_{\mathcal {G},K} \ne 0 \) for which the monomer correlation function for an even collection of disjoint sites \(\{ x_1,..., x_{2n}\} \subset \mathcal {V} \) is well-defined as

$$\begin{aligned} S_{2n}(x_1,..., x_{2n}) := \langle \prod _{j=1}^n \eta _{x_j} \rangle _{\mathcal {G},K} \ := \ \frac{Z_{\mathcal {G},K}(\{ x_1,..., x_{2n}\} )}{Z_{\mathcal {G}, K}} \end{aligned}$$
(2.3)

The variables \( \eta _{x_j} \) should be thought of an operator in the functional integral representing the average \( \langle \cdot \rangle _{\mathcal {G},K} \) corresponding to the dimer partition function \( Z_{ \mathcal {G}, K} \). These variables take a similar role as the spin variables in the related Ising model.

In the planar set-up, monomer correlations have been studied early on by M. E. Fisher and J. Stephenson [11], who determined the fall-off of \( S_2(x_1,x_2) \) on the square lattice \( \mathbb {Z}^2 \) for \( K \equiv 1 \) and two monomers in the bulk to behave asymptotically as \( |x_1-x_2|^{-1/2} \) for large separation (making the similarity to the Ising model even more apparent [24]). The values of other special placements of momomer pairs on a square lattice are also known (cf. [4, 11, 15]). In case of the infinite half-lattice \( \mathbb {Z} \times \mathbb {Z}_+ \), the monomer boundary correlations in case \( K \equiv 1 \) have been computed not long ago by V. B. Priezzhev and P. Ruelle [25]. They turned out to be Pfaffians with two-point function given by

$$\begin{aligned} S_2((\xi ,0),(\eta ,0)) = {\left\{ \begin{array}{ll} - \frac{2}{\pi \, |\xi -\eta |} &{} \text{ if } |\xi -\eta | \text{ is } \text{ odd } \\ 0 &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$
(2.4)

3 The Double Dimer Model and Its Loop Gas Representation

The removal of a site in a finite graph, or equivalently its cover by a monomer, has a drastic effect on the graph’s dimer covers: if \(Z_{\Lambda ,K}\ne 0\) then for parity reasons the modified graph has no dimer cover. The removal of an even number of sites does not automatically invalidate the existence of a cover. Its effect on the distribution of the dimer covers may be localized to a collection of random paths linking pairwise the affected sites. A convenient way to arrive at such a stochastic geometric picture of correlations is to consider the overlay of two sets of dimer covers, one of the original graph and the other of its depleted version resulting in the double dimer model. This technique is reminiscent of the duplication which is an effective tool in the study of the Ising model’s correlation functions in its random current representation [1, 13].

Fig. 1
figure 1

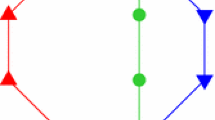
A double dimer configuration \(\omega ^{(2)}= (\omega _1,\omega _2)\) on a finite graph (whose edges are indicated in grey) with disjoint sets of monomers covering selected sites in one or the other copy of the graph. The edges of \( \omega _1\) and \( \omega _2\), are marked in solid and dashed lines, correspondingly. The overlay results in a configuration of alternatingly marked paths connecting the monomers and alternatingly marked loops, as described in Lemma 3.1

Full size image

The configurations of doubled dimer covers of a graph \( \mathcal {G}= ( \mathcal {V}, \mathcal {E}) \), depleted by corresponding sets of monomers \(M_1, M_2 \subset \mathcal {V}\) will be denoted here as:

$$\begin{aligned} \omega ^{(2)} = (\omega _1, \omega _2) \, \in \, \Omega _\mathcal {G}( M_1) \times \Omega _\mathcal {G}(M_2) \ =:\ \Omega _\mathcal {G}^{(2)} ( M_1, M_2) \, . \end{aligned}$$
(3.1)

Clearly, each such configuration \(\omega ^{(2)}\) is in one-to-one correspondence with a 2-multigraph with vertex set \(\mathcal {V}\) and the collection of edges in \(\omega ^{(2)}\). The following deterministic statement concerning such pairs of matchings relates the duplicated dimer cover model with a system of loops and paths with prescribed boundaries given by the monomers, cf. Fig. 1.

Lemma 3.1

(Double matching as a loop/path system) For any finite graph \(\mathcal {G}= ( \mathcal {V}, \mathcal {E})\), let \(\omega ^{(2)} \in \, \Omega _\mathcal {G}^{(2)} ( M_1, M_2)\) be a pair of dimer covers of \(\mathcal {G}\) depleted by a disjoint pair of monomers, \(M_1, M_2 \subset \mathcal {G}\). Then the multiplicity with which the edges are covered by \(\omega ^{(2)}\) coincides with that of a collection \(\Gamma =\Gamma (\omega ^{(2)})\) of edge-disjoint loops and paths where each \(\gamma \in \Gamma \) is either

  1. i.

    a double loop covering a single edge,

  2. ii.

    a simple loop of an even number of non-repeated edges,

  3. iii.

    a simple path with boundary set \(\partial \gamma \subset M_1 \sqcup M_2\).

In case iii., the numbers of edges of \(\gamma \) is odd if and only if its two boundary sites are in the same monomer set (i.e. either both in \(M_1\) or both in \(M_2\)).

The loop-path characterisation of double covers \( \omega ^{(2)} \) in terms of \(\Gamma \) partitions their collection \(\Omega _\mathcal {G}^{(2)} ( M_1, M_2) \) into equivalence classes, each of \(2^{n_s(\Gamma )}\) elements, where \(n_s(\Gamma )\) is the number of simple loops in \(\Gamma \).

Proof

In the case of disjoint monomer sets, the degree of each site \(x\in \mathcal {V}\) in the multigraph formed from the edge set of \(\omega ^{(2)}\) is either 1 or 2, and given by

$$\begin{aligned} \deg _{\omega ^{(2)}}(x) = \deg _{\omega _1}(x) + \deg _{\omega _2}(x) = {\left\{ \begin{array}{ll} 2, &{}\text { if }x \in \mathcal {V} \backslash [ M_1 \sqcup M_2] \\ 1, &{}\text { if }x \in M_1 \sqcup M_2 \end{array}\right. }. \end{aligned}$$
(3.2)

It follows that the collection of edges with multiplicity 1 is the disjoint union of loops (of no boundary) and paths with end points in \(M_1 \sqcup M_2\), each made of simple edges in \(\omega _j\), at alternating values of \(j=1,2\). The stated constraints on the parity of the number of edges in the loops and paths readily follow from the constraint that the path’s edges alternate between the two dimer covers. In case of the open paths, the identity of the cover to which an edge of \(\gamma \) belongs can be determined successively starting from the end points. There is no such constraint for the \(n_s(\Gamma )\) simple closed loops, and hence for each of these there are exactly two choices (independent among the loops) for the alternating values of \(j\in \{1,2\}\). \(\square \)

The above representation of \(\Omega _\mathcal {G}^{(2)} ( M_1, M_2) \) in terms of loops and paths may be extended by allowing the two sets of monomers to overlap, or coincide. The corresponding pure loop gas was recently studied in [5].

The loop gas picture of the double-dimer partition functions

$$\begin{aligned} Z_{\mathcal {G},K}^{(2)}\left( M_1,M_2\right) \ := \ Z_{\mathcal {G},K}(M_1) \, \, Z_{\mathcal {G},K}(M_2) \ = \sum _{\omega ^{(2)} \in \Omega ^{(2)}(M_1, M_2)} \chi _K(\omega _1) \, \chi _K(\omega _2) \, , \end{aligned}$$
(3.3)

is particularly convenient in revealing switching symmetries of the double dimer model’s connection amplitudes. Similar symmetries have been noted for the correlation functions of the Ising model, revealed there through its random current representation.

The connection amplitudes are defined as restricted sums such as

$$\begin{aligned} Z_{\mathcal {G},K}^{(2)}\left( M_1,M_2; x_j\leftrightarrow y_j \; \text{ for } j =1, \dots , \text{ N } \right) : = \nonumber \\ \sum _{\omega ^{(2)} \in \Omega ^{(2)}(M_1, M_2)} \chi _K(\omega _1) \, \chi _K(\omega _2) \, \prod _{j =1}^N \mathbbm {1} \left[ x_j{\longleftrightarrow {\omega ^{(2)}}} y_j \right] \, . \end{aligned}$$
(3.4)

where \( \{x_j , y_j\}_{j=1,..., N} \) are pairs of sites in \(M_1\sqcup M_2 \), and \(\mathbbm {1} \big [ x_j{\longleftrightarrow {\omega ^{(2)}}} y_j \big ] \) is an indicator function corresponding to the condition that the monomers \( x_j , y_j \) are connected by a path \(\gamma \in \Gamma (\omega ^{(2)})\).

Lemma 3.2

(Switching principle I) For any finite graph \(\mathcal {G}= (\mathcal {V} , \mathcal {E}) \), pair of disjoint monomer sets \(M_1, M_2\) and \( \{x,y\} \subset \mathcal {V}\backslash (M_1 \sqcup M_2)\):

$$\begin{aligned}&Z_{\mathcal {G},K}^{(2)}\left( M_1 \sqcup \{x,y\} ,M_2; x\leftrightarrow y , C \right) = Z_{\mathcal {G},K}^{(2)}\left( M_1, M_2 \sqcup \{x,y\} ; x\leftrightarrow y , C\right) \, , \end{aligned}$$
(3.5)
$$\begin{aligned}&Z_{\mathcal {G},K}^{(2)}\left( M_1 \sqcup \{x\} ,M_2 \sqcup \{y\} ; x\leftrightarrow y , C \right) =Z_{\mathcal {G},K}^{(2)}\left( M_1 \sqcup \{y\} ,M_2 \sqcup \{x\} ; x\leftrightarrow y ,C\right) \end{aligned}$$
(3.6)

where C stands for any collection of other connection conditions among monomers in \( M_1\sqcup M_2 \).

Proof

Considering first the case \(C = \emptyset \) (i.e. no other conditions), let \( \Omega ^{(2)}(M_1 \sqcup \{x,y\} , M_2;x\leftrightarrow y) \) be the set of double dimer covers for which there is a path \( \gamma ^{(x,y)} \in \Gamma \) with \(\partial \gamma ^{(x,y)} = \{ x, y\} \). The first assertion is based on the bijection

$$\begin{aligned} \Omega ^{(2)}(M_1 \sqcup \{x,y\} , M_2;x\leftrightarrow y) \ \rightarrow \ \Omega ^{(2)}(M_1 , M_2 \sqcup \{x,y\} ;x\leftrightarrow y) \, \nonumber \end{aligned}$$

implemented by the symmetric difference \( \triangle \) of sets:

$$\begin{aligned} \left( \omega _1,\omega _2\right) \ \mapsto \ \left( \omega _1 \triangle \gamma ^{(x,y)}, \omega _2 \triangle \gamma ^{(x,y)} \right) \, . \end{aligned}$$
(3.7)

This map reverses the “edge coloring” along the path \( \gamma ^{(x,y)} \) connecting x and y with the color indicating to which of the two dimer covers the edge belongs. The first identity thus follows immediately from the fact that the path weights are unchanged under a color-flip operation.

The same switching argument implies also the second identity, and the generalization to more general condition C. \(\square \)

The loop gas formulation of the double dimer model casts its correlation functions in terms of (discrete) path integrals, thereby bringing it closer to a broad range of physics models. A more explicit version of this representation, which could be used for an alternative presentation of the analysis which follows, is stated in Appendix.

4 Pfaffian Structure of Boundary Monomer Correlation Functions

The switching principle allows a simple proof of the fact that boundary monomer correlation functions have a Pfaffian nature on all planar graphs. The corresponding result for Ising model’s boundary spin–spin correlation functions goes back to [14]. Our proof parallels the more recent rederivation of that relation in [2].

For the dimer model the following statement was derived in [25] in case of the infinite planar half-lattice for which the two-point function is given by (2.4). For other planar graphs, the theorem was recently established by different means in [12].

Theorem 4.1

(Pfaffian boundary correlations) For any finite planar graph \(\mathcal {G}= (\mathcal {V} , \mathcal {E}) \) the boundary values of the monomer correlation functions satisfy

$$\begin{aligned} S_{2n}(x_1, ..., x_{2n})&= \sum _{\pi \in \Pi _{2n} } \mathrm{sgn}(\pi ) \, \prod _{j=1}^{n} S_{2}(x_{\pi (2j-1)}, x_{\pi (2j)}) \; \equiv {{\mathrm{Pf}}}_n\left( S_{2}(x_i,x_j) \right) \end{aligned}$$
(4.1)

where \(M:=\{x_1, ..., x_{2n} \}\) ranges over sequences of disjoint vertices positioned in a cyclic order along any boundary of \(\mathcal {G}\). Moreover, \(\Pi _{2n}\) is the collection of pairings of \(\{1,...,2n\}\), and \(\mathrm{sgn}(\pi ) \) is the pairing’s parity.

Proof

Through a known characterization of Pfaffians (provable by an induction argument) it suffices to show that for each \(n >1\) and any cyclicly ordered sequence of boundary sites

$$\begin{aligned} S_{2n}(x_1, ..., x_{2n}) \ = \ Q_{2n}(x_1, ..., x_{2n}) \, \end{aligned}$$
(4.2)

with \(Q_{2n}\) defined as:

(4.3)

At fixed k the term is a sum of over configurations of the duplicated system, , which may be grouped according to the paths of \(\Gamma (\omega ^{(2)})\) which connect to \(x_1\) and \(x_k\). These fall into two classes: the monomers \(x_1\) and \(x_k\) may be connected to each other by some \(\gamma \in \Gamma \), or else each is connected to another monomer:

(4.4)

Being based on combinatorial arguments, the above relation holds for arbitrary graphs. It will now be combined with the following topological implication of planarity. For any planar graph, a pair of monomers \( \{x_i,x_j\} \) located along the boundary can be linked by one of the non-intersecting simple paths of \(\Gamma (\omega ^{(2)})\) only if the two are either consecutively placed along the boundary or separated by an even number of other monomers. In other words, in the cases considered here:

$$\begin{aligned} x_i\leftrightarrow x_j \ \Longrightarrow \ (-1)^{i-j} = -1 \,. \end{aligned}$$
(4.5)

For the pair of sums on the right side of (4.4) this implies:

  1. i.

    In the first sum \( (-1)^{k-1} = -1 \), and hence

    (4.6)

    Here the first step is a consequence of the switching principle of Lemma 3.2.

  2. ii.

    In the second sum \( (-1)^{k-l} = -1\), and thus

    (4.7)

    due to the antisymmetry of the summands under the exchange of k with l as is apparent from the switching principle of Lemma 3.2.

Upon insertion in (4.4) these relations prove (4.2), and through it the claimed Pfaffian structure. \(\square \)

5 Disorder Operators for the Dimer Model

In the context of planar Ising spin systems order–disorder correlation functions have a Pfaffian structure throughout the bulk and reduce to simple correlations functions in case of sites along the boundary. They have been recently discussed, from a pair of somewhat different perspectives, in [6] and [2]. To present a related concept for the dimer model’s correlation functions we turn now to the dimer analog of disorder operators.

The definition of the disorder operators may be placed in the broader context of gauge symmetries. For that let us first recall Kasteleyn’s observation [20] that the dimer model has the following \(Z_2\) gauge symmetry in the dependence of the partition function \(Z_{\mathcal {G},K}\) on the kernel K.

For subsets \(B\subset \mathcal {V} \) let us denote

$$\begin{aligned} \partial B := \{ [x,y] \in \mathcal {E} \, | \, \text{ if } \text{ exactly } \text{ one } \text{ of } \text{ the } \text{ two } \text{ points } \text{ is } \text{ in } B \} \, \end{aligned}$$
(5.1)

which forms the edge boundary of B.

Next, for any edge set \(E \subset \mathcal {E} \) let \(T_{E }: \mathbb {C}^{\mathcal {E} }\rightarrow \mathbb {C}^{\mathcal {E} } \) be the transformation of K which flips its signs over the edges in E,

$$\begin{aligned} (T_{E}K)_b \ = \ {\left\{ \begin{array}{ll} - K_b &{} \text{ if } \; b \in E \\ ~~K_b &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$
(5.2)

The key observation now is that if \(E = \partial B\) for a set \(B\subset \mathcal {V} \) then

$$\begin{aligned} Z_{\Lambda ,T_{\partial B} K} \ = \ (-1)^{|B|}\, Z_{\Lambda ,K} \, , \end{aligned}$$
(5.3)

where |B| is the number of sites in B. For B containing a single site the relation (5.3) holds since in each dimer cover exactly one dimer is affected by the sign flip \(T_{\partial B} \). The general case follows by noting the commutative product relation

$$\begin{aligned} T_{\partial B} = \prod _{x\in B} T_{\partial \{x\}} \ \end{aligned}$$
(5.4)

and taking the corresponding product of the single site case of (5.3).

In view of the simplicity of the effect of \(T_{\partial B}\) on the partition function (and also on the expectations defined below), such mappings may be regarded as the model’s gauge transformations.

The disorder operators which are defined next may be viewed as partial gauge transformations, given by \(T_E\) where E is the collection of edges which are traversed by a line \(\ell \) which has only transversal intersections with the edges of \(\mathcal {E}\) and in the general case has a non-empty boundary set \(\partial \ell \). The end-points of \(\ell \) are associated with sites of the dual graph \( \mathcal {G}^* \), namely the faces of \( \mathcal {G}\) in which the end points of \(\ell \) lie. One may note that away from \(\partial \ell \) the transformation locally acts as if it could be associated with a gauge transformation—but it is not (unless \(\partial \ell = \emptyset \)).

Definition 5.1

For a planar graph \(\mathcal {G}=(\mathcal {V},\mathcal {E})\) with edge weights \( K \,: \mathcal E \mapsto \mathbb {C}\):

  1. i.

    The disorder operators \(\tau _{\ell }\) are associated with site-avoiding, lines \( \ell _1, \dots , \ell _n \) in the plane in which \(\mathcal {G}\) is embedded. To each such line we associate the transformation \( K \mapsto T_{\ell ^*} K\) where \(\ell ^*\) is the set of edges in \(\mathcal {E}\) which are crossed by \(\ell \) an odd number of times.

  2. ii.

    The expectation values of products of such disorder operators is defined as:

    $$\begin{aligned} \langle \prod _{j=1}^n \tau _{\ell _j} \rangle _{\mathcal {G},K} \ := \ \frac{Z_{\mathcal {G}, T_{\ell _1^*} \circ \dots \circ T_{\ell _n^*} K} }{Z_{\mathcal {G}, K} }\,. \end{aligned}$$
    (5.5)

As an expression of the above mentioned gauge symmetry, the expectation value \( \langle \prod _{j=1}^N \tau _{\ell _j} \rangle _{\mathcal {G},K}\) is a homotopy invariant under deformations of any \(\ell _j\) in the plane which preserve the line’s endpoints. More precisely, as a simple consequence of (5.3) we have:

Proposition 5.2

(Homotopy invariance) For any finite planar graph \(\mathcal {G}=(\mathcal {V},\mathcal {E})\), edge weights \( K \,: \mathcal E \mapsto \mathbb {C}\) and lines \( \ell _j \), \( j \in \{1,\dots , n\} \), as in Definition 5.1, under deformations of each \(\ell _j\) in the plane which preserve the line’s endpoints the expectation value functional \( (\ell _1,\dots ,\ell _N) \mapsto \langle \prod _{j=1}^n \tau _{\ell _j} \rangle _{\mathcal {G},K} \) is multiplied by \((-1)\) each time one deformed line is moved over a site of the planar graph.

Fig. 2
figure 2

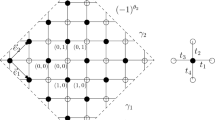
Order–disorder variables for a planar graph. Each of the ovals in the figure encircles a pair consisting of a site \(x_j\in \mathcal {G}\) and a point, marked \(\times \), within an adjacent cell of the dual graph \(x_j^*\in \mathcal {G}^*\). The disorder variables \(\tau _{\ell _j}\) are associated with lines \(\ell _j \), each linking the corresponding \(\times \) marked sites with a point in the grand central cell \(x_0^* \). The disorder lines \( \ell _1, \ell _2, \dots \) are enumerated cyclicly in the order of the lines’ emergence from the grand central \(x_0^* \). The correlation function associated with such an array is defined in (5.5)

Full size image

The above construction parallels the definition of disorder operators for the Ising model [18]. Disorder lines for the dimer-monomer model appear also in the recent discussion of the dimer model’s partition function in terms of Grassmann integrals [3].

6 Pfaffian Structure of the Correlation Functions of the Order–Disorder Operators

Our main concern in this paper will be canonical pairs of order–disorder variables, cf. Fig. 2.

Definition 6.1

For a planar graph \(\mathcal {G}=(\mathcal {V},\mathcal {E})\) with a set of edge weights \( K \,: \mathcal E \mapsto \mathbb {C}\), open-ended, site-avoiding, non-intersecting lines \( \ell _1, \dots , \ell _{2n} \) in the plane in which \(\mathcal {G}\) is embedded, together with disjoint sites \( x_1, \dots , x_{2n} \subset \mathcal {V} \) are called a collection of canonical pairs of order–disorder variables in case:

  1. i.

    all lines have a common end-point \( x_0^* \in \mathcal {G}^* \), called the grand central, and

  2. ii.

    the other endpoint of \( \ell _j \) is a face \( x_j^* \in \mathcal {G}^* \) adjacent to \( x_j \) for all \( j \in \{ 1, \dots , 2n \} \).

We call the canonical pairs of order–disorder variables cyclicly ordered if they are labeled relative to their intersections with the edge boundary of \( x_0^*\).

The expectation values of products of order–disorder variables operators \( \mu _j := \eta _{x_j} \tau _{\ell _j} \) are defined as

$$\begin{aligned} \langle \prod _{j=1}^{2n} \mu _j \rangle _{\mathcal {G},K} \ := \ \frac{Z_{\mathcal {G}, T_{\ell _1^*} \circ \dots \circ T_{\ell _{2n}^*} K}\left( \{ x_1,\dots ,x_{2n}\}\right) }{Z_{\mathcal {G}, K} }\, . \end{aligned}$$
(6.1)

Our main new result is:

Theorem 6.2

(Pfaffian correlations) For a finite planar graph \(\mathcal {G}=(\mathcal {V},\mathcal {E})\) with edge weights \( K \,: \mathcal E \mapsto \mathbb {C}\), for any collection of canonical pairs of order–disorder variables \(p_j= (x_j,\ell _j) \), \( j \in \{ 1, \dots , 2n\} \), ordered cyclicly relative to the grand central

$$\begin{aligned} \langle \prod _{j=1}^{2n} \mu _j \rangle _{\mathcal {G},K} \ = \ \sum _{ \pi \in \Pi _n} {{\mathrm{sgn}}}(\pi ) \, \prod _{j=1}^n \langle \mu _{ \pi (2j-1)} \, \mu _{ \pi (2j)} \rangle _{\mathcal {G},K} \ \equiv \ {{\mathrm{Pf}}}_n\left( \langle \mu _j \mu _k \rangle _{\mathcal {G},K} \right) \, . \end{aligned}$$
(6.2)

This result includes Theorem 4.1 as a special case. To see that, let us first note that for sites \(x_j\) which lie along the boundary of the grand-central \(x_0^*\), the corresponding disorder sites may be chosen as \(x_j^* = x_0^*\). When the lines \(\ell _j\) do not cross any edge, as in this case, the operators \(\tau _{\ell _j} \) act as identity and may be omitted. Theorem 4.1 then emerges through the inverted picture of the plane in which the complement of the finite graph is viewed as a single cell (of potentially large boundary).

In case the monomers \( \{ x_{2j-1},x_{2j} \}\) are pairwise adjacent, the disorder lines may be chosen so that their actions are pairwise equivalent, and thus cancel each other. In that case the pairwise product of two order–disorder variables reduces to a an ordinary product of monomers, i.e., a dimer \( \mu _{2j-1} \mu _{2j} = \eta _{x_{2j-1}} \eta _{x_{2j}}\), so that

$$\begin{aligned} \big \langle \prod _{j=1}^{2n} \tau _j \big \rangle _{\mathcal {G}, K} = \big \langle \prod _{j=1}^{n}\eta _{x_{2j-1}} \eta _{x_{2j}} \big \rangle _{\mathcal {G}, K} \, . \end{aligned}$$
(6.3)

The proof of Theorem 6.2 is organized along the lines used to establish the boundary case, Theorem 4.1. However, the relevant topological considerations are considerably more intricate. Defining, in analogy with \( Q_{2n} \) of (4.3),

(6.4)

(with \( p_j := (x_j , \ell _j) \) standing for an order–disorder variables) the Pfaffian structure will be shown by proving that for each n and choice of order–disorder pairs:

$$\begin{aligned} R_{2n}(p_1,...p_{2n}) \ = \ \langle \prod _{j\in \{ 1,.., 2 n\}} \mu _j \rangle _{\mathcal {G},K} \, . \end{aligned}$$
(6.5)

At specified k the product of the order–disorder correlators is given by:

(6.6)

where \((\omega _1 |\ell _{1,k}) \) denotes the number of intersections of the edges of \( \omega _1 \) with two disorder lines \( \ell _{1,k} := \{ \ell _1, \ell _k \} \) and likewise \((\omega _2 | \mathcal L) \) denotes the number of intersections of the edges of \( \omega _2 \) with the collection of all disorder lines \( \mathcal L := \{ \ell _1, \dots , \ell _{2n} \} \).

The terms in the above sum can be split into two classes, according to whether the loop/path configuration \(\Gamma (\omega ^{(2)})\) includes a path with \(\partial \gamma ^{(1,k)} = \{x_1,x_k\}\), or not. The corresponding partial sums will be studied through the following quantities:

$$\begin{aligned}&W^{(2)}_{\mathcal {G}, K}(\{M_1,\mathcal {L}_1\} ,\{ M_2,\mathcal {L}_2\} ; C ) := \nonumber \\&\quad \sum _{{\omega ^{(2)} \in \Omega ^{(2)}(M_1, M_2)}} \mathbbm {1} \left[ \omega ^{(2)} \text{ satisfies } C \right] \, \chi _{K} (\omega _1) \, (-1)^{(\omega _1 \, | \, \mathcal {L}_1)}\, \chi _{K}(\omega _2) \, \, (-1)^{(\omega _2 \, | \, \mathcal {L}_2)} \end{aligned}$$
(6.7)

in which we specify a set of connections C of the involved monomer sets \(M_1, M_2\).

A key result here is the corresponding version of the switching lemma:

Lemma 6.3

(Switching principle II) For planar graphs, and the setup of Theorem 6.2, we have for any \( m \ne k \ne l \ne m \):

(6.8)
(6.9)

Proof

The relation (6.8), which involves terms for which \(x_1\leftrightarrow x_k\), will be established through the switching transformation:

$$\begin{aligned} (\omega _1,\omega _2) \ \mapsto \ (\omega _1\Delta \gamma ^{(1,k)} ,\omega _2\Delta \gamma ^{(1,k)} ) \end{aligned}$$
(6.10)

Expanding the quantities \(W^{(2)}\) (defined in (6.7)), which appear in (6.8), into sums over \(\omega ^{(2)} \), the ratio of the corresponding terms is

$$\begin{aligned} \frac{\chi _K(\omega _1\Delta \gamma ^{(1,k)} ) \ \ \chi _K(\omega _2\Delta \gamma ^{(1,k)} ) }{\chi _K(\omega _1) \quad \chi _K(\omega _2) } \, \frac{ (-1) ^{(\omega _2\Delta \gamma ^{(1,k)} | \mathcal L )} }{ (-1) ^{(\omega _1 |\ell _{1,k})} (-1) ^{(\omega _2 | \mathcal L \backslash \ell _{1,k})} } \nonumber \\ \ = \ (-1)^{(\gamma ^{(1,k)} |\mathcal L)} \ \ (-1)^{(\omega ^{(2)} | \ell _{1,k})}\, , \end{aligned}$$
(6.11)

where the last step is by an elementary calculation in \(Z_2\). The relation (6.8) then follows from the special case \( l = 1 \) through the lemma which is stated next. (This is where the model’s planarity plays a role.)

The relation (6.9) concerns terms \(\omega ^{(2)}\) for which \(x_k\leftrightarrow x_l\) for some \(l\ne 1\). For that we employ the switching transformation

$$\begin{aligned} (\omega _1,\omega _2) \ \mapsto \ (\omega _1 \Delta \gamma ^{(k,l)} , \omega _2 \Delta \gamma ^{(k,l)}) \,. \end{aligned}$$
(6.12)

By a calculation similar to (6.11), the ratio of the corresponding contributions to the sums which yield the two quantities \(W^{(2)}\) in (6.9) is:

$$\begin{aligned} \frac{(-1)^{(\omega _1 \Delta \gamma ^{(k,l)} | \ell _{1,l} )} \, (-1)^{(\omega _2 \Delta \gamma ^{(k,l)} | \mathcal {L} \backslash \ell _{1,l} )} }{(-1)^{(\omega _1 | \ell _{1,k} )} \, (-1)^{(\omega _2 | \mathcal {L} \backslash \ell _{1,k} )} }&= \ \frac{ (-1)^{(\gamma ^{(k,l)} |\mathcal L)} \, (-1)^{(\omega ^{(2)} | \ell _{1,l} )}}{(-1)^{(\omega ^{(2)} | \ell _{1,k} )}} \nonumber \\&= \ (-1)^{(\gamma ^{(k,l)} |\mathcal L)} \, (-1)^{(\omega ^{(2)} | \ell _{k,l} )} \, . \end{aligned}$$
(6.13)

The relation (6.9) then again follows from the next lemma. \(\square \)

The topological statement which was quoted within the above proof is:

Lemma 6.4

(Intersection parities) In the planar graph setup of Proposition 6.3, for any \(\omega ^{(2)}\) such that \(x_k\leftrightarrow x_l\) with respect to the corresponding loop / path configuration \(\Gamma (\omega ^{(2)})\):

$$\begin{aligned} (-1)^{(\gamma ^{(k,l)} |\mathcal L)} \ \ (-1)^{(\omega ^{(2)} | \ell _{k,l})} \ = \ (-1)^{k-l-1} \, . \end{aligned}$$
(6.14)

Proof

To establish this relation it is useful to join the open ended paths \(\gamma \) of \( \Gamma (\omega ^{(2)} ) \) with the disorder lines corresponding to the paths’ edges into loops with only transversal crossing. For this purpose, we employ the following construction.

  1. 1.

    Join directly each \( x_j \) with the endpoint \( x_j^*\) of the corresponding disorder line \( \ell _j \).

  2. 2.

    Connect pairwise the other endpoints of the disorder lines within the grand central \( x_0^* \), so that \( \ell _k \) is connected to \( \ell _l \) and the remaining lines are paired consecutively with respect to the cyclic ordering.

Let \( \sigma ^{(k,l)} \) be the loop which includes \( \gamma ^{(k,l)} \) concatenated with \( \ell _k \) and \( \ell _l \) in the above construction, and let \( \Sigma ^{(k,l)} \) stand for the collection of the other loops which the construction yields. Any two planar loops, simple or not, with transversal crossings can intersect only even number of times (as can be deduced from the Jordan curve theorem). Thus \( \sigma ^{(k,l)} \) has an even intersection with \( \Sigma ^{(k,l)} \). The intersections within the grand central cell contribute to this the factor \((-1)^{k-l-1}\), and the rest is the parity of the intersections of \( \gamma ^{(k,l)} \) and \(\ell _{k,l}\) with the rest. Hence:

$$\begin{aligned} 1= & {} (-1)^{k-l-1} \, (-1)^{\left[ (\gamma ^{(k,l)} | \mathcal L) - (\gamma ^{(k,l)} | \ell _{k,l} ) \right] } \, (-1) ^{\left[ ( \omega ^{(2)}| \ell _{k,l} ) - ( \gamma ^{(k,l)} | \ell _{k,l} ) \right] } \nonumber \\= & {} (-1)^{k-l-1} \, (-1)^{(\gamma ^{(k,l)} |\mathcal L)} \ \ (-1)^{(\omega ^{(2)} | \ell _{k,l})}\, , \end{aligned}$$
(6.15)

as claimed in (6.14). \(\square \)

We are now ready to complete the proof of Theorem 6.2.

Proof of Theorem 6.2

Similarly as in the Proof of Theorem 4.1, it remains to show that

$$\begin{aligned} \langle \prod _{j=1}^{2n} \mu _j \rangle _{\mathcal {G},K} \ =\ R_{2n}(p_1,...p_{2n}) \, . \end{aligned}$$
(6.16)

The right side times \( (Z_{\mathcal {G},K})^2 \) may be rewritten as

(6.17)

Here the last line results from the switching Lemma 6.3. More precisely, the second sum on the left vanishes thanks to the antisymmetry in the \( k\ne l \) summation as is apparent from (6.9). Applying (6.8) to the first sum on the left yields the sum on the right, which coincides with \(\langle \prod _{j=1}^{2n} \mu _j\rangle _{\mathcal {G},K} \times (Z_{\mathcal {G},K})^2 \). \(\square \)