1 Introduction

The nonlinear Boltzmann equation [4] is the foundation for understanding the motion of trace amounts of charged particles through dilute gases [20], but its exact solution is still not possible in general circumstances. A solution of the Fourier-transformed Boltzmann equation for a particular Maxwell-type interaction model has been obtained [3, 16, 17] and it is now called the BKW solution. For other interactions, the nonlinear collision term is not separable in energy and angle and no major simplification is achieved by this method [6, 13, 48]. In the present case, we are interested in situations where trace amounts of ions move through dilute gases and ion-ion interactions are so few that they can be ignored; the collision term in the Boltzmann equation is thus automatically linear and the equation much easier to solve.

An integral transform for solving the homogeneous and isotropic (but still nonlinear) Boltzmann equation, called the “temperature transform” method [2], can be directly applied both to Maxwell molecules and very-hard particles. However, we are interested here in any type of interaction and in situations that may be inhomogeneous or anisotropic, so we cannot use this method.

An iterative method for solving the Boltzmann equation has been described [7, 33]. It is based on a perturbation scheme in terms of the deviation from equilibrium, and therefore resembles the method used below for solving the Boltzmann equation for gaseous ion transport and reaction.

Prigogine and Xhrouet [27] were the first to consider the kinetic theory of chemically reacting gases. They assumed that the reactive terms are perturbations of the non-reactive collision terms, as would be true if the cross sections for gas phase reactions are much smaller than those for non-reactive collisions. There were many subsequent treatments of chemical reactions in gases [10, 24, 32]. What is significant from the present point of view is that consideration has seldom been given to what happens when one of the reactants is present in trace amounts.

A statistical-mechanical theory of gaseous ion-molecule reactions was given by Viehland and Mason [44] for trace ions moving in a dilute gas under the influence of an electrostatic field. It assumed that ion-neutral reactions were infrequent, either because the cross sections were small, as above, or because the gas was composed primarily of inert substances but also contained a small amount of a reactive neutral. In the late 1980s [26, 28–30] the concept of a reaction was extended to include electron attachment and detachment (ionization of the neutrals), and such effects were allowed to become large. Research along these lines through 2006 was summarized in the book by Robson [31], and it has continued at a slow but steady rate since then. In order to keep this paper as short as possible, however, we will assume below that reactions are infrequent.

In the first paper [47] of this series, general moment equations were developed from the Boltzmann equation. This moment theory was uniform in the sense that it applied to any type of experiment in which trace amounts of electrons or atomic ions move through dilute atomic gases under the influence of electric and/or magnetic fields of arbitrary strength and of arbitrary dependence upon space or time. Since we are going to specifically include diffusion in this paper, the word uniform should not be taken as implying that there are no ion density gradients.

As is always the case with moment theories, a method of truncation had to be devised in [47] in order to provide a series of successive approximations that led to equations that are mathematically tractable and converge rapidly to accurate results that can be compared to experimental measurements. Two such methods were developed, the two-temperature (2T) and multi-temperature methods. In this paper we shall consider only the 2T method, which is based on the recognition that the temperature of the trace amount of ions (i.e., their average ion kinetic energy) can be much larger than the gas temperature.

The first-approximation results (explained more fully below) were applied in [47] to several types of experiment. For drift-tube mass spectrometers (DTMS), the results of the 2T approach for the gaseous ion mobility and average kinetic energy were shown to be exactly the same as those of the (more limited) 2T kinetic theory [43, 45]; these results are known to be accurate within approximately 10 % at all values of the gas temperature, T, and the ratio, E / N, of the electrostatic field strength to the gas number density. For ion mobility spectrometers (IMS) at or near atmospheric pressure, the 2T results gave the fundamental low-field mobility equation [12, 15, 18, 21, 36] that follows from the fundamental ion mobility equation [14, 34] in the zero-field limit where the ions and neutrals are both characterized by a single temperature; it too is known to be accurate. Applications of the first approximation moment methods to ion cyclotron resonance [46], differential mobility spectrometry [25], ion traps [9, 38–41] and other apparatus were also described.

The objectives of this paper are to:

  1. 1.

    Obtain the coupled set of differential equations that arise in second approximation of the 2T moment theory presented in first approximation in [47]. The accuracy of the first approximations for DTMS and IMS suggest that similar calculations should be even more accurate in higher approximations.

  2. 2.

    Show how the moment theory can incorporate such effects as diffusion and ion-neutral reactions; such effects were not part of the first-approximation equations.

  3. 3.

    Show the similarities and differences between this theory and momentum-transfer theory [20, 31, 34].

  4. 4.

    Make numerical applications that show explicitly that the second approximation of the 2T moment theory is not much different than the first, and hence that convergence is likely to be occurring.

This paper is restricted to atomic ions of mass m and charge q moving through a dilute, atomic gas. Also present may be a small amount of a reactive neutral that may be molecular or atomic. Because the ions are assumed to be present in trace amounts, mixtures of ions are described by a superposition of results for each separate ion. For the sake of readability, many of the derivations carried out in this research are relegated to electronic supplementary material (ESM).

2 General Moment Equations

The Boltzmann equation for the motion of trace amounts of ions or electrons through a dilute mixture of atomic gases under the influence of an external electric field \({\varvec{E}}\) and an external magnetic field \({\varvec{B}}\) is [4, 20]

$$\begin{aligned} \left[ {\frac{\partial }{\partial t}+{\varvec{v}}\cdot {\varvec{\nabla }} +\frac{q}{m}( {{\varvec{E}}+{\varvec{v}}\times {\varvec{B}}})\cdot {\varvec{\nabla }}_{\varvec{v}}} \right] f( {{\varvec{r}},{\varvec{v}},t})=( {J+J_R })f( {{\varvec{r}},{\varvec{v}},t}). \end{aligned}$$
(1)

The operators \({\varvec{\nabla }} \) and \({\varvec{\nabla }} _{\varvec{v}} \) are gradient vectors in physical space and in velocity space, respectively, and \({\varvec{r}}\) and \({\varvec{v}}\) are the ion position and velocity at time t. Both \({\varvec{E}}\) and B are assumed to be known (possibly as functions of \({\varvec{r}}\) and t, but not \({\varvec{v}})\). Finally, the ion velocity distribution function f is normalized to the ion number density, i.e.,

$$\begin{aligned} n( {{\varvec{r}},t})=\int {f( {{\varvec{r}},{\varvec{v}},t})d{\varvec{v}}}. \end{aligned}$$
(2)

We have assumed in Eq. (1) that ion-neutral reactions are infrequent enough that the Boltzmann collision operator can be written as a sum of a large, non-reactive operator, J, and a small, reactive operator, \(J_R \), that describes interactions in which the ion identity changes. The terms large and small indicate that \(J_R \) can be ignored except in situations where J acts on a collisional invariant (ion mass, velocity or kinetic energy) and hence vanishes.

The non-reactive operator is defined [4, 20] so that

$$\begin{aligned} \begin{array}{l} Jf\left( {{\varvec{r}},{\varvec{v}},t} \right) = \mathop \sum \limits _j {x_j}\mathop \int \int \left[ {f\left( {{\varvec{r}},{{\varvec{v}}'},t} \right) {f_j}\left( {{{\varvec{V}}_{\varvec{j}}}'} \right) - f\left( {{\varvec{r}},{\varvec{v}},t} \right) {f_j}\left( {{{\varvec{V}}_{\varvec{j}}}} \right) } \right] \\ \quad \quad \quad \quad \quad \quad \qquad \times \left| {{\varvec{v}} - {{\varvec{V}}_{\varvec{j}}}} \right| {\sigma _j}\left( {\left| {{\varvec{v}} - {{\varvec{V}}_{\varvec{j}}}} \right| ,{{\Omega }_j}} \right) d{{\Omega }_j}d{{\varvec{V}}_{\varvec{j}}}, \end{array} \end{aligned}$$
(3)

where the primed and unprimed velocities refer to post- and pre-collision values for the ions (\({\varvec{v}})\) and neutrals (\({\varvec{V}}_{\varvec{j}}\), with subscripts indicating the species, j, with mass \(M_j \) and mole fraction \(x_j )\). The differential scattering cross section, \(\sigma _j \), is a function of the relative speed, \(\left| {{\varvec{v}}-{\varvec{V}}_{\varvec{j}} } \right| \), and the scattering angles, \(\Omega _j \); it is this quantity that connects the pre- and post-collision velocities by means of the ion-neutral interaction potentials.

The reactive operator is defined [44] in terms of the total cross sections for ion reaction, \(Q^*( {\epsilon _R })\), with reactive neutrals having mole fractions \(x_R \) and velocities \({\varvec{V}}_{\varvec{R}} \) :

$$\begin{aligned} J_R \psi ({\varvec{v}})=\mathop \sum \limits _R x_R \psi ( {\varvec{v}})\mathop \int f_R ( {{\varvec{V}}_{\varvec{R}} })Q^*( {\epsilon _R })\left| {{\varvec{v}}-{\varvec{V}}_{\varvec{R}} } \right| d{\varvec{V}}_{\varvec{R}} . \end{aligned}$$
(4)

Here the relative kinetic energy is

$$\begin{aligned} \epsilon _R =\frac{1}{2}\mu _R \left| {{\varvec{v}}-{\varvec{V}}_{\varvec{R}} } \right| ^2, \end{aligned}$$
(5)

and \(\mu _R \) is the reduced mass for the ion-reactive neutral pair.

The various neutral gases are in equilibrium, since the ions are present in trace amounts and since the neutrals are not directly affected by the external fields. Therefore, their velocity distribution functions are Maxwellian, i.e.,

$$\begin{aligned} f_j ( {{\varvec{V}}_{\varvec{j}} })=N( {M_j /2\pi k_B T})^{3/2}\exp ( {-M_j V_j^2 /2k_B T}), \end{aligned}$$
(6)

and similarly for \(f_R ( {{\varvec{V}}_{\varvec{R}} })\). Here N, the total number density of the gas, arises because we have placed the mole fractions in Eqs. (3) and (4).

To obtain moment equations, we multiply Eq. (1) from the left by any function, \(\psi ({\varvec{v}})\), of the velocity alone and integrate over all velocities. After integration by parts and making use of the inverse collision properties [5] of the collision operators, each of the terms in the resulting equation can be expressed as moments of the ion velocity distribution function, \(f( {{\varvec{r}},{\varvec{v}},t})\), that are defined as

$$\begin{aligned} <\psi >=\frac{1}{n( {{\varvec{r}},t})}\mathop \int f( {{\varvec{r}},{\varvec{v}},t})\psi ( {\varvec{v}})d{\varvec{v}}. \end{aligned}$$
(7)

The dependences of the moments upon \({\varvec{r}}\) and t, have been left implicit, reflecting (but not limited to) the common situation where the other moments vary much less rapidly with these quantities than does \(n( {{\varvec{r}},t})\). The resulting equation is

$$\begin{aligned} \begin{array}{l} \frac{\partial }{\partial t}n( {{\varvec{r}},t})<\psi >+\,{\varvec{\nabla }} \cdot n( {{\varvec{r}},t})<\psi {\varvec{v}}>-\frac{q}{m}n ( {{\varvec{r}},t})\langle ( {{\varvec{E}}+{\varvec{v}}{ \times {\varvec{B}}}})\cdot {\varvec{\nabla }} _{\varvec{v}} \psi \rangle \\ \quad \quad \quad \quad \qquad \qquad \quad +\,n({{\varvec{r}},t})N\langle J\psi \rangle +n( {{\varvec{r}},t})N\langle J_R \psi \rangle =0. \\ \end{array} \end{aligned}$$
(8)

Eq. (8) is equivalent to Maxwell’s equation of change [22, 31], an alternative approach to the Boltzmann equation for the description of the transport properties of gases. Neither equation can be obtained unambiguously from a more fundamental theory, but they can be derived from one another. In the complete absence of chemical reactions, Eq. (8) is identical to the equation obtained by Kihara [15], although his derivation starting from the Boltzmann equation required that matrix elements of J must be symmetric and positive definite. A derivation that does not include these limiting requirements was given in 1975 [43] using essentially the same procedure as above.

Since \(\langle J1 \rangle =0 \) by conservation of mass, the rate equation of continuity obtained by using \(\psi =1\) in Eq. (8) is

$$\begin{aligned} \frac{\partial }{\partial t}n( {{\varvec{r}},t})+{\varvec{\nabla }} \cdot n( {{\varvec{r}},t})<{\varvec{v}}>+n( {{\varvec{r}},t})Nk=0, \end{aligned}$$
(9)

where the (two-body) reaction rate coefficient, k, is discussed in [44] and in Appendix A of ESM. Using Eq. (9) to eliminate the time derivative of \(n( {{\varvec{r}},t})\) in favor of its spatial gradients, Eq. (8) can be written as

$$\begin{aligned} \epsilon _0 \frac{\partial }{\partial t}<\psi >-\frac{q}{m}\langle ( {{\varvec{E}}+{\varvec{v}\times } {\varvec{B}}})\cdot {\varvec{\nabla }} _{\varvec{v}} \psi \rangle +N\langle J\psi \rangle =R( \psi ), \end{aligned}$$
(10)

where

$$\begin{aligned} \begin{array}{l} R( \psi )=\epsilon _1 \left[ {( {\langle \psi \rangle \langle {\varvec{v}}\rangle -\langle \psi {\varvec{v}}\rangle })\cdot {\varvec{\nabla }} \ln n( {{\varvec{r}},t})+\langle \psi \rangle {\varvec{\nabla }} \cdot \langle {\varvec{v}} \rangle -{\varvec{\nabla }} \cdot \langle {\varvec{v}}\psi \rangle } \right] \\ \quad \qquad \qquad +\,\epsilon _2 \left[ {Nk\langle \psi \rangle -N\langle J_R \psi \rangle } \right] . \\ \end{array} \end{aligned}$$
(11)

Here the \(\epsilon _i \) are smallness factors discussed below; for present purposes, they can be assumed to be equal to one. The operator J is scalar (doesn’t change the angles of any vector upon which it operates), linear (because the ions are present in trace amounts), local (independent of \({\varvec{r}})\) and instantaneous (independent of t).

It should be noted that Eq. (10) is exact, which means that it has the same level of mathematical rigor as the Boltzmann equation from which it was derived, i.e. both assume that reactive ion-neutral reactions are infrequent compared to nonreactive ones, that we are working in the hydrodynamic regime where initial and/or boundary conditions are supplied independently, and that ion-ion interactions are negligible (no space charge effects). Eq. (10) also shares the general disadvantage of any moment method: the equation for a simple moment involves more complicated moments, i.e., ones with higher powers of the ion velocity, so the hierarchy must somehow be truncated before it can be put to practical use.

3 Two-Temperature Moment Equations

From this point on, we will consider only the 2T approach for a single-component gas (possibly containing a small amount of a reactive neutral). In order to relate the quantity \(\langle J\psi \rangle \) in Eq. (10) to the matrix elements of J that are tabulated in [43], we cannot use spherical harmonics as was done in [47]. Instead, we use the Burnett functions [20, 43],

$$\begin{aligned} \psi _{l,\hat{m}}^{( r)} ( \mathbf{W})=W^lS_{l+\frac{1}{2}}^{( r)} ( {W^2})P_l^{\left| {\hat{m}} \right| } ( {\cos \theta })e^{i\hat{m}{\phi } }, \end{aligned}$$
(12)

where W is the magnitude of the dimensionless ion velocity,

$$\begin{aligned} {\varvec{W}}=\left( {\frac{m}{2k_B T_i }}\right) ^{\frac{1}{2}}{\varvec{v}}. \end{aligned}$$
(13)

Here \(\theta \) and \({\phi } \) are the spherical polar angles chosen with respect to the space-fixed, \(\hat{z}\) axis defined by \({\varvec{E}}\), and the \(\hat{m}\) index should not be confused with the ion mass. The \(P_l^{\left| {\hat{m}} \right| } \) are associated Legendre polynomials, the \(S_{l+\frac{1}{2}}^{( r)} \) are the Sonine polynomials that are identical with the generalized Laguerre polynomials \(L_r^{l+1/2} \), \(k_B \) is Boltzmann’s constant, and \(T_i \) is the ion temperature defined by requiring that

$$\begin{aligned} \frac{3}{2}k_B T_i =\left\langle \frac{1}{2} mv^2\right\rangle . \end{aligned}$$
(14)

The Burnett functions are orthogonal on the inner-product space defined by the equation,

$$\begin{aligned} \begin{array}{l} \left( {\psi _{l,\hat{m}}^{( r)} ,\psi _{l^{\prime },\hat{m}^{\prime }}^{( {r^{\prime }})} }\right) =\pi ^{-\frac{3}{2}}\int {\exp ( {-W^2})\psi _{l,\hat{m}}^{( r)*} ( {\mathbf{W}})\psi _{l^{\prime },\hat{m}^{\prime }}^{( {r^{\prime }})} ( \mathbf{W})d\mathbf{W}} \\ \quad \quad \qquad \qquad \quad \quad =\delta _{l,l^{\prime }} \delta _{\hat{m},\hat{m}^{\prime }} \delta _{r,r^{\prime }} , \\ \end{array} \end{aligned}$$
(15)

where the * represents complex conjugation. Eq. (15) implies that a good, zero-order approximation to the ion velocity distribution function is [43, 45, 47]

$$\begin{aligned} f( {{\varvec{r}},{\varvec{v}},t})=n( {{\varvec{r}},t})( {m/2\pi k_B T_i })^{3/2}\exp ( {-mv^2/2k_B T_i }). \end{aligned}$$
(16)

Due to the properties of J already mentioned, Eqs. (12)–(16) also imply [43] that the collision term in Eq. (10) can be written as

$$\begin{aligned} \langle J\psi _{l,\hat{m}}^{( r)} ( {\mathbf{W}})\rangle =\mathop \sum \limits _{s=0}^\infty a_{r,s} ( l)\langle \psi _{l,\hat{m}}^{( s)} ( {\mathbf{W}})\rangle , \end{aligned}$$
(17)

where the matrix elements,

$$\begin{aligned} a_{r,s} ( l)=\frac{\left( {\psi _{l,\hat{m}}^{( s)} ,J\psi _{l,\hat{m}}^{( r)} }\right) }{\left( {\psi _{l,\hat{m}}^{( s)} ,\psi _{l,\hat{m}}^{( s)} }\right) }, \end{aligned}$$
(18)

must be diagonal with respect to the l and \(\hat{m}\) indices, but otherwise independent of \(\hat{m} \).

It is known [1, 20, 23, 43] how to evaluate the matrix elements in terms of \(m,M,T,T_i \) and the ion-neutral interaction potential, so we will assume here that these quantities are known. It should be noted [43, 45] that all of the \(a_{r,s} ( l)\) have approximately the same magnitude when \(s\le r\), and that they become progressively smaller as s increases above r. This suggests the following treatment of \(J\psi \) in Eq. (10). We write a particular function \(\psi ({\varvec{v}})\) in terms of the \({\psi } _{l,m}^{( r)} ( \mathbf{W})\), use Eq. (17) to evaluate \(\langle J\psi _{l,m}^{( r)} ( \mathbf{W}) \rangle \), place the terms that arise with \(s\le r\) on the left-hand side of the equation, place the other terms (proportional to \(\epsilon _3^{s-r} \), where \(\epsilon _3 \) is another smallness parameter) on the right-hand side along with \(R(\psi )\), and then convert the \(\psi _{l,m}^{( r)} ( {\mathbf{W}})\) back into functions of \({\varvec{v}}\). This complicated procedure is used because \(T_i \) can be a function of \({\varvec{r}}\) and t, and hence one must avoid replacing functions of \({\varvec{v}}\) with functions of \({\varvec{W}}\) in the terms in Eq. (10) that involve time derivatives and spatial gradients.

Reasons were given in [47] why the terms in \(R(\psi )\) are generally small in the experiments of interest here. Briefly, the terms multiplied by \(\epsilon _1 \) involve the ratio of \({\varvec{\nabla }} n( {{\varvec{r}},t})\) to \(n( {{\varvec{r}},t})\), the experiments are conducted with \({\varvec{\nabla }} n( {{\varvec{r}},t})<n( {{\varvec{r}},t})\ll N\), and the terms involve the difference between the product of two averages and the average of the product. The terms multiplied by \(\epsilon _2 \) are small because they are proportional to the small mole fraction of the reactive neutral or because the cross section for reaction is much smaller than the non-reactive cross sections.

It follows that \(R(\psi )\) and the \(a_{r,s} ( l)\) terms with \(s>r\) must be ignored in the first of the series of successive approximations. This is why the ion diffusion coefficients and ion-neutral reactions were not treated in [47]. Here we shall show how these terms lead to a second approximation and the effects that this has on solutions of the moment equations.

We note before proceeding that there is no requirement that each of the \(\epsilon _i \) have the same degree of “smallness”. In paper 1 [47] we set \(\epsilon _0 =1\) but the others equal to zero. The reason for the special treatment of the smallness for the time derivative is that it does not couple different moments like the others do; of course, \(\epsilon _0 =0\) in steady-state situations where \({\varvec{E}}\) and \({\varvec{B}}\) do not vary with time. The second approximation considered here will be obtained by allowing only one power of any \(\epsilon _i \) to be retained, with no products like \(\epsilon _1 \epsilon _3 \). In applications of the second approximation equations, one must separately set each \(\epsilon _i \) to 0 or 1, depending upon the experimental conditions to which the theory is being applied.

4 Moment Equation for Ion Velocity

We start by considering the function \(\psi ({\varvec{v}})=v_z \) and following the procedure just described. We get

$$\begin{aligned} \begin{array}{l} <Jv_z >=( {2k_B T_i /m})^{1/2}\langle J\psi _{1,0}^{( 0)} ({\varvec{W}})\rangle \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=a_{0,0} ( 1)\langle v_z \rangle +\mathop \sum \limits _{s=1}^\infty \epsilon _3^s a_{0,s} ( 1)\langle v_z S_{3/2}^{(s)} ( {W^2})\rangle . \\ \end{array} \end{aligned}$$
(19)

The quantity \(Na_{0,0} ( 1)\) is the momentum-transfer collision frequency discussed in [47] and given the symbol \(\xi ( {T_{eff} })\). It may be written as

$$\begin{aligned} Na_{0,0} ( 1)=\frac{8N}{3}\frac{M}{m+M}\left( {\frac{2k_B T_{eff} }{\pi \mu _j }}\right) ^{\frac{1}{2}}\bar{\Omega }^{( {1,1})}( {T_{eff} })=\xi ( {T_{eff} }), \end{aligned}$$
(20)

so it is directly proportional to the momentum-transfer collision integral, \( \bar{\Omega }^{( {1,1})}( {T_{eff} })\), that is one of the many transport collision integrals that can be described using quantum, semi-classical or classical mechanics [20]. In classical mechanics, they are energy averages of the transport cross sections, \(\bar{Q}^{(l)}( \varepsilon )\):

$$\begin{aligned} \begin{array}{l} \bar{\Omega }^{(l,s)}(T)=\left[ {(s+1)!( {k_B T})^{{s+2}}} \right] ^{-1} \\ \qquad \qquad \quad \quad \times \int \limits _0^\infty \bar{Q}^{(l)} (\bar{\varepsilon } )\exp \left( {-\frac{\bar{\varepsilon }}{k_B T}}\right) \bar{\varepsilon } ^{s+1}d\bar{\varepsilon }. \\ \end{array} \end{aligned}$$
(21)

The \( \bar{Q}^{( l)}( \bar{\varepsilon } )\) are averages over impact parameters of the scattering angle, \(\theta ( {b,\bar{\varepsilon } }):\)

$$\begin{aligned} \bar{Q}^{( l)}( \bar{\varepsilon } )=2\pi \left[ {1-\frac{1+( {-1})^l}{2( {l+1})}} \right] ^{-1}\int \limits _0^\infty \left\{ {1-\cos ^l\theta ( {b,\bar{\varepsilon } })} \right\} bdb. \end{aligned}$$
(22)

The scattering angle is determined in turn by an integral of the ion-neutral interaction potential, V(r), over the ion-neutral separation, r:

$$\begin{aligned} \theta ( {b,\bar{\varepsilon } })=\pi -2b\mathop \smallint \limits _{r_m }^\infty \left[ {1-\frac{b^2}{r^2}-\frac{V( r)}{\bar{\varepsilon } }} \right] ^{-\frac{1}{2}}\frac{dr}{r^2}. \end{aligned}$$
(23)

Here \(r_m \) is the distance of closest approach, the largest positive real root of the bracketed quantity. Note also that the constants in Eqs. (21) and (22) have been chosen so that both the transport cross sections and collision integrals are \(\pi \sigma ^2\) when the interaction potential is that between rigid spheres of diameter \(\sigma \); the over-bars in Eqs. (21)–(23) serve as a reminder of this.

We see from Eqs. (20) and (21) that \(\xi ( {T_{eff} })\) depends upon m, M, the reduced mass \(\mu \), V( r), and the effective temperatures that are related to \(T_i \) and T by the equation

$$\begin{aligned} T_{eff} =\frac{mT+MT_i }{m+M}. \end{aligned}$$
(24)

Since J is a scalar operator, Eq. (19) may be written as

$$\begin{aligned} N\langle J{\varvec{v}}\rangle =\xi ( {T_{eff} })\left[ {\langle {\varvec{v}}\rangle +\mathop \sum \limits _{s=1}^\infty \epsilon _3^s c_{0,s} ( 1)\left\langle {\varvec{v}}S_{\frac{3}{2}}^{( s)} ( {W^2})\right\rangle } \right] , \end{aligned}$$
(25)

where

$$\begin{aligned} c_{r,s} ( l)=\frac{a_{r,s} ( l)}{a_{0,0} ( 1)}. \end{aligned}$$
(26)

This means that the moment equation for ion velocity obtained by using \(\psi ({\varvec{v}})={\varvec{v}}\) in Eq. (10) can be written as the vector equation,

$$\begin{aligned} \begin{array}{l} \epsilon _0 \frac{\partial }{\partial t}\langle {\varvec{v}}\rangle -\frac{q}{m}( {{\varvec{E}}+\langle {\varvec{v}}\rangle \times {\varvec{B}}})+\xi ( {T_{eff} })\langle {\varvec{v}}\rangle \\ =R( {\varvec{v}})-\xi ( {T_{eff} })\mathop \sum \limits _{s=1}^\infty \epsilon _3^s c_{0,s} ( 1)\left\langle {\varvec{v}}S_{3/2}^{( s)} ( {W^2})\right\rangle . \\ \end{array} \end{aligned}$$
(27)

The first approximation to Eq. (27) is obtained by setting \(\epsilon _0 \) equal to one and neglecting the right-hand side. The second approximation is obtained by retaining the right-hand side but truncating the sum so that only one power of \(\epsilon _3 \) is kept (i.e., keeping only \(s\le 1)\). This gives

$$\begin{aligned} \begin{array}{l} \epsilon _0 \frac{\partial }{\partial t}\langle {\varvec{v}}\rangle -\frac{q}{m}( {{\varvec{E}}+\langle {\varvec{v}}\rangle \times {\varvec{B}}})+\xi ( {T_{eff} })\left[ {\langle {\varvec{v}}\rangle +\epsilon _3 c_{0,1} ( 1)\left\langle {\varvec{v}}S_{\frac{3}{2}}^{( 1)} ( {W^2})\right\rangle } \right] \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\epsilon _1 \left[ {( {\langle {\varvec{v}}\rangle \langle {\varvec{v}}\rangle -\langle {\varvec{v}}{\varvec{v}}\rangle })\cdot \nabla \ln n( {{\varvec{r}},t})+\langle {\varvec{v}}\rangle \nabla \cdot \langle {\varvec{v}}\rangle -\nabla \cdot \langle {\varvec{v}}{\varvec{v}}\rangle } \right] \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\epsilon _2 \left[ {Nk \langle {\varvec{v} \rangle }-N \langle J_R {\varvec{v}}\rangle } \right] . \\ \end{array} \end{aligned}$$
(28)

The new moment on the left-hand side of this equation may be written as

$$\begin{aligned} \left\langle {\varvec{v}}S_{\frac{3}{2}}^{( 1)} ( {W^2})\right\rangle =\left\langle {\varvec{v}}\left( {\frac{5}{2}-W^2}\right) \right\rangle =\frac{5}{2}\langle {\varvec{v}}\rangle -\frac{m}{2k_B T_i }\langle {\varvec{v}}v ^2\rangle . \end{aligned}$$
(29)

5 Moment Equation for Effective Temperature

Next we consider \(\psi ({\varvec{v}})=(1/2)mv^{2}\). Following the same procedure as above, we get

$$\begin{aligned} \left\langle J\left( {\frac{1}{2}mv^2}\right) \right\rangle =k_B T_i \,\left\langle J\left[ {\frac{3}{2}\psi _{0,0}^{( 0)} ( {\varvec{W}})-\psi _{0,0}^{( 1)} ({\varvec{W}})} \right] \right\rangle . \end{aligned}$$
(30)

Therefore from Eq. (17),

$$\begin{aligned} \begin{array}{l} \left\langle J \left( {\frac{1}{2}mv^2}\right) \right\rangle =k_B T_i \left[ {\frac{3}{2}a_{0,0} ( 0)-a_{1,0} ( 0)}\right] \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+k_B T_i \mathop \sum \limits _{s=1}^\infty \left[ {\frac{3}{2}\epsilon _3^s a_{0,s} ( 0)-\epsilon _3^{s-1} a_{1,s} ( 0)} \right] \left\langle S_{\frac{1}{2}}^{( s)} ( {W^2})\right\rangle . \\ \end{array} \end{aligned}$$
(31)

It is known [43] that \(a_{0,s} ( 0)=0\) for all s, because of conservation of mass. Therefore Eq. (20) simplifies Eq. (31) to

$$\begin{aligned} \begin{array}{l} N\left\langle J( {\frac{1}{2}mv^2})\right\rangle =-k_B T_i \xi ( {T_{eff} })c_{1,0} ( 0)\left\langle S_{\frac{1}{2}}^{( 0)} ( {W^2})\right\rangle \\ \qquad \qquad \qquad \quad \quad -k_B T_i \xi ( {T_{eff} })\mathop \sum \limits _{s=1}^\infty \epsilon _3^{s-1} c_{1,s} ( 0)\left\langle S_{\frac{1}{2}}^{( s)} ( {W^2})\right\rangle . \\ \end{array} \end{aligned}$$
(32)

Now

$$\begin{aligned} \left\langle S_{\frac{1}{2}}^{( 0)} ( {W^2})\right\rangle =\left\langle 1\right\rangle =1, \end{aligned}$$
(33)

and the ion temperature defined by Eq. (14) means that

$$\begin{aligned} \left\langle S_{\frac{1}{2}}^{( 1)} ( {W^2})\right\rangle =\left\langle \frac{3}{2}-W^2\right\rangle =0. \end{aligned}$$
(34)

In addition, we note from the Appendix of [43] and Eq. (24) that

$$\begin{aligned} c_{1,0} ( 0)=-\frac{3m}{m+M}\left( {1-\frac{T}{T_i }}\right) =-\frac{3m( {T_{eff} -T})}{MT_i }. \end{aligned}$$
(35)

Therefore, putting \(\psi ({\varvec{v}})=(1/2)mv^{2}\) in Eq. (10) and using qs. (14), (24) and (34)–(35) gives the moment equation for the effective temperature,

$$\begin{aligned} \begin{array}{l} \epsilon _0 \frac{m}{\mu }\frac{\partial }{\partial t}\left( {\frac{3}{2}k_B T_{eff} }\right) -q{\varvec{E}}\cdot \langle {\varvec{v}}\rangle +2\xi ( {T_{eff} })\frac{m}{M}\left[ {\frac{3}{2}k_B ( {T_{eff} -T})} \right] \\ \qquad \qquad \qquad \qquad \quad =R\left( {\frac{1}{2}mv^2}\right) +k_B T_i \xi ( {T_{eff} })\mathop \sum \limits _{s=2}^\infty \epsilon _3^{s-1} c_{1,s} ( 0)\left\langle S_{\frac{1}{2}}^{( s)} ( {W^2})\right\rangle . \\ \end{array} \end{aligned}$$
(36)

The first approximation to Eq. (36) is obtained by setting \(\epsilon _0 \) = 1 and neglecting the right-hand side. The second approximation is obtained by retaining the right-hand side of Eq. (36) and truncating the sum so that only the terms with \(s\le 2\) are kept. This gives

(37)

The new moment that arises in Eq. (37) is not one that is discussed in momentum-transport theories of gaseous ion transport [31]; using Eq. (14) it can be shown that

$$\begin{aligned} \left\langle S_{\frac{1}{2}}^{( 2)} ( {W^2})\right\rangle =\frac{1}{2}\left\langle \frac{15}{4}-5W^2+W^4\right\rangle =\frac{1}{2}\left( {\frac{m}{2k_B T_i }}\right) ^2\langle v^4\rangle -\frac{15}{8}. \end{aligned}$$
(38)

This equation can be written in terms of the effective temperature rather than \(T_i \), by using Eq. (24).

In order to obtain the second approximation expressions for the ion drift velocity and the effective temperature, we must add first-approximation equations for the new moments that arise in Eqs. (28–30) and (37, 38). (The new moments involving ion-neutral reactions are discussed in Appendix A of ESM.)

6 Moment Equation for \(\langle v^4 \rangle , \langle vv^{2} \rangle \) and \(\langle vv \rangle \)

Following the same procedure with \(\psi ({\varvec{v}})=v^4\) and using Eqs. (33) and (34), we find that

$$\begin{aligned} N\langle Jv^4\rangle&=\left( {\frac{2k_B T_i }{m}}\right) ^2\xi ( {T_{eff} })\left[ 2c_{2,0} ( 0)-5c_{1,0} ( 0)+2c_{2,2} ( 0)\left\langle S_{\frac{1}{2}}^{( 2)} ( {W^2})\right\rangle \right. \nonumber \\&\left. \quad +\,2\mathop \sum \limits _{s=3}^\infty \left\{ {\epsilon _3^{s-2} c_{2,s} ( 0)\left\langle S_{\frac{1}{2}}^{( s)} ( {W^2})\right\rangle } \right\} \right. \nonumber \\&\left. \quad -5\mathop \sum \limits _{s=2}^\infty \epsilon _3^{s-1} c_{1,s} ( 0)\left\langle S_{\frac{1}{2}}^{( s)} ( {W^2})\right\rangle \right] . \end{aligned}$$
(39)

Putting \(\psi ({\varvec{v}})=v4\) in Eq. (10) then gives a second approximation for \(\langle v^4 \rangle \). The first approximation is all that is needed to go with the second approximation moment equations for ion velocity and effective temperature. It is

$$\begin{aligned} \begin{array}{l} \epsilon _0 \frac{\partial }{\partial t}\langle v ^4 \rangle -\frac{4q}{m}{\varvec{E}}\cdot \langle {\varvec{v}}v ^2 \rangle +\left( {\frac{2k_B T_i }{m}}\right) ^2\xi ( {T_{eff} }) \\ \quad \times \left[ {2c_{2,0} ( 0)-5c_{1,0} ( 0)+2c_{2,2} ( 0)\left\langle S_{\frac{1}{2}}^{( 2)} ( {W^2})\right\rangle } \right] =0. \\ \end{array} \end{aligned}$$
(40)

For \(\psi ({\varvec{v}})={\varvec{v}}v^{2}\) we get

$$\begin{aligned} N \langle J{\varvec{v}}v^2\rangle =&\left( {\frac{2k_B T_i }{m}}\right) \xi ( {T_{eff} })\left[ \left\{ {\frac{5}{2}c_{0,0} ( 1)-c_{1,0} ( 1)} \right\} \langle {\varvec{v}}\rangle -c_{1,1} ( 1)\left\langle {\varvec{v}}S_{\frac{3}{2}}^{( 1)} ( {W^2})\right\rangle \right. \nonumber \\&\left. +\frac{5}{2}\mathop \sum \limits _{s=1}^\infty \epsilon _3^s c_{0,s} ( 1)\left\langle {\varvec{v}}S_{\frac{3}{2}}^{( s)} ({W^2})\right\rangle \right. \nonumber \\&\left. -\mathop \sum \limits _{s=2}^\infty \epsilon _3^{s-1} c_{1,s} ( 1)\left\langle {\varvec{v}}S_{\frac{3}{2}}^{( s)} ( {W^2})\right\rangle \right] . \end{aligned}$$
(41)

Putting \(\psi ({\varvec{v}})={\varvec{v}}v^{2}\) in Eq. (10) then gives the first approximation equation

$$\begin{aligned} \begin{array}{l} \epsilon _0 \frac{\partial }{\partial t}\langle {\varvec{v}}v^2\rangle -\frac{q}{m}( {\frac{3k_B T_i }{m}}){\varvec{E}}-\frac{2q}{m}{\varvec{E}}\cdot \langle {\varvec{v}}{\varvec{v}}\rangle +\frac{3q}{m}{\varvec{B}}\times \langle {\varvec{v}}v^2\rangle +\xi ( {T_{eff} }) \\ \quad \times \left\{ {\left( {\frac{2k_B T_i }{m}}\right) \left[ {\frac{5}{2}-c_{1,0} ( 1)-\frac{5}{2}c_{1,1} ( 1)} \right] \langle {\varvec{v}}\rangle +c_{1,1} ( 1)\langle {\varvec{v}}v^2\rangle } \right\} =0. \\ \end{array} \end{aligned}$$
(42)

Finally, we consider

$$\begin{aligned} \psi ({\varvec{v}})=v_z^2 =\left( {\frac{2k_B T_i }{m}}\right) \left[ {\frac{1}{2}\psi _{0,0}^{(0)} ( {\varvec{W}})-\frac{1}{3}\psi _{0,0}^{( 1)} ( {\varvec{W}})+\frac{2}{3}\psi _{2,0}^{(0)} ( {\varvec{W}})} \right] \end{aligned}$$
(43)

and

$$\begin{aligned} \psi ( {\varvec{v}})=v_x v_z =-\left( {\frac{k_B T_i }{3m}}\right) \left[ {\psi _{2,-1}^{( 0)} ( {\varvec{W}})+\psi _{2,1}^{( 0)} ( {\varvec{W}})} \right] . \end{aligned}$$
(44)

Following the same path as above, we get results from Eqs. (43) and (44) that can be combined into a single tensor equation,

$$\begin{aligned} N\langle J{\varvec{v}}{\varvec{v}}\rangle= & {} \xi ( {T_{eff} })\left[ c_{0,0} ( 2)\left\langle \left( {{\varvec{v}}{\varvec{v}}-\frac{1}{3}v^2\mathbf{U}}\right) \right\rangle -\frac{1}{3}c_{1,0} ( 0)\left( {\frac{2k_B T_i }{m}}\right) \mathbf{U}\right. \nonumber \\&\left. +\mathop \sum \limits _{s=1}^\infty \epsilon _3^s c_{0,s} ( 2)\left\langle \left( {{\varvec{v}}{\varvec{v}}-\frac{1}{3}v^2\mathbf{U}}\right) S_{\frac{5}{2}}^{( s)} ( {W^2})\right\rangle \right. \nonumber \\&\left. -\,\frac{1}{3}\mathop \sum \limits _{s=2}^\infty \epsilon _3^{s-1} c_{1,s} ( 0)\left( {\frac{2k_B T_i }{m}}\right) \left\langle S_{\frac{1}{2}}^{( s)} ( {W^2})\right\rangle \mathbf{U}\right] , \end{aligned}$$
(45)

where U is a unit tensor of rank two. Putting \(\psi ({\varvec{v}})={\varvec{v}}{\varvec{v}}\) in Eq. (10) then gives the following tensor equation of rank two in first approximation,

$$\begin{aligned} \begin{array}{l} \epsilon _0 \frac{\partial }{\partial t}\langle {\varvec{v}}{\varvec{v}}\rangle -\frac{q}{m}( {{\varvec{E}}\langle {\varvec{v}}\rangle +\langle {\varvec{v}}\rangle {\varvec{E}}-{\varvec{B}}\times \langle {\varvec{v}}{\varvec{v}}\rangle +\langle {\varvec{v}}{\varvec{v}}\rangle \times {\varvec{B}}})+\xi ( {T_{eff} }) \\ \times \left[ {c_{0,0} ( 2)\left\langle \left( {{\varvec{v}}{\varvec{v}}-\frac{1}{3}v^2\mathbf{U}}\right) \right\rangle -\left( {\frac{2k_B T_i }{3m}}\right) c_{1,0} ( 0)\mathbf{U}} \right] =0.\, \\ \end{array} \end{aligned}$$
(46)

It will be shown below that \(<{\varvec{v}}{\varvec{v}}>\) is related to the temperature tensor, \(<{\varvec{v}}v^{2}>\) to the heat flux vector, and \(<v^4>\) to the dyadic energy, each in the laboratory frame of reference.

7 Drift-Tube Mass Spectrometers

7.1 Theory of the Instrument

Drift-tube mass spectrometers (DTMS) are instruments that are cylindrically-symmetric along the \(\hat{z} \) axis defined by a (possibly strong) electrostatic field, but in which there are no magnetic fields. Therefore, \(\epsilon _0 =0\) and, on the average, the ions move only along the \(\hat{z} \) axis with an average speed that is usually written as \(v_d \). In our previous work [47], several additional assumptions were made that are valid in the absence of diffusion, reaction and other complicating factors that we now want to consider. Hence we must carefully examine the way in which experimental data in DTMS are analyzed in order to be sure that our theoretical quantities match exactly with the quantities that are being measured. We will focus on the most common ways [8] that raw DTMS data are analyzed; a guide to other analyses is given in Sec. 3-6-C of [20].

The most elementary analysis of drift-tube data computes \(v_d \) by dividing the known distance between the ion source and the ion detector by the measured difference between the injection time of the ions (i.e., the peak of the injection-time distribution function) and the time at which the maximum ion intensity arrives at the detector (i.e., the peak of the arrival-time distribution function). All effects due to spatial gradients (of the ion number density and other moments) and due to reactions are ignored. This is completely consistent with the first approximation result [47],

$$\begin{aligned} v_d =\frac{qE}{m\xi ( {T_{eff} })}. \end{aligned}$$
(47)

The effective ion temperature under these circumstances is

$$\begin{aligned} \frac{3}{2}k_B T_{eff} =\frac{3}{2}k_B T+\frac{qME}{2m\xi ( {T_{eff} })}v_d =\frac{3}{2}k_B T+\frac{1}{2}Mv_d^2 . \end{aligned}$$
(48)

These results were discussed more extensively in [47].

A more elaborate analysis of drift-tube data is based on Fick’s First Law of Diffusion, which indicates that the ion flux in the absence of an external field is directly proportional to the gradient of the ion number density. In DTMS, it is assumed that space-charge effects are negligible and that the flux is given by the equation [20]

$$\begin{aligned} {\varvec{J}}( {{\varvec{r}},t})=n( {{\varvec{r}},t})\langle {\varvec{v}}\rangle =n( {{\varvec{r}},t}){\varvec{v}}_{\varvec{d}} -\mathbf{D}\cdot {\varvec{\nabla }} n( {{\varvec{r}},t}). \end{aligned}$$
(49)

Here \({\varvec{v}}_{\varvec{d}} \) is the drift velocity vector and D is the diffusion tensor characterizing the motion of the ions through the gas; both quantities are in the laboratory frame. It is further assumed that there is no gain of ions from an external source during the movement of an ion swarm down the tube but that there can be a loss due to chemical reaction. Therefore, the rate equation of continuity obtained from Eqs. (9) and (49) is

$$\begin{aligned} \frac{\partial }{\partial t}n( {{\varvec{r}},t})+{\varvec{\nabla }} \cdot n( {{\varvec{r}},t}){\varvec{v}}_{\varvec{d}} -{\varvec{\nabla }} \cdot \mathbf{D}\cdot {\varvec{\nabla }} n( {{\varvec{r}},t})=-kNn( {{\varvec{r}},t}). \end{aligned}$$
(50)

Next, it is assumed that neither \({\varvec{v}}_{\varvec{d}}\) nor D vary with time or position and that the effects of reaction on them are neglible. We thus get Fick’s Second Law of Diffusion (also known as the diffusion equation) in the form

$$\begin{aligned} \frac{\partial }{\partial t}n( {\varvec{r}},t)+{\varvec{v}}_{\varvec{d}} \cdot {\varvec{\nabla }} n({{\varvec{r}},t})-\mathbf{D}:{\varvec{\nabla }} {\varvec{\nabla }} n( {{\varvec{r}},t})=-kNn( {{\varvec{r}},t}). \end{aligned}$$
(51)

Here : indicates a full contraction between the tensor D and two copies of the gradient vector \({\varvec{\nabla }}\). It is important to note [20, 31] that experimental measurements in this type of DTMS are analyzed by means of Eq. (51), not Eq. (49).

Using general arguments [20], it can be shown that \({\varvec{v}}_{\varvec{d}}\) must lie along \(\hat{z}\), and that D is a diagonal tensor whose value along the electric field (\(D_\parallel )\) is different than its value (\(D_\bot )\) along the perpendicular directions. Moreover, it is necessary to add a source term, \(\beta ({\varvec{r}},t)\), that represents an input of ions at the beginning of the drift region. Therefore Eq. (51) becomes (in Cartesian coordinates)

$$\begin{aligned} \frac{\partial }{\partial t}n( {x,y,z,t})=\left[ {D_\bot \left( {\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}}\right) +D_\parallel \frac{\partial ^2}{\partial z^2}-v_d \frac{\partial }{\partial z}-kN} \right] n( {x,y,z,t})+\beta ( {x,y,z,t}). \end{aligned}$$
(52)

The solution of Eq. (52) has been developed by Gatland [8] for a delta-function input of ions with an initial ion surface density, s. Since the ions detected in a DTMS are those that exit the drift tube on the cylindrical axis (\(x=y=0)\), the solution of primary interest is the axial ion number density,

$$\begin{aligned} n( {0,0,z,t})=\frac{s\exp ( {-Nkt})}{( {4{\pi }D_\Vert t})^{1/2}}\left[ {1-\exp \left( {-\frac{r_0^2 }{4D_\perp t}}\right) } \right] \exp \left( {-\frac{( {z-v_d t})^2}{4D_\Vert t}}\right) . \end{aligned}$$
(53)

Here \(r_0 \) is the radius of the ion entrance aperture. Then the axial ion flux density from an exit aperture of area a is

$$\begin{aligned} \begin{array}{l} \Phi ( {0,0,z,t})=\frac{sa\exp ( {-Nkt})}{4( {\pi D_\parallel t})^{\frac{1}{2}}}( {v_d +\frac{z}{t}}) \\ \qquad \qquad \qquad \quad \quad \times \left[ {1-\exp \left( {-\frac{r_0^2 }{4D_\bot t}}\right) } \right] \exp \left( {-\frac{( {z-v_d t})^2}{4D_\parallel t}}\right) . \\ \end{array} \end{aligned}$$
(54)

By adjusting the quantities in Eq. (54) until the equation fits the observed ion flux density at the detector, one obtains values of \(v_d \), \(D_\parallel \), \(D_\bot \) and k at particular values of T and E / N.

Appendix B of ESM shows that the second-order moment equations that are consistent with the theory of the instrument just presented are:

$$\begin{aligned} \langle {\varvec{v}}\rangle \left[ {1-\epsilon _2 \frac{Nk}{\xi ( {T_{eff} })}} \right] +\epsilon _3 c_{0,1} ( 1)\left\langle {\varvec{v}}S_{\frac{3}{2}}^{( 1)} ( {W^2})\right\rangle =\frac{q{\varvec{E}}}{m\xi ( {T_{eff} })}, \end{aligned}$$
(55)
$$\begin{aligned} \begin{array}{l} \frac{3}{2}k_B T_{eff} =\frac{3}{2}k_B T+\frac{\epsilon _3 }{2}k_B \left( {\frac{M}{\mu }T_{eff} -T}\right) c_{1,2} ( 0)\left\langle S _{\frac{1}{2}}^{( 2)} ( {W^2})\right\rangle +\frac{Mq{\varvec{E}}\cdot \langle {\varvec{v}}\rangle }{2m\xi ( {T_{eff} })} \\ \qquad \qquad \qquad +\,\epsilon _2 \frac{Nk}{\xi ( {T_{eff} })}\frac{3}{4}k_B \left( {\frac{M}{\mu }T_{eff} -T}\right) \\ \end{array} \end{aligned}$$
(56)

and

$$\begin{aligned} \begin{array}{l} \mathbf{D}=-\frac{\Big ( {\langle {\varvec{v}}\rangle \langle {\varvec{v}}\rangle -\langle {\varvec{v}}{\varvec{v}}\rangle }\Big )}{\xi ( {T_{eff} })}+\frac{\xi ^ \prime ( {T_{eff} })}{3k_B \xi ( {T_{eff} })}\left[ {\xi ( {T_{eff} })+\xi ^ \prime ( {T_{eff} })( {T_{eff} -T})} \right] ^{-1} \\ \,\qquad \times \left[ {\left\{ {\frac{M}{\mu }( {\frac{3}{2}k_B T_{eff} })-\frac{3}{2}k_B T} \right\} \langle v \rangle -\frac{M}{2}\langle {\varvec{v}}v\rangle ^2-\frac{Mq}{m}{\varvec{E}}\cdot {\mathbf{D}}} \right] \langle {\varvec{v}}\rangle . \\ \end{array} \end{aligned}$$
(57)

Before these equations can be put to use, however, we must consider the new moments that arise in them.

7.2 Drift Velocity

Appendix C of ESM shows how the equations in Secs. 6 and 7.1 can be used to give the following second-order expression for a DTMS experiment:

$$\begin{aligned} v_d \left[ {1-\epsilon _2 \frac{Nk}{\xi ( {T_{eff} })}} \right] =\varepsilon \left\{ {1+\epsilon _3 \frac{c_{0,1} ( 1)}{c_{1,1} ( 1)}\left[ {\frac{2}{3}\frac{c_{1,0} ( 0)}{c_{0,0} ( 2)}+c_{1,0} ( 1)+\left( {\frac{m}{k_B T_i }}\right) \frac{2\varepsilon ^2}{c_{0,0} ( 2)}} \right] } \right\} , \end{aligned}$$
(58)

where

$$\begin{aligned} \varepsilon =\frac{qE}{m\xi ( {T_{eff} })} \end{aligned}$$
(59)

Note that the first approximation (where \(\epsilon _2 =\epsilon _3 =0)\) to the ion drift speed is \(v_d =\varepsilon \), which is exactly the same as Eq. (47) and as the equation obtained by a “bottom-up” approach to momentum-transfer theory [34]. Note also that the second approximation, which has \(\epsilon _2 =\epsilon _3 =1\) and cannot be obtained by momentum-transfer theory, depends upon the square of E / N through its dependence upon \(\varepsilon ^{2}\). In addition, the second approximation differs from the result obtained from the 2T theory [43] (where \(\epsilon _2 =0)\) because we have used Cartesian tenors for the moment equations, rather than spherical tensors. Finally, it should be noted that the infrequent ion-neutral reactions affect Eq. (58) only by shifting the drift velocity by a dimensionless amount that is equal to the ratio of N times the reaction rate coefficient to the collision frequency for momentum transfer; this is consistent with ignoring reaction effects in Eq. (50) except for the rate coefficient shown explicitly.

7.3 Effective Temperature

Starting from Eqs. (56) and (58), Appendices C and D of ESM allow us to obtain the following second-order expression for a DTMS experiment:

$$\begin{aligned} \frac{3}{2}k_B T_{eff} =\frac{3}{2}k_B T+\frac{1}{2}M\varepsilon v_d +\frac{1}{2}k_B \left( {\frac{M}{\mu }T_{eff} -T}\right) \end{aligned}$$
$$\begin{aligned}&\times \left( \epsilon _3 \frac{c_{1,2} ( 0)}{c_{2,2} ( 0)}\left( \frac{5}{2}c_{1,0} ( 0)-c_{2,0} ( 0)+\left( {\frac{m}{2k_B T_i }}\right) \frac{2\varepsilon ^2}{c_{1,1} ( 1)}\right. \right. \nonumber \\&\quad \left\{ {\frac{3}{2}+\frac{1}{c_{0,0} ( 2)}\left[ {c_{0,0} ( 2)+\frac{2}{3}c_{1,0} ( 0)+\frac{2m}{k_B T_i }\varepsilon v_d } \right] } \right\} -\frac{2}{c_{1,1} ( 1)}\left( {\frac{m}{2k_B T_i }}\right) \left[ \frac{5}{2}-c_{1,0} ( 1) \right. \nonumber \\&\left. \left. \left. \quad -\frac{5}{2}c_{1,1} ( 1)\right] \varepsilon v_d \right) +\epsilon _2 \frac{3}{2}\frac{Nk}{\xi ( {T_{eff} })}\right) , \end{aligned}$$
(60)

Eq. (60) shows that in first approximation (\(\epsilon _2 =\epsilon _3 =0)\)we have the same result as obtained by momentum-transfer theory [31]:

$$\begin{aligned} \frac{3}{2}k_B T_{eff} =\frac{3}{2}k_B T+\frac{1}{2}M\epsilon v_d =\frac{3}{2}k_B T+\frac{1}{2}Mv_d^2 . \end{aligned}$$
(61)

From Eqs. (24) and (61) we obtain the Wannier formula [20],

$$\begin{aligned} \frac{3}{2}k_B T_i =\frac{3}{2}k_B T+\frac{1}{2}mv_d^2 +\frac{1}{2}Mv_d^2 . \end{aligned}$$
(62)

The second approximation, given by the full version of Eq. (60) with \(\epsilon _2 =\epsilon _3 =1\), is a new result. We note that, in order to remain consistent, we can modify the correction terms in Eqs. (58) and (60) by replacing \(v_d \) by \(\varepsilon \) and \(T_i \) by the right-hand side of Eq. (62). The versions of Eqs. (58) and (60) so obtained differ slightly from those obtained in the 2T theory [43] with \(\epsilon _2 =0\), due again to our use of Cartesian tensors. Finally, note that Eq. (60) indicates that ion-neutral reactions cause an additional term to occur in the Wannier formula, whereas the terms proportional to \(\epsilon _3 \) act only to modify the final term in Eqs. (61) and (62).

7.4 Temperature Tensor

We define the temperature tensor in the laboratory frame, T, as

$$\begin{aligned} k_B \mathbf{T}=m\langle {\varvec{v}}{\varvec{v}}\rangle . \end{aligned}$$
(63)

From Eq. (63) and Eq. (C4) in ESM, the temperature tensor can be written in first approximation as

$$\begin{aligned} k_B {\mathbf{T}}=\frac{2}{c_{0,0} ( 2)}m{\varvec{v}}_{\varvec{d}} {\varvec{v}}_{\varvec{d}} +k_B T_i \left[ {1+\frac{2}{3}\frac{c_{1,0} ( 0)}{c_{0,0} ( 2)}} \right] {\mathbf{U}}. \end{aligned}$$
(64)

This shows that the temperature tensor does not have off-diagonal components in DTMS experiments, a fact that can be established by more general arguments than used here. The components of T along \(\hat{x} \hat{x} \) and \(\hat{y} \hat{y}\) are the same and are generally labeled \(T_\bot \). Then using Eqs. (62) and (64) and inserting the explicit expression [43] for \(c_{1,0} ( 0)\) we get the first approximation result

$$\begin{aligned} k_B T_\bot =k_B T+A_\bot Mv_d^2 , \end{aligned}$$
(65)

where

$$\begin{aligned} A_\bot =\frac{m+M}{3M}-\frac{2}{3c_{0,0} ( 2)}\frac{m}{M}. \end{aligned}$$
(66)

Similarly, the component of \(\mathbf{T}\) along \(\hat{z}\) \(\hat{z} \) is generally labeled \(T_\parallel \), with

$$\begin{aligned} k_B T_\parallel =k_B T+A_\parallel Mv_d^2 , \end{aligned}$$
(67)

where

$$\begin{aligned} A_\parallel =\frac{m+M}{3M}+\frac{4}{3c_{0,0} ( 2)}\frac{m}{M}. \end{aligned}$$
(68)

A second-order approximation for T cannot be obtained until the second-order approximation is established for \(\langle {\varvec{v}}{\varvec{v}}\rangle \), which would require a third-order approximation for the ion drift velocity and effective temperature.

It is obvious from Eqs. (65)–(68) that

$$\begin{aligned} \frac{3}{2}k_B T_i =\frac{1}{2}k_B T_\parallel +k_B T_\bot =\frac{3}{2}k_B T+\frac{1}{2}mv_d^2 +\frac{1}{2}Mv_d^2 , \end{aligned}$$
(69)

i.e., the present results for energy partitioning are consistent in first approximation with the Wannier equations [20] for the ion and effective temperatures.

Eqs. (65) and (67) for \(T_\parallel \) and \(T_\bot \) have the same forms as obtained from momentum-transfer theory [31]. The expressions become exactly the same when the ion temperature tensor is transformed from the laboratory frame to the frame of reference of the moving ion swarm using the definition

$$\begin{aligned} k_B \mathbf{T}_\mathbf{rel} =m\langle ( {{\varvec{v}}-{\varvec{v}}_{\varvec{d}}})( {{\varvec{v}}-{\varvec{v}}_{\varvec{d}}})\rangle =k_B {\mathbf{T}}-m{\varvec{v}}_{\varvec{d}}{\varvec{v}}_{\varvec{d}} , \end{aligned}$$
(70)

and when we identify the ratio, \(\nu _v /\nu _m \), used in momentum-transfer theory as

$$\begin{aligned} \frac{\upsilon _v }{\upsilon _m }=\left( {1+\frac{m}{M}}\right) c_{0,0} ( 2)-\frac{2m}{M}. \end{aligned}$$
(71)

A microscopic definition of \(\nu _v /\nu _m \) cannot be obtained from momentum-transfer theory, but we can use the tabulated expressions for matrix elements of the Boltzmann collision operator [43] to find that

$$\begin{aligned} \frac{\upsilon _v }{\upsilon _m }=\frac{6}{5}A^*( {T_{eff} })+\frac{2m}{5( {m+M})}\left( {\frac{T_i -T}{T_{eff} }}\right) \left[ {6C^*( {T_{eff} })-5} \right] , \end{aligned}$$
(72)

where

$$\begin{aligned} A^*( {T_{eff} })=\frac{\bar{\Omega }^{( {2,2})}( {T_{eff} })}{\bar{\Omega }^{( {1,1})}( {T_{eff} })} \end{aligned}$$
(73)

and

$$\begin{aligned} C^*( {T_{eff} })=\frac{\bar{\Omega }^{( {2,2})}( {T_{eff} })}{\bar{\Omega }^{( {1,1})}( {T_{eff} })} \end{aligned}$$
(74)

are ratios of collision integrals. For the Maxwell model, \(6C^*( {T_{eff} })=5\), so Eqs. (72) and (73) give

$$\begin{aligned} \frac{\upsilon _v }{\upsilon _m }=\frac{6}{5}\frac{\bar{\Omega }^{( {2,2})}( {T_{eff} })}{\bar{\Omega }^{( {1,1})}( {T_{eff} })}. \end{aligned}$$
(75)

Since \(\bar{\Omega }^{( {2,2})}( {T_{eff} })\) is the primary way in which the interaction potential governs the viscosity of an atomic gas and \(\bar{\Omega }^{( {1,1})}( {T_{eff} })\) is the primary factor governing momentum-transfer, it is clear why \(\nu _v /\nu _m \) has been called [31] the ratio of the collision frequency for viscosity to the momentum-transfer collision frequency. We note again, however, that Eq. (75) is restricted to the Maxwell model upon which momentum-transfer theory is based.

7.5 Heat Flux Vector

In the laboratory frame, we define the heat flux vector as

$$\begin{aligned} {\varvec{Q}}=\frac{m}{2}\langle {\varvec{v}}v^2\rangle . \end{aligned}$$
(76)

Inserting eq. (C2) of ESM and Eq. (59) above into Eq. (76) shows that \({\varvec{Q}}\) must lie entirely along the direction of the electric field and have a magnitude, Q, such that

$$\begin{aligned} c_{1,1} ( 1)Q=\varepsilon \left[ {\frac{3}{2}k_B T_i +k_B T_\parallel } \right] -v_d k_B T_i \left[ {\frac{5}{2}-c_{1,0} ( 1)-\frac{5}{2}c_{1,1} ( 1)} \right] . \end{aligned}$$
(77)

Using the first approximation Eqs. (62), (67) and (68), this reduces to

$$\begin{aligned} Q=v_d \left\{ {\frac{5}{2}k_B T_i +\left[ {\frac{4}{3c_{0,0} ( 2)}-1} \right] \frac{mv_d^2 }{c_{1,1} ( 1)}} \right\} . \end{aligned}$$
(78)

By transforming Eq. (77) to the frame of reference of the moving ion swarm, we get

$$\begin{aligned} {\varvec{Q}}_{\varvec{rel}} =\frac{m}{2}\langle ( {{\varvec{v}}-{\varvec{v}}_{\varvec{d}}} )( {{\varvec{v}}-{\varvec{v}}_{\varvec{d}} })\cdot ( {{\varvec{v}}-{\varvec{v}}_{\varvec{d}} })\rangle ={\varvec{Q}}-\left( {\frac{3}{2}k_B T_i }\right) {\varvec{v}}_{\varvec{d}} -k_B {\mathbf{T}}_{{\varvec{rel}}} \cdot {\varvec{v}}_{\varvec{d}}. \end{aligned}$$
(79)

From Eq. (79) it may be shown that \({\varvec{Q}}_{\varvec{rel}} \) is directed along the electric field, but that its magnitude is zero in first approximation. This must be true for the first approximation of any odd moment in the relative frame of reference; as another example, \(\langle {\varvec{v}}-{\varvec{v_d}} \rangle =0\). This is because the essential feature of the 2T moment theory is that the zero-order distribution functions for both the ions and neutrals are isotropic. Only if we proceed to higher approximation or consider \({\varvec{Q}}_{\varvec{rel}} \) in a multi-temperature moment theory [47] would we be able to test the prediction [31] that \({\varvec{Q}}_{{\varvec{rel}}} \) is proportional to \(v_d^3 \) for the Maxwell model.

7.6 Dyadic Energy

In the laboratory frame, we define the scalar dyadic energy as

$$\begin{aligned} E_d =\left\langle \left( {\frac{1}{2}mv^2}\right) ^2\right\rangle =\left( {\frac{m}{2}}\right) ^2\langle v^4\rangle . \end{aligned}$$
(80)

It is shown in Appendix E of ESM that in first approximation

$$\begin{aligned} E_d =\left( {\frac{m}{2}}\right) ^2&\left[ \left( {\frac{2k_B T_i }{m}}\right) ^2\left\{ {\frac{15}{4}+5\frac{c_{1,0} ( 0)}{c_{2,2} ( 0)}-2\frac{c_{2,0} ( 0)}{c_{2,2} ( 0)}} \right\} \right. \nonumber \\&\left. +\frac{20k_B T_i }{mc_{2,2} (0)}\varepsilon ^2+\frac{8}{c_{2,2} ( 0)c_{1,1} ( 1)}\left\{ {\frac{4}{3c_{0,0} ( 2)}-1} \right\} \varepsilon ^4 \right] . \end{aligned}$$
(81)

It is possible to define a relative dyadic energy as

$$\begin{aligned} E_d =\left\langle \left( {\frac{1}{2}m( {{\varvec{v}}-{\varvec{v}}_{\varvec{d}} })\cdot ( {{\varvec{v}}-{\varvec{v}}_{\varvec{d}} })}\right) ^2\right\rangle , \end{aligned}$$
(82)

but no simplifications occur and the result has the same general form as Eq. (81).

7.7 Diffusion Coefficients

Like the temperature tensor and heat flux vector, the ion diffusion coefficients do not arise in first approximation of our theory. This means that the quantities appearing in the right-hand side of Eq. (57) should be replaced by their first-approximation values. When this is done, Appendix F of ESM shows that \({\varvec{D}}\) is a diagonal tensor with equal components, \(D_\bot \), perpendicular to the electric field and with a different component, \(D_\parallel \), along the field.

The expression for the perpendicular diffusion coefficient is simple,

$$\begin{aligned} \frac{qD_\bot }{K}=k_B T_\bot , \end{aligned}$$
(83)

where K is the usual ion mobility defined by the equation,

$$\begin{aligned} {\varvec{v}}_{\varvec{d}} =K{\varvec{E}}. \end{aligned}$$
(84)

When the field strength is low and \(T_\bot =T\), Eq. (83) is the well-known [20] Nernst-Townsend-Einstein relation. Extensions to higher E / N values [20, 45] involve finding approximate expressions for \(T_\bot \), similar to Eqs. (65) and (67).

The parallel diffusion coefficient obtained in Appendix F of ESM is

$$\begin{aligned} \frac{qD_\parallel }{K}=\left[ {k_B T_\parallel -mv_d^2 } \right] \left[ {1+\frac{K^\prime }{2}} \right] +\left[ {\frac{Q}{v_d }-\frac{3}{2}k_B T_i } \right] \frac{K^\prime }{2}, \end{aligned}$$
(85)

where \(K^\prime \) is the logarithmic derivative defined there. Eq. (85) becomes much simpler in appearance when written in terms of the relative quantities, \(Q_{rel} \) and \(T_{\parallel ,rel} \):

$$\begin{aligned} \frac{qD_\parallel }{K}=k_B T_{\parallel ,rel} \left[ {1+( {1+\Delta })K^\prime } \right] , \end{aligned}$$
(86)

where

$$\begin{aligned} \Delta =\frac{Q_{rel} }{v_d }\frac{1}{2k_B T_{\parallel ,rel} }. \end{aligned}$$
(87)

Thus the present results are in agreement with results obtained [31] from momentum-transfer theory, with the advantage of our approach being that the transport collision integrals, and hence the influence of the ion-neutral interaction potential, are given explicitly. We note that although relative quantities arise on the right-hand side of Eq. (86), the parallel diffusion coefficients that it describes is measured in the laboratory frame. Although Eq. (85) is somewhat more cumbersome, all of the quantities in it are in the laboratory frame.

8 Tests for Special Cases

Since the first approximation moment equations (with all \(\epsilon _i \) equal to zero) are exact for the Maxwell model, we turn for a first test of our second approximation equations to the Lorentz model (m\(\ll \)M) for rigid spheres with diameter \(\mathrm{\sigma } \). The “exact” results (for \(\epsilon _3 =1\), but all other \(\epsilon _i \) equal to zero) are known [11] from numerical calculations for this model, in terms of the dimensionless field strength,

$$\begin{aligned} \varepsilon ^*=\frac{3\sqrt{\pi }}{16k_B T}\left( {\frac{m+M}{m}}\right) ^{\frac{1}{2}}\frac{qE}{N\pi \sigma ^2}, \end{aligned}$$
(88)

and the dimensionless drift speed,

$$\begin{aligned} v_d^*=\left( {\frac{M}{2k_B T}}\right) ^{\frac{1}{2}}v_d . \end{aligned}$$
(89)

In terms of these quantities, the first approximation to Eq. (58) is

$$\begin{aligned} v_d^*\left[ {1+\frac{2}{3}( {v_d^*})^2} \right] ^{1/2}=\varepsilon ^*. \end{aligned}$$
(90)

The second approximation obtained from Eqs. (58) and the matrix elements tabulated in the Appendix of [43] is

$$\begin{aligned} v_d^*\left[ {1+\frac{2}{3}( {v_d^*})^2} \right] ^{1/2}=\frac{14}{13}\varepsilon ^*. \end{aligned}$$
(91)

Because we have used Cartesian tensors for the moment equations, our second approximation differs from the result obtained previously [43] using spherical tensors, which is (after correcting a misprint):

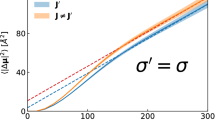
$$\begin{aligned} v_d^*\left[ {1+\frac{2}{3}( {v_d^*})^2} \right] ^{1/2}=\frac{14}{13}\varepsilon ^*\left\{ {1+\frac{5}{7}\frac{( {v_d^*})^2\left[ {3+2( {v_d^*})^2} \right] -3( {\varepsilon ^*})^2}{3\left[ {1+( {v_d^*})^2} \right] \left[ {3+2( {v_d^*})^2} \right] }} \right\} . \end{aligned}$$
(92)

Fig. 1 shows the percentage deviations from the exact results of the various approximate values. Both second-approximation results are in better agreement with the exact results than are the first-approximation values, on an overall basis, even though the convergence is known to be slow for the Lorentz model [42]. The present second-approximation values are more accurate than the original second-approximation results, at least for this particular model.

Fig. 1
figure 1

Percentage deviations of the calculated drift velocities from the true values [11], as a function of the dimensionless field strength, \(\varepsilon ^*\), for the Lorentz model of rigid spheres. The lowest (blue) results are the first approximation values, the upper (red) results are the earlier second approximation values, while the middle (purple) results are the present results in second approximation (Color figure online)

Full size image

For rigid spheres, Monte Carlo values have been determined [35] (again for \(\epsilon _3 =1\) but all other \(\epsilon _i \) equal to zero) for values of the ratio,

$$\begin{aligned} F=\left( {\frac{3}{8\varepsilon ^*}}\right) ^{\frac{1}{2}}\left( {\frac{\pi M}{\mu }}\right) ^{\frac{1}{4}}v_d^*, \end{aligned}$$
(93)

in the limit of large \(\varepsilon ^*\). Our first approximation results for F are the same as given previously [43],

$$\begin{aligned} F^4=\frac{27\pi }{128}\frac{M}{\mu }. \end{aligned}$$
(94)

In order to obtain the second approximation, it is necessary to keep the correction terms in both Eqs. (58) and (60) and to work out the high-field limits of many \(c_{r,s} ( l).\) Fig. 2 compares the first two approximations with the Monte Carlo values, as a function of the mass ratio, m / M. On an overall basis (i.e., except for small mass ratios), the second approximation results are in better agreement with the Monte Carlo values than are the first approximation values. Once again, the successive approximations to the moment equations appear to be converging.

Fig. 2
figure 2

Dimensionless quantity, F, as a function of the ion-neutral mass ratio, m / M. The first approximation is the lower (blue) curve, the second approximation is the upper (red) curve, and the Monte Carlo values [35] are given by points with error bars (Color figure online)

Full size image

Another special case of interest in IMS is when the electrostatic field is so weak that \(T_{eff} =T_i =T\). In first approximation, we obtain from Eqs. (20), (58) and (59) the fundamental low-field mobility equation [12],[15],[18],[21],[36] for the standard mobility,

$$\begin{aligned} K_0 =\frac{NK}{N_0 }=\frac{3}{8N_0 }\left( {\frac{\pi }{2\mu k_B T}}\right) ^{\frac{1}{2}}\frac{q}{\bar{\Omega }^{( {1,1})}( T)}. \end{aligned}$$
(95)

Here \(N_0 \) is Loschmidt’s constant, the number density of an ideal gas at 273.15 K and 101.325 kPa. If we denote as \(K_0 ^{(1)}\) the mobility given by Eq. (95) and as \(K_0^{{(2)}} \) the second approximation mobility (again for \(\epsilon _3 =1\) but all other \(\epsilon _i \) equal to zero), then Eq. (58) and the matrix elements in the Appendix of [43] give

$$\begin{aligned} \frac{K_0^{( 2)} }{K_0^{( 1)} }=1+\frac{e^2\left[ {6C^*( T)-5} \right] ^2}{10( {3-6e+4e^2})-3e^2\left[ {4B^*( T)-5} \right] +16( {1-e})eA^*( T)}, \end{aligned}$$
(96)

where \(e=\mu /m\) and

$$\begin{aligned} B^*( T)=\frac{5 \bar{\Omega }^{( {1,2})}( {T_{eff} })-4 \bar{\Omega }^{( {1,3})}( {T_{eff} })}{\bar{\Omega }^{( {1,1})}( {T_{eff} })}. \end{aligned}$$
(97)

For Maxwell molecules where the ion-neutral interaction potential varies as the inverse-fourth power of the separation, \(6C^*( T)=5\) and the two approximations become identical. For rigid spheres, all three ratios of collision integrals are identically equal to 1.0, so the ratio \(K_0 ^{(2)}/K_0 ^{(1)}\) becomes a function only of the ion-neutral mass ratio (equivalently, e). Fig. 3 shows that \(K_0^{({2})}/K_0 ^{(1)}\) is very close to 1.00 for rigid spheres, except for small mass ratios where we see in Fig. 1 that the first approximation is too low by just a bit more than 10%. Hence Fig. 3 indicates that, once again, the successive approximations to the moment equations appear to be converging.

Fig. 3
figure 3

Ratio of the first two approximations to the standard mobility at low field strengths, for rigid-sphere interactions as a function of the ion-neutral mass ratio

Full size image

9 Conclusions

This paper gives the second in a series of successive approximations obtained by truncating the 2T moment equations obtained from the Boltzmann equation using Burnett functions. In first approximation, the only moments needed are the three Cartesian components of the average ion velocity in the laboratory frame and the average ion energy; thus there is a closed system of ordinary differential equations for one vector quantity and one scalar. The second approximation is needed in order to treat, even approximately, the ion diffusion tensor and the scalar rate coefficient for ion-neutral reactions. If we let all the smallness factors be 1, the second approximation involves three more moments, equivalent to the ion temperature tensor, the heat flux vector, and the (scalar) dyadic energy. The new moments are introduced using the first approximation equations for them, which truncates the coupled set. Thus there is a closed system of partial differential equations for two tensor, two vector, and three scalar quantities. It would be straightforward to work out successively higher approximations, if desired.

The approach illustrated here is not expected to describe accurately quantities such as the ion diffusion and ion temperature tensors that are inherently anisotropic. Indeed, this is the reason that the 2T kinetic theory [43, 45] was replaced, first by a three-temperature kinetic theory [19, 42] and then by a Gram-Charlier theory [37]. Such theories are, however, specifically designed for one particular type of experiment, DTMS. In contrast, the present uniform theory can be applied to any type of experiment in which trace amounts of ions move though dilute gases under the influence of external electric or magnetic fields of arbitrary strength, as discussed previously [47] for the first approximation.

When applied to drift-tube mass spectrometers, our second approximation results are the same as the results obtained by momentum-transfer theory in the special case where the ion-neutral interactions follow the Maxwell model. For real ion-neutral interactions, the results given here for the temperature tensor, heat flux vector, and dyadic energy are new.

Further analytical analysis of this uniform moment theory is not recommended, except possibly for the second approximation using a multi-temperature approach with Cartesian basis functions (see [47]). Instead, it is better to set up the partial differential equations for the moments in successively higher approximations and then proceed from that point by numerical methods. The key thing is that the present applications to drift-tube mass spectrometry show that the successive approximations appear to be converging, in a global sense, in a way that rivals or exceeds the well-established successive approximations in the 2T kinetic theory [43, 45]. This gives us confidence in applying this uniform moment theory to other experiments, including ion mobility spectrometry, ion traps, crossed electric and magnetic fields, and collision-dominated ion cyclotron resonance. In such experiments, the desired accuracy is not particularly high, so the first or second approximations should suffice.