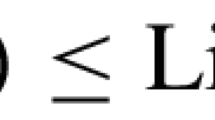1 Introduction

Let \(\zeta \) be a random variable binomially distributed as

$$\begin{aligned} \mathrm{P}[\zeta =1]=\frac{1}{2}, \quad \mathrm{P}[\zeta =-1]=\frac{1}{2}, \end{aligned}$$
(1.1)

so that the Laplace transform of the probability distribution is given by

$$\begin{aligned} \mathrm{E}[e^{\alpha \zeta }]= \cosh \alpha , \quad \alpha \in \mathbb {R}. \end{aligned}$$
(1.2)

For \(N \in \mathbb {N}\equiv \{1,2, \ldots \}\), let \(\{\zeta _j(t): 1 \le j \le N, t \in \mathbb {N}\}\) be a family of i.i.d.random variables which follow the same probability law with \(\zeta \). We consider a random walk (RW) on \(\mathbb {Z}^N\), \({\varvec{S}}(t)=(S_1(t), \ldots , S_N(t)), t \in \mathbb {N}_0 \equiv \{0\} \cup \mathbb {N}\), in which the components \(S_j(t), j=1,2,\ldots , N\) are independent simple and symmetric RWs;

$$\begin{aligned} S_j(0)&= u_j \in \mathbb {Z},\\ S_j(t)&= u_j+\zeta _j(1)+\zeta _j(2)+ \cdots + \zeta _j(t), \quad t \in \mathbb {N}, \quad 1 \le j \le N. \end{aligned}$$

Let \(\mathbb {Z}_\mathrm{e}=2 \mathbb {Z}=\{\dots , -2, 0, 2, 4, \ldots \}\) and \(\mathbb {Z}_\mathrm{o}=1+2 \mathbb {Z}=\{\dots , -1,1,3,5, \ldots \}\). For each component, \(S_j(\cdot ), 1 \le j \le N\), the transition probability is given by

$$\begin{aligned} p(t-s,y|x)&= \mathrm{P}[S_j(t)=y | S_j(s)=x] \nonumber \\&= \left\{ \begin{array}{l} \displaystyle { \frac{1}{2^{t-s}} {t-s \atopwithdelims ()[(t-s)+(y-x)]/2 }}, \\ \qquad \qquad \hbox {if}\; t \ge s, \, -(t\!-\!s) \!\le \! y\!-\!x \!\le \! t\!-\!s, \, (t\!-\!s)\!+\!(y\!-\!x) \!\in \! \mathbb {Z}_\mathrm{e}, \\ 0, \quad \qquad \hbox {otherwise}. \end{array} \right. \end{aligned}$$
(1.3)

We always take the initial point \({\varvec{u}}=(u_1, \ldots , u_N) ={\varvec{S}}(0)\) from \(\mathbb {Z}^N_\mathrm{e}\), then \({\varvec{S}}(t) \in \mathbb {Z}^N_\mathrm{e}\), if \(t\) is even, and \({\varvec{S}}(t) \in \mathbb {Z}^N_\mathrm{o}\), if \(t\) is odd. The probability space is denoted as \((\Omega , \mathcal{F}, \mathrm{P}_{{\varvec{u}}})\) and expectation is written as \(\mathrm{E}_{{\varvec{u}}}\).

Let

$$\begin{aligned} \mathbb {W}_N=\{{\varvec{x}}=(x_1, \ldots , x_N) \in \mathbb {R}^N: x_1 < \cdots < x_N\} \end{aligned}$$

be the Weyl chamber of type A\(_{N-1}\). Define \(\tau _{{\varvec{u}}}\) to be the first exit time from the Weyl chamber of the RW started at \({\varvec{u}}\in \mathbb {Z}_\mathrm{e}^N \cap \mathbb {W}_N\),

$$\begin{aligned} \tau _{{\varvec{u}}}=\inf \{ t \ge 1: {\varvec{S}}(t) \notin \mathbb {W}_N\}. \end{aligned}$$

In the present paper, we study the RW conditioned to stay in \(\mathbb {W}_N\) forever. That is, \(\tau _{{\varvec{u}}}=\infty \) is conditioned. We call such a conditional RW the (simple and symmetric) noncolliding RW, since when we regard the \(j\)-th component \(S_j(\cdot )\) as the position of \(j\)-th particle on \(\mathbb {Z}, 1 \le j \le N\), if \(\tau _{{\varvec{u}}} < \infty \), then at \(t=\tau _{{\varvec{u}}}\) there is at least one pair of particles \((j, j+1)\), which collide with each other; \(S_j(\tau _{{\varvec{u}}})=S_{j+1}(\tau _{{\varvec{u}}}), 1 \le j \le N-1\). Such a conditional RW is also called a system of vicious walkers in statistical physics [6, 14], non-intersecting paths, non-intersecting walks, and ordered random walks in enumerative combinatorics and probability theory (see [8, 36] and Chap. 10 in [15]).

Let \(\mathfrak {M}\) be the space of nonnegative integer-valued Radon measure on \(\mathbb {Z}\) and \(\mathfrak {M}_0 \equiv \{\xi \in \mathfrak {M}: \xi (\{x\}) \le 1, \forall x \in \mathbb {Z}\}\). We consider the noncolliding RW as a process in \(\mathfrak {M}_0\) and represent it by

$$\begin{aligned} \Xi (t, \cdot )=\sum _{j=1}^N \delta _{S^0_j(t)}(\cdot ), \quad t \in \mathbb {N}_0, \end{aligned}$$
(1.4)

where

$$\begin{aligned} {\varvec{S}}^0(t)=(S^0_1(t), \ldots , S^0_N(t)) \in \mathbb {Z}^N \cap \mathbb {W}_N, \quad t \in \mathbb {N}_0. \end{aligned}$$
(1.5)

The configuration \(\Xi (t, \cdot ) \in \mathfrak {M}_0, t \in \mathbb {N}_0\) is unlabeled, while \({\varvec{S}}^0(t) \in \mathbb {Z}^N \cap \mathbb {W}_N, t \in \mathbb {N}_0\) is labeled. We write the probability measure for \(\Xi (t, \cdot ), t \in \mathbb {N}_0\) started at \(\xi \in \mathfrak {M}_0\) as \({\mathbb P}_{\xi }\) with expectation \({\mathbb E}_{\xi }\), and introduce a filtration \(\{\mathcal{F}(t) : t \in \mathbb {N}_0\}\) defined by \(\mathcal{F}(t)=\sigma (\Xi (s): 0 \le s \le t, s \in \mathbb {N}_0)\). Then the above definition of the noncolliding RW gives the follows. Let \(\xi =\sum _{j=1}^N \delta _{u_j}\) with \({\varvec{u}}\in \mathbb {Z}^N_\mathrm{e} \cap \mathbb {W}_N\), and \(t \in \mathbb {N}\), \(t \le T \in \mathbb {N}\). For any \(\mathcal{F}(t)\)-measurable bounded function \(F\),

$$\begin{aligned} {\mathbb E}_{\xi } \Big [F(\Xi (\cdot )) \Big ] = \lim _{n \rightarrow \infty } \mathrm{E}_{{\varvec{u}}} \left[ \left. F \left( \sum _{j=1}^N \delta _{S_j(\cdot )} \right) \right| \tau _{{\varvec{u}}} > n \right] \!. \end{aligned}$$
(1.6)

The important fact is that, if we write the Vandermonde determinant as

$$\begin{aligned} h({\varvec{x}})=\det _{1 \le j, k \le N} [x_j^{k-1}] =\prod _{1 \le j < k \le N} (x_k-x_j), \end{aligned}$$
(1.7)

the expectation (1.6) is obtained by an \(h\)-transform in the sense of Doob of the form [35]

$$\begin{aligned} {\mathbb E}_{\xi }\Big [F(\Xi (\cdot ))\Big ] =\mathrm{E}_{{\varvec{u}}} \left[ F \left( \sum _{j=1}^N \delta _{S_j(\cdot )} \right) \mathbf{1}(\tau _{{\varvec{u}}} > T) \frac{h({\varvec{S}}(T))}{h({\varvec{u}})} \right] \!. \end{aligned}$$
(1.8)

(See also [8, 34].) It determines the noncolliding RW, \((\Xi (t), t \in \mathbb {N}_0, {\mathbb P}_{\xi })\).

The formula (1.8) is a discrete analogue of the construction of noncolliding Brownian motion (BM) by Grabiner [18] as an \(h\)-transform of absorbing BM in \(\mathbb {W}_N\). The noncolliding BM is equivalent to Dyson’s BM model with parameter \(\beta =2\) and the latter is known as an eigenvalue process of Hermitian matrix-valued BM and as solutions of the following system of stochastic differential equations (SDEs)

$$\begin{aligned} dX_j(t)= dW_j(t)+ \sum _{\begin{array}{c} 1 \le k \le N, \\ k \not =j \end{array}} \frac{1}{X_j(t)-X_k(t)}dt, \quad 1 \le j \le N, \quad t \in [0, \infty ), \end{aligned}$$
(1.9)

where \(W_j(\cdot ), 1 \le j \le N\) are independent one-dimensional standard BMs [7, 18, 19, 21, 27, 32, 38, 41–43, 51, 52]. (From now on BM stands for one-dimensional standard Brownian motion and Dyson’s BM model with \(\beta =2\) is simply called the Dyson model in this paper.) Then the noncolliding RW has been attracted much attention as a discretization of models associated with the Gaussian random-matrix ensembles [2, 3, 12, 15, 22, 23, 26, 40].

Eigenvalue distributions of random-matrix ensembles provide important examples of determinantal point processes, in which any correlation function is given by a determinant specified by a single continuous function called the correlation kernel [4, 49, 50]. The noncolliding BM is regarded as a dynamical extension of determinantal point process such that any spatio-temporal correlation function is expressed by a determinant. Such processes are said to be determinantal [28]. The dynamical correlation kernel is asymmetric with respect to the exchange of two points on the spatio-temporal plane and shows causality in the system. This type of correlation kernel was first obtained by Eynard and Mehta for a multi-matrix model [11] and by Nagao and Forrester for the noncolliding BM started at a special initial distribution (the GUE eigenvalue distribution) [39]. It is proved that the noncolliding BM is determinantal for any fixed initial configuration with finite numbers of particles as well as two families of infinite-particle initial configurations [30, 33].

Nagao and Forrester [40] studied a ‘bridge’ of noncolliding RW started from \({\varvec{u}}_0=(2j)_{j=0}^{N-1}\) at \(t=0\) and returned to the same configuration \({\varvec{u}}_0\) at time \(t=2M, M \in \mathbb {N}_0\). They showed that at time \(t=M\) the spatial configuration provides a determinantal point process and the correlation kernel is expressed by using the symmetric Hahn polynomials. Johansson [23] generalized the process to a bridge from \({\varvec{u}}_0\) at \(t=0\) to \(M_2-M_1+{\varvec{u}}_0\) at \(t=M_1+M_2\), \(M_1, M_2 \in \mathbb {N}_0, M_2 > M_1\), and proved that the process is determinantal. The dynamical correlation kernel is of the Eynard-Mehta type and called the extended Hahn-kernel. For the noncolliding RW defined for infinite time-period \(t \in \mathbb {N}_0\) by (1.6) or (1.8) [8, 34, 35], however, determinantal structure of spatio-temporal correlations has not been clarified so far.

In the present paper we show that the construction by the \(h\)-transform (1.8) directly leads to the fact that the discrete-time noncolliding RW is determinantal for any fixed initial configuration \(\xi =\sum _{j=1}^{N} \delta _{u_j} \in \mathfrak {M}_0\) with \(N=\xi (\mathbb {Z}_\mathrm{e}) \in \mathbb {N}\). (See [10] for the noncolliding system of continuous-time random walks.) There are two key points in the present study of discrete-time systems; proper complexification of RWs and introduction of determinantal martingale. Let \(\widetilde{\zeta } \in \mathbb {R}\) be a continuous random variable in the hyperbolic secant distribution [13],

$$\begin{aligned} \widetilde{\mathrm{P}}[\widetilde{\zeta } \in dx] = \frac{1}{2} \mathrm{sech} \left( \frac{\pi x}{2} \right) dx = \frac{1}{2 \cosh (\pi x/2)} dx, \end{aligned}$$
(1.10)

which is selfdecomposable (see [47, pp.98–99 ]). The Fourier transform of (1.10) (the characteristic function of \(\widetilde{\zeta }\)) is also expressed by the hyperbolic secant [13] (\(i \equiv \sqrt{-1}\))

$$\begin{aligned} \widetilde{\mathrm{E}}[e^{i \alpha \widetilde{\zeta }}] =\mathrm{sech} \alpha =\frac{1}{\cosh \alpha }, \quad \alpha \in \mathbb {R}, \end{aligned}$$
(1.11)

which is exactly the inverse of (1.2). Let \(\{\widetilde{\zeta }(t) : t \in \mathbb {N}\}\) be a series of i.i.d.random variables obeying the same probability law with \(\widetilde{\zeta }\). We define a discrete-time Markov process \(\widetilde{S}(t), t \in \mathbb {N}_0\) on \(\mathbb {R}\) starting from 0 at time \(t=0\) by

$$\begin{aligned} \widetilde{S}(t)=\widetilde{\zeta }(1) + \cdots + \widetilde{\zeta }(t), \quad t \in \mathbb {N}. \end{aligned}$$
(1.12)

At each time \(t \in \mathbb {N}_0\), it is in the generalized hyperbolic secant distribution with density

$$\begin{aligned} \widetilde{p}(t, x|0)&\equiv \widetilde{\mathrm{P}}[\widetilde{S}(t) \in dx ] \nonumber \\&= \frac{2^{t-2}}{\pi \Gamma (t)} \left| \Gamma \left( \frac{t}{2}+i \frac{x}{2} \right) \right| ^2, \quad t \in \mathbb {N}_0, \quad x \in \mathbb {R}, \end{aligned}$$
(1.13)

where \(\Gamma \) denotes the gamma function [20]. It can be shown that \(\widetilde{S}(t)/\sqrt{t} \mathop {\rightarrow }\limits ^\mathrm{d}\mathsf{N}(0,1)\) as \(t \rightarrow \infty \) [20]. Let \(\widetilde{S}_j(\cdot ), 1 \le j \le N\) be a set of independent copies of \(\widetilde{S}(\cdot )\) and express the expectation with respect to these processes also by \(\widetilde{\mathrm{E}}\). For the original RW, \({\varvec{S}}(t)=(S_1(t), \ldots , S_N(t)), t \in \mathbb {N}_0\) started at a fixed configuration \({\varvec{u}}\in \mathbb {Z}_\mathrm{e}^N \cap \mathbb {W}_N\), its complexification is given by the discrete-time complex processes, \({\varvec{Z}}(t)=(Z_1(t), \ldots , Z_N(t)), t \in \mathbb {N}_0\) with

$$\begin{aligned} Z_j(t)=S_j(t)+ i \widetilde{S}_j(t), \quad 1 \le j \le N, \quad t \in \mathbb {N}_0. \end{aligned}$$
(1.14)

We put \(\xi = \sum _{j=1}^{N} \delta _{u_j} \in \mathfrak {M}_0\) and consider a set of functions of \(z \in \mathbb {C}\),

$$\begin{aligned} \Phi _{\xi }^{u_k}(z)&= \prod _{\begin{array}{c} 1 \le j \le N, \\ j \not = k \end{array}} \frac{z-u_j}{u_k-u_j}, \quad 1 \le k \le N. \end{aligned}$$
(1.15)

The function \(\Phi _{\xi }^{u_k}(z)\) is a polynomial of \(z\) with degree \(N-1\) having zeros at \(u_j, 1 \le j \le N, j \not =k\) and \(\Phi _{\xi }^{u_k}(u_k)=1\). We can prove that (Lemma 2.3), for each \(1 \le k \le N\),

$$\begin{aligned} \mathcal{M}_{\xi }^{u_k}(t, S_j(t)) \equiv \widetilde{\mathrm{E}} \Big [ \Phi _{\xi }^{u_k}(Z_j(t)) \Big ], \quad 1 \le j \le N \end{aligned}$$
(1.16)

provide independent martingales with discrete time \(t \in \mathbb {N}_0\). We consider a determinant of matrix, whose entries are these martingales,

$$\begin{aligned} \mathcal{D}_{\xi }(t,{\varvec{S}}(t)) =\det _{1 \le j, k \le N} [\mathcal{M}_{\xi }^{u_k}(t, S_j(t))], \quad t \in \mathbb {N}_0, \end{aligned}$$
(1.17)

which we call the determinantal martingale [24]. Our martingales (1.16) are prepared so that the equality

$$\begin{aligned} \frac{h({\varvec{S}}(t))}{h({\varvec{u}})} =\mathcal{D}_{\xi }(t, {\varvec{S}}(t)), \quad t \in \mathbb {N}_0, \end{aligned}$$
(1.18)

holds and a kind of reducibility (Lemma 2.4) is established.

This equality (1.18) gives a determinantal-martingale representation (DMR) for the noncolliding RW (Proposition 3.1), and from it we can prove that the noncolliding RW is determinantal with the correlation kernel,

$$\begin{aligned} \mathbb {K}_{\xi }(s,x;t,y) = \left\{ \begin{array}{l} \displaystyle { \sum _{j=1}^N p(s, x|u_j) \mathcal{M}_{\xi }^{u_j}(t,y) - \mathbf{1}(s>t) p(s-t,x|y), } \\ \qquad \quad \,\,\, \hbox {if} \quad (s,x), (t,y) \in \mathbb {N}_0 \times \mathbb {Z}, \quad s+x, t+y \in \mathbb {Z}_\mathrm{e}, \\ 0, \qquad \,\,\, \hbox {otherwise}, \end{array} \right. \end{aligned}$$
(1.19)

where \(p\) is the transition probability (1.3), and \(\mathbf{1}(\cdot )\) is an indicator; \(\mathbf{1}(\omega )=1\) if \(\omega \) is satisfied, and \(\mathbf{1}(\omega )=0\) otherwise (Theorem 3.2). Note again that

$$\begin{aligned} \mathcal{M}_{\xi }^{u_j}(t,y)&= \widetilde{\mathrm{E}} \left[ \Phi _{\xi }^{u_j}(y+i \widetilde{S}(t)) \right] \nonumber \\&= \int _{\mathbb {R}} dv \, \widetilde{p}(t, v|0) \Phi _{\xi }^{u_j}(y+i v), \quad 1 \le j \le N \end{aligned}$$
(1.20)

with (1.13), are functions of initial configuration \(\xi =\sum _{j=1}^N \delta _{u_j}\) through (1.15).

For \(a \in \{2,3, \ldots \}\), we consider a configuration on \(\mathbb {Z}_\mathrm{e}\) having equidistant spacing \(2a\) with an infinite number of particles,

$$\begin{aligned} \delta _{2a \mathbb {Z}}(\cdot ) \equiv \sum _{k \in \mathbb {Z}} \delta _{2a k} (\cdot ). \end{aligned}$$
(1.21)

(The noncolliding RW starting from \(\delta _{2 \mathbb {Z}}(\cdot )\), that is, the case \(a=1\) of (1.21), is trivial. The process is stationary in the sense that \(\Xi (2n)= \sum _{k \in \mathbb {Z}} \delta _{2k}\), \(\Xi (2n+1)= \sum _{k \in \mathbb {Z}} \delta _{2k+1}\), \(n \in \mathbb {N}_0\).) We prove that the noncolliding RW started at (1.21), denoted as \((\Xi (t), t \in \mathbb {N}_0, {\mathbb P}_{\delta _{2a \mathbb {Z}}})\), \(a \in \{2,3, \ldots \}\), is well-defined as a determinantal process with an infinite number of particles (Proposition 4.1). There the \(N\) linearly independent polynomials of \(y\) given by (1.20) are extended to an infinite sequence of linearly independent entire functions of \(y\), \(\mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2ak}(t,y), k \in \mathbb {Z}\), corresponding to the infinite-particle initial configuration (1.21). Then by using the infinite sequence of independent martingales with discrete time, \((\mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2ak}(t, S_j(t)))_{t \in \mathbb {N}_0}, k \in \mathbb {Z}\), for each \(j \in \mathbb {Z}\), we can give DMRs for \((\Xi (t), t \in \mathbb {N}_0, {\mathbb P}_{\delta _{2 a \mathbb {Z}}})\), \(a \in \{2,3, \ldots \}\) (Proposition 4.2). For each \(a \in \{2,3, \ldots \}\), this discrete-time infinite-particle system on \(\mathbb {Z}\) shows a relaxation phenomenon to the equilibrium determinantal process, \((\Xi (t), t \in \mathbb {Z}, \mathbf{P}_{\rho }\)), whose correlation kernel is given by

$$\begin{aligned} \mathbf{K}_{\rho }(t-s, y-x) = \left\{ \begin{array}{ll} \displaystyle {\int _0^{\rho } d u \, \frac{2 \cos (\pi u(y-x))}{[\cos (\pi u)]^{t-s}}}, \quad &{} \hbox {if}\; s<t, \\ &{} \\ \displaystyle {\frac{2 \sin (\pi \rho (y-x))}{\pi (y-x)}}, \quad &{} \text{ if } \;s=t, \\ &{} \\ \displaystyle {-\int _{\rho }^{1} d u \, \frac{2 \cos (\pi u(y-x))}{[\cos (\pi u)]^{t-s}}}, \quad &{} \text{ if }\; s>t, \end{array} \right. \end{aligned}$$
(1.22)

for \((s,x), (t,y) \in \mathbb {Z}^2\), \(s+x, t+y \in \mathbb {Z}_\mathrm{e}\), and \(\mathbf{K}_{\rho }(t-s, y-x)=0\) otherwise, where \(\rho =1/2a\) gives the particle density on \(\mathbb {Z}\) (Theorem 4.4). This is a discrete analogue of the extended sine-kernel (see Sect.  11.7.1 in [15]) of the Dyson model (1.9).

We note that independent increments \(\zeta _j(t)\) of \(S_j(t)\) and \(\widetilde{\zeta }_j(t)\) of \(\widetilde{S}_j(t)\), \(1 \le j \le N, t \in \mathbb {N}_0\) are both having mean zero and variance 1. Then Donsker’s invariance principle [5, 46] proves both of \(S_j(n^2 t)/n\) and \(\widetilde{S}_j(n^2 t)/n\) converge to BMs as \(n \rightarrow \infty \). It implies that the DMRs for appropriately scaled noncolliding RWs converge to the complex BM representation for the Dyson model (1.9) given by [33]. The central limit theorem of noncolliding RWs to the Dyson model will be established.

The paper is organized as follows. In Sect. 2 the polynomial martingales and determinantal martingales are introduced for noncolliding RW and their properties are discussed. Determinantal properties of noncolliding RW is clarified in Sect. 3. An extension to infinite particle systems is discussed in Sect. 4. Convergence of noncolliding RWs to the Dyson model is discussed in Sect. 5.

2 Preliminaries

2.1 Discrete Itô’s Formula and Polynomial Martingales of Fujita

Let \(S(t), t \in \mathbb {N}_0\) be a one-dimensional, simple and symmetric RW starting from 0 at time \(t=0\),

$$\begin{aligned} S(t)=\zeta (1)+\zeta (2)+ \cdots + \zeta (t), \quad t \in \mathbb {N}, \end{aligned}$$

where \(\{\zeta (t) : t \in \mathbb {N}\}\) are i.i.d.obeying the same probability law with \(\zeta \). The following discrete Itô’s formula was given by Fujita for the one-dimensional, simple and symmetric RW [16, 17].

Lemma 2.1

For any \(f: \mathbb {N}_0 \times \mathbb {Z}\rightarrow \mathbb {R}\) and any \(t \in \mathbb {N}_0\),

$$\begin{aligned}&f(t+1,S(t+1))-f(t,S(t))\nonumber \\&\qquad = \frac{1}{2} \Big [ f(t+1, S(t)+1)-f(t+1, S(t)-1) \Big ] \zeta (t+1)\nonumber \\&\quad \qquad +\, \frac{1}{2} \Big [ f(t\!+\!1, S(t)\!+\!1)\!-\! 2 f(t\!+\!1, S(t))\!+\! f(t\!+\!1, S(t)\!-\!1) \Big ]\nonumber \\&\quad \qquad +\,f(t+1, S(t))-f(t, S(t)). \end{aligned}$$
(2.1)

We perform the Esscher transform with parameter \(\alpha \in \mathbb {R}\), \(S(\cdot ) \rightarrow \widehat{S}_{\alpha }(\cdot )\) as

$$\begin{aligned} \widehat{S}_{\alpha }(t) =\frac{e^{\alpha S(t)}}{\mathrm{E}[e^{\alpha S(t)}]}, \quad t \in \mathbb {N}_0. \end{aligned}$$
(2.2)

By (1.2), we have \( \widehat{S}_{\alpha }(t)= G_{\alpha }(t, S(t)) \) with

$$\begin{aligned} G_{\alpha }(t,x)=\frac{e^{\alpha x}}{(\cosh \alpha )^t}, \quad t \in \mathbb {N}_0, \quad x \in \mathbb {Z}. \end{aligned}$$
(2.3)

If we set \(f=G_{\alpha }\) in (2.1), the second and third terms in the RHS vanish. Then

$$\begin{aligned} G_{\alpha }(t\!+\!1, S(t\!+\!1))-G_{\alpha }(t,S(t))= \frac{1}{2} \Big [G_{\alpha }(t\!+\!1, S(t)\!+\!1) - G_{\alpha }(t\!+\!1, S(t)\!-\!1) \Big ]\zeta (t+1), \end{aligned}$$

which implies that \(G_{\alpha }(t, S(t))\) is \(\{\zeta (1), \ldots , \zeta (t)\}\)-martingale for any \(\alpha \in \mathbb {R}\) [16, 17]. From now on, we simply say ‘\((G_{\alpha }(t, S(t)))_{t \in \mathbb {N}_0}\) is a martingale’ in such a situation.

Expansion of (2.3) with respect to \(\alpha \) around \(\alpha =0\),

$$\begin{aligned} G_{\alpha }(t,x)=\sum _{n=0}^{\infty } m_n(t,x) \frac{\alpha ^n}{n!}, \end{aligned}$$
(2.4)

determines a series of monic polynomials of degrees \(n\) studied by Fujita in [16]

$$\begin{aligned} m_n(t,x)=x^n + \sum _{j=1}^{n-1} c_n^{(j)}(t) x^j, \quad n \in \mathbb {N}_0, \end{aligned}$$
(2.5)

such that

$$\begin{aligned}&c_n^{(j)}(0)=0, \quad 1 \le j \le n-1,\end{aligned}$$
(2.6)
$$\begin{aligned}&m_n(t, S(t)) \,\,\text{ is } \text{ martingale }, \quad t \in \mathbb {N}_0. \end{aligned}$$
(2.7)

For example,

$$\begin{aligned} m_0(t,x)&= 1, \nonumber \\ m_1(t,x)&= x, \nonumber \\ m_2(t,x)&= x^2-t, \nonumber \\ m_3(t,x)&= x^3-3 t x, \nonumber \\ m_4(t,x)&= x^4-6 t x^2+t (3t+2),\nonumber \\ m_5(t,x)&= x^5-10 t x^3 + 5 t (3t+2) x,\ldots . \end{aligned}$$
(2.8)

They satisfy the recurrence relations

$$\begin{aligned} m_n(t,x)=\frac{1}{2} [ m_n(t+1,x+1)+m_n(t+1,x-1) ], \quad n \in \mathbb {N}_0. \end{aligned}$$

As mentioned below in Remark 2, \(m_n(t, x), n \in \mathbb {N}_0\) are related with the Euler polynomials studied in [48]. Since the importance of \(m_n(t, x), n \in \mathbb {N}_0\) in the context of random walks was first clearly shown by Fujita [16], however, we would like to call \(m_n(t,x), n \in \mathbb {N}\), Fujita’s polynomials and \((m_n(t,S(t)))_{t \in \mathbb {N}_0}, n \in \mathbb {N}_0\), Fujita’s polynomial martingales for the simple and symmetric RW.

Remark 1

Let \(B(t), t \ge 0\) be BM started at 0. Then its Esscher transform with parameter \(\alpha \) is given by \( \widehat{B}_{\alpha }(t) = G^\mathrm{BM}_{\alpha }(t,B(t)) \) with

$$\begin{aligned} G^\mathrm{BM}_{\alpha }(t,x) = \frac{e^{\alpha x}}{\mathrm{E}[e^{\alpha B(t)}]} =\frac{e^{\alpha x}}{\displaystyle { \int _{-\infty }^{\infty } dx e^{\alpha x} p^\mathrm{BM}(t, x|0)}} = e^{\alpha x - \alpha ^2 t/2}, \end{aligned}$$

where

$$\begin{aligned} p^\mathrm{BM}(t,y|x) =\frac{1}{\sqrt{2 \pi t}} e^{-(y-x)^2/2t}, \quad t \ge 0, \quad x, y \in \mathbb {R} \end{aligned}$$
(2.9)

is the transition probability density of BM. We see that

$$\begin{aligned} G^\mathrm{BM}_{\alpha }(t,x) =\sum _{n=0}^{\infty } \left( \frac{t}{2} \right) ^{n/2} H_n \left( \frac{x}{\sqrt{2t}}\right) \frac{\alpha ^n}{n!} \end{aligned}$$

with the Hermite polynomials \(\displaystyle { H_n(z)= \sum _{j=0}^{[n/2]} (-1)^j \frac{n !}{j ! (n-2j)!} (2z)^{n-2j}, n \in \mathbb {N}_0. }\) Therefore,

$$\begin{aligned} m_n^\mathrm{BM}(t, B(t)) =\left( \frac{t}{2} \right) ^{n/2} H_n \left( \frac{B(t)}{\sqrt{2t}} \right) , \quad n \in \mathbb {N}_0, \quad t \ge 0, \end{aligned}$$
(2.10)

are the polynomial martingales for BM as known well (see, for instance, [48]).

Remark 2

The polynomials (2.10) for BM have the multiple stochastic-integral representations,

$$\begin{aligned} m_n^\mathrm{BM}(t, B(t)) = n! \int _0^t \int _0^{t_1} \cdots \int _0^{t_{n-1}} dB(t_n) \cdots d B(t_2) d B(t_1), \quad n \in \mathbb {N}. \end{aligned}$$

Their discrete analogues determine the polynomial martingales for RW,

$$\begin{aligned} \widehat{m}_n(t, S(t)) = n! \sum _{t_1=1}^{t} \sum _{t_2=1}^{t_1} \cdots \sum _{t_n=1}^{t_{n-1}} \zeta (t_1) \zeta (t_2) \cdots \zeta (t_n). \end{aligned}$$

For \(N \in \mathbb {N}_0\), \(0 < p < 1\), the monic Krawtchouk polynomials \(\tilde{K}_n(x;N,p), n \in \mathbb {N}_0\) are defined by the generating function as

$$\begin{aligned} \sum _{n=0}^{N} \tilde{K}_n(x;N,p) \frac{\alpha ^n}{n!} =(1+(1-p) \alpha )^{x}(1-p \alpha )^{N-x}. \end{aligned}$$

Then [45, 48]

$$\begin{aligned} \widehat{m}_n(t,x)=2^n \tilde{K}_n((t+x)/2; t, 1/2), \quad n \in \mathbb {N}_0. \end{aligned}$$

It should be noted that \(\widehat{m}_n(t,x), n \in \mathbb {N}_0\) are generally different from Fujita’s polynomials \(m_n(t,x), n \in \mathbb {N}_0\). We see that \(\widehat{m}_0(t,x)=1\), \(\widehat{m}_1(t,x)=x\), \(\widehat{m}_2(t,x)=x^2-t\), and \(\widehat{m}_3(t,x)=x(x^2+2)-3tx\), \(\widehat{m}_4(t,x)=x^2(x^2+8)-6tx^2+3t(t-2), \ldots \). In general, the Krawtchouk polynomials do not satisfy the condition (2.6). The monic polynomials of order \(n\), \(E_n^{(\lambda )}(x)\) with parameter \(\lambda \in \mathbb {N}_0\) defined by the generating function

$$\begin{aligned} \sum _{n=0}^{\infty } E_n^{(\lambda )}(x) \frac{\alpha ^n}{n!} =\left( \frac{2}{1+e^{\alpha }} \right) ^{\lambda } e^{\alpha x} \end{aligned}$$
(2.11)

are called the Euler polynomials (see [9, p. 253 ]). Schoutens showed that, if \(\bar{\zeta }_j, j \in \mathbb {N}\) have a binomial distribution \(\mathsf{Bin}(\lambda , 1/2)\) and \(\bar{S}(t) \equiv \sum _{j=1}^t \bar{\zeta }_j, t \in \mathbb {N}\) with \(\bar{S}(0) \equiv 0\), then \((E_n^{(t \lambda )}(\bar{S}(t)))_{t \in \mathbb {N}_0}, n \in \mathbb {N}_0\) are martingales [48]. Fujita’s polynomials are related with Euler’s by

$$\begin{aligned} m_n(t, x)=2^n E_n^{(t)} \left( \frac{t+x}{2} \right) \!, \quad n \in \mathbb {N}_0. \end{aligned}$$
(2.12)

2.2 Complex-Process Representation for Polynomial Martingales

For RW, \((S(t))_{t \in \mathbb {N}_0}\), we consider its complexification,

$$\begin{aligned} Z(t)=S(t)+i \widetilde{S}(t), \quad t \in \mathbb {N}_0, \end{aligned}$$
(2.13)

where \(\widetilde{S}(\cdot )\) is defined by (1.12) with \(\widetilde{S}(0) \equiv 0\). Note that \(\mathfrak {R}Z(t)=S(t) \in \mathbb {Z}\) and \(\mathfrak {I}Z(t)=\widetilde{S}(t) \in \mathbb {R}, t \in \mathbb {N}_0\). We can prove the following.

Lemma 2.2

With the complex process (2.13), Fujita’s polynomial martingales with discrete time \(t \in \mathbb {N}_0\), \((m_n(t,S(t)))_{t \in \mathbb {N}_0}\), \(n \in \mathbb {N}_0\), for the simple and symmetric RW have the following representations,

$$\begin{aligned} m_n(t, S(t)) = \widetilde{\mathrm{E}} [ Z(t)^n ], \quad n \in \mathbb {N}_0, \quad t \in \mathbb {N}_0. \end{aligned}$$
(2.14)

Proof

By definition (1.12) of \(\widetilde{S}(t)\), (1.11) gives

$$\begin{aligned} \widetilde{\mathrm{E}} \left[ e^{i \alpha \widetilde{S}(t)} \right] =\left( \widetilde{\mathrm{E}} \left[ e^{i \alpha \widetilde{\zeta }} \right] \right) ^t =\frac{1}{(\cosh \alpha )^t}, \quad \alpha \in \mathbb {R}, \quad t \in N_0. \end{aligned}$$
(2.15)

Then for (2.3), the equality \( G_{\alpha }(t, S(t)) = \widetilde{\mathrm{E}}[e^{\alpha Z(t)}], \alpha \in \mathbb {R}\) is established, which proves (2.14). \(\square \)

Remark 3

For a pair of independent BMs, \(B(t), \widetilde{B}(t), t \ge 0\), we can see

$$\begin{aligned} \mathrm{E}[e^{\alpha B(t)}] = e^{\alpha ^2 t/2} =\left( \widetilde{\mathrm{E}} \left[ e^{i \alpha \widetilde{B}(t)} \right] \right) ^{-1}, \quad \alpha \in \mathbb {R}. \end{aligned}$$
(2.16)

Then \( m_n^\mathrm{BM}(t, B(t))=\widetilde{\mathrm{E}} [\mathcal{B}(t)^n], n \in \mathbb {N}_0,t \ge 0, \) is concluded, where \(\mathcal{B}(t)\) is a complex BM, \(\mathcal{B}(t)=B(t)+i \widetilde{B}(t), t \ge 0\). The reciprocity relations between (1.2) and (1.11), and \(\mathrm{E}[e^{\alpha S(t)}]=(\cosh \alpha )^t\) and (2.15) are discrete-time analogues of (2.16).

A direct consequence of Lemma 2.2 is the following.

Lemma 2.3

Assume that \(f\) is polynomial. Then \(\widetilde{\mathrm{E}}[f(Z(t))]\) is a martingale with discrete time \(t \in \mathbb {N}_0\).

2.3 Determinantal Martingales

We consider an \(N\)-component complex process \({\varvec{Z}}(t)=(Z_1(t), \ldots , Z_N(t)), t \in \mathbb {N}_0\) with (1.14). The probability space for (1.14) is a product of the probability space \((\Omega , \mathcal{F}, \mathrm{P}_{{\varvec{u}}})\) for the RW on \(\mathbb {Z}^N\), \({\varvec{S}}(t), t \in \mathbb {N}_0\), and \((\widetilde{\Omega }, \widetilde{\mathcal{F}}, \widetilde{\mathrm{P}})\) for \(\widetilde{{\varvec{S}}}(t), t \in \mathbb {N}_0\) defined on \(\mathbb {R}^N\), which we write as \((\check{\Omega }, \check{\mathcal{F}}, \mathbf{P}_{{\varvec{u}}})\). Let \(\mathbf{E}_{{\varvec{u}}}\) be the expectation for the process \({\varvec{Z}}(t), t \in \mathbb {N}_0\) with the initial condition \({\varvec{Z}}(0)={\varvec{u}}\in \mathbb {Z}_\mathrm{e}^N \cap \mathbb {W}_N\).

By multilinearity of determinant, the Vandermonde determinant (1.7) does not change in replacing \(x_j^{k-1}\) by any monic polynomial of \(x_j\) of degree \(k-1\), \(1 \le j, k \le N\). Note that \(m_{k-1}(t,x_j)\) is a monic polynomial of \(x_j\) of degree \(k-1\). Then

$$\begin{aligned} \frac{h({\varvec{S}}(t))}{h({\varvec{u}})}&= \frac{1}{h({\varvec{u}})} \det _{1 \le j, k \le N} [m_{k-1}(t, S_j(t))]\\&= \frac{1}{h({\varvec{u}})} \det _{1 \le j, k \le N}\Big [ \widetilde{\mathrm{E}} [Z_j(t)^{k-1} ] \Big ]\\&= \widetilde{\mathrm{E}} \left[ \frac{1}{h({\varvec{u}})}\det _{1 \le j, k \le N}[Z_j(t)^{k-1}] \right] \!, \end{aligned}$$

where we have used Lemma 2.2, the multilinearity of determinant, and independence of \(Z_j(t)\)’s. Therefore, we have obtained the equality,

$$\begin{aligned} \frac{h({\varvec{S}}(t))}{h({\varvec{u}})} = \widetilde{\mathrm{E}} \left[ \frac{h({\varvec{Z}}(t))}{h({\varvec{u}})} \right] , \quad t \in \mathbb {N}_0. \end{aligned}$$
(2.17)

Now we consider the determinant identity [33],

$$\begin{aligned} \frac{h({\varvec{z}})}{h({\varvec{u}})} =\det _{1 \le j, k \le N} \Big [ \Phi _{\xi }^{u_k}(z_j) \Big ], \end{aligned}$$
(2.18)

where \(\xi =\sum _{j=1}^N \delta _{u_j}, {\varvec{u}}=(u_1, \ldots , u_N) \in \mathbb {W}_N\), and \(\Phi _{\xi }^{u_k}(z)\) is given by (1.15) (see Sect. 4.1 in [24] for derivation). Since \(\Phi _{\xi }^{u_k}(z)\) is a polynomial of \(z\) of degree \(N-1\), Lemma 2.3 proves that \((\mathcal{M}_{\xi }^{u_k}(t, S_j(t)))_{t \in \mathbb {N}_0}, 1 \le j \le N\), defined by (1.16) are independent martingales with discrete time \(t \in \mathbb {N}_0\) and

$$\begin{aligned} \mathrm{E}_{{\varvec{u}}}[\mathcal{M}_{\xi }^{u_k}(t, S_j(t))]&= \mathrm{E}_{{\varvec{u}}}[\mathcal{M}_{\xi }^{u_k}(0, S_j(0))]\nonumber \\&= \mathcal{M}_{\xi }^{u_k}(0, u_j) \nonumber \\&= \Phi _{\xi }^{u_k}(u_j)=\delta _{jk},\quad 1 \le j, k \le N. \end{aligned}$$
(2.19)

Using the identity (2.18) for \(h({\varvec{Z}}(t))/h({\varvec{u}})\) in (2.17), we have

$$\begin{aligned} \frac{h({\varvec{S}}(t))}{h({\varvec{u}})}&= \widetilde{\mathrm{E}} \left[ \det _{1 \le j, k \le N}[ \Phi _{\xi }^{u_k}(Z_j(t)) ] \right] \\&= \det _{1 \le j, k \le N} \Big [\widetilde{\mathrm{E}} [ \Phi _{\xi }^{u_k}(Z_j(t)) ] \Big ], \end{aligned}$$

where independence of \(Z_j(t)\)’s was again used. By definition (1.17) of \(\mathcal{D}_{\xi }\) with (1.16), we obtain the equality (1.18).

Remark 4

The real parts of the complex processes (1.14) are RWs with \(\mathrm{E}_{{\varvec{u}}}[(S_j(t)-u_j)^2]=t \in \mathbb {N}_0, 1 \le j \le N\). It is obvious from definition (1.12) that the imaginary parts, \(\widetilde{S}_j(t), t \in \mathbb {N}_0\), are \(\{\widetilde{\zeta }_j(1), \ldots , \widetilde{\zeta }_j(t) \}\)-martingales with \(\widetilde{\mathrm{E}}[\widetilde{S}_j(t)^2]=t \in \mathbb {N}_0,1 \le j \le N\). Then \(Z_j(\cdot ), 1 \le j \le N\) shall be regarded as discrete-time conformal martingales (see Definition (2.2) in Sect. V.2 of [46]). Their conformal maps by polynomial functions, \(\Phi _{\xi }^{u_k}(Z_j(\cdot )), 1 \le j, k \le N\) are discrete-time complex martingales such that

$$\begin{aligned} \mathbf{E}_{{\varvec{u}}} [\Phi _{\xi }^{u_k}(Z_j(t))] =\mathbf{E}_{{\varvec{u}}}[\Phi _{\xi }^{u_k}(Z_j(0))] =\delta _{j k}, \quad 1 \le j, k \le N \end{aligned}$$
(2.20)

for any \(t \in \mathbb {N}_0\),

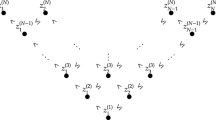
For \(n \in \mathbb {N}\), let \(\mathbb {I}_{n} = \{1,2, \ldots , n\}\). Denote the cardinality of a finite set \(A\) by \(|A|\). Let \({\varvec{x}}=(x_1, \ldots , x_N) \in \mathbb {Z}^N\) and \(1 \le N' \le N\). We write \(\mathbb {J}\subset \mathbb {I}_N, |\mathbb {J}|=N'\), if \(\mathbb {J}=\{j_1, \ldots , j_{N'}\}, 1 \le j_1 < \dots < j_{N'} \le N\), and put \({\varvec{x}}_{\mathbb {J}}=(x_{j_1}, \ldots , x_{j_{N'}})\). In particular, we write \({\varvec{x}}_{N'}={\varvec{x}}_{\mathbb {I}_{N'}}, 1 \le N' \le N\). (By definition \({\varvec{x}}_N={\varvec{x}}\).) Suppose \({\varvec{u}}\in \mathbb {Z}_\mathrm{e}^N \cap \mathbb {W}_N\) and \(\xi (\cdot )=\sum _{j=1}^N \delta _{u_j}(\cdot )\). For \(\mathbb {J}\subset \mathbb {I}_N, |\mathbb {J}|=N', 1 \le N' \le N\), introduce determinantal martingales

$$\begin{aligned} \mathcal{D}_{\xi }(t, {\varvec{S}}_{\mathbb {J}}(t)) =\det _{j,k \in \mathbb {J}} \Big [ \mathcal{M}_{\xi }^{u_k}(t, S_j(t)) \Big ], \quad t \in \mathbb {N}_0, \end{aligned}$$
(2.21)

where the sizes of matrices for determinants are \(|\mathbb {J}|=N', 1 \le N' \le N\). We can prove the following, which is a discrete-time version of Lemma 2.1 in [24].

Lemma 2.4

Assume that \(\xi (\cdot )=\sum _{j=1}^N \delta _{u_j}(\cdot )\) with \({\varvec{u}}\in \mathbb {Z}_\mathrm{e}^N \cap \mathbb {W}_N\). Let \(1 \le N' < N\). For \(t \in \mathbb {N}, t \le T \in \mathbb {N}\) and a symmetric bounded function \(F_{N'}\) on \(\mathbb {Z}^{N'}\),

$$\begin{aligned}&\sum _{\mathbb {J}\subset \mathbb {I}_N, |\mathbb {J}|=N'}\mathrm{E}_{{\varvec{u}}} \left[ F_{N'}({\varvec{S}}_{\mathbb {J}}(t))\mathcal{D}_{\xi }(T, {\varvec{S}}(t)) \right] \nonumber \\&\quad = \int _{\mathbb {W}_{N'}} \xi ^{\otimes N'} (d{\varvec{v}})\mathrm{E}_{{\varvec{v}}} \left[ F_{N'}({\varvec{S}}_{N'}(t)) \mathcal{D}_{\xi }(T, {\varvec{S}}_{N'}(T)) \right] . \end{aligned}$$
(2.22)

This shows the reducibility of the determinantal martingale in the sense that, if we observe a symmetric function \(F_{N'}\) depending on only \(N'\) variables, \(N' < N\), then the size of determinant for determinantal martingale can be reduced from \(N\) to \(N'\).

3 Determinantal Properties

3.1 Determinantal Martingale Representation

Since we consider the noncolliding RW as a process represented by an unlabeled configuration (1.4), measurable functions of \(\Xi (\cdot )\) are only symmetric functions of \(N\) variables, \(S^0_j(\cdot ), 1 \le j \le N\). Then by the equality (1.18), we obtain the following representation. We call it the DMR for the present noncolliding RW.

Proposition 3.1

Suppose that \(N \in \mathbb {N}\) and \(\xi =\sum _{j=1}^{N} \delta _{u_j}\) with \({\varvec{u}}=(u_1, \ldots , u_N) \in \mathbb {Z}_\mathrm{e}^N \cap \mathbb {W}_N\). Let \(t \in \mathbb {N}, t \le T \in \mathbb {N}\). For any \(\mathcal{F}(t)\)-measurable bounded function \(F\) we have

$$\begin{aligned} {\mathbb E}_{\xi } \left[ F \left( \Xi (\cdot ) \right) \right]&= \mathrm{E}_{{\varvec{u}}} \left[ F \left( \sum _{j=1}^{N} \delta _{S_j(\cdot )} \right) \mathcal{D}_{\xi }( T, {\varvec{S}}(T)) \right] \nonumber \\&= \mathbf{E}_{{\varvec{u}}} \left[ F \left( \sum _{j=1}^{N} \delta _{\mathfrak {R}Z_j(\cdot )} \right) \det _{1 \le j, k \le N} [\Phi _{\xi }^{u_k}(Z_j(T))] \right] \!. \end{aligned}$$
(3.1)

Note that the second representation of (3.1) is a discrete-time analogue of the complex BM representation reported in [33] for the Dyson model (i.e. the noncolliding BM). See Remark 4 above again.

Proof of Proposition

3.1. It is sufficient to consider the case that \(F\) is given as \(F(\Xi (\cdot )) = \prod _{m=1}^M g_m({\varvec{S}}^0(t_m))\) for \(M \in \mathbb {N}\), \(t_m \in \mathbb {N}, 1 \le m \le M\), \(t_1< \cdots <t_M \le T \in \mathbb {N}\), with symmetric bounded functions \(g_m\) on \(\mathbb {Z}^N\), \(1 \le m \le M\). Here we prove the equalities

$$\begin{aligned} {\mathbb E}_{\xi }\left[ \prod _{m=1}^M g_m({\varvec{S}}^0(t_m)) \right]&= \mathrm{E}_{{\varvec{u}}} \left[ \prod _{m=1}^M g_m({\varvec{S}}(t_m)) \mathcal{D}_{\xi }( T, {\varvec{S}}(T)) \right] \nonumber \\&= \mathbf{E}_{{\varvec{u}}} \left[ \prod _{m=1}^M g_m({\varvec{S}}(t_m))\det _{1 \le j, k \le N} [\Phi _{\xi }^{u_k}(Z_j(T))] \right] . \end{aligned}$$
(3.2)

By (1.8), the LHS of (3.2) is given by

$$\begin{aligned} \mathrm{E}_{{\varvec{u}}} \left[ \prod _{m=1}^M g_m({\varvec{S}}(t_m)) \mathbf{1}(\tau _{{\varvec{u}}} > t_M) \frac{h({\varvec{S}}(t_M))}{h({\varvec{u}})} \right] , \end{aligned}$$
(3.3)

where we used the fact that \(h({\varvec{S}}(\cdot ))/h({\varvec{u}})\) is martingale. At time \(t=\tau _{{\varvec{u}}}\), there are at least one pair \((j, j+1)\) such that \(S_j(\tau _{{\varvec{u}}})=S_{j+1}(\tau _{{\varvec{u}}}), 1 \le j \le N-1\). We choose the minimal \(j\). Let \(\sigma _{j, j+1}\) be the permutation of the indices \(j\) and \(j+1\) and for \({\varvec{v}}=(v_1, \ldots , v_N) \in \mathbb {Z}^N\) we put \(\sigma _{j,j+1}({\varvec{v}})=(v_{\sigma _{j,j+1}(k)})_{k=1}^N =(v_1, \ldots , v_{j+1}, v_j, \ldots , v_N)\). Let \({\varvec{u}}'\) be the labeled configuration of the process at time \(t=\tau _{{\varvec{u}}}\). Since \(u'_j=u'_{j+1}\) by the above setting, under the probability law \(\mathrm{P}_{{\varvec{u}}'}\) the processes \({\varvec{S}}(t), t > \tau _{{\varvec{u}}}\) and \(\sigma _{j,j+1}({\varvec{S}}(t)), t > \tau _{{\varvec{u}}}\) are identical in distribution. Since \(g_m, 1 \le m \le M\) are symmetric, but \(h\) is antisymmetric, the Markov property of the process \({\varvec{S}}(\cdot )\) gives

$$\begin{aligned} \mathrm{E}_{{\varvec{u}}} \left[ \prod _{m=1}^M g_m({\varvec{S}}(t_m)) \mathbf{1}(\tau _{{\varvec{u}}} \le t_M) \frac{h({\varvec{S}}(t_M))}{h({\varvec{u}})} \right] =0. \end{aligned}$$

Therefore, (3.3) is equal to

$$\begin{aligned} \mathrm{E}_{{\varvec{u}}} \left[ \prod _{m=1}^M g_m({\varvec{S}}(t_m)) \frac{h({\varvec{S}}(t_M))}{h({\varvec{u}})} \right] \!. \end{aligned}$$

By the equality (1.18) and the martingale property of \((\mathcal{D}_{\xi }(t, {\varvec{S}}(t)))_{t \in \mathbb {N}_0}\), we obtain the first line of (3.2). By definitions of \(\mathbf{E}_{{\varvec{u}}}\) and \(\mathcal{D}_{\xi }\), the second line is valid. Then the proof is completed. \(\square \)

3.2 Determinantal Process

For any integer \(M \in \mathbb {N}\), a sequence of times \({\varvec{t}}=(t_1,\ldots ,t_M) \in \mathbb {N}^M\) with \(t_1 < \cdots < t_M \le T \in \mathbb {N}\), and a sequence of bounded functions \({\varvec{f}}=(f_{t_1},\ldots ,f_{t_M})\), the moment generating function of multitime distribution of the process \(\Xi (\cdot )\) is defined by

$$\begin{aligned} \Psi _{\xi }^{{\varvec{t}}}[{\varvec{f}}] \equiv {\mathbb E}_{\xi } \left[ \exp \left\{ \sum _{m=1}^{M} \int _{\mathbb {Z}} f_{t_m}(x) \Xi (t_m, dx) \right\} \right] \!. \end{aligned}$$
(3.4)

It is expanded with respect to

$$\begin{aligned} \chi _{t_m}(\cdot )=e^{f_{t_m}(\cdot )}-1, \quad 1 \le m \le M \end{aligned}$$
(3.5)

as

$$\begin{aligned} \Psi _{\xi }^{{\varvec{t}}}[{\varvec{f}}] =\sum _ {\begin{array}{c} N_m \ge 0, \\ 1 \le m \le M \end{array} } \sum _ {\begin{array}{c} {\varvec{x}}^{(m)}_{N_m} \in \mathbb {Z}^{N_m} \cap \mathbb {W}_{N_m},\\ 1 \le m \le M \end{array} } \prod _{m=1}^{M} \prod _{j=1}^{N_{m}} \chi _{t_m} \Big (x_{j}^{(m)} \Big ) \rho _{\xi } \Big ( t_{1}, {\varvec{x}}^{(1)}_{N_1}; \ldots ; t_{M}, {\varvec{x}}^{(M)}_{N_M} \Big ), \end{aligned}$$
(3.6)

where \({\varvec{x}}^{(m)}_{N_m}\) denotes \((x^{(m)}_1, \ldots , x^{(m)}_{N_m})\), and (3.6) defines the spatio-temporal correlation functions \(\rho _{\xi }(\cdot )\) for the process \((\Xi (t), t \in \mathbb {N}_0, {\mathbb P}_{\xi })\). Given an integral kernel

$$\begin{aligned} \mathbf{K}(s,x;t,y); \quad (s,x), (t,y) \in \mathbb {N}_0 \times \mathbb {Z}, \end{aligned}$$

the Fredholm determinant is defined as

$$\begin{aligned}&\mathop {\mathrm{Det}}_{\begin{array}{c} (s,t)\in \{t_1, \ldots , t_M\}, \\ (x,y)\in \mathbb {Z}^2 \end{array}} \Big [\delta _{st} \delta _x(\{y\})+ \mathbf{K}(s,x;t,y) \chi _{t}(y) \Big ]\nonumber \\&\quad =\sum _{\begin{array}{c} N_m \ge 0, \\ 1 \le m \le M \end{array} } \sum _{\begin{array}{c} {\varvec{x}}^{(m)}_{N_m} \in \mathbb {Z}^{N_m} \cap \mathbb {W}_{N_m},\\ 1 \le m \le M \end{array} }\prod _{m=1}^{M}\prod _{j=1}^{N_{m}} \chi _{t_m} \Big (x_{j}^{(m)} \Big )\det _{\begin{array}{c} 1 \le j \le N_{m}, 1 \le k \le N_{n}, \\ 1 \le m, n \le M \end{array}}\left[ \mathbf{K}\left( t_m, x_{j}^{(m)}; t_n, x_{k}^{(n)} \right) \right] .\nonumber \\ \end{aligned}$$
(3.7)

By the reducibility of determinantal martingales (Lemma 2.4) and a combinatorial argument, we can prove the following identity.

Lemma 3.1

Let \({\varvec{u}}\in \mathbb {Z}_\mathrm{e}^N \cap \mathbb {W}_N\) and \(\xi =\sum _{j=1}^N \delta _{u_j}\). For \(M \in \mathbb {N}, t_m \in \mathbb {N}, 1 \le m \le M\), \(t_1 < \cdots < t_M \le T \in \mathbb {N}\),

$$\begin{aligned}&\mathrm{E}_{{\varvec{u}}} \left[ \prod _{m=1}^M \prod _{j=1}^N\{1+\chi _{t_m}(S_j(t_m)) \} \mathcal{D}_{\xi }(T, {\varvec{S}}(T)) \right] \\&\qquad =\mathop {\mathrm{Det}}_{\begin{array}{c} (s,t)\in \{t_1, \ldots , t_M\}, \\ (x,y)\in \mathbb {Z}^2 \end{array}} \Big [\delta _{st} \delta _x(y)+ \mathbb {K}_{\xi }(s,x;t,y) \chi _{t}(y) \Big ], \end{aligned}$$

where \(\mathbb {K}_{\xi }\) is given by (1.19) with (1.20).

The same identity was proved for continuous-time DMR in Sect. 2 of [24]. So we omit the proof of Lemma 3.1 for discrete-time DMR.

Now we arrive at one of the main theorems of the present paper.

Theorem 3.2

For any initial configuration \(\xi \in \mathfrak {M}_0\) with \(\xi (\mathbb {Z}_\mathrm{e})=N \in \mathbb {N}\), the noncolliding RW, \((\Xi (t), t \in \mathbb {N}_0, {\mathbb P}_{\xi })\) is determinantal with the correlation kernel (1.19) with (1.20) in the sense that the moment generating function (3.4) is given by a Fredholm determinant

$$\begin{aligned} \Psi _{\xi }^{{\varvec{t}}}[{\varvec{f}}] =\mathop {\mathrm{Det}}_ {\begin{array}{c} (s,t)\in \{t_1,t_2,\ldots , t_M\}^2, \\ (x,y)\in \mathbb {Z}^2 \end{array}} \Big [\delta _{st} \delta _x(\{y\}) + \mathbb {K}_{\xi }(s,x;t,y) \chi _{t}(y) \Big ], \end{aligned}$$
(3.8)

and then all spatio-temporal correlation functions are given by determinants as

$$\begin{aligned}&\rho _{\xi } \Big (t_1,{\varvec{x}}^{(1)}_{N_1}; \ldots ;t_M,{\varvec{x}}^{(M)}_{N_M} \Big ) =\left\{ \begin{array}{l}\displaystyle {\det _{\begin{array}{c} 1 \le j \le N_{m}, 1 \le k \le N_{n}, \\ 1 \le m, n \le M \end{array}}\Bigg [\mathbb {K}_{\xi }(t_m, x_{j}^{(m)}; t_n, x_{k}^{(n)} )\Bigg ],} \\ \qquad { if} \quad {\varvec{x}}^{(m)}_{N_m} \in \mathbb {Z}_\mathrm{e}^{N_m} \cap \mathbb {W}_{N_m}, t_m={ even}, \\ \qquad { or} \quad {\varvec{x}}^{(m)}_{N_m} \in \mathbb {Z}_\mathrm{o}^{N_m} \cap \mathbb {W}_{N_m}, t_m={ odd}, \quad 1 \le m \le M, \\ 0, \quad { otherwise}, \end{array} \right. \end{aligned}$$
(3.9)

\(t_m \in \mathbb {N}, 1 \le m \le M\), \(t_1 < \cdots < t_M\), and \(0 \le N_m \le N, 1 \le m \le M\).

Proof

By (1.4) with (1.5), the moment generating function (3.4) is written using (3.5) as

$$\begin{aligned} \Psi _{\xi }^{{\varvec{t}}}[{\varvec{f}}] ={\mathbb E}_{\xi } \left[ \prod _{m=1}^N \prod _{j=1}^N \{1+\chi _{t_m}(S^0_j(t_m)) \} \right] \!. \end{aligned}$$

Proposition 3.1 gives its DMR,

$$\begin{aligned} \Psi _{\xi }^{{\varvec{t}}}[{\varvec{f}}] =\mathrm{E}_{{\varvec{u}}} \left[ \prod _{m=1}^N \prod _{j=1}^N \{1+\chi _{t_m}(S_j(t_m)) \} \mathcal{D}_{\xi }(T, {\varvec{S}}(T)) \right] \!. \end{aligned}$$

Then Lemma 3.1 gives (3.8). By definitions of correlation functions (3.6) and Fredholm determinant (3.7), (3.9) is concluded from (3.8). The proof is completed. \(\square \)

4 Dynamics with an Infinite Number of Particles

4.1 Determinantal Process with an Infinite Number of Particles

In this subsection, we will show that the noncolliding RW with an infinite number of particles can be well-defined as a determinantal process for the initial configurations \(\delta _{2 a \mathbb {Z}}, a \in \{2, 3, \ldots \}\) given by (1.21). In order to that, we prepare infinite sequences of entire functions and discrete-time martingales labeled by \(k \in \mathbb {Z}\) below.

For a configuration \(\xi =\sum _{j} \delta _{u_j} \in \mathfrak {M}_0\) we write its restriction in \([-L, L] \subset \mathbb {Z}, L \in \mathbb {N}\) as \(\xi \cap [-L, L] \equiv \sum _{j: u_j \in [-L, L]} \delta _{u_j}\). For each infinite-particle configuration (1.21) with \(a \in \{2,3,\ldots \}\), and \(k \in \mathbb {Z}\), a limit of the polynomial (1.15)

$$\begin{aligned} \Phi _{\delta _{2a \mathbb {Z}}}^{2ak}(z) \equiv \lim _{L \rightarrow \infty } \Phi _{\delta _{2a \mathbb {Z}} \cap [-L, L]}^{2a k}(z), \quad z \in \mathbb {C} \end{aligned}$$
(4.1)

exists and explicitly calculated as

$$\begin{aligned} \Phi _{\delta _{2a \mathbb {Z}}}^{2ak}(z)&= \prod _{j \in \mathbb {Z}, j \not = k} \frac{z-2aj}{2ak-2aj}= \prod _{n \in \mathbb {Z}, n \not = 0}\left( 1 + \frac{z/2a -k}{n} \right) \nonumber \\&= \frac{\sin (\pi (z/2a -k))}{\pi (z/2a-k)}= \frac{1}{2 \pi } \int _{-\pi }^{\pi } d \lambda \,e^{i \lambda (z/2a -k)},\quad k \in \mathbb {Z} \end{aligned}$$
(4.2)

by using the product formula of the sine function [30, 37], As the analytic continuation of (2.15) with respect to \(\alpha \),

$$\begin{aligned} \widetilde{\mathrm{E}} [e^{-\lambda \widetilde{S}(t)}] = \frac{1}{(\cos \lambda )^t}, \quad \lambda \in \left( -\frac{\pi }{2}, \frac{\pi }{2} \right) \!, \quad t \in \mathbb {N}_0, \end{aligned}$$
(4.3)

implies that \(e^{i \lambda \{(y+i \widetilde{S}(t))/2a-k\}}\) is \(d \lambda \times d \widetilde{\mathrm{P}}\)-integrable for \(a \ge 2\). Then

$$\begin{aligned} \mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2ak}(t,y) \equiv \widetilde{\mathrm{E}} [ \Phi _{\delta _{2a \mathbb {Z}}}^{2ak} (y+i \widetilde{S}(t)) ], \quad k \in \mathbb {Z} \end{aligned}$$
(4.4)

are well-defined and given by

$$\begin{aligned} \mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2ak}(t,y) = \frac{1}{2 \pi } \int _{-\pi }^{\pi } d \lambda \, \frac{e^{i \lambda (y/2a-k)}}{[\cos (\lambda /2a)]^t}, \quad k \in \mathbb {Z}. \end{aligned}$$
(4.5)

Since \(|\mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2ak}(t,y)| \le 2^{t/2}, a \in \{2,3, \ldots \}\), \(|\sum _{j \in \mathbb {Z}} p(s,x|2aj) \mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2aj}(t,y)| < \infty \) for any \((s,t) \in \mathbb {N}^2\), \(s, t \le T \in \mathbb {N}\), \((x,y) \in \mathbb {Z}^2\). Then the kernel

$$\begin{aligned} \mathbb {K}_{\delta _{2a\mathbb {Z}}}(s,x;t,y) = \left\{ \begin{array}{l} \displaystyle { \sum _{j \in \mathbb {Z}} p(s, x|2a j) \mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2aj}(t,y) - \mathbf{1}(s>t) p(s-t,x|y), } \\ \qquad \qquad \text{ if } \quad (s,x), (t,y) \in \mathbb {N}_0 \times \mathbb {Z}, \quad s+x, t+y \in \mathbb {Z}_\mathrm{e}, \\ 0, \qquad \quad \text{ otherwise }, \end{array} \right. \end{aligned}$$
(4.6)

defines the moment generating function of the process by the Fredholm determinant

$$\begin{aligned} \Psi _{\delta _{2a\mathbb {Z}}}^{{\varvec{t}}}[{\varvec{f}}] =\mathop {\mathrm{Det}}_ {\begin{array}{c} (s,t)\in \{t_1,t_2,\ldots , t_M\}^2, \\ (x,y)\in \mathbb {Z}^2 \end{array} } \Big [\delta _{st} \delta _x(y) + \mathbb {K}_{\delta _{2a\mathbb {Z}}}(s,x;t,y) \chi _{t}(y) \Big ] \end{aligned}$$

for any integer \(M \in \mathbb {N}\), a sequence of times \({\varvec{t}}=(t_1,\ldots ,t_M) \in \mathbb {N}^M\) with \(t_1 < \cdots < t_M \le T \in \mathbb {N}\), and a sequence of bounded functions \({\varvec{f}}=(f_{t_1},\ldots ,f_{t_M})\) with (3.5). It implies that \({\mathbb P}_{\delta _{2a\mathbb {Z}}}\) is determined in the sense of finite dimensional distributions.

Proposition 4.1

For each \(a \in \{2,3, \ldots \}\), the noncolliding RW started at \(\delta _{2a \mathbb {Z}}\), denoted by \((\Xi (t), t \in \mathbb {N}_0, {\mathbb P}_{\delta _{2a\mathbb {Z}}})\), is well-defined as a determinantal process with the correlation kernel (4.6).

It is readily shown by Lemma 2.1 (discrete Itô’s formula) that if \((S(t))_{t \in \mathbb {N}_0}\) is a RW, \((\mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2ak}(t, S(t)))_{t \in \mathbb {N}_0}, k \in \mathbb {Z}\) are discrete-time martingales, if \(a \in \{2,3, \ldots \}\). Let \((S_j(t))_{t \in \mathbb {N}_0}\), \(j \in \mathbb {Z}\) be an infinite sequence of independent RWs. Then we have an infinite sequence of independent martingales with discrete time,

$$\begin{aligned} (\mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2ak}(t, S_j(t)))_{t \in \mathbb {N}_0}, \quad k \in \mathbb {Z}, \end{aligned}$$
(4.7)

for each \(a \in \{2,3, \ldots \}\) and \(j \in \mathbb {Z}\). We write the labeled configuration \((2a j)_{j \in \mathbb {Z}}\) with an infinite number of particles as \(2a \mathbb {Z}\), and under \(\mathrm{P}_{2a \mathbb {Z}}\), \(S_j(0)=2aj, j \in \mathbb {Z}\). Then, for any \(t \in \mathbb {N}_0\),

$$\begin{aligned} \mathrm{E}_{2a \mathbb {Z}} \Big [\mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2ak} (t, S_j(t)) \Big ]&= \mathrm{E}_{2a \mathbb {Z}} \Big [\mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2ak} (0, S_j(0)) \Big ]\nonumber \\&= \mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2ak} (0, 2a j)\nonumber \\&= \delta _{jk}, \quad j, k \in \mathbb {Z}. \end{aligned}$$
(4.8)

Fix \(N \in \mathbb {N}\). For \(\mathbb {J}\subset \mathbb {I}_N\), define the determinantal martingale of (4.7)

$$\begin{aligned} \mathcal{D}_{\delta _{2a\mathbb {Z}}}(t,{\varvec{S}}_{\mathbb {J}}(t))=\det _{j, k \in \mathbb {J}} \Big [\mathcal{M}_{\delta _{2a \mathbb {Z}}}^{k}(t, S_j(t)) \Big ],\quad t \in \mathbb {N}_0. \end{aligned}$$
(4.9)

Let \(t \in \mathbb {N}, t \le T \in \mathbb {N}\), \(N' \in \mathbb {N}, N' < N\), and \(F_{N'}\) be a symmetric bounded function on \({\mathbb {Z}}^{N'}\). Then the reducibility

$$\begin{aligned}&\sum _{\mathbb {J}\subset \mathbb {I}_N, |\mathbb {J}|=N'}\mathrm{E}_{2a \mathbb {Z}} \left[ F_{N'}({\varvec{S}}_{\mathbb {J}}(t)) \mathcal{D}_{\delta _{2a \mathbb {Z}}}(T, {\varvec{S}}_{N}(T)) \right] \nonumber \\&\quad =\sum _{\mathbb {J}\subset \mathbb {I}_N, |\mathbb {J}|=N'} \mathrm{E}_{2a \mathbb {Z}} \left[ F_{N'}({\varvec{S}}_{\mathbb {J}}(t))\mathcal{D}_{\delta _{2a \mathbb {Z}}}(T, {\varvec{S}}_{\mathbb {J}}(T)) \right] \nonumber \\&\quad = \int _{\mathbb {W}_{N'}} \delta ^{\otimes N'}_{2a\mathbb {Z}} (d{\varvec{v}})\mathrm{E}_{{\varvec{v}}} \left[ F_{N'}({\varvec{S}}_{N'}(t)) \mathcal{D}_{\delta _{2a\mathbb {Z}}}(T, {\varvec{S}}_{N'}(T)) \right] . \end{aligned}$$
(4.10)

holds as well as Lemma 2.4. Note that the last expression of (4.10) does not change even if we replace \(N\) in the first line of (4.10) by any other integer \(\widehat{N}\) with \(\widehat{N} > N\). Based on such consistency in reduction of DMRs and the fact (4.1), the DMR is valid also for the noncolliding RW with an infinite number of particles.

Proposition 4.2

Assume that \(F\) is represented as

$$\begin{aligned} F(\Xi (\cdot )) =G \left( \sum _{x \in \mathbb {Z}} \phi _1(x) \Xi (t_1, x), \ldots , \sum _{x \in \mathbb {Z}} \phi _M(x) \Xi (t_M,x) \right) , \end{aligned}$$

where \(G\) is a polynomial function on \(\mathbb {R}^M, M \in \mathbb {N}\) and \(\phi _{m}, 1 \le m \le M\) are real-valued bounded functions with finite supports on \(\mathbb {Z}\). Then the expressions (3.1) are valid also in the cases with \(\xi =\delta _{2 a \mathbb {Z}}\) and \({\varvec{u}}=2a \mathbb {Z}\),\(a \in \{2,3,\ldots \}\), even though \(N= \delta _{2a\mathbb {Z}}(\mathbb {Z})=\infty \).

Proof is given in the similar way to that given for Corollary 1.3 in [33].

4.2 Relaxation to Equilibrium Dynamics

Now we prove that the infinite-particle systems \((\Xi (t), t \in \mathbb {N}_0, {\mathbb P}_{\delta _{2 a \mathbb {Z}}}), a \in \{2, 3, \ldots \}\), constructed in the previous subsection show relaxation phenomena to the equilibrium determinantal processes with discrete analogues of the extended sine-kernel (1.22).

Since the transition probability of RW (1.3) is a unique solution of the difference equation

$$\begin{aligned} p(t+1,y|x)=\frac{1}{2} [ p(t,y-1|x)+p(t,y+1|x)], \quad t \in \mathbb {N}_0, \quad x, y \in \mathbb {Z}, \end{aligned}$$

with the initial condition \(p(0, y|x)=\delta _{x y}\), it has the following expressions,

$$\begin{aligned} p(t,y|x)&= \frac{1}{2 \pi } \int _{-\pi }^{\pi } dk \, e^{ik(y-x)}(\cos k)^t\nonumber \\&= \frac{1}{4 \pi a} \int _{-2a \pi }^{2 a \pi } d \theta \, e^{i \theta (y-x)/2a} \left[ \cos \left( \frac{\theta }{2a} \right) \right] ^t\nonumber \\&= \int _0^1 du \, \cos (u \pi (y-x)) [\cos (u \pi )]^{t}, \end{aligned}$$
(4.11)

where \(a \in \mathbb {N}\). Note that the integral representations (4.11) of (1.3) are valid for any \(t \in \mathbb {N}_0, x, y \in \mathbb {Z}\). Then combining with (4.5) we have

$$\begin{aligned} \sum _{j \in \mathbb {Z}} p(s,x|2aj) \mathcal{M}_{\delta _{2a \mathbb {Z}}}^{2aj}(t,y)&= \frac{1}{8 \pi ^2 a} \sum _{j \in \mathbb {Z}} \int _{-2a \pi }^{2a \pi } d \theta \\&\int _{-\pi }^{\pi } d \lambda \, e^{i \theta (x/2a-j) + i \lambda (y/2a-j)} \frac{[\cos (\theta /2a)]^s}{[\cos (\lambda /2a)]^t}. \end{aligned}$$

We rewrite the first line of (4.6) as follows: for \((s,x), (t,y) \in \mathbb {N}_0 \times \mathbb {Z}\), \(s+x, t+y \in \mathbb {Z}_\mathrm{e}\),

$$\begin{aligned} \mathbb {K}_{\delta _{2a \mathbb {Z}}}(s,x;t,y) + \mathbf{1}(s>t)p(s-t, x|y) = G(s,x;t,y)+R(s,x;t,y) \end{aligned}$$
(4.12)

with

$$\begin{aligned} G(s,x;t,y) = \frac{1}{4 \pi ^2 a} \int _{|\theta | \le \pi } d \theta \int _{|\lambda | \le \pi } d \lambda \, \frac{e^{i(\theta x+ \lambda y)/2a}}{[\cos (\lambda /2a)]^{t-s}} \sum _{j \in \mathbb {Z}} e^{-i(\theta +\lambda )j} \left[ \frac{\cos (\theta /2a)}{\cos (\lambda /2a)}\right] ^s, \end{aligned}$$

and

$$\begin{aligned} R(s,x;t,y)&= \frac{1}{8 \pi ^2 a} \sum _{j \in \mathbb {Z}} \int _{\pi <|\theta | < (2a-1) \pi } d \theta \\&\int _{|\lambda | \le \pi } d \lambda \, \frac{e^{i(\theta x+ \lambda y)/2a}}{[\cos (\lambda /2a)]^{t-s}} e^{-i(\theta +\lambda )j} \left[ \frac{\cos (\theta /2a)}{\cos (\lambda /2a)}\right] ^s. \end{aligned}$$

Since \(\sum _{j \in \mathbb {Z}} e^{-i(\theta +\lambda )j} =2\pi \delta _{-\lambda }(\{\theta \})\) for \(\theta , \lambda \in (-\pi , \pi ]\), we obtain

$$\begin{aligned} G(s,x; t,y) = \frac{1}{2 \pi a} \int _{-\pi }^{\pi } d \lambda \, \frac{e^{i \lambda (y-x)/2a}}{[\cos (\lambda /2a)]^{t-s}} \equiv \mathcal{G}(t-s,y-x). \end{aligned}$$
(4.13)

On the other hand, when \(\pi < |\theta | < (2a-1) \pi \) and \(|\lambda | \le \pi \), \( |\cos (\theta /2a)/\cos (\lambda /2a)| < 1. \) Then for any fixed \(s,t \in \mathbb {N}\), \( |R(s+n, x; t+ n, y)| \rightarrow 0\) as \(n \rightarrow \infty \) uniformly on any \((x,y) \in \mathbb {Z}^2\) and it implies

$$\begin{aligned} \mathbb {K}_{\delta _{2a \mathbb {Z}}}(s+n, x; t+n, y) \rightarrow \mathbf{K}_{\rho }(t-s, y-x) \quad \text{ as }\; n \rightarrow \infty , \end{aligned}$$
(4.14)

where

$$\begin{aligned} \mathbf{K}_{\rho }(t-s, y-x)&= \mathcal{G}(t-s,y-x)-\mathbf{1}(s>t) p(s-t, x|y)\nonumber \\&= 2 \int _{0}^{\rho } d u \, \frac{\cos (\pi u (y-x))}{[\cos (\pi u)]^{t-s}} -\mathbf{1}(s>t) p(s-t,x|y), \end{aligned}$$
(4.15)

if \(s+x, t+y \in \mathbb {Z}_\mathrm{e}\), and \(\mathbf{K}_{\rho }(t-s,y-x)=0\), otherwise, with the density on \(\mathbb {Z}\),

$$\begin{aligned} \rho =\frac{1}{2 a}, \quad a \in \{2,3, \ldots \}. \end{aligned}$$
(4.16)

By (4.11) and others, we can see that (4.15) is written as (1.22).

The convergence of the correlation kernel (4.14) implies the convergence of generating function for correlation functions \(\Psi _{\delta _{2a \mathbb {Z}}}^{{\varvec{t}}}[{\varvec{f}}]\), and thus the convergence of the determinantal process to an equilibrium determinantal process. This is an example of relaxation phenomena [10, 25, 29–31].

In order to state the result, we define determinantal point processes on \(\mathbb {Z}\).

Definition 4.3

Let \(\sharp =\mathrm{e}\) or \(\mathrm{o}\). For a given density \(0 < \rho < 1/2\), the probability measures \(\mu ^\mathrm{sin}_{\rho , \sharp }\) on \(\mathbb {Z}\) are defined as determinantal point processes with the sine kernels

$$\begin{aligned} \mathbf{K}^\mathrm{sin}_{\rho , \sharp }(y-x) =\left\{ \begin{array}{ll} \displaystyle {\frac{2 \sin (\pi \rho (y-x))}{\pi (y-x)}}, \quad &{} \text{ if } \,\,x,y \in \mathbb {Z}_{\sharp }, \\ 0, \quad &{} \text{ otherwize }. \end{array} \right. \end{aligned}$$
(4.17)

Theorem 4.4

For each \(a \in \{2,3, \ldots \}\), the process \((\Xi (t), t \in \mathbb {N}_0, {\mathbb P}_{\delta _{2a \mathbb {Z}}})\) shows a relaxation phenomenon to equilibrium state such that

$$\begin{aligned} \Xi (2n)&\Rightarrow \mu ^\mathrm{sin}_{\rho , \mathrm{e}},\\ \Xi (2n+1)&\Rightarrow \mu ^\mathrm{sin}_{\rho , \mathrm{o}}, \quad \text{ as }\,\, n \rightarrow \infty \end{aligned}$$

with \(\rho =1/2a\). The equilibrium process, denoted by \((\Xi (t), t \in \mathbb {Z}, \mathbf{P}_{\rho })\), is time-reversible and determinantal with the correlation kernel given by (1.22).

Here we note that the local densities of particles (the one-point correlation functions) in \(\mu ^{\sin }_{\rho , \sharp }\) and in \((\Xi (t), t \in \mathbb {Z}, \mathbf{P}_{\rho })\) are obtained from the expressions (4.17) and (1.22) for correlation kernels, respectively, by taking the limits as

$$\begin{aligned} \mu ^\mathrm{sin}_{\rho , \sharp }(\{x\})&= \lim _{y \rightarrow x} \mathbf{K}^\mathrm{sin}_{\rho , \sharp }(y-x) =\left\{ \begin{array}{ll} 2 \rho , \qquad \text{ if } \,\,x \in \mathbb {Z}_{\sharp }, \\ 0, \qquad \text{ otherwize }, \end{array} \right. \quad \sharp =\mathrm{e} \,\,\text{ or } \,\,\mathrm{o},\\ \mathbf{P}_{\rho }[\Xi (s,\{x\})=1]&= \lim _{\begin{array}{c} t \rightarrow s, \\ y \rightarrow x \end{array}} \mathbf{K}_{\rho }(y-x, t-s) =\left\{ \begin{array}{ll}2 \rho , \qquad \text{ if }\,\, s+x \in \mathbb {Z}_\mathrm{e}, \\ 0, \qquad \text{ otherwize }. \end{array} \right. \end{aligned}$$

On the spatio-temporal plane \((t,x) \in \mathbb {Z}^2\), the equilibrium state makes a homogeneous bipartite lattice.

5 Convergence to the Dyson Model

In this final section, we will discuss the convergence of noncolliding RWs to the continuous version (i.e. the Dyson model) in the sense of Donsker’s invariant principle from the viewpoint of DMR.

For \(n \in \mathbb {N}\), define scaled discrete-processes as

$$\begin{aligned}&S_j^{(n)}(t) = \frac{1}{n}S_j(n^2 t), \quad \widetilde{S}_j^{(n)}(t) = \frac{1}{n}\widetilde{S}_j(n^2 t),\nonumber \\&Z_j^{(n)}(t) = S_j^{(n)}(t)+ i \widetilde{S}_j^{(n)}(t),\quad t \in \mathbb {N}_0, \quad 1 \le j \le N. \end{aligned}$$
(5.1)

We set \(S_j(0)=n u_j,1 \le j \le N\). Since

$$\begin{aligned}&\mathrm{E}[\zeta _j(t)]= \widetilde{\mathrm{E}}[\widetilde{\zeta }_j(t)]=0,\\&\mathrm{E}[\zeta _j(t)^2]= \widetilde{\mathrm{E}}[\widetilde{\zeta }_j(t)^2]=1, \quad t \in \mathbb {N}, \quad 1 \le j \le N, \end{aligned}$$

Donsker’s invariance principle [5, 46] proves the convergence in distribution

$$\begin{aligned} S_j^{(n)}(\cdot ) \mathop {\rightarrow }\limits ^\mathrm{d}B_j(\cdot ), \quad \widetilde{S}_j^{(n)}(\cdot ) \mathop {\rightarrow }\limits ^\mathrm{d}\widetilde{B}_j(\cdot ), \quad Z_j^{(n)}(\cdot ) \mathop {\rightarrow }\limits ^\mathrm{d}\mathcal{B}_j(\cdot ), \quad \text{ as }\; n \rightarrow \infty , \end{aligned}$$
(5.2)

where \(B_j(\cdot )\) and \(\widetilde{B}_j(\cdot )\) are independent BMs with \(B_j(0)=u_j, \widetilde{B}_j(0)=0, 1 \le j \le N\), and \(\mathcal{B}_j\) denotes the complex BMs, \(\mathcal{B}_j(\cdot )=B_j(\cdot )+i \widetilde{B}_j(\cdot )\), \(1 \le j \le N\). For \(\Phi _{\xi }^{u_k}(\cdot ), 1 \le k \le N\) are polynomials and thus continuous functions, (5.2) implies

$$\begin{aligned} \Phi _{\xi }^{u_k} (Z_j^{(n)}(\cdot )) \mathop {\rightarrow }\limits ^\mathrm{d}\Phi _{\xi }^{u_k}(\mathcal{B}_j(\cdot )) \quad \text{ as }\; n \rightarrow \infty , \quad 1 \le j, k \le N. \end{aligned}$$
(5.3)

For each \(n \in \mathbb {N}\), let \({\varvec{S}}^{0 \, (n)}(\cdot )=(S_1^{0 \, (n)}(\cdot ), \ldots , S_N^{0 \,(n)}(\cdot ))\) be the \(N\)-particle scaled RW conditioned never to collide with each other started at \({\varvec{u}}=(u_1, \ldots , u_N) \in \mathbb {Z}_\mathrm{e}^N \cap \mathbb {W}_N\) and put \(\Xi ^{(n)}(t, \cdot )=\sum _{j=1}^N \delta _{S_j^{0 \, (n)}(t)}(\cdot )\), \(t \in \mathbb {N}_0\). Then we have a series of scaled noncolliding RWs, \((\Xi ^{(n)}(t), t \in \mathbb {N}_0, {\mathbb P}_{\xi })\), \(n \in \mathbb {N}\), each of which has DMR

$$\begin{aligned} {\mathbb E}_{\xi } \left[ F \left( \Xi ^{(n)}(\cdot ) \right) \right]&= \mathrm{E}_{n {\varvec{u}}} \left[ F \left( \sum _{j=1}^{N} \delta _{S_j^{(n)}(\cdot )} \right) \mathcal{D}_{\xi }\left( n^2 T, {\varvec{S}}^{(n)}(T)\right) \right] \nonumber \\&= \mathbf{E}_{n {\varvec{u}}} \left[ F \left( \sum _{j=1}^{N} \delta _{\mathfrak {R}Z_j^{(n)}(\cdot )} \right) \det _{1 \le j, k \le N} \left[ \Phi _{\xi }^{u_k}\left( Z_j^{(n)}(T)\right) \right] \right] \end{aligned}$$
(5.4)

for any \(\mathcal{F}(t)\)-measurable bounded function \(F\) for any \(t \in \mathbb {N}, t \le T \in \mathbb {N}\). Let \((\mathbf{\Xi }(t), t \in [0, \infty ), \mathcal{P}_{\xi })\) be the Dyson model started at \(\xi =\sum _{j=1}^N \delta _{u_j} \in \mathfrak {M}_0\) with \({\varvec{u}}=(u_1, \ldots , u_N) \in \mathbb {Z}_\mathrm{e}^N \cap \mathbb {W}_N\). That is, \(\mathbf{\Xi }(t, \cdot )=\sum _{j=1}^N \delta _{X_j(t)}(\cdot ), t \in [0, \infty )\), where \({\varvec{X}}(\cdot )=(X_1(\cdot ), \ldots , X_N(\cdot ))\) is a unique solution of the SDEs (1.9) under the initial configuration \({\varvec{X}}(0)={\varvec{u}}\in \mathbb {Z}_\mathrm{e}^N \cap \mathbb {W}_N\). By the invariance principle (5.2), (5.3), if \(F\) is continuous, the DMRs given by the RHS of (5.4) converge to the complex BM representation for \((\mathbf{\Xi }(t), t \in [0, \infty ), \mathcal{P}_{\xi })\) given by Theorem 1.1 in [33]. Since the complex BM representation is a special case of DMR (see Remark 4 and a comment mentioned just after Proposition 3.1), we will say that

$$\begin{aligned} (\Xi ^{(n)}(t), t \in \mathbb {N}_0, {\mathbb P}_{\xi })\,\, \text{ converges } \text{ to }\,\, (\mathbf{\Xi }(t), t \in [0, \infty ), \mathcal{P}_{\xi })\,\, \text{ in } \text{ DMR. } \end{aligned}$$
(5.5)

As shown in Sect. 3, the DMR gives a Fredholm determinantal expression for any generating function of multitime correlation functions. Then (5.5) implies the convergence in the sense of finite dimensional distributions. It also implies the convergence as determinantal processes. By the convergence of processes (5.2), the following convergence of functions are concluded; if \(p(n^2 t, n y|nx) \not =0\),

$$\begin{aligned} \mathrm{P}_{n x}[S^{(n)}(t) \in dy] = p(n^2 t, ny|n x) n dy \rightarrow p^\mathrm{BM}(t,y|x), \end{aligned}$$

and

$$\begin{aligned} \widetilde{\mathrm{E}} \left[ \Phi _{\xi }^{u_k}(x+i \widetilde{S}_j^{(n)}(t)) \right]&= \mathcal{M}_{\xi }^{u_k}(n^2 t, x)\\&\quad \rightarrow \int _{\mathbb {R}} dv \, p^\mathrm{BM}(t, v|0) \Phi _{\xi }^{u_k}(x+iv) \equiv \mathsf{M}_{\xi }^{u_k}(t, x) \end{aligned}$$

as \(n \rightarrow \infty \) with (2.9). Therefore, the correlation kernel of the Dyson model, \((\mathbf{\Xi }(t), t \in [0, \infty ), \mathcal{P}_{\xi })\), is determined as the limit of the kernels of \((\Xi ^{(n)}(t), t \in \mathbb {N}_0, {\mathbb P}_{\xi })\) of the form (1.19),

$$\begin{aligned} \mathsf{K}_{\xi }(s,x;t,y) =\sum _{j=1}^N p^\mathrm{BM}(s,x|u_j) \mathsf{M}_{\xi }^{u_j}(t,y) - \mathbf{1}(s>t) p^\mathrm{BM}(s-t, x|y), \end{aligned}$$
(5.6)

\((s,x), (t,y) \in [0, \infty ) \times \mathbb {R}\). The limit (5.6) is exactly the same as the correlation kernel of the Dyson model given as Eq.(2.2) in [30] for general \(\xi \in \mathfrak {M}_0\), \(\xi (\mathbb {R})=N \in \mathbb {N}\), which was obtained by using the multiple Hermite polynomials.

As claimed by Proposition 4.2, DMR is valid for \((\Xi (t), t \in \mathbb {N}_0, {\mathbb P}_{\delta _{2 a \mathbb {Z}}})\), \(a \in \{2,3,\ldots \}\). Then we will conclude that

$$\begin{aligned} (\Xi ^{(n)}(t), t \in \mathbb {N}_0, {\mathbb P}_{\delta _{2 a \mathbb {Z}}})\,\, \text{ converges } \text{ to }\,\, (\mathbf{\Xi }(t), t \in [0, \infty ), \mathcal{P}_{\delta _{2 a \mathbb {Z}}}) \,\,\text{ in } \text{ DMR }, \end{aligned}$$
(5.7)

if \(a \in \{2,3, \ldots \}\). From (4.4) with (4.2),

$$\begin{aligned}&\widetilde{\mathrm{E}} \left[ \Phi _{\delta _{2 a \mathbb {Z}}}^{2 a k} (x+i \widetilde{S}^{(n)}(t)) \right] = \mathcal{M}_{\delta _{2 a \mathbb {Z}}}^{2 a k} (n^2 t, x)\nonumber \\&\quad \rightarrow \int _{\mathbb {R}} dv \, p^\mathrm{BM}(t, v|0) \Phi _{\delta _{2 a \mathbb {Z}}}^{2 a k}(x+iv) \equiv \mathsf{M}_{\delta _{2 a \mathbb {Z}}}^{2 a k}(t, x) \end{aligned}$$
(5.8)

as \(n \rightarrow \infty \). We find

$$\begin{aligned} \mathsf{M}_{\delta _{2 a \mathbb {Z}}}^{2ak}(t,y) = \frac{1}{2 \pi } \int _{-\pi }^{\pi } d \lambda \, e^{\lambda ^2 t/8 a^2 + i \lambda (y/2a-k)}, \quad (t,y) \in [0, \infty ) \times \mathbb {R}, \quad k \in \mathbb {Z}. \end{aligned}$$

Then the Dyson model with an infinite number of particles, \((\mathbf{\Xi }(t), t \in [0, \infty ), \mathcal{P}_{\delta _{2 a \mathbb {Z}}})\), is determinantal and its correlation kernel is determined as

$$\begin{aligned} \mathsf{K}_{\delta _{2 a \mathbb {Z}}}(s,x;t,y) = \sum _{j \in \mathbb {Z}} p^\mathrm{BM}(s,x|2aj) \mathsf{M}_{\delta _{2 a \mathbb {Z}}}^{2 a k}(t, y) - \mathbf{1}(s>t) p^\mathrm{BM}(s-t, x|y), \end{aligned}$$
(5.9)

\((s,x), (t,y) \in [0, \infty ) \times \mathbb {R}\). Let

$$\begin{aligned} \vartheta _3(v, \tau ) = \sum _{j \in \mathbb {Z}} e^{2 \pi i v j+ \pi i \tau j^2}, \quad \mathfrak {I}\tau > 0, \end{aligned}$$

which is a version of the Jacobi theta function. If we use the reciprocity relation

$$\begin{aligned} \vartheta _3(v,\tau )= \vartheta _3 \left( \frac{v}{\tau }, - \frac{1}{\tau } \right) e^{-\pi i v^2/\tau } \sqrt{ \frac{i}{\tau }} \end{aligned}$$

(see, for example, Sect. 10.12 in [1]), we can obtain the expression

$$\begin{aligned} \sum _{j \in \mathbb {Z}} p^\mathrm{BM}(s, x|2aj) \mathsf{M}_{\delta _{2a \mathbb {Z}}}^{2a j} (t, y) = \frac{\rho }{2 \pi } \int _{-\pi }^{\pi } d \lambda \, e^{\lambda ^2 \rho ^2 (t-s)/2 + i \lambda \rho (y-x)} \vartheta _3( \rho x- i \lambda \rho ^2 s, 2 \pi i \rho ^2 s), \end{aligned}$$

where \(\rho \) is the density of particles given by (4.16). Then (5.9) is written as

$$\begin{aligned} \mathsf{K}_{\delta _{2 a \mathbb {Z}}}(s,x;t,y)&= \mathsf{K}_{\rho }^\mathrm{sin}(t-s, y-x)\nonumber \\&\quad +\, \frac{\rho }{2 \pi } \int _{-\pi }^{\pi } d \lambda \, e^{\lambda ^2 \rho ^2 (t-s)/2 + i \lambda \rho (y-x)} \{ \vartheta _3(\rho x- i \lambda \rho ^2 s, 2 \pi i \rho ^2 s) -1 \},\nonumber \\ \end{aligned}$$
(5.10)

\((s,x), (t,x) \in [0, \infty ) \times \mathbb {R}\), where

$$\begin{aligned} \mathsf{K}_{\rho }^\mathrm{sin}(t-s, y-x) = \left\{ \begin{array}{ll} \displaystyle { \int _0^{\rho } du \, e^{\pi ^2 u^2(t-s)/2} \cos (\pi u(y-x))}, &{} \text{ if }\; s<t, \\ &{} \\ \displaystyle { \frac{\sin (\pi \rho (y-x))}{\pi (y-x)}}, &{} \text{ if }\; s=t,\\ &{} \\ \displaystyle { -\int _{\rho }^{\infty } du \, e^{\pi ^2 u^2(t-s)/2} \cos (\pi u \pi (y-x))}, &{} \text{ if }\; s>t. \\ \end{array} \right. \end{aligned}$$
(5.11)

The correlation kernel (5.10) coincide with Eq.(1.5) in [30] if we set \(\rho =1\). The kernel (5.11) is called the extended sine kernel with density \(\rho \) (see Sect. 11.7.1 in [15]), which is a continuum limit of (1.22). The relaxation phenomenon associated with \( \lim _{\tau \rightarrow \infty } \mathsf{K}_{\delta _{2 a Z}}(s+\tau , x; t + \tau , y) = \mathsf{K}_{1}^\mathrm{sin}(t-s, y-x) \) was studied in [30].

The above shows that the convergence in DMR implies the convergence in the sense of finite dimensional distributions and that as determinantal processes. As demonstrated by Proposition 1.4 and Theorem 1.5 in [33], DMR is useful to test the Kolmogorov criterion for tightness. Relations between the present convergence in DMR and the previous results concerning convergence to the Dyson model [3, 26, 44] will be discussed elsewhere.