Dynamic personnel rescheduling: insights and recovery strategies

Abstract

Personnel rescheduling problems have typically been studied from a static perspective, assuming a single rescheduling decision to be taken for which all disruption information is known. However, companies operate in a dynamic environment and new disruptions arise at different moments in time during the course of the execution of the schedule. In response, the personnel planner resides to (multiple) rerostering and/or allocation decisions to reinstate the workability of the schedule. In this paper, we investigate the dynamic personnel shift and task rescheduling problem and propose different recovery strategies to efficiently restore the personnel schedule. To that purpose, we simulate the operational variability based on input probability distributions for different sources of uncertainty and conduct timely recourse actions whenever indicated by the studied recovery strategies. Insights are provided into the recourse actions with respect to the number and timing of rescheduling decisions, the type of rescheduling decision and the rescheduling time horizon. We assess the trade-off between the rescheduling quality and effort, mapping the efficient recovery strategies using a Pareto front. Based upon these insights, we devise well-performing rules-of-thumb, defining efficient recovery decision strategies that lead to reconstructed personnel schedules of high quality. In addition, we investigate the impact of the timeline uncertainty on the outcome of the recovery strategies.

1 Introduction

As personnel resources embody typically one of the largest operating costs in an organisation, proper personnel planning is indispensable to managing these resources in an efficient and effective manner. Companies, however, operate typically in a dynamic environment such that unexpected events may disrupt the activity schedules and an appropriate schedule recovery mechanism should be installed. The planning of personnel resources is divided, because of its complexity, into different hierarchical decision stages, i.e. the strategic staffing phase, the tactical scheduling phase and the operational allocation phase (Burke et al., 2004). Each of these stages is usually treated separately as they involve different types of decisions with a different time horizon, taking stage-specific expected or more accurate information into account. The stages are organised in a hierarchical manner such that the decisions taken in each phase constrain the decision freedom in the subsequent phase(s). The strategic staffing phase considers long-term capacity decisions to determine the personnel mix and budget required to meet service demand. In the tactical scheduling phase, decisions entail constructing a baseline personnel schedule for a medium-term horizon. Typical objectives are to meet the desired service level at minimal personnel cost and maximal personnel satisfaction. This baseline schedule is constructed given a number of assumptions relative to service demand and employee availability based on expected information. However, in the operational allocation phase, from the moment the schedule has been published to the day of operations, the personnel planner receives up-to-date and accurate information. Certain input schedule parameters may change and take a different actual value. According to Van den Bergh et al. (2013), three types of variability can be distinguished in personnel planning, i.e. uncertainty of demand, uncertainty of arrival and uncertainty of capacity. Uncertainty of demand may cause expected demand to differ from actual demand for staff. Uncertainty of capacity is due to potential absenteeism, such that employees are unavailable to work a planned duty. Uncertainty of arrival influences start times and/or the duration of scheduled tasks. These unexpected events may lead to schedule disruptions, i.e. employee shortages or violations of certain scheduling rules, that render the current personnel schedule infeasible. Consequently, the published schedule cannot be executed as planned and needs to be adapted by either a rerostering or an allocation decision. A rerostering decision is taken with a short-to-medium horizon of multiple days that reinstates schedule feasibility and minimises the number of deviations compared to the original personnel schedule (Maenhout & Vanhoucke, 2013). Imbalances between supply and demand can also be (partially) recovered by adjusting the personnel schedule ad hoc via allocation decisions that consider only the short-term horizon of the single, upcoming day, for which the parameter data is known with certainty (Bard & Purnomo, 2005b). A rerostering decision entails larger scheduling flexibility but requires more effort whereas future schedule parameters may be only partially up-to-date and still subject to change. The interplay between rerostering decisions and allocation decisions in response to schedule disruptions has not been the subject of research before.

The problem under study is a dynamic rescheduling problem that considers the reactive recovery of personnel schedules at different time points. Operational variability accidentally changes parameter input values regarding task information and worker availability at different moments in time during the course of execution of the schedule, defined by the timeline uncertainty. The decision-making embodies both rerostering and allocation decisions to revise and restore the feasibility of the baseline personnel schedule relative to both shift and task assignments. In this paper, we evaluate the outcome of various dynamic recovery policies in order to deduce best practices and managerial guidelines. We primarily focus on the time dimension where a personnel planner faces typically two contingent decisions, i.e.

(i) When is schedule recovery desired? Depending on the characteristics of disruptions incurred, the rescheduling decision to restore disruptions can be taken ’ad hoc’ or using a long-sighted approach. The former implies that the rescheduling decision is delayed to the day the disruptions actually occur when the decision-maker has more accurate information on all sources of uncertainty, whereas the latter entails the rescheduling decision is taken a couple of days in advance, possibly on the moment disruptions have arisen, on a somewhat larger time horizon. The timing of rescheduling decisions over the horizon is indicated by the recovery decision timeline.

(ii) What is the optimal length of the rescheduling time horizon? If a recovery decision is undertaken, the ideal length of the rescheduling time horizon has to be determined and, correspondingly, whether allocation or rerostering decisions should be undertaken. If the rescheduling time horizon is too short and/or allocation decisions are considered, the feasibility of the schedule can often only be (partially) restored by calling upon very costly personnel resources. If the rescheduling horizon is too large, it is not unimaginable that conducted changes will have to be changed again in a dynamic setting, leading to an excessive number of (unnecessary) changes.

In order to evaluate dynamic recovery strategies, we simulate the operational variability based on input probability distributions for the different types of uncertainty and apply recourse actions whenever indicated by the recovery decision timeline. The reactive rerostering and allocation decisions are solved via integer programming in order to retrieve exact solutions such that managerial guidelines can be identified in an unbiased manner. The research objective is to devise well-performing rules-of-thumb that define efficient recovery decision strategies leading to restored personnel schedules of high quality. As the problem has not been studied before, we acquire insight into (1) the evaluation of recovery decision strategies with particular interest in the recovery decision timeline, the type of recovery decision and the rescheduling horizon; (2) the trade-off between rescheduling quality and rescheduling effort, mapping effective and efficient solutions using a Pareto front; (3) the impact of timeline uncertainty on the outcome of recovery decision strategies. In addition, we benchmark a recovery strategy devised upon the best-performing rule to different individual recovery strategies known from the literature.

Dynamic rescheduling related to integrated personnel and task scheduling is relevant for different application domains, for example, healthcare, production and transportation (Brucker et al., 2011; Van den Bergh et al., 2013). Personnel is in most of those application domains auxiliary resources to process relevant tasks. For all these applications, the planning and scheduling of resources follow the same hierarchical decision stages. Different assumptions have been taken about the service demand and employee availability based on expected information to construct a baseline schedule. Approaching the moment of execution, certain input schedule parameters may change at different moments in time, invoking the need for a dynamic (re-)scheduling approach. In the following, we discuss in detail one application of the problem under study related to the nurse-patient assignment problem in the operating room (OR) department of a hospital (e.g. Di Martinelly & Meskens, 2017; Akbarzadeh et al., 2020). In an OR department, the OR manager coordinates the surgical teams in order to perform surgical operations. In order to meet the patients’ needs, nurses are assigned directly to specific surgical cases in accordance with their availability and qualifications. The nurse shift schedule is communicated to the nurses at the start of each month specifying the days and shifts nurses are required to be on duty. Based on the advance patient schedule for the next upcoming week, nurses are assigned to specific patients, i.e. the shift schedule is integrated with the task planning in order to get a more accurate estimation of the nurse staffing requirements. However, when the date of surgery is approaching, usually somewhere in the week before the surgery, the attending physicians carefully revise their patient schedules independently from each other on a moment that suits them best. Hence, new information may reach the OR manager at any point in time, involving one or multiple surgery sessions for the upcoming week. In practice, the exact OR schedule, indicating the specific start times of the surgeries, is composed the day before operations by the OR manager who has an overview of the requests of the different physicians. On the day of operations, this schedule can further change due to the emergence of urgent patients. In this way, the nurse schedule can be impaired because of (1) nurse-specific disruptions that are mainly caused by the illness of personnel, personnel training days and leave requests of personnel (uncertainty of capacity); (2) attending physicians who may postpone specific surgical cases to a later period or even append add-on cases with a high priority (uncertainty of demand); and (3) attending physicians reconsidering their surgical case planning, i.e. the sequencing of these cases and the provision of a more accurate estimation of the duration of surgeries to the OR manager (uncertainty of arrival).

The paper is organised as follows. Section 2 reviews the relevant literature on dynamic (re-)scheduling and personnel rerostering and allocation decisions. In Sect. 3, we give a detailed description of the baseline scheduling problem, the different sources of uncertainty and the dynamic rescheduling problem. In Sect. 4, we discuss the solution methodology used to devise and analyse recovery decision strategies. The computational experiments and derived managerial findings are discussed in Sect. 5. Section 6 provides final notes and contributions made.

2 Literature review

2.1 Dynamic (re-)scheduling

Most operating systems are managed in a dynamic environment due to the arising of unpredictable events. Dynamic scheduling problems have been foremost studied in the areas of production, project and transportation scheduling. For an overview, we refer to Herroelen and Leus (2005), Ouelhadj and Petrovic (2009) and Larsen and Pranzo (2019). To consider operational uncertainty that arises accidentally at different moments in time, dynamic scheduling approaches typically apply a scheduling and rescheduling process in which schedules are revised in response to incurred disruptions. In the literature, different types of multi-stage decision methodologies have been proposed. In this respect, solution approaches have been developed relying on stochastic programming or (adjustable) robust optimisation to incorporate some of the uncertainty information upfront when constructing the baseline schedule (Yanikoglu et al., 2019). However, when the number of stages, the number of possible scenarios and/or the number of (binary) recourse variables is (too) large, the computational performance of these approaches is hampered (Larsen & Pranzo, 2019). Apart from these proactive methods, dynamic rescheduling approaches study to resolve disruptions solely in a reactive manner, which is the focus of this literature review. These solution procedures treat the problem in a deterministic manner and apply a rescheduling method whenever specific conditions are met. The invoked reactive mechanisms embody a schedule repair, adjusting the current schedule locally, or a complete rescheduling that devises a new schedule from scratch (Cowling & Johansson, 2002). The schedule repair heuristics typically focus upon either a limited period to match up with the baseline schedule, a partial schedule consisting only of a limited set of tasks (e.g. operations in failure) or a combination of both. Corresponding to complete rescheduling or schedule repair, different objectives have been proposed to restore the workability of the schedule considering efficiency measures, robustness measures minimising the effect of disruptions on the performance of the realised schedule (e.g. Wu et al., 1993), and/or stability measures minimising deviation from the baseline schedule (e.g. Ariano et al., 2007).

In a dynamic rescheduling algorithm, the disruptions are generated via Monte Carlo simulation or are direct input from real-world applications (known as trace-driven simulation), whereas the schedule repair is effectuated using single-pass heuristics (e.g. the right-shift repair strategy, activity crashing (Bowman, 2006)), meta-heuristics (Nguyen et al., 2014) or exact optimisation approaches (Zhu & Goverde, 2020). These optimisation methods are guided by the set of allowed recovery actions, which are problem-specific mechanisms instigating changes to the allocation of resources [e.g. swapping of tasks, overtime (Ingels & Maenhout, 2017)] and/or the execution of the jobs (e.g. task cancellation, retiming tasks sks Borgonjon & Maenhout, 2021). In contrast to the static rescheduling problem, dynamic rescheduling problems are discerned based on their multi-stage character, requiring the definition of the point(s) in time to perform the rescheduling. To this end, periodic, event-driven and hybrid policies have been formulated in the literature (Sabuncuoglu & Bayiz, 2000; Vieira et al., 2003). In the periodic policy, schedules are reviewed at regular intervals. The periodic policy yields larger schedule stability and less schedule nervousness but is not very responsive to unexpected schedule disruptions. In this regard, different authors studied the rescheduling frequency and indicated that performance deteriorates when the frequency is lowered (e.g. Sabuncuoglu & Karabuk, 1999). In an event-driven policy, rescheduling is triggered whenever an unexpected event arises, which has been recognised to outperform periodic rescheduling policies (Vieira et al., 2000). A hybrid policy combines both policies by invoking a rescheduling decision periodically and also when a disruption occurs. In this framework, low-impact disruptions are typically handled on a periodic basis, whereas high-impact disruptions are resolved via an event-driven rescheduling mechanism (Church & Uzsoy, 1992). In general, determining the rescheduling horizon has been found to be a non-trivial task (Ouelhadj & Petrovic, 2009).

2.2 Personnel rerostering and allocation decisions

The problem of dynamic (re-)scheduling has not been studied before in the domain of personnel scheduling. In contrast to personnel rostering problems, rescheduling decisions have received limited attention in the staff scheduling literature (Van den Bergh et al., 2013; Clarke et al., 2015). The few relevant studies focus on the design of an efficient method to restore the feasibility of a personnel roster in a static environment considering a single decision moment, on which all disruption information is known, whereas the system dynamics of personnel scheduling applications are neglected. Only Wolbeck et al. (2020) consider multiple rescheduling decisions that revise the nurse roster from the moment only one single capacity disruption arises and installs a fair shift penalisation scheme over time. However, in their study, no attention is given to the definition of a suitable length of the time horizon, frequency and timing of rescheduling decisions, nor to the impact of timeline uncertainty. Most studies that consider the rerostering problem, are related to the nurse shift rerostering problem, for which Clarke et al. (2015) provide an overview of the literature. Wolbeck et al. (2020) presents a generic formulation of the nurse rerostering problem that can be adjusted to various cases with different characteristics. Bäumelt et al. (2016), Chiaramonte and Caswell (2016) and Wickert et al. (2019), amongst others, propose different meta-heuristic algorithms as a solution methodology for the nurse rerostering problem, which is basically a personnel shift scheduling problem. The previous studies dealing with the nurse rerostering problem consider only disruptions that are the result of staff absenteeism as pointed out by the review of Clarke et al. (2015). More recently, Maenhout and Vanhoucke (2018) study the static personnel shift and task rescheduling problem considering the uncertainty of demand, arrival and capacity. They propose a local search-based heuristic that combines a variable neighbourhood search and a perturbation method based on mathematical programming in order to restore the feasibility of personnel rosters. Rather than devising an efficient solution methodology to solve the static rescheduling problem as done by Maenhout and Vanhoucke (2018), the focus in this paper is on the development of efficient and effective recovery decision strategies for the dynamic rescheduling problem, giving insight into the timing, frequency and horizon of rescheduling decisions so that disruptions arising dynamically over the scheduling horizon are adequately dealt with.

Short-term allocation recovery decisions have been researched primarily for task scheduling problems relative to the transportation industry, for which the causes of disruptions are more of a technical or external nature resulting from uncertainty of arrival (see Clausen et al., 2010; Cacchiani et al., 2014 for a survey). Bard and Purnomo (2005a, 2005b) study allocation decisions in the healthcare sector to recover nurse schedules in the short term that are primarily impacted by uncertainty of demand. Similarly, Gross et al. (2018) propose a model for rescheduling physicians as a response to unplanned absenteeism in a hospital. The preferred methodology to solve allocation models in the literature is mixed-integer programming. Apart from these static reactive allocation methods, a limited number of studies proposed a two-stage proactive method to construct a robust personnel schedule considering uncertainty upfront, combining scheduling and allocation decisions (e.g. Ingels & Maenhout, 2017; Parisio & Jones, 2015). However, to the best of our knowledge, there is no study that combines rerostering and allocation decisions together to improve the decision-making and design a suitable dynamic recovery strategy.

Different studies in the literature [e.g. (Rezanov & Ryan, 2010; Clausen et al., 2010; Maenhout & Vanhoucke, 2013; Wickert et al., 2019)] show the importance and (computational) benefits of reducing the time horizon and/or the number of employees, i.e. the so-called window technique, to solve personnel rerostering and/or allocation problems. The proper definition of the rescheduling time horizon and the (number of) employees included in the recovery problem is crucial to ensure high-quality solutions. Maenhout and Vanhoucke (2013) evaluate different strategies regarding the lead time or pre-period and after-period, i.e. the considered horizon before or after the schedule disruptions, assuming that all disruptions causing a rescheduling are known. They conclude that considering a pre-period of a single day and an after-period of one or two days significantly improves solution quality and is sufficient to restore the personnel roster efficiently.

3 Problem description and formulation

In this paper, we study the dynamic personnel shift and task rescheduling problem. We assume that a baseline personnel roster has been composed based on expected information (Sect. 3.1). Changes to the schedule parameters, potentially disrupting the schedule, arise in a dynamic manner over the time horizon as a result of operational variability (Sect. 3.2). To reinstate the workability of the schedule, the personnel planner can decide to conduct a rescheduling decision, which embodies either a rerostering decision or an allocation decision, at different moments in time following a particular recovery decision strategy (Sect. 3.3).

3.1 The integrated personnel shift and task scheduling problem

Shift scheduling and task assignment are two related optimisation problems. The personnel shift scheduling problem assigns shifts and days off to create a line-of-work for each worker. The task assignment problem assigns tasks to workers to compose duties based on worker availability, which is determined by their line-of-work. The integration of both problems leads to an improved personnel roster (Ernst et al., 2004). The integrated personnel shift and task scheduling problem involves a medium-term planning horizon consisting of a set of days D (index d). A set of tasks $\overline{J}_d$ (index j) needs to be performed on every day d. A task j on a particular day d, designated by (d, j), has a start time ($\overline{st}_{dj}$), finish time ($\overline{ft}_{dj}$) and duration ($\overline{t}_{dj}$). These tasks are assigned to a set of homogeneous workers $\overline{W}$ (index w), who are able to carry out all tasks. These workers are organised to work following a set of shifts I (index i), which comprehends particular shift duties $i \in I \setminus i^{*}$ to carry out the allocated tasks and a free shift or day off $i^{*}$. Each shift $i \in I$ is determined by a start time $S_i$, end time $F_i$ and duration $T_i$. The tasks and shifts allocated to an individual worker over the planning horizon compose a line-of-work. The set of individual lines-of-work for all workers yields the baseline personnel roster. The following constraints are imposed on this schedule, i.e.

• Staffing requirements stipulate that a task j on day d must be carried out by a specific number of individual workers, i.e., $\overline{R}_{dj}$. Tasks with a staffing requirement higher than one are broken down into (sub-)tasks with staffing requirements equal to one, for which the characteristics (duration, start and finish time) are identical.

• Time-related or calendar constraints are imposed on the scheduling of shifts for an individual worker. These constraints embody both counter and sequence constraints. A worker w can carry out a single shift duty i ($i \in I \setminus i^{*}$) or a day off $i^{*}$ per day. The planning horizon is divided into different periods $p \in P$ (e.g. a calendar week) and in each period a worker should work between a minimum ($g^{\textrm{min}}$) and maximum ($g^{\textrm{max}}$) number of shift duties. Furthermore, a minimum rest time of 11 h between shift duties is imposed, establishing a forward rotation of shifts over consecutive days. The set of shifts $B_i$ lists the shift duties that cannot be assigned on day $d+1$ after shift i has been assigned on day d. Additional sequence restrictions are imposed on the minimum ($h^{\textrm{min}}$) and maximum ($h^{\textrm{max}}$) consecutive work days and on the minimum ($w^{\textrm{min}}$) and maximum ($w^{\textrm{max}}$) consecutive days off.

• Task assignment constraints prohibit overlap between allocated tasks. Based on the start and finish times of the tasks, a set of task cliques $\overline{C}$ (index c) can be defined. Each clique consists of a set of tasks $\overline{K}_c$ out of which only one task can be carried out by a specific worker. When a worker is assigned to a task, the worker is assigned to the associated shift ensuring the link between task and shift assignments. The pre-emption of tasks is forbidden.

The objective is to construct an efficient baseline schedule, minimising the number of hired workers and the number of planned shift duties. A worker is hired from the moment (s)he performs a shift duty in the planning horizon. The problem relies on three types of decision variables, i.e. (1) variable $\overline{x}_{jwdi}$ is equal to 1 if worker w is allocated to task j related to shift i and day d, and 0 otherwise; (2) variable $\overline{y}_{wdi}$ equals 1 if worker w performs shift i on day d, and 0 otherwise; and (3) variable $\overline{z}_{w}$ is equal to 1 if worker w is hired, carrying out a line-of-work, and 0 otherwise. Note that the baseline personnel schedule is made public a couple of days (or weeks) before the day of operations and scheduling decisions are taken based upon deterministic, expected information related to task staffing requirements, start times and durations of tasks and worker availability. A formulation of the baseline scheduling problem can be found in Maenhout and Vanhoucke (2018). The set of selected workers in the baseline schedule, i.e. $W = \{w \in \overline{W} | \overline{z}_w = 1\}$ stipulates the set of workers that is input to the dynamic rescheduling problem, which implies that any disruption in the operational phase should be resolved by the workers assigned in the tactical decision phase as no additional workers can be deployed.

3.2 Operational variability

Certain schedule parameter values, input to construct the baseline schedule, may emerge differently than expected when new or more accurate information is obtained at different points in time between the moment the schedule has been announced and the day of operations. These unexpected parameter values may embody schedule disruptions, making the baseline roster infeasible. This operational variability encountered during the execution of a personnel roster is determined by (1) timeline uncertainty and (2) schedule parameter uncertainty, which are explained below.

3.2.1 Timeline uncertainty

In contrast to the static rescheduling variant, disruptions are not all known at a particular point in time (e.g. the beginning of the time horizon) but arise in a gradual manner over the time horizon according to the disruption information profile. The associated degree of timeline uncertainty is dependent on the specific application as some environments are more volatile than others, characterised by two factors, i.e.

• (i) The frequency of disruption information points: A disruption information point defined on day d is a point in time the personnel planner is notified about newly available disruption information, indicated by the exogenous parameter $DIP_d$ with a value equal to 1. A day d on which no additional information is revealed, is indicated as $DIP_d = 0$. The disruption information points are predefined depending on the problem setting and can occur on a regular basis, e.g. on a daily or weekly basis, the latter assuming that the disruption information for the upcoming week is gathered and provided to the personnel planner, e.g. at the beginning of the week. The basic scenario under study is that a personnel planner considers new information every day of the planning horizon, conform to the discussed real-life application. However, in order to assess the impact of timeline uncertainty, we consider different scenarios related to the frequency of disruption information points. The larger the number of disruption information points, indicated by $\#DIP = \sum _d DIP_d$, the larger the uncertainty as disruption information becomes gradually known in a more fragmented manner.

• (ii) The information horizon ($IH$): The number of days for which new disruption information becomes available starting from the disruption information point. The smaller the information horizon, the larger the uncertainty, as less future disruption information is known.

3.2.2 Schedule parameter uncertainty

Similar as in the research of Maenhout and Vanhoucke (2018), we consider three sources of parameter uncertainty, characterised by different probability distributions and parameters, i.e.

• (i) Personnel may become unavailable for one or more days in the planning horizon due to uncertainty of capacity (e.g. illness, holiday). Based on this absenteeism, the set of shift disruptions L and the set of task disruptions M can be defined, comprising the relevant duties and tasks the associated workers are assigned to in the baseline roster. The availability of worker w on day d is modelled via a Bernoulli distribution with probability $Pr(\chi )$ (with $\chi$ as a binary stochastic variable, assuming a value of 1 if the worker is available, and 0 otherwise). The majority of studies, comprising a wide variety of application domains, employ independent Bernoulli trials to model the absenteeism of workers on a particular day (e.g. Maass et al.,2017; Mac-Vicar et al., 2017; Gross et al., 2018; Wickert et al., 2021) . However, there are some rare cases in which the absenteeism probability takes some dependency into account. Relevant is the research of Wolbeck et al. (2020), who model worker absenteeism considering both single-day and consecutive-day absences, such that there is some dependency between capacity disruptions for a single worker on subsequent days. Notification of worker absences is determined in an independent manner using the Bernoulli distribution, whereas the number of days of absence is generated according to a discrete distribution.

• (ii) The actual demand for staff, represented by the actual set of tasks $J_d$, may deviate from the expected staffing requirements, indicated by the original set of tasks $\overline{J}_d$, requiring changes to the personnel shift and task schedule due to uncertainty of demand (Bard & Purnomo, 2005a; Ingels & Maenhout, 2017). The demand for staff is assumed to be uncertain over a particular shift i on day d. The staffing requirements $\sum _{j \in \overline{J}_{di}} R_{dj}$ of shift duty $i \in I \setminus i^{*}$ (with $\overline{J}_{di}$ = {$(d,j)\;|\; \overline{st}_{dj} \ge S_i \wedge \overline{ft}_{dj} \le F_i, j \in \overline{J}_d, d \in D$}) can be modelled by a Poisson distribution with the expected staffing requirements $\sum _{j \in \overline{J}_{di}} \overline{R}_{dj}$ as the mean value. A change in the staffing requirements of a particular shift impacts the set of tasks $J_d$ as tasks may either be removed or added (Maenhout & Vanhoucke, 2018).

• (iii) Due to uncertainty of arrival, the original parameters ($\overline{st}_{dj}, \overline{ft}_{dj}$ and $\overline{t}_{dj}$) of task j on day d can be changed and a new actual start time $st_{dj}$, finish time $ft_{dj}$ and duration $t_{dj}$ may be postulated (eg., Sadjadi et al., 2011). Uncertainty related to durations of tasks is modelled by a triangular distribution with an expected duration equal to $\overline{t}_{dj}$. The lower and upper limits are equal to $\beta _1$ $\times$ $\overline{t}_{dj}$ and $\beta _2$ $\times$ $\overline{t}_{dj}$, respectively, with $\beta _1 \le 1$ and $\beta _2 \ge 1$ as variability measures. Furthermore, variation in start time of task (d, j) is modelled by a uniform distribution within interval [$\overline{st}_{dj} - st^{dev}$; $\overline{st}_{dj} + st^{dev}$].

3.3 The dynamic rescheduling problem

In response to the incurred disruptions gradually arising over the planning horizon, the personnel planner undertakes one or multiple (static) rescheduling decisions in a reactive manner following a particular recovery decision strategy to restore schedule feasibility. Each rescheduling decision, taken at a certain point in time, considers a particular rescheduling horizon for which the—at that moment in time—known disruptions are tried to be resolved by adapting the personnel shift and task schedule, while keeping the number of changes to the baseline schedule to a minimum.

3.3.1 Recovery decision strategy

A recovery decision strategy is defined by the following characteristics, i.e.

• (i) The timing and frequency of rescheduling decision points: The personnel planner can undertake a rescheduling decision at any day d of the planning horizon, which can be either a rerostering decision or an allocation decision, determined by the rescheduling horizon. The personnel planner can select the points in time, at which (s)he actually tries to restore the personnel schedule by adapting the schedule, i.e. the so-called rerostering decision points ($RDP_d = 1$) or allocation decision points ($ADP_d = 1$). When such a recovery or allocation decision is not taken, the respective variables $RDP_d$ and $ADP_d$ are set to 0.

• (ii) The rescheduling horizon (RH): This horizon corresponds to the number of days subject to rescheduling, starting from the day of the rescheduling decision point considered. Hence, in contrast to typical rescheduling decisions defined in the literature that consider the remaining horizon, starting from the rescheduling decision point under consideration towards the end of the planning horizon, the recovery methodology applies the time-window technique such that a rescheduling decision on day d considers only a limited set of days $D^v_d \subseteq D$. The other days in the planning horizon are not considered for rescheduling, which implies that these assignments are fixed to the assignments made via an earlier (re-)scheduling decision. The rescheduling decision may comprehend either an allocation decision or a rerostering decision, between which a distinction is made based on RH, i.e.

  • An allocation decision makes short-term ad hoc adjustments to both shift and task assignments. Allocation decisions adopt a wait-and-see approach and are modelled as a recovery decision with a horizon of only a single day, i.e. the day of operation d ($RH = 1$, $D^v_d = \{d\}$), for which all schedule (disruption) information is known with certainty. With such short lead times, the rescheduling effort is limited but there is little flexibility to adjust personnel shift assignments, which should be conform to the (hard) time-related constraints given the (fixed) assignments on previous and later days.

  • A rerostering decision considers a medium-term horizon of a couple of days starting from the day of operation d ($RH > 1$, $D^v_d = \{d, \ldots , d^*\}$ with $d^* = min\{d+RH-1, |D|\}$) to adapt the schedule, taking the relevant schedule (disruption) information into account. As the recovery horizon comprises multiple days, a rerostering decision considers the personnel shift and task allocations on multiple contiguous days, taking the task assignment constraints, the staffing requirements and especially the time-related constraints explicitly into account. In this way, rerostering decisions allow to anticipate to some future schedule disruptions and are characterised by a larger scheduling flexibility and effort compared to allocation decisions.

During the planning horizon, the personnel planner may carry out one or multiple rescheduling decisions, possibly invoking both types of recovery decisions at different moment in time, depending on the type of disruptions arisen on a particular day. In this way, the strengths of both types of decisions can be combined to compose an efficient recovery decision strategy. Note that it is not useful to consider a rerostering decision and an allocation at the same point in time (day d), i.e. $RDP_d + ADP_d \le 1$. Implementing an allocation decision on the same day when undertaken a rerostering decision would unnecessarily increase the rescheduling effort while the quality of the restored roster will not further improve.

3.3.2 The (static) rescheduling decision

At every rescheduling decision point ($RDP_d = 1$ or $ADP_d = 1$), a (static) recovery decision is taken considering a limited horizon with length RH, a set of shift disruptions L and a set of task disruptions M. The embedded recovery mechanisms to adjust the personnel shift and task schedule rely on

• (i) The cancellation of a task when the staffing requirement of the task is not fulfilled. This is explicitly stated in the model by decision variable $n^{u}_{dj}$, which equals 1 if the corresponding task j on day d is cancelled and is 0 otherwise.

• (ii) The overstaffing of a task such that the task can be assigned to more workers than defined by the staffing requirement. The variable $n^{o}_{dj}$ indicates the excess number of workers assigned to task j on day d.

• (iii) The swapping of tasks and shifts between workers is performed when workers are assigned to new tasks or shifts during their line-of-work and take over tasks and shift duties that were originally assigned to other personnel members.

To restore the personnel shift and task schedule, two objectives are considered, i.e.

• (i) The maximisation of the feasibility of the personnel shift and task schedule, considering both the scheduling of the shift duties for an individual worker, respecting the time-related constraints, and the task staffing requirements.

• (ii) The minimisation of the number of schedule deviations of the restored schedule compared to the originally announced schedule as a result of the swapping of shift duties and tasks between workers. This objective considers schedule stability over multiple rescheduling decisions, in line with previous research on dynamic (re-)scheduling (Ouelhadj & Petrovic, 2009), advocating schedule adherence to the baseline schedule. In this way, we consider not only the personnel satisfaction as personnel dislike schedule changes, but also account for efficiency considerations as the baseline schedule is constructed minimising the number of workers and planned shift duties.

The mathematical formulation for the (static) rescheduling problem, which is provided below, encompasses a modified version of the model proposed by Maenhout and Vanhoucke (2018) to account for the (restricted) rescheduling horizon and the fixing of variables outside this time window via constraints (13) and (14), making the model relevant in the context of dynamic rescheduling.

Sets

I:

The set of shifts (index i)

W:

The set of workers (index w)

D:

The set of days in the planning horizon (index d)

$D^v_d$:

The set of days in the planning horizon subject to recovery

P:

The set of periods in the planning horizon (index p)

$J_d$:

The set of tasks on day d (index j)

C:

The set of cliques (index c)

$K_{c}$ :

The set of tasks incorporated in clique c

$B_i$:

The set of shifts forbidden on day $d+1$ after shift i has been scheduled on day d

L:

The set of disrupted shift assignments with L = {$(w,d,i)\;|\; y_{wdi} = 0 \wedge \overline{y}_{wdi} = 1, w \in W, d \in D, i \in I$} (index l)

M:

The set of disrupted task assignments with M = {$(j,w,d,i)\;|\; x_{jwdi} = 0 \wedge \overline{x}_{jwdi} = 1, w \in W, d \in D, j \in J_d, i \in I$} (index m)

Parameters

$st_{dj}$:

The start time of task j on day d

$ft_{dj}$:

The finish time of task j on day d

$t_{dj}$:

The duration of task j on day d

$R_{dj}$:

The staffing requirement of task j on day d

$S_i$:

The start time of shift i

$F_i$:

The finish time of shift i

$T_{i}$:

The duration of shift i

$g^{\textrm{min}}$:

The minimum number of shift duties in one period for an individual worker

$g^{\textrm{max}}$:

The maximum number of shift duties in one period for an individual worker

$h^{\textrm{min}}$:

The minimum number of consecutive days on for an individual worker

$h^{\textrm{max}}$:

The maximum number of consecutive days on for an individual worker

$w^{\textrm{min}}$:

The minimum number of consecutive days off for an individual worker

$w^{\textrm{max}}$:

The maximum number of consecutive days off for an individual worker

$\overline{x}_{jwdi}$:

1, if task j is allocated to worker w, shift i and day d in the baseline schedule, 0 otherwise

$\overline{y}_{wdi}$:

1, if worker w is scheduled to shift i on day d in the baseline schedule, 0 otherwise

$\overline{z}_{w}$:

1, if worker w is hired according to the baseline schedule, 0 otherwise

$x'_{jwdi}$:

1, if task j is allocated to worker w, shift i and day d in the previous schedule, 0 otherwise

$y'_{wdi}$:

1, if shift i on day d has been scheduled for worker w in the previous schedule, 0 otherwise

$c^{1}_{w}$:

The cost for changing the staffing of worker w in the operational phase

$c^{2,1}_{wdi}$:

The cost for scheduling worker w to the disrupted shift duty i on day d

$c^{2,2}_{wdi}$:

The cost for scheduling worker w to shift i on day d, different to the baseline schedule

$c^{3,1}_{jwdi}$:

The cost for allocating worker w to the disrupted task assignment j, day d, shift i

$c^{3,2}_{jwdi}$:

The cost for allocating worker w to task j, day d, shift i, different to the baseline schedule

$c^{o}$:

The cost per worker overstaffing of a task

$c^{u}$:

The cost for cancelling a task

Decision variables

$x_{jwdi}$:

1, if worker w is allocated to task j, shift i on day d, 0 otherwise

$y_{wdi}$:

1, if worker w is scheduled to shift i on day d, 0 otherwise

$z_{w}$:

1, if worker w is assigned to perform a line-of-work, 0 otherwise

Auxiliary variables

$n^{u}_{dj}$:

1, if task j on day d is cancelled, 0 otherwise

$n^{o}_{dj}$:

The excess number of workers for task j on day d

Mathematical formulation

$$\begin{aligned}&\text {Min} \quad \sum _{d \in D} \sum _{j \in J_d} (c^{o} \; n^{o}_{dj} + c^{u} \; n^{u}_{dj}) + \sum _{(w,d,i) \in M} c^{2,1}_{wdi} \; y_{wdi}\nonumber \\&\qquad + \sum _{(j,w,d,i) \in L} c^{3,1}_{jwdi} \; x_{jwdi} + \nonumber \\&\quad \sum _{w \in W} c^{1}_{w} \; |z_{w} - \overline{z}_{w}| + \sum _{w \in W} \sum _{d \in D} \sum _{i \in I} c^{2,2}_{wdi} \; |y_{wdi} - \overline{y}_{wdi}| \nonumber \\&\qquad + \sum _{j \in J_d} \sum _{w \in W} \sum _{d \in D} \sum _{i \in I} c^{3,2}_{jwdi} \; |x_{jwdi} - \overline{x}_{jwdi}| \end{aligned}$$

(1)

$$\begin{aligned}&\sum _{i \in I}\sum _{w \in W} x_{jwdi} + n^{u}_{dj} - n^{o}_{dj} = R_{dj} \quad \quad \forall d \in D, \forall j \in J_d \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{(d,j) \in K_{c}} x_{jwdi} \le y_{wdi} \quad \quad \forall w \in W, \forall c \in C \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{d \in D} \sum _{i \in I\setminus i^{*}} y_{wdi} \le M \; z_{w} \quad \quad \forall w \in W \end{aligned}$$

(4)

$$\begin{aligned}&\sum _{i \in I} y_{wdi} = 1 \quad \quad \forall w \in W, \forall d \in D \end{aligned}$$

(5)

$$\begin{aligned}&\sum _{d = 7p}^{7p + 6} \sum _{i \in I\setminus i^{*}} y_{wdi} \ge g^{\textrm{min}} \quad \quad \forall w \in W, \forall p \in P \end{aligned}$$

(6)

$$\begin{aligned}&\sum _{d = 7p}^{7p + 6} \sum _{i \in I\setminus i^{*}} y_{wdi} \le g^{\textrm{max}} \quad \quad \forall w \in W, \forall p \in P \end{aligned}$$

(7)

$$\begin{aligned}&\sum _{d}^{d+h^{\textrm{min}}-1} \sum _{i \in I \setminus i^{*}} y_{wdi} - h^{\textrm{min}} \sum _{i \in I \setminus i^{*}} y_{wdi} (1- \sum _{i \in I \setminus i^{*}} y_{w(d-1)i}) \ge 0 \quad \quad \nonumber \\&\forall w \in W,\forall d \in \{2,\ldots , |D| - (h^{\textrm{min}}-1)\} \end{aligned}$$

(8)

$$\begin{aligned}&\sum _{d' = d}^{d+h^{\textrm{max}}} \sum _{i \in I\setminus i^{*}} y_{wd'i} \le h^{\textrm{max}} \quad \quad \forall w \in W, \forall d \in \{1,\ldots , |D|-h^{\textrm{max}}\} \end{aligned}$$

(9)

$$\begin{aligned}&\sum _{d}^{d+w^{\textrm{min}}-1} y_{wdi^{*}} - w^{\textrm{min}} y_{wdi^{*}} (1 - y_{w(d-1)i^{*}}) \ge 0 \quad \quad \forall w \in W,\nonumber \\&\forall d \in \{2,\ldots , |D| - (w^{\textrm{min}}-1)\} \end{aligned}$$

(10)

$$\begin{aligned}&\sum _{d' = d}^{d+w^{\textrm{max}}} y_{wd'i^{*}} \le w^{\textrm{max}} \quad \quad \forall w \in W, \forall d \in \{1,\ldots , |D|-w^{\textrm{max}}\} \end{aligned}$$

(11)

$$\begin{aligned}&y_{wdi} + \sum _{i' \in B_i} y_{w(d+1)i'} \le 1 \quad \quad \forall w \in W, \forall d \in \{1,\ldots , |D|-1\}, \forall i \in I \end{aligned}$$

(12)

$$\begin{aligned}&y_{wdi} = y'_{wdi}\quad \quad \forall w \in W, \forall d \in D \setminus D^v_d, \forall i \in I \end{aligned}$$

(13)

$$\begin{aligned}&x_{jwdi} = x'_{jwdi} \quad \quad \forall j \in J_d, \forall w \in W, \forall d \in D \setminus D^v_d, \forall i \in I \end{aligned}$$

(14)

$$\begin{aligned}&x_{jwdi}\; \text {binary} \quad \quad \forall j \in J_d, \forall w \in W, \forall d \in D, \forall i \in I \nonumber \\&y_{wdi}\; \text {binary} \quad \quad \forall w \in W, \forall d \in D, \forall i \in I \nonumber \\&z_{w}\; \text {binary} \quad \quad \forall w \in W \nonumber \\&n^{u}_{dj}\; \text {binary}\quad \quad \forall j \in J_d, \forall d \in D \nonumber \\&n^{o}_{dj} \; \ge 0 \; \text {and integer}\quad \quad \forall j \in J_d, \forall d \in D \end{aligned}$$

(15)

Equation (1) formulates the objective function, which consists of two components. The first objective component minimises the total sum of feasibility penalties involving the staffing requirements and assignment to disrupted shifts and/or tasks. In order to restore feasibility as best as possible, we include variables $n^{u}_{dj}$ and $n^{o}_{dj}$ in the staffing requirements (Eq. 2), allowing respectively under- and over-coverage of staffing requirements at the expense of a penalty cost. In order to prevent violation of (hard) time-related constraints, the variables related to sets L and M of disrupted assignments are still eligible at the expense of a very large penalty cost when selected. The assignment of a worker to a disrupted shift or task is further denoted as an infeasible shift or task assignment. The second component minimises the differences between parameters $\overline{z}_{w}, \overline{x}_{jwdi}$ and $\overline{y}_{wdi}$ related to the baseline schedule and decision variables $z_{w}$, $y_{wdi}$ and $x_{jwdi}$ in order to optimise the personnel satisfaction and avoid deteriorating the schedule efficiency. Note that via the definition of appropriate penalty costs, the objective (Eq. 1) can be linearised as stated in Maenhout and Vanhoucke (2018).

Equation (2) formulates the staffing requirements. This constraint imposes that each task is executed by the required number of workers, but allows deviations from the stipulated task demand for staff. Constraint (3) embodies the relation between task and shift assignment variables, i.e. if a worker is allocated to a task, (s)he has to carry out the corresponding shift duty. Additionally, the constraint stipulates that a worker can be allocated to at most one task out of a set of overlapping tasks $K_c$, forming the maximal clique c. Constraint (4) models the relation between the shift assignment variables and worker hiring variables, i.e. a worker is hired when (s)he performs a shift in the planning horizon. Constraints (5)–(12) represent the time-related requirements imposed on the line-of-work of an individual worker, determining the scheduling of shift duties over the planning horizon. Equation (5) assigns a worker to one shift duty per day or to a day off. Constraints (6) and (7) restrict minimum and maximum number of shift duties per calendar week. Constraints (8) and (9) limit minimum and maximum number of shift duties on consecutive days. Constraints (10) and (11) impose restrictions on minimum and maximum number of consecutive days off. Equation (12) forbids the consecutive assignment of particular shift duties to allow only forward rotation of shifts. Equations (13) and (14) implement the time-window technique, ensuring that only task and shift assignments related to the set of days $D^v_d$ can be changed. Other assignments, outside this time window, are fixed to the assignments made in the previous personnel schedule, which is either the baseline schedule or the schedule constructed at a previous rescheduling decision point. Note that the values for $x'_{jwds}$ and $y'_{wds}$ are updated after every (re-)scheduling decision. Equation (15) state the domains of the decision variables.

4 Methodology

The dynamic rescheduling problem under study can be modelled as a multi-stage stochastic optimisation problem, which implements a recourse decision stage for every potential decision moment and implicitly considers the decisions related to timing of rescheduling decision points, type of recovery decisions and rescheduling horizon. However, due to the large number of stochastic variables, the exponential number of possible scenarios and the large number of binary decision variables, a stochastic approach is computationally intractable. In this paper, we utilise a two-step methodology to investigate the dynamic rescheduling problem. This methodology first stipulates the values for the relevant recovery decisions to be taken and subsequently assesses empirically roster quality after simulation and rescheduling. In this way, we present heuristic rules-of-thumb defining recovery strategies leading to restored personnel schedules of high quality. In addition, we study the sensitivity in performance of the (proposed) scheduling rules for different timeline uncertainty profiles. In this section, we discuss the methodology and conducted experimental design to derive relevant findings. Algorithm 1 provides an overview of the functioning of the dynamic rescheduling algorithm given a timeline uncertainty profile and a stipulated recovery decision strategy. Taking these inputs into account, we mimic the dynamic progress of the personnel shift and task schedule and conduct the arising of operational variability and rescheduling decisions in a chronological order until the end of the planning horizon. The disruption information is generated over a particular information horizon at respective disruption information points using Monte Carlo simulation. The latter relies on the characteristics of the schedule parameter uncertainty, which is defined by hypothesised distributions and parameters. The static rescheduling problems (Eqs. 1–15), encountered when taking a rerostering decision ($RDP_d = 1$) or an allocation decision ($ADP_d = 1$), are solved exactly using mathematical programming. In this way, the devised recovery strategies are evaluated in an unambiguous manner thriving on empirical experimentation. Section 4.1 gives an overview of the relevant output metrics. Section 4.2 discusses relevant decision values for recovery strategies and presents rules-of-thumb to define dynamic recovery strategies.

4.1 Output metrics and performance evaluation

In order to discern suitable recovery strategies, the analysis is based on multiple metrics and performance is evaluated against objective benchmark recovery strategies.

4.1.1 Output metrics

As one of the primary research objectives is to devise effective and efficient recovery decision strategies in an unambiguous manner, we conduct a multi-objective evaluation considering rescheduling quality and rescheduling effort, i.e.

• Rescheduling quality (Z) The performance of recovery decision strategies is measured via evaluation of attained roster feasibility and number of schedule deviations of the final personnel schedule, obtained at the end of the planning horizon after recovery, in comparison to the baseline schedule. The objective function of the rescheduling model, i.e. Eq. (1), provides a mathematical representation of this performance measure. In our analysis of rescheduling quality, we account for two main objectives, i.e. (1) the maximisation of the schedule feasibility and (2) the minimisation of the number of deviations between the original and final roster (cf. Section 3.3.2), which encompass the following components:

  • Coverage: This component accounts for the feasibility related to the staffing requirements, expressed by the number of cancelled or understaffed tasks (#UST $= \sum _{d\in D} \sum _{j\in J_d} n^{u}_{dj}$) and the amount of task overstaffing (#OST $= \sum _{d\in D} \sum _{j\in J_d} n^{o}_{dj}$).

  • Infeasible assignments: This component measures the feasibility related to the hard time-related constraints, reflected by the number of infeasible assignments, i.e. $\sum _{(w,d,i) \in M} y_{wdi}$ ($\#Shifts$) and $\sum _{(j,w,d,i) \in L} x_{jwdi}$ ($\#Tasks$), respectively.

  • Deviations: This component measures the stability relative to the baseline roster, which is measured via the number of worker, shift and task deviations between the baseline and the final roster, formalised as $\sum _{w \in W} |z_{w} - \overline{z}_{w}|$ ($\#Workers$), $\sum _{w \in W} \sum _{d \in D} \sum _{i \in I} |y_{wdi} - \overline{y}_{wdi}|$ ($\#Shifts$) and $\sum _{j \in J_d} \sum _{w \in W} \sum _{d \in D} \sum _{i \in I} |x_{jwdi} - \overline{x}_{jwdi}|$ ($\#Tasks$), respectively.

  There is a clear trade-off between these two components, i.e. increasing the number of deviations improves the schedule feasibility and vice versa. As a result, these objective components are entangled and cannot be viewed in a separate manner when evaluating the attained roster quality after rescheduling, which necessitates the representation of the rescheduling quality as a compound of these components. To attain an adequate and balanced trade-off, however, suitable weights need to be devised, which is discussed in Sect. 5.1. Apart from the quality evaluation based on the comparison between the final and baseline schedule, we also take the dynamic roster changes into account in our analysis, i.e. the total number of shift and task changes conducted over the course of the planning horizon aggregated over all rescheduling decisions. These dynamic roster changes are evaluated by counting the number of changes between successive (intermediate) schedules. In order to break ties between recovery decision strategies that lead to similar performance in terms of Z, we consider the unnecessary shift and task changes resulting from conducting multiple rescheduling decisions. An unnecessary change is a change performed at a particular rescheduling decision point that is made undone or changed again at a later decision point due to the dynamic character of the problem, taking into account new disruption information. These unnecessary changes can be derived as the difference between the total number of dynamic roster changes and the number of changes between the baseline and final roster. These unnecessary task and shift changes entangle the organisation of resources and communication. (Unnecessary) shift changes, in particular, are detrimental to personnel satisfaction.

• Rescheduling effort (RE) In the context of (dynamic) re-scheduling, constructing a new schedule in an efficient manner has been a relevant topic of research (see e.g. Ouelhadj & Petrovic, 2009). We rely on RE to reflect the efficiency of a recovery decision strategy. RE is a function of the number of days considered for rescheduling and is a main determinant of the instance size. This metric is most relevant for practitioners to define efficiency as it gives an unambiguous idea—not related to the solution methodology—of the required manual interventions or computational efforts relative to automated solution procedures. Limiting the rescheduling effort can realise substantial efficiency savings. The rescheduling effort (Eq. 16) is equal to the summation of the considered rescheduling horizons relative to the days on which rescheduling decisions are taken. In other words, we sum the number of days considered in every rerostering decision, which is equal to the minimum of RH and the remaining number of days in the planning horizon starting with the day the rerostering decision is taken included (i.e. $|D| - d + 1$), and add the number of allocation decisions, which per definition consider a horizon of only a single day.

  $$\begin{aligned} {\textrm{RE}} = \sum _{d\in D}({\textrm{RDP}}_d \cdot \text {min}({\textrm{RH}},|D| - d + 1)+{\textrm{ADP}}_d) \end{aligned}$$

  (16)

When relating Z and RE of all possible recovery decision strategies, a set of efficient non-dominated solutions can be constructed, which can be shown using a Pareto front (Emmerich & Deutz, 2018). As we aim to identify a limited set of recovery decision strategies leading to high-quality personnel schedules, among which the personnel planner can choose based on both Z and RE, we try to find characteristics of recovery decision strategies that (1) lie on (or close to) the Pareto front and (2) show a stable performance over all identified decision strategies. In order to represent resulting quality of a particular set of recovery strategies, we calculate the convergence of the selected set of recovery strategies, represented by a point cloud of solution points, to the Pareto front. This measure refers to the closeness of the set to the Pareto front, which is most frequently evaluated in the literature by the mean generational distance (GD) (Li & Yao, 2019), calculating the Euclidian distance for each solution point in the solution set to the closest point in the Pareto set based on absolute values in performance (eq. (17)). The lower GD, the closer the solution set is to the Pareto front.

$$\begin{aligned} {\textrm{GD}} = \frac{1}{|N|}\sum _{n\in N}\sqrt{(Z(n) - Z^*(n))^2+({\textrm{RE}}(n) - {\textrm{RE}}^*(n))^2} \end{aligned}$$

(17)

with

N:

Set of recovery decision strategies considered (index n)

Z(n):

Rescheduling quality associated with recovery decision strategy n

$Z^*(n)$:

Rescheduling quality associated with closest point on Pareto front for recovery decision strategy n

${\textrm{RE}}(n)$:

Rescheduling effort associated with recovery decision strategy n

${\textrm{RE}}^*(n)$:

Rescheduling effort associated with closest point on Pareto front for recovery decision strategy n

Note that this metric, as presented, is based on the absolute values in performance related to Z and RE. As the scales of both criteria are different, the calculated GD is biased towards Z. This is because the term related to Z has a higher contribution to the distance formula. To solve this issue, studies in the domain of multi-objective optimisation have proposed several methodologies [e.g. TOPSIS (Hwang & Yoon, 1981), VIKOR (Opricovic, 1998)], which apply some type of unity-based normalisation (e.g. min–max feature scaling). When normalising the coordinates to some degree, the drawback is that the ranges of the metrics Z and RE are significantly different and points are not uniformly distributed over the solution space (cf. Section 5.2) so that many points have very small normalised coordinate values for Z. As a consequence, the GD with normalised coordinates shows small and meaningless values, which are very difficult to interpret and utilise for comparison of recovery strategy characteristics.

The purpose of GD, however, is primarily to give the reader insight into the degradation in Z associated with a set of recovery decision strategies resulting from the application of a specific rule-of-thumb versus the solutions lying on the Pareto front. RE operates merely as a tiebreaker to distinguish efficient from inefficient recovery decision strategies and to identify the Pareto front solutions. In this way, when using the absolute coordinates for calculating GD, GD provides valuable information relative to the proximity of the considered set of strategies to the Pareto front and differences can mainly be attributed to the difference in Z.

4.1.2 Benchmark recovery strategies

Apart from the comparison with the Pareto front, we benchmark performance of the visited recovery decision strategies to following strategies, i.e.

• (i) No rerostering/No allocation: This strategy does not conduct any rerostering nor allocation decision, i.e. $RDP_d = 0 \wedge ADP_d = 0$ $(\forall d \in D)$. A benchmark with this strategy reveals the degree according to which the proposed recovery strategy improves the roster quality after rescheduling as a result from recovery decisions.

• (ii) Allocation: This strategy assumes only allocation decisions, resolving only those schedule disruptions on the day of operations, i.e. $RDP_d = 0 \wedge ADP_d = 1$ $(\forall d \in D)$. This benchmark reveals to which degree rerostering decisions are beneficial to improve roster quality.

• (iii) Rerostering with Perfect Information (PI): This strategy assumes that all disruption information is known at the beginning of the planning horizon and conducts a single rerostering decision with a horizon spanning the entire planning horizon D. This benchmark allows an objective comparison of recovery strategies with a lower bound solution.

4.2 Analysis and experimental design

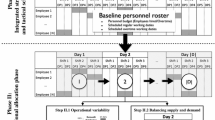
In order to obtain insight into the dynamic rescheduling problem under study and to identify characteristics of suitable recovery decision strategies leading to restored personnel schedules of high quality, we conduct several computational experiments. An overview of main experiments is provided in Fig. 1, which is described in the following subsections.

Fig. 1

Overview on the experimental design

4.2.1 Analysis of recovery decision strategies

Step 1. An analysis of recovery decision strategies is performed via a multi-objective evaluation of rescheduling quality versus rescheduling effort, constructing the Pareto front of efficient recovery strategies given the base case timeline uncertainty scenario, which conforms to most application domains. In this base scenario, we assume that new information becomes known every day ($\#DIP = |D|$) and the information horizon starts from the relevant disruption information point until the end of the planning horizon ($IH = |D|$). In this first step, we consider all recovery decision strategies related to the timing of rescheduling decisions, the type of recovery decision and the rescheduling horizon via complete enumeration. Overall, we consider $2 \times |D| \times 2^{|D|}$ different recovery decision strategies for which the dynamic rescheduling algorithm is applied and the performance is analysed, i.e.

• We consider all possible recovery decision timelines or combinations of alternative timings for conducting a rerostering decision over the planning horizon, leading to $2^{|D|}$ alternatives giving insight in the binary value for $RDP_d$ $(\forall d\in D)$. These rerostering decision timelines are potentially complemented or not by an allocation decision whenever $RDP_d = 0$, leading to 2 times $2^{|D|}$ recovery decision timelines in total, with and without allocation decisions.

• The rescheduling horizon is varied between 1 and the length of the planning horizon (|D|). Note that when $RDP_d = 1$ and $RH = 1$, the rerostering decision coincides with an allocation decision on day d.

In the initial analysis, only rerostering decisions are considered to investigate the course of the Pareto front and the characteristics of efficient recovery strategies, comparing non-dominated versus dominated recovery strategies, in a qualitative manner.

Step 2. An in-depth study is conducted in order to gain insight in the characteristics of suitable recovery strategies, exploring impact of length of rescheduling horizon, number of rescheduling decision points and timing of rescheduling points. The RH and the number of rerostering decision points ($\#RDP = \sum _d RDP_d$) are decision variables with a value ranging between 1 and the length of the planning period (|D|). For timing of rescheduling points, preliminary analysis pointed to different interesting patterns that need further investigation, i.e. (1) recovery decisions can be conducted on a regular basis over the time horizon; (2) recovery decisions can be linked to the disruption information points, i.e. the timeline uncertainty; and (3) recovery decisions can be linked to the (type of) disruptions incurred, i.e. the schedule parameter uncertainty.

Step 3. Based upon these characteristics, different heuristic rules-of-thumb are devised and evaluated, guided by GD as performance metric, to identify a limited set of well-performing recovery strategies amongst which the personnel planner can make a choice, making the trade-off between Z and RE, i.e.

• Rule 0. No rule: No specific characteristic is discerned such that this rule considers all recovery strategies visited. This rule is applied for benchmark purposes.

• Rule 1. Always rerostering: These recovery strategies ensure that new disruption information is always considered in one of the rescheduling decisions taken. In this way, we conduct a rerostering decision at least every time new information becomes available ($RDP_d \ge DIP_d$, $\forall d \in D$) with a minimum RH up to the next (predefined) rerostering point ($RH \ge \text {max}_q (d \times RDP_d^{(q+1)} - d' \times RDP_{d'}^{(q)})$, $\forall d, d' \in D$, with $RDP^{(q)}_d$ is the $q^{th}$ rerostering decision in the planning horizon). Note that the timeline uncertainty and associated disruption information points are assumed to be known in advance. This rescheduling policy can be considered as a hybrid rescheduling policy. This policy is, on the one hand, event-driven as a rescheduling decision is applied every time new disruption information arises and allows, on the other hand, to increase frequency of rescheduling decisions, invoking a rescheduling decision also on other moments in time.

• Rule 2. Regular rerostering decisions: This rescheduling strategy embodies a periodic policy to restore the personnel schedule at least at regular intervals, ensuring rerostering decision points are balanced and equally distributed over the planning horizon. A RH of at least two days is applied. The number of time periods or distance between consecutive rerostering decisions can be computed as $d \times RDP^{(q+1)}_d - d' \times RDP^{(q)}_{d'} = (|D| - 1)/\sum _d RDP_d$. This implies that when $\#RDP = 2$ and $|D| = 7$, the distance between decision points should be equal to 3 (e.g. decision points are positioned at time points 2 and 5) or, when $\#RDP = 3$, the distance between consecutive decision points is equal to 2 (e.g. decision points are positioned at time points 2, 4 and 6), etc. Hence, the smaller $\#RDP$, the larger the average distance is between consecutive decision points.

• Rule 3. Regular rerostering decisions with overlap: This periodic policy ensures rerostering decision points are not only balanced and equally distributed over the planning horizon (cf. rule 2), but also an overlap of at least a single day is installed between rescheduling horizons of consecutive rerostering decision points, i.e. $RH \ge d \times RDP^{(q+1)}_d - d' \times RDP^{(q)}_{d'} + 1$.

• Rule 4. Rerostering linked to disruption information point: This hybrid policy stipulates that, similar to rule 1, a rerostering decision is required whenever new disruption information is available ($RDP_d \ge DIP_d$, $\forall d\in D$) but does not specify a particular RH.

• Rule 5. Rerostering linked to information horizon: RH is set longer than IH when IH does not comprehend the entire planning horizon such that an after-period is created when rerostering $(RH > IH|IH < |D|$). Only when the information horizon is equal to the length of the planning horizon, RH and IH are equal $(RH = IH|IH = |D|$). This policy does not postulate any specific timing for the rescheduling decision points.

• Rule 6. Rerostering linked to disruptions: This event-driven policy ensures that a rerostering decision ($RH \ge 2$) is invoked if there is an infeasible shift assignment that needs to be resolved on day d or $d+1$, i.e. $\forall d \in D: RDP_d$ = 1$\;|\; \exists l \in L: y_{wdi} = 1 \vee y_{w(d+1)i} = 1$. In this way, possibly a pre-period and after-period are installed to solve capacity disruptions and improve rescheduling quality.

We further sophisticate recovery strategies following these rules by combining rerostering and allocation decisions. This implies that an allocation decision is conducted when no rerostering decision is applied ($\forall d \in D: ADP_d = 1 | RDP_d = 0$). The alternation between rerostering and allocation decisions may be induced because disruptions related to task information require a significantly lower rescheduling effort to achieve a feasible schedule compared to disruptions related to personnel-shift assignments, violating the shift-scheduling rules. Combining rerostering and allocation decisions reduces the required RE to attain a particular level of schedule feasibility.

4.2.2 Sensitivity analysis

The sensitivity in the performance of recovery decision strategies is explored by evaluating the impact of (1) dependency between capacity disruptions on consecutive days for individual workers and (2) the timeline uncertainty. Regarding the latter, the following steps are taken:

Step 1. In order to obtain insights into the sensitivity of timeline uncertainty on the performance of dynamic recovery strategies, we consider alternative timeline uncertainty scenarios, denoted as [$\#DIP$, IH], and apply the dynamic rescheduling algorithm for all recovery decision strategies (cf. Section 4.2.1) to conduct a multi-objective evaluation involving both Z and RE. In order to investigate the impact of timeline uncertainty on resulting value for Z and performance of proposed dynamic rescheduling rules, we vary the (input) timeline uncertainty characteristics as follows, i.e.

• The frequency of the occurrence of disruption information points is varied and three different settings are considered, i.e. disruption information points occur on a daily basis ($\#DIP = |D|$), once per three days ($\#DIP = \lceil |D|/3 \rceil$) and once per week ($\#DIP = |D|/7$).

• The length of the information horizon is varied and three different settings are considered, i.e. 1 day, 3 days and |D| days.

• In order to generate disruption information timelines with suitable characteristics, we only consider those combinations [$\#DIP$, IH] that allow the simulation of disruptions on every day of the planning horizon for reasons of comparability between uncertainty scenarios. For example, the combination [$\#DIP$, IH] = [3,1] are not considered as disruptions can only be generated on day d ($DIP_d = 1$), day $d+3$ ($DIP_{d+3} = 1$), etc and not on intermediate days (e.g. days $d+1$ and $d+2$).

Based on these settings, we consider in total six alternative timeline uncertainty scenarios [$\#DIP$, IH], i.e. [1,7], [3,3], [3,7], [7,1], [7,3] and [7,7]. In order to evaluate unambiguously the impact of timeline uncertainty, we use the technique of common random numbers. This implies that the same disruptions stipulated by the schedule parameter uncertainty are generated but that the occurrence of these (future) disruptions may arise at a different information disruption point. For example, when $\#DIP = 1$, all disruptions are generated for the entire planning horizon at this point. When $\#DIP = 7$ and $IH = 1$, daily information points are defined and the same disruptions arise but all disruption information is generated only for the day of the disruption information point and disruption information on future days is uncharted.

Step 2. Comparing results for different timeline uncertainty profiles allows analysing the impact of timeline uncertainty characteristics $\#DIP$ and IH. Via changing the input timeline disruption profile, we study (1) impact on the average value for Z; (2) impact on the course of the convex Pareto front, for which multiple phases are existent with a different slope indicating the improvement in quality as a function of RE; and (3) the divergence in quality between different recovery strategies, which is measured via metric GD. A larger variation in quality increases the importance of properly selecting a suitable recovery strategy to restore schedule feasibility.

Step 3. The sensitivity of timeline uncertainty is explored relative to the defining characteristics of recovery strategies, i.e. RH, $\#RDP$, $RDP_d$ and $ADP_d$, and performance of proposed heuristic rules-of-thumb.

5 Computational experiments

In this section, we provide insight into the recovery of disrupted personnel rosters in a dynamic environment. In Sect. 5.1, we describe test instances and parameter settings used in the experimental analysis. In Sect. 5.2, we demonstrate how the recovery decision timeline and the rescheduling horizon relate to the rescheduling quality and discern a Pareto front of efficient solutions mapping Z versus RE. In Sect. 5.3, we explore the sensitivity of obtained results to characteristics modelling the encountered uncertainty. Section 5.4 benchmarks individual recovery decision strategies known from literature to the best-performing heuristic rule devised in this study. Online Appendix C provides an overview of the most important managerial findings. All tests are carried out on an Intel Core i5 processor 2.6 Ghz and 8 Gb RAM.

5.1 Experimental dataset design

As a result of the variety of applications for the problem under study, we study a generic personnel shift and task scheduling problem. The design of the considered test instances is discussed in Maenhout and Vanhoucke (2018) and relies on the generation of synthetic data for which many settings are inspired by real-life or are derived from well-devised experiments in the literature. Online Appendix A section gives a summary of considered task characteristics, personnel scheduling characteristics, characterisation of uncertainty and objective function structure.

5.2 Analysis of recovery decision strategies

In this section, we analyse resulting rescheduling quality as a function of rescheduling effort and characteristics of recovery strategies. To conduct this analysis properly, all recovery decision alternatives are considered but we foremost focus on recovery strategies implementing only rerostering decisions, not complemented by allocation decisions, unless otherwise stated. In this way, we assess $7 \cdot 2^7 = 896$ recovery decision strategies, resulting from the combination of $2^7$ timeline decisions, indicating the rerostering decision points, and 7 possible rescheduling horizons, ranging between 1 and the length of the planning horizon (|D| = 7).

5.2.1 Multi-objective evaluation: rescheduling quality versus rescheduling effort

Figure 2 shows the scatter plot for recovery strategies not complemented by allocation decisions (indicated by light grey dots ($\bullet$)), displaying performance metrics Z and RE on y-axis and x-axis, respectively. The horizontal lines display the value for Z associated with the benchmarks, i.e. (1) quality without rerostering and without allocation decisions, (2) quality with solely allocation decisions and (3) quality resulting from rerostering with PI. In addition, we identified the Pareto front or non-dominated recovery strategies (indicated by black dots ($\bullet$) and connected via a line). Table 1 displays the (average) detailed performance (cf. Section 4.1.1) of the benchmark strategies and recovery decision strategies categorised based on RE. The percentage of dynamic roster changes on top of the deviations is shown between brackets, which resembles the absolute number of unnecessary changes versus the number of deviations between the baseline and final schedule. Table A in Online Appendix B shows a detailed comparison of objective components between Pareto and non-Pareto recovery decision strategies supporting qualitative findings discussed below.

Fig. 2

Computational results for all recovery strategies without allocation decisions: Z versus RE ([#DIP, IH] = [7, 7])

Table 1 Detailed computational results for recovery decision strategies ([#DIP, IH] = [7, 7]) and benchmark solutions

Figure 2 and Table 1 reveal that, in general, a larger effort improves the quality of the resulting personnel roster, i.e. the number of infeasible assignments and understaffed tasks decrease at the expense of a larger number of deviations to the original roster. However, the rate of improvement decreases when effort increases. The Pareto front reveals a steep improvement in Z when RE is limited and increases from 1 to 7 days. Note that with RE = 7 days, the variance in Z between different recovery strategies is large. For the most efficient strategies, almost all infeasible assignments are resolved and a significant amount of understaffed tasks are re-assigned to other workers (cf. Table A in Online Appendix B). A well-designed rescheduling strategy with a limited RE, possibly including days for which not all disruptions are known, outperforms the ‘Allocation’ benchmark that only restores the roster for the day of operation, for which all disruptions are known with certainty. Enlarging RE to more than 7 days significantly improves quality, primarily reducing the number of understaffed tasks. At some point, further enlarging RE is no longer useful as no efficient combinations are discerned as the value for Z stagnates. Consequently, although some disruptions may already be known in the further future, it is not necessary to consider the entire (remaining) period as RH, starting from the day under consideration until the end of the planning horizon. When RE is large, a smaller variance in Z, shown by the values for GD, is observed as nearly all recovery decision strategies lead to a restored solution of high quality. Compared to the benchmark ‘Rerostering with PI’, however, we observe a larger number of understaffed tasks due to the timeline uncertainty where new disruptions can arise daily on every future day.

Efficient strategies, lying on the Pareto front, show a compromise between $\#RDP$ and RH. Foremost, the days in the planning horizon that are subject to rerostering need to be concentrated around the days that are impacted by (the largest number of) capacity disruptions (cf. the performance of Rule 6 indicated in Sect. 5.2.3, which counts 9 of the 21 Pareto solutions). To resolve these quandaries in a satisfactory manner, changes to the original roster on multiple consecutive days are required. As a result, when possible, it is good practice to install multiple rescheduling decision points with a limited horizon of two to preferably four consecutive days, for which most of the disruptions are known. Inefficient strategies suffer from poor timing as they do not consider the days with the largest number of (capacity) disruptions or utilise the RE inefficiently, which is shown by the larger number of infeasible shift and task assignments for non-Pareto solutions. The latter is caused by (1) a too large number of rerostering decisions with a smaller RH such that either the disruptions are not entirely restored or a larger number of deviations is required due to the smaller degree of freedom to change the roster; or (2) a too small number of rerostering decisions with a longer RH, e.g., a single rerostering decision with a relatively longer RH undertaken at the beginning of the horizon, not taking into account that disruptions may arise in a dynamic manner every day of the planning horizon.

In following sections, we aim to identify suitable characteristics of recovery strategies, lying close to the Pareto front presented in Fig. 2 by making use of GD, together with performance metrics Z and RE. The value for Z averaged over all recovery decision strategies is 7692 and the average RE is 10.0 days. The GD for the 896 recovery decision strategies amounts to 566.9, which is employed as a benchmark. For a single recovery decision strategy, the required computational effort, measured via the $CPU$ time (in seconds), averages 7.3 s and ranges between 0.004 s and 61.9 s, which depends upon the recovery decision strategy and the instance characteristics. Note that these times are limited resulting from the considered planning horizon of 7 days and the many strategies characterised by a low RE. In search for proper recovery strategies, we enumerated and executed all possible strategies, leading to a total required $CPU$ of 13577.4 s ([$\#DIP$, IH] = [7,7]) for a single instance.

5.2.2 Rescheduling horizon and number of rescheduling decisions

Tables 2 and 3 display impact of RH and $\#RDP$ on the performance metrics. In addition, details are provided related to the objective component values, averaged over all 896 considered recovery strategies without allocation decisions. The percentage of dynamic roster changes on top of the deviations is shown between brackets. The results reveal that both RH as well as $\#RDP$ have a significant impact. A longer RH or a larger $\#RDP$ improves the value for Z at the expense of a larger RE. Increasing RH or $\#RDP$ reduces the number of understaffed tasks and the number of infeasible shift and task assignments in an incremental manner at the expense of a larger number of deviations to the original roster. In addition, the number of unnecessary changes increases as well, as schedule disruptions on later days may be anticipated and possibly considered again at a later decision point with additional information. Unnecessary (shift) changes are undesirable from the workers’ perspective. The results for GD reveal that the decision strategies with a RH of four or more days are well-performing and lead to high-quality solutions, lying close to the Pareto front. Recovery strategies with RH = 4 have significantly more solutions on the Pareto front than strategies considering a shorter or longer RH. A larger RH unnecessarily increases RE from 11.0 to 14.0 and the unnecessary dynamic shift changes from 21% to 36%, whereas Z does not significantly improve. Similarly, strategies with five or more rescheduling decisions perform significantly better than strategies with fewer decisions. The appropriated timing of these rescheduling decisions is discussed in the following sections. Based on all these metrics together, we conclude that suitable, well-performing recovery strategies should limit both RH and $\#RDP$ to a certain extent. Comparing RH and $\#RDP$, we observe that an increase of $\#RDP$ has the largest impact resulting in a better value for Z but also a larger number of (unnecessary) dynamic roster changes, which is due to the specific timeline uncertainty characteristics of the base case scenario, i.e. disruptions may arise on each day.

Table 2 Computational results as a function of RH

Table 3 Computational results as a function of #RDP

5.2.3 Timing of rescheduling decision points

Additional understanding in well-performing recovery strategies can be gained by analysing the timing of the rescheduling decision points. Relevant heuristic rules-of-thumb have been proposed in Sect. 4.2. Figure 3 has been composed similarly to Fig. 2. The set of recovery strategies following these rules is indicated by black dots ($\bullet$). Table B in Online Appendix B provides details related to the objective function components of solutions yielded via the rules-of-thumb. Note that the performance of rules 4 and 5 are not discussed for the base case timeline uncertainty scenario as for this timeline uncertainty profile, rule 4 coincides with rule 1 and rule 5 is highlighted in the previous section ($RH = 7$). Other observations are as follows:

Rule 1. Always rerostering

A natural decision strategy is to conduct rescheduling decisions such that all changed schedule parameters are considered in at least one of the rescheduling decisions. Since in the base case timeline uncertainty scenario new information may arise on every day of the horizon, a rescheduling decision is required every day. Figure 3a shows the performance (RE, Z) of those decision strategies. The results reveal that these recovery decision strategies lead to high-quality personnel rosters with an average value for Z of 2303 and RE is large, i.e. 20 days ($CPU$ = 14.5 s). Compared to the entire set of explored decision strategies (Rule 0), GD is significantly lower and decreases from 566.9 to 268.9. Hence, exploiting this characteristic enables the identification of a set of recovery strategies that are closer to the Pareto front but require a large effort. The resulting schedules denote a large degree of feasibility at the expense of a large number of deviations and unnecessary changes (e.g. when RH = 4, unnecessary task and shift changes amount to 137% and 48%, respectively).

Fig. 3

Computational results for the heuristic rules-of-thumb

Rule 2. Regular rerostering decisions

In order to reduce RE and number of deviations and unnecessary changes, the average distance between consecutive rescheduling decision points is a relevant timeline characteristic to define decision points in a balanced manner over the planning horizon. Figure 3b reveals that these strategies lead to personnel rosters with an average value for Z of 3827 while RE is moderate, equal to 13.2 days ($CPU$ = 9.0 s). Compared to the entire set of 896 explored decision strategies, GD is significantly lower and amounts to 341.0. When $RH = 4$, this rule lowers the unnecessary task and shift changes to 80% and 25%, respectively.

Rule 3. Regular rerostering decisions with overlap

Figure 3c reveals that installing some overlap of at least a single day between the rescheduling horizons of consecutive rescheduling decisions, balanced over the time horizon, significantly improves the value for Z compared to rule 2 from 3827 to 3208. In addition, GD improves from 341.0 to 271.1. This can be explained as (capacity) disruptions that may already have arisen and are known, are better restored a couple of days in advance via an earlier rerostering decision rather than restoring the disruption on the day of operation. The downside of defining overlap is that RE increases to 14.5 days ($CPU$ = 10.9 s), whereas the unnecessary task and shift changes are similar to Rule 2. Defining no overlap, i.e. the RH is ended (just) before the day of the next rerostering decision point, leads to an inferior quality. Decision strategies with limited or no overlap ($< 1$ day) involve a smaller RE (average 5.8 days) and lead to personnel rosters with an inferior value for Z (equal to 10,046) and a GD value of 773.6, which is worse than the average GD of the 896 decision strategies.

Rule 6. Rerostering linked to (capacity) disruptions

An analysis of the timing of decision points reveals that rescheduling decisions can be connected to the arising of capacity disruptions. A rerostering decision is taken preferably on the day before or on the day of the disruption with a limited $RH \ge 2$. In this way, primarily the numbers of infeasible shift and task assignments are reduced. Figure 3d shows that applying these rules lead to high-quality schedules that are lying close to the Pareto front. The average value for Z equals 1742 and RE amounts to 19.5 days ($CPU$ = 21.0 s), whereas there is only a slight increase regarding the unnecessary task and shift changes (i.e. 88% and 27%, respectively, when RH = 4). Compared to the entire set of explored decision strategies, GD has significantly decreased to 41.0.

5.2.4 Value of appending allocation decisions

Fig. 4 displays the resulting rescheduling quality and effort and compares the strategies that conduct additional allocation decisions when no rerostering decision is applied (indicated by grey triangles ($\blacktriangle$)), to recovery strategies without allocation decisions (indicated by light grey dots ($\bullet$)). The Pareto front of recovery strategies with and without allocation decisions are represented by black triangles ($\blacktriangle$) and black dots ($\bullet$), respectively. Note that as a result of appending allocation decisions, the average required $CPU$ only marginally increases.

Fig. 4

Computational results for combining rerostering and allocation decisions: Z versus RE ([#DIP, IH] = [7, 7])

The results reveal that, in general, combining allocation decisions with rerostering decisions does not outperform suitably devised recovery strategies without allocation decisions. The Pareto front with allocation decisions is dominated by the Pareto front when considering only rerostering decisions. However, as a result of included allocation decisions, recovery strategies are consistent and always lead to high-quality solutions having a better performance than the ‘Allocation’ benchmark. Appending allocation decisions improves the value for Z yielded by individual recovery strategies that do not apply a rerostering decision on every day of the planning horizon to ensure the latest disruption information is considered via a rescheduling decision. For example, when appending allocation decisions to rule 6, a rerostering decision ($RH \ge 2$) is conducted to resolve capacity disruptions on day d or $d+1$ and allocation decisions are taken on other days to resolve disruptions resulting from uncertainty of demand or arrival. This combined recovery strategy improves the average value for Z from 1742 to 1568 and decreases GD to 16.7, leading to high-quality schedules that are lying very close to the Pareto front. The drawback of appending allocation decisions is that the number of unnecessary task and shift changes significantly increase to 217% and 105% ($RH = 4$), respectively, as days are subject to rescheduling more frequently.

5.3 Sensitivity analysis

In this section, we investigate the sensitivity of results for the recovery decision strategies to the encountered uncertainty. More precisely, we study the impact of dependency between capacity disruptions (Sect. 5.3.1) and the timeline uncertainty characteristics (Sect. 5.3.2).

5.3.1 Impact of dependency between capacity disruptions

In this experiment, we consider the modelling of both single-day and consecutive-day absences for individual workers. Inspired by the research of Wolbeck et al. (2020), we set probabilities of 1, 2, 3, 4 and 5 days of absence equal to 55%, 20%, 20%, 5% and 1% respectively. Table 4 compares the obtained results with dependent capacity disruptions to the case for which the number of absent workers is determined day-by-day in an independent manner. The results are presented for rules 1, 2, 3 and 6, in combination or not with allocation decisions (‘with alloc’ vs. ‘w/o alloc’) for [$\#DIP$, IH] = [7,7]. The table shows that results are very similar when considering only single-day capacity disruptions versus the case of considering both single-day and multi-day absences and confirms the analysis done for independent capacity disruptions in previous section. Note that solution quality is worse for instances for which dependent capacity disruptions are generated, which is due to the larger number of disruptions simulated for these instances. Results reveal that rule 6 with allocation decisions appended (a hybrid policy) still performs best in terms of rescheduling quality, followed by rule 1, which is an event-driven policy for the base case scenario. Periodic rules 2 and 3 perform relatively worse because periodic recovery is not very responsive to the arising of dependent capacity disruptions on subsequent days. Appending allocation decisions leads to steep performance improvements for most recovery strategies. In addition, other findings related to RH, $\#RDP$, and Pareto front are identical when encountering either dependent or independent capacity disruptions.

Table 4 Computational comparison (Z, RE, GD) for dependent versus independent capacity disruptions ([#DIP, IH] = [7,7])

5.3.2 Impact of timeline uncertainty characteristics

In this section, we investigate the impact of timeline uncertainty characteristics, i.e. $\#DIP$ and $IH$, on the quality after rescheduling and the performance of the proposed rules-of-thumb. For that purpose, we vary the timeline uncertainty characteristics as discussed in Sect. 4.2.2. All possible combinations of rerostering decision points and rescheduling horizons are considered. Table 5 displays the impact of the timeline uncertainty characteristics, i.e. $\#DIP$ and IH, on the value for Z and related objective components. The table displays the measures averaged over all 896 considered recovery strategies without allocation decisions. Table 6 displays the performance (Z, RE and GD) for the rules-of-thumb identified in Sect. 4.2.1. The results are presented for each of these recovery strategies whether or not combined with complementary allocation decisions (‘with alloc’ vs. ‘w/o alloc’). The results related to the overall best performing rule are indicated in bold. In the analysis below, allocation decisions are only considered when explicitly stated.

Impact on rescheduling quality and Pareto front

Table 5 reveals that both $\#DIP$ as IH have a significant impact on the resulting performance. The results reveal that a lower uncertainty, i.e. a larger IH or a lower $\#DIP$, improves the quality of restored personnel rosters. This results from the acquisition and accumulation of a larger amount of disruption information a number of days in advance, which can be taken into account at an earlier (rerostering) point in time. When the uncertainty is lower, we observe a smaller number of understaffed tasks and infeasible assignments, at the expense of a larger number of deviations. However, despite the improved quality of the personnel rosters, a lower uncertainty leads to a larger absolute and relative number of unnecessary changes, especially task changes, performed dynamically throughout the course of the entire planning horizon. When timeline uncertainty is higher, not all disruptions are known well in advance and can be anticipated. Consequently, as disruptions may arise abruptly, not all disruptions could be resolved or changes cannot be reconsidered at a later rescheduling decision point, possibly made undone or changed again, for which the timeline uncertainty profile with $IH = 1$ and $\#DIP$ = 7 is exemplary. Comparing average results, we observe that an increase of $IH$ has the largest impact, improving Z by 103% (from 14,058 ($IH = 1$) to 6910 ($IH = 7$)), whereas a reduction of $\#DIP$ ameliorates Z by only 67% (from 10,521 ($\#DIP = 7$) to 6298 ($\#DIP = 1$)). The required computational time depends upon the disruption profile, i.e. the larger $IH$ and $\#DIP$ is, the larger is the required average run time per recovery decision strategy.

Table 5 Detailed computational results as a function of the timeline uncertainty characteristics

The timeline uncertainty impacts also the divergence in quality between individual recovery strategies. Figure 5 illustrates results for timeline uncertainty profiles [$\#DIP$, IH] = [1,7] and [7,1] and has been composed similar to Fig. 2, which considers profile [$\#DIP$, IH] = [7,7]. These figures indicate the performance of all decision strategies ($\bullet$) and the Pareto front ($\bullet$). In addition, the figures display a set of recovery strategies leading to high-quality personnel rosters identified according to rule 6 with allocation decisions appended, indicated by dark grey triangles ($\blacktriangle$) (cf. infra). GD is displayed both for all rerostering decision strategies (GD ($\bullet$)) and the limited set of high-quality recovery strategies (GD ($\blacktriangle$)). The results (see also Table 6 (Rule 0 ’w/o alloc’)) reveal that when the uncertainty is higher, i.e. IH is shorter or $\#DIP$ is larger, GD is larger, which is illustrated by a larger point cloud mapping Z and RE for the different recovery strategies. In this respect, the uncertainty profile with the largest uncertainty ([$\#DIP$, IH] = [7,1]) is characterised by the largest point cloud (GD = 852.2), implying a larger variance in resulting quality. The profile with the smallest uncertainty ([$\#DIP$, IH] = [1,7]) shows the smallest point cloud (GD = 476.9). The variance of the other uncertainty profiles are in-between these two extremes (see Table 6). $IH$ has the largest impact on the variance in quality as GD increases from 566.9 ([$\#DIP$, IH] = [7,7]) to 852.2 ([$\#DIP$, IH] = [7,1]), whereas a larger $\#DIP$ increases GD only modestly from 476.9 ([$\#DIP$, IH] = [1,7]) to 566.9 ([$\#DIP$, IH] = [7,7]).

In addition, the timeline uncertainty profile impacts the curve of the Pareto front of non-dominated strategies. All identified Pareto fronts have more or less the same form, i.e. (Phase 1) a steep improvement of Z when RE varies between 1 and 7 days; (Phase 2) for a larger RE the rate of improvement in Z declines; (Phase 3) Z more or less stagnates and only marginal improvements are observed; and (Phase 4) at some point, further enlarging RE is no longer useful as no efficient combinations are discerned. The larger the uncertainty, the larger the required RE before Z is more or less stagnating. In this perspective, we observe that for the disruption profile with the largest uncertainty ([$\#DIP$, IH] = [7,1]) significant improvements are obtained when RE increases from 7 to 15 days, whereafter Z stagnates. In contrast, the quality for the disruption profile with the smallest uncertainty ([$\#DIP$, IH] = [1,7]) is already stagnating when RE is equal to 7 days.

Fig. 5

Computational results for different timeline uncertainty profiles

Impact on the performance of recovery decision strategies

In the following, we discuss the impact of rescheduling characteristics defining efficient recovery strategies and stipulated rules of thumb. In line with earlier findings related to the rescheduling horizon and number of rerostering decisions, results for different uncertainty profiles indicate that increasing $\#RDP$ is more important than setting a longer RH (see Table C and Table D in Online Appendix B). A larger $\#RDP$ gradually improves the values for Z and GD. When the embedded uncertainty of the timeline disruption profile rises, the improvements associated with installing additional rescheduling decisions are larger. Increasing $\#RDP$ (RH) from 1 to |D| improves Z by a percentage ranging between 84% and 88% (19% and 78%). The smaller the uncertainty of the timeline disruption profile, the more interesting it is to increase RH. When disruptions do not arise every day, it is no longer necessary to invoke a rescheduling decision on a daily basis, especially if changed information has been considered earlier via a rerostering decision. We observe that improvements relative to Z and GD more or less stagnate when $RH \ge 4$ days. Only when the uncertainty is relatively small ([$\#DIP$, IH] = [1,7] or [3,7]), a further increase of RH leads to a substantial better value for Z.

Regarding the timing of rerostering decision points, Table 6 displays the performance (Z, RE and GD) for the different rules-of-thumb. The results are presented for each of these recovery strategies whether or not combined with complementary allocation decisions (’with alloc’ versus ’w/o alloc’). The best performing rule is indicated in bold. The table reveals that rules applying a rescheduling decision every day on which parameter information has been changed due to operational variability, are preferred to restore feasibility. This can be realised via a suitable recovery strategy defining enough rerostering decision points and a proper, sufficiently long RH to cope with capacity disruptions. In this respect, rule 1 provides a very good and consistent performance in terms of the values for Z and GD for all uncertainty profiles. As a result, rule 1 outperforms rule 4, which defines a rerostering decision on at least those days new information becomes available but neglects a proper definition of RH. In a similar manner, rule 1 performs better than rule 5 as this rule gives only guidance to the definition of RH and not to the number and timing of rerostering decision points. In addition, the results related to rule 5 indicate that setting RH larger than IH (or equal when IH = |D|) performs better than the average result found for all 896 decision strategies in terms of values for Z and GD. This confirms the results found by Maenhout and Vanhoucke (2013) that an after-period is preferably implemented. Moreover, rule 1 also outperforms rule 2 that defines rerostering decision points at regular time intervals, without connection to the disruption information points. Even when an overlap is additionally installed between rescheduling horizons of consecutive rerostering decision points (rule 3), rule 1 still performs better. These periodic rules 2 and 3 perform better when the embedded uncertainty of the disruption profile is lower ([$\#DIP$, IH] = [1,7], [3,7] and [7,7]). In contrast to previous rules, rule 6 links the rerostering decision to the incurred capacity disruptions and not to the disruption timeline characteristics. Results indicate that rule 6 outperforms rule 1, especially for those disruption profiles where the uncertainty is low to modest. Only when uncertainty is high ([$\#DIP$, IH] = [7,1]), rule 1 performs slightly better than rule 6 without allocation decisions appended.

Table 6 Computational performance (Z, RE, GD) for different recovery strategies and disruption uncertainty profiles

When allocation decisions are executed on those days for which no rerostering decision is applied, we observe steep improvements in quality Z for every timeline uncertainty profile whereas the additional effort RE is limited. The relative improvements are the largest for those uncertainty profiles with the largest degree of uncertainty, i.e. allocation decisions are most useful when new information arises on a daily basis ($\#DIP = 7$). This trend is confirmed for all devised rules, except for rule 1 for which appending allocation decisions does not show significant improvements as the uncertainty has been considered entirely via the rerostering decisions taken. Similarly, for rule 6 there are no improvements resulting from appending allocation decisions when uncertainty is low ([$\#DIP$, IH] = [1,7]). When uncertainty is higher, executing allocation decisions indeed improves performance of rule 6. Moreover, rule 6 with allocation decisions appended even outperforms rule 1 for all uncertainty profiles, demonstrating the added value of cleverly appending allocation decisions. Note that incorporating allocation decisions may occasionally deteriorate quality after rescheduling to a minor extent due to the myopic nature of allocation decisions. The latter may restrict scheduling flexibility to resolve disruptions at a later point in time as a result of imposed (hard) time-related constraints.

5.4 Benchmark of individual recovery decision strategies

In this section, we perform a benchmark comparison between individual recovery decision strategies known from the literature and a suitably devised dynamic recovery strategy based on the insights yielded in previous sections. This benchmark has been performed on 7 synthetic instances accounting for a longer planning horizon of 28 days and 9 different timeline uncertainty profiles. The instances have been generated in a similar manner as described in Sect. 5.1. A time limit has been imposed of 3600 s to obtain a solution for a single static recovery decision. Table 7 displays the performance metrics Z, RE and $CPU$ for the following strategies, i.e.

• Recovery strategy of Moz and Pato (2003): This event-driven strategy conducts a rerostering decision only when new information is available, i.e. $RDP_d = DIP_d$. Each rerostering decision considers the entire (remaining) planning horizon, i.e. RH starts from the day under consideration until the end of the planning horizon ($RH = |D| - d+1$).

• Recovery strategy of Maenhout and Vanhoucke (2013): This event-driven strategy conducts a recovery decision whenever new information is available, i.e., $RDP_d = DIP_d$, and sets RH equal to $IH+1$, considering (1) the disruption period, i.e., the time horizon from the first until last day disruptions occur and (2) an after-period of 1 day, i.e., the period of time that is under consideration after the day of the last schedule disruption.

• Allocation strategy: This periodic strategy assumes only allocation decisions, resolving only those schedule disruptions on the day of operations (cf. Section 4.1.2).

• Proposed strategy: This hybrid strategy is designed following rule 6, linking rerostering decisions to capacity disruptions with allocation decisions appended. As denoted in previous sections, the value for Z depends on the effort the decision-maker is willing to spent to recover the roster and is a design choice. In this benchmark comparison, we have set RH equal to 7.

Table 7 Benchmark results for individual recovery strategies

Table 7 reveals that the proposed strategy provides a robust performance over different timeline uncertainty profiles, leading to reconstructed rosters of high-quality in an acceptable timespan. The recovery strategy of Moz and Pato (2003) delivers the best performance in terms of the value for Z, which results from a lower number of understaffed tasks, but devotes a far larger RE to recover the roster. The strategy of Maenhout and Vanhoucke (2013), which spends a similar RE to restore the roster, performs worse than the proposed strategy in terms of attained quality. The latter is especially the case when IH is small to medium (= 1, 3 or 7 days), i.e., when uncertainty is larger. This is not the case for $IH = 28$, as the strategy of Maenhout and Vanhoucke (2013) then coincides with the effortful strategy of Moz and Pato (2003). Both these latter recovery strategies, known from literature, require a far larger amount of $CPU$ time, especially for the timeline uncertainty profiles characterised by a large IH (= 28 days), and do not denote a stable behaviour. In addition, these strategies record a larger number of dynamic roster changes. For example, for [$\#DIP$, IH] = [28,28], the strategies of Moz and Pato (2003) and Maenhout and Vanhoucke (2013) accumulate a total of 2395 and 580 dynamic task and shift changes, compared to, respectively, 1040 and 203 conducted dynamic changes by the proposed strategy. The allocation strategy delivers a detrimental performance in terms of the value for Z as a large number of shift disruptions cannot be resolved given the small recovery period.

6 Conclusions

In this paper, we studied a dynamic personnel rescheduling problem, where disruptions arise gradually over the planning horizon. The contribution of this paper is fourfold. First, we defined the dynamic rescheduling problem for the integrated personnel shift and task scheduling problem introducing different concepts to characterise the timeline uncertainty and dynamic recovery strategies. Second, we gave insight into the performance of recovery decision strategies and relevant characteristics. The decision strategy at hand should be determined by making the trade-off between quality and the effort one is willing to spend to recover the roster. Maximising the rescheduling effort does not lead to an efficient recovery strategy as (1) the incumbent solution is reached with a smaller rescheduling effort, advocating the definition of efficient recovery strategies, and (2) blindly adopting a large number of rescheduling decisions and/or a large rescheduling horizon leads to a significant number of unnecessary task and shift changes, which is detrimental to the organisation of resources and communication. The number of recovery decisions is preferably linked to the number of disruption information points as it is not necessary to invoke a rescheduling decision if changed schedule parameters have been considered earlier via a rerostering decision. The larger the timeline uncertainty, the more important to conduct a larger number of recovery decisions, which is more predominant than increasing the rescheduling horizon. Only when the embedded timeline uncertainty is low, it is interesting to consider a relatively large rescheduling horizon. Third, we developed different rules-of-thumb to define suitable recovery strategies leading to reconstructed personnel schedules of high quality. Insights in these rules stipulate that rescheduling decisions are preferably conducted on all days on which schedule parameters have been changed due to operational variability. The timing of rerostering decisions that consider a rescheduling horizon of multiple days, should be linked to the occurrence of capacity disruptions to facilitate effective recovery. Allocation decisions, which consider only a single day of the planning horizon, should be applied to resolve disruptions originating from the uncertainty of arrival and uncertainty of demand. Combining allocation and rerostering decisions in this way defines individual recovery strategies that consistently provide high-quality solutions. Fourth, insight into the impact of timeline uncertainty is delivered and linked to the design of suitable recovery strategies. A larger uncertainty, characterised by a shorter information horizon and a larger number of disruption information points, impacts the (variance in) quality of individual recovery strategies and requires more rescheduling effort to adequately restore the roster. In that case, appending allocation decisions to rerostering decisions becomes more important to define an effective but efficient recovery strategy.

There are different ways to extend this study in future research. First, the insights identified in this paper related to timing of rescheduling decision points and rescheduling horizon can be exploited to develop a tractable multi-stage procedure to construct a tactical personnel roster that embeds uncertainty in a proactive manner, following a predictive-reactive approach. Every potential decision moment corresponds to a recourse decision stage and decisions need to be taken related to the timing of rescheduling decisions, length of rescheduling horizon and adjustment of the schedule to restore feasibility/quality of the personnel schedule. Accordingly, the current research may contribute to improving the efficiency of a stochastic or (adjustable) robust optimisation approach by reducing the number of decision stages in advance and restricting the rescheduling horizon, which decreases the number of decision variables that need to be considered. Second, the choice in this study of setting the (efficient) baseline schedule as a reference schedule is a research design choice. The problem definition can be altered to investigate the impact of setting the last created schedule as the reference schedule since personnel may adapt rather quickly to their new duty roster. However, this requires the optimisation of new objectives in the (static) rescheduling decision model considering the efficiency of the newly constructed rosters. In this way, we will no longer optimise the deviation compared to the baseline schedule, i.e. the schedule stability, but we focus on constructing a new roster that shows robust performance in terms of solution quality, i.e. yielding a similar efficiency as was postulated by the baseline schedule.