Two-Electron and Two-Hole Cooper Pairs in Superconductivity

Abstract

We revisit the generalized Bose-Einstein condensation (GBEC) theory which addresses a ternary boson-fermion gas including two-hole Cooper pairs (2hCPs) as an essential component in superconductivity. Here, we extend the BCS-Bose crossover theory, itself subsumed in BEC, by explicitly including 2hCPs. Shown here are phase diagrams of T_c/T_F, where T_c is the critical temperature and T_F the Fermi temperature and Δ(0)/E_Fvsn/n_f, where Δ(0) is the energy gap at zero temperature and E_F is the Fermi energy of an ideal Fermi gas, with n the total electron number density and n_f is that of unbound electrons at zero temperature. These phase diagrams are obtained for two pure phases, one with two-electron Cooper pairs (2eCPs) and the other with 2hCPs, plus a mixed phase with arbitrary proportions of 2e/2hCPs. We find that the extended BCS-Bose crossover predicts T_c/T_F as well Δ(0)/E_F values for the elemental superconductors (SCs) Al, In, Sn, Pb, Hg, and Nb which compare reasonably well with experimental data.

1 Introduction

The BCS-BEC crossover theory (where BCS stands for Bardeen-Cooper-Schrieffer and BEC for Bose-Einstein condensation) was likely introduced by Schrieffer [1] and later discussed by Keldysh et al. [2], Popov [3], Friedel et al. [4], Eagles [5] and the absolute temperature T = 0 equations formulated by Leggett [6] which were more recently also solved numerically by Carter et al. [7].

All authors now dealt with two equations to be solved simultaneously, one for the energy gap Δ and another for the electron chemical potential μ. This picture leads to a weak-coupling regime where pairs greatly overlapped while μ was originally assumed in BCS theory [8] be fixed as μ = E_F, the Fermi energy of an ideal Fermi gas. But in strong-coupling, pairs must really be small and non overlapping. The BCS-BEC crossover was subsequently discussed by Nozières et al. [9] (1985) and many others. (This crossover can in fact more accurately be named “BCS-Bose” instead of “BCS-BEC” since a BEC cannot occur in either 2D or in 1D [10] whereas bosons can form in both instances.)

Boson-fermion (BF) gas models of superconductors (SCs) as a BEC go back to the mid-1950s [11,12,13,14]—pre-dating even the BCS-Bogoliubov theory [8, 15, 16]. All BF models [11,12,13,14, 17,18,19,20,21,22,23,24,25,26] so far had been binary gases and posit the existence of actual bosonic CPs. With a single exception [27] all BF models neglect the explicit effect of hole CPs (2hCPs) included on an equal footing with electron CPs (2eCPs). This constituted a complete ternary BF model [27,28,29,30] at the heart of a GBEC theory.

The preparation of this paper as well as writing of the main framework was co-authored with Vladimir V. Tolmachev, and, in sorrow, we dedicate this paper in his memory. Manuel de Llano Mexico City, April 2018.

2 GBEC Theory Formalism

The GBEC theory starts from an ideal BF ternary gas consisting of unbound electrons (fermions) with 2eCPs and 2hCPs as bosons, to which are added very particular BF vertex interactions. It is described [27,28,29,30] by the Hamiltonian H = H₀ + H_int where H₀ is an ideal ternary gas and H_int contains the BF vertex interactions [27, 28].

Defining a simpler reduced H_int, called H_red, by neglecting in H_int nonzero K-terms (center-of-momentum-of-mass (CMM) K≠ 0) in H_int but not also in H₀ as done in BCS theory, renders an exactly diagonalizable expression in H_int. Then, ignoring these bosons and using the Bogoliubov recipe of replacing b₀ and c₀ the 2eCP and 2hCP zero-K creation/annhilation operators respectively by c-numbers $\sqrt {N_{0}}$ and $\sqrt {M_{0}}$ in H₀, where N₀ and M₀ are the numbers of K = 0 bosons, one can diagonalize the reduced dynamical operator $\hat {H}_{\text {red}}-\mu \hat {N}$ [29] via a Bogoliubov-Valatin transformation [31, 32]. Here, $\hat {N}$ is the total-electron-number operator. Thus, the thermodynamic (or Landau) potential in the grand canonical ensemble becomes

$$\begin{array}{@{}rcl@{}} &&{\Omega} (T,L^{3},\mu ,N_{0},M_{0})\\ &&=-k_{\mathrm{B}}T\ln \left[ \text{Tr}(\exp \{-\beta (\hat{H}_{\text{red}}-\mu \hat{N})\})\right] \end{array} $$

(1)

where Tr stands for the “trace” of the diagonalized dynamical operator, thus Ω can now be evaluated explicitly. The neglected K≠ 0 bosons can later be brought back into the picture [33,34,35,36]). If β ≡ 1/k_BT with T the absolute temperature and k_B the Boltzmann constant, the Helmholtz free energy belowT_c then becomes F(T,L³,μ,N₀,M₀) ≡Ω + μN, where L³ is the gas volume and N₀ and M₀ are the number of electron/hole composite bosons with zero-CMM, respectively. Taking the negative partial derivative of (1) with respect to μ, and also minimizing F wrt N₀, M₀ requires imposing

$$ -\frac{\partial {\Omega} }{\partial \mu }=N\qquad \ \ \ \ \ \ \frac{\partial F }{\partial N_{0}}= 0\qquad \ \ \ \ \ \ \frac{\partial F}{\partial M_{0}}= 0. $$

(2)

The first relation is familiar from statistical mechanics and ensures the net charge conservation of the GBEC theory, i.e., gauge invariance [37] which contrasts with the BCS theory which lacks it. The last two requirements of (2) are needed for a stable thermodynamic state.

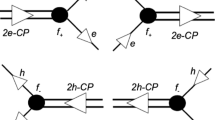
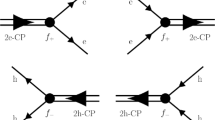
As stated, the GBEC theory via (2) leads to three coupled transcendental equations. These determine a thermodynamic equilibrium phase diagram with three condensed phases: two pure BEC phases, one for 2eCPs and the other for 2hCPs, and a mixed phase of arbitrary proportions of these two components. Each phase is defined by f_±(𝜖) the BF vertex interaction functions as originally defined in Refs. [27, 28]. For 2eCPs f₊(𝜖) = E_f < 𝜖 < E_f + δ𝜖 where δ𝜖 is the CP binding energy [27] and E_f a “pseudo Fermi energy” to be defined below. For 2hCPs f₋(𝜖) = E_f − δ𝜖 < 𝜖 < E_f. Otherwise f_±(𝜖) = 0. For the mixed phase f(𝜖) = E_f − δ𝜖 < 𝜖 < E_f + δ𝜖. The three phases can be determined at worst numerically by solving the three coupled transcendental equations which formally depend on three unknown functions of T: the electron chemical potential μ(T) along with the 2eCP and 2hCP BE condensate densities n₀(T) ≡ N₀/L³ and m₀(T) ≡ M₀/L³. This gives two gap-like equations [27]

$$ 2\sqrt{n_{0}}[E_{+}(0)-2\mu ] = \int\limits_{0}^{\infty }d\epsilon N(\epsilon ) \frac{{\Delta} (\epsilon )f_{+}(\epsilon )}{E(\epsilon )}\tanh \left[ \tfrac{1 }{2}\beta E(\epsilon )\right] $$

(3)

and

$$ 2\sqrt{m_{0}}[2\mu -E_{-}(0)] = \int\limits_{0}^{\infty }{\kern-.5pt} d\epsilon N(\epsilon ) \frac{{\Delta} (\epsilon )f_{-}(\epsilon )}{E(\epsilon )}\tanh \left[ \tfrac{1 }{2}\beta E(\epsilon )\right] $$

(4)

where N(𝜖) is the electronic density of states, E_±(0) are phenomenological energies [38] of bosonic CPs with CMM K = 0, $E(\epsilon )\equiv \sqrt {(\epsilon -\mu )^{2}+{\Delta }^{2}(\epsilon )}$ is the familiar gapped Bogoliubov fermion dispersion relation and ${\Delta } (\epsilon )\equiv f_{+}\sqrt {n_{0}(T)}+f_{-} \sqrt {m_{0}(T)}$. The first relation of (2) yields the total-electron-number density as

$$ N/L^{3}\equiv n = 2n_{\mathrm{B}}(T)-2m_{\mathrm{B}}(T)+n_{\mathrm{f}}(T) $$

(5)

where n_f(T) is that of the unbound electrons while n_B(T) and m_B(T) are respectively those of 2e and 2hCPs in all bosonic states, ground together with excited. These turn out to be

$$\begin{array}{@{}rcl@{}} n_{\mathrm{B}}(T) &\equiv &n_{0}+n_{\mathrm{B+}}(T)\quad \text{with}\\ n_{\mathrm{B+}}(T) &=&\int\limits_{0+}^{\infty }d\varepsilon M(\varepsilon )\left[\exp \beta (2E_{\mathrm{f}}+\delta \varepsilon -2\mu +\varepsilon )-1\right]^{-1} \end{array} $$

(6)

and

$$\begin{array}{@{}rcl@{}} m_{\mathrm{B}}(T) &\equiv &m_{0}+m_{\mathrm{B+}}(T)\quad \text{with}\\ m_{\mathrm{B+}}(T) &=&\int\limits_{0+}^{\infty }d\varepsilon M(\varepsilon )\left[\exp \beta (2\mu +\varepsilon -2E_{\mathrm{f}}+\delta \varepsilon )-1\right]^{-1} \end{array} $$

(7)

where $M(\varepsilon )\equiv (2m^{3/2}/\pi ^{2}\hbar ^{3})\sqrt {\varepsilon }$ is the bosonic density of states. Finally, the number density of unbound electrons at any T turns out to be

$$\begin{array}{@{}rcl@{}} n_{\mathrm{f}}(T) &\equiv &\int\limits_{0}^{ \infty }d\epsilon N(\epsilon )\left[ 1- \frac{\epsilon -\mu }{E(\epsilon )}\tanh \{{\tfrac{1}{2}}\beta E(\epsilon )\} \right]\\ &\xrightarrow[{T \to 0}]{}&\left( 2mE_{\mathrm{f}}\right)^{3/2}/3\pi^{2}\hbar^{3}\equiv n_{\mathrm{f}} \end{array} $$

(8)

with the last result first reported by Chávez et al. [39]. Here, E_f coincides precisely with E_F only when n₀(T) = m₀(T) andn_B+(T) = m_B+(T), i.e., ideal perfect 50-50 symmetry.

3 Statistical Superconductivity Theories Subsumed in GBEC

The BCS and ordinary BEC theories are subsumed [27] as special cases in the GBEC theory. Assuming perfect 50-50 symmetry between 2eCPs and 2hCPs. Equations (3) and (4) can be combined into a single equation. Then, setting μ ≃ E_F as assumed by BCS, one readily arrives at the BCS gap equation if one identifies δε with the Debye energy of the ionic lattice $\hbar \omega _{\mathrm {D}}$ and f²/2δε with V, the BCS net attraction constant. Thus

$$ 1=\frac{f^{2}N(\mu )}{2\delta \varepsilon }\int\limits_{0}^{\delta \varepsilon }d\epsilon \frac{1}{\sqrt{\xi^{2}+{\Delta} (T)^{2}}}\tanh \left[ \tfrac{1}{2}\beta \sqrt{\xi^{2}+{\Delta} (T)^{2}}\right] $$

(9)

where ξ ≡ 𝜖 − μ. In addition to this one also recovers the T = 0 condensation energy exactly [40] and most recently as well [41] for all 0 ≤ T ≤ T_c.

For the noninteracting BF system, i.e., when f_±(𝜖) = 0 in (3) and (4) implying that Δ(𝜖) ≡ 0, one must put μ = E_f so that E(𝜖) = |𝜖 − E_f|. The total electron-number density for this noninteracting BF system is then

$$\begin{array}{@{}rcl@{}} n &=&2n_{0}+\int\limits_{0+}^{\infty }d\varepsilon M(\varepsilon )\left( \exp \beta \lbrack 2E_{\mathrm{f}}+\delta \varepsilon -2\mu +\varepsilon ]-1\right)^{-1}\\ &&+\int\limits_{0}^{ \infty }d\epsilon N(\epsilon )\left[ 1-\frac{\epsilon -\mu }{E(\epsilon )}\left( 1-2\exp [\beta E(\epsilon )]+ 1\right)^{-1}\right]\\ \end{array} $$

(10)

where one allows for the fully asymmetric case by ignoring the presence of 2hCPs altogether by setting m_B(T,n) = 0 for all T. Determining n₀(T,n) associated with the remaining 2eCP condensate fraction for 0 ≤ T ≤ T_c, the critical temperature T_c can then be defined as the temperature below which n₀(n,T) just ceases to vanish as T decreases. The solution is obtained [27] from (10) since n₀(n,T_c) = 0 and gives

$$ T_{\mathrm{c}}\simeq 3.31\frac{\hbar^{2}}{Mk_{\mathrm{B}}}\left( N_{\mathrm{B}}/L^{3}\right)^{2/3} $$

(11)

which is just the BEC formula for an ideal Bose gas with masses M ≡ 2m and boson particle density $N_{\mathrm {B}}/L^{3}\equiv \tfrac {1}{2}(n-n_{\mathrm {f}})$ where again n_f ≡ n_f(T = 0). From all this, one arrives at the universal BEC ratio

$$T_{\mathrm{c}}/T_{\mathrm{F}}=(1/2)\left[ 2/3{\Gamma} (3/2)\zeta (3/2)\right]^{2/3}\simeq 0.218. $$

Figure 1 is a flowchart illustrating the aforementioned five statistical theories subsumed in the GBEC formalism.

Fig. 1

Five statistical theories subsumed in the GBEC formalism. The BCS-Bose crossover extended with 2hCPs along with 2eCPs, with three equations, one gap-like for 2eCPs and another for 2hCPs, and the number density. Taking the a symmetric case (right branch) with 2eCPs only, one recovers the Friedberg and T.D. Lee model as well as the BEC theory. On the other hand (left branch), assuming 50-50 symmetry between 2eCPs and 2hCPs leads to the BCS-Bose crossover. Putting μ = E_F and $f=\protect \sqrt {2\hbar \protect \omega _{\mathrm {D}}V}$, where V is associated with the BCS electron-phonon interaction, one recovers the BCS theory

4 Extended BCS-Bose Crossover

The extended BCS-Bose crossover theory [42, 43] emerges from including bosonic 2hCPs explicitly in addition to the 2eCPs. Hence, one deals with the number densities of condensed 2hCPs m₀(T), the excited 2hCPs, m_B+(T), alongside the condensed 2eCPs n₀(T) and the excited 2eCPs n_B+(T). In perfect symmetry between 2eCPs and 2hCPs, i.e., with half-and-half proportions, one recovers the original (unextended) BCS-Bose crossover [1]. Specifically, the equations for the extended crossover for the 50-50 case at T = T_c implies that Δ(T_c) = 0 so that n₀(T_c) = m₀(T_c) = 0 which thus leaves

$$\begin{array}{@{}rcl@{}} \lbrack E_{+}(0)-E_{-}(0)]&=&f^{2}\int\limits_{E_{\mathrm{f}}-\hbar \omega _{\mathrm{D}}}^{E_{\mathrm{f}}+\hbar \omega_{\mathrm{D}}}d\epsilon N(\epsilon )\frac{1}{|\epsilon -\mu |}\tanh\\ &&\times \left( \tfrac{1}{2}\beta_{\mathrm{c}}|\epsilon -\mu |\right) \end{array} $$

(12)

with β_c ≡ 1/k_BT_c, so the number equation at T = T_c is

$$\begin{array}{@{}rcl@{}} n &=&n_{\mathrm{f}}(T_{\mathrm{c}})\\ &=&\int\limits_{0}^{\infty }d\epsilon N(\epsilon )\left[ 1-\frac{\epsilon -\mu }{|\epsilon -\mu |}\right.\\ &&\times\left. \left( 1-2\left( \exp\{\beta_{\mathrm{c}}|\epsilon -\mu|\} + 1 \right)^{-1}\right)\vphantom{\frac{\epsilon -\mu }{|\epsilon -\mu |}} \right]. \end{array} $$

(13)

If μ = E_F, one recovers the original BCS weak-coupling gap equation. Otherwise, one solves the two equations (12) and (13) when μ≠E_F also.

Figure 2 shows Δ(0)/E_F vs n/n_f. The blue (online) short-dashed curve as solution of the 50-50 symmetry case, namely (12) and (13) for the energy gap at T = 0 made dimensionless with Fermi energy vs dimensionless number density n/n_f. Also shown is the 100-0 (2eCPs only) case (thick curve) as well the 0-100 (2hCPs only) case (thin curve) for both energy gap and critical temperature. Note that one has three condensed phases: i) for 50-50 below the blue (online) short-dashed curve; ii) for 100-0 light-gray shaded area; and iii) for 0-100 dark-gray shaded area, and of course a normal phase (darkest gray shaded area). Blue (online) rectangular inset shows the same phase boundaries but in greater detail. Inset also shows a red (online) circle, while Δ(0)/E_F shows that 100-0 and 0-100 intersect at the same value for n/n_f = 1 with Δ(0)/E_F ≃ 9.11 × 10^− 6 while the 50-50 case has Δ(0)/E_F ≃ 1.34 × 10^− 5, suggesting that this latter case gives a larger energy gap with respect to 2eCPs or 2hCPs. The 50-50 energy gap values coincide precisely with experimental data as will be shown below.

Fig. 2

Gap Δ(0)/E_F vs n/n_f for 50-50 case blue (online) short-dashed curve, 100-0 thick curve, and 0-100 thin curve. Gray shaded areas mark different phases. Remarkably, it shows a mirror-symmetry between 100-0 and 0-100 cases around n/n_f = 1 and, of course, for the 50-50 case. Inset shows more detail around n/n_f = 1, red (online) dot marks where 100-0 and 0-100 cases intersect at n/n_f = 1 when Δ(0)/E_F = 9.11 × 10^− 5. Here, $\hbar \protect \omega _{\mathrm {D}}/E_{\mathrm {F}}= 10^{-3}$ and Fermi temperature of T_F = 10³ K were used

Figure 3 shows the phase diagram of T_c/T_Fvsn/n_f for the same cases: i) 50-50 case; ii) 100-0 (2eCPs only); and iii) 0-100 (2hCPs only). Also shown is a red (online) circle where the three phases cross at the same triple-point value labeled T_t = T_c/T_F ≃ 7.64 × 10^− 6 at n/n_f = 1. The BCS critical temperature comes from their weak-coupling expression $T_{\mathrm {c}}/T_{\mathrm {F}}\simeq 1.134\hbar \omega _{\mathrm {D}} \exp [-1/\lambda _{\text {BCS}}]$, where λ_BCS is the BCS electron-phonon dimensionless coupling constant, and lies only at n/n_f = 1. Again, there are three phases for T_c that depend on the value taken by n/n_f. Below those curves, one finds superconductivity by slightly changing n/n_f from unity; we now analyze this latter result.

Fig. 3

T_c/T_Fvsn/n_f for 50-50 case blue (online) short-dashed curve, 100-0 thick curve, and 0-100 thin curve. Inset shows more detail around n/n_f = 1, red (online) circle marks where 50-50, 100-0, and 0-100 curves intersect at n/n_f = 1 with T_t = T_c/T_F = 7.64 × 10^− 6. Gray shaded areas mark different phases. Notably, it shows a symmetry between 100-0 and 0-100 cases around n/n_f = 1 and, of course, for the 50-50 case. Here, $\hbar \protect \omega _{\mathrm {D}}/E_{\mathrm {F}}= 10^{-3}$ and Fermi temperature of T_F = 10³ K were used

Table 1 shows for elemental SCs values for Δ(0)/E_F, T_c/T_F and the gap-to-T_c ratio 2Δ(0)/k_BT_c, all for the 50-50 and 100-0 cases, and compared with experimental data when n/n_f = 1. Values for the 50-50 case were obtained by solving (12) and (13) while for 100-0 by solving (3) and (5). Note that the 50-50 case compares quite well with the data but not for the 100-0 case where 2hCPs are neglected, i.e., m₀(T) = 0. This implies that by merely excluding 2hCPs altogether, the energy gap and the gap-to-T_c ratio which in turn are related with coupling, decrease substantially with respect to actual data. Thus, 2hCPs are unequivocally indispensable to describe superconductivity.

Table 1 T_c/T_F, Δ(0)/E_F, and 2Δ(0)/k_BT_c for 50-50 ideal perfect symmetry and 100-0 proportions (2eCPs only) for the aforementioned superconductors

5 Conclusions

The GBEC formalism subsumes the BCS-Bose crossover extended with explicit inclusion of 2hCPs. Starting from an ideal ternary BF gas with particular BF vertex interactions, the extended crossover is found to be defined by two thermodynamic-equilibrium requirements along with a well-known result from statistical mechanics that guarantees charge conservation. Upon just slightly varying n/n_f around 1, and without abandoning electron-phonon dynamics, it leads to critical temperatures T_c enhanced by several orders compared with BCS theory. Notably, the lack of 2hCPs, i.e., with m₀(T) = 0 or 100-0 proportions, meaning only 2eCPs, results in an energy gap and gap-to-T_c ratio significantly reduced with respect to the 50-50 case, suggesting that 2hCPs are indispensable for an acceptable description of superconductivity.