1 Introduction

Modern microfabrication techniques enable one to create nanosized superconducting structures with unique properties. The behavior of such structures in an external magnetic field is strongly influenced by the boundary conditions besides its size and geometry and differs from the bulk materials. For example, strong confinement leads to the formation of the giant vortex state [1–5] and multivortex state [6–11], which are energetically less favorable in bulk type-II superconductors [12]. An even more exotic vortex state was predicted to exist in nanoscale samples with artificial pinning: the vortex–antivortex state [13–15]. Vortices also show very rich static and dynamic behavior in the presence of a weak link [16, 17]. A weak link is commonly achieved by two superconducting layers separated by a normal metallic layer or weak a superconducting region. It is well known that the properties of both superconducting and normal metals are modified due to the proximity effect [18] when they are in contact with each other. Thus, the vortex–vortex interaction and the vortex interaction with different kinds of defects and interfaces become very complex.

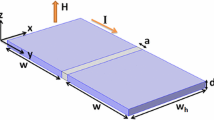
In this paper, we study the vortices properties in a nanosized type-II superconducting strip with a weak superconducting narrow metallic region (see Fig. 1). In order to investigate the response of the sample to magnetic fields, we apply the time-dependent Ginzburg–Landau (TDGL) equations where the anisotropy is included through a spatially dependent anisotropy coefficient ζ in different layers of the sample. This anisotropic GL approach [16] allows both the modulus and the phase of the order parameter to vary in both the weak and the strong superconducting regions. Then, the magnetic vortex properties of the nanoscale superconductors are determined by using the finite element method (FEM) [14, 19] to solve the coupled TDGL equations. The FEM is characterized by approximate solutions that are piecewise polynomial functions with respect to some grid. A specific finite scheme is defined by choosing a particular space of such functions in which to seek approximate solutions. Of course, our sample can also be considered as a model for a Josephson junction system [20]. Therefore, the present study may give us insight into some basic mechanisms of flux line motion.

Fig. 1
figure 1

(Color online) Schematic view of the studied system: a superconducting stripe (length w, width w h, thickness d<<ξ,λ) with one central weak link of size a = ξ in the presence of a perpendicular magnetic field H

Full size image

2 Time-Dependent Ginzburg–Landau Model

We consider a mesoscopic superconducting stripe with one or more weakened superconducting regions as illustrated in Fig. 1. We restrict ourselves to a sufficiently thin stripe such that the thickness d < < ξ (the coherence length), λ (the penetration depth). The stripe is surrounded by vacuum with an external uniform magnetic field H = (0, 0, H z ) in the z-direction. According to Ginzburg and Landau, the Gibbs free energy of the superconductor near the critical temperature T c can be described by the complex order parameter ψ:

$$\begin{array}{@{}rcl@{}} F_{s} -F_{n} \!\!&=&\!\!\int\left[\alpha \left| \psi \right|^{2}+\frac{1}{2}\beta \left| \psi \right|^{4}+\frac{1}{2m^{\ast }}\right.\\ &&\quad\!\times \!\left.\left| {\left( {\!-i\hbar \nabla \,-\,\frac{e^{\ast }}{c}\mathbf{A}} \right)\psi } \right|^{2}\,-\,\!\frac{\left( {\mathbf{B}}-\mathbf{H} \right)^{2}}{4\pi} \right] dV, \end{array} $$
(1)

where H denotes the applied magnetic field, B = ∇ × A is the local magnetic field, α and β are phenomenological parameters, and m ∗is the mass of the Cooper pair. Since α(T) = α 0(1 − T/T c ), α anisotropy is effectively equivalent to T c anisotropy in the system T c(y). In this way, the thin normal region is not treated independently from the surrounding. From simplicity, we assume the same length scales for the condensate both in the weak and strong superconducting regions. Using α = α 0 ζ with spatially dependent parameter ζ(x, y), the TDGL equations are written in the following form near the critical temperature:

$$ \left( {\frac{\partial }{\partial t}+i{\Phi} } \right)\psi =-(-i\nabla -\mathbf{A})^{2}\psi +(\zeta -\left| \psi \right|^{2})\psi , $$
(2)
$$ \sigma \left( {\frac{\partial \mathbf{A}}{\partial t}+\nabla {\Phi} } \right) = \mathbf{J}_{s} -\kappa^{2}\nabla \times \nabla \times {\mathbf{A}}, $$
(3)

with boundary conditions

$$ \mathbf{n}\cdot \left( {-i\nabla -\mathbf{A}} \right)\psi \left|{~}_{\bot ,\;\text{boundary}} \right.=0, $$
(4)

where Φ is the electric potential, σ is the conductivity of the normal current, and n is the normal unit vector on the surface. The density of the superconducting current J s is given by:

$$ \mathbf{J}_{s} =\frac{i}{2}\left( {\psi \nabla \psi^{\ast }-\psi^{\ast }\nabla \psi } \right)-\left| \psi \right|^{2}\mathbf{A}. $$
(5)

We scale the length in units of \(\xi =\hbar /{\sqrt {2m\left | {\alpha _{0}} \right |} }\), the order parameter ψ in units of \(\psi _{0} =\sqrt {-{\alpha _{0} } /{\alpha _{0} }\beta } \), the vector potential A in units of \(A_{0} =\sqrt 2 \kappa H_{\mathrm {c}} \xi \), the time t in unit of τ = ξ 2/D (D, a phenomenological diffusion constant), and the local magnetic field B in units of \(H_{\mathrm {c}2} =\sqrt {2} \kappa H_{\mathrm {c}} \), where H c is the thermodynamic critical field and κ = λ/ξ is the GL parameter. The TDGL equations and their discretized form are gauge invariant under the transformations as follows:

$$ \psi^{\prime}=\psi e^{i\chi }, \quad \mathbf{A}^{\prime}=\mathbf{A}+\nabla \chi ,\text{and}\quad{\Phi}^{\prime}={\Phi} -{\partial \chi}/ {\partial t} $$
(6)

We chose the zero scalar potential gauge, that is, Φ = 0 at all times and positions. The free energy of the superconducting state, measured in \(F_{0} ={{H_{c}^{2}} V} / {8\pi }\) units, is expressed as

$$ F=\frac{2}{V}\int {\left[ {-\left| \psi \right|^{2}+\frac{1}{2}\left| \psi \right|^{4}+\left| {\left( {-i\nabla -\mathbf{A}} \right)\psi } \right|^{2}+\kappa^{2}\left( {\mathbf{B}}-{\mathbf{H}} \right)^{2}} \right]} dV $$
(7)

Note that the dimensions of the system are given in ξ, so that the superconducting stripe is downscaled to nanometer sizes. The weak link, i.e., the region in the system with weak superconductivity, can be directly modeled by a decreased parameter α or, in other words, the anisotropy function ζ less than unity. For simplicity, we assume in this work a step-like behavior of ζ across the system, so that it becomes a coefficient equal unity inside the superconducting layer, and less than 1 inside the weak link. Then, for a fixed applied magnetic field, we solve the TDGL equations by using the FEM and can obtain the order parameter and the vector potential. Our simulations have been carried out by using σ = 1 and κ = 1 for the system. The initial conditions are \(\left | \psi \right |^{2}=1\) corresponding to the Meissner state and zero magnetic field inside the superconductor. The calculation is repeated until the relative difference of order parameter between two consecutive iteration steps is less than 10 −6.

3 Results and Discussions

We first consider a mesoscopic superconducting stripe of size w = w h = 5ξ with a single weak link of size a = ξ, centered in the sample, as illustrated in Fig. 1. The weak links are characterized by the anisotropy coefficient ζ(y) in the GL (1) with ζ(y) = 1 outside the weak link and ζ(y) = ζ in the weak link region. The anisotropy can lead to the free energy difference between the weak link in its superconducting and in its normal state smaller than that of the bulk superconductor [16]. As a result, it is easier to suppress superconductivity inside a weak link than in the strongly superconducting layers. For the reason, the vortex core, as locally destroyed superconductivity, is more likely to reside inside the weak links than elsewhere. On the other hand, a small anisotropy coefficient leads to a larger effective coherence length in the weak link region, which implies that the superconducting order parameter recovers slower from 0 inside the vortex to its equilibrium value far from the vortex. In other words, the vortex core will expand inside the weak link, compared to the vortex size in the superconducting layers. Meanwhile, the diffusion of Cooper pairs from strongly superconducting regions into the weak link will also influence the deformation of the vortex core. To investigate this phenomenon in more detail, we present the dynamics of magnetic vortices entering in the sample. Figure 2 shows the time dependence of the order parameter \(\left | \psi \right |\) in the sample with a weak link of size a = ξ and an anisotropy coefficient ζ = 0 at the magnetic field value H/H c2 = 1.20 In the color scale, blue to red represents low to high for the absolute value of the order parameter and 0 to 2π for the phase. The normalized time t/τ ranges from 0 to 10 5 for the evolution of the dynamics. To begin with, the vortices make entry into the weak link region (shown in Fig. 2a, b) and sit preferably inside the weak link until the saturation number is reached, i.e., there are enough vortices in the weak link so that the increased vortex–vortex interaction expels some of them into the superconducting layers of the sample (shown in Fig. 2c–g). Eventually, the vortices will find an equilibrium position, in which the inward and outward forces cancel exactly and the vortices become stable (shown in Fig. 2h). Note also that vortices not only favorably reside in the weak link to minimize energy but they also enter the superconducting layers through the weak link owing to the lower energy barrier for vortex entry there.

Fig. 2
figure 2

(Color online) Evolution of the absolute value of the order parameter for the sample of size w = w h = 5ξ with one central weak link of size a = ξ and an anisotropy coefficient ζ = 0 at t/τ = 1 (a), t/τ = 10 (b), t/τ = 15 (c), t/τ = 20 (d), t/τ = 30 (e), t/τ = 40 (f), t/τ = 50 (g), and t/τ = 90 (h) for H/H c2 = 1.2. Blue to red means the absolute value of the order parameter ranges from minimum to maximum

Full size image

After the analysis of the dynamics of magnetic vortices entering in the sample, we now calculate the full free energy spectrum, magnetization, and the corresponding vortex states as a function of applied magnetic field for the sample. For comparison, we also calculated the vortex states for a sample without any weak link (i.e. a = ξ and an anisotropy coefficient ζ = 1), as shown in Fig. 3. Figure 3 shows the vortex states for vorticities L = 4, 5, and 6 at the fields H/H c2 = 1.270, H/H c2 = 1.275, and H/H c2 = 1.280. The vortices enter the superconductor through the center of the sides. At the edges of the sample without a weak link, the Meissner current is strongest which confines vortices toward the interior of the sample. Figure 4 shows the free energy, magnetization, and selected vortex states in the sample with one central weak link of size a = ξ and an anisotropy coefficient ζ = −1. At the range of field from 0 to 1.4, the L = 0, 1, 2, 3, 4, 5, 6, 7, and 8 ground states are observed. When H/H c2 ≤ 0.4, the vortices enter the weak link and attract each other until the saturation number is reached. With increase of the applied magnetic field strength, the increased vortex–vortex interaction expels some of them into the superconducting layers, and the kinked vortex strings are formed in the sample owing to the competing interactions of vortices with meissner currents and the weak link boundaries.

Fig. 3
figure 3

(Color online) Evolution of the absolute value of the order parameter for a sample without a weak link (i.e., a=ξ and an anisotropy coefficient ζ=1) at H/H c2=1.270 (a), H/H c2=1.275 (b), and H/H c2=1.280 (c). (d)–(f) show plots of order parameter phase of (a)–(c). Blue to red means the absolute value of the order parameter ranges from minimum to maximum

Full size image
Fig. 4
figure 4

(Color online) Free energy curve (a), magnetization (b), and selected vortex states and corresponding phases (c) in the sample of size w = w h = 5ξ with one central weak link of size a = ξ and an anisotropy coefficient ζ = −1

Full size image

In what follows, we consider a mesoscopic superconducting stripe of size w = 5ξ and w h = 10ξ with one central weak link of size a = ξ and the value of the anisotropy coefficient ζ = −1. Figure 5 shows the absolute value of the order parameter and phase of the order parameter at the field H/H c2 = 0.9,H/H c2 = 1.0, and H/H c2 = 1.1 for a sample without a weak link (i.e., a = ξ and an anisotropy coefficient ζ = 1) (Fig. 5a) and a sample with one central weak link of size a = ξ and the value of the anisotropy coefficient ζ = −1 (Fig. 5b). For the sample without a weak link, the vortices inside the superconductor occupy central positions owing to strong interactions with the Meissner currents, such as L = 4 state at the field H/H c2 = 1.0 and L = 8 state at the field H/H c2 = 1.1. As expected, for the sample with a weak link, the number of vortex inside the weak link grows with increasing weak link of size w h = 10ξ, compared to the sample with weak link of size w h = 5ξ (see Fig. 4c). Thus, the increased vortex–vortex interaction expels many more vortices into the superconducting layers, which leads to very little superconductivity remaining in the superconductor, such as L = 10 state at the field H/H c2 = 1.0 and L = 12 state at the field H/H c2 = 1.1.

Fig. 5
figure 5

(Color online) A The absolute value of the order parameter and phase of the order parameter. a–c are for H/H c2 = 0.9, H/H c2 = 1.0, and H/H c2 = 1.1 state in a sample without a weak link (i.e., a = ξ and an anisotropy coefficient ζ = 1); d–f are the corresponding phases of the order parameter as in a–c. B The absolute value of the order parameter and phase of the order parameter. a–c are for H/H c2 = 0.9, H/H c2 = 1.0, and H/H c2 = 1.1 state in a sample of size w = 5ξ and w h = 10ξ with one central weak link of a = ξ and an anisotropy coefficient ζ = −1; d–f are the corresponding phases of the order parameter as in a–c

Full size image

4 Conclusions

In summary, the time-dependent Ginzburg–Landau equations have been solved numerically by a finite element analysis for a nanosized superconducting strip with one central weak link. For given applied magnetic fields, we have simulated the dynamical behavior of the penetrating magnetic vortices into the superconductor and illustrated their final pattern formation. These results could help us to gain insight into some basic mechanisms of flux line motion and the interpretation of the experimental data on Josephson coupled structures.