1 Introduction

The vortex matter in mesoscopic and nanopatterned superconductors has attracted a lot of attention. A mesoscopic (or nanopatterned) sample is such that its size is comparable to the magnetic field penetration depth \(\lambda \) or the coherence \(\xi \). The behavior of such structures in an external magnetic field is strongly influenced by the boundary conditions besides its size and geometry, and differs from the bulk materials. The samples of different shapes [1–15] have been studied extensively both experimentally and theoretically. These researches have shown two kinds of superconducting state, i.e., the giant vortex state [5–9] and multivortex state [10–15], which are energetically less favorable in bulk type-II superconductors [16]. An even more exotic vortex state was predicted to exist in nanoscale samples with artificial pinning: the vortex–antivortex state [17–19]. Recently, the vortex states in weakly linked layered mesoscopic superconductors were studied in the presence of a uniform magnetic field [20–22]. The weak link is commonly achieved by two superconducting layers separated by a normal metallic layer, or a weak superconducting region. In the weakly linked layered samples, kinked vortex strings are formed owing to the competing interactions of vortices with Meissner currents and the weak-link boundaries [23–25]. The weakly linked layered structure of the superconducting sample has important effects on the structure and behavior of magnetic vortices, which in turn can strongly influence the properties of the sample.

In this paper, we use the time-dependent Ginzburg–Landau (TDGL) equations to study the static and dynamic properties of the superconducting condensate in a nanosized type-II superconducting strip with one central weak link in the presence of external magnetic and electric fields, with the objective to understand the penetration of magnetic field in such samples [26], and the formation and rearrangement of vortex states with respect to the superconducting layers and the weak-link boundaries. This anisotropic GL approach [27] allows both the modulus and the phase of the order parameter to vary in both the weak and the strong superconducting regions, which is an effective and useful vehicle for the interpretation of the experimental data on Josephson coupled structures.

The paper is organized as follows. In Sect. 2, we show the derived TDGL equations with an anisotropy function and explain the numerical method we use in the calculations. In Sect. 3, we analyze the results obtained for the samples with one central weak link. Our results are finally summarized in Sect. 4.

2 Theoretical Formalism

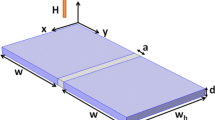
We consider a mesoscopic superconducting stripe with one or more weakened superconducting regions as illustrated in Fig. 1. The superconducting state is usually described by the complex order parameter \(\psi \). The quantity \(\vert \) \(\psi \) \(\vert ^{2}\) represents the electronic density of Cooper pairs. In the regions where \(\vert \) \(\psi \) \(\vert ^{2}\) is small, superconductivity is suppressed. At the center of the vortex \(\vert \) \(\psi \) \(\vert ^{2}\)=0, whereas the local magnetic field h is maximum. We restrict ourselves to a sufficiently thin strip such that the thickness \(d<<\) \(\xi \), \(\lambda \) (\(\xi \), the coherence length; \(\lambda \), the penetration depth). The strip is surrounded by vacuum with an external uniform magnetic field H \(=\)(0,0,\(H_{z})\) in the z-direction. The order parameter and the local magnetic field can be determined by the Ginzburg–Landau equations in their time-dependent formalism, which are expressed as [20]

$$\begin{aligned} \big ( {\frac{\partial }{\partial t}+i\Phi } \big )\psi =- \big (-i\nabla -\mathbf {A} \big )^2\psi +\big (\zeta -\left| \psi \right| ^2 \big )\psi , \end{aligned}$$
(1)
$$\begin{aligned} \sigma \big ( {\frac{\partial \mathbf {A}}{\partial t}+\nabla \varPhi } \big )=\mathbf {J}_s -\kappa ^2\nabla \times \nabla \times \mathbf {A}, \end{aligned}$$
(2)

with boundary conditions:

$$\begin{aligned} \mathbf {n}\cdot \big ( {-i\nabla -\mathbf {A}} \big )\psi \left| {_{\bot ,\;\mathrm{boundary} }} \right. =0, \end{aligned}$$
(3)

where \(\Phi \) is the scalar potential; \(\zeta \) is the anisotropy function [28]; J \(_{s}\) is the supercurrent density; \(\psi \) is the order parameter, A is the vector potential, related to the magnetic field as h=\(\times \) A; \(\kappa \) is Ginzburg–Landau parameter; \(\sigma \) is the conductivity constant, and n is the normal unit vector on the surface. The density of the superconducting current \(\mathbf {J}_s \) is given by

$$\begin{aligned} \mathbf {J}_s =\frac{i}{2} \big ( {\psi \nabla \psi ^*-\psi ^*\nabla \psi } \big )-\left| \psi \right| ^2\mathbf {A}. \end{aligned}$$
(4)

Here, all of the distances are scaled with the coherence length \(\xi \)(T); A is given in units of \({\varPhi _0 } {/} {2\pi \xi (T)}\) (\(\varPhi _0 \) is the flux quantum); the magnetic field is in units of \(H_{C2}={\varPhi _0 } {/} {2\pi \xi ^2}\); the time is in units of Ginzburg–Landau relaxation time \(\tau _{GL} ={\pi \hbar } {/} 8k_B (T_c -T)\)[29]. The transport current is introduced via the boundary condition for the vector potential in the x -direction: \(\nabla \times \mathbf {A}\vert _z ( {x=0,w})=H\pm H_I \). The external dc current I is induced by imposed \(H_I \) (approx \({2\pi I} {/} c)\) on the lateral edges of the sample. The applied current is given in units of \(j_0 ={\sigma _n \hbar } {/} {2e\tau _{GL} }\xi \) (\(\sigma _n \) is the normal-state conductivity) . The TDGL equations and their discretized form are gauge invariant under the transformations as follows:\(\psi '=\psi e^{i\chi }\), \(\mathbf {A}'=\mathbf {A}+\nabla \chi \), \(\varPhi '=\Phi -{\partial \chi } {/} {\partial t}\).We chose the zero-scalar potential gauge, that is, \(\varPhi =0\) at all times and positions.

Fig. 1
figure 1

Schematic view of the studied system: a superconducting stripe (length W, width \(W_{h}\), thickness \(d<<\) \(\xi \),\(\lambda \)) with one central weak link of size a in the presence of a perpendicular magnetic field H (Color figure online)

Full size image

The weak link, i.e., the region in the system with weak superconductivity, can be directly modeled by the anisotropy function \(\zeta \) less than unity [20, 21, 29]. For simplicity, we assume in this work a steplike behavior of \(\zeta \) across the system, so that it becomes a coefficient equal to unity inside the superconducting layer, and less than 1 inside the weak link. Then, for a fixed applied magnetic field, we solve the TDGL equations using the finite element method [20] and can obtain the order parameter and the vector potential. The dimensionless magnetization in our work, which is a direct measure of the expelled magnetic field from the nanosized superconducting strip, can be defined as M=(\(\langle B\rangle -H)\)/4\(\pi \), where \(\langle B\rangle \) is the magnetic induction averaged over the nanosized superconducting strip. The infinite strip is implemented through periodic boundary conditions in the y-direction and Neumann boundary conditions at all sample edges. Our simulations have been carried out using \(\sigma \)=\(\kappa \)=1 for the system. The initial conditions are \(\vert \) \(\psi \) \(\vert ^{2}\)=1 corresponding to the Meissner state and zero magnetic field inside the superconductor. The calculation is repeated until the relative difference of the order parameter between two consecutive iteration steps is less than 10\(^{-6}\).

3 Results and Discussion

In what follows, we first consider a superconducting strip of size \(w=w_{h}\)=50 nm [30, 31] with a weak link of size a=0, 4, and 10 nm, centered in the sample. As an example, we choose the coherence length \(\xi \)=10 nm and penetration depth \(\lambda \)=\(\xi \) so that the sample is a type-II one. The weak links are characterized by the anisotropy coefficient \(\zeta \)(y) in the GL equation with \(\zeta \)(y)=1 outside the weak link and \(\zeta \)(y)= \(\zeta \) in the weak-link region. As a result, it is easier to suppress superconductivity inside a weak link than in the strongly superconducting layers. For this reason, the vortex core, as locally destroyed superconductivity, is more likely to reside inside the weak links than elsewhere. Figure 2a–c shows the vortex states of the samples with one central weak link of size a=0 nm, a=4 m and a=10 nm for an anisotropy coefficient \(\zeta \)=0, J=0, \(H/H_{C2}\)=1.1 and \(W=W_{h}\)=50 nm. The vortices make entry into the superconducting strip through the boundary for the sample without the weak link, while the vortices make entry into the weak- link region for the sample with a weak link of size a=4 nm and 10 nm, and sit preferably inside the weak link until the saturation number is reached, i.e., there are enough vortices in the weak link so that the increased vortex–vortex interaction expels some of them into the superconducting layers of the sample. Eventually, the vortices will find an equilibrium position, in which the inward and outward forces cancel exactly and the vortices become stable. Figure 2d shows the magnetization in the sample with one central weak link of a=10 nm for the anisotropy coefficients \(\zeta \)=1, 0, \(-\)1. As can be seen from Fig. 2d, the magnetization shows that the vortices more easily make entry into the samples due to the introduction of the weak link.

Fig. 2
figure 2

Absolute value of the order parameter for the samples with one central weak link of size a=0 nm (a), a=4 nm (b), and a=10 nm (c) and an anisotropy coefficient \(\zeta =\)0, \(J=\)0, \(H/H_{C2}=\)1.1, and \(W=W_{h}\)=50 nm. d Magnetization in the sample with one central weak link of a=10 nm for the anisotropy coefficients \(\zeta \)=1, 0, \(-\)1. Blue to red means that the absolute value of the order parameter ranges from minimum to maximum (Color figure online)

Full size image

Figure 3 shows magnetization versus time characteristics of the samples without the weak link (a \(=\)0) and with one central weak link of size a=10 nm for an anisotropy coefficient \(\zeta \)=\(-\)1, J=0.05\(j_{0}\), \(H/H_{C2}\)=1.1 and \(W=W_{h}\)=50 nm. As can be seen in these figures, the magnetization shows periodic oscillations, although the amplitude of the oscillations is not much affected by the applied current for the samples without one central weak link. With the introduction of the weak link, the period of oscillations decreases (Fig. 3a–c). To see the origin of this behavior, we chose one point on the curve for the sample with one central weak link of size a=10 nm and an applied current density J=0.05\(j_{0}\), and monitored the vortex motion and magnetization as a function of time (shown in Fig. 3b–c). We obtained the period of oscillations \(\tau \sim 300\tau _{GL} \). For the chosen length of the simulation region and the considered magnetic field, we actually had N=4 vortices moving in a single row, as shown in the plots of the order parameter (shown in Fig. 3c). Another interesting result we found is that the magnetization of the sample decreases by introducing the weak link (Fig. 3a–b). The reason for this effect is that the path of the moving vortices goes through the weak link (Fig. 3c), preserving superconductivity in the superconducting region outside the weak link.

Fig. 3
figure 3

a–b Magnetization versus time characteristics in samples without the weak link (a \(=\)0) and with one central weak link of size a \(=\)10 nm for an anisotropy coefficient \(\zeta \)=\(-\)1, J=0.05\(j_{0}\), \(H/H_{C2}\)=1.1, and \(W=W_{h}\)=50 nm. c The absolute value of the order parameter at time intervals indicated in Fig. 3b. Blue to red means that the absolute value of the order parameter ranges from minimum to maximum (Color figure online)

Full size image
Fig. 4
figure 4

Magnetization versus time characteristics of the samples with one central weak link of size a=10 nm for an anisotropy coefficient \(\zeta \)=\(-\)1, \(H/H_{C2}\)=1.1, and \(W=W_{h}\)=50 nm at the current values J  = 0.001\(j_{0}\), J = 0.005\(j_{0}\), J = 0.01\(j_{0}\), J = 0.03\(j_{0}\), and J = 0.05\(j_{0}\) (Color figure online)

Full size image

To obtain a better insight into the process leading to the periodic oscillations of magnetization, we plotted in Fig. 4 the temporal magnetization signal in the samples with one central weak link of size a=10 nm for an anisotropy coefficient \(\zeta \)=\(-\)1, \(H/H_{C2}\)=1.1, and \(W=W_{h}\)=50 nm at the current values J=0.001\(j_{0}\), J=0.005\(j_{0}\), J=0.01\(j_{0}\), J=0.03\(j_{0}\), and J=0.05\(j_{0}\). Figure 4 shows that the period of the magnetization oscillations \(\tau \) varies between 330 and \(4500\tau _{GL} \) when the applied current varies from 0.005\(j_{0 }\)to 0.05\(j_{0}\). The oscillations of magnetization are not observed for a small value of the applied current (such as J=0.001\(j_{0})\), which shows that the vortices do not move. With an increasing current, the period of the magnetization oscillations decreases, although the amplitude of the oscillations is not much affected by the applied current. Here we provide some estimates of the relevant quantities of the magnetization periods for Nb films [32]. Taking \(T_\mathrm{c}\)=9.7 K and the working temperature T=5.5 K, and coherence length \(\xi ( 0)=10\)nm, we estimate \(\tau _{GL} \approx 0.71\) ps. The range of the considered frequencies of the magnetization oscillations for this particular case is from 0.3 GHz up to 4.3 GHz, which could be detected by nanoscale superconducting quantum interference devices (SQUIDs) [33].

4 Conclusions

In summary, we presented the static and dynamic properties of the superconducting condensate in nanosized type-II superconducting strips with a weakly superconducting narrow metallic region in the presence of external magnetic field and current. Our samples show magnetization oscillations in the presence of a dc current I and a perpendicular magnetic field H. The giga-to-terahertz frequencies of magnetization oscillations can be expected, which can be probed in magnetic measurements by the nanoscale SQUIDs. Our results are closely related to the studies of special magnetoresistive features in mesoscopic stripes with weak links [30, 31], and will have further implications in the studies of vortex dynamics in two-gap superconductors (where weak link can be realized in one gap condensate and not in the other, especially close to ’hidden criticality’ [34], causing nontrivial dynamics of fractional vortices [35–37]), or in the studies of vortex slippage along magnetic nanostructures and/or magnetic domain walls in various superconductor–ferromagnet hybrids [38, 39].