1 Introduction

Magnetic materials with large magnetocaloric effect (MCE) have been extensively studied experimentally and theoretically due to their great potential applications in energy-efficient magnetic refrigeration (MR) technology [1–3]. The reason for this is twofold. On the one hand, magnetic cooling offers a competitive alternative to conventional gas compression–expansion refrigeration systems due to its high energy efficiency and environmental friendliness, as neither ozone-depleting nor global warming volatile refrigerants are required. On the other hand, as magnetic refrigeration close to room temperature is only possible with materials which undergo a phase transition close to the working temperature of a refrigerator, the characterization of magnetocaloric materials generally tends to become associated with a detailed study of their phase transition, which is also interesting from a fundamental point of view. Numerous magnetocaloric materials have been intensively studied these years because of their possibility for applications in magnetic refrigeration near room temperature region, e.g., Gd 5Si 2Ge 2 alloy [4], NiMnGa [5, 6], FeMnP 1−x As x [7], LaFe 13−x Si x [8], and ferromagnetic perovskite maganites [9–13]. With prominent advantages in terms of giant magnetic entropy change ΔS M, LaFe 13−x Si x has been the progenitor of recent focused efforts regarding the magnetocaloric effect in a variety of systems because it uses relatively common, low-toxicity elements; low-cost, excellent soft ferromagnetism; and high magnetization, and it has a large magnetocaloric effect [8]. For LaFe 13−x Si x , the phase transition is very sensitive to the Si content, i.e., it changes from first-order transition to second-order transition corresponding to the Si content from 1.0 ≤x ≤ 1.6 to 1.6 < x ≤ 2.0, respectively. The Si element was introduced to stabilize a cubic NaZn13-type structure. The Curie temperature (T C) in the base LaFeSi material occurs more than 70 K below room temperature, but magnetic transition can be raised to room temperature or above by the addition of H as an interstitial element or substitution of Co for Fe [14]. To obtain a large ΔS M material without a thermal and magnetic hysteresis which is workable in a wide range of temperatures near room temperature [15], we have studied the effect of combined substitution of Pr and Co on the MCE of NaZn13-type La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 compound. The praseodymium was introduced as the substitute element to increase the magnetic entropy change. In this work, we investigated the magnetocaloric properties for the optimized La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 compound. The sample was prepared by arc melting in a high-purity argon atmosphere. La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 was turned over and remelted several times to make certain its homogeneity. The obtained ingot was wrapped using a molybdenum foil, sealed in a high-vacuum quartz tube, annealed at 1,373 K for 40 days, and then quenched into liquid nitrogen [16].

2 Model Calculations

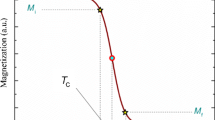
According to the phenomenological model [17], the dependence of magnetization on a variation of temperature and Curie temperature T C is presented by

$$ M(T,H\,=\,H_{\max } )\,=\,\left(\! {\frac{M_{\mathrm{i}} -M_{\mathrm{f}} }{2}}\! \right)\! [ {\tanh ( {A( {T_{\mathrm{C}} \,-\,T} )} )} ]+BT+C $$
(1)

where H m a x is the maximum external field, T C is the Curie temperature, and M i/M f is the initial/final value of magnetization at ferromagnetic–paramagnetic transition as shown in Fig. 1. Here, \(A=2\left ( {\frac {B-S_{\mathrm {c}} }{M_{\mathrm {i}} -M_{\mathrm {f}} }} \right )\), B is the magnetization sensitivity dM/dT at ferromagnetic state before transition, S c is the magnetization sensitivity dM/dT at Curie temperature T C, and \(C=\left ( {\frac {M_{\mathrm {i}} -M_{\mathrm {f}} }{2}} \right )-BT_{\mathrm {C}} \)

Fig. 1
figure 1

Temperature dependence of magnetization in constantly applied magnetic field

Full size image

The magnetic entropy change ( ΔS M) can be obtained through the adiabatic change of temperature by the application of a magnetic field. ΔS M as a function of temperature for a field variation from 0 to H max is given by

$$\begin{array}{@{}rcl@{}} &&\Delta S_{\mathrm{M}} ( {T,\Delta H=H_{\max } } )\\ &&=H_{\max } \left[ {-A\left( {\frac{M_{\mathrm{i}} -M_{\mathrm{f}} }{2}} \right)\text{sech}^{2}( {A( {T_{\mathrm{C}} -T} )} )+B} \right] \end{array} $$
(2)

A more abrupt variation of magnetization near the magnetic transition occurs and results in a large magnetic entropy change. ΔS M depends on the temperature gradient of magnetization and reaches a maximum value around T C.

Relative cooling power (RCP) is a useful parameter which decides the efficiency of magnetocaloric materials based on the magnetic entropy change [1, 18]. The RCP is defined as the product of maximum magnetic entropy change ΔS Mmax and full width at half maximum in ΔS M(T) curve (δT FWHM). According to this model, ΔS Mmax is available by

$$ \Delta S_{\mathrm{M max}} =H_{\max } \left[ {-A\left( {\frac{M_{\mathrm{i}} -M_{\mathrm{f}} }{2}} \right)+B} \right] $$
(3)

and δT F W H M is presented by

$$ \delta T_{\text{FWHM}} =\frac{2}{A}\cosh^{-1}\left( {\frac{2A( {M_{\mathrm{i}} -M_{\mathrm{f}} } )}{A( {M_{\mathrm{i}} -M_{\mathrm{f}} } )+2B}} \right)^{1/2} $$
(4)

Then, RCP is computed by

$$\begin{array}{@{}rcl@{}} \text{RCP}&=&-\Delta S_{\mathrm{M max}} \delta T_{\text{FWHM}}\\ &=&H_{\max } \left( {M_{\mathrm{i}} -M_{\mathrm{f}} -\frac{2B}{A}} \right)\cosh^{-1}\left( {\frac{2A( {M_{\mathrm{i}} -M_{\mathrm{f}} } )}{A( {M_{\mathrm{i}} -M_{\mathrm{f}} } )+2B}} \right)^{1/2}\\ \end{array} $$
(5)

The RCP corresponds to the amount of heat that can be transferred between the cold and hot parts of a refrigerator in one ideal thermodynamic cycle. This parameter allows an easy comparison of different magnetic materials for applications in magnetic refrigeration; hence, larger RCP values lead to better magnetocaloric materials.

Another figure of merit which is used to compare the magnetic refrigerant materials is the refrigerant capacity (RC). The RC can be determinate by numerically integrating the area under the ΔS M(T) curve using the temperatures at half maximum of the peak as integration limits [19]. Here, RC value can be obtained as

$$\begin{array}{@{}rcl@{}} \text{RC}&=&-\int\limits_{T_{\mathrm{C}} +\frac{\delta T_{\text{FWHM}} }{2}}^{T_{\mathrm{C}} -\frac{\delta T_{\text{FWHM}} }{2}} {\Delta S( T )dT} \\ &=&H_{\max }\! \left[ {\!-( {M_{\mathrm{i}}\! -\!M_{\mathrm{f}} } )\tanh \left( {A\frac{\delta T_{\text{FWHM}} }{2}} \right)\,+\,B\delta T_{\text{FWHM}} } \right]\\ \end{array} $$
(6)

The heat capacity can be calculated from the magnetic contribution to the entropy change induced in the material, ΔC P,H, by the following expression:

$$ \Delta C_{\mathrm{P,H}} =T\frac{\partial \Delta S_{\mathrm{M}} }{\partial T} $$
(7)

From this model, a determination of ΔC P,H can be carried out as follows:

$$\begin{array}{@{}rcl@{}} &&\Delta C_{\mathrm{P,H}} ( {T,\Delta H=H_{\max } } )\\ &&=\!H_{\max } [ {\,-\,TA^{2}( {M_{\mathrm{i}} \,-\,M_{\mathrm{f}} } )\text{sech}^{2}( {A( {T_{\mathrm{C}} \,-\,T} )} )\!\tanh ( {A( {T_{\mathrm{C}} \,-\,T} )} )} ]\\ \end{array} $$
(8)

From this phenomenological model, it can easily assess the values of δT FWHM, ΔS Mmax, RCP, RC, and ΔC P,Hmin/max for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 at several magnetic fields.

3 Model Application and Discussions

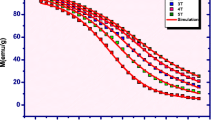
In order to apply phenomenological model, numerical calculations were made with parameters as displayed in Table 1. Figure 2 depicts the magnetization versus temperature in different applied magnetic field shifts for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 that has been prepared by arc melting in a high-purity argon atmosphere. The symbols represent experimental data from [16], while the dashed curves represent modeled data using model parameters given in Table 1. It is seen that for the given parameters, the results of calculation are in a good agreement with the experimental results. Magnetic transition in La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 is reversible in a cycle of increasing and decreasing temperature, being accompanied without any thermal hysteresis which is highly desired in the sense of practical application. It can be reported that the magnetization exhibits a continuous change around T C in different magnetic fields, and T C significantly increases with the increase in magnetic field [16].

Fig. 2
figure 2

Magnetization versus temperature for the La 0.6Pr 0.4 Fe 10.7Co 0.8Si 1.5 system at several magnetic fields. The solid lines are modeled results, and symbols represent experimental data from [16]

Full size image
Table 1 Model parameters for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 system at several magnetic fields
Full size table

Furthermore, Figs. 3 and 4 show predicted values for changes of magnetic entropy and specific heat. Magnetic entropy change in La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 is reported for ΔH = 0.5, 1, 2, 3, 4, and 5 T in Fig. 3 and show an increase in - ΔS M with increasing ΔH. The - ΔS M is found to be positive in the entire temperature range for all magnetic fields that confirmed the ferromagnetic character. It is seen that the results of calculation are in a good agreement with the experimental results. The magnetocaloric effect increases with an increase of the applied magnetic field and with the change of magnetization during the application of magnetic field. This means that the effect reaches its maximum in the vicinity of magnetic phase transition points. The large values of ΔS M for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 compounds originate from a reversible second-order magnetic transition [16]. For ΔH = 0.5 T, the ΔS M shows a maximum value of 2.020(3) J kg −1 K −1 around 269 K, and it decreases symmetrically on either side. The magnitude of ΔS M increases with an increasing strength of H and reaches a maximum value of 14.197(4) J kg −1 K −1 for ΔH = 5 T. However, the peak of ΔS M becomes asymmetrical at higher fields, i.e., while ΔS M decreases sharply with lowering temperature below the peak, it decreases gradually with an increasing temperature above the peak. Furthermore, the position of peak shifts to higher temperature with an increasing strength of H, i.e., the peak shifts from 269 K for ΔH = 0.5 T to 275 K for ΔH = 5 T.

Fig. 3
figure 3

Magnetic entropy change, ΔS, for the La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 sample. The solid lines are predicted results, and symbols represent experimental data from [16]

Full size image
Fig. 4
figure 4

Isothermal magnetic entropy change versus maximal field applied for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5, as selected temperatures below or above transition (a, b), respectively

Full size image

At the individual temperatures, the field dependence of the isothermal magnetic entropy change of sample La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5, as deduced from Fig. 3 curves, is consistent with a simple ferromagnetic order (i.e., a monotonic, almost linear increase is seen) over the total investigated field and temperature range. Figure 5a, b, for temperatures below and above the transition, respectively, shows - ΔS M changes to a positive value with the increase of the magnetic field, corresponding to the magnetic transition from ferromagnetic to paramagnetic states

Fig. 5
figure 5

Heat capacity change for ΔC P for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 system

Full size image

At the peak, the field dependence of - ΔS M can be assumed to be a power law, with an exponent n

$$ \Delta S_{\mathrm{M max}} \approx a( {\mu_{0} H} )^n $$
(9)

At T C, the exponent n becomes field-independent and is expressed as

$$ n( {T_{\mathrm{C}} } )=\left( {\frac{\beta -1}{\beta +\gamma }} \right)+1 $$
(10)

where β and γ are the critical exponents [20].

As shown in Fig. 6, the fitting of full square points ( ΔS Mmax) leads to that n(T C) = 0.773(5) for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5, which is larger than the predicted value of 2/3 in the mean field approach [21] due to the local inhomogeneities in La0.6Pr0.4Fe10.7Co0.8Si1.5.

Fig. 6
figure 6

Field dependence of maximum magnetic entropy change for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5

Full size image

In addition to the magnitude of the ΔS M, other important parameters used to characterize the refrigerant efficiency of the material are the RCP and RC defined as Eqs. (5) and (6). RCP and RC give an estimate of quantity of the heat transfer between the hot (T hot) and cold (T cold) ends during one refrigeration cycle, and it is the area under the ΔS M versus T curve between two temperatures ( ΔT =T h o t –T cold) of the FWHM of the curve. Figure 7 shows the values for the compound LaFe 10.7Co 0.8Si 1.5 as a function of applied magnetic field.

Fig. 7
figure 7

Field dependence of RCP and RC for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5

Full size image

The MCE data of different materials of the same universality class should fall onto the same curve irrespective of the applied magnetic field. Because of the intrinsic relation between the MCE and the universality class, one can obtain the critical exponents based on the MCE data, which may be another method to determine the critical behavior of phase transition, i.e., the universality class. Based on Fig. 8, the field dependence of the distance T peak−T C for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 is depicted. The distance between T C and T peakincreases with field following a power law b( μ 0 H) 1/Δ (where b is the constant, and Δ is the gap exponent), as predicted by scaling laws [22]. This feature provides an insight into the critical behavior of the compound. The lowest field data have been omitted because of the large uncertainty of the peak position. The slope of the linear function fitted to the Ln–Ln data yields the inverse of the gap exponent which implies Δ= 1.941(8).

Fig. 8
figure 8

Field dependence of the distance (T peak–T C ) for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5

Full size image

The knowledge of two critical exponents n and Δ inferred from the field dependence of MCE is enough to determine other exponents, e.g., β and γ [23]. By means of the relation Δ=β+γ and Eq. (10), one can effortlessly finds that β = 1 - Δ(1 - n) ≈0.560(5) and that γ=Δ(2 - n) - 1 ≈ 1.381(2). Fundamentally, β keeps close to the value of the mean field universality class associated with long-range FM interactions, while γ is paradoxically close to the value expected for the 3D Heisenberg ferromagnets with ferromagnetic short-range interactions. A similar result of critical behaviors was observed in Pr 0.3Nd 0.2Sr 0.5MnO 3 [24]. Together with β and γ, the other exponent δ can be also determined from the Widom’s relation [25]: δ=1+γ / β ≈ 3.463(9).

Using Eq. (8), one can calculate the specific heat changes, ΔC P,H, caused by the applied magnetic field. Shown in Fig. 4 is ΔC P,H as a function of temperature for μ 0 H = 0.5, 1, 2, 3, 4, and 5 T. It is clearly seen that ΔC P,H changes sharply from negative to positive at the Curie temperature. Since ∂ M / ∂T < 0, ΔS M < 0 results, and accordingly, the total entropy decreases upon magnetization. Furthermore, ΔC P,H < 0 for T < T C and ΔC P,H > 0 for T >T C [13, 26]. The sum of the two parts is the magnetic contribution to the total specific heat which affects the cooling or heating power of the magnetic refrigerator [27]. Specific heat presents the advantage of delivering values necessary for further refrigerator design, should the material in question be selected.

For comparison, we have also tabulated the thermomagnetic properties for several magnetocaloric materials under different magnetic fields (see Table 2).

Table 2 Comparison of maximum entropy change, specific heat change, RCP, and RC for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 system and several materials
Full size table

Recently, we [28] and others [29, 30] have shown that for second-order magnetic transition materials, the ΔS M(T) curves obtained with different maximum applied fields will collapse onto a universal curve by normalizing all the ΔS M curves with their peak entropy change, respectively, as ΔS \(_{\mathrm {M}}^{\prime } = \Delta \) S M / 2, and the temperature axis has to be rescaled in a different way below and above T C, just by imposing that the position of two additional reference points in the curve correspond to new parameter 𝜃, defined by the expression [28, 31]

$$ \theta = \left\{\begin{aligned}-{( {T-T_{\mathrm{C}} } )/( {T_{\mathrm{r}2} -T_{\mathrm{C}} } );\quad T > T_{\mathrm{C}} }^{-( {T-T_{\mathrm{C}} } )/( {T_{\mathrm{r}1} -T_{\mathrm{C}} } );\quad T\le T_{\mathrm{C}} }\end{aligned} \right. $$
(11)

where T r1 and T r2 are the reference temperatures below and above T C, respectively.

The phenomenological construction of the universal scaling of different magnetic fields is depicted in Fig. 9. Figure 9 shows an attempt to form a master curve for the entropy change of the La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5. One can see that the universal behavior manifests itself only in a limited interval around the peak temperature. Farther below and above the peak, the scaling behavior apparently breaks. Increasing fields produce an increase in the reduced magnetic entropy change. Deviations from the collapse might indicate either the influence of the demagnetizing field associated to the shape of the sample [32] or the presence of additional magnetic phases [33, 34]. The divergence of the curves is clear in the compound, particularly above the T C. The inset of Fig. 9 shows the magnetic field dependences of the two reference temperatures (T r1 and T r2). Both the temperatures increase with increasing field.

Fig. 9
figure 9

Normalized entropy change as a function of the rescaled temperature 𝜃. The inset shows the magnetic field dependences of the two reference temperatures (T r1 and T r2)

Full size image

4 Conclusions

In summary, the exhibition of large MCE in La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 which is associated with a ferromagnetic to paramagnetic phase transition near the Curie temperature was reported.

Dependence of the magnetization on temperature variation for La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 upon different magnetic fields was simulated. A good magnetocaloric property is observed. The large change of magnetization during the phase transition leads to large MCE. Large ΔS M of 7.416(9) J kg −1 K −1 and RCP of 176.103(2) J kg −1 are found for a magnetic field change of 0–2 T. Large MCE originates from a reversible second-order magnetic transition. The peak of the ΔS Mmax(T) curve shows a broad distribution, and the full width at half maximum of the ΔS Mmax peak is about 392.729(2) (Table 2) under a magnetic field of 5 T. We show that the higher field La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 MCE has a power law field dependence characterized by an exponent n = 0.773(7). The critical exponents associated with ferromagnetic transition have been determined from the magnetocaloric effect (MCE) methods. This sample exhibits considerably no magnetic hysteresis near room temperature, which is beneficial for the magnetic cooling efficiency. Moreover, by virtue of the excellent MCE with the low cost, high safety, easy preparation, and tunable Curie temperature, the La 0.6Pr 0.4Fe 10.7Co 0.8Si 1.5 system appears to be a good candidate for magnetic refrigerant materials at near room temperature range.