1 Introduction

Rare earth manganites with a general formula of R1−xAx MnO3(R = rare earths, A = alkaline earth or alkali elements) gained the attention of researchers due to their interesting electric transport and magnetic properties [1, 2]. The close relation between transport and magnetism in this kind of materials has been explained by many theories, such as double exchange (DE) interaction [3], polaronic effects, [4], and phase separation [5]. Strong competition between lattice, charge, orbital, and magnetic degrees of freedom determines the properties of the perovskites manganites, which lead to a series of novel behaviors related to basic concepts in modern physics and materials science [6, 7]. Today, the universality class of the paramagnetic (PM) to ferromagnetic (FM) transition in manganites is still a controversial question [8]. Previous studies on the critical behaviors and the universality class of the Curie temperature (T C ) transition have indicated that the critical exponents play important roles in elucidating interaction mechanisms near T C [10, 11].

In this paper, we decided to study the La0.78Dy0.02Ca0.2 MnO3 (LDCMO) manganite compound elaborated using a new synthesis route, the ball-milling (BM) process. Experimental details of the BM elaboration have been detailed in our previous work [14]. This method has been known as a very versatile technique to prepare supersaturated solid solutions and other metastable systems, including rare earth (RE) and transition metal (TM)-based systems [12]. The use of BM can be found in literature as a single-step production technique even if annealing maybe necessary sometimes to produce the desired phase [13]. Based on a phenomenological model, we predicted the critical phenomena parameters behavior near the phase transition such as the magnetic entropy change, the relative cooling power (RCP), and the heat capacity. This study allowed estimating the critical exponents for LDCMO near the Curie temperature. Three different methods have been used to analyze them.

2 Theoretical Consideration

In thermodynamic theory [15], the entropy change ΔS M associated with a magnetic field variation is given by:

$$ {\Delta} S_{M}={{\int}_{0}^{H}}_{\max} {\left( \frac{\partial S}{\partial H} \right)_{T}dH} $$
(1)

From Maxwell’s thermodynamic lows, it can be written as:

$$ {\left( \frac{\partial M}{\partial T}\right)}_{H}={\left( \frac{\partial S}{\partial H}\right)}_{T} $$
(2)

From (1) and (2):

$$ {\Delta} S_{M}={\int}_{0}^{H_{\max}} \left( \frac{\partial M}{\partial T} \right)_{H}dH $$
(3)

As a consequence, numerical evaluation of magnetic entropy change can be carried out from (3) using isothermal magnetization measurements.

Hamad [16, 17] has proposed a new model to evaluate magnetic materials behavior by using electrocaloric modeling. The proposed model assumes the temperature dependence of magnetization to be expressed as:

$$ M=\frac{(M_{i}-M_{f})}{2}\tanh \left[ A\left( T_{C}-T \right) \right]+BT+C $$
(4)

where

$$\begin{array}{@{}rcl@{}} \left\{\begin{array}{l} M_{i}~ \text{is the initial magnetization at FM-PM transition;}\\ M_{\mathrm{f}}~\text{is the final magnetization at FM-PM transition;}\\ B ~\text{is the magnetization sensitivity (dM/dT) in the}\\ \quad\text{ferromagnetic region before the transition; and}\\ S_{C} ~\text{is the magnetization sensitivity (dM/dT) at Curie}\\ \quad~\text{temperature} T_{C};\\ C=\left( \frac{M_{i}+M_{f}}{2} \right)-BT_{c};\\ A= \frac{\left( 2B-S_{C} \right)}{\left( M_{i}-M_{f} \right)}. \end{array}\right. \end{array} $$

The magnetic entropy change of a magnetic system under adiabatic magnetic field variation can be evaluated by [16]:

$$ {\Delta}\! S_{M}\,=\,\left\{\!-A\!\left( \frac{M_{i}\,-\,M_{\!f}}{2} \right)\!\text{sech}^{2}\!\left[\!A\left( T_{c}\,-\,T \right) \right]\,+\,B\! \right\}\!\mu_{0}H_{\max} $$
(5)

At T = T C , the entropy change reaches its maximum; so, (5) may be written as follows [16]:

$$ {\Delta S}_{\max}=\left[ -\left( \frac{M_{i}-M_{f}}{2} \right)+B \right]\mu_{0}H_{\max} $$
(6)

The full width at half maximum, δ T FWHM, is determined at the two extreme points of the \({\Delta S}_{\max }\) curves where \({\Delta S}_{\max }\) is the half of its maximum value. Thus [16]:

$${\delta T}_{\text{FWHM}}=\frac{2}{A}\text{sech}\left[ \sqrt{\frac{2A\left( M_{i}-M_{f} \right)}{A\left( M_{i}-M_{f} \right)+2B}} \right] $$
(7)

Thanks to these parameters, the relative cooling power (RCP) can be calculated allowing the evaluation of the magnetocaloric efficiency of the materials. In fact, the RCP is defined as [17]:

$$\begin{array}{@{}rcl@{}} \text{RCP}\!&=& \,-\,{\Delta}\! S(T,H_{\max})\!\times\! \delta T_{\text{FWHM}}\\ &=&\!(M_{i}\,-\,M_{\!f}\,-\,2\! \frac{B}{A})H_{\max}\!\times \!\text{sech}\!\left[\! \sqrt{\frac{2A\!\left( M_{i}\,-\,M_{f}\right)}{A\!\left( \! M_{i}\,-\,M_{f}\! \right)\,+\,2B}}\!\right]\\ \end{array} $$
(8)

The heat capacity can be also calculated from the magnetic contribution to the entropy change by the following expression [16]:

$$ {\Delta C}_{p,H}=T\frac{\delta {\Delta} S_{M}}{\delta T} $$
(9)

According to this model [16], ΔC p,H can be rewritten as:

$$\begin{array}{@{}rcl@{}} {\Delta C}_{p,H}&=&-TA^{2}\left( M_{i}-M_{f} \right)\text{sech}^{2}\left[ A\left( T_{C}-T \right) \right]\\&&\times \tanh \left[ A\left( T_{C}-T \right) \right]H_{\max} \end{array} $$
(10)

3 Scaling Analysis

In accordance with the scaling hypothesis [9], the critical behavior of a magnetic system showing a second-order magnetic phase transition near the Curie point is characterized by a set of critical exponents: the spontaneous magnetization exponent (β), the isothermal magnetic susceptibility exponent (γ), and the critical isotherm exponent (δ). The mathematical definitions of the critical exponents from magnetization measurements are given as follows [18]:

$$ M_{S} = \lim\nolimits_{H\rightarrow0}{(M)}= \text{M}_{0}(-\varepsilon )^{\beta},\varepsilon <0\text{T}{<T}_{C} $$
(11)
$$\chi_{0}^{-1} = \lim\nolimits_{H\rightarrow0}(\mu_{0}H/M) = (h_{0}/m_{0})\upvarepsilon^{\gamma}, \varepsilon>\!\!0 \quad T\!\!>\!\! T_{C} $$
(12)
$$ M = D(\mu H)^{1/\gamma}\upvarepsilon =\!\! 0\quad T\!\! =\! T_{C} $$
(13)

where M 0, h 0, and D are the critical amplitudes and ε = (T−T C )/T C is the reduced temperature. Furthermore, the field and temperature dependence of magnetization in the critical regime obeys to a scaling relation which can be expressed as:

$$ M(\mu_0 H, \upvarepsilon)\! = (\upvarepsilon)^{\upbeta}f_{+-}(\mu_{0} H/\upvarepsilon^{\upbeta+\upgamma}) $$
(14)

where f + and f − are regular analytical functions above and below T C [19, 20]. According to this scaling low, the plots of M/(ε)β versus H/ε β+γ would lead to two universal curves: one for T > T C (ε > 0) and the other for T < T C (ε<0).

4 Results and Discussion

4.1 Simulation

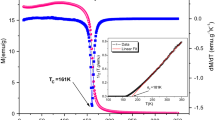
Based on the phenomenological model proposed by M. A. Hamad [16], we can easily predict the magnetocaloric properties in a magnetic material. First of all, the experimental magnetization data M(T) are fitted using (4) for several magnetic applied fields between 1 and 5 T. In Fig. 1, we report the measured magnetization (symbols) and the simulation (solid line) obtained by using the model parameters given in Table 1. The results of simulation are in very good agreement with the experimental data indicating the accuracy of the method. As shown in Fig. 1, the ferromagnetic to paramagnetic transition is characterized by a continuous decreasing of the magnetization around T C . The observed smooth change in M(T) for different applied magnetic fields indicates that this magnetic phase transition is of second order [14] (Fig. 2).

Fig. 1
figure 1

Temperature dependence of the LDCMO magnetization for different applied magnetic field. Symbols represent the experimental data and solid lines the simulation obtained by the model in [16]

Full size image
Table 1 LDCMO parameters from (4) at different applied magnetic fields (see text)
Full size table
Fig. 2
figure 2

Magnetic entropy change, (−ΔS M ) versus temperature for different magnetic fields

Full size image

Using (13), the change of the specific heat (ΔC P ) versus temperature at various magnetic fields is displayed in Fig. 3. It can be seen that ΔC P goes through an unexpected change of sign in the vicinity of the transition with a positive value below T C and a negative one above T C .

Fig. 3
figure 3

Heat capacity changes as function of temperature for different applied magnetic field

Full size image

Based on the model parameters reported in Table 1 and on (5), the magnetic entropy change (−ΔS M ) has been predicted and it is displayed in Fig. 2. It is found to be positive in the entire temperature range. However, the full-width at half-maximum of magnetic entropy change and the relative cooling power of the present magnetic refrigerants increase with Δ(μ 0 H). At 4 T, (LDCMO) compound reached a high value of RCP around 345 (J/kg), which is relatively close to the reported RCP of the Gd material [21] of 535 (J/kg). Thus, our compound can be a good candidate for magnetic refrigeration.

4.2 Critical Exponents

The reliable method used for obtaining the exact values of the critical exponents and critical temperatures is based on the measurement of the magnetic isotherm M(H) curves at various temperatures. The LDCMO magnetization M(H) has been measured with a step of 2 K in the vicinity of Curie temperature as shown in Fig. 4.

Fig. 4
figure 4

Isothermal magnetization curves

Full size image

4.2.1 Arrott–Noakes Plot or Modified Arrot Plots

The (M)1/β versus (H/ M)1/γ Arrott–Noakes plots [22], also known as modified Arrott plots (MAP), are constructed for the LDCMO compound using four different kinds of trial exponents. Based on the magnetic state equation:

$$ \left( \frac{H}{M}s\right)^{1/\gamma} = \frac{a(T-T_{C})}{T}\text{g} + bM^{1/\beta} $$
(15)

where a and b are considered to be constants.

In theory, we have four kinds of trial exponents that are used to plot the MAP by using four models of critical exponents: mean–field model (β = 0.5 and γ = 1); 3D Heisenberg model (β = 0.365 and γ = 1.336); 3D-Ising model (β = 0.325 and γ = 1.24) and tricritical mean–field model (β = 0.25 and γ = 1) as shown in Figs. 5, 6, 7 and 8.

Fig. 5
figure 5

Modified Arrott plots (MAP): isotherms of M 1/βversus μ 0 H/M 1/γby the mean–field model

Full size image
Fig. 6
figure 6

Modified Arrott plots (MAP): isotherms of M 1/βversus μ 0 H/M 1/γby the 3D-Ising model

Full size image
Fig. 7
figure 7

Modified Arrott plots (MAP): isotherms of M 1/βversus μ 0 H/M 1/γby the tricritical mean–field model

Full size image
Fig. 8
figure 8

Modified Arrott plots (MAP): isotherms of M 1/βversus μ 0 H/M 1/γ by the 3D-Heisenberg model

Full size image

In these four models, the lines in the high field region are quasi-parallel, so it is complicated to distinguish which one of them is the best model to determine the critical exponents. Thus, we calculated the so-called relative slope (RS) defined at the critical point as RS = S(T)/ S(T C ).The RS of the best model should be near the unity. As shown in Fig. 9, the RS of LDCMO using the mean–field model, the Heisenberg, and the tricritical ones, clearly deviates from 1. On the contrary, the RS of 3D-Ising model is close to unity. Thus, the latter is the best model to describe our perovskite material.

Fig. 9
figure 9

Relative slope (RS) versus temperature defined by RS = S(T)/S(T C )

Full size image

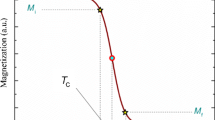
Based on the MAP, the spontaneous magnetization M S (T) as well as the inverse of the magnetic susceptibility \(\chi _{0}^{-1}(T)\) were determined from the intersections of the linear extrapolation line with the (M)1/β and the (H/ M)1/γ axis, respectively. The M S (T) and \(\chi _{0}^{-1}(T)\) are shown in Fig. 10. Those curves denote the power low fitting of M S (T) and \(\chi _{0}^{-1}(T)\) according to (1) and (2), respectively. The new critical exponent values were hence determined and reported in Table 2. In addition, the Curie temperatures associated with the fitting of M S (T) and \(\chi _{0}^{-1}(T)\) with (1) and (2), respectively, are also determined.

Fig. 10
figure 10

The spontaneous magnetization M S (T) (left axis) and the initial inverse susceptibility χ −1(T) (right axis) together with the fitting curves (solid lines)

Full size image
Table 2 Comparison of \({\Delta } S_{\max }\), RCP, and ΔC p for LDCMO and related materials
Full size table

4.2.2 Kouvel–Fisher Method

The Kouvel–Fisher (KF) method is the most accurate procedure to determinate the critical exponents. It is based on the following equations [23]:

$$ M_{S}(T)[\textit{dM}_{S}(T)/d(T)]^{-1} = 1/\beta (T - T_{C}) $$
(16)
$$ \chi_{0}^{-1}(T) [d\chi_{0}^{-1}(T)/\textit{dT}]^{-1} = 1/\gamma(T - T_{C}) $$
(17)

According to (16) and (17), plots of M S (T)[d M S (T) /d(T)]−1 and \(\chi _{0}^{-1}(T)[d\chi _{0}^{-1}(T)/\mathit {dT}]^{-1}\) versus temperature should yield to straight lines with 1/ β and 1/ γ as slopes, respectively, and with intercepts on T axes equal to Curie temperature (T C ). In Fig. 11 the critical exponents obtained from the KF methods are β = 0.312 ± 0.007 and γ = 1.28 ± 0.02.

Fig. 11
figure 11

Kouvel–Fisher plots for the spontaneous magnetization M S (T) (left axis) and the initial inverse susceptibility \(\chi _{0}^{-1}\)1 (right axis) for LDCMO sample. Solid lines correspond to the linear fit of M S (T) and \(\chi _{0}^{-1}\) data

Full size image

It is easy to remark that the critical exponents values as well as T C calculated by the MAP and KF-plots, match reasonably well.

4.2.3 Critical Isotherm Exponent

The third critical exponent δ can be determined by plotting the M(H) data at T = T C according to (13). Based on the obtained critical exponents, the M(H, T C = 161 K) versus H measured from 0 to 5 T, were chosen as the critical isothermal magnetizations, as shown in Fig. 12. The inset of the same figure shows the M(H) curve on a log–log scale. From the linear fitting in inset Fig. 12, the value of δ is found to be 4.80. Furthermore, exponent δ has been calculated from Widom scaling relation defined as [24]:

$$ \gamma =1+\frac{\gamma}{\beta} $$
(18)

Using the above scaling relation and estimated values of β and γ from the modified Arrott plot method as shown in Fig. 12, we have obtained δ = 4.80. The δ value deduced from the KF method in Fig. 11 is δ = 5.10. This value is larger than the one estimated from the Widom scaling. This difference is probably due to the experimental errors.

Fig. 12
figure 12

Isothermal magnetic curves at T = T C . The insetshows the plot in a logarithmic scale. The critical exponents mentioned in graph are obtained from the linear fit (solid line)

Full size image

4.2.4 Scaling Law

In Fig. 13, we have plotted M/|ε|−β versus H/|ε|−(β + γ) curves with β and γ obtained from the KF method. It is clear that all the data fall into one of the two parts of the plots, i.e., one part for temperatures above T C (T > T C ) and the other for temperatures below T C (T < T C ). To ensure a good visualization of the separation of curves, we plot the curves with log–log scale inset (Fig. 13). This evidently suggests that the obtained values of the critical exponents and the T C one, confirm the reliability and the good concordance with the scaling hypothesis. Indeed, all data fall into two distinct branches, one for temperature below T C and the other for temperature above T C .

Fig. 13
figure 13

Scaling plots indicating two universal curves below and above TC for LDCMO sample. The inset shows the plot in a log-log scale

Full size image

It is obvious that the values of the critical exponents agree well with those of 3-D Ising model, suggesting that the interactions among spins are of short range type. Actually, this is completely accepted for perovskite manganites [25].

As reported above, LDCMO exhibits a large MCE around T C but it’s still useless for a magnetic sensor device designed to work at room temperature [26]. Our results are similar to those of M. Khlifi et al. [27], in which they found that the critical exponents of La0.8Ca0.2MnO3 agree pretty well with the 3-D Ising model predictions. Therefore, the slight substitution with Dy3+ in LDCMO does not affect the universality class.

In another work, Kim et al. [28, 29] pointed out that the critical exponents of the La0.6Ca0.4MnO3 contain a tricritical point separating regions of first-order transition from regions of second-order one. These results are not consistent with the LDCMO ones discussed here showing a Dy 3+ substitution effect. An interesting feature is also that in La1−x Ca x MnO3compounds, the 3D-Heisenberg model is applicable only for x <0.2. Severe deviations for x ≥ 0.2 have been observed (in fact, for x = 0.3 a first-order transition occurs) [30, 31]. In particular, at x = 0.2, the obtained critical exponents are between the 3D-Heisenberg and the 3D-Ising model [29]. At this point, we decided to go further and to compare the critical behavior found in our study with other manganite systems reported in literature (see Table 3).

Table 3 Critical exponents for LDCMO compound compared to earlier values reported in literature by using various theoretical models
Full size table

One of the drawbacks of several studies is that they have been done on polycrystalline samples which present a strong smearing in the phase transitions, making it difficult to evaluate the critical parameters [32]. Numerous papers are dealing with the critical exponents in manganites. For the same composition, we can notice a difference between critical exponents near the transition’s temperature depending on the synthesis process used. For instance, Ezaami et al. [33] have studied the effect of synthesis route on the critical behavior of La0.7Ca0.2Sr0.1MnO3 manganite system in the vicinity of the Curie temperature and their results showed a change in the universality class. Moreover, Messaoui et al. [34] noticed that by changing the milling time, the critical behavior changed from the tricritical mean–field prediction to the 3D-Ising model one in Nd0.7Sr0.15Ca0.15MnO3 polycrystalline sample.

Up to now, although the wide difference of critical phenomena is reported in the literature, it is difficult to determine the common universality class for a continuous PM-FM phase transitions in manganites. The better way for this issue needs more experimental measurements on high purity samples with different compositions [32].

5 Conclusion

In summary, La0.78Dy0.02Ca0.2MnO3 compound was synthesized by high-energy ball-milling process. We simulated the dependence of magnetization, magnetic entropy, and heat capacity change as a function of temperature for (LDCMO) materials under an external magnetic field. A large magnetocaloric effect is observed, and the large relative cooling power (RCP) is found to be 345 (J/kg) under 4 T. Thus, we can consider our sample as a potential candidate for magnetic refrigeration applications. The critical properties of the perovskite manganite were studied using the isothermal magnetization around Curie temperature (T C ), based on various techniques: Arrott plot, Kouvel–Fisher analysis, and critical isotherm method. Furthermore, the validity of our critical exponents was confirmed by the universal scaling analysis. The obtained critical exponents are similar to those predicted by the 3D-Ising.