A Family of Fast Multi-resolution ENO Schemes for Compressible Flows

Abstract

In this paper, a new class of high-order fast multi-resolution essentially non-oscillatory (FMRENO) schemes is proposed with an emphasis on both the performance and the computational efficiency. First, a new candidate stencil arrangement is developed for a multi-resolution representation of the local flow scales. A set of candidate stencils ranging from high- to low-order (from large to small stencils) is constructed in a hierarchical manner. Second, the monotonicity-preserving (MP) limiter is introduced as the regularity criterion of the candidate stencils. A candidate stencil, with which the reconstructed cell interface flux locates within the MP lower and upper bounds, is regarded to be smooth. Third, a multi-resolution stencil selection strategy, which prioritizes the stencils with better spectral property or higher-order accuracy meanwhile satisfying the MP criterion, is proposed. If all the candidate stencils are judged to be nonsmooth, the targeted stencil that violates the MP criterion the least is deployed as the final reconstruction instead. With this new framework, the desirable high-order accuracy is restored in the smooth regions while the sharp shock-capturing capability is achieved by selecting the targeted stencil satisfying the MP criterion most. Moreover, the new FMRENO schemes feature low numerical dissipation for resolving the broadband physical fluctuations by adaptively choosing the candidate stencil with better spectra or higher accuracy order based on the local flow regularity. Compared to the standard weighted/targeted essentially non-oscillatory (W/TENO) schemes, the computational efficiency is dramatically enhanced by avoiding the expensive evaluations of the classical smoothness indicators. A set of benchmark simulations demonstrate the performance of the new FMRENO schemes for handling complex fluid problems with a wide range of length scales.

1 Introduction

High-order and high-resolution shock-capturing schemes are essential numerical methods to solve compressible fluid problems, which may involve discontinuities and broadband flow scales [1,2,3,4]. The main objectives are to restore the high-order accuracy in smooth regions with low numerical dissipation while capturing discontinuities sharply without generating spurious oscillations. Among all the concepts proposed in the past decades to cope with this issue [5,6,7,8,9,10], the family of essentially non-oscillatory (ENO) schemes belongs to one of the most popular methods [2, 11, 12].

The development of the ENO-family schemes and the related variants are briefly reviewed in the following. Harten et al. [7] first propose the high-order ENO scheme, which selects the smoothest stencil from a set of predefined candidate stencils to avoid the Gibbs phenomenon near discontinuities. Widely accepted discretization schemes, weighted essentially non-oscillatory (WENO) schemes, first proposed by Liu et al. [8] and further improved by Jiang and Shu [9], are developed from the ENO concept. Instead of selecting the smoothest candidate, WENO deploys a convex combination of all candidate stencils to achieve high-order accuracy in smooth regions. The optimal linear weights are modulated based on the smoothness indicators such that the desired accuracy order is restored in smooth regions and the ENO property is preserved near discontinuities. The performance of the WENO schemes can be further enhanced by improving the nonlinear weighting strategy, e.g., the WENO-M [13] and WENO-Z [14, 15] schemes avoid the order degeneration near critical points through correcting the nonlinear weights to be closer to the optimal linear ones. On the other hand, the excessive numerical dissipation of WENO (as another typical flaw of WENO-family schemes) can be remedied by freezing the nonlinear adaptation when the ratio between the largest and the smallest calculated smoothness indicator is below a problem-dependent threshold [16]. Alternatively, to reduce the numerical dissipation of the fifth-order WENO scheme, an adaptive central-upwind sixth-order WENO-CU6 [17] scheme is proposed by introducing the contribution of an additional downwind stencil. Other recent work following this direction includes the development of WENO-Z+ scheme [18]. To improve the numerical robustness of the very-high-order WENO reconstructions, monotonicity-preserving WENO schemes [19], positivity-preserving WENO schemes [20], and WENO schemes with recursive-order-reduction [21] are proposed. More recently, Zhu and Shu [22] develop the finite-difference and finite-volume multi-resolution WENO schemes based on a hierarchy of nested unequal-sized central spatial stencils. Following the nonlinear weighting concept of central WENO (CWENO) schemes [23, 24], arbitrary positive linear weights can be employed and the resulting schemes have a gradual degrading of accuracy near discontinuities. However, the aforementioned WENO schemes are rather expensive especially for the very-high-order reconstructions since the calculations of smoothness indicators are inevitable.

As the most recent innovation, the high-order TENO schemes improve the numerical robustness and reduce the unnecessary numerical dissipation by a new candidate stencil arrangement and a novel ENO-like stencil selection strategy [10, 25,26,27,28,29,30,31,32,33]. In contrast to the WENO-like smooth convex combination of candidate stencils, the TENO scheme either deploys a candidate stencil with its optimal linear weight or discards it completely when crossed by a discontinuity. The TENO scheme has been extended to unstructured meshes [34] and multi-resolution methods [35].

In this paper, a family of FMRENO schemes for both the odd- and even-order reconstructions in a unified framework is proposed. With a set of predefined candidate stencils as the multi-resolution representation of local flow scales, a novel stencil selection strategy is proposed to form the final reconstruction. The selection criterion is provided by the MP limiter [19], with which a candidate stencil is regarded to be smooth if the reconstructed cell interface flux locates within the upper and lower bounds of the MP limiter. Then, the optimal smooth stencil with higher-order accuracy or better spectral property will be adopted as the final reconstruction scheme. As a result, the FMRENO scheme achieves the multi-resolution property by adaptively selecting the targeted candidate stencil according to the local flow regularity and degenerates from high- to low-order reconstruction when approaching the discontinuities. Moreover, the computational efficiency is improved when compared to W/TENO since the evaluations of the smoothness indicators are unnecessary.

The rest of this paper is organized as follows. In Sect. 2, the basic concepts of the WENO and TENO schemes are briefly reviewed. In Sect. 3, a general framework to construct arbitrarily high-order FMRENO schemes is proposed. In Sect. 4, the explicit expressions of FMRENO schemes ranging from fifth- to eighth-order are given. In Sect. 5, a set of benchmark cases is considered to assess the proposed schemes. The concluding remarks are given in the last section.

2 Basic Concepts of W/TENO Schemes

To facilitate the presentation, we consider a one-dimensional scalar hyperbolic conservation law

$$\begin{aligned} \frac{\partial u }{\partial t} + \frac{\partial }{\partial x}f(u) = 0 , \end{aligned}$$

(1)

where u and f denote the conservative variable and the flux function, respectively. Without losing the generality, the characteristic signal velocity is assumed to be positive $\frac{\partial f(u)}{\partial u} > 0$ in the entire computational domain hereafter.

For a uniform Cartesian mesh with cell centers ${x_i} = i\Delta x$ and cell interfaces ${x_{i+1/2}} = {x_i} + {\Delta x}/{2}$, the spatial discretization results in a set of ordinary differential equations

$$\begin{aligned} \frac{d{u_i(t)}}{dt} = - \frac{\partial f}{\partial x}\left| {_{x = {x_i}}} \right. , \text { } i = 0,\ldots ,n, \end{aligned}$$

(2)

where ${u_i}$ denotes the numerical approximation to the point value $u(x_i,t)$. Eq. (2) can be further discretized by a conservative finite-difference scheme as

$$\begin{aligned} \frac{d{u_i}}{dt} = - \frac{1}{\Delta x}({h_{i + 1/2}} - {h_{i - 1/2}}) , \end{aligned}$$

(3)

where the primitive function h(x) is implicitly defined by

$$\begin{aligned} f(x) = \frac{1}{\Delta x}\int _{x - \Delta x/2}^{x + \Delta x/2} {h(\xi )d\xi }, \end{aligned}$$

(4)

and ${h_{i \pm 1/2}} = h({x_i} \pm {{\Delta x}}/{2})$. For the purpose of achieving global high-order accuracy of spatial discretization, a high-order approximation of the function h(x) at the cell interface has to be reconstructed from the cell-averaged values of f(x) at the cell centers. Eq. (3) can be written as

$$\begin{aligned} \frac{d{u_i}}{dt} \approx - \frac{1}{\Delta x}({{\hat{f}}_{i + 1/2}} - {{\hat{f}}_{i - 1/2}}) , \end{aligned}$$

(5)

where ${{\hat{f}}_{i \pm 1/2}}$ denotes the approximate numerical fluxes and can be computed from different stencils. For a K-point stencil, a K-th order polynomial interpolation of function h(x) can be assumed as

$$\begin{aligned} h(x) \approx {{\hat{f}}}(x) = \sum \limits _{l = 0}^{{K} - 1} {{a_{l}}} {x^l}. \end{aligned}$$

(6)

After substituting Eq. (6) into Eq. (4) and evaluating the integral functions at the stencil nodes, the coefficients ${a_{l}}$ are uniquely determined by solving the resulting system of linear algebraic equations.

For solving hyperbolic conservation laws, discontinuities may occur in the computational domain even when the initial condition is smooth enough. The long-term numerical challenge is to develop a reconstruction scheme that is high-order accurate in smooth regions and captures discontinuities sharply and stably in nonsmooth regions. In the following, we recall the essential elements of different strategies to ensure the above properties.

2.1 The WENO-Z Scheme

With the WENO-family schemes [9, 14], a global $(K = 2r-1)$-th order approximate numerical flux can be computed from a convex combination of r candidate stencils with the same width r as

$$\begin{aligned} {\hat{f}}_{i + 1/2} = \sum \limits _{k = 0}^{r-1} {w_k} {\hat{f}}_{k,i + 1/2} , \end{aligned}$$

(7)

where $\omega _{k}$ denotes the nonlinear weight for each candidate flux, and ${{\hat{f}}_{k, i \pm 1/2}}$ denotes the r-th order approximate numerical flux similar to the definition in Eq. (6). For WENO-Z schemes [14], the nonlinear weight $\omega _{k}$ of each stencil is renormalized from the optimal linear weight $d_k$ as

$$\begin{aligned} \omega _{k} = \frac{\alpha _k^Z}{\sum _{k=0}^{r-1}\alpha _k^Z}, \text { and } \alpha _k^Z = \frac{d_k}{\beta _k^Z}. {\textbf { }} \end{aligned}$$

(8)

In the WENO-Z scheme, the optimal linear weight $d_k$ is the corresponding coefficient for each candidate stencil to achieve maximum accuracy order of the background linear scheme.

Following [36], the calculation of the $\beta _k^Z$ function is obtained by

$$\begin{aligned} \frac{1}{\beta _k^Z} = \left( 1+(\frac{\tau _{2r-1}}{\beta _{k,r} + \epsilon })^p\right) , \text {and } p = 1 \text { or } 2. \end{aligned}$$

(9)

Following Jiang and Shu [9], the smoothness indicator $\beta _{k,r}$ for the k-th candidate stencil can be given as

$$\begin{aligned} {\beta _{k,r}} = \sum \limits _{j = 1}^{r - 1} {\Delta {x^{2j - 1}}} \int _{{x_{i - 1/2}}}^{{x_{i + 1/2}}} {{{\left( \frac{{{d^j}}}{{d{x^j}}}{{{\hat{f}}}_k}(x)\right) }^2}dx} \end{aligned}$$

(10)

based on the $L_2$ norm of the derivatives of the reconstructed candidate polynomials.

The global high-order smoothness indicator $\tau _{2r-1}$ is defined with a linear combination of existing low-order smoothness indicators $\beta _{0,r},\ldots ,\beta _{r-1,r}$ as:

$$\begin{aligned} {\tau _{2r-1}} = \left\{ {\begin{array}{ll} |\beta _{0,r} - \beta _{r-1,r}|, &{}{\text {if } \bmod (r,2) = 1,}\\ |\beta _{0,r} -\beta _{1,r} - \beta _{r-2,r} + \beta _{r-1,r}|, &{}{\text {if } \bmod (r,2) = 0.}\\ \end{array}} \right. \end{aligned}$$

(11)

2.2 The WENO-S Scheme

In [37], a new smoothness indicator that can decrease the measured smoothness variances on different candidate stencils in smooth regions is proposed. The resulting new schemes based on the same candidate stencils of classical WENO schemes are called WENO-S. For WENO-S schemes [37], the nonlinear weight $\omega _{k}^{S}$ of each stencil is renormalized from the optimal linear weight $d_k$ as

$$\begin{aligned} \omega _{k}^{S} = \frac{\alpha _k^S}{\sum _{k=0}^{r-1}\alpha _k^S}, \text { and } \alpha _k^S = {d_k \left( 1+(\frac{\tau ^{S}}{\beta _{k}^{S} + \epsilon })\right) }, \end{aligned}$$

(12)

where the formula of the $\beta _k^S$ function is given by

$$\begin{aligned} \begin{aligned}&{\beta _k^S} = (f_{i+k-3} - f_{i+k-2} - f_{i+k-1} + f_{i+k})^2 + \\&|(-f_{i+k-3} - f_{i+k-2} + f_{i+k-1} + f_{i+k})(-f_{i+k-3} +3f_{i+k-2} -3 f_{i+k-1} + f_{i+k})|. \end{aligned} \end{aligned}$$

(13)

For the seven-point WENO-S scheme, the global smoothness indicator $\tau ^S$ can be written as

$$\begin{aligned} \begin{aligned} {\tau ^S} =&(-f_{i-3} + 4f_{i-2} - 5f_{i-1} + 5f_{i+1} - 4f_{i+2} + f_{i+3})^2 + \\&+|(f_{i-3} - 2f_{i-2} - f_{i-1} + 4f_{i} - f_{i+1} -2f_{i+2} + f_{i+3}) \\&(f_{i-3} - 6f_{i-2} + 15f_{i-1} - 20f_{i} +15f_{i+1} -6f_{i+2} + f_{i+3})|. \end{aligned} \end{aligned}$$

(14)

2.3 The TENO Scheme

Different from WENO schemes, arbitrarily high-order TENO schemes can be constructed from a set of candidate stencils with incremental width [10, 25], as shown in Fig. 1. The sequence of stencil width r varying versus the global accuracy order K is as

$$\begin{aligned} \{ {r_k}\} = \left\{ {\begin{array}{*{20}{c}} {\{ \underbrace{3,3,3,4,\ldots ,\frac{{K + 2}}{2}}_{0,\ldots ,K - 3}\} ,}&{}{\text {if } \bmod (K,2) = 0,}\\ {\{ \underbrace{3,3,3,4,\ldots ,\frac{{K + 1}}{2}}_{0,\ldots ,K - 3}\} ,}&{}{\text {if } \bmod (K,2) = 1.} \end{array}} \right. \end{aligned}$$

(15)

Fig. 1

Sketch of the candidate stencils with incremental width towards high-order TENO reconstructions. The candidate stencils for the eight-point TENO reconstruction scheme are shown in this plot

As WENO schemes, the Kth-order reconstructed numerical flux by TENO at the cell face $i + {1}/{2}$ is given as

$$\begin{aligned} {\hat{f}}_{i + 1/2} = \sum \limits _{k = 0}^{K - 3} {w_k} {{\hat{f}}_{k,i + 1/2}}, \end{aligned}$$

(16)

where the nonlinear weight $\omega _{k}$ of each stencil is renormalized from the optimal linear weight $d_k$ as

$$\begin{aligned} {w_k} = \frac{{d_k}{\delta _k}}{{\sum \nolimits _{k = 0}^{K - 3} {d_k}{\delta _k} }} , \end{aligned}$$

(17)

and $\delta _k$, given as

$$\begin{aligned} {\delta _k} = \left\{ {\begin{array}{*{20}{c}} 0, &{}{\text {if }{\chi }_k < {C_T},}\\ 1, &{}{\text {otherwise},} \end{array}} \right. \end{aligned}$$

(18)

is a sharp cut-off function with the parameter $C_T$ which controls the numerical dissipation and can be determined by spectral analysis [10].

${\chi }_k$ is a normalized function of the smoothness indicator $\gamma _k$, which can be defined as

$$\begin{aligned} {{\chi }_k } = \frac{{{\gamma _k}}}{{\sum \nolimits _{k = 0}^{K - 3} {{\gamma _k}} }}, \end{aligned}$$

(19)

and

$$\begin{aligned} {\gamma _k} = {\left( C + \frac{{{\tau _K}}}{{{\beta _{k,r}} + \varepsilon }}\right) ^q}{\text { , }}k = 0,\ldots ,K - 3 . \end{aligned}$$

(20)

Here, $\tau _K$ is the high-order smoothness indicator which allows for good stability with a reasonably large CFL number and can be constructed as [25]

$$\begin{aligned} \tau _K = \left| {{\beta _K} - \frac{1}{6}({\beta _{1,3}} + {\beta _{2,3}} + 4{\beta _{0,3}})} \right| = {\mathcal {O}}(\Delta {x^6}), \text { } K \ge 5 \end{aligned}$$

(21)

where ${\beta _K}$ measures the global smoothness on the K-point full stencil, for any Kth-order TENO scheme (higher than fourth-order). $\varepsilon = {10^{ - 40}}$ is introduced to prevent the zero denominator. Moreover, the parameters $C = 1$ and $q = 6$ are adopted for strong scale separation, which means that discontinuities can be isolated from smooth regions effectively. Similarly to WENO schemes, $\beta _{k,r}$ can be defined following Eq. (10) [9].

3 Framework for Constructing the High-Order FMRENO Schemes

The previous work of TENO [26] demonstrates that the high-order accuracy and the ENO property can be enforced by properly selecting the targeted stencil from a set of predefined candidates and the linear/nonlinear convex combination is not necessary. The main flaw of TENO schemes [26], which applies to the WENO-family schemes [9, 14] as well, is that the evaluation of the smoothness indicators is expensive, particularly for very-high-order reconstructions [29].

The objective of this work is to propose a new family of FMRENO schemes, which is computationally cheap and also competitive in terms of performance. In this section, the three main phases for constructing the high-order FMRENO schemes are elaborated in detail, i.e. (1) prepare the hierarchically nested candidate stencils; (2) provide the regularity criterion based on the MP concept; (3) form the final high-order reconstruction by a new multi-resolution stencil selection strategy.

3.1 The Hierarchical Nested Candidate Stencil Arrangement

Motivated by the construction of TENO schemes [26], the candidate stencil arrangement of a K-th order reconstruction should satisfy the following principles: (1) in order to achieve a multi-resolution representation of the local flow scales, a set of candidate stencils with interpolation polynomials of order $k = 3,\dots ,K$ is constructed in a hierarchical nested manner; (2) all candidate stencils contain at least one-point upwinding such that no pure downwind stencil can be deployed for the final reconstruction. As shown in the standard TENO schemes [10], this condition ensures the good numerical stability of even-order reconstructions in nonsmooth regions; (3) the candidate stencil arrangement allows that, in nonsmooth regions, at least one candidate stencil is not crossed by discontinuities to ensure the ENO property.

Following the above principles, the candidate stencil arrangements for the five-, six-, seven- and eight-point FMRENO schemes are given in Figs. 2, 3, 4 and 5, respectively. It is worth noting that, such a candidate stencil arrangement is applicable for arbitrarily high-order reconstructions, i.e., for both the odd- and even-order FMRENO schemes.

For each candidate stencil $S_{r,m}$, a polynomial interpolation function (typically r-th order with r stencil points) for h(x) can be constructed similar to the definition in Eq. (6) and the resulting flux function evaluated at $i+1/2$ is denoted as ${\hat{f}}^r_{m,i+1/2}$. Among all candidate stencils with the same width r, a priority sequence (as indicated by the value m) to form the final reconstruction is: the high-order central schemes, the optimized central schemes (if there are), the downwind-biased schemes, and the upwind-biased schemes. Such an arrangement ensures that the candidate stencil with higher accuracy order or better spectral property features the priority to be selected for the final reconstruction.

Fig. 2

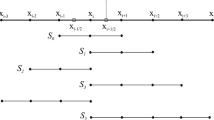
Hierarchically nested candidate stencils for five-point FMRENO scheme: admissible stencils with stencil point number $r = 3,4,5$. For candidate stencil $S_{r,m}$, m denotes the sequence order among all the r-point candidates and a smaller value indicates a higher priority to be selected for the final reconstruction

Fig. 3

The hierarchically nested candidate stencils for six-point FMRENO scheme: admissible stencils with stencil point number $r = 3,4,5,6$. For candidate stencil $S_{r,m}$, m denotes the sequence order among all the r-point candidates and a smaller value indicates a higher priority to be selected for the final reconstruction. Also included is the stencil $S_{6,1}$ represented with the dashed line, which is generally an optimized six-point scheme for a better spectral property by relaxing the accuracy-order constraint. Note that, for the odd-order reconstruction, such an additional optimal scheme is not necessary

Fig. 4

Hierarchically nested candidate stencils for seven-point FMRENO scheme: admissible stencils with stencil point number $r = 3,4,5,6,7$. For candidate stencil $S_{r,m}$, m denotes the sequence order among all the r-point candidates and a smaller value indicates a higher priority to be selected for the final reconstruction.

Fig. 5

Hierarchically nested candidate stencils for eight-point FMRENO scheme: admissible stencils with stencil point number $r = 3,4,5,6,7,8$. For candidate stencil $S_{r,m}$, m denotes the sequence order among all the r-point candidates and a smaller value indicates a higher priority to be selected for the final reconstruction. Also included is the stencil $S_{8,1}$ represented with the dashed line, which is generally an optimized eight-point scheme for a better spectral property by relaxing the accuracy-order constraint.

3.2 MP-Based Regularity Criterion

Extensive numerical experiments demonstrate that the MP scheme proposed by Suresh and Huynh [19] is able to distinguish smooth local extrema from genuine discontinuities and is robust for shock-dominated flows [38,39,40]. Instead of deploying the MP limiter to modify the reconstructed cell interface flux for suppressing numerical oscillations as in [19] and [40], in this work, we propose to utilize the MP limiter as a local regularity criterion, which judges the candidate stencil to be smooth or not. More specifically, one candidate stencil is judged to be smooth only when the reconstructed cell interface flux locates within the MP upper and lower bounds, which will be defined as follows.

As given in [19] and [40], the lower and upper bounds of the cell interface flux at $i + {1}/{2}$ are given by

$$\begin{aligned} \begin{array}{l} {\hat{f}}_{i + 1/2}^\mathrm{{min}} = \max [\min ({f_i},{f_{i + 1}},{\hat{f}}_{i + 1/2}^{\mathrm{{MD}}}),\min ({f_i},{\hat{f}}_{i + 1/2}^{\mathrm{{UL}}}, {\hat{f}}_{i + 1/2}^{\mathrm{{LC}}})],\\ {\hat{f}}_{i + 1/2}^\mathrm{{max}} = \min [\max ({f_i},{f_{i + 1}},{\hat{f}}_{i + 1/2}^{\mathrm{{MD}}}),\max ({f_i},{\hat{f}}_{i + 1/2}^{\mathrm{{UL}}},{\hat{f}}_{i + 1/2}^{\mathrm{{LC}}})], \end{array} \end{aligned}$$

(22)

where ${\hat{f}}_{i + 1/2}^{\text {UL}}$, ${\hat{f}}_{i + 1/2}^{\text {MD}}$ and ${\hat{f}}_{i + 1/2}^{\text {LC}}$ denote the left-side upper limiter, the median value of the solution, and the left-side value allowing for a large curvature in the solution, respectively.

Specifically, the left-side upper limiter is given by

$$\begin{aligned} {\hat{f}}_{i + 1/2}^{\text {UL}} = {f_i} + \alpha ({f_i} - {f_{i - 1}}), \end{aligned}$$

(23)

where $\alpha = 2.5$ is employed to enable stability.

The median value of the solution at $x_{i+1/2}$ is given by

$$\begin{aligned} {\hat{f}}_{i + 1/2}^{\text {MD}} = \frac{1}{2}({f_i} + {f_{i + 1}}) - \frac{1}{2}d_{i + 1/2}^{\text {MD}} . \end{aligned}$$

(24)

The left-side value allowing for a large curvature in the solution at $x_{i+1/2}$ can be given by

$$\begin{aligned} {\hat{f}}_{i + 1/2}^{\text {LC}} = {f_i} + \frac{1}{2}({f_i} - {f_{i - 1}}) + \frac{\beta }{3}d_{i - 1/2}^{\text {LC}} , \end{aligned}$$

(25)

where it is recommended to set $\beta = 4$. Following [19] and [40], $d_{i + 1/2}^{\text {MD}} = d_{i + 1/2}^{\text {LC}} = {d_{i + 1/2}^{\text {M}}}$ is adopted, and the curvature measurement at the cell interface $i+ 1/2$ can be defined as

$$\begin{aligned} {\begin{array}{l} {d_{i + 1/2}^{\text {M}}} = \mathrm{{minmod}} ({d_i},{d_{i + 1}}), \end{array}} \end{aligned}$$

(26)

with ${d_i} = {f_{i + 1}} - 2{f_i} + {f_{i - 1}}, \text { and } {d_{i+1}} = {f_{i + 2}} - 2{f_{i+1}} + {f_{i}}$.

3.3 A Multi-resolution Stencil Selection Strategy

In order to restore the optimal high-order accuracy in smooth regions and enforce the ENO property near discontinuities, a multi-resolution stencil selection strategy is proposed based on the new candidate stencil arrangement and the MP-based regularity criterion as described in previous subsections. The detailed algorithms are summarized as in Algorithm 1.

Specifically, the regularity of each candidate stencil is examined by the MP-based criterion in a one-by-one manner and the priority is given to the stencil with higher accuracy order (typically with larger stencil width r) or with better spectral property (e.g., with a smaller value of m in Figs. 2, 3, 4 and 5). Once one candidate stencil satisfies the regularity criterion, i.e. judged to be smooth by the MP criterion, it is assigned as the final reconstruction scheme without further turning to candidate stencils with lower priorities. If all predefined candidate stencils fail to enforce the MP criterion, then the smoothest candidate, with which the predicted cell interface value departs from the MP upper and lower bounds the least, will be adopted as the final reconstruction for numerical stability.

As a result, (i) in smooth regions, the first largest stencil will be adopted as the final reconstruction scheme ensuring that the desired high-order accuracy is restored; (2) for wave-like structures, the reconstruction tends to select the stencil assigned with a higher priority, i.e. higher accuracy order or better spectral property, according to the local flow regularity. This multi-resolution type stencil selection ensures low numerical dissipation for resolving the broadband physical fluctuations; (3) near discontinuities, the reconstruction gradually degenerates to a smaller stencil with lower priority until it is judged to be smooth by the MP regularity criterion or the so-called smoothest candidate flux which minimizes $| {\hat{f}^r_{m,i+1/2}} - \frac{1}{2} ({\hat{f}^\mathrm{{max}}_{i+1/2} + \hat{f}^\mathrm{{min}}_{i + 1/2} })|$ for all r and m.

When compared to the standard W/TENO schemes, the expensive evaluation of the smoothness indicators is avoided and the linear combination of candidate stencils is not necessary. Moreover, with increasing targeted reconstruction accuracy order, the cost increase of the FMRENO scheme is negligible whilst that of W/TENO scheme is generally substantial.

4 Explicit Expressions of FMRENO Schemes

In this section, the formulas for fifth- to eighth-order FMRENO schemes are explicitly given. It is worth noting that the candidate schemes may also be constructed as other non-polynomial functions [41].

4.1 Five-Point FMRENO Scheme

All candidate stencils used to construct a five-point FMRENO scheme (referred to as FMRENO5) are given as

$$\begin{aligned} {\begin{array}{l} {\hat{f}}^5_{0,i+1/2} = -\frac{1}{60}(-2f_{i-2} + 13f_{i-1} - 47f_{i} - 27f_{i+1} + 3f_{i+2}),\\ {\hat{f}}^4_{0,i+1/2} = -\frac{1}{12}(f_{i-1} - 7f_{i} - 7f_{i+1} + f_{i+2}),\\ {\hat{f}}^4_{1,i+1/2} = \frac{1}{12}(f_{i-2} - 5f_{i-1} + 13f_{i} + 3f_{i+1}),\\ {\hat{f}}^3_{0,i+1/2} = \frac{1}{6}(2f_{i} + 5f_{i+1} - f_{i+2}),\\ {\hat{f}}^3_{1,i+1/2} = \frac{1}{6}(-f_{i-1} + 5f_{i} + 2f_{i+1}),\\ {\hat{f}}^3_{2,i+1/2} = \frac{1}{6}(2f_{i-2} - 7f_{i-1} + 11f_{i}).\\ \end{array}} \end{aligned}$$

(27)

4.2 Six-Point FMRENO Scheme

All candidate stencils used to construct a six-point FMRENO scheme (referred to as FMRENO6) are given as

$$\begin{aligned} {\begin{array}{ll} {\hat{f}}^6_{0,i+1/2} &{}= \frac{1}{60}(f_{i-2}-8f_{i-1}+37f_{i}+37f_{i+1}-8f_{i+2}+f_{i+3}),\\ {\hat{f}}^6_{1,i+1/2} &{}= -\frac{57}{6000}(-2f_{i-2} + 13f_{i-1} - 47f_{i} - 27f_{i+1} + 3f_{i+2}) + \\ &{}\quad \frac{43}{6000}(-3f_{i-1} + 27f_{i} + 47f_{i+1} - 13f_{i+2} + 2f_{i+3}),\\ {\hat{f}}^5_{0,i+1/2} &{}= \frac{1}{60}(-3f_{i-1} + 27f_{i} + 47f_{i+1} - 13f_{i+2} + 2f_{i+3}),\\ {\hat{f}}^5_{1,i+1/2} &{}=-\frac{1}{60}(-2f_{i-2} + 13f_{i-1} - 47f_{i} - 27f_{i+1} + 3f_{i+2}),\\ {\hat{f}}^4_{0,i+1/2} &{}= -\frac{1}{12}(f_{i-1} - 7f_{i} - 7f_{i+1} + f_{i+2}),\\ {\hat{f}}^4_{1,i+1/2} &{}= \frac{1}{12}(3f_{i} + 13f_{i+1} - 5f_{i+2} + f_{i+3}),\\ {\hat{f}}^4_{2,i+1/2} &{}= \frac{1}{12}(f_{i-2} - 5f_{i-1} + 13f_{i} + 3f_{i+1}),\\ {\hat{f}}^3_{0,i+1/2} &{}= \frac{1}{6}(2f_{i} + 5f_{i+1} - f_{i+2}),\\ {\hat{f}}^3_{1,i+1/2} &{}= \frac{1}{6}(-f_{i-1} + 5f_{i} + 2f_{i+1}),\\ {\hat{f}}^3_{2,i+1/2} &{}= \frac{1}{6}(2f_{i-2} - 7f_{i-1} + 11f_{i}),\\ \end{array}} \end{aligned}$$

(28)

where ${\hat{f}}^6_{1,i+1/2}$ denotes a central scheme with optimized dispersion-dissipation relation [25].

4.3 Seven-Point FMRENO Scheme

All candidate stencils used to construct a seven-point FMRENO scheme (referred to as FMRENO7) are given as

$$\begin{aligned} {\begin{array}{l} {\hat{f}}^7_{0,i+1/2}= \frac{1}{420}(-3f_{i-3}+25f_{i-2}-101f_{i-1}+319f_{i}+214f_{i+1}-38f_{i+2}+4f_{i+3}),\\ {\hat{f}}^6_{0,i+1/2}= \frac{1}{60}(f_{i-2}-8f_{i-1}+37f_{i}+37f_{i+1}-8f_{i+2}+f_{i+3}),\\ {\hat{f}}^6_{1,i+1/2}= -\frac{1}{60}(f_{i-3} - 7f_{i-2} + 23f_{i-1} - 57f_{i} - 22f_{i+1} + 2f_{i+2}),\\ {\hat{f}}^5_{0,i+1/2}= \frac{1}{60}(-3f_{i-1} + 27f_{i} + 47f_{i+1} - 13f_{i+2} + 2f_{i+3}),\\ {\hat{f}}^5_{1,i+1/2}=-\frac{1}{60}(-2f_{i-2} + 13f_{i-1} - 47f_{i} - 27f_{i+1} + 3f_{i+2}),\\ {\hat{f}}^5_{2,i+1/2}=\frac{1}{60}(-3f_{i-3} + 17f_{i-2} - 43f_{i-1} + 77f_{i} + 12f_{i+1}),\\ {\hat{f}}^4_{0,i+1/2} = -\frac{1}{12}(f_{i-1} - 7f_{i} - 7f_{i+1} + f_{i+2}),\\ {\hat{f}}^4_{1,i+1/2} = \frac{1}{12}(3f_{i} + 13f_{i+1} - 5f_{i+2} + f_{i+3}),\\ {\hat{f}}^4_{2,i+1/2} = \frac{1}{12}(f_{i-2} - 5f_{i-1} + 13f_{i} + 3f_{i+1}),\\ {\hat{f}}^4_{3,i+1/2} = \frac{1}{12}(-3f_{i-3} + 13f_{i-2} - 23f_{i-1} + 25f_{i}),\\ {\hat{f}}^3_{0,i+1/2}= \frac{1}{6}(2f_{i} + 5f_{i+1} - f_{i+2}),\\ {\hat{f}}^3_{1,i+1/2} = \frac{1}{6}(-f_{i-1} + 5f_{i} + 2f_{i+1}),\\ {\hat{f}}^3_{2,i+1/2} = \frac{1}{6}(2f_{i-2} - 7f_{i-1} + 11f_{i}).\\ \end{array}} \end{aligned}$$

(29)

4.4 Eight-Point FMRENO Scheme

All candidate stencils used to construct an eight-point FMRENO scheme (referred to as FMRENO8) are given as

$$\begin{aligned} {\begin{array}{ll} {\hat{f}}^8_{0,i+1/2}&{}= -\frac{1}{840}(3f_{i-3}-29f_{i-2}+139f_{i-1}-533f_{i}-533f_{i+1}+139f_{i+2}-29f_{i+3}+3f_{i+4}), \\ {\hat{f}}^8_{1,i+1/2}&{}= -0.007723837710877f_{i-3}+0.05728582585522101f_{i-2}\\ &{}\quad -0.2148478198727312f_{i-1}+0.6852858258552214f_{i}\\ &{}\quad +0.6152858258552207f_{i+1}-0.1728478198727316f_{i+2} \\ &{}\quad +0.04328582585522106f_{i+3}-0.005723831837710886f_{i+4}, \\ {\hat{f}}^7_{0,i+1/2}&{}= -\frac{1}{420}(-4f_{i-2}+38f_{i-1}-214f_{i}-319f_{i+1}+101f_{i+2}-25f_{i+3}+3f_{i+4}), \\ {\hat{f}}^7_{1,i+1/2}&{}= \frac{1}{420}(-3f_{i-3}+25f_{i-2}-101f_{i-1}+319f_{i}+214f_{i+1}-38f_{i+2}+4f_{i+3}), \\ {\hat{f}}^6_{0,i+1/2}&{}= \frac{1}{60}(f_{i-2}-8f_{i-1}+37f_{i}+37f_{i+1}-8f_{i+2}+f_{i+3}),\\ {\hat{f}}^6_{1,i+1/2}&{}= -\frac{1}{60}(2f_{i-1}-22f_{i}-57f_{i+1}+23f_{i+2}-7f_{i+3}+f_{i+4}),\\ {\hat{f}}^6_{2,i+1/2}&{}= -\frac{1}{60}(f_{i-3} - 7f_{i-2} + 23f_{i-1} - 57f_{i} - 22f_{i+1} + 2f_{i+2}),\\ {\hat{f}}^5_{0,i+1/2}&{}= -\frac{1}{60}(-12f_{i} - 77f_{i+1} + 43f_{i+2} - 17f_{i+3} + 3f_{i+4}),\\ {\hat{f}}^5_{1,i+1/2}&{}= \frac{1}{60}(-3f_{i-1} + 27f_{i} + 47f_{i+1} - 13f_{i+2} + 2f_{i+3}),\\ {\hat{f}}^5_{2,i+1/2}&{}=-\frac{1}{60}(-2f_{i-2} + 13f_{i-1} - 47f_{i} - 27f_{i+1} + 3f_{i+2}),\\ {\hat{f}}^5_{3,i+1/2}&{}=\frac{1}{60}(-3f_{i-3} + 17f_{i-2} - 43f_{i-1} + 77f_{i} + 12f_{i+1}),\\ {\hat{f}}^4_{0,i+1/2} &{}= -\frac{1}{12}(f_{i-1} - 7f_{i} - 7f_{i+1} + f_{i+2}),\\ {\hat{f}}^4_{1,i+1/2} &{}= \frac{1}{12}(3f_{i} + 13f_{i+1} - 5f_{i+2} + f_{i+3}),\\ {\hat{f}}^4_{2,i+1/2} &{}= \frac{1}{12}(f_{i-2} - 5f_{i-1} + 13f_{i} + 3f_{i+1}),\\ {\hat{f}}^4_{3,i+1/2} &{}= \frac{1}{12}(-3f_{i-3} + 13f_{i-2} - 23f_{i-1} + 25f_{i}),\\ {\hat{f}}^3_{0,i+1/2}&{}= \frac{1}{6}(2f_{i} + 5f_{i+1} - f_{i+2}),\\ {\hat{f}}^3_{1,i+1/2}&{} = \frac{1}{6}(-f_{i-1} + 5f_{i} + 2f_{i+1}),\\ {\hat{f}}^3_{2,i+1/2} &{}= \frac{1}{6}(2f_{i-2} - 7f_{i-1} + 11f_{i}),\\ \end{array}} \end{aligned}$$

(30)

where ${\hat{f}}^8_{1,i+1/2}$ denotes a central scheme with optimized dispersion-dissipation relation [25].

5 Numerical Validations

In this section, a set of critical benchmark cases involving strong discontinuities and broadband flow length scales is simulated. With the finite-difference framework, the proposed FMRENO schemes are extended to multi-dimensional problems in a dimension-by-dimension manner. For systems of hyperbolic conservation laws, the characteristic decomposition method based on the Roe average [42] is employed for effectively suppressing numerical oscillations. The Rusanov scheme [43] is adopted as the flux splitting method if not mentioned otherwise. The third-order strong stability-preserving (SSP) Runge-Kutta method [44] with a typical CFL number of 0.4 is adopted for the time advancement. Meanwhile, the numerical results from WENO5-Z, WENO7-S [37], WENO-CU6 [45] and TENO8 [27] are compared.

To facilitate the accurate measurement of the computational time with one CPU (avoiding the effects of parallelization), the simulation resolution of some 2D cases, i.e., 2D Riemann problems, will be decreased.

5.1 Accuracy Verifications

5.1.1 Advection Problem

We first consider the one-dimensional Gaussian pulse advection problem [46]. The linear advection equation

$$\begin{aligned} \frac{\partial u}{\partial t} + \frac{\partial u}{\partial x} = 0 , \end{aligned}$$

(31)

with initial condition

$$\begin{aligned} {u}(x,0) = {\sin (\pi x)}, \text { } \end{aligned}$$

(32)

is solved in a computational domain $0 \le x \le 2$ and the final time is $t = 2$. Periodic boundary conditions are imposed at $x = 0$ and $x = 2$.

As shown in Tables 1, 2, 3 and 4, the desired accuracy order is achieved for all the present FMRENO schemes.

Table 1 Convergence statistics of numerical error with $L_\infty$ norm from five-point schemes for the linear advection problem

Table 2 Convergence statistics of numerical error with $L_\infty$ norm from six-point schemes for the linear advection problem

Table 3 Convergence statistics of numerical error with $L_\infty$ norm from seven-point schemes for the linear advection problem

Table 4 Convergence statistics of numerical error with $L_\infty$ norm from eight-point schemes for the linear advection problem

5.1.2 Burgers Problem

Further, we consider the 2D inviscid nonlinear Burgers equation [47]

$$\begin{aligned} \frac{\partial u}{\partial t} + \frac{\partial {( \frac{u^2}{2})}}{\partial x} + \frac{\partial {( \frac{u^2}{2})}}{\partial y}= 0 . \end{aligned}$$

(33)

The equation with an initial condition $u(x,y,0)=\sin (\pi (x+y)/2)$ is solved in a computational domain $[0,4] \times [0,4]$ and periodic boundary conditions are imposed at the left and right boundaries. The simulation is conducted up to $t = {0.5}/{\pi }$, when the solution is still smooth.

Numerical error statistics and accuracy orders for the WENO5-Z, WENO-CU6, WENO7-S, TENO8 and FMRENO schemes are shown in Tables 5, 6, 7 and 8, respectively. The presented data shows that FMRENO schemes can achieve the desired accuracy order even in nonlinear advection problems.

Figure 6 shows the $L_{\infty }$ numerical error versus the total CPU computational time from the WENO5-Z, WENO-CU6, WENO7-S, TENO8, and FMRENO schemes. It is observed that to achieve the same level of numerical error, the required computational cost from the present scheme is lower than that from the corresponding classical W/TENO scheme of the same accuracy order.

Note that, the order of convergence with WENO7-S and TENO8 schemes is not as expected in Tables 7 and 8. This is consistent with the report by [13, 15] that the magnitude of $\epsilon$ may change the order of convergence of the scheme when the machine round-off error accumulates in smooth regions of flow with $\Delta$x $\rightarrow$ 0. In order to study the sensitivity based on the adopted computer with double precision, in Tables 9 and 10, we show the convergence statistics of WENO7-S and TENO8 schemes with $\epsilon =10^{-8}$, $\epsilon =10^{-10}$ and $\epsilon =10^{-40}$ for the Burgers problem, respectively. The expected accuracy order is restored for both schemes when a proper value of $\epsilon$ is adopted. The default value of $\epsilon =10^{-40}$ is applied in this work, simply as recommended by the original reference papers [25, 37].

Table 5 Convergence statistics of numerical error with $L_\infty$ norm from the five-point schemes for the Burgers problem

Table 6 Convergence statistics of numerical error with $L_\infty$ norm from the six-point schemes for the Burgers problem

Table 7 Convergence statistics of numerical error with $L_\infty$ norm from the seven-point schemes for the Burgers problem

Table 8 Convergence statistics of numerical error with $L_\infty$ norm from the eight-point schemes for the Burgers problem

Fig. 6

Burgers equation: the $L_{\infty }$ numerical error versus the total CPU computational time from the WENO5-Z, WENO-CU6, WENO7-S, TENO8, and FMRENO schemes. Discretization is on $20 \times 20$, $40 \times 40$, $80 \times 80$, $120 \times 120$, and $180 \times 180$ uniformly distributed grid points

Table 9 Convergence statistics of numerical error with $L_\infty$ norm from WENO7-S scheme for the Burgers problem with various $\epsilon$

Table 10 Convergence statistics of numerical error with $L_\infty$ norm from TENO8 scheme for the Burgers problem with various $\epsilon$

5.2 Shock-Tube Problem

Lax’s problem [48] and Sod’s problem [49] are considered here. The initial condition for Lax’s problem [48] is

$$\begin{aligned} (\rho ,u,p) = \left\{ {\begin{array}{*{20}{c}} {(0.445,0.698,3.528),}&{}{\text {if }0 \le x < 0.5} ,\\ {(0.5,0,0.5710),}&{}{\text {if }0.5 \le x \le 1} , \end{array}} \right. \end{aligned}$$

(34)

and the final simulation time is $t = 0.14$.

The initial condition for Sod’s problem [49] is

$$\begin{aligned} (\rho ,u,p) = \left\{ {\begin{array}{ll} {(1,0,1),}&{}{\text {if }0 \le x < 0.5} ,\\ {(0.125,0,0.1),}&{}{\text {if }0.5 \le x \le 1} , \end{array}} \right. \end{aligned}$$

(35)

and the final simulation time is $t = 0.2$. Both computations are performed on 100 uniformly distributed grid points.

As shown in Figs. 7 and 8, for both problems, the proposed FMRENO schemes show good shock-capturing properties. In addition, the efficiency improvement based on the scheme reconstruction time (referred to as Efficiency improvement 1) and that based on the total CPU computation time (referred to as Efficiency improvement 2) with FMRENO schemes are shown in Table 11. The results show that the computational time of FMRENO schemes only varies slightly when the present framework is extended to very-high-order reconstructions, whereas that of the standard high-order W/TENO schemes increases remarkably due to the expensive evaluations of the smoothness indicators.

Fig. 7

Lax’s problem: solutions from the WENO5-Z, WENO-CU6, WENO7-S, TENO8, and FMRENO schemes. Discretization is on 100 uniformly distributed grid points and the final simulation time is $t = 0.14$

Fig. 8

Sod’s problem: solutions from the WENO5-Z, WENO-CU6, WENO7-S, TENO8, and FMRENO schemes. Discretization is on 100 uniformly distributed grid points and the final simulation time is $t = 0.2$

5.3 Shock Density-Wave Interaction Problem

This case is proposed by Shu and Osher [50]. A one-dimensional Mach-3 shock wave interacts with a perturbed density field generating both small-scale structures and discontinuities. The initial condition is

$$\begin{aligned} (\rho ,u,p) = \left\{ {\begin{array}{ll} {(3.857,2.629,10.333),}&{}{\text {if } 0 \le x < 1} ,\\ {(1 + 0.2\sin (5(x-5)),0,1),}&{} \quad {\text {if } 1 \le x \le 10} . \end{array}} \right. \end{aligned}$$

(36)

The computational domain is [0,10] with $N = 200$ uniformly distributed mesh cells and the final evolution time is $t = 1.8$. The inflow boundary condition and outflow boundary condition are applied at $x = 0$ and $x = 10$, respectively. The “exact” solution for reference is obtained by the fifth-order WENO5-JS scheme with $N = 2000$.

The computed density profiles from the WENO5-Z, WENO-CU6, WENO7-S, TENO8, and FMRENO schemes are given by Fig. 9. For the five-point schemes, the FMRENO schemes show obvious improvement with regard to resolving the high-wavenumber fluctuations when compared to the corresponding WENO5-Z schemes. For the six-, seven-, and eight-point schemes, compared with WENO-CU6, WENO7-S, and TENO8, the present FMRENO schemes perform better in capturing the shocklets and maintaining the wave amplitude, except in the vicinity of $x=6$.

Efficiency comparisons between various schemes are given in Table 12. All the proposed schemes show an efficiency improvement when compared to the corresponding classical W/TENO schemes of the same accuracy order.

5.4 Interacting Blast Waves

The two-blast-waves interaction problem taken from [51] is considered. The initial condition is

$$\begin{aligned} (\rho ,u,p) = \left\{ {\begin{array}{*{20}{c}} {(1,0,1000),}&{}{\text {if }0 \le x< 0.1},\\ {(1,0,0.01),}&{}{\text {if }0.1 \le x < 0.9},\\ {(1,0,100),}&{}{\text {if }0.9 \le x \le 1} . \end{array}} \right. \end{aligned}$$

(37)

The computational domain is [0,1], and symmetry boundary conditions are applied at $x = 0$ and $x = 1$, respectively. The simulation is performed on a uniform mesh with $N = 400$ and the final simulation time is $t = 0.038$. The “exact” solution for reference is computed by the fifth-order WENO5-JS scheme on a uniform mesh with $N = 2000$. For this case, the Roe scheme with entropy-fix is employed for flux splitting.

As shown in Fig. 10, while WENO7-S fails this case as reported by [37] due to the lack of numerical robustness, the results from all other considered schemes agree well with the reference solution. Moreover, the FMRENO5 and FMRENO6 schemes perform better than WENO5-Z and WENO-CU6 in resolving the density peak at $x = 0.78$, respectively.

Efficiency comparisons between various schemes are given in Table 13 and the efficiency improvement from the present schemes is substantial.

Table 11 Averaged computational time for various reconstruction schemes and the corresponding efficiency improvements

Fig. 9

Shock density-wave interaction problem: solutions from the WENO5-Z, WENO-CU6, WENO7-S, TENO8, and FMRENO schemes. Discretization is on 200 uniformly distributed grid points and the final simulation time is $t = 1.8$

5.5 Rayleigh–Taylor Instability

The inviscid Rayleigh-Taylor instability case proposed by Xu and Shu [52] is considered here. The initial condition is

$$\begin{aligned} (\rho ,u,v,p) = \left\{ {\begin{array}{*{20}{c}} {(2,0, - 0.025c\cos (8\pi x),1 + 2y),}&{}{\text {if } 0 \le y < 1/2},\\ {(1,0, - 0.025c\cos (8\pi x),y + 3/2),}&{}{\text {if } 1/2 \le y \le 1}, \end{array}} \right. \end{aligned}$$

(38)

where the sound speed $c = \sqrt{\gamma \frac{p}{\rho }}$ with $\gamma = \frac{5}{3}$. The computational domain is $[0,0.25] \times [0,1]$. Reflective boundary conditions are imposed at the left and right sides of the domain. Constant primitive variables $(\rho ,u,v,p) = (2,0,0,1)$ and $(\rho ,u,v,p) = (1,0,0,2.5)$ are set for the bottom and top boundaries, respectively.

The computed density contours with the FMRENO and various W/TENO schemes at a resolution of $120 \times 480$ are shown in Fig. 11. It is observed that the newly proposed FMRENO5 and FMRENO7 schemes resolve finer small-scale structures than WENO5-Z and WENO7-S, respectively. On the other hand, the FMRENO6 and FMRENO8 schemes perform similarly to WENO-CU6 and TENO8.

As shown in Table 14, a substantial efficiency improvement can be observed for all the considered FMRENO schemes when compared to classical W/TENO schemes of the same accuracy order.

Table 12 Averaged computational time for various reconstruction schemes and the corresponding efficiency improvements

Fig. 10

Interacting blast waves problem: solutions from the WENO5-Z, WENO-CU6, TENO8, and FMRENO schemes. Discretization is on 400 uniformly distributed grid points and the final simulation time is $t = 0.038$. WENO7-S also fails due to the lack of numerical robustness as reported by [37]

5.6 Riemann Problem: Configuration 3

Two-dimensional Riemann (2D) problems, first proposed in [53], are classical benchmark cases for verifying numerical methods by solving the Euler equations. Here, we consider the 2D Riemann problem of configuration 3. The computational domain is $[0, 1] \times [0,1]$ and the final simulation time is $t = 0.3$. The initial condition is given as

$$\begin{aligned} (\rho ,p,u,v) = \left\{ {\begin{array}{*{20}{c}} {(0.5323,0.300,1.206,0.000),}&{}{\text {if }0.0< x< 0.5, 0.5< y< 1.0},\\ {(1.5000,1.500,0.000,0.000),}&{}{\text {if }0.5< x< 1.0, 0.5< y< 1.0},\\ {(0.1380,0.029,1.206,1.206),}&{}{\text {if }0.0< x<0.5, 0.0<y< 0.5}, \\ {(0.5323,0.300,0.000,1.206),}&{}{\text {if }0.5< x<1.0, 0.0<y< 0.5}. \\ \end{array}} \right. \end{aligned}$$

(39)

As shown in Figs. 12 and 13, the FMRENO5, FMRENO6, and FMRENO7 schemes capture the shockwave patterns, and the small-scale flow structures better than WENO5-Z, WENO-CU6 and WENO7-S, respectively. For the eight-point schemes, the present FMRENO8 scheme is a bit more dissipative and at the same time generates less spurious numerical noise than the standard TENO8 scheme.

Efficiency comparisons between various schemes have been given in Table 15. Except for the five-point schemes, the present schemes show a much better efficiency in terms of both criteria.

Table 13 Averaged computational time for various reconstruction schemes and the corresponding efficiency improvements

Fig. 11

Rayleigh–Taylor instability problem: solutions from the WENO5-Z, WENO-CU6, WENO7-S, TENO8, and FMRENO schemes. Resolution is $120 \times 480$, and the final simulation time is $t = 1.95$

Table 14 Averaged computational time for various reconstruction schemes and the corresponding efficiency improvements

Fig. 12

2D Riemann problem of configuration 3: solutions from the WENO5-Z, WENO-CU6, FMRENO5, and FMRENO6 schemes. The simulation time is $t = 0.3$ and the grid resolution is $1200 \times 1200$. This figure is drawn with 30 density contours between 0.2 and 1.8

Fig. 13

2D Riemann problem of configuration 3 (continued): solutions from the WENO7-S, TENO8, FMRENO7, and FMRENO8 schemes. The simulation time is $t = 0.3$ and the grid resolution is $1200 \times 1200$. This figure is drawn with 30 density contours between 0.2 and 1.8

5.7 Riemann Problem: Configuration 6

The 2D Riemann problem of configuration 6 is considered. The computational domain is $[0, 1] \times [0,1]$ and the final simulation time is $t = 0.3$. The initial condition is given as

$$\begin{aligned} (\rho ,u,v,p) = \left\{ {\begin{array}{*{20}{c}} {(2.0,0.75,0.5,1.0),}&{}{\text {if }0.0< x< 0.5, 0.5< y< 1.0},\\ {(1.0,0.75,-0.5,1.0),}&{}{\text {if }0.5< x< 1.0, 0.5< y< 1.0},\\ {(1.0,-0.75,0.5,1.0),}&{}{\text {if }0.0< x<0.5, 0.0<y< 0.5}, \\ {(3.0,-0.75,-0.5,1.0),}&{}{\text {if }0.5< x<1.0, 0.0<y< 0.5}. \\ \end{array}} \right. \end{aligned}$$

(40)

As shown in Figs. 14 and 15, the performance of the present FMRENO schemes is much better than that of the corresponding W/TENO schemes in terms of capturing the interfacial instabilities. It is worth noting that the solution of FMRENO8 is free from the numerical noise generated by TENO8.

Efficiency comparisons between various schemes have been given in Table 16. Overall speaking, the efficiency improvement from the present schemes increases remarkably as the reconstruction order increases.

Table 15 Averaged computational time for various reconstruction schemes and the corresponding efficiency improvements (the simulation resolution is $400 \times 400$)

Fig. 14

2D Riemann problem of configuration 6: solutions from the WENO5-Z, WENO-CU6, FMRENO5, and FMRENO6 schemes. The simulation time is $t = 0.3$ and the grid resolution is $1200 \times 1200$. This figure is drawn with 30 density contours between 0.24 and 3.3

Fig. 15

2D Riemann problem of configuration 6 (continued): solutions from the WENO7-S, TENO8, FMRENO7, and FMRENO8 schemes. The simulation time is $t = 0.3$ and the grid resolution is $1200 \times 1200$. This figure is drawn with 30 density contours between 0.24 and 3.3

5.8 Double Mach Reflection of a Strong Shock

This 2D case is taken from Woodward and Colella [51] with the initial condition as

$$\begin{aligned} (\rho ,u,v,p) = \left\{ {\begin{array}{ll} {(1.4,0,0,1),}&{}{\text {if } y < 1.732(x - 0.1667),}\\ {(8,7.145, - 4.125,116.8333),}&{} {\text {otherwise}.} \end{array}} \right. \end{aligned}$$

(41)

The computational domain is $[0,4] \times [0,1]$ and the final simulation time is $t = 0.2$. Initially, a right-moving Mach 10 shock wave is placed at $x = 0.1667$ with an incident angle of $60^{\circ }$ to the x-axis. The post-shock condition is imposed from $x = 0$ to $x = 0.1667$ whereas a reflecting wall condition is enforced from $x = 0.1667$ to $x = 4$ at the bottom. For the top boundary condition, the fluid variables are defined to exactly describe the evolution of the Mach 10 shock wave. The inflow and outflow conditions are imposed for the left and right sides of the computational domain. The computed density contours are shown in Figs. 16 and 17. For the five-, six- and eight-point reconstructions, the present FMRENO schemes perform similarly to or slightly better than the corresponding W/TENO schemes. On the other hand, the seven-point FMRENO7 scheme performs significantly better than WENO7-S in resolving the small-scale vortical structures in the blow-up regions.

Moreover, it is worth noting that the effect of the MP limiter can be adjusted by tuning the curvature measurement $d_{i + 1/2}^{\text {M4}}$ and the parameters $\alpha$, $\beta$. In the following, we test the dissipation property of FMRENO8 with a more restrictive curvature measurement $d_{i + 1/2}^{\text {4M}}$ at the cell interface $i+ 1/2$ which is defined as

$$\begin{aligned} {d_{i + 1/2}^{\text {M4}}} = \mathrm{{minmod}} (4{d_i} - {d_{i + 1}},4{d_{i + 1}} - {d_i},{d_i},{d_{i + 1}}). \end{aligned}$$

(42)

As shown in Figs. 17h and 18c, a more restrictive curvature measurement will tighten the MP-based regularity criterion, which results in a more dissipative FMRENO8 scheme. In Fig. 18a, d, the dissipation property changes with the parameter $\beta$, which determines the amount of freedom allowing for large curvature. And Fig. 18b, d show that, a larger $\alpha$ results in a less dissipative FMRENO8 scheme.

Efficiency comparisons between various schemes are given in Table 17. The efficiency improvements from the present schemes of the same accuracy order are remarkable.

Table 16 Averaged computational time for various reconstruction schemes and the corresponding efficiency improvements (the simulation resolution is $400 \times 400$)

Fig. 16

Double Mach reflection of a strong shock: zoomed-in views of density contours from the WENO5-Z, WENO-CU6, FMRENO5, and FMRENO6 schemes at the simulation time $t = 0.2$. The grid resolution is $1280 \times 320$. This figure is drawn with 42 density contours between 1.887 and 20.9

Fig. 17

Double Mach reflection of a strong shock (continued): zoomed-in views of density contours from the WENO7-S, TENO8, FMRENO7, and FMRENO8 schemes at the simulation time $t = 0.2$. The grid resolution is $1280 \times 320$. This figure is drawn with 42 density contours between 1.887 and 20.9

5.9 Single-Material Triple Point Problem

A modified triple point problem with a single material rather than multiple materials is presented [54]. The computational domain is $[0,7] \times [0,3]$ and the initial condition is shown in Fig. 19. An outflow condition is applied to the right boundary while a slip-wall condition for all other boundaries. A uniform mesh with the resolution of $1120 \times 480$ is employed for all computations.

Fig. 18

Double Mach reflection of a strong shock: zoomed-in views of density contours from FMRENO8 schemes with $d_{M4}$ curvature measurement and various parameters at the simulation time $t = 0.2$. a $\alpha = 0.5$ and $\beta = 4.0$; b $\alpha = 2.5$ and $\beta = 2.0$; c $\alpha = 2.5$ and $\beta = 4.0$; d $\alpha = 0.5$ and $\beta = 2.0$. The grid resolution is $1280 \times 320$. This figure is drawn with 42 density contours between 1.887 and 20.9

As shown in Fig. 20, the present FMRENO schemes generate finer small-scale structures in the roll-up regions and along the contact discontinuities than the corresponding WENO5-Z, WENO-CU6, and WENO7-S schemes, respectively. Also as shown by Fig. 21, FMRENO8 further improves the performance of the lower-order FMRENO schemes while the standard TENO8 scheme fails this case in the high-resolution simulation with $1120 \times 480$ because of the positivity-preserving issue.

Efficiency comparisons between various schemes have been given in Table 18. For very-high-order reconstructions, the efficiency improvements from the present schemes of the same accuracy order are remarkable for both criteria.

5.10 Regular Shock Reflection

The regular shock reflection is a typical two-dimensional steady flow [55]. The computational domain is $[0, 4] \times [0,1]$. Initially, an impinging shock with impinging angle $\theta$ of $29^{\circ }$ and upstream flow of Mach number 2.9 is imposed by the Rankine–Hugoniot relationship [56]. The evolution histories of the averaged residue for the various schemes are analyzed. Here, the averaged residue is defined as

$$\begin{aligned} {Res_A} = {\sum _{i=1}^{N}{\frac{|R_i|}{N}}}, \end{aligned}$$

(43)

where $R_i$ is the local residue defined as

$$\begin{aligned} {R_i} = {\frac{{\rho ^{n+1}_i} - {\rho ^{n}_i}}{\delta {t}}}, \end{aligned}$$

(44)

and N is the total number of grid points, and n denotes the time step.

The computed density distributions are shown with 20 contours between 0.98 and 2.7 in Fig. 22. The results show that the numerical oscillations of WENO-CU6 and TENO8 are more severe than those of WENO5-Z. This can be seen more clearly in Fig. 23. The averaged residue of WENO5-Z settles down to the smallest value around $10^{-2.8}$, followed by that of WENO7-S which settles down to a value around $10^{-2.0}$. The averaged residues of WENO-CU6 and TENO8 decrease to a relatively larger value, which is around $10^{-1.7}$ and $10^{-0.9}$, respectively. For the newly proposed five-, six-, seven-, and eight-point FMRENO schemes, the averaged residue settles down to a value around $10^{-2.8}$, $10^{-2.2}$, $10^{-2.6}$ and $10^{-2.4}$, respectively. These results clearly show that the FMRENO5 scheme has a comparable convergence behavior with WENO5-Z. When comparing with the low-dissipation WENO-CU6, WENO7-S, and TENO8 schemes, the present FMRENO6, FMRENO7, and FMRENO8 schemes show better convergence behavior.

Table 17 Averaged computational time for various reconstruction schemes and the corresponding efficiency improvements

Fig. 19

The sketch of the computational domain and the initial condition for the triple point problem

Fig. 20

Single-material triple point problem: normalized density gradient contours from the WENO5-Z, WENO-CU6, WENO7-S, and various FMRENO schemes at the simulation time $t = 5$. The grid resolution is $1120 \times 480$. This figure is drawn with 19 normalized density gradient contours between 0.05 and 1.95.

Fig. 21

Single-material triple point problem (continued): normalized density gradient contour from the FMRENO8 scheme. Note that the standard TENO8 scheme fails in this case

Table 18 Averaged computational time for various reconstruction schemes and the corresponding efficiency improvements

Fig. 22

Regular shock reflection: density contours from the WENO5-Z, WENO-CU6, WENO7-S, TENO8, FMRENO5, FMRENO6, FMRENO7, and FMRENO8 schemes at the simulation time $t = 50$. The grid resolution is $128 \times 32$. This figure is drawn with 20 density contours between 0.98 and 2.7

Fig. 23

Regular shock reflection: the evolution histories of the averaged residue with the WENO5-Z, WENO-CU6, WENO7-S, TENO8, FMRENO5, FMRENO6, FMRENO7, and FMRENO8 schemes

6 Conclusions

In this work, a new family of high-order shock-capturing FMRENO schemes has been proposed. The major contributions are summarized as follows:

• Based on the MP concept, the construction of the new FMRENO schemes consists of three main phases, i.e., (1) preparing polynomial-based candidate stencils from high- to low-orders in a hierarchical manner; (2) providing a local regularity criterion by calculating the MP upper and lower bounds. A candidate stencil is judged to be smooth only when the reconstructed cell interface flux locates within the MP bounds; (3) formulating the final cell interface reconstruction scheme by selecting the higher-order (or better spectra) candidate stencil, which is judged to be smooth. If all candidate stencils are judged to be nonsmooth by the MP criterion, the smoothest stencil, with which the reconstructed cell interface flux departs from the MP bounds the least, will be adopted as the final reconstruction scheme.

• The new framework achieves the multi-resolution property by adaptively selecting the targeted reconstruction scheme from the candidate stencils of different orders according to the local flow regularities. Specifically, in smooth regions, the candidate stencil with the largest stencil width will be adopted for restoring the desired high-order accuracy. In the vicinity of discontinuities, the good non-oscillatory property will be achieved by selecting the candidate reconstruction satisfying the MP criterion. For the wave-like structures, the low-dissipation property can be approached by choosing the smooth candidate stencils with higher accuracy order or better spectral properties.

• The present framework can be straightforwardly extended to arbitrarily very-high-order reconstructions with a tiny complexity increase. Compared to the standard W/TENO schemes, the computational efficiency of FMRENO schemes is substantially higher by avoiding the expensive evaluations of the smoothness indicators. Moreover, the efficiency improvement is more impressive with higher-order reconstructions.

• A set of critical benchmark cases is simulated to validate the performance of the proposed FMRENO schemes. Numerical results demonstrate the capability of the new schemes in terms of recovering the targeted high-order accuracy in smooth regions, preserving the low numerical dissipation for resolving wave-like structures, and capturing the discontinuities sharply. In all the considered cases, the present FMRENO schemes show either a similar or an improved performance when compared to the corresponding W/TENO schemes.

Considering the high computational efficiency and the competitive performance of the present FMRENO schemes, future work will focus on the applications to complex geometries and multi-physics problems.