Abstract
Curvilinear, multiblock summation-by-parts finite difference operators with the simultaneous approximation term method provide a stable and accurate framework for solving the wave equation in second order form. That said, the standard method can become arbitrarily stiff when characteristic boundary conditions and nonlinear interface conditions are used. Here we propose a new technique that avoids this stiffness by using characteristic variables to “upwind” the boundary and interface treatment. This is done through the introduction of an additional block boundary displacement variable. Using a unified energy, which expresses both the standard as well as characteristic boundary and interface treatment, we show that the resulting scheme has semidiscrete energy stability for the scalar anisotropic wave equation. The theoretical stability results are confirmed with numerical experiments that also demonstrate the accuracy and robustness of the proposed scheme. The numerical results also show that the characteristic scheme has a time step restriction based on standard wave propagation considerations and not the boundary closure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Due to their superior dispersion properties, high-order methods are ideally suited for wave-dominated partial differential equations (PDEs) [13]. That said, unless great care is taken in the treatment of boundary conditions, interface couplings, and variable coefficients, high-order methods are often less robust than their low-order counterparts. An important tool in robust high-order methods is utilization of the summation-by-parts (SBP) property [14, 15]. SBP is the discrete analogue of integration by parts and allows the discrete stability analysis to mimic the continuous well-posedness analysis [22].
When combined with multiblock domain decompositions and curvilinear coordinates, SBP finite difference methods can be used to stably and accurately model complex geometries and variable material parameters. SBP finite difference methods use standard central difference stencils in the interior of a domain and transition to one-sided stencils at boundaries and interfaces in a manner that maintains the SBP property. An important feature of SBP finite difference methods is the built-in norm matrix, which is similar to the mass matrix in finite element methods. A variety of SBP finite difference operators have been developed with the most relevant to this work being the first and second derivative operators on unstaggered grids [14,15,16, 20, 26]. With SBP finite difference methods it is possible to either enforce boundary conditions strongly [23, 24] or weakly [4, 6]; weak enforcement of boundary conditions with SBP methods is often called the simultaneous approximation term (SAT) method and is the approach taken here due to its ability to handle non-compatible boundary and interface conditions.
We are primarily interested in the wave equation in second-order form, that is, a displacement formulation of the wave equation as opposed to velocity-stress or velocity-strain. Our motivation for this is to address our ultimate goal of advancing simulations of the earthquake cycle, though our work is applicable to other coupling situations and whenever characteristic-based boundary conditions are natural. In earthquake cycle models interseismic loading (decade long tectonic loading) is coupled to dynamic rupture (earthquake rupture taking place over seconds to minutes); the importance of this coupling has been recently highlighted in, for example, Erickson et al. [8]. In the interseismic phase, a quasidynamic formulation is often used that neglects inertial effects, e.g., acceleration, resulting in an elliptic PDE for the displacement. During active fault slip, the coseismic rupture phase, the equations have a hyperbolic character due to the inclusion of inertial effects.
In order to avoid having to transition between displacements and velocity-stress (or velocity-strain) it is desirable to use a displacement-based formulation for the coseismic phase. Virta and Mattsson [28], building on Mattsson et al. [18, 19], developed an SBP-SAT finite difference scheme for the scalar second-order wave equation with variable coefficients on curved geometries. Duru et al. [7] extended this scheme for use with nonlinear friction laws which govern the sliding of fault interfaces in earthquake problems; nonlinear friction laws relate the interface traction to the sliding velocity. However, as noted in Duru et al. [7], the modified scheme that incorporates the nonlinear friction law results in a numerically stiff system of ordinary differential equations (ODEs) that prevents the use of, for instance, explicit Runge-Kutta time stepping methods; in Duru et al. [7] a custom second-order accurate time stepping method is used. Similar numerical stiffness is also seen in the velocity-stress formulation of the wave equation for earthquake problems, though this can be circumvented by rewriting the nonlinear friction law in terms of the characteristic variables, [11].
The main contribution of this work is the use of a characteristic formulation of boundary and interface conditions within a displacement-based scheme, namely merging the ideas of Duru et al. [7], Virta and Mattsson [28] with those of Kozdon et al. [11]. The key idea of the work is to track the evolution of the boundary and interface displacements, which allows the use of a non-stiff characteristic formulation.
The paper is structured as follows: Section 2 introduces our notation for SBP finite difference methods. Since the main contribution of the work can be seen in a simplified setup, Sect. 3 presents the continuous and semidiscrete energy analysis for the one-dimensional scalar wave equation. Here the characteristic method is formulated for both boundary and nonlinear interface conditions and compared against the standard approach. Section 4 introduces a multi-dimensional anisotropic, scalar wave equation along with its continuous energy analysis. The semidiscretization of the multi-dimensional problem is given in Sect. 5, where a unified energy analysis is presented that incorporates both the proposed characteristic method and the previous approach. The paper concludes with multi-dimensional tests problems in Sect. 6 and concluding remarks in Sect. 7.
The Julia programming language [3, v1.6.0] was used for all simulations with the codes available at https://github.com/Thrase/sbp_waveprop_characteristic.
2 Summation-By-Parts Operators
In this work summation-by-parts (SBP) finite difference operators are used to approximate spatial derivatives. In order to centralize the explanation of these operators, here we introduce the one-dimensional operators and then generalize the operators to multiple dimensions using tensor products.
Throughout we refer to the SBP operators as 2p where p is the boundary accuracy and 2p is the interior accuracy. SBP methods for the wave equation in second order form typically see a global convergence rate of \(\min (2p, p + 2)\), i.e., two orders of accuracy greater than the boundary accuracy except in the case of \(2p = 2\). For first derivatives we use the operators from Strand [27]Footnote 1 and for second derivatives the variable coefficient operators from Mattsson [16].
2.1 One Dimensional SBP Operators
Let the domain \(0 \le \xi \le 1\) be discretized with an \(N + 1\) equally spaced grid of points. The grid of points are represented as \({{\varvec{\xi }}}\) with spacing \(h = 1 / N\) and points located at \({\left\{ {{\varvec{\xi }}}\right\} }_{k} = k h\) for \(k = 0, 1, \dots , N\). Let \({{\varvec{u}}}\) be the projection of u onto the computational grid. We define the operator \({{\varvec{e}}}_{k}\) to be the grid basis functions, that is the vector which is 1 at grid point k and zero at all other grid points. Importantly \({{\varvec{e}}}_{k}^{T}\) selects the value of a grid function \({{\varvec{u}}}\) at the point k, namely \({{\varvec{e}}}_{k}^{T} {{\varvec{u}}} = {\left\{ {{\varvec{u}}}\right\} }_{k}\).
Let the first and \(C(\xi )\)-weighted second derivatives of u be approximated as
The derivative approximations \({{\varvec{{D}}}}_{1}\) and \({{\varvec{{D}}}}^{(C)}_{11}\) are called SBP if they satisfy the following definitions.
Definition 1
(SBP First Derivative) The operator \({{\varvec{{D}}}}_{1}\) is called an SBP approximation if it can be decomposed as \({{\varvec{{H}}}}_{1}{{\varvec{{D}}}}_{1} = {{\varvec{{Q}}}}_{1}\) with \({{\varvec{{H}}}}_{1}\) being a symmetric positive definite matrix and
for all vectors \({{\varvec{u}}}\) and \({{\varvec{v}}}\).
Definition 2
(SBP Second Derivative) The operator \({{\varvec{{D}}}}_{11}^{(C)}\) is called an SBP approximation if it can be decomposed as
where \({{\varvec{{A}}}}_{11}^{(C)}\) is a symmetric positive semidefinite matrix and \({{\varvec{b}}}_{N}^{T} {{\varvec{u}}}\) and \({{\varvec{b}}}_{0}^{T} {{\varvec{u}}}\) are accurate approximations of the first derivative of u at the boundary points \({\left\{ {{\varvec{\xi }}}\right\} }_{N}\) and \({\left\{ {{\varvec{\xi }}}\right\} }_{0}\), respectively.
In addition the derivative approximations are assumed to be compatible, namely that \({{\varvec{{H}}}}_{1}\) is the same for both the first and second derivative operators and the weighting matrix \({{\varvec{{H}}}}_{1}\) is diagonal.
Remark 1
It is not assumed that the boundary derivative operators \({{\varvec{b}}}_{0}^{T}\) and \({{\varvec{b}}}_{N}^{T}\) are the first and last rows of \({{\varvec{{D}}}}_{1}\), namely \({{\varvec{b}}}_{0}^{T} \ne {{\varvec{e}}}_{0} {{\varvec{{D}}}}_{1}\) and \({{\varvec{b}}}_{N}^{T} \ne {{\varvec{e}}}_{N} {{\varvec{{D}}}}_{1}\). That is, we do not assume that the operators are fully-compatible SBP operators [21].
The reason operators satisfying Definitions 1 and 2 are called SBP is that the following identities
discretely mimic the continuous integration by parts identities
It is useful to note that \({{\varvec{{H}}}}_{1}\) and \({{\varvec{{A}}}}^{(C)}_{11}\) lead to quadrature approximations of the following integrals [9]:
2.2 Multidimensional SBP Operators
Multiple dimensional SBP operators can be constructed via tensor products. In particular the one-dimensional operators are applied along the grid lines. Derivative approximations are taken to be of the form
The variable coefficients C present in the approximation make it cumbersome to define the form of \({{\varvec{\tilde{ D}}}}_{ij}^{(C)} {{\varvec{\tilde{u}}}}\), so here we outline some of the important discrete properties of the operator; Appendix presents the tensor product construction of the operators in two spatial dimensions from which the higher dimensional extensions can be generalized.
We define multidimensional SBP operators on the reference domain \(\hat{B} = {[0, 1]}^d\) with d being the number of spatial dimensions. A regular Cartesian grid is used to discretize the reference domain with \(N_{i} + 1\) grid points in each direction and grid spacing \(h_{i} = 1 / N_{i}\). A field is represented as a vector with the leading dimension being the fastest index, i.e., column-major order. So in two dimensions the grid function of \(u(\xi _{1}, \xi _{2})\) is the vector
where \({\left\{ {{\varvec{\tilde{u}}}}\right\} }_{ij} \approx u(i h_{1}, j h_{2})\). On the reference domain the faces are numbered so that face 1 is \(\xi _{1} = 0\), face 2 is \(\xi _{1} = 1\), face 3 is \(\xi _{2} = 0\), etc..
Let \({{\varvec{\tilde{ H}}}}\) be the tensor product volume norm matrix,
which can be thought of as an approximation of the inner product
The tensor product derivative operators have the following SBP structure
where the two terms in the multidimensional SBP decomposition can be thought of as approximations of the following volume and surface integrals:
If \(C_{ij}\) defines a symmetric positive definite, spatially varying coefficient matrix then the matrix \({{\varvec{\tilde{ A}}}}_{ij}^{(C_{ij})}\) (summation implied over i and j) is symmetric positive semidefinite; see Appendix A.
The scalar \(\hat{n}_{i}^{f}\) is component i of the outward pointing normal to the reference domain along face f; the Cartesian nature of the reference domain and the face numbering imply that
The matrix \({{\varvec{{\bar{L}}}}}^{f}\) selects the points from the volume vector along face f. The matrix \({{\varvec{{\bar{B}}}}}^{f}_{j}\) computes the derivative approximation in the direction \(\xi _{j}\) and evaluates it along face f. When \(i = j\) in (11) then \(f \in (2j-1, 2j)\) and \({{\varvec{{\bar{B}}}}}^{f}_{j}\) is based on the boundary derivatives from the one-dimensional second derivative SBP operator. When \(i \ne j\) in (11) then \(f \notin (2j-1, 2j)\) and \({{\varvec{{\bar{B}}}}}^{f}_{j}\) is based on the first derivative SBP operator. The diagonal matrix \({{\varvec{{H}}}}^{f}\) is the tensor product surface norm matrix, which approximates
and the diagonal matrix \({{\varvec{{C}}}}^{f}\) is the variable coefficient evaluated at the points of face f. Since \(\hat{n}_{i}^{f} = 0\) for \(f \notin (2i-1, 2i)\) the summation in SBP decomposition (11) can be extended to be a summation over all faces,
this new form will be used to simplify the statement of the discretization.
As noted above, here we have only outlined our basic notation and more details about the construction of the operators are given in Appendix A.
3 One-Dimensional Example
To highlight the key contributions of the work we begin with the one dimensional scalar wave equation with linear boundary and nonlinear interface conditions. Even in these simplified problem setups the stiffness of the standard non-characteristic approach can be seen as well as the key ideas and benefits of the proposed characteristic method.
3.1 Boundary Treatment
3.1.1 Continuous Problem
On the domain \(\varOmega = [0, 1]\) we consider the scalar wave equation
where \(\dot{u}\) and \(\ddot{u}\) denote the first and second time derivatives of the displacement u. To scalar wave Eq. (16a) we add the family of boundary conditions
for boundary traction \(\tau \) given by
where n is the outward unit normal to the domain, namely \(n = -1\) at \(x = 0\) and \(n = 1\) at \(x = 1\). At each domain edge, the particular type of boundary condition imposed is controlled by the parameter \(\alpha \ge 0\). For example \(\alpha = 0\) corresponds to a Neumann boundary condition and Dirichlet boundary conditions correspond to \(\alpha \rightarrow \infty \), with the latter seen by rewriting (16b) as
Defining the solution energy,
leads to the following energy estimate and thus well-posedness:
Lemma 1
Governing Eq. (16) with energy (19) satisfies \(\dot{E} \le 0\).
Proof
Taking the time derivative of the energy (19), using the scalar wave Eq. (16a), and simplifying with integration by parts yields
Applying boundary conditions (16b) leads to
since \(\alpha \ge 0\). \(\square \)
For the numerical scheme that follows, it is useful to express the boundary conditions (16b) in characteristic form:
Here R, known as the reflection coefficient, is related to \(\alpha \) by the transformations
where if \(\alpha \ge 0\) then \(-1 \le R \le 1\) and vice versa. For example, the Neumann condition (\(\alpha = 0\)) corresponds to \(R = 1\), and the Dirichlet condition (\(\alpha \rightarrow \infty \)) corresponds to \(R = -1\). The terms \(\dot{u} \pm \tau \) in boundary condition (22) correspond to characteristic variables propagating in the  directions, respectively; recall that the unit normal n is included in traction definition (17). This implies that the boundary condition takes the form of expressing the incoming characteristic as a reflection of the outgoing characteristic. Since (22) is completely equivalent to (16b) the continuous energy estimate of Lemma 1 still holds.
directions, respectively; recall that the unit normal n is included in traction definition (17). This implies that the boundary condition takes the form of expressing the incoming characteristic as a reflection of the outgoing characteristic. Since (22) is completely equivalent to (16b) the continuous energy estimate of Lemma 1 still holds.
In the semidiscrete scheme that follows it will be useful to define

with w being the outward and q the inward propagating characteristic variables. We reiterate that for the continuous problem, the boundary conditions specified in terms of \({\alpha }\) and R are completely equivalent. That said, the two different perspectives on the boundary conditions will lead to discretizations with differing numerical properties.
3.1.2 Semidiscrete Problem
Using the SBP finite difference operators defined in Sect. 2, a family of SBP-SAT semidiscretizations for governing Eq. (16) is
where \(n_{0} = -1\) and \(n_{N} = 1\) are the outward pointing normals at the boundary points. Additionally, \(\tau ^{*}_{k}\) and \(u^{*}_{k}\) with \(k \in \{0, N\}\) are yet-to-be-defined numerical fluxes that penalize the boundary derivative and displacement toward values that satisfy a range of desired boundary conditions. For example a Neumann condition \(-\partial _1 u = 0\) at \(x = 0\) can be imposed by making the choices
We will illustrate however, that the numerical fluxes can be chosen to impose the boundary conditions using either the non-characteristic (16b) or characteristic (22) formulations, which though equivalent in the continuous setting, do not lead to the same numerical scheme.
The semidiscrete version of solution energy (19) is
with \(\tau _{k}\) being the following approximation of traction:
where \(\gamma \ge 0\) is a penalty parameter. The following theorem characterizes energy (27):
Theorem 1
Energy (27) is a seminorm for all \({{\varvec{u}}}\) and \(u^{*}_{k}\) if \(\gamma \) is positive and sufficiently large.
Proof
The borrowing lemma from [1, Lemma 1] states that
Here, parameters \(\theta > 0\) and \(\zeta > 0\) depend on the specific SBP operator but are independent of the grid spacing; see Table 3.
The operator \({{\varvec{d}}}_{k}^{T} {{\varvec{u}}}\) for \(k \in \{0, N\}\) is an approximation of the boundary derivative and \({{\varvec{\varDelta }}}_{k}^{T} = {{\varvec{b}}}_{k}^{T} - {{\varvec{d}}}_{k}^{T}\); the specific form of \({{\varvec{d}}}_{k}^{T}\) does not matter for the one-dimensional analysis but is critical in the multi-dimensional case.Footnote 2
Expanding the difference term in energy (27) and rewriting in terms of \({{\varvec{\varDelta }}}_{k}^{T}\) and \({{\varvec{d}}}_{k}^{T}\) yields
where we have defined \(\delta _{k} = u_{k}^{*} - u_{k}\) for \(k \in \{0, N\}\). Putting these results together and completing the square gives
Choosing \(\gamma \) so that
leads to the estimate
for all \({{\varvec{u}}}\) and \(u^{*}\) since \(\theta > 0\) and \(\zeta > 0\). The theorem then follows because \({{\varvec{{H}}}}\) is positive definite. \(\square \)
Corollary 1
Semidiscretization (25) satisfies
where \(\mathcal {E}\) is defined by (27).
Proof
Follows directly by taking the time derivative of energy (27), substituting semidiscretization (25), and applying SBP property (3). \(\square \)
3.1.3 Semidiscrete Problem: Non-Characteristic Boundary Treatment
If the numerical fluxes in semidiscretization (25) are defined to impose boundary conditions in the non-characteristic form (16b), namely,
then the numerical scheme is equivalent to that of Virta and Mattsson [28]. In this case, the definition of \(u^{*}\) implies that the terms with \(\gamma \) drop out from energy (27) and the penalty parameter has no impact on the scheme. Neumann boundary conditions can be imposed by setting \(\alpha = 0\) in (35), however it becomes clear that the imposition of Dirichlet boundary conditions (\(\alpha \rightarrow \infty \)) is problematic with this formulation.
Theorem 2
Semidiscretization (25) with numerical fluxes (35) satisfies \(\dot{\mathcal {E}} \le 0\) where \(\mathcal {E}\) is defined by (27).
Proof
Substituting numerical fluxes (35) into energy rate (34) leads to
since \(\alpha \ge 0\). \(\square \)
3.1.4 Semidiscrete Problem: Characteristic Boundary Treatment
The numerical fluxes in semidiscretization (25) can instead be chosen to impose the characteristic boundary condition (22), giving rise to a different numerical discretization that defined by non-characteristic numerical flux (35). The basic idea of the characteristic method is to mimic the upwinding procedure used in methods for first order hyperbolic equations. Namely, we seek to modify the incoming characteristic variable while preserving to outgoing characteristic variable. To do this, we introduce an equation for \(\dot{u}_{k}^{*}\) which tracks the time evolution of the numerical flux.
The characteristic-based numerical fluxes are defined as
where the characteristic variables are defined so that the outgoing characteristic is preserved and the incoming characteristic satisfies the boundary condition:
for any \(-1 \le R \le 1\). Importantly the characteristic numerical flux \(u^{*}_{k}\) must be tracked as an independent variable in the solution process. To illustrate the characteristic approach, both Neumann and Dirichlet conditions can be enforced in a straightforward manner by choosing either \(R = 1\) or \(R = -1\), respectively, in (38). For \(R = -1\), for example, solving (37) and (38) for the numerical fluxes yields the specific choices
corresponding to Dirichlet boundary conditions.
Theorem 3
Semidiscretization (25) with numerical fluxes (37) satisfies \(\dot{\mathcal {E}} \le 0\) where \(\mathcal {E}\) is defined by (27).
Proof
By definition, \(\tau ^{*}_{k}\) and \(\dot{u}_{k}^{*}\) satisfy the boundary condition:
where we have used numerical flux definitions (37) and (38) along with the relationship (23) between \(\alpha \) and R.
If the grid based incoming characteristic is defined as
then it follows that
Using (40) and (42) in energy rate (34) gives
since \(\alpha \ge 0\). \(\square \)
3.1.5 Numerical Results
In order to integrate semidiscretization (25) in time one can either use methods designed for second order ODEs, such as those proposed in Duru et al. [7], or transform the equations into a first order system of ODEs and use first order time integration technology such as Runge-Kutta methods. In this latter approach, the auxiliary variable \({{\varvec{v}}} = {{\varvec{\dot{u}}}}\) is introduced and semidiscretization (25) becomes
in the case of the characteristic numerical flux (37) additional ODEs are required to track \(u^{*}_{k}\) for \(k \in \{0, N\}\). System of ODEs (44) can be written more compactly as
where linear operator \({{\varvec{{G}}}}\) corresponds to the characteristic numerical flux (37) and \(\bar{{{\varvec{{G}}}}}\) non-characteristic numerical flux (35). For each method, the time step size is controlled by the eigenvalue spectrum of the corresponding linear operator.
Comparison of the eigenvalue spectra for the proposed characteristic and non-characteristic [28] treatment of boundary conditions for various values of reflection coefficient R. In all cases the domain is [0, 1] with grid spacing 1/50 and SBP interior accuracy of \(2p = 4\). The non-characteristic method is indicated by red \(\times \) and the characteristic method with blue \(+\) (Color figure online)
Figure 1a–c compare the eigenvalue spectra of the operators with \(R = 0.99\), 0, and \(-0.99\) (or equivalently \(\alpha = 1/99\), 1, and 199) using a grid with \(N = 50\) and the SBP operators with fourth order interior accuracy from Mattsson [16]. The markers \(+\) represent the characteristic numerical flux and \(\times \) the non-characteristic numerical flux. As \(\alpha \) increases the spectrum associated with the non-characteristic methods has a large magnitude negative real eigenvalue, which will severely restrict the time step, i.e., the scheme can become arbitrarily stiff. On the other hand, the spectrum associated with the characteristic numerical flux is well behaved in all cases. To further explore this, in Fig. 1d the maximum magnitude real component of the eigenvalue spectra is given as a function of R (or \(\alpha \)). As can be seen the maximum magnitude real eigenvalue of the non-characteristic methods grows rapidly for \(R < 0\) (or \(\alpha > 1\)) and is more uniform for the characteristic method.
L\(^2\)-convergence comparison of the characteristic (\(+\) markers) and non-characteristic (\(\times \) markers) treatment of boundary conditions with various values of the reflection coefficient R. The red, blue, and green curves correspond to SBP interior orders 2, 4, and 6, respectively (Color figure online)
We now considering the accuracy of both the non-characteristic and characteristic schemes. In this test we consider the initial condition
which for times \(t \in [0, 1]\) and reflection coefficients \(R\in [-1, 1]\) has the analytic solution
The L\(^{2}\)-convergence can be seen in Fig. 2 at time \(t = 0.9\) for \(R = 0.99\), 0, and \(-0.99\); the L\(^2\)-error in the solution is defined as
with \(\varDelta {{\varvec{u}}}\) being the pointwise difference between the numerical and exact solutions. In the figure, the interior accuracy of the SBP scheme is denoted by 2p and all the operators are from Mattsson [16]. The spatial resolutions used in the test are \(N = 17 \times 2^r\) with \(r = 0, 1, 2, 3, 4, 5\) and time integration is performed using matrix exponentiation. As can be seen, both the non-characteristic and characteristic methods converge at similar rates. For the characteristic method with \(2p = 6\) the overall error constant is higher, though this can be improved by increasing the penalty parameter (not shown) at the cost of increased stiffness.
3.2 Nonlinear Interface
3.2.1 Continuous Problem
We now consider an interface at \(x = 0\) on which the traction acting on the interface is related to the jump in particle velocity across the interface. To do this, we consider the domain \(\varOmega = [-1, 1]\) and modify wave Eq. (16) to be
In interface condition (49c) the superscript ± denotes the solution on the two-sides of the interface with \(\dot{u}^{-}\) being the particle velocity as \(x \rightarrow 0^{-}\) and \(\dot{u}^{+}\) the particle velocities as \(x \rightarrow 0^{+}\). The tractions \(\tau ^{\pm }\) are defined with normals that point out of the respective sides of the interface, i.e., \(\tau ^{\pm } = \mp \partial _{1} u^{\pm }\). The nonlinear interface function F is assumed to be odd and take the same sign as its argument:
Defining the solution energy,
leads to the following energy estimate and thus well-posedness:
Lemma 2
Governing Eqs (49) with energy (51) satisfies \(\dot{E} \le 0\).
Proof
Taking the time derivative of energy (51), using scalar wave Eq. (49a), and simplifying with integration by parts yields
Applying the definition of traction (17), boundary conditions (49b), and interface conditions (49c) leads to
since \(\alpha \ge 0\) and \(V\;F(V) \ge 0\). \(\square \)
3.2.2 Characteristic Nonlinear Interface Condition
As was done with boundary conditions in Sect. 3.1.1, it will be useful for the discretization to rewrite nonlinear interface condition (49c) in terms of the characteristic variables propagating into and out of the interface. Namely we let \(w^{\pm }\) be the characteristic variables propagating into and \(q^{\pm }\) out of the two sides of interface:
We then define the nonlinear functions \(\mathcal {Q}^{\pm }(w^{-}, w^{+})\) so that the characteristic-defined interface particle velocities and tractions,
satisfy nonlinear interface condition (49c). For a general F there is no closed form expression of \(\mathcal {Q}^{\pm }\), but existence can be guaranteed by the implicit function theorem if \(F'(V) > 0\) [11, Proposition 1]; Appendix D show how determining \(\mathcal {Q}^{\pm }\) can be reduced to a scalar root finding problem.
3.2.3 Discrete Problem
The interface problem is discretized with two blocks each with \(N + 1\) grid points. The grid solution on \([-1, 0]\) is \({{\varvec{u}}}^{-}\) and the grid solution on [0, 1] is \({{\varvec{u}}}^{+}\). With this a semidiscretization in each block is then
where \(n_{0} = -1\) and \(n_{N} = 1\) are the outward pointing normals at the block edges. As in Sect. 3.1, the terms \(\tau ^{\pm *}_{k}\) and \(u^{\pm *}_{k}\) are yet-to-be-defined numerical fluxes which can either be set in a non-characteristic or characteristic manner.
In each block we define the energy in the solution as
with traction \(\tau _{k}^{\pm }\) being as defined (28) for a penalty parameter \(\gamma \). The energy in the whole domain is then
and the following theorem guarantees that \(\mathcal {E}\) is a seminorm of the solution.
Theorem 4
Energy (58) is a seminorm for all \({{\varvec{u}}}^{\pm }\) and \(u^{\pm *}_{k}\) if \(\gamma \) is positive and sufficiently large.
Proof
Since the block energy (57) is of the same form as (27) the result follows directly from Theorem 1. \(\square \)
Corollary 2
Semidiscretization (56) satisfies
where \(\mathcal {E}\) is defined by (58) with the boundary term BT and interface term IT being
Proof
Follows directly by taking the time derivative of energy (58), substituting semidiscretization (56), and applying SBP property (3). \(\square \)
As shown in Sect. 3.1, if boundary conditions are enforced with either the non-characteristic (35) or characteristic (37) numerical fluxes then \(BT \le 0\). All that remains to be shown is how the numerical fluxes for the interface can be defined so that \(IT \le 0\), and as with the boundaries we will show how this can be done in a non-characteristic and characteristic manner.
3.2.4 Non-Characteristic Interface Treatment
In Duru et al. [7] it was proposed to set the numerical fluxes for the interface as
This leads to the following energy estimate for the interface:
Theorem 5
Non-characteristic numerical flux (62) leads to the energy dissipation \(IT \le 0\) where IT is defined by (61).
Proof
Substituting numerical flux (62) into (61) gives
and the result follows since \(V\;F(V) \ge 0\). \(\square \)
3.2.5 Characteristic Interface Treatment
The characteristic numerical interface fluxes are defined as
where the characteristic variables are
see Sect. 3.2.2. As with the case of characteristic treatment of boundary conditions, the numerical fluxes \(u_{N}^{-*}\) and \(u_{0}^{+*}\) must be tracked as variables during the solution process. The following theorem guarantees energy stability of the characteristic interface treatment:
Theorem 6
Characteristic numerical flux (64) leads to the energy dissipation \(IT \le 0\) where IT is defined by (61).
Proof
By definition, characteristic numerical flux (64) satisfies the nonlinear interface condition:
With this, we then have that
since \(V\;F(V) \ge 0\). Defining the grid based interface outgoing characteristic variables
it follows from characteristic numerical flux (64) that
Using relations (67) and (69) in interface term (61) gives
\(\square \)
3.2.6 Numerical Results
In order to assess the stiffness and accuracy of the non-characteristic and characteristic interface treatment, we use the nonlinear interface function
where the parameter \(\beta > 0\) will vary in the experiment. The outer boundary conditions are Neumann and enforced using the non-characteristic method. The initial condition is taken as
with \(\mu = -1/2\) and \(\sigma = 1/15\). These initial conditions lead to a pulse centered at \(x = \mu \) moving to the right. The exact solution for displacement is
The functions \(\psi ^{\pm }\) are a result of the wave propagating out of the interface, and are defined as
with the characteristic variables propagating into the interface being
the integral in (74) must be solved numerically since \(\mathcal {Q}^{\pm }\) does not have a closed form.
Time stepping is done by converting semidiscretization (56) into a first order system and using the low-storage, fourth order Runge-Kutta scheme of [5, (5,4) 2N-Storage RK scheme, solution 3]. The time step size is selected to be of the form
where \(\kappa \) is a Courant number chosen so that the simulation is stable and accurate. The L\(^2\)-error in the solution is
with \(\varDelta {{\varvec{u}}}^{\pm }\) being the pointwise difference between the numerical and exact solutions on the two sides of the interface. To find a suitable value of \(\kappa \) we start with an initial value of \(\kappa = 1\) and this is successively halved until the simulation is stable and accurate.
Table 1 gives the Courant \(\kappa \) determined for each SBP order and \(\beta \) pair. As can be seen the Courant number for the characteristic method is purely a function of the SBP operator and for the non-characteristic the time step size scales inversely with \(\beta \).
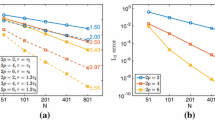
L\(^2\)-convergence comparison of the characteristic (\(+\) markers) and non-characteristic (\(\times \) markers) treatment of the nonlinear interface condition for various values of the strength parameter \(\beta \). The red, blue, and green curves correspond to SBP interior orders 2, 4, and 6, respectively (Color figure online)
Figure 3 shows the convergence results for the solution at time \(t = 1\) for the non-characteristic and characteristic methods. The spatial resolutions used in the test are \(N = 17 \times 2^r\) with \(r = 0, 1, 2, 3, 4, 5\). In the figure SBP interior orders \(2p = 2\), 4, and 6 are used and the nonlinear strength parameters as \(\beta = 32\), 64, and 128. As can be seen both methods converge similarly at the expected rates.
4 Multi-Dimensional Model Problem
4.1 Continuous Problem
Let \(\varOmega \subset {\mathbb {R}}^{d}\) be a bounded domain with boundary \(\partial \varOmega \). The boundary is split into two distinct parts: a Dirichlet boundary \(\partial \varOmega _{D}\) and a characteristic boundary \(\partial \varOmega _{C}\). Additionally, let \(\varGamma _{I} \subset {\mathbb {R}}^{d-1}\) be a set of interfaces in the domain. Unless otherwise noted summation over repeated subscripts is implied, e.g., \(u_{i} v_{i} = \sum _{i=1}^{d} u_{i} v_{i}\), \(u_{ii} = \sum _{i=1}^{d} u_{ii}\), and \(u_{i}C_{ij}v_{j} = \sum _{i=1}^{d}\sum _{j=1}^{d} u_{i}C_{ij}v_{j}\).
As a model problem we consider the scalar second-order, anisotropic wave equation for displacement u:
Here, the density \(\rho > 0\) and the components of the stiffness matrix \(C_{ij}\) are taken to be spatially varying. The stiffness matrix is assumed to be symmetric positive definite: \(C_{ij} = C_{ji}\) and \(v_{i} C_{ij} v_{j} \ge 0\) with equality only when \(v_{i} = 0\) for all i. At interfaces and boundaries the traction \(\tau \) is
where the vector \(n_{i}\) is the outward unit normal to boundary. On \(\partial \varOmega _C\) the reflection coefficient satisfies \(-1 \le R \le 1\) where the shear impedance \(Z > 0\) is defined by \(Z^2 = \rho n_{i}C_{ij}n_{j}\). On the interface \(\varGamma _{I}\), relationship (78d) specifies force balance and a nonlinear conditions, respectively. The normal vector is defined so that \(n_{i}^{-}\) points away from the minus side and \(n_{i}^{+}\) points away from the plus side with \(n_{i}^{+} = -n_{i}^{-}\). The superscripts on the material parameters denote which side of the interface the material parameters are evaluated on. We define the jump in \(\dot{u}\) across the interface by
Physically, The nonlinear function F(V) is the frictional strength of the interface and is assumed to satisfy \(VF(V) \ge 0\). Force balance and \(V^{+} = -V^{-}\) imply that \(F(V^{+}) = -F(V^{-})\).
4.2 Domain Decomposition
Let \({\mathcal {B}(\varOmega )}\) be a partitioning of \(\varOmega \subset {\mathbb {R}}^{d}\) into \(N_{b}\) non-overlapping, curvilinear blocks (quadrilaterals when \(d=2\) and hexahedrons when \(d=3\)). For each \(B \in {\mathcal {B}(\varOmega )}\) there is a diffeomorphic mapping \({\varvec{x}}^{B}\) between B and the reference block \(\hat{B} = [0, 1]^d\) such that \({\varvec{x}}^{B}({\varvec{\xi }}) \in B\) for all \({\varvec{\xi }} \in \hat{B}\); the reference block is the same as the reference domain discussed in Sect. 2.2 and the same face numbering is used. We use the notation \(\hat{\partial }_{i}\) to denote the partial derivative with respect to \(\xi _{i}\). The Jacobian determinant is denoted as \(J^{B}\). For example with \(d=2\)
Note that typically the metric terms are computed by first computing \(\hat{\partial }_{l} x_{i}^{B}\) and then metric identities are employed to calculate \(\partial _{j} \xi _{m}^{B}\); see, for example, Kopriva [10].
Each block \(B \in {\mathcal {B}(\varOmega )}\) has 2d faces, and we let \(\partial B^{f}\) for \(f = 1, 2, \dots , 2d\) be the faces in physical space and \(\partial \hat{B}^{f}\) be the faces in the reference space. We assume that each face \(B^{f}\) corresponds to either a Dirichlet boundary, characteristic boundary, nonlinear interface, or a purely computational interface (i.e., an artificial interface introduced in the partitioning of \(\varOmega \)). We let \(n_{i}^{B^f}\) denote the outward pointing normal to face f of block B in physical space and \(\hat{n}_{i}^{B^f} \equiv \hat{n}_{i}^{f}\) denote the same outward pointing normal in the reference space; see also (13). The relationship between \(n_{i}\) and \(\hat{n}_{i}\) is
where the surface Jacobian \(S_{J}^{B^{f}}\) is the normalization factor so that \(n_{i}^{B^{f}}\) is a unit vector. Given the face numbering convention and properties of the reference unit norm \(\hat{n}_{i}^{f}\), the surface Jacobian with \(d = 2\) is
Before writing down the transformed governing equations, it is useful to define a few metric term scaled quantities. For each \(B \in {\mathcal {B}(\varOmega )}\) we define the transformed density and stiffness matrix as
in this equation, and those that follow, unless needed the superscript B denoting the block number is suppressed. Similarly, on face \(\partial B^{f}\) the shear impedance and traction are defined as
unless needed for clarity, the superscript \(B^{f}\) is reduced to f. Finally, the scaled boundary data and interface function are
With these, for each \(B \in {\mathcal {B}(\varOmega )}\) governing Eq. (78) become
For each face \(\partial B^{f}\) the boundary and interface condition are
where \(V^{f^{\pm }} = \dot{u}^{f^{\mp }} - \dot{u}^{f^{\pm }}\). Here the notation \(f^{\pm }\) denotes the two sides of the interface with \(f^{-}\) denoting the interior value and \(f^{+}\) denoting the exterior (neighboring block) value. Namely, let face \(\partial B^{f}\) of block \(B \in {\mathcal {B}(\varOmega )}\) be connected to block \(C \in {\mathcal {B}(\varOmega )}\) along face \(\partial C^{f'}\), then \(\partial B^{f^{-}} = \partial B^{f}\) and \(\partial B^{f^{+}} = \partial C^{f'}\). By definition \(S_{J}^{f^{+}} = S_{J}^{f^{-}}\) and \(\hat{n}^{f^{+}}_{i} = - \hat{n}^{f^{-}}_{i}\). Interface conditions (87e) are not present in the original governing Eq. (78), and are added to account for continuity of the solution across computational block interfaces.
4.3 Characteristic Variables
As in the one-dimensional case, it is useful to introduce the characteristic variables
where \(\hat{q}^{f}\) and \(\hat{w}^{f}\) propagate out of and into the block face f, respectively; recall that \(\hat{\tau }^{f}\) includes the outward normal. As before, the displacement and traction can be recovered from the characteristic variables:
With this, the characteristic boundary condition (87c) can be written as
Interface conditions (87d) and (87e) can both be rewritten in terms of the characteristic variables:
where the superscript \(f^{\pm }\) denote the variable on either side of the interface. For computational interface (87e), \(\hat{\mathcal {Q}}^{f^{\pm }}\) is a linear function:
when \(\hat{Z}^{f^{+}} = \hat{Z}^{f^{-}}\) this reduces to transmission of the characteristic variable across the interface: \(\hat{\mathcal {Q}}^{f^{\pm }}\left( \hat{w}^{f^{\pm }}, \hat{w}^{f^{\mp }}\right) = \hat{w}^{f^{\mp }}\).
As discussed in one-dimension, for nonlinear interface condition (87d), in general there is no closed form expression for \(\hat{\mathcal {Q}}^{\pm }\). As shown in Appendix D, for a given \(\dot{u}^{f^{\pm }}\) and \(\hat{\tau }^{f^{\pm }}\) the function \(\hat{\mathcal {Q}}^{\pm }\) can be found to be consistent with the interface condition by solving the nonlinear system
4.4 Energy Analysis
To guide the development of the numerical scheme, we now develop an energy estimate for governing Eq. (87a). We define a seminorm E(u) and then show that \(\dot{E}(u(\cdot , t)) \le 0\) when \(g^{f}_{D} = \hat{g}_{C}^{f} = 0\) for all \(t > 0\); with non-zero boundary data energy growth due to the boundary conditions must be allowed.
For the transformed system (87), the energy in block \(B \in {\mathcal {B}(\varOmega )}\) is
this is valid seminorm of u, namely \(E^{B} \ge 0\) for all u, because the stiffness matrix is symmetric positive definite. The total energy in the domain is then
Lemma 3
Governing Eq. (87) with energy (95) satisfy \(\dot{E} \le 0\) if \(g^{f}_{D} = \hat{g}^{f}_{C} = 0\).
Proof
Taking the time derivative of block energy (94), substituting in governing Eq. (87a), and applying the divergence theorem gives
If face f is a Dirichlet boundary then applying boundary condition (87b) with \(g^{f}_{D} = 0\) gives
Similarly, if face f is a characteristic boundary, applying physical to characteristic variable transformation (89) and using characteristic boundary condition (90) gives
since \(-1 \le R^f \le 1\).
If face f is an interface, adding both contributions gives
where we have used that \(\hat{\tau }^{f^{+}} = - \hat{\tau }^{f^{-}}\) by (87e) and (87d).
For the case of computational interface condition (87e) the particle velocity is continuous, thus \(V^{f^{-}} = 0\) and the interface leads to a zero rate of change in energy.
When the interface is governed by nonlinear interface condition (87d) we have that
by the condition that \(V\hat{F}(V) \ge 0\). \(\square \)
5 Multi-Block Semidiscretization
A single block semidiscretization of (87) with weak enforcement of boundary conditions is
which after multiplying by \({{\varvec{\tilde{H}}}}\) and applying the multidimensional SBP property (15) gives a form that is more convenient for analysis:
Here we have defined
and \({{\varvec{\tilde{ \rho }}}}\) is a diagonal matrix of density \(\rho \) evaluated at the grid points. The numerical flux vectors \({{\varvec{\hat{\tau }}}}^{*f}\) and \({{\varvec{u}}}^{*f}\), which depend on the specific boundary or interface condition, are discussed in detail below.
We define the energy in the domain as
where the energy in block B is
Here we have defined the diagonal matrix
where \({{\varvec{{\varGamma }}}}^{f}\) is a diagonal penalty parameter matrix the entries of which must be sufficient large; a lower bound for \({{\varvec{{\varGamma }}}}^{f}\) is given by (149a). Additionally we define the block face tractions
Essentially, discrete energy (105) is a direct discretization of continuous energy (94) with an additional penalty on the faces for the mismatch between two alternative approximations of the traction \(\hat{\tau }^{f}\) (85b).
The discrete energy satisfies the following theorem; proof in Appendix B.
Theorem 7
Energy (105) is a seminorm of the solution if \({{\varvec{{\varGamma }}}}^{f}\) is positive and sufficiently large.
Corollary 3
For each block \(B \in {\mathcal {B}(\varOmega )}\), the energy rate of change is
with the energy face rate of change being
Proof
For a single block, taking the time derivative of block energy (105) and using discretization (102) gives
Using the definition of \({{\varvec{\hat{\tau }}}}^{f}\) (107b) the rate of change of face energy simplifies to face rate (109). \(\square \)
Discrete face energy rate (109) is of the same form as the continuous counterpart (96), namely a boundary integral of the particle velocity times the traction at the boundary. Stability is now reduced to showing that if a face f is on a physical boundary that \(\dot{\mathcal {E}}^{f} \le 0\) and if on a block interface that \(\dot{\mathcal {E}}^{f^{-}} + \dot{\mathcal {E}}^{f^{+}} \le 0\).
In the remainder of this section numerical fluxes are given for characteristic boundary conditions as well as the characteristic treatment of computational and nonlinear interfaces. In Appendix C the typical SBP-SAT numerical fluxes for Dirichlet, Neumann, and Characteristic boundary conditions as well as computational interfaces are given, e.g., those from Virta and Mattsson [28] with the improved Dirichlet penalty parameter of Almquist and Dunham [1]. The standard approaches specify \(u^{*}\) directly, i.e., they do not require an additional block face variable be integrated in time.
5.1 Characteristic Boundary Conditions
When block face f corresponds to a characteristic boundary (90) we choose values of \({{\varvec{\hat{\tau }}}}^{*f}\) and \({{\varvec{\dot{u}}}}^{*f}\) which preserves the outgoing characteristic variable while also satisfying the boundary condition:
Solving these equations for the numerical fluxes gives
As in the one-dimensional formulation, numerical flux \({{\varvec{u}}}^{*f}\) must be stored along the face and integrated in time.
Using the characteristic boundary treatment (112) with \(g_{c} = 0\) in face energy rate of change (109) gives
Since the reflection coefficient satisfies \(-1 \le R \le 1\), the boundary treatment is energy stable: \(\dot{\mathcal {E}}_{f} \le 0\).
5.2 Characteristic Interface
For characteristic interfaces, computational or nonlinear, the aim is to define the numerical fluxes to satisfy the interface condition in a way that preserves the characteristic variables propagating into the interface. As noted in Sect. 4.2, the nonlinear and computational interface conditions can be enforced using the functions \(\hat{\mathcal {Q}}^{f^{\pm }}\) (91). Thus we define \({{\varvec{\hat{\tau }}}}^{*f^\pm }\) and \({{\varvec{\dot{u}}}}^{*f^\pm }\) so that they satisfy
Solving for the numerical fluxes then gives
Since \({{\varvec{\hat{\tau }}}}^{*f^{\pm }}\) and \({{\varvec{\dot{u}}}}^{*f^{\pm }}\) satisfy the interface conditions, it follows that for a computational interface:
and for the nonlinear interface:
where \({{\varvec{V}}}^{*f^{\pm }} = {{\varvec{\dot{u}}}}^{*f^{\mp }} - {{\varvec{\dot{u}}}}^{*f^{\pm }}\). Since it is required that \(V \hat{F}(V) \ge 0\), for both the computational and nonlinear interface treatment
in the computational interface \({{\varvec{V}}}^{*f^{\pm }} = {{\varvec{0}}}\).
In order to analyze the interface treatment, it is useful to define the grid based characteristic variables
so that we can write
identical expressions can be written for the numerical fluxes \({{\varvec{\hat{q}}}}^{*f^{\pm }}\), \({{\varvec{\dot{u}}}}^{*f^{\pm }}\), and \({{\varvec{\hat{\tau }}}}^{*f^{\pm }}\). Using these in the face energy rate of change (109) gives
Adding the two sides of an interface together yields
Here we have used that \({{\varvec{\hat{\tau }}}}^{*f^{+}} = -{{\varvec{\hat{\tau }}}}^{*f^{-}}\). Energy stability results since this face energy rate of change is non-positive due to the positivity result of (118) and the fact that the second and third terms are in quadratic form.
6 Two-Dimensional Numerical Experiments
To test semidiscrete scheme (102) we introduce a velocity variable  and write the method as a first order system of equations:
and write the method as a first order system of equations:
as needed, additional variables are also introduced to track the numerical fluxes. The error is measured using the discrete L\(^{2}\)-norm
where \(\varDelta {{\varvec{\tilde{u}}}}\) is the difference between the numerical and analytic solution evaluated at the grid points. In all cases the penalty parameter is chosen to be at the stability limit, i.e., the equality condition of (149a).
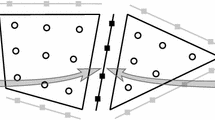
Two-dimensional domain used for numerical results in Sect. 6. The thick green line is the interface between the two subdomains \(\varOmega _{1}\) and \(\varOmega _{2}\). The thin black lines show the finite difference block interfaces (Color figure online)
We consider the two-dimensional square domain \(\varOmega = [-2, 2]^2\). Inside of \(\varOmega \) we define the unit circle \(\varGamma _{I} = \{(x_{1}, x_{2}) | x_{1}^2+x_{2}^2=1 \}\) to partition the domain into a closed unit disk \(\varOmega _{1} = \{(x_{1}, x_{2}) | x_{1}^2+x_{2}^2\le 1 \}\) and the remainder \(\varOmega _2 = \text {cl}(\varOmega \setminus \varOmega _{1})\). The interface \(\varGamma _{I}\) is governed by the nonlinear condition
where \(\beta > 0\) and \(g_{\tau }^{\pm }\) is a time and space dependent forcing function; around \(V = 0\) with \(g_{\tau }^{\pm } = 0\) the linearization of the interface condition is \(\tau ^{\pm } = \beta V\). The right and left boundaries of \(\varOmega \) are taken to be Dirichlet, the top and bottom boundaries Neumann; the Dirichlet and Neumann boundary conditions are enforced using the standard approach described in the Appendix C. As shown in Fig. 4, the domain is decomposed into 56 finite difference blocks and the all interfaces, nonlinear and computational, are enforced using the characteristic approach described in Sect. 5.2 through the introduction of the auxiliary variable \({{\varvec{u}}}^{*f}\) on each interface. Given the unstructured connectivity of the blocks it is necessary to use the same \((N+1) \times (N+1)\) grid of points in each block; we refer to N as the block size. Time stepping is performed using the low-storage, fourth order Runge-Kutta scheme of [5, (5,4) 2N-Storage RK scheme, solution 3].
In order to assess the stiffness and accuracy of the scheme in two spatial dimensions we use the method of manufactured solutions (MMS) [25]. In particular, we assume an analytic solution and compute the necessary boundary, interface, and volume data. The manufactured solution is taken to be
where \(r^2 = x_{1}^2 + x_{2}^2\) and \(\theta = {{\,\mathrm{atan2}\,}}(x_{2}, x_{1})\). The boundary, interface, and forcing data are found by using assumed solution (126) in governing Eq. (78). In order to avoid order reduction with time dependent data, we found it necessary to define the Dirichlet boundary data by integrating \(\dot{g}_{D}\) using the Runge-Kutta method. Solution (126) satisfies force balance along \(\varGamma _{I}\), i.e., continuity of traction \(\tau \), and the interface data \(g_{\tau }^{\pm }\) is used to enforce the assumed solution. In the MMS test the material properties are \(\rho = 1\) and \(C_{ij} = \delta _{ij}\), with \(\delta _{ij}\) being the kroneckor delta; after the mesh warping the effective material parameters \(\hat{C}_{ij}\) are spatially varying.
To compare the stiffness of the standard and characteristic nonlinear interface treatment we vary the nonlinear interface parameter \(\beta \) and decrease the time step size until the simulation is stable for a fixed block size \(N = 48\). For a non-stiff method, the time step size should be on the order of the effective grid spacing for all \(\beta > 0\). In particular, we define the time step size to be
where \(\kappa \) is the Courant number and a non-stiff scheme should have \(\kappa \sim 1\); since the material properties are taken to be unity the wave speed in this problem is 1. The effective grid spacing \(\bar{h}\) is defined as
Table 2 gives the Courant number \(\kappa \) required for stability of the two methods with various values of \(\beta \) using SBP interior order \(2p = 6\). Here the value of \(\kappa \) was repeatedly halved until the error in the simulation at time \(t = 0.1\) no longer decreased dramatically. To demonstrate that the stable Courant \(\kappa \) is close to its maximum value, Table 2 also reports the L\(^{2}\)-error with a time step defined by \(\kappa \) and \(2\kappa \), and as can be seen the former time step leads to an accurate simulation and the latter an inaccurate one. As can be seen the characteristic method requires a similar time step for all values of the parameter \(\beta \) whereas the non-characteristic method requires a significantly reduced time step as \(\beta \) increases. Though not shown, results with SBP interior orders \(2p = 2\) and \(2p = 4\) are similar; for \(2p = 2\) the characteristic method can use a Courant of \(\kappa = 1\) for all values of \(\beta \) as can the non-characteristic method with \(\beta = 1\).
Convergence results for MMS solution (126) with \(\beta = 128\) using SBP interior orders \(2p = 2, 4, 6\) with the characteristic nonlinear interface treatment. The value of \(\bar{h}_{0} \approx 0.019\) corresponds to block size \(N = 17\)
To investigate the convergence of the two-dimensional, characteristic method we now run the same MMS solution (126) to time \(t_f = 1\) using \(\beta = 128\) with different levels of refinement and a fixed Courant number \(\kappa = 1/2\). Figure 5 shows the convergence of the scheme using mesh levels \(N = 17 \times 2^r\) where \(r = 0, 1, 2, 3\). As can be seen the convergence order is similar to the one-dimensional case.
Variable material parameters \(C_{ij}\) and displacement field u snap shots with block size \(N = 136\) with the mesh show in Fig. 4. The colormap for the displacement field is saturated to show features at later times and the green curve indicates the location of the nonlinear interface (Color figure online)
As a final test, we explore the self-convergence and energy dissipation properties of the characteristic method with variable material properties and no body or boundary data. The same two-dimensional spatial domain is used, but now the material parameters are taken to be
where the angle \(\theta = \frac{\pi }{4} \left( 2 - x_{1}\right) \left( 2 - x_{2}\right) \); colormaps of the material parameters are shown in Fig. 6. The Courant number \(\kappa = 1/2\) is used for all the simulations and the material parameters lead to a maximum wave speed of 1, i.e., maximum eigenvalue of the matrix defined by \(C_{ij} / \rho \). The initial displacement is taken to be the product of two off-center Gaussians
where \(\mu _1 = 0.1\), \(\mu _2 = 0.2\), \(\sigma _1 = 0.0025\), and \(\sigma _2 = 0.005\), and the initial velocity is \(\dot{u}_{0} = 0\). A nonlinear parameter \(\beta = 1\) is used in order to highlight the effect of the nonlinear interface condition; larger values of \(\beta \) lead to a more continuous solution across the interface since the sliding velocity V will be lower. Snapshots of the displacement field at various times are shown in Fig. 6 for the block size \(N = 136 = 17 \times 8\) and SBP interior order \(2p = 6\). As can be seen in the figure, there is a discontinuity in the displacement across the interface as well as reflected waves.
For the self-convergence study we run the simulation until time \(t = 3\) using \(N_{r} = 17 \times 2^r\) with \(r = 1, 2, 3\). The error is estimated by taking the difference between neighboring resolutions, and the rate is estimated by
where \(\varDelta _{r}\) is the difference between the solutions using \(N_{r}\) and \(N_{r+1}\) and \(H_{r}\) indicates that the norm is taken with respect to the metrics defined by \(N_{r}\). With this, we get an estimate convergence rate for this problem of 4.4 using the SBP operators with interior accuracy \(2p = 6\).
Using same material properties and initial condition, Fig. 7 show the dissipated energy when \(\varGamma _I\) is taken to be a computational interface and a nonlinear interface with \(\beta = 1\); energy is measured using the discrete energy norm (104). In both cases the energy decreases in time as the theory predicts. In the case of the computational interface the dissipation is purely numerical, and as the results show the dissipation decreases as the resolution increases. In the case of the nonlinear interface the amount of energy dissipated is larger since the continuous formulation supports energy dissipation on interface \(\varGamma _{I}\).
Normalized dissipated energy for a computational and nonlinear interface \(\varGamma _{I}\) with energy is computed discretely using (104) and positive values indicating dissipation
7 Concluding Remarks
We have developed a characteristic based method for handling boundary and interface conditions with SBP finite difference methods for the second order, scalar wave equation. The key idea of the method is the introduction of an additional unknown on the block boundaries which evolves in time and acts as local Dirichlet data for the block. The rate of change of the boundary unknown is defined in an upwind fashion that modifies the incoming characteristic variable, which is similar to the technique previously used to remove stiffness for the wave equation in first order form with nonlinear interfaces [11].
The main benefit of the scheme is that, when compared with the standard approach [7, 28], the scheme is non-stiff for all characteristic boundary conditions and a class of nonlinear interface conditions that can be written in characteristic form; we note that at the continuous level the equation we consider are the same as Duru et al. [7] and that our schemes only differ at the discrete level. One benefit of this approach is that it enables the use of a wider class of time stepping methods for earthquake rupture problems with nonlinear interfaces.
The energy method was used to show that the proposed scheme is stable. Numerical experiments showed that the proposed scheme is non-stiff, confirmed the stability results, and also demonstrated the accuracy of the scheme. The analysis presented is dimension independent, thus the results equally apply to three dimensions. That said, the penalty parameter scales with d, and thus there may be more restrictive time step in three dimensions; see (149a).
One area for future work includes more general wave equations, such as linear elasticity. In this case, there will be multiple displacement and characteristic variables. One important question to consider is whether auxiliary interface variables are required for all components or only a subset. The work Almquist and Dunham [2] will be relevant to these exstensions, particularly if one is willing to be restricted to fully-compatible SBP operators.
One of the disadvantages of the traditional SBP finite difference formulations is that the mesh must be conforming across block interfaces. Computationally, this means that some regions of the domain will have finer mesh resolution than the physics dictates which increases the computational cost through both increased overhead per time step and reduced time steps size. These limitations have lead to a recent interest in SBP-SAT methods for non-conforming interfaces [12, 17, 29]. Though we see no obvious reason that the methods presented here would not extend to the non-conforming interface case, it remains for this to be rigorously demonstrated.
Notes
The free parameter \(x_1=0.70127127127127\) is used for \(2p = 6\).
References
Almquist, M., Dunham, E.M.: Non-stiff boundary and interface penalties for narrow-stencil finite difference approximations of the laplacian on curvilinear multiblock grids. J. of Comput. Phys. 408, 109–294 (2020). https://doi.org/10.1016/j.jcp.2020.109294
Almquist, M., Dunham, E.M.: Elastic wave propagation in anisotropic solids using energy-stable finite differences with weakly enforced boundary and interface conditions. J. of Comput. Phys. 424, 109–842 (2021). https://doi.org/10.1016/j.jcp.2020.109842
Bezanson, J., Edelman, A., Karpinski, S., Shah, V.B.: Julia: A fresh approach to numerical computing. SIAM review 59(1), 65–98 (2017). https://doi.org/10.1137/141000671
Carpenter, M.H., Gottlieb, D., Abarbanel, S.: Time-stable boundary conditions for finite-difference schemes solving hyperbolic systems: Methodology and application to high-order compact schemes. J. of Comput. Phys. 111(2), 220–236 (1994). https://doi.org/10.1006/jcph.1994.1057
Carpenter, M.H., Kennedy, C.A.: Fourth-order 2N-storage Runge-Kutta schemes. Tech. Rep. NASA TM-109112, National Aeronautics and Space Administration, Langley Research Center, Hampton, VA (1994)
Carpenter, M.H., Nordström, J., Gottlieb, D.: A stable and conservative interface treatment of arbitrary spatial accuracy. J. of Comput. Phys. 148(2), 341–365 (1999). https://doi.org/10.1006/jcph.1998.6114
Duru, K., Allison, K.L., Rivet, M., Dunham, E.M.: Dynamic rupture and earthquake sequence simulations using the wave equation in second-order form. Geophys. J. Int. 219(2), 796–815 (2019). https://doi.org/10.1093/gji/ggz319
Erickson, B.A., Jiang, J., Barall, M., Lapusta, N., Dunham, E.M., Harris, R., Abrahams, L.S., Allison, K.L., Ampuero, J.P., Barbot, S., Cattania, C., Elbanna, A., Fialko, Y., Idini, B., Kozdon, J.E., Lambert, V., Liu, Y., Luo, Y., Ma, X., Mckay, M.B., Segall, P., Shi, P., van den Ende, M., Wei, M.: The community code verification exercise for simulating sequences of earthquakes and aseismic slip (seas). Seismol. Res. Lett. 91, 874–890 (2020). https://doi.org/10.1785/0220190248
Hicken, J.E., Zingg, D.W.: Summation-by-parts operators and high-order quadrature. J. of Comput. and Appl. Math. 237(1), 111–125 (2013). https://doi.org/10.1016/j.cam.2012.07.015
Kopriva, D.A.: Metric identities and the discontinuous spectral element method on curvilinear meshes. J. of Sci. Comput. 26(3), 301–327 (2006). https://doi.org/10.1007/s10915-005-9070-8
Kozdon, J.E., Dunham, E.M., Nordström, J.: Interaction of waves with frictional interfaces using summation-by-parts difference operators: Weak enforcement of nonlinear boundary conditions. J. of Sci. Comput. 50(2), 341–367 (2012). https://doi.org/10.1007/s10915-011-9485-3
Kozdon, J.E., Wilcox, L.C.: Stable coupling of nonconforming, high-order finite difference methods. SIAM J. on Sci. Comput. 38(2), A923–A952 (2016). https://doi.org/10.1137/15M1022823
Kreiss, H., Oliger, J.: Comparison of accurate methods for the integration of hyperbolic equations. Tellus 24(3), 199–215 (1972). https://doi.org/10.1111/j.2153-3490.1972.tb01547.x
Kreiss, H., Scherer, G.: Finite element and finite difference methods for hyperbolic partial differential equations. In: Mathematical aspects of finite elements in partial differential equations; Proceedings of the Symposium, pp. 195–212. Madison, WI (1974). https://doi.org/10.1016/b978-0-12-208350-1.50012-1
Kreiss, H., Scherer, G.: On the existence of energy estimates for difference approximations for hyperbolic systems. Tech. rep., Department of Scientific Computing, Uppsala University (1977)
Mattsson, K.: Summation by parts operators for finite difference approximations of second-derivatives with variable coefficients. Journal of Scientific Computing 51(3), 650–682 (2012). https://doi.org/10.1007/s10915-011-9525-z
Mattsson, K., Carpenter, M.H.: Stable and accurate interpolation operators for high-order multiblock finite difference methods. SIAM J. on Sci. Comput. 32(4), 2298–2320 (2010). https://doi.org/10.1137/090750068
Mattsson, K., Ham, F., Iaccarino, G.: Stable and accurate wave-propagation in discontinuous media. J. of Comput. Phys. 227(19), 8753–8767 (2008). https://doi.org/10.1016/j.jcp.2008.06.023
Mattsson, K., Ham, F., Iaccarino, G.: Stable boundary treatment for the wave equation on second-order form. J. of Sci. Comput. 41(3), 366–383 (2009). https://doi.org/10.1007/s10915-009-9305-1
Mattsson, K., Nordström, J.: Summation by parts operators for finite difference approximations of second derivatives. J. of Comput. Phys. 199(2), 503–540 (2004). https://doi.org/10.1016/j.jcp.2004.03.001
Mattsson, K., Parisi, F.: Stable and accurate second-order formulation of the shifted wave equation. Commun. in Comput. Phys. 7(1), 103 (2010). https://doi.org/10.4208/cicp.2009.08.135
Nordström, J.: A roadmap to well posed and stable problems in computational physics. J. of Sci. Comput. 71(1), 365–385 (2017). https://doi.org/10.1007/s10915-016-0303-9
Olsson, P.: Summation by parts, projections, and stability. I. Math. of Comput. 64(211), 1035–1065 (1995). https://doi.org/10.2307/2153482
Olsson, P.: Summation by parts, projections, and stability. II. Math. of Comput. 64(212), 1473–1493 (1995). https://doi.org/10.2307/2153366
Roache, P.: Verification and validation in computational science and engineering, 1st edn. Hermosa Publishers, Albuquerque, NM (1998)
Strand, B.: Summation by parts for finite difference approximations for d/dx. J. of Comput. Phys. 110(1), 47–67 (1994). https://doi.org/10.1006/jcph.1994.1005
Strand, B.: Summation by parts for finite difference approximations for \(d/dx\). J. of Comput. Phys. 110(1), 47–67 (1994). https://doi.org/10.1006/jcph.1994.1005
Virta, K., Mattsson, K.: Acoustic wave propagation in complicated geometries and heterogeneous media. J. of Sci. Comput. 61(1), 90–118 (2014). https://doi.org/10.1007/s10915-014-9817-1
Wang, S., Virta, K., Kreiss, G.: High order finite difference methods for the wave equation with non-conforming grid interfaces. J. of Sci. Comput. 68(3), 1002–1028 (2016). https://doi.org/10.1007/s10915-016-0165-1
Acknowledgements
We thank the two anonymous reviewers whose insightful feedback substantially improved the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
B.A.E. was supported by National Science Foundation Awards EAR-1547603 and EAR-1916992
J.E.K. was supported by National Science Foundation Award EAR-1547596
T.H. was supported by National Science Foundation EAR-1916992
The views expressed in this document are those of the authors and do not reflect the official policy or position of the Department of Defense or the U.S. Government.
Approved for public release; distribution unlimited.
Appendices
Appendix A Definition of Two-Dimensional SBP Operators
As an example of how to construct multidimensional SBP operators, we consider the two dimensional SBP finite difference operators. We describe the operators on the reference block \(\hat{B} = [0,1] \times [0,1]\), where faces 1 and 2 are the right and left faces with faces 3 and 4 being the top and bottom faces, respectively. For simplicity we let the domain \(\hat{B}\) be discretized with an \((N+1) \times (N+1)\) grid points with the grid nodes located at \({\left\{ {{\varvec{\xi }}}\right\} }_{kl} = (kh, lh)\) for \(0 \le k,l \le N\) with \(h = 1/N\). The projection of u onto the grid is denoted \({{\varvec{\tilde{u}}}}\), where \({\left\{ {{\varvec{\tilde{u}}}}\right\} }_{kl} \approx u(kh, lh)\) and is stored as a vector with with \(\xi _1\) being the fastest index; see (8). With this, the volume norm matrix can be written as
We define the face restriction operators as
where the \({{\varvec{{I}}}}\) is the \((N+1) \times (N+1)\) identity matrix. More generally the restriction to a single grid line in the \(\xi _1\) and \(\xi _2\) directions, respectively, are
In order to construct \({{\varvec{\tilde{ A}}}}_{ii}^{(C)}\), no summation over i, we construct individual one-dimensional second derivative matrices for each grid line with varying coefficients C and place them in the correct block; expanding a single second derivative matrix with the tensor product and the identity matrix only works in the constant coefficient case. To do this it is useful to define \({{\varvec{\tilde{C}}}}\) as the projection of C onto the grid with the coefficients along the individual grid lines being
The second derivative operators are the sum of the operators along each grid line
and a tensor product is used for the mixed derivative operators
The boundary derivatives parallel to a face are given by the first derivative operator \({{\varvec{{D}}}}_{1}\) and those perpendicular with the boundary derivative operators from the SBP definition 2:
Appendix B Proof of Theorem 7
To show that energy (105) is positive we need the following definition from [16, Definition 2.4]:
The remainder matrix \({{\varvec{\tilde{ R}}}}_{ij}^{(c)}\) is symmetric positive semidefinite if the coefficient c is always positive; the remainder matrix is zero when \(i \ne j\). The remainder matrix can be further decomposed using the borrowing lemma from [1, Lemma 1]:
Here the matrix \({{\varvec{\tilde{ S}}}}_{ii}^{(c)}\) (no summation over i) is a positive semidefinite and the matrix \({{\varvec{{\bar{\varDelta }}}}}_{i}^{f} = {{\varvec{{\bar{B}}}}}_{i}^{f} - {{\varvec{{\bar{D}}}}}_{i}^{f}\) is the difference between the boundary derivative matrix from \({{\varvec{\tilde{ D}}}}_{ii}\) (no summation over i) and the first derivative matrix \({{\varvec{\tilde{ D}}}}_{i}\) at the boundary. Each element of the diagonal matrix \({{\varvec{{C}}}}^{f,min}\) is the minimum value of c in the \(m_{b}\) points orthogonal to the boundary where \(m_{b}\) depends on the order of accuracy of the SBP operator. The positive constant \(\zeta ^f = h^f_{\bot } \bar{\zeta }\) where \(h^{f}_{\bot }\) is the grid spacing orthogonal to the face and \(\bar{\zeta }\) is a constant which depends on the SBP operator. The \((m_{b}, \bar{\zeta })\) values used for the operators in this paper are given in Table 3; see [1, Table 1].
Since \({{\varvec{\tilde{ H}}}}\) is diagonal and positive, it is clear that for any face f
where \(\theta ^{f}\) is the value of the \({\left\{ {{\varvec{H}}}\right\} }_{00}\) where \({{\varvec{H}}}\) is the norm matrix orthogonal to the face. It then follows that
where the factor of 1/d is needed to avoid over counting corners and, when \(d = 3\), edges. Since the coefficient matrix \(C_{ij}\) is positive definite, this can be extended to included the variable coefficients:
We now turn to considering the discrete block energy (105). The first term satisfies
because it is in quadratic form and \({{\varvec{\tilde{ H}}}}\) and \({{\varvec{\tilde{ \rho }}}}\) are diagonal, positive matrices. The remaining terms will be shown to combine in a manner that is also positive semidefinite.
Combing relations (138), (139), and (142) we have that
We now considering the face term of the discrete block energy (105). Defining \({{\varvec{\delta }}}^{f}_{u} = {{\varvec{u}}}^{*f} - {{\varvec{u}}}^{f}\) and using the definition of \({{\varvec{\hat{\tau }}}}^{f}\) and \({{\varvec{\hat{T}}}}^{f}\) in (107) gives
It is useful to note that \({{\varvec{\hat{T}}}}\) can be rewritten using \({{\varvec{{\bar{\varDelta }}}}}^{f}_{k}\) as
this follows because only when \(f \in (2j, 2j-1)\) is \({{\varvec{{\bar{B}}}}}^{f}_{j} \ne {{\varvec{{\bar{D}}}}}^{f}_{j}\). Using this along with the definition of \({{\varvec{{X}}}}^{f}\) in (106) leads to,
where \(k = \left\lceil {\frac{f}{2}}\right\rceil \).
Returning to the remaining terms of block energy (105), we use (144) and (147) to write
If we choose
then we have that
where we have used that \(\hat{n}^{f}_{i} {{\varvec{{\hat{C}}}}}_{ij}^{f} \hat{n}^{f}_{j} = {{\varvec{{\hat{C}}}}}_{kk}^{f}\) with \(k = \left\lceil {\frac{f}{2}}\right\rceil \) (no summation over k). Though a similar transformation could be used on the first summation it is not needed and complicates the analysis that follows. Returning to (148) then gives with (150)
where we have used that \({{\varvec{{\hat{C}}}}}_{kk}^{f} = \hat{n}^{f}_{k} {{\varvec{{\hat{C}}}}}_{kk}^{f} \hat{n}_{k}^{t}\) (no summation over k) and \({{\varvec{{\hat{C}}}}}_{kk}^{f,\min } {{\varvec{{P}}}}^{f} = {{\varvec{{C}}}}_{kk}^{f}\) (no summation over k). Since this expression is in quadratic form, it is non-negative and the when combine with (143) shows that the block energy (105) is non-negative.
Appendix C Non-Characteristic Boundary and Interface Treatment
The standard approach for SBP-SAT for Dirichlet (78b), and characteristic boundaries (78c) as well as computational and nonlinear interfaces from Virta and Mattsson [28] and Duru et al. [7] are presented in the notation of this paper; Neumann boundary treatment is the same as the characteristic boundary treat with \(R = 1\).
1.1 C.1 Dirichlet Boundary Conditions
When block face f is on a Dirichlet boundary (87b) then the numerical fluxes are chosen to be
Using these numerical fluxes, the face energy rate of change (109) is
which with \(g_{D} = 0\) gives \(\dot{\mathcal {E}}^{f} = 0\) and does not lead to energy growth.
1.2 C.2 Characteristic (and Neumann) Boundary Conditions
In order to define the standard treatment of characteristic boundary conditions (78c), it is useful to solve (78c) for \(\tau \):
with \(\alpha = -Z (1 - R) / (R + 1) \le 0\) and \(\nu = 1 / (R + 1)\). We note again that the Neumann boundary condition is attained when \(R = 1\) in which case \(\alpha = 0\) and \(\nu = 1\). With this, if block face f is on a characteristic boundary then the numerical fluxes are chosen to be
where the parameters \({{\varvec{{\hat{\alpha }}}}}\) and \({{\varvec{{\hat{\nu }}}}}\) are diagonal matrices of \(S_{J}^{f} \alpha \) and \(S_{J}^{f} \nu \) evaluated at each point on face f. Using these numerical fluxes in (109) give
With \(g_{C} = 0\) we then have that \(\dot{\mathcal {E}}^{f} \le 0\) and there is no energy growth due to the characteristic boundary treatment; equality is obtained in the Neumann case.
1.3 C.3 Computational Interface
For computational interfaces (e.g., interfaces between blocks in the domains that have been introduced to mesh to either a material interface and/or needed in the mesh generation) continuity of displacement and traction need to be enforced. That is, across the interface it is required that
Here the superscript ± denotes the value on either side of the interface with the unit normal \({\varvec{n}}^{\pm }\) is taken to be outward to each side of the interface, i.e., \({\varvec{n}}^{-} = -{\varvec{n}}^{+}\). The standard approach to enforcing this is to choose the numerical flux to be the average of the values on the two sides of the interface,
the minus sign in \({{\varvec{\hat{\tau }}}}^{*f^{-}}\) is due to the unit normals being equal and opposite. Here the two blocks connected across the interface are \(B^{\pm }\) through faces \(f^{\pm }\).
The face energy rate of change (109) for computational interfaces is then
Adding the two sides of the interface together gives
and energy stability results.
1.4 C.4 Nonlinear Interface Condition
The approach Duru et al. [7] for nonlinear interfaces is to define the sliding velocity \(V^{\pm f}\) directly from the particle velocities on the grid and then the traction \(\tau ^{f}\) is defined directly from the nonlinear function so the numerical fluxes are
The face energy rate of change (109) for a nonlinear interface is then
Adding the two sides of the interface together gives
where we have used that \({{\varvec{V}}}^{f^{-}} = -{{\varvec{V}}}^{f^{+}}\) and the fact that \(V \hat{F}(V) \ge 0\).
Appendix D Nonlinear Interface Root Finding Problem
In general, evaluating \(\mathcal {Q}^{\pm }\) for a nonlinear condition \(\tau ^{\pm } = F\left( V^{\pm }\right) \) requires solving a nonlinear root finding problem. In particular, using the characteristic variables \(w^{\pm }\) a root finding problem for \(V^{\pm }\) is solved after which \(\mathcal {Q}^{\pm }\) can be determined.
Recall that force balance, \(\tau ^{-} = -\tau ^{+}\), and the fact that \(V^{-} = -V^{+}\) implies that \(\tau ^{-} = -F\left( V^{+}\right) \). Using this we can compute the \(Z^{\pm }\) weighted-average
Expressing \(\tau ^{\pm }\) in terms of \(\mathcal {Q}^{\pm }\) and \(w^{\pm }\), see (93b), then gives
The sliding velocity \(V^{+}\) can be written in terms of the characteristic variables using (93a):
Using this, we can rewrite (165) as
This expression can be more compactly written by defining
which depends only on the characteristic variables propagating into the interface and is the traction that would result if the interface were a computational interface; seen by using (92) in (93b). We can now write the final form of the root finding problem as
where \(\eta = Z^{+}Z^{-} / (Z^{+} + Z^{-})\) is known as the radiation damping coefficient. Once this nonlinear system is solved for \(V^{+}\) all other quantities can be determined using (93). When numerically solving (169) it is useful to realize that \({{\,\mathrm{sgn}\,}}\left( V^{+}\right) = {{\,\mathrm{sgn}\,}}\left( \tau _{l}^{+}\right) \) and that the root can be bracketed: \(\left| V^{+}\right| \in \left[ 0, F^{-1}\left( \tau _{l}^{+}\right) \right] \).
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Erickson, B.A., Kozdon, J.E. & Harvey, T. A Non-Stiff Summation-By-Parts Finite Difference Method for the Scalar Wave Equation in Second Order Form: Characteristic Boundary Conditions and Nonlinear Interfaces. J Sci Comput 93, 17 (2022). https://doi.org/10.1007/s10915-022-01961-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-022-01961-1