Unconditional Convergence of a Fast Two-Level Linearized Algorithm for Semilinear Subdiffusion Equations

Abstract

A fast two-level linearized scheme with nonuniform time-steps is constructed and analyzed for an initial-boundary-value problem of semilinear subdiffusion equations. The two-level fast L1 formula of the Caputo derivative is derived based on the sum-of-exponentials technique. The resulting fast algorithm is computationally efficient in long-time simulations or small time-steps because it significantly reduces the computational cost $O(MN^2)$ and storage O(MN) for the standard L1 formula to $O(MN\log N)$ and $O(M\log N)$, respectively, for M grid points in space and N levels in time. The nonuniform time mesh would be graded to handle the typical singularity of the solution near the time $t=0$, and Newton linearization is used to approximate the nonlinearity term. Our analysis relies on three tools: a recently developed discrete fractional Grönwall inequality, a global consistency analysis and a discrete $H^2$ energy method. A sharp error estimate reflecting the regularity of solution is established without any restriction on the relative diameters of the temporal and spatial mesh sizes. Numerical examples are provided to demonstrate the effectiveness of our approach and the sharpness of error analysis.

1 Introduction

A two-level linearized method is considered to numerically solve the following semilinear subdiffusion equation on a bounded domain

$$\begin{aligned} {\mathcal {D}}^{\alpha }_tu&= \Delta u+f(u)\quad \text {for }\varvec{x}\in \Omega \text { and } 0<t\le T, \end{aligned}$$

(1.1a)

$$\begin{aligned} u&=u^0(\varvec{x}) \quad \text {for }\varvec{x}\in \Omega \text { and } t=0, \end{aligned}$$

(1.1b)

$$\begin{aligned} u&= 0\quad \text {for }\varvec{x}\in \partial \Omega \text { and }0<t\le T, \end{aligned}$$

(1.1c)

where $\partial \Omega$ is the boundary of $\Omega :=(x_{l},x_{r})\times (y_{l},y_{r})$, and the nonlinear function f(u) is smooth. In (1.1a), ${\mathcal {D}}^{\alpha }_t={}_{~0}^{C}\!{\mathcal {D}}_t^{\alpha }$ denotes the Caputo fractional derivative of order $\alpha$:

$$\begin{aligned} ({\mathcal {D}}^{\alpha }_tv)(t) :=\int _{0}^{t} \omega _{1-\alpha } (t-s) v^{\prime }(s)\,\mathrm {d}{s},\quad 0<\alpha <1, \end{aligned}$$

(1.2)

where the weakly singular kernel $\omega _{1-\alpha }$ is defined by $\omega _{\mu }(t):=t^{\mu -1}/{\Gamma (\mu )}$. It is easy to verify that $\omega _{\mu }^{\prime }(t)=\omega _{\mu -1}(t)$ and $\int _0^t\omega _{\mu }(s)\,\mathrm {d}s=\omega _{\mu +1}(t)$ for $t>0$.

In any numerical methods for solving semilinear fractional diffusion equations (1.1a), a key consideration is the singularity of the solution near the time $t=0$, see [5, 9, 19, 23]. For example, under the assumption that the nonlinear function f is Lipschitz continuous and the initial data $u^0\in H^2(\Omega )\cap H_0^1(\Omega )$, Jin et al. [5, Theorem 3.1] prove that problem (1.1) has a unique solution u for which $u\in C\left( [0,T];H^2(\Omega )\cap H_0^1(\Omega )\right)$, ${\mathcal {D}}^{\alpha }_tu\in C\left( [0,T];L^2(\Omega )\right)$ and $\partial _t u \in L^2(\Omega )$ with

$$\begin{aligned} \Vert \partial _t u(t)\Vert _{L^2(\Omega )} \le C_ut^{\alpha -1}\quad \text {for } 0< t \le T, \end{aligned}$$

where $C_u>0$ is a constant independent of t but may depend on T. Their analysis of numerical methods for solving (1.1) is applicable to both the L1 scheme and backward Euler convolution quadrature on a uniform time grid of diameter $\tau$; a lagging linearized technique is used to handle the nonlinearity f(u), and [5, Theorem 4.5] shows that the discrete solution is $O(\tau ^{\alpha })$ convergent in $L^\infty (L^2)$.

This work may be considered as a continuation of [14], in which a sharp error estimate for the L1 formula on nonuniform meshes was obtained for linear subdiffusion-reaction equations based on a discrete fractional Grönwall inequality and a global consistency analysis. In this paper, we combine the L1 formula and the sum-of-exponentials (SOEs) technique to develop a one-step fast difference algorithm for the semilinear subdiffusion problem (1.1) by using the Newton’s linearization to approximate nonlinear term, and present the corresponding sharp error estimate of the proposed scheme without any restriction on the relative diameters of temporal and spatial mesh sizes.

It is known that the Caputo fractional derivative involves a convolution kernel. The total number of operations required to evaluate the sum of L1 formula is proportional to $O(N^2)$, and the active memory to O(N) with N representing the total time steps, which is prohibitively expensive for the practically large-scale and long-time simulations. Recently, a simple fast algorithm based on SOEs approximation is proposed to significantly reduce the computational complexity to $O(N \log N)$ and $O(\log N)$ when the final time $T\gg 1$, see [4, 10]. For an evolution equation with memory, a fast summation algorithm was also proposed [17] by interval clustering. Very recently, another fast algorithm for the evaluation of the fractional derivative has been proposed in [1], where the compression is carried out in the Laplace domain by solving the equivalent ODE with some one-step A-stable scheme. Here the technique of SOEs approximation is used to develop a two-level fast L1 formula by combining a nonuniform mesh suited to the initial singularity with a fast time-stepping algorithm for the historical memory in (1.2). As an interesting property, this scheme computes the current solution by only using the solution at previous time-level, so it would be useful to develop efficient parallel-in-time algorithms, cf. [21], for time-fractional differential equations.

On the other hand, the nonlinearity of the problem also results in the difficulty for the numerical analysis. To establish an error estimate of the two-level linearized scheme at time $t_n$, it always requires to prove the boundedness of the numerical solution at the previous time level, that is $\Vert u^{n-1}\Vert _{\infty }\le C_u$. Traditionally it is gotten by using the mathematical induction and some inverse estimate, assuming the underlaying scheme is accurate of order $O(\tau ^{\beta }+h^2)$ with $\beta$ representing the temporal convergence order,

$$\begin{aligned} \Vert u^{n-1}\Vert _{\infty }&\le \, \Vert U^{n-1}\Vert _{\infty }+\Vert U^{n-1}-u^{n-1}\Vert _{\infty }\\&\le \, \Vert U^{n-1}\Vert _{\infty }+h^{-1}\Vert U^{n-1}-u^{n-1}\Vert \\&\le \, \Vert U^{n-1}\Vert _{\infty }+C_uh^{-1}\big (\tau ^{\beta }+h^2\big ). \end{aligned}$$

This leads to a restriction of the time-space grid $\tau =O(h^{1/\beta })$ in the theoretical analysis even though it is nonphysical and may be unnecessary in numerical simulations. In this paper, we will extend the discrete $H^2$ energy method developed in [11,12,13] to prove unconditional convergence of our fully discrete solution without any time-space grid restrictions. The main idea of discrete $H^2$ energy method is to separately treat the temporal and spatial truncation errors. This method avoids some nonphysical time-space grid restrictions in the error analysis. Another related approach in a finite element setting is discussed in [6,7,8].

The convergence rate of L1 formula for the Caputo derivative is limited by the smoothness of the solution. We approximate the Caputo fractional derivative (1.2) on a (possibly nonuniform) time mesh $0=t_0<\cdots<t_{k-1}<t_{k}<\cdots <t_N=T$, with the time-step sizes $\tau _k:=t_k-t_{k-1}$ for $1\le k\le N$, the maximum time-step $\tau =\max _{1\le k\le N}\tau _k$ and the step size ratios 

$$\begin{aligned} \rho _k:=\tau _k/\tau _{k+1}\quad \text { for }1\le k\le N-1. \end{aligned}$$

The analysis here is based on the following assumptions on the continuous solution

$$\begin{aligned} \left\| u\right\| _{H^{4}(\Omega )}\le C,\;\; \left\| \partial _{t}u\right\| _{H^{4}(\Omega )}\le C(1+t^{\sigma -1})\;\; \text { and }\;\;p \left\| \partial _{tt}u\right\| _{H^{2}(\Omega )}\le C(1+t^{\sigma -2}) \end{aligned}$$

(1.3)

for $0< t \le T$, where $\sigma \in (0,1)\cup (1,2)$ is a regularity parameter. To satisfy the regularity conditions in (1.3), appropriate regularity and compatibility assumptions should be imposed on the given data in problem (1.1). Investigating this is beyond the scope of the paper. Noting that, the first two regularity conditions in (1.3) can be relaxed by using the finite elements instead of finite differences [15]. Throughout the paper, any subscripted C, such as $C_u$, $C_{\gamma }$, $C_{\Omega }$, $C_v$, $C_0$ and $C_{F}$, denotes a generic positive constant, not necessarily the same at different occurrences, which is always dependent on the given data and the continuous solution u, but independent of the time-space grid steps.

To resolve the singularity at $t=0$, it is reasonable to use a nonuniform mesh that concentrates grid points near $t=0$, see [2, 3, 14, 16, 20]. We make the following assumption on the time mesh:

AssG :

For a parameter $\gamma \ge 1$, there are positive constant $C_{\gamma }$ and ${\widetilde{C}}_{\gamma }$, independent of k, such that $\tau _k\le C_{\gamma }\tau \min \{1,t_k^{1-1/\gamma }\}$ for $1\le k\le N$, and $t_{k}\le {\widetilde{C}}_{\gamma }t_{k-1}$ for $2\le k\le N$.

The assumption AssG implies that $\tau _1=O(\tau ^{\gamma })$, and allows the time-step size $\tau _k$ to increase as the time $t_k$ increases, meanwhile, one may has $\tau _k=O(\tau )$ as those bounded $t_k$ away from $t=0$. The parameter $\gamma$ controls the distribution density of the grid points concentrated near $t=0$: increasing $\gamma$ will refine the time-step sizes near $t=0$ and so move mesh points closer to $t=0$. A simple example of a family of meshes satisfying AssG is the graded grid $t_k=T(k/N)^{\gamma }$, see discussions in [2, 14, 16, 18,19,20]. Although nonuniform time meshes are flexible and reasonably convenient for practical implementations, they also significantly complicate the numerical analysis of schemes, both with respect to stability and consistency. In this paper, our analysis will rely on a generalized fractional Grönwall inequality [15], which would be applicable for any discrete fractional derivatives having the discrete convolution form. As the main result shown in Theorem 4.2, the proposed two-level linearized fast scheme is proved to be unconditionally convergent in the sense that ($\epsilon$ is the SOE approximation error and h is the maximum spatial length)

$$\begin{aligned} \big \Vert U^k-u^k\big \Vert _{\infty }\le \frac{C_u}{\sigma (1-\alpha )} \left( \tau ^{\min \{2-\alpha ,\gamma \sigma \}}+h^2+\epsilon \right) , \end{aligned}$$

where $C_u$ may depend on u and T, but is uniformly bounded with respect to $\alpha$ and $\sigma$.

The paper is organized as follows. Section 2 presents the two-level fast L1 formula and the corresponding linearized fast scheme. The global consistency analysis of fast L1 formula and the Newton’s linearization are presented in Sect. 3. A sharp error estimate for the linearized fast scheme is proved in Sect. 4. Two numerical examples in Sect. 5 are given to demonstrate the sharpness of our analysis.

2 A Two-Level Fast Method

In space we use a standard finite difference method on a tensor product grid. Let $M_1$ and $M_2$ be two positive integers. Set $h_{1}=(x_{r}-x_{l})/M_1, \ h_{2}=(y_{r}-y_{l})/ M_2$ and the maximum spatial length $h=\max \{h_1,h_2\}$. Then the fully discrete spatial grid

$$\begin{aligned} {\bar{\Omega }}_h :=\{\varvec{x}_{h}=(x_{l} + ih_1, y_{l} + jh_2)\,|\, 0\le i\le M_1, 0\le j\le M_2\}. \end{aligned}$$

Set ${\Omega }_h={{\bar{\Omega }}}_h\cap \Omega$ and the boundary $\partial \Omega _h={{\bar{\Omega }}}_h\cap \partial \Omega$. Given a grid function $v = \{v_{ij}\}$, define

$$\begin{aligned}&v_{i-\frac{1}{2},j}=\left( v_{i,j}+v_{i-1,j}\right) /{2}, \ \delta _xv_{i-\frac{1}{2},j}=\left( v_{i,j}-v_{i-1,j}\right) /{h_1}, \ \\&\quad \delta _x^2v_{ij} =\big (\delta _xv_{i+\frac{1}{2},j}-\delta _xv_{i-\frac{1}{2},j}\big )/{ h_1}. \end{aligned}$$

Also, discrete operators $v_{i,j-\frac{1}{2}},\ \delta _yv_{i,j-\frac{1}{2}}, \ \delta _x\delta _yv_{i-\frac{1}{2},j-\frac{1}{2}}$ and $\delta _y^2v_{ij}$ can be defined analogously. The second-order approximation of $\Delta v(\varvec{x}_{h})$ for $\varvec{x}_h\in \Omega _h$ is $\Delta _hv_{h} := (\delta _x^2+\delta _y^2)v_{h}$. Let ${\mathcal {V}}_{h}$ be the space of grid functions,

$$\begin{aligned} {\mathcal {V}}_{h}=\big \{v=\left( v_h\right) _{\varvec{x}_h\in {\bar{\Omega }}_h}\,\big |\, v_h=0\;\text{ for }\;\varvec{x}_h\in \partial \Omega _h\big \}. \end{aligned}$$

For $v, w \in {\mathcal {V}}_h$, define the discrete inner product $\left\langle v,w\right\rangle =h_1h_2\sum _{\varvec{x}_h\in \Omega _h}v_{h}w_{h}$, the discrete $L^2$ norm $\Vert v\Vert :=\sqrt{\left\langle v,v\right\rangle }$, the discrete $H^1$ seminorms

$$\begin{aligned} \Vert \delta _xv\Vert :=\sqrt{h_1h_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2-1}\big (\delta _xv_{i-\frac{1}{2},j}\big )^2},\quad \Vert \delta _yv\Vert :=\sqrt{h_1h_2\sum _{i=1}^{M_1-1}\sum _{j=1}^{M_2}\big (\delta _yv_{i,j-\frac{1}{2}}\big )^2}, \end{aligned}$$

$\Vert \nabla _h v\Vert =\sqrt{\Vert \delta _xv\Vert ^2+\Vert \delta _yv\Vert ^2}$ and the maximum norm $\Vert v\Vert _{\infty }=\max _{\varvec{x}_h\in \Omega _h}\left| v_h\right|$. For any $v\in {\mathcal {V}}_{h}$, by [13, Lemmas 2.1, 2.2 and 2.5] there exists a constant $C_{\Omega }>0$ such that

$$\begin{aligned} \Vert v\Vert \le C_{\Omega }\Vert \nabla _hv\Vert , \quad \Vert \nabla _hv\Vert \le C_{\Omega }\Vert \Delta _hv\Vert , \quad \Vert v\Vert _{\infty }\le C_{\Omega }\Vert \Delta _hv\Vert . \end{aligned}$$

(2.1)

2.1 A Fast Variant of the L1 Formula

On our nonuniform mesh, the standard L1 approximation of the Caputo derivative is

$$\begin{aligned} (D^{\alpha }_\tau v)^n:=\sum _{k=1}^n\frac{1}{\tau _k}\int _{t_{k-1}}^{t_{k}}\omega _{1-\alpha }(t_n-s)\nabla _{\tau } v^k\,\mathrm {d}s = \sum _{k=1}^na_{n-k}^{(n)}\nabla _{\tau }v^k, \end{aligned}$$

(2.2)

where $\nabla _{\tau }v^k:=v^k-v^{k-1}$ and the convolution kernel $a_{n-k}^{(n)}$ is defined by

$$\begin{aligned} a_{n-k}^{(n)}:=\frac{1}{\tau _k}\int _{t_{k-1}}^{t_{k}}\!\!\omega _{1-\alpha }(t_n-s)\,\mathrm {d}s =\frac{1}{\tau _k}\left[ \omega _{2-\alpha }(t_n-t_{k-1})-\omega _{2-\alpha }(t_n-t_{k})\right] ,\quad 1\le k\le n. \end{aligned}$$

(2.3)

Lemma 2.1

For any fixed integer $n\ge 2$, the convolution kernel $a^{(n)}_{n-k}$ of (2.3) satisfies

• (i) $\displaystyle a_{n-k-1}^{(n)}>\omega _{1-\alpha }(t_n-t_{k})>a_{n-k}^{(n)},\quad 1\le k\le n-1;$

• (ii) $\displaystyle a^{(n)}_{n-k-1}-a^{(n)}_{n-k}>\tfrac{1}{2}\left[ \omega _{1-\alpha }(t_{n}-t_k) -\omega _{1-\alpha }(t_{n}-t_{k-1})\right] ,\quad 1\le k\le n-1.$

Proof

The integral mean value theorem yields

$$\begin{aligned} a^{(n)}_{n-k} = \frac{1}{\tau _k}\int _{t_{k-1}}^{t_k} \omega _{1-\alpha }(t_n-s)d{s} =\omega _{1-\alpha }(t_n-s_k)\quad \text {for some } s_k\in (t_{k-1},t_k), \end{aligned}$$

which implies the result (i) directly since the kernel $\omega _{1-\alpha }$ is decreasing, also see [14, 23]. For any function $q\in C^2[t_{k-1},t_{k}]$, let $\Pi _{1,k}q$ be the linear interpolant of q(t) at $t_{k-1}$ and $t_k$. Let

$$\begin{aligned} \widetilde{\Pi _{1,k}}q := q - \Pi _{1,k}q \end{aligned}$$

be the error in this interpolant. For $q(s)=\omega _{1-\alpha }(t_{n}-s)$ one has $q^{\prime \prime }(s)=\omega _{-\alpha -1}(t_{n}-s)>0$ for $0<s<t_n$, so the Peano representation of the interpolation error [14, Lemma 3.1] shows that

$$\begin{aligned} \int _{t_{k-1}}^{t_{k}}\big (\widetilde{\Pi _{1,k}}q\big )(s)\,\mathrm {d}s<0. \end{aligned}$$

Thus the definition (2.3) of $a^{(n)}_{n-k}$ yields

$$\begin{aligned}&a^{(n)}_{n-k}-\frac{1}{2}\omega _{1-\alpha }(t_{n}-t_k) -\frac{1}{2}\omega _{1-\alpha }(t_{n}-t_{k-1})\\&\quad =\frac{1}{\tau _k}\int _{t_{k-1}}^{t_{k}}\big (\widetilde{\Pi _{1,k}}q\big )(s)\,\mathrm {d}s<0,\quad 1\le k\le n-1. \end{aligned}$$

Subtract this inequality from (i) to obtain (ii) immediately. $\square$

One can see that the direct evaluation of the L1 formula (2.2) is quite inefficient as it requires the information of solutions at all previous time levels while solving problem (1.1). This motivates us to develop a fast L1 formula based on the SOEs approach given in [4, 10, 22]. A basic result of SOE approximation (see [4, Theorem 2.5] or [22, Lemma 2.2]) is as follows:

Lemma 2.2

Given $\alpha \in (0,1)$, an absolute tolerance error $\epsilon \ll 1$, a cut-off time $\Delta {t}>0$ and a final time T, there exists a positive integer $N_{q}$, positive quadrature nodes $\theta ^{\ell }$ and positive weights $\varpi ^{\ell }$$(1\le \ell \le N_q)$ such that

$$\begin{aligned} \Big |\omega _{1-\alpha }(t)-\sum _{\ell =1}^{N_q}\varpi ^{\ell }e^{-\theta ^{\ell }t}\Big | \le \epsilon \quad \forall \, t\in [\Delta {t},T], \end{aligned}$$

where the number $N_q$ of quadrature nodes satisfies

$$\begin{aligned} N_q=O\left( \log \frac{1}{\epsilon }\Big (\log \log \frac{1}{\epsilon } +\log \frac{T}{\Delta {t}}\Big ) +\log \frac{1}{\Delta {t}}\Big (\log \log \frac{1}{\epsilon } +\log \frac{1}{\Delta {t}}\Big )\right) . \end{aligned}$$

To design the fast L1 algorithm, we divide the Caputo derivative $({\mathcal {D}}^{\alpha }_tv)(t_n)$ of (1.2) into a sum of a local part (an integral over $[t_{n-1}, t_n]$) and a history part (an integral over $[0, t_{n-1}]$), and approximate $v^{\prime }$ by linear interpolation in the local part (as the same as the standard L1 method) and use the SOE technique of Lemma 2.2 to approximate the kernel $\omega _{1-\alpha } (t-s)$ in the history part. It arrives at

$$\begin{aligned} \big ({\mathcal {D}}^{\alpha }_tu\big )(t_n)&\approx \int _{t_{n-1}}^{t_{n}}\omega _{1-\alpha }(t_n-s) \frac{\nabla _{\tau }u^n}{\tau _n}\,\mathrm {d}s +\int _0^{t_{n-1}}\sum _{\ell =1}^{N_q}\varpi ^{\ell }e^{-\theta ^{\ell } (t_n-s)}u^{\prime }(s)\,\mathrm {d}s\\&=a_{0}^{(n)}\nabla _{\tau }u^n+\sum _{\ell =1}^{N_q} \varpi ^{\ell }e^{-\theta ^{\ell }\tau _n}{\mathcal {H}}^{\ell }(t_{n-1}), \quad n\ge 1, \end{aligned}$$

where ${\mathcal {H}}^{\ell }(t_k) := \int _0^{t_{k}}e^{-\theta ^{\ell }(t_k-s)}u^{\prime }(s)\,\mathrm {d}s$ with ${\mathcal {H}}^{\ell }(t_0)=0$ for $1\le \ell \le N_q\,$. To compute ${\mathcal {H}}^{\ell }(t_k)$ efficiently we apply linear interpolation in each cell $[t_{k-1}, t_{k}]$ to have

$$\begin{aligned} {\mathcal {H}}^{\ell }(t_{k})=&\,e^{-\theta ^{\ell }\tau _{k}}{\mathcal {H}}^{\ell }(t_{k-1}) +\int _{t_{k-1}}^{t_{k}}e^{-\theta ^{\ell }(t_{k}-s)}u^{\prime }(s)\,\mathrm {d}s \approx e^{-\theta ^{\ell }\tau _{k}}{\mathcal {H}}^{\ell }(t_{k-1}) +b^{(k,\ell )}\nabla _{\tau }u^{k}, \end{aligned}$$

where the positive coefficient is given by

$$\begin{aligned} b^{(k,\ell )}:=\frac{1}{\tau _k}\int _{t_{k-1}}^{t_{k}}e^{-\theta ^{\ell }(t_{k}-s)}\,\mathrm {d}s, \quad k\ge 1, \;1\le \ell \le N_q. \end{aligned}$$

(2.4)

In summary, we now have the two-level fast L1 formula

$$\begin{aligned} (D^{\alpha }_fu)^n:=a_{0}^{(n)}\nabla _{\tau }u^n+\sum _{\ell =1}^{N_q}\varpi ^{\ell } e^{-\theta ^{\ell }\tau _n}H^{\ell }(t_{n-1}), \quad n\ge 1, \end{aligned}$$

(2.5a)

where $H^{\ell }(t_{k})$ satisfies $H^{\ell }(t_{0})=0$ and the recurrence relationship

$$\begin{aligned} H^{\ell }(t_{k})=e^{-\theta ^{\ell }\tau _{k}}H^{\ell }(t_{k-1}) +b^{(k,\ell )}\nabla _{\tau }u^{k},\quad k\ge 1, \;1\le \ell \le N_q. \end{aligned}$$

(2.5b)

2.2 The Two-Level Linearized Scheme

Let $U_{h}^n=u(\varvec{x}_h,t_n)$ for $\varvec{x}_h\in {\bar{\Omega }}_h$, $0\le n\le N$, and $u_{h}^n$ be the discrete approximation of $U_{h}^n$. Using the fast L1 formula (2.5) and the Newton linearization, we obtain a linearized scheme for problem (1.1): find $\{u_h^{N}\}\in {\mathcal {V}}_{h}$ such that

$$\begin{aligned} (D^{\alpha }_fu_h)^n&=\Delta _hu_h^n+f(u_h^{n-1}) +f^{\prime }(u_h^{n-1})\nabla _{\tau }u_h^{n},\quad \varvec{x}_h\in \Omega _h, \; 1\le n\le N; \end{aligned}$$

(2.6a)

$$\begin{aligned} u_h^0&=u^0(\varvec{x}_h),\quad \varvec{x}_h\in {\bar{\Omega }}_h. \end{aligned}$$

(2.6b)

The Newton linearization of a general nonlinear function $f=f(\varvec{x},t,u)$ at $t=t_n$ is taken as the form

$$\begin{aligned} f(\varvec{x}_h,t_n,u_h^n)\approx f(\varvec{x}_h,t_n,u_h^{n-1}) +f_u^{\prime }(\varvec{x}_h,t_n,u_h^{n-1})\nabla _{\tau }u_h^{n}. \end{aligned}$$

The scheme (2.6) is a two-level procedure for computing $\{u_h^{n}\}$, because (2.6a) can be equivalently reformulated as

$$\begin{aligned} \left[ a_{0}^{(n)}-\Delta _h-f^{\prime }(u_h^{n-1})\right] \nabla _{\tau }u_h^{n}&=\Delta _hu_h^{n-1}+f(u_h^{n-1}) -\sum _{\ell =1}^{N_q}\varpi ^{\ell }e^{-\theta ^{\ell }\tau _n}H_h^{\ell } (t_{n-1}), \end{aligned}$$

(2.7)

$$\begin{aligned} H_h^{\ell }(t_{n})&=e^{-\theta ^{\ell }\tau _{n}}H_h^{\ell }(t_{n-1}) +b^{(n,\ell )}\nabla _{\tau }u_h^{n},\quad 1\le \ell \le N_q. \end{aligned}$$

(2.8)

Thus, once the values $\{u_h^{n-1},\;H_h^{\ell }(t_{n-1})\}$ at the previous time-level $t_{n-1}$ are available, the current solution $\{u_h^{n}\}$ can be found by (2.7) with a fast matrix solver and the historic term $\{H_h^{\ell }(t_{n})\}$ will be updated explicitly by the recurrence formula (2.8).

Remark 2.3

At each time level the scheme (2.6) requires $O(MN_q)$ storage and $O(MN_q)$ operations, where $M=M_1M_2$ is the total number of spatial grid points. Given a tolerance error $\epsilon _0$, by virtue of Lemma 2.2, the number of quadrature nodes $N_q=O(\log N)$ if the final time $T\gg 1$. Hence our fast method is efficient for long time simulations since it computes the final solution using in total $O(M\log N)$ storage and $O(MN\log N)$ operations.

2.3 Discrete Fractional Grönwall Inequality

Our analysis relies on a generalized discrete fractional Grönwall inequality developed in [15], which is applicable for any discrete fractional derivative having the discrete convolution form 

$$\begin{aligned} ({\mathcal {D}}^{\alpha }_tv)^n \approx \sum _{k=1}^n A^{(n)}_{n-k}(v^k-v^{k-1}),\quad 1\le n\le N, \end{aligned}$$

(2.9)

provided that $A^{(n)}_{n-k}$ and the time-steps $\tau _n$ satisfy the following three assumptions:

Ass1 :

The discrete kernel is monotone, that is,

$$\begin{aligned} A^{(n)}_{k-2}\ge A^{(n)}_{k-1}>0\quad \text {for }2\le k\le n\le N. \end{aligned}$$

Ass2 :

There is a constant $\pi _A>0$ such that

$$\begin{aligned} A^{(n)}_{n-k}\ge \frac{1}{\pi _A}\int _{t_{k-1}}^{t_k} \frac{\omega _{1-\alpha }(t_n-s)}{\tau _k}\,\mathrm {d}{s}\quad \text {for }1\le k\le n\le N. \end{aligned}$$

Ass3 :

There is a constant $\rho >0$ such that the time-step ratios

$$\begin{aligned} \rho _k\le \rho \quad \text {for }1\le k\le N-1. \end{aligned}$$

The complementary discrete kernel $P^{(n)}_{n-k}$ was introduced by Liao et al. [14, 15]; it satisfies the following identity

$$\begin{aligned} \sum _{j=k}^nP^{(n)}_{n-j}A^{(j)}_{j-k}\equiv 1\quad \text {for }1\le k\le n\le N. \end{aligned}$$

(2.10)

Rearranging this identity yields a recursive formula that defines $P^{(n)}_{n-k}$ :

$$\begin{aligned}&P_{0}^{(n)}:=1/{A_0^{(n)}},\nonumber \\&P_{n-j}^{(n)}:=1/{A_0^{(j)}} \sum _{k=j+1}^{n}\Big (A_{k-j-1}^{(k)}-A_{k-j}^{(k)}\Big )P_{n-k}^{(n)},\quad 1\le j\le n-1. \end{aligned}$$

(2.11)

From [15, Lemma 2.2] one can see that $P^{(n)}_{n-k}$ is well-defined and non-negative if the assumption Ass1 holds true. Furthermore, if Ass2 holds true, then

$$\begin{aligned} \sum _{j=1}^nP^{(n)}_{n-j}\le \pi _A\,\omega _{1+\alpha }(t_n)\quad \text {for }1\le n\le N. \end{aligned}$$

(2.12)

Recall that the Mittag–Leffler function $E_\alpha (z) = \sum _{k=0}^\infty \frac{z^k}{\Gamma (1+k\alpha )}$. We state the following (slightly simplified) version of [15, Theorem 3.2]. This result differs substantially from the fractional Grönwall inequality of Jin et al. [5, Theorem 4] since it is valid on very general nonuniform time meshes.

Theorem 2.4

Let Ass1–Ass3 hold true. Suppose that the sequences $(\xi _1^n)_{n=1}^N$, $(\xi _2^n)_{n=1}^N$ are nonnegative. Assume that $\lambda _0$ and $\lambda _1$ are non-negative constants and the maximum step size $\tau \le 1/\root \alpha \of {2\pi _A\Gamma (2-\alpha )(\lambda _0+\lambda _1)}$. If the nonnegative sequence $(v^k)_{k=0}^N$ satisfies

$$\begin{aligned} \sum _{k=1}^nA^{(n)}_{n-k}\nabla _\tau v^k\le \lambda _{0}v^{n}+\lambda _1v^{n-1}+\xi _1^n+\xi _2^n\quad \text {for } 1\le n\le N, \end{aligned}$$

then it holds that for $1\le n\le N$,

$$\begin{aligned} v^n\le 2 E_\alpha \big (2\max \{1,\rho \}\pi _A(\lambda _0+\lambda _1)t_n^\alpha \big ) \biggl (v^0+\max _{1\le k\le n}\sum _{j=1}^k P^{(k)}_{k-j}\xi _1^j +\pi _A\omega _{1+\alpha }(t_n)\max _{1\le j\le n}\xi _2^j\biggr ). \end{aligned}$$

To facilitate our analysis, we now eliminate the historic term $H^{\ell }(t_{n})$ from the fast L1 formula (2.5a) for $(D^{\alpha }_fu)^n$. From the recurrence relationship (2.5b), it is easy to see that

$$\begin{aligned} H^{\ell }(t_{k})=\sum _{j=1}^ke^{-\theta ^{\ell }(t_{k}-t_{j})} b^{(j,\ell )}\nabla _{\tau }u^{j},\quad k\ge 1, \; 1\le \ell \le N_q. \end{aligned}$$

Inserting this in (2.5a) and using the definition (2.4), one obtains the alternative formula

$$\begin{aligned}&(D^{\alpha }_fu)^n =a_{0}^{(n)}\nabla _{\tau }u^n+\sum _{k=1}^{n-1} \frac{\nabla _{\tau }u^{k}}{\tau _k} \int _{t_{k-1}}^{t_{k}}\sum _{\ell =1}^{N_q}\varpi ^{\ell } e^{-\theta ^{\ell }(t_{n}-s)}\,\mathrm {d}s\nonumber \\ {}&\quad = \sum _{k=1}^{n}A_{n-k}^{(n)}\nabla _{\tau }u^{k}, \quad n\ge 1, \end{aligned}$$

(2.13)

where the discrete convolution kernel $A_{n-k}^{(n)}$ is henceforth given as

$$\begin{aligned} A_{0}^{(n)}:=a_{0}^{(n)}, \quad A_{n-k}^{(n)}:=\frac{1}{\tau _k}\int _{t_{k-1}}^{t_{k}} \sum _{\ell =1}^{N_q}\varpi ^{\ell }e^{-\theta ^{\ell }(t_{n}-s)}\,\mathrm {d}s, \quad 1\le k\le n-1,\; n\ge 1. \end{aligned}$$

(2.14)

The formula (2.13) takes the form of (2.9), and we now verify that our $A_{n-k}^{(n)}$ defined by (2.14) satisfy Ass1 and Ass2, allowing us to apply Theorem 2.4 and establish the convergence of our computed solution. Part (I) of the next lemma ensures that Ass1 is valid, while part (II) implies that Ass2 holds true with $\pi _A=\frac{3}{2}$.

Lemma 2.5

If the tolerance error $\epsilon$ of SOE satisfies $\epsilon \le \min \left\{ \frac{1}{3}\omega _{1-\alpha }(T),\alpha \,\omega _{2-\alpha }(T)\right\}$, then the discrete convolutional kernel $A_{n-k}^{(n)}$ of (2.14) satisfies

• (I) $A_{k-1}^{(n)}>A_{k}^{(n)}>0,\;\;1\le k\le n-1;$

• (II) $A_{0}^{(n)}=a_{0}^{(n)}$ and $A_{n-k}^{(n)}\ge \frac{2}{3}a_{n-k}^{(n)},\;\; 1\le k\le n-1.$

Proof

The definition (2.3) and Lemma 2.1 (i) yield

$$\begin{aligned} a_{0}^{(n)}-a_{1}^{(n)}>a_{0}^{(n)}-\omega _{1-\alpha }(\tau _n) =\tfrac{\alpha }{\tau _n}\omega _{2-\alpha }(\tau _n)\ge \alpha \,\omega _{2-\alpha }(T)\ge \epsilon . \end{aligned}$$

The definition (2.14) and Lemma 2.2 imply that $A_{0}^{(n)}=a_{0}^{(n)}>a_{1}^{(n)}+\epsilon >A_{1}^{(n)}$. Lemma 2.2 also shows that $\theta ^{\ell }, \varpi ^{\ell }>0$ for $\ell =1,\dots , N_q$; the mean-value theorem now yields property (I). By Lemma 2.1 (i) and our hypothesis on $\epsilon$ we have

$$\begin{aligned} \epsilon \le \frac{1}{3}\omega _{-\alpha }(t_n)<\frac{1}{3}a_{n-1}^{(n)}\le \frac{1}{3}a_{n-k}^{(n)},\quad 1\le k\le n-1. \end{aligned}$$

Hence Lemma 2.2 gives

$$\begin{aligned} A_{n-k}^{(n)}\ge a_{n-k}^{(n)}-\epsilon \ge \frac{2}{3}a_{n-k}^{(n)}\quad \text { for } 1\le k\le n-1. \end{aligned}$$

The proof is complete. $\square$

3 Global Consistency Error Analysis

We now proceed with the consistency error analysis of our fast linearized method, and begin with the consistency error of the standard L1 formula $(D^{\alpha }_\tau u)^n$ of (2.2).

Lemma 3.1

For $v\in C^2(0,T]$ with $\int _0^T t \,|v^{\prime \prime }(t)|\,\mathrm {d}s < \infty$, one has

$$\begin{aligned} \big |({\mathcal {D}}^{\alpha }_tv)(t_n)-(D^{\alpha }_\tau v)^n\big |\le a_{0}^{(n)}G^n+\sum _{k=1}^{n-1}\big (a_{n-k-1}^{(n)}-a_{n-k}^{(n)}\big )G^k,\quad n\ge 1, \end{aligned}$$

where the L1 kernel $a_{n-k}^{(n)}$ is defined by (2.3) and $G^k :=2\int _{t_{k-1}}^{t_k}\left( t-t_{k-1}\right) \left| v^{\prime \prime }(t)\right| \,\mathrm {d}t$.

Proof

From Taylor’s formula with integral remainder, the truncation error of the standard L1 formula at time $t=t_n$ is (see [14, Lemma 3.3])

$$\begin{aligned} ({\mathcal {D}}^{\alpha }_tv)(t_n)-(D^{\alpha }_\tau v)^n&=\sum _{k=1}^n\int _{t_{k-1}}^{t_k}\omega _{1-\alpha }(t_n-s)\left( v^{\prime }(s)-\nabla _\tau v^k/\tau _k\right) \,\mathrm {d}s\nonumber \\&=\sum _{k=1}^n\int _{t_{k-1}}^{t_k}v^{\prime \prime }(t)\, \big (\widetilde{\Pi _{1,k}}Q\big )(t)\,\mathrm {d}{t},\quad n\ge 1, \end{aligned}$$

(3.1)

where $Q(t)=\omega _{2-\alpha }(t_n-t)$ and we use the notation of the proof of Lemma 2.1. By the error formula for linear interpolation [14, Lemma 3.1], we have

$$\begin{aligned} \big (\widetilde{\Pi _{1,k}}Q\big )(t)=\int _{t_{k-1}}^{t_k}\chi _k(t,y)Q^{\prime \prime }(y)\,\mathrm {d}{y},\quad t_{k-1}<t<t_k,\;1\le k\le n, \end{aligned}$$

where the Peano kernel $\chi _k(t,y)=\max \{t-y,0\}-\frac{t-t_{k-1}}{\tau _k}(t_{k}-y)$ satisfies

$$\begin{aligned} -\tfrac{t-t_{k-1}}{\tau _k}(t_{k}-t)\le \chi _k(t,y)<0\qquad \text {for any }t,y\in (t_{k-1},t_k). \end{aligned}$$

Observing that for each fixed $n\ge 1$ the function Q is decreasing and $Q^{\prime \prime }(t)=\omega _{-\alpha }(t_n-t)<0$, we arrive at the interpolation error $\big (\widetilde{\Pi _{1,k}}Q\big )(t)\ge 0$ for $1\le k\le n$, with

$$\begin{aligned} \big (\widetilde{\Pi _{1,n}}Q\big )(t)&\le Q(t_{n-1})-\big (\Pi _{1,n}Q\big )(t)=(t-t_{n-1})a_{0}^{(n)},\\ \big (\widetilde{\Pi _{1,k}}Q\big )(t)&\le (t_{k-1}-t)\int _{t_{k-1}}^{t_k}Q^{\prime \prime }(t)\,\mathrm {d}{t} \le (t-t_{k-1})\big [\omega _{1-\alpha }(t_n-t_{k})-\omega _{1-\alpha } (t_n-t_{k-1})\big ]\nonumber \\&\le 2(t-t_{k-1})\big (a_{n-k-1}^{(n)}-a_{n-k}^{(n)}\big ),\quad t\in (t_{k-1},t_{k}), \; 1\le k\le n-1, \end{aligned}$$

where Lemma 2.1 (ii) is used in the last inequality. Thus, (3.1) yields

$$\begin{aligned}&\big |({\mathcal {D}}^{\alpha }_tv)(t_n)-(D^{\alpha }_\tau v)^n\big | \le \int _{t_{n-1}}^{t_n}\left| v^{\prime \prime }(t)\right| \big (\widetilde{\Pi _{1,n}}Q\big )(t)\,\mathrm {d}{t} +\sum _{k=1}^{n-1}\int _{t_{k-1}}^{t_k}\left| v^{\prime \prime }(t)\right| \big (\widetilde{\Pi _{1,k}}Q\big )(t)\,\mathrm {d}{t}\\&\quad \le a_{0}^{(n)}\int _{t_{n-1}}^{t_n}\!\!(t-t_{n-1}) \left| v^{\prime \prime }(t)\right| \!\,\mathrm {d}{t} +2\sum _{k=1}^{n-1}\big (a_{n-k-1}^{(n)}-a_{n-k}^{(n)}\big ) \int _{t_{k-1}}^{t_k}\!\!(t-t_{k-1})\left| v^{\prime \prime }(t)\right| \!\,\mathrm {d}{t}, \end{aligned}$$

and the desired result follows from the definition of $G^k$. $\square$

Remark 3.2

Compared with the previous estimate in [14, Lemma 3.3], Lemma 3.1 removes the restriction of time-step ratios $\rho _k\le 1$, which is an undesirable restriction on the mesh for problems that allow the rapid growth of the solution at the time far away from $t=0$.

We now focus on the fast L1 method by taking the initial singularity into account. Here and hereafter, we denote ${\hat{T}}=\max \{1,T\}$ and ${\hat{t}}_{n}=\max \{1,t_{n}\}$ for $1\le n\le N$. Next lemma presents the estimate of the global consistency error $\sum _{j=1}^nP_{n-j}^{(n)}\big |\Upsilon ^j\big |$ accumulating from $t=t_1$ to $t=t_n$ with the discrete convolution kernel $P_{n-j}^{(n)}$.

Lemma 3.3

Assume that $v\in C^2((0,T])$ and that there exists a constant $C_v>0$ such that

$$\begin{aligned} \big |v^{\prime }(t)\big |\le C_v (1+t^{\sigma -1}),\quad \big |v^{\prime \prime }(t)\big |\le C_v (1+t^{\sigma -2}), \quad 0<t\le T, \end{aligned}$$

(3.2)

where $\sigma \in (0,1)\cup (1,2)$ is a parameter. Let

$$\begin{aligned} \Upsilon ^j :=({\mathcal {D}}^{\alpha }_tv)(t_j)- (D^{\alpha }_fv)^j \end{aligned}$$

denote the local consistency error of the fast L1 formula (2.13). Assume that the SOE tolerance error satisfies $\epsilon \le \frac{1}{3}\min \{\omega _{1-\alpha }(T),3\alpha \,\omega _{2-\alpha }(T)\}$. Then the global consistency error can be bounded by

$$\begin{aligned} \sum _{j=1}^nP_{n-j}^{(n)}\big |\Upsilon ^j\big |&\le C_v\Big (\frac{\tau _1^{\sigma }}{\sigma }+ \frac{1}{1-\alpha }\max _{2\le k\le n}(t_{k}-t_1)^{\alpha }t_{k-1}^{\sigma -2}\tau _k^{2-\alpha } +\frac{\epsilon }{\sigma }t_{n}^{\alpha }{\hat{t}}_{n-1}^{\,2}\Big ) \end{aligned}$$

(3.3)

for $1\le n\le N$. Moreover, if the mesh satisfies AssG, then

$$\begin{aligned} \sum _{j=1}^nP_{n-j}^{(n)}\big |\Upsilon ^j\big |&\le \frac{C_v}{\sigma (1-\alpha )}\tau ^{\min \{2-\alpha ,\gamma \sigma \}} +\frac{\epsilon }{\sigma }C_vt_{n}^{\alpha }{\hat{t}}_{n-1}^{\,2},\quad 1\le n\le N. \end{aligned}$$

Proof

The main difference between the fast L1 formula (2.13) and the standard L1 formula (2.2) is that the convolution kernel is approximated by SOEs with an absolute tolerance error $\epsilon$. Thus, comparing the standard L1 formula (2.2) with the corresponding fast L1 formula (2.13), by Lemma 2.2 and the regularity assumption (3.2) one has

$$\begin{aligned} \big | (D^{\alpha }_fv)^j -(D^{\alpha }_\tau v)^j\big |&\le \sum _{k=1}^{j-1}\frac{\big |\nabla _{\tau }v^{k}\big |}{\tau _k} \int _{t_{k-1}}^{t_{k}} \Big |\sum _{\ell =1}^{N_q}\varpi ^{\ell }e^{-\theta ^{\ell }(t_{j}-s)} -\omega _{1-\alpha }(t_j-s)\Big |\,\mathrm {d}s,\\&\le \epsilon \sum _{k=1}^{j-1}\int _{t_{k-1}}^{t_{k}}\left| v^{\prime }(s)\right| \,\mathrm {d}s \le C_v \big (t_{j-1} + t_{j-1}^{\sigma }/\sigma \big )\epsilon \le \frac{C_v}{\sigma }{\hat{t}}_{j-1}^{\,2}\epsilon , \quad j\ge 1. \end{aligned}$$

Lemma 2.2 implies that $\big |A_{n-k}^{(n)}-a_{n-k}^{(n)}\big |\le \epsilon$ for $1\le k\le n-1$. Recalling that $A_{0}^{(n)}=a_{0}^{(n)}$, one has

$$\begin{aligned} a_{j-k-1}^{(j)}-a_{j-k}^{(j)}\le A_{j-k-1}^{(j)}-A_{j-k}^{(j)}+2\epsilon ,\quad 1\le k\le j-1. \end{aligned}$$

Then Lemma 3.1 and the regularity assumption (3.2) lead to

$$\begin{aligned} \left| ({\mathcal {D}}^{\alpha }_tv)(t_j)-(D^{\alpha }_\tau v)^j\right|&\le A_{0}^{(j)}G^j+\sum _{k=1}^{j-1}\big (A_{j-k-1}^{(j)}-A_{j-k}^{(j)}\big )G^k+2\epsilon \sum _{k=1}^{j-1}G^k\\&\le A_{0}^{(j)}G^j+\sum _{k=1}^{j-1}\big (A_{j-k-1}^{(j)}-A_{j-k}^{(j)}\big )G^k +4\epsilon \sum _{k=1}^{j-1}\int _{t_{k-1}}^{t_k}t\left| v^{\prime \prime }(t)\right| \,\mathrm {d}{t}\\&\le A_{0}^{(j)}G^j+\sum _{k=1}^{j-1}\big (A_{j-k-1}^{(j)}-A_{j-k}^{(j)}\big )G^k +\frac{C_v}{\sigma }{\hat{t}}_{j-1}^{\,2}\epsilon ,\quad j\ge 1. \end{aligned}$$

Now a triangle inequality gives

$$\begin{aligned} \big |\Upsilon ^j\big | \le A_{0}^{(j)}G^j+\sum _{k=1}^{j-1}\big (A_{j-k-1}^{(j)}-A_{j-k}^{(j)}\big )G^k + \frac{C_v}{\sigma }{\hat{t}}_{j-1}^{\,2}\epsilon ,\quad j\ge 1. \end{aligned}$$

(3.4)

Multiplying the above inequality (3.4) by $P_{n-j}^{(n)}$ and summing the index j from 1 to n, one can exchange the order of summation and apply the definition (2.11) of $P_{n-j}^{(n)}$ to obtain

$$\begin{aligned} \sum _{j=1}^nP_{n-j}^{(n)}\,\big |\Upsilon ^j\big |&\le \sum _{j=1}^nP_{n-j}^{(n)}A_0^{(j)}G^j+ \sum _{j=2}^nP_{n-j}^{(n)}\sum _{k=1}^{j-1} \big (A_{j-k-1}^{(j)}-A_{j-k}^{(j)}\big )G^k\nonumber \\&\quad +C_v\frac{\epsilon }{\sigma }\sum _{j=2}^nP_{n-j}^{(n)} {\hat{t}}_{j-1}^{\,2}\nonumber \\&=\sum _{j=1}^nG^jP_{n-j}^{(n)}A_0^{(j)} +\sum _{k=1}^{n-1}G^k\sum _{j=k+1}^nP_{n-j}^{(n)} \big (A_{j-k-1}^{(j)}-A_{j-k}^{(j)}\big )\nonumber \\&\quad +C_v{\hat{t}}_{n-1}^{\,2}\frac{\epsilon }{\sigma } \sum _{j=2}^nP_{n-j}^{(n)}\nonumber \\&\le \sum _{k=1}^{n}P_{n-k}^{(n)}A_{0}^{(k)}G^k+ \sum _{k=1}^{n-1}P_{n-k}^{(n)}A_{0}^{(k)}G^k +\frac{C_v}{\sigma }t_{n}^{\alpha }{\hat{t}}_{n-1}^{\,2}\epsilon , \end{aligned}$$

(3.5)

where the property (2.12) with $\pi _A=3/2$ is used in the last inequality. If the SOE approximation error $\epsilon \le \frac{1}{3}\min \{\omega _{1-\alpha }(T),3\alpha \,\omega _{2-\alpha }(T)\},$ Lemma 2.5 (II) and Lemma 2.1 (i) imply that

$$\begin{aligned} A_{0}^{(k)}=a_{0}^{(k)}=\omega _{2-\alpha }(\tau _k)/\tau _k,\quad A_{k-2}^{(k)}\ge \tfrac{2}{3}a_{k-2}^{(k)}\ge \tfrac{2}{3}\omega _{1-\alpha }(t_k-t_1), \end{aligned}$$

and then

$$\begin{aligned} A_{0}^{(k)}/{A_{k-2}^{(k)}}\le \tfrac{3}{2(1-\alpha )}(t_k-t_1)^{\alpha }\tau _k^{-\alpha },\quad 2\le k\le n\le N. \end{aligned}$$

Furthermore, the identical property (2.10) for the complementary kernel $P^{(n)}_{n-j}$ gives

$$\begin{aligned} P_{n-1}^{(n)}A_{0}^{(1)}\le 1\quad \text{ and }\quad \sum _{k=2}^{n-1}P_{n-k}^{(n)}A_{k-2}^{(k)} \le \sum _{k=2}^{n}P_{n-k}^{(n)}A_{k-2}^{(k)}=1. \end{aligned}$$

The regularity assumption (3.2) gives

$$\begin{aligned} G^1\le C_v\tau _1^{\sigma }/\sigma \quad \text { and}\quad G^k\le C_vt_{k-1}^{\sigma -2}\tau _k^2\quad \text {for }2\le k\le n. \end{aligned}$$

Thus it follows from (3.5) that

$$\begin{aligned} \sum _{j=1}^nP_{n-j}^{(n)}\big |\Upsilon ^j\big |&\le 2G^1+2 \sum _{k=2}^{n}P_{n-k}^{(n)}A_{0}^{(k)}G^k +\frac{C_v}{\sigma }t_{n}^{\alpha }{\hat{t}}_{n-1}^{\,2}\epsilon \\&\le C_v\frac{\tau _1^{\sigma }}{\sigma }+\frac{C_v}{1-\alpha } \sum _{k=2}^{n}P_{n-k}^{(n)}A_{k-2}^{(k)} (t_{k}-t_1)^{\alpha }t_{k-1}^{\sigma -2}\tau _k^{2-\alpha } +\frac{C_v}{\sigma }t_{n}^{\alpha }{\hat{t}}_{n-1}^{\,2}\epsilon \\&\le C_v\Big (\frac{\tau _1^{\sigma }}{\sigma } +\frac{1}{1-\alpha }\max _{2\le k\le n}(t_{k}-t_1)^{\alpha }t_{k-1}^{\sigma -2}\tau _k^{2-\alpha } +\frac{1}{\sigma }t_{n}^{\alpha }{\hat{t}}_{n-1}^{\,2}\epsilon \Big ),\quad 1\le n\le N. \end{aligned}$$

The claimed estimate (3.3) is verified. In particular, if AssG holds, one has

$$\begin{aligned} t_{k}^{\alpha }t_{k-1}^{\sigma -2}\tau _k^{2-\alpha }&\le C_{\gamma }t_k^{\sigma -2+\alpha }\tau _k^{2-\alpha -\beta }\tau ^{\beta } \min \{1,t_k^{\beta -\beta /\gamma }\}\\&\le C_{\gamma }t_k^{\sigma -\beta /\gamma }\big (\tau _k/t_k\big )^{2-\alpha -\beta } \tau ^{\beta } \le C_{\gamma }t_k^{\max \{0,\sigma -(2-\alpha )\gamma \}}\tau ^{\beta },\quad 2\le k\le N, \end{aligned}$$

where $\beta =\min \{2-\alpha ,\gamma \sigma \}$. The final estimate follows since $\tau _1^{\sigma }\le C_{\gamma }\tau ^{\gamma \sigma }\le C_{\gamma }\tau ^{\beta }$. $\square$

Next lemma describes the global consistency error of Newton’s linearized approach, which is smaller than that generated by the above L1 approximation. In addition, there is no error in the linearized approximation if $f=f(u)$ is a linear function.

Lemma 3.4

Assume that $v\in C([0,T])\cap C^2((0,T])$ satisfies the regularity condition (3.2), and the nonlinear function $f=f(u)\in C^2({\mathbb {R}})$. Denote $v^n=v(t_n)$ and the local truncation error

$$\begin{aligned} {\mathcal {R}}_f^n=f(v^n)-f(v^{n-1})-f^{\prime }(v^{n-1})\nabla _{\tau }v^{n} \end{aligned}$$

such that the global consistency error

$$\begin{aligned} \sum _{j=1}^nP_{n-j}^{(n)}\big |{\mathcal {R}}_f^j\big |\le C_v\tau _1^{\alpha }\left( \tau _1^{2}+\tau _1^{2\sigma }/\sigma ^2\right) +C_vt_n^{\alpha }\max _{2\le j\le n} \big (\tau _j^2+t_{j-1}^{2\sigma -2}\tau _j^{2}\big ),\quad 1\le n\le N. \end{aligned}$$

Moreover, if the assumption AssG holds, one has

$$\begin{aligned} \sum _{j=1}^nP_{n-j}^{(n)}\big |{\mathcal {R}}_f^j\big | \le \,C_v\tau ^{\min \{2,2\gamma \sigma \}} \max \{1,\tau ^{\gamma \alpha }/\sigma ^2\},\quad 1\le n\le N. \end{aligned}$$

Proof

Applying the formula of Taylor expansion with integral remainder, one has

$$\begin{aligned} {\mathcal {R}}_f^j=(\nabla _{\tau }v^{j})^2\int _0^1f^{\prime \prime }\big (v^{j-1}+s\nabla _{\tau }v^{j}\big )(1-s)\,\mathrm {d}{s},\quad j\ge 1. \end{aligned}$$

Under the regularity conditions, one has

$$\begin{aligned} \big |{\mathcal {R}}_f^{1}\big |\le C_v\big (\int _{t_{0}}^{t_1} \left| v^{\prime }(t)\right| \!\,\mathrm {d}{t}\big )^2 \le C_v\left( \tau _1^{2}+\tau _1^{2\sigma }/\sigma ^2\right) , \end{aligned}$$

and

$$\begin{aligned} \big |{\mathcal {R}}_f^{j}\big |\le C_v\Big (\int _{t_{j-1}}^{t_j}\left| v^{\prime }(t)\right| \!\,\mathrm {d}{t}\Big )^2 \le C_v\big (\tau _j^2+t_{j-1}^{2\sigma -2}\tau _j^{2}\big ),\quad 2\le j\le N. \end{aligned}$$

Note that, Lemma 2.5 (II) and the definition (2.3) give $A_{0}^{(k)}=a_{0}^{(k)}=\omega _{2-\alpha }(\tau _k)/\tau _k$, so the identical property (2.10) shows

$$\begin{aligned} P_{n-1}^{(n)}\le 1/A_{0}^{(1)}\le \Gamma (2-\alpha )\tau _1^{\alpha }. \end{aligned}$$

Moreover, the bounded estimate (2.12) with $\pi _A=\frac{3}{2}$ gives

$$\begin{aligned} \sum _{j=2}^nP_{n-j}^{(n)}\le \frac{3}{2}\omega _{1+\alpha }(t_n). \end{aligned}$$

Thus, it follows that

$$\begin{aligned} \sum _{j=1}^nP_{n-j}^{(n)}\big |{\mathcal {R}}_f^j\big |&\le P_{n-1}^{(n)} \big |{\mathcal {R}}_f^1\big | +\sum _{j=2}^nP_{n-j}^{(n)}\big |{\mathcal {R}}_f^j\big | \le C_v\tau _1^{\alpha }\big |{\mathcal {R}}_f^1\big |+C_vt_n^{\alpha } \max _{2\le j\le n}\big |{\mathcal {R}}_f^j\big |\\&\le C_v\tau _1^{\alpha }\left( \tau _1^{2}+\tau _1^{2\sigma }/\sigma ^2\right) +C_vt_n^{\alpha }\max _{2\le j\le n} \big (\tau _j^2+t_{j-1}^{2\sigma -2}\tau _j^{2}\big ),\quad 1\le n\le N. \end{aligned}$$

If AssG holds, one has

$$\begin{aligned} \tau _j^2\le C_{\gamma }\tau ^{2}\min \{1,t_j^{2-2/\gamma }\}\le C_{\gamma }\tau ^{\beta }\min \{1,t_j^{2-2/\gamma }\}, \end{aligned}$$

and

$$\begin{aligned} t_{j-1}^{2\sigma -2}\tau _j^{2}&\le C_{\gamma }t_j^{2\sigma -2}\tau _j^{2-\beta }\tau ^{\beta } \min \{1,t_j^{\beta -\beta /\gamma }\}\\&\le C_{\gamma }t_j^{2\sigma -\min \{2,2\gamma \sigma \}/\gamma } \big (\tau _k/t_k\big )^{2-\beta }\tau ^{\beta } \le C_{\gamma }t_k^{\max \{0,2\sigma -2/\gamma \}}\tau ^{\beta }, \quad 2\le j\le N, \end{aligned}$$

where $\beta =\min \{2,2\gamma \sigma \}$. The second estimate follows since $\tau _1^{2\sigma }\le C_{\gamma }\tau ^{2\gamma \sigma }\le C_{\gamma }\tau ^{\beta }$. $\square$

4 Unconditional Convergence

Assume that the time mesh fulfills Ass3 and AssG in the error analysis. We here extend the discrete $H^2$ energy method in [11,12,13] to prove the unconditional convergence of discrete solutions to the two-level linearized scheme (2.6). In this section, $K_0$, $\tau ^{*}$, $\tau _0^{*}$, $\tau _1^{*}$, $h_0$, $\epsilon _0$ and any numeric subscripted c, such as $c_0$, $c_1$, $c_2$ and so on, are fixed values, which are always dependent on the given data and the continuous solution, but independent of the time-space grid steps and the inductive index k in the mathematical induction as well. To make our ideas more clearly, four steps are listed to obtain unconditional error estimate as follows.

4.1 STEP 1: Construction of Coupled Discrete System

We introduce a function $w:={\mathcal {D}}^{\alpha }_tu-f(u)$ with the initial-boundary values $w(\varvec{x},0):=\Delta u^0(\varvec{x})$ for $\varvec{x}\in \Omega$ and $w(\varvec{x},t):=-f(0)$ for $\varvec{x}\in \partial \Omega$. The problem (1.1a) can be formulated into

$$\begin{aligned} w&={\mathcal {D}}^{\alpha }_tu-f(u), \quad \varvec{x}\in {\bar{\Omega }},\; 0<t\le T;\\ w&=\Delta u,\quad \varvec{x}\in \Omega ,\; 0\le t\le T. \end{aligned}$$

Let $w_{h}^n$ be the numerical approximation of function $W_{h}^n=w(\varvec{x}_h,t_n)$ for $\varvec{x}_h\in {\bar{\Omega }}_h$. As done in subsection 2.2, one has an auxiliary discrete system: to seek $\{u_h^{n},\,w_h^n\}$ such that

$$\begin{aligned} w_h^n&=(D^{\alpha }_fu_h)^n-f(u_h^{n-1})-f^{\prime }(u_h^{n-1}) \nabla _{\tau }u_h^{n}, \quad \varvec{x}_h\in {\bar{\Omega }}_h, \; 1\le n\le N; \end{aligned}$$

(4.1)

$$\begin{aligned} w_h^n&=\Delta _hu_h^n, \quad \varvec{x}_h\in \Omega _h, \; 0\le n\le N; \end{aligned}$$

(4.2)

$$\begin{aligned} u_h^0&=u^0(\varvec{x}_h),\;\; \varvec{x}_h\in {\bar{\Omega }}_h\,;\quad u_h^n=0,\; \;\varvec{x}_h\in \partial {\Omega }_h,1\le n\le N. \end{aligned}$$

(4.3)

Obviously, by eliminating the auxiliary function $w_h^n$ in above discrete system, one directly arrives at the computational scheme (2.6). Alternately, the solution properties of two-level linearized method (2.6) can be studied via the auxiliary discrete system (4.1)–(4.3).

4.2 STEP 2: Reduction of Coupled Error System

Let ${\tilde{u}}_{h}^n=U_{h}^n-u_{h}^n$, ${\tilde{w}}_{h}^n=W_{h}^n-w_{h}^n$ be the solution errors for $\varvec{x}_h\in {\bar{\Omega }}_h$. The solution errors satisfy the governing equations as

$$\begin{aligned} {\tilde{w}}_h^n&=(D^{\alpha }_f{\tilde{u}}_h)^n-{\mathcal {N}}_h^n+\xi _h^n, \quad \varvec{x}_h\in {\bar{\Omega }}_h, \; 1\le n\le N; \end{aligned}$$

(4.4)

$$\begin{aligned} {\tilde{w}}_h^n&= \Delta _h{\tilde{u}}_h^n+\eta _h^n, \quad \varvec{x}_h\in \Omega _h, \; 0\le n\le N; \end{aligned}$$

(4.5)

$$\begin{aligned} {\tilde{u}}_h^0&= 0,\;\; \varvec{x}_h\in {\bar{\Omega }}_h\,;\quad {\tilde{u}}_h^n=0,\;\; \varvec{x}_h\in \partial {\Omega }_h,1\le n\le N, \end{aligned}$$

(4.6)

where $\xi _h^n$ and $\eta _h^n$ denote temporal and spatial truncation errors, respectively, and

$$\begin{aligned} {\mathcal {N}}_h^n&:=\,f^{\prime }(u_h^{n-1})\nabla _{\tau }{\tilde{u}}_h^{n}+f(U_h^{n-1})-f(u_h^{n-1}) +\left( f^{\prime }(U_h^{n-1})-f^{\prime }(u_h^{n-1})\right) \nabla _{\tau }U_h^{n}\nonumber \\&=f^{\prime }(u_h^{n-1})\nabla _{\tau }{\tilde{u}}_h^{n} +{\tilde{u}}_h^{n-1}\int _0^1f^{\prime }\big (s U_h^{n-1}+(1-s)u_h^{n-1}\big )\,\mathrm {d}{s}\nonumber \\&\quad +{\tilde{u}}_h^{n-1}\nabla _{\tau }U_h^{n}\int _0^1f^{\prime \prime }\big (s U_h^{n-1}+(1-s)u_h^{n-1}\big )\,\mathrm {d}{s}. \end{aligned}$$

(4.7)

Acting the difference operators $\Delta _h$ and $D^{\alpha }_f$ on the Eqs. (4.4)–(4.5), respectively, gives

$$\begin{aligned} \Delta _h{\tilde{w}}_h^n=&\,(D^{\alpha }_f\Delta _h {\tilde{u}}_h)^n-\Delta _h{\mathcal {N}}_h^n+\Delta _h\xi _h^n, \quad \varvec{x}_h\in \Omega _h, \; 1\le n\le N;\\ (D^{\alpha }_f{\tilde{w}}_h)^n=&\,(D^{\alpha }_f \Delta _h{\tilde{u}}_h)^n+(D^{\alpha }_f\eta _h)^n, \quad \varvec{x}_h\in \Omega _h, \; 1\le n\le N. \end{aligned}$$

By eliminating the term $(D^{\alpha }_f\Delta _h{\tilde{u}}_h)^n$ in the above two equations, one gets

$$\begin{aligned} (D^{\alpha }_f{\tilde{w}}_h)^n&= \Delta _h{\tilde{w}}_h^n+\Delta _h{\mathcal {N}}_h^n +(D^{\alpha }_f\eta _h)^n-\Delta _h\xi _h^n \quad \varvec{x}_h\in \Omega _h, \; 1\le n\le N; \end{aligned}$$

(4.8)

$$\begin{aligned} {\tilde{w}}_h^0&=\eta _h^0,\;\; \varvec{x}_h\in {\bar{\Omega }}_h\,;\quad {\tilde{w}}_h^n=0,\;\; \varvec{x}_h\in \partial {\Omega }_h,1\le n\le N; \end{aligned}$$

(4.9)

where the initial and boundary conditions are derived from the error system (4.4)–(4.6).

4.3 STEP 3: Continuous Analysis of Truncation Error

According to the first regularity condition in (1.3), one has

$$\begin{aligned} \big \Vert \eta ^n\big \Vert \le c_1h^2,\quad 0\le n\le N. \end{aligned}$$

(4.10)

Since the spatial error $\eta _h^n$ is defined uniformly at the time $t=t_n$ [there is no temporal error in the Eq. (4.2)], we can define a continuous function $\eta _{h}(t)$ for $\varvec{x}_h=(x_i,y_j)\in \Omega _h,$

$$\begin{aligned} \eta _{h}(t)&=\frac{h_1^2}{6}\int _0^1\big [\partial _{x}^{(4)}u(x_i-s h_1,y_j,t) +\partial _{x}^{(4)}u(x_i+s h_1,y_j,t)\big ](1-s)^3\,\mathrm {d}{s}\\&\quad +\frac{h_2^2}{6}\int _0^1\big [\partial _{y}^{(4)}u(x_i,y_j-s h_2,t) +\partial _{y}^{(4)}u(x_i,y_j+s h_2,t)\big ](1-s)^3\,\mathrm {d}{s}, \end{aligned}$$

such that $\eta _h^n=\eta _h(t_n)$. The second condition in (1.3) implies

$$\begin{aligned} \left\| \eta ^{\prime }(t)\right\| \le C_uh^2(1+t^{\sigma -1}). \end{aligned}$$

Hence, applying the fast L1 formula (2.13) and the equality (2.10), one has

$$\begin{aligned} \sum _{j=1}^nP_{n-j}^{(n)}\big \Vert (D^{\alpha }_f\eta )^j\big \Vert \le&\, \sum _{j=1}^nP_{n-j}^{(n)}\sum _{k=1}^jA_{j-k}^{(j)}\big \Vert \nabla _{\tau }\eta ^k\big \Vert =\sum _{k=1}^n\big \Vert \nabla _{\tau }\eta ^k\big \Vert \le \frac{c_2}{\sigma }{\hat{t}}_n^{\,2}h^2. \end{aligned}$$

(4.11)

Since the time truncation error $\xi _h^n$ in (4.4) is defined uniformly with respect to grid point $\varvec{x}_h\in {{\bar{\Omega }}}_h$, we can define a continuous function $\xi ^n(\varvec{x})=\xi _1^n(\varvec{x})+\xi _2^n(\varvec{x})$, where $\xi _1^n$, $\xi _2^n$ denote the truncation errors of fast L1 formula and Newton’s linearized approach, namely,

$$\begin{aligned} \xi _1^n=({\mathcal {D}}^{\alpha }_tu)(t_n)-(D^{\alpha }_fu)^n,\quad \xi _2^n=\big (\nabla _{\tau }u(t_n)\big )^2\int _0^1f^{\prime \prime }\big (u(t_{n-1}) +s\nabla _{\tau }u(t_{n})\big )(1-s)\,\mathrm {d}{s}, \end{aligned}$$

such that $\xi _h^n=\xi ^n(x_i,y_j)$ for $\varvec{x}_h\in {{\bar{\Omega }}}_h$. By the Taylor expansion formula, one has

$$\begin{aligned} \Delta _h\big (\xi _{1}^n\big )_{ij}&=\int _0^1\big [\partial _{xx}\xi _1^n(x_i-s h_1,y_j) +\partial _{xx}\xi _1^n(x_i+s h_1,y_j)\big ](1-s)\,\mathrm {d}{s}\\&\quad +\int _0^1\big [\partial _{yy}\xi _1^n(x_i,y_j-s h_2) +\partial _{yy}\xi _1^n(x_i,y_j+s h_2)\big ](1-s)\,\mathrm {d}{s},\quad 1\le n\le N. \end{aligned}$$

Applying Lemma 3.3 with the second and third regularity conditions in (1.3), we have

$$\begin{aligned} \sum _{j=1}^nP_{n-j}^{(n)}\big \Vert \Delta _h\xi _1^j\big \Vert&\le \frac{C_u}{\sigma (1-\alpha )}\tau ^{\min \{2-\alpha ,\gamma \sigma \}} +\frac{C_u}{\sigma }t_{n}^{\alpha }{\hat{t}}_{n-1}^{\,2}\epsilon ,\quad 1\le n\le N. \end{aligned}$$

Similarly, one may have an integral expression of $\Delta _h\big (\xi _{2}^n\big )_{ij}$ by using the Taylor expansion. Assuming $f\in C^4({\mathbb {R}})$ and taking the maximum time-step size

$$\begin{aligned} \tau \le \tau _1^{*}:=\root \gamma \alpha \of {\sigma }\quad \text {such that}\quad \tau ^{\gamma \alpha }\le (\tau _1^{*})^{\gamma \alpha }=\sigma , \end{aligned}$$

we apply Lemma 3.4 with the second regularity condition in (1.3) to find,

$$\begin{aligned} \sum _{j=1}^nP_{n-j}^{(n)}\big \Vert \Delta _h\xi _2^j\big \Vert \le C_u\tau ^{\min \{2,2\gamma \sigma \}}\max \{1,\tau ^{\gamma \alpha }/\sigma ^2\} \le \frac{C_u}{\sigma }\tau ^{\min \{2,2\gamma \sigma \}},\quad 1\le n\le N. \end{aligned}$$

Thus, the triangle inequality leads to

$$\begin{aligned} \sum _{j=1}^nP_{n-j}^{(n)}\big \Vert \Delta _h\xi ^j\big \Vert \le \frac{c_3}{\sigma (1-\alpha )}\tau ^{\min \{2-\alpha ,\gamma \sigma \}} +\frac{c_4}{\sigma }t_{n}^{\alpha }{\hat{t}}_{n-1}^{\,2}\epsilon , \quad 1\le n\le N. \end{aligned}$$

(4.12)

4.4 STEP 4: Error Estimate by Mathematical Induction

For a positive constant $C_0$, let ${\mathcal {B}}(0,C_0)$ be a ball in the space of grid functions on ${{\bar{\Omega }}}_h$ such that

$$\begin{aligned} \max \big \{\Vert \psi \Vert _{\infty },\Vert \nabla _h\psi \Vert ,\Vert \Delta _h\psi \Vert \big \}\le C_0 \end{aligned}$$

for any grid function $\{\psi _h\}\in {\mathcal {B}}(0,C_0)$. Always, we need the following result to treat the nonlinear terms but leave the proof to Appendix A.

Lemma 4.1

Let $F\in C^2({\mathbb {R}})$ and a grid function $\{\psi _h\}\in {\mathcal {B}}(0,C_0)$. Thus there is a constant $C_F>0$ dependent on $C_0$ and $C_{\Omega }$ such that,

$$\begin{aligned} \left\| \Delta _h\left[ F(\psi )v\right] \right\| \le C_F\left\| \Delta _hv\right\| . \end{aligned}$$

Under the regularity assumption (1.3) with $U_h^k=u(\varvec{x}_h,t_k)$, we define a constant

$$\begin{aligned} K_0=\frac{1}{3}\max _{0\le k\le N}\big \{\big \Vert U^k\big \Vert _{\infty },\big \Vert \nabla _hU^k\big \Vert ,\big \Vert \Delta _hU^k\big \Vert \big \}. \end{aligned}$$

For a smooth function $F\in C^2({\mathbb {R}})$ and any grid function $\{v_h\}\in {\mathcal {V}}_{h}$, we denote the maximum value of $C_F$ in Lemma 4.1 as $c_0$ such that

$$\begin{aligned} \left\| \Delta _h\left[ F(w)v\right] \right\| \le c_0\left\| \Delta _hv\right\| \quad \text {for any grid function }\{w_h\}\in {\mathcal {B}}(0,K_0+1). \end{aligned}$$

(4.13)

Let $c_5$ be the maximum value of $C_{\Omega }$ to verify the embedding inequalities in (2.1), and

$$\begin{aligned} c_6\!=\!\max \{1,c_5\}E_{\alpha }\big (3\max \{1,\rho \}(2K_0+3)c_0T^{\alpha }\big ),\quad c_7\!=\!3c_1\!+\! \frac{2c_2}{\sigma }{\hat{T}}^{2}+3(2K_0+3)c_0c_1T^{\alpha }. \end{aligned}$$

Also let

$$\begin{aligned} \tau _0^{*}:=\frac{1}{\root \alpha \of {3\Gamma (2-\alpha )(2K_0+3)c_0}},\quad \tau ^{*}:=\root \gamma \alpha \of {\frac{\sigma (1-\alpha )}{6c_3c_6}}\le \tau _1^{*}, \end{aligned}$$

(4.14)

and

$$\begin{aligned} h_0:=\frac{1}{\sqrt{3c_6c_7}},\quad \epsilon _0:=\min \Big \{\frac{\sigma }{6c_4c_6{\hat{T}}^{2}T^{\alpha }},\frac{1}{3}\omega _{1-\alpha }(T),\alpha \,\omega _{2-\alpha }(T)\Big \}. \end{aligned}$$

(4.15)

For the simplicity of presentation, we define the following notations for $1\le k\le N$,

$$\begin{aligned} E_k&:=E_{\alpha }\big (3\max \{1,\rho \}(2K_0+3)c_0t_k^{\alpha }\big ),\\ {\mathcal {T}}^k&:=\frac{2c_3}{\sigma (1-\alpha )} \tau ^{\min \{2-\alpha ,\gamma \sigma \}} +\Big (2c_1+\frac{2c_2}{\sigma }{\hat{t}}_k^{\,2} +3(2K_0+3)c_0c_1t_k^{\alpha }\Big )h^2+\frac{2c_4}{\sigma }t_{k}^{\alpha } {\hat{t}}_{k-1}^{\,2}\epsilon . \end{aligned}$$

We now apply the mathematical induction to prove that

$$\begin{aligned} \big \Vert \Delta _h{\tilde{u}}^k\big \Vert \le E_k{\mathcal {T}}^k+c_1h^2 \quad \text {for }1\le k\le N, \end{aligned}$$

(4.16)

if the time-space grids and the SOE approximation satisfy

$$\begin{aligned} \tau \le \min \{\tau _0^{*},\tau ^{*}\}, \quad h\le h_0,\quad \epsilon \le \epsilon _0. \end{aligned}$$

(4.17)

Here $\tau _0^{*}$, $\tau ^{*}$, $h_0$ and $\epsilon _0$ are fixed constants defined by (4.14)–(4.15). Note that, the restrictions in (4.17) ensures the error function $\{{\tilde{u}}_h^{k}\}\in {\mathcal {B}}(0,1)$ for $1\le k\le N$.

Consider $k=1$ firstly. Since ${\tilde{u}}_h^0=0$, $\{u_h^0\}\in {\mathcal {B}}(0,K_0)\subset {\mathcal {B}}(0,K_0+1)$ and the nonlinear term (4.7) gives ${\mathcal {N}}_h^1=f^{\prime }(u_h^{0}){\tilde{u}}_h^{1}$. For the function $f\in C^3({\mathbb {R}})$, the inequality (4.13) implies

$$\begin{aligned} \big \Vert \Delta _h{\mathcal {N}}^1\big \Vert =\Vert \Delta _h\left( f^{\prime }(u^{0}){\tilde{u}}^{1}\right) \Vert \le c_0\big \Vert \Delta _h{\tilde{u}}^{1}\big \Vert \le c_0\big \Vert {\tilde{w}}^{1}\big \Vert +c_0c_1h^2, \end{aligned}$$

(4.18)

where the Eq. (4.5) and the estimate (4.10) are used. Taking the inner product of the Eq. (4.8) (for $n=1$) by ${\tilde{w}}_h^{1}$, one gets

$$\begin{aligned} A_0^{(1)}\big \langle \nabla _{\tau }{\tilde{w}}^{1},{\tilde{w}}^{1}\big \rangle \le \big \langle \Delta _h{\mathcal {N}}^1,{\tilde{w}}^{1}\big \rangle +\big \langle (D^{\alpha }_f\eta )^1-\Delta _h\xi ^1,{\tilde{w}}^{1}\big \rangle , \end{aligned}$$

because the zero-valued boundary condition in (4.9) leads to $\big \langle \Delta _h{\tilde{w}}^{1},{\tilde{w}}^{1}\big \rangle \le 0$. With the view of Cauchy–Schwarz inequality and (4.18), one has

$$\begin{aligned} \big \langle \nabla _{\tau }{\tilde{w}}^{1},{\tilde{w}}^{1}\big \rangle \ge \big \Vert {\tilde{w}}^{1}\big \Vert \nabla _{\tau }\big (\big \Vert {\tilde{w}}^{1}\big \Vert \big ) \end{aligned}$$

and then

$$\begin{aligned} A_0^{(1)}\nabla _{\tau }\big (\big \Vert {\tilde{w}}^{1}\big \Vert \big ) \le&\big \Vert \Delta _h{\mathcal {N}}^1\big \Vert +\big \Vert (D^{\alpha }_f\eta )^1-\Delta _h\xi ^1\big \Vert \le c_0\big \Vert {\tilde{w}}^{1}\big \Vert +\big \Vert (D^{\alpha }_f\eta )^1-\Delta _h\xi ^1\big \Vert +c_0c_1h^2. \end{aligned}$$

Setting $\tau _1\le \tau _0^{*}\le 1/\root \alpha \of {3\Gamma (2-\alpha )c_0}$, we apply Theorem 2.4 (discrete fractional Grönwall inequality) with $\xi _1^1=\big \Vert (D^{\alpha }_f\eta )^1-\Delta _h\xi ^1\big \Vert$ and $\xi _2^1=c_0c_1h^2$ to get

$$\begin{aligned} \big \Vert {\tilde{w}}^{1}\big \Vert&\le E_\alpha \big (3\max \{1,\rho \}c_0t_1^\alpha \big ) \Big (2\big \Vert \eta ^{0}\big \Vert +2P_0^{(1)}\big \Vert (D^{\alpha }_f\eta )^1-\Delta _h\xi ^1\big \Vert +3c_0c_1\omega _{1+\alpha }(t_1)h^2\Big )\\&\le E_1\Big (\frac{2c_3}{\sigma (1-\alpha )} \tau ^{\min \{2-\alpha ,\gamma \sigma \}} +2c_1h^2+\frac{2c_2}{\sigma }{\hat{t}}_1^{\,2}h^2 +3c_0c_1\omega _{1+\alpha }(t_1)h^2\Big )\le E_1{\mathcal {T}}^1, \end{aligned}$$

where the initial condition (4.9) and the error estimates (4.10)–(4.12) are used. Thus, the Eq. (4.5) and the inequality (4.10) yield the estimate (4.16) for $k=1$,

$$\begin{aligned} \big \Vert \Delta _h{\tilde{u}}^1\big \Vert \le \big \Vert {\tilde{w}}^{1}\big \Vert +\big \Vert \eta ^{1}\big \Vert \le E_1{\mathcal {T}}^1+c_1h^2. \end{aligned}$$

Assume that the error estimate (4.16) holds for $1\le k\le n-1$ ($n\ge 2$). Thus we apply the embedding inequalities in (2.1) to get

$$\begin{aligned} \max \big \{\big \Vert {\tilde{u}}^{k}\big \Vert _{\infty },\big \Vert \nabla _h{\tilde{u}}^{k}\big \Vert ,\big \Vert \Delta _h{\tilde{u}}^{k}\big \Vert \big \}\le \max \{1,c_5\}\big (E_k{\mathcal {T}}^k+c_1h^2\big ),\quad 1\le k\le n-1. \end{aligned}$$

Under the priori settings in (4.17), we have the error function $\{{\tilde{u}}_h^{k}\}\in {\mathcal {B}}(0,1)$, the discrete solution $\{u_h^{k}\}\in {\mathcal {B}}(0,K_0+1)$ for $1\le k\le n-1$, and the continuous solution

$$\begin{aligned} \{U_h^{k}\}\in {\mathcal {B}}(0,K_0)\subset {\mathcal {B}}(0,K_0+1). \end{aligned}$$

Then, for the function $f\in C^4({\mathbb {R}})$, one applies the inequality (4.13) to find that

$$\begin{aligned}&\big \Vert \Delta _h\!\left[ f^{\prime }(u^{n-1})\nabla _{\tau }{\tilde{u}}^{n}\right] \big \Vert \le c_0\big \Vert \Delta _h\nabla _{\tau }{\tilde{u}}^{n}\big \Vert \le c_0\big \Vert \Delta _h{\tilde{u}}^{n}\big \Vert +c_0\big \Vert \Delta _h{\tilde{u}}^{n-1}\big \Vert ,\\&\big \Vert \Delta _h\!\left[ {\tilde{u}}^{n-1}f^{\prime }\big (s U^{n-1}+(1-s)u^{n-1}\big )\right] \big \Vert \le c_0\big \Vert \Delta _h{\tilde{u}}^{n-1}\big \Vert ,\\&\big \Vert \Delta _h\!\left[ {\tilde{u}}^{n-1}\nabla _{\tau }U^{n}f^{\prime \prime }\big (s U^{n-1}+(1-s)u^{n-1}\big )\right] \big \Vert \le c_0 \big \Vert \Delta _h({\tilde{u}}^{n-1}\nabla _{\tau }U^{n})\big \Vert \le 2c_0K_0\big \Vert \Delta _h{\tilde{u}}^{n-1}\big \Vert , \end{aligned}$$

where $0\le s\le 1$. From the expression (4.7) of ${\mathcal {N}}^n$ and the triangle inequality, one has

$$\begin{aligned} \big \Vert \Delta _h{\mathcal {N}}^n\big \Vert&\le c_0\big \Vert \Delta _h{\tilde{u}}^{n}\big \Vert +2(K_0+1)c_0\big \Vert \Delta _h{\tilde{u}}^{n-1}\big \Vert \nonumber \\&\le c_0\big \Vert {\tilde{w}}^{n}\big \Vert +2(K_0+1)c_0\big \Vert {\tilde{w}}^{n-1}\big \Vert +(2K_0+3)c_0c_1h^2, \end{aligned}$$

(4.19)

where the Eq. (4.5) and the estimate (4.10) are used.

Now, taking the inner product of (4.8) by ${\tilde{w}}_h^{n}$, one gets

$$\begin{aligned} \big \langle (D^{\alpha }_f{\tilde{w}})^n,{\tilde{w}}^{n}\big \rangle \le \big \langle \Delta _h{\mathcal {N}}^n,{\tilde{w}}^{n}\big \rangle +\big \langle (D^{\alpha }_f\eta )^n-\Delta _h\xi ^n,{\tilde{w}}^{n}\big \rangle , \end{aligned}$$

(4.20)

because the zero-valued boundary condition in (4.9) leads to $\big \langle \Delta _h{\tilde{w}}^{n},{\tilde{w}}^{n}\big \rangle \le 0$. Lemma 2.5 (I) says that the kernels $A^{(n)}_{n-k}$ are decreasing, so the Cauchy–Schwarz inequality gives

$$\begin{aligned} \big \langle (D^{\alpha }_f{\tilde{w}})^n,{\tilde{w}}^{n}\big \rangle&\ge A_{0}^{(n)}\Vert {\tilde{w}}^n\Vert ^2 -\sum _{k=1}^{n-1}\big (A_{n-k-1}^{(n)}-A_{n-k}^{(n)}\big ) \Vert {\tilde{w}}^k\Vert \Vert {\tilde{w}}^n\Vert -A_{n-1}^{(n)}\Vert {\tilde{w}}^0\Vert \Vert {\tilde{w}}^n\Vert \\&=\Vert {\tilde{w}}^n\Vert \Big [A_{0}^{(n)}\Vert {\tilde{w}}^n\Vert -\sum _{k=1}^{n-1}\big (A_{n-k-1}^{(n)}-A_{n-k}^{(n)}\big )\Vert {\tilde{w}}^k\Vert -A_{n-1}^{(n)}\Vert {\tilde{w}}^0\Vert \Big ]\\&=\Vert {\tilde{w}}^n\Vert \sum _{k=1}^{n}A_{n-k}^{(n)} \nabla _\tau \big (\Vert {\tilde{w}}^k\Vert \big ). \end{aligned}$$

Thus with the help of Cauchy–Schwarz inequality and (4.19), it follows from (4.20) that

$$\begin{aligned}&\sum _{k=1}^{n}A_{n-k}^{(n)}\,\nabla _\tau \big (\Vert {\tilde{w}}^k\Vert \big )\le \big \Vert \Delta _h{\mathcal {N}}^n\big \Vert +\big \Vert (D^{\alpha }_f\eta )^n-\Delta _h\xi ^n\big \Vert \\&\quad \le c_0\big \Vert {\tilde{w}}^{n}\big \Vert +2(K_0+1)c_0\big \Vert {\tilde{w}}^{n-1}\big \Vert +\big \Vert (D^{\alpha }_f\eta )^n-\Delta _h\xi ^n\big \Vert +(2K_0+3)c_0c_1h^2. \end{aligned}$$

Setting the maximum time-step size

$$\begin{aligned} \tau \le \tau _0^{*}=1/\root \alpha \of {3\Gamma (2-\alpha )(2K_0+3)c_0}, \end{aligned}$$

we apply Theorem 2.4 with $\xi _1^n=\big \Vert (D^{\alpha }_f\eta )^n-\Delta _h\xi ^n\big \Vert$ and $\xi _2^n=(2K_0+3)c_0c_1h^2$ to get

$$\begin{aligned} \big \Vert {\tilde{w}}^{n}\big \Vert&\le E_n \left( 2\big \Vert \eta ^{0}\big \Vert +2\max _{1\le j\le n}\sum _{k=1}^jP_{j-k}^{(j)}\big \Vert (D^{\alpha }_f\eta )^k -\Delta _h\xi ^k\big \Vert +3(2K_0+3)c_0c_1\omega _{1+\alpha }(t_n)h^2\right) \\&\le E_n\Big (\frac{2c_3}{\sigma (1-\alpha )}\tau ^{\min \{2 -\alpha ,\gamma \sigma \}} +\frac{2c_4}{\sigma }t_{n}^{\alpha }{\hat{t}}_{n-1}^{\,2}\epsilon \Big )\\&\quad +E_n\Big (2c_1+\frac{2c_2}{\sigma }{\hat{t}}_n^{\,2} +3(2K_0+3)c_0c_1\omega _{1+\alpha }(t_n)\Big )h^2\le E_n{\mathcal {T}}^n, \end{aligned}$$

where the initial data (4.9) and the three estimates (4.10)–(4.12) are used. Then the error equation (4.5) with (4.10) implies that the claimed error estimate (4.16) holds for $k=n$,

$$\begin{aligned} \Vert \Delta _h{\tilde{u}}^n\Vert \le E_n{\mathcal {T}}^n+c_1h^2. \end{aligned}$$

The principle of induction and the third inequality in (2.1) give the following result.

Theorem 4.2

Assume that the nonlinear function $f\in C^4({\mathbb {R}})$ and the solution of nonlinear subdiffusion problem (1.1) fulfills the regularity assumption (1.3) with a regularity parameter $\sigma \in (0,1)\cup (1,2)$. Suppose that the SOE approximation error $\epsilon$, the maximum time-step size $\tau$, and the maximum spatial length h satisfy

$$\begin{aligned} \epsilon \le \epsilon _0,\quad \tau \le \min \{\tau _0^{*},\tau ^{*}\}, \quad h\le h_0, \end{aligned}$$

where $\epsilon _0$, $\tau _0^{*}$, $\tau ^{*}$ and $h_0$ are fixed constants defined by (4.14)–(4.15). Then the discrete solution of two-level linearized fast scheme (2.6), on the nonuniform time mesh satisfying Ass3 and AssG, is unconditionally convergent in the maximum norm, that is,

$$\begin{aligned} \big \Vert U^k-u^k\big \Vert _{\infty }\le \frac{c_8}{\sigma (1-\alpha )}E_{\alpha }\big (3\max \{1,\rho \} (2K_0+3)c_0t_k^{\alpha }\big ) \left( \tau ^{\min \{2-\alpha ,\gamma \sigma \}}+h^2+\epsilon \right) , \end{aligned}$$

for $1\le k\le N$, where

$$\begin{aligned}c_8=\max \big \{1,c_5\}\max \{2c_3,4 c_1+2c_2{\hat{T}}^{2} +3(2K_0+3)c_0c_1T^{\alpha },2c_4T^{\alpha }{\hat{T}}^{2}\big \}.\end{aligned}$$

The numerical solution achieves an optimal time accuracy of order $O(\tau ^{2-\alpha })$ if the grading parameter is taken by $\gamma \ge \max \{1,(2-\alpha )/\sigma \}$.

5 Numerical Experiments

Two numerical examples are reported here to support our theoretical analysis. The two-level linearized scheme (2.6) runs for solving the fractional Fisher equation

$$\begin{aligned} {\mathcal {D}}^{\alpha }_tu=\Delta u+u(1-u)+g(\varvec{x},t),\quad (\varvec{x},t)\in (0,\pi )^2\times (0,T], \end{aligned}$$

subject to zero-valued boundary data, with two different initial data and exterior forces:

• (Example 1) $u^0(\varvec{x})=\sin x \sin y$ and $g(\varvec{x},t)=0$ such that no exact solution is available;

• (Example 2) $g(\varvec{x},t)$ is specified such that $u(\varvec{x},t)=\omega _{\sigma }(t)\sin x \sin y$, $0<\sigma <2$.

Note that, Example 2 with the regularity parameter $\sigma$ is set to examine the sharpness of predicted time accuracy on nonuniform meshes. Actually, our present theory also fits for the semilinear problem with a nonzero force $g(\varvec{x},t)\in C({\bar{\Omega }}\times [0,T])$.

In our simulations, the spatial domain $\Omega$ is divided uniformly into M parts in each direction $(M_1 = M_2=M)$ and the time interval [0, T] is divided into two parts $[0, T_0]$ and $[T_0, T]$ with total $N_T$ subintervals. According to the suggestion in [14], the graded mesh $t_k=T_0\left( k/N\right) ^{\gamma }$ is applied in the cell $[0, T_0]$ and the uniform mesh with time step size $\tau \ge \tau _{N}$ is used over the remainder interval. Given certain final time T and a proper number $N_T$, here we would take $T_0=\min \{1/\gamma ,T\}$, $N=\big \lceil \frac{N_T}{T+1-\gamma ^{-1}}\big \rceil$ such that

$$\begin{aligned} \tau =\frac{T-T_0}{N_T-N}\ge \frac{T+1-\gamma ^{-1}}{N_T}\ge N^{-1}\ge \tau _N. \end{aligned}$$

Always, the absolute tolerance error of SOE approximation is set to $\epsilon =10^{-12}$ such that the two-level L1 formula (2.5a) is comparable with the L1 formula (2.2) in time accuracy.

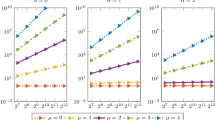
In Example 1, we investigate the asymptotic behavior of solution near $t=0$ and the computational efficiency of the linearized method (2.6). Setting $M = 100$, $T=1/\gamma$ and $N_T= 100$, Figs. 1 and 2 depict, in log–log plot, the numerical behaviors of first-order difference quotient $\nabla _{\tau }u_h^n/\tau _n$ at three spatial points near the initial time for different fractional orders and grading parameters. Observations suggest that $\log \left| u_t(\varvec{x},t)\right| \approx C_u(\varvec{x})+(\alpha -1)\log t$ as $t\rightarrow 0$, and the solution is weakly singular near the initial time. Compared with the uniform grid, the graded mesh always concentrates much more points in the initial time layer and provides better resolution for the initial singularity.

Fig. 1

The log–log plot of difference quotient $\nabla _{\tau }u_h^n/\tau _n$ versus the time for Example 1 ($\alpha =0.4$) with two grading parameters $\gamma =1$ (left) and $\gamma =3$ (right)

Fig. 2

The log–log plot of difference quotient $\nabla _{\tau }u_h^n/\tau _n$ versus the time for Example 1 ($\alpha =0.8$) with two grading parameters $\gamma =1$ (left) and $\gamma =2$ (right)

Fig. 3

The log–log plot of CPU time versus the total number $N_T$ of time levels for the linearized method in solving Example 1 with two different formulas of Caputo derivative

To see the effectiveness of our linearized method (2.6), we also consider another linearized method by replacing the two-level fast L1 formula $(D^{\alpha }_fu_h)^n$ with the nonuniform L1 formula $(D^{\alpha }_\tau u_h)^n$ defined in (2.2). Setting $\alpha = 0.5$, $\gamma =2$, and $M = 50$, the two schemes are run for Example 1 to the final time $T = 50$ with different total numbers $N_T$. Figure 3 shows the CPU time in seconds for both linearized procedures versus the total number $N_T$ of subintervals. We observe that the proposed method has almost linear complexity in $N_T$ and is much faster than the direct scheme using traditional L1 formula.

Since the spatial error $O(h^{2})$ is standard, the time accuracy due to the numerical approximations of Caputo derivative and nonlinear reaction is examined in Example 2 with $T=1$. The maximum norm error $e(N,M)=\max _{1\le l\le N}\big \Vert U(t_l)-u^l\big \Vert _{\infty }.$ To test the sharpness of our error estimate, we consider three different scenarios, respectively, in Tables 1, 2, and 3:

• Table 1: $\sigma =2-\alpha$ and $\gamma =1$ with fractional orders $\alpha =0.4$, 0.6 and 0.8.

• Table 2: $\alpha =0.4$ and $\sigma =0.4$ with grid parameters $\gamma =1$, $\frac{3}{4}\gamma _{\texttt {opt}}$, $\gamma _{\texttt {opt}}$ and $\frac{5}{4}\gamma _{\texttt {opt}}$.

• Table 3: $\alpha =0.4$ and $\sigma =0.8$ with grid parameters $\gamma =1$, $\frac{3}{4}\gamma _{\texttt {opt}}$, $\gamma _{\texttt {opt}}$ and $\frac{5}{4}\gamma _{\texttt {opt}}$.

Table 1 Numerical temporal accuracy for $\sigma =2-\alpha$ and $\gamma =1$

Table 1 lists the solution errors, for $\sigma =2-\alpha$, on the gradually refined grids with the coarsest grid of $N=50$. Numerical data indicates that the optimal time order is of about $O(\tau ^{2-\alpha })$, which dominates the spatial error $O(h^{2})$. Always, we take $M=N$ in Tables 1, 2, and 3 such that $e(N,M)\approx e(N)$. The experimental rate (listed as Order in tables) of convergence is estimated by observing that $e(N)\approx C_u\tau ^{\beta }$ and then $\beta \approx \log _{2}\left[ {e(N)}/{e(2N)}\right] .$

Table 2 Numerical temporal accuracy for $\alpha =0.4$, $\sigma =0.4$ and $\gamma _{\texttt {opt}}=4$

Table 3 Numerical temporal accuracy for $\alpha =0.4$, $\sigma =0.8$ and $\gamma _{\texttt {opt}}=2$

Numerical results in Tables 2 and 3 (with $\alpha =0.4$ and $\sigma <2-\alpha$) support the predicted time accuracy in Theorem 4.2 on the smoothly graded mesh $t_k=T(k/N)^{\gamma }$. In the case of a uniform mesh $(\gamma =1)$, the solution is accurate of order $O(\tau ^{\sigma })$, and the nonuniform meshes improve the numerical precision and convergence rate of solution evidently. The optimal time accuracy $O(\tau ^{2-\alpha })$ is observed when the grid parameter $\gamma \ge (2-\alpha )/\sigma$.

A Proof of Lemma 4.1

Proof

Consider $F(\psi )=\psi$ firstly. It is easy to check that, at point $\varvec{x}_h=(x_i,y_j)\in \Omega _h$,

$$\begin{aligned} \delta _x^2(\psi _{ij}v_{ij})=\psi _{ij}\big (\delta _x^2v_{ij}\big ) +\delta _x\psi _{i-\frac{1}{2},j}\big (\delta _xv_{i-\frac{1}{2},j}\big ) +\delta _x\psi _{i+\frac{1}{2},j}\big (\delta _xv_{i+\frac{1}{2},j}\big ) +v_{ij}\big (\delta _x^2\psi _{ij}\big ), \end{aligned}$$

so that

$$\begin{aligned} \Vert \delta _x^2(\psi v)\Vert \le C_0\left( \Vert v\Vert +\Vert \delta _xv\Vert +\Vert \delta _x^2v\Vert \right) . \end{aligned}$$

Similarly,

$$\begin{aligned} \Vert \delta _y^2(\psi v)\Vert \le C_0\left( \Vert v\Vert +\Vert \delta _yv\Vert +\Vert \delta _y^2v\Vert \right) . \end{aligned}$$

Moreover, one has

$$\begin{aligned} \Vert \delta _y\delta _x(\psi v)\Vert \le C_0\left( \Vert v\Vert +\Vert \delta _xv\Vert +\Vert \delta _yv\Vert +\Vert \delta _y\delta _xv\Vert \right) , \end{aligned}$$

due to the fact

$$\begin{aligned} \delta _y\delta _x(\psi _{i-\frac{1}{2},j-\frac{1}{2}}v_{i-\frac{1}{2},j-\frac{1}{2}})&=\psi _{i-\frac{1}{2},j-\frac{1}{2}}\big (\delta _y\delta _xv_{i-\frac{1}{2},j-\frac{1}{2}}\big ) +\delta _y\psi _{i-\frac{1}{2},j-\frac{1}{2}}\big (\delta _xv_{i-\frac{1}{2},j-\frac{1}{2}}\big )\\&\quad +\delta _x\psi _{i-\frac{1}{2},j-\frac{1}{2}}\big (\delta _yv_{i-\frac{1}{2},j-\frac{1}{2}}\big ) +\big (\delta _y\delta _x\psi _{i-\frac{1}{2},j-\frac{1}{2}}\big )v_{i-\frac{1}{2},j-\frac{1}{2}}. \end{aligned}$$

Noticing that $\left\| \Delta _hv\right\| ^2=\Vert \delta _x^2v\Vert ^2+2\Vert \delta _x\delta _yv\Vert ^2+\Vert \delta _y^2v\Vert ^2$, we apply the embedding inequalities in (2.1) to obtain, also see [11, Lemma 2.2],

$$\begin{aligned} \left\| \Delta _h(\psi v)\right\| \le C_u\left( \left\| v\right\| +\left\| \Delta _hv\right\| \right) \le C_{F}\left\| \Delta _hv\right\| , \end{aligned}$$

where the constant $C_F$ is dependent on $C_0$ and $C_{\Omega }$. For the general case $F\in C^2({\mathbb {R}})$, one has

$$\begin{aligned} \delta _x^2\big [F(\psi _{ij})v_{ij}\big ]&=F(\psi _{ij})\big (\delta _x^2v_{ij}\big ) +\delta _xF(\psi _{i-\frac{1}{2},j})\big (\delta _xv_{i-\frac{1}{2},j}\big )\\&\quad +\delta _xF(\psi _{i+\frac{1}{2},j})\big (\delta _xv_{i+\frac{1}{2},j}\big ) +v_{ij}\big [\delta _x^2F(\psi _{ij})\big ]. \end{aligned}$$

The formula of Taylor expansion with integral remainder gives

$$\begin{aligned} \delta _xF(\psi _{i-\frac{1}{2},j})&=\big (F(\psi _{ij})-F(\psi _{i-1,j})\big )/h_1 =\delta _x\psi _{i-\frac{1}{2},j}\int _0^1F^{\prime }\big (s \psi _{ij}+(1-s)\psi _{i-1,j}\big )\,\mathrm {d}{s},\\ \delta _x^2F(\psi _{ij})&=\big (\delta _x^2\psi _{ij}\big )F^{\prime }(\psi _{ij}) +\big (\delta _x\psi _{i-\frac{1}{2},j}\big )^2\int _0^1F^{\prime \prime }\big (s \psi _{ij}+(1-s)\psi _{i-1,j}\big )(1-s)\,\mathrm {d}{s}\\&\quad +\big (\delta _x\psi _{i+\frac{1}{2},j}\big )^2\int _0^1F^{\prime \prime }\big (s \psi _{ij}+(1-s)\psi _{i+1,j}\big )(1-s)\,\mathrm {d}{s}, \end{aligned}$$

such that $\Vert \delta _xF(\psi )\Vert \le C_{F}$ and $\Vert \delta _x^2F(\psi )\Vert \le C_{F}\,$. Therefore, simple calculations arrive at

$$\begin{aligned} \Vert \delta _x^2\left[ F(\psi ) v)\right] \Vert \le C_{F}\left( \Vert v\Vert +\Vert \delta _xv\Vert +\Vert \delta _x^2v\Vert \right) . \end{aligned}$$

By presenting similar arguments as those in the above simple case, it is straightforward to get claimed estimate and complete the proof. $\square$